1 Introduction

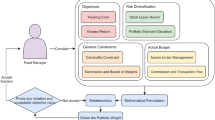
1.1 The problem of active portfolio management and index tracking

The economic goal of investing in stocks is to earn money by achieving high returns. Because the stock market is volatile by nature, this is a risky business. Therefore, investors and fund managers try to reduce the risk by choosing an optimal combination of stocks. Such a combination of stocks is called portfolio.

A widely known and accepted way to measure risk is the variance or the standard deviation of a stock (see, e.g., Callsen-Bracker and Grädler 2011). Usually, the two variables “return” and “risk move” are positively correlated, meaning that a stock with a high return has also a high risk.

To reduce the risk, investors often follow a diversification approach described by Stratman (1987) who shows that the higher the number of stocks in a portfolio, the lower the risk, and that 30 stocks are sufficient to reduce the risk significantly.

If, however, an investor or fund manager feels he or she cannot outperform the market by building a portfolio (a method of active portfolio management; see, e.g., Gilli and Këllezi 2001), another widely used strategy is to invest into an existing index (see, e.g., Shapcott 1992). An index is a collection of different stocks that have a common denominator, for example the Swiss Market Index SMI which comprises Swiss companies. If one is interested in investing in Swiss companies, but does not know which ones to pick one could simply try to track the SMI.

Tracking an index (a method of passive portfolio management; see, e.g., Gilli and Këllezi 2001) means that one builds a portfolio that tries to replicate the behavior of the index as closely as possible. This means that the return on the portfolio rises when the index rises, but also that the return falls when the index falls. A perfect tracking portfolio would require all the stocks (or assets) of the index with exactly the same proportions (or weights) as the index in it. This is called a full replication (see, e.g., Shapcott 1992). However, there are two major problems with this approach: firstly, the initial transaction costs are very high, because it is necessary to buy all the different stocks of the index. Secondly, it is hard to rebalance the tracking portfolio while the proportions in the index change; this will cause rebalancing cost (Aiello and Chieffe 1999).

To tackle these two difficulties, another approach called partial replication is used in practice. This partial replication basically builds a tracking portfolio (sometimes also called index fund; see, e.g., Oh et al. 2005) with a subset of stocks from the index. Such passive portfolio management strategy enables to invest in topics like, for example, “water” or “renewable energies” without exact knowledge of the underlying stocks by replicating a corresponding index.

With the partial replication, another problem is introduced: the tracking error. Because the tracking portfolio does not consist of all the stocks of the index, there is a difference in the performance of the index and the tracking portfolio. This relative deviation between a portfolio and its benchmark is called tracking error (TE) (see, e.g., Kunz 2009).

When trying to find a tracking portfolio with partial replication, the tracking error should be as low as possible. 0.03 (annualized) is regarded as a good value for the TE (Kunz 2009). Additionally, the return and volatility (risk) need to be taken into account as constraints when searching for a good tracking portfolio. A forth constraint is the number of stocks that comprises the tracking portfolio: the lower the number of stocks is, the less transaction costs are generated.

Index tracking problems are difficult optimization problems due to their combinatorial nature (selection of assets to be included in the portfolio) and further constraints to be observed. In particular, index tracking problems which limit the number of included assets are NP-hard (Coleman et al. 2006) which means that there are no efficient algorithms which can solve sufficiently large problem instances exactly due to exponential running times. Because of time restrictions it is not possible to enumerate all the different possible combinations of tracking portfolios. Therefore, heuristics and metaheuristic approaches are of high interest as they usually manage to solve NP-hard optimization problems with sufficiently good results and with an acceptable running time.

Which of the many different available generic heuristics is the best for the specific problem cannot be determined without tests. In this article, the suitability of the invasive weed optimization (IWO) algorithm for index tracking is investigated and it is stated how it has to be adapted to the problem of finding a good tracking portfolio. Therefore, the research question is: Is it possible and, if so, how can IWO be adapted to the problem of finding an index tracking portfolio under given constraints?

1.2 Invasive weed optimization

Invasive Weed Optimization (IWO) is a stochastic evolutionary search algorithm introduced by Mehrabian and Lucas (2006). It is inspired by the behavior of weed colonies and their ability to adapt to environmental conditions. A brief overview of the algorithm in (adapted from Mehrabian and Lucas 2006) states as follows:

  1. (1)

    A finite number of seeds are being dispersed over the search area (initializing a population).

  2. (2)

    Every seed grows to a flowering plant and produces seeds depending on its fitness (reproduction).

  3. (3)

    The produced seeds are being randomly dispersed over the search area and grow to new plants (spatial dispersal).

  4. (4)

    This process continues until the maximum number of plants is reached; now only the plants with higher fitness can survive and produce seeds, others are being eliminated (competitive exclusion).

In the end, hopefully the plant with the best fitness is rather close to an optimal solution. Please note that the original characterization of the concept by Mehrabian and Lucas (2006) is confusing since they suggest eliminating plants with high fitness in step (4) although the fitness is to be maximized. Moreover, the respective characterization of step (4) does not coincide with the further detailed descriptions in the same paper.

IWO was adapted successfully to several problems other than the one introduced by Mehrabian and Lucas (2006). Heuristics were used in the past for index tracking (e.g., genetic algorithms or the threshold accepting heuristics) but not IWO. An earlier study (Affolter 2011) came to no final conclusions regarding the suitability of IWO for the index tracking problem, and therefore, this remains unclear until now.

In addition to the unknown general suitability of the algorithm for the problem, it is also not known how to adapt IWO to the needs of index tracking and what would be a good choice for the various parameters of the algorithm.

We consider the hypothesis that it is possible to adapt IWO to maximize the predicted return of a portfolio while meeting certain constraints (meet a given tracking error, volatility and portfolio size). The reasons for this hypothesis are as follows:

  • IWO can handle discrete solution spaces.

  • IWO could already be applied to a problem within the field of financial optimization (although this was a standard problem) (Affolter 2011).

The acceptance criterion for the solution is that it has to improve the return of a sample portfolio over time (=over iterations) while meeting all of the constraints by following the concept of IWO according to Mehrabian and Lucas (2006).

The rest of this article is organized as follows: In Sect. 2, we discuss related literature. Basic concepts for adapting IWO to the index tracking problem are outlined in Sect. 3. The implemented IWO method is presented in Sect. 4 including the necessary adaption to the index tracking problem and the architecture of the prototype program. The settings for our numerical experiments are shown in Sect. 5. Test results are presented in Sect. 6. The article ends with a discussion and the conclusions in Sect. 7.

2 Related literature

Apart from our previous study (Affolter 2011), there are no published studies on applying IWO to portfolio optimization problems in general and index tracking problems in particular. This is not very surprising since IWO is a relatively new metaheuristics with currently about 350 works citing the original paper by Mehrabian and Lucas (2006).

However, the index tracking problem has been solved by various other metaheuristics: Shapcott (1992) applied a combination of quadratic programming and a genetic algorithm to the index tracking problem. The programming environment was a special tool for implementing genetic algorithms called RPL/Framework. He was able to outperform the benchmark (local search).

In Oh et al. (2005), a genetic algorithm (GA) was used to support portfolio optimization for index fund management. The GA was used for index fund optimization (index fund is a synonym for a tracking portfolio) in this paper as well. Their experiments were successful, but a slightly different approach than the one described in this article was used. They used the heuristic (GA) only to decide the weight of the assets in the tracking portfolio, but did not use this approach to choose which assets are part of the portfolio.

Gilli and Këllezi (2001) used the threshold accepting (TA) heuristic optimization algorithm for index tracking and achieved good results with it. The computations were made using a MatLab environment. However, the focus for their optimizations relied heavily on the transaction costs and not on the mean or the risk/variance of the tracking portfolio.

In Derigs and Nickel (2003), a decision support system for portfolio optimization including index tracking problems is described. The system is based on the metaheuristics of simulated annealing for solving the respective optimization problems.

Beasley et al. (2003) suggest using an adapted evolutionary algorithm for solving the index tracking problems. They performed experiments for several stock indexes and obtained rather good tracking errors.

Jeurissen and van den Berg (2008) used a (hybrid) genetic algorithm for solving the index tracking problem. The GA was used for the selection of stocks, whereas their weights were determined by a quadratic programming approach nested into the GA framework. The obtained results beat a random portfolio and performed equally well as a portfolio of high capitalized stocks. A similar hybrid approach combining an evolutionary algorithm with quadratic programming was investigated in Ruiz-Torrubiano and Suárez (2009).

Krink et al. (2009) applied a differential evolution (DE) approach to the index tracking problem. The basic DE approach was refined with a combinatorial search operator in order to make it applicable to the considered type of problem. The obtained results were slightly better than a portfolio of the least correlated assets and a randomly constructed portfolio.

The index tracking problem and an enhanced version of it were studied in Guastaroba and Speranza (2012) in the form of a mixed integer linear model which was solved by using a heuristic approach for binary optimization problems, called Kernel Search. The approach was tested with numerical instances which show the competitiveness compared to a standard solver.

Coleman et al. (2006) applied a penalty-based model for tracking error minimization and solved it by using a sequence of non-convex optimization runs. The model allows to avoid binary variables which are a main reason of the computational complexity.

3 General concepts for adapting IWO

There are multiple ways to adapt the algorithm to the problem at hand. As a first step, different approaches were conceived, and their concepts of application sketched. All in all four different approaches can be proposed:

3.1 A two-layered approach, where the selection of the assets for the tracking portfolio is based on a uniform distribution of the different assets

This approach features substantial modifications of the original IWO algorithm, namely the addition of a first layer to select the stocks which are to be included in the tracking portfolio and a second layer which determines their weights. The first layer is the selection of k assets (stocks) to build the tracking portfolio out of n assets (the index). This selection is based on a uniform distribution. Therefore, each asset has the same probability to be selected. In the beginning, k is equal to the targeted size of the final tracking portfolio, usually between 20 and 30 assets. With continuous iterations, k will be reduced so that the number of assets to be replaced decreases over time. This in fact corresponds to the implementation approach of the decreasing normal distribution (as proposed by Mehrabian and Lucas 2006) in this situation with a problem space where it has to be assumed that there is no measure for the distance between solutions (=portfolios).

The second layer is responsible for the choice of the weight of the assets in the portfolio. This optimization is done by lcprog, Matlab’s default solver for mean-variance portfolio optimization which is an implementation of a linear complementarity programming (LCP) algorithm (Mathworks 2011).

This approach features quite a bit of a modification compared to the original algorithm proposed by Mehrabian and Lucas (2006), namely the addition of a first layer to select the stocks which are to be included in the tracking portfolio. In Affolter (2011), this approach was already investigated but showed insufficient performance. The failure could stem from three different sources:

  • Possibly, the selection of the parameters of IWO was bad, even though they were based on the parameters proposed by Mehrabian and Lucas (2006).

  • Or it could be that the two-layered approach with a uniform distribution responsible for the asset selection is not suitable for the index tracking problem.

  • An additional reason is the implementation of the prototype itself which was not geared for high performance but instead for good traceability of intermediate steps.

Because the second possibility seems to be the most likely and no other propositions for the parameters were found in the literature, it was decided to dismiss this approach.

3.2 A two-layered approach, where the selection of assets for the tracking portfolio is based on the distance to an already selected asset using a normal distribution

The next logical step to take is to have a look at what would happen if the uniform distribution were replaced by a normal distribution. This would mean that the first layer would be responsible for the selection of the assets to be included, but now with a normal instead of a uniform distribution (see Sect. 3.1). I. e. when a new random solution is calculated it should be more likely to replace an asset by a similar asset than by any random asset.

For this approach, a measure for the distance (or similarity) between the different stocks of the index is needed. Otherwise, it would not be possible to use a normal distribution which favors similar assets. Different measures came to mind (e.g., size of the company, the sector it is active in or the recent returns it achieved) to measure whether “Bank of America” is more similar to “Garmin” or to “General Electric.”

After having chosen which stocks to include via normal distribution based, e.g., on the recent returns, the second layer would then again be responsible for the choice of the weight of the asset in the portfolio via a normal distribution (see Sect. 3.1).

However, this is still a two-layered approach and therefore not what Mehrabian and Lucas (2006) described in their paper. While it is probably better than the two-layered approach with a uniform distribution, the authors are of the opinion that it affects the IWO in an unwanted and negative way, as did the approach with the uniform distribution described above. Moreover, this approach would require more extensive data collection and analysis.

This led to the decision to drop the idea of a two-layered approach.

3.3 A one-layered approach with a normal distribution of the asset weights, where the initial tracking portfolio consists of only k out of the n assets in the index

The idea behind this approach was to get rid of the first layer and use the correlation of the returns in conjunction with the weights of the different assets. As a consequence, based on the current weight of an asset and given correlations of returns between different assets, it should be decided whether to change the weight or to replace the asset with a similar one.

This would mean that both, the small changes of the weights or the replacement of one asset with a very similar one (high correlation), lie near the current portfolio in the solution space, and the normal distribution would pick them with a higher probability than portfolios with very different stocks (low correlation) or with very different asset weights.

An obstacle is that if more than one stock is changed per iteration, it is not clear which correlation coefficient would be used (is asset A replacing asset B and asset C replacing asset D or is asset A replacing asset D and asset C replacing asset B?) There are two possibilities to deal with this problem: either to always choose the lowest possible sum or to allow only one stock per iteration to be changed.

While this one-layered approach is very close to what Mehrabian and Lucas (2006) proposed, it would make it necessary to do a lot of calculations: the algorithm would have to enumerate all the different combinations of tracking portfolios and asset weights and then let the normal distribution pick a similar one.

Since this step would basically be a deterministic approach, where all the possible combinations would have to be calculated, in the opinion of the authors, this slows down the IWO too much and is opposed to the idea of generating new solutions mainly by using a stochastic approach which is a basic assumption of IWO. Therefore, this third approach was also dismissed.

3.4 A one-layered approach with a normal distribution of the asset weights, where the initial tracking portfolio contains most of the index assets and the tracking portfolio’s size is reduced over time via a penalty for the size

This last approach is a very different take on the problem and introduces a new penalty (in addition to the ones given by the index tracking problem, where there are penalties for the tracking error, the volatility and the available capital). This penalty is designed to reduce the initial size of the tracking portfolio over time by punishing portfolios that contain more assets than a given number/parameter.

All of these four approaches have their merits and problems. Due to its simplicity and better compliance with the original IWO, the one-layered approach with a penalty for the portfolio size was considered the most promising. It was selected for implementation and is described in more detail in the next section.

4 A penalty-based adaptation of IWO

The chosen adaptation approach is very close to the original idea behind IWO proposed by Mehrabian and Lucas (2006). The basic idea is that a new penalty function is used to deal with the problem of limiting the number of assets in the portfolio.

In addition to the penalties in the objective function given by the index tracking problem itself (where there are penalties for the tracking error, the volatility, and the exceeding of the available capital), there is a forth penalty for the size of the tracking portfolio. This penalty is intended to reduce the initial size of the tracking portfolio over time by punishing portfolios that include more assets than a given parameter.

As with the second layer of the two-layered approaches described above, the weight of each asset would be determined via a normal distribution, where the current weight is the mean and the standard deviation lies between the parameters stdv \(_{Ini}\) and stdv \(_{Fin}\) (depending on the current iteration) as shown in Fig. 1. The weights may range from 0 to 100 %, where 0 means that the asset is not included in the tracking portfolio. No additional layers or previously mentioned adaptations like the correlation coefficient would be needed.

Fig. 1
figure 1

Vector of asset weights in one plant (i.e., a solution corresponding to a specific portfolio)

Full size image

Starting point is an initial set of random portfolios chosen from all the assets included in the index with random weights. The size of the initial population is specified by \(p_{Ini}\). Each combination of asset weights is a solution to the optimization problem. It is represented as a plant object which carries all the necessary information to specify that solution (the tracking portfolio), including a vector of the calculated asset weights. The plants are rated according to the target function and get a fitness value assigned that specifies the number of seeds they are allowed to dispread in the next generation.

4.1 Objective function and penalty terms

As the initial solutions are evaluated, a penalizing strategy will make the portfolios develop toward the target values. Penalties are set for the deviation between the actual and the targeted key parameters like tracking error, volatility, invested capital, and portfolio size. These penalties are included in the objective function:

$$\begin{aligned} \mathrm{fitness}= & {} \mathrm{{return-penalty}}_ \mathrm{TE} -\mathrm{penalty}_\mathrm{Volatility} \nonumber \\&-\mathrm{penalty}_\mathrm{Capital} -\mathrm{penalty}_\mathrm{Size} \end{aligned}$$
(1)

The constraints are considered in the various penalty components which use penalty cost parameters (\(\lambda _\mathrm{tracking error}\), \(\lambda _\mathrm{volatility}\), \(\lambda _\mathrm{capital}\), \(\lambda _\mathrm{size})\) for calibration. They are defined as follows:

  • The tracking error TE shall be as low as possible:

    penalty\(_\mathrm{TE}\) = TE \(\lambda _\mathrm{tracking error}\)

  • The given portfolio risk must not be exceeded. Portfolios with volatility \(>\) target volatility (targetVol) target get penalized:

    penalty\(_\mathrm{Volatility}\) = (volatility \(-\) targetVol) \(\lambda _\mathrm{volatility}\)

  • The given capital must not be exceeded. Portfolios with invested capital \(>\) available capital (targetCap) get penalized:

    penalty\(_\mathrm{Capital}\) = (capital – targetCap) \(\lambda _\mathrm{capital}\)

  • The given portfolio size must not be exceeded. Portfolios with size \(>\) targetSize (maximum number of included assets) get penalized:

    penalty\(_\mathrm{Size}\) = (size – targetSize) \(\lambda _\mathrm{size}\)

The given capital has to be fully invested. This should be accomplished by the return, because it is assumed that risky assets always lead to better returns than investing in cash. Therefore, portfolios with a higher return will get a higher fitness as long as the other values stay the same.

4.2 Reproduction and selection

After the evaluation of every plant according to the above objective function, the plants will reproduce. Reproducing means that the parent plants generate a number of offspring. Fitter plants are allowed to reproduce more often than the ones with lower fitness. When offspring is produced, its vector of asset weights will be changed in such a way that the actual (or parent) weight of asset i becomes the mean for the new normally distributed random number which defines the new weight of asset i.

The standard deviation used in the normal distribution will be reduced from stdv \(_{Ini}\) to stdv \(_{Fin}\) over the iterations which should lead to the effect that the colony first dispreads in wide steps and then concentrates around an optimum as described by Mehrabian and Lucas (2006) with the sphere function experiment.

The main assumption for a successful application of IWO is that good solutions must be somehow located close to each other. Because the problem is high dimensional, there is no way to check in advance if the solution space fulfills this prerequisite.

While it is possible to measure the distance between two weights of the same asset, this is not the case between different asset combinations. The question here is what would be the distance between two portfolios. As long as the two portfolios consist of the same assets but with different weights, the difference in the weights can be regarded as distance. If the two portfolios contain different assets (and weights), it is hard to define some measure for the distance between them. Furthermore, adding assets to the portfolio and taking them out of it (by assigning weights \(>\)0 and \(\le \)0, respectively) leads to jumps within the solution space.

When the maximum number of plants in the colony is reached, the selection mechanism eliminates the plants with low fitness. This leads to a constant size of the colony. If a plant has a relative high fitness, it survives several generations and is allowed to reproduce more than once. The procedure would go on infinitely, and therefore, the maximum number of iterations it \(_\mathrm{{Max}}\) is used as stopping criterion.

4.3 Parameters

The parameters directly related to IWO are shown in Table 1.

Table 1 List of parameters related to IWO
Full size table

Parameters related to the index tracking problem are shown in Table 2.

Table 2 List of parameters related to the index tracking problem
Full size table

4.4 Implementation aspects

The architecture of the test model consists of the executable code, a runtime environment (Mathworks 2011), an MS Access database where data from simulation runs with different parameter settings are stored as well as an ActiveX control to interface MatLab and the database.

Since IWO can be considered an evolutionary algorithm, the heuristic is implemented as an evolutionary algorithm following the basic evolutionary loop (Beyer 2001). It is extended with the specific features from the concept of IWO like reducing the step width and the unique reproduction and selection mechanism. It was a goal to keep the parent–child relationship among the individuals in the plant colony for the purpose of comprehensiveness of the optimization process. This is done by the use of a data structure as a variable length tree as described in more detail in Affolter (2011).

A new subclass (Plant1) of the problem class Plant has been adapted to the problem which in fact is the multiobjective optimization problem. Furthermore, the penalty handling which is part of the optimization approach was implemented. As mentioned above, penalties are calculated for the excess of the invested capital, for volatility, portfolio size (number of investments \(>\)0 %), and for the tracking error.

Some supporting classes and functions are needed for the handling of the input data and the database interface via ActiveX control. The entity relationship diagram where the data are written is shown in Fig. 2.

Fig. 2
figure 2

Entity relationship diagram of the reporting database

Full size image

5 Tests and experiments

After implementing this approach, a test robot was coded to automate and facilitate the experiments. With the help of this robot, several thousand test runs were made and the data obtained were thoroughly analyzed.

This analysis also includes a benchmarking against two defined tracking portfolios. It was decided to measure the portfolios determined by IWO against a randomly assembled portfolio of size 30 and against the top 30 of the index.

5.1 Test data

For the experiments, a medium-sized index with a reasonably long history was needed to ensure that the results were representative. As suggested by Affolter (2011), the well-known MSCI USA Value in US-$ (Source: Datastream, MSVUSA$) was used. It features 295 stocks and there are data available for well over the last 10 years.

The stocks without a complete history were eliminated from the index to ensure that the calculations were not biased by missing prices for certain stocks. This resulted in a dataset of 257 stocks, where the prices were listed weekly and ranged from 5th January 2001 to 8th April 2011.

5.2 Parameter settings

During the experiments, the following parameters were systematically investigated with 4–6 different values and considered in all possible combinations. These parameters are it \(_\mathrm{{max}}\), the maximum number of iterations, and the penalties \(\lambda _\mathrm{Volatility}\), \(\lambda _\mathrm{Capital}\), \(\lambda _\mathrm{Tracking Error}\), and \(\lambda _\mathrm{Size}\). The following values for these parameters were analyzed:

  • it \(_\mathrm{{max}}\): 25, 50, 100, and 150

  • \(\lambda _\mathrm{Volatility}\), \(\lambda _\mathrm{Capital}\), \(\lambda _\mathrm{Tracking Error}\) and \(\lambda _\mathrm{Size}\): 0.1, 0.3, 0.5, 1, 5, and 10.

These settings led to 4 \(\times \) 6 \(\times \) 6 \(\times \) 6 \(\times \) 6 = 5184 experiments. The other parameters have been kept constant for all tests and are based on recommendations in Mehrabian and Lucas (2006):

  • \(s_\mathrm{Min }\)= 0 (minimum number of seeds produced by one plant)

  • \(s_\mathrm{Max }\)= 2 (maximum number of seeds produced by one plant)

  • n = 3 (non-linear modulation index to alter the standard deviation)

  • \(p_\mathrm{Max }\)= 15 (maximum number of plants in the population, should be between 10 and 20)

  • \(p_{Ini }\)= 5 (size of initial population, represented by the first level of the tree after the root, should be between 5 and 10)

  • stdv \(_{Ini}\) = 20,000 (initial value for the standard deviations)

  • stdv \(_{Fin}\) = 1000 (final value for the standard deviations)

Parameters directly related to the problem are as follows:

  • \(r_{0}\) = 0.01/52 (risk-free weekly returns)

  • capital = 100,000 (total capital to be invested)

  • targetVol = 0.025 (volatility of the target portfolio)

  • targetSize = 30 (target size of the tracking portfolio)

6 Results

The portfolios found by IWO were compared with regard to the mean return, volatility, tracking error, and portfolio size against two benchmarks. The benchmarks are the TOP30 assets (the 30 assets with the highest weights) of the MSCI USA and a random selection of 30 assets out of the MSCI USA.

Table 3 shows the main results from the IWO experiments in comparison with the two benchmarks. For the IWO results, the best outcomes with respect to mean return, volatility, and tracking error are shown. While it is possible to beat the benchmarks with respect to mean return and volatility, the results concerning tracking errors are unreasonably disappointing. Moreover, the resulting portfolios appear to be unreasonably large.

Table 3 Results of IWO optimization in comparison with benchmarks
Full size table

Because of the partially unfruitful results, it is not sufficiently clear whether the research hypothesis is correct, i.e. that it is possible to solve complex index tracking problems with IWO. Therefore, a step back was taken and it was tried to find out whether IWO is able to minimize the TE at all if no restrictions/penalties are applied. This assumption is part of the research hypothesis.

The objective function was adapted so that the IWO only searches for the portfolio with the best (=lowest) TE. It was found out that the initial standard deviation of 20,000 as suggested in the original works on IWO was too high (although those values worked very well in Affolter (2011), and therefore, the deviation of the weights of the 257 assets was very high.

The first runs showed a significant worsening after the very first iteration, which was when the initial colony reproduced for the first time. It looked like the algorithm found the best solution right away in the initial colony (evenly distributed random asset weights) and no later iteration was successful in finding a better solution. At the same time, the minimal fitness in the colony worsened.

Another indicator that stdv \(_{Ini}\) was too high was the number of zeros in the portfolio, meaning an asset would be excluded from the tracking portfolio. While parent plants from the initial colony usually had about 17 zeros (according to the explanation above), the next generation had already 130 zeros. Since this happened in only one step, the step width had to be considered too large.

When the initial standard deviation was corrected to 100, the IWO performed in the way wanted (meaning that it found better TEs over time), see Fig. 3. It can be shown that starting from a portfolio with zero assets, the tracking portfolio grows rapidly (size larger than 100 already after one iteration and larger than 200 after 10 iterations) and that IWO finally approaches the tracking portfolio with all the stocks in it as the optimal solution when no penalties are active. Additionally, the TE lowers over iterations. This corresponds with the literature (see, e.g., Shapcott 1992) that a TE of 0 is achieved by having all the stocks of the index with their respective weights in the tracking portfolio (full replication). This means that the implemented MatLab algorithm works correctly for the TE problem and that the assumption is valid, that a penalty for the size and capital is needed to solve the problem.

Fig. 3
figure 3

Reduction of tracking errors over 200 iterations

Full size image

7 Discussion and conclusions

The major assumption for a successful application of IWO is that good solutions must somehow be located close to each other so that IWO can concentrate the plant colony around an optimum. Since there is no obvious measure for the distance between different portfolios with respect to selected assets and their weights, a major prerequisite for the application of the original IWO seems not given.

This has led to an objective function which unfortunately did not work well. Therefore, it has to be thought about changing the objective function. A few tests with a first amendment of the fitness function to (2)

$$\begin{aligned} \mathrm{fitness} = 1 - \mathrm{penalty}_\mathrm{TE} - \mathrm{penalty}_{\mathrm{Size}} - \mathrm{penalty}_{\mathrm{Capital}} \end{aligned}$$
(2)

showed better results than the original function (1). Further investigations into that direction are suggested for future research.

There are two hypotheses why the search for tracking portfolios with the considered IWO has been unsuccessful:

  1. (1)

    The penalty for size is the reason for the failed experiments. When activating the penalty for size in the objective functions, the algorithm does not behave in the desired way. It is conceivable that the approach with a penalty for limiting the size to a desired value is not suitable, especially not in combination with other penalties for volatility, tracking, error and capital.

  2. (2)

    The solution space is not suitable for IWO. During the test, it could be seen that smallest changes in the penalties can have a huge impact on the optimization process. For example, changing the penalty \(\lambda _\mathrm{Size}\) from 0.00006 to 0.000065 caused a change in the behavior regarding the portfolio size. With \(\lambda _\mathrm{Size}\) = 0.00006, the size starting at 0 climbed to to a maximum of 230 and ended finally at 180. With \(\lambda _\mathrm{Size}\) = 0.000065, the size starting at 0 climbed to a maximum of 30 and finally ended at 27. However, it is still unknown if the above described change in behavior is significant. Because of the stochastic nature of the algorithm, many more test runs would be needed. The approach of defining penalties somewhere from 0 to 100 turned out to be useless as there is no reason for the assumption that the correct range for a penalty lies somewhere between 0 and 100.

Because the data structure of the prototype is designed for comprehensiveness of the results rather than for performance, the optimization runs needed an average of 5 minutes. This time constraint did not allow testing with more than 500 iterations. However, some runs showed the first positive changes only after approximately 250 iterations. Therefore, it may be that the presented and used parameter combination only works for runs with more than 500 iterations.

Because the IWO implemented as described in this paper is not able to find a good tracking portfolio, other approaches for the adaptation of IWO to the problem are needed. One such promising approach could be to use the NSIWO described in Nikoofard (2012) instead of the IWO. NSIWO (non-dominated sorting IWO) is claimed to have good properties when dealing with multiobjective problems.

Another possible source for different approaches than the one followed in this paper could be Maringer and Di Tollo (2009). This paper contains a description of the basics of index tracking and how (meta)heuristics can be used to solve the problem. Unfortunately, the concept of IWO is not covered in this work.

As the formerly proposed amendment of the objective function shows slightly better results, this could also be a way. The function (2) is heading toward the smallest tracking error regarding the constraints portfolio size and maximum invested capital. In fact, this is a reduction of objectives (mean and volatility have been avoided) which can be used to analyze the effect of one or more objectives to one or more others.

Since the single penalties seemed to work as long as everything stays the same, another approach could be to start from a full replication of the index (with similar assets and weights) and then let IWO adapt weights and reduce the number of stocks. This approach could at least be interesting to further study the influence of the single parameter, e.g., the penalties, to see how far they can bring IWO to go from the initial solution which in fact is the global optimum.