Indicator-based set evolution particle swarm optimization for many-objective problems

Abstract

Multi-objective particle swarm optimization (MOPSO) has been well studied in recent years. However, existing MOPSO methods are not powerful enough when tackling optimization problems with more than three objectives, termed as many-objective optimization problems (MaOPs). In this study, an improved set evolution multi-objective particle swarm optimization (S-MOPSO, for short) is proposed for solving many-objective problems. According to the proposed framework of set evolution MOPSO (S-MOPSO), including quality indicators-based objective transformation, the Pareto dominance on sets, and the particle swarm operators for set evolution, an enhanced S-MOPSO method is developed by updating particles hierarchically, i.e., a set of solutions is first regarded as a particle to be updated and then the solutions in a selected set are further evolved by a modified PSO. In the set evolutionary stage, the strategy for efficiently updating the set particle is proposed. When further evolving a single solution in the initial decision space of the optimized MaOP, the global and local best particles are dynamically determined based on those ideal reference points. The performance of the proposed algorithm is empirically demonstrated by applying it to several scalable benchmark many-objective problems.

1 Introduction

Multi-objective optimization problems (MOPs) are variable in practice, i.e., environmental and systems biology (Pedro et al. 2014), controller tuning (Gilberto et al. 2014), and machinability of stainless steel (Lobato et al. 2014). In MOPs, conflicts among objectives usually lead to a set of trade-off solutions,rather than a single optimal solution. To determine such a set of solutions, the concept of the Pareto dominance (Goldberg 1988) is used as the foundation to discriminate solutions, and a variety of multi-objective evolutionary algorithms (MOEAs), e.g., multi-objective particle swarm optimization (MOPSO) (Reyes-Sierra and Coello Coello 2006), non-dominated sorting genetic algorithm-II (NSGA-II) (Deb et al. 2002), strength Pareto evolutionary algorithm (SPEA) (Zitzler and Thiele 1999), and Pareto archived evolutionary strategy (PAES) (Knowles and Corne 1999), have been proven to be powerful in solving MOPs with two or three objectives. However, these algorithms scale poorly in solving MaOPs (Purshouse and Fleming 2003) due to the increase in the number of non-dominated solutions that deteriorates the selection pressure. To well extend the merits of MOEAs for solving MOPs, three main kinds of MOEAs have been developed. The first is Pareto-based algorithms. In general, Pareto dominance often fails to provide enough selection pressure in a high-dimensional objective space, and this could lead to the appearance of some modifications of Pareto-based algorithms when facing many-objective problems. These modifications typically include enhancing the Pareto dominance relation, such as the $\epsilon$-dominance (Deb et al. 2005), and improving the diversity maintenance strategy in the algorithms, such as the shift-based density estimation (Li et al. 2014). The second is based on decomposition, e.g., MOEA/D (Zhang and Li 2007). With this kind of MOEAs, several single-objective optimization problems are constructed by decomposing MaOPs using suitable weighted functions. For the last category, it is generally called indicator-based MOEAs (Zitzler and Knzli 2004). Zitzler et al. first proposed an indicator-based framework for reducing the number of objectives, by regarding a set of candidates as an individual and directly using some quality indicators, e.g., hypervolume, diversity or spread of a set of solutions, to evaluate the performance of the individuals. In this case, the number of objectives to be optimized is determined by the adopted indicators, usually no more than three. In addition, no extra parameters are introduced into this framework. Therefore, it has been steadily gaining attention recently.

The main character of the indicator-based algorithm is that all evolutionary operators perform on not a single solution as traditional MOEAs do, but sets of solutions. So the corresponding operators for the set evolution are of great importance. However, few studies have been focused on such an issue, and most existing methods just adopt simple crossover and mutation operators of traditional EAs to evolve only the elements of a set, but neglecting the correlations among sets.

MOPSO has been demonstrated to be suitable for MOPs in a faster convergence compared to other MOEAs (Goh et al. 2010). But when applying PSO for MaOPs, it is difficult to select the global and local leaders, because almost all individuals are non-dominated under the Pareto comparison. It is natural to combine the PSO with the indicator-based MOEA due to their merits. On one hand, if the indicator-based framework is incorporated into PSO, the performance of PSO for MaOPs is expected to be improved; on the other hand, for an indicator-based MOEA, if both a set of solutions and a solution of the set are regarded as different level of particles, the PSO strategies can be applied to them hierarchically, which will greatly benefit the fine search. To this end, we have proposed an indicator-based set evolution PSO algorithm (Sun et al. 2014a, b), including the general framework and some specific operators of PSO. In work Sun et al. (2014a), the set-based PSO operator was presented and the associated selection method of sets leaders was given in detail based on a weighted indicator by balancing the convergence and diversity of the evolved sets. In Sun et al. (2014b), an alternative leader selection strategy was addressed and a mutation was further applied to the solutions of each set. However, in these algorithms, the set-based PSO operator and the evolution for the original solutions are not further studied.

The main goal of this study is to improve the performance of the set-based PSO by proposing an enhanced set PSO operator and a more efficient PSO for the solutions in the original space of the MaOPs. Compared with our previous work, in Sun et al. (2014a, b), the following three different contents are focused here: (1) a framework of indicator-based set evolution IS-MOPSO; (2) an improved PSO operator for evolving sets in a more powerful way; (3) an approach to updating the solution of a set to guide the population to evolve toward the true Pareto front.

The remainder of this paper is organized as follows. Section 2 gives the main concepts and notations for MaOPs. Related work on MOEAs for solving MaOPs is introduced in Sect. 3. Section 4 presents the framework of our improved indicator-based set evolution PSO, and the specific realization of this framework is followed in Sect. 5. The applications of the proposed algorithm in several benchmark MaOPs and the associated analysis are demonstrated in Sect. 6. Section 7 draws the main conclusions of the study.

2 Concepts of evolutionary many-objective optimization

Without loss of generality, a minimization problem formulated with Eq. (1) is considered here:

$$\begin{aligned}&\min \;\;\mathbf{{f}}(\mathbf{{x}}) = ({f_1}(\mathbf{{x}}) ,{f_2}(\mathbf{{x}}) , \ldots ,{f_m}(\mathbf{{x}})) \nonumber \\&s .t.\;\;\; {g_i}\left( \mathbf {x} \right) \le 0,i = 1,2,\ldots ,k \nonumber \\&\mathbf {x} \in S \subset R^n , \end{aligned}$$

(1)

where $\mathbf {x}$ is an n-dimensional decision variable and its feasible space is denoted as $S$; ${g_i}(\mathbf{{x}}) \le 0,i = 1,2, \ldots ,k$ represents the $i$th constraint; ${f_j}(\mathbf{{x}}),$ j $= 1,2, \ldots ,m,$ means the $j$th objective, and $m$ refers to the number of objectives to be optimized. When the value of $m$ is larger than 3, Eq. (1) is termed as an MaOP.

Evolutionary many-objective optimization expects to seek a number of compromising solutions for all objectives under the concept of the Pareto dominance. Therefore, the related notations, including the Pareto dominance (PD), the Pareto optimality, the Pareto optimal set, and the Pareto front (PF) are of great importance here.

Pareto dominance: For two solutions $\mathbf {x}_1$ and $\mathbf {x}_2$, if $\forall k \in \left\{ {1,2, \ldots ,m} \right\} \!\!:{f_k}\left( {{\mathbf{{x}}_1}} \right) \le {f_k}\left( {{\mathbf{{x}}_2}} \right)$ and $\exists k^{\prime } \in \left\{ {1,2, \ldots ,m} \right\}$: ${f_{k^{\prime }}}\left( {{\mathbf{{x}}_1}} \right) < {f_{k^{\prime }}}\left( {{\mathbf{{x}}_2}} \right)$, solution $x_1$ is said to dominate $x_2$, denoted as ${\mathbf{{x}}_1} \succ {\mathbf{{x}}_2}$.

Pareto optimal set and Pareto front: For a solution ${\mathbf{{x}}^*} \in S$, if there is no $\mathbf{{x^{\prime }}} \in S:\mathbf{{x^{\prime }}} \succ {\mathbf{{x}}^*}$, ${\mathbf{{x}}^*}$ is said to be non-dominated and called as a Pareto optimal solution. The set consisting of all non-dominated solutions is called the Pareto optimal set. Accordingly, the images of all the Pareto optimal solutions in the objective space form the Pareto front.

Besides the aforementioned concepts, indicators which are commonly utilized to evaluate the performances of traditional MOEAs are especially significant for an indicator-based MOEA. Therefore, they are briefly introduced here. So far, such metrics as the generational distance (GD), the inverted generational distance (IGD), the maximal spread (MS), hypervolume, and the spacing are very popular. The main reason is that they provide several criteria related to (1) proximity, which reflects the distance between the Pareto front obtained by an algorithm and the true Pareto front of a MOP, (2) distribution, which depicts the distribution of solutions along the Pareto front, and (3) spread, which suggests the extent covered by the Pareto optimal set.

GD indicator: The metric of GD well indicates the gap between the true Pareto front and the obtained one, which is formulated as:

$$\begin{aligned} {\text{ GD }} = \frac{1}{{{n_{PF}}}}{\left( {\sum \limits _{i = 1}^{{n_{PF}}} {d_i^2} } \right) ^{\frac{1}{2}}}, \end{aligned}$$

(2)

where ${n_{PF}} = \left| {PF} \right|$, and ${d_i} = \mathop {\min }\nolimits _{g = 1}^{{n_{PF}}}$ $\sqrt{\sum \nolimits _{j = 1}^m {{{\left( {{f_j}({\mathbf{{x}}_i}) - f_j^{\text {true}}({\mathbf{{x}}_g})} \right) }^2}} }$ represents the Euclidean distance between the $i$-th member of the obtained Pareto front and the closest one of the true Pareto front. Clearly, a small value of GD is expected, which suggests that the obtained Pareto front has a good approximation to the true one.

IGD indicator: The IGD indicator can reflect not only the proximity, but also the distribution of the obtained Pareto front. Let $P^{\text {true}}$ be a set of points with uniform distribution in the objective space along the true Pareto front, and P an approximation to the true Pareto front, then the IGD is defined as:

$$\begin{aligned} {\text {IGD}}\left( {P,{P^{\text {true}}}} \right) = \frac{{\sum \limits _{v \in {P^{\text {true}}}} {d\left( {v,P} \right) } }}{{\left| {{P^\text {true}}} \right| }}, \end{aligned}$$

(3)

where $d\left( {v,P} \right)$ means the minimal Euclidean distance between $v$ and the points in $P$. $P$ must be very near to the true Pareto front and does not miss any part of the true Pareto front, if the value of IGD is low enough.

Schotts spacing: Schott (1995) addressed the following spacing metric to gauge how even the points on the Pareto front were:

$$\begin{aligned} {F_d}{(}\mathbf{{X}}{)} = \sqrt{\sum \limits _{j = 1}^N {{{\left[ {{d^*}(\mathbf{{X}}) - d({\mathbf{{x}}_j})} \right] }^2}/(N - 1)} } \end{aligned}$$

(4)

where $\mathbf {X} = \{ {\mathbf{{x}}_1},{\mathbf{{x}}_2}, \ldots ,{\mathbf{{x}}_N}\}$ is a set with $N$ optimal solutions; $d({\mathbf{{x}}_j}) = \mathop {\min }\nolimits _{l \in \{ 1,2, \ldots ,N\} ,l \ne j} \sum \nolimits _{i = 1}^m {\left| {{f_i}({\mathbf{{x}}_j}) - {f_i}({\mathbf{{x}}_l})} \right| }$, $j = 1,2, \ldots ,N$, and ${d^*}(\mathbf{{X}}) = \frac{1}{N}\sum \nolimits _{j = 1}^N {d({\mathbf{{x}}_j})}$. From Eq. (4), a large value of ${F_d}\mathrm{{(}}\mathbf{{X}}\mathrm{{)}}$ is expected to obtain an evenly distributed Pareto front.

Hypervolume The hypervolume indicator Johannes and Zitzler (2008) gives the volume of an objective subspace that is dominated by a solution set. On the basis of a reference point, $\mathbf{{x}}_{ref}$, it can be defined as follows:

$$\begin{aligned} {F_h}(\mathbf{{X}}) = \lambda \left( \bigcup \limits _{{\mathbf{{x}}_j} \in \mathbf{{X}}} {\{ h|f({\mathbf{{x}}_j}) < h < f({\mathbf{{x}}_{ref}})\} } \right) , \end{aligned}$$

(5)

where $\lambda$ is the Lebesgue measure. A large value of this indicator means that the obtained Pareto front gains not only an outstanding proximity, but also a good distribution.

Diversity The diversity indicator is used to measure the extent of a set of optimal solutions. Zitzler et al. (2000) argued the following expression to calculate the value of the diversity. Similarly, a large value of this indicator is expected to maintain the diversity of a solution set:

$$\begin{aligned} {F_e}\left( \mathbf{{X}} \right) = \sqrt{\sum \limits _{i = 1}^m {{{\left( {\max _{j = 1}^N{f_i}\left( {{\mathbf{{x}}_j}} \right) - \min _{j = 1}^N{f_i}\left( {{\mathbf{{x}}_j}} \right) } \right) }^2}} }. \end{aligned}$$

(6)

3 Related work

Since MOEAs have been proven to be powerful for tackling MOPs with two or three objectives, it is natural to scale such a framework to MaOPs. Li et al. (2013) reviewed that various MOEAs have been improved to solve MaOPs in recent years. They provided a systematic comparison among eight representative MOEAs, e.g., NSGA-II, MOEA/D, and indicator-based MOEA, and concluded that different explorative capabilities suggest a careful choice for solving MaOPs. Von Lcken et al. (2014) also presented a survey on MOEAs for MaOPs from two aspects, i.e., methods of using alternative dominance relation and transforming the original MaOP into a related one. As Christian addressed, the transformation-based approaches, including decomposition-based MOEAs, objective aggregation, indicator-based evolution, dimension reduction, and space partition, are very popular and have gained much attention.

Among all these compared approaches, three typical algorithms, NSGA-II which is the most powerful tool for solving MOPs with less than four objectives, the indicator-based MOEA presented recently, and PSO, are closely correlated with this study, and therefore related work of these algorithms will be focused.

3.1 NSGA-II for MaOPs

The framework of NSGA-II has been successfully adopted to solve MOPs in the past decades and it is of nature to be expanded to solve MaOPs. However, previous studies have shown that the dominance relation used in NSGA-II greatly weakens its performance in comparing individuals as the number of objectives increases. However, NSGA-II is widely used in tackling MaOPs by either changing the dominance relation or enhancing the crowding distance to improve its scalability.

Mario and Kaori (2007) proposed several substitutive distance assignment schemes to replace the traditional crowding distance used in typical NSGA-II. These schemes result in a significantly improved performance for most MaOPs. Yang et al. (2013) developed a grid-based MOEA by articulating the grid-based approach to strengthen the selection pressure and presented the concepts of grid dominance and grid differences. From the point of improving the evolutionary diversity, Li also presented two kinds of improved MOEAs, i.e., shift-based density estimation Li et al. (2014) and diversity management operation (Li et al. 2014).

3.2 PSO for MaOPs

PSO is performed by updating the position of a particle that represents a possible solution according to its own flying experience and that of the swarm. In the basic PSO, the $i$-th particle at generation t is updated as follows:

$$\begin{aligned}&{{\mathbf {v}}_i}(t + 1) = w{{\mathbf {v}}_i}(t) + {c_1}{r_1}({{\mathbf {P}}_i} - {{\mathbf {x}}_i}(t)) + {c_2}{r_2}({{\mathbf {P}}_g} - {{\mathbf {x}}_i}(t)) \nonumber \\&{{\mathbf {x}}_i}(t + 1) = {{\mathbf {x}}_i}(t) + {{\mathbf {v}}_i}(t + 1), \end{aligned}$$

(7)

where ${{\mathbf {v}}_i}(t)$ and ${{\mathbf {x}}_i}(t)$ are the velocity and the position of the $i$-th particle at generation $t$, respectively; ${{\mathbf {P}}_i}$ means the local best of particle $i$ and ${{\mathbf {P}}_g}$ the global best; $w$ refers to the inertia weight; $c_1$ represents the cognitive weight and $c_2$ the social weight; $r_1$ and $r_2$ are two random values with the uniform distribution in the range of [0, 1].

PSO has been recognized to be powerful when handling MOPs and has a rapid convergence compared to other MOEAs (Margarita and Coello Coello 2006). To extend PSO for MOPs, the following four aspects are usually focused: selecting non-dominated solutions, updating the global and the local best particles, maintaining the population diversity, and updating the archive.

In the case of selecting non-dominated solutions, the Pareto dominance is a major principle. Mostaghim and Teich (2003) incorporated the $\epsilon$-dominance into MOPSO to obtain a dominance relation among individuals based on the grid dominance. Once the dominance concept is defined, the global and the local best particles will be accordingly updated. To this end, the newly generated particle is compared to the current local best one, and the non-dominated one is the new local best particle; otherwise, a randomly picked out one is regarded as newly local best. As for the global best particle, an archive is usually constructed along with the evolution, and each non-dominated particle in this archive is a candidate of the global best. Then, according to a specific mechanism, e.g., random, roulette, or tournament selection (Margarita and Coello Coello 2006), the global best particle of the swarm is selected. The population diversity is of considerable importance to the evolution of a swarm due to the guidance mechanism of PSO, and the mutation operator is a suitable way to maintain the population diversity (Coello Coello et al. 2004).

PSO is also extended to solving MaOPs. Woolard and Fieldsend (2013) addressed the capability of PSO in solving MaOPs from several aspects as selecting the global and the local best particles and updating the archive, seeking for appropriate dominance relations and evolutionary operators. Andre and Aurora (2012) investigated the convergence and the diversity of PSO in solving MaOPs by controlling the area where the dominated solutions locate. Mostaghim and Schmeck (2008) proposed a distance-based ranking method to substitute the Pareto dominance to effectively compare particles in many-objective PSO. Wickramasinghe and Li (2009) used reference points to define a distance metric and applied it to select the leaders. It is worth noting that no matter the Pareto dominance or the distance-based ranking metrics used in these PSO methods cannot avoid the complex comparisons among the updating procedure; therefore, the challenges faced by MOEAs in solving MaOPs are yet unsolved, suggesting that novel techniques are required to be explored.

3.3 Indicator-based set evolution for MaOPs

Indicator-based EMOs and PSOs have been extensively investigated for solving MOPs in recent years. Zitzler and Kunzli (2004) first suggested directly using one or more EMO indicators related to proximity, distribution, and spread of a set of optimal solutions to guide an evolutionary process. Basseur and Burke (2007) carried out a range of experiments on different binary indicators. Phan and Suzuki (2013) proposed an indicator-based selection with the R2 indicator to obtain a diverse set of solutions. Jiang et al. (2014) presented a simple and fast hypervolume indicator-based EMO to effectively decrease the high time complexity for measuring the hypervolume contributions of different solutions. Besides these EMOs, some PSO algorithms are also focused on using the indicators to select leaders for the updating operator. Jia et al. (2011) proposed an indicator-based PSO with local search by articulating the preference of the decision maker into MOPSO in selecting the leader particles. Chaman et al. (2014) developed a hypervolume indicator-based leader selection strategy for PSO, in which the hypervolume contribution of archived solutions for selecting global and local leaders was used. By using R2 indicator to select leader particles, Castro and Pozo (2014) addressed a MOPSO to optimize many-objective problems. This algorithm used a simple hyper-heuristic strategy to automatically select leader and archiving methods during the search. However, these algorithms only focused on selection by use of indicators, and not on the set evolution, as addressed in this paper.

As for indicator-based set evolution, according to the indicators, a set consisting of a number of individuals is determined to be either selected or not. Compared to previous methods of handling MaOPs, the optimized variable here is not a single solution of the original optimization problem, but a set consisting of more than one solution. In the literature, hypervolume has been widely adopted as an appropriate indicator, since it can reflect both proximity and distribution of a Pareto optimal set (Zitzler et al. 2010).

The framework of indicator-based EMO includes the following two aspects: (1) converting an MaOP to a new optimization problem with not more than three indicator-based objectives, by regarding a set of solutions as a decision variable to be optimized; (2) developing strategies or operators to perform the evolution of the set-based population. According to the indicators used to evaluate the performance of a solution set, the superior set containing a number of Pareto optimal solutions can be obtained.

To clearly describe the indicator-based set evolution, the related concepts and notations different from traditional MOEAs are introduced here. The indicators to be adopted as the optimized objectives are denoted as: $\min F({\mathbf {X}}) = \{ {F_1}({\mathbf {X}}),{F_1}({\mathbf {X}}),\ldots ,{F_M}({\mathbf {X}})\} (M \le 3)$, where ${\mathbf {X}} = \{ {{\mathbf {x}}_1},{{\mathbf {x}}_2}, \ldots ,{{\mathbf {x}}_P}\}$ is the set variable to be optimized with ${{\mathbf {x}}_i},i = 1,2, \ldots ,P$ being a solution of the original MaOP. For such set-based optimization, the Pareto dominance defined in Gong et al. (2014) is as follows.

Set-based Pareto dominance: For two sets of solutions, ${\mathbf{{X}}_i}$ and ${\mathbf{{X}}_j}$ , ${\mathbf{{X}}_i}$ is said to dominate ${\mathbf{{X}}_j}$ , denoted as ${\mathbf{{X}}_i}{ \succ _\text {spar}}{\mathbf{{X}}_j}$ if $\forall k \in \left\{ {1,2, \ldots ,M} \right\} :{F_k}({\mathbf{{X}}_i}) \le {F_k}({\mathbf{{X}}_j})$ and $\exists k^{\prime } \in {1,2, \ldots ,M}$:${F_{k^{\prime }}}({\mathbf{{X}}_i}) < {F_{k^{\prime }}}({\mathbf{{X}}_j})$.

It has been experimentally demonstrated that the indicator-based set evolutionary algorithms are greatly beneficial to enhancing the selection pressure by converting an MaOP into the one with two or three indicator-based objectives, which effectively conquers the deterioration of applying traditional MOEA to tackle MaOPs. However, the evolutionary operators must be finely explored to promote the set evolution, which are greatly different from those traditional EA operators. In the following, we will take full advantages of PSO and indicator-based MOEA to develop set-based MOPSO for MaOPs.

4 Framework of the algorithm

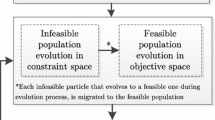
The general framework of the set-based PSO has been given in Sun et al. (2014b). Based on our previous work, the framework of the proposed algorithm is shown in Fig. 1, consisting of three main parts. (1) Initialization: Some sets of solutions are randomly initialized in the decision variable space of the optimized MaOP. In the subsequent evolutionary process, these sets are individuals to be optimized. (2) Indicator-based objective transformation: The indicators used to measure the quality of the sets are calculated as objectives, and thus the MaOP is transformed into an MOP with two or three objectives. (3) Set-based PSO operators for updating the sets of solutions and also for further evolving the solutions of some selected sets.

Fig. 1

Framework of the algorithm

In this paper, the PSO operators for the set evolution will be highlighted. (1) Updating a particle for the set evolution, specifically, the evolutionary strategy and the selection of the global and local best set particles; (2) updating a solution of a set on considering the selection of the global and local best particles with a low computational cost. In the next section, an improved S-MOPSO algorithm will be presented in detail. In this method, the non-dominated sorting mechanism used in NSGA-II is adopted here to compare and sort particles, so as to select the global and the local best particles during the set evolution, and thus the archive is not involved anymore. That is to say, only the set and the solution of a set of updates are focused on, especially the selection of the global and the local best particles.

5 Improved S-MOPSO

5.1 Optimization objectives of indicator-based S-MOPSO

In indicator-based set evolution MOEAs, the original MaOP is first transformed into a new optimization problem, in which the objectives are some performance indicators addressed in Sect. 2, and the decision variable represents a set consisting of a number of solutions of the original MaOP. Since the framework of the algorithm given in Sect. 4 is based on indicators, the formulation of the transformed optimization problem is first presented here.

In this study, two most popular indicators to evaluate the performance of the Pareto front obtained by a MOEA, i.e., the distribution metric, ${F_d}(\mathbf {X})$, expressed with Eq. (4) and hypervolume, ${F_h}(\mathbf {X})$, formulated with Eq. (5), are adopted as two new objectives to be optimized by PSO, and a particle refers to a solution set is denoted as $\mathbf {X}$.

As addressed before, the larger the values of these two indicators, the better is the corresponding set. Therefore, the converted optimization problem is an MOP with two objectives and is expressed as follows:

$$\begin{aligned}&\max F(\mathbf{{X}}) = \{ {F_1}(\mathbf{{X}}),{F_2}(\mathbf{{X}})| \nonumber \\&{F_1}(\mathbf{{X}}) = {F_d}(\mathbf{{X}}),{F_2}(\mathbf{{X}}) = {F_h}(\mathbf{{X}})\} \nonumber \\&s .t.\quad \mathrm{{ }}\mathbf{{X}} \in \mathcal {P}(S), \end{aligned}$$

(8)

where $\mathcal {P}$ means the power set of $S$ and consists of all the subsets of $S$; $\mathbf{{X}} = \{ {\mathbf{{x}}_1},{\mathbf{{x}}_2}, \ldots ,{\mathbf{{x}}_P}\}$ represents a set consisting of $P$ solutions of the original MaOP.

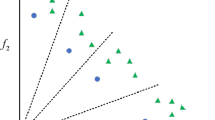
To clearly and visually show the relationship between the original MaOP and its transformed one with two indicator-based objectives, a problem with three objectives and three decision variables are illustrated in Fig. 2.

Fig. 2

Relationship between the original MaOP and its converted one

In Fig. 2a, c refer to the objective spaces before and after transformation of the optimization problem, respectively, and (b) the decision space. In (b), there are two kinds of symbols labeled with stars and black dots, respectively, representing two solution sets. The associated mapping relationship from (b) to (a) is very clear and fully determined by the original MaOP. However, such a mapping is quite different between (b) and (c), i.e., the decision variable in (b) is not a single solution, but a set consisting of a number of solutions, labeled as stars or dots in (b), and the objectives in (c) are two indicators. For the converted objectives, the decision space is composed of all the subspaces of the original decision space. Therefore, the evolution in such a framework has an essential difference with traditional MOEA, and the operators performing on a set must be properly designed. In such a scenario, a hierarchical evolution mechanism should be developed, with evolving not only a solution set, but also a solution of this set. To this end, in the proposed algorithm, a set, $\mathbf {X}$, is first regarded as a particle, and the corresponding PSO for the set evolution is developed, so as to take full advantage of information provided by different sets. Then, an element of a set, which is a solution of the original MaOP and shown as ${\mathbf{{x}}_1},{\mathbf{{x}}_2},{\mathbf{{x}}_3},{\mathbf{{x}}_4}$ in Fig. 2b, is further served as a particle and updated by traditional PSO. The following subsections will give a detailed description of these contents.

5.2 S-MOPSO

The strategy for updating a set under the mechanism of PSO is first presented and then the methods of selecting the global and the local best sets to perform the above updating is focused on by taking the indicator objectives into account.

As aforementioned, in the indicator-based S-MOPSO, a decision variable, $\mathbf {X}$, is a set with each of its elements being a solution of the original MaOP. The following update strategy is presented by regarding ${\mathbf{{X}}_i}\left( t \right)$ as a particle of a swarm with its size being $N$ (Sun et al. 2014b).

$$\begin{aligned} {\mathbf{{V}}_i}\left( {t + 1} \right)= & {} \mathbf{{\omega }}{\mathbf{{V}}_i}\left( t \right) + {\mathbf{{c}}_\mathbf{{1}}}{\mathbf{{r}}_\mathbf{{1}}}\left[ {{\mathbf{{P}}_i}\left( t \right) - {\mathbf{{X}}_i}\left( t \right) } \right] \nonumber \\&+\,{\mathbf{{c}}_\mathbf{{2}}}{\mathbf{{r}}_\mathbf{{2}}}\left[ {{\mathbf{{P}}_\mathrm{{g}}}\left( t \right) - {\mathbf{{X}}_i}\left( t \right) } \right] \nonumber \\ {\mathbf{{X}}_i}\left( {t + 1} \right)= & {} {\mathbf{{X}}_i}\left( t \right) + {\mathbf{{V}}_i}\left( {t + 1} \right) , \end{aligned}$$

(9)

where the meanings of these parameters are the same as those in Eq. (7). However, Eq. (9) is distinct from Eq. (7) even though they are very similar in form. The parameters, $\mathbf{{\omega }},{\mathbf{{c}}_k},{\mathbf{{r}}_k},k = 1,2$, represent matrices with their sizes being the same as those of particle ${\mathbf{{X}}_i}\left( t \right)$,  $i = 1,2, \ldots ,N$. Accordingly, the computations of ${\mathbf{{P}}_i}\left( t \right) - {\mathbf{{X}}_i}\left( t \right)$ and ${\mathbf{{P}}_g}\left( t \right) - {\mathbf{{X}}_i}\left( t \right)$ are also performed on matrices with their dimensions being $N \times n$. ${\mathbf{{V}}_i}\left( t \right)$ is also a matrix denoting the velocity of ${\mathbf{{X}}_i}\left( t \right)$, with its $j$-th column referring to the velocity of the $j$-th solution of the original MaOP and formulated as:

$$\begin{aligned}&\mathbf{{V}}_i^j\left( t \right) = \left[ \begin{array}{l} v_i^j\left( {t,1} \right) \\ v_i^j\left( {t,2} \right) \\ \vdots \\ v_i^j\left( {t,n} \right) \end{array} \right] = {\mathbf{{\omega }}^j}\mathbf{{V}}_i^j\left( {t - 1} \right) \nonumber \\&\quad + \mathbf{{c}}_1^j\mathbf{{r}}_1^j\left[ {\mathbf{{P}}_i^j\left( t \right) - \mathbf{{X}}_i^j\left( t \right) } \right] + \mathbf{{c}}_2^j\mathbf{{r}}_2^j\left[ {\mathbf{{P}}_\mathrm{{g}}^j\left( t \right) - \mathbf{{X}}_i^j\left( t \right) } \right] .\nonumber \\ \end{aligned}$$

(10)

In the previous work Sun et al. (2014b), the critical two terms ${\mathbf{{P}}_i}\left( t \right) - {\mathbf{{X}}_i}\left( t \right)$ and ${\mathbf{{P}}_g}\left( t \right) - {\mathbf{{X}}_i}\left( t \right)$ are directly and simply calculated according to the indices of the elements without considering their qualities, which cannot guarantee the merits of the traditional PSO, in that some elements of ${\mathbf{{P}}_i}\left( t \right)$ or ${\mathbf{{P}}_g}\left( t \right)$ (the leaders) may be worse than those of ${\mathbf{{X}}_i}\left( t \right)$. Here, an improvement updating strategy is developed to overcome this shortage. For the elements in the sets of the two leaders ${\mathbf{{P}}_i}\left( t \right)$, ${\mathbf{{P}}_g}\left( t \right)$ and the current particle ${\mathbf{{X}}_i}\left( t \right)$, they are resorted in an ascending order according to their values on the first objective of the original MaOP.

As has been addressed, lots of researches have been devoted to the selection of the leaders of PSO, and these methods can be directly applied to our algorithm. Here, a weighted approach of selecting the local best particle is first proposed by balancing the performances of a set in distribution and convergence. Then, the global best particle is determined based on sorting the performances of all the local best particles. Since the above performances can well be depicted by the two indicators defined in Eq. (8), a weighted indicator is then defined as follows”

$$\begin{aligned} F\left( {{\mathbf{{X}}_i}} \right) = \alpha {F_1}\left( {{\mathbf{{X}}_i}} \right) + \left( {1 - \alpha } \right) {F_2}\left( {{\mathbf{{X}}_i}}. \right) \end{aligned}$$

(11)

It is clear that the value of parameter $\alpha$ is very important to the integrated $F\left( {{\mathbf{{X}}_i}} \right)$. When the performance of a set in distribution is good, the evolution of a swarm should be strengthened on the performance in convergence and the value of $\alpha$ should be relatively small; otherwise, if the performance of a set in convergence is superior, the distribution of the set should be further highlighted to promote the evolution of a swarm and the value of $\alpha$ should be relatively large. Accordingly, a method is given here to determine the value of $\alpha$.

For all the set particles in a swarm, the average value of $F_1(\mathbf {X})$ and that of $F_2(\mathbf {X})$ can be calculated as follows:

$$\begin{aligned} \begin{array}{l} {{\bar{F}}_1}\left( t \right) = \frac{1}{N}\sum \limits _{i = 1}^N {{F_1}\left( {{\mathbf{{X}}_i}\left( t \right) } \right) } \\ {{\bar{F}}_2}\left( t \right) = \frac{1}{N}\sum \limits _{i = 1}^N {{F_2}\left( {{\mathbf{{X}}_i}\left( t \right) } \right) } \\ \end{array}. \end{aligned}$$

(12)

Then, the value of $\alpha$ is defined as:

$$\begin{aligned} \alpha (t) = \frac{{{{\bar{F}}_2}\left( t \right) }}{{{{\bar{F}}_1}\left( t \right) + {{\bar{F}}_2}\left( t \right) }}. \end{aligned}$$

(13)

According to the weighted value, calculated from Eq. (11), of each particle the global best particle with the largest value of $F(\mathbf {X})$ can be selected as follows:

$$\begin{aligned} {\mathbf{{P}}_g} = \arg \mathop {\max }\limits _{i = 1,2, \ldots ,N} F\left( {{\mathbf{{X}}_i}} \right) . \end{aligned}$$

(14)

When updating a local best particle, the Pareto dominance on sets is adopted to compare the quality of each set particle. For the newly generated particle, ${\mathbf{{X}}_i}\left( {t + 1} \right)$, and the current local best particle, ${P_i}\left( t \right)$, if ${\mathbf{{X}}_i}\left( {t + 1} \right) { \succ _\text {spar}}{P_i}\left( t \right)$, ${\mathbf{{X}}_i}\left( {t + 1} \right)$ is selected as the new local best particle, ${P_i}\left( t + 1 \right)$; if ${\mathbf{{X}}_i}\left( {t + 1} \right) { \prec _\text {spar}}{P_i}\left( t \right)$, the local best particle remains unchanged; if these two particles are non-dominated, the domination proportion of each particle is calculated based on the elements belonging to each of these two particles and the one with a larger proportion is selected as ${P_i}\left( t + 1 \right)$.

Set evolution PSO can fully exchange information among solution sets. However, it does not focus on a specific solution of a set. When tackling MaOPs, it is expected to seek for the Pareto optimal set of this problem. Therefore, it is of considerable necessity to further evolve solutions of a set. Next, PSO for evolving solutions of a set will be addressed, especially, the selection of the global and the local best particles for updating a solution particle.

5.3 PSO for evolving solutions of a set

PSO for evolving solutions of a set is expected to finely explore solutions in the original searching space S and gain a valuable Pareto front. Besides, the computational cost should be acceptable when performing PSO. Therefore, a method of evolving only solutions of a particularly selected set is developed here.

The following three issues must be addressed to meet the above requirements: (1) selecting the set whose elements will be further evolved by using PSO; (2) performing appropriate PSO strategies on the solutions of the selected set; (3) choosing the global and the local best particles for updating a solution. The general idea of handling these issues is as follows. In the prophase of the evolution, the worst set is selected to evolve its elements by using PSO, so as to speed up the convergence toward the true Pareto front. In such a scenario, the ideal reference point of the current best set is selected as the global best particle, and the ideal reference of the selected set as the corresponding local best particle. In the anaphase, the superior set is chosen to evolve its elements by performing PSO, with the purpose of enhancing the performance of this set in proximity and distribution. According to Eq. (12), the evolution of solutions in a set can be divided into the following two phases: if ${\bar{F}_1}\left( t \right) > {\bar{F}_2}\left( t \right)$, the evolution is in the prophase; otherwise, it is in the anaphase.

5.3.1 Selection of a particular set

With the method of non-dominated sorting, all the sets in $\mathcal {P}(S)$ can be sorted according to the values of $F_1(\mathbf {X})$ and $F_2(\mathbf {X})$, and their orders obtained. From these sets, the worst and the best ones with the highest and the lowest orders, respectively, can be chosen and denoted as $S_\mathrm{{W}}$ and $S_\mathrm{{ND}}$.

In the prophase, solutions in $S_\mathrm{{W}}$ are further updated by PSO, whereas in the anaphase, solutions in $S_\mathrm{{ND}}$ are finely adjusted also by PSO. For solutions in the other sets, they are evolved only by a mutation operator.

5.3.2 PSO strategies in different sets

It is quite difficult to select the global and the local best particles for MaOPs if the traditional Pareto dominance is adopted to compare the solutions. Therefore, we propose an approach of selecting the virtual global and local best particles for updating a particle in PSO by taking both $S_\mathrm{{W}}$ and $S_\mathrm{{ND}}$ into account. In this approach, the ideal reference point of $S_\mathrm{{ND}}$ is selected as the global best particle, and the ideal reference point of a set in $S_\mathrm{{W}}$ is taken as the local best particle when updating solutions in this set.

It is worth noting that the number of sets in $S_\mathrm{{W}}$, denoted as $N_\mathrm{{W}}$, or that of sets in $S_\mathrm{{ND}}$, denoted as $N_\mathrm{{ND}}$, may be larger than one. For the $i$-th set in $S_\mathrm{{W}}$, its ideal reference point is denoted as $\mathbf{{z}}_{\mathrm{{W}},i}^*$, with its expression being as follows:

$$\begin{aligned} \begin{array}{l} \mathbf{{z}}_{\mathrm{{W}},i}^* = \{ {\mathbf{{x}}_j}\left| {\mathop {\min }\limits _{{\mathbf{{x}}_j} \in {\mathbf{{X}}_i},{\mathbf{{X}}_i} \in {S_{/rm{W}}}} {f_k}\left( {{\mathbf{{x}}_j}} \right) } \right. ,\\ k = 1,2, \ldots ,m,j = 1,2, \ldots ,N,i = 1,2, \ldots ,{N_\mathrm{{W}}}\}. \end{array} \end{aligned}$$

(15)

All these ideal reference points are selected as the local best particles.

For $S_\mathrm{{ND}}$, the ideal reference point of its $i$th set is $\mathbf{{z}}_{\mathrm{{ND}},i}^*,i = 1,2, \ldots ,{N_\mathrm{{ND}}}$. Since only one global best particle is required for updating a particle in PSO, the reference point with the smallest crowding degree is selected., the ideal reference point of its $i$th set is . Since only one global best leader is required for updating a particle in PSO, the reference point with the smallest crowding degree is selected.

In the anaphase of the evolution, solutions in $S_\mathrm{{ND}}$ are evolved with the PSO operators. For the $i$-th set in $S_\mathrm{{ND}}$, denote its best decision variable as $\mathbf{{x}}_{\mathrm{{ND}},i}$, whose ideal reference point is $\mathbf{{z}}_{\mathrm{{ND}},i}^*$, then $\mathbf{{z}}_{\mathrm{{ND}},i}^*$ is selected as the global best particle. Since solutions with the largest contribution to hypervolume is selected as the local best particle, solutions of the current best set will be promoted to converge toward the true Pareto front as soon as possible.

6 Experiments and analysis

6.1 Benchmark optimization problems

The DTLZ benchmark optimization problems are adopted to evaluate the performance of the proposed S-MOPSO since the number of objectives of these problems can be freely varied. Here, five optimization problems, named DTLZ1 to DTLZ7, are selected excepted for DTLZ4 and DTLZ6, due to their similar Pareto fronts to those of DTLZ2 and DTLZ3. The number of objectives of each problem is denoted as m, and its value here is set to 5, 10, and 20, respectively. The number of decision variables of each problem is $n=k+m-1$, with the value of k being 5 for DTLZ1, 10 for DTLZ2, DTLZ3, and DTLZ5, and 20 for DTLZ7. Each of these variables varies from 0 to 1. The detailed expression of DTLZ1 is shown in Eq. (16). For those of the other optimization problems, please refer to Zhang et al. (2008).

$$\begin{aligned} \begin{array}{l} \mathrm{{min}} {f_1}(x) = \frac{1}{2}{x_1}{x_2} \ldots {x_{m - 1}}(1 + g({\mathrm{{x}}_m}))\\ \quad {f_2}(x) = \frac{1}{2}{x_1}{x_2} \cdots (1 - {x_{m - 1}})(1 + g({\mathrm{{x}}_m}))\\ \qquad \quad \vdots \\ \quad {f_{m - 1}}(x) = \frac{1}{2}{x_1}(1 - {x_2})(1 + g({\mathrm{{x}}_m}))\\ \quad {f_m}(x) = \frac{1}{2}(1 - {x_1})(1 + g({\mathrm{{x}}_m})) \\ s.t. k = \left| {{x_m}} \right| = 5; \quad 0 \le {x_i} \le 1,i = 1,2, \ldots m \\ \end{array}, \end{aligned}$$

(16)

where $g({x_m}) = 100(\left| {{x_m}} \right| + \sum \nolimits _{{x_i} \in {\mathrm{{x}}_m}} {{{({x_i} - 0.5)}^2}-\cos (20\pi }$ ${({x_i} - 0.5)))}$.

6.2 Parameter settings

The values of the parameters used by all the compared algorithms are listed in Table 1. The other parameters, $\mathbf{{\omega }}$, ${\mathbf{{c}}_1}$, ${\mathbf{{c}}_2}$, ${\mathbf{{r}}_1}$, and ${\mathbf{{r}}_2}$, involved in the proposed algorithm, are all vectors. For simplicity, each element of these vectors is set to the same value. To be specific, each element of $\mathbf{{\omega }}$ is 0.4, that of ${\mathbf{{c}}_1}$ and ${\mathbf{{c}}_2}$ is 2, and that of ${\mathbf{{r}}_1}$ and ${\mathbf{{r}}_2}$ is a random value varying in the range of 0 and 1. Besides, the indicators formulated with Eq. (4) and Eq. (5) are calculated to measure the performances of these compared algorithms in solving MaOPs.

Table 1 Parameter settings

Here, four groups of experiments are conducted to evaluate the main contents of the proposed S-MOPSO.

• 1. Selecting the global best set particle. The method of selecting the global best particle given in Eq. (14) is greatly influenced by the value of parameter $\alpha$ which is determined by an adaptive approach. In this experiment, the presented approach of setting the value of $\alpha$ is analyzed by comparing the indicators under four values of $\alpha$.

• 2. Developing strategies for set evolution PSO. Set evolution PSO is expected to exchange information among sets, which is quite different from existing indicator-based MOEAs. To show its effectiveness, set-based many-objective evolutionary optimization (S-MOEMO) (Gong et al. 2014) and NSGA-II (Deb et al. 2002) are compared here. Since no operations are performed to any solution of a set in this stage, the crossover and mutation are only performed to the sets in S-MOEMO, and only selection is adopted in NSGA-II.

• 3. Updating solutions of a selected set by using PSO. The performance of updating solutions of a selected set by using PSO is discussed here. Both the S-MOPSO algorithm with the above approach and that without it are conducted, and their results are compared so as to evaluate the performance of using the above approach.

• 4. The overall performance of S-MOPSO. To show the overall performance of S-MOPSO, the proposed algorithm is compared with S-MOEMO, NSGA-II, and MOPSO, and the values of the indicators are analyzed.

6.3 Results and analysis

6.3.1 Set evolution PSO + selecting the global best set particle

Selecting the global best set particle given in Eq. (14) is actually a critical part of set evolution PSO. Therefore, the experiments on both set evolution PSO and selection on global best particles are combined together to show their effectiveness.

The effectiveness of selecting the global best set particle for the set evolution has been demonstrated in our previous work by setting several different values for the weighting $\alpha$ and applying them to DTLZ1 and DTLZ2. Here, some other experimental results are further analyzed by applying the algorithm to DTLZ3, DTLZ5, and DTLZ7 with their objective numbers being 5, 10, and 20. The proposed set evolution together with the global best selection is compared with S-MOEMO and NSGA-II through the values of the hypervolume (H) and distribution (SP). The corresponding results are depicted in Figs. 3 and 4. For simplicity, the legend of the curves is only involved in Figs. 3c and 4c.

Fig. 3

Values of hypervolume (H)

Fig. 4

Values of distribution (SP)

From Figs. 3 and 4, the following observations can be concluded: (1) For the Hypervolume, an indicator used to show the convergence of the obtained Pareto solutions, the proposed set-based PSO together with the selection of global leader always outperforms the other two compared algorithms. (2) For the SP, an indicator for measuring the distribution of the solutions, our algorithm performs better than S-MOEMO and NSGA-II except for the DTLZ3 with 20 objectives. (3) The variations of the Hypervolume somewhat contradict that of the SP. (4) For S-MOEMO, its evolutionary operators among sets regard a solution of a set as a gene, so that the crossover actually transfers solutions without generating any new solution, which is quite different from the proposed algorithm. (5) For NSGA-II, because only selection is performed, i.e., no crossover and mutation( as described in Sect. 6.2), the values of SP and H In Figs. 3 and 4 remain unchanged.

In summary, (1) the proposed S-MOPSO outperforms the compared two algorithms on the whole, suggesting that the proposed set evolution PSO is effective; (2) the proposed approach of adaptively setting the value of $\alpha$ is effective for selecting the global best set particle.

6.3.2 PSO for evolving solutions of a selected set

This experiment is done to investigate the performances of PSO for evolving solutions of a selected set. Under the set evolution S-MOPSO framework shown in the previous experiment, the two algorithms, i.e., S-MOPSO with and without the above mechanism, are compared. To be clearly demonstrated, S-MOPSO without the above mechanism is simplified as S-MOPSO-N. DTLZ2 and DTLZ3 with the number of objectives being 5, 10, and 20 are solved here by using S-MOPSO and S-MOPSO-N, respectively, and the values of the SP and H indicators are shown in Figs. 5 and 6. For the other problems, similar experimental results can be obtained.

Fig. 5

SP of S-MOPSO with and without evolving solutions of a set using PSO

Fig. 6

H of S-MOPSO with and without evolving solutions of a set using PSO

Figures 5 and 6 reports that, (1) for each optimization problem, the value of SP has an evident increase when PSO for evolving solutions of a set is included in S-MOPSO. Furthermore, this value augments in each generation, especially for DTLZ2. (2) From the aspect of the H indicator, the performance of S-MOPSO is also enhanced when PSO is used to evolve solutions of a set. (3) The improvement in the SP indicator is greater than that of H, indicating that the proposed PSO evolution of solutions of a set contributes more to the diversity of the Pareto optimal set, which is very important to tackle MaOPs.

To sum up, the proposed PSO for evolving solutions of a selected set is powerful in enhancing the H and SP indicators of S-MOPSO, indicating that this approach can further improve the performance of the obtained Pareto optimal set in diversity and convergence, which is well in accord with the intention of the proposed evolutionary mechanism.

6.3.3 Overall performance of S-MOPSO

In the aforementioned comparisons, the S-MOPSO has been compared with NSGA-II (as shown in Figs. 3, 4); therefore, here it is qualified by comparing it to S-MOEMO and MOPSO (without set evolution) on the indicators of SP and H. The Mann–Whitney U test is used to conduct a non-parametric statistical hypothesis test for S-MOPSO and S-MOEMO since they both belong to indicator-based EMOs. In addition, DTLZ1, DTLZ2, DTLZ3, DTLZ5, and DTLZ7 with 5, 10, and 20 objectives are solved, and their experimental results are listed in Table 2.

Table 2 Values of SP and H of compared algorithms

From Table 2, the proposed S-MOPSO outperforms S-MOEMO except for DTLZ2 with 5 objectives and DTLZ3 with 20 objectives. The values of SP and H obtained by S-MOPSO and S-MOEMO are larger than that of NSGA-II, indicating that the set-based evolutionary strategies are superior to MOPSO which is powerful for a MOP with less than 4 objectives. The reason is that set-based MOEA can maintain enough selection pressure and the diversity of a population, so as to promote the evolution to be effective for MaOPs.

In summary, the proposed PSO for evolving sets and solutions of a set is effective for solving MaOPs, and the performances of S-MOPSO in convergence and distribution are enhanced by its merit in well maintaining the diversity of a population.

7 Conclusion

A framework for set evolution many-objective particle swarm optimization is presented by incorporating indicator-based set MOEA with PSO for conquering the deficiency of traditional MOEA when tackling MaOPs. An improved S-MOPSO is addressed by focusing on PSO for evolving sets and solutions of a set. Two commonly used indicators, i.e., distribution and hypervolume, are adopted as the converted objectives; thus a MaOP is first transformed into a traditional MOP with only two objectives. Then the PSO operators are developed by considering both a set and a solution of a set as different levels of particles. In addition, the approach of selecting the global and the local best particles under two different levels, i.e., an entire set and a solution of a set, are explored. The proposed algorithm is applied to five scalable benchmark optimization problems, and the experimental results demonstrate that S-MOPSO is effective in obtaining solutions with good distribution and convergence by comparing it to MOPSO and S-MOEMO.

It is worth noting that the computational complexity of the proposed algorithm, caused by the two levels of PSO operators, especially selecting the global and the local best particles, is higher than the compared algorithms. Therefore, it is of significance to design appropriate PSO operators with a low computational cost for such a framework, including the selection of the global and the local best particles, the construction and the update of an archive. Besides, other indicators, e.g., IGD, may also bring surprising outcomes with a low computational cost. All these issues will be further studied in the future.