1 Introduction

The short-term hydrothermal scheduling plays an important role in the economic operation of electric power systems (Feroldi 2000; Yuan et al. 2011). The objective of the optimization scheduling is to find out the optimal power output of both hydroplants and thermal plants in order to minimize the operating cost of hydrothermal system while satisfying various constraints. As the cost of hydroelectric plants is insignificant, the objective of minimizing the operating cost of hydrothermal system reduces to minimize the fuel cost of the thermal plants during the scheduling period. The short-term hydrothermal scheduling is a high dimension, non-convex, nonlinear optimization problem with a lot of equality and inequality constraints, which is concerned with both hydroplants scheduling and thermal plants dispatching. It is difficult to solve the hydrothermal scheduling problems, especially because they deal with various constraints.

Many methods have been presented to solve the hydrothermal scheduling problems in the past decades. Some of these are linear programming (Chang et al. 2001), nonlinear programming (Catalão et al. 2010, 2011), dynamic programming (Cheng et al. 2009; Santiago et al. 2012), genetic algorithm (Gil et al. 2003; Senthil and Mohan 2011; Sushil and Naresh 2007; Yuan et al. 2008a), artificial neural networks (Sharma et al. 2007), cultural algorithm (Yuan et al. 2010), evolutionary programming (EP) (Basu 2004), ant colony optimization (Wai et al. 2008), Tabu search (Nayak and Rajan 2010), simulated annealing (Christober 2011), differential evolution (DE) (Yuan et al. 2008c, 2009; Mandal and Chakraborty 2008), and particle swarm optimization (PSO) (Mandal and Chakraborty 2011; Yuan et al. 2011; Mehdi et al. 2010). However, these studies only considered the fuel costs of the hydrothermal system; the emission produced by thermal plants was not considered. Owing to increasing concerns about environmental protection, the harmful, polluting emissions of thermal plants should be considered. Thus, it is necessary to take the emission as the objective of the hydrothermal scheduling.

Due to the increasing concerns about emission from thermal plants, many researchers have developed various methods to solve short-term economic/environmental hydrothermal scheduling problems (SEEHTS). Blaže and Marko (2013) applied genetic algorithm for the combined economic-environmental power dispatch problem. This paper used the weighted sum method to solve multi-objective optimization, but the constraints handling of the hydrothermal system was according to a penalization method based on membership functions, which needed a lot of computation. Basu (2004) used fuzzy satisfying evolutionary programming procedure to solve multi-objective short-term hydrothermal scheduling problem. Although this method avoided selecting the plenty factor, the optimum result relied on the reference membership values chosen by users too much. Lu and Sun (2011) developed quadratic approximation-based differential evolution with valuable trade-off approach (QADEVT) to solve SEEHTS problem. They converted the bi-objective programming into single objective one by the valuable trade off. But in the article the method to handle the reservoir storage volumes constraints was based on feasible selection comparison. It needed much time for computation, and at times, there was no feasible solution. Mandal and Chakraborty (2011) utilized PSO to solve the bi-objective hydrothermal scheduling problem and used price penalty factors to transform the problem into a single objective one. But the process of handling the constraints was not given. Sun and Lu (2010) proposed an improved quantum-behaved particle swarm optimization (IQPSO) to solve the SEEHTS problem. The authors made the particles have quantum behavior to find the global optimization solution and used heuristic strategies to handle the constraints of hydrothermal system. But this approach was sensitive to the value of parameter, and the shortcoming of premature convergence was not overcome (Li et al. 2012). From descriptions above, it is significant to find methods obtaining better performance and more effective ways to deal with the constraints for the SEEHTS problem.

Gravitational search algorithm (Rashedi et al. 2009) is a new, heuristic optimization algorithm based on Newton’s law of gravity, which finds the optimization search direction through gravitation interactions between particles. As GSA is advantageous being simple and effective, researchers have used it in order to solve different optimization problems. Rashedi et al. (2011) presented a new linear and nonlinear filter modeling based on GSA. Mohammad et al. (2012) applied GSA to search for the minimum factor of safety and minimum reliability index in both deterministic and probabilistic slope stability analysis. Güvenç et al. (2012) used GSA to deal with the economic load dispatch problem of thermal plants successfully. They formulated the economic emission dispatch problem considered the valve point effect with transmission loss. But this paper just considered the load dispatch with only one time period. Duman et al. (2012) employed GSA to find the best solution for optimal power flow problem in a power system. However, the application of GSA for SEEHTS problem is rarely reported in literature so far.

This paper presents an improved GSA to solve SEEHTS problem. In order to enhance the performance of GSA, particle individual memory character and group social information are introduced to update velocity. And a mutation procedure based on chaotic behavior is used in the improved gravitational search algorithm (IGSA). Moreover, in the presented method, a modification strategy by dividing the violation water volume into several parts and randomly selecting intervals to adjust the water discharge gradually is proposed to handle the water dynamic balance constraints. A new strategy is adopted to meet the reservoir storage volumes limit constraints. Based on the violations of the reservoir storages, it adjusts the water discharge of the hydroplant at previous time intervals in feasible region. Meanwhile, it modifies the equal amount to the corresponding discharge at the later time intervals to keep water dynamic balance. A strategy based on adjusting the output of the thermal power plants according to their priority index is also applied to handle system load balance constraints effectively. To make the particles always move towards the optimum solution, the proposed method adopts a selection operation based on a greedy rule in population evolution. Finally, in order to show IGSA is effective for solving SEEHTS problem, the proposed approach is tested on a sample system with four cascaded hydroplants and three thermal plants (Basu 2004). Simulation results obtained by IGSA are compared with the results of quantum PSO (Sun and Lu 2010), quadratic approximation based differential evolution (Lu and Sun 2011), fuzzy satisfying evolutionary programming (Basu 2004) and differential evolution (Mandal and Chakraborty 2009) in the literatures, and IGSA gets less fuel cost and smaller pollution emission. It is found that the IGSA is more powerful and effective than other algorithms for solving SEEHTS problem.

This paper is organized as follows: Section 2 provides the mathematical formulation of SEEHTS problem. Section 3 describes the standard GSA and the proposed IGSA. Section 4 presents the IGSA for solving SEEHTS problem in detail. Section 5 gives the numerical example. Section 6 outlines the conclusions and future work. Finally, acknowledgments are given.

2 Problem formulation of SEEHTS

The SEEHTS problem is a bi-objective optimization problem. It is aimed to minimize both the fuel cost and emission of thermal plants while making full use of the availability of hydro resources under various constraints of the systems in the scheduling period. The formulation of the SEEHTS problem is expressed as follows.

2.1 Objective functions

2.1.1 Minimization of fuel cost

The minimization objective of the total fuel cost produced by the thermal plants in the scheduling horizon can be defined by Eq. (1):

$$\begin{aligned} F=\min \sum \limits _{k=1}^T {\sum \limits _{i=1}^{N_s } {f\left( {P_{si}^k }\right) } } \end{aligned}$$
(1)

where \(F\) is the total fuel cost; \(f( {P_{si}^k })\) is the fuel cost function of thermal plant \(i\) including valve-point loading effects; \(P_{si}^k \) is the power generation of thermal unit \(i\) at time interval \(k\); \(N_s \) is the number of thermal plants; \(T\) is the total time intervals over scheduling horizon.

The fuel cost function of a thermal plant with a consideration of valve-point is described by Eq. (2) as follows:

$$\begin{aligned} f\left( {P_{si}^k }\right)&=a_{si} +b_{si} P_{si}^k +c_{si} \left( {P_{si}^k }\right) ^2 \nonumber \\&\quad +\left| {e_{si} \times \sin \left\{ {f_{si} \times \left( {P_{si}^{\min } -P_{si}^k }\right) } \right\} } \right| \end{aligned}$$
(2)

where \(a_{si},b_{si},c_{si},e_{si}, {f_{si} }\) are the fuel cost coefficients of thermal plant \(i\); \(P_{si}^{\min } \) is the minimum power generation limit of thermal plant \(i\).

2.1.2 Minimization of emission

The minimization objective of total emission amount released by the thermal plants during the scheduling period is defined by Eq. (3):

$$\begin{aligned} E=\min \sum \limits _{k=1}^T {\sum \limits _{i=1}^{N_s } {e\left( {p_{si}^k }\right) } } \end{aligned}$$
(3)

where \(E\) is the total emission amount; \(e( {p_{si}^k })\) is the emission function of thermal plant \(i\).

The emission function of each thermal plant can be described as the sum of a quadratic and an exponential function:

$$\begin{aligned} e\left( {p_{si}^k }\right)&=\alpha _{si} +\beta _{si} P_{si}^k +\gamma _{si}\left( {p_{si}^k }\right) ^2 \nonumber \\&\quad +\eta _{si} \exp \left( {\delta _{si} \times p_{si}^k }\right) \end{aligned}$$
(4)

where \(\alpha _{si},\;\beta _{si},\;\gamma _{si},\;\eta _{si} ,\;\delta _{si} \) are the emission coefficients of thermal plant \(i\).

2.1.3 Bi-objective function of SEEHTS problem

The SEEHTS is a bi-objective problem which considers both minimizing fuel cost and minimizing pollutant emission of thermal plants simultaneously. The fuel cost \(f(P_{si}^k )\) is evaluated in $ and the emission amount \(e(P_{si}^k )\) of thermal plants is measured in lb. As the two functions are calculated in different units, the objective of total operational cost cannot sum the fuel cost and emission amount simply. By introducing variable weights \(h_k \) (Kulkarni et al. 2000) based on the time interval, the bi-objective optimization problem can be converted to a single objective one, which is defined by Eq. (5) as follows:

$$\begin{aligned} \mathrm{TC}=\min \sum \limits _{k=1}^T {\sum \limits _{i=1}^{N_s} {\left( {f\left( P_{si}^k \right) +h_k \cdot e\left( P_{si}^k \right) }\right) } } \end{aligned}$$
(5)

where TC is the total operational cost of the hydrothermal system and \(h_k \) is the variable weight during time \(k\).

In Eq. (5), the weight of fuel cost is set as 1 all through the scheduling time, and \(h_k \) is a ratio determined according to the fuel cost and emission properties of thermal plants and system load. By using the variable weight \(h_k\), the emission amount can be calculated as some operation cost of the system. The two different objectives are converted into a single one to optimize the total operational cost of the hydrothermal system. The process to calculate \(h_k \) can be described briefly as follows:

  1. 1.

    Calculate the ratio \(\lambda _{ik} \) between the fuel cost and emission of each thermal plant at its maximum power output.

    $$\begin{aligned} \lambda _{ik} =\frac{f(P_{si}^{\max } )}{e(P_{si}^{\max } )}\quad i=1,2,\ldots ,N_s. \end{aligned}$$
    (6)
  2. 2.

    Arrange the thermal plants according to the value of \(\lambda _{ik} \) in ascending order.

  3. 3.

    Add the maximum output \(P_{si}^{\max } \) of thermal plants starting from the unit with the smallest \(\lambda _{ik} \), until \(\sum \nolimits _{i=1}^{Ns} {P_{si}^{\max } \ge P_D^k } \) is reached. Where \(P_D^k \) is the system load demand at time interval \(k\).

  4. 4.

    The \(\lambda _{ik} \) belonging to the last thermal plants in the process is chosen as \(h_k \) for the system load at time interval \(k\).

From the description above, it is clear that the value of \(h_k \) is dependent on the system load at each time interval and hence it is variable in the scheduling period.

2.2 Constraints

  1. 1.

    System load balance constraints

    $$\begin{aligned} \sum \limits _{i=1}^{N_s } {P_{si}^k } +\sum \limits _{j=1}^{N_h } {P_{hj}^k } -P_D^k =0 \end{aligned}$$
    (7)

    where \(P_D^k \) is the system load demand at time interval \(k\); \(P_{hj}^k \) is the power generation of hydroplant \(j\) at time interval \(k\); \(N_h \) is the number of hydroplants. The hydropower generation is a function of water discharge rate and reservoir storage volume, which can be expressed as follows:

    $$\begin{aligned} P_{hj}^k&= C_{1j} \left( {V_j^k }\right) ^2+C_{2j} \left( {Q_j^k }\right) ^2+C_{3j} V_j^k Q_j^k \nonumber \\&+C_{4j} V_j^k +C_{5j} Q_j^k +C_{6j} \end{aligned}$$
    (8)

    where \(C_{1j},\;C_{2j},\;C_{3j},\;C_{4j},\;C_{5j},\;C_{6j} \) are the power generation coefficients of hydroplant \(j\); \(V_j^k \) is the water volume of reservoir \(j\) at time interval\( k\); \(Q_j^k \) is the water discharge of hydroplant \(j\) at time interval \(k\).

  2. 2.

    Thermal plant power generation limits

    $$\begin{aligned} P_{si}^{\min } \le P_{si}^k \le P_{si}^{\max } \end{aligned}$$
    (9)

    where \(P_{si}^{\min },\;P_{si}^{\max } \) are minimum and maximum power generation limits of thermal plant \(i\) respectively.

  3. 3.

    Hydroplant power generation limits

    $$\begin{aligned} P_{hj}^{\min } \le P_{hj}^k \le P_{hj}^{\max } \end{aligned}$$
    (10)

    where \(P_{hj}^{\min },\;P_{hj}^{\max } \) are minimum and maximum power generation limits of hydroplant \(j\), respectively.

  4. 4.

    Reservoir storage volumes limits constraints

    $$\begin{aligned} V_j^{\min } \le V_j^k \le V_j^{\max } \end{aligned}$$
    (11)

    where \(V_j^{\min },\;V_j^{\max } \) are minimum and maximum water storage volumes of reservoir \(j\).

  5. 5.

    Hydroplant discharge limits constraints

    $$\begin{aligned} Q_j^{\min } \le Q_j^k \le Q_j^{\max } \end{aligned}$$
    (12)

    where \(Q_j^{\min },\;Q_j^{\max } \) are minimum and maximum water discharge limits of hydroplant \(j\).

  6. 6.

    Water dynamic balance constraints

    $$\begin{aligned} V_j^k&= V_j^{k-1} +I_j^k -Q_j^k -S_j^k \nonumber \\&+\sum \limits _{m=1}^{R_{uj} } {\left( {Q_m^{k-\tau _{mj} } +S_m^{k-\tau _{mj} } }\right) } \end{aligned}$$
    (13)

    where \(I_j^k \) is the inflow of hydro reservoir \(j\) at time interval \(k\); \(S_j^k\) is the water spillage of hydroplant \(j\) at time interval \(k\); \(\tau _{mj} \) is the water transport delay from reservoir \(m\) to \(j\); \(R_{uj} \) is the number of upstream hydroplants above reservoir \(j\).

  7. 7.

    Initial and final reservoir storage volumes constraints

    $$\begin{aligned} V_j^0 =V_j^{\mathrm{begin}},\;V_j^T =V_j^{\mathrm{end}} \end{aligned}$$
    (14)

    where \(V_j^{\mathrm{begin}} \) is the initial water storage volume of reservoir \(j\); \(V_j^{\mathrm{end}} \) is the final water storage volume of reservoir \(j\) at the end of scheduling period.

3 Gravitational search algorithm

3.1 Standard GSA

Gravitational search algorithm is a novel heuristic optimization algorithm based on Newton’s law of gravity proposed by Rashedi et al. (2009). In GSA, the solution to problem is expressed as the particle’s position. The performances of particles are measured by their masses, the particles with higher fitness values have heavier masses. Due to the gravity force, all particles attract the others and they move towards heavier particles. The movement of particles follows Newton’s law of motion, the heavier particles move slower and the lighter ones move faster. At last all the particles would move to the area near the heaviest one, which represents the optimum solution to the problem. The following describes the standard GSA briefly:

Without loss of generality, it assumes that an optimization problem can be expressed as:

$$\begin{aligned} \mathop {\min }\limits _{X\in R^D}f( X). \end{aligned}$$

The particle’s position represents the solution to the optimization problem. The position of particle \(i\) is defined as:

$$\begin{aligned} X_i =\left( x_i^1,\ldots x_i^d,\ldots ,x_i^D \right) ,\quad i=1,2,\ldots ,\mathrm{NP}, \end{aligned}$$
(15)

where \(n\) is the dimension of the problem and \(x_i^d \) is the position of particle \(i\) in the \(d\)th dimension, NP is the number of the populations.

At time \(t\) the gravitational force acting on particle \(i\) from particle \(j\) is defined as follows:

$$\begin{aligned} F_{ij}^d (t)=G(t)\frac{M_i (t)\times M_j (t)}{R_{ij} (t)+\varepsilon }\left( {x_j^d (t)-x_i^d (t)}\right) \end{aligned}$$
(16)

where \(M_i (t)\) and \(M_j (t)\) are masses of particle \(i\) and \(j\); \(\varepsilon \) is a small constant; and \(R_{ij} (t)\) is the Euclidean distance between particle \(i\) and \(j\) described as follows:

$$\begin{aligned} R_{ij} (t)=\left\| {X_i (t),X_j (t)} \right\| _2. \end{aligned}$$
(17)

\(G(t)\) is the gravitational constant at time \(t\) defined as follows:

$$\begin{aligned} G(t)=G_0 \;\exp (-\alpha t/t_{\max }) \end{aligned}$$
(18)

where \(G_0 \) is the initial value of the gravitational constant; \(\alpha \) is a constant to control the decay rate of \(G(t)\); \(t\) is the current iteration; \(t_{max}\) is the total number of iteration.

The total force acting on particle \(i\) in dimension \(d\) at time \(t\) is described as follows:

$$\begin{aligned} F_i^d (t)=\sum \limits _{j \in \mathrm{kbest}, j\ne i}^{\mathrm{NP}} {\mathrm{rand}_j F_{ij}^d (t)} \end{aligned}$$
(19)

where kbest is set of first \(k\) particles which have the better fitness value and heavier mass, kbest(\(t)\) ’s initial value is the population number NP, which express that all the particles attract each other. And the final value of it is a small integer, which express that only a few heavier particles attract the others at last. rand\(_j\) is a random number between 0 and 1.

The masses of the agents are calculated by their fitness values. In GSA, the masses are updated as follows:

$$\begin{aligned} m_i (t)=\frac{\mathrm{fit}_i (t)-\mathrm{worst}(t)}{\mathrm{best}(t)-\mathrm{worst}(t)} \end{aligned}$$
(20)
$$\begin{aligned} M_i (t)=\frac{m_i (t)}{\sum \nolimits _{j=1}^N {m_i (t)} } \end{aligned}$$
(21)

where \(\mathrm{fit}_i (t)\) is the fitness value of particle \(i\) at time \(t\). \(\mathrm{best}(t)\) and \(\mathrm{worst}(t)\) are the minimum fitness and maximum fitness of all the particles. They are defined as follows:

$$\begin{aligned} \mathrm{best}(t)=\mathop {\min }\limits _{j\in \left\{ {1,2,\ldots ,N} \right\} } \mathrm{fit}_j (t) \end{aligned}$$
(22)
$$\begin{aligned} \mathrm{worst}(t)=\mathop {\max }\limits _{j\in \left\{ {1,2,\ldots ,N} \right\} } \mathrm{fit}_j (t). \end{aligned}$$
(23)

According to the laws of motions, the acceleration of the particle \( i\) in dimension \(d\) at time \(t\) is described as follows:

$$\begin{aligned} a_i^d (t)=\frac{F_i^d (t)}{M_i (t)}. \end{aligned}$$
(24)

In GSA, the particle \(i\) would updates its position and velocity in each iteration as follows:

$$\begin{aligned}&v_i^d (t+1)=\mathrm{rand}_i \times v_i^d (t)+a_i^d (t)\end{aligned}$$
(25)
$$\begin{aligned}&x_i^d (t+1)=x_i^d (t)\times v_i^d (t+1) \end{aligned}$$
(26)

where \(\mathrm{rand}_i \) is a random number in range of [0, 1]; \(v_i^d (t)\) is the velocity and \(x_i^d (t)\) is the position of the particle \(i\) in the \(d\)th dimension at time \(t\).

3.2 Improved GSA

In standard GSA, the optimization solution is obtained by the particles movement based on the attraction of other particles. The particle with better fitness value is heavier and has a bigger attraction to others. The attractions make the population move towards the optimum solution. But in the velocity update procedure only the gravitational force from particles works, it lacks the memory of the best position of particle and sharing of social information. And the particle may move to a worse position by the attraction force, which makes the convergence of algorithm slower. Due to the characters of SEEHTS problem and its various constraints, there are many local optimum solutions which standard GSA is easy to fall into. In order to improve the performance of the method for SEEHTS problem, this paper proposes IGSA, which uses particle memory character and population social information to update velocity. And taking advantage of ergodicity and stochastic property of chaotic behavior, a chaotic mutation procedure is introduced into IGSA to enhance the ability to search the global optimum solution. Moreover, this approach adopts the selection operation based on a greedy rule in population evolution to insure the particles always evolve to better ones.

3.2.1 Velocity update based on particle memory character and population social information

In standard GSA, the moving direction of a particle is based on the total force provided by other particles. Only the current position of the particle plays a role in the velocity and position update procedure, it does not make full use of the particle memory character and population social information. Inspired by the PSO algorithm, this paper introduces the particle memory character and population social information to GSA, the improved rules of motion are based on the new strategy: the movement not only obeys Newton’s law of motion, and also takes the particle memory and sharing of social information into account. The memory means the best position \(\mathrm{Pbest}_i =(\mathrm{pbest}_i^1,\ldots ,\mathrm{pbest}_i^d,\ldots ,\mathrm{pbest}_i^D )\) where particle \(i\) has reached so far, and social information means the global best position \(\mathrm{Gbest}_i =(\mathrm{gbest}^1,\ldots ,\mathrm{gbest}^d,\ldots ,\mathrm{gbest}^D)\) where all the particles have reached so far. The velocity update equation is redefined as follows:

$$\begin{aligned} v_i^d (t+1)&= \mathrm{rand}_1 \times v_i^d (t)+a_i^d (t) \nonumber \\&+c_1 \times \mathrm{rand}_2 \times \left( \mathrm{pbest}_i^d (t)-x_i^d (t)\right) \nonumber \\&+c_2 \times \mathrm{rand}_3 \times \left( \mathrm{gbest}^d(t)-x_i^d (t)\right) \end{aligned}$$
(27)
$$\begin{aligned}&x_i^d (t+1)=x_i^d (t)+v_i^d (t+1)\nonumber \\&\quad i=1,2,\ldots ,\mathrm{NP} \quad d=1,2,\ldots ,D \end{aligned}$$
(28)

where \(\mathrm{rand}_1 \), \(\mathrm{rand}_2 \) and \(\mathrm{rand}_3 \) are random numbers which obey uniform distribution in the range [0–1]; \(c_{1}\) and \(c_{2}\) are constants; \(\mathrm{pbest}_i^d (t)\) is the best position in dimension \(d\) where the particle \(i\) has reached at time \(t\); \(\mathrm{gbest}^d(t)\) is the best position in dimension \(d\) where all particles have moved to at time \(t\). By changing the value of \(c_{1}\) and \(c_{2}\), it can balance the impact of gravity with the impact of memory and social information on the performance of IGSA.

3.2.2 Mutation operator based on chaotic behavior

Although GSA has a strong ability in exploration, there is still some room for enhancing the exploitation capacity in local space. Similar to other optimization algorithms, GSA has shortcomings of premature convergence. Because of the ergodicity and stochastic property of chaotic behavior, it can improve the performance of GSA in searching the global optimum solution by utilizing the chaotic mutation operator. This paper introduces a chaotic mutation operator after the velocity update procedure. By mutating the best particle based on chaotic sequences, it enlarges the search space of the approach from the region near the local optimum solution to the global space, which can overcome premature convergence of GSA. To ensure the mutation operator would not make the fitness of populations worse, only if the new particle created by mutation is better than the worst particle in populations, it will replace the worst one in next generation.

In this paper, the chaotic sequence is based on logistic map, which is one of the simplest dynamic systems evidencing chaotic behavior (Yuan et al. 2008b). In the reference, the chaotic behavior has been applied in combination with PSO algorithm to improve the performance successfully. The logistic map can be described as Eq. (29):

$$\begin{aligned} y(t+1)=\mu \cdot y(t)\cdot ( {1-y(t)})\quad y(t)\in (0,1) \end{aligned}$$
(29)

where \(\mu \) is a control parameter. And if \(\mu =4\), the sequence would be in chaotic state and the generated value will traverse from 0 to 1. At the beginning of iteration, \(y(0)\) is randomly generated in [0, 1] and \(y(0)\notin \left\{ {\left. {0,\;0.25,\;0.5,\;0.75,\;1} \right\} } \right. \).

The chaotic mutation operator procedure is described as follows:

  1. 1.

    Create a new particle \(X_{\mathrm{new}} =( {x_{\mathrm{new}}^1,\ldots ,x_{\mathrm{new}}^d,\ldots ,x_{\mathrm{new}}^D })\) and let it be the best particle Gbest in populations as: \(X_{\mathrm{new}} =\mathrm{Gbest}\).

  2. 2.

    Set mutation iteration count \(g=0\).

  3. 3.

    Convert the position of \(X_{\mathrm{new}} \) in the \(d\)th dimension of search space to the range of [0, 1] to generate the initial chaotic variables as follows:

    $$\begin{aligned} \xi ^d(0)=\frac{x_{\mathrm{new}}^d -x_{\min }^d }{x_{\max }^d -x_{\min }^d }\quad d=\text{1 },\text{2 },\ldots ,D. \end{aligned}$$
    (30)

    where \(x_{\min }^d \) and \(x_{\max }^d \) are the minimum and maximum limit of \(X_{\mathrm{new}} \) in \(d\) dimension. As the description above the chaotic variable vector \({{\mathbf {\xi }}}(0)=(\xi ^1(0),\ldots ,\xi ^d(0),\ldots \xi ^D(0))\) is obtained.

  4. 4.

    Compute the chaotic variable vector \(\mathrm{\mathbf{\xi }}(g+1)\) in next iteration according to logistic map as follows:

    $$\begin{aligned} \xi ^d(g+1)=4\cdot \xi ^d(g)\cdot ( {1-\xi ^d(g)}). \end{aligned}$$
    (31)
  5. 5.

    Update the position of the new mutated particle in \(d\)th dimension by the chaotic variable \(\xi ^d(g+1)\) as follows:

    $$\begin{aligned}&x_{\mathrm{new}}^d =x_{\min }^d +\xi ^d(g+1)\cdot (x_{\max }^d -x_{\min }^d)\nonumber \\&\quad d=\text{1 },\text{2 },\ldots ,D. \end{aligned}$$
    (32)
  6. 6.

    After the new positions in all \(D\) dimensions are generated, the new mutated particle \(X_{\mathrm{new}} \) is obtained.

  7. 7.

    If the new mutated particle \(X_{\mathrm{new}} \) has a better fitness than the worst particle Gworst at \(t \) iteration, replace Gworst by \(X_{\mathrm{new}} \) in next generation. Where Gworst is the particle with the worst fitness value in current population.

  8. 8.

    If the maximum iteration gmax is not reached, set \(g=g+1\) and go to (4) to continue the next iteration. Else if \(g=\hbox {gmax}\), the chaotic mutation procedure is over.

3.2.3 Population evolution based on selection operation

In standard GSA, the particle may move to a worse position by the gravitational force. In order to ensure the population evolution is toward the optimum solution throughout, this paper adopts a greedy selection operation based on the rule of elimination similar to differential evolution (Yuan et al. 2008a). This method compares the fitness of the moved particle with fitness of the current particle correspondingly. If the moved particle has a better fitness than the current one, the moved particle would replace the current one as a member in the next generation. On the contrary, if the moved particle is worse than the current one, the current one would be kept in the next generation. The selection operation is described as follows:

Firstly, according to the improved velocity update Eqs. (27) and (28), compute the position in each dimension of the particle \(i\) after moving.

The moved particle \({\overset{\frown }{X}}_i (t+1)\) can be expressed as:

$$\begin{aligned}&{\overset{\frown }{X}}_i (t+1)=\left( x_i^1 (t+1),\ldots ,x_i^d (t+1),\ldots ,x_i^D (t+1)\right) , \nonumber \\&\quad d=\text{1 },\text{2 },\ldots ,D. \end{aligned}$$
(33)

Then adopt the selection operation based on elimination rule to update population:

$$\begin{aligned}&X_i (t+1)\nonumber \\&=\left\{ {{\begin{array}{*{20}l} {{\overset{\frown }{X}}_i (t+1)} &{}\quad {\mathrm{if}\;f\left( {\overset{\frown }{X}}_i (t+1))<f(X_i (t)\right) } \\ {X_i (t)} &{}\quad \mathrm{otherwise} \end{array} }} \right. . \end{aligned}$$
(34)

After all the particles and the corresponding moved ones are compared and selected, the selection operation is finished and the new generation is created.

4 IGSA for solving SEEHTS problem

In this section, the procedures of the proposed IGSA for solving SEEHTS problem are explained in detail. Especially, rules will be given to handle the various constraints of the problem. The processes can be described as follows:

4.1 Structure of individual

For the SEEHTS problem, the decision variables are water discharges \(Q_j^k \) of the hydroplants and power generations \(P_{si}^k \) of thermal plants at each time interval. The structure of individual is composed of those decision variables. It is defined as follows:

$$\begin{aligned}&X_a = \left( \begin{array}{l} {{\begin{array}{*{20}c} {Q_1^1 } &{} {,\ldots ,} &{} {Q_j^1 } &{} {,\ldots ,} &{} {Q_{N_h }^1,} &{} {P_{s1}^1 } &{} {,\ldots ,} &{} {P_{si}^1 } &{} {,\ldots ,} &{} {P_{sN_s }^1 } \\ \vdots &{} \ldots &{} \vdots &{} \ldots &{} \vdots &{} \vdots &{} \ldots &{} \vdots &{} \ldots &{} \vdots \\ {Q_1^k } &{} {,\ldots ,} &{} {Q_j^k } &{} {,\ldots ,} &{} {Q_{N_h }^k,} &{} {P_{s1}^1 } &{} {,\ldots ,} &{} {P_{si}^k } &{} {,\ldots ,} &{} {P_{sN_s }^k } \\ \vdots &{} \ldots &{} \vdots &{} \ldots &{} \vdots &{} \vdots &{} \ldots &{} \vdots &{} \ldots &{} \vdots \\ {Q_1^T } &{} {,\ldots ,} &{} {Q_j^T } &{} {,\ldots ,} &{} {Q_{N_h }^T,} &{} {P_{s1}^T } &{} {,\ldots ,} &{} {P_{si}^T } &{} {,\ldots ,} &{} {P_{sN_s }^T } \\ \end{array} }} \\ \end{array}\right) \nonumber \\&a=1,2,\ldots ,\mathrm{NP}. \end{aligned}$$
(35)

4.2 Initialization individuals

In the initialization process, each initial individual is obtained by creating all the decision variables randomly in feasible range. The equation of initialization is defined as follows:

$$\begin{aligned}&Q_j^k =Q_j^{\min } +\mathrm{rand}_h \times \left( Q_j^{\max } -Q_j^{\min } \right) \end{aligned}$$
(36)
$$\begin{aligned}&P_{si}^k =P_{si}^{\min } +\mathrm{rand}_s \times \left( P_{si}^{\max } -P_{si}^{\min } \right) \end{aligned}$$
(37)

where \(\mathrm{rand}_h \) and \(\mathrm{rand}_s \) are random numbers uniformly distributed in range [0–1].

4.3 Rules to handle constraints of SEEHTS problem

In the process of solving the SEEHTS problem with IGSA, the initial and renewed solutions of individuals may not satisfy various constraints of the problem. The rules to handle the various constraints can be summarized as follows:

4.3.1 Handling water dynamic balance constraints

To deal with the water dynamic balance constraints, this paper adopts a randomly adjustment strategy, which divides the violation water volume into several parts and randomly selects intervals to adjust the water discharge gradually.

Assume the water spillage in Eq. (13) is zero. Based on the Eqs. (13) and (14), we can get the differences between the total water discharge volume and the water volume available in restriction of hydroplant \(j\) during the schedule horizon, which can be described as follows:

$$\begin{aligned} \Delta Q(j)&= V_j^{\mathrm{begin}} -V_j^{\mathrm{end}} +\sum \limits _{k=0}^T {I_j^k } +\sum \limits _{m=1}^{Ru} \sum \limits _{k=1}^T {Q_m^{k-\tau _{mj} } }\nonumber \\&-\sum \limits _{k=0}^T {Q_j^k } . \end{aligned}$$
(38)

And then divide the water volume differences into num parts, select a time interval \(l\) randomly to adjust the water discharge in feasible region. Repeat the selection and adjustment procedure until the equality constraint is satisfied. The procedures for handling water dynamic balance constraint of hydroplant \(j\) are given as follows:

Step 1::

Calculate the differences between the total water discharge volume and the water volume available in restriction of hydroplant \(j\) by (38). Set num = 30, count = 0. And the average water adjustment volume is calculated by:

$$\begin{aligned}&\mathrm{Avg}Q=\Delta Q(j)/\mathrm{num}. \end{aligned}$$
Step 2::

Select a time interval \(l\) randomly.

Step 3::

Adjust the water discharge in \(l\) interval to satisfy the constraint. Calculate \({\overset{\frown }{Q}}_j^1 =Q_j^1 +\mathrm{Avg}Q,\) if \(Q_j^{\min } \le Q_j^1 \le Q_j^{\max }\), then let \(Q_j^l =\widehat{Q}_j^l \), count = count + 1. If the modified discharge \(\widehat{Q}_j^l \) cannot satisfy the constraint (12), then select another new interval to adjust randomly.

Step 4::

If count \(<\) num, go to step 2, if count = num, go to next step.

Step 5::

The procedures of handling water dynamic balance constraints are over.

4.3.2 Handling reservoir storage volumes limit constraints

The modified discharge sequences have satisfied water dynamic balance constraints, but the reservoir storage volumes at each time interval \(V_j^k \) may violate the constraint (11). Assume the water spillage in Eq. (13) is zero, the reservoir storage volumes can be calculated by (13) and (14).

This paper proposes a new strategy to handle reservoir storage volumes limit constraints. It picks out the storage volumes which violate the constraints and calculates the violation of them. And then based on the violations, it adjusts the water discharge of the hydroplant at current and previous time interval in feasible region to satisfy the constraint (11). That is to say, if \(V_j^k <V_j^{\min } \), reduce the discharge \(Q_j^{k-1} \) in previous interval \(k-1\) and correspondingly add the same amount to discharge \(Q_j^k \) in current interval \(t\), which can increase the volume \(V_j^k \) to satisfy the constraint (11); if \(V_j^k >V_j^{\max } \), add \(Q_j^{k-1} \) and correspondingly subtract the same amount to \(Q_j^k \), which decrease the volume \(V_j^k \) to satisfy the constraint (11). And if the violation water volume cannot be adjusted in one time interval, the adjustment will be used in previous time intervals until the constraints are satisfied. Because the strategy has not changed the total discharges of hydroplant in whole schedule period, it can modify the discharge sequences to satisfy the reservoir storage volumes limit constraints without break water dynamic balance. The procedures for handling the reservoir storage volumes limit constraints of hydroplant \(j\) are described as follows:

Step 1::

Set \(k=1\).

Step 2::

Calculate the storage volume \(V_j^k \) of reservoir \(j\) at time interval \(t\), if \(V_j^k \) satisfies the constraint (11), go to step 10. If \(V_j^k \) violates (11), go to step 3.

Step 3::

If \(V_j^k >V_j^{\max } \), go to step 4. If \(V_j^k <V_j^{\max } \), go to step 7.

Step 4::

Calculate the adjust amount \(\Delta Q\) according to the violations by

$$\begin{aligned}&\Delta Q=\left( V_j^k -V_j^{\max } \right) /\Delta k \end{aligned}$$

where \(\Delta k\) is the time span during one time interval. Set \(Q_j^{k-1} =Q_j^{k-1} +\Delta Q,Q_j^k =Q_j^k -\Delta Q\). If the adjusted discharge \(Q_j^{k-1},\;Q_j^k \) satisfy constraint (12), then go to step 10. Else if \(Q_j^{k-1} >Q_j^{\max } \) or \(Q_j^k >Q_j^{\min } \), go to step 5.

Step 5::

If \(Q_j^{k-1} >Q_j^{\max } \). And if \(k=1\), means there is no room to adjust the discharges to previous time interval according to the proposed strategy, go to step 10, else calculate \(\Delta Q_1 =\Delta Q-(Q_j^k -Q_j^{\max } )\), set\(Q_j^{k-1} =Q_j^{\max } ,\;Q_j^{k-2} =Q_j^{k-2} +\Delta Q_1 \), it means to adjust the water discharge violating constraint (12) to the discharge before time interval \(k-1\). If \(Q_j^{k-2} =Q_j^{\max } \), adjust the discharge \(Q_j^{k-2} \) similarly as step5. Else due to the water storage at time \(k-1\) has changed, let \(k=k-1\), go to step 2.

Step 6::

If \(Q_j^k =Q_j^{\max } \). And if \(k=T-1\), means there is no room to adjust the discharges to latter time interval according to the proposed strategy, go to step 11, else calculate \(\Delta Q_2 =\Delta Q-(Q_j^{\min } -Q_j^k )\), set \(Q_j^k =Q_j^{\min },\;Q_j^{k+1} =Q_j^{k+1} 0-\Delta Q_2 \), means to adjust the water discharge violating constraint (12) to the discharge after time interval \(k\). If \(Q_j^{k+1} <Q_j^{\max }\), adjust the discharge \(Q_j^{k+1} \) similarly as step 6. Else go to step 10.

Step 7::

Calculate the adjust amount according to the violations by

$$\begin{aligned}&\Delta Q=\left( V_j^{\min } -V_j^k \right) /\Delta k. \end{aligned}$$

Set \(Q_j^{k-1} =Q_j^{k-1} -\Delta Q,\;Q_j^k =Q_j^k +\Delta Q\). If the adjusted discharge \(Q_j^{k-1} \), \(Q_j^k \) satisfy constraint (12), and then go to step 10. Else if \(Q_j^{k-1} <Q_j^{\min } \) or \(Q_j^k >Q_j^{\max } \), go to step 8.

Step 8::

If \(Q_j^{k-1} <Q_j^{\min } \). And if \(k=1\), means there is no room to adjust the discharges to previous time interval according to the proposed strategy, go to step 10, else calculate \(\Delta Q_2 =\Delta Q-(Q_j^{\min } -Q_j^{k-1} )\), set \(Q_j^{k-1} =Q_j^{\min } ,\;Q_j^{k-2} =Q_j^{k-2} -\Delta Q_2 \), it means to adjust the water discharge violating constraint (12) to the discharge before time interval \(k-1\). If \(Q_j^{k-2} <Q_j^{\min } \), adjust the discharge \(Q_j^{k-2} \) similarly as step8. Else due to the water storage at time \(k-1\) has changed, let \(k=k-1\), go to step 2.

Step 9::

If\(Q_j^k >Q_j^{\max } \). And if \(k=T-1\), means there is no room to adjust the discharges to latter time interval according to the proposed strategy, go to step 11, else calculate \(\Delta Q_1 =\Delta Q-(Q_j^k -Q_j^{\max } )\), set \(Q_j^k =Q_j^{\max } ,\;Q_j^{k+1} =Q_j^{k+1} -\Delta Q_1 \), it means to adjust the extra water violating constraint (12) to the discharge after time interval \(k\). If \(Q_j^{k+1} >Q_j^{\max } \), adjust the discharge \(Q_j^{k+1} \) similarly as step 9. Else go to step 10.

Step 10::

If \(k < T\), set \(k=k+1\), go to step 2. If \(k = T\), go to next step.

Step 11::

The adjustment procedures are over.

On the basis of the rules described above, handle the constraints of the cascade hydroplants from upstream to downstream, the discharge sequences can be modified to satisfy the water dynamic balance constraints and reservoir storage volumes limit constraints.

4.3.3 Handling system load balance constraints

After the procedures for handling the constraints of hydroplants, this paper uses a strategy by adjusting the output of the thermal power plants according to their priority index to handle system load balance constraints. System load balance constraints are defined as:

$$\begin{aligned} \sum \limits _{i=1}^{N_h } {P_{si}^k } +\sum \limits _{i=1}^{N_h } {P_{hf}^k } -P_D^k =0. \end{aligned}$$
(39)

Firstly, calculate the total power load demand of thermal plants \(P_S^k \) in restriction at time interval \(k\) as follows:

$$\begin{aligned} P_S^k =P_D^k -\sum \limits _{j=1}^{N_h } {P_{hj}^k }. \end{aligned}$$
(40)

Then, according to the priority index of thermal plants (Sun and Lu 2010), adjust the violation power of system load balance to the thermal plants.

Priority index is obtained according to the average fuel cost and emission of each thermal plant at its full load operating. The priority index \(\alpha _{ik} \) of thermal plant \(i\) at time interval \(k\) is defined as:

$$\begin{aligned} \alpha _{ik} =\frac{f( {P_{si}^{\max } })+h_k \times e( {P_{si}^{\max } })}{P_{si}^{\max } } \end{aligned}$$
(41)

where \(h_k \) is the variable weight during time interval \(k\) in Eq. (5).

During the whole scheduling horizon, the thermal plants are ranked by their priority index \(\alpha _{ik} \) in ascending order to get the priority list. In this list, thermal plant with the smaller \(\alpha _{ik} \) is arranged to adjust more power load. The procedures for handling system load balance constraints are described as follows:

Step 1::

Calculate the priority index \(\alpha _{ik} \) of each thermal plant in schedule period by (41), and rank them in ascending order to get the priority list.

Step 2::

Set \(k=1\).

Step 3::

Calculate the violations of system load balance in each time interval by:

$$\begin{aligned}&\Delta P^k=\sum \limits _{i=1}^{Ns} {P_{si}^k -P_S^k }. \end{aligned}$$
(42)
Step 4::

If \(\Delta P^k\) =0, go to step 13; if \(\Delta P^k<0\), go to step 5; if \(\Delta P^k>0\), go to step 9.

Step 5::

Set \(n=1\).

Step 6::

Select the thermal plant \(m\) with the smallest \(\alpha _{ik} \) in the priority list, set the output of thermal plant \(m\) at time interval \(k\) to be \(P_m^k =P_{sm}^{\max } \), and delete thermal plant \(m\) from the priority list.

Step 7::

Calculate the violations again by (42). If \(\Delta P^k>0\), set \(P_m^k =P_{sm}^{\max } -\Delta P^k\), then go to step 13. If \(\Delta P^k<0\), go to step 8.

Step 8::

Set \(n=n+1\), if \(n\le \quad N_{s}\), go to step 6; if \(n>N_{s}\), go to step 13.

Step 9::

Set \(n=1\).

Step 10::

Select the thermal plant \(m\) with the biggest \(\alpha _{ik} \) in the priority list, set the output of thermal plant \(m\) at time interval \(k\) to be\(P_m^k =P_{sm}^{\min } \), and delete thermal plant\( m\) from the priority list.

Step 11::

Calculate the violations again by (42). If\(\Delta P^k<0\), set \(P_m^k =P_{sm}^{\min } -\Delta P^k\), then go to step 13. If \(\Delta P^k>0\), go to step 12.

Step 12::

Set \(n=n+1\), if \(n\le N_{s}\), go to step 10; if \(n>N_{s}\), go to step 13.

Step 13::

Set \(k=k+1\), if \(k\le T\), go to step 3; if \(k>T\), go to step 14.

Step 14::

The procedures of handling system load balance constraints are over.

4.4 Calculate the sum of violation and fitness of individuals

Sometimes due to some reasons, which includes the inflow of upstream reservoirs is too large or too small, the outputs of hydroplants are too much or not enough, etc., the solution of individual after modified still violates the constraints such as reservoir storage volumes limits and system load balance etc. This paper checks the violation of the modified individuals. If the individual cannot satisfy the constraints after the constraints handling procedure, the violation will be calculated to be a criterion of the individual for evolutionary selection. The violation calculation takes hydroplant power generation limits (10) and reservoir storage volumes limits (11) into account.

With the volume of reservoir storage and the power generation of hydro in each time interval, we can calculate the violations of every individual by:

$$\begin{aligned} \mathrm{viol}V_j^k =\left\{ {{\begin{array}{ll} {V_j^{\min } -V_j^k } &{}\quad {\mathrm{if}\;V_j^k <V_j^{\min } } \\ 0 &{}\quad {\mathrm{if}\;V_j^{\min } \le V_j^k \le V_j^{\max } } \\ {V_j^k -V_j^{\max } } &{}\quad {\mathrm{if}\;V_j^k >V_j^{\max } } \\ \end{array} }} \right. \end{aligned}$$
(43)
$$\begin{aligned} \mathrm{viol}P_j^k =\left\{ {{\begin{array}{ll} {P_{hj}^{\min } -P_{hj}^k } &{}\quad {\mathrm{if}\;P_{hj}^k <P_{hj}^{\min } } \\ 0 &{}\quad {\mathrm{if}\;P_{hj}^{\min } \le P_{hj}^k \le P_{hj}^{\max } } \\ {P_{hj}^k -P_{hj}^{\max } } &{}\quad {\mathrm{if}\;P_{hj}^k >P_{hj}^{\max } } \\ \end{array} }} \right. . \end{aligned}$$
(44)

By the Eqs. (43) and (44), we can calculate the total violation Sumviol of the individual. If Sumviol = 0, the individual is feasible. The Sumviol of the individual is described as follows:

$$\begin{aligned} \mathrm{Sumviol}=\sum \limits _{k=1}^T {\left[ \mathrm{viol}V_j^k +\mathrm{viol}P_{hj}^k \right] }. \end{aligned}$$
(45)

According to the description above and the Eq. (5), the total violation Sumviol and the fitness value Fitness of individuals is calculated. Sumviol and Fitness are the criterions for comparing and selecting the individuals.

4.5 Update of \(M\), \(G\), Pbest, Gbest in IGSA

Select the best fitness value \(\mathrm{best}(t)\) and the worst fitness value \(\mathrm{worst}(t)\) of individuals in population, and then according to (20) and (21) update the mass of each individual. The gravitational constant \(G(t)\) is calculated by (18).

Due to the introduction of the particle memory character and population social information in velocity update of IGSA, the best previous position of each individual \(\mathrm{Pbest}_i (t)\) and the best position where all the particles have reached \(\mathrm{Gbest}(t)\) are also updated respectively.

The total gravity force acting on each individual and the acceleration are calculated using (19), (24). And according to the improved velocity update Eqs. (27) and (28), we can obtain the moved individual \({\overset{\frown }{X}}_i (t+1)\) which corresponding the current individual \(X_i (t)\) after move.

4.6 Chaotic mutation

According to the descriptions in Sect. 3.2.2, mutate the individual with best fitness value based on the chaotic behavior. If the mutated individual \(X_{\mathrm{new}} \) has a better fitness than the worst one \(Gworst\) in current generation, select \(X_{\mathrm{new}} \) to replace Gworst in next generation.

4.7 Individuals comparison and population evolution

Calculate the total violation Sumviol and the fitness value Fitness of the moved individuals \({\overset{\frown }{X}}_i (t+1)\), and compare the moved individual \({\overset{\frown }{X}}_i (t+1)\) with the current individual \(X_i (t)\). Only the moved individual \({\overset{\frown }{X}}_i (t+1)\) has a better performance than the current individual \(X_i (t)\) in solving the problem, the moved individual would replace the current one in next generation. Which guarantees new generation is better than the previous generation and the populations always evolve towards the optimization solution.

If the comparison result is in the three cases described as following, we can estimate \({\overset{\frown }{X}}_i (t+1)\) is better than \(X_i (t)\), and select \({\overset{\frown }{X}}_i (t+1)\) to be \(X_i (t+1)\) in next generation. Otherwise, \(X_i (t)\) is retained to be \(X_i (t+1)\) in new generation.

  1. 1.

    \(\mathrm{Sumviol}( {{\overset{\frown }{X}}_i (t+1)})\!=\!0\), \(\mathrm{Sumviol}( {X_i (t)})\!=\!0\), Fitness\(({{\overset{\frown }{X}}_i (t+1)})<\mathrm{Fitness}( {X_i (t)})\).

  2. 2.

    \(\mathrm{Sumviol}( {{\overset{\frown }{X}}_i (t+1)})=0,\;\mathrm{Sumviol}( {X_i (t)})>0\)

  3. 3.

    \(\mathrm{Sumviol}( {{\overset{\frown }{X}}_i (t+1)}){>}0\), \(\mathrm{Sumviol}( {X_i (t)}){>}0\), Sumviol\(( {\overset{\frown }{X}} _i(t+1))<\mathrm{Sumviol}({\overset{\frown }{X}} _i(t)).\)

4.8 The flow of using IGSA for solving SEEHTS problem

The procedure of using IGSA for SEEHTS problem is described as follows:

Step 1::

Initialize individuals and the parameters of IGSA, such as NP, \(G_{0}\), \(\alpha \), \(t_{\max }\), \(\mu \), \(c_{1}\) and \(c_{2}\).

Step 2::

Handle the constraints of the problem to the initial individuals, calculate the fitness value and total violation.

Step 3::

Update \(G(t)\), Pbest\(_{i}(t)\), Gbest\((t)\) in IGSA, and calculate the mass \(M_{i}(t)\) of each individual.

Step 4::

Calculate the total gravity force and the acceleration acting on each individual.

Step 5::

Update the velocity and position of each individual according to the improved velocity equation.

Step 6::

Modify the moved individuals using the constraints handling strategy, and calculate the fitness value and total violation of all individuals.

Step 7::

Operate chaotic mutation to the best individual, if the mutated individual is better than the worst one in population, replace the worst by the mutated individual.

Step 8::

Compare the current individual and the corresponding moved individual based on population evolution rules, select the better one to create the new generation.

Step 9::

If reaching the ending of iteration, stop and select the best individual as the optimization solution to the problem. Otherwise, repeat steps 3–8 until \(t_{\max }\) is reached.

5 Numerical example

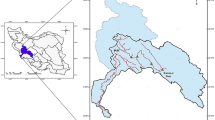
In order to verify the effectiveness of IGSA, this paper uses it to solve SEEHTS problem of hydrothermal system composed by a cascade of four hydroplants and three thermal plants. The scheduling period is 1 day, the time interval is chosen as 1 h which divides 1 day to 24 scheduling intervals. The hydro system configuration is shown in Fig. 1. The system loads at each time interval, coefficients of hydro and thermal plants, reservoir inflows and reservoir limits are taken from the reference (Basu 2004).

Fig. 1
figure 1

Hydraulic system network

Full size image

In order to find the optimum parameters setting of IGSA for SEEHTS problem, many trials have been applied. After a lot of trials and comparisons, the parameters with best results used in IGSA for this experiment are chosen as follows: \(G_{0}=110\), \(\alpha =10\), the initial and final value of Kbest are 70 and 2, respectively, \(c_{1}=1.0\), \(c_{2}=0.4\), \(\mu =4\). In order to compare with the results obtained by PSO, DE and other methods reported in the literatures, the population size \(\hbox {NP}=70\), the maximum iteration \(t_{\max }=400\). The experiment is performed on Microsoft Visual Studio 2008, 2 GB RAM, 2.20 MHz CPU.

Due to the randomness of heuristic optimization algorithm, the result obtained by IGSA in a single trial cannot be taken as the best solution. To test the stability and effectiveness of IGSA, this paper runs the experiment 20 times with different initial populations and the best compromise solution among these 20 trial results is selected as the best solution obtained. In the meanwhile, we apply standard GSA in the experiment with the same setting of parameters to illustrate the improvement achieved by IGSA compared with GSA. The results of fitness values of the 20 trial results obtained by IGSA and standard GSA are given in Table 1.

Table 1 The results of fitness values in 20 trials for SEEHTS problem
Full size table

As shown in Table 1, the minimum, average and maximum fitness value of IGSA in 20 trials are 104,731.87, 105,784.34 and 107,380.95 respectively, and the corresponding standard deviation is 805.67. It is clearly seen in Table 1 that IGSA obtains better quality solutions over standard GSA. In the 20 trials, IGSA can improve the minimum, average and maximum fitness value about 2.93, 3.26 and 2.49 % when compared to GSA.

In order to demonstrate that IGSA’s results are statistically better than those obtained by GSA, this paper performs a Wilcoxon signed-ranks test (García et al. 2009) for detecting significant differences between the performances of two algorithms. Firstly, we establish an assumption that there is no significant difference between the results of IGSA and those of GSA. Then, according to the 20 paired fitness values, the sum of ranks and the complement of the probability of reporting that two samples are the same, called the \(p\) value are computed and shown in Table 2.

Table 2 Wilcoxon test applied over the comparison between IGSA and GSA in fitness value
Full size table

From Table 2, it can be seen that the \(p\) value is 0.001. Choose the significance level \(\alpha =0.05\). Since \(p<0.05\), we can reject the previous assumption that two sample are the same and accept the opposite assumption, that there are significant differences between the performances of two algorithms. It is concluded that the performance of IGSA is statistically better than GSA.

The fuel cost and emission in 20 trials are calculated and given in Fig. 2. It is obvious in Fig. 2 that the variations of the cost and emission objectives of the 20 solutions are in small range. And for SEEHTS problem, the result in 18th trial is selected as the final optimization solution of IGSA, of which fuel cost is 43,299.89 $ and emission amount is 17,868.74 lb. From Fig. 2, it is clearly seen that the best solution gets the minimum fuel cost and the medium emission amount among 20 trial results. Compared to the other trial results, the obtained best solution reduces large fuel cost with a little compromise of emission. It reveals that the obtained best solution gets a best balance of minimizing both fuel cost and emission. The distribution of the fuel cost and emission of the 20 trial results in functional space is shown in Fig. 3. It is seen in Fig. 3 that the 20 independent executions are not non-dominated solutions, which indicates the need of multi-objective optimization approach as future research.

Fig. 2
figure 2

Fuel cost and emission in 20 trials obtained by IGSA for SEEHTS

Full size image
Fig. 3
figure 3

The distribution of the 20 solutions in functional space

Full size image

Variation of the fitness value of the best solution obtained with iteration numbers of IGSA and standard GSA for SEEHTS is shown in Fig. 4. It can be seen that the proposed IGSA has a smooth convergence curve and a fast convergence speed when dealing with SEEHTS problem. During the first 50 iterations, the fitness value of the best solution obtained decreases sharply. It is obvious that IGSA has strong convergence ability at the beginning of iterations. From the 50th iteration to the end of iterations, the fitness value decreases slowly and trends to be steady without any improvement, which means IGSA converges to the global optimization solution. The fitness value obtained by GSA decreases much slowly than those of IGSA during the evolutionary process, which results in the fitness value larger than those of IGSA at the end of iterations. It is apparent that IGSA has a better convergence property than standard GSA in solving SEEHTS problem.

Fig. 4
figure 4

Variation of the best fitness value with iteration numbers

Full size image

The water discharge and storage volume of hydroplants in each time interval during the schedule horizon are provided in Figs. 5 and 6, respectively. The power outputs of hydro and thermal plants are given in Table 3. From Figs. 5 and 6, it can be seen that the optimization solution satisfies the constraints of hydroplants strictly. In Table 3, the last column shows the sum of power outputs generated by thermal and hydroplants. From Table 3, we can see the thermal plant with the smaller priority index is dispatched more power load in system. And it is apparent that the power output of each plant in the hydrothermal system is in feasible region and the system load balance constraints are satisfied during the whole scheduling period.

Fig. 5
figure 5

Hourly hydroplant discharge for SEEHTS (\(\times \)10\(^{4}\) m\(^{3}\)/h)

Full size image
Fig. 6
figure 6

Hourly hydroplant storage for SEEHTS (\(\times \)10\(^{4}\) m\(^{3})\)

Full size image
Table 3 Power generations of hydro and thermal plants for SEEHTS
Full size table

The results obtained by proposed IGSA are compared with those of standard GSA, QPSO (Sun and Lu 2010), QADEVT (Lu and Sun 2011), EP (Basu 2004) and DE (Mandal and Chakraborty 2009) in Table 4. In the references above, the fitness evaluations are not given in the simulation results section. So the fitness evaluations of other methods in references are not presented in Table 4. The fuel cost and emission of the best solution provided by IGSA are 43,299.89 $ and 17,868.74 lb, respectively. From the comparison with GSA, QPSO, QADEVT, Fuzzy EP and DE, IGSA reduces the fuel cost about 1,557.54, 959.11, 95.11, 4,606.11 and 1,614.11$, respectively, during scheduling horizon, while the corresponding emission is decreased about 223.24, 360.26, 455.26, 8,455.26 and 1,746.26 lb in 1 day. In order to make the comparison result more visual, the distribution of the five non-dominated solutions of IGSA and solutions of other methods in functional space are shown in Fig. 7. It can be clearly seen from Fig. 7 that all the solutions of the previous references are dominated by at least one of the non-dominated solutions of IGSA. It is obvious that when dealing with the SEEHTS problem, IGSA obtains less fuel cost and smaller emission than all the other optimization algorithms in the references. It is clearly seen in the simulation results that, IGSA has a good performance to find optimum solutions and satisfy constraints completely for SEEHTS problem.

Table 4 Comparison of results obtained by IGSA with those of other methods
Full size table
Fig. 7
figure 7

The distribution of the non-dominated solutions of IGSA and solutions of other methods

Full size image

6 Conclusions and future work

In this paper, an IGSA with new constraints handling strategy has been proposed and applied to solve SEEHTS problem successfully. The main improvements of the proposed method are as follows: (1) in order to improve the convergence speed and exploitation ability of GSA, this paper introduces the particle memory character and population social information in velocity update process; (2) a mutation operator based on chaotic behavior is also adopted to overcome premature convergence and enhances the ability to search for the global optimum solution. (3) When dealing with the difficult problem of constraints handling, a modification strategy by dividing the violation water volume into several parts and randomly selecting intervals to adjust the water discharge gradually is proposed to handle the water dynamic balance constraints. A new symmetrical strategy is utilized by adjusting the violation water volume to the discharge at previous time intervals in feasible region to meet reservoir storage volumes constraints. In order to keep the water dynamic balance, it also modifies the equal amount to the discharge at later time intervals. A strategy based on adjusting the output of the thermal power plants according to their priority index is also applied to handle active power balance constraints effectively in IGSA. Finally, this paper converts the bi-objective problem into a single one by using the variable weights based on the time intervals, and then the proposed IGSA is employed to solve SEEHTS problem of hydrothermal system consisting of a cascade of four hydroplants and three thermal plants. Simulation results show that IGSA has a good performance to find good solutions and satisfies all constraints completely for SEEHTS problem. Compared with other methods such as QPSO, QADEVT, EP and DE reported in the literatures, IGSA obtains the better fuel cost and less pollution emission. It is found that IGSA is feasible and effective in solving SEEHTS problem.

The limitation of this paper is that the two competing objectives are converted into a single one to be optimized. Although the best compromise solution with better fuel cost and less pollution emission is obtained, the real Pareto optimum solutions cannot be achieved by independent iterations. Therefore, our future work is to extend the proposed IGSA to be a multi-objective optimization algorithm. By using the multi-objective optimization algorithm to solve SEEHTS problem, the fuel cost and emission can be optimized simultaneously and a set of Pareto optimum solutions can be achieved in one trial without any variable weights.