Uncertain minimum cost flow problem

Abstract

The aim of this paper is to give an uncertainty distribution of the least cost of shipment of a commodity through a network with uncertain capacities. Uncertainty theory is used to deal with uncertain capacities, and an $\alpha$-minimum cost flow problem model is proposed. After defining the $\alpha$-minimum cost flow, the properties of the model are analyzed, and then an algorithm for uncertain minimum cost flow problem is developed. The algorithm can be considered as a general solution to the uncertain minimum cost flow problem. To demonstrate the efficiency of the proposed algorithm, a numerical example is illustrated.

1 Introduction

The minimum cost flow problem is the central issue of network flow theory. Many other problems, such as transportation problem, assignment problem, the shortest path and maximum flow problems are special cases of the problem. There are several efficient algorithms for the minimum cost flow problem. Jewell (1958), Iri (1960), Busacker and Gowen (1960) independently developed the initial form of successive shortest path algorithm. The successive shortest path algorithm maintains optimal solution at every step and tries to attain a feasible flow. Yakovleva (1959), Minty (1960), and Fulkerson (1961) studied the special structure of the minimum cost network flow and designed out-of-kilter algorithm for adjusting arcs that fail to satisfy the optimality properties. After that, Ford and Fulkerson (1962) described the primal-dual algorithm for solving the minimum cost flow problem. In addition, Klein (1967) studied how to maintain feasible flow at every step and strive to achieve optimal solution, and then proposed the cycle canceling algorithm. Moreover, in order to design efficient solution algorithm, some researchers used scaling approach to design polynomial time algorithms for the minimum cost flow problem. Edmonds and Karp (1972) introduced a capacity scaling technique to reduce the number of iterations. Röck (1980) was the first to propose cost scaling algorithm for solving the minimum cost flow problem. Other scholars used ideas from lagrangian relaxation to design new algorithms. Bertsekas (1986) proposed $\varepsilon$-relaxation method for the classical minimum cost flow problem. After that, Bertsekas and Castañon (1993) introduced auction algorithm to improve the efficiency of the $\varepsilon$-relaxation method. The auction algorithm can change two node prices per iteration while $\varepsilon$-relaxation method only change one node price. Furthermore, Ciurea and Ciupalâ (2004) presented sequential and parallel algorithms for minimum flows by modifying preflow algorithms for maximum flow. Paparrizos et al. (2009) introduced an exterior simplex type algorithm for the minimum cost flow problem.

In classical minimum cost flow problem, each arc has a known capacity and cost. In practice, unfortunately, the situation is complicated by the fact that arc capacities or costs may change in some probabilistic fashions. Williams (1963) considered the demand for the commodity is a random variable. Following Williams, Connors and Zangwill (1971) studied multistage minimum cost network flow problem. They assumed the node requirements are discrete random variables with known conditional probability distributions. In order to study stochastic minimum cost multicommodity transport network, Wollmer (1980) created a stochastic generalized multicommodity network. The stochastic network performance depends on random variables. Some other researchers studied the probability of the existence of a feasible flow. Prékopa and Boros (1991) proposed a method to find sharp lower and upper bounds for the probability that a feasible flow exists in a stochastic transportation network. Moreover, Boyles and Waller (2010) analyzed a minimum cost flow problem in which only the mean and variance of arc cost are assumed to be known.

However, in reality, the capacities of network may not be accurately measured according to probability theory. For instance, indeterminacy factors, such as storm or traffic congestions, will influence arc capacities. In fact, we may do not get probability distribution of arc capacities due to lack of information. In order to treat non-random phenomena, Zadeh (1965) defined the concept of fuzzy set. Moreover, Zadeh (1978) gave the concept of possibility measure to describe fuzzy events. But Zadeh’s fuzzy theory has been challenged by many researchers. The center of controversy lies that the measure of union of events does not necessarily equal the maximum of measures of individual events. When we do not have enough samples to estimate a probability distribution of arc capacities, we have to invite experts to give the belief degree of arc capacities. It depends on the personal knowledge about the capacities. In this situation, if we insist on using both probability theory and fuzzy set theory to deal with belief degree, counterintuitive results may occur (Liu 2012). To model the nature of human uncertainty, Liu (2007); Liu (2009a) founded uncertainty theory based on normality axiom, duality axiom, subadditivity axiom and product axiom. Since then, researchers have actively studied uncertainty theory and its applications. Liu (2007) introduced uncertain variable and uncertainty distribution to describe quantities with uncertainty. After that, a sufficient and necessary condition for uncertainty distribution was given by Peng and Iwamura (2010). In addition, Liu (2010) proved a measure inversion theorem. Moreover, in order to calculate the uncertainty distribution of monotone function of independent uncertain variables, Liu (2010) proposed the operational law. Expected value is the average value of uncertain variable in the sense of uncertain measure. Liu and Ha (2010) proved a formula for calculating the expected values of monotone functions of uncertain variables. Uncertain programming is a type of mathematical programming involving uncertain variables. Liu (2009b) founded uncertain programming theory. On the basis of uncertain programming theory, Liu and Yao (2012) presented an uncertain multilevel programming for modeling uncertain decentralized decision systems. Following that, Liu and Chen (2013) developed an uncertain multiobjective programming and an uncertain goal programming. Wang et al. (2013) proposed a new price discrimination model in labor market, where employee’s capability is assumed to be an uncertain variable. In addition, Chen and Gao (2013) valued zero-coupon bond under framework of uncertainty theory.

Uncertain network and uncertain graph can be conveniently used to represent many the real-world systems. Liu (2010) first exploited uncertain network theory for modeling project scheduling problem. Han and Peng (2010) used numerical method to solve the uncertain maximum flow problem. Gao (2011) derived the uncertainty distribution of the shortest path length under the framework of uncertainty theory. In addition, Gao (2012) applied uncertainty theory to solve uncertain facility location problem. In order to study the influence of indeterminacy factors on the graph, Gao and Gao (2013) proposed uncertain graph. In addition, Gao (2013) provided the concepts of cycle index of uncertain graph.

In this paper, we extend previous work to uncertain minimum cost flow problem, where capacities are uncertain variables. The rest of this paper is arranged as follows: In Sect. 2, we first give a brief introduction of uncertainty theory. In Sect. 3, $\alpha$-minimum cost flow model is proposed and properties of the model are analyzed. In Sect. 4, solution algorithm is developed. In Sect. 5, a numerical example is illustrated. Finally, a brief summary is provided in Sect. 6.

2 Preliminary

This section will present basic concepts, useful definitions and theorems of uncertainty theory.

Let $\Gamma$ be a nonempty set, and $\mathcal {L}$ a $\sigma$-algebra over $\Gamma$. Each element $\Lambda \in$ $\mathcal {M}$ is called an event. Let ($\Gamma$, $\mathcal {L}$) be measurable space. A set function $\mathcal {M}$ from $\mathcal {L}$ to [0, 1] is called an uncertain measure if it satisfies normality axiom, duality axiom, subadditivity axiom and product axiom (Liu 2007, 2009a).

Definition 1

(Liu 2007) An uncertain variable is a function from an uncertainty space $(\Gamma$, $\mathcal {L}$, $\mathcal {M})$ to the set of real numbers, i.e., for any Borel set B of real numbers, the set

$$\begin{aligned} \{\xi \in B\} = \{\gamma \in \Gamma |\xi (\gamma )\in B\} \end{aligned}$$

is an event.

Definition 2

(Liu 2007) The uncertain variables $\xi _1, \xi _2$, $\ldots ,\xi _n$ are said to be independent if

$$\begin{aligned} \mathcal {M}\left\{ \bigcap _{i=1}^n\{\xi _i\in B_i\}\right\} =\bigwedge _{i=1}^{n}\mathcal {M}\{\xi _i\in B_i\} \end{aligned}$$

for any Borel sets $B_1,B_2,\ldots ,B_n$ of real numbers.

Definition 3

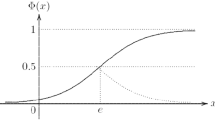
(Liu 2007) The uncertainty distribution $\varPhi$ of an uncertain variable $\xi$ is defined by

$$\begin{aligned} \varPhi (x)=\mathcal {M}\{\xi \le x\} \end{aligned}$$

for any real number $x$.

The zigzag uncertainty distribution $\xi \sim \mathcal {Z}(a, b, c)$ has an uncertainty distribution

$$\begin{aligned} \varPhi (x) = {\left\{ \begin{array}{ll} 0,&{} if \ x \le a\\ {(x - a)/2(b - a)}, &{} a \le x \le b\\ {(x+c-2b )/2(c - b)}, &{} b \le x \le c\\ 1,&{} if \ x \ge c. \end{array}\right. } \end{aligned}$$

The expected value of an uncertain variable is defined as follows.

Definition 4

(Liu 2007) Let $\xi$ be an uncertain variable. Then the expected value of $\xi$ is defined by

$$\begin{aligned} E[\xi ]=\int _0^{+\infty }\mathcal {M}\{\xi \ge r\}\mathrm{d}r-\int _{-\infty }^0\mathcal {M}\{\xi \le r\}\mathrm{d}r \end{aligned}$$

provided that at least one of the two integrals is finite.

Definition 5

(Liu 2010) An uncertainty distribution $\varPhi (x)$ is said to be regular if it is a continuous and strictly increasing function with respect to $x$ at which $0 < \mathcal {M}(x) < 1$, and

$$\begin{aligned} \mathop {\lim }\limits _{x \rightarrow - \infty } \varPhi (x) = 0,\quad \mathop {\lim }\limits _{x \rightarrow + \infty } \varPhi (x) = 1. \end{aligned}$$

Zigzag uncertain variable has a regular uncertainty distribution. In reality, we usually assume that all uncertainty distributions are regular. Otherwise, we can impose a small perturbation to get a regular one.

A real-valued function $f(x_1, x_2,\ldots ,x_n)$ is said to be strictly increasing if

$$\begin{aligned} f(x_1, x_2,\ldots ,x_n)\le f(y_1, y_2,\ldots ,y_n) \end{aligned}$$

whenever $x_i\le y_i$ for $i=1, 2,\ldots , n$, and

$$\begin{aligned} f(x_1, x_2,\ldots ,x_n)< f(y_1, y_2,\ldots ,y_n) \end{aligned}$$

whenever $x_i< y_i$ for $i=1, 2,\ldots , n$.

If $f(x_1, x_2,\ldots ,x_n)$ is a strictly increasing function, then $-f(x_1, x_2,\ldots ,x_n)$ is a strictly decreasing function.

Theorem 1

(Liu 2010) Let $\xi _1, \xi _2,\ldots ,\xi _n$ be independent uncertain variables with regular uncertainty distributions $\varPhi _1, \varPhi _2,\ldots ,\varPhi _n$, respectively. If the function $f(x_1, x_2,$ $\ldots ,x_n)$ is strictly increasing with respect to $x_1, x_2,\ldots ,x_m$ and strictly decreasing with respect to $x_{m+1}, x_{m+2},\ldots ,x_n$, then

$$\begin{aligned} \xi =f(x_1, x_2,\ldots ,x_n) \end{aligned}$$

is an uncertain variable with inverse uncertainty distribution

$$\begin{aligned} \Psi ^{-1}(\alpha )&= f(\varPhi _1^{-1}(\alpha ), \varPhi _2^{-1}(\alpha ),\ldots ,\varPhi _m^{-1}(\alpha ),\\&\quad \varPhi _{m+1}^{-1}(1-\alpha ),\ldots , \varPhi _n^{-1}(1-\alpha )). \end{aligned}$$

3 Mathematical formulation

This paper considers uncertain minimum cost flow problem. The optimization problem is to determine the minimum cost plan for sending flow through the network to satisfy supply and demand requirements. The arc flows must be nonnegative and be no greater than uncertain arc capacities with a predetermined confidence level. The arc flows must satisfy conservation of flow at all nodes.

Generally, a deterministic directed network is denoted as $G=(N,A)$, where $N$ is a finite set of nodes with $|N|=n$ and $A=\{(i, j)|i,j \in N\}$ is the set of arcs with $|A|=m$. Each arc $(i, j) \in A$ has a cost $c_{ij}$ that denotes unit cost of flow through arc $(i, j)$, and a capacity $u_{i, j}$ that denotes the maximum amount that can flow through the arc $(i, j)$. We also associate with each node $i \in N$ a number $b(i)$ indicating its demand or supply (Since total supply must equal to total demand, $\sum \nolimits _{i=1}^{n}b(i)=0$). (1) If $b(i)>0$, node $i$ is a supply node; (2) If $b(i)<0$, node $i$ is a demand node; (3) If $b(i)=0$, node $i$ is a transshipment node. Because computers store capacities as rational numbers and rational numbers can be converted to integer numbers by multiplying a proper large number (Ahuja et al. 1993), in this paper all these data are assumed to be rational numbers.

Denote $x =\{x_{ij} | (i, j) \in A\}$ as the set of flow through arc $(i,j)$. Then, the linear programming of the classical minimum cost flow problem can be formulated as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathop {\min }\sum \nolimits _{(i,j)\in A}c_{ij}x_{ij} &{} \\ \mathrm {subject \, to:} &{}\\ \sum \nolimits _{j:(i,j)\in A}x_{ij}-\sum \nolimits _{j:(j,i)\in A}x_{ji}= b(i),\forall i \in N &{} (A1) \\ x _{ij} \le {u_{ij}},{\forall (i,j) \in A} &{} (A2) \\ {{x_ {ij}} \ge 0},{\forall (i,j) \in A}, &{} (A3 )\\ \end{array}\right. }\nonumber \\ \end{aligned}$$

(1)

where $\sum \nolimits _{i=1}^{n}b(i)=0$.

The objective is to minimize the arc costs over all arcs in the network. Constraints $(A1)$ stipulate that the net flow out of node $i$ must equal $b(i)$, $\forall i \in N$. Constraints $(A2)$ and constraints $(A3)$ ensure that the flow through each arc satisfies the arc capacity restrictions.

In classical deterministic minimum cost flow problem, the capacity of each arc requires a nonnegative crisp value. However, in practice, capacities usually are not fixed. If we have enough data, we may create probability distributions of arc capacities. Unfortunately, sometimes we cannot obtain probability distributions of arc capacities due to influence of indeterminacy factors (congestion, accidents and weather conditions). But experts can give belief degree to describe distributions of arc capacities. In this paper, we employ uncertainty theory to deal with belief degree. Define a set of uncertain capacities $\xi =\{\xi _{ij}|(i, j) \in A\}$. Then, we denote uncertain network as $\tilde{G}=(N, A, \xi )$.

Uncertain programming is a commonly used method for practical decision making problems. When the decision-makers wish that the flow satisfies some chance constraints, the $\alpha$-minimum cost flow model is formulated as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathop {\min } \, \sum \nolimits _{(i,j)\in A}c_{ij}x_{ij} &{} \\ \mathrm {subject \, to:} &{}\\ \sum \nolimits _{j:(i,j)\in A}x_{ij}-\sum \nolimits _{j:(j,i)\in A}x_{ji}= b(i), \forall i \in N &{} (B1)\\ \mathcal {M}\{ x _{ij} \le {\xi _{ij}}\} \ge \alpha , \, {\forall (i,j) \in A} &{} (B2) \\ {{x_ {ij}} \ge 0}, \, {\forall (i,j) \in A} &{} (B3) \\ \end{array}\right. }\nonumber \\ \end{aligned}$$

(2)

where $\sum \nolimits _{i=1}^{n}b(i)=0$.

Constraints (B2) are chance constraints, which mean that the flow need satisfy flow bound constraints with a given confidence level $\alpha$.

A flow is feasible if it satisfies mass balance constraints $(B1)$ and capacity constraints $(B2)$ and $(B3)$. A feasible flow $x^*$ is the optimal cost flow of model (2), if for any feasible flow $x$, we can obtain

$$\begin{aligned} \sum \limits _{(i,j)\in A}c_{ij}x^*_{ij} \le \sum \limits _{(i,j)\in A}c_{ij}x_{ij}. \end{aligned}$$

The feasible flow $x^*$ is called as the $\alpha$-minimum cost flow.

The reason that the classical deterministic problem can be solved so efficiently is that it can be formulated as a linear programming problem, and a number of algorithmic approaches for solving this problem have been developed. It implies that if we can transform $\alpha$-minimum cost flow model into its crisp equivalent, and then the model can be solved by classic algorithms. Therefore, we need to convert the chance constraints $(B2)$ into their crisp equivalents.

Theorem 2

Let $\xi _{ij}$ be independent uncertain variables with regular uncertainty distributions $\varPhi (x)$ for all arc $(i, j)\in A$, respectively. Then model (2) is equivalent to the following deterministic programming problem

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathop {\min } \, \sum \nolimits _{(i,j)\in A}c_{ij}x_{ij} &{} \\ \mathrm {subject \, to:} &{}\\ x _{ij} \le {\varPhi _{ij}^{-1}(1-\alpha )} , \, {\forall (i,j) \in A}\\ \mathrm {Constraints \, (B1) \, and \, (B3)}.\\ \end{array}\right. } \end{aligned}$$

(3)

Proof

Since constraints (B2) of model (2) are $\mathcal {M}\{ x _{ij} \le {\xi _{ij}}\} \ge \alpha , \, {\forall (i,j) \in A}$ and $\xi _{ij}$ are regular uncertain variables.

We have

$$\begin{aligned} \mathcal {M}\{ x _{ij} \le {\xi _{ij}}\}= 1-\mathcal {M}\{{\xi _{ij}} \le x _{ij}\} \ge \alpha , \, {\forall (i,j) \in A}. \end{aligned}$$

Thus, we obtain

$$\begin{aligned} \mathcal {M}\{{\xi _{ij}} \le x _{ij}\} \le 1-\alpha , \quad {\forall (i,j) \in A}. \end{aligned}$$

Then, according to Theorem 1, constraints (B2) are equivalent to the following form,

$$\begin{aligned} {x_{ij}} \le \varPhi _{ij}^{-1}(1-\alpha ), \quad {\forall (i,j) \in A}. \end{aligned}$$

Thus, the $\alpha$-minimum cost flow of model (2) is equivalent to a deterministic minimum cost flow of model (3) with capacities $\varPhi _{ij}^{-1}(1-\alpha )$ for all arc $(i, j) \in A$.

The proof is completed. $\square$

Theorem 2 shows that given $\alpha$, we may obtain the minimum cost over all arcs by using effective classic algorithms such as network simplex algorithm. Thus, choosing different $\alpha$ and solving the model (3), we can obtain the uncertainty distribution of the minimum cost.

Next, we further analyze the properties of model (3).

Theorem 3

Assume that $\xi _{ij}$ are independent uncertain variables with regular uncertainty distributions $\varPhi (x)$ for all arc $(i, j)\in A$, respectively. The model (3) subject to constraints $(B2)$ is nondecreasing with respect to confidence level $\alpha$.

Proof

Let $S(\alpha )$ denote the feasible set of constraints $(B2)$ with respect to confidence level $\alpha$. Assume that $\alpha _{1} \le \alpha _{2}$. Then, it is easy to obtain

$$\begin{aligned} \varPhi _{ij}^{-1}(1-\alpha _{1}) \ge \varPhi _{ij}^{-1}(1-\alpha _{2}). \end{aligned}$$

Thus, according to Theorem 2, $S(\alpha _{1}) \supseteq S(\alpha _{2})$, which means that feasible set of model (3) with respect to $\alpha _{1}$ is more extended than that with respect to $\alpha _{2}$. Thus, the optimal value with respect to $\alpha _{2}$ is greater than or equal to the optimal value with respect to $\alpha _{1}$.

The proof is completed. $\square$

Corollary 1

If the feasible set provided by constraints (B2) is empty for $\alpha _{1}$, the feasible set of constraints (B2) remains empty for any $\alpha > \alpha _{1}$.

Proof

It follows from Theorem 3 immediately.

Corollary 1 permits us to select the bisection method to find the greatest confidential level $\alpha$ that yields a feasible flow. $\square$

4 Solution algorithm

Simulation method was usually used to obtain an optimal solution to uncertain programming problem. But it may impossible to quantify how close to an optimal solution. However, Theorem 2, Theorem 3 and Corollary 1 provide a better way to get the optimal solution. Because simplex algorithm and network simplex algorithm are widely considered to be some of the fastest algorithms in practice, we just only need to use bisection method and Big M method to obtain initial feasible solution, and then employ network simplex algorithm for solving model (3). Hence, we can design the following optimal solution algorithm for uncertain minimum cost flow problem (UMCFP).

UMCFP Algorithm:

Step 1. Set $\underline{a}=0$, $\overline{a}=1$ and $\varepsilon =10^{-3}$ (error tolerance).

Step 2. If $\overline{a}-\underline{a}> \varepsilon$, set $\alpha =(\overline{a}+\underline{a})/2$, construct the corresponding deterministic network ${G}=(N, A)$, set the capacity of each arc $u_{ij}$ equal to $\varPhi _{ij}^{-1}(1-\alpha )$, and go to Step 3. Otherwise go to Step 4.

Step 3. Employ Big M method to obtain initial feasible solution. If cannot find feasible solution, set $\alpha =\overline{a}$, go to Step 2. Otherwise set $\alpha =\underline{a}$, go to Step 2.

Step 4. Set $\alpha = \underline{a}$, construct the deterministic network ${G}=(N, A)$, and set the capacity of each arc $u_{ij}$ equal to $\varPhi _{ij}^{-1}(1-\alpha )$.

Step 5. Employ network simplex algorithm to obtain the minimum total cost and $\alpha$-minimum cost flow in network $G$.

In next section, we give an example to illustrate the algorithm.

5 Numerical example

The network $\tilde{G}=(N, A, \xi )$ is shown in Fig. 1. Capacity and cost of each arc $(i, j)$ are listed in Table 1. We can obtain the following:

• 1. the $\alpha$-minimum cost flow and the minimum total cost when $\alpha =0.4$;

• 2. the uncertainty distribution of the minimum total cost.

Fig. 1

Network $\tilde{G}$ for example

Table 1 List of capacities, costs and $\varPhi _{ij}^{-1}(1-0.4)$

If $\xi _{ij}$ is a constant, we stipulate $\varPhi ^{-1}( \alpha )=c$ for any $\alpha \in (0, 1)$. When $\alpha =0.4$, we calculate $\varPhi ^{-1}_{ij}(1-0.4)$ for each $\xi _{ij}$. The values are listed in Table 1.

Using the data in Table 1, we create a deterministic network $G=(N, A)$ shown in Fig. 2. The capacity of arc $(i,j) \in A$ is $\varPhi _{ij}^{-1}(1-0.4).$

Fig. 2

Network $\tilde{G}$ when $\alpha =$ 0.4

We employ the network simplex algorithm to obtain the optimal solution. Figure 3 shows the $0.4$-minimum cost flow. The minimum total cost $=12 \cdot 0 + 1\cdot 5 + 1\cdot 4.8 + 8 \cdot 0.2 + 3 \cdot 4.8 = 25.8$.

Fig. 3

$0.4$-minimum cost flow

Selecting different $\alpha$, we obtain Table 2. Repeating this process, we can obtain the uncertainty distribution of the minimum total cost shown in Fig. 4.

Table 2 List of $\alpha$-minimum cost flows and the minimum total costs

Fig. 4

Uncertainty distribution of the minimum total cost

It is worth pointing out that according to UMCFP algorithm, we can find the minimum $\alpha =0.666 (1-\alpha =0.334)$ is the greatest confidential level that yields a feasible flow with the error tolerance $\varepsilon =10^{-3}$. If we want to increase accuracy, we only need to decrease the value of $\varepsilon$.

6 Conclusion

This paper extends the classical minimum cost flow problem to uncertain minimum cost flow problem. The general form of minimum cost flow model with uncertain capacities is investigated. To deal with uncertain capacities, we use uncertainty theory to handle indeterminacy factors on capacities. Prosperity investigation is carried out to reveal characteristics of the proposed model, and the UMCFP algorithm for the model is developed. The algorithm can easily transform the uncertain minimum cost problem into a classical deterministic problem, and then solve it efficiently. At last, a numerical example is presented to illustrate the algorithm. These results may have many applications in uncertain network optimization.