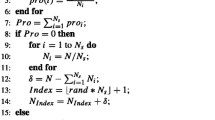Use of the q-Gaussian mutation in evolutionary algorithms

Abstract

This paper proposes the use of the q-Gaussian mutation with self-adaptation of the shape of the mutation distribution in evolutionary algorithms. The shape of the q-Gaussian mutation distribution is controlled by a real parameter q. In the proposed method, the real parameter q of the q-Gaussian mutation is encoded in the chromosome of individuals and hence is allowed to evolve during the evolutionary process. In order to test the new mutation operator, evolution strategy and evolutionary programming algorithms with self-adapted q-Gaussian mutation generated from anisotropic and isotropic distributions are presented. The theoretical analysis of the q-Gaussian mutation is also provided. In the experimental study, the q-Gaussian mutation is compared to Gaussian and Cauchy mutations in the optimization of a set of test functions. Experimental results show the efficiency of the proposed method of self-adapting the mutation distribution in evolutionary algorithms.

1 Introduction

Evolutionary algorithms (EAs), which are a class of stochastic search algorithms inspired by the principles of natural evolution, have been successfully applied to a large number of optimization problems. Many of these problems are continuous optimization problems and, as a consequence, several interesting EA variants for real-valued optimization have been investigated, as evolution strategy (ES) with adaptive encoding (Hansen 2008), differential evolution (DE) (Das et al. 2009; Price et al. 2005; Qin et al. 2009), real-coded genetic algorithms (Herrera et al. 1998; García-Martínez et al. 2008), memetic algorithms (Lozano et al. 2004; Nguyen et al. 2009; Noman and Iba 2008), and hybrid approaches (Vrugt et al. 2009).

Stochastic search algorithms, like EAs, differ from other optimization algorithms by using random samples to generate new candidate solutions. Traditionally, when EAs are applied in real-valued optimization, new candidate solutions are generated by mutation using multivariate samples taken from Gaussian distributions with zero mean (Beyer and Schwefel 2002). The isotropic Gaussian distribution, which has a finite second moment, maximizes the Boltzmann–Gibbs entropy (and the differential entropy, i.e., the extension of the Shannon’s concept of information entropy to the continuous case) in the unconstrained real-valued search space (Thistleton et al. 2007) and, in this way, does not favor any direction in the search space. In this way, the generation of new candidate solutions by mutation does not require the knowledge of any information about the geometry of the search space.

However, in recent years, researchers have proposed the use of distributions with longer tails and an infinite second moment in EAs. For example, in the fast evolutionary programming (FEP) (Yao et al. 1999), the Cauchy distribution is employed, while in the evolutionary programming (EP) with Lévy mutation (LEP) (Lee and Yao 2004), mutation based on the Lévy distribution is used. The Lévy distribution is a class of probability distributions with an infinite second moment, which includes the Cauchy distribution, and allows to control the tail of the distribution by changing a scalar parameter α.

The use of mutation taken from heavy tail distributions implies jumps of scale-free sizes, allowing to reach distant regions of the search space faster. This property can be interesting when EAs are applied to multimodal problems or dynamic optimization problems as it can allow the population to escape faster from local optima. However, some controversy about the benefits of the use of distributions with heavy tails in EAs have appeared in recent years (Hansen et al. 2006). For example, some researchers argue that most of the proposed algorithms use heavy tail distributions that are anisotropic, i.e., where some directions of the mutation are privileged in the search space (Obuchowicz 2003). Moreover, in some fitness landscapes, it can be difficult to reach a fair region of the search space from a long jump as the probability to reach a point with a worse fitness is generally much larger for a long jump (Hansen et al. 2006).

In this paper, self-adaptation is employed to control the mutation distribution. In this way, the choice of a mutation distribution for a given problem and, at a given moment of the evolutionary process, is made by the algorithm, and not by the programmer. In the proposed algorithm, a real parameter that defines the shape of the distribution employed by the mutation operator is encoded in the chromosome of the individuals and is allowed to evolve. For this purpose, the q-Gaussian probability density function (Thistleton et al. 2007) derived from the Tsallis generalized entropy (Tsallis 1988) is employed. The q-Gaussian distribution allows to control the shape of the distribution by setting a real parameter q and can reproduce either finite second moment distributions, like the Gaussian distribution, or infinite second moment distributions, like the Cauchy distribution.

The rest of this paper is organized as follows: Related work and the main contributions of the paper are presented in Sect. 2. The q-Gaussian distribution is briefly introduced in Sect. 3. In Sect. 4, self-adaptation of the mutation distribution in EAs is proposed. Evolutionary programming algorithms with mutations generated from anisotropic and isotropic distributions are presented in Sect. 5. In Sect. 6, the theoretical analysis of the q-Gaussian mutation is provided. In Sect. 7, the q-Gaussian mutation is used in a $(\mu, \lambda)$-ES with restart. The experimental study based on a suite of benchmark test functions is presented in Sect. 8. In the experiments with EP algorithms, Gaussian, Cauchy and q-Gaussian mutations generated from anisotropic and isotropic distributions are compared, while in the remaining experiments, a $(\mu, \lambda)$-ES with q-Gaussian mutation and restart is compared with other continuous optimization EAs. Finally, Sect. 9 concludes this paper with discussions on the relevant future work.

2 Related work

In this paper, instead of only controlling the mutation strength parameter that defines the spread of a fixed mutation distribution like in ESs and EP, the shape of the mutation distribution is also controlled during the evolutionary process. There are three main classes of parameter control in EAs (Eiben et al. 1999): deterministic, where the parameters are changed by deterministic rules; adaptive, where feedback from the optimization process is employed for parameter control; and self-adaptive, where parameters of the EA are encoded in the chromosome and allowed to evolve. The use of self-adaptation to define the mutation strength parameters is usual in EP and ESs. Here, self-adaptation is used to control the parameter q, that allows to modify the shape of the q-Gaussian distribution employed to generate random mutations.

The use of mutations generated from q-Gaussian distributions in EAs is not new (Iwamatsu 2002; Moret et al. 2006). However, in such algorithms, like in most other algorithms that use heavy tail distributions, new candidate solutions are produced by generating random deviates for each coordinate of the individual, which implies anisotropic distributions where large steps are generated close to the coordinate axes. Moreover, in such algorithms, the parameter q, which defines the shape of the distribution, is fixed during the searching process or starts with a large value and decreases during the searching process, like the temperature control in simulated annealing. That is, the control is deterministic. In Lee and Yao (2004), the authors proposed two schemes for LEP: in the first scheme, all offspring are generated from a distribution with a fixed α, and in the second, each parent generates five offspring, each of which is generated from a distribution with a different pre-defined value of α. All individuals in LEP use the same pre-fixed values of α during the whole evolutionary process.

Control of the mutation probability density function is not new too. In Davis (1994), the mutation probability density function is generated from a histogram with 101 bars representing the values of probability between a range of interest in a one-dimensional space. Self-adaptation is employed to control the heights of the bars, allowing to change the shape of the mutation distribution during the running of the EA (Bäck 2000). Experiments indicated the formation of histograms with a peak in the center, suggesting that Gaussian and Cauchy distributions are good candidates as mutation distributions. However, the use of histograms is not suitable when the number of dimensions of the search space is high because the required number of histograms exponentially increases with the dimension of the search space. As pointed in Bäck (2000), the control of the mutation probability density function by a few control parameters would be more interesting.

In Dong et al. (2007), four types of mutation can occur: Cauchy, Lévy, and two types of Gaussian mutation (i.e., the standard Gaussian mutation and the single-point mutation, where in each occurrence, only one dimension is changed). A four-string vector containing the probabilities of choosing each type of mutation is added to the individual and is modified according to the performance of each type of mutation.

The solution presented in this paper to control the shape of the mutation distribution employs only one parameter for each individual: the q-Gaussian distribution parameter q. Differently from the strategy used in Dong et al. (2007), the control of the parameter q allows to smoothly and continuously change the shape of the distribution, as q is a real parameter and a small change in its value causes a small change in the shape of the mutation distribution. In this way, the main contributions of this paper are (1) the use of the q-Gaussian mutation generated from anisotropic and isotropic distributions are proposed and compared in EP; (2) self-adaptation is used to control the parameter q, which allows changing the shape of the distribution during the solving process; (3) Gaussian, Cauchy, and q-Gaussian mutations generated from anisotropic and isotropic distributions are compared in a series of experiments based on a suite of benchmark test functions; and (4) an ES with q-Gaussian mutation is proposed and compared with other continuous optimization EAs.

3 The q-Gaussian distribution

One of the most interesting properties of the Gaussian distribution is that it maximizes, under certain constraints, the entropy in the form

$$ S = \int\limits_{-\infty}^{+\infty}{p(x)\ln(p(x)){\text{d}}x}, $$

(1)

where $p(x)$ is the distribution density function. This entropy is known as the Boltzman–Gibbs entropy. While the Gaussian distribution is an attractor for independent systems with a finite second moment, it does not represent well correlated systems with an infinite second moment (Thistleton et al. 2007). In this concern, Tsallis (1988) proposed a generalized entropy form as follows:

$$ S_{q} = {\frac{1 - \int_{-\infty}^{+\infty}{p(x)^{q}{\text{d}}x}}{q-1}}, $$

(2)

where ${q \in \mathbb {R}}$. Equation 2 recovers the entropy form given by Eq. 1 in the limit $q \rightarrow 1$. The q-Gaussian distribution arises when maximizing the generalized entropy form given by Eq. 2. The q-Gaussian distribution has interesting properties. The parameter q controls the shape of the q-Gaussian distribution. The second-order moment is finite for q < 5/3 and the q-Gaussian distribution reproduces the usual Gaussian distribution when $q\rightarrow1$. When $q<1$, the q-Gaussian distribution has a compact form, and decays asymptotically as a power law for $1<q<3$. When $q=2$, the q-Gaussian distribution reproduces the Cauchy distribution, while for $q=(3+d)/(1+d)$ where $0<d<\infty$, it becomes a Student’s t-distribution with d degrees of freedom (Souza and Tsallis 1997).

When $-\infty <q <3$, the q-Gaussian distribution density (Thistleton et al. 2007) is given by

$$ p_{q(\bar{\mu}_{q}, \bar{\sigma}_{q})}(x) = {\frac{\sqrt{B_{q}}} {A_{q}}}\;{\text{e}}_{q}^{-B_{q}(x-\bar{\mu}_{q})^2}, $$

(3)

where $\bar{\mu}_{q}$ and $\bar{\sigma}_{q}$ are the q-mean and the q-variance, respectively, A _q is the normalization factor, $B_{q}$ controls the width of the q-Gaussian distribution, and ${\text{e}}_{q}^{-y}$ is the q-exponential function of $-y$ defined as follows:

$$ {\text{e}}_{q}^{-y}\equiv\left\{\begin{array}{ll} \left(1+(q-1)y\right)^{-{\frac{1} {q-1}}}, & \hbox{if}\;1+(q-1) y \geq 0\\ 0, & \hbox{otherwise}\\ \end{array} \right.. $$

(4)

When $q\rightarrow1$, the limit of the q-exponential function of $-y$, if we write $z=(q-1)y$, is given by

$$ \lim_{q\rightarrow1} {\text{e}}_{q}^{-y} = \lim_{z\rightarrow0} \left( \left(1+ z \right)^{{\frac{1}{z}}}\right)^{-y}. $$

(5)

The limit of the function $(1+ z )^{{\frac{1}{z}}}$ is well known and converges to e when $z\rightarrow0$. Thus, we have

$$ \lim_{q\rightarrow1} {\text{e}}_{q}^{-y} = {\text{e}}^{-y} ,$$

(6)

i.e., the q-Gaussian exponential converges to the exponential when $q \rightarrow 1$.

In Eq. 3, the q-mean $\bar{\mu}_{q}$ and the q-variance $\bar{\sigma}_{q}$ (Thistleton et al. 2007) are, respectively, defined as follows:

$$ \bar{\mu}_{q} \equiv {\frac{\int{x p(x)^{q}} {\text{d}}x}{\int{p(x)^{q}}{\text{d}}x}}, $$

(7)

$$ \bar{\sigma}_{q}^{2}\equiv{\frac{\int{(x- \bar{\mu}_{q}})^{2}p(x)^{q}{\text{d}}x}{\int{p(x)^{q}}{\text{d}}x}}, $$

(8)

and, respectively, reduce to the usual mean and variance when $q\rightarrow1$.

In Eq. 3, the normalization factor $A_{q}$ is given by $A_{q}= \int_{-\infty}^{+\infty}{e_{q}^{-(x-\bar{\mu}_{q})^2}}{\text{d}}x$ (Umarov et al. 2008) and $B_{q}$ is given by

$$ B_{q} = \left((3-q) \bar{\sigma}_{q}^{2}\right)^{-1}. $$

(9)

A random variable x taken from a q-Gaussian distribution with q-mean $\bar{\mu}_{q}$ and q-variance $\bar{\sigma}_{q}^{2}$ is here denoted by $x\sim\mathcal{N}_{q}(\bar{\mu}_{q},\bar{\sigma}_{q})$. In this paper, the generalized Box–Müller method proposed in Thistleton et al. 2007, which is very simple (see its pseudo-code in Thistleton et al. 2007) and allows to generate samples from q-Gaussian distributions for $-\infty<q<3$, is employed to generate q-Gaussian random variables $x \sim \mathcal{N}_{q}(0,1)$.

Figure 1 presents the empirical q-Gaussian distribution for random variables $x \sim \mathcal{N}_{q}(0,1)$ with different values of q. It can be observed that larger values of q result in longer tails of the q-Gaussian distribution.

Fig. 1

Empirical distribution for 500,000 observations of a q-Gaussian random variable $x \sim \mathcal{N}_{q}(0,1)$ for: $q=-0.5$, $q=1.0$ (Gaussian), $q=2.0$ (Cauchy), and $q=2.8$. Only the values for x between −10 and +10 are shown

4 Self-adaptation of the mutation distribution

In an m-dimensional real-valued search space, a new candidate solution is generated by the EA’s mutation operator from individual ${\mathbf{x}}_{i}$ as follows:

$$ \tilde{{{\mathbf{x}}}}_{i} = {{\mathbf{x}}}_{i} + {{\mathbf{Cz}}} , $$

(10)

where $i=1,\ldots,\mu$, z is an m-dimensional random vector generated from a given multivariate distribution with zero mean, and C is the matrix which defines the mutation strength in each coordinate $j=1, \ldots, m$. In the most simple case,

$$ {{\mathbf{C}}} = \sigma {{\mathbf{I}}}, $$

(11)

where I is the identity matrix and the unique parameter, $\sigma$, defines the mutation strength for all components of ${\mathbf{x}}_{i}$. There are some cases, however, where it is interesting to define one different parameter $\sigma(j)$ for each component of ${\mathbf{x}}_{i}$. In this way, we have

$$ {{\mathbf{C}}}=\hbox{diag}({\varvec{\sigma}}^{{\rm T}}). $$

(12)

That is, C is a diagonal matrix with the main diagonal composed by the elements of vector ${\varvec{\sigma}} = [\sigma(1)\,\sigma(2) \cdots \sigma(m)]^{{\rm T}}$. In the most general situation, e.g., in the covariance matrix adaptation ES (CMA-ES) (Hansen and Ostermeier 2001), C is a matrix with elements indicating the correlation between the components of z.

In general, when self-adaptation is used in the standard EP (Yao et al. 1999) and in ES (Beyer and Schwefel 2002), the mutation strength parameter for each offspring $i=1, \ldots, \mu$ of the population is multiplicatively updated. If all elements of the mutation parameter vector are equal [i.e., $\sigma_{i}(j) =\sigma_{i}$ for $j=1, \ldots, m$, see Eq. 11], then the updated value of the mutation parameter is given by

$$ \tilde{\sigma}_{i} = \sigma_{i} {\text{e}}^{\tau_{b} {\mathcal{N}}(0,1)} , $$

(13)

where $\tau_{b}$ denotes the standard deviation of the Gaussian distribution used to generate the change in $\sigma_{i}$. If each element of the vector $\mathbf{x}_{i}$ has an individual mutation strength parameter, as shown in Eq. 12, $\sigma_{i}(j)$ is updated according to the following formula:

$$ \tilde{\sigma}_{i}(j) = \sigma_{i}(j) {\text{e}}^{\tau_{b} {\mathcal{N}}(0,1)_{i} + \tau_{c} {\mathcal{N}}(0,1)} , $$

(14)

where $\tau_{b}$ denotes the standard deviation of the Gaussian distribution used to generate the random deviate $\mathcal{N}(0,1)_{i}$, which is common for all elements of the vector $\mathbf{x}_{i}$, and $\tau_{c}$ is the standard deviation of the Gaussian distribution used to generate the separated random deviate $\mathcal{N}(0,1)$ for each element $j=1, \ldots, m$.

In EAs, the use of the Gaussian distribution is generally employed to generate the m-dimensional vector $\mathbf{z}$ (Beyer and Schwefel 2002). Here, an m-dimensional random vector generated from the Gaussian distribution is denoted by $\mathbf{z} \sim \mathcal{N}^{m}$. A Gaussian random vector $\mathbf{z} \sim \mathcal{N}^{m}$ is generated by sampling m independent Gaussian variables $\mathcal {N}(0,1)$. It is important to observe that when the same procedure is adopted to generate multivariate random samples with a heavy tail distribution, some directions in the search space are much more explored than others, i.e., the distribution is highly anisotropic.

To the best of the authors’ knowledge, all stochastic search algorithms with the q-Gaussian mutation, like the generalized simulated annealing (Tsallis and Stariolo 1996) and the generalized genetic algorithm (Moret et al. 2006), make use of anisotropic q-Gaussian distributions generated by sampling m independent q-Gaussian variables. Most mutation operators for EAs that are based on heavy tail distributions, e.g., in fast evolution strategies (Yao and Liu 1997), FEP (Yao et al. 1999), and LEP (Lee and Yao 2004), make use of anisotropic distributions generated by sampling independent random variables too. The use of random variables generated by sampling independent random variables taken from a heavy tail distribution is very interesting for optimization problems with separable functions, as most of the large steps occur close to the coordinate axes (Obuchowicz 2003; Thistleton et al. 2007) and the optimization can be solved by m one-dimensional optimization processes parallel to the coordinate axes. However, the performance of the optimization process can be strongly affected for some non-separable functions.

In this paper, we investigate the use of two multivariate q-Gaussian distributions, the anisotropic q-Gaussian distribution generated by sampling independent q-Gaussian random variables (Sect. 5.1) and the q-Gaussian distribution generated from isotropic distributions (Sect. 5.2), to produce new candidate solutions in EAs. As mentioned earlier, the use of the q-Gaussian distribution allows us to reproduce different distributions by changing only one real parameter q.

We propose to self-adapt the parameter q, which defines the shape of the distribution. Based on the mutation strength self-adaptation (Beyer and Schwefel 2002), we propose to multiplicatively update the parameter q in individual i as follows:

$$ \tilde{q}_{i} = q_{i} {\text{e}}^{\tau_{q} {\mathcal{N}}(0,1)}, $$

(15)

where $\tau_{q}$ denotes the standard deviation of the Gaussian distribution. In this way, different distributions can be reproduced during the evolutionary process. However, it is not possible to identify the separated influence of a change in $\varvec{\sigma}_{i}$ or $q_{i}$ in the fitness of individual i if both mutation strength vector and parameter q are mutated in the same generation for individual i. For example, a beneficial mutation in $\varvec{\sigma}_{i}$ can be masked in the fitness of individual i if the parameter q is mutated to a bad value in the same generation. Here, $\varvec{\sigma}_{i}$ and $q_{i}$ are not mutated together (i.e., in the same generation) in each individual. The mutation strength vector $\varvec{\sigma}_{i}$ is updated for individual i in each generation if a uniform random number in the range [0, 1] is equal to or larger than a real parameter $r_{q} \in [0,1]$. Otherwise, the value of $q_{i}$ is updated.

5 Evolutionary programming algorithms with q-Gaussian mutation

In order to test the proposed ideas, an EP algorithm with the q-Gaussian mutation, called qGEP for the anisotropic version and IqGEP for the version generated from isotropic distributions, is proposed and presented in Algorithm 1. EP was selected to test the q-Gaussian mutation because it only uses mutation as a transformation operator, which makes it easier to compare the q-Gaussian mutation with Cauchy and Gaussian mutation.

There are two main differences of the EP algorithm presented in Algorithm 1 from the Gaussian EP, FEP (Yao et al. 1999), and LEP (Lee and Yao 2004). First, in the proposed algorithm, the q-Gaussian mutation is employed (step 10) instead of the Gaussian (Gaussian EP), Cauchy (FEP), or Lévy (LEP) mutation. Second, a procedure to adapt the q parameter is adopted in the proposed algorithm, i.e., steps 5 to 9 in Algorithm 1. For Gaussian EP, FEP, and LEP, steps 5, 7, 8, and 9 in Algorithm 1 are removed.

5.1 EP with q-Gaussian mutation generated from anisotropic distribution

In an EA with q-Gaussian mutation generated from anisotropic distribution, the vector $\mathbf{z}$ in Eq. 10 is created by sampling m independent q-Gaussian random variables. Each element $z(j)$, $j=1,\ldots,m$, of the random mutation vector $\mathbf{z}$ is generated as follows:

$$ z(j) \sim {\mathcal{N}}_{q}(0,1) . $$

(16)

Here, an m-dimensional random vector generated from the multivariate anisotropic q-Gaussian distribution is denoted by $\mathbf{z} \sim \mathcal{M}_{q}^{m}$.

In order to investigate the contribution of the scheme of self-adapting the parameter q, the qGEP algorithm is compared, in Sect. 8, with three other approaches where the parameter q is fixed, i.e., the shape of the mutation distribution is fixed during the evolutionary process. For fixed values of q, the q-Gaussian mutation can reproduce Gaussian and Cauchy mutations. Lévy mutation can be still reproduced, as Lévy and q-Gaussian distributions are related for some values of q (Rathie and Da Silva 2008). In all approaches described here, Eq. 16 is employed to generate new candidate solutions. The approaches are defined as follows:

• Algorithm GEP: uses only one fixed parameter $q=1.0$ for all individuals. That is, in Algorithm 1, the initial value of $\tilde{q}_{i}$ is equal to 1.0 for $i=1,\ldots,\mu$ and $r_{q}=0$. In this way, the Gaussian mutation generated from sampling m independent Gaussian random variables is reproduced.

• Algorithm CEP: uses only one fixed parameter $q=2.0$ for all individuals. That is, in Algorithm 1, the initial value of $\tilde{q}_{i}$ is equal to 2.0 for $i=1,\ldots,\mu$ and $r_{q}=0$. In this way, the anisotropic Cauchy distribution is reproduced.

• Algorithm EP ($q=1.5$): uses only one fixed parameter $q=1.5$ for all individuals. That is, in Algorithm 1, the initial value of $\tilde{q}_{i}$ is equal to 1.5 for $i=1,\ldots,\mu$ and $r_{q}=0$.

• Algorithm qGEP uses one changing q for each individual and $r_{q}>0$, i.e., Eq. 15 is employed.

5.2 EP with q-Gaussian mutation generated from isotropic distribution

Here, the use of q-Gaussian mutations generated from isotropic distributions is proposed. In Obuchowicz (2003), a method to generate the Cauchy random mutation vector from an isotropic distribution was proposed. For this purpose, the random mutation vector is generated with (1) a random direction uniformly distributed on the surface of the m-dimensional unit hypersphere, and (2) an Euclidean norm obtained from a Cauchy distribution.

Based on the works Obuchowicz (2003) and Thistleton et al. (2007), we propose to generate the random mutation vector $\mathbf{z}$ as follows:

$$ \mathbf{z} \sim r \mathbf{u}, $$

(17)

where $r \sim \mathcal{N}_{q}(0,1)$, i.e., a random variable with the q-Gaussian distribution, and $\mathbf{u}$ is an uniform random vector obtained by sampling a random vector with a Gaussian distribution and normalizing it to length one, i.e., $\mathbf{u}=\mathbf{v} / \|\mathbf{v}\|$ where $\mathbf{v} \sim \mathcal{N}^{m}$ and $\|\mathbf{v}\|$ denotes the Euclidean norm of the vector $\mathbf{v}$. In this paper, an m-dimensional random vector generated from an isotropic distribution and step length given by a q-Gaussian distribution is denoted by $\mathbf{z} \sim \mathcal{N}_{q}^{m}$.

Figure 2 presents two-dimensional multivariate samples obtained from an anisotropic q-Gaussian distribution, a Gaussian distribution, and a q-Gaussian distribution generated as described in this section. It can be observed that, in the anisotropic q-Gaussian distribution, larger steps occur more often close to the coordinate axes. This effect is more evident in high-dimensional spaces and/or for larger values of q for $q<3$.

Fig. 2

Two-dimensional points from: random vector $\mathbf{z} \sim \mathcal {M}_{q}^{m}$ with anisotropic q-Gaussian distribution and q = 2.0 (left), random vector $\mathbf{z} \sim \mathcal{N}^{m}$ with Gaussian distribution (center), and q-Gaussian random vector $\mathbf{z} \sim \sqrt{2}\mathcal{N}_{q}^{m}$ generated from isotropic distribution and q = 2.0 (right)

The EP algorithm with q-Gaussian mutation generated from isotropic distribution, called IqGEP here, is compared, in Sect. 8, with three other approaches where the parameter q is fixed. In all approaches, Eq. 17 is employed to generate the new candidate solutions. The approaches are defined as follows:

• Algorithm IGEP: uses only one fixed parameter $q=1.0$ for all individuals. That is, in Algorithm 1, the initial value of $\tilde{q}_{i}$ is equal to 1.0 for $i=1,\ldots,\mu$ and $r_{q}=0$. In this way, the Gaussian mutation generated from an isotropic distribution and with step length given by the Gaussian distribution is reproduced.

• Algorithm ICEP: uses only one fixed parameter $q=2.0$ for all individuals. That is, in Algorithm 1, the initial value of $\tilde{q}_{i}$ is equal to 2.0 for $i=1, \ldots, \mu$ and $r_{q}=0$. In this way, the Cauchy mutation generated from an isotropic distribution and with step length given by the Cauchy distribution is reproduced.

• Algorithm IEP ($q=1.5$): uses only one fixed parameter $q=1.5$ all individuals. That is, in Algorithm 1, the initial value of $\tilde{q}_{i}$ is equal to 1.5 for $i=1, \ldots, \mu$ and $r_{q}=0$.

• Algorithm IqGEP uses one changing q for each individual and $r_{q}>0$, i.e., Eq. 15 is employed.

6 Analysis of the q-Gaussian mutation

In this section, the impact of changing the mutation strength parameter $\sigma$ and the q-Gaussian distribution parameter q on the probability of generating a jump $\sigma x$, where $x \sim \mathcal{N}_{q}(0,1)$, in the neighbourhood of a point $x^{*}$ is analysed. The analyses presented here are similar to the analysis of Gaussian and Cauchy mutations presented in Yao et al. (1999).

When $\bar{\mu}_{q}=0$ and $\bar{\sigma}_{q}^{2}=1$, the q-Gaussian distribution density for $-\infty<q<3$ (see Eq. 3) is given by

$$ p_{q}(x) = {\frac{1}{\sqrt{3-q}A_{q}}} \quad {\text{e}}_{q}^{\frac{-x^2}{3-q}}, $$

(18)

where considering $\left(1+x^{2}(q-1) / \sqrt{3-q} \right) \geq 0$, the q-exponential is given by

$${\text{e}}_{q}^{\frac{-x^2}{3-q}}=\left(1+{\frac{q-1}{3-q}} \quad x^{2} \right)^{\frac{1}{1-q}}. $$

(19)

We consider that the q-Gaussian mutation is applied in an EA in the one-dimensional case, i.e., the mutation produces a jump $\sigma x$, where $\sigma$ is the mutation strength parameter and $x \sim \mathcal{N}_{q}(0,1)$. For simplicity, we will consider $1<q<3$. The probability of reaching the neighbourhood of a point $x^{*}$ from a jump $\sigma x$, i.e., the probability that $x^{*}-\epsilon \leq \sigma x \leq x^{*}+\epsilon$, where $\epsilon>0$ defines the neighbourhood size, is given by

$$ P_{q}(|\sigma x - x^{*}| \leq \epsilon) = \int\limits_{\frac{x^{*}- \epsilon}{\sigma}}^{\frac{x^{*}+\epsilon}{\sigma}}{p_{q}(x){\text{d}}x}. $$

(20)

The mean value theorem for definite integrals states that there is a number $\delta$ ($0<\delta<2\epsilon$), at which the value of the integral given by Eq. 20 is equal to the difference between the limits of the integral multiplied by $p_{q}((x^{*} - \epsilon + \delta)/ \sigma)$. In this way, Eq. 20 can be written as follows:

$$ P_{q}(|\sigma x - x^{*}| \leq \epsilon) = {\frac{2 \epsilon} {\sigma}} p_{q} \left({\frac{x^{*} - \epsilon + \delta}{\sigma}} \right). $$

(21)

Substituting Eqs. 18 and 19 in Eq. 21, we obtain

$$ P_{q}(|\sigma x - x^{*}| \leq \epsilon) = {\frac{2 \epsilon}{\sigma \sqrt{3-q}A_{q}}} \left(1+ {\frac{q-1}{3-q}} {\frac{c^{2}} {\sigma^{2}}}\right)^{\frac{1}{1-q}}, $$

(22)

where $c = x^{*} - \epsilon + \delta$.

6.1 The impact of changing σ

Taking the derivative of Eq. 22 with respect to σ, we can write

$$ \begin{aligned} &{\frac{\partial}{\partial \sigma}}P_{q}(|\sigma x - x^{*}| \leq \epsilon) \\ &\quad={\frac{2 \epsilon}{\sqrt{3-q}A_{q}}}{\frac{\partial}{\partial \sigma}} \left({\frac{1}{\sigma}}\left(1+ \frac{q-1}{3-q} \frac{c^{2}} {\sigma^{2}}\right)^{\frac{1}{1-q}}\right), \end{aligned} $$

(23)

and, then,

$$ \begin{aligned} {\frac{\partial}{\partial \sigma}}P_{q}(|\sigma x-x^{*}| \leq \epsilon)& = {\frac{2 \epsilon}{\sqrt{3-q}A_{q}}}\left({\frac{2q_{a}c^{2}} {(q-1)\sigma^{4}}} \left(1+q_{a}{\frac{c^{2}} {\sigma^{2}}}\right)^{\frac{q}{1-q}}\right.\\ &\quad -\left.{\frac{1}{\sigma^2}}\left(1+ q_{a}{\frac{c^{2}} {\sigma^{2}}}\right)^{\frac{1}{1-q}}\right), \end{aligned} $$

(24)

where $q_{a} = (q-1)/(3-q)$. After some manipulation, we obtain

$$ \begin{aligned} &{\frac{\partial}{\partial \sigma}} P_{q}(|\sigma x - x^{*}| \leq \epsilon) \\ &\quad={\frac{2 \epsilon}{\sqrt{3-q}A_{q} \sigma^{2}}}\left(1+ q_{a}{\frac{c^{2}}{\sigma^{2}}}\right)^{\frac{1}{1-q}} {\frac{c^{2}-\sigma^{2}}{q_{a}c^{2}+\sigma^{2}}}. \end{aligned} $$

(25)

From Eq. 25, we can write for $1<q<3$

$$ {\frac{\partial}{\partial \sigma}} P_{q}(|\sigma x - x^{*}| \leq \epsilon)\left\{{\begin{array}{ll} {> 0\,{\mathrm{if}}\,|c|> \sigma}\\ {< 0\,{\mathrm{if}}\,|c|< \sigma}\\ \end{array}} \right. . $$

(26)

Equation 26 states that an increase in the mutation strength $\sigma$ results in an increase in the probability of reaching the point c, which is located in the neighbourhood of the point $x^{*}$, from a jump $\sigma x$ only if $|c|<\sigma$. In other words, an increase in the mutation strength is beneficial to reach the neighbourhood of a point $x^{*}$ if it is distant ($|c|>\sigma$) from the current solution (before the mutation). A similar result was found for the Gaussian and Cauchy mutations (Yao et al. 1999). The above analysis also states that the probability changing rate given by Eq. 25 depends on the value of q.

6.2 The impact of changing q

Taking the derivative of Eq. 22 with respect to q, we can write

$$ \frac{\partial}{\partial q} P_{q}(|\sigma x - x^{*}| \leq \epsilon) = \frac{2 \epsilon}{\sigma} \frac{\partial}{\partial q} \left({\frac{1}{\sqrt{3-q}A_{q}}} y \right) , $$

(27)

where

$$ y = \left(1+ \frac{q-1}{3-q} \frac{c^{2}} {\sigma^{2}}\right)^{\frac{1}{1-q}} $$

(28)

is the q-exponential given by Eq. 19 at the point $x=c/\sigma$. We now analyse the derivative of the q-exponential y given by Eq. 28). Applying the natural logarithm in both sides of Eq. 28 and taking the derivative on q, we have

$$ {\frac{\partial y}{\partial q}}= y \frac{\partial}{\partial q} \left({\frac{1}{1-q}} \ln \left(1+\frac{q-1}{3-q} \frac{c^{2}}{\sigma^{2}}\right)\right). $$

(29)

After some manipulation, we can write

$$ {\frac{\partial y}{\partial q}}= \frac{1}{q-1} p^{\frac{1}{1-q}} \left({\frac{\ln(p)}{q-1}}-\frac{2}{(3-q)^{2}} \frac{c^{2}}{\sigma^{2}}p^{-1}\right), $$

(30)

where

$$ p = 1+ \frac{q-1}{3-q} \frac{c^{2}}{\sigma^{2}} , $$

(31)

i.e., $y=p^{\frac{1}{1-q}}$. In Eq. 30, $p \geq 1$ for $1<q<3$. In this way, we can write

$$ {\frac{\partial y}{\partial q}} \left\{{\begin{array}{ll} {> 0\;{\mathrm{if}}\;a> b}\\ {< 0\;{\mathrm{if}}\;a< b}\\ \end{array}} \right., $$

(32)

where $a = {\frac{\ln (p)}{q-1}}$ and $b =\frac{2}{(3-q)^{2}} \frac{c^{2}}{\sigma^{2}} p^{-1}$. While $|a|>|b|$ for small values of $|c|$ (until the value of c where $a=b$), $|a|<|b|$ for larger values of $|c|$ as $\lim _{|c| \to \infty} a = +\infty$. and $\lim _{|c| \to \infty} b={\frac{2}{(3-q)(q-1)}}$.

Figure 3 shows the regions where the derivative of the q-exponential given by Eq. 28 is positive or negative for $\sigma=3$ and $|c| \leq 10$. When the derivative is positive, increasing (or decreasing) q by a small value implies increasing (or decreasing) the value of the q-exponential at the point c, while the opposite occurs for a negative derivative. It can be observed that the location c where the derivative changes its sign moves according to the value of q. The larger the value of q, the farther the locations of $|c|$ where the derivative changes its sign. Figure 3 (and Eq. 30) also suggests that values of q close to 3 are not interesting as the location where the derivative changes its sign is very far away from the current solution.

Fig. 3

Positive (gray) and negative (white) regions of the derivative of the q-exponential given by Eq. 28 for $\sigma=3$

Using the derivative of the q-exponential given by Eq. 28, we can now write, after some manipulations, the derivative of Eq. 22 with respect to q (see Eq. 27)

$$\begin{aligned} {\frac{\partial}{\partial q}} P_{q}(|\sigma x - x^{*}| \leq \epsilon)&= {\frac{2 \epsilon p^{{\frac{1}{1-q}}}}{A_{q}\sigma \sqrt{3-q}(q-1)}} \\&\quad\times\left({\frac{(q-1)(A_{q}-(3-q) A_{q}')} {(3-q)A_{q}}}+ a-b \right).\end{aligned} $$

(33)

As the first term inside the parenthesis does not depend on c, the analysis is similar to that one presented before for the q-exponential given by Eq. 30. Equation 33 indicates where a small change in the value of q is beneficial to increase the probability of reaching the neighbourhood of a point $x^{*}$ from a jump $\sigma x$. In other words, an increase in the value of q is beneficial to reach the neighbourhood of a point $x^{*}$ if it is distant (at a location where the derivative given by Eq. 33 is positive) from the current solution (before the mutation). Otherwise, the value of q should be decreased.

7 Restart q-Gaussian evolution strategy

In Sect. 5, EP algorithms with q-Gaussian mutation were presented. However, it is important to observe that the proposed self-adapted q-Gaussian mutation can be used in other EAs. In this section, the q-Gaussian mutation is proposed in a ($\mu$, $\lambda$)-ES with recombination. The proposed algorithm, called RqGES, is presented in Algorithm 2.

Besides mutation, like in the EP algorithms presented in Sect. 5, the proposed RqGES employs an intermediate recombination with $\rho=2$, i.e., two parents are randomly chosen from the parent population and are mixed to generate an offspring. The intermediate recombination is applied to the variables ($\mathbf{x}_{i}$) and parameters ($\sigma_{i}$ and $q_{i}$). After recombination, the q-Gaussian mutation generated from isotropic distribution is used. In multimodal problems, larger population sizes can be useful to help the population escaping from local optima. In this way, following the scheme proposed in (Auger and Hansen 2005a), the population is restarted with a larger number of individuals if a convergence criterion is met. Here, like in (Auger and Hansen 2005a), the population is increased by a factor of 2 until a maximum allowed size ${\lambda}_{\max}$.

8 Experimental study

In order to investigate the performance of the proposed algorithms, 25 benchmark functions as described in Suganthan et al. (2005) are selected as the test suite in our experiments. The test functions, which should be minimized, are presented in Table 1 and are used with the same parameters as described in Suganthan et al. (2005).

In the test suite, functions $f_{1}$ to $f_{5}$ are unimodal and the remaining functions are multimodal. Functions $f_{15}$ to $f_{25}$ are hybrid composition functions (Suganthan et al. 2005). Such functions are composed of basic functions, which results in hybrid composite functions with different basic function properties, and are given by

$$ f({\mathbf x}) = \sum_{i=1}^{10} \left(w_{i} \left( f_{i}' \left({\mathbf M}_{i} ({\mathbf x}-{\mathbf o}_{i} ) / \lambda_{i} \right) + {\text{bias}}_{i} \right) \right)+f_{{\text{bias}}} , $$

(34)

where $f_{i}'(.)$ is the normalized i-th basic function, ${\mathbf M}_{i}$, $\lambda_{i}$, and $w_{i}$ are the linear transformation matrix, the compress rate, and the weight value for each function $f_{i}(.)$, respectively, ${\mathbf o}_{i}$ defines the position of the local and global optima, bias _i defines which optimum is the global optimum, and $f_{\text{bias}}$ is the bias in the function value. For example, function $f_{15}$ is composed of five basic functions: Rastrigin, Weierstrass, Griewank, Ackley, and Sphere. See Suganthan et al. (2005) for details and parameters.

Table 1 Test functions, where the vector ${\mathbf x^{*}}$ is the global optimum and the range is for each element of ${\mathbf x}$

The functions presented in Table 1 allow comparing the three types of mutation operators described in this paper, i.e., Gaussian, Cauchy, and q-Gaussian mutations, on problems with different properties. For example, while some functions in Table 1 are separable, others are non-separable. Some important properties of the functions are presented in the last column of Table 1. The comparison of Gaussian, Cauchy, and q-Gaussian mutations on EP is performed in Sect. 8.2.

The functions presented in Table 1 also allow comparing the results of the algorithms with other EAs found in the literature. The comparison of RqGES, which presented better performance than qGEP and IqGEP, and other EAs for continuous optimization is performed in Sect. 8.3. In the following section, the design of all experiments presented in this paper is described:

8.1 Experimental design

In order to compare the EP algorithms with different types of mutation, each one was executed 25 times for each test function presented in Table 1 with $m=10$ and $m=30$ (Suganthan et al. 2005). The same was done for RqES, but also with $m=50$. For each run of an algorithm, the individuals of the initial population were randomly chosen with uniform distribution in the range of each function (see Table 1), except for the experiments with functions $f_{7}$ and $f_{25}$, where the populations were, respectively, initialized in the ranges $[0, 600]^{m}$ and $[2, 5]^{m}$. The number of fitness evaluations was set to $10{,}000m$. In the EP algorithms, the population size was set to 100 individuals and the tournament size in the winning function (Lee and Yao 2004) for selection was set to 10. In RqGES, the initial $\lambda$ was set to 50, ${\lambda}_{\max}=200$, the initial $\mu$ was set to 15, and $g_{s}=120$.

As suggested by the theoretical and empirical work (Beyer and Schwefel 2002), the parameters $\tau_{b}$ and $\tau_{c}$ are defined by $\tau_{b} = {\frac{1}{\sqrt{2 m}}}$ and $\tau_{c} = {\frac{1}{\sqrt{2 \sqrt{m}}}}$. Here, we propose to define the parameter $\tau_{q}$ as follows:

$$ \tau_{q} = {\frac{1}{\sqrt{2 m}}}. $$

(35)

The initial mutation strength parameter $\sigma_{i}(j)$ was set to $0.4 |x_{\max}-x_{\min}|/\sqrt{m}$ for the algorithms with anisotropic mutation distributions, as employed in (Mezura-Montes and Coello 2004), and $0.4 |x_{\max}-x_{\min}|$ for the algorithms with mutations generated from isotropic distributions, where $x_{\min}$ and $x_{\max}$ are, respectively the minimum and maximum allowed values of each element of the solution in the initial population. The initial q-Gaussian parameter q in algorithms with q-Gaussian mutation was set to 1.0 (value where the Gaussian distribution is reproduced). In the algorithms with q-Gaussian mutation, $r_q=0.8$ and the minimum and maximum values of the q-Gaussian parameter q were set to 0.8 and $0.8{\text{e}},$ respectively, i.e., values, respectively, smaller and higher than the values of q where the Gaussian and Cauchy mutations are reproduced. Experiments, not presented here, using the EP algorithm with different parameter settings (e.g., with the minimum and maximum values of the q-Gaussian parameter q, respectively, set to 0.5 and $0.5{\text{e}}$) showed similar results to those presented in the following section:

8.2 Experimental results: evolutionary programming

8.2.1 Experimental results on qGEP

The experimental results of the fitness error $f({\mathbf{x}}^{\bf best}) -f({\mathbf{x}^{*}})$, where $f({\mathbf{x}}^{\bf best})$ is the best value of fitness found during the run, averaged over 25 runs in the experiments with anisotropic mutation distributions for $m=10$ and $m=30$ are presented in Tables 2 and 3, respectively. Figure 4 shows the convergence of the mean best-of-generation fitness error in the experiments with $m=30$ for functions $f_{9}$ and $f_{10}$.

Fig. 4

Mean $f({\mathbf x^{best}_{g}})-f({\mathbf x^{*}})$, where ${\mathbf x^{best}_{g}}$ is the best-of-generation individual and ${\mathbf x^{*}}$ is the global optimum, in the experiments with functions $f_{9}$ and $f_{10}$ with $m=30$ for the algorithms: GEP (solid line), CEP (dashed line), EP ($q=1.5$) (dotted line) and qGEP (dash-dotted line)

Table 2 Experimental results of the error of the best fitness in each run obtained for algorithms GEP, CEP, EP ($q=1.5$), and qGEP on the test functions with $m=10$

Table 3 Experimental results of the error of the best fitness obtained for algorithms GEP, CEP, EP ($q=1.5$), and qGEP on the test functions with $m=30$

In Tables 4 and 5, the statistic comparison regarding the fitness error of the best individual found during each run is carried out by the Wilcoxon signed rank test (García et al. 2009). Tables 4 and 5 show the p value of the Wilcoxon signed rank test for each function, which indicates the significance for testing the null hypothesis that the difference between the matched samples of the results regarding Alg. A and Alg. B comes from a distribution with median equal to zero. For each problem $f_{i}$, the result regarding the comparison Alg. A–Alg. B is shown, in parentheses, as “=” when the values of the median of Alg. A and Alg. B are equal. When the values of the median are different but the p value is higher than 0.05, i.e., the test indicates that the hypothesis that the median of the difference between the results are zero cannot be rejected at the 5% level, the result is respectively shown as “+” when the median of Alg. A is smaller than that of Alg. B and “−” when the median of Alg. A is higher than that of Alg. B. Otherwise, when the result is statistically significant, the result is respectively shown as “s+” or “s−” when the median of Alg. A is smaller or higher than the median of Alg. B.

Table 4 Statistical comparison of algorithms GEP, CEP, EP ($q=1.5$), and qGEP regarding the error of the best fitness on the test functions with $m=10$

Table 5 Statistical comparison of algorithms GEP, CEP, EP ($q=1.5$), and qGEP regarding the error of the best fitness on the test functions with $m=30$

In the last line of Tables 4 and 5, following the method proposed in (García et al. 2009), the comparison Alg. A–Alg. B regarding the results of all functions is presented, where the p values of the Wilcoxon signed rank test are obtained comparing the vectors with the mean results (shown in Tables 4, 5) obtained for each function by Alg. A and Alg. B, respectively. In the second parentheses, the values in the last line also indicate the difference between the number of times (functions) that the median of Alg. A is smaller than the median of Alg. B (i.e., the number of “+” and “s+” in the respective column) and the number of times (functions) that the median of Alg. B is smaller than the median of Alg. A (i.e., the number of “−” and “s−” in the respective column). For example, the result 5.60E−03 (+s, +22) in the last line, third column of Table 4 indicates that the p value of the Wilcoxon signed rank test regarding the comparison between qGEP and GEP is 5.60E−03, which means that the result is statistically significant (“s+”). The result also indicates that the difference between the number of times that the median of qGEP is smaller than the median of GEP and the number of times that the median of qGEP is higher than the median of GEP is 22. The analysis of the experimental results shown here is presented in Sect. 8.2.3.

8.2.2 Experimental results on IqGEP

The experimental results of the fitness error averaged over 25 runs in the experiments with mutation generated from isotropic distributions for $m=10$ and $m=30$ are, respectively, presented in Tables 6 and 7. Figure 5 shows the convergence of the mean best-of-generation fitness error in the experiments with $m=30$ for functions $f_{9}$ and $f_{10}$. In Tables 8 and 9, the statistic comparison regarding the fitness error is carried out by the Wilcoxon signed rank test. Tables 10 and 11 show the p value of the Wilcoxon signed rank test regarding the comparison between the isotropic and anisotropic algorithms. Table 12 summarizes the results regarding the comparison among qGEP, IqGEP, and other investigated algorithms for different groups of functions. In Table 12, the results regarding the comparison Alg. A–Alg. B indicate the difference between the number of times (functions) that the median of Alg. A is smaller than the median of Alg. B (i.e., the number of “+” and “s+” for the group of functions in the respective tables) and the number of times (functions) that the median of Alg. B is smaller than the median of Alg. A (i.e., the number of “−” and “s−” for the group of functions in the respective tables). The analysis of the experimental results shown here is presented in Sect. 8.2.3.

Fig. 5

Mean $f({\mathbf x^{best}_{g}})-f({\mathbf x^{*}})$, in the experiments with functions $f_{9}$ and $f_{10}$ with $m=30$ for the algorithms: IGEP (solid line), ICEP (dashed line), IEP ($q=1.5$) (dotted line), and IqGEP (dash-dotted line)

Table 6 Experimental results of the error of the best fitness obtained for algorithms IGEP, ICEP, IEP ($q=1.5$) and IqGEP on the test functions with $m=10$

Table 7 Experimental results of the error of the best fitness obtained for algorithms IGEP, ICEP, IEP ($q=1.5$) and IqGEP on the test functions with $m=30$

Table 8 Statistical comparison of algorithms IGEP, ICEP, IEP ($q=1.5$) and IqGEP regarding the error of the best fitness on the test functions with $m=10$

Table 9 Statistical comparison of algorithms IGEP, ICEP, IEP ($q=1.5$) and IqGEP regarding the error of the best fitness on the test functions with $m=30$

Table 10 Statistical comparison of the EP algorithms with mutation generated from anisotropic or isotropic distributions regarding the best fitness on the test functions with $m=10$

Table 11 Statistical comparison of the EP algorithms with mutation generated from anisotropic or isotropic distributions regarding the best fitness on the test functions with $m=30$

Table 12 Comparison of the EP algorithms for different groups of functions

8.2.3 Analysis

Some observations can be made from the experimental results presented in the tables and figures shown in last sections. They are described and analysed below.

First, it is observable that the algorithms with the Gaussian mutation, i.e., GEP and IGEP, generally have a better performance than those with the Cauchy mutation, i.e., CEP and ICEP, on unimodal functions (lines for functions $f_{1}-f_{5}$ in column 2 of Tables 4, 5, 8, 9). Similar results of comparing long tail and Gaussian distributions in the minimization of unimodal functions were reported in the literature (Lee and Yao 2004; Yao et al. 1999). In an unimodal function, long jumps, which often occur when the Cauchy mutation is employed, generally cause a degradation in the performance of the algorithm at the later stage of the evolution because less offspring are generated to explore the local neighborhood. For all functions and algorithms, the norm of the mutation strength parameter vector generally remains large in the initial stage of the evolution, allowing a faster convergence in the initial steps, and decays to small values in later generations.

It can also be observed that the performance of the proposed algorithms (i.e., qGEP and IqGEP) is generally better than that of the algorithms with Cauchy mutation (i.e., CEP and ICEP), and is, in general, equal to or better than that of the algorithms with Gaussian mutation (i.e., GEP and IGEP) on the unimodal functions (lines for functions $f_{1}-f_{5}$ in Tables 4, 5, 8, 9). These results can be explained because, in general, the q-Gaussian mutation generates less long jumps than the Cauchy mutation and more long jumps than the Gaussian mutation for $q \geq 1$. However, when $q<1$, the q-Gaussian distribution is more compact than the Gaussian distribution, which implies shorter jumps.

Second, while the algorithms with Gaussian mutation (i.e., GEP and IGEP) generally outperform the algorithms with Cauchy mutation (i.e., CEP and ICEP) on the unimodal functions, they are generally outperformed on the multimodal functions, especially on the highly multimodal functions, e.g., functions $f_{9}$ and $f_{10}$. These results indicate that the long jumps generated by the Cauchy mutation are advantageous for the individuals to escape from local optima, especially in the later stage of the evolution when the mutation strength parameters have converged to small values.

The proposed algorithms (qGEP and IqGEP) generally outperform the algorithms with Gaussian mutation on the multimodal functions, especially on the highly multimodal (e.g., functions $f_{9}$ and $f_{10}$) or hybrid functions (functions $f_{15}$ – $f_{20}$).

The good performance of the proposed algorithms on multimodal functions can be explained because higher values of the parameter q were eventually employed to allow longer jumps (see Fig. 6, where the distribution parameter q of the current best individual on the first run of two experiments is plotted against the generation index). On the multimodal functions, after the initial stage, the evolution generally occurs in steps. It can be observed that such steps are generally coincident with larger changes in the value of q in Fig. 6, which indicates that jumps in individuals with higher values of q, or in individuals where the value of q has increased, were eventually beneficial. Similar results can be observed in the minimization of other multimodal functions.

Fig. 6

$f({\mathbf x^{best}_{g}})-f({\mathbf x^{*}})$, distribution parameter q, and norm of the mutation strength parameter vector for the current best individual in the last run of IqGEP on function $f_{10}$ with $m=10$. The last graphic shows the differences dq (solid line), between the values of q in two consecutive generations, and $df$ (dashed line), between the values of fitness errors in two consecutive generations, both in the range −0.5 to 0.5

These results indicate that an eventual increase in the value of q in the proposed algorithms can lead to longer jumps (when compared to those produced by Gaussian mutation), which can be advantageous to the evolution since they allow the population to escape from local optima, especially in later stages of the evolution when the mutation strength parameters are generally small. For the algorithms with mutation generated from isotropic distributions, the computed mean change in the best-of-generation fitness generated by advantageous mutations is generally higher for IqGEP on all functions, even when the final fitness is smaller for the other two algorithms. For IqGEP, when the mean changes in the fitness generated by advantageous mutations are analysed for different intervals of q after the middle of the evolutionary process (i.e., when the population has converged to local optima in most of the runs with multimodal functions), an interesting result can be observed. When these values are interpolated by a linear function, while the resulting line has a negative inclination for the unimodal functions (with exception of function $f_{3}$, where the inclination is close to zero), indicating that smaller values of q generally result in higher changes in the fitness function, the resulting line generally has a positive inclination for the multimodal functions, i.e., the selection of higher values of q resulted in higher changes in the fitness function.

When the performance of the algorithms with q-Gaussian mutation is statistically compared to that of the algorithms with Cauchy mutation on the multimodal functions, it can be observed that the proposed algorithms generally present a better or statistically similar performance (Tables 4, 5, 8, 9). The better performance of the algorithm qGEP is the result of a better compromise between long and local jumps of the candidate solutions as the tail of the mutation distribution is self-adapted in qGEP. The use of q-Gaussian mutation is advantageous in noisy functions, too. It can be observed that the performance of the proposed algorithms is better, when compared to other algorithms (Tables 4, 5, 9), with the exception in isotropic algorithms on the function $f_{4}$ with $m=10$ , which is composed by adding noise to the unimodal function $f_{2}$.

Following the method proposed in (García et al. 2009), we can observe that the performance of the algorithms with q-Gaussian mutation is significantly better (with the exception for IqGEP when compared to IGEP and ICEP in the experiment with $m=10$, where the performance of IqGEP is better, but not statistically significant) than the performance of all other algorithms when all functions are considered (last lines in Tables 4, 5, 8, 9).

Finally, the algorithms with mutations generated from isotropic distributions present a better performance than the algorithms with anisotropic mutations on the unimodal functions (see Tables 10, 11). The performance of the mutations generated from isotropic distributions is better than the anisotropic mutations on more multimodal functions with $m=10$ than with $m=30$. In the functions where the anisotropic mutations present a better performance, good solutions can be found in the subspace formed by the points close to the coordinate axes (Fig. 2) and the optimization can be done mainly by coordinate-wise search steps. Such results agree with the conjecture presented in (Hansen et al. 2006) and affirm that anisotropic mutation distributions with longer tails are interesting on those multimodal functions with the low dimensional space where most of the longer jumps occur and better optima than the current best local solution may be located. When Cauchy and q-Gaussian mutations generated from isotropic distributions are employed, it is more difficult to reach a fair region of the search space from a long jump, especially when $m=30$, as the number of points that can be reached exponentially increases with the size of the jump. That is, the sub-space that is more explored by the algorithm is much larger when mutation generated from isotropic distributions with longer tails are used.

However, mutation generated from isotropic distributions with longer tails are generally better than the anisotropic mutation distributions on functions with heavy influence of the crossed component terms in the function evaluation, and where better optima are not located in the subspace explored by the anisotropic algorithm. These facts can be observed when the results of the experiments with the axis parallel Rastrigin function ($f_{9}$), which is separable, and the rotated Rastrigin function ($f_{10}$), where crossed component terms present a heavy influence in the function evaluation, are analysed (Figs. 4, 5). While the anisotropic Cauchy mutation presents a better performance than the q-Gaussian mutation on function $f_{9}$, they present a worse performance on function $f_{10}$. On the other hand, IqGEP presents a better performance than ICEP on both functions. In the experiments on function $f_{9}$, larger jumps to points close to the coordinate axes are advantageous for the population to escape from local optima. In the algorithms ICEP and IqGEP, where the mutations are generated from isotropic distributions, such jumps are rare, while they are common in the anisotropic algorithms CEP and qGEP. However, such jumps are less advantageous on $f_{10}$, where better optima are located far away from the coordinate axes. As the search space is much larger, it is more difficult to reach fair regions, though such regions can be eventually reached by longer jumps produced by ICEP and IqGEP. In general, for larger spaces, it would be more difficult to reach such fair regions if there are only a few of them. It is important to observe that these results depend on the fitness space, its size, and the number and size of the regions where better optima are located.

8.3 Comparison of restart q-Gaussian evolution strategy to other continuous EAs

The experimental results of the error of the best fitness averaged over 25 runs in the experiments with RqGES for $m=10$, $m=30$, and $m=50$ are presented in Tables 13, 14, and 15. When the results of the RqGES are compared with those obtained by IqGEP, the benefits of using recombination and the restart scheme are clear, mainly on multimodal functions. The results for the fitness errors of RqGES can also be compared with those obtained for continuous optimization EAs applied to the problems described in Table 1.

Table 13 Experimental results of the error of the best fitness obtained for algorithm RqGES on the test functions with $m=10$

Table 14 Experimental results of the error of the best fitness obtained for algorithm RqGES on the test functions with $m=30$

Table 15 Experimental results of the error of the best fitness obtained for algorithm RqGES on the test functions with $m=50$

In order to test the performance of RqGES against other EAs, the results obtained are compared with those obtained by the algorithms presented in the Special Session on Real Parameter Optimization for the 2005 IEEE Congress on Evolutionary Computation (Suganthan et al. 2005): BLX-GL50 (García-Martínez and Lozano 2005), BLX-MA (Molina et al. 2005), CoEVO (Pošík 2005), DE (Rönkkönen et al. 2005), DMS-L-PSO (Liang and Suganthan 2005), EDA (Yuan and Gallagher 2005), G-CMA-ES (Auger and Hansen 2005a), K-PCX (Sinha et al. 2005), L-CMA-ES (Auger and Hansen 2005b), L-SADE (Qin and Suganthan 2005), and SPC-PNX (Ballester et al. 2005). Their results for the problems presented in Table 1 for $m=10$ were available in the respective papers.¹ Eight of those algorithms presented results for $m=30$ and two algorithms also for $m=50$. For all algorithms, the same maximum number of fitness evaluations and number of runs presented in Sect. 8.1 were considered. When the results for all functions of the algorithms presented in the special session were compared, G-CMA-ES was pointed as the algorithm with the best average performance (García et al. 2009).

Figures 7, 8, and 9 show the mean of the error $f({\mathbf x^{best}})-f({\mathbf x^{*}})$ (error between the best fitness found during the run and the fitness at the global optimum) for the test functions, respectively, with $m=10$, $m=30$, and $m=50$ for the algorithms (including RqGES). The results shown in those figures were obtained in the respective papers (see last paragraph) and in Tables 13, 14, and 15 for RqGES. The results for RqGES with different values of m are still presented in Figure 10.

Fig. 7

Mean of $f({\mathbf x^{best}})-f({\mathbf x^{*}})$ on the test functions with $m=10$. The termination error value $10^{-8}$ is adopted as the low limit

Fig. 8

Mean of $f({\mathbf x^{best}})-f({\mathbf x^{*}})$ on the test functions with $m=30$

Fig. 9

Mean of $f({\mathbf x^{best}})-f({\mathbf x^{*}})$ on the test functions with $m=50$

Fig. 10

Mean of $f({\mathbf x^{best}})-f({\mathbf x^{*}})$ for RqGES on the test functions with $m=10$, $m=30$, and $m=50$

Tables 16, 17 and 18 present the rank (for the performance regarding the mean best fitness error) for RqGES when compared with the results of other algorithms. A rank i means that RqGES was the i-th best algorithm. When k algorithms present the same mean best fitness error values, the mean between the maximum and minimum rank for such group is considered and a “t” is indicated in the table (e.g., when RqGES and another algorithm presented the best performance, the rank was set to 1.5t).

Table 16 Rank of the mean of the fitness error of RqGES (when compared with 11 algorithms: BLX-GL50, BLX-MA, CoEVO, DE, DMS-L-PSO, EDA, G-CMA-ES, K-PCX, L-CMA-ES, L-SADE, and SPC-PNX) on the test functions with $m=10$

Table 17 Rank of the mean of the fitness error of RqGES (when compared to 8 algorithms: BLX-GL50, BLX-MA, CoEVO, DE, G-CMA-ES, K-PCX, L-CMA-ES, and SPC-PNX) on the test functions with $m=30$

Table 18 Rank of the mean of the fitness error of RqGES (when compared with 2 algorithms: G-CMA-ES and L-CMA-ES) on the test functions with $m=50$

Tables 19, 20, and 21 present the statistical comparison of RqGES to the other algorithms regarding the results of two groups of functions ($f_{1}-f_{25}$ and the hybrid composition functions $f_{15}-f_{25}$), as in (García et al. 2009). The p value of the Wilcoxon signed rank test presented in the tables is obtained comparing the vectors with the mean results obtained for each function for RqGES and Alg. A. The values in the second parentheses indicate the difference between the number of times (functions) that the mean of the error for RqGES is smaller than the mean of the error for Alg. A and the number of times (functions) that the mean of the error for Alg. A is smaller than the mean of the error for RqGES. A negative value indicates that Alg. A presented smaller mean (when compared with RqGES) on more functions.

Table 19 Statistical comparison of RqGES to other algorithms regarding the mean of the fitness error on the test functions with $m=10$

Table 20 Statistical comparison of RqGES with other algorithms regarding the mean of the fitness error on the test functions with $m=30$

Table 21 Statistical comparison of RqGES to other algorithms regarding the mean of the fitness error on the test functions with $m=50$

One can observe that, for the experiments with $m=10$, the performance of RqES was significantly worse than the performance of BLX-GL50 and G-CMA-ES for the group $f_{1}-f_{25}$, while it was significantly better than the performance of K-PCX for the group $f_{15}-f_{25}$ (Table 19). For the experiments with $m=30$, RqES was significantly better than CoEVO in both groups (Table 20). In general, RqES presented better performance for high dimension and multimodal functions.

It can be observed (Tables 16, 17, 18; Figs. 7, 8, 9) that RqGES presents good results on the functions with noise (functions $f_{4}$ and $f_{17}$). In the multimodal function $f_{17}$, RqES was the best algorithm for $m=10$ and $m=50$, while it was the second best algorithm for $m=30$ (one can observe in Figs. 8, 9 that the performance of RqGES, differently for the other algorithms, did not deteriorated from function $f_{16}$ to function $f_{17}$, obtained by adding noise to function $f_{16}$). In the unimodal function $f_{4}$, RqES is the best algorithm for $m=50$ and the second best for $m=30$. RqGES presents the best results on function $f_{11}$ (with the exception for $m=50$ where RqGEs is the second best algorithm), which is differentiable only on a set of points (Suganthan et al. 2005). The properties of function $f_{11}$ can also explain the better results of RqGES on the hybrid composition functions where function $f_{11}$ was used.

Such properties (noise and rugged landscapes) can represent obstacles for algorithms that intensively explore local information about the search landscape to guide the optimization process, like some of the best EAs used in continuous optimization problems. The good performance of RqGES on such problems can be explained by the eventual use of higher values of q to produce larger jumps on the search landscape. However, eventual large jumps makes RqGES to generate less candidate solutions, when compared with other algorithms, close to the best found solutions, which explains the worse performance of RqGES on the unimodal functions (with exception for function $f_{4}$). Besides, RqGES does not employ additional mechanisms to explore local information about the search space, what explains the worse performance, when compared with the best algorithms, in unimodal and multimodal functions where such information is useful to guide the optimization process.

On function $f_{25}$, higher values of q were useful too, as the global optimum is outside the initialization range. It can also be observed that RqGES has a good performance on rotated functions, e.g., $f_{10}$, because the q-Gaussian mutation is generated from an isotropic distribution. One can observe, in Figs. 8 and 9, that RqGES is the only algorithm where the performance did not deteriorate when function $f_{9}$ was rotated to generate function $f_{10}$. In the figures, one can observe that the error for $f_{10}$ is higher than for $f_{9}$ for all algorithms, except for RqGES.

9 Conclusion and future work

The use of self-adaptation is proposed in this paper to control not only the mutation strength parameter, but also the mutation distribution for EAs. For this purpose, self-adapted q-Gaussian mutations generated from anisotropic and isotropic distributions are employed. The q-Gaussian distribution allows to smoothly change the shape of the mutation distribution by setting a real parameter q and can reproduce either finite or infinite second moment distributions. In the proposed method, the real parameter q of the q-Gaussian distribution, which defines the shape of the distribution employed by the mutation operator, is encoded in the chromosome of the individual and is allowed to evolve.

In the proposed method, the decision of choosing which distribution is more indicated for a given problem and at a given moment of the evolutionary process is made by the algorithm. This property can be observed in the experimental results presented in Sect. 8, where the proposed q-Gaussian mutation generally presents a performance similar to or better than the Gaussian mutation when the Gaussian mutation is better than the Cauchy mutation and generally presents a performance similar to or better than the Cauchy mutation when it is better than the Gaussian mutation. Generally speaking, the experimental results indicate the efficiency of the proposed self-adaptation scheme.

In this paper, EP was selected to compare the Gaussian, Cauchy, and q-Gaussian mutations because it only uses mutation as a transformation operator. In this way, it is easier to analyse the influence of each type of mutation operators. In fact, the q-Gaussian mutation can be used in other types of EAs. The results for the EP with q-Gaussian mutation can be improved if recombination and other heuristics are used, which was shown by the experimental results of the restart q-Gaussian ES presented in this paper. RqGES presented competitive performance when compared with some of the best EAs for real-parameter optimization. The possible use of the q-Gaussian mutation in ESs with adaptive encoding (Hansen 2008), which is a form of applying the representation changes given by the covariance matrix adaptation (CMA) in the continuous domain, is a relevant future work. Other future works include the investigation of other control methods for the q parameter (including self-organization Tinós and Yang 2007), and the use of the q-Gaussian mutation for dynamic optimization problems (Wang et al. 2009), like the optimization of synaptic weights in evolutionary neural networks in dynamic environments (Tinós and Carvalho 2006).