Minimax mean-variance models for fuzzy portfolio selection

Abstract

This paper discusses fuzzy portfolio selection problem in the situation where each security return belongs to a certain class of fuzzy variables but the exact fuzzy variable cannot be given. Two credibility-based minimax mean-variance models are proposed. The crisp equivalents of the models to linear programming ones are given in three special cases. In addition, a general solution algorithm is also provided. To help understand the modeling idea and to illustrate the effectiveness of the proposed algorithm, one example is presented.

1 Introduction

Portfolio selection has been one of the hottest research topics in financial area since Markowitz proposed his famous mean-variance theory (Markowitz 1952, 1959). Markowitz’s great contribution is that he initially proposed a mathematical way for analyzing portfolio selection problem. Since Markowitz, mean-variance idea has been remaining the most popular principle for portfolio selection. Traditionally, security returns were assumed to be random variables. A variety of mean-variance models have been constantly developed (e.g., Abdelaziz et al. 2007; Corazza and Favaretto 2007; Hirschberger et al. 2007; Liu et al. 2003). As an improvement of mean-variance models, mean-semivariance models have been proposed employing semivariance as the measure of risk (Chow and Denning 1994; Grootveld and Hallerbach 1999; Markowitz 1959). Different from defining the deviation from the expected value as risk, the probability of a pre-set level of loss was considered as risk by Roy (1952), Elton and Gruber (1995), William (1997) and so on. Recently, Huang (2008a) proposed a new definition of risk and presented a new mean-risk model by maximizing the expected return under the constraint that the risk curve of the portfolio is below the confidence curve.

Since many non-probabilistic factors may affect the security market, in many situations security returns contain much fuzziness instead of randomness. With the introduction and development of fuzzy set theory, scholars began to study portfolio selection problem with fuzzy returns. The researches mainly focused on extending mean-variance selection idea to fuzzy environment and a variety of fuzzy mean-variance models have been developed (Arenas-Parra et al. 2001; Bilbao-Terol et al. 2006; Carlsson et al. 2002; Tanaka et al. 2000). In particular, Huang (2007a, 2009) argued that credibility is a more suitable measure than possibility for a fuzzy event and proposed (Huang 2007a) two credibility-based fuzzy mean-variance models. As an extension of using semivariance to measure portfolio risk, Huang (2008b) defined the semivariance of fuzzy variable and proposed fuzzy mean-semivariance models for fuzzy portfolio selection.

Since the security market is so sensitive to various economic and political factors, sometimes exact random variables or fuzzy variables cannot be given to describe the security returns. Thus people have to handle portfolio selection with more complex uncertainty, and different mean-variance models were proposed. When the security returns are regarded to be random but the expected return of each underlying random asset varies in an estimated interval, Deng et al. (2005) proposed a stochastic minimax model by maximizing the worst possible expected rates of returns on portfolios. When the security returns are regarded to contain fuzziness with random parameters, Ammar (2008) and Li and Xu (2009) employed fuzzy random programming method to select the optimal portfolio. When the security returns are regarded to be random but the expected returns of the securities are fuzzy, Huang (2007b, 2008c) proposed different random fuzzy mean-variance models. In this paper, we will discuss the portfolio selection problem in a different complex uncertain environment where each underlying security is predicted to belong to a class of fuzzy variables but the exact fuzzy variable cannot be given.

The rest of the paper is organized as follows: to help better understand the paper, the mean-variance selection idea proposed in Huang (2007a) will be reviewed first in Sect. 2. Necessary knowledge about fuzzy variables will also be presented in the section. Then two credibility-based minimax portfolio selection models will be proposed in Sect. 3, and the crisp equivalents of the new models will be given in some special cases in Sect. 4. In Sect. 5, a hybrid intelligent algorithm will be provided for solving the optimization problems in general cases. In Sect. 6, one numerical example will be presented to illustrate the effectiveness of the proposed algorithm. Finally, the concluding comments will be presented in Sect. 7.

2 Fuzzy mean-variance selection idea

In the field of fuzzy portfolio selection, many scholars have extended Markowitz’s mean-variance models (e.g., Arenas-Parra et al. 2001; Carlsson et al. 2002; Bilbao-Terol et al. 2006; Lacagnina and Pecorella 2006; Zhang et al. 2007). In particular, Huang (2007a, 2009) proposed that credibility is a more suitable measure than possibility measure for fuzzy portfolio selection because credibility is self-dual while possibility is not. Using possibility measure, we find that two fuzzy events with different occurring chances may have the same possibility value 1. Furthermore, we find that whenever the possibility value of a portfolio return greater than a target value is lower than 1, the possibility value of the opposite event (i.e., the portfolio return less than or equal to the target value) is the maximum value of 1; or whenever the possibility value of a portfolio return less than or equal to a target value is lower than 1, the possibility value of the opposite event (i.e., the portfolio return greater than the target value) is the maximum value of 1. For example, for a portfolio return described by the triangular fuzzy variable ξ = (0, 1, 2), though the occurring chances of the return being lower than 1 and than 1.5 are different, the possibility values of the two events are the same value of 1, i.e., Pos {ξ < 1} = Pos {ξ < 1.5} = 1. In addition, it can be calculated that the possibility value of the portfolio return not greater than 0.5 is 0.5, while the possibility value of the opposite event is 1, i.e., Pos {ξ ≤ 0.5} = 0.5, while Pos {ξ > 0.5} = 1. These results are quite awkward and will confuse the decision maker. Thus, Huang measured portfolio risk and return based on credibility. Furthermore, Huang argued that it is easier and more direct to describe a security return by fuzzy variable than by fuzzy probability. As a counterpart of Markowitz’s mean-variance models in stochastic environment, Huang proposed two new credibilistic mean-variance models (Huang 2007a). Other fuzzy portfolio selection models can be found in Huang (2009).

Let x _i be the investment proportion in the ith security, and ξ _i the fuzzy variable that represents the ith security return. The ξ _i is defined as ξ _i  = (p ^′ _i  + d _i  − p _i )/p _i  , i = 1, 2,..., n, respectively, where p ^′ _i is the estimated closing price of the security i in the future, p _i the closing price of the security i at present, and d _i the estimated dividend of the security i from now to the future time. The mean-variance selection idea is to regard the expected value of the fuzzy portfolio return as the investment return and the variance the investment risk. Thus, the investors should select the portfolio with the maximum expected return under the constraint that the variance of the portfolio return will not be greater than a preset tolerable level. The mathematical expression of the idea is as follows:

$$ \left\{\begin{array}{lll}\max \hbox{E}[x_1\xi_1+x_2\xi_2+\cdots+x_n\xi_n]\\ \hbox{subject to:}\\ \hbox{V}[x_1\xi_1+x_2\xi_2+\cdots+x_n\xi_n]\le\gamma\\ x_1+x_2+\cdots+x_n=1\\ x_i\ge 0,\quad i=1,2,\ldots,n \end{array}\right.$$

(1)

where γ is the maximum tolerable variance level, and E the expected value operator and V the variance operator based on credibility measure defined as follows:

Let ξ be a fuzzy variable with membership function μ. The credibility measure is defined as (Liu and Liu 2002)

$$ \hbox{Cr }\{\xi\in A\}=\frac{1}{2}\left(\sup\limits_{t\in A} \mu(t)+1-\sup\limits_{t\in A^c} \mu(t)\right) $$

(2)

for any set A of real numbers. It is easy to see that credibility is self-dual.

The expected value of ξ is defined as (Liu and Liu 2002)

$$ \hbox{E} [\xi]=\int\limits_0^\infty\hbox{Cr }\{\xi\ge r\}\,\hbox{d}r -\int\limits_{-\infty}^0\hbox{Cr }\{\xi\le r\}\,\hbox{d}r $$

(3)

provided that at least one of the two integrals is finite. If the fuzzy variable ξ has a finite expected value, then its variance is defined as (Liu and Liu 2002)

$$ \hbox{V}[\xi]=\hbox{E}\left[(\xi-\hbox{E}[\xi])^2\right]. $$

(4)

3 Fuzzy minimax mean-variance models

As discussed in Sect. 1, there are various kinds of uncertainty in the security market. Sometimes, the market is so complex that the investors only know that the security returns belong to a certain class of fuzzy variables. Then how should the investors select their optimal portfolio? In this section, we will handle such a complex fuzzy portfolio selection problem.

Suppose each security return ξ _i is fuzzy and known to belong to a certain class of fuzzy variables $\Upgamma_i.$ Let β be the maximum variance level the investors can tolerate. Then, for the safety purpose of decision making, the investors should first require that the maximum variance of the portfolio return in all cases should not be greater than the pre-set β level and then pursue maximum expected return in the worst case. To express the idea mathematically, we have the model as follows:

$$ \left\{\begin{array}{lll} \max \limits_{x_i, 1\le i\le n}\, \min\limits_{\xi_i, 1\le i\le n} \hbox{E}[x_1\xi_1+x_2\xi_2+\cdots+x_n\xi_n]\\ \hbox{subject to:}\\ \max \limits_{\xi_i, 1\le i\le n} \hbox{V}[x_1\xi_1+x_2\xi_2+\cdots+x_n\xi_n]\le\beta\\ \xi_i \in \Upgamma_i,\quad i=1,2,\cdots,n \\ x_1+x_2+\cdots+x_n=1\\ x_i\ge 0,\quad i=1,2,\ldots,n, \end{array}\right. $$

(5)

where E denotes the expected value operator of the fuzzy variables, and V the variance operator. The formula $\max \limits_{\xi_i, 1\le i\le n} \hbox{V}[x_1\xi_1+x_2\xi_2+\cdots+x_n\xi_n]$ gives the maximum variance value (i.e., the maximum risk level) of the portfolio return in all cases. The constraint $\max \limits_{\xi_i, 1\le i\le n} \hbox{V}[x_1\xi_1+x_2\xi_2+\cdots+x_n\xi_n]\le\beta$ means that the variance value of the portfolio return in any cases will not be greater than the preset level β. It is clear that the portfolios satisfying this constraint are safe ones. The formula $\min\limits_{\xi_i, 1\le i\le n} \hbox{E}[x_1\xi_1+x_2\xi_2+\cdots+x_n\xi_n]$ finds the expected value in worst case, and the objective function $\max \limits_{x_i, 1\le i\le n} \, \min\limits_{\xi_i, 1\le i\le n} \hbox{E}[x_1\xi_1+x_2\xi_2+\cdots+x_n\xi_n]$ means that the optimal portfolio should be the one with maximum expected return in the worst case.

If the investors preset a threshold of expected value b, they should first require that the minimum expected return in all cases should not be less than this pre-set level, and then pursue the portfolio with minimum variance value in the worst case. The mathematical expression is as follows:

$$ \left\{\begin{array}{lll} \min \limits_{x_i, 1\le i\le n}\, \max\limits_{\xi_i, 1\le i\le n} \hbox{V}[x_1\xi_1+x_2\xi_2+\cdots+x_n\xi_n]\\ \hbox{subject to:}\\ \quad \min \limits_{\xi_i, 1\le i\le n} \hbox{E}[x_1\xi_1+x_2\xi_2+\cdots+x_n\xi_n]\ge b\\ \xi_i \in \Upgamma_i,\quad i=1,2,\ldots,n \\ x_1+x_2+\cdots+x_n=1\\ x_i\ge 0,\quad i=1,2,\ldots,n. \end{array}\right. $$

(6)

4 Crisp equivalents

To use traditional methods to solve the models (5) and (6), we need to convert the models into traditional programming models. Normally distributed fuzzy variable and triangular fuzzy variable are two popular types of fuzzy variables. Let us first review them briefly and then discuss the crisp equivalents of the proposed models when all the security returns can be described by either of the two special types of fuzzy variables.

Example 1.

A fuzzy variable ξ is called a normally distributed fuzzy variable if it has a normal membership function

$$ \mu(r)=2 \left(1+\exp \left(\frac{\pi |r-e|}{\sqrt{6} \sigma}\right)\right)^{-1}, \quad r\in R, \; \sigma>0, $$

where e is the expected value of ξ and σ² the variance value. We denote it by $\xi \sim {\mathcal{N}} (e, \sigma).$ It has been proven (Li and Liu 2007) that a normally distributed fuzzy variable has a maximum entropy among all types of fuzzy variables with expected value e and variance value σ².

A security return with maximum entropy distributes most dispersively, and it will be most difficult to predict whether a specific return value will occur. Thus, if only the expected and variance values of the security return can be given, a conservative investor can use the normally distributed fuzzy variable to describe this security return. Usually the intervals of the expected return and the variance value can be obtained. Then the investor can use a class of normally distributed fuzzy variable to describe the security return.

Theorem 1

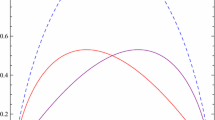
Assume that each security return ξ _i can be described by a class of normally distributed fuzzy variables, i.e., $\xi_i \sim {\mathcal{N}} (e_i, \sigma_i),$where$e_i \in [e_{li},e_{ui}], \sigma_i \in [\sigma_{li}, \sigma_{ui}]$ (see Fig. 1). Then Model (5) can be converted into the following model:

$$ \left\{\begin{array}{lll} \max x_1e_{l1}+x_2e_{l2}+\cdots+x_ne_{ln}\\ \hbox{subject to:}\\ \quad x_1\sigma_{u1}+x_2\sigma_{u2}+\cdots+x_n\sigma_{un}\le \sqrt{\beta}\\ x_1+x_2+\cdots+x_n=1\\ x_i\ge 0,\quad i=1,2,\ldots,n. \end{array}\right. $$

(7)

Fig. 1

Membership functions of a class of normally distributed fuzzy variables

Proof

We know from Li and Liu (2007) that a weighted sum of normally distributed fuzzy variables is also normally distributed. That is, if fuzzy variables $\eta_1 \sim {\mathcal{N}}(e_1, \sigma_1)$ and $\eta_2 \sim {\mathcal{N}} (e_2, \sigma_2)$ are normally distributed fuzzy variables, then for any real numbers λ₁ and λ₂, the fuzzy variable λ₁η₁ + λ₂η₂ is also a normally distributed fuzzy variable with expected value λ₁ e ₁ + λ₂ e ₂ and variance $(|\lambda_1|\sigma_1+|\lambda_2|\sigma_2)^2,$ whose membership function is

$$ \mu(r)=2 \left(1+\exp \left(\frac{\pi |r-(\lambda_1e_1+\lambda_2e_2)|}{\sqrt{6} (|\lambda_1|\sigma_1+|\lambda_2|\sigma_2)}\right)\right)^{-1}.$$

Therefore, $\max \limits_{\xi_i, 1\le i\le n} \hbox{V}[x_1\xi_1+x_2\xi_2+\cdots+x_n\xi_n]$ can be converted into $(x_1\sigma_{u1}+x_2\sigma_{u2}+\cdots+x_n\sigma_{un})^2$ since x _i  ≥ 0 for i = 1, 2,...,n, which implies that only those securities whose returns are $\xi_i^{\prime} \sim {\mathcal{N}} (e_i, \sigma_{ui}), e_i \in [e_{li},e_{ui}], 1\le i\le n$ need pass the constraint check. Then $\max \limits_{x_i, 1\le i\le n} \, \min\limits_{\xi_i, 1\le i\le n} \hbox{E}[x_1\xi_1+x_2\xi_2+\cdots+x_n\xi_n]$ now becomes $\max \limits_{x_i, 1\le i\le n} \, \min\limits_{\xi_i^{\prime}, 1\le i\le n} \hbox{E}[x_1\xi_1^{\prime}+x_2\xi_2^{\prime}+\cdots+x_n\xi_n^{\prime}],$ and can be converted into $\max x_1e_{l1}+x_2e_{l2}+\cdots+x_ne_{ln}$ since x _i  ≥ 0 for i = 1, 2,...,n. Thus, the theorem is obvious.

Example 2

A fuzzy variable ξ is called a triangular fuzzy variable if it has a triangular membership function which is given by

$$ \mu(r)=\left\{\begin{array}{l} \frac{r-a}{b-a}, \quad \hbox{if }a\le r \le b\\ \frac{r-c}{b-c}, \quad \hbox{if }b \le r \le c\\ 0, \quad \quad \hbox{otherwise}. \end{array}\right. $$

We denote it by ξ = (a, b, c). Especially, if b − a = c − b, we call it the symmetrical triangular fuzzy variable. If the investor believes that the security returns can be described by the symmetrical triangular fuzzy variables but is not very sure about the lowest and highest values that the security returns may reach, he or she can use a class of symmetrical triangular fuzzy variables to describe the security returns.

Theorem 2

Assume that each security return ξ _i can be described by a class of symmetrical triangular fuzzy variables ξ _i  = (a _i , b _i , 2b _i  − a _i ), wherea _i  ∈ [a _li , a _ui ], 1 ≤ i ≤ n (see Fig. 2). Then model (5) can be converted into the following model:

$$ \left\{\begin{array}{lll} \max x_1b_1+x_2b_2+\cdots+x_nb_n\\ \hbox{subject to:}\\ \quad x_1(b_{1}-a_{l1})+x_2(b_{2}-a_{l2})+\cdots+x_n(b_{n}-a_{ln}) \le \sqrt{6\beta}\\ x_1+x_2+\cdots+x_n=1\\ x_i\ge 0,\quad i=1,2,\ldots,n. \end{array}\right. $$

(8)

Fig. 2

Membership functions of a class of triangular fuzzy variables

Proof

We know from Liu (2002) that a weighted sum of triangular fuzzy variables is also a triangular fuzzy variable. That is, if fuzzy variables η₁ = (a ₁, b ₁, c ₁) and η₂ = (a ₂, b ₂, c ₂) are triangular fuzzy variables, then for any real numbers λ₁ ≥ 0 and λ₂ ≥ 0, the fuzzy variable λ₁η₁ + λ₂η₂ = (λ₁ a ₁ + λ₂ a ₂, λ₁ b ₁ + λ₂ b ₂, λ₁ c ₁ + λ₂ c ₂) is also a triangular fuzzy variable. It can be calculated that for a symmetrical triangular fuzzy variable η = (a, b, c), its expected value is b and variance value is (c − a)²/24. Therefore, $\max \limits_{\xi_i, 1\le i\le n} \hbox{V}[x_1\xi_1+x_2\xi_2+\cdots+x_n\xi_n]$ can be converted into $(\sum_{i=1}^n x_ic_{ui}-\sum_{i=1}^n x_ia_{li})^2/24=(\sum_{i=1}^n x_ib_i-\sum_{i=1}^n x_ia_{li})^2/6,$ which implies that only those securities whose returns are ξ ^′ _i  = (a _li , b _i , c _ui ), 1 ≤ i ≤ n need pass the constraint check. Then $\max \limits_{x_i, 1\le i\le n} \, \min\limits_{\xi_i, 1\le i\le n} \hbox{E}[x_1\xi_1+x_2\xi_2+\cdots+x_n\xi_n]$ now becomes $\max \limits_{x_i, 1\le i\le n} \, \min\limits_{\xi_i^{\prime}, 1\le i\le n} \hbox{E}[x_1\xi_1^{\prime}+x_2\xi_2^{\prime}+\cdots+x_n\xi_n^{\prime}],$ and can be converted into $\max x_1b_1+x_2b_2+\cdots+x_nb_n.$ Thus, the theorem is obvious.

Theorem 3

Assume that each security return ξ _i can be described by a class of symmetrical triangular fuzzy variables ξ _i  = (a _i , a _i  + t _i , a _i  + 2t _i ), where a _i  ∈ [a _li , a _ui ], 1 ≤ i ≤ n (see Fig. 3). Then model (5) can be converted into the following model:

$$ \left\{\begin{array}{lll} \max x_1(a_{l1}+t_1)+x_2(a_{l2}+t_2)+\cdots+x_n(a_{ln}+t_n)\\ \hbox{subject to:}\\ x_1t_1+x_2t_2+\cdots+x_nt_n \le \sqrt{6\beta}\\ x_1+x_2+\cdots+x_n=1\\ x_i\ge 0,\quad i=1,2,\ldots,n. \end{array}\right. $$

(9)

Fig. 3

Membership functions of a class of triangular fuzzy variables

Proof

From the properties of the symmetrical triangular fuzzy variable, we know that the expected value of the fuzzy variable η = (a, a + t, a + 2t) is a + t and the variance value is t ²/6. Thus, the theorem is obvious.

5 Hybrid intelligent algorithm

Though in some special cases we can convert the proposed models into their crisp equivalents as shown in Sect. 4, however, in other cases, it is difficult to do so. Therefore, we need to find an algorithm to solve the proposed optimization problems in general cases. Genetic algorithm (GA) was proposed by Holland (1975). It does not require much mathematical analysis on the underlying optimization problems and has solved many complex optimization problems that are difficult to solve in traditional methods. In Huang (2007a), we have designed a fuzzy simulation based GA to solve the fuzzy mean-variance models in which fuzzy simulation is used to calculate the expected and variance values and GA is used for finding the optimal portfolio. In the algorithm, the solution time is mainly spent on the simulation procedures for calculating the expected and the variance values. Though the algorithm can be revised to solve the minimax models (5) and (6), however, when checking the constraints, we have to employ fuzzy simulation to calculate a sufficient number of expected values or the variance values in order to find the maximum variance value for Model (5) or the minimum expected value for Model (6). Thus, when using fuzzy simulation to calculate the expected value and the variance value, the algorithm will take a long time to find the optimal solution. Neural network (NN) is famous for approximating any nonlinear continuous functions over a closed bounded set (Leshno et al. 1993). In order to speed up the computational process, we employ an NN to approximate the expected and variance values, respectively. Then the trained NN is integrated into GA to find the optimal portfolio. In the following, we introduce in detail the NN training process and summarize the hybrid intelligent algorithm.

5.1 Generating training data by fuzzy simulation

In order to train neurons to approximate the fuzzy expected value and variance value, one set of expected values and one set of variance values are first generated by fuzzy simulation as the training data sets. The detailed introduction for calculating expected and variance values by fuzzy simulation has been presented in Huang (2007a). Let ${\user2{x}}=(x_1,x_2,\ldots,x_n)$ represent the decision vector, where x _i are the investment proportions in the ith securities and n the number of the securities. Let C = (c ₁, c ₂,...,c _n ) denote the chromosomes, d ₁ and d ₂ the expected and variance values obtained by fuzzy simulation, respectively. The algorithm for generating training data is summarized as follows:

• Step 1 Define the number of training data N in each training set.

• Step 2 Set j = 1.

• Step 3 Randomly generate a vector C = (c₁, c₂,...,c _n ) from the hypercube [0, 1]ⁿ. Set

  $$ x_i=\frac{c_i}{c_1+c_2+\cdots+c_n},\quad i=1,2,\ldots,n $$

  (10)

  which ensures that x₁ + x₂ +⋯+ x _n  = 1 always holds.

• Step 4 Use fuzzy simulation to calculate the expected value d₁ = E[x₁ξ₁ + x₂ξ +⋯+ x _n ξ _n ] and variance value d₂ = V[x₁ξ₁ + x₂ξ +⋯+ x _n ξ _n ], respectively.

• Step 5 If j ≤ N, then j = j + 1 and go to step 3. Otherwise, stop.

5.2 Training NN

Determining network structure Before training the NN, we should determine the network structure, i.e., the number of hidden layers and the number of hidden neurons. Since in practice it is usually enough to train the NN with one hidden layer to approximate the uncertain function, in our paper, we consider the NN with one hidden layer connecting the input layer and the output layer in a feed-forward way. For example, for Model (5), we train one NN with n neurons in the input layer, h neurons in the hidden layer, and two neurons in the output layer to approximate the expected value function E[x₁ξ₁ + x₂ξ +⋯+ x _n ξ _n ] and the variance value function V[x₁ξ₁ + x₂ξ +⋯+ x _n ξ _n ], respectively. The number of hidden neurons h can be determined by the pruning algorithm (Castellano et al. 1997).

Training NN by backpropagation algorithm Let ω ⁰ _ij be the weight vector of the jth input neuron connected to the ith hidden neuron, ω ¹ _ij the weight vector of the jth hidden neuron connected to the ith output neuron, and ρ the activation function of neurons in the hidden layer, e.g., ρ(x) = tanh(x). Then the outputs of the neurons in the hidden layer are

$$ x_i^1=\rho\left(\sum\limits_{j=1}^n\omega_{ij}^0x_j+\omega_{i0}^0\right) =\hbox{tanh}\left(\sum\limits_{j=1}^n\omega_{ij}^0x_j+\omega_{i0}^0\right), \quad i=1,2,\ldots,h, $$

(11)

and the outputs of the neurons in the output layer are

$$ y_i=\sum\limits_{i=1}^h\omega_{ij}^1x_j^1+\omega_{i0}^1, \quad i=1,2. $$

(12)

The aim of the NN training is to minimize the error between the target output produced by the NN and the actual output (in our case, the expected and variance values obtained by fuzzy simulation) by updating the weight values continuously.

Backpropagation algorithm is a well-known learning algorithm for NN training and is adopted in the paper. Assume that by fuzzy simulation we have obtained big enough training data $({\user2{x}}, y_{1i})$ and $({\user2{x}}, y_{2i}), i=1,2,\ldots,N,$ for the expected and variance values, respectively. The weight values will be updated continuously in the training phase until the following error function

$$ \hbox{Err}({\varvec{\omega}})=\frac{1}{2N}\sum\limits_{k=1}^{2}\sum\limits_{i=1}^{N} ||y_{ki}-d_{k,i}||^2 $$

(13)

is small enough, i.e.,

$$ \hbox{Err}({\varvec{\omega}})\le \varepsilon, $$

where $\varepsilon$ is a preset small enough error rate.

To minimize the error function, we first randomly generate an initial weight vector ${\varvec{\omega}}$ for the neural network. Set ${\Updelta}\omega_{ij}^1=0$ for i = 1, 2 and j = 0, 1, 2,...,h, and ${\Updelta}\omega_{ij}^0=0$ for i = 1, 2,...,h and j = 0, 1, 2,...,n. Then the weights are adjusted by an on-line learning process. Take the tth sample as an example. It is known from Eqs. (11) and (12) that the outputs of the hidden neurons are

$$ x_{t,i}^1=\hbox{tanh}\left(\sum\limits_{j=1}^n\omega_{ij}^0x_{t,j}+\omega_{i0}^0\right), \quad i=1,2,\ldots,h, $$

and the outputs of the NN are

$$ y_{t,i}=\sum\limits_{j=1}^h\omega_{ij}^1x_{t,j}^1+\omega_{i0}^1, \quad i=1,2. $$

Then the error between the tth target output and actual output is

$$ \hbox{Err}_t({\varvec{\omega}})={\frac{1}{2}}\left((y_{1,t}-d_{1,t})^2 +(y_{2,t}-d_{2,t})^2\right). $$

(14)

The weights of the NN will be adjusted continuously based on the error function $\hbox{Err}_t({\varvec{\omega}}).$ For the hidden output weights ω ¹ _ij , i = 1, 2, j = 0, 1, 2,...,h, we have

$$ \Updelta \omega_{ij}^1 \leftarrow -\alpha\frac{\partial Err_t}{\partial w_{ij}^1}+\eta\Updelta w_{ij}^1, \quad \omega_{ij}^1 \leftarrow \omega_{ij}^1+\Updelta \omega_{ij}^1, $$

(15)

where $\frac{\partial \hbox{Err}_t}{\partial w_{ij}^1}=(y_{ti}-d_{ti})x_{tj}^1,$ and α and η are numbers between 0 and 1, e.g., α = 0.05 and η = 0.01.

For the input-hidden weights ω ⁰ _ij , i = 1, 2,...,h, j = 0, 1, 2,...,n, we have

$$ \Updelta \omega_{ij}^0 \leftarrow -\alpha\frac{\partial {\hbox{Err}}_t}{\partial w_{ij}^0}+\eta\Updelta w_{ij}^0, \quad \omega_{ij}^0 \leftarrow \omega_{ij}^0+\Updelta \omega_{ij}^0, $$

(16)

where $\frac{\partial Err_t}{\partial w_{ij}^0}=x_{tj}(1-(x_{ti}^1)^2)\sum_{l=1}^2(y_{tl}-d_{tl})\omega_{li}^1.$

When the NN has been trained over all the numbers of input–output training data, the average error is calculated according to the error function (13). Repeat the training process until the error is less than the predetermined precision $\varepsilon$ or the maximum iteration times N′ is met.

The algorithm for training the NN is summarized as follows:

• Step 1 Initialize weight vector ω, and set the parameters including error rate $\varepsilon$ and α and η. Set t = 0, and i = 1.

• Step 2t ← t + 1.

• Step 3 Adjust the weights according to (15) and (16).

• Step 4 Calculate the error Err _t according to (14).

• Step 5 If t ≤ N, go to step 2.

• Step 6 Set ${\hbox{Err}}=\sum_{t=1}^N {\hbox{Err}}_t.$

• Step 7 If $\hbox{Err}> \varepsilon,$ and i < N′, then i ←i + 1 and t = 0, and go to Step 2.

• Step 8 End.

5.3 Hybrid intelligent algorithm

Initialization After training NN, the trained NN is embedded into the GA to produce the hybrid intelligent algorithm. For the detailed introduction of the GA, the interested readers can refer to Huang (2007a). Here, we introduce in detail the initialization operation in which the feasibility checking and the computation of objective values are also introduced, and then summarize the hybrid intelligent algorithm.

When initializing chromosomes, for Model (5), first, randomly generate a point C = (c ₁, c ₂,...,c _n ) from the hypercube [0, 1]ⁿ. Next, randomly select fuzzy variables {ξ_1k , ξ_2k ,...,ξ _nk } from the corresponding class $\{\Upgamma_1, \Upgamma_2,\ldots,\Upgamma_n\},$ where 1 ≤ k ≤ N and N is a sufficiently large number. After that, use the trained NN to calculate the expected values E [x ₁ξ_1k  + x ₂ξ_2k  +⋯+ x _n ξ _nk ] and the corresponding variance values V [x ₁ξ_1k  + x ₂ξ_2k  +⋯+ x _n ξ _nk ]. Among N couples of expected and variance values, find the maximum variance value denoted by V_max and the minimum expected value whose corresponding variance value is V_max. We denote this expected value by E_min. Then the feasibility of the chromosome C = (c ₁, c ₂,...,c _n ) is checked as follows:

$$ \begin{aligned} & If\;\hbox{V}_{max}>\beta\;return\;0;\\ &return\;1; \end{aligned} $$

in which 1 means feasible, and 0 non-feasible.

For Model (6), first, randomly generate a point C = (c ₁, c ₂,...,c _n ) from the hypercube [0,1]ⁿ. Next, randomly select fuzzy variables {ξ_1k , ξ_2k ,...,ξ _nk } from the corresponding class $\{\Upgamma_1, \Upgamma_2,\ldots,\Upgamma_n\}$, where 1 ≤ k ≤ N and N is a sufficiently large number. After that, use the trained NN to calculate the expected values E [x ₁ξ_1k  + x ₂ξ_2k +⋯+ x _n ξ _nk ] and the corresponding variance values V [x ₁ξ_1k  + x ₂ξ_2k +⋯+ x _n ξ _nk ]. Among N couples of expected and variance values, find the minimum expected value denoted by E_min and the maximum variance value whose corresponding expected value is E_min. We denote this variance value by V_max. Then the feasibility of the chromosome C = (c ₁, c ₂,...,c _n ) is checked as follows:

$$ \begin{aligned}&If\;\hbox{E}_{min}<b\;return\;0;\\ &return\;1;\\ \end{aligned} $$

in which 1 means feasible, and 0 non-feasible.

If C is checked to be feasible, it is taken as an initial chromosome. For Model (5), the expected value E_min is the objective value for this chromosome C; for Model (6), the variance value V _max is the objective value for this chromosome C. If C is checked to be infeasible, randomly generate another point C from the hypercube [0,1]ⁿ until the point is proven to be feasible and taken as an initial chromosome. Repeat this process pop_size times, then initial feasible pop_size chromosomes C ₁, C ₂,...,C _{pop_size} are produced. In the meantime, we get the corresponding objective values for these initial feasible pop_size chromosomes.

Hybrid intelligent algorithm When the initial feasible chromosomes are obtained through initialization operation, the chromosomes will go through the operations of selection, crossover, and mutation. After finishing the whole round, the new population will be ready for its next round of selection, crossover, and mutation. The hybrid intelligent algorithm will continue until a given number of cyclic repetitions of the whole round is met (see Fig. 4). Summarization of the algorithm is as follows:

• Step 1 Generate two training data sets for the expected and variance value functions by fuzzy simulation, respectively.

• Step 2 Train an NN to approximate the expected and variance value functions, respectively, by back propagation algorithm.

• Step 3 Initialize feasible pop_size chromosomes, in which the trained NN is used to calculate the constraint values of the chromosomes and check the feasibility of chromosomes.

• Step 4 For all chromosomes use the trained NN to calculate the objective values.

• Step 5 Give the rank order of the chromosomes according to the objective values, and compute the values of the rank-based evaluation function of the chromosomes.

• Step 6 Compute the fitness of each chromosome according to the rank-based-evaluation function.

• Step 7 Select the chromosomes by spinning the roulette wheel.

• Step 8 Update the chromosomes by crossover and mutation operations, in which the trained NN is used to calculate the constraint values and to check the feasibility of the chromosomes.

• Step 9 Repeat the fourth to the eighth steps.

• Step 10 Terminate the repetition cycle when a fixed maximum number of generations is reached. Take the best chromosome as the solution for portfolio selection.

Fig. 4

Hybrid intelligent algorithm

6 Numerical example

To help understand the optimization idea and to illustrate the effectiveness of the proposed algorithm, let us consider one numerical example which is performed on a HP personal computer with CPU 2.8 GHz and memory size 2.0 GB. The parameters are set as follows: the fuzzy simulation cycle is 3,000, the training data for the NN 3000, 15 hidden neurons, error rate $\varepsilon=0.003,$ maximum iteration times 3,000, the population size 30, the probability of crossover P _c = 0.3, the probability of mutation P _m = 0.3, the parameter a in the rank-based evaluation function is 0.05.

Example 3

According to the data in security markets and the experts’ knowledge, usually the expected values of the security returns can be given. However, it is often difficult to predict the exact numbers of the other parameters of the security returns. From Shanghai Stock Market we have ten securities, among which five security returns belong to normally distributed fuzzy variables and the rest five ones belong to triangular fuzzy variables. The expected returns of the securities are given, but other parameters can only be provided in an interval. The data set is given in Table 1.

Table 1 Fuzzy returns of the ten securities

Suppose the investors accept 0.50 as the maximum tolerable variance level. Since the expected values of the security returns are known, according to Model (5), the minimax fuzzy portfolio selection model is given as follows:

$$ \left\{\begin{array}{lll} \max \hbox{E}[\xi_1x_1+\xi_2x_2+\cdots+\xi_{10}x_{10}]\\ \hbox{subject to:}\\ \max \limits_{\xi_i, 1\le i\le 10} \hbox{V}[\xi_1x_1+\xi_2x_2+\cdots+\xi_{10}x_{10}]\le 0.50\\ x_1+x_2+\cdots+x_{10}=1\\ x_i\ge 0,\quad i=1,2,\ldots,10. \end{array}\right. $$

(17)

In order to solve this model, we first generate by fuzzy simulation one training data set {x _1i , x _2i ,...,x _10i , u _i |i = 1, 2,...,3,000 } for the variance value function. An NN with one hidden layer is used. Employing pruning algorithm (Castellano et al. 1997), we set 15 hidden neurons in the hidden layer. Then the NN is trained to approximate the variance function. After training, we randomly generated 12 samples and the comparison of the variance values by fuzzy simulation and the trained NN is shown in Table 2, where ”Difference” is the difference between the NN result and the simulation result. It can be seen that the maximum relative errors for the variance value do not exceed 1% which is considered acceptable. Next, we imbedded the trained NN into the GA to produce the hybrid intelligent algorithm. A run of the hybrid intelligent algorithm with 5,000 generations shows that among ten securities, in order to gain the maximum expected return in worst cases at the maximum variance value not greater than 0.50, the investors should assign their money according to Table 3. The corresponding maximum expected return is 1.8933. The solution time including NN training is about 12 min while the solution time by using the fuzzy simulation based GA without NN proposed in our previous paper (Huang 2007a) is about 4 h. By using NN, the time for calculating the variance values is greatly shortened. The solution time is mainly spent on the training of NN. Once the NN is trained, the optimal solution is found within only a few seconds.

Table 2 Comparisons of the values by the trained NN and the values by simulation

Table 3 Allocation of money to the ten securities (%)

It is seen from Table 3 that most of the money is allocated to securities 6, 9, and 10. We calculate the expected and the maximum variance values of the individual ten securities and present them in Table 4. It is seen that security 6 has the third highest expected value with the maximum variance value bigger than 0.5 but lowest among the securities whose maximum variances are bigger than 0.5. Security 9 has the highest expected value among the securities whose maximum variance values are lower than 0.5 and security 10 has the second lowest maximum variance value with a not so low expected value. Thus, the allocation plan is reasonable. We increase the preset tolerable variance at 0.7. Since securities 5, 6, and 7 are securities with the highest expected value among all the ten securities, we expect that more money will be allocated to them with increase of the preset variance value. Since the maximum variance values of securities 5 and 7 are both higher than 0.7 with security 5 having he highest maximum variance value of 1.40, it is estimated that some other securities with low maximum variance may be included in the optimal portfolio. We run the algorithm and present the solution in Table 4. It is seen that the result is consistent with our expectation. We further increase the preset variance at 0.8 and expect that allocation of money to securities 5, 6 and 7 will be increased. The result shown in Table 4 confirms our expectation. Furthermore, it is seen that among securities 5, 6, and 7, when the preset variance value becomes bigger, allocation proportion on security 7 with both higher expected and variance values among the three securities becomes bigger. The result is also consistent with our judgement.

Table 4 Different allocation plans (%)

7 Conclusions

This paper proposes two credibility-based minimax mean-variance models for a fuzzy portfolio selection problem where each security return belongs to a certain class of fuzzy variables but the exact fuzzy variable cannot be given. The proposed models are converted into linear programming models in three special cases. A neuron network imbedded genetic algorithm is provided for solving the proposed optimization problems in general cases. In the algorithm, the neuron network is used to approximate the expected value function and the variance value function so that the solution time is greatly shortened.