1 Introduction

Reservoir operation represents one of the major tasks in water resources management and hydropower engineering. Decisions in reservoir operation problems deal with the amount of water that should be released and stored over a period of time considering the variation and uncertainties of future streamflows and demands (Nagesh Kumar and Janga Reddy 2007). Several researchers have been applied diverse analysis techniques involving simulation and optimization algorithms to study decision-making in multipurpose reservoir systems (Labadie 2004). Simulation models associated with reservoir operation are generally based on mass balance equations, representing the hydrological behavior of reservoir systems using inflows, operating conditions and, in some cases, the economic performance of the reservoir system (Rani and Moreira 2010). Although simulation models permit detailed and realistic representation of the complex characteristics of a reservoir system, this approach can be too time-consuming to find optimal solutions (Neelakantan and Pundarikanthan 2000). On the other hand, optimization techniques have become increasingly important in the last decades to represent the management and operations of complex reservoir systems, reducing significantly the computational cost (Cheng et al. 2008). Different studies provided an extensive literature review and evaluate different optimization methods associated with reservoir operation and water resources management (Yeh 1985; Wurbs 1993; Labadie 2004).

Overall, optimization techniques used in reservoir systems can be classified into two types. Explicit stochastic optimization (ESO) and implicit stochastic optimization (ISO). Explicit stochastic optimization (ESO) considers the uncertainties of streamflows and other parameters of the problems in an explicit way. This approach is commonly used when inflows cannot be reliably forecasted for a relatively long period, requiring the use of probability distribution functions to represent uncertainties of the data (Celeste and Billib 2009). In such cases, the problem is typically addressed by stochastic dynamic programming (SDP) (Stedinger et al. 1984), being described in the literature as one of the most robust methods to derive optimal policies for water reservoirs. Nevertheless, Giuliani et al. (2016) pointed out that the adoption of SDP in complex real-world water resources problems is challenged by the three well know curses (dimensionality, modeling, and multiple objectives). In that way, approximate dynamic programming has been explored to overcome some or all the SDP curses (Powell 2007). For instance, Giuliani et al. (2016) discuss the adoption of direct policy search (DPS) to reduce the limiting effects of the three curses of SDP. In general DPS considers a parametrization of the operating policies using a set of family functions. Although DPS represents a simplification of SDP, this method still involves the use of dynamic programming and requires in some cases the estimation of several parameters. Moreover, the final results can be significant affected when a bad approximation function is chosen.

Contrary to ESO, ISO derive operational policies of reservoirs based on deterministic models (Zambelli et al. 2006). This approach takes into consideration the use of independent inflow scenarios, providing an optimal solution for each one (Zambelli et al. 2011). Thus, the stochastic aspects of this kind of problem can be implicitly handled by the analysis of the optimal deterministic solutions associated with different hydrological scenarios (Diniz et al. 2008). One of the main advantages of ISO is the facility to derive operation rules for large-scale systems, which might be more attractive to operators who are skeptical to use complex optimization approaches as a replacement to easier-to-understand simulation procedures (Celeste and Billib 2012; De Souza Zambelli et al. 2013). Operation rules specify operational decisions (e.g. releases) as a function of current reservoir water level and the hydro-meteorological conditions (Guo et al. 2004). Different functional methods have been applied to derive operation rules, including linear regression (LR) (Liu et al. 2011), two-dimensional surface models (SURF) (Celeste and Billib 2009), fuzzy models (Mousavi et al. 2007; Russell and Campbell 1996), bayesian networks (Mesbah et al. 2009) and support vector machines (SVMs) (Karamouz et al. 2009; Zhang et al. 2015). In general, the performance and goodness-of-fit of each method vary according to the studied area. For instance, Celeste and Billib (2009) pointed out that the SURF model achieve the best performance for the Epitácio Pessoa Reservoir. Liu et al. (2014) concluded that LR operating rules were suitable for the hydropower operation of China’s Three Gorges Reservoir. Ji et al. (2014) proposed SVM operating rules for the Jinsha Reservoir system, whereas Li et al. (2014) explored the use of genetic programming (GP) to derive the explicit nonlinear formulation of operating rules for multi-reservoir systems that included the Three Gorges and the Qing River cascade hydropower reservoirs. Nonetheless, there is no evidence that any particular fitting approach is superior and must be used under all conditions to derive operating rules for water reservoirs.

This study explores and proposes a probabilistic approach by the usage of copulas to derive operating rules for the long-term policies for water reservoir systems. Copulas represent a robust approach for multivariate modeling, and its development resulted in a surge in building multivariate distributions to handle nonlinear dependence of hydroclimatic variables in a suite of applications (Genest and Favre 2007; Hao and Singh 2015; Jaworski et al. 2010). In hydrology, the first studies with copulas were related to exploring multivariate aspects of extreme events including floods and droughts (Zhang and Singh 2007; Favre et al. 2004; Salvadori and De Michele 2004). Copulas are being extended to other applications of water resources and environmental sciences, including simulation or predicting processes (Lee and Salas 2011; Sadiq et al. 2008; Shi and Xia 2016). Other type of studies related copulas to construct the transition probability matrix of inflow values, useful to solve SDP problems for reservoir operation (Lei et al. 2018). For multivariate cases, vines copulas offer a flexible way to represent different dependence structures (Joe 2014), being commonly used to modeling the spatial and temporal distribution of random variables (Pham et al. 2016; Erhardt et al. 2015; Ávila et al. 2019).

In this case, copulas are employed to relate hydrological variables that affect the operation of water reservoirs and used derive probabilistic long-term operational policies for a single hydropower reservoir located in a semiarid region of Brazil. Using a deterministic optimization model, an ISO approach is performed to estimate the optimal allocations under different streamflow scenarios previously generated by a periodic vine copula model. For each month, the optimal water releases are related to the initial storage volume and inflows in order to construct the corresponding joint probability distribution functions. Thus, a simulation process based on vine copulas is performed in order to forecast the expected amount of water that should be released, given the prior knowledge of the initial store volume and future hydrological conditions in the reservoir. Goodness-of-fit tests and error analysis show that the proposed model can well represent the operation of hydropower reservoirs located in semiarid regions with seasonal streamflow regimes. The remainder of this paper is organized as follows: Sect. 2 describes the principal methods used for this study in order to derive probabilistic reservoir operation policies by ISO and copulas. Section 3 presents the application and results of the proposed model considering a hydropower reservoir located in the Northeastern region of Brazil as a case study. Finally, Sect. 4 draws the main conclusions.

2 Methodology

This section introduces the principal methods used in this study, which was conducted into three stages: (1) Simulate monthly streamflow scenarios based on a periodic vine copula-entropy model; (2) Compute optimal releases policies using an ISO approach; and (3) Estimate reservoir operational policies based on a probabilistic simulation process with copulas. Figure 1 depicts the general framework used for the development of this study. Overall, the simulation of monthly streamflows time series is carried out by the definition of a periodic vine copula model. This approach allows the construction of multivariate distribution functions without any restriction to represent nonlinear dependencies between adjacent months. The streamflow simulation process was supported by the Principle of Maximum Entropy (POME) in order to derive the marginal distribution function of each month. Simulated streamflow scenarios were used as input of an Implicit Stochastic Optimization model (ISO) to derive the operational policies of a single water reservoir. Finally, the ensemble of initial water volume, inflow and water release of each month was related and modeled using multivariate distribution functions in order to represent operating rules for the selected reservoir. Notice that this study considered different vine copulas structures (eg. D-vine, C-vine) for the construction of multivariate distribution functions. Section 2.1 presents a formal introduction of vines copulas, showing the main differences of each one.

Fig. 1
figure 1

General framework to derive reservoir operation policies combining ISO and copulas

Full size image

2.1 Joint distribution based on copulas

A copula C is a multivariate distribution function with marginals as the uniformly distributed U(0, 1) (Joe 1997; Nelsen 2006). Copulas were firstly introduced by Sklar (1959) and are useful to derive joint distributions given the marginals, especially when dealing with non-normal distributions (Suroso and Bárdossy 2018). The main advantage of copulas can be explained through the Sklar’s theorem (1959), which stated that for a d random vector \(X=(X_{1},...,X_{d})\) with joint cumulative distribution H and marginals \(F_{1},...,F_{d}\), a copula \(C: [0,1]^{d} \rightarrow [0,1]\) exists such that for all \(x=(x_{1},...,x_{d}) \in {\mathbb {R}}^{d}\).

$$\begin{aligned} H(x_{1},...,x_{d})=C[F_{1}(x_{1}),...,F_{d}(x_{d})]=C(u_{1},...,u_{d}) \end{aligned}$$
(1)

where \(u_{1}=F_{i}(x_{i})\) and \(u_{i} \sim U(0,1)\) for \(i=1,...,d.\) Hence, marginal and joint distribution analysis can be done separately.

Some bivariate copulas and its relationship between the dependence structure parameter \(\theta\) and Kendall’s \(\tau\) are listed in Table 1. Kendall’s \(\tau\) is a rank correlation coefficient and it is defined as the probability of concordance minus that of discordance. For two variables \(x_{1}\) and \(x_{2}\) with n observations, the empirical Kendall’s \(\tau\) can be calculated as (Genest and Favre 2007):

$$\begin{aligned} \tau _{1,2}= \frac{P_{n}-Q_{n}}{\left( {\begin{array}{c}n\\ 2\end{array}}\right) }=\frac{4}{n(n-1)}P_{n}-1 \end{aligned}$$
(2)

where \(P_{n}\) and \(Q_{n}\) represent the number of concordant and discordant pairs, respectively.

Table 1 Bivariate copula functions and the association between their parameters and Kendall’s \(\tau\)
Full size table

Computational modeling for d-dimensional cases (\(d >2\)) can be addresed by the so-called vine copulas. Proposed by Joe (1996) and subsequently addressed by Bedford and Cooke (2001; 2002) and Aas et al. (2009), a vine copula allows the decomposition of a multivariate density function by a set of conditional and unconditional bivariate copulas.

For dimensions greater than two, vines copulas are commonly organized by a set of trees composed by edges and vertices. Two special vines (C-vine and D-vine) are illustrated in Fig. 2 for a 3-dimensional case. In general, a C-vine is characterized for modeling dependence structures centered in one variable, while a D-Vine presents a sequential structure useful to modeling time dependence. For the three-dimensional case the vines are composed by 2 trees (\(T_{1}\) and \(T_{2}\)); the first tree has 3 nodes (circles) and 2 edges (lines), and the second tree has 2 nodes and 1 edge. Note that the edges in \(T_{1}\) become nodes in \(T_{2}\). Vine copulas offers the flexiblity of selecting different bivariate family copulas for each edge.

Fig. 2
figure 2

Three-dimensional vine copula construction

Full size image

2.2 Principle of maximum entropy (POME)

The concept of entropy was firstly introduced in the context of information theory by Shannon (1948). Subsequently, Jaynes (1957a, b, 1982) developed the Principle of Maximum Entropy (POME) useful to derive probability distribution functions of random variables when some information is given in terms of constraints. For a random variable X, the most probable probability density function (PDF) is the one that maximizes the Shannon entropy H(x) defined as:

$$\begin{aligned} H(x)=-\int _{a}^{b} f(x) \log f(x) dx \end{aligned}$$
(3)

where f(x) is the PDF of X; and x is a value of X defined in the upper and lower limits b and a respectively. According to Jaynes (1957a), the PDF of X can be obtained by maximizing the Shannon entropy for a set of statistical moments as constraints such as:

$$\begin{aligned} \int _{a}^{b}f(x)dx= & {} 1 \quad \quad f(x) \ge 0 \,\, \forall \, x \in [a,b] \end{aligned}$$
(4)
$$\begin{aligned} \int _{a}^{b}h_{i}f(x)dx= & {} \overline{h_{i}(x)} \quad \quad i=1,...,m \end{aligned}$$
(5)

where \(h_{i}(x)\) is a function of X, and \(\overline{h_{i}(x)}\) is the expected value of \(h_{i} (x)\). For a given set of constraints, a unique distribution can be defined (Chen and Singh 2018). Therefore, finding the appropriate constraint is critical to define a suitable PDF. According to Kapur and Kesavan (1992), the maximum entropy-based (ME-based) PDF of X can be obtained as follows:

$$\begin{aligned} f(x)=\exp \left[ -\ln \left( \int _{a}^{b} \exp \left( -\sum _{i=1}^{m} \lambda _{i} h_{i} (x)\right) dx \right) - \sum _{i=1}^{m} \lambda _{i} h_{i}(x) \right] \end{aligned}$$
(6)

The corresponding cumulative distribution function (CDF) can be expressed as:

$$\begin{aligned} E_{X}(x)=\int _{a}^{x}f(t)dt \end{aligned}$$
(7)

where \(\lambda _{i} \quad (i=1,2,\ldots ,m)\) are the Lagrange multipliers that must be estimated. In general, Equation (6) has not an analytical solution for \(m > 2\); therefore, numerical methods are needed to perform the computation. For this case, the conjugate gradient (CG) method is applied (Kong et al. 2015) to estimate the Lagrange multipliers in Equation (6). Moreover \(h_{i} (x)\) is defined as a known function of X, such as \(h_{1}=x\), \(h_{2}=x^{2}\), \(h_{3}=x^{3}\) and \(h_{4}=x^{4}\) for the constraints presented in Equation (5), and \(\overline{h_{i}(x)}\)\(i=1,...,4\) are associated to the sample mean, variance, skewness, and kurtosis respectively (Hao and Singh 2009).

2.3 Goodness-of-fit statistical tests

This study employs goodness-of-fit (GOF) tests to evaluated the performance and relative errors of simulated data generated by POME and copula functions. Firstly, the estimated marginal distributions are compared with the empirical distributions obtained from the the Gringorten (Gringorten 1963) plotting position formula expressed as:

$$\begin{aligned} P(K \le k) = \frac{k-0.44}{N+0.12} \end{aligned}$$
(8)

where N stands for the sample size and k is the kth smallest observation in the data set arranged in an increasing order.

The Kolmogorov-Smirnov (K-S) test is used to assess the performance of the marginal distributions. The K-S test quantifies the vertical distance between the empirical distribution of a sample and the cumulative distribution function of the reference distribution. Given n increasing ordered data points, \(x_{(\cdot )}\), the K-S test stastistic is defined as (Kolmogorov 1933):

$$\begin{aligned} T=\sup _{x} |F^{*}(x)-F_{n}(x)| \end{aligned}$$
(9)

where \(F^{*}(x)\) stands for the specified distribution; \(F_{n}(x)\) represents the empirical distribution; and \(\sup\) is the supremum function. The null hypothesis \(H_{o}\) is: \(F(x)=F^{*}(x)\) for all x from \(- \infty\) to \(\infty\). For a significance level \(\alpha\), the null hypothesis is rejected if T exceeds the \(1- \alpha\) quantil (Razali et al. 2011).

In addition, the RMSE and NSE coefficients are applied to asses the error of simulated data. The RMSE (Willmott and Matsuura 2005) and NSE (Nash and Sutcliffe 1970) coefficients can be expressed as:

$$\begin{aligned} RMSE= & {} \sqrt{\frac{\sum _{k=1}^{N}(x_{k}^{est}-x_{k}^{obs})^{2}}{N}} \end{aligned}$$
(10)
$$\begin{aligned} NSE= & {} 1 - \frac{\sum _{i=1}^{N} (x_{k}^{est}-x_{k}^{obs})^{2}}{\sum _{i=1}^{N} (x_{k}^{obs}-\overline{x^{obs}})^{2}} \end{aligned}$$
(11)

where \(x_{k}^{est}\) is the simualted value; \(x_{k}^{obs}\) is the corresponding observed value; \(\overline{x^{obs}}\) is the mean of observed values; and N is the sample size

2.4 Streamflow simulation with copulas

The simulation of monthly streamflow time series is based in the periodic vine copula model proposed by Pereira and Veiga (2018). This approach allows to consider lags that are greater than one, and non-linear dependence structures between adjacent months. Basically, a d-dimensional D-vine structure is defined for each month to model the periodic structure of historical data. The dimension of the D-vine is related to the maximum time lag dependence considered for each month. To determine those dimensions, the authors suggest performing an iterative procedure together with a bivariate asymptotic independence test proposed by Genest and Favre (2007).

The general sampling procedure for new dependent uniform datasets \((u_{1},\ldots u_{d})\) using R-vine structures, including D-vines, is performed as follow. First, sample \(w_{i} \sim U(0,1)\) for \(i=1,...,d\) and subsequently iterate:

  1. 1.

    \(u_{1}:=w_{1}\)

  2. 2.

    \(u_{2}:=C_{2|1}^{-1} (w_2 |u_1)\)

  3. 3.

    \(u_{3}:=C_{3|1,2}^{-1} (w_{2}|u_{1},u_{2})\)

    \(\vdots\)

  4. 4.

    \(u_{d}:=C_{d|1,...,d-1}^{-1}(w_{d}|u_{1},...,u_{d-1})\)

In a streamflow simulation, we are interested in the simulation of \(u_{t}\) conditioned on the previos \(d-1\) observations. Assuming that t belongs to the month m, we have that

$$\begin{aligned} u_{t}:=C_{t|t-1,t-2,...,t-d+1}^{-1}(w_{t}|u_{t-1},u_{t-2},...,u_{t-d+1}) \end{aligned}$$
(12)

For a better simulation process, Equation (12) can be expressed in terms of h-functions such as (Aas et al. 2009):

$$\begin{aligned} u_{t}=h^{-1}(w_{t} ; \varvec{u}, \theta ) = F^{-1}_{i-1|i}(w_{i}|\varvec{u}) \quad i=1,...,t \end{aligned}$$
(13)

where \(\theta\) is the parameter of the copula C; w is uniformly distributed and \(\varvec{u}=u_{t-1},u_{t-2},...,u_{t-d+1}\).

The simulated sample dataset \((u_{1},\ldots ,u_{t})\) must be rescaled to obtain the desired streamflow scenarios using the corresponding inverse cumulative distribution function, such as \(x_{i}=F^{-1}(u_{i})\), \(i=1,...,t\), where x is a simulated streamflow time series. This study employed the Principle of Maximum Entropy (POME) method to derive the marginal distribution function for each month. The Gaussian, t-Student, Gumbel, Frank, Clayton, Frank, Joe and Independence copulas, as well as their rotated versions were considered to model different dependence structures. The selection of the best copula was carried out via the Bayesian information criterion (BIC) (Schwarz et al. 1978), and the parameters of each copula are estimated using the maximum likelihood (ML) method. More information about regular vine and simulation process of h-functions is presented in Brechmann and Schepsmeier (2013).

2.5 Forecasting method with copulas

Additional to simulation, copulas can be used to forecast future realizations of random variables, considering its temporal dependence structure. Forecasting procedures with copulas have been commonly applied in univariate and multivariate time series (Simard and Rémillard 2015; Patton 2013; Sokolinskiy and van Dijk 2011). For instance, Khedun et al. (2014) and Nguyen-Huy et al. (2017) used copulas to predict precipitation anomalies caused by circulation patterns and in the state of Texas (US) and Australia, respectively. Liu et al. (2015) employed a vine copula model to predict one month ahead the streamflow presented in a basin located in South China, whereas Wang et al. (2017) proposed a vine copula-based model to asses wind power uncertainties in power systems.

Basically, this approach follows the assumption that the expected value of a future realization can be estimated by the mean of a simulated data set. This study adopted a multivariate approach based on vines copula to estimated the expected amount of water that should be released, conditioned on the initial reservoir storage and the predicted inflow. Hence, a R-vine structure is constructed for each month, considering the dependence structures of these random variables. The forecasting method with copulas is performed by a simulation process based on the inverse transformation procedure, and follows the algorithm presented by Matthias and Jan-frederik (2017). For a specific month m, the general prodedure is followed as: Set \(F_{S}(\cdot )\), \(F_{R}(\cdot )\) and \(F_{I}(\cdot )\) as the marginal distribution functions of the storage volume (S), the releases (R) and the inflows (I) of the reservoir; and \(S_{t}\), \(I_{t+1}\), \(R_{t+1}\) as the initial storage volume, the future inflow and the expected release in the reservoir at time \(m=t\). Perform the iterative procedure described as:

  1. 1.

    Set \(u_{t}=F_{S}(S_{t})\) and \(v_{t+1}=F_{I}(I_{t+1})\);

  2. 2.

    For \(i=1,...,k\), calculate \(z_{t+1}^{(i)}=C^{-1}(w^{(i)}|u_{t},v_{t+1})\). Where \(w^{i} \sim U(0,1)\); k is the length of the vector \(\mathbf {z_{t+1}}\); and \(z_{t+1}^{(i)}\) is the i copula data of water release at time \(t+1\) ;

  3. 3.

    Transform the uniform values to the original scales: \(R_{t+1}^{(i)}=F_{R}^{-1}(z_{t+1}^{(i)}) \quad i=1,...,k\);

  4. 4.

    Estimate the mean of the simulated values: \(\hat{R_{t+1}}= \frac{1}{k} \sum _{i=1}^{k} R_{t+1}^{(i)}\)

Notice that the described procedure generated a simulated dataset of water release \(R^{(k)}_{t+1}\) based on a stochastic process. In particular, Step (4) estimated the expected water release as the mean of the simulated data. Moreover, we can well construct the corresponding uncertainty bounds (e.g 90%, 95%) at each period of time. Matthias and Jan-frederik (2017) provide several simulation algorithms to estimate the corresponding values of z for different R-vine structures, including D-vines and C-vines.

2.6 Implicit stochastic optimization (ISO)

Implicit stochastic optimization, also referred to as Monte Carlo optimization, uses a deterministic optimization model to find the optimal reservoir allocations under different inflow scenarios (Celeste et al. 2009). For each inflow sequence, a different operating policy is found. Hence, the stochasticity and uncertainties of streamflow regimes are addressed in an implicit way. According to Celeste et al. (2009), the ISO procedure is described as follows:

  1. 1.

    Generate M synthetic N-month inflow sequences.

  2. 2.

    For each inflow sequence realization, find the optimal releases for all N months by means of a deterministic optimization model.

  3. 3.

    Use the ensemble of optimal releases (\(M \times N\)) to develop monthly operating rules.

For a specific month, the releases obtained by the optimization model are conditioned on the initial reservoir storage and the predicted inflow. In general, multiple regression analysis is applied to determine the operating rules for each month. Instead, this study explores the use of copulas to construct a joint probability distribution function to related the dependence structure of these random variables. Thus, given the information of initial reservoir storage and forecasted inflow for a month m, the expected amount of water that should be released can be estimated by a simulation process.

2.6.1 Deterministic reservoir operation optimization model

The deterministic optimization model assumes that the main objetive of the operation is to find the allocations of water that best satisfy their respetive demands without compromising the systems. Furthermore, the objetive function need to satisfies the mass balance and operative constraints of the system respectively. Therfore, the general problem is formulated as:

$${\text{minimize}} = \sum\limits_{{t = 1}}^{N} {\left[ {\frac{{R(t) - D(t)}}{{D(t)}}} \right]^{2} }$$
(14)

subject to

$$\begin{aligned} S(t)=&S(t-1)+I(t)-E(t)-R(t)-S_{p}(t); \quad \quad \forall t \end{aligned}$$
(15)
$$\begin{aligned} 0 \le&R(t) \le D(t); \quad \quad \forall t \nonumber \\ S_{min} \le&S(t) \le S_{max}; \quad \quad \forall t \nonumber \\ \quad S_{p}(t) \ge&0; \quad \quad \forall t \end{aligned}$$
(16)

where t is the month index; N is the operating horizon in months; R(t) and D(t) are the release and demand in the month t; S(t) is the final storage in reservoir at the end of month t (when \(t=1\), \(S(t-1)\) is equal to the initial storage \(S_{0}\)); I(t) and E(t) are the inflow and evaporation volume in the month t; \(S_{p}\) is the water volume that might eventually spill from the reservoir during month t; \(S_{min}\) is the dead storage and \(S_{max}\) is the storage capacity of the reservoir.

In order to limit spills from the reservoir in periods of time that the demand have been met and the final reservoir storage S(t) is equal to \(S_{max}\), Celeste and Billib (2010) recommended to use an additional constraint that include a deficit variable \(\delta (t)\), such as:

$$\begin{aligned} S(t-1)+I(t)-E(t)-D(t)-S_{p}(t)-\delta (t)=S_{max} \end{aligned}$$
(17)

In that way, Equation (14) is reformulated as:

$$\begin{aligned} \begin{aligned}&\text {minimize}&\sum _{t=1}^{N} \left\{ {\alpha (t) \left[ \frac{R(t)-D(t)}{D(t)}\right] }^{2} + [S_{p}(t)+ \delta (t)] \right\} \end{aligned} \end{aligned}$$
(18)

Note that the first term of the summation in Equation (18) varies within the interval [0, 1] while the second terms varies within \([0, \mu (t)]\), where \(\mu (t)=max[S_{p_{max}}(t)+\delta _{max}(t)]\), such as \(S_{p_{max}}(t) \approx I(t)-D(t)\) and \(\delta _{max}(t)=S_{max}+D(t)\). Therefore, Celeste and Billib (2010) suggest multiply the first term of Equation (18) by \(\alpha (t)=\mu ^{2}(t)\). The interior-point-convex algorithm is used to optimize Eq. (18) (Nesterov and Nemirovskii 1994).

3 Case study

3.1 Overview

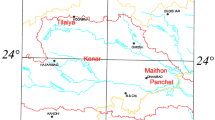
The Sobradinho reservoir was selected as a case study to demonstrate de applicability of the proposed method. The Sobradinho reservoir is located in the Northeastern region of Brazil, has a surface area of 4.214 km\(^{2}\) and a storage capacity of 34.1 km\(^{3}\) approximately. This reservoir encloses the waters of the São Francisco River, which is the longest river that runs entirely in Brazilian territory, with a mainstream length of 2.830 km and a drainage area of 641.000 km\(^{2}\) (Figure 3). The Sobradinho reservoir has dead and a maximum storage volume equal to 5.447 hm\(^{3}\) and 34.116 hm\(^{3}\) respectively. In terms of power generation, the Sobradinho hydropower plant has an installed capacity of 1.050 MW and was projected to add about 4 billions of KWh of electrical energy per year to the Northeastern region of Brazil (Lima and Abreu 2016). Furthermore, the reservoir is also used to control and regulate water resources in the region, providing water supply for irrigation, fishing, and recreation (Azevedo et al. 2018).

Fig. 3
figure 3

Location of the Sobradinho reservoir

Full size image

Monthly streamflow records from 1931 to 2017 at the Sobradinho hydropower station were used in this study. The streamflow data was provided by the Brazilian National Electrical System Operator (ONS) and consists of naturalized streamflows, i.e., without the influence of the dam nor consumptive water uses. Figure 4 depicts the original streamflow time series and the annual cycle observed in the Sobradinho reservoir. The recorded monthly time series presents a strong periodicity in this region, characterized by drought periods (smaller average and variance) in the middle of the year, in comparison with the wet periods (at the beginning and end of the year).

Fig. 4
figure 4

(a) Monthly streamflow time series and (b) annual cycle in São Francisco River

Full size image

3.2 Results analysis

3.2.1 Monthly streamflow simulation

The first step in this study consists in simulate monthly streamflow scenarios in the São Francisco River using a periodic vine copula model. Without loss of generality, the application of this method involves: (a) the construction of marginal distribution of monthly streamflows based on the POME, estimating the values of Lagrange multipliers through the CG method, and (b) the definition of joint distribution between adjacent monthly streamflows considering lags greater than one using d-dimensional D-vine structures.

In order to define the ME-based marginal distributions, expressed by Eq. (6), the Lagrange multipliers must be first estimated. The CG method was used to calculate the corresponding Lagrange multipliers for each month. This study considered the first four statistical moments as constraints. The generated PDFs and CDFs were compared with the empirical histograms and the empirical CDFs obtained from the Gringorten plotting position formula. Figure 5 depicts the marginal PDF and CDF for April streamflow in São Francisco river.

Fig. 5
figure 5

Comparison of the theoretical and empirical PDF and CDF for April streamflow in São Francisco river

Full size image

A goodness-of-fit based on the Kolmogorov-Smirnov test (K-S) and RMSE was applied to evaluate the estimated ME-based marginal distributions. Table 2 reports the obtained p-values and statistical T calculated from the K-S test for each month. For a significant level \(\alpha =0.05\), the results show that the null hypothesis cannot be rejected, and the estimated ME-based distribution functions can appropriately represent the observed monthly streamflows in São Francisco river. In addition, the RMSE results indicate that the corresponding relative errors are relatively small for the months of April to December. On the other hand, the RMSE is higher for the months of January to March. This result is congruent with Fig. 3, indicating a greater variability of streamflow values presented for those months.

Table 2 The goodness-of-fit for monthly streamflow marginal distributions
Full size table

Based on the marginal distribution analysis, the streamflow data can be converted into copula data \(U \sim (0,1)\) in order to construct the joint probability distributions between adjacent months. The joint analysis data was performed based on the construction of d-dimensional D-vine structures for each month using the bivariate asymptotic indepdendece test (Genest and Favre 2007). The analysis exposed that the temporal dependence for all months can be modeled with bivariate copulas, with the exception for the months of January and May (4-dimensional D-vine).

Figure 6 presents 300 simulated scenarios (grey lines), each one containing 60 months, generated by the periodic vine-copula entropy based model in São Fransico river. The figure compares the historical averages (black line) and the simulated averages (red line), showing that synthetic scenarios successfully reproduce the periodic characteristics of historical streamflow regimes in the studied area. Moreover, Fig. 7 compares the monthly statistics of simulated and observed streamflow data in São Francisco river, including maximum and minimum values.

We also demonstrate that the simulated scenarios replicate time dependence of historical data by a monthly autoregressive analysis. Thus, for each month the Kendall’s \(\tau\) coefficient is calculated up to lag five (previous 1–5 months). Figure 8 presents a comparison between the historical values (black dot) and the average of the simulated values (red triangle). Results evidence the good performance of vine copula models to represent nonlinear autocorrelation structures. In that way, the stochastic vine copula model can be used to construct synthetic streamflow sequences to derive long-term operational policies in the Sobradinho reservoir employing a deterministic optimization model.

Fig. 6
figure 6

Simulated streamflow scenarios in São Francisco river

Full size image
Fig. 7
figure 7

Comparison of monthly statistics of simulated (boxplot) and observed (red line) streamflow data in São Francisco river

Full size image
Fig. 8
figure 8

Comparison of the simulated and observed monthly autocorrelation analysis based on Kendall’s s coefficient for lags 1–5

Full size image

3.2.2 Reservoir operation optimization with ISO

A deterministic optimization model is performed to derive the optimal operational policies in the Sobradinho reservoir. A Monte Carlo process was executed over an operating horizon of 1320 months (110 years) for 70 inflow sequences. The initial storage was set to \(S_{max}\). The monthly demand D(t) of the objective function (Eq. 18) was assumed to be the reservoir yield at 95% reliability. This value represents the amount of energy that can be produced 95% of the time and is estimated by the Brazilian Electricity Regulatory Agency (Agência Nacional de Energia Elétrica (ANEEL)) (ANEEL 2019). The optimization results for the first and last five years obtained for each inflow sequence were discarded in order to avoid the influence of the boundary conditions (initial and final storages) (Celeste et al. 2009). Initial storage, inflow, and water release values were grouped month by month to construct the respective operational curves. Figure 9 presents the scatterplots and Kendall’s \(\tau\) of the studied variables for the month of June. In general, the figure shows that the variables present positive correlations with different tail dependence structures that could be modeled by copulas. Notice that inflow data are significant correlate with monthly water release. The dominance of this hydrological variable in the operation of water reservoirs is further discussed in Tejada-Guibert et al. (1995) and Piccardi and Soncini-Sessa (1991).

Fig. 9
figure 9

Scatterplots of optimized operating reservoir variables in June

Full size image

3.2.3 Reservoir operation simulation with copulas

Based on the results of Fig. 9, a set of joint probability distribution functions is constructed using a vine copula approach. Hence, the data must be first transformed into a uniform distribution \(U \sim (0,1)\) using the inverse transformation procedure. For each variable, a marginal ME-based distribution function is estimated using the first four statistical moments as constraints. Table 3 presents the estimated Lagrange multipliers using the CG method. Based on the Lagrange multipliers, the PDFs and CDFs of the random variables associated with the monthly operation of the Sobradinho reservoir could be determined using Equations (6) and (7).

Table 3 Estimation of Lagrange multipliers for ME-based marginal distribution of random variables associated with reservoir operation in June
Full size table

Figure 10 compares the empirical and theoretical ME-based marginal probability density function (PDF) and cumulative distribution function (CDF) for the optimized water releases in the Sobradinho reservoir in June, including some parametric probability distribution functions such as Normal, Weibull and Gamma. Moreover, Table 4 presents a goodness-of-fit based on Kolmogorov-Smirnov (K-S) test for the marginal distribution functions. Results show that the POME method can better fit the distributions of the variables that represent the operation in the Sobradinho reservoir, whereas parametric distributions exhibit p-values lower than \(\alpha =0,05\), rejecting the null hypothesis.

Fig. 10
figure 10

Comparison of theoretical and empirical marginal density function (PDF) and cumulative distribution function (CDF) of water release in Sobradinho reservoir in June

Full size image
Table 4 Goodness-of-fit based on Kolmogorov-Smirnov (K-S) test for marginal distribution functions in June. Red values indicate p-values lower than \(\alpha =0,05\)
Full size table

A multivariate distribution function is constructed for each month in order to estimate the expected water release given the initial volume and inflows in the Sobradinho reservoir. According to the obtained data of the optimization model, the C-vine structure is chosen to represent the dependence structure of the studied variables. Considering the Kendall’s \(\tau\) presented in Figure 8, the inflows \(I_{t}\) was selected to represent the first dimension, the initial volume storage \(S_{t-1}\) the second dimension, and the water release \(R_{t}\) was set as the third dimension of the C-vine. Figure 11 depicts the trees of the 3-dimensional C-vine defined for June and Fig. 12 shows the copula density surfaces, as well as the copula family and parameters used for this month.

Fig. 11
figure 11

C-vine structure used to model operational policies in June

Full size image
Fig. 12
figure 12

Copula density surfaces associated to the C-vine structure of June

Full size image

A simulation procedure based on copula was performed to forecast the expected amount of water that should be released in the Sobradinho reservoir one-month ahead. For each step, the performed model assumes the prior knowledge of the initial storage volume and the future inflow conditions in the river. In order to avoid overfitting, the simulation process was carried out for a dataset used to define the vine copula model (inside) and another sample dataset that was not considered for this purpose (outside). Figures 13 and 14 compare the simulated and optimized water release in the Sobradinho reservoir for both sample datasets respectively. Moreover, the corresponding 90% uncertainty bound are represented for each period of time. Results indicate that simulated data can well represent the variation of water releases in the study area, particularly for the peak values of turbinate water flow. In addition, simulated data show randomness over period of time that operating policies defined by the optimization model remain constants. However, the simulation by copulas allows to construct uncertainty bounds for each month rather than estimate a single water release value. Moreover, the QQ-plots show a good performance of the proposed model to represent water allocations in the Sobradinho reservoir.

Fig. 13
figure 13

Comparison of optimized and simulated water release in Sobradinho reservoir for a dataset inside the vine copula model

Full size image
Fig. 14
figure 14

Comparison of optimized and simulated water release in Sobradinho reservoir for a dataset outside the vine copula model

Full size image

Figure 15 shows the relative errors between the optimized and simulated monthly water releases for both datasets. Furthermore, the RMSE and NSE are estimated to evaluate the performance of the proposed model. Considering the optimized data of Figs. 13 and 14 as observed values, the relative error between simulated and optimized values is 11%, the calculated NSE is 0.55 and the RMSE is 350 m\(^{3}\)/s approximately. Hence, the results show that the variability of simulated data is low when it is compared to the optimized monthly water release.

Fig. 15
figure 15

Relative error of simulated water release in the Sobradinho reservoir for a dataset a inside and b outside the vine copula model. The red lines represent the average of the relative errors

Full size image

4 Conclusions

Reservoir operation is a key task for water resources management. Numerical methods, including optimization and simulation techniques, are commonly used to derive suitable operational policies. In particular, Implicit Stochastic Optimization (ISO) combines optimization deterministic models and Monte Carlo methods to derive operational policies under different inflow scenarios. ISO is commonly supported by fitting approaches including linear regression or nonlinear methods to derive long-term operating rules for multipurpose water reservoirs. Although such approaches give feasible solutions for future water releases, the adoption of optimal parameters for specific functions may not consider the uncertainties or nonlinear dependence structure of hydrological variables. This study explored a probabilistic approach to derive monthly operating rules for a single hydropower reservoir based on the definition of joint probability distribution functions, combining copulas and ISO. In that way, the expected water release and the correspoding uncertainty bounds can be estimated for future months, rather than a single optimal value. Thus, the proposed method is presented as a supportive approach for operators to derive long-term water release policies.

Considering the importance of inflow scenarios to derive feasible water allocations, simulation models should represent the main statistical features of historical data. Therefore, this study started with the simulation of monthly streamflow sequences based on a vine copula model. In this case, D-vine structures were employed to represent the periodic and sequence dependence of adjacent months in the Sobradinho river. The Principle of Maximum Entropy (POME) was used to support the simulation process by fitting the marginal distribution function for each month. Overall, the simulated scenarios showed good adherence to the periodic behavior of historical data and well performance to represent nonlinear autocorrelation structures.

Simulated streamflow scenarios were used as input to derive the optimal water allocations in the Sobradinho reservoir using a deterministic optimization model. Based on a Monte Carlo process, the resulting ensemble of initial storage volume, inflow, and water release was related month by month in order to represent the corresponding operating rules. In this case, C-vine structures shown a feasible approach to construct multivariate distribution functions in order to relate and represent the dependence structure of the studied variables. A simulation procedure based on copulas was performed to forecast the expected water release one-month ahead. The proposed model was tested on a sample inside and outside the stochastic model. Results show that simulated data can well represent the variability of monthly water release in the Sobradinho reservoir with small relative errors in comparison with the data obtained by the optimization model. In general, the average relative error for both samples is 11%, the estimated RMSE was equal to 350 and NSE was equal to 0.55.

In comparison with other fitting approaches, the main advantages of the proposed model are the non-restriction to represent nonlinear dependencies between hydrological variables and the non-assumptions regarding the marginal distributions. Moreover, the flexibility of copula allows the construction of multivariate probability distributions considering other variables that may constrain reservoir operation. The main observed disadvantage of the proposed model is the randomness presented by simulated values, increasing the variability of the results when it is compared with optimized data. However, the simulation process allows considering uncertainty bounds rather than a single water release for each period of time. In this study, the performance of the proposed model was evaluated by the comparison with the water release obtained by the optimization model. Nonetheless, the application of this model can be well extended for real cases when the initial volume and expected future inflows of a single water reservoir are well known. Further studies may explore the performance of copulas to derive short-term operating policies in water reservoirs as well as the operating policies for cascade water reservoir systems.