Development of an inexact two-stage stochastic model with downside risk control for water quality management and decision analysis under uncertainty

Abstract

Water quality management along rivers involves making water-allocation plans, establishing water quality goals, and controlling pollutant discharges, which is complicated itself but further challenged by existence of uncertainties. In this study, an inexact two-stage stochastic downside risk-aversion programming (ITSDP) model is developed for supporting regional water resources allocation and water quality management problems under uncertainties. The ITSDP method is a hybrid of interval-parameter programming, two-stage stochastic programming, and downside risk measure to tackle uncertainties described in terms of interval values and probability distributions. A water quality simulation model was provided for reflecting the relationship between the water resources allocation, wastewater discharge, and environmental responses. The proposed approach was applied to a hypothetical case for a shared stream water quality management with one municipal, three industrial and two agricultural sectors. A number of scenarios corresponding to different river inflows and risk levels were examined. The results demonstrated that the model could effectively communicate the interval-format and random uncertainties, and risk-aversion into optimization process, and generate a trade-off between the system economy and stability. They could be helpful for seeking cost-effective management strategies under uncertainties, and gaining an in-depth insight into the water quality management system characteristics, and make cost-effective decisions.

1 Introduction

Over recent decades, the main challenge in water resources system management is resolving the varying levels of water shortage and deterioration of water quality caused by the rapid development of regional economy and society (Cai et al. 2011). For example, hundreds of Chinese cities face serious water shortages and water pollution, and most of the rivers and lakes (especially shared rivers) in China have been deleteriously affected by wastewater discharge from various sources, leading to serious problems in terms of water pollution and eutrophication. Water pollution has done great harm to people’s health, and caused economic losses amounted to about 30 % of gross domestic product each year in China. Therefore, effective water quality management in a river basin is desired for reducing the tremendous stresses on water environment protection. In addition, conflicting and controversial water quality issues among different stakeholders interests have been intensified in a shared river (Huang and Chang 2003; Niksokhan et al. 2009). One of the major reasons is that the water quality needs of the downstream water users are in conflict with the water quantity requirements of the upstream water users. The other reason is that the water resources systems are complicated with uncertainties that may exist in many system parameters, their interrelationships would intensify the competitive issue of water quality management. For example, stream flows and allowable pollution emissions have been characterized by spatial and temporal variations, measurements of net system benefits may exhibit random natures. These complexities are further compounded by interactions among various uncertain parameters (Maqsood et al. 2005; Zheng and Keller 2007).

Previously, a number of optimization techniques were developed for dealing with the above-mentioned difficulties and helping manage water quality in a more environmental-friendly pattern (Lohani and Thanh 1978; Huang 1996, 1998; Sasikumar and Mujumdar 2000; Lee and Chang 2005; Matthies et al. 2006; Qin et al. 2007, 2009; Maeda et al. 2009; Xie et al. 2011; Lv et al. 2012; Li et al. 2013a, b; Nikoo et al. 2012; William et al. 2013). Among these techniques, the inexact two-stage stochastic programming (ITSP) model has received extensive attentions over the past years (Mobasheri and Harboe 1970; Kovacs et al. 1986; Birge and Louveaux 1988; Lustig et al. 1991; Ferrero et al. 1998; Huang and Loucks 2000; Mance 2007; Yeomans and Gunalay 2009; Li and Huang 2009; Guo et al. 2010; Li et al. 2013a, b). The ITSP method, integrated the interval-parameter programming (IPP) and TSP, could deal with uncertainties expressed as not only probability distributions but also discrete intervals. In ITSP, an initial decision is first undertaken before the random events happen; then after these future uncertainties are resolved and the values of random variables are known, a second-stage decision can be made in order to minimize “penalties” that may appear due to any infeasibility (Loucks et al. 1981; Birge and Louveaux 1988, 1997). For example, in a water resources allocation problem, it is assumed that the water allocation plan is decided before the actual realization of available water resources inflow, allowing only some operational recourse actions (e.g. reduce the amount of water supplies) to take place to improve the objective and correct any infeasibility (Xie et al. 2013). In this formulation, the objective is usually to maximize the expected profit or to minimize the expected cost over the two stages of a decision-making project. Although ITSP methods were widely explored over the past decades, a major limitation of the ITSP is that it considers, in one way or another, “expected outcome” of the problem objective without explicitly taking into accounts its variability. Specifically, ITSP model do not take into account the variability of the second-stage cost or benefit but only its expected value (Xu et al. 2009). The limitation could lead to the problems of low system stability and unbalanced allocation pattern. For example, in water resources management problems, the water resources amounts would be allocated to the water users with higher benefit, water consumers. With low benefit would obtain insufficiently allowable amounts or even zero amount. Such a situation would be exacerbated when the region is under a severe water-shortage situation.

Aiming to reflect such risk-aversion within the ITSP framework, the concept of downside risk was proposed to measure the recourse cost variability and firstly obtain solutions appealing to a risk-averse investment management. Downside risk, as the name implies, measures risk below a certain point. For example, if an investor is worried only about losing money, that point would be zero, and the possibility of negative returns would be viewed as risky. If an investor needs to earn a 5 % annual return in order to meet goals, any return under 5 % would be considered risky. In addition, downside risk is a function not only of the first-stage decisions but also of the aspiration or target profit level, minimizing downside risk at one level does not imply its minimization at another. The downside risk method is an advantageous measure to assess and manage risk in many filed, such as financial risk and investment management, water resources trading, energy market management (Sortino and Lee 1994; Yu 2002; Finger 2013). Through the previous studies, it was found that in addition to being a more intuitive definition of risk, the major advantage to downside risk over standard deviation is that it accommodates different views of risk. Besides, it could integrate goal programming formulations with a scenario-based description of problem data, and generates a series of solutions, which are useful for helping decision makers to quantitatively evaluate trade-offs between system economy and stability. Moreover, in a shared river basin, many water users need to earn a fixed return in order to meet the development target; due to the random variation of the allowable discharge amounts of the main pollutants in a river reach, the net benefit would vary along with the random changes in water quantity and quality levels, and any profit under the fixed return would be considered risky. If it does not take the risk of model feasibility and reliability into consideration in water quality management problems, it could lead to the problems of low system stability, and unbalanced water and pollutant allocation pattern.

Nevertheless, in water quality management, most of the studies relatively pay close attention to the water quality risk assessment, water quality risk control management, and water quality simulation and so on. No previous studies were focused on risk-aversion of water users’ profit in water quality management problems, and development of inexact two-stage stochastic downside risk-aversion programming (ITSDP) method through integrating IPP, TSP and downside risk method into a general framework for water quality management in a river basin. Therefore, based on the inexact two-stage stochastic water resources allocation programming (proposed in Xie et al. 2013), the objective of this study is to develop an ITSDP for water quality management in a shared river with multi-water resources users under uncertainty. This is the first attempt that IPP, TSP and downside risk methods are integrated into a general framework to manage water pollutant emissions under uncertainties presented as interval values and probabilities within a planning horizon. A case study will then be provided for demonstrating how the ITSDP method will support environmental management systems planning under uncertainty. Furthermore, it will be shown how it can be used to optimize the water allocation strategies and enhance water quality management in the water resources systems, as well as determine which of these designs can most efficiently lead to the optimized system objectives.

2 Methodology

By keeping sustainable development between water environment and social-economy, the framework of water quality management is related to many policies, technical, environmental, institutional and financial components (Zarghami and Szidarovszky 2009). Consider a water quality management system wherein a manager is responsible for allocating the allowable water resources to water users, and optimizing pollutant loadings from wastewater dischargers within a shared stream basin. In the water resources management system under consideration, water pollution results mainly from municipal, industrial and agricultural pollution sources, and multi-users water allocation is related to human activities, river flows and economic returns. In this sense, the major decisions involved in the water quality management are economic development targets (e.g. water allocation target) and pollution-discharge schemes. Under such a situation, the decision makers need to optimize the target of water users’ development and the pollutant discharge permits for each user to mitigate the pollution, and achieve a maximum net system benefit. However, uncertainties expressed as multiple formats existing in water resources systems should be reflected. Thus, the decision makers can formulate the problem as maximizing the net system benefit while satisfying the goals of pollution mitigation, the requirement of water quality, and the complex uncertainty reflection.

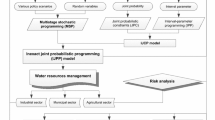
In order to reflect the complex problem complicated relations between in the realistic water quality management problems, an ITSDP model was based on IPP, TSP, and downside risk method. Figure 1 presents the general framework and solution algorithm of the ITSDP method, and each technique has its unique contribution in enhancing the ITSDPs capacities for tackling the uncertainties and system risk. For example, the uncertainties of imperfect knowledge presented as discrete intervals were reflected through IPP, the probability distributions and policy implications were handled through TSP, the system risk was addressed by downside risk method.

Fig. 1

Framework of the ITSDP model

2.1 Inexact TSP

TSP is effective for addressing problems where an analysis of policy scenarios is desired periodically over time and uncertain parameters are expressed as probability distribution functions. In TSP, decision variables are divided into two subsets: those that must be determined before the realizations of random variables are known and those (recourse variables) that are determined after the realized values of the random variables are available. A general TSP model can be formulated as follows (Birge and Louveaux 1997):

$$ \hbox{max} \;f = c^{T} x - \sum\limits_{s = 1}^{N} {p_{s} Q\left( {y,\;\omega_{s} } \right)} , $$

(1a)

subject to:

$$ ax \le b, $$

(1b)

$$ T\left( {\omega_{s} } \right)x + W\left( {\omega_{s} } \right)y = h\left( {\omega_{s} } \right), $$

(1c)

$$ x \ge 0,\quad y\left( {\omega_{s} } \right) \ge 0, $$

(1d)

where x is vector of first-stage decision variables, c ^T x is first-stage benefits, ω is random events after the first-stage decisions are made, s is the scenario of the happening of random events, p _s is probability of event ω _s , Q(y, ω _s ) is system recourse at the second-stage under the occurrence of event ω _s , $\sum\nolimits_{s = 1}^{N} {p_{s} Q(y,\;\omega_{s} )}$ is expected value of the second-stage system penalties.

The existing TSP methods are effective in handling probabilistic uncertainties in the model’s right-hand sides which are often related to resources availability; however they have difficulties in dealing with independent uncertainties of the model’s left-hand sides and cost coefficients. IPP is an alternative for handling uncertainties in the model’s left- and/or right-hand sides as well as those that cannot be quantified as membership or distribution functions, since interval numbers are acceptable as its uncertain inputs (Huang et al. 1992). Let x ^± be a set of intervals with crisp lower bound (e.g., x ⁻) and upper bounds (i.e., x ⁺), but unknown distribution information. Let x be a set of closed and bounded interval numbers x ^± (Huang 1996):

$$ x^{ \pm } = \left[ {x^{ - } ,\;x^{ + } } \right] = \left\{ {t|x^{ - } \le t \le x^{ + } } \right\}. $$

(2)

Through introducing interval parameters into Model 1, the ITSP model can be formulated as follows (Li et al. 2010):

$$ \hbox{max} \;f^{ \pm } = c^{ \pm } x^{ \pm } - \sum\limits_{s = 1}^{N} {p_{s} Q\left( {y^{ \pm } ,\;\omega_{s}^{ \pm } } \right)}, $$

(3a)

subject to:

$$ a^{ \pm } x^{ \pm } \le b^{ \pm } , $$

(3b)

$$ T\left( {\omega_{s}^{ \pm } } \right)x^{ \pm } + W\left( {\omega_{s}^{ \pm } } \right)y^{ \pm } = h\left( {\omega_{s}^{ \pm } } \right), $$

(3c)

$$ x^{ \pm } \ge 0,\quad y\left( {\omega_{s}^{ \pm } } \right) \ge 0. $$

(3d)

On the other hand, when trying to analyze the usefulness of the ITSP model in the context of risk management one first notices that, even though it maximizes the total expected profit, it does not provide any control over the variability of the profit over the different scenarios. The reason is that in the two-stage stochastic approach, it is assumed that the plan is decided before the actual realization of uncertain parameters (scenarios), allowing only some operational recourse actions to take place to improve the objective and correct any infeasibility. In this formulation, the objective is usually to maximize the expected profit or to minimize the expected cost over the TSP management. The expected profit of the problem objective without explicitly taking into account its variability leads to the problems of low system stability and unbalanced allocation pattern.

2.2 Downside risk method

According to previous studies, Cheng et al. (2003) suggest that risk should be managed directly in its downside risk form for a particular aspiration level together with other project attributes such as the expected profit. Downside risk is an advantageous method to assess and manage risk that can incorporate risk concern (i.e., the tradeoff between the expected value and variability of the expected value) into optimization models. In order to deal with the limitation of TSP, the concept of downside risk has been proposed to measure the recourse cost variability in the TSP model. To present the concept of downside risk, let us first define δ(x, Ω) as the positive deviation from a profit target Ω for design x and Profit(x) as the benefit during the planning horizon, that is

$$ \delta (x,\;\Omega ) = \left\{ {\begin{array}{ll} {\Omega - Profit(x)} & {{\text{if}}\;Profit(x) < \Omega }, \\ 0 & {{\text{if}}\;Profit(x) \ge \Omega}. \\ \end{array} } \right. $$

(4)

Downside risk is then defined as the expected value of δ(x, Ω)

$$ DRisk\;\delta (x,\;\Omega ) = E[\delta (x,\;\Omega )]. $$

(5)

To incorporate the concept of downside risk in the framework of two-stage stochastic models let δ _s (x, Ω _s ) be the positive deviation from the profit target Ω _s for design x and scenario s defined as follows (Bean et al. 1992):

$$ \delta_{s} \left( {x,\;\Omega_{s} } \right) = \left\{ {\begin{array}{ll} {\Omega_{s} - Profit_{s} (x)} & {{\text{if}}\;Profit_{s} (x) < \Omega_{s} } \\ 0 & {{\text{if}}\;Profit_{s} (x) \ge \Omega_{s} } \\ \end{array} ,\quad \forall s}. \right. $$

(6)

Because the scenarios are probabilistically independent, the expected value of δ(x, Ω) (i.e., downside risk) can be expressed as the following linear function of δ

$$ DRisk\;\delta (x,\;\Omega ) = \sum\limits_{{s = 1\text{ }}}^{N} {p_{s} \delta_{s} (x,\;\Omega )} . $$

(7)

Similarly, in the case where the profit has a continuous probability distribution, downside risk is given by

$$ DRisk\;\delta (x,\;\Omega ) = \int\limits_{ - \infty }^{\Omega } {(\Omega - \xi )f(x,\;\xi )d\xi } . $$

(8)

From the above definitions of downside risk, it is indicated that downside risk is an expectation in income/cost, differing with the definition of other risk measures that represents a probability value. Moreover, DRisk δ(x, Ω) is a continuous linear measure because it does not require the use of binary variables in the two-stage stochastic formulation (Aseeri and Bagajewicz 2004). This is a highly desirable property to potentially reduce the computational requirements of the models to manage risk. If the decision-maker is risk averse, he/she would prefer the lower risk.

2.3 Inexact two-stage stochastic downside risk-aversion programming

In this case, a downside risk method can be introduced into the ITSP model to averse the risk. Therefore, an ITSDP can be formulated as follows:

$$ \hbox{max} \;f^{ \pm } = c^{ \pm } x^{ \pm } - \sum\limits_{s = 1}^{N} {p_{s} Q\left( {y^{ \pm } ,\;\omega_{s}^{ \pm } } \right)}, $$

(9a)

subject to:

$$ a^{ \pm } x^{ \pm } \le b^{ \pm } , $$

(9b)

$$ T\left( {\omega_{s}^{ \pm } } \right)x^{ \pm } + W\left( {\omega_{s}^{ \pm } } \right)y^{ \pm } = h\left( {\omega_{s}^{ \pm } } \right), $$

(9c)

$$ DRisk\;\delta \left( {x^{ \pm } ,\;\Omega_{s}^{ \pm } } \right) = \sum\limits_{{s = 1\text{ }}}^{N} {p_{s} \delta_{s} \left( {x^{ \pm } ,\;\Omega_{s}^{ \pm } } \right)} \le \lambda \cdot \psi^{ \pm } , $$

(9d)

$$ Profit_{s} \left( {x^{ \pm } } \right) = c^{ \pm } x^{ \pm } - \sum\limits_{s = 1}^{N} {Q\left( {y^{ \pm } ,\;\omega_{s}^{ \pm } } \right)} ,\quad \forall s, $$

(9e)

$$ \delta_{s} \left( {x^{ \pm } ,\;\Omega_{s}^{ \pm } } \right) = \left\{ {\begin{array}{ll} {\Omega_{s}^{ \pm } - Profit_{s} \left( {x^{ \pm } } \right)} & {{\text{if}}\;Profit_{s} \left( {x^{ \pm } } \right) < \Omega_{s}^{ \pm } } \\ 0 & {{\text{if}}\;Profit_{s} \left( {x^{ \pm } } \right) \ge \Omega_{s}^{ \pm } } \\ \end{array} }, \right.\quad \forall s, $$

(9f)

$$ x^{ \pm } \ge 0,\quad y\left( {\omega_{s}^{ \pm } } \right) \ge 0, $$

(9g)

where ψ ^± is the expected downside risk value that calculates through the solution of the ITSP model, and λ is a control factor to acquire a more stringent limitation of risk, λ ∈ [0, 1].

Model (9) can be transformed into two deterministic submodels that correspond to the lower and upper bounds of desired objective function value. This transformation process is based on an interactive algorithm, which is different from the best/worst case analysis (Huang et al. 1992). The objective function value corresponding to f ⁺ is desired first because the objective is to maximize net system costs. The submodel to find f ⁺ can be firstly formulated as follows (assume that B ^± ≥ 0, and f ^± ≥ 0):

$$ { \hbox{max} }\; \, f^{ + } = \sum\limits_{j = 1}^{{k_{1} }} {c_{j}^{ + } x_{j}^{ + } } + \sum\limits_{{j = k_{1} + 1}}^{{_{{\mathop n\nolimits_{1} }} }} {c_{j}^{ + } x_{j}^{ - } } - \sum\limits_{{l\text{ } = 1}}^{{_{{\mathop k\nolimits_{2} }} }} {\sum\limits_{s = 1}^{n} {p_{s} d_{l}^{ - } y_{ls}^{ - } } } - \sum\limits_{{l = k_{2} + 1}}^{{_{{n_{2} }} }} {\sum\limits_{s = 1}^{n} {p_{s} d_{l}^{ + } y_{ls}^{ + } } }, $$

(10a)

subject to:

$$ \sum\limits_{j = 1}^{{_{{k_{1} }} }} {\left| {a_{rj}^{ \pm } } \right|^{ - } sign\left( {a_{rj}^{ \pm } } \right)x_{j}^{ + } } + \sum\limits_{{j = k_{1} + 1}}^{{_{{\mathop n\nolimits_{1} }} }} {\left| {a_{rj}^{ \pm } } \right|^{ + } sign\left( {a_{rj}^{ \pm } } \right)x_{j}^{ - } } \le b_{r}^{ + } ,\quad \forall r, $$

(10b)

$$ \sum\limits_{j = 1}^{{k_{1} }} {T\left( {\omega_{s}^{ + } } \right)x_{j}^{ + } } + \sum\limits_{{j = k_{1} + 1}}^{{n_{1} }} {T\left( {\omega_{s}^{ + } } \right)x_{j}^{ - } } + \sum\limits_{l = 1}^{{k_{2} }} {W\left( {\omega_{s}^{ + } } \right)y_{ls}^{ - } } + \sum\limits_{{l = k_{2} + 1}}^{{n_{2} }} {W\left( {\omega_{s}^{ + } } \right)y_{ls}^{ + } } = h\left( {\omega_{s}^{ + } } \right)\quad \forall s, $$

(10c)

$$ DRisk\;\delta \left( {x^{ \pm } ,\;\Omega_{s}^{ + } } \right) = \sum\limits_{{s = 1\text{ }}}^{N} {p_{s} \delta_{s} \left( {x^{ \pm } ,\;\Omega_{s}^{ + } } \right)} \le \lambda \cdot \psi^{ + } , $$

(10d)

$$ Profit_{s} \left( {x^{ \pm } } \right) = \sum\limits_{j = 1}^{{_{{k_{1} }} }} {c_{j}^{ + } x_{j}^{ + } } + \sum\limits_{{j = k_{1} + 1}}^{{_{{\mathop n\nolimits_{1} }} }} {c_{j}^{ + } x_{j}^{ - } } - \sum\limits_{{l\text{ } = 1}}^{{_{{\mathop k\nolimits_{2} }} }} {d_{l}^{ - } y_{ls}^{ - } } - \sum\limits_{{l = k_{2} + 1}}^{{_{{n_{2} }} }} {d_{l}^{ + } y_{ls}^{ + } } , $$

(10e)

$$ \delta_{s} \left( {x^{ \pm } ,\;\Omega_{s}^{ + } } \right) = \left\{ {\begin{array}{ll} {\Omega_{s}^{ + } - Profit_{s} \left( {x^{ \pm } } \right)} & {{\text{if}}\;Profit_{s} \left( {x^{ \pm } } \right) < \Omega_{s}^{ + } } \\ 0 & {{\text{if}}\;Profit_{s} \left( {x^{ \pm } } \right) \ge \Omega_{s}^{ + } } \\ \end{array} }, \right.\quad \forall s, $$

(10f)

$$ \sum\limits_{s = 1}^{n} {p_{s} = 1} , $$

(10g)

$$ x_{j}^{ - } \ge 0,\quad j = 1,\;2, \ldots ,k_{1} , $$

(10h)

$$ x_{j}^{ + } \ge 0,\quad j = k_{1} + 1,\;k_{1} + 2, \ldots ,n_{1} , $$

(10i)

$$ y_{ls}^{ - } \ge 0,\quad \forall s;\quad l = 1,\;2, \ldots ,k_{2} , $$

(10j)

$$ y_{ls}^{ + } \ge 0,\quad s;\quad l = k_{2} + 1,\;k_{2} + 2, \ldots ,n_{2} , $$

(10k)

where $x_{j}^{ \pm } ,$ j = 1, 2,…,k ₁, are interval variables with positive coefficients in the objective function; $x_{j}^{ \pm } ,$ j = k ₁ + 1, k ₁ + 2,…,n ₁ are interval variables with negative coefficients; $y_{ls}^{ \pm } ,$ l = 1, 2,…,k ₂ and s = 1, 2,…,n, are random variables with positive coefficients in the objective function; $y_{ls}^{ \pm } ,$ l = k ₂ + 1, k ₂ + 2,…,n ₂ and s = 1, 2,…,n, are random variables with negative coefficients. $\sin g(a_{j}^{ \pm } ) = - 1$ when $a_{j}^{ \pm } < 0;\;\sin g(a_{j}^{ \pm } ) = 1$ when $a_{j}^{ \pm } > 0.$ Solutions of $x_{jopt}^{ + }$ (j = 1, 2,…,k ₁), $x_{jopt}^{ - }$ (j = k ₁ + 1, k ₁ + 2,…,n ₁), $y_{lsopt}^{ - }$ (l = 1, 2,…,k ₂), and $y_{lsopt}^{ + }$ (l = k ₂ + 1, k ₂ + 2,…,n ₂) can be obtained through submodel (10). Based on the above solutions, the second submodel for f ⁻ can be formulated as follows:

$$ {\text{max}}\; \, f^{ - } = \sum\limits_{j = 1}^{{_{{k_{1} }} }} {c_{j}^{ - } x_{j}^{ - } } + \sum\limits_{{j = k_{1} + 1}}^{{_{{\mathop n\nolimits_{1} }} }} {c_{j}^{ - } x_{j}^{ + } } - \sum\limits_{{l\text{ } = 1}}^{{_{{\mathop k\nolimits_{2} }} }} {\sum\limits_{s = 1}^{n} {p_{s} d_{l}^{ + } y_{ls}^{ + } } } - \sum\limits_{{l = k_{2} + 1}}^{{_{{n_{2} }} }} {\sum\limits_{s = 1}^{n} {p_{s} d_{l}^{ - } y_{ls}^{ - } } } , $$

(11a)

subject to:

$$ \sum\limits_{j = 1}^{{_{{k_{1} }} }} {\left| {a_{rj}^{ \pm } } \right|^{ + } sign\left( {a_{rj}^{ \pm } } \right)x_{j}^{ - } } + \sum\limits_{{j = k_{1} + 1}}^{{_{{\mathop n\nolimits_{1} }} }} {\left| {a_{rj}^{ \pm } } \right|^{ - } sign\left( {a_{rj}^{ \pm } } \right)x_{j}^{ - } } \le b_{r}^{ - } ,\quad \forall r, $$

(11b)

$$ \sum\limits_{j = 1}^{{k_{1} }} {T\left( {\omega_{s}^{ - } } \right)x_{j}^{ - } } + \sum\limits_{{j = k_{1} + 1}}^{{n_{1} }} {T\left( {\omega_{s}^{ - } } \right)x_{j}^{ + } } + \sum\limits_{l = 1}^{{k_{2} }} {W\left( {\omega_{s}^{ - } } \right)y_{ls}^{ + } } + \sum\limits_{{l = k_{2} + 1}}^{{n_{2} }} {W\left( {\omega_{s}^{ - } } \right)y_{ls}^{ - } } = h\left( {\omega_{s}^{ - } } \right)\quad \forall s, $$

(11c)

$$ DRisk\;\delta \left( {x^{ \pm } ,\;\Omega_{s}^{ - } } \right) = \sum\limits_{{s = 1\text{ }}}^{N} {p_{s} \delta_{s} \left( {x^{ \pm } ,\;\Omega_{s}^{ - } } \right)} \le \lambda \cdot \psi^{ - } , $$

(11d)

$$ Profit_{s} \left( {x^{ \pm } } \right) = \sum\limits_{j = 1}^{{_{{k_{1} }} }} {c_{j}^{ - } x_{j}^{ - } } + \sum\limits_{{j = k_{1} + 1}}^{{_{{\mathop n\nolimits_{1} }} }} {c_{j}^{ - } x_{j}^{ + } } - \sum\limits_{{l\text{ } = 1}}^{{_{{\mathop k\nolimits_{2} }} }} {d_{l}^{ + } y_{ls}^{ + } } - \sum\limits_{{l = k_{2} + 1}}^{{_{{n_{2} }} }} {d_{l}^{ - } y_{ls}^{ - } } , $$

(11e)

$$ \delta_{s} \left( {x^{ \pm } ,\;\Omega_{s}^{ - } } \right) = \left\{ {\begin{array}{ll} {\Omega_{s}^{ - } - Profit_{s} \left( {x^{ \pm } } \right)} & {{\text{if}}\;Profit_{s} \left( {x^{ \pm } } \right) < \Omega_{s}^{ - } } \\ 0 & {{\text{if}}\;Profit_{s} \left( {x^{ \pm } } \right) \ge \Omega_{s}^{ - } } \\ \end{array} }, \right.\quad \forall s, $$

(11f)

$$ \sum\limits_{s = 1}^{n} {p_{s} = 1} , $$

(11g)

$$ x_{jopt}^{ + } \ge x_{j}^{ - } \ge 0,\quad j = 1,\;2, \ldots ,k_{1} , $$

(11h)

$$ 0 \le x_{jopt}^{ - } \le x_{j}^{ + } ,\quad j = k_{1} + 1,\;k_{1} + 2, \ldots ,n_{1} , $$

(11i)

$$ y_{ls}^{ + } \ge y_{lsopt}^{ - } \ge 0,\quad \forall s;\quad l = 1,\;2, \ldots ,k_{2} , $$

(11j)

$$ y_{lsopt}^{ + } \ge y_{{ls\text{ }}}^{ - } \ge 0,\quad \forall s;\quad l = k_{2} + 1,\;k_{2} + 2, \ldots ,n_{2} . $$

(11k)

Solutions of $x_{jopt}^{ - }$ (j = 1, 2,…,k ₁), $x_{jopt}^{ + }$ (j = k ₁ + 1, k ₁ + 2,…,n ₁), $y_{lsopt}^{ + }$ (j = 1, 2,…,k ₂), and $y_{lsopt}^{ - }$ (j = k ₂ + 1, k ₂ + 2,…,n ₂) can be obtained through submodel (11). Through integrating solutions of submodels (10) and (11), interval solution for model (9) can be obtained.

$$ f_{opt}^{ \pm } = \left[ {f_{jopt}^{ - } ,\;f_{jopt}^{ + } } \right], $$

(12a)

$$ x_{jopt}^{ \pm } = \left[ {x_{jopt}^{ - } ,\;x_{jopt}^{ + } } \right], $$

(12b)

$$ y_{lsopt}^{ \pm } = \left[ {y_{lsopt}^{ - } ,\;y_{lsopt}^{ + } } \right]. $$

(12c)

3 ITSDP model for water quality management

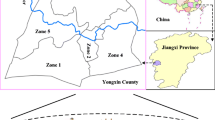
Consider a water-quality management system in a region, where one municipal, three industrial and two agricultural sectors exist and take water from a shared stream (Fig. 2). The study area is an important industrial and agricultural base, and the main crops are cotton, rice, maize, soybean, peanut, wheat and rape. The growing period of cotton, rice, maize, soybean and peanut is from May to October, and the planting time of wheat and rape is from November to April next year. Two agricultural aqueducts are used for transferring the water to agricultural regions I and II, and no water from the agricultural areas back up to the river through the agricultural canals, apart from the condition of flooding. Therefore, the main pollutant dischargers are the municipal wastewater treatment plant and three major industrial units (i.e. a food processing plant, a thermal power plant, and a paper mill factory). Moreover, two water intakes are used for municipal and industrial water supply, one is for municipal and food processing plant’s water supply, another is for thermal power and paper mill factory. The main control pollutants are chemical oxygen demand (e.g. COD) and biochemical oxygen demand (e.g. BOD), and the main loss of the agricultural are total nitrogen (e.g. TN) and total phosphorus (e.g. TP). In order to meet the environmental requirement, the raw wastewater from each industry source must be treated with specific facilities before discharge. The water quality in the river is related to contaminant concentrations of each important monitoring sections (including pollution discharging section, drinking water sources) and flow rate of the discharged wastewater. Therefore, the stream is segmented into nine reaches with reach 1 being at the upstream end and reach 9 at the downstream end. Water quality at each reach is also affected by various sources from its upper stream. Moreover, municipal and industrial activities are not only responsible for the water pollution but also interrelated to each other. Any change in one activity may lead to a series of environmental effects and water resources allocation strategies. Moreover, population growth and economic development with the study area in the future can lead to increment demand for water resources and wastewater discharge of each sectors. Challenges exit in satisfying the water resources demand and water quality requirement while facilitating regional development.

Fig. 2

Schematic diagram of the study system

For the stream water, COD and BOD are important index to evaluate the quality of water in environmental monitoring and sewage treatment, and water quality models are used to address the relationship between pollutant discharges and water-quality indicators’ responses in a stream. In many cases, simplifications or assumptions are made in specific planning situations given the limits of available time and money; in some cases, models should be relatively simple; in other cases, they may have to be more complex (Loucks et al. 1981). For a typical water quality management problem, the modeling method should be able to predict the degree of waste removal at various point sources sites along a water body that will meet both effluent and water quality standards. In this study, a one-dimensional water quality model is used to support effective water quality management considering a main loading contribution from point sources. Thus, the BOD load and DO deficit in relation to the m wastewater-discharge sources can be predicted as follows (O’Connor and Dobbins 1958; Thomann and Mueller 1987; Li and Huang 2009):

$$ B_{n} = \mathop \prod \limits_{r = 1}^{n} e^{{ - k_{{d_{b} }} t_{j} }} BOD_{0} + \mathop \prod \limits_{r = 2}^{n} e^{{ - k_{{d_{b} }} t_{j} }} \left( {1 - \eta_{1} } \right)BOD_{1} + \cdots + e^{{ - k_{{d_{b} }} t_{n} }} \left( {1 - \eta_{m - 1} } \right)BOD_{m - 1} + \left( {1 - \eta_{m} } \right)BOD_{m} , $$

(13a)

$$ C_{n} = \mathop \prod \limits_{r = 1}^{n} e^{{ - k_{{d_{c} }} t_{j} }} COD_{0} + \mathop \prod \limits_{r = 2}^{n} e^{{ - k_{{d_{c} }} t_{j} }} \left( {1 - \xi_{1} } \right)COD_{1} + \cdots + e^{{ - k_{{d_{c} }} t_{n} }} \left( {1 - \xi_{m - 1} } \right)COD_{m - 1} + \left( {1 - \xi_{m} } \right)COD_{m} , $$

(13b)

where r is defined as a segmentation of the stream between source i and i + 1 (r = 1, 2,…,n), BOD ₀ and COD ₀ is the initial BOD and COD in the stream immediately after discharge (mg/L), respectively, B _n and C _n are the respective BOD and COD loads in the river at the beginnings of reaches n, respectively, $k_{{d_{b} }}$ and $k_{{d_{c} }}$ are the first-order deoxygenation rate constant and decay rate (day⁻¹), respectively, t _j is the length of reach r expressed in time units, i denotes wastewater-discharge source, and i = 1, 2,…,m, η _i and ξ _i are the wastewater-treatment efficiency of BOD and COD at discharge source i, respectively, BOD _m and COD _m are the total amount of BOD and COD to be disposed of at source i (kg/day), respectively.

In order to establish and make the plan of rational production, all sectors need to know the water allocation target that promised by the region manager under an water environmental requirement. If the promised water cannot be delivered due to insufficient supply, users will have to either obtain water from higher priced alternatives or curb their development plans (Maqsood et al. 2005). If the promised water is delivered, a net benefit to the local economy will be generated for each unit of water allocated. However, if the promised water is not delivered, either the water must be obtained from higher priced alternatives or the demand must be curtailed by reduced production, resulting in a reduced net system benefit (Huang and Loucks 2000; Maqsood et al. 2005). In addition to maximization of net benefit, feasibility and reliability issues associated with the water allocations are taken into consideration. Actually, the manager should ensure that each user would obtain a amount of water for the purpose of a maximum income with a certain risk level. Besides, uncertainties may exist in a variety of impact factors, water users’ activities and pollution-related processes such as effluent characteristics, treatment measures, pollutant-discharge levels (Victoria et al. 2005). Therefore, the problems under consideration are how to effectively allocate water to the three users to achieve a maximum benefit and how to keep balance between regional development and water environmental protection under multiple uncertainties with a stable water allocation policy being accounted for.

Based on the above analysis, it should make an effective measure to plan water resources allocation in the study area with a maximized system benefit under a water-pollution risk control. Consider a 1-year planning horizon, the first period is from May to October, and November to April next year is the second planning period, corresponds to the crops growing times. Policies in terms of the related municipal, industrial and agricultural activities, and the wastewater discharges are critical for ensuring maximized system benefit and safe water quality. Generally, the complexities of the study problem include: (a) many parameters are uncertain and are available as probabilistic distributions and/or discrete intervals, (b) the maximize objective of net benefit can affect the model results and the unbalanced allocation outcome, and (c) dynamic interactions exist between pollutant loading and water quality. The proposed ITSDP method is considered suitable for tackling such a problem. Therefore, based on the ITSDP method and water quality model, an inexact two-stage stochastic downside risk-aversion water quality management model can be formulated as follows:

$$ \begin{aligned} \hbox{max} \;f^{ \pm } & = \sum\limits_{i = 1}^{I} {\sum\limits_{t = 1}^{T} {W_{it}^{ \pm } \cdot NB_{it}^{ \pm } } } - \sum\limits_{i = 1}^{I} {\sum\limits_{t = 1}^{T} {\sum\limits_{h = 1}^{H} {p_{ht} \cdot CS_{it}^{ \pm } \cdot DW_{iht}^{ \pm } } } } - \sum\limits_{i = 1}^{I} {\sum\limits_{t = 1}^{T} {\sum\limits_{h = 1}^{H} {CT_{it}^{ \pm } \cdot \varphi_{it}^{ \pm } \cdot \left( {W_{it}^{ \pm } - p_{ht} \cdot DW_{iht}^{ \pm } } \right)} } } \\ \text{ } & \quad + \sum\limits_{j = 1}^{J} {\sum\limits_{r = 1}^{R} {\sum\limits_{t = 1}^{T} {Y_{j}^{ \pm } \cdot S_{jrt}^{ \pm } \cdot BC_{jt}^{ \pm } } } } - \sum\limits_{j = 1}^{J} {\sum\limits_{r = 1}^{R} {\sum\limits_{t = 1}^{T} {\sum\limits_{h = 1}^{H} {p_{ht} \cdot Y_{j}^{ \pm } \cdot SD_{jrht}^{ \pm } \cdot CA_{jt}^{ \pm } } } } } \\ \text{ } & \quad - \sum\limits_{r = 1}^{R} {\sum\limits_{j = 1}^{J} {\sum\limits_{n = 1}^{N} {\sum\limits_{t = 1}^{T} {\sum\limits_{h = 1}^{H} {CF_{n}^{ \pm } \cdot \left( {S_{jrt}^{ \pm } - p_{ht} \cdot SD_{jrht}^{ \pm } } \right) \cdot FD_{jnt}^{ \pm } } } } } }, \\ \end{aligned} $$

(14a)

subject to

• (1) Area constraint

  $$ \sum\limits_{j = 1}^{J} {S_{jrt}^{ \pm } - SD_{jrht}^{ \pm } } = A_{r} ,\quad \forall r,\;t,\;h, $$

  (14b)
  $$ SD_{jrht}^{ \pm } \le S_{jrt}^{ \pm } \le \text{ }S_{jrtmax}^{ \pm } ,\quad \forall j,\;r,\;t,\;h. $$

  (14c)

• (2) TN and TP discharge constraint

  $$ \sum\limits_{j = 1}^{J} {\left( {1 - \varepsilon_{jnt}^{ \pm } } \right) \cdot \left( {S_{jrt}^{ \pm } - SD_{jrht}^{ \pm } } \right) \cdot FD_{jnt}^{ \pm } - \sum\limits_{j = 1}^{J} {B_{jnt}^{ \pm } \left( {S_{jrt}^{ \pm } - SD_{jrht}^{ \pm } } \right)} } \le \text{ }\sum\limits_{j = 1}^{J} {TN_{jnt}^{ \pm } \cdot \left( {S_{jrt}^{ \pm } - SD_{jrht}^{ \pm } } \right)} ,\quad \forall r,\;n,\;t,\;h. $$

  (14d)

• (3) Amount of water availability constraint

  $$ \sum\limits_{i = 1}^{I} {\left( {W_{it}^{ \pm } - DW_{iht}^{ \pm } } \right)} + \sum\limits_{j = 1}^{J} {\zeta_{jt}^{ \pm } \cdot \left( {S_{jrt}^{ \pm } - SD_{jrht}^{ \pm } } \right)} \le q_{ht}^{ \pm } ,\quad \forall h,\;t, $$

  (14e)
  $$ DW_{iht}^{ \pm } \le W_{it}^{ \pm } \le W_{itmax}^{ \pm } ,\quad \forall i,\;h,\;t. $$

  (14f)

• (4) Wastewater discharge standard constraint

  $$ C_{imt}^{ \pm } \cdot \left( {1 - \eta_{imt}^{ \pm } } \right) \le GB_{im}^{ \pm } ,\quad \forall i,\;m,\;t. $$

  (14g)

• (5) Maximum allowable COD discharge constraints

  $$ C_{0m} \cdot \exp \left( { - kx_{1} /v} \right) \le R_{1m}^{ \pm } ,\quad \forall m,\;t, $$

  (14h)
  $$ \frac{\begin{aligned} & C_{0m} \cdot \exp \left[ { - k\left( {x_{1} + x_{2} } \right)/v} \right] \cdot \left\{ {Q_{ht}^{ \pm } - \sum\limits_{i = 1}^{2} {\left( {W_{it}^{ \pm } - DW_{iht}^{ \pm } } \right)} } \right\} \\ &+ \varphi_{1t}^{ \pm } \cdot (1 - \eta_{1mt}^{ \pm } ) \cdot C_{1mt}^{ \pm } \cdot (W_{1t}^{ \pm } - DW_{1ht}^{ \pm } ) \\ \end{aligned} }{{Q_{ht}^{ \pm } - \sum\nolimits_{i = 1}^{2} {(W_{it}^{ \pm } - DW_{iht}^{ \pm } )} + \varphi_{1t}^{ \pm } \cdot (W_{1t}^{ \pm } - DW_{1ht}^{ \pm } )}} \le R_{2m}^{ \pm } ,\quad \forall m,\;t, $$

  (14i)
  $$ \frac{\begin{aligned} & C_{0m} \cdot \exp \left[ { - k\left( {x_{1} + x_{2} + x_{3} } \right)/v} \right] \cdot \left\{ {Q_{ht}^{ \pm } - \sum\limits_{i = 1}^{2} {\left( {W_{it}^{ \pm } - DW_{iht}^{ \pm } } \right)} } \right\} \\ &+ \varphi_{1t}^{ \pm } \cdot (1 - \eta_{1mt}^{ \pm } ) \cdot C_{1mt}^{ \pm } \cdot \exp ( - kx_{3} /v) \cdot (W_{1t}^{ \pm } - DW_{1ht}^{ \pm } ) \\ \end{aligned} }{{Q_{ht}^{ \pm } - \sum\nolimits_{i = 1}^{2} {(W_{it}^{ \pm } - DW_{iht}^{ \pm } )} + \varphi_{1t}^{ \pm } \cdot (W_{1t}^{ \pm } - DW_{1ht}^{ \pm } )}} \le R_{3m}^{ \pm } ,\quad \forall m,\;t, $$

  (14j)
  $$ \frac{\begin{aligned} & C_{0m} \cdot \exp \left[ { - k\left( {x_{1} + x_{2} + x_{3} + x_{4} } \right)/v} \right] \cdot \left\{ {Q_{ht}^{ \pm } - \sum\limits_{i = 1}^{2} {\left( {W_{it}^{ \pm } - DW_{iht}^{ \pm } } \right)} } \right\} \\ & + \varphi_{1t}^{ \pm } \cdot \left( {1 - \eta_{1mt}^{ \pm } } \right) \cdot C_{1mt}^{ \pm } \cdot \exp \left[ { - k\left( {x_{3} + x_{4} } \right)/v} \right] \cdot \left( {W_{1t}^{ \pm } - DW_{1ht}^{ \pm } } \right) \\ &+ \varphi_{2t}^{ \pm } \cdot (1 - \eta_{2mt}^{ \pm } ) \cdot C_{2mt}^{ \pm } \cdot (W_{2t}^{ \pm } - DW_{2ht}^{ \pm } ) \\ \end{aligned} }{{Q_{ht}^{ \pm } - \sum\nolimits_{i = 1}^{2} {(W_{it}^{ \pm } - DW_{iht}^{ \pm } )} + \sum\nolimits_{i = 1}^{2} {\varphi_{it}^{ \pm } \cdot (W_{it}^{ \pm } - DW_{iht}^{ \pm } )} }} \le R_{4m}^{ \pm } ,\quad \forall m,\;t, $$

  (14k)
  $$ \frac{\begin{aligned} & C_{0m} \cdot \exp \left[ { - k\left( {x_{1} + x_{2} + x_{3} + x_{4} + x_{5} } \right)/v} \right] \cdot \left\{ {Q_{ht}^{ \pm } - \sum\limits_{i = 1}^{2} {\left( {W_{it}^{ \pm } - DW_{iht}^{ \pm } } \right)} } \right\} \\ & + \varphi_{1t}^{ \pm } \cdot \left( {1 - \eta_{1mt}^{ \pm } } \right) \cdot C_{1mt}^{ \pm } \cdot \exp \left[ { - k\left( {x_{3} + x_{4} + x_{5} } \right)/v} \right] \cdot \left( {W_{1t}^{ \pm } - DW_{1ht}^{ \pm } } \right) \\ &+ \varphi_{2t}^{ \pm } \cdot (1 - \eta_{2mt}^{ \pm } ) \cdot C_{2mt}^{ \pm } \cdot \exp ( - kx_{5} /v) \cdot (W_{2t}^{ \pm } - DW_{2ht}^{ \pm } ) \\ \end{aligned} }{{Q_{ht}^{ \pm } - \sum\nolimits_{i = 1}^{2} {(W_{it}^{ \pm } - DW_{iht}^{ \pm } )} + \sum\nolimits_{i = 1}^{2} {\varphi_{it}^{ \pm } \cdot (W_{it}^{ \pm } - DW_{iht}^{ \pm } )} }} \le R_{5m}^{ \pm } ,\quad \forall m,\;t, $$

  (14l)
  $$ \frac{\begin{aligned} & C_{0m} \cdot \exp \left[ { - k\left( {x_{1} + x_{2} + x_{3} + x_{4} + x_{5} + x_{6} } \right)/v} \right] \cdot \left\{ {Q_{ht}^{ \pm } - \sum\limits_{i = 1}^{2} {\left( {W_{it}^{ \pm } - DW_{iht}^{ \pm } } \right)} } \right\} \\ & + \varphi_{1t}^{ \pm } \cdot \left( {1 - \eta_{1mt}^{ \pm } } \right) \cdot C_{1mt}^{ \pm } \cdot \exp \left[ { - k\left( {x_{3} + x_{4} + x_{5} + x_{6} } \right)/v} \right] \cdot \left( {W_{1t}^{ \pm } - DW_{1ht}^{ \pm } } \right) \\ & + \varphi_{2t}^{ \pm } \cdot \left( {1 - \eta_{2mt}^{ \pm } } \right) \cdot C_{2mt}^{ \pm } \cdot \exp \left[ { - k\left( {x_{5} + x_{6} } \right)/v} \right] \cdot \left( {W_{2t}^{ \pm } - DW_{2ht}^{ \pm } } \right) \\ &+ \varphi_{3t}^{ \pm } \cdot (1 - \eta_{3mt}^{ \pm } ) \cdot C_{3mt}^{ \pm } \cdot (W_{3t}^{ \pm } - DW_{3ht}^{ \pm } ) \\ \end{aligned} }{{Q_{ht}^{ \pm } - \sum\nolimits_{i = 1}^{4} {(W_{it}^{ \pm } - DW_{iht}^{ \pm } )} + \sum\nolimits_{i = 1}^{3} {\varphi_{it}^{ \pm } \cdot (W_{it}^{ \pm } - DW_{iht}^{ \pm } )} }} \le R_{6m}^{ \pm } ,\quad \forall m,\;t, $$

  (14m)
  $$ \frac{\begin{aligned} & C_{0m} \cdot \exp \left[ { - k\left( {x_{1} + x_{2} + x_{3} + x_{4} + x_{5} + x_{6} + x_{7} } \right)/v} \right] \cdot \left\{ {Q_{ht}^{ \pm } - \sum\limits_{i = 1}^{2} {\left( {W_{it}^{ \pm } - DW_{iht}^{ \pm } } \right)} } \right\} \\ & + \varphi_{1t}^{ \pm } \cdot \left( {1 - \eta_{1mt}^{ \pm } } \right) \cdot C_{1mt}^{ \pm } \cdot \exp \left[ { - k\left( {x_{3} + x_{4} + x_{5} + x_{6} + x_{7} } \right)/v} \right] \cdot \left( {W_{1t}^{ \pm } - DW_{1ht}^{ \pm } } \right) \\ & + \varphi_{2t}^{ \pm } \cdot \left( {1 - \eta_{2mt}^{ \pm } } \right) \cdot C_{2mt}^{ \pm } \cdot \exp \left[ { - k\left( {x_{5} + x_{6} + x_{7} } \right)/v} \right] \cdot \left( {W_{2t}^{ \pm } - DW_{2ht}^{ \pm } } \right) \\ & + \varphi_{3t}^{ \pm } \cdot \left( {1 - \eta_{3mt}^{ \pm } } \right) \cdot C_{3mt}^{ \pm } \cdot \exp \left( { - kx_{7} /v} \right) \cdot \left( {W_{3t}^{ \pm } - DW_{3ht}^{ \pm } } \right) \\ &+ \varphi_{4t}^{ \pm } \cdot (1 - \eta_{4mt}^{ \pm } ) \cdot C_{4mt}^{ \pm } \cdot (W_{3t}^{ \pm } - DW_{3ht}^{ \pm } ) \\ \end{aligned} }{{Q_{ht}^{ \pm } - \sum\nolimits_{i = 1}^{4} {(W_{it}^{ \pm } - DW_{iht}^{ \pm } )} + \sum\nolimits_{i = 1}^{4} {\varphi_{it}^{ \pm } \cdot (W_{it}^{ \pm } - DW_{iht}^{ \pm } )} }} \le R_{7m}^{ \pm } ,\quad \forall m,\;t, $$

  (14n)
  $$ \frac{\begin{aligned} & C_{0m} \cdot \exp \left[ { - k\left( {x_{1} + x_{2} + x_{3} + x_{4} + x_{5} + x_{6} + x_{7} + x_{8} + x_{9} } \right)/v} \right] \cdot \left\{ {Q_{ht}^{ \pm } - \sum\limits_{i = 1}^{2} {\left( {W_{it}^{ \pm } - DW_{iht}^{ \pm } } \right)} } \right\} \\ & + \varphi_{1t}^{ \pm } \cdot \left( {1 - \eta_{1mt}^{ \pm } } \right) \cdot C_{1mt}^{ \pm } \cdot \exp \left[ { - k\left( {x_{3} + x_{4} + x_{5} + x_{6} + x_{7} + x_{8} + x_{9} } \right)/v} \right] \cdot \left( {W_{1t}^{ \pm } - DW_{1ht}^{ \pm } } \right) \\ & + \varphi_{2t}^{ \pm } \cdot \left( {1 - \eta_{2mt}^{ \pm } } \right) \cdot C_{2mt}^{ \pm } \cdot \exp \left[ { - k\left( {x_{5} + x_{6} + x_{7} + x_{8} + x_{9} } \right)/v} \right] \cdot \left( {W_{2t}^{ \pm } - DW_{2ht}^{ \pm } } \right) \\ & + \varphi_{3t}^{ \pm } \cdot \left( {1 - \eta_{3mt}^{ \pm } } \right) \cdot C_{3mt}^{ \pm } \cdot \exp \left[ { - k\left( {x_{7} + x_{8} + x_{9} } \right)/v} \right] \cdot \left( {W_{3t}^{ \pm } - DW_{3ht}^{ \pm } } \right) \\& + \varphi_{4t}^{ \pm } \cdot (1 - \eta_{4mt}^{ \pm } ) \cdot C_{4mt}^{ \pm } \cdot \exp [ - k(x_{8} + x_{9} )/v] \cdot (W_{3t}^{ \pm } - DW_{3ht}^{ \pm } ) \\ \end{aligned} }{{Q_{ht}^{ \pm } - \sum\nolimits_{i = 1}^{4} {(W_{it}^{ \pm } - DW_{iht}^{ \pm } )} + \sum\nolimits_{i = 1}^{4} {\varphi_{it}^{ \pm } \cdot (W_{it}^{ \pm } - DW_{iht}^{ \pm } )} }} \le R_{9m}^{ \pm } ,\quad \forall m,\;t. $$

  (14p)
  $$ \frac{\begin{aligned} & C_{0m} \cdot \exp \left[ { - k\left( {x_{1} + x_{2} + x_{3} + x_{4} + x_{5} + x_{6} + x_{7} + x_{8} } \right)/v} \right] \cdot \left\{ {Q_{ht}^{ \pm } - \sum\limits_{i = 1}^{2} {\left( {W_{it}^{ \pm } - DW_{iht}^{ \pm } } \right)} } \right\} \\ & + \varphi_{1t}^{ \pm } \cdot \left( {1 - \eta_{1mt}^{ \pm } } \right) \cdot C_{1mt}^{ \pm } \cdot \exp \left[ { - k\left( {x_{3} + x_{4} + x_{5} + x_{6} + x_{7} + x_{8} } \right)/v} \right] \cdot \left( {W_{1t}^{ \pm } - DW_{1ht}^{ \pm } } \right) \\ & + \varphi_{2t}^{ \pm } \cdot \left( {1 - \eta_{2mt}^{ \pm } } \right) \cdot C_{2mt}^{ \pm } \cdot \exp \left[ { - k\left( {x_{5} + x_{6} + x_{7} + x_{8} } \right)/v} \right] \cdot \left( {W_{2t}^{ \pm } - DW_{2ht}^{ \pm } } \right) \\ & + \varphi_{3t}^{ \pm } \cdot \left( {1 - \eta_{3mt}^{ \pm } } \right) \cdot C_{3mt}^{ \pm } \cdot \exp \left[ { - k\left( {x_{7} + x_{8} } \right)/v} \right] \cdot \left( {W_{3t}^{ \pm } - DW_{3ht}^{ \pm } } \right) \\ &+ \varphi_{4t}^{ \pm } \cdot (1 - \eta_{4mt}^{ \pm } ) \cdot C_{4mt}^{ \pm } \cdot \exp ( - kx_{8} /v) \cdot (W_{3t}^{ \pm } - DW_{3ht}^{ \pm } ) \\ \end{aligned} }{{Q_{ht}^{ \pm } - \sum\nolimits_{i = 1}^{4} {(W_{it}^{ \pm } - DW_{iht}^{ \pm } )} + \sum\nolimits_{i = 1}^{4} {\varphi_{it}^{ \pm } \cdot (W_{it}^{ \pm } - DW_{iht}^{ \pm } )} }} \le R_{8m}^{ \pm } ,\quad \forall m,\;t, $$

  (14o)

• (6) Downside risk-aversion constraint

  $$ Profit(i,\;h,\;t) = W_{it}^{ \pm } \cdot NB_{it}^{ \pm } - p_{ht} \cdot CS_{it}^{ \pm } \cdot DW_{iht}^{ \pm } - p_{ht} \cdot CT_{ik}^{ \pm } \cdot \varphi_{it}^{ \pm } \cdot \left( {W_{it}^{ \pm } - DW_{iht}^{ \pm } } \right),\quad \forall i,\;h,\;t, $$

  (14q)
  $$ Profit(r,\;h,\;t) = \sum\limits_{j = 1}^{J} {Y_{j}^{ \pm } \cdot S_{jrt}^{ \pm } \cdot BC_{jt}^{ \pm } } - \sum\limits_{j = 1}^{J} {p_{ht} \cdot Y_{j}^{ \pm } \cdot SD_{jrht}^{ \pm } \cdot CA_{jt}^{ \pm } } - \sum\limits_{j = 1}^{J} {\sum\limits_{n = 1}^{N} {p_{ht} \cdot CF_{n}^{ \pm } \cdot \left( {S_{jrt}^{ \pm } - SD_{jrht}^{ \pm } } \right) \cdot FD_{jnt}^{ \pm } } } ,\quad \forall r,\;h,\;t, $$

  (14r)
  $$ \delta_{iht} \left( {i,\;\Omega_{it}^{ \pm } } \right) = \left\{ {\begin{array}{ll} {\Omega_{it}^{ \pm } - Profit(i,\;h,\;t)} & {{\text{if}}\;Profit(i,\;h,\;t) < \Omega_{it}^{ \pm } } \\ 0 & {{\text{if}}\;Profit(i,\;h,\;t) \ge \Omega_{it}^{ \pm } } \\ \end{array} }, \right.\quad \forall i,\;h,\;t, $$

  (14s)
  $$ \delta_{rht} \left( {r,\;\Omega_{rt}^{ \pm } } \right) = \left\{ {\begin{array}{ll} {\Omega_{rt}^{ \pm } - Profit(r,\;h,\;t)} & {{\text{if}}\;Profit(r,\;h,\;t) < \Omega_{rt}^{ \pm } } \\ 0 & {{\text{if}}\;Profit(r,\;h,\;t) \ge \Omega_{rt}^{ \pm } } \\ \end{array} } \right.,\quad \forall r,\;h,\;t, $$

  (14t)
  $$ DRisk\;\delta \left( {i,\;\Omega_{it}^{ \pm } } \right) = \sum\limits_{{h = 1\text{ }}}^{H} {p_{h} \delta_{iht} \left( {i,\;\Omega_{it}^{ \pm } } \right)} \le \lambda \cdot \psi_{it}^{ \pm } ,\quad \forall i,\;t, $$

  (14u)
  $$ DRisk\;\delta \left( {r,\;\Omega_{rt}^{ \pm } } \right) = \sum\limits_{{h = 1\text{ }}}^{H} {p_{h} \delta_{rht} \left( {r,\;\Omega_{rt}^{ \pm } } \right)} \le \lambda \cdot \psi_{rt}^{ \pm } ,\quad \forall r,\;t. $$

  (14v)

• (7) Technical constraints

  $$ SD_{jrht}^{ \pm } ,\quad DW_{iht}^{ \pm } \text{ } \ge 0. $$

  (14w)

The detailed explanations for the variables and parameters are provided in “List of symbols”. The objective is to maximize total system benefit, which includes (a) the related benefit from various water users, and the penalties when the promised water is not delivered, (b) the related benefit from agricultural activities, and the penalties when surface water irrigation target is not met, (c) cost of wastewater treatment, and (d) charge of agricultural fertilization application. The constraints are for relationships between the decision variables and a number of water-related restrictions, including the regional total available water resources, the agricultural acreage, the wastewater discharge standard, the amount of pollutant discharge, downside risk-aversion, and so on. Table 1 provides the water target demands of municipal and industrial sectors, and the related economic data. The data were obtained through analyses for a number of representative cases for water resources management (Loucks et al. 1981; Huang and Loucks 2000; Li et al. 2006, 2007). Most information in water resources system problems is not of sufficient quality to be presented as probability density functions. Instead, it is easier to describe such information as discrete intervals, water-allocation targets and economic data are expressed as intervals format. At the same time, if the promised water is delivered, it would bring a net benefit to the local development. However, if the promised water is not delivered, either water must be obtained from alternative and more expensive sources, or demand must be curtailed by reduced production and/or increased recycling within the industrial concern, or by reduced irrigation in the agricultural sector. Table 2 presents irrigation target and the related parameters of agricultural activities. Moreover, the available amount of water resources has characteristics of random and increasing or decreasing trend changes. In order to obtain the probability values, one way is to survey from different experts, based on an assumption that there were no enough data available. The other way is exemplified by the probability cumulative distribution function, which is based on that there is enough data available. According to the local policy of the hypothetical cases, three discrete water inflow values are selected as the range of interval. In addition, division of the targets into a number of predefined values associated with probabilities can also meet the requirement of the ITSDP. Table 3 shows the water inflow levels and the associated probabilities of occurrence.

Table 1 Water target demands and the related economic data

Table 2 Irrigation target and the related parameters of agricultural activities

Table 3 Stream flows and available water resources in the two planning periods

4 Result analysis and discussion

In this study, the optimal results have obtained without the downside risk-aversion constraints through the ITSP model, and the value of downside risk has calculated when the λ value is fixed at 1. In addition, different sets of λ values have been tested and found that the values of 0.80, 0.85, 0.90, and 0.95 are representative for reflecting the desired trade-offs. Therefore, such values are used for the result analysis. Table 4 shows the downside risk values under different λ values. In this study, the expected income would be $ [10.00, 15.00] × 10⁶ for municipal sector, $ [10.00, 11.00] × 10⁶ for food processing plants, $ [0.25, 0.35] × 10⁶ for thermal power plant, $ [50.00, 65.00] × 10⁶ for paper mill, $ [1.50, 2.50] × 10⁶ for agricultural region I, and $ [2.00, 2.70] × 10⁶ for agricultural region II in period 1; and $ [10.00, 15.00] × 10⁶ for municipal sector, $ [8.00, 10.00] × 10⁶ for food processing plants, $ [0.20, 0.30] × 10⁶ for thermal power plant, $ [55.00, 70.00] × 10⁶ for paper mill, $ [0.80, 1.00] × 10⁶ for agricultural region I, and $ [0.80, 1.20] × 10⁶ for agricultural region II during period 2. From Table 4, it is indicated that the solution obtained through the ITSP model would lead to the highest system risk. As the λ values decreases, the downside risk value of each users, especially municipal sectors and the thermal power plant, would have a downward trend. For example, in period 1, the value of downside risk for municipal sectors would be $ [10.260, 22.113] × 10⁶, $ [9.720, 21.515] × 10⁶, $ [9.180, 20.918] × 10⁶, $ [8.640, 20.320] × 10⁶ under the λ values of 0.95, 0.90, 0.85, and 0.80, respectively. The system downside risk would be lessened and system feasibility be enhanced. Moreover, the downside risk value of industrial and agricultural sectors would be 0 under different λ values. This is because the industrial sectors (the food processing plant and paper mill plant) could bring about a higher benefit when its water demand is satisfied, and the study area is a significant agricultural base. Therefore, in order to gain a stable and higher benefit and keep a safe food production, the allowable water resources allocated to the two industrial and agricultural sectors would firstly meet the demand of the expected return.

Table 4 Downside risk values under different λ values

Table 5 shows the results of water allocation target obtained from the ITSDP model under different λ values. Generally, water allocation would firstly be guaranteed to the food processing plants, followed by the paper mill, the municipal sector and the thermal power plant. This is because the water consumption of the food processing plant brings the highest benefit when the water demand is satisfied and is subject to the highest penalty if the promised water amount is not delivered; whereas, the other industrial and municipal sectors have lower benefits and penalties. Under different λ levels, the optimized allocation targets for the food processing plant would have no changes and equal 0.98 × 10⁶ and 0.93 × 10⁶ m³ during periods 1 and 2, respectively, which are their upper-bound targets. Thus, the manager would have to promise upper-bound quantities to the water user. In comparison, the water allocation target of municipal sector and the thermal power plant would always approach its lower bound with the value of λ decreasing from 1.00 to 0.80; this is because the two water users are associated with lower benefit and lower penalty. In addition, the amount of water allocation target of paper mill plant would decreases from 5.42 × 10⁶ to 4.83 × 10⁶ m³ in period 1, and from 5.87 × 10⁶ to 4.65 × 10⁶ m³ in period 2, when λ changes from 1.00 to 0.80. On the other hand, the decision of water-allocation targets represents a compromise of water shortage under uncertain water availability. A higher target level would lead to a higher benefit but, at the same time, a higher risk of water shortage (and thus a higher penalty) when the water flow is low. Table 6 describes optimal solutions of irrigation target and irrigation area under different λ values. The optimized cotton irrigation targets would be respectively 90 and 105 ha in agricultural regions I and II during period 1, which approach their lower bounds. Rice, maize, and peanut irrigation targets in the two subareas would reach their upper bounds in period 1. For the wheat crop, the optimal target would approach its upper bound (i.e. 390 ha in region I, and 504 ha in region II) in period 2, and the optimal irrigation targets of rape would be 140 ha in region I and 157.5 ha in region II. Under low, medium and high inflows, the optimized irrigation areas would have no changes. For example, in agricultural region I, the optimized irrigation areas of cotton, rice, maize, soybean, peanut, wheat and rape would be respectively 90, 176, 90, 50, 124, 390, and 140 ha, and have no changes with the λ values increasing from 0.80 to 1.00 under the different inflow levels. It indicated that the study are is an important agricultural base, and the manager would be firstly provide a certain amount of water resources to the agricultural sectors in order to avoid the economic loss. In addition, the agricultural region II is located in the downstream, and water users in the upstream dominate control of a river, the water shortage would definitely occur in the agricultural region II. Moreover, due to the low irrigation benefit and crop yield, water shortage would lead to the irrigation deficit of soybean and rape during periods 1 and 2, respectively.

Table 5 Optimal solutions of water allocation target under different λ values

Table 6 Optimal solutions of irrigation target and irrigation area under different λ values

Figures 3 and 4 present optimized water-allocation patterns (corresponding to lower- and upper-bound system benefits, respectively) to the municipal and industrial sectors under different λ levels during the planning horizon. The results indicate that deficits would occur if the available water amounts are less than the promised targets. Each allocated flow is the difference between the promised target and the probabilistic shortage under a given stream condition with an associated probability level. For example, for the thermal power plant, when λ is fixed at 0.80, the water-allocation would be [0.08, 0.69] × 10⁶ m³ (in period 1) and [0.40, 0.62] × 10⁶ m³ (in period 2) under the low flow level, [0.52, 0.83] × 10⁶ m³ (in period 1) and 0.85 × 10⁶ m³ (in period 2) under the medium flow level, and 0.83 × 10⁶ m³ (in period 1) and 0.85 × 10⁶ m³ (in period 2) under the high flow level. The results also indicated that water-allocation plans would vary under different λ levels. For example, when the flow levels are medium in the two periods, under λ = 0.80, 0.85, 0.90, 0.95 and 1.00, the water allocation for municipal would respectively be 4.55 × 10⁶, 4.27 × 10⁶, 4.26 × 10⁶, 3.99 × 10⁶, and 4.18 × 10⁶ m³ in period 1, and 5.02 × 10⁶, 4.79 × 10⁶, 4.56 × 10⁶, 4.33 × 10⁶, and 2.30 × 10⁶ m³ in period 2. In addition, as the λ level decrease, the water allocation for municipal and thermal power plant would increase, and the amount of water resources allocated to the food processing plants and paper mill would decrease. This shows that the effect of the risk measure on the modeling outputs could be adjusted by changing λ value. Generally, as λ value decrease, the allocation values of users with high benefit would decrease, and the amount of water allocation of users with low benefit would increase. In such a case, the extreme risk could be lowered and the system feasibility be enhanced. On the contrary, a lower λ value would result in a higher possibility of system loss in extreme conditions.

Fig. 3

Optimized water-allocation patterns under different λ levels in period 1

Fig. 4

Optimized water-allocation patterns under different λ levels in period 2

Figures 5, 6, 7 and 8 present the COD and BOD concentration of each reach under different λ levels during periods 1 and 2. From Figs. 5 and 6, the COD concentration in each reach would vary and increase from the low inflow level to high. For example, in reach 2, when λ is fixed at 0.90, the concentration of COD would be [13.25, 13.40], [13.86, 13.94], and [14.59, 14.98] mg/L under low, medium and high inflow levels in period 1; and in period 2, it would be [12.05, 12.60], [13.22, 13.66], and [13.97, 15.33] mg/L under low, medium and high inflow levels, respectively. It indicated that the contradiction between water supply and water quality has increased significantly under a higher inflow levels. More water resources would be used for supporting the municipal, industrial and agricultural development under the high inflow level, and water pollution would increase due to more wastewater and pollutant discharged through the sectors’ production process. The maximum concentration of COD could be controlled at 25 mg/L in reaches 6 and 7, 20 mg/L in reaches 1 (drinking water sources) and 5 (industrial and drinking water sources), 40 mg/L in reaches 3 and 8 (agricultural water sources), 20 mg/L in reaches 2 and 4, and 25 mg/L in reach 9. In addition, the maximum concentration of COD (Figs. 5, 6) and BOD (Figs. 7, 8) would occur in reach 7 during the planning horizon. During period 2, when λ is fixed at 0.85, the COD concentration would be [10.96, 11.73], [13.89, 15.08], [12.96, 13.74], [14.76, 14.84], [13.33, 13.75], [15.94, 16.12], [22.22, 25.00], [20.48, 23.52], and [18.66, 21.93] mg/L under the medium level in reaches 1–9, respectively. The reason is that (i) the paper mall plant’s wastewater discharge of per water consumption and COD concentration of wastewater discharge in emission standard are the highest than other water competitors and (ii) the water allocated to the paper mill is more than other users under the same inflow levels. Moreover, the concentration of COD would have an increases trend with the value of λ value decreases. It indicated that as λ value decrease, the water allocation for municipal and thermal power plant with a high COD discharge standers would increase, and the amount of water resources allocated to the food processing plants and paper mill with a lower COD discharge standers would decrease. The solutions for the BOD concentration in each reach can be similarly interpreted based on the results presented in Figs. 7 and 8. In order to achieve the aim of stream water quality protection, the quantity and quality of aviable water resources must be controlled by recharge and discharge water.

Fig. 5

COD concentration of each reach under different λ levels in period 1

Fig. 6

COD concentration of each reach under different λ levels in period 2

Fig. 7

BOD concentration of each reach under different λ levels in period 1

Fig. 8

BOD concentration of each reach under different λ levels in period 2

Figure 9 presents the optimal results of net system benefit, recourse cost, and wastewater treatment cost under different risk level (λ values). Since the λ levels represent a set of downside-risk tradeoffs, at which the admissible risk will be restrained. Thus, the relation between the benefit and the λ levels demonstrates a tradeoff between benefit and downside risk. There is an obvious growth from low levels to high ones. Under each λ level, different combinative considerations on the uncertain inputs would lead to varied objective function values. The net system benefit over the planning horizon would be $ [148.23, 200.83] × 10⁶, $ [143.77, 185.87] × 10⁶, $ [143.33, 185.36] × 10⁶, $ [143.28, 184.82] × 10⁶, and $ [143.21, 184.22] × 10⁶ under λ values of 1.00, 0.95, 0.90, 0.85 and 0.80, respectively. It indicated that an increased λ means a decreased strictness for the constraints (and thus an expanded decision space), which may then result in an increased system benefit. At the same time, the solutions for the recourse cost and wastewater treatment cost under different λ levels could be generated. The wastewater treatment cost would be $ [4.01, 5.96] × 10⁶, $ [3.90, 5.89] × 10⁶, $ [3.90, 5.91] × 10⁶, $ [3.91, 5.93] × 10⁶, and $ [3.92, 5.97] × 10⁶ during the planning horizon. In addition, the recourse cost gradually decreases as λ decreases. For example, the cost would be $ [100.59, 120.11] × 10⁶, $ [89.67, 99.32] × 10⁶, $ [89.18, 98.78] × 10⁶, $ [88.70, 97.84] × 10⁶, and $ [88.21, 96.86] × 10⁶ during the planning horizon. It is indicated that the system reliabilities would be enhanced as the λ values decreases. Considering the risk-averse structure on the target profit and downside-risk value, an impartial water-allocation scheme would lead to a lower recourse cost and ensures a healthier development of economy than those unbalanced ones.

Fig. 9

Net benefit (a), resource cost (b), and wastewater treatment cost (c) under different λ values

Compared with an ITSDP model, an ITSP model takes maximum benefit as an exclusive objective without analyzing trade-offs between the system benefits and stability in the objective function. The detailed optimal water targets, water allocation plans, downside risk, net benefit and resources cost from ITSP are presented in Tables 4, 5 and 6 and Figs. 3, 4 and 5. Being different from ITSDP model, ITSP model aims to obtain the maximum benefit in the optimal process of water allocation, and it does not take the risk of model feasibility and reliability into consideration. These limitations could lead to low system stability and unbalanced allocation patterns, and high system risk of violating the profit-target during water resources allocation problems. For example, when λ value is equal to 1, the amount of water resources allocated to the thermal power plant would be 0 under different inflow levels, due to a higher benefit during period 1 (Fig. 3). Moreover, the system net benefit and the resources cost would be higher than that of ITSDP model (Fig. 9). This also implies that the system objective of the ITSP model is only to obtain a maximum benefit without regarding risk aversion. In addition, the width of interval net benefit in ITSDP model is narrower than that of ITSP model. It is indicated that the system benefit relies on the water resources condition, and tends to fluctuate more intensively with the change of available water resources. Through integrating downside risk-aversion into the objective of a water resources system management model, a steady water-allocation and water quality management plan would be more attractive for decision makers in real-world applications.

5 Conclusions

In this study, an ITSDP model is developed for supporting regional water resources allocation and water quality management problems under uncertainty. This method is based on an integration of IPP, TSP, and downside risk measure. It allows uncertainties presented as both probability distributions and interval values to be incorporated within a general optimization framework. A water quality simulation model was provided for reflecting the relationship between the water resources allocation, wastewater discharge, and environmental responses. Moreover, risk aversion is also incorporated by limiting the volatility of the expected profit through the downside risk methodology, in order to reflect the preference of decision makers, such that the tradeoff between system economy and extreme expected loss could be analyzed. Then, the developed method has been confirmed though a case study of a water quality management in a shared stream. A number of scenarios corresponding to different river inflow and risk levels are examined; the results of the case study suggest that the methodology is applicable to reflecting complexities of water quality management and can be used for providing bases for identifying desired water-allocation plans with maximized system, and reflecting the decision maker’s attitude toward risk aversion.

Although this study is the first attempt for planning a water quality management system through the ITSDP approach, the results suggest that this hybrid method is also applicable to many other environmental management problems, and can be incorporated within other optimization frameworks to handle various management problems under uncertainty. However, compared with other approaches, there is still much space for improvement of the proposed model. Firstly, the water-quality simulation was limited by the assumptions of steady-state flow in each river segment, without any dispersive effects being considered. In addition, the developed ITSDP model would have difficulties in dealing with the uncertainties in the model’s right-hand-side coefficients; the probability of random variable is estimated through statistical analysis, which would unavoidably bring errors to the system; the selection of a suitable alternative among the obtained interval solutions is of significant complexity and becomes an extra burden for water quality managers. Further studies are desired to mitigate these limitations.