Inexact stochastic dynamic programming method and application to water resources management in Shandong China under uncertainty

Abstract

In this study, an interval parameter multistage joint-probability programming (IMJP) approach has been developed to deal with water resources allocation under uncertainty. The IMJP can be used not only to deal with uncertainties in terms of joint-probability and intervals, but also to examine the risk of violating joint probabilistic constraints in the context of multistage. The proposed model can handle the economic expenditure caused by regional water shortage and flood control. The model can also reflect the related dynamic changes in the multi-stage cases and the system safety under uncertainty. The developed method is applied to a case study of water resources allocation in Shandong, China, under multistage, multi-reservoir and multi-industry. The violating reservoir constraints are addressed in terms of joint-probability. Different risk levels of constraint lead to different planning. The obtained results can help water resources managers to identify desired system designs under various economic, environment and system reliability scenarios.

1 Introduction

Water is essential for human being, economic activity, and environmental development. The utilization of water resources means that a certain quantity and quality of water resources are used in different ways like irrigation, navigation, electricity generation etc. It can be used to fill the requirements of drink, the production of industry and agriculture, and the maintenance of ecology to affirm the social, economic, and environmental values of water resources.

China has the monsoon climate of warm temperate zone. The 70–90 % of annual rainfall occur from June to September, in which more than 70 % of water resources are made up of floodwater which is hard to use. Moreover, due to the change of annual rainfall is high, the runoff varies a lot. The wet year and dry year present alternately. Therefore, the water resources utilization is hard for the spatio-temporal uneven distribution of the precipitation. With the acceleration of industrial growth and urbanization, it is enforced to further optimize the allocation of water resources and improve the control level of overall water resources and the reliability of water supply. Especially, to handle the above problem, the model is desired to deal with both flood control and water conservation. To address this, the optimal reservoir operation is an important way for water resources utilization. It is meaningful to propose a sound method to solve above problem.

Regarding optimal approach to operation, it can be classified into linear programming, nonlinear programming, dynamic programming, multiple objectives programming, etc. The above methods can be variously integrated to handle different practical problems. For example, Heidari et al. (1971) proposed a discrete differential dynamic programming (DDDP), which is useful in dealing with two reservoir system. Windsor (1973) first dealt with the application of linear programming to reservoir group operation. Cancelliere et al. (2002) developed a neural network model to derive the operational strategies for an irrigation supply reservoir. Soliman and Christensen (1986) presented the multi-variables spatial optimization based on integrating many optimize methods. Barros et al. (2003) first addressed the application of successive liner programming (SLP) to Brazilian hydropower, one of the largest hydropower systems in the world.

However, in the real-world, a number of uncertainties are existed in water resources management, especially, in hydrology, conservancy, construction, and water supply. Water resource system is a very complex uncertain system due to the input and output, as well as the intern structure of the system contain uncertain elements.

There have been different mathematical methodologies to deal with different uncertainties. To deal with random uncertainty, the mathematical methodology is the random theory and the probability statistics. For example, Anderson et al. (2000) developed probabilistic seasonal forecasts of droughts with a simplified coupled hydrologic–atmospheric model for water resources planning. To deal with interval uncertainty, there is interval-parameter programming. Huang (1996) developed an interval parameter water quality management model for water pollution control planning within an agricultural system.

The above methods can only process uncertainty of the system presented in single form, like random, fuzzy, or interval. However, there are always multiple uncertainties in practical problems, and many of them are intertwined. To handle these problems, it is needed to consider all the multiple uncertainties comprehensively. Luo et al. (2007) developed interval stochastic dynamic programming by integrating interval dynamic programming and stochastic programming; this method can tackle the uncertainties presented in interval and stochastic number. Guo et al. (2010) developed inexact fuzzy-stochastic programming by integrating interval, fuzzy and stochastic programming together, which is to deal with the uncertainties presented in interval, fuzzy and stochastic number. These approaches can tackle multiple uncertainties, but they cannot handle the multi-stage problem under uncertainty.

Due to the multi periods existed in the optimal reservoir operation and management, the concept of multistage programming to the process of water resources management was proposed in the previous studies. When dealing with the uncertainties in optimization model, the uncertainty method is always integrated with mathematical optimization model under multi-stages. For example, the optimized model integrated interval method and random methodology, such as interval-parameter multi-stage stochastic programming (Li et al. 2006), interval-parameter two-stage stochastic semi-infinite programming (Guo et al. 2009) and so on. Similarly, a multistage stochastic programming (MSP) model was developed for planning water supplies from highland lakes, where dynamics and uncertainties of water availability (and thus water allocation) could be taken into account by generating of multiple representative scenarios (Watkins et al. 2000). Li and Huang (2008) developed an interval-parameter two-stage stochastic nonlinear programming (ITNP) for supporting decisions of water-resources allocation. Fan et al. (2012) developed inexact two-stage stochastic partial programming (ITSPP) for water resources management under uncertainty.

The above model can effectively process the uncertainty data appearing in interval and random formality under two-stage or multi-stage in the optimization model. But once the uncertainty in the model expressed in interval, fuzzy and random form, the above method can not handle. Because of the complexity of water resource system, uncertainties may be shown in the three forms (interval, fuzzy and random) simultaneously or in phases. To solve this kind of problem, it needs to integrate interval, fuzzy and random methods together based on the optimization model, such as, interval-parameter fuzzy two-stage stochastic program (Maqsood et al. 2005), inexact two-stage fuzzy-stochastic programming (Lu et al. 2009), two-stage fuzzy chance-constrained programming (CCP) for tackling dual uncertainties (Guo and Huang 2009), and so on.

The two stage programming was used for examining hydrothermal scheduling of multi-reservoir systems and the two stage optimization model was developed for the design and operation of a multi-purpose reservoir (Mobasheri and Harboe 1970). However, the above method can effectively solve the problem when uncertainty is shown in the form of fuzzy number, interval number and random number. But these methods cannot effectively handle the planning equations when elements show in form of joint probability, especially when the uncertainty programming integrated joint probability and chance constraint programming. In the past, the joint probability programming approach was proposed to process the problems of water resources management. For example, Sharma (2000) developed a framework for rainfall probabilistic forecasting using available hydro-climatic information. The predictor identification approach presented using a nonparametric implementation of the mutual information criterion as a measure of dependence between variables. The criterion is based on a characterisation of the joint probability distribution. Chan and Bras (1979) developed the frequency distribution of the volume of water threshold discharge. It is done by using basic and accessible information of the joint probability density function of rainfall intensity and duration together with expressions to be derived, relating the volume of interest to rainfall intensity and duration. Sayers et al. (2002) evolved the flood engineering in Britain from traditional approaches based on design standards to the development of risk-based decision-making. A joint probability analysis of all of the load conditions was required to analysis the flooding system. Among them, the methods of MSP and CCP were cooperated to deal with uncertainties represented as probability distribution under multi-stages.

In the previous studies, the two methods have been integrated by researchers (Hausman et al. 1998; Myerson 1986; Hausman et al. 1998; Charnes and Shenoy 2004), but it has not been applied to optimal reservoir operation and management. Moreover, the traditional multistage and joint probability method’s solving algorithm was complexity and huge workload in the coupling analysis. Especially, in optimal reservoir operation and management, the integration of multistage programming and method of joint probability optimization under multiple uncertainties were not found. It is required to present such a sound method to solve the actual existing complex question. Therefore, the sound efficient and fast algorithm based on uncertainty multistage joint probability optimization is desired. Especially, the above integrated method was not applied to the case study of water resources allocation in Shandong, China, under multistage, multi-reservoir and multi-industry.

The objective of this study is to develop an inexact multistage joint probabilistic programming (IMJP) method in response to the above challenges. Techniques of MSP with recourse and inexact joint probabilistic programming (IJP) will be incorporated within a general framework. The IMJP can deal with uncertainties expressed both as probability distributions and as intervals. It can also help examine the risk of violating joint probabilistic constraints. A case study will then be provided for demonstrating how the developed method will support the planning of water resources management within a multi-stream, multi-reservoir and multi-period context. The detailed tasks entail: (1) dealing with uncertainties expressed as probability distributions and interval values; (2) examining the risk of violating joint-probability under the uncertainty; (3) working out the effective measures based on the dynamics of system uncertainties under multi-stages; (4) analyzing the system benefit on different constraint violation level; (5) providing decision support for water supply optimal control under a complete set of scenarios and on a range of constraint violation level.

2 Methodology

2.1 Multistage stochastic programming (MSP)

Consider a MSP with recourse as follows:

$$ \hbox{max} f = \sum\limits_{t = 1}^{T} {C_{t} X_{t} - \sum\limits_{t = 1}^{T} {\sum\limits_{k = 1}^{{K_{t} }} {p_{tk} D_{tk} Y_{tk} } } } $$

(1a)

Subject to:

$$ A_{rt} X_{t} \le B_{rt} ,\quad r = 1,2, \ldots ,m_{1} ;\quad t = 1,2, \ldots ,T $$

(1b)

$$ A_{it} X_{t} + A^{\prime}_{itk} Y_{tk} \le \omega_{itk} ,\quad i = 1,2, \ldots m_{2} ;\quad t = 1,2, \ldots ,T;\quad k = 1,2, \ldots K_{t} $$

(1c)

$$ x_{jt} \ge 0,x_{jt} \in X_{t} ,\quad j = 1,2, \ldots n_{1} ;\quad t = 1,2, \ldots ,T $$

(1d)

$$ y_{jtk} \ge 0,y_{jtk} \in Y_{tk} ,\quad j = 1,2, \ldots n_{2} ;\quad t = 1,2, \ldots ,T;\quad k = 1,2, \ldots ,K_{t} $$

(1e)

where $f$ is the expected system benefit; $X$ are decision variables; $Y$ are recourse variables; $k$ is the number of scenarios; $i$ is index of constraints; $t$ is period; $P_{tk}$ is probability of occurrence for scenario $k$ in period $t$; $D_{tk}$ are coefficients of recourse variables; $A^{\prime}_{itk}$ are coefficients of $Y_{tk}$ in constraint $i$; $\omega_{itk}$ is random variable with known distribution; C are coefficients of X; B are sets with random elements.

In model (1), the decision variables include two subsets: (1) the $x_{jt}$ are determined before the realizations of random variables are disclosed; (2) the recourse variables $y_{jtk}$ will be obtained after the random variables are computed.

Nevertheless, there is a limitation in model (1). The optimum aim can not be attained for the $x_{jt}$ due to it has been determined before the model computing. In order to address this, the model (1) was improved. The operation step of the improved model is: firstly, putting the random variables disclosed in model (1), and get the result data of $x_{jt}$; secondly, selecting the alternative of $x_{jt}$ for the “final $x_{jt}$”; thirdly, calculating the recourse variable, such as $y_{jtk}$ from “final $x_{jt}$” and obtained random variables. Through above procedure, the optimal solution of modeling can be obtained.

2.2 Interval parameter multistage joint-probability programming (IMJP)

In model (1), when uncertainties in the right-hand sides presented as probability distribution, the CCP method can be used for dealing with it (Charnes et al. 1972; Charnes and Cooper 1983). The CCP can solve this problem by converting the model into a deterministic version. The method is: (i) fixing a certain level of probability $p_{i}$ for each constraint; (ii) imposing the condition that the constraint should be satisfied with at least a probability of $1 - p_{i}$, and $p_{i} \in \left[ {0,1} \right]$. The feasible solution set is restricted by the following constraints (Charnes et al. 1972; Charnes and Cooper 1983):

$$ \Pr [t\left| {A_{i} (t)X \le b_{i} (t)} \right.] \ge 1 - q_{i} ,\quad A_{i} (t) \in A(t),\quad b_{i} (t) \in B(t),\quad i = 1,2, \ldots ,m $$

(2a)

where X is a vector of decision variable, and A(t), B(t), are set with random elements, which are defined on a probability space T (Infanger 1992). Generally constraint (2a) is nonlinear, and is feasible on certain conditions, one of which is when elements of $A_{i} (t)$ are deterministic and $b_{i} (t)$ are random. Constraint (2a) can be converted into a linear model as follow:

$$ A_{i} (t)X \le b_{i} (t)^{{q_{i} }} ,\quad \forall i $$

(2b)

where $b_{i} (t)^{{q_{i} }} = F_{i}^{ - 1} (q_{i} )$, and $b_{i} (t)$ follows cumulative probability distribution, $q_{i}$ is probability of violating constraint i.

The problem with (2b) is that linear constraints can only reflect the case when A is deterministic. If both A and B are uncertain, the set of feasible constraints may become more complicated (Ellis 1991; Infanger 1992; Watanabe and Ellis 1994; Zare and Daneshmand 1995).

However, although the CCP can deal with left-hand side uncertainties presented as probability distributions, it is unable to handle coefficients presented as independent uncertainties in function, and in many practical cases, uncertainties in practical problems can not be presented as probability distributions (Infanger 1992; Zare and Daneshmand 1995; Huang 1998).

Sometimes, uncertainties in right hand side of CCP constraint is presented as joint-probability. Complexities of model will intensely increase in this case. The technique of joint probabilistic constraints programming (JCP) can be used for dealing with such complexities (Miller and Wager 1965; Charnes and Cooper 1983). A general JPC formulation can be expressed as (Miller and Wager 1965):

$$ A_{i} (t)X \le b_{i} (t)^{{q_{i} }} ,\quad A_{i} (t) \in A(t),\quad b_{i} (t) \in B(t),\quad i = 1,2, \ldots ,m $$

(3a)

$$ \sum\limits_{j}^{m} {q_{ij} } \le q_{i} \quad j = 1,2, \ldots n $$

(3b)

where $q_{i}$ is joint probability. $q_{ij}$ is individual probability that make up of joint probability.

Interval-parameter mathematical programming (IP) can deal with uncertainties presented as upper bound and lower bound but unknown probability distribution information.

Therefore, the above problem can be effectively solved by introducing IP technique into the JCP framework to form the interval parameter joint probability constrained programming (IJCP) as follows:

$$ \hbox{max} f^{ \pm } = C^{ \pm } X^{ \pm } $$

(4a)

Subject to:

$$ \Pr [t\left| {A_{i} (t)^{ \pm } X^{ \pm } \le b_{i} (t)^{ \pm } } \right.] \ge 1 - q_{i} ,\quad A_{i} (t)^{ \pm } \in A(t)^{ \pm } ,\quad b_{i} (t)^{ \pm } \in B(t)^{ \pm } $$

(4b)

$$ \sum\limits_{j}^{m} {q_{ij} } \le q_{i} \quad i = 1,2, \ldots ,m,\quad j = 1,2, \ldots n $$

(4c)

where superscript ‘+’ represents upper bounds of interval parameters, and ‘−’ represents lower bounds (Huang et al. 1995).

In according to the translation of model (2a) to model (2b2).

Model (4) can be translated to Model (5) as follows:

$$ \hbox{max} f^{ \pm } = C^{ \pm } X^{ \pm } $$

(5a)

Subject to:

$$ A_{i} (t)^{ \pm } X^{ \pm } \le B_{i} (t)^{{q_{ij} \pm }} ,\quad A_{i} (t)^{ \pm } \in A(t)^{ \pm } ,\quad b_{i} (t)^{ \pm } \in B(t)^{ \pm } $$

(5b)

$$ \sum\limits_{j}^{m} {q_{ij} } \le q_{i} \quad i = 1,2, \ldots ,m,\quad j = 1,2, \ldots n $$

(5c)

where

$$ B_{i} (t)^{{q_{i ^{*} } \pm }} = \left\{ {b_{i} (t)^{{q_{ij} \pm }} \left| {\quad i = 1,2, \ldots ,m,\quad j = 1,2, \ldots n} \right.} \right\} $$

(5d)

Through introducing IJCP into MSP, it can deal with the randomness in MSP and can analyze the risk of violating the uncertain constraints. An IMJP model for water resources management within a multi-reservoir system can be formulated as follows: (Charnes et al. 1972; Charnes and Cooper 1983).

$$ \hbox{max} f^{ \pm } = \sum\limits_{t = 1}^{T} {C_{{_{t} }}^{ \pm } X_{{_{t} }}^{ \pm } - \sum\limits_{t = 1}^{T} {\sum\limits_{k = 1}^{{K_{t} }} {p_{tk} D_{{_{tk} }}^{ \pm } Y_{{_{tk} }}^{ \pm } } } } $$

(6a)

Subject to:

$$ A_{rt}^{ \pm } X_{t}^{ \pm } \le B_{rt}^{ \pm } ,\quad r = 1,2, \ldots ,m_{1} ;\quad t = 1,2, \ldots ,T $$

(6b)

$$ A_{it}^{ \pm } X_{t}^{ \pm } + A_{it}^{\prime \pm } Y_{tk}^{ \pm } \le \omega_{itk}^{ \pm } ,\quad i = 1,2, \ldots m_{2} ;\quad t = 1,2, \ldots ,T;\quad k = 1,2, \ldots K_{t} $$

(6c)

$$ A_{st}^{ \pm } X_{t}^{ \pm } + A_{it}^{\prime \pm } Y_{tk}^{ \pm } \le B_{i}^{ \pm } (t)^{{q_{ij} }} ,\quad i = 1,2, \ldots ,m;\quad t = 1,2, \ldots ,T;\quad k = 1,2, \ldots K_{t} $$

(6d)

$$ x_{jt}^{ \pm } \ge 0,x_{jt}^{ \pm } \in X_{t}^{ \pm } ,\quad j = 1,2, \ldots n_{1} ;\quad t = 1,2, \ldots ,T $$

(6e)

$$ y_{jtk}^{ \pm } \ge 0,y_{jtk}^{ \pm } \in Y_{tk}^{ \pm } ,\quad j = 1,2, \ldots n_{2} ;\quad t = 1,2, \ldots ,T;\quad k = 1,2, \ldots ,K_{t} $$

(6f)

IMJP can not only deal with uncertainties presented as probability distributions and intervals, it can also analyzing the reliability of satisfying in varying degree. The model can also reflect the dynamics of system uncertainties of each stage and decision processes under a complete set of scenarios.

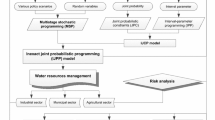
Figure 1 shows the flow diagram of framework of the IMJP model.

Fig. 1

The flow diagram of framework of the IMJP model

3 Case study

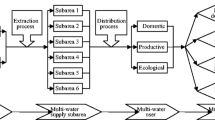
As Huaihe river basin is located in China’s north–south climate transition zone, the climate here is very complex. Because of this kind of climate and the history of being captured by the Yellow River, Huaihe River Basin suffered from frequent flood and drought disasters. Yihe River, One of the tributary of Huaihe River, flows through Shandong Province in China. Being in the upper stream of Yihe river, Tianzhuang reservoir is a level II reservoir mainly aimed at flood control and irrigation, as well as hydropower, aquaculture and industrial water supply. Bashan reservoir, located in the middle stream of Yihe River, is also a level II reservoir with the same function of Tianzhuang reservoir, which was built up in May, 1960. The control basin area of this reservoir is 1,782 km² and its total capacity is 267 million m³. In the downstream of Bashan reservoir, 1.5 million population and 1,400 km² area in seven counties of Linyi City, Shandong Province and Xinyi City and Pizhou City of Jiangsu Province are protected by Bashan reservoir. Meanwhile, Yanshi and Longhai railways, the Beijing–Shanghai, Rizhao–Dongming, Qingzhou–Xinqi, and Rizhao–Jinan expressways are secured by Bashan reservoir. Between these two reservoirs, there are series of tributaries that provide water to the above seven counties in Shandong Province and two cities in Jiangsu Province. Figure 2 shows the study area.

Fig. 2

Study area

The water supplies during the planning horizon are random variables. With the rapid development of local economy, the demand of water is increasing. The local economic development would be restricted if the water supply is insufficient. Meanwhile, when inflow of the reservoir is at a high level and exceeds the maximum water demand, the surplus will appear at that period. When the reservoir water storage is greater than the maximum of storage capacity, there would be overflow. The floods are possibly taken place. Because the relationship between water-supply and water-demand constantly change, the challenges facing the local water resource units are how to identify desired water-allocation patterns with a maximum net benefit and a minimized system-failure risk under uncertainty.

Figure 3 shows the schematic of water resources management system. In the figure, reservoir 1 represents Tianzhuang reservoir, and reservoir 2 represents Bashan reservoir. We set the upper stream of Yihe River that falls into Tianzhuang reservoir as Flow 1, and set the series of tributaries of Yihe River Between Tianzhuang reservoir and Bashan reservoir as Flow 2. Here, the volume of runoff of Flow 2 is the sum total of the runoffs of the above series of tributaries. Before the series of tributaries between Tianzhuang reservoir and Bashan reservoir (Flow 2) fall into the main stream of Yihe River, there is no water exchange between Flow 1 and Flow 2. Therefore, Flow 1 and Flow 2 are mutually independent. Because both of these two rivers are parts of Huaihe River Basin, there is some link between the two rivers’ natural runoff. Meanwhile, there are series of cut-off facilities and water consumptions in Flow 1 and Flow 2. The human factors influence the runoff volume of both the main stream and tributaries. In particular, the human factors influence greatly on the runoff volume of tributaries that fall into the main stream. Therefore, the runoff volume of main stream and tributaries cannot meet the natural laws. Here in this paper, set the runoff volumes of these two rivers are discrete distributed.

Fig. 3

Schematic of water resources management system

Uncertainties exist in many aspects, such as, hydrology (i.e., stream flow), water conservancy facilities, water consumption and water supply, and social economics. The stream flow coming from the two rivers supplies the county. They have uncertainties in the form of joint-probability because of multi-tributaries. These uncertainties presented as either probability distribution or random numbers. Such uncertainties can lead to interactive and dynamic complexities in terms of water allocation and diversion.

There is no research on joint scheduling of Bashan reservoir and Tianzhuang reservoir. Because of the existing joint probability, the IMJP is more effective when supporting water resources management under such complexities, comparing with the existing uncertainty methods, such as, interval-parameter fuzzy-random two-stage programming (IFRTSP), ITSPP, two stage fuzzy chance constrained programming (TFCCP).

The IMJP model for water resources management can be formulated as follows:

$$ \hbox{max} f^{ \pm } = \sum\limits_{t = 1}^{T} {NB_{it}^{ \pm } X_{it}^{ \pm } } - \sum\limits_{t = 1}^{T} {\sum\limits_{{K_{1} = 1}}^{{K_{1}^{t} }} {\sum\limits_{{K_{2} = 1}}^{{K_{2}^{t} }} {P_{{tk_{1} }} } P_{{tk_{2} }} PE_{it}^{ \pm } SH_{{itk_{1} k_{2} }}^{ \pm } - } } \sum\limits_{t = 1}^{T} {\sum\limits_{{K_{1} = 1}}^{{K_{1}^{t} }} {\sum\limits_{{K_{2} = 1}}^{{K_{2}^{t} }} {P_{{tk_{1} }} } } } P_{{tk_{2} }} VC_{t}^{ \pm } SU_{{tk_{1} k_{2} }}^{ \pm } $$

(7a)

The objective function is to maximize the system benefit, that is to maximize the result which the benefit from suitably allocating water resources to primary, secondary and tertiary industries subtract the penalty for violating the promised targets and the cost for diverting surplus flows.

Subject to:

$$ S_{{(t + 1)k_{1} }}^{ \pm } = S_{{tk_{1} }}^{ \pm } + \tilde{Q}_{{tk_{1} }}^{ \pm } - \left[ {\left( {{{\left( {S_{{tk_{1} }}^{ \pm } + S_{{(t + 1)k_{1} }}^{ \pm } } \right)} \mathord{\left/ {\vphantom {{\left( {S_{{tk_{1} }}^{ \pm } + S_{{(t + 1)k_{1} }}^{ \pm } } \right)} 2}} \right. \kern-0pt} 2}} \right)(C_{CL} + C_{SL} + C_{EL} )} \right] - R_{{tk_{1} }}^{ \pm } ,\quad \forall t;\quad k_{1} = 1,2, \ldots,K_{1}^{t} $$

(7b)

$$ S_{{(t + 1)k_{1} k_{2} }}^{ \pm } = S_{{tk_{1} }}^{ \pm } + (\tilde{Q}_{{tk_{2} }}^{ \pm } + R_{{tk_{1} }}^{ \pm } ) - \left[ {\left( {{{\left( {S_{{tk_{1} }}^{ \pm } + S_{{(t + 1)k_{1} }}^{ \pm } } \right)} \mathord{\left/ {\vphantom {{\left( {S_{{tk_{1} }}^{ \pm } + S_{{(t + 1)k_{1} }}^{ \pm } } \right)} 2}} \right. \kern-0pt} 2}} \right)(C_{CL} + C_{SL} + C_{EL} )} \right] - R_{{tk_{1} k_{2} }}^{ \pm } ,\quad \forall t;\quad k_{1} = 1,2,..,K_{1}^{t} ;\quad k_{2} = 1,2, \ldots ,K_{2}^{t} ; $$

(7c)

Constraints (7b) and (7c), indicated the relationship among the existing reservoir water, the inflow, the outflow and the wastage between the current stage and next stage.

$$ X_{t}^{ \pm } - SU \ge \left( {De_{lt}^{ \pm } + De_{et}^{ \pm } } \right),\quad \forall t $$

(7d)

Constraint (7d) indicates that the allocated water to county must satisfy the minimum water used for ecological, particularly when river inflow is continuously low over the planning horizon;

$$ De_{it}^{\hbox{min} } \le X_{it}^{ \pm } \le De_{it}^{\hbox{max} } ,\quad \forall t $$

(7e)

Constraint (7e) indicates that the allocated water must satisfy each industry’s minimum necessity but not exceed its maximum requirement in each period.

$$ De_{t}^{\hbox{min} } \le X_{t}^{ \pm } \le De_{t}^{\hbox{max} } ,\quad \forall t $$

(7f)

Constraint (7f) indicates that the allocated water must satisfy minimum necessity for county but not exceed its maximum requirement.

$$ ZX_{t}^{ \pm } - ZSH_{{tk_{1} k_{1} }}^{ \pm } \le R_{{tk_{1} k_{1} }}^{ \pm } - ZSU_{{tk_{1} k_{1} }}^{ \pm } ,\quad \forall t;\quad k_{1} = 1,2, \ldots K_{1}^{t} ;\quad k_{2} = 1,2, \ldots K_{2}^{t} $$

(7g)

$$ ZX_{t}^{ \pm } - ZSH_{{tk_{1} k_{1} }}^{ \pm } \ge SU_{{tk_{1} k_{1} }}^{ \pm } ,\quad \forall t;\quad k_{1} = 1,2, \ldots K_{1}^{t} ;\quad k_{2} = 1,2, \ldots K_{2}^{t} $$

(7h)

Constraints (7g) and (7h), indicates that the actual delivery water to the district and the diversion of water can not exceed the amount of water released from the reservoir.

$$ \Pr \left\{ \begin{aligned} &S_{{tk_{1} }}^{ \pm } \le TR_{1}^{ \pm } ,\quad \forall t;\quad k_{1} = 1,2, \ldots K_{1}^{t} \hfill \\ &S_{{tk_{1} k_{2} }}^{ \pm } \le TR_{2}^{ \pm } ,\quad \forall t;\quad k_{1} = 1,2, \ldots K_{1}^{t} ;\quad k_{2} = 1,2, \ldots K_{2}^{t} \hfill \\ \end{aligned} \right\} \ge 1 - q $$

(7i)

Constraint (7i), shows that the storage water in the reservoir can not exceed the maximum amount of reservoir capacity.

$$ S_{{tk_{1} }}^{ \pm } \ge DR_{1t}^{ \pm } ,\quad \forall t;\quad k_{1} = 1,2, \ldots K_{1}^{t} $$

(7j)

$$ S_{{tk_{1} k_{2} }}^{ \pm } \ge DR_{2t}^{ \pm } ,\forall t;\quad k_{1} = 1,2, \ldots K_{1}^{t} ;\quad k_{2} = 1,2, \ldots K_{2}^{t} $$

(7k)

Constraints (7j) and (7k), show that the reservoir storage should be greater than the dead storage of the reservoir.

$$ ZX_{it} = \sum {X_{it} } \quad \forall t;\quad i = 1,2,3; $$

(7l)

Constraint (7l) shows that water allocation to three industries is the sum of the allocated water to each industry.

$$ ZSH_{{itk_{1} k_{2} }} = \sum {SH_{{itk_{1} k_{2} }} } \quad \forall t;\quad i = 1,2,3; $$

(7m)

Constraint (7m) shows that the shortage of water allocation to three industries is the sum of the shortage of allocated water to each industry.

$$ ZSU_{{itk_{1} k_{2} }} = \sum {SU_{{itk_{1} k_{2} }} } \quad \forall t;\quad i = 1,2,3; $$

(7n)

Constraint (7n) indicates that the total water shortage is the sum of each industry water shortage.

$$ X^{ \pm } \ge SH_{{tk_{1} k_{2} }}^{ \pm } \ge 0,\quad \forall t;\quad k_{1} = 1,2, \ldots K_{1}^{t} ;\quad k_{2} = 1,2, \ldots K_{2}^{t} $$

(7o)

Constraint (7o) showed that the water shortage can not exceed the amount of target and the shortage is positive.

The traditional algorithm makes predetermined X _t value first, and then according to X _t and each random variable value, get recourse variables, such as $SH_{{tk_{1} k_{1} }}$ and $SU_{{tk_{1} k_{1} }}$. However, it is difficult to get optimal and safe results. In this model, the procedure of getting recourse variables is: (i) calculating the under different scenarios with the basis that the q is 0 (i.e., in the absolute safety case), then (ii) get recourse variables from obtained X _t and each random variable.

Table 1 provides the inflow levels of the two streams over the planning horizon. When the river runoff is less, the pre-allocation of water may not meet the requirements; and when the runoff is more, there may possibly be extra water and the reservoir distributaries are needed to avoid the possible downstream flood disasters. Table 2 provides reservoir data. Table 3 provides water demand of three industries and ecological water requirement of county (Tables 1, 2, 3).

Table 1 The inflow levels of the two streams

Table 2 Reservoir data

Table 3 Water demand of three industries and ecological water requirement of the county

4 Result and discussion

In this case study, the model of water resources planning under three-stages is developed. Because there are two reservoirs and two streams, the flow of streams is considered mutually independent; and there are dry season and wet/dry season. Thus, there are 64 different permutations and combinations, which mean there will be 64 corresponding scenes. Besides, a series of probability constraints are considered for reservoir shortage. It also helps to analysis the risk of violating the capacity constraints and gets good water distribution planning. Because of the existing of joint-probability, nine representative joint-probability combinations introduced to model for analysis. With the probability level increasing, the risk of violating the constraints of reservoir capacities increased. Each model can be divided into two sub-models corresponding to the upper bound and lower bound of objective function. Two problems can be solved by running the models: (1) predicting the output value of county; (2) formulating a good water supply planning to make system get maximized benefit with minimized penalty (water shortage penalty, cost of surplus).

The results are presented as interval numbers. With the different water flow and reservoir storage capacity, the benefit of planning system fluctuate between $f^{ - }$ and $f^{ + }$.

Table 4 shows the system benefits. The values of these variables change with the changes in the value of joint probabilities.

Table 4 System benefit of different joint probabilities

Table 4 shows that with the joint-probability increasing, the system benefit increases. Different individual probability combination brings different system benefits.

The reason that system benefit increases with the joint-probability increase is that with the increase of the q value, violating the constraints of reservoir capacities become high and the storage of reservoir increases correspondingly. Thus, the costs for water shortage compensation and diversion are decreased, so that it reduces the fee of shortage penalty and diversion.

Different combination of a range of individual probability result into the differences of violating the constraints of reservoir capacities. That is, the water storage of the two reservoirs increase based on the different individual probability combination. Thus, it cause different total water storage, and has different total benefit. In Table 3, system benefit decrease with the increase of individual probability of q1 and decrease of individual probability of q2. That is because the total holding capacity of reservoir 1 is less than reservoir 2, and the total holding capacity of two reservoir decrease accordingly. It causes reduction of water supply, and the system benefit decrease accordingly.

In this study, X_opt can be obtained through solving the model when q = 0 (i.e., the violation is 0). And then by substituting X_t with the optimized X_opt value and parameters in the equation for computing, a system program is derived which can enable the system to get the optimal value better than in the case of pre-set value of X_t under the premise of ensuring system security.

Formula:

$$ X_{opt} = \sum\limits_{i = 1}^{64} {P_{opti} X_{opti} } $$

(8)

where $X_{opt}$ value of X when Q = 0; $P_{opti}$ value of P when Q = 0; $X_{opti}$ value of X when Q = 0 under scenario i.

Take the water supply of reservoir, water shortage and water diversion of county, in which joint probability Q = 0.05 and individual probability q1 = 0.025, q2 = 0.025 as the example. Because of the uncertainties existed in water flow and reservoir capacities, there are 64 scenarios in system, and each scenario has a water supply pattern.

Figure 4 shows the water supply to primary industry, secondary industry and tertiary industry in three stages when q1 = 0.025 and q2 = 0.025. It presents that the distribution interval of upper-bound water supply to each industry among the 64 water distribution modes at the first stage are [7.7016, 9.5978] × 10⁸, [0.9660] × 10⁸, [0.3459] × 10⁸ m³ and that of the corresponding lower-bound water shortage is [7.4943, 9.8338] × 10⁸, [0.9660] × 10⁸, [0.3459] × 10⁸ m³. Among the 64 water distribution modes, the distribution intervals of the upper-bound water supply of three industries are [4.4204, 11.3666] × 10⁸, [1.1328] × 10⁸, [0.4056] × 10⁸ m³ and [5.3604, 13.7470] × 10⁸, [1.3283] × 10⁸, [0.4756] × 10⁸ m³ under the second and the third stages, respectively. The distribution intervals of the corresponding lower-bound water shortage are [4.1787, 11.5017] × 10⁸, [1.3278] × 10⁸, [0.4056] × 10⁸ m³ and [5.0842, 13.1481] × 10⁸, [1.3283] × 10⁸, [0.4756] × 10⁸ m³ under the second and third stages.

Fig. 4

The water supply to primary industry, secondary industry and tertiary industry in three stages when q1 = 0.025 and q2 = 0.025

It can be seen from the graph that except for the primary industry, the water supply of secondary industry and tertiary industry are the same with the water supply targets. That is because when water supply shortage for the low water flow occurs in the county, the model ensures the basic living water supply, and then decreases the water from the low benefit industry in order to get the high benefit. So during the three-stage, it decreases the water from the primary industry and the water to the secondary industry and tertiary industry are almost of the water supply targets.

The total water shortage in three stages is shown in Fig. 5. Figure 5 shows the water shortage of the three industries water supply in three stages when q1 = 0.025, q2 = 0.025. The figure shows that the distribution interval of upper-bound are [0, 17.2289] × 10⁸ m³ and the distribution interval of the corresponding of lower-bound is [0, 24.1653] × 10⁸ m³.

Fig. 5

The water shortage of the three industries water supply in three stages when q1 = 0.025, q2 = 0.025

In the above figure, with the exception of the first scenario, where the water shortage of lower bound is less than upper bound, the others are the exact opposite. The water shortage of lower bound is all more than upper bound. The result indicated that the water shortage of lower bound is higher than upper bound on the whole.

The reason that the water shortage of lower bound is higher than upper bound on the whole is that the promised water supply to county in the case of upper bound is greater than that in the case of lower bound. Thus, the water shortage in the case of upper bound is correspondingly higher than the water shortage in the case of lower bound.

The total diversion of the three stages is shown in Fig. 6.

Fig. 6

The total diversion of the three industries water supply in three stages when q1 = 0.025, q2 = 0.025

The figure shows that the distribution interval of upper-bound are [0, 13.7331] × 10⁸ m³ and the distribution interval of the corresponding of lower-bound is [0, 13.2356] × 10⁸ m³.

Set against the water shortage of total three stages. In Fig. 6, with the exception of the first scenario, where the water diversion of lower bound is more than high bound, the others are the exact opposite, that is, the water diversion of lower bound are all less than high bound. The result indicated that the water diversion of lower bound is higher than high bound on the whole.

Table 5 shows the values that multiplying the difference of total water shortage and total diversion during the three stages by its probability for each scenario under the upper and lower bound. The difference of total water shortage are the differences of total water shortage of primary industry among 64 water distribution modes during the three stages under upper bound and lower bound in different scenarios (when q1 = 0.025, q2 = 0.025 minus the total water flow when q1 = 0.005, q2 = 0.005 and when q1 = 0.05, q2 = 0.05 minus the total water flow when q1 = 0.025, q2 = 0.025. When q1 = 0.025, q2 = 0.025 minus the total water flow when q1 = 0.005, q2 = 0.005, the corresponding values are 0.0229 × 10⁸ m³ and 0.0254 × 10⁸ m³. When q1 = 0.05, q2 = 0.05 minus the total water flow when q1 = 0.025, q2 = 0.025, the values are 0.0275 × 10⁸ m³ and 0.0305 × 10⁸ m³. The total diversion are the differences of total diversion of lower bound and upper bound among 64 water distribution modes during the three stages when joint probabilities q1 = 0.025, q2 = 0.025 minus the corresponding values when q1 = 0.01, q2 = 0.04, and q1 = 0.01, q2 = 0.04 minus the corresponding values when q1 = 0.025, q2 = 0.025. The corresponding values are 0.0113 and 0.0328 when joint probabilities q1 = 0.025, q2 = 0.025 minus the corresponding values when q1 = 0.01, q2 = 0.04, and 0.0320 × 10⁸ m³ and 0.0328 × 10⁸ m³ when q1 = 0.04, q2 = 0.01 minus the corresponding values when q1 = 0.025, q2 = 0.025, respectively.

Table 5 The difference of the total water shortage and total diversion

From Table 5, it is indicated that this circumstance occurs because $S_{{tk_{1} k_{2} }}$ is greater than $S_{{tk_{1} }}$. When the probabilities are q1 = 0.01, q2 = 0.04, the total reservoir storage capacity achieves the maximum volume. When q1 = 0.025, q2 = 0.025, the total reservoir storage capacity gets the second large volume. When q1 = 0.04, q2 = 0.01, there is the minimum of total reservoir storage capacity. The reservoir distributary volume becomes bigger with the reduction of total storage capacity.

With the increasing of q value, reservoir storage becomes correspondingly greater. The water shortage increases gradually. The distributary volume is gradually reduced, and the water shortage compensation and diversion cost are correspondingly reduced. Thus, the total system benefits become greater, but the system is accompanied by the greater security risk as well.

When the q value is the same, different joint probabilities modes correspond to different deposit amounts. The water shortage volumes, distributary volumes, water shortage compensations, diversion costs and the total system benefits are also different.

When Q = 0, water supply to the primary of the three-stage total is shown in Fig. 7. From Fig. 7, it indicate that when Q = 0, the distribution interval of water supply in three stages during the three stages under 64 water distribution modes (multiply the total water shortage for the three stages under each scene by its probability) for upper bound and lower bound are [17.4824, 34.7113] × 10⁸ m³ and [18.3821, 34.4835] × 10⁸ m³, respectively.

Fig. 7

Water supply to the primary of the three-stage total when Q = 0

When Q = 0, the total water shortage of three stages is larger than each of the total shortage with joint-probability. On the contrary, the total water diversion is less than each of the total diversion with joint-probability. When Q = 0, the distribution intervals of water supply are [7.4943, 7.7016] × 10⁸ m³ in first stage, [4.4204, 4.1787] × 10⁸ m³ in second stage and [5.0842, 5.3604] × 10⁸ m³ in third stage, respectively.

When q = 0, the system benefit is [11324.80, 14254.13] × 10⁸ RMB yuan; the penalty is [14.3944, 28.2220] × 10⁸ RMB yuan; the diversion cost is [4.0166, 0.1929]. × 10⁸ RMB yuan. Comparing the system benefit, penalty, diversion cost correspondingly to the joint probability P, (i) the benefit meets the minimum; (ii) the penalty gets the maximum; and (iii) diversion cost gets the maximum. That is because when q is 0, the violation is 0, which means it is not allowed to exceed the total reservoir storage capacity. In this case, although the benefits are not greater than that in the case when there is violation under joint probability, the reservoir security is the highest.

The lower bounds are higher than the upper bounds for selective scenarios in Figs. 5, 6, and 7 (scenario 1 in Figs. 5, 6, scenarios 1, 21, 23, 29, 53, 55, 61, 63 in Fig. 7). The reason for this is that the promised water supply to county (X_opt) comes from the water supply in each scenario when Q = 0 multiplied by the probability of occurrence of the corresponding scenarios, say $X_{opt} = \sum\nolimits_{i = 1}^{64} {P_{opti} X_{opti} }$. So, the water distribution plan is applicable in most scenarios to maximize the system revenue, but may affect the system revenue in some small probability scenario (e.g., scenario 1 in Figs. 5, 6). In the 64 scenarios, the probability of scenario 1 is 0.004096, which is a small probability event.

5 Conclusion

The IMJP approach has been developed to deal with water resources allocation under uncertainty. The model can deal with both the economic penalty caused by water shortage of county and flood control. Through solving the model, the water resources are disposed for different industries. This model can not only reflect the related dynamic changes in the multi-stage cases, but also the reliability of satisfying the system safety under uncertainty.

The IMJP method is applied to a case study of water resources allocation planning within multistage, multi-reservoir and multi-industry. In the case study, a number of violation levels are examined under uncertainty. The violating reservoir constraints are addressed in terms of joint-probability. Different risk levels of constraint lead to different planning. A number of solutions are developed to help water resources managers to identify desired system designs under various economic, environment and system reliability. The supply to primary industry with minimum revenue would be decreased first under the water resources shortage situation. The lower violation the system constraint, the safer the system, and the lower the system benefit in a safety range. Otherwise, the higher violation leads to lower safety, but the higher benefit.

Furthermore, the proposed method can also be applied to other environmental management, such as solid waste management and air pollution.