Abstract
In this paper we present a fully-coupled, two-scale homogenization method for dynamic loading in the spirit of FE\(^2\) methods. The framework considers the balance of linear momentum including inertia at the microscale to capture possible dynamic effects arising from micro heterogeneities. A finite-strain formulation is adapted to account for geometrical nonlinearities enabling the study of e.g. plasticity or fiber pullout, which may be associated with large deformations. A consistent kinematic scale link is established as displacement constraint on the whole representative volume element. The consistent macroscopic material tangent moduli are derived including micro inertia in closed form. These can easily be calculated with a loop over all microscopic finite elements, only applying existing assembly and solving procedures. Thus, making it suitable for standard finite element program architectures. Numerical examples of a layered periodic material are presented and compared to direct numerical simulations to demonstrate the capability of the proposed framework. In addition, a simulation of a split Hopkinson tension test showcases the applicability of the framework to engineering problems.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Under dynamic loading, micro-heterogeneities can give rise to additional wave effects at the microscale leading to complex microscopic stress distributions. This then contributes to the complex macroscopic dynamic material behavior. There are various examples from different fields of application which cover a broad range of length scales. Currently the interest is high in metamaterials in general, but especially in locally resonant metamaterials exhibiting special properties like band gaps and negative bulk moduli. The applications range from cloaking devices [8, 24] over tunable sound attenuation [29, 34] to earthquake protection [5, 43]. More classical materials are being investigated as well. One example is metaconcrete, which replaces aggregates by rubber-coated lead inclusions to weaken impact waves [26, 44]. A different approach for an improved impact resistance are strain-hardening cement-based composites (SHCC), that show a pronounced energy dissipation under dynamic loading, as well as a change in fiber failure and overall crack pattern [10,11,12]. In addition to that, porous materials have shown an influence of microscopic inertia on voids under high strain rates [45, 53]. This list serves only to illustrate the possible influence of the material microstructure on the macroscopic response under high dynamic loading for a wide range of materials and applications. In general, any material under impact loading, which has large variation in stiffness, e.g. rubber-coated particles, or materials with a pronounced variation in density, e.g. if pores or cracks are present at the microscale, can exhibit distinct effective macroscopic properties resulting from the dynamics in the microstructure. In principle, locally large deformations may occur at the microscale in such materials. One example is the fiber-pullout process in SHCC under dynamic loading. Due to the progress of cracks through the cementitious matrix, structural problems arise at the microscale with deformations which are large compared to the structural components such as the fibers or the crack. This requires the consideration of finite strains in a geometrically nonlinear setting where the description is not limited to linearized strains.
To model the before-mentioned effects, the dynamics at the microscale need to be accounted for. Computational homogenization methods for quasi-static loading have become a common tool in numerical material analysis, see e.g. [15, 16, 40, 46, 55, 59]. A recent overview of computational homogenization methods in general is given in [18]. In addition a recapitulation of the FE\(^2\) method in particular is presented in [54]. However, with the rise in interest in metamaterials more and more dynamic homogenization frameworks have been published in the last years. Early works date back to elastodynamic problems [62], with more recent work confirming that the effective macroscopic density under the influence of inertia is not the simple average density as for quasi static applications, c.f. [37, 41]. Then there are works dealing with microdynamics analytically [64, 67], motivating further research. One widely applied homogenization method is asymptotic expansion, see e.g., [7, 17, 20,21,22], which is mainly based on the original work of Bensoussan et al. [1]. In addition to that, there is the more general theory of elastodynamic homogenization by Willis [63], which has been applied in e.g. [42, 47, 49, 65] and others. The two approaches are based on related ideas and their similarities are studied in [48]. Both mentioned methods are limited to elastic, periodic media, a considerable limitation when dealing with various composites. A further approach is based on the work of Irving and Kirkwood [23]. It is called the continuum homogenization theory, where the main extensive quantities as mass, momentum and energy are computed as weighted averages of their microscopic counterparts, c.f. [35, 38]. A more general approach is the micro-macro simulation based on a representative volume element (RVE). In such homogenization methods, macroscopic quantities such as the deformation gradient and the displacement vector at a macroscopic integration point are projected onto a microscopic boundary value problem whose homogenized response replaces the constitutive material law. In the case where the finite element method (FEM) is used on both scales, this procedure is called the FE\(^2\) method. A good theoretic introduction to this theory including dynamics is given by [14], which has been the foundation on which this paper is built. The framework in [17] calculates a quasi-static microstructure but then applies an inertia-induced eigenstrain based on the microstructure as an extra body force at the macroscale to account for micro-inertia effects. This was extended by [25] to account for matrix cracking at the microscale under impact loading. Other, rather FE\(^2\)-type schemes as [32, 33, 51, 52, 56, 60, 61] calculate the full balance of linear momentum at the microscale. In [32] an explicit, periodic, small-strain framework is presented, which was extended to an implicit time integration method for modeling resonant elastic metamaterials in [33]. [51, 52] use the assumption of linear elasticity to improve the computational performance, by splitting the problem into a purely static and a special dynamic boundary value problem (BVP). To better capture a wider range of applied frequencies, [56] use a Floquet–Bloch transformation to build a base of eigenmodes to analyze elastic, periodic metamaterials. The mentioned frameworks all use at least one of the following idealizations: small strains, linear elasticity, periodic or symmetric microstructures. In addition, many require quite elaborate implementations. A recent publication [60] does fulfill the named requirements, however for the derivation of the macroscopic tangent moduli, specific nodes are assumed to experience no microscale fluctuation. This assumption is quite reasonable in the context of metamaterials, whose analysis was primary goal in [60], because there the regions at the unitcell boundaries are particularly stiff. For microscopic problems not specifically addressing classical metamaterial microstructures, however, more flexibility at the boundaries may be more reasonable which is why we propose an alternative approach here.
The aim of this paper is to build a multiscale framework for dynamic loading as general as possible, while still being compatible with standard FE architecture. To enable the analysis of micro-mechanical processes as plasticity or fiber pullout, as well as to incorporate effects resulting from geometric nonlinearities, the proposed framework uses a finite-strain formulation. Its importance is supported by the analytical example in [27] of a nonlinear, elastic metamaterial, where finite strains were shown to be relevant for large wave amplitudes. The conducted numerical studies are so far not specifically chosen to highlight this aspect of the framework. To permit a flexible damage evolution in the RVE, which is not dominated by periodic boundary conditions [6] or aforementioned assumptions regarding fixated fluctuations at specific boundary nodes [60], we propose to apply kinematic scale links as constraints on the whole RVE. This allows us to model any type of RVE morphology.
The paper starts by discussing the general ideas of the framework in Sect. 2. The used notations of the large-strain framework are presented and the averaging relations derived in [13] are briefly recapitulated to include the full balance of momentum at the microscale. Then in Sect. 3 the FE formulations of the microscale are presented and the kinematic constraints are derived. In Sect. 4 the respective macroscale formulations are displayed. There, a focus is laid on the derivation of consistent macroscale tangent moduli in closed form. These enable a quadratically converging macroscopic Newton-iteration, resulting in a robust and efficient algorithm compared to numerical differentiation through perturbation of the macroscopic quantities [39]. Once the whole theoretical background of the framework is explained, Sect. 5 provides numerical examples, demonstrating the convergence behavior and analyzing some properties of RVEs under dynamic loading. In Sect. 6, the applicability of the framework to construction materials is given. A split Hopkinson tension test is conducted on a sample of strain-hardening cementitious composite (SHCC). The presented example is an extension of the example published in [58], presenting a more complex, 3D microstructure. The publication [58] is focused on the comparison to experimental results and the understanding of the composite behavior, without going into detail on the developed homogenization framework. The paper is completed in Sect. 7 with concluding remarks.
2 Homogenization framework including microscopic inertia
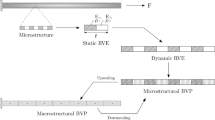
The general idea of the homogenization framework for dynamics is to consider the full balance of linear momentum including the inertia terms at the microscale. This enables not only the analysis of full dynamic fields at the microscale but a direct study of microscopic inertia effects on the macroscale. By using appropriate averaging relations and kinematic links, a consistent scale bridging for dynamic loading is established. In the FE\(^2\) method, each macroscopic Gauss point is associated with a separate microscopic RVE simulation which uses the macroscopic mechanical quantities to define the microscopic BVP. In order to differentiate the two scales, variables associated with the macroscale are denoted with a bar \(\overline{\bullet }\). Here, the finite-strain framework is taken into account in order to enable the analysis of a wide range of material behavior and micro-mechanical effects under dynamic loading. In the following sections the fundamental ingredients of the scale-coupling framework are explained, see also the schematic illustration in Fig. 1.
2.1 Kinematics at different scales
The connection of the (undeformed) reference and the (deformed) current configuration is described by the displacement \({{\varvec{u}}}\) as \({{\varvec{u}}}= {{\varvec{x}}}- {{\varvec{X}}}\), where \({{\varvec{X}}}\in {\mathcal B}\) denotes the coordinates in the reference configuration and \({{\varvec{x}}}\in {\mathcal S}\) the deformation. The link between the two configurations in terms of transformations of vector elements is described by the deformation and displacement gradients, respectively \({{\varvec{F}}}= \partial _{{{\varvec{X}}}}{{{\varvec{x}}}}={\varvec{1}}+{{\varvec{H}}}\) and \({{\varvec{H}}}= \partial _{{{\varvec{X}}}}{{{\varvec{u}}}}\), such that \({{\varvec{x}}}= {{\varvec{F}}}{{\varvec{X}}}\). In this work, the origin of the microscopic coordinates is chosen as the geometrical center of the RVE, with
where \(\int _{\mathcal {B}} \,\mathrm {d}V\) is the volume integral over the microscopic reference body \(\mathcal {B}\). Note that this choice of origin has no influence on the results but it simplifies the notation. Now the microscopic deformation \({{\varvec{x}}}\) can be split into the sum of terms,
Herein, two terms result directly from the macroscale: a constant part \(\overline{{{\varvec{u}}}}\), which describes the macroscopic rigid body translations, and a homogeneous part \(\overline{{{\varvec{F}}}}{{\varvec{X}}}\), defined in terms of the macroscopic deformation gradient.
The difference of these homogeneous deformations \(\overline{{{\varvec{u}}}}+\overline{{{\varvec{F}}}}{{\varvec{X}}}\) to the actual deformations \({{\varvec{x}}}\) is the microscopic displacement fluctuation field \(\widetilde{{{\varvec{u}}}}\). This is the field the microscopic BVP will be solved for. Now the microscopic displacements \({{\varvec{u}}}\) can be written as
Analogously, the microscopic deformation gradient can be split as
At the macroscale the kinematics are standard, see Fig. 2, where the kinematic relations for both the micro- and macroscale are illustrated.
2.2 Averaging relations
To expand quasi-static homogenization frameworks to the case of dynamics, an extended version of the Hill–Mandel condition of macro homogeneity [19, 36], which takes into account inertia and body forces at the microscale, is adopted
see [3] and [14]. Herein, \(\left\langle \bullet \right\rangle =\frac{1}{V} \int _{\mathcal {B}} \bullet \,\mathrm {d}V\) is an expression used to abbreviate the volume average of a microscopic quantity. \({{\varvec{P}}}\) is the first Piola–Kirchhoff stress tensor, \({{\varvec{f}}}\) is the microscopic body force vector, and \(\overline{{{\varvec{f}}}}\) is its macroscopic counterpart. The variational Eq. (5) is also called the Principle of Multiscale Virtual Power. It ensures that the virtual work of the macroscale coincides with its respective microscopic volume average, thus ensuring energetic consistency across the scales. By decomposing \(\delta {{\varvec{F}}}\) and \(\delta {{\varvec{u}}}\), following (3) and (4), three important equations can be derived. First, one obtains
which is automatically fulfilled for mechanical equilibrium. Then, more importantly, the averaging equation for the effective macroscopic stress \(\overline{{{\varvec{P}}}}\) and the effective macroscopic body force vector \(\overline{{{\varvec{f}}}}\) are derived as
These averaging relations can be found in multiple frameworks dealing with homogenization of dynamics, see e.g., [14, 31, 32, 45, 51, 52, 60]. It was shown in [30] that the extended Hill–Mandel averaging relation can be applied in a discretized setting without introducing additional error by scale transition.
2.3 Scale separation
A principal ingredient of the Hill–Mandel condition, as well as the presented extension (5), is the assumption of scale separation. This means that the equation only holds if the length scale of the microscopic mechanical fields is significantly smaller than the one of the macroscopic mechanical fields. For dynamic homogenization this means in practice, that the macroscopic wavelength is sufficiently larger than the size of the RVE.
2.4 Time integration
In this paper, an implicit numerical time integration method of first order is applied. Considering
we can express the second time derivative of any quantity \(\bullet \) as the difference of the current time step and the last \(\hat{\bullet }\), divided by the square of the time step \(\Delta t\), bearing in mind that \(\hat{\bullet }\) includes the first and second time derivatives of the last time step. The parameters \(\alpha _1\) and \(\alpha _2\) define the specific time integration scheme. For an explicit time integration, \(\alpha _1\) can be set to zero. Applying this to derivatives of acceleration terms with respect to a quantity \(\Box \) in the current configuration leads to
Analogously, the derivative of a value \(\bullet \) with respect to the second time derivative \(\ddot{\Box }\) reads
For the numerical simulations in the numerical analysis section the widely used Newmark method [50] is applied, with \(\alpha _1 = \frac{1}{\beta }\). Herein, \(\beta \) is one of the two parameters of the Newmark method influencing the type and stability of the time integration.
3 The microscopic problem
We start with the formulation of the microscopic problem, which includes the necessary kinematic links to the macroscale. Furthermore, an algorithmic treatment for the associated constraint conditions is given.
3.1 Microscopic balance of linear momentum
For a dynamic analysis, the microscopic balance of linear momentum is given by
The body force vector \({{\varvec{f}}}\) can be decomposed into an inertia part \({{\varvec{f}}}^{\rho }\) and a body force vector representing e.g. the gravitational pull \({{\varvec{f}}}^{\text {b}}\). As this framework is intended to model impact loading, gravitational forces are assumed to be negligible compared to the inertia forces. Thus, the relevant body force vector is defined as \({{{\varvec{f}}}} \,{:=}\, {{{\varvec{f}}}}^{\rho }{= }-\rho _0 \ddot{{{\varvec{u}}}}\) with \(\rho _{0}\) referring to the density of the microscale constituents in the reference configuration. If gravitational forces have to be considered, they can be included in the standard way by the additional force vector \({{\varvec{f}}}^{\text {b}} = \rho _0\,{{\varvec{g}}}\), where \({{\varvec{g}}}\) is the gravitation field. Since this force however, does not depend on the displacements, it does not represent any specialty with view to the proposed homogenization framework and is thus omitted from the presentation to avoid unnecessary complications.
Using standard FE procedures for the discretization and linearization of the weak form of the balance of linear momentum, the well-known equation
is obtained, where \(\widehat{{{\varvec{K}}}}\) and \(\widehat{{{\varvec{R}}}}\) are the global tangent stiffness matrix and the residuum matrix, respectively. In the following, the hat \(\widehat{\bullet }\) is used to highlight quantities that include dynamic terms. After incorporating the Dirichlet boundary conditions, the global matrix of incremental nodal displacements \(\Delta \widetilde{{{\varvec{D}}}}\) are computed from \(\widehat{{{\varvec{K}}}}\Delta \widetilde{{{\varvec{D}}}}=\widehat{{{\varvec{R}}}}\) in each Newton iteration step in order to obtain the updated displacements until convergence of the Newton scheme is achieved, i.e. until \(|\Delta \widetilde{{{\varvec{D}}}}|<tol\). For the classical scheme, the global tangent stiffness matrix \(\widehat{{{\varvec{K}}}}\) is assembled from the element matrix defined as
Herein, \({{\varvec{N}}}^e\) is the classical element matrix of shape functions, \({{\varvec{B}}}^e\) denotes the classical B-matrix containing the derivatives of the shape functions, and \(\mathbb {A}\) is the matrix representation of the material tangent modulus, defined as the sensitivity of the microscopic stress with respect to the microscopic deformation gradient as \(\mathbb {A}= \partial _{{{{\varvec{F}}}}}{{{\varvec{P}}}}\). Analogously, the global residuum matrix \(\widehat{{{\varvec{R}}}}\) is obtained by the assembly of the element-wise counterparts, given as
Herein, \({{\varvec{P}}}\) denotes the matrix representation of the first Piola–Kirchhoff stresses. It can be noted that both, \(\widehat{{{\varvec{k}}}}^e\) and \(\widehat{{{\varvec{r}}}}^e\) have dynamic terms related to the density \(\rho _0\), which directly enables the evaluation of inertia at the microscale.
3.2 Kinematic links to the macroscale
As depicted in Fig. 1, the macroscopic displacements and deformation gradient and their time derivatives are used to define boundary conditions on the RVE. Inserting them into (2) is only the first step. If no additional constraint is considered, the BVP will find an equilibrium where the fluctuations \(\widetilde{{{\varvec{u}}}}\) oppose the applied displacements which results in zero effective displacement of the microstructure. This might not seem obvious at first, however without any imposed constraint, the energetically most favorable position of each node will be its initial configuration, as any deviation from it requires energy. Thus, resulting in a microscopic displacement fluctuation field of \(\widetilde{{{\varvec{u}}}} = \overline{{{\varvec{u}}}} + \overline{{{\varvec{H}}}}{{\varvec{X}}}\), c.f. (3). Based on the principal of kinematic admissibility, described in detail in [3] and applied in dynamic settings e.g. in [14, 52], two kinematic links are chosen here, i.e.
The first constraint (17)\(_{1}\) is well-known from quasi-static RVE homogenization frameworks. It postulates, that the volume average of the microscopic deformation gradients must equal the macroscopic deformation gradient. This is usually enforced by choosing appropriate boundary conditions, e.g., linear displacement or periodic boundary conditions. The second constraint (17)\(_{2}\) is a necessary expansion for the dynamic microscopic problem. This link to the macroscopic displacements is essential in order to prevent the RVE from moving arbitrarily in space. In quasi-static calculations, fluctuations e.g. of a corner node in the RVE are restricted, which does not influence the results. This is, however, not directly possible for the dynamic case without artificially restricting the fluctuations. This is due to the fact that the microscopic deformations are already influenced by just moving the RVE. Thus, restricting the movement at selected locations will yield different deformation fields. Some dynamic homogenization frameworks, e.g. the one in [51], apply a displacement constraint only on the boundary, which can be a reasonable assumption for dynamic metamaterials. There, the boundary lies in the matrix phase, which behaves quasi statically compared to the dynamically active inclusions. The framework proposed here does not make any a priori assumptions on which part of the microstructure will be dynamically significant, as this cannot always be determined in advance for arbitrary problems. Using the displacement split (3) and the definition of the origin of the local coordinate system as the center of the volume (1), the displacement constraint (17)\(_{2}\) can be reduced to
which states that the constraint is fulfilled, once the volume average of the fluctuations equals zero.
3.3 Algorithmic treatment of kinematic constraints
To enforce the displacement constraint in (18) on the whole RVE domain, we propose to use the method of Lagrange multipliers [2]. Similar applications can be found in [4, 52]. For this purpose, the mechanical boundary value problem is recast in terms of the principle of minimum potential energy. By adding the potential \(\Pi ^{\lambda }\) associated with the Lagrange multipliers \({\varvec{\lambda }}\) and the constraint (18) to the function of potential energy \(\Pi \), one obtains
In the following, only the terms concerning the Lagrange multiplier will be regarded, as the other terms capturing the internal potential energy \(\Pi ^{\text {int}}\) and the external potential energy \(\Pi ^{\text {ext}}\) will result in the standard FE formulation (13) described above. However, note that due to the Lagrange term, the additional degrees of freedom \({\varvec{\lambda }}\) appear.
3.3.1 Variation
The potential energy is varied once with respect to the displacement fluctuations \(\widetilde{{{\varvec{u}}}}\) and once with respect to the Lagrange multipliers \({\varvec{\lambda }}\), i.e.
3.3.2 Discretization
Using \(\widetilde{{{\varvec{u}}}} \approx {{\varvec{N}}}^{e} \widetilde{{{\varvec{d}}}}^{e}\) and \(\delta \widetilde{{{\varvec{u}}}} \approx {{\varvec{N}}}^{e} \delta \widetilde{{{\varvec{d}}}}^{e}\) as FE approximations, the discretized expressions can be written as
To obtain the equivalent of the global volume integral in terms of the elements, the assembly operator \({\varvec{\mathsf {A}}}\) is applied for the respective matrices. For better readability, a new element matrix is defined as
This simplifies the formulations to
3.3.3 Global matrix notation
To write the whole system of equations as a global problem, the global matrices are defined in terms of the element matrices, i.e.
where \({\varvec{\mathsf {A}}}\) is the aforementioned assembly operator and \({\varvec{\mathsf {U}}}\) a unification operator, as the node displacement fluctuations shared by different elements are not added up, but belong to the same degree of freedom. Now the expressions (25) and (26) can be reformulated in global fields as
Since the Lagrange multiplier only appears in \(\Pi ^{\lambda }\), no terms result from the variation of \(\Pi ^{\text {int}}\) and \(\Pi ^{\text {ext}}\) with respect to \({\varvec{\lambda }}\). It follows, that the second expression has to vanish, see (29).
3.3.4 Linearization
In order to solve the nonlinear global system of equations, the Newton–Raphson method is utilized. For that purpose, we not only need the equations in weak form as in (28) and (29) but also their linearizations. They are used to iteratively compute the nodal displacement fluctuations as well as the Lagrange multipliers. Here the definition of the \(\Delta \) operator is used. When linearizing a function \(f(x)=0\) at \(\hat{x}\) as Lin\(f= f|_{\begin{array}{c} \hat{x} \end{array}} + \Delta f|_{\begin{array}{c} \hat{x} \end{array}}\), then \(\Delta f = \frac{\partial f}{\partial x}\big {|}_{\begin{array}{c} \hat{x} \end{array}} \Delta x\). Applying this to the weak forms results in
3.4 Global discretized microscopic problem including constraint
From the linearized variations of \(\Pi ^{\lambda }\) we define the global residua
Including all linearized variations of \(\Pi ^{\text {int}}+\Pi ^{\text {ext}}+\Pi ^{\lambda }\) yields the discrete equation

as expansion of (13). After including Dirichlet boundary conditions and applying standard arguments of variational calculus, the resulting discrete system of equations reads

Note that in contrast to \({{\varvec{K}}}\), the new tangent stiffness matrix is not necessarily positive definite, which needs to be taken into account when choosing and setting up a solver. In general, Lagrange multipliers have the disadvantage of adding new degrees of freedom to the system of equations. For the presented displacement constraint, only one extra degree of freedom is added for each spacial direction This is due to the fact that the constraint is applied on the whole RVE which avoids the approximation of the Lagrange multipliers as field variables. Thus, for three-dimensional problems, \({\varvec{\lambda }}\) will only add three additional degrees of freedom. Compared to the displacement fluctuations which are linked to the nodes and which may thus easily reach thousands of degrees of freedom, the number of three additional degrees of freedom over the whole RVE is negligible, making it computationally cheap.
3.5 Coupling of the deformation gradient
The constraint related to the deformation gradient (17)\(_{1}\), can be derived and applied in the same manner as just presented for (17)\(_{2}\) in the previous section. The only change in the final formulation is that the related \({{\varvec{g}}}^{e\text {T}}_{\langle {{\varvec{F}}}\rangle }\) matrix needs to be computed as the volume average of the element B-Matrix instead of the shape functions,
Applying the constraint regarding the deformation gradient on the volume instead of enforcing it using periodic boundary conditions will lead to minimally invasive boundary conditions enabling e.g. arbitrary damage propagation without artificial restrictions imposed by periodic boundary conditions. As shown in [13], such minimally invasive boundary conditions result in a softer constraint compared to periodic boundary conditions. To simplify the numerical examples in this paper, only the displacement constraint is applied and the constraint related to the deformation gradient is enforced by using periodic boundary conditions.
4 The macroscopic problem
For the solution of the dynamic macroscopic boundary value problem, the associated linearized, discretized balance equations are derived. Herein, specific macroscopic tangent moduli appear which are consistently derived for the case where the displacement constraint proposed in the previous section is taken into account.
4.1 Macroscopic boundary value problem
4.1.1 Macroscopic equilibrium equation
The complete macroscopic balance of linear momentum including inertia is given by
Applying the Galerkin method with a test function \(\delta \overline{{{\varvec{u}}}}\) on the entire domain \(\overline{\mathcal {B}}\) leads to the weak form of linear momentum \(\int _{\overline{\mathcal {B}}}\delta \overline{{{\varvec{u}}}}^{\text {T}}\left( {\text {Div}}\overline{{{\varvec{P}}}} + \overline{{{\varvec{f}}}}\right) \,\mathrm {d}V= 0\). By applying \({\text {Div}}( {{{\varvec{P}}}}) \delta {{{\varvec{u}}}}= {\text {Div}}( {{{\varvec{P}}}}^{\text {T}}\delta {{{\varvec{u}}}}) - {{{\varvec{P}}}}\!:\!{\text {Grad}}\delta {{{\varvec{u}}}}\) and the Gauss theorem \(\int _{{\mathcal {B}}}{\text {Div}}( {{{\varvec{P}}}}^{\text {T}}\delta {{{\varvec{u}}}}) \,\mathrm {d}V=\int _{\partial {\mathcal {B}}} \delta {{{\varvec{u}}}} \cdot {{\varvec{t}}}\,\mathrm {d}A\), the weak form is written as
Herein, zero traction forces are taken into account at the boundary and \(\delta {{\varvec{F}}}= {\text {Grad}}\delta {{\varvec{u}}}\). Analogous to the microscale, only body forces related to inertia, not gravitation, are considered at the macroscale. Thus, the body force vector is set to \(\overline{{{\varvec{f}}}} {:=}\overline{{{\varvec{f}}}}^{\rho }= \left\langle {{\varvec{f}}}^{\rho }\right\rangle \).
4.1.2 Linearization
To solve the weak form of equilibrium by using the standard Newton–Raphson scheme, the linearized balance of linear momentum is obtained as
Now the \(\Delta \) operator is applied again to \(\Delta \overline{{{\varvec{P}}}}\) and \(\Delta \overline{{{\varvec{f}}}}^{\rho }\):
Here an interesting property of the two-scale homogenization framework for dynamics is observed. The macroscopic stress not only depends on the deformation gradient but on the acceleration as well. In turn, the inertia forces can also depend on the deformation gradient in addition to the acceleration. We define the resulting four sensitivities as
These moduli (42) are inserted into the linearized weak form which results in
4.1.3 FE discretization
The linearization is of the weak form of the balance of linear momentum is now discretized in terms of finite elements. First, the linear increment
is discretized using standard FE formulations. Then, to get rid of the dependence on the time derivatives, the numerical time integration in terms of (10) is used, which results in
Herein, the matrix representation of the moduli in index notation has been used. Lowercase indices refer the spacial dimension \(n_{\text {dm}}\), whereas uppercase indices to the total degrees of freedom of a element \(n_{\text {edf}}\). Again, standard element B-matrix \(\overline{B}^e\) and shape function matrix \(\overline{N}^e\) are considered. By extracting the nodal virtual and incremental displacements, this yields the definition of the full macroscopic element tangent stiffness matrix
Now the remaining part of the linearization (43), the residuum \(\overline{R}\), is discretized as
By extracting the nodal virtual displacements, the element residuum is identified as
where again matrix representation and index notation is used.
4.2 Consistent macroscopic tangent moduli
For the dynamic homogenization framework, four macroscopic tangent moduli (42) need to be determined. To obtain the sought-after moduli in closed form, we start with taking the derivative of the incremental linearized weak form of linear momentum at the microscale with respect to the two relevant macroscopic quantities, the deformation gradient \(\overline{{{\varvec{F}}}}\) and the acceleration \(\ddot{\overline{{{\varvec{u}}}}}\). Then we derive the moduli by considering the microscopic problem in its equilibrium state.
4.2.1 Incremental weak forms including displacement constraint
As it will be shown later, the derivatives of the microscopic fluctuations with respect to the macroscopic deformation gradient and the acceleration will be required. For their calculation, the incremental linearized weak forms have to be derived with respect to these two quantities. In order to account for the proposed displacement constraint, the associated increments of the weak form of linear momentum and of the Lagrange multiplier potential with respect to the microscopic displacement fluctuations as well as the Lagrange multipliers, i.e. (20) and (21), are identified as
Using the decompositions (3) and (4), equation (49) can be reformulated as
4.2.2 Derivatives of incremental weak forms
By taking the derivatives of the increments (50) and (51) in the equilibrium state \(\Delta G = 0\), a closed form formulation of the tangent moduli will be obtained later. Thus, the associated derivatives are computed in the following.
Derivative with respect to \(\overline{{{\varvec{F}}}}\): Taking the derivatives of (50) and (51) with respect to the macroscopic deformation gradient, while considering (10) results in
Using standard FE discretization yields
Rewriting this in global notation using the abbreviations defined in Appendix 1 Table 2 leads to the expressions
By combining the nodal fluctuations and the Lagrange multipliers into one column matrix \({{\varvec{D}}}^*\), the two equations can be written as one system of equations \({{\varvec{K}}}^*\partial _{\overline{{{\varvec{F}}}}}{{\varvec{D}}}^*=-{{\varvec{L}}}^{\overline{*}}\) with the matrices



Then, the required derivative can be computed from
Note that \({{\varvec{K}}}^*\) is the microscopic tangent stiffness matrix in (35), which is already available from solving the microscopic boundary value problem.
Derivative with respect to \(\ddot{\overline{{{\varvec{u}}}}}\): Analogously, the derivative of (51) with respect to \(\ddot{\overline{{{\varvec{u}}}}}\) can be obtained by applying (11), i.e. one obtains
Standard FE discretization using matrix representation and index notation yields
Again, the two equations are combined by joining the displacements and the Lagrange multipliers into a single matrix, c.f. (58). By solving the resulting system of equations with respect to the required derivatives \(\partial _{\ddot{\overline{{{\varvec{u}}}}}} {{\varvec{D}}}^{*}\), we obtain
Herein, the definitions (58)–(59), the abbreviations defined in Appendix 1 Table 2, as well as  are used.
are used.
4.2.3 Derivation of tangent moduli
In this subsection the four moduli will be derived by inserting the derivatives computed in the last subsection. Note that all moduli are only consistent for a microscopic equilibrium state. Thus, quadratic convergence of the macroscopic Newton–Raphson iteration is only ensured if the microscopic boundary value problem is solved for each macroscopic iteration step. After the last microscopic iteration, the consistent tangent moduli can be computed.
Derivation of \(\overline{\mathbb {A}}^{P\!,F}\): To derive the sensitivity of the macroscopic stresses with respect to the macroscopic deformation gradient, the derivative is rewritten using the definition of the macroscopic stresses in terms of the microscopic fields, i.e.
Using the chain rule \(\frac{\partial {{\varvec{P}}}({{\varvec{F}}})}{\partial \overline{{{\varvec{F}}}}} = \frac{\partial {{\varvec{P}}}}{\partial {{{\varvec{F}}}}} : \frac{\partial {{\varvec{F}}}}{\partial \overline{{{\varvec{F}}}}}\), applying (3), (4), (10) and inserting FE discretization, the equation can be written as
By using the global abbreviations defined in Appendix 1 Tables 2, 3 and inserting (61), the closed form result is obtained as
Note that this result has already been presented in [57] for a special scenario of dynamic homogenization, which did not include macroscopic acceleration and the displacement constraint.
Derivation of \(\overline{\mathbb {A}}^{P\!,u}\): The derivation of the sensitivity of the macroscopic stresses with respect to the macroscopic accelerations is analogous to that of \(\overline{\mathbb {A}}^{P\!,F}\!\). First the derivative is rewritten using the definition of the macroscopic stresses in terms of the microscopic fields as
Then using the chain rule, (3), (4), (10) and FE discretization, the equation reads
Finally, using the global abbreviations in Appendix 1 Tables 2, 3 and inserting (66), the modulus is obtained as
Algorithm for single macroscopic iteration of the dynamic FE\(^2\) framework with respective equation references. It should be noted that the overall structure of the standard FE procedure does not change, only some additional fields need to be computed. Furthermore, for the implementation of the microscopic problem, the macroscopic displacments \(\overline{{{\varvec{u}}}}\) may be omitted from the code. It is the second derivative \(\ddot{\overline{{{\varvec{u}}}}}\), computed in the macroscopic problem, which influences the microscopic results
Derivation of \(\overline{\mathbb {A}}^{f\!,F}\): The derivation of the sensitivity of the macroscopic inertia with respect to the macroscopic deformation gradient is again similar to that of \(\overline{\mathbb {A}}^{P\!,F}\!\). First, the derivative is rewritten as
and by using (3), (4), (10) and FE discretization, the equation reads
Using the global abbreviations in Appendix 1 Tables 2, 3 and plugging in (61), the modulus is identified as
Derivation of \(\overline{\mathbb {A}}^{f\!,u}\): Analogously, the derivative is rewritten as
Then, using (3) and FE discretization, the expression becomes
Taking into account the global abbreviations in Appendix 1 Tables 2, 3 and inserting (66), the modulus is derived as
Note that if \(\overline{\alpha }_1\) and \(\alpha _1\) are equal to zero, which would be equivalent to a quasi-static calculation, the first tangent moduli in (69) take the same form as e.g. found in [40]. Here, the closed form moduli (69), (72), (75) and (78) extend this consistently to the dynamic regime. Note that for a comparable approach at small strains, most derivative terms are conceptually quite similar. Also the incorporation of the new kinematic constraint in terms of Lagrange multipliers can be considered analogous for small strains. An overview over the algorithm of the proposed framework is presented in Fig. 3.
5 Numerical analysis: layered structure
This section presents numerical studies as a proof of concept, as well as an initial analysis of different RVE choices. As it turns out, for dynamic homogenization the definition of RVE is even more complex than for quasi-static cases. Single-scale comparisons are calculated to assess the reliability of the homogenization framework. First, a rather arbitrary example is shown to analyze the macroscopic Newton iteration and demonstrate the quadratically converging algorithm, which is based on the tangent moduli derived in Sect. 4. Then the concept of a unit cell as RVE is analyzed under dynamic conditions. Finally, a comparison of two different displacement constraints, including the proposed one, is presented. All numerical examples make use of the Newmark scheme with the parameters \(\gamma = 0.5\) and \(\beta = 0.25\), resulting in an unconditionally stable algorithm. For more details on time integration methods in the context of nonlinear FE methods see e.g. [66].
A one-dimensional model of a layered structure with the total length of L is investigated. The studied heterogeneous material consists of two alternating phases, a soft and light phase, and a stiff and heavy phase. Each phase has a length of \(l_{\text {M}}\), a Young’s modulus \(E_1\) and \(E_2\), and a density \(\rho _1\) and \(\rho _2\), respectively. All calculations are run using \(E_1=2\cdot 10^{3}~\frac{\text {N}}{\text {mm}^{2}}\), \(E_2=2\cdot 10^{5}~\frac{\text {N}}{\text {mm}^{2}}\), \(\rho _1=1\cdot 10^{3}~\frac{\text {kg}}{\text {m}^{3}}\) and \(\rho _2=1\cdot 10^{5}~\frac{\text {kg}}{\text {m}^{3}}\). The Poisson’s ratio is chosen to be negligible, i.e. \(\nu = 10^{-6}\), to enable a quasi-1D investigation. The left boundary is fixed, on the right end an impact load is applied in terms of a displacement boundary condition using the polynomial function \(\overline{u}(t) = \frac{2^{8}\overline{u}_{\text {max}}}{ {T}^{8}} (t)^4(t-T)^4\), where \(\overline{u}_{\text {max}}\) is the amplitude of the impact wave and T the duration in which the load is applied. Initially, the bar is at rest. The problem will be solved using both, a standard single-scale finite element problem referred to as direct numerical simulation (DNS), as well as the proposed dynamic FE\(^2\) framework, c.f. Fig. 4 respectively. The DNS discretizes the microscopic phases at the macroscale into a large number of finite elements with a length of \(l_E\). It thereby serves as overkill reference for the multiscale approach. The FE\(^2\) simulations have a macroscopic element length of \({l}_{\overline{\text {{E}}}}\) and make use of the same element length \(l_E\) at the microscale for better direct comparability of the microscopic fields to the DNS. To approximate the displacement fields of the elements, linear shape functions and two Gauss points are used for all scales. As shown in Fig. 4b, each microscopic RVE calculation is associated to a single macroscopic integration point. The corresponding parameters for each simulation, regarding geometry, material parameters and loading will be listed in the caption of each figure.
Analysis of algorithmic consistency: a comparison of displacement fields, b convergence of the macroscopic Newton iteration with a tolerance of \(10^{-8}\). The simulation parameters are \(L = 10{,}000\) mm, \(l_M = 10\) mm, \(l_{\overline{\text {E}}} = 33.33\) mm, \(\overline{u}_{\text {max}}~=~100\) mm, \(T = 0.01\) s, \(\Delta t = 5\cdot 10^5\) s and basic unit cell type A as RVE
5.1 Consistency of numerical framework
This example analyzes the convergence behavior of the macroscopic Newton iteration. In Fig. 5a, the distribution of macroscopic displacement fields is shown at three different time instances for both, the DNS and the FE\(^2\) calculation. As RVE, the basic unit cell of the type A (c.f. Fig. 6) is used. It can be seen, that the dynamic multiscale framework approximates the overall behavior well and even captures some of the smaller waves arising from the microstructure. A better representation of the wave propagation might be achieved by using finer time steps, but this would generally make the calculation converge faster as the initial values are already closer to the solution, defying the objective to properly test the tangent moduli. The convergence behavior for the three arbitrarily chosen time frames is depicted in Fig. 5b. Quadratic convergence of the norm of the updates of the nodal displacements \(\left| \Delta {{\varvec{D}}}^* \right| \) is observed. This demonstrates that the macroscopic tangent moduli, incorporating both the microscale inertia forces as well as possible constraints, have been derived in a consistent manner. Note that in this example, locally strains appear of over 10% which exceed the range of small strains. However, due to the one-dimensionality of the problem, no significant influence from the finite strain setting can be expected.
Comparison of macroscopic displacement fields for two different RVEs with different basic unit cells types. The simulation parameters are \(L = 10{,}000\) mm, \(l_M=10\) mm, \(l_{\overline{\text {E}}}~=~33.33\) mm, \(\overline{u}_{\text {max}} = 100\) mm, \(T = 0.01\) s, \(t=0.045\) s and \(\Delta t = 5\cdot 10^5\) s
Analysis of different RVE choices: a direct comparison of RVEs with unit cell type A and B, for an increasing number of basic unit cells per RVE (the error is computed as difference between the response of the two unit cell types, not with respect to the DNS). b Error of unit cell type A and B, compared to DNS as reference. The simulation parameters are \(L = 10{,}000\) mm, \(l_M = 2.5\) mm, \(l_{\overline{\text {E}}} = 20\) mm, \(\overline{u}_{\text {max}} = 100\) mm, \(T = 0.01\) s, \(\Delta t = 5\cdot 10^5\) s, \(n_{\text {timesteps}} = 400\)
5.2 Analysis of the unit cell concept under dynamic loading
For quasi-static homogenization simulations of periodic microstructures, it is known that the resulting macroscopic answer, as well as the corresponding microscopic fields are invariant with respect to the specific choice of unit cell, as long as an admissible periodic unit cell is chosen. In contrast to quasi-static cases, the distribution of the mass relative to the geometrical center matters in a dynamic setting. An extreme example is shown in Fig. 7, which compares the macroscopic displacement field at \(t=0.045\) s presented in the first example in Fig. 5a with a simulation using the basic unit cell type B as an RVE (c.f. Fig. 6). To properly measure the influence of different RVE choices on the FE\(^2\) simulation, an objective error measure \(\epsilon \) is considered. It is defined as average difference of the macroscopic displacement fields \( \epsilon = \sum _i^{n_{\text {nodes}}}\left| \overline{u}^{\text {I}}_{i}(t_j) - \overline{u}^{\text {II}}_{i}(t_j) \right| /n_{\text {nodes}}\), where \(\overline{u}^{\text {I}}\) and \(\overline{u}^{\text {II}}\) stand for any two displacement signals that are being compared. This measure can be evaluated for each time step and thus, the average is once more computed over the number of time steps \(\epsilon _{\text {time}}~=~\sum _j^{n_{\text {timesteps}}} \epsilon _j/n_{\text {timesteps}}\). Note, that due to the comparison of nodal displacements, a unitless error value obtained by dividing the difference by the reference value is problematic as the regarded value might be zero. Furthermore, a delay in the response may lead to relatively large errors in the displacements summarizing over time even if the shape of the displacement wave is perfectly fine. Therefore, in principle it is difficult for dynamic problems to obtain a quantitative measure to evaluate the accuracy. The interpretation of the error value should therefore be done with caution, as the single value does not convey any information about the actual shape of the wave. However for the present analysis the considered error measure is sufficient to analyze the general trend. Figure 8 shows the calculated errors of different choices of the RVE. For the comparison, RVEs with multiple periods of the same unit cell type, as depicted in Fig. 6, were considered. Two effects can be observed: The first, presented in Fig. 8a, is that the difference in macroscopic displacements between different choices of unit cell type decreases, when the number of unit cells per RVE is increased. This means that the choice of particular basic unit cell type does not matter as long as the RVE is chosen large enough. The second effect, shown in Fig. 8b, is that the error, computed as difference to the DNS reference, increases when the size of the RVE, relative to the macroscopic element length, gets too large. Then, errors resulting from a violation of the scale separation assumption are obtained. Generally, the second effect can be neglected, as calculations with RVE sizes larger than the macroscopic element length have little practical application when using FE\({}^2\). At this point it is favorable to use domain decomposition approaches instead of a homogenization method in order to avoid the scale separation assumption.
5.3 Influence of displacement constraints
Finally the proposed displacement link \(\overline{{{\varvec{u}}}} = \left\langle {{\varvec{u}}}\right\rangle \) is analyzed for the examples in Fig. 8b, in comparison to the standard displacement link for quasi-static periodic homogenization, where the fluctuations at the RVE corner nodes is set to zero, i.e. \(\widetilde{{{\varvec{u}}}}_{\text {corner}} = {\varvec{0}}\). For the quasi-1D example analyzed here, this is equivalent to setting the integral over the surface equal to the corresponding macroscopic displacements, which has been taken into account in other dynamic homogenization schemes.
The first observation is, that using the proposed volume constraint \(\overline{{{\varvec{u}}}} = \left\langle {{\varvec{u}}}\right\rangle \) results in a more robust framework in terms of stability of the Newton–Raphson iterations. Furthermore, slightly smaller error values are obtained compared to the DNS reference. Table 1 shows the number of time steps reached before either the calculations crashed (due to diverging Newton iterations at the microscale) or they were finished successfully after the intended complete set of 1000 time steps. Especially the calculations using the unit cell type B in combination with the zero fluctuations of the corner nodes, underperformed the other scenarios. To understand the difference between the performance of the displacement links, it is necessary to examine the behavior at the RVE level.
Comparison of microscopic displacement fields obtained from the FE\(^2\) simulations with the DNS. The displacements have been normalized by \(\overline{{{\varvec{u}}}}\) (for the DNS, average displacement) to analyze the quality of microscopic displacements more or less independent of the macroscopic displacements. The two different displacement links, the volume constraint (VC) and the fixed corners (FC) are analyzed. The simulation parameters are \(L = 10{,}000\) mm, \(l_M = 2.5\) mm, \(l_{\overline{\text {E}}} = 20\) mm, \(\overline{u}_{\text {max}} = 100\) mm, \(T = 0.01\) s, \(\Delta t = 5\cdot 10^5\) s, location of the macroscale integration point \(\overline{X}_1 = 7504,23\) mm, section of the DNS displacement field from \(\overline{X}_1 = 7496.25\) mm to \(\overline{X}_1 = 7511.25\) mm, RVE with three periods of basic unit cell types B
Here the examples with the RVEs consisting of three periods of the basic unit cell B are further analyzed. Figure 9 compares the microscopic displacements for four relevant time instances right before the peak of the input wave passes through the RVEs. More specifically, the differences between the microscopic displacement fields \({{\varvec{u}}}\) of an RVE and the respective macroscopic displacements \(\overline{{{\varvec{u}}}}\). To compare the DNS, an effective \(\overline{{{\varvec{u}}}}\) has been computed as the average displacement over the associated length. Thereby, the quality of the microscopic fields can be analyzed independently of the macroscopic displacements. With this, the two different displacement constraint options can be effectively compared with the reference solution obtained from DNS. The graphs show, that the fixed corner constraint leads to artificially increased displacement intensities at the microscale due to the constricted boundary. These increased displacements eventually lead to extreme deformations in single elements at the microscale, crashing the simulation. The proposed displacement volume constraint however, leads to a softer constraint which results in a more robust computation while still enabling dynamic effects which agree well with the ones from the reference DNS. In the presented examples, the only rate-dependent influence are inertia forces. In cases where also rate-dependent material properties are included we expect the influence of different displacement constraints on the overall simulation to increase, in favor for the proposed volume constraint.
6 Numerical analysis: split Hopkinson bar
After presenting an analysis focused on the study of general properties of dynamic homogenization, this section shows the applicability of the framework to an engineering problem. A standard experiment to study material behavior under impact loading is therefore replicated, the split Hopkinson tension bar test, see e.g. [11, 58]. By releasing a pre-strained steel bar, a loading pulse is transmitted to an aluminum input bar. The wave travels along the bar and through a specimen, which is sandwiched between the input and another aluminum bar called the output bar. Strain gauges in the two bars record the wave signal. By applying the elastic, uniaxial stress wave propagation theory to the split Hopkinson bar experiment, the time history of the forces and the displacements of the faces of the test specimen are calculated, in the following denoted as \(\overline{\sigma }_1\) and \(\overline{\sigma }_2\), cf. [28]. These are then used to approximate the stress and strain within the specimen in loading direction. A schematic visualization is presented in Fig. 10. As target material, a strain-hardening cementitious composite (SHCC) is chosen. This fiber-reinforced concrete exhibits an outstanding ductility and a pronounced energy dissipation under high strain rates. Therefore it is ideal as reinforcing layer to improve the impact resistance of structures [12]. The interpretation of experimentally measured data under dynamic conditions is difficult. Therefore there is a need for accurate simulations including inertia at the macro- and the microscale. In [58] a quite simplified microstructure was considered as RVE. Although a three-dimensional discretization of the RVE was taken into account, the multidimensional character with respect to mechanics was strongly limited by the fact that only one fiber in the direction of the main macroscopic traveling wave direction was taken into account. Therefore, in contrast to [58], here we consider an RVE with multiple fibers to more realistically reflect the three-dimensional nature of microscopic problems in real SHCC. In total, 13 randomly oriented fibers are included representing a more or less isotropic distribution of fiber orientations. First the applied micromechanical models and the chosen microstructure are presented. The macroscopic boundary value problem is shown and used to analyze the dynamic effects.
6.1 Microscale problem
The microscale problem discretizes the fiber-reinforced concrete. Therefore the relevant micromechanical features need to be replicated. Before the first crack through the cementitious matrix, the concrete matrix itself dominates the material behavior of the composite. Once a crack has formed the fibers are engaged and bridge the crack. Finally, a crack will open when the fibers are pulled out. The fiber properties as well as the pullout behavior are shown to be rate dependent [9, 11]. To capture these micromechanical effects two main models are required: (i) a model for the concrete matrix, including cracking and (ii) a representation for the embedded fibers. The concrete is represented as a first approximation by a standard Neo–Hooke material law. The complex compressive behavior of concrete is neglected as only tensile loading is considered within this example. A realistic representation of the crack development is not within the scope of this work. Therefore, to represent the matrix cracking, a simple erosion method is implemented. It sets the material stiffness of an integration point close to zero, once the stress in loading direction surpasses a critical value \(\sigma _{\text {cr}}\). The fibers are represented by a linear truss element, sharing the nodes with the matrix mesh. This allows for a 1D effective material law to be applied, capturing the complex material behavior of the fiber as well as that of the fiber-matrix bond. However, the forces are thus not transferred to the matrix continuously, leading to stress concentrations at the nodes resulting in spurious crack patterns. Therefore, the crack path in the matrix is here defined in advance. The chosen material model uses a general 1D Neo–Hookean material law with an additional strain rate sensitivity of the stress as well as a damage formulation, cf. [58]. The stress in terms of the first Piola–Kichhoff stress tensor is given by \({P} = \frac{1}{2} E ( F -\frac{1}{F} )( 1+\Omega ) ( 1 - D )\) where E is the Young’s modulus, \(\Omega \) denotes the dynamic increase which takes on only positive values, and D is the damage value which takes on values from 0 to 1. The dynamic increase function \(\Omega \) is defined by a logarithmic function, which depends on the rate of the deformation gradient \(\dot{F}\). For values of \(\dot{F} \ge \alpha ^\text {II}\), it is defined as \(\Omega = \alpha ^\text {I}\,\ln [\frac{\dot{F}}{\alpha ^\text {II}}]\) otherwise it is zero, i.e. no dynamic increase for rates lower than \(\alpha ^\text {II}\). The exponential damage formulation is given by \(D = D_\infty ( 1- \exp ( -( \frac{\psi _{\text {D}}}{D_{\text {rate}}})^{D_{\text {shape}}}) )\). The damage value D is determined by the effective energy considered for damage \(\psi _{\text {D}}\). It is defined as the current maximum value of the strain energy function \(\psi _0\). The damage algorithm is therefore classified as a discontinuous damage approach. The damage evolution is controlled by three parameters. \(D_{{\infty }}\) defines the maximum damage reached, \(D_{\text {rate}} > 0\) sets the velocity of the damage evolution, and \(D_{\text {shape}}\) modifies the shape of the function.
As RVE, a cubic body with an edge length of 1 mm is chosen, see Fig. 10a. A crack face perpendicular to the loading direction is located in the center, splitting the matrix in two halves, which are connected by a number of 13 randomly oriented fibers. The concrete matrix is modeled by brick elements, whereas in the center, the feature for cracking is included to represent a possible crack through the matrix. This microstructure fulfills minimal geometric requirements to reproduce the relevant micromechanical processes of SHCC. More complex structures are only of value once advanced micromechanical models are utilized. In the subsequent simulations the following material parameters are used: for the concrete matrix \(E = 29\) kN/mm\(^2\), \(\nu = 0.3\), and \(\rho _0 = 2100\) kg/m\(^3\), additionally for the crack \(E_{\text {cr}} = 10^{-3}\) kN/mm\(^2\) and \(\sigma _{\text {cr}} = 5\) kN/mm\(^2\), for the fiber model \(E = 40\) kN/mm\(^2\), \(A = 0.00385\,\text {mm}^2\), \(\rho _0 = 980\) kg/m\(^3\), \(D_\infty = 0.9982\), \(D_{\text {shape}} = 0.36\), \(D_{\text {rate}} = 0.2\), \(\alpha ^{\text {I}} = 0.08\), and \(\alpha ^{\text {II}} = 0.51\).
6.2 Macroscopic boundary value problem
The macroscale represents the experimental setup of the split Hopkinson tension bar. The cylindrical equipment and SHCC sample are discretized by truss elements. Standard elements are used to simulate the aluminum input and output bars, the two-scale homogenization framework is applied to model only the SHCC specimen. A sketch of the setup is shown in Fig. 10b. All elements have a length of 10 mm. To simulate the experimental loading conditions a piece-wise polynomial function \(\overline{u}^{\text {BC}}\) is chosen. The load is applied as a boundary displacement. The three parts are defined as \(\overline{u}^{\text {I}}(t)=\frac{14}{275}\,t\,v_{\text {c}}(\frac{2t}{t_{\text {vc}}})^3\), \(\overline{u}^{\text {II}}(t) =\frac{t\,v_{\text {c}}}{275}[ 7 (\frac{2t}{t_{\text {vc}}} )^8-12(\frac{2t}{t_{\text {vc}}})^7+16(\frac{2t}{t_{\text {vc}}})^6+19-\frac{34}{3}(\frac{2t}{t_{\text {vc}}})^{-1}]\) and \(\overline{u}^{\text {III}}(t)=v_{\text {c}}(t-\frac{529}{825}t_{\text {vc}}).\) The transitions between the respective functions are at \(\overline{u}^{\text {I}}(0.592\,t_{\text {vc}}) = \overline{u}^{\text {II}}( 0.592\,t_{\text {vc}})\) and \(\overline{u}^{\text {II}}(t_{\text {vc}}) = \overline{u}^{\text {III}}(t_{\text {vc}})\).
The function describes the pulse, which is characterized by two phases. First the acceleration phase and second a phase of constant velocity. The two parameters of the function \(t_{\text {vc}}\) and \(v_{\text {c}}\), define respectively the time when the transition from the first to the second phase is reached and the constant velocity.
6.3 Results
By using the presented microstructure in combination with the split Hopkinson tension bar simulation, the capabilities of the developed framework to analyze material behavior of composites under dynamic loading are illustrated. Following the experimental procedure, the stress signals \(\overline{\sigma }_1\) and \(\overline{\sigma }_2\) of the nodes at the specimen interfaces is averaged as \(\overline{\sigma }\). The stress is then plotted against an approximated specimen strain, computed by the difference of displacement of the interfaces divided by the specimen length. First a quasi-static simulation is compared to the dynamic response, shown in Fig. 11. A clear increase in the dynamic simulation is observed. In addition, a shift is visible from the sudden drop of stress under quasi static loading, due to the homogeneous stress state, to a more gradual stress increase under dynamic conditions, mimicking the multiple cracking behavior of SHCC. Then, to understand the origin of the dynamic increase, two parameter studies are conducted. In Fig. 12, the strain rate sensitivity of the fibers is varied. Clearly, the overall stress response is increased by an increase in \(\alpha ^{\text {I}}\). In addition, the unsteady phase of multiple cracking is completed at smaller overall strains, due to the effective increase in fiber stiffness. A similar effect is observed when comparing microstructures with random fiber direction to perpendicular fibers in loading direction. The fibers at an angle to the applied load result in the softer macroscopic response, c.f. [58]. In Fig. 13, the focus is on the influence of the microinertia. It is evident that the main dynamic influences of this example are the structural inertia and the strain rate sensitivity of the fiber pullout. The microscopic inertia, in contrast to the earlier example of the layered structure in Sect. 5, does not appear to have a significant influence on the macroscopic stress. As the chosen microstructure only allows for moderate dynamic activity, this is not surprising. However with more advanced micromechanical models this might change.
7 Conclusion
In this paper, a general purpose, consistent, two-scale homogenization framework for dynamics at the macro- and microscale was proposed in the sense of the FE\({}^2\) method. The novelty of this framework lays in its generality. The framework does not include any simplifications such as linearized strains, explicit time integration or partly quasi-static scenarios. The only assumption taken into account is a sufficiently pronounced scale separation, which is anyway essential requirement of any FE\({}^2\) approach. Therefore, it enables the simulation of various structural problems of complex micro-heterogeneous materials under dynamic loading such as impact. Furthermore, the derived formulations are compatible with standard FE\(^2\) architecture. The main aspects are: (i) the incorporation of the complete balance of momentum at the micro- and macroscale including inertia forces, (ii) extended microscopic boundary conditions resulting in a more robust scheme and giving the possibility for non-periodic RVE boundaries, (iii) a finite-strain formulation enabling the simulation of a wide range of macro- and micro-mechanical phenomena, and (iv) the derivation of consistent macroscopic tangent moduli ensuring quadratically converging macroscopic iterations. The presented results on different choices of RVEs show that different admissible unit cells of a periodic microstructure lead also to a different mechanical response - even if periodic boundary conditions are employed. This is in contrast to quasi-static scenarios. However, these results should not entail that the most basic unit cell is necessarily a bad choice for a simulation, but the specific choice of this basic unit cell is not unique. In addition, a more complex simulation of a split Hopkinson tension test on an SHCC specimen was presented. The example at hand, compared to the simplified microstructure in [58], exhibits a softer macroscopic response, as not all fibers are oriented in loading direction. This is apparent due to the more pronounced phase of multiple cracking up to 1.5% strain. The example shows the capability of the multiscale framework to further the understanding of experimental material behavior under impact.
References
Bensoussan A, Lions J-L, Papanicolaou G (1978) Asymptotic analysis for periodic structures. North-Holland Publishing Company, Amsterdam
Bertsekas DP (1996) Constrained optimization and Lagrange multiplier methods. Athena Scientific, New York
Blanco PJ, Sánchez PJ, de Souza Neto EA, Feijóo RA (2016) Variational foundations and generalized unified theory of RVE-based multiscale models. Arch Comput Methods Eng 23:191–253
Blanco PJ, Clausse A, Feijóo RA (2017) Homogenization of the Navier–Stokes equations by means of the multi-scale virtual power principle. Comput Methods Appl Mech Eng 315:760–779
Brûlé S, Javelaud EH, Enoch S, Guenneau S (2014) Experiments on seismic metamaterials: molding surface waves. Phys Rev Lett 112:133901
Coenen EWC, Kouznetsova VG, Geers MGD (2012) Novel boundary conditions for strain localization analyses in microstructural volume elements. Int J Numer Methods Eng 90:1–21
Craster RV, Kaplunov J, Pichugin AV (2010) High-frequency homogenization for periodic media. Proc R Soc A 466:2341–2362
Cummer SA, Schurig D (2007) One path to acoustic cloaking. New J Phys 9:45
Curosu I (2018) Influence of fiber type and matrix composition on the tensile behavior of strain-hardening cement-based composites (SHCC) under impact loading. Doctoral dissertation, Schriftenreihe des Instituts für Baustoffe Heft 2018/1, V. Mechtcherine (Hrsg.), Technische Universität Dresden, 2018. ISBN 978-3-86780-555-1
Curosu I, Mechtcherine V, Millon O (2016) Effect of fiber properties and matrix composition on the tensile behavior of strain-hardening cement-based composites (SHCCs) subject to impact loading. Cem Concr Res 82:23–35
Curosu I, Mechtcherine V, Forni D, Cadoni E (2017) Performance of various strain-hardening cement-based composites (SHCC) subject to uniaxial impact tensile loading. Cem Concr Res 102:16–28
Curosu I, Mechtcherine V, Hering M, Curbach M (2019) Mineral-bonded composites for enhanced strucutural impact safety—overview of the format, goals and achievements of the research training group GRK 2250. In: 10th international conference on fracture mechanics of concrete and concrete structures. https://doi.org/10.21012/FC10.235408
de Souza Neto EA, Feijóo RA (2010) Variational foundations of large strain multiscale solid constitutive models: kinematical formulation, Chapter 9. Wiley, London, pp 341–378
de Souza Neto EA, Blanco PJ, Sánchez PJ, Feijóo RA (2015) An RVE-based multiscale theory of solids with micro-scale inertia and body force effects. Mech Mater 80:136–144
Feyel F (1999) Multiscale FE\({}^2\) elastoviscoplastic analysis of composite structures. Comput Mater Sci 16:344–354
Fish J, Shek K (1999) Finite deformation plasticity for composite structures: computational models and adaptive strategies. Comput Methods Appl Mech Eng 172:145–174
Fish J, Chen W, Nagai G (2002) Non-local dispersive model for wave propagation in heterogeneous media: multi-dimensional case. Int J Numer Methods Eng 54:347–63
Geers MGD, Kouznetsova VG, Matouš K, Yvonnet J (2017) Homogenization methods and multiscale modeling: nonlinear problems. Wiley, London, pp 1–34
Hill R (1972) On constitutive macro-variables for heterogeneous solids at finite strain. Proc R Soc A 326:131–147
Hu R, Oskay C (2018) Spatial–temporal nonlocal homogenization model for transient anti-plane shear wave propagation in periodic viscoelastic composites. Comput Methods Appl Mech Eng 342:1–31
Hu R, Oskay C (2019) Multiscale nonlocal effective medium model for in-plane elastic wave dispersion and attenuation in periodic composites. J Mech Phys Solids 124:220–243
Hui T, Oskay C (2014) A high order homogenization model for transient dynamics of heterogeneous media including micro-inertia effects. Comput Methods Appl Mech Eng 273:181–203
Irving JH, Kirkwood JG (1950) The statistical mechanical theory of transport processes. IV. The equation of hydrodynamics. J Chem Phys 18:817
Kadic M, Bückmann T, Schittny R, Wegener M (2015) Experiments on cloaking in optics, thermodynamics and mechanics. Philos Trans R Soc A 373:20140357
Karamnejad A, Sluys LJ (2014) A dispersive multi-scale crack model for quasi-brittle heterogeneous materials under impact loading. Comput Methods Appl Mech Eng 278:423–444
Kettenbeil C, Ravichandra G (2018) Experimental investigation of the dynamic behavior of metaconcrete. Int J Impact Eng 111:199–207
Khajehtourian R, Hussein MI (2014) Dispersion characteristics of a nonlinear elastic metamaterial. AIP Adv 4:124308
Kolsky H (1949) An investigation of the mechanical properties of materials at very high rates of loading. Proc Phys Soc Lond Sect B 62(11):676–700
Li J, Chan CT (2004) Double-negative acoustic metamaterial. Phys Rev E 70(5):055602
Liu C, Reina C (2016a) Discrete averaging relations for micro to macro transition. J Appl Mech 83(8):081006
Liu C, Reina C (2016b) Discrete averaging relations for micro to macro transition. J Appl Mech 83(8):081006
Liu C, Reina C (2017) Variational coars-graining procedure for dynamic homogenization. J Mech Phys Solids 104:187–206
Liu C, Reina C (2018) Dynamic homogenization of resonant elastic metamaterials with space/time modulation. Comput Mech 64(1):147–161
Liu Z, Zhang X, Mao Y, Zhu YY, Yang Z, Chan CT, Sheng P (2000) Locally resonant sonic materials. Science 289(5485):1734–1736
Manadapu KK, Sengupta A, Papadopoulos P (2012) A homogenization method for thermomechanical continua using extensive physical quantities. Proc R Soc A 468:1696–1715
Mandel J (1971) Plasticité classique et viscoplasticité. Springer, Udine
Mei J, Liu Z, Wen W, Sheng P (2006) Effective mass density of fluid–solid composites. Phys Rev Lett 96:024301
Mercer B, Mandadapu KK, Papadopoulos P (2016) Homogenization of high-frequency wave propagation in linearly elastic layered media using a continuum Irving–Kirkwood theory. Int J Solids Struct 96:162–172
Miehe C (1996) Numerical computation of algorithmic (consistent) tangent moduli in large-strain computational inelasticity. Comput Methods Appl Mech Eng 134(3):223–240
Miehe C, Schotte J, Schröder J (1999) Computational micro-macro transitions and overall moduli in the analysis of polycrystals at large strains. Comput Mater Sci 16:372–382
Milton GW, Willis JR (2007) On modifications of Newton’s second law and linear continuum elastodynamics. Proc R Soc A 463:855–880
Milton GW, Willis JR (2010) Minimum variational principles for time-harmonic waves in a dissipative medium and associated variational principles of Hashin–Shtrikman type. Proc R Soc A Math Phys Eng Sci 466(2122):3013–3032
Miniaci M, Krushynska A, Bosia F, Pugno NM (2016) Large scale mechanical metamaterials as seismic shields. New J Phys 18:083041
Mitchell SJ, Pandolfi A, Ortiz M (2016) Effect of brittle fracture in a metaconcrete slab under shock loading. J Eng Mech 142(4):04016010
Molinari A, Mercier S (2001) Micromechanical modelling of porous materials under dynamic loading. J Mech Phys Solids 49:1497–1516
Moulinec H, Suquet P (1998) A numerical method for computing the overall response of nonlinear composites with complex microstructure. Comput Methods Appl Mech Eng 157:69–94
Nassar H, He Q-C, Auffray N (2015) Willis elastodynamic homogenization theory revisited for periodic media. J Mech Phys Solids 77:158–178
Nassar H, He Q-C, Auffray N (2016) On asymptotic elastodynamic homogenization approaches for periodic media. J Mech Phys Solids 88:274–290
Nemat-Nasser S, Srivastava A (2011) Overall dynamic constitutive relations of layered elastic composites. J Mech Phys Solids 59(10):1953–1965
Newmark NM (1959) A method of computation for structural dynamics. J Eng Mech 85:67–94
Pham K, Kouznetsova VG, Geers MGD (2013) Transient computational homogenization for heterogeneous materials under dynamic excitation. J Mech Phys Solids 61:2125–2146
Roca D, Lloberas-Valls O, Cante J, Oliver J (2018) A computational multiscale homogenization framework accounting for inertia effects: application to acoustic metamaterials modelling. Comput Methods Appl Mech Eng 330:415–446
Sartori C, Mercier S, Jacques N, Molinari A (2015) Constitutive behavior of porous ductile materials accounting for micro-inertia and void shape. Mech Mater 80:324–339
Schröder J (2013) Plasticity and beyond—microstructures, crystal-plasticity and phase transitions CISM Lecture Notes 550, Schröder J, Hackl K (eds) Chapter A numerical two-scale homogenization scheme: the FE\({}^2\)-method. Springer, London
Smit R, Brekelmans W, Meijer H (1998) Prediction of the mechanical behavior of nonlinear heterogeneous systems by multi-level finite element modeling. Comput Methods Appl Mech Eng 155:181–192
Sridhar A, Kouznetsova VG, Geers MGD (2018) A general multiscale framework for the emergent effective elastodynamics of metamaterials. J Mech Phys Solids 111:414–433
Tamsen E, Weber W, Balzani D (2018) First steps towards the direct micro–macro simulation of reinforced concrete under impact loading. Proc Appl Math Mech 18(1):e201800181
Tamsen E, Curosu I, Mechtcherine V, Balzani D (2020) Computational micro-macro analysis of impact on strain-hardening cementitious composites (SHCC) including microscopic inertia. Materials 13:4934
Terada K, Hori M, Kyoyac T, Kikuchi N (2000) Simulation of the multi-scale convergence in computational homogenization approaches. Int J Solids Struct 37:2285–2311
van Nuland TFW, Silva PB, Sridhar A, Geers MGD, Kouznetsova VG (2019) Transient analysis of nonlinear locally resonant metamaterials via computational homogenization. Math Mech Solids 24(10):3136–3155
Wang Z-P, Sun CT (2002) Modeling micro-inertia in heterogeneous materials under dynamic loading. Wave Motion 36:473–485
Willis JR (1981) Variational principles for dynamic problems for inhomogeneous elastic media. Wave Motion 3:1–11
Willis JR (1997) Dynamics of composites. Springer, Vienna
Willis JR (2009) Exact effective relations for dynamics of a laminated body. Mech Mater 41:385–393
Willis JR (2012) The construction of effective relations for waves in a composite. C R Méc 340(4):181–192
Wriggers P (2008) Nonlinear finite element methods. Springer, Berlin
Zhou X, Hu G (2009) Analytic model of elastic metamaterials with local resonance. Phys Rev B 79:195109
Acknowledgements
The authors gratefully acknowledge financial support from the German Research Foundation (DFG) within project B1 of the Training Research Group (GRK) 2250 “Mineral-Bonded Composites for Enhanced Structural Impact Safety”. Furthermore, fruitful discussions with Celia Reina (University of Pennsylvania) are greatly appreciated.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: Matrix abbreviations
Appendix: Matrix abbreviations
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Tamsen, E., Balzani, D. A general, implicit, finite-strain FE\(^2\) framework for the simulation of dynamic problems on two scales. Comput Mech 67, 1375–1394 (2021). https://doi.org/10.1007/s00466-021-01993-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00466-021-01993-8