1 Introduction

Lightweight designs are desirable in many industrial applications and structural optimization is an effective way to achieve this. Topology optimization is an important tool to obtain the optimal design of engineering structures. Because of its importance in engineering designs, this subject has drawn great attention by academia for more than twenty years, and remarkable progress has been made since the pioneering work of Bendsoe and Kikuchi [1]. In recent years, many topology optimization methods have been proposed, such as the solid isotropic material with penalization (SIMP), the level-set method (LSM) [2], and the moving morphable components (MMC) [3], etc. Because of the simple material distribution description, the SIMP method gained much popularity for structural design in engineering. The SIMP method is a pixel-based method, where the material layout is fully described by pixels. Because of the pixel-based description, numerical problems are often occurred such as checkboards, staggered boundaries, and mesh dependency [4]. Although pixel-based material layout has already achieved remarkable progress in recent years, there still exist several challenges such as controlling the structural complexity and ensuring manufacturability of an optimal design [5]. To resolve the above problems, several new geometry representation methods have been proposed in recent years. To control design complexity in an explicit geometrical way, a moving morphable component (MMC) approach was proposed by Guo et al. [3]. In Guo’s work, all components are described by level set function and allowed to move, overlap and merge freely, where XFEM analysis based on a fixed mesh is carried out to solve physical problems. Based on the MMC approach, those researchers [6,7,8] further extended MMC to treat 3-D problems and solve more complex physical problem such as stress constraint and multi-material problems. Recently, Tortorelli et al. [9] proposed a geometry projection method for the continuum-based topology optimization made of discrete elements. This method is in the context of density-based topology optimization, and hence standard finite element analysis (FEA) and nonlinear programming algorithm can be applied, where a differentiable mapping from discrete element to density field is realized in this paper. Furthermore, Zhang et al. [10] developed this method to solve stress constraint problem, where the optimal design is based on optimizing an assembly of discrete geometric components such as bars or plates. Lately, Watts and Tortorelli [11] extended the geometric projection method to 3-D and design unit cell for lattice materials based on inverse homogenization, where a negative Poisson’s ratio lattice material is achieved. White et al. [12] proposed a novel method to represent the density field with a truncated Fourier representation, where the number of decision variables are reduced significantly. Recently, Gao et al. [13] proposed an effective method to apply density distribution function, in combination with isogeometric topology optimization, to describe the material layout, where the smoothness and continuity of the optimal design are demonstrated in details. The methods mentioned above can be classified as dimension reduction method. From the mathematical view, solving these problems is equivalent to finding an appropriate density field representation methodology to take the place of traditional pixel-based method.

In recent years, introducing the deep learning method to resolve physical problem such as physics-informed deep learning method is a hot and advanced topic [14,15,16,17,18,19,20,21,22,23]. For topology optimization, some new methods are proposed to apply deep learning in design as described in Ref. [24,25,26]. In computer graphics, the 3D computer vision and robotic communities have come up with multiple approaches to represent 3D geometry for rendering and reconstruction. Fidelity, efficiency, and compression capabilities are the three key factors to balance when choosing among different representation methods. Recently, deep learning for 3D geometric representations draws great attentions from academy [27, 28]. In general, data-driven 3D representation learning approaches can be classified into three categories: point-based, voxel-based and mesh-based methods. For point-based method, a point cloud is a lightweight 3D representation which can closely relate to the geometric raw data, and hence is a natural choose for 3D geometric representation. PointNet [29], for example, apply the max-pool operations to extract and represent geometry. Mesh-based learning methods [30] using parameterization algorithm to represent 3D surface through morphing 2D planes. However, this mesh-based method is often sensitive to input mesh quality. Voxels, using 3D grids to describe volumes, are the most natural extension into 3D domain; however, voxel-based approaches cannot preserve fine shape details and their normal are not smooth. Furthermore, using voxel approach to represent geometry can generally handle low resolutions (\( 128^{3} \) or below), and memory requirements of this method increase cubically. Recently, a new geometry representation called the deep signed distance function (DeepSDF) [31] is proposed to describe modeling shapes as the zero iso-surface boundaries, and a deep feed-forward network is trained to represent SDFs. In this way, the CAD surface is implicitly represented by zero level-set, and Marching Cubes [32] is applied to generate geometry model through raycasting of the surface mesh. The purpose of the present work is proposing the deep representation learning (DRL) method, which incorporates geometry deep learning into existing density-based topology optimization method. The density field is described by a deep feed-forward neural network to ensure the enough smoothness and continuity of material layout.

Recently, Zhou et al. [33] proposed a so-called generalized discrete cosine transform (DCT) compression-based density method to achieve an efficient topology optimization, which does not need any additional filter for optimization and design variables can be phenomenally reduced. As described by Zhou et al. [33], the number of design variables is positive correlative to the computation time. However, the computation time is not linearly dependent on the number of design variables, because the time cost of FEA calculation is not reduced in this method. From this perspective, there is not much differences in computational time if the FEA analysis is time-consuming in that reducing the design variables mainly decreases the time for optimization solver to update. Similar methods based on Fourier transformation is also reported by White et al. [12], and a new method called a material-field series-expansion method [34] is also proposed recently. A dual mesh method proposed by White et al. [35] uses Bernstein polynomials on a coarse mesh to reduce the number of design variables and provide length scale control and allow for AMR. In fact, some other methods such as using IGA [13] to represent density distribution shares some similarity with respect to above methods. The major advantages of these methods come from a) capability of avoiding the checkerboard patterns and mesh dependency b) enough smoothness at boundary and dimension reduction c) Adaptive mesh refinement causes problems for traditional SIMP since the number of design variables is not constant. This is an advantage of the method proposed in this paper, the design has been decoupled from the analysis mesh. d) Effectively reduce design variables. One of the major reasons to reduce the design variables is to build surrogate model for physical problem for topology optimization, which is reported in recent literature [36]. As described in this paper, an effective non-gradient method is proposed using material-field series expansion to represent density field. Because the number of design variables can be reduced significantly, it is possible to build a surrogate model for physical problem (the cost of building surrogate model is dependent on the number of variables). This material-field series expansion method combined with kriging-based optimization method successfully achieve a non-gradient method for topology optimization from linear problems to nonlinear problems as shown in Ref [36]. The method proposed in our paper is a new density field representation method compared to material-field series expansion method, which can be potentially combined with kriging-based optimization algorithm to achieve non-gradient optimization. This point will be investigated in the future. Above methods are indeed using function to describe the material distribution instead of pixel. From this point, the core novelty of this paper is to propose a generalized function description method for topology optimization design. As described in previous paragraph, the deep neural networks have ability to approximate any complex functions. Thus, we proposed a deep learning-based method to achieve a generalized description of density distribution, which is a generalization formulation of above methods.

The paper is organized as follows. In Sect. 2, we describe the deep learning algorithm for geometry representation. Section 3 describes the topology optimization formulation based on deep geometry representation. In Sect. 4, several typical numerical cases are presented to demonstrate the effectiveness of proposed algorithm, followed by conclusions in Sect. 5.

2 Geometry description based on deep representation learning

In computer-aided design, B-rep (boundary representation) [37] is a general way to represent shapes. In this way, a geometry is represented as collection of connected surface elements, which formulate the boundary between solid and void. Compared to B-rep representation method, implicit surface modeling method [38, 39] describes the geometry by implicit function, and the level set of the function represents boundary surface, whereas B-rep method usually consists of piecewise surface patches. Geometry description based on implicit surfaces provide a straightforward way (metamorphosis [40]) to fillet and round surfaces, which is a powerful tool to join two geometry with sufficient continuous. Moreover, implicit geometry modeling method is simpler to determine whether a point is inside, outside, or on a surface. This facilitates the construction of complex geometry such as lattice or porous media. Another advantage of implicit surface is memory requirement is far less than B-rep [41, 42], because the geometry is described by spatial continuous functions \( f\left( {x,y,z} \right) \), where \( x,y,z \) are spatial coordinates and the zero-level set of \( f\left( {x,y,z} \right) \) represents the isosurface of geometry. A Stanford bunny [43], which serves as a computer graphics 3D test model, is shown in Fig. 1. For density-based topology optimization method, a geometry model is generally described by voxels. Voxels, which non-parametrically described geometry with 3D grids of values, are used commonly in density-based topology optimization. The voxel representation method suffers from huge computing costs and memory requirement [44], while it is difficult to obtain high-fidelity shapes using the voxel model because the rendered normal is not smooth.

Fig. 1
figure 1

Model for stanford bunny

Full size image

Recently, modern representation learning techniques have been developed to automatically extract a set of features that compactly represent geometry without loss of fidelity. Several representation learning techniques are proposed such as Generative Adversial Networks [45], Auto-encoders [46], and Optimizing Latent Vectors [47]. In this paper, a new geometry representation method is employed to describe the design shape, while the feedforward neural networks are trained to represent the implicit surface. To demonstrate this idea in detail, a general implicit surface can be expressed as,

$$ F\left( {x,y,z} \right) = 0 $$
(1)

The implicit surface is the set of spatial coordinates \( \left\{ {x,y,z} \right\} \) that satisfy above equation, and the implicit surface is the level set of density field \( F\left( {x,y,z} \right) \). Some typical implicit surfaces are shown as following (Fig. 2),

Fig. 2
figure 2

implicit surface a Torus \( \left( {x^{2} + y^{2} + z^{2} + R^{2} - a^{2} } \right)^{2} - 4R^{2} \left( {x^{2} + y^{2} } \right) = 0 \), b Genus \( 2y\left( {y^{2} - 3x^{2} } \right)\left( {1 - z^{2} } \right) + \left( {x^{2} + y^{2} } \right)^{2} - \left( {9z^{2} - 1} \right)\left( {1 - z^{2} } \right) = 0 \) and c Schwarz’s P surfaces [48] \( \left( {\cos \left( {\pi x} \right) + \cos \left( {\pi y} \right) + \cos \left( {\pi z} \right)} \right)^{2} - t^{2} = 0 \)

Full size image

However, analytical expression for implicit geometry is limited and difficult to achieve free-form topology optimization. In this paper, a new implicit geometry representation method is proposed. Instead of applying analytical expression to describe a geometry, a deep feedforward neural network [49,50,51] is implemented here to substitute the implicit function \( F\left( {x,y,z} \right) \) in Eq. (1). Deep feedforward networks [49, 52, 53], also known as multilayer perceptions, are the foundation of most of the deep learning models such as convolutional neural networks (CNNs) [54]. The main goal of a feedforward network is to approximate a function. For example, a spatial function \( g = F\left( {x,y,z} \right) \) maps the 3D coordinate \( \left\{ {x,y,z} \right\} \) to a value \( g \). Similarly, a feedforward network defines a mapping function \( g_{n} = F_{networks} \left( {x,y,z,\varvec{\theta}} \right) \) from input coordinate to output \( g_{n} \). Note that the parameters \( \varvec{\theta} \) need to be trained to achieve the best function approximation. In fact, deep networks can represent certain functions far more efficiently than shallow ones, and the fitting capability increase significantly with greater depth [55]. Assume that a Stanford bunny can be represented by a density field (voxel representation), which is described by an implicit function. To directly obtain the analytical implicit geometry expression for this Stanford bunny is difficult; however, deep neural networks can be employed to approximate the implicit geometry function, which shares some similarity with DeepSDF [56]. The objective here is to find a compact representation for the spatial density distribution of the Stanford bunny shown in Fig. 1. The Stanford bunny is represented by \( 100 \times 100 \times 100 \) voxels. The input of deep feedforward networks is spatial coordinates of a voxel, and the output is density value at the present coordinates. Thus, the number of training data is \( 1 \times 10^{6} \). The activation kernel is chosen as Tansig (Hyperbolic tangent sigmoid transfer function [57]) neuron. The optimization formulation for deep geometry representation can be written as,

$$ \left\{ {\begin{array}{*{20}l} {Find:\varvec{\theta}} \\ {Min:\mathop \sum \limits_{i = 1}^{N} F_{networks} \left( {x_{i} ,y_{i} ,z_{i} ,\varvec{\theta}} \right) - D\left( {x_{i} ,y_{i} ,z_{i} } \right)_{2} } \\ \end{array} } \right. $$
(2)

where \( F_{networks} \) represent neural network, and the \( \varvec{\theta} \) is the parameters of network. \( D\left( {x,y,z} \right) \) represents density value of Stanford bunny at point \( \left( {x,y,z} \right) \) and operator \( \left\| \cdot \right\|_{2} \) denotes 2-norm. \( N \) is total number of voxels.

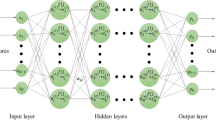
Figure 3 illustrates three feedforward networks with three hidden layers are chosen with different neurons in each layer for comparison. The Levenberg–Marquardt backpropagation algorithm [58] is implemented to train the networks based on the objective function Eq. (2). The training results are presented in Fig. 4. Obviously, the network with \( 5 \times 5 \times 5 \) hidden layers is only able to represent coarse configuration, and lots of geometry details are missing. However, the network with \( 40 \times 40 \times 40 \) hidden layers is able to represent geometry with a high fidelity. Mean squared error (MSE) is applied to measure the error between the objective density field (Stanford bunny) with respect to density field represented by trained neural networks.

Fig. 3
figure 3

The architecture of feedforward networks a\( 5 \times 5 \times 5 \left( {freedom:81} \right) \), b\( 20 \times 20 \times 20 \)\( \left( {freedom:921} \right) \), c\( 40 \times 40 \times 40 \left( {freedom:3441} \right) \)

Full size image
Fig. 4
figure 4

Stanford bunny represented by deep feedforward neural networks a\( 5 \times 5 \times 5\left( {freedom:81;MSE:0.2075} \right) \), b\( 20 \times 20 \times 20 \left( {freedom:921, MSE:0.007952} \right) \), c\( 40 \times 40 \times 40 \left( {freedom:3441, MSE:0.001617} \right) \)

Full size image

3 Topology optimization formulation based on deep representation learning

3.1 Density field described by deep feedforward networks

For density-based method, the material distribution is transformed to spatial arrangement of finite elements. The finite element method (FEM) formulation is formulated by assembling the discrete elements with different density. For the well-established solid isotropic material with penalization (SIMP) approach, the spatial arrangement of density is represented by mesh, which results in optimized layout with staggered boundary (i.e. Lego effect). Thus, a substantial effort in post-processing is needed to generate a smooth CAD model, which may compromise geometric precision along the boundary. Since mesh are utilized to represent the structural topology, the number of design variables is usually quite large for three-dimensional design, and many mature optimization techniques are not applicable for large-scale problem [59]. To resolve the above issues, a new density representation method using deep feedforward network is described in this section. As described in Sect. 2, a complex geometry can be represented by a deep feedforward network with high fidelity, and smoothness of surface can be guaranteed. Thus, it is a natural choice to apply deep feedforward network to represent the density field in the design domain. A requirement should be satisfied to ensure a well-justified density field, i.e., the bounds of element densities are within \( \left[ {0,1} \right] \). Like the formulation in Sect. 2, a density function in design domain is described by a deep feedforward network, and the input for the network are all the point coordinates. The output is density value at a given point. To ensure the output density is in the bounds \( \left[ {0,1} \right] \), a mapping function \( {\mathcal{M}} \) is applied as follows,

$$ {\mathcal{M}} = \frac{{\left( {\tanh \left( {\beta x} \right) + 1} \right)}}{2} \left( {\beta = 0.5} \right) $$
(3)

Note that the parameter \( \beta \) is chosen as 0.5 in this paper. An example is presented here to demonstrate the functionality of mapping function \( {\mathcal{M}} \). Consider a two-dimensional problem, the density field \( \phi \left( {x,y} \right) \) is described by a \( 20 \times 20 \times 20 \) feedforward network with Tansig activation function. Thus, the mathematical formulation of density field can be expressed as:

$$ \phi \left( {x,y} \right) = {\mathcal{M}}\left( {{\mathbb{N}}\left( {x,y,\varvec{\theta}} \right)} \right) \left( {2D problem} \right) $$
(4)
$$ \phi \left( {x,y,z} \right) = {\mathcal{M}}\left( {{\mathbb{N}}\left( {x,y,z,\varvec{\theta}} \right)} \right) \left( {3D problem} \right) $$
(5)

where \( {\mathbb{N}} \) denotes feedforward networks, and the \( \varvec{\theta} \) is parameter. The architecture of deep layered network composes many hidden layers. Denoting the output of hidden layers by \( \varvec{h}^{{\left( \varvec{l} \right)}} \left( \varvec{x} \right) \), a network with L hidden layers can be expressed as,

$$ {\mathbb{N}}\left( {x,y,z,\varvec{\theta}} \right) = {\mathbb{N}}\left( {\varvec{a}^{{\left( {\varvec{L} + 1} \right)}} \left( {\varvec{h}^{{\left( \varvec{L} \right)}} \left( {\varvec{a}^{{\left( \varvec{L} \right)}} ( \ldots \varvec{h}^{\left( 1 \right)} (\varvec{a}^{\left( 1 \right)} \left( {x,y,z} \right)} \right)} \right)} \right) $$
(6)

where \( \varvec{a}^{{\left( \varvec{l} \right)}} \left( \varvec{x} \right) \) is a linear operation, expressed as,

$$ \varvec{a}^{{\left( \varvec{l} \right)}} \left( \varvec{x} \right) = \varvec{W}^{{\left( \varvec{l} \right)}} \varvec{x} + \varvec{b}^{{\left( \varvec{l} \right)}} $$
(7)

where \( \varvec{W}^{{\left( \varvec{l} \right)}} \) is weight matrix and \( \varvec{b}^{{\left( \varvec{l} \right)}} \) is bias vector for the lth layer. The weight matrix \( \varvec{W}^{{\left( \varvec{l} \right)}} \left( {\varvec{l} = 1,2, \ldots \varvec{L}} \right) \) and bias \( \varvec{b}^{{\left( \varvec{l} \right)}} \left( {\varvec{l} = 1,2, \ldots \varvec{L}} \right) \) can be combined into a single parameter \( \varvec{\theta} \). \( \varvec{h}^{{\left( \varvec{l} \right)}} \left( {\varvec{l} = 1,2, \ldots \varvec{L}} \right) \) are hidden-layer activation functions (kernel functions).

3.2 Minimum compliance

In this section, the deep representation learning (DRL) is adopted to develop the topology optimization formulation of compliance minimization [60]. The density field is represented by a deep neural network in the design domain. Hence, the TO will iteratively optimize the density field through updating the parameters of the network in the design domain until the material layout has the best stiffness performance. Here, the weights of the feedforward network are defined as the design variables for evolving the density field in the design domain during the optimization. Thus, the optimization problem can be expressed as:

$$ \left\{ {\begin{array}{*{20}l} {Find:\theta } \\ {Min:C\left( {u,\Phi } \right) = \frac{1}{2}\int\limits_{\Omega } {\varvec{\varepsilon}\left( \varvec{u} \right)^{\varvec{T}} \varvec{D}\left( {\Phi \left(\varvec{\theta}\right)} \right)\varvec{\varepsilon}\left( \varvec{u} \right)d\Omega } } \\ {s.t:\left\{ {\frac{1}{{\left|\Omega \right|}}\int\limits_{\Omega } {\Phi \left(\varvec{\theta}\right)d\Omega } } \right. - V_{prescribe} \le 0} \\ \end{array} } \right. $$
(8)

where the \( \varvec{\theta} \) are the parameters of the deep feedforward network, and \( C \) is the objective function defined by the structural compliance. \( \Phi \) is the density distribution in the design domain \( \Omega \), and \( V_{prescribe} \) is the prescribed volume fraction. In the finite element model, \( \varvec{u} \) is the unknown displacement field, \( \varvec{\varepsilon} \) is the strain, and \( \varvec{D} \) is the elastic tensor matrix.

3.3 Minimum compliance with stress constraint

For the minimum compliance with stress constraint problem, the von Mises stress is always used for local stress measurement and as stress constraint in the optimization. However, constraining the local stress is numerically expensive in practice. Thus, a p-norm approach is implemented here to approximate the local stress constraint. In recent years, several modified methods have been proposed to accurately control the local stress [10, 61,62,63,64,65,66,67,68]. For simplicity, we apply a well-developed method to constrain the local von Mises stress as described in Ref. [69]. In this method, the p-norm measure \( \sigma_{PN} \) is adopted to formulate the constraint. Thus, the problem in Sect. 3.2 can be reformulated as:

$$ \left\{ {\begin{array}{*{20}l} {Find:\theta } \\ {Min:C\left( {u,\Phi } \right) = \frac{1}{2}\int\limits_{\Omega } {\varvec{\varepsilon}\left( \varvec{u} \right)^{\varvec{T}} \varvec{D}\left( {\Phi \left(\varvec{\theta}\right)} \right)\varvec{\varepsilon}\left( \varvec{u} \right)d\Omega } } \\ {S.t:\left\{ {\begin{array}{*{20}c} {\frac{1}{{\left|\Omega \right|}}\int\limits_{\Omega } {\Phi \left(\varvec{\theta}\right)d\Omega - V_{prescribe} \le 0} } \\ {\sigma_{PN} = \left( {\mathop \sum \limits_{e = 1}^{N} \left( {v_{e} \sigma_{e}^{vM} } \right)^{p} } \right)^{{\frac{1}{p}}} \le \overline{{\sigma_{PN} }} \left( {\left( {\mathop \sum \limits_{e = 1}^{N} \left( {v_{e} \sigma_{e}^{vM} } \right)^{p} } \right)^{{\frac{1}{p}}} - \overline{{\sigma_{PN} }} < 0} \right)} \\ \end{array} } \right.} \\ \end{array} } \right. $$
(9)

where \( p \) is the p-norm parameter, \( \sigma_{e} \) is element von Mises stress, \( \sigma_{PN} \) is p-norm measure, and \( \overline{{\sigma_{PN} }} \) is the global stress limit. \( v_{e} \) is element \( e \) solid volume. A good choice for \( p \) can make the algorithm perform well and provide an adequate approximation of the maximum stress value. In this paper, \( p = 10 \) is applied in all stress-constrained numerical examples.

3.4 Design sensitivity analysis

For gradient-based optimization, the sensitivity analysis of the objective with respect to the design variables, i.e., weights of the feedforward network, are needed. To derive the sensitivity of the objective function, the chain rule will be employed. The adjoint method [70] can be used to obtain the sensitivity with respect to the density field \( \Phi \):

$$ \frac{\partial C}{{\partial\phi }} =\varvec{\lambda}^{T} \frac{{\partial \varvec{K}}}{{\partial\phi }}\varvec{u} $$
(10)

where \( \varvec{\lambda} \) is the adjoint vector computed from the adjoint equation \( \varvec{K\lambda } = - \varvec{f} \), and \( \varvec{K} \) is the assembled stiffness matrix, see Ref. [60]. Based on the chain rule, the sensitivity of objective \( C \) with respect to design variables \( w \) can be expressed as:

$$ \frac{\partial C}{\partial w} = \frac{\partial C}{{\partial\phi }} \cdot \frac{{\partial\phi }}{\partial w} $$
(11)

where the density field \( \phi \) can be expressed as \( {\mathcal{M}}\left( {\mathbb{N}} \right) \). The sensitivity of \( {\mathcal{M}}\left( {\mathbb{N}} \right) \) with respect to the network weights \( w \) can be readily obtained using the algorithmic differentiation (AD) technique [71, 72] implemented in the open-source software CasADi [73]. For sensitivity analysis of the p-norm stress, similar derivation can be achieved based on chain rule as follows:

$$ \frac{{\partial \sigma_{PN} }}{\partial w} = \frac{{\partial \sigma_{PN} }}{{\partial\phi }} \cdot \frac{{\partial\phi }}{\partial w} $$
(12)

where the analytical sensitivity derivation based on the adjoint method of \( \frac{{\partial \sigma_{PN} }}{\partial \phi } \) can be found in Ref. [74].

Fig. 5
figure 5

The relationship between standard deviation with respect to number of holes in each direction

Full size image

3.5 The relationship between geometry complexity with respect to architecture of neural networks

The architecture of neural networks is close related to the fitting ability, and how to design a deep neural network to satisfy a certain requirement is a hot topic in recent years. To investigate the relationship between the geometry complexity with respect to architecture of neural networks, several numerical experiments are conducted in this section. To simplify the problem, the geometry complexity is measured using standard deviation of density field as follows,

$$ s = \sqrt {\frac{1}{N - 1}\mathop \sum \limits_{i = 1}^{N} \left( {\phi_{i} - \bar{\phi }} \right)^{2} } $$
(13)

where \( N \) is the total number of density points, and \( \bar{\phi } \) is mean value of density field, which can be expressed as,

$$ \bar{\phi } = \frac{{\mathop \sum \nolimits_{i = 1}^{N} \phi_{i} }}{N} $$
(14)

The relationship between the number of holes with respect to standard deviation can be found in Fig. 5. For number of holes less than \( 9 \times 9 \), the density standard deviation increases with increasing number of holes, which means that the geometry complexity increases with more holes. The mean squared error (MSE) loss can be defined as,

$$ MSE = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \left| {\phi_{i} - \hat{\phi }_{i} } \right|^{2} $$
(15)

where the \( \hat{\phi }_{i} \) denotes the target density value, and \( \phi_{i} \) is density value computed from neural networks. \( MSE \) defines the error between target density field and density field obtained from networks.

Fig. 6
figure 6

One hole in each direction

Full size image

To verify that the geometry fitting ability is increasing with larger neural networks, several numerical experiments are conducted here. We apply different neural networks architecture to approximate objective geometry with different complexity. Figure 6 shows a square with one hole, which works as target density field. Four different neural networks are implemented to fitting this simple geometry. The fitting results (level set function,\( \phi = 0.5 \)) are shown in Fig. 7. Obviously, for one hidden layer, the MSE value decreases with increasing the number of neurons. Compared with shallow neural networks (one hidden layer), the networks with three hidden layers show better fitting ability with \( {\text{MSE}} = 1.327 \times 10^{ - 8} \). For squares with three or five holes (Figs. 8 and 10), the fitting results are plotted in Figs. 9 and 11. The numerical results show that networks with more hidden layers and neurons have more powerful geometry fitting ability with lower MSE values. Another finding is that the networks can capture the major geometry feature once the MSE value is less than \( 1 \times 10^{ - 2} \) from numerical experiments. For example, comparing Fig. 11d, g, networks with one hidden layer (15 neurons) cannot capture the major geometry features with \( MSE = 4.727 \times 10^{ - 2} \), while networks with three hidden layers \( {\text{MSE}} = 9.638 \times 10^{ - 3} \) is able to capture major geometry features with some small defects at the boundary. The same conclusion can be drawn from Fig. 12. As shown in Fig. 12, we compare the fitting ability of two different networks. The horizontal axis represents number of holes, and the vertical axis denotes mean squared error (MSE). Apparently, the larger networks with more neurons in each layer have better fitting ability with lower MSE values. For example, if we use \( 1 \times 10^{ - 2} \) as MSE threshold to work as a standard to determine whether fitting results is sufficient to approximate the target geometry, it is evident to observe that networks with 20 neurons in each layer can fit up to the square with \( 9 \times 9 \) holes. However, the smaller networks with 10 neurons has lower fitting ability, which can only fit up to the square with \( 4 \times 4 \) holes. As shown in Fig. 5, standard deviation of density field is an approach to measure the geometry complexity. To further examine the geometry complexity with respect to networks architecture, the relationship between standard deviation and networks (three hidden layers) is plotted in Fig. 13. If we choose the \( MSE = 1 \times 10^{ - 2} \) as the threshold, the max standard deviation value for the networks with 5 neurons in each layer is 0.16, while max standard deviation value can reach 0.38 for the networks with 20 neurons. Therefore, standard deviation can work as a complexity measurement when designing networks. Meanwhile, the Fig. 13 can also work as a guidance when choosing the size of the neural networks to achieve a certain geometry complexity. More works will be done to incorporate the standard deviation of density field as a complexity constraint in optimization in the future.

Fig. 7
figure 7

Geometric fitting results with different networks

Full size image
Fig. 8
figure 8

Three holes in each direction

Full size image
Fig. 9
figure 9

Geometric fitting results with different networks (\( 3 \times 3\;{\text{holes}}) \)

Full size image
Fig. 10
figure 10

Five holes in each direction

Full size image
Fig. 11
figure 11

Geometric fitting results with different networks (\( 5 \times 5\;{\text{holes}}) \)

Full size image
Fig. 12
figure 12

Geometric fitting results with different networks (\( 5 \times 5\;{\text{holes}}) \)

Full size image
Fig. 13
figure 13

Geometric fitting ability \( \left( {{\text{Three}}\;{\text{Hidden}}\;{\text{Layers}}} \right) \)

Full size image

4 Numerical examples

In this section, several 2D and 3D numerical examples are demonstrated in detail to present the effectiveness of the proposed method. The classic MBB beam is first investigated to illustrate the benefits of the proposed DRL method. The box constraints are chosen as \( \left[ { - 10,10} \right] \) for both weights and biases during optimization.

4.1 Compliance optimization for MBB design

The MBB-beam [75] is a popular test and benchmark problem in topology optimization. The symmetry is used for design, and the right half of the beam is modelled. The design of the MBB beam with the loading and boundary conditions is illustrated in Fig. 14. The design domain is uniformly meshed by \( 300 \times 100 \) elements. The prescribed volume fraction is set as 30%. The elastic constants are chosen as follows: elastic modulus \( E = 1 \) and Poisson’s ratio \( \mu = 0.3 \). The initial weights of the network are computed to generate uniformed density distribution in design domain. For comparison, different network architectures are generated as shown in Fig. 15. The activation function is chosen as Tansig (Hyperbolic tangent sigmoid), and networks are fully connected. For the 2D problem, the inputs are spatial coordinates \( \left\{ {x,y} \right\} \), and output is density field. For networks with \( 20 \times 20 \times 20 \) hidden layers, the evolution of density field is presented in Fig. 20, and optimized design is plotted in Fig. 21. For shallow neural networks with only one layer, the evolution of density field and optimal design is plotted in Figs. 16 and 17. For \( 20 \times 20 \) hidden layers, the evolution history and optimal design are demonstrated in Figs. 18 and 19. It can readily be found that the different architectures result in different optimal topologies, and shallow network can generate simple optimal layout with less geometric complexity. As shown in the density evolutionary progress, the density field is smoother and less small sharp features are found using shallow neural networks. This can be easily explained in that networks with more hidden layers present better fitting ability, which leads to more complex geometric topology. The optimal compliance for different designs is 454.75 (Hidden Layers: 20), 391.82 (Hidden Layers: \( 20 \times 20 \)), and 336.45 (Hidden Layers: \( 20 \times 20 \times 20 \)) respectively. The number of design variables for different architectures are 81, 501 and 921. Compared with voxel-based density method, the design variables reduce significantly. At present, the number of neurons is chosen based on experience and fully connected networks are used in density representation. However, the regularization method [76] of neural networks may be implemented to prune the topology structure. The regularization method is a technique that makes modification to the connectivity of networks such that the model generalizes better and reduces overfitting. In regularization, the coefficients of weights are penalized through modifying the objective function so that a sparse optimal result of weights is obtained. In such manner, some neurons in the network will be dropped so that the network has better compact representation. In this paper, we will not discuss the regularization of neural networks, and more research will be devoted to regularization in the future.

Fig. 14
figure 14

MBB beam example

Full size image
Fig. 15
figure 15

Architectures of feedforward networks

Full size image
Fig. 16
figure 16

Evolution of density field (hidden layers structure: \( 20 \))

Full size image
Fig. 17
figure 17

Optimal design (hidden layers structure: \( 20 \) compliance: 454.75)

Full size image
Fig. 18
figure 18

Evolution of density field (hidden layer structure: \( 20 \times 20 \))

Full size image
Fig. 19
figure 19

Optimal design (hidden layer structure: \( 20 \times 20 \) compliance: 391.82)

Full size image
Fig. 20
figure 20

Evolution of density field (hidden layers: \( 20 \times 20 \times 20 \))

Full size image
Fig. 21
figure 21

Optimal design (hidden layers structure: \( 20 \times 20 \times 20 \) compliance: 336.45)

Full size image

In this part, different neuron activation functions are implemented to examine the effect of activation function on the optimal design. Three activation functions implemented in this paper are Tansig (Hyperbolic tangent sigmoid transfer function), Gaussian [77], and Tribas (Triangular basis function [78]). The mathematical properties of the three typical activation functions are plotted in Fig. 22. Note that the Tribas function is made of piece-wise linear function so that the spatial density distribution is piece-wise smooth as shown in Fig. 23. The optimal design obtained using Tribas is simpler geometrically compared to the Tansig kernel, the main reason lies in that the nonlinearity of Tansig is higher than Tribas (Fig. 24).

Fig. 22
figure 22

Graph of activation function a Tansig, b Gaussian, c Tribas

Full size image
Fig. 23
figure 23

Evolution of density field (Kernel: Tribas, hidden layers: \( 20 \times 20 \times 20 \))

Full size image
Fig. 24
figure 24

Optimal design (hidden layers: \( 20 \times 20 \times 20 \), Tribas, Compliance: 445.77)

Full size image

The Gaussian kernel, which is widely used in probability theory, shows excellent fitting capacity for highly nonlinear problems. The graph of Gaussian kernel is a characteristic symmetric “bell curve” shape, and the width of the “bell” is controlled by a parameter called the standard deviation [79]. The Gaussian kernel is continuous and infinitely differentiable, which is a significant difference from Tribas. Using the Gaussian kernel, the minimum feature of optimal design can be controlled through kernel width as shown in Fig. 25. In the Fig. 25, four different values of kernel width are chosen to generate four optimized designs. The minimum length of optimal design increases after increasing kernel width from 0.25 to 2. The evolution history for four different designs are plotted in Figs. 26, 27, 28 and 29. Evidently, the networks with smaller kernel width has more detailed feature as shown in Fig. 29. However, for large kernel width, the detailed feature or noise cannot be found in optimization as shown in Fig. 26. This can be explained based on image processing theory. In image processing, an image can be blurred by a Gaussian function, which is known as Gaussian smoothing. The Gaussian function can be applied to reduce image noise and reduce detail. Mathematically, a Gaussian smoothing is a low pass filter, which has the effect of reducing the high-frequency components of function. This can be proven based on Weierstrass transform [80], and the kernel width can directly control property of low pass filter. Thus, the geometry details can be effectively controlled through kernel width. Strict mathematical proven will be done in the future to verify our numerical results. In fact, several effective minimum feature control methods are proposed in recently years based on conventional density-based method [5, 81,82,83,84,85,86,87,88,89,90,91,92,93]. Compared to these methods, our method provides an alternative way to control the minimum feature based on deep representation learning.

Fig. 25
figure 25

Optimal design with different kernel width (hidden layers: \( 20 \times 20 \times 20 \), Gaussian kernel)

Full size image
Fig. 26
figure 26

Evolution history with kernel width 2 (hidden layers: \( 20 \times 20 \times 20 \), Gaussian kernel)

Full size image
Fig. 27
figure 27

Evolution history with kernel width 1 (hidden layers: \( 20 \times 20 \times 20 \), Gaussian kernel)

Full size image
Fig. 28
figure 28

Evolution history with kernel width 0.5 (hidden layers: \( 20 \times 20 \times 20 \), Gaussian kernel)

Full size image
Fig. 29
figure 29

Evolution history with kernel width 0.25 (hidden layers: \( 20 \times 20 \times 20 \), Gaussian kernel)

Full size image

4.2 Stress constrained optimization for two-dimensional L-bracket design

To further verify the effectiveness of the proposed method, the compliance minimization with stress constraint problem is considered in this section. The L-bracket is modeled by a \( 100 \times 100 \) finite element mesh with \( 50 \times 50 \) section removed as shown in Fig. 30. The boundary condition and force are demonstrated in Fig. 30. A vertical load \( F = 4 \) is applied uniformly on four nodes, and element size is unity in this numerical example. The elastic constants are chosen as follows: elastic modulus \( E = 1 \) and Poisson’s ratio \( \mu = 0.3 \). The p-norm value for this numerical example is chosen as \( p = 10 \). The volume fraction is chosen as 0.3, and stress constraint (SC) in the p-norm is set to \( \sigma_{pnorm} < 2 \left( {SC:\sigma_{pnorm} - 2 < 0} \right) \). The neural network with three hidden layers of size \( 20 \times 20 \times 20 \) is implemented to represent the density distribution, and the Gaussian kernel is chosen as the activation function. Considering that the stress constraint optimization is highly nonlinear, a small moving limit of 0.005 in the MMA algorithm [94] is employed in the optimization. At the beginning of the optimization, the stress concentration occurs at the sharp corner, and the sensitivity at this region is negative so that the material in this area tends to be removed. The final optimal result is plotted in Fig. 31. Note that round corners are generated to reduce stress concentration, and the optimized material layout boundary becomes smooth. The evolutionary history of density distribution is shown in Fig. 32. The stress contour and distribution for the final optimal design is presented in Fig. 33. The stress distribution of optimal design is uniform and smooth, and the maximum stress are in the region near loading points as plotted in Fig. 33. The convergence history is shown in Fig. 34. Note that after optimization, the stress constraint is satisfied, which the compliance decreases significantly to around 1/3 of initial design. Because of the local stress singularity, the local oscillation of convergence curve can be observed in Fig. 34.

Fig. 30
figure 30

2D L-bracket example

Full size image
Fig. 31
figure 31

Optimal design for stress constrained optimization

Full size image
Fig. 32
figure 32

Evolution of density field (Kernel: Gaussian, hidden layers: \( 20 \times 20 \times 20 \))

Full size image
Fig. 33
figure 33

Stress distribution of optimal design (Kernel: Gaussian, hidden layers: \( 20 \times 20 \times 20 \))

Full size image
Fig. 34
figure 34

Convergence history

Full size image

4.3 Compliance optimization for three dimensional MBB design

In this section, a three-dimensional MBB example is presented for compliance optimization. The MBB is modeled by a 600 × 150 × 150 hexahedral mesh, and the dimension of the design is demonstrated in Fig. 35. A uniform line force \( F = 1 \) is applied on the mid-top of the rectangle domain. The neural network with three hidden layers of size \( 20 \times 20 \times 20 \) is implemented to represent the density field in the design domain. Note that three inputs are needed to represent coordinates \( x,y \) and \( z \). In the actual FEM analysis, only half of the design domain is modeled considering the geometric symmetry. The elastic constants are chosen as follows: elastic modulus \( E = 1 \) and Poisson’s ratio \( \mu = 0.3 \). The first numerical result is obtained using the Tansig kernel. The optimization converges after 60 iterations and the density evolution history is plotted in Fig. 36. To make a comparison, a Gaussian kernel is also employed, and the optimization progress is demonstrated in Fig. 37. The optimization converges after 80 iterations.

Fig. 35
figure 35

3D MBB example

Full size image
Fig. 36
figure 36

Evolution of density field for MBB design (Tansig kernel)

Full size image
Fig. 37
figure 37

Evolution of density field for MBB design (Gaussian kernel)

Full size image

4.4 Stress constrained optimization for three-dimensional L-bracket design

To test the proposed algorithm in a three-dimensional case, a three-dimensional L-bracket example is plotted in Fig. 38. The dimensions of the L-bracket, boundary and loading conditions are found in Fig. 38. A distributed edge force \( F = 3 \) is applied to the finite element model. The design domain is meshed with \( 100 \times 100 \times 40 \) uniform trilinear hexahedral elements with element size of \( h = 1 \). The material properties are the same as in the previous example. The p-norm stress constraint is set to be \( SC: \sigma_{pnorm} - 5 < 0 \), and volume fraction constraint is chosen as 0.3. Due to the presence of a sharp comer in the initial design, the stress is expected to concentrate at the corner with a high value. The neural network with three hidden layers of size \( 20 \times 20 \times 20 \) and Tansig kernel as the activation function is implemented to implicitly represent the density field. The moving limit of MMA algorithm is chosen as 0.005. The optimization converges after 120 iterations, and optimized density field is presented in Fig. 39. The final optimization result is transformed into a CAD model as shown in Fig. 42, where the stress distribution is plotted in Fig. 40. Apparently, the sharp corner disappears after optimization, and stress distribution tends to be uniform in the optimal structure. To validate the design, the commercial software ANSYS is applied to implement stress analysis. The tetrahedron mesh with 10 nodes is used to discretize the design (Total mesh number:142785), the discretized finite element model and stress contour is plotted in Fig. 43. Stress optimization is a highly nonlinear optimization problem due to its local effects. This example successfully demonstrates that the deep learning method can represent complex geometry by generating effective optimal layout with significant decrease of design variables, i.e., from the original number of design variables of 400,000 to 941. The deep neural networks demonstrate excellent data compression ability. There are no small intricate features are found in optimal design, and the final optimal design are represented in an implicit way. Meanwhile, no staggered phenomenon on the surface occurs due to the implicit representation method. The convergence history is plotted in Fig. 41.

Fig. 38
figure 38

3D L-bracket example

Full size image
Fig. 39
figure 39

Optimized material layout (Kernel: Tansig, hidden layers: \( 20 \times 20 \times 20 \)) a front view, b rear view

Full size image
Fig. 40
figure 40

Stress distribution a front view, b rear view

Full size image
Fig. 41
figure 41

Convergence history

Full size image
Fig. 42
figure 42

CAD model a front view, b rear view

Full size image
Fig. 43
figure 43

a Tetrahedron mesh, b stress distribution

Full size image

5 Conclusion

In this paper, a density field representation algorithm based on deep learning is proposed to generate optimal design for compliance and stress constrained problems. The main conclusions are as follows,

  1. (a)

    The density field is represented by a neural network so that the design variables are reduced phenomenally compared to the conventional voxel-based optimization method.

  2. (b)

    Different kernel functions influence the optimized design, and the geometry complexity is directly related to the topology of neural networks. The simple optimal geometry is obtained with shallow neural networks.

  3. (c)

    No filtering technique is needed in the proposed algorithm, and optimal designs are free from chessboard pattern [95].

  4. (d)

    Because the topology is represented in an implicit way, there is no staggered boundary found in the final design.

From the future perspective, the method proposed in this paper open a new opportunity to achieve a combination of deep learning with topology optimization in a geometric way. In fact, deep neural networks are only one of the deep learning models. In recently years, more powerful and sophisticated deep learning model are proposed (e.g., generative adversarial network [45] and convolutional neural network [96]). The method proposed in this paper is a real “marriage” between deep learning and topology optimization. Future work will focus on applying more deep learning models to represent density field such as CNN and GAN. Meanwhile, future directions include employing the classification method (e.g. decision tree algorithm [97], random forest [98]) for geometry representation to directly generate 0–1 solution in the design domain.