1 Introduction

The shakedown analysis is one of the most reliable and convenient methods that could assess the safety of structure under varying loadings. The mathematical problem for the evaluation of shakedown load could be formulated by using the Melan’s static theorem [1, 2] or the Koiter’s kinematic theorem [3]. It should be noted that the authors would like to consider mainly the numerical analysis of lower bound shakedown based on the Melan’s static theorem in this paper. The lower bound shakedown analysis may be led to the solution of the convex optimization problem with the linear objective function and the linear or non-linear constraints, in general. The nonlinearity of constraints depends on the type of yield function used. Since the von-Mises function is usually adopted as the yield function, the shakedown analysis reduces to the nonlinear convex optimization problem.

The nonlinear convex optimization problem for the shakedown analysis is usually very large in computational scale because it has many unknowns and constraints. In earlier studies [4,5,6,7], the sequential quadratic programming (SQP) has been combined with the methods for reducing the number of bases of self-equilibrated stress field stipulating the number of unknowns for the numerical optimization of the shakedown. But, these approaches should evaluate the reduced bases newly at every step of optimization by using the elastic analysis or the plastic incremental computation based on the finite element method (FEM). Thus, the optimization solution process should be accompanied by the finite element computation and the basis reduction process needs to be repeated with varying the load angle for the given independent loadings. Although the boundary element method and the element-free Galerkin method were combined with the basis reduction method presented in Ref. [4] for the shakedown analysis [8,9,10], the basis reduction method itself has little advances till now.

Some studies extended the basis reduction method into the kinematic hardening material. Although Stein et al. [4] proposed the overlay model, being capable of preserving the general form of perfectly-plastic material for the shakedown analysis of kinematic hardening material, its implementation was limited to the 2D problem or the specific 3D problem. Even though Heizer et al. [7] proposed a method, being applicable to any 3D shakedown problem, by using the two-surface method [11] in order to overcome this difficulty, this method should solve the shakedown problem for the perfectly-plastic material twice one after another and the basis reduction process also has to be repeated twice. More importantly, it can not be applied for the shakedown analysis of unbounded kinematic hardening material.

Also, studies for developing the effective optimization methods being capable of solving the shakedown problem without reduction of computational scale were extensively performed. Earlier studies were focused on the sequential quadratic programming (SQP), considering that the von-Mises yield function is expressed by the quadratic form of design variables [12]. Thereafter, the augmented Lagrangian type algorithm LANCELOT [13] as well as interior-point algorithm IPDCA [14,15,16] and IPOPT [17, 18] was developed, respectively. Recently, Simon and Weichert proposed a new interior-point algorithm IPSA [19, 20] for the von-Mises material, which becomes a strongly problem-oriented solution strategy, based on the IPDCA. The computational effectiveness and accuracy of IPSA were verified in refs. [21,22,23,24,25].

On the other hand, the residual stress decomposition methods (RSDM) for the shakedown analysis that does not depend on the mathematical programming has been proposed [26,27,28]. The RSDM evaluates the plastic shakedown of perfectly-plastic material by expanding the residual stress field into the Fourier series, provided that the residual stress field has periodicity under the specific loading. Coefficients in the Fourier series expansion of residual stress field will be updated iteratively by the elastic stress field previously evaluated during one cycle and the elastic–plastic solution at every iteration. Recently, the RSDM has been extended to the shakedown analysis of perfectly-plastic material with multi-dimensional loading domain subjected to the simultaneous action of several periodic loadings, and the effectiveness of its implementation procedure has been improved [29].

In the meantime, there have been extensive studies for the linear matching method (LMM), which evaluates the upper bound of shakedown factor by solving iteratively the nearly non-compressible elasticity problem with spatially-varying Young’s modulus [30]. The LMM was firstly proposed in Ref. [31, 32]. Recently, the authors presented an improved method which is capable of evaluating the upper and lower bound of limit load simultaneously, keeping the original computation framework of LMM as before [33].

In spite of extensive studies outlined above, the decrease of computational scale in the shakedown analysis still remains indispensable for the large-scale shakedown problem containing many integration points since the number of integration points used for the finite element discretization is the main factor controlling the computational scale of shakedown analysis.

In this paper, the authors would like to extend the basis reduction method of residual stress field based on the proper orthogonal decomposition that was proposed in Ref. [34] for the lower bound shakedown analysis of periodic composite material with the perfectly-plastic material into the elastic–plastic structure with the kinematic hardening.

Firstly, the authors propose a method for reducing the bases of self-equilibrated stress field by using the elastic finite element analysis of perfectly-plastic material subjected to the initial strain as well as the proper orthogonal decomposition of plastic strain field. The current method is distinguished from the previous basis reduction methods in that the optimization solution process could be performed, independently of the basis reduction. In other words, it evaluates the reduced bases for the given structure only once and does not need the elastic computation or the plastic incremental analysis for the basis estimation during the optimization solution process, unlike the previous methods. Secondly, a new solution strategy for the lower bound shakedown analysis of unbounded/bounded kinematic hardening material is proposed, based on the shakedown analysis of bounded kinematic hardening material presented in Ref. [7]. The main idea of current solution strategy lies in that the number of design variables is reduced by expressing the back stress field in terms of the linear combination of fictitious elastic stress fields at the load vertices and the shakedown load of unbounded/bounded kinematic hardening material is evaluated by solving the optimization problem only once but not twice. It should be emphasized that the combination of this solution strategy with the current basis reduction method could be led to a new method that can decrease the computational scale of lower bound shakedown analysis of kinematic hardening material significantly.

It should be noted that the basis reduction method of the residual stress field based on the proper orthogonal decomposition in the paper is essentially different from the RSDM proposed in Ref. [26,27,28,29]. In the RSDM, the residual stress field is expanded by the Fourier series under the specific periodic loading while the current method extracts the most important bases in the given loading domain among all the sets of bases of the self-equilibrated stress field.

This paper is organized as follows: The basic formulation of lower bound shakedown analysis for the perfectly-plastic material is briefly introduced in Sect. 2. Section 3 describes a new basis reduction method for the lower bound shakedown analysis of the perfectly-plastic material. The solution method of lower bound shakedown analysis for the bounded and unbounded kinematic hardening material is discussed in Sect. 4. The current method is validated through 4 numerical examples in Sect. 5, followed by a few concluding remarks in Sect. 6.

2 Formulation of lower shakedown analysis for perfectly-plastic material

Let us consider the volume \( \varOmega \) with its boundary \( \partial \varOmega = \partial \varOmega_{p} + \partial \varOmega_{u} \) where the traction is given on \( \partial \varOmega_{p} \) and the displacement is specified on \( \partial \varOmega_{u} \). For the volume \( \varOmega \), the lower bound shakedown theorem could be formulated as follows [1, 4, 5].

Under any loading history \( {\mathbf{P}}\left( t \right) \) varying within the given load domain \( \text{L} \), if there exists a safety factor \( \alpha > 1 \) and a time-independent self-equilibrated stress field \( {\varvec{\uprho}}^{*} \left( {\mathbf{x}} \right) \) such that satisfies the yield condition at any point \( {\mathbf{x}} \in \varOmega \)

$$ F\left( {\alpha {\varvec{\upsigma}}^{E} \left( {{\mathbf{x}},t} \right) + {\varvec{\uprho}}^{*} \left( {\mathbf{x}} \right)} \right) \le \sigma_{y}^{2} \left( {\mathbf{x}} \right) $$
(1)

then the structure will shake down elastically.

Here, \( F \) is the convex yield function, \( \sigma_{y} \left( {\mathbf{x}} \right) \) the yield stress, \( {\varvec{\upsigma}}^{E} \left( {{\mathbf{x}},t} \right) \) the fictitious elastic stress field of a pure elastic body subjected to \( {\mathbf{P}}\left( t \right) \) and \( {\varvec{\uprho}}^{*} \left( {\mathbf{x}} \right) \) the time-independent self-equilibrated stress field satisfying the following condition.

$$ \left. \begin{aligned} {\text{div}}{\varvec{\uprho}}^{*} \left( {\mathbf{x}} \right) = {\mathbf{0}},\quad \forall {\mathbf{x}} \in \varOmega \hfill \\ {\varvec{\uprho}}^{*} \left( {\mathbf{x}} \right) \cdot {\mathbf{n}} = {\mathbf{0}},\quad \forall {\mathbf{x}} \in \partial \varOmega_{p} \hfill \\ \end{aligned} \right\} $$
(2)

In this study, the load domain \( \text{L} \) is assumed to be the \( n \)-dimensional convex polyhedron that could be generated by the convex combination of \( NV \) load vertices \( {\mathbf{P}}\left( j \right) \) where \( NV = 2^{n} \) and \( n \) is the number of independent variable loads. Namely, we have following relation.

$$ {\mathbf{P}}\left( t \right) = \sum\limits_{j = 1}^{NV} {\lambda_{j} \left( t \right)} \, {\mathbf{P}}\left( j \right),\quad \sum\limits_{j = 1}^{NV} {\lambda_{j} } = 1 $$
(3)

Also, the fictitious elastic stress field \( {\varvec{\upsigma}}^{E} \left( {{\mathbf{x}},t} \right) \) corresponding to \( {\mathbf{P}}\left( t \right) \) could be expressed by the convex combination of fictitious elastic stress fields \( {\varvec{\upsigma}}^{E} \left( {{\mathbf{x}},j} \right) \) relevant to load vertices \( {\mathbf{P}}\left( j \right) \). Thus, one has below expression.

$$ {\varvec{\upsigma}}^{E} \left( {{\mathbf{x}},t} \right) = \sum\limits_{j = 1}^{NV} {\lambda_{j} \left( t \right)} \, {\varvec{\upsigma}}^{E} \left( {{\mathbf{x}},j} \right) $$
(4)

On the other hand, the fictitious elastic stress field \( {\varvec{\upsigma}}^{E} \left( {{\mathbf{x}},j} \right) \) and the self-equilibrated stress field \( {\varvec{\uprho}}^{*} \left( {\mathbf{x}} \right) \) could be expressed in terms of discrete values at \( NG \) Gaussian points by using the finite element interpolation, respectively. Applying the principle of virtual work into Eq. (2) and using the finite element interpolation, one can get \( NF \) simultaneous equations for the self-equilibrated stress field as follows.

$$ \sum\limits_{i = 1}^{NG} {{\mathbf{C}}_{i} \, {\varvec{\uprho}}_{i}^{*} } = \left[ {\mathbf{C}} \right]\left\{ {{\varvec{\uprho}}^{*} } \right\} = \left\{ {\mathbf{0}} \right\} $$
(5)

Here, \( NF \) is the number of degree of freedom of finite element discrete system and the matrix \( \left[ {\mathbf{C}} \right] \) could be uniquely determined, given the displacement boundary condition and the finite element discrete system. \( \left\{ {{\varvec{\uprho}}^{*} } \right\} \) denotes the vector representation of global self-equilibrated stress by using the finite element discretization. Using Eqs. (3) and (4) and considering the convexity of yield function \( F \), the shakedown analysis could be reduced into the following optimization problem [1, 4, 5].

$$ \mathop {\hbox{max} }\limits_{{\alpha ,\rho^{*} }} \, \alpha $$
$$ \left[ {\mathbf{C}} \right]\left\{ {{\varvec{\uprho}}^{*} } \right\} = \left\{ {\mathbf{0}} \right\} $$
(6a)
$$ F\left( {\alpha {\varvec{\upsigma}}_{i}^{E} \left( j \right) + {\varvec{\uprho}}_{i}^{*} } \right) \le \sigma_{y,i}^{2} \, \forall i \in \left[ {1,NG} \right], \, \forall j \in \left[ {1,NV} \right] $$
(6b)

Here, \( {\varvec{\upsigma}}_{i}^{E} \left( j \right) \) is the value of fictitious elastic stress at \( i \)-th integration point and \( j \)-th load vertex. The number of equality constraints is equal to the number of degree of freedom of the finite element system \( NF \) while the number of inequality constraints is \( NG \times NV \). The design variables consists of the self-equilibrated stress components \( \left\{ {{\varvec{\uprho}}^{*} } \right\} \) at all integration points and a shakedown load factor \( \alpha \), total number being \( NG \times NSK + 1 \), where \( NSK \) is the number of independent stress tensor components.

Solving the linear simultaneous Eq. (6a), the self-equilibrated stress \( \left\{ {{\varvec{\uprho}}^{*} } \right\} \) could be expressed in terms of the free variable vector \( \left\{ {\mathbf{y}} \right\} \) and the basis matrix \( \left[ {\mathbf{b}} \right] \) as follows.

$$ \left\{ {{\varvec{\uprho}}^{*} } \right\} = \left[ {\mathbf{b}} \right]\left\{ {\mathbf{y}} \right\} $$
(7)

The size of free variables vector \( \left\{ {\mathbf{y}} \right\} \), denoting the number of self-equilibrated stress fields, is \( NB = NG \times NSK - NF \). Finally, the optimization problem for the shakedown analysis could be led to

$$ \, \mathop {\hbox{max} }\limits_{{\alpha ,{\mathbf{y}}}} \, \alpha $$
$$ \, F\left( {\alpha {\varvec{\upsigma}}_{i}^{E} \left( j \right) + \left[ {{\mathbf{b}}_{i} } \right]\left\{ {\mathbf{y}} \right\}} \right) \le \sigma_{y,i}^{2} , { }\forall i \in \left[ {1,NG} \right], \, \forall j \in \left[ {1,NV} \right] $$
(8)

where total number of design variables is \( NB + 1 \) and \( \left[ {{\mathbf{b}}_{i} } \right] \) represents the basis matrix related to the self-equilibrated stress field \( {\varvec{\uprho}}_{i}^{*} \) at the \( i \)-th integration point.

3 Basis reduction method using proper orthogonal decomposition

Some researchers applied the proper orthogonal decomposition (so-called the Karhunen–Loeve decomposition) to the non-uniform transformation field analysis (NTFA) of nonlinear composite materials [35,36,37,38,39,40]. They represented the plastic strain field by the linear combination of previously known bases called the plastic strain modes and evaluated the evolution of plastic strain by the linear combination coefficients of bases. Bases of plastic strain field were computed by the proper orthogonal decomposition of snapshots of plastic strain field. In this study, we adopt the proper orthogonal decomposition used in the NTFA of nonlinear composite materials for the lower bound shakedown analysis of the homogeneous material.

3.1 General consideration of elastic–plastic problem

One assumes that the plastic strain field \( {\varvec{\upvarepsilon}}^{p} \left( {{\mathbf{x}} ,t} \right) \) would be expressed by the linear combination of \( M \) given bases \( {\varvec{\upmu}}_{k} \left( {\mathbf{x}} \right) \) as follows [35,36,37].

$$ {\varvec{\upvarepsilon}}^{p} \left( {{\mathbf{x}},t} \right) = \sum\limits_{k = 1}^{M} {a_{k} \left( t \right) \, {\varvec{\upmu}}_{k} } \left( {\mathbf{x}} \right) $$
(9)

Due to the incompressibility of plastic strain, bases \( {\varvec{\upmu}}_{k} \) should be incompressible, too. Thus,

$$ {\text{tr}}\left( {{\varvec{\upmu}}_{k} \left( {\mathbf{x}} \right)} \right) = 0 $$
(10)

Given the plastic strain field \( {\varvec{\upvarepsilon}}^{p} \left( {{\mathbf{x}},t} \right) \), the elastic–plastic problem could be formulated as

$$ \left. {\begin{array}{*{20}l} {{\text{div}}{\varvec{\upsigma}}\left( {{\mathbf{x}} ,t} \right) = {\mathbf{0}}} \hfill & {\forall {\mathbf{x}} \in \varOmega } \hfill \\ {{\varvec{\upsigma}}\left( {{\mathbf{x}},t} \right) = {\mathbf{L}}\left( {\mathbf{x}} \right):\left( {{\varvec{\upvarepsilon}}\left( {{\mathbf{x}},t} \right){ - }{\varvec{\upvarepsilon}}^{p} \left( {{\mathbf{x}},t} \right)} \right)} \hfill & {\forall {\mathbf{x}} \in \varOmega } \hfill \\ {{\varvec{\upsigma}}\left( {{\mathbf{x}},t} \right) \cdot {\mathbf{n}} = {\mathbf{P}}\left( t \right)} \hfill & {\forall {\mathbf{x}} \in \varOmega_{p} } \hfill \\ {{\mathbf{u}} = {\mathbf{0}}} \hfill & { \, \forall {\mathbf{x}} \in \varOmega_{u} } \hfill \\ \end{array} } \right\} $$
(11)

where \( {\mathbf{L}}\left( {\mathbf{x}} \right) \) is the elastic tensor. In convenience, a time variable will be omitted. Then, Eq. (11) may be decomposed as two elastic problems as

$$ \left. {\begin{array}{*{20}l} {{\text{div}}{\varvec{\upsigma}}^{E} \left( {\mathbf{x}} \right) = {\mathbf{0}}} \hfill & {\forall {\mathbf{x}} \in \varOmega } \hfill \\ {{\varvec{\upsigma}}^{E} \left( {\mathbf{x}} \right) = {\mathbf{L}}\left( {\mathbf{x}} \right):{\varvec{\upvarepsilon}}^{E} \left( {\mathbf{x}} \right)} \hfill & {\forall {\mathbf{x}} \in \varOmega } \hfill \\ {{\varvec{\upsigma}}^{E} \left( {\mathbf{x}} \right) \cdot {\mathbf{n}} = {\mathbf{P}}} \hfill & {\forall {\mathbf{x}} \in \varOmega_{p} } \hfill \\ {{\mathbf{u}}^{E} = {\mathbf{0}}} \hfill & {\forall {\mathbf{x}} \in \varOmega_{u} } \hfill \\ \end{array} } \right\} $$
(12a)
$$ \left. {\begin{array}{*{20}l} {{\text{div}}{\varvec{\upsigma}}^{r} \left( {\mathbf{x}} \right) = {\mathbf{0}}} \hfill & { \, \forall {\mathbf{x}} \in \varOmega } \hfill \\ {{\varvec{\upsigma}}^{r} \left( {\mathbf{x}} \right) = {\mathbf{L}}\left( {\mathbf{x}} \right):\left( {{\varvec{\upvarepsilon}}^{r} \left( {\mathbf{x}} \right) - {\varvec{\upvarepsilon}}^{p} \left( {\mathbf{x}} \right)} \right)} \hfill & {\forall {\mathbf{x}} \in \varOmega } \hfill \\ {{\varvec{\upsigma}}^{r} \left( {\mathbf{x}} \right) \cdot {\mathbf{n}} = {\mathbf{0}}} \hfill & { \, \forall {\mathbf{x}} \in \varOmega_{p} } \hfill \\ {{\mathbf{u}}^{r} = {\mathbf{0}}} \hfill & {\forall {\mathbf{x}} \in \varOmega_{u} } \hfill \\ \end{array} } \right\} $$
(12b)

where Eq. (12a) is the fictitious elastic problem and Eq. (12b) is the elastic problem that the plastic strain acts as the initial strain.

The solution of elastic–plastic problem (11) is the sum of solutions of elastic problem (12a) and (12b). Namely,

$$ {\varvec{\upsigma}}\left( {\mathbf{x}} \right) = {\varvec{\upsigma}}^{E} \left( {\mathbf{x}} \right) + {\varvec{\upsigma}}^{r} \left( {\mathbf{x}} \right),\quad {\varvec{\upvarepsilon}}\left( {\mathbf{x}} \right) = {\varvec{\upvarepsilon}}^{E} \left( {\mathbf{x}} \right) + {\varvec{\upvarepsilon}}^{r} \left( {\mathbf{x}} \right) $$
(13)

Substituting Eq. (9) into Eq. (12b) and considering the linear characteristics of problem, likewise the plastic strain field, the residual stress field \( {\varvec{\upsigma}}^{r} \left( {\mathbf{x}} \right) \) could be also expressed by the linear combination of residual stress fields \( {\mathbf{D}}_{k} \left( {\mathbf{x}} \right) \) corresponding to the bases \( {\varvec{\upmu}}_{k} \left( {\mathbf{x}} \right) \) of plastic strain as follows.

$$ {\varvec{\upsigma}}^{r} \left( {\mathbf{x}} \right) = \sum\limits_{k = 1}^{M} {a_{k} {\mathbf{D}}_{k} } \left( {\mathbf{x}} \right) $$
(14)

Here, \( {\mathbf{D}}_{k} \left( {\mathbf{x}} \right) \) is the residual stress field corresponding to \( {\varvec{\upmu}}_{k} \left( {\mathbf{x}} \right) \).

$$ \left. {\begin{array}{*{20}l} {{\text{div}}{\mathbf{D}}_{k} \left( {\mathbf{x}} \right) = {\mathbf{0}}} \hfill & {\forall {\mathbf{x}} \in \varOmega } \hfill \\ {{\mathbf{D}}_{k} \left( {\mathbf{x}} \right) = {\mathbf{L}}\left( {\mathbf{x}} \right):\left( {{\mathbf{E}}_{k} \left( {\mathbf{x}} \right) - {\varvec{\upmu}}_{k} \left( {\mathbf{x}} \right)} \right)} \hfill & {\forall {\mathbf{x}} \in \varOmega } \hfill \\ {{\mathbf{D}}_{k} \left( {\mathbf{x}} \right) \cdot {\mathbf{n}} = {\mathbf{0}}} \hfill & {\forall {\mathbf{x}} \in \varOmega_{p} } \hfill \\ {{\mathbf{u}}_{k} = {\mathbf{0}}} \hfill & {\forall {\mathbf{x}} \in \varOmega_{u} } \hfill \\ \end{array} } \right\} $$
(15)

\( {\mathbf{E}}_{k} \left( {\mathbf{x}} \right) \) is the unknown residual strain field corresponding to \( {\mathbf{D}}_{k} \left( {\mathbf{x}} \right) \).

In this study, we express the self-equilibrated stress field by the linear combination of bases as in Eq. (14) using the decomposition of plastic strain field (9).

3.2 Basis reduction by proper orthogonal decomposition

In this study, decomposition (9) is used for the reduction of bases of self-equilibrated stress field while it was adopted for the evaluation of evolution of plastic strain field \( {\varvec{\upvarepsilon}}^{p} \left( {\mathbf{x}} \right) \) by \( M \) coefficients \( a_{k} \) in the NTFA.

Firstly, snapshots of plastic strain along the chosen loading path are calculated for all points \( {\mathbf{x}} \in \varOmega \). Choice of loading path has no general rule, but it prefers to choose the monotonic loading that would approximate to the actual loading if possible [34,35,36,37,38,39,40]. For every monotonic increasing load, solutions until the plastic strain is fully developed from the beginning of plastic strain must be used to obtain snapshots of plastic strain. Thus, the number of snapshots of plastic strain can be taken as the number of increments used until the plastic strain is fully developed from the beginning of plastic strain. In Ref. [34], 40 snapshots of plastic strain were used for the loading path in the case of periodic composite materials. As will be seen in Sect. 5, 15–30 snapshots of plastic strain were used for every loading path, leading to the evaluation of sufficiently accurate results.

Once \( N \) snapshots \( {\varvec{\uptheta}}^{l} \left( {\mathbf{x}} \right) \) of plastic strain are obtained for chosen monotonic loadings, one can constitute the \( N \times N \) correlation matrix \( K_{lm} \) between these snapshots as

$$ K_{lm} = \frac{1}{V}\int_{\varOmega } {{\varvec{\uptheta}}^{l} \left( {\mathbf{x}} \right):{\varvec{\uptheta}}^{m} \left( {\mathbf{x}} \right)dV} ,\quad l,m \in \left[ {1,N} \right] $$
(16)

where \( V \) is the volume of domain \( \varOmega \). The correlation matrix \( K_{lm} \) has \( N \) real eigenvalues and eigenvectors \( {\mathbf{v}}_{l} \) because it is the weak positive symmetric matrix. The correlation matrix \( K_{lm} \) can be easily evaluated by the element integration in case of using the finite discretization.

Using N eigenvectors \( {\mathbf{v}}_{l} \) of the correlation matrix \( K_{lm} \), one can evaluate \( N \) bases \( {\varvec{\upmu}}_{k} \left( {\mathbf{x}} \right) \) of plastic strain field that are orthogonal to each other as follows

$$ {\varvec{\upmu}}_{k} \left( {\mathbf{x}} \right) = \sum\limits_{l = 1}^{N} {v_{k}^{l} \, {\varvec{\uptheta}}^{l} \left( {\mathbf{x}} \right) ,\quad k \in \left[ {1,N} \right]} $$
(17)

where \( v_{k}^{l} \) is the \( l \)-th component of \( k \)-th eigenvector \( {\mathbf{v}}_{k} \). Since the obtained \( {\varvec{\upmu}}_{k} \) are orthogonal to each other and the snapshots of plastic strain itself used in the decomposition are incompressible, bases are incompressible, too.

It is well known that information involved in N eigenvectors \( {\mathbf{v}}_{l} \) obtained by the proper orthogonal decomposition takes effect on the size of eigenvalue. This fact enables to restrict to the consideration of only few eiginvectors corresponding to some eigenvalues of large size if the eigenvalues are sorted in decreasing order, namely \( \lambda_{l} \ge \lambda_{l + 1} \). Therefore, one can choose \( M \le N \) eigenvectors satisfying following condition

$$ \left( {\sum\limits_{k = 1}^{N} {\lambda_{k} } } \right) \le \beta \, \left( {\sum\limits_{l = 1}^{M} {\lambda_{l} } } \right) $$
(18)

where \( \lambda_{l} \ge \lambda_{l + 1} \). \( \beta \) represents the share of the information that the M eigenvectors have among the total information of the eigenvectors. \( \beta = 1 \) means that all the information of N eigenvectors should be used, that is, \( M = N \). Commonly, \( \beta \) is required to take a value close to 1, and it was taken as a value of 0.9999 in Refs. [38, 39] to obtain the homogenized constitutive relation of viscoplastic composite and of viscoelastic composite, respectively. In this paper, we take \( \beta \) of 0.9999. Once \( \beta \) is specified, the minimum number M required to satisfy Eq. (18) is uniquely determined.

Finally, one has to solve the following equation similar to Eq. (12b) for obtained bases \( {\varvec{\upmu}}_{k} \) of plastic strain.

$$ \left. {\begin{array}{*{20}l} {{\text{div}}{\tilde{\varvec{\uprho }}}_{k} \left( {\mathbf{x}} \right) = {\mathbf{0}}} \hfill & {\forall {\mathbf{x}} \in \varOmega } \hfill \\ {{\tilde{\varvec{\uprho }}}_{k} \left( {\mathbf{x}} \right) = {\mathbf{L}}\left( {\mathbf{x}} \right):\left( {{\varvec{\upvarepsilon}}_{k}^{r} \left( {\mathbf{x}} \right) - {\varvec{\upmu}}_{k} \left( {\mathbf{x}} \right)} \right)} \hfill & {\forall {\mathbf{x}} \in \varOmega } \hfill \\ {{\tilde{\varvec{\uprho }}}_{k} \left( {\mathbf{x}} \right) \cdot {\mathbf{n}} = {\mathbf{0}}} \hfill & {\forall {\mathbf{x}} \in \partial \varOmega_{p} } \hfill \\ \end{array} } \right\} $$
(19)

Here, \( {\varvec{\upvarepsilon}}_{k}^{r} \left( {\mathbf{x}} \right) \) is the unknown residual strain tensor. Equation (19) can be solved by reducing into the elasticity problem having \( {\varvec{\upmu}}_{k} \) as the permanent strain [34].

The solutions \( {\tilde{\varvec{\uprho }}}_{k} \) of Eq. (19) are elements of a set of self-equilibrated stress fields satisfying Eq. (2) and

$$ {\varvec{\uprho}}\left( {\mathbf{x}} \right) = \sum\limits_{k = 1}^{M} {a_{k} \, {{\tilde{\varvec{\uprho }}}_{k}} \left( {\mathbf{x}} \right)} $$
(20)

is a subset \( \text{B} \) of self-equilibrated stress fields. And \( {\tilde{\varvec{\uprho }}}_{k} \) has the meaning of basis of \( {\varvec{\uprho}}\left( {\mathbf{x}} \right) \).

We adopt the solution \( {\tilde{\mathbf{\rho }}}_{k} \) of Eq. (19) as the reduced basis of self-equilibrated stress field. Thus, by using the reduced bases, the shakedown problem (8) can be led to the following equations.

$$ \mathop {\hbox{max} }\limits_{{\alpha ,a_{l} }} \, \alpha $$
$$ \, F\left( {\alpha {\varvec{\upsigma}}_{i}^{E} \left( j \right) + \sum\limits_{l = 1}^{M} {a_{l} \, {\boldsymbol{\tilde{\rho }}}_{l,i} } } \right) \le \sigma_{y,i}^{2} , { }\forall i \in \left[ {1,NG} \right], \, \forall j \in \left[ {1,NV} \right] $$
(21)

The number of design variables for the reduced shakedown problem (21) of perfectly plastic material is \( M + 1 \).

4 Lower bound shakedown problem for kinematic hardening material

4.1 Common solution strategy

Extending the lower bound shakedown theorem for the perfectly-plastic material into the bounded kinematic hardening material, the discrete formulation of lower bound shakedown problem may be written as [7]

$$ \mathop {\hbox{max} }\limits_{{\alpha ,{\varvec{\uprho}}^{*} ,{\varvec{\uppi}}^{ *} }} \, \alpha $$
$$ \left[ {\mathbf{C}} \right]\left\{ {{\varvec{\uprho}}^{*} } \right\} = \left\{ {\mathbf{0}} \right\} $$
(22a)
$$ F\left( {\alpha {\varvec{\upsigma}}_{i}^{E} \left( j \right) + {\varvec{\uprho}}_{i}^{*} - {\varvec{\uppi}}_{i}^{*} } \right) \le \sigma_{y,i}^{2} \, $$
(22b)
$$ F\left( {{\varvec{\uppi}}_{i}^{*} } \right) \le \left( {\sigma_{u,i} - \sigma_{y,i} } \right)^{ 2} , { }\forall i \in \left[ {1,NG} \right], \, \forall j \in \left[ {1,NV} \right] $$
(22c)

where \( {\varvec{\uppi}}^{*} \) is the back stress field and \( \sigma_{u} \) is the final yield stress. Total number of design variables is \( 2NG \times NSK - NF + 1 \) including the number of bases of self-equilibrated stress field \( NG \times NSK - NF \), the number of components of back stress at integration points \( NG \times NSK \) and a shakedown load factor \( \alpha \).

Heitzer et al. [7] developed the well-known solution strategy in order to solve the bounded kinematic hardening problem (22). In convenience, let us outline this strategy briefly.

If one would obtain the solution \( \left( {\alpha_{pp} ,{\varvec{\uprho}}_{pp} } \right) \) of shakedown problem (6) for the perfectly-plastic material, the back stress \( {\varvec{\uppi}}_{i}^{*} \) could be taken as the constant value \( {\tilde{\varvec{\pi }}}_{i} \). The constant value \( {\tilde{\varvec{\pi }}}_{i} \) is expressed as

$$ {\tilde{\varvec{\pi }}}_{i} = \frac{{\sigma_{u,i} - \sigma_{y,i} }}{{\sigma_{y,i} }}\left( {\alpha_{pp} {\varvec{\upsigma}}_{i}^{E} \left( {j^{*} } \right) + {\varvec{\uprho}}_{pp,i} } \right) $$
(23)

where \( j^{*} \) is the load vertex satisfying the equality constraint (active vertex). Then, one can solve following problem again.

$$ \mathop {\hbox{max} }\limits_{{\alpha ,{\varvec{\uprho}}^{*} }} \, \alpha $$
$$ \left[ {\mathbf{C}} \right]\left\{ {{\varvec{\uprho}}^{*} } \right\} = \left\{ {\mathbf{0}} \right\} $$
(24a)
$$ F\left( {\alpha {\varvec{\upsigma}}_{i}^{E} \left( j \right) + {\varvec{\uprho}}_{i}^{*} - {\tilde{\varvec{\pi }}}_{i} } \right) \le \sigma_{y,i}^{2} \, \forall i \in \left[ {1,NG} \right], \, \forall j \in \left[ {1,NV} \right] \, $$
(24b)

Formulation (24) is the shakedown problem for the perfectly-plastic material having the dead load \( {\tilde{\varvec{\pi }}}_{i} \).

Even though the solution strategy described above can reduce the number of unknowns by taking the back stress, unknown variable, as the deterministic constant value, it should solve the shakedown problem for the perfectly-plastic material twice one after another and furthermore, it can not be applied for the shakedown analysis of unbounded kinematic hardening material where the back stress becomes the free unknown variable.

In order to overcome this difficulty, we propose a new solution strategy for the shakedown analysis of unbounded and bounded kinematic hardening material by solving the shakedown problem of perfectly-plastic material only once.

4.2 A new solution strategy for shakedown analysis of kinematic hardening material

Let \( \text{B} \) denote the whole set of all self-equilibrated stress fields that satisfy Eq. (24a). \( {\varvec{\uprho}}_{i}^{*} \), an unknown variable of the optimization problem (24), must be an element of \( \text{B} \) from the requirement of problem itself, and \( {\varvec{\uprho}}_{i}^{*} + b \, {\varvec{\uprho}}_{pp,i} \in \text{B} \) for any constant since \( {\varvec{\uprho}}_{pp,i} \), which is a solution of perfectly-plastic shakedown analysis previously given is an element of \( \text{B} \). This means that a term related to previously given \( {\varvec{\uprho}}_{pp,i} \) in \( {\tilde{\mathbf{\pi }}}_{i} \) of Eq. (24b) does not take effect on the optimization solution, involved in the design variable \( {\varvec{\uprho}}_{i}^{*} \), and that only the meaningful term is \( \frac{{\sigma_{u,i} - \sigma_{y,i} }}{{\sigma_{y,i} }}\alpha_{pp} {\varvec{\upsigma}}_{i}^{E} \left( {j^{*} } \right) \) related to the fictitious elastic stress \( {\varvec{\upsigma}}_{i}^{E} \left( {j^{*} } \right) \) corresponding to the active load vertex \( j^{*} \). From this, without losing generality, \( {\varvec{\uprho}}_{i}^{*} - {\tilde{\varvec{\pi }}}_{i} = {\varvec{\uprho}}_{i}^{*} - \frac{{\sigma_{u,i} - \sigma_{y,i} }}{{\sigma_{y,i} }}{\varvec{\uprho}}_{pp,i} - \frac{{\sigma_{u,i} - \sigma_{y,i} }}{{\sigma_{y,i} }}\alpha_{pp} {\varvec{\upsigma}}_{i}^{E} \left( {j^{*} } \right) \) in Eq. (24b) can be replaced by \( {\varvec{\uprho}}_{i}^{*} - {\tilde{\varvec{\pi }}}_{i} = {\varvec{\uprho}}_{i}^{*} - \frac{{\sigma_{u,i} - \sigma_{y,i} }}{{\sigma_{y,i} }}\alpha_{pp} {\varvec{\upsigma}}_{i}^{E} \left( {j^{*} } \right) \). Thus, Eq. (24) can be written as follows.

$$ \mathop {\hbox{max} }\limits_{{\alpha ,{\varvec{\uprho}}^{*} }} \, \alpha $$
$$ \left[ {\mathbf{C}} \right]\left\{ {{\varvec{\uprho}}^{*} } \right\} = \left\{ {\mathbf{0}} \right\} $$
(25a)
$$ F\left( {\alpha {\varvec{\upsigma}}_{i}^{E} \left( j \right) + {\varvec{\uprho}}_{i}^{*} - {\tilde{\varvec{\pi }}}_{i} } \right) \le \sigma_{y,i}^{2} , { }\forall i \in \left[ {1,NG} \right], \, \forall j \in \left[ {1,NV} \right] $$
(25b)
$$ {\boldsymbol{\tilde{\pi }}}_{i} = \frac{{\sigma_{u,i} - \sigma_{y,i} }}{{\sigma_{y,i} }}\alpha_{pp} {\varvec{\upsigma}}_{i}^{E} \left( {j^{*} } \right) $$
(25c)

Equation (25c) implies that the back stress could be taken as the several times of elastic stress at the active load vertex. Nevertheless, since the active load vertex \( j^{*} \) and a shakedown load factor \( \alpha_{pp} \) can not be determined previously without solving the shakedown problem for the perfectly-plastic material, we approximate the back stress \( {\varvec{\uppi}}_{i}^{*} \) by the linear combination \( {\varvec{\uppi}}_{i} \) of fictitious elastic stresses \( {\varvec{\upsigma}}_{i}^{E} \left( j \right) \) at load vertices. Namely,

$$ {\varvec{\uppi}}_{i} = \sum\limits_{j = 1}^{NV} {b_{j} \, {\varvec{\upsigma}}_{i}^{E} \left( j \right)} $$
(26)

Therefore, the bounded kinematic hardening shakedown problem (22) could be reduced as follows.

$$ \mathop {\hbox{max} }\limits_{{\alpha ,{\varvec{\uprho}}_{i}^{*} ,b_{j} }} \, \alpha $$
$$ \left[ {\mathbf{C}} \right]\left\{ {{\varvec{\uprho}}^{*} } \right\} = \left\{ {\mathbf{0}} \right\} $$
(27a)
$$ F\left( {\alpha {\varvec{\upsigma}}_{i}^{E} \left( j \right) + {\varvec{\uprho}}_{i}^{*} - {\varvec{\uppi}}_{i} } \right) \le \sigma_{y,i}^{2} \, $$
(27b)
$$ F\left( {{\varvec{\uppi}}_{i} } \right) \le \left( {\sigma_{u,i} - \sigma_{y,i} } \right)^{ 2} , { }\forall i \in \left[ {1,NG} \right], \, \forall j \in \left[ {1,NV} \right] $$
(27c)
$$ {\varvec{\uppi}}_{i} = \sum\limits_{j = 1}^{NV} {b_{j} \, {\varvec{\upsigma}}_{i}^{E} \left( j \right)} $$
(27d)

Since the self-equilibrated stress field does not depend on the hardening of material, the bounded kinematic hardening shakedown problem (27) could be led to the following equation by applying the current basis reduction method for the perfectly-plastic material.

$$ \mathop {\hbox{max} }\limits_{{\alpha ,a_{l} ,b_{m} }} \, \alpha $$
$$ F\left( {\alpha {\varvec{\upsigma}}_{i}^{E} \left( j \right) + \sum\limits_{l = 1}^{M} {a_{l} \, {\tilde{\varvec{\uprho }}}_{l,i} - \sum\limits_{m = 1}^{NV} {b_{m} {\varvec{\upsigma}}_{i}^{E} \left( m \right)} } } \right) \le \sigma_{y,i}^{2} \, $$
(28a)
$$ F\left( {\sum\limits_{m = 1}^{NV} {b_{m} \, {\varvec{\upsigma}}_{i}^{E} \left( m \right)} } \right) \le \left( {\sigma_{u,i} - \sigma_{y,i} } \right)^{ 2} , { }\forall i \in \left[ {1,NG} \right], \, \forall j \in \left[ {1,NV} \right] $$
(28b)

Furthermore, the unbounded kinematic hardening shakedown problem could be obtained by ignoring the constraint (28b) in Eq. (28). Namely,

$$ \, \mathop {\hbox{max} }\limits_{{\alpha ,a_{l} ,b_{j} }} \, \alpha $$
$$ F\left( {\alpha {\varvec{\upsigma}}_{i}^{E} \left( j \right) + \sum\limits_{l = 1}^{M} {a_{l} \, {\tilde{\varvec{\uprho }}}_{l,i} - \sum\limits_{m = 1}^{NV} {b_{m} \, {\varvec{\upsigma}}_{i}^{E} \left( m \right)} } } \right) \le \sigma_{y,i}^{2} \, $$
(29)

Total number of design variables in Eqs. (28) and (29) is \( M + NV \), respectively. It should be noted that the implementation of Eqs. (28) and (29) for the bounded and unbounded kinematic hardening material is similar to the one of Eq. (21) for the perfectly-plastic material respectively since the representation form of back stress is the same as the one of the self-equilibrated stress field.

5 Numerical examples

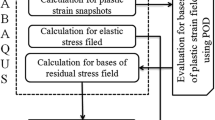
Figure 1 shows the flowchart for implementing the current method. Finite element package ABAQUS 6.14-1 is used in order to compute the snapshots \( {\varvec{\uptheta}}^{l} ,\left( {l = 1, \cdots ,N} \right) \) for the evaluation of bases of plastic strain and the fictitious elastic stress field \( {\varvec{\upsigma}}^{E} \left( {\mathbf{x}} \right) \). The bases \( {\varvec{\upmu}}_{k} \) of plastic strain can be estimated by applying the proper orthogonal decomposition described in Sect. 3 for the snapshots \( {\varvec{\uptheta}}^{l} \) of plastic strain. For each basis \( {\varvec{\upmu}}_{k} \), Eq. (19) is solved in order to compute the bases \( {\tilde{\varvec{\uprho }}}_{k} \) of self-equilibrated stress field.

Fig. 1
figure 1

Flowchart for implementing the current method

Full size image

Also, Eq. (19) for the computation of bases for the self-equilibrated stress field \( {\tilde{\varvec{\uprho }}}_{k} \) is solved by using ABAQUS user-subroutine UEXPAN and SDVINI. Details regarding the solution of Eq. (19) can be found in Ref. [34]. Finally, a shakedown load factor \( \alpha \) can be extracted by applying the SQP based on NLPQL subroutine [42].

In this paper, all the computations were done by using a personal computer with Intel(R) Core(TM) i5-4460CPU of 8192 MB RAM and 3.2 GHZ Clock.

5.1 Square plate with a hole in its center

Let us consider the case of perfectly-plastic material. As shown from Fig. 2, two tensile stresses \( P_{1} \) and \( P_{2} \) that vary independently each other are acted vertically on the sides of plate, respectively. Table 1 lists the geometric dimensions of plate.

Fig. 2
figure 2

Square plate with a hole in its center subjected to bi-axial tension

Full size image
Table 1 Dimensions of plate
Full size table

The plate is assumed to be made by Aluminum 2024-T6 whose material properties can be found from Table 2. Due to its symmetry, only a quarter of plate is considered. The finite element model uses ABAQUS 8-nodes element C3D8I. The model consists of 400 elements and 882 nodes. There exists only one element layer through the thickness. Figure 3 denotes the finite element model.

Table 2 Material properties of aluminum 2024-T6 [21]
Full size table
Fig. 3
figure 3

Finite element model of square plate

Full size image

For the elastic computation, \( P_{1} = \sigma_{y} \) and \( P_{2} = \sigma_{y} \) are used. The snapshots of plastic strain are estimated for 3 monotonic increasing loads, namely, \( P_{1} \ne 0 \wedge P_{2} = 0 \), \( P_{1} = 0 \wedge P_{2} \ne 0 \) and \( P_{1} = P_{2} \ne 0 \) while 15 snapshots for every load, thus 45 snapshots are used for the proper orthogonal decomposition, in total. For \( \beta = 0.9999 \), 13 bases of plastic strain were obtained. Time consumed for the computation of plastic strain bases by the proper orthogonal decomposition were accounted by about 1.5 s.

Table 3 lists the number of design variables for the cases with the current basis reduction and without the basis reduction, respectively. It should be emphasized that the number of bases entirely depends on the number of integration points for the case without the basis reduction while it does not depend on the number of integration points for the case with the current basis reduction.

Table 3 Comparison of design variables
Full size table

Table 4 lists the comparison of shakedown load factors computed by the current method and by Simon et al. [21] for 3 cases of \( P_{2} = P_{1} \), \( P_{2} = {{P_{1} } \mathord{\left/ {\vphantom {{P_{1} } 2}} \right. \kern-0pt} 2} \) and \( P_{ 1} = 0 \). Figure 4 compares the shakedown load domains of square plate with a hole in its center subjected to the bi-axial tension computed by the current method, Simon et al. [21] and Mouhtamid [41]. The computation time of optimization problem with reduced bases were about 4 s for the loading angle of 30 degrees.

Table 4 Comparison of shakedown load factor for the square plate with a hole in its center
Full size table
Fig. 4
figure 4

Predictions of shakedown load domain of square plate

Full size image

Form Table 4 and Fig. 4, one can confirm that the current method has a good prediction capacity.

5.2 Symmetric continuous beam receiving distributed load

Let us consider the symmetric continuous beam with unit thickness subjected to 2 independent distributed loads as shown in Fig. 5. This problem has been studied by several researchers for the case of perfectly-plastic materials [29, 43, 44]. Table 5 lists the material properties of the symmetric continuous beam. The finite element model consists of 589 C3D8I elements and 1342 nodes as shown in Fig. 6. 4 monotonic loads of \( P_{1} \ne 0 \wedge P_{2} = 0 \), \( P_{1} = 0 \wedge P_{2} \ne 0 \), \( P_{1} = P_{2} \ne 0 \) and \( P_{1} = 2P_{2} \ne 0 \) are used to evaluate snapshots of plastic strain, and 15 snapshots for every load, thus 60 snapshots are adopted for proper orthogonal decomposition. 8 bases of plastic strain are obtained for the tolerance of \( \beta = 0.9999 \). It took about 2.5 s to evaluate 8 bases of plastic strain by the proper orthogonal decomposition of 60 snapshots.

Fig. 5
figure 5

Symmetric continuous beam subjected to distributed load

Full size image
Table 5 Material properties of symmetric continuous beam
Full size table
Fig. 6
figure 6

FE mesh of symmetric continuous beam

Full size image

Table 6 compares the numerical results of shakedown load factor obtained by the current method with those by previous studies in the load domain \( P_{1} \in \left[ {1.2\;{\text{Mpa}},2\;{\text{Mpa}}} \right] \wedge P_{2} \in \left[ {0,1\;{\text{Mpa}}} \right] \). As seen from Table 6, numerical results obtained by the current method are in good agreement with those by the previous studies. The computation time for the optimization problem having 8 reduced bases was about 15 s.

Table 6 Comparison of predicted shakedown factor of symmetric continuous beam
Full size table

5.3 Plate subjected to thermo-mechanical load

Let us consider the square plate subjected to independent heating and uniformly-distributed load as in Fig. 7a. Figure 7b shows the boundary conditions and the quarter model used for the finite element analysis. There are no constraints in the thickness direction, and thickness does not affect the shakedown analysis. 300 C3D8I elements and 484 nodal points are used. Table 7 lists the material properties of the plate. Kinematic hardening is considered by \( \sigma_{u} = 1. 5\sigma_{y} \) where \( \sigma_{u} \) is the ultimate strength.

Fig. 7
figure 7

Square plate subjected to heating and tensile load and its FE models. a The geometry and boundary conditions of the plate, b FEM-model

Full size image
Table 7 Material properties of plate
Full size table

Three monotonic loads of \( \Delta T \ne 0 \wedge P = 0 \), \( \Delta T = 0 \wedge P \ne 0 \) and \( \Delta T\alpha_{T} E = P \ne 0 \) are used to evaluate snapshots of plastic strain, and 30 snapshots for every load, thus 90 snapshots are adopted for proper orthogonal decomposition. 4 bases of plastic strain are obtained for the tolerance of \( \beta = 0.9999 \). It took about 1 s to evaluate 4 bases of plastic strain by the proper orthogonal decomposition of 90 snapshots.

Since the bases having the zero value at all points \( {\mathbf{x}} \in \varOmega \) can be neglected, and the number of bases of back stress is 3 in this example, excluding zero-load vertices among 4 load vertices. Figure 8 compares numerical results of the shakedown load domain obtained by the current method with those by Mouhtamid [41]. As shown in Fig. 8, the shakedown load domains obtained by the current method are in good agreement with those by Mouhtamid [41] for the perfectly-plastic, limited kinematic hardening as well as unlimited kinematic hardening.

Fig. 8
figure 8

Comparison of predicted shakedown load domain of square plate subjected to heating and uniformly-distributed tension

Full size image

When solving the optimization problem having 4 reduced bases of residual stress field for the loading angle of 30 degrees, it took about 3 s, 9 s, and 13 s for the perfectly-plastic, unbounded and bounded kinematic hardening, respectively.

5.4 Thin pipe subjected to thermo-mechanical loading

In this example, the kinematic hardening material is considered. Let us consider the thin pipe subjected to the internal pressure \( P \) and the thermal loading \( \Delta T = T_{1} - T_{0} \) that varies independently each other, as shown from Fig. 9a. The thickness versus outer diameter ratio \( {h \mathord{\left/ {\vphantom {h R}} \right. \kern-0pt} R} \) is equal to 0.1 and the pipe is sufficiently long and its ends are opened. The pipe material is X6CrNiNb18-10 Steel. The material properties can be found from Table 8 and assumed to be independent of temperature. Moreover, we consider only the steady state, ignoring the transient state due to the thermal shock effect.

Fig. 9
figure 9

Geometry and FEM model of thin pipe. a The geometry of the thin pipe, b FEM-model

Full size image
Table 8 Thermo-mechanical properties of X6CrNiNb 18-10 steel [25]
Full size table

Figure 9b shows the finite element model used in the computation. Due to the symmetry, only a half model is considered. The finite element model uses ABAQUS 8-nodes element C3D8I. The model consists of 600 elements and 984 nodes. There exist 5 element layers through the thickness.

The snapshots of plastic strain are estimated for 2 monotonic increasing loads, namely, \( P \ne 0 \wedge \Delta T = 0 \) and \( P = 0 \wedge \Delta T \ne 0 \) while 30 snapshots for every load, thus 60 snapshots are used for the proper orthogonal decomposition, in total. For \( \beta = 0.9999 \), 6 bases of plastic strain were obtained. The time taken to determine 6 bases from 60 snapshots using the proper orthogonal decomposition was about 2 s.

For the elastic computation, analytical shakedown load \( P_{0} = 23.671\;{\text{MPa}} \) and \( \Delta T_{0} = 128.125\;{\text{K}} \) for the perfectly-plastic material are used [45]. Since the bases having the zero value at all points \( {\mathbf{x}} \in \varOmega \) can be neglected, the number of back stress is 3 in this example, excluding zero-load vertices among 4 load vertices.

Table 9 lists the number of design variables in the optimization problem of perfectly-plastic and kinematic hardening material for the cases with the current basis reduction and without the basis reduction, respectively.

Table 9 Comparison of design variables
Full size table

Figure 10 compares the shakedown load domain predicted by the current method and Moutamid [41] for the unbounded kinematic hardening material. Figure 11 shows the shakedown load domain predicted by the current method and Simon [25] for the bounded kinematic hardening material with \( \sigma_{u} = 1. 2\sigma_{y} \) and the perfectly-plastic material. Figure 12 shows the shakedown load domain predicted by the current method and Heitzer et al. [7] for the bounded kinematic hardening material with \( \sigma_{u} = 1. 3 5\sigma_{y} \).

Fig. 10
figure 10

Shakedown load domain predicted by the current method and Moutamid [41] for the unbounded kinematic hardening material

Full size image
Fig. 11
figure 11

Shakedown load domain prediction for the bounded kinematic hardening material with \( \sigma_{u} = 1. 2\sigma_{y} \) and the perfectly-plastic material

Full size image
Fig. 12
figure 12

Shakedown load domain prediction for the bounded kinematic hardening material with \( \sigma_{u} = 1. 3 5\sigma_{y} \)

Full size image

As seen from Figs. 10, 11, and 12, the current method has a good consistency with shakedown analysis results predicted by previous studies for the perfectly-plastic material, the bounded and the unbounded kinematic hardening material. When solving the optimization problem having 4 reduced bases of residual stress field for the loading angle of 30 degrees, it took about 5 s, 8 s, and 9 s for the perfectly-plastic, unbounded and bounded kinematic hardening, respectively.

6 Conclusions

In this study, we proposed a new method which can reduce the number of bases of self-equilibrated stress field significantly by using the decomposition of plastic strain field based on the proper orthogonal decomposition. This approach adopts the elastic–plastic finite element analysis under the given monotonic increasing loading, the proper orthogonal decomposition and the elastic finite element analysis with the initial strain. The evaluation of reduced bases could be performed, independently of the optimization solution process of lower bound shakedown problem. The reduced bases obtained once can be used for any load angles. This method can be used efficiently for the engineering practice requiring many integration points since the number of reduced bases does not depend on the number of integration points.

Furthermore, the authors presented a new solution strategy for the shakedown analysis of kinematic hardening material. In this strategy, the number of design variables related to the back stress is reduced to the number of load vertices by expressing the back stress with the linear combination of fictitious elastic stress fields corresponding to each load vertex in the load space for the bounded and the unbounded kinematic hardening material. Only one optimization solution process is needed for the shakedown analysis of the bounded and the unbounded kinematic hardening material. Moreover, the total number of design variables for the shakedown analysis of kinematic hardening material can be reduced significantly by the combination of basis reduction method of self-equilibrated stress field based on the proper orthogonal decomposition, leading to the substantial decrease in the computational size.