1 Introduction

Due to the outstanding designability, high strength/stiffness-to-weight ratio and excellent resistance to fatigue and corrosion, carbon fiber reinforced polymer matrix composites have been increasingly applied in various fields. Under different loading conditions, the layered and orthotropic characteristics would result in different failure modes in the composites. In general, failure modes of composites include delamination, matrix cracking, fibre breakage and fibre/matrix debonding whilst the first two modes are dominating due to the high tensile strength of the fiber. For instance, fiber breakage is generally very limited and confined to the region under and near the contact area between the impactor and composite laminates in low velocity impact of laminated composite structures [1]. To model matrix cracks and delaminations, damage mechanics and fracture mechanics were usually used [2–9]. Although there are a lot of investigations on the static response, free vibration and buckling of laminated composite structures with delaminations or matrix cracks, only a few of them consider multiple delaminations and matrix cracks [10–14].

For problems with material and geometric discontinuities, the extended finite element method (XFEM) was developed based on the conventional FEM and the concept of partition of unity [15–19]. This method was generalized to model transverse cracks and crack growth in plates and shell [20–23]. Later on, it was extended to the delamination and in-plane crack of composite structures. Remmers [24] presented a new finite element method for simulating delamination growth in thin-layered composite structures based on a solid-like shell element and the partition-of-unity property of the element shape functions. For the problem of interfacial cracks between dissimilar materials, XFEM was extended by using the orthotropic enrichment functions [25]. Hettich and Ramm [26] carried out a detailed geometric modeling of multi-phase materials and a local mechanical modeling of material interfaces and interfacial failure for multi-phase materials. The mechanical modeling of material interfaces and interfacial cracks is accomplished by XFEM without any crack tip enrichment. Nagashima and Suemasu [27] applied XFEM to stress analysis of delaminated composite plate. To model the delamination, nodes on above and below the delamination were enriched. Curiel Sosa and Karapurath [28] applied the XFEM to simulating delamination in the fibre metal laminates. Their study considered a double cantilever plate with mode I crack. Development of the orthotropic crack-tip enrichment functions for the composite materials are reported in a series of works [29–31]. Motamedi and Mohammadi [32, 33] studied the dynamic crack stability and propagation in composites based on static and dynamic orthotropic crack-tip enrichment functions. Although, remarkable progress on the application of XFEM in composite damages analysis has been achieved in the last decade, two important aspects should be improved. Firstly, existing shell elements methods enriched by XFEM can only deal with the through-thickness cracks yet many the matrix cracks are restricted to the single layers around the impact contact zone [1]. Secondly, the existing shell elements enriched by XFEM were applied to model either cracks or delaminations. No work has been reported for the typical damage pattern which include matrix cracks and delaminations simultaneously. In particular, the damage zone induced by low velocity impact contains complex three-dimensional cracks with layered characteristics. Since it is very difficult to apply XFEM directly to deal with complex three-dimensional crack, one cannot just rely on XFEM to solve this complex problem.

Recently, the Heaviside step-function was introduced into the displacement field along the thickness direction for modeling the delamination [34–39]. In those methods, the delaminations were modeled by jump discontinuous conditions across the interlaminar interfaces. Thus, the displacements on adjacent layers remain independent, allowing for separation and slippage.

Therefore, if the transverse cracks are perpendicular to each layer, one can convert the complex three-dimensional damage with layered characteristics to two two-dimensional cracks (delaminations and transverse cracks) by using an appropriate displacement assumption along thickness direction. Hence, the multiple delaminations can be simulated by the jump discontinuous functions in the thickness direction and the in-plane transverse cracks inside each ply can be modeled independently by XFEM.

The displacement field employed in Layerwise theories can be used to calculate the three-dimensional stresses and strains of each mathematical layer. Particularly, the finite element model of the displacement-based full layerwise theory of Reddy is equivalent to the displacement-based 3D continuum finite element model [40]. Thus, it would be suitable to simulate the complex three-dimensional crack with layered characteristics by combining with XFEM. In our previous work [41], an extended layerwise method (XLWM) was developed by using the layerwise theory and XFEM for laminated composite beams with multiple delaminations and transverse cracks. In the displacement field of XLWM, the nodes in the thickness direction are located at the mid-surface of each layer, top surface and bottom surface of whole composite beams. The displacement field contains the linear Lagrange interpolation functions, the one-dimensional weak discontinuous function and strong discontinuous function. The strong and weak discontinuous functions are applied to model the displacement discontinuity induced by delaminations and the strain discontinuity induced by the interlaminar interface, respectively. Because the nodes in the thickness direction are located at the mid-surface of each layer, the XLWM can be conveniently employed to deal with the transverse cracks.

Fig. 1
figure 1

A N-ply composite plates with multiple delaminations

Full size image

In the present work, the XLWM is extended to the laminated composite plates for static responses analysis, SIF calculation and transverse crack arbitrary growth prediction. The rest of this paper is organized as follows. In the next section, the displacement field for the laminated composite plates is introduced. The in-plane displacement approximation used to model the laminated composite plate with multiple delaminations and/or transverse cracks as well as the level set function and the crack-tip enrichment functions used to represent the transverse cracks are described. In Sects. 3 and 4, the Hamilton’s principle, Euler–Lagrange equations and constitutive equations are established for the XLWM of laminated composite plates. The governing equations for laminated plates with multiple delaminations and/or transverse cracks are developed in Sect. 5. The SIF calculation method and transverse crack propagation criterion are presented in Sect. 6. As the transverse crack grows, some nodes would be very close to the crack surface. In this light, a local remeshing scheme will be presented in Sect. 7. In Sect. 8, several numerical examples for demonstrating the capability of the XLWM in static responses analysis, SIF calculation and crack arbitrary growth predication are presented. Conclusions are drawn in Sect. 9.

2 Displacements field and in-plane displacements discretization

2.1 Displacements field

In our previous work [41], in order to model the displacement discontinuity of delaminations based on the strong discontinuous functions, nodes along the thickness direction are placed at the top surface, bottom surface and mid-surface of each layer. This node distribution is also necessary for the simulation of transverse cracks. However, the weak discontinuous function is needed in this displacement field to model the strain discontinuity resulted from the interlaminar interfaces.

Fig. 2
figure 2

Shape functions in the displacement field along the thickness direction. a \(\phi _{k}\); b \(\varTheta _{k}=\phi _{k}(z)\chi _{k}(z)\) ; c \(\varXi _{k}=\phi _{k}(z)H_{k}(z)\)

Full size image

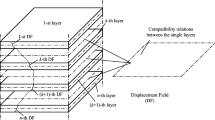
For plate with multiple delaminations, the displacements field is similar to that in our previous work [41], see Fig. 1. In the Figure, \(h_{k}\) is the thickness of the k-th layer and \(z_{k}\) is the thickness coordinate of the interface between kth layer and \((k-1)\)th layer, the numbers on the left side denote the nodes along the thickness direction, the numbers on the right side denote the interfaces between the N layers in the plate.

The present layerwise concept is very general in the sense that the number of mathematical layers can be greater than, equal to or less than the number of the material layers. Within a mathematical layer, the material is homogeneous. Adjacent material layers of the same fiber angle may be more efficiently modelled as a single mathematical layer. On the other hand, a material layer can be modelled by multiple mathematical layers for higher resolution, if necessary. Figure 1 shows that the numbers of the nodal freedoms and the nodeless freedoms for interfaces are \(N+2\) and N, respectively.

The displacements at point (x, y, z) in the composite laminated plate with multiple delaminations can be expressed as

$$\begin{aligned} u_{\alpha }(x,y,z,t)= & {} \sum _{k=1}^{N+2}\phi _{k}(z)u_{\alpha ik}(x,y,t)\nonumber \\&+\sum _{k=1}^{N_{D}}\varXi _{k}(z)u_{\alpha lk}(x,y,t)\nonumber \\&+\sum _{k=2}^{N+1}\varTheta _{k}(z)u_{\alpha rk}(x,y,t) \end{aligned}$$
(1)

where \(N_{D}\) is the number of nodes to be enriched for modelling the delaminations; \(\alpha =1,\,2,\,3\) denotes the components in the x, y and z directions; \(u_{\alpha ik}, u_{\alpha lk}\) and \(u_{\alpha rk}\) are the nodal freedom, the additional nodal freedom to model displacements discontinuity induced by delaminations and the additional nodal freedom to model strains discontinuity induced by interface between the layers, respectively; the subscripts i, l and r denote the standard nodal freedom, the additional nodal freedom for delaminations and the additional nodal freedom for interfaces, respectively; \(\phi _{k}\) is the linear Lagrange interpolation functions along the thickness direction of the laminated composite plate, see Fig. 2a; \(\varTheta _{k}=\phi _{k}(z)\chi _{k}(z)\) is the weak discontinuous shape function used to model the strains discontinuity in the interface between the layers (see Fig. 2b) and \(\chi _{k}(z)\) is the one-dimensional signed distance function; \(\varXi _{k}=\phi _{k}(z)H_{k}(z)\) is the shape function used to model delaminations and \(H_{k}(z)\) is the one-dimensional Heaviside function, see Fig. 2c. The detailed expressions of \(\phi _{k}, \varTheta _{k}\) and \(\varXi _{k}\) can be found in the Appendix A. Therefore, in the proposed XLWM, the nodal freedoms are located at the top surface, bottom surface and mid-surface of each mathematical layer. The additional nodal freedoms to model strains discontinuity are located at the mid-surface of each mathematical layer. The additional nodal freedoms to model displacements discontinuity induced by delaminations are located at the mid-surface of the mathematical layers nearby the delamination. The location of the freedoms also can be found in Fig. 1.

Let

$$\begin{aligned} \varPhi _{ik}=\phi _{k}(z),\quad \varPhi _{lk}=\varXi _{k}(z),\quad \varPhi _{rk}=\varTheta _{k}(z) \end{aligned}$$
(2)

Using the Einstein summation convention for repeated indexes, Eq. (1) can be expressed as

$$\begin{aligned} u_{\alpha }(x,y,z,t)=\varPhi _{\zeta k}(z)u_{\alpha \zeta k}(x,y,t),\quad \zeta =i,\, l,\, r \end{aligned}$$
(3)

where \(k\in [1,N+2], [1,N_{D}]\) and \([2,N+1]\) for \(\zeta =i, l\) and r, respectively.

If there is no delaminations, the displacement field can be simplified to

$$\begin{aligned} u_{\alpha }(x,y,z,t)=\varPhi _{\zeta k}(z)u_{\alpha \zeta k}(x,y,t),\quad \zeta =i,\, r \end{aligned}$$
(4)

In the displacement-based full layerwise theory of Reddy [40], the layerwise continuous functions, such as the one-dimensional Lagrange interpolation functions along the thickness direction, are used to develop the displacement field of the laminated composite structures. In the present displacement field, the nodes along the thickness direction are located at the upper surface and bottom surface and mid-surfaces of each layer. The displacement components are continuous along the thickness direction but the derivatives of the displacements (strains) are discontinuous at the interfaces. Therefore, the displacement field present here is an improvement and extension to the Reddy’s theory.

2.2 In-plane displacements discretization

The basic idea of the XLWM is to convert a complex 3D fracture problem to two 2D fracture problem (two 1D fracture problem for composite beams [41]). For the laminated composite plate with multiple delaminations and transverse cracks, the nodal displacements (\(u_{\alpha ik}\)) and the addition freedoms (\(u_{\alpha lk}, u_{\alpha rk}\)) are expressed over each element as a linear combination of the Lagrange interpolation, the discontinuous enrichment and the crack-tip enrichment functions as

$$\begin{aligned} u_{\alpha \zeta k}(x,y,t)= & {} \psi _{m}(x,y)\tilde{U}_{\alpha \zeta km}(t)+\varLambda _{s}(x,y)\bar{U}_{\alpha \zeta ks}(t)\nonumber \\&+\,\varPi _{h_{b}}(x,y)\hat{U}_{\alpha \zeta kh_{b}}(t) \end{aligned}$$
(5)

where \(m=1,\ldots ,N_{E}\); and \(N_{E}\) is the number of the in-plane finite element nodes; \(s=1,\ldots ,N_{E}^{P}\), and \(N_{E}^{P}\) is the number of in-plane nodes which are enriched by the discontinuity of in-plane transverse cracks; \(h_{b}=1,\ldots ,N_{E}^{Q}\); and \(N_{E}^{Q}\) is the number of in-plane nodes which are enriched by the in-plane transverse crack tips; \(b=1,\ldots ,N^{F}\); and \(N^{F}\) is the number of the crack-tip enrichment functions; \(\tilde{U}_{\alpha \zeta km}\) is the freedoms of the standard nodes; \(\bar{U}_{\alpha \zeta ks}\) is the addition freedoms introduced by the transverse cracks; and \(\hat{U}_{\alpha \zeta kh_{b}}\) is the addition freedoms introduced by the transverse crack tips; \(\psi _{m}(x,y)\) is the two-dimensional Lagrange interpolation function; \(\varLambda _{s}=\psi _{s}(x,y)F^{H}_{s}(x,y)\) is the shape function used to model in-plane cracks and \(F^{H}_{s}(x,y)\) is the Heaviside function; \(\varPi _{h_{b}}=\psi _{h}(x,y)F_{h_{b}}(x,y)\) is the shape function used to model transverse crack tips and the enrichment function \(F_{h_{b}}(x,y)\) will be introduced in Sect. 2.4.

Because of the nodes along the thickness direction are located at the mid-surface of each ply, the tip of mathematic transverse crack is located at the mid-surface, instead of the interface, as shown in our previous investigations [41]. To truly simulate the tip of real crack, we had presented a scheme based on the concept of sublaminates.

For the laminated composite plate without transverse cracks, the nodal displacements and the addition freedoms in the XLWM can be expressed over each element as a linear combination of the Lagrange interpolation function \(\psi _{m}\) as follows

$$\begin{aligned} u_{\alpha \zeta k}(x,y,t)=\psi _{m}(x,y)\tilde{U}_{\alpha \zeta km}(t). \end{aligned}$$
(6)

2.3 Level set representation of cracks

The level set method (LSM) [42, 43], which is a numerical technique for tracking the motion of discontinuous interfaces, is employed here to track the interfaces resulted from the transverse cracks. The crack faces are represented by level curve \(\psi (\varvec{x},t)=0\). The crack tips are represented by the intersection of \(\psi (\varvec{x},t)=0\) and \(\phi _{i}(\varvec{x},t)=0\) where \(\phi _{i}\) are also level set functions, and each i denotes a different crack tip.

The initial conditions of the level curve \(\psi \) can be defined as the signed-distance to the crack face

$$\begin{aligned} \psi (\varvec{x},t=0)=\pm \underset{\varvec{x}_{\gamma } \in \gamma (t)}{\mathrm {min}}\left\| \varvec{x}-\varvec{x}_{\gamma }\right\| \end{aligned}$$
(7)

where \(\gamma (t)\) represents the crack face.

Similarly, the the level curve \(\phi _{i}\) can be constructed by the signed-distance of the line orthogonal to crack at its tips, namely

$$\begin{aligned} \phi _{i}(\varvec{x},t)=\left( \varvec{x}- \varvec{x}_{i}\right) \cdot \hat{\varvec{t}} \end{aligned}$$
(8)

where \(\varvec{x}_{i}\) is the location of the ith crack tip. \(\hat{\varvec{t}}\) is the unit vector tangent to the crack at its tip.

Therefore, the crack can be represented by multiple level set functions as

$$\begin{aligned} \left\{ \varvec{x}:\psi (\varvec{x},t)=0\,\mathrm {and}\,\phi _{i}(\varvec{x},t)\le 0\right\} \end{aligned}$$
(9)

where the level sets \(\psi =0\) and \(\phi _{i}=0\) are forced to be orthogonal at their intersection point.

2.4 Enrichment functions

The enrichment function used to model in-plane cracks is constructed by the Heaviside function

$$\begin{aligned} F^{H}(\varvec{x})=\left\{ \begin{array}{ll} 1, &{} \quad \psi (\varvec{x},t)>0\\ -1, &{} \quad \psi (\varvec{x},t)<0 \end{array}\right. \end{aligned}$$
(10)

All laminae are orthotropic, so the near-tip functions \(F_{h_{b}}\) must span from the displacement fields derived for orthotropic materials. According to Asadpoure and Mohammadi [29, 31], \(F_{h_{b}}\) can be taken as [29–31, 44]

$$\begin{aligned} \begin{array}{ll} F_{1}=\sqrt{r}\cos \displaystyle \frac{\theta _{1}}{2}\sqrt{g_{1}\left( \theta \right) }, &{}\quad F_{2}=\sqrt{r}\cos {\displaystyle \frac{\theta _{2}}{2}\sqrt{g_{2}\left( \theta \right) },}\\ F_{3}=\sqrt{r}\sin {\displaystyle \frac{\theta _{1}}{2}\sqrt{g_{1}\left( \theta \right) },} &{} \quad F_{4}=\sqrt{r}\sin {\displaystyle \frac{\theta _{2}}{2}\sqrt{g_{2}\left( \theta \right) }} \end{array} \end{aligned}$$
(11)

where

$$\begin{aligned} \begin{aligned} g_{j}\left( \theta \right)&\!=\!\sqrt{\left( \cos \theta \!+\!s_{jx}\sin \theta \right) ^{2}\!+\!\left( s_{jy}\sin \theta \right) }\\ \theta _{j}&=\arctan \left( \frac{s_{jy}\sin \theta }{\cos \theta +s_{jx}\sin \theta }\right) \end{aligned} ,\quad j\!=\!1,2 \end{aligned}$$
(12)

\(s_{jx}\) and \(s_{jy}\) are the real and imaginary components of the roots of the characteristic equation derived by substituting the Airy stress function into the compatibility equation of anisotropic solids free of body force [44].

For the isotropic plates, \(F_{h_{b}}\) should be taken as

$$\begin{aligned} \begin{array}{ll} F_{1}=\sqrt{r}\cos \displaystyle \frac{\theta }{2}, &{}\quad F_{2}=\sqrt{r}\sin \theta \cos \displaystyle \frac{\theta }{2},\\ F_{3}=\sqrt{r}\sin {\displaystyle \frac{\theta }{2},} &{}\quad F_{4}=\sqrt{r}\sin \theta \sin {\displaystyle \frac{\theta }{2}}. \end{array} \end{aligned}$$
(13)

3 Hamilton’s principle and Euler–Lagrange equations

Substituting the displacements in Eq. (3) into the strain-displacement relationship results in

$$\begin{aligned} \varepsilon _{xx}= & {} \varPhi _{\zeta k}u_{1\zeta k,x} \quad \varepsilon _{xy}=\varPhi _{\zeta k}u_{1\zeta k,y}+\varPhi _{\zeta k}u_{2\zeta k,x}\nonumber \\ \varepsilon _{yy}= & {} \varPhi _{\zeta k}u_{2\zeta k,y} \quad \varepsilon _{yz}=\varPhi _{\zeta k,z}u_{2\zeta k}+\varPhi _{\zeta k}u_{3\zeta k,y}\nonumber \\ \varepsilon _{zz}= & {} \varPhi _{\zeta k,z}u_{3\zeta k} \quad \varepsilon _{xz}=\varPhi _{\zeta k,z}u_{1\zeta k}+\varPhi _{\zeta k}u_{3\zeta k,x} \end{aligned}$$
(14)

Thus, the virtual strain energy is given by

$$\begin{aligned} \delta U= & {} \int _{\varOmega }\int _{-H/2}^{H/2}\left( \sigma _{xx}\delta \varepsilon _{xx} +\sigma _{yy}\delta \varepsilon _{yy}+\sigma _{zz}\delta \varepsilon _{zz}\right. \nonumber \\&\left. +\,\sigma _{xy}\delta \varepsilon _{xy}+\sigma _{yz}\delta \varepsilon _{yz} +\sigma _{xz}\delta \varepsilon _{xz}\right) \mathrm {d}z\mathrm {d}x\mathrm {d}y\\= & {} \int _{\varOmega }\left( N_{\zeta k}^{x}\delta u_{1\zeta k,x}+N_{\zeta k}^{xy}\delta u_{1\zeta k,y} +Q_{\zeta k}^{xz}\delta u_{1\zeta k}\right. \nonumber \\&\left. +\,N_{\zeta k}^{y}\delta u_{2\zeta k,y}+N_{\zeta k}^{xy}\delta u_{2\zeta k,x}\right. \nonumber \\&\left. +\, Q_{\zeta k}^{yz}\delta u_{2\zeta k}+N_{\zeta k}^{yz}\delta u_{3\zeta k,y}+N_{\zeta k}^{xz}\delta u_{3\zeta k,x}\right. \nonumber \\&\left. +\,Q_{\zeta k}^{zz}\delta u_{3\zeta k}\right) \mathrm {d}x\mathrm {d}y \end{aligned}$$
(15)

where the stress resultants are

$$\begin{aligned} \begin{aligned}&\left( N_{\zeta k}^{x},N_{\zeta k}^{y},N_{\zeta k}^{xy},N_{\zeta k}^{yz},N_{\zeta k}^{xz}\right) \\&\quad =\int _{-H/2}^{H/2}\left( \sigma _{xx},\sigma _{yy},\sigma _{xy},\sigma _{yz},\sigma _{xz}\right) \varPhi _{\zeta k}\mathrm {d}z,\\&\left( Q_{\zeta k}^{zz},Q_{\zeta k}^{yz},Q_{\zeta k}^{xz}\right) \\&\quad =\int _{-H/2}^{H/2}\left( \sigma _{zz},\sigma _{yz},\sigma _{xz}\right) \varPhi _{\zeta k,z}\mathrm {d}z \end{aligned} \end{aligned}$$
(16)

The virtual work done by the external forces is given by

$$\begin{aligned} \delta W= & {} \int _{\varOmega }\left[ q_{b}(x,y,t)\delta u_{3}\left( x,y,-\displaystyle \frac{H}{2},t\right) \right. \nonumber \\&\left. +\,q_{t}(x,y,t)\delta u_{3}\left( x,y,\displaystyle \frac{H}{2},t\right) \right] \mathrm {d}x\mathrm {d}y\nonumber \\&+\,\int _{\varGamma }\int _{-H/2}^{H/2}\left( \bar{\sigma }_{nn}\delta u_{n}+\,\bar{\sigma }_{ns}\delta u_{s}+\bar{\sigma }_{nz}\delta u_{3}\right) \mathrm {d}z\mathrm {d}\varGamma \nonumber \\= & {} \int _{\varOmega }\left( q_{b}\delta u_{3}^{N+2}+q_{t}\delta u_{3}^{1}\right) \mathrm {d}x\mathrm {d}y\nonumber \\&+\, \int _{\varGamma }\left( \bar{N}_{\zeta k}^{nn}\delta u_{1\zeta k}^{n}+\bar{N}_{\zeta k}^{ns}\delta u_{1\zeta k}^{s}+\bar{Q}_{\zeta k}^{n}\delta u_{3\zeta k}\right) \mathrm {d}\varGamma \nonumber \end{aligned}$$
(17)

where \(q_{b}\) and \(q_{t}\) are the distributed force at the bottom surface (\(z=-H/2\)) and top surface (\(z=H/2\)) of the laminated plate, respectively; H is the thickness of the composite laminated plates. \(\bar{\sigma }_{nn}, \bar{\sigma }_{ns}\) and \(\bar{\sigma }_{nz}\) are the stresses at the boundary \(\varGamma \). Moreover,

$$\begin{aligned} \begin{array}{l} \bar{N}_{\zeta k}^{nn}=\displaystyle \int _{-H/2}^{H/2}\bar{\sigma }_{nn}\phi _{\zeta k}\mathrm {d}z,\\ \bar{N}_{\zeta k}^{ns}=\displaystyle \int _{-H/2}^{H/2}\bar{\sigma }_{ns}\phi _{\zeta k}\mathrm {d}z,\\ \bar{Q}_{\zeta k}^{n}=\displaystyle \int _{-H/2}^{H/2}\bar{\sigma }_{nz}\phi _{\zeta k}\mathrm {d}z \end{array} \end{aligned}$$
(18)

are the boundary stress resultants and

$$\begin{aligned} u_{1\zeta k}^{n}= & {} u_{1\zeta k}n_{x}+u_{2\zeta k}n_{y}\nonumber \\ u_{1\zeta k}^{s}= & {} -u_{1\zeta k}n_{y}+u_{2\zeta k}n_{x} \end{aligned}$$
(19)

are the normal and tangential displacements at boundary.

The virtual kinetic energy is given by

$$\begin{aligned} \begin{aligned} \delta M&= \int _{\varOmega }\int _{-H/2}^{H/2}\rho _{0}\left( \dot{u}_{1}\delta \dot{u}_{1}+\dot{u}_{2}\delta \dot{u}_{2}+\dot{u}_{3}\delta \dot{u}_{3}\right) \mathrm {d}z\mathrm {d}x\mathrm {d}y\\&= \int _{\varOmega }\left( I_{\zeta \eta ke}\dot{u}_{1\eta e}\delta \dot{u}_{1\zeta k}+I_{\zeta \eta ke}\dot{u}_{2\eta e}\delta \dot{u}_{2\zeta k}\right. \\&\left. \quad +\,I_{\zeta \eta ke}\dot{u}_{3\eta e}\delta \dot{u}_{3\zeta k}\right) \mathrm {d}x\mathrm {d}y \end{aligned} \end{aligned}$$
(20)

where

$$\begin{aligned} I_{\zeta \eta ke}=\int _{-H/2}^{H/2}\rho _{0}\varPhi _{\zeta k}\varPhi _{\eta e}\mathrm {d}z \end{aligned}$$
(21)

Substituting Eqs. (16), (18) and (20) into the Hamilton’s principle

$$\begin{aligned} \int _{0}^{T}(\delta U-\delta W-\delta M)dt=0 \end{aligned}$$
(22)

and integrating by parts lead to the following Euler–Lagrange equations

$$\begin{aligned} \begin{aligned} \delta u_{1\zeta k}:&N_{\zeta k,x}^{x}+N_{\zeta k,y}^{xy}-Q_{\zeta k}^{xz}=I_{\zeta \eta ke}\ddot{u}_{1\eta e}\\ \delta u_{2\zeta k}:&N_{\zeta k,y}^{y}+N_{\zeta k,x}^{xy}-Q_{\zeta k}^{yz}=I_{\zeta \eta ke}\ddot{u}_{2\eta e}\\ \delta u_{3\zeta k}:&N_{\zeta k,y}^{yz}+N_{\zeta k,x}^{xz}-Q_{\zeta k}^{zz}+q_{b}\delta _{k}^{N+2}+q_{t}\delta _{k}^{1}=I_{\zeta \eta ke}\ddot{u}_{3\eta e} \end{aligned} \end{aligned}$$
(23)

with the natural boundary conditions

$$\begin{aligned}&\delta u_{1\zeta k}:\, N_{\zeta k}^{nn}-\tilde{N}_{\zeta k}^{nn}=0\nonumber \\&\delta u_{2\zeta k}:\, N_{\zeta k}^{ns}-\tilde{N}_{\zeta k}^{ns}=0\nonumber \\&\delta u_{3\zeta k}:\, Q_{\zeta k}^{n}-\bar{Q}_{\zeta k}^{n}=0 \end{aligned}$$
(24)

In Eq. (23), \(\delta _{k}^{0}\) and \(\delta _{k}^{N+1}\) are the Kronecker delta and

$$\begin{aligned} N_{\zeta k}^{nn}=N_{\zeta k}^{x}n_{x}+N_{\zeta k}^{xy}n_{y}\nonumber \\ N_{\zeta k}^{ns}=N_{\zeta k}^{y}n_{y}+N_{\zeta k}^{xy}n_{x}\nonumber \\ Q_{\zeta k}^{n}=N_{\zeta k}^{yz}n_{y}+N_{\zeta k}^{xz}n_{x}\nonumber \\ \tilde{N}_{\zeta k}^{nn}=\bar{N}_{\zeta k}^{nn}n_{x}-\bar{N}_{\zeta k}^{ns}n_{y}\nonumber \\ \tilde{N}_{\zeta k}^{ns}=\bar{N}_{\zeta k}^{nn}n_{y}+\bar{N}_{\zeta k}^{ns}n_{x}. \end{aligned}$$
(25)

4 Constitutive equations

The constitutive law of the \(\mu \)th layer in the composite laminate with respect to the global \(x-y-z\) coordinate system is

$$\begin{aligned} \left\{ \begin{array}{c} \sigma _{xx}\\ \sigma _{yy}\\ \sigma _{zz}\\ \sigma _{yz}\\ \sigma _{xz}\\ \sigma _{xy} \end{array}\right\} ^{(\mu )}\!\!=\!\left[ \begin{array}{cccccc} C_{11} &{} C_{12} &{} C_{13} &{} 0 &{} 0 &{} C_{16}\\ C_{12} &{} C_{22} &{} C_{23} &{} 0 &{} 0 &{} C_{26}\\ C_{13} &{} C_{23} &{} C_{33} &{} 0 &{} 0 &{} C_{36}\\ 0 &{} 0 &{} 0 &{} C_{44} &{} C_{45} &{} 0\\ 0 &{} 0 &{} 0 &{} C_{45} &{} C_{55} &{} 0\\ C_{16} &{} C_{26} &{} C_{36} &{} 0 &{} 0 &{} C_{66} \end{array}\right] ^{(\mu )}\left\{ \begin{array}{c} \varepsilon _{xx}\\ \varepsilon _{yy}\\ \varepsilon _{zz}\\ \varepsilon _{yz}\\ \varepsilon _{xz}\\ \varepsilon _{xy} \end{array}\right\} ^{(\mu )}\nonumber \\ \end{aligned}$$
(26)

Invoking the constitutive equation in Eq. (26), the force resultants in Eq. (17) can be expressed in terms of the displacements as

$$\begin{aligned} \begin{aligned}&\left( N_{\zeta k}^{x},\, N_{\zeta k}^{y},\, Q_{\zeta }^{zz},\, N_{\zeta k}^{xy}\right) \\&\quad = \left( A_{11\zeta \eta ke}^{1},\, A_{12\zeta \eta ke}^{1},\, A_{13\zeta \eta ke}^{3},\, A_{16\zeta \eta ke}^{1}\right) u_{1\eta e,x}\\&\qquad +\left( A_{16\zeta \eta ke}^{1},\, A_{26\zeta \eta ke}^{1},\, A_{36\zeta \eta ke}^{3},\, A_{66\zeta \eta ke}^{1}\right) \left( u_{1\eta e,y}+u_{2\eta e,x}\right) \\&\qquad +\left( A_{12\zeta \eta ke}^{1},\, A_{22\zeta \eta ke}^{1},\, A_{23\zeta \eta ke}^{3},\, A_{26\zeta \eta ke}^{1}\right) u_{2\eta e,y}\\&\qquad +\left( A_{13\zeta \eta ke}^{2},\, A_{23\zeta \eta ke}^{2},\, A_{33\zeta \eta ke}^{4},\, A_{36\zeta \eta ke}^{2}\right) u_{3\eta e}\\&\left( N_{\zeta k}^{yz},\, Q_{\zeta k}^{yz},\, N_{\zeta k}^{xz},\, Q_{\zeta k}^{xz}\right) \\&\quad = \left( A_{45\zeta \eta ke}^{2},A_{45\zeta \eta ke}^{4},A_{55\zeta \eta ke}^{2},A_{55\zeta \eta ke}^{4}\right) u_{1\eta e}\\&\qquad +\left( A_{44\zeta \eta ke}^{2},A_{44\zeta \eta ke}^{4},A_{45\zeta \eta ke}^{2},A_{45\zeta \eta ke}^{4}\right) u_{2\eta e}\\&\qquad +\left( A_{45\zeta \eta ke}^{1},A_{45\zeta \eta ke}^{3},A_{55\zeta \eta ke}^{1},A_{55\zeta \eta ke}^{3}\right) u_{3\eta e,x}\\&\qquad +\left( A_{44\zeta \eta ke}^{1},A_{44\zeta \eta ke}^{3},A_{45\zeta \eta ke}^{1},A_{45\zeta \eta ke}^{3}\right) u_{3\eta e,y} \end{aligned} \end{aligned}$$
(27)

where the laminate stiffness coefficients \(A_{pq\zeta \eta ke}^{1},\, A_{pq\zeta \eta ke}^{2}, A_{pq\zeta \eta ke}^{3},\, A_{pq\zeta \eta ke}^{4}\) are given in terms of modified elastic constants and the through-thickness interpolation polynomials as

$$\begin{aligned} \begin{aligned} A_{pq\zeta \eta ke}^{1}&=\int _{-H/2}^{H/2}\varPhi _{\zeta k}C^{(\mu )}_{pq}\varPhi _{\eta e}\mathrm {d}z,\\ A_{pq\zeta \eta ke}^{2}&=\int _{-H/2}^{H/2}\varPhi _{\zeta k,z}C^{(\mu )}_{pq}\varPhi _{\eta e}\mathrm {d}z,\\ A_{pq\zeta \eta ke}^{3}&=\int _{-H/2}^{H/2}\varPhi _{\zeta k}C^{(\mu )}_{pq}\varPhi _{\eta e,z}\mathrm {d}z,\\ A_{pq\zeta \eta ke}^{4}&=\int _{-H/2}^{H/2}\varPhi _{\zeta k,z}C^{(\mu )}_{pq}\varPhi _{\eta e,z}\mathrm {d}z. \end{aligned} \end{aligned}$$
(28)

5 Finite element formulation

5.1 Finite element formulation for laminated plates with multiple delaminations

Substituting Eq. (6) into Eq. (22), the finite element formulation for the static laminated composite plate with multiple delaminations can be expressed as

$$\begin{aligned} K_{\alpha \beta \zeta \eta kemn}U_{\beta \eta en}=F_{\alpha \zeta km} \end{aligned}$$
(29)

where \(m,n=1,\ldots ,N_{E}\); The contraction of tensor is used inhere, for example, the index pairs \(\alpha , \beta \) in matrix \(\varvec{K}\) contract with the index \(\beta \), so the index \(\alpha \) remain of vector \(\varvec{F}; K_{\alpha \beta \zeta \eta kemn}\) is the element stiffness matrix given by

$$\begin{aligned} K_{11\zeta \eta kemn}= & {} \psi _{m,x}A_{11\zeta \eta ke}^{1}\psi _{n,x}+\psi _{m,x}A_{16\zeta \eta ke}^{1}\psi _{n,y}\\&+\,\psi _{m,y}A_{16\zeta \eta ke}^{1}\psi _{n,x}\\&+\,\psi _{m,y}A_{66\zeta \eta ke}^{1}\psi _{n,y}+\psi _{m}A_{55\zeta \eta ke}^{4}\psi _{n}\\ K_{12\zeta \eta kemn}= & {} \psi _{m,x}A_{12\zeta \eta ke}^{1}\psi _{n,y}+\psi _{m,x}A_{16\zeta \eta ke}^{1}\psi _{n,x}\\&+\,\psi _{m,y}A_{26\zeta \eta ke}^{1}\psi _{n,y}\\&+\,\psi _{m,y}A_{66\zeta \eta ke}^{1}\psi _{n,x}+\psi _{m}A_{45\zeta \eta ke}^{4}\psi _{n}\\ K_{13\zeta \eta kemn}= & {} \psi _{m,x}A_{13\zeta \eta ke}^{2}\psi _{n}+\psi _{m,y}A_{36\zeta \eta ke}^{2}\psi _{n}\\&+\,\psi _{m}A_{45\zeta \eta ke}^{3}\psi _{n,y} +\,\psi _{m}A_{55\zeta \eta ke}^{3}\psi _{n,x}\\ K_{21\zeta \eta kemn}= & {} \psi _{m,y}A_{12\zeta \eta ke}^{1}\psi _{n,x}+\psi _{m,x}A_{16\zeta \eta ke}^{1}\psi _{n,x}\\&+\,\psi _{m,y}A_{26\zeta \eta ke}^{1}\psi _{n,y}\\&+\,\psi _{m,x}A_{66\zeta \eta ke}^{1}\psi _{n,y}\\&+\,\psi _{m}A_{45\zeta \eta ke}^{4}\psi _{n}=K_{12\zeta \eta kemn}\\ K_{22\zeta \eta kemn}= & {} \psi _{m,y}A_{22\zeta \eta ke}^{1}\psi _{n,y}+\psi _{m,y}A_{26\zeta \eta ke}^{1}\psi _{n,x}\\&+\,\psi _{m,x}A_{26\zeta \eta ke}^{1}\psi _{n,y}\\&+\,\psi _{m,x}A_{66\zeta \eta ke}^{1}\psi _{n,x}+\psi _{m}A_{44\zeta \eta ke}^{4}\psi _{n} \end{aligned}$$
$$\begin{aligned} \begin{aligned} K_{23\zeta \eta kemn} =\,&\psi _{m,y}A_{23\zeta \eta ke}^{2}\psi _{n}+\psi _{m,x}A_{36\zeta \eta ke}^{2}\psi _{n}\\&+\,\psi _{m}A_{45\zeta \eta ke}^{3}\psi _{n,x}+\psi _{m}A_{44\zeta \eta ke}^{3}\psi _{n,y}\\ K_{31\zeta \eta kemn} =\,&\psi _{m}A_{13\zeta \eta ke}^{3}\psi _{n,x}+\psi _{m}A_{36\zeta \eta ke}^{3}\psi _{n,y}\\&+\,\psi _{m,y}A_{45\zeta \eta ke}^{2}\psi _{n} +\psi _{m,x}A_{55\zeta \eta ke}^{2}\psi _{n}\\ =\,&K_{13\zeta \eta kemn}\\ K_{32\zeta \eta kemn} = \,&\psi _{m}A_{23\zeta \eta ke}^{3}\psi _{n,y}+\psi _{m}A_{36\zeta \eta ke}^{3}\psi _{n,x}\\&+\,\psi _{m,y}A_{44\zeta \eta ke}^{2}\psi _{n}+\psi _{m,x}A_{45\zeta \eta ke}^{2}\psi _{n}\\ =\,&K_{23\zeta \eta kemn}\\ K_{33\zeta \eta kemn} = \,&\psi _{m,y}A_{44\zeta \eta ke}^{1}\psi _{n,y}+\psi _{m,y}A_{45\zeta \eta ke}^{1}\psi _{n,x}\\&+\, \psi _{m,x}A_{45\zeta \eta ke}^{1}\psi _{n,y}+\psi _{m,x}A_{55\zeta \eta ke}^{1}\psi _{n,x}\\&+\,\psi _{m}A_{33\zeta \eta ke}^{4}\psi _{n}. \end{aligned} \end{aligned}$$
(30)

5.2 Finite element formulation for laminated plates with multiple delaminations and transverse cracks

The finite element formulation for the static laminated composite plate with multiple delaminations and matrix cracks is obtained by substituting Eq. (5) into Eq. (22), as

$$\begin{aligned} K_{\alpha \beta \zeta \eta ke\kappa \iota }U_{\beta \eta e\iota }=F_{\alpha \zeta k\kappa } \end{aligned}$$
(31)

where \(\kappa =m,s,h_{b}; \iota =n,g,f_{b}; m,n=1,2,\ldots , N_{E}; s, g=1,\ldots , N_{E}^{P}; h_{b},f_{b}=1,\ldots , N_{E}^{Q}; b=1,2,3,4\). The submatrices in Eq. (31) have the same form with the element stiffness matrix of the XLWM for the laminated composite plates Eq. (29). In Eq. (31), the index pairs (m, n), (s, g) and \((h_{b},f_{b})\) correspond to the shape functions \(\psi , \varLambda \) and \(\varvec{\varPi }\), respectively. So, the entries of \(K_{\alpha \beta \zeta \eta ke\kappa \iota }\) can be obtained by replacing the shape functions \(\psi \) in Eq. (30) with the shape functions corresponding to the index pairs (m, n), (s, g) and \((h_{b},f_{b})\), for example

$$\begin{aligned} K_{11\zeta \eta kemg}= & {} \psi _{m,x}A_{11\zeta \eta ke}^{1}\varLambda _{g,x}\nonumber \\&+\,\psi _{m,x}A_{16\zeta \eta ke}^{1}\varLambda _{g,y}+\psi _{m,y}A_{16\zeta \eta ke}\varLambda _{g,x}\nonumber \\&+\,\psi _{m,y}A_{66\zeta \eta ke}^{1}\varLambda _{g,y}+\psi _{m}A_{55\zeta \eta ke}^{4}\varLambda _{g}\nonumber \\ K_{11\zeta \eta kemf_{b}}= & {} \psi _{m,x}A_{11\zeta \eta ke}^{1}{\varPi }_{f_{b},x}\nonumber \\&+\,\psi _{m,x}A_{16\zeta \eta ke}^{1}{\varPi }_{f_{b},y}+\psi _{m,y}A_{16\zeta \eta ke}{\varPi }_{f_{b},x}\nonumber \\&+\,\psi _{m,y}A_{66\zeta \eta ke}^{1}{\varPi }_{f_{b},y}+\psi _{m}A_{55\zeta \eta ke}^{4}{\varPi }_{f_{b}} \end{aligned}$$
(32)

For the laminated composite plate with multiple delaminations and transverse cracks, it can be seen from Eq. (31) that the element stiffness matrix is composed of nine submatrixes. \(K_{\alpha \beta \zeta \eta kemn}\) is the submatrix of the nodal freedoms whilst \(K_{\alpha \beta \zeta \eta kesg}\) and \(K_{\alpha \beta \zeta \eta keh_{b}f_{b}}\) are the submatrices of the additional nodal freedoms for delaminations and transverse cracks, respectively. On the other hand, \(K_{\alpha \beta \zeta \eta kemg}, K_{\alpha \beta \zeta \eta kemf_{b}}\) and \(K_{\alpha \beta \zeta \eta kesf_{b}}\) are the coupling submatrixes.

6 SIF calculation and crack propagation criterion of the isotropic and orthotropic plates

6.1 SIF calculation

SIF is one of the most important parameters characterizing the crack tip stress field. In XFEM, SIF is usually computed by using the interaction integral method. Kim and Paulino [45] presented a domain integral method for the mix SIF of orthotropic materials. The method has been applied to the SIF calculation of composite structures in many researches [29, 31, 33, 46–48]. In the present work, the method is employed to calculate the SIFs associated with the delaminations and transverse cracks, The method is introduced briefly as follows.

The interaction integral method is carried out by using actual and auxiliary displacement/stress/strain fields. The actual field describes the physical problem and satisfies the equilibrium and compatibility equations in each point of a general inhomogeneous domain. In contrast, auxiliary fields do not satisfy all governing equations (e.g. equilibrium, compatibility and constitutive equations) and are employed to established the relationship between mix SIF and the interaction integral.

For the isotropic materials, the SIF \(K_{\mathrm {I}}\) and \(K_{\mathrm {II}}\) are related to the J-integral \(M_{1}\) of the auxiliary field as

$$\begin{aligned} M^{l}=\displaystyle \frac{2}{E^{*}}\left( K_{\mathrm {I}}^{\mathrm {aux}}K_{\mathrm {I}}+K_{\mathrm {II}}^{\mathrm {aux}}K_{\mathrm {II}}\right) \end{aligned}$$
(33)

where \(K_{\mathrm {I}}^{\mathrm {aux}}\) and \(K_{\mathrm {II}}^{\mathrm {aux}}\) are the SIF of the auxiliary field. Detailed expression of \(M^{l}\) can be found in reference [44].

$$\begin{aligned} E^{*}={\left\{ \begin{array}{ll} E &{} \quad \text {plane stress}\\ \displaystyle \frac{E}{1-v^{2}} &{} \quad \text {plane strain} \end{array}\right. } \end{aligned}$$

E is the elastic modulus of isotropic materials.

For the anisotropic materials, one can obtain the modes I and II SIF \(K_{\mathrm {I}}\) and \(K_{\mathrm {II}}\) by solving the linear algebraic equations

$$\begin{aligned} {\left\{ \begin{array}{ll} M_{1}^{l}=2c_{11}K_{\mathrm {I}}+c_{12}K_{\mathrm {II}} &{}\quad \left( K_{\mathrm {I}}^{\mathrm {aux}}=1,K_{\mathrm {II}}^{\mathrm {aux}}=0\right) \\ M_{2}^{l}=c_{12}K_{\mathrm {I}}+2c_{22}K_{\mathrm {II}} &{}\quad \left( K_{\mathrm {I}}^{\mathrm {aux}}=0,K_{\mathrm {II}}^{\mathrm {aux}}=1\right) \end{array}\right. } \end{aligned}$$
(34)

where \(M_{1}^{l}\) and \(M_{2}^{l}\) denote the J-integral for the case I (\(K_{\mathrm {I}}^{\mathrm {aux}}=1, K_{\mathrm {II}}^{\mathrm {aux}}=0\)) and case II (\(K_{\mathrm {I}}^{\mathrm {aux}}=0, K_{\mathrm {II}}^{\mathrm {aux}}=1\)). \(M_{1}^{l}, M_{2}^{l}, c_{11}, c_{12}\) and \(c_{22}\) can be found in Ref. [44].

Thus SIF \(K_{\mathrm {I}}^{\mu }\) and \(K_{\mathrm {II}}^{\mu }\) of each mathematical layer in the XLWM can be calculated.

6.2 Crack propagation criterion

The maximum circumferential tensile stress criterion [49] assumes that a crack starts to propagate when the maximum circumferential SIF exceed the critical SIF at the direction perpendicular to the maximum circumferential stress-direction. For isotropic materials, the propagation criterion is

$$\begin{aligned} K_{\theta \mathrm {max}}=\displaystyle \frac{K_{\mathrm {I}}}{K_{\mathrm {Ic}}}\mathrm {\cos }^{3}\displaystyle \frac{\theta _{0}}{2}-\displaystyle \frac{3}{2}\displaystyle \frac{K_{\mathrm {II}}}{K_{\mathrm {Ic}}}\cos \displaystyle \frac{\theta _{0}}{2}\mathrm {\sin }\theta _{0}=K_{\theta C} \end{aligned}$$
(35)

and the propagation direction is given by

$$\begin{aligned}&K_{\mathrm {I}}\mathrm {\sin }\theta _{0}-K_{\mathrm {II}} \left( 3\cos \theta _{0}-1\right) =0\nonumber \\&K_{\mathrm {I}}\cos \displaystyle \frac{\theta _{0}}{2} \left( 1-3\cos \theta _{0}\right) +K_{\mathrm {II}} \mathrm {\sin }\displaystyle \frac{\theta _{0}}{2} \left( 9\cos \theta _{0}+5\right) <0 \end{aligned}$$
(36)

where \(K_{\theta C}\) is the fracture toughness.

In 1987, Saouma el at. [50] extended the maximum circumferential tensile stress criterion of isotropic materials to the crack growth problem of anisotropic materials. The crack growth angle, global coordinates and the crack tip coordinates for the anisotropic materials are shown in Fig. 3.

Fig. 3
figure 3

The crack growth angle, global and local coordinates of the crack tip for the anisotropic materials

Full size image

For the anisotropic materials, the crack growth angle \(\theta _{0}\) need to meet

$$\begin{aligned} \displaystyle \frac{\sigma _{\theta }}{\sigma _{\theta \mathrm {max}}}= & {} \displaystyle \frac{K_{\mathrm {I}}\mathrm {Re} \left[ A\left( \mu _{1}B_{2}-\mu _{2}B_{1}\right) \right] +K_{\mathrm {II}}\mathrm {Re}\left[ A\left( B_{2}-B_{1}\right) \right] }{K_{\mathrm {Icr}}^{1}\cos ^{2}\beta +K_{\mathrm {Icr}}^{2}\mathrm {\mathrm {\sin }}^{2}\beta }\nonumber \\= & {} 1 \end{aligned}$$
(37)

where \(\sigma _{\theta }\) is the circumferential tensile stress; \(\sigma _{\theta \mathrm {max}}\) is the maximum circumferential tensile stress; \(\beta =\theta _{0}+\omega \) and \(\omega \) is the angle between the crack and the material direction; \(A=\displaystyle \frac{1}{\mu _{1}-\mu _{2}}, B_{i}=\left( \cos \theta +\mu _{i}\sin \theta \right) ^{1.5}\); \(K_{\mathrm {Icr}}^{1}\) and \(K_{\mathrm {Icr}}^{2}\) are the critical SIF for cracks along direction \(x_{1}\) and \(x_{2}\), respectively. The coefficients \(\mu _{1}\) and \(\mu _{2}\) can be found in Ref. [44].

Fig. 4
figure 4

Scheme of local remesh

Full size image

There are two fronts of the transverse crack in the proposed XLWM: the front in the thickness direction and the front in in-plane. In the proposed study, only the front in in-plane is considered. For the front in the thickness direction, if the virtual crack closure technique (VCCT) is employed to calculate the strain energy release rate (SERR) along the transverse crack front, and the transverse crack growth in the thickness direction can be predicted by the mixed-mode fracture criterion.

7 Local remesh for crack arbitrary growth

As the crack grows, some nodes such as node O in Fig. 4 may become very close to the crack surface. When one part of an element divided by a crack is far smaller than another part, Guass integral cannot accurately obtain the stiffness matrix of the element and would result in significant error. Because the level set function cannot be accurately calculated nearby the turning point of a crack, the whole calculation process may be terminated. In order to overcome this problem, a local remesh is undergone near the crack by moving the node O to \(O'\), as shown in Fig. 4. Let \(l_{\mathrm {gap}}\) denote the minimum distance between node O and the intersection point of the element edge and the crack. As the crack grows, \(l_{\mathrm {gap}}\) determines whether one needs to move the node (local remesh). To restrict excess element distortion, the node is moved by

$$\begin{aligned} \varDelta \varvec{x}=fl_{e}\varvec{n} \end{aligned}$$
(38)

where \(l_{e}\) is the length of the element edge; f is the coefficient that limits the distance of move and excess element distortion; \(\varvec{n}\) is the outward normal vector of crack surface. As an illustration, there are nodes very close to the crack surface in Fig. 5a, After the local remeshing with \(f=0.2\), nodes are shifted away from the crack surface while the mesh quality is reserved as shown in Fig. 5b. The large value of f would result into the grid distortion and the small value cannot make the nodes away from the crack surface adequately, so the value of \(f=0.2\) is determine by a number of examples.

Fig. 5
figure 5

Local remesh. a Before local remesh; b After local remesh

Full size image
Fig. 6
figure 6

Composite laminated plate with elliptic delamination and transverse crack. a Schematic diagram; b FE mesh (the length dimension is in m)

Full size image
Table 1 Maximum displacement of the isotropic plates with elliptic delamination
Full size table
Table 2 Maximum displacement of the isotropic plates with transverse crack
Full size table

The integration scheme for elements enriched by strong discontinuous function is based on subdomains (sub-triangle), its details can be found in Refs. [44, 51]. In this approach, the enriched elements are to subdivide into sub-triangles at both sides of the crack whose edges are adapted to crack faces. For the crack tip elements, more sub-triangles are required in front of the crack tip because of the existence of a highly nonlinear and singular stress field.

8 Numerical examples

8.1 Static responses analysis

The XLWM is used to model the plates with multiple delaminations and/or transverse crack. Figure 6 shows the geometry and FE mesh for a rectangular plate with a semi-elliptic delamination and a transverse crack. The major axis of the delamination coincides with the y-axes. The transverse crack is along the minor axis of the ellipse. Three kinds of boundary conditions are investigated: (1) \(x=6\) is clamped and other edges are free (CFFF); (2) \(y=10\) and \(y=0\) are clamped and other edges are free (CCFF); (3) \(x=0\) is free and other edge are clamped (CCCF). The plate is subjected to a unit transverse pressure on the delaminated region in top surface.

The plate of overall thickness H = 0.4 m is evenly divided into eight layers. For comparison purpose, these problems are also analyzed by using MSC.Nastran with Hex8 solid elements. Nodes pairs along the delamination interface and through-thickness crack are employed to model the displacement discontinuity. Meanwhile, the discretization scheme of the XLWM is the same with that used in the finite element analysis.

Table 3 Maximum displacement of the isotropic plates with delamination and transverse crack
Full size table
Table 4 Maximum displacement of the laminated composite plates with transverse crack
Full size table

Firstly, the isotropic plates with delamination and/or transverse crack are employed to validate the proposed XLWM. The material properties are taken as \(E=52 \mathrm {GPa}, \nu =0.3\).

Fig. 7
figure 7

Deformation of the composite laminated plate with multiple elliptic delaminations and transverse crack

Full size image
Fig. 8
figure 8

Stresses of the composite laminated plate with multiple elliptic delaminations and transverse crack

Full size image

Tables 1 and 2 compare the maximum displacements obtained by the proposed XLWM and MSC.Nastran for the isotropic plates with delamination or through crack, respectively. In the damage zone, the delamination can be denoted as \([\theta /\theta /\theta /\theta /\cap /\theta /\theta /\theta /\theta ]\), which means that the delamination is located at the interface between 4th layer and 5th layer (4th interface). It can be seen from the table that the proposed method is accurate and reliable for the plates with delamination or through crack. In Table 1, the maximum displacements \(u_{1}\) and \(u_{3}\) occur at the central point of the delamination region (\(x=0, y=5\)), and the maximum displacement \(u_{2}\) occurs at the point (\(x=0, y=2.8\)) and (\(x=0, y=7.2\)). In Table 2, the maximum displacement \(u_{1}\) occurs at the central point of the delamination region (\(x=0, y=5\)) for CFFF, point (\(x=2.9, y=5.0\)) for CCFF and point (\(x=2.6, y=5.0\)) for CCCF. The maximum displacement \(u_{2}\) occurs at the point (\(x=0, y=0\)) and (\(x=0, y=10.0\)) for CFFF, point (\(x=0, y=3.4\)) and (\(x=0, y=6.6\)) for CCFF and CCCF. The maximum displacements \(u_{3}\) occurs at the central point of the delamination region.

For the isotropic plates with delamination and non-thick-through crack, the maximum displacements calculated by XLWM and MSC.Nastran are compared in Table 3. In the damage region, the delamination and crack can be denoted as \([\theta /\theta /\theta /\theta /\cap /\varvec{\theta }/\varvec{\theta }/\varvec{\theta }/\varvec{\theta }]\), which means that the delamination is located at the interface between 4th layer and 5th layer and the crack cuts though the last four layers. It can be seen from Table 3 that the proposed method is accurate and reliable for the isotropic plates with both delamination and crack. The locations of maximum displacements are same with those in Table 2.

The XLWM is also employed to model the cross-ply laminated plate with multiple delaminations and/or transverse cracks in this example. The material properties of the single layer are taken as \(E_{11}=181\,\mathrm {GPa}, E_{22}=E_{33}=10.3\,\mathrm {GPa}, G_{12}=G_{13}=7.17\,\mathrm {GPa}, G_{23}=6.21\,\mathrm {GPa}, \nu _{12}=0.28, \nu _{13}=0.02\), and \(\nu _{23}=0.40\).

For the three stacking sequences \([0]_{8}, [0/90/0/90]_{s}\) and \([90/0/90/0]_{s}\), Table 4 compares the maximum displacements calculated by XLWM and MSC.Nastran for the plates with delamination \([\theta /\theta /\theta /\theta /\cap /\theta /\theta /\theta /\theta ]\). It can be seen from Table 4 that the proposed method is also accurate and reliable for the plates with transverse crack.

For the laminated composite plate \([0/90/0/90]_{s}\) with multiple delaminations and transverse cracks, the boundary condition is CCCF. In the damage region, the delaminations and non-thick-though transverse cracks can be denoted as \([\varvec{\theta }/\varvec{\theta }/\cap /\theta /\theta /\theta /\theta /\cap /\varvec{\theta }/\varvec{\theta }]\) which means that delaminations are located at the 2th and 6th interfaces and the cracks cut though the first two and the last two layers. Deformations and stresses of the laminated composite plate with multiple elliptic delaminations and transverse cracks are plotted in Figs. 7 and 8.

8.2 SIF calculation

The rectangular isotropic and composite plates with an edge through crack are used to examine the performance of the present method for the SIF calculation. The results obtained by the present method are compared with those given by the analytical solutions and the available numerical results. In addition, the effects of the crack size and the orthotropic angle on the distribution of SIF along the thickness direction are investigated.

8.2.1 Rectangular isotropic plates with a through-thickness edge crack

The rectangular isotropic plate with a through-thickness crack (see Fig. 9a) is employed to validate the present method for the calculation of SIF. As shown in Fig. 9a, the plate is subjected to a unit tensile stress \(\sigma _{0}\) at two ends and the crack angle \(\varphi \) is the angle between the crack and the direction transverse to the tensile stress. The square region around the crack tip is the domain used for computing the J-integral. The length of the rectangular plate is twice the width. The material parameters are \(E=1.0\,\mathrm {GPa}\), and \(\nu =0.3\). Two different meshes shown in Fig. 9b, c are used. When the crack angle \(\varphi =0\), SIF \(K_{II}=0\) and the analytical solution of \(K_{\mathrm {I}}\) is given by

$$\begin{aligned} K_{\mathrm {I}}= & {} \left[ 1.12-0.23\left( \displaystyle \frac{a}{b} \right) +10.56\left( \displaystyle \frac{a}{b}\right) ^{2}\right. \nonumber \\&\left. -\, 21.74\left( \displaystyle \frac{a}{b}\right) ^{3}+30.42 \left( \displaystyle \frac{a}{b}\right) ^{4}\right] \sigma _{0}\sqrt{\pi a} \end{aligned}$$
(39)
Fig. 9
figure 9

Rectangular isotropic plates with an edge through crack. a Geometric size and crack size; b \(20\times 40\) elements; c \(40\times 80\) elements

Full size image

For different crack lengths, the values of \(K_{\mathrm {I}}\) of the rectangular isotropic plates with an edge through crack calculated by the present method, Mohammadi [44] and the analytical method are compared in Table 5. The present predictions agree well with those of the others.

Table 5 \(K_{\mathrm {I}}\) of the rectangular isotropic plates with an edge through crack
Full size table
Fig. 10
figure 10

Distribution of \(K_{\mathrm {I}}\) of the rectangular isotropic plates with an edge through crack

Full size image
Fig. 11
figure 11

Influence of angle \(\phi \) on SIF

Full size image

Because the XLWM is quasi three dimensional and the transverse cracks of each single layer are independently described, the distribution of the SIF along the thickness direction can be obtained by the present method. It is an important advantage compared with the existing shell elements enriched by XFEM. For different crack sizes, distributions of \(K_{\mathrm {I}}\) of the rectangular isotropic plates with an edge through crack are plotted in Fig. 10, which shows that the crack size has significant influence on the distribution of \(K_{\mathrm {I}}\) along the thickness direction. In general, the SIF at top and bottom surfaces is larger than that at the mid-plane. If the ratio of crack size to the width of plate is approaches 0.5, \(K_{\mathrm {I}}\) decreases from the surface to the mid-plane. If the ratio of crack size to the width of plate is greater or less than 0.5, \(K_{\mathrm {I}}\) first decreases and then increases from the top/bottom surfaces to mid-plane. Because the boundary condition and the loads are symmetrical with respect to the mid-plane in the present numerical example, the distribution of \(K_{\mathrm {I}}\) along the thickness direction is symmetrical as well.

The influence of the angle between the crack and the transverse direction of plate \(\varphi \) on SIF is investigated in this numerical example and plotted in Fig. 11, where the values of SIF is the average along the thickness direction. It can be seen that \(K_{\mathrm {I}}\) decreases as angle \(\varphi \) increases, while \(K_{\mathrm {II}}\) first increases and then decreases with turning point at \(\varphi \approx 30^{\circ }\).

For different angles \(\varphi \), distributions of SIF \(K_{\mathrm {I}}\) and \(K_{\mathrm {II}}\) along the thickness direction after normalized by their respective thickness averages are shown in Fig. 12. As angle \(\varphi \) increases, the change in amplitude of \(K_{\mathrm {I}}\) along the thickness direction first decreases and then increases. If angle \(\varphi \approx 18^{\circ }, K_{\mathrm {I}}\) does not change along the thickness direction. If angle \(\varphi \) is less than \(18^{\circ }, K_{\mathrm {I}}\) decreases from the top/bottom surface to the mid-plane. If angle \(\varphi \) is greater than \(18^{\circ }, K_{I}\) increases from the top/bottom surface and attains it maximum at the mid-plane, while \(K_{\mathrm {I}}\) at the upper/bottm surface is maximum when angle \(\varphi \) is less than \(18^{\circ }\). As angle \(\varphi \) increases, the change in amplitude of \(K_{\mathrm {II}}\) along the thickness direction first decreases and then become almost zero when angle \(\varphi \approx 45^{\circ }\). \(K_{\mathrm {II}}\) decreases from the top/bottom surface to the mid-plane, namely, \(K_{\mathrm {II}}\) at top/bottom surface is maximum. \(K_{\mathrm {I}}\) and \(K_{\mathrm {II}}\) are symmetrical along the thickness direction with respect to the mid-plane, and always equal to their respective average values at \(z/H \approx 0.2\) and \(z/H \approx 0.8\).

Fig. 12
figure 12

Distributions of SIF along the thickness direction for different angles \(\phi \)

Full size image
Fig. 13
figure 13

Comparison of SIF for rectangular composite plates with an edge crack

Full size image

8.2.2 Rectangular composite plates with an edge through crack

The rectangular composite plate with an edge though crack to be considered has the same geometric size, boundary condition, loads and mesh with the isotropic plate in above subsection. The material properties are \(E_{11}=114.8\,\mathrm {GPa}, E_{22}=E_{33}=11.7\,\mathrm {GPa}, G_{12}=G_{13}=9.66\,\mathrm {GPa}, G_{23}=6.21\,\mathrm {GPa}, \nu _{12}=v_{13}=0.21\), and \(\nu _{23}=0.40\).

For five fibre angles (\(0^{\circ }, 30^{\circ }, 45^{\circ }, 60^{\circ }\) and \(90^{\circ }\)), Fig. 13 compares the normalized \(K_{\mathrm {I}}\) and \(K_{\mathrm {II}}\) obtained by the presented method with those obtained by XFEM [29, 31], BEM [52] and XEFG [53]. The SIF results obtained by the XLWM agree well with those obtained by other methods.

Figure 14 shows the distributions of SIF along the thickness direction. When fibre angle \(\theta =45^{\circ }\), the change in amplitude of \(K_{\mathrm {I}}\) along the thickness direction is maximum. When fibre angle \(\theta =90^{\circ }\), the change in amplitude is minimum. The change in amplitude of SIF \(K_{\mathrm {II}}\) along the thickness direction decreases as the fibre angle increasing. Similar to the isotropic plate with an edge crack, \(K_{\mathrm {I}}\) and \(K_{\mathrm {II}}\) are symmetrical along the thickness direction with respect to the mid-plane, and \(K_{\mathrm {I}}\) and \(K_{\mathrm {II}}\) always equal to their respective average values near the points \(z/H\approx 0.2\) and \(z/H\approx 0.8\).

Fig. 14
figure 14

Distribution of SIF along the thickness direction for the rectangular composite plates with an edge crack

Full size image

The influence of the crack angle \(\varphi \) on SIF for the rectangular composite plate with an edge crack is also examined. Figure 15 shows the influence of \(\varphi \) on SIF for five fibre angles. \(K_{\mathrm {I}}\) and its change in amplitude decrease as \(\varphi \) increases. On the other hand, the decrease in amplitude of SIF reduces as the fibre angle increasing. \(K_{\mathrm {II}}\) increases as angle \(\varphi \) increases, and the increase in amplitude of \(K_{\mathrm {II}}\) for \(\theta =0^{\circ }\) is significantly higher than that for other fibre angles.

Fig. 15
figure 15

Influence of angle \(\varphi \) on SIF of the composite plate

Full size image
Fig. 16
figure 16

Distribution of SIF along the thickness direction for the composite plate with an edge crack (\(\theta =0^{\circ }\))

Full size image
Fig. 17
figure 17

Distribution of SIF along the thickness direction for the composite plate with an edge crack (\(\theta =30^{\circ }\))

Full size image
Fig. 18
figure 18

Distribution of SIF along the thickness direction for the composite plate with an edge crack (\(\theta =45^{\circ }\))

Full size image
Fig. 19
figure 19

Distribution of SIF along the thickness direction for the composite plate with an edge crack (\(\theta =60^{\circ }\))

Full size image
Fig. 20
figure 20

Distribution of SIF along the thickness direction for the composite plate with an edge crack (\(\theta =90^{\circ }\))

Full size image

Figures 16, 17, 18, 19, and 20 show the distributions of SIF along the thickness direction for the five fibre angles \(\theta \) and different crack angles \(\varphi \). \(K_{\mathrm {I}}\) and \(K_{\mathrm {II}}\) are symmetrical along the thickness direction with respect to the mid-plane and always equal to their respective average values near the points \(z=0.2\) and \(z=0.8\). When \(\theta =0^{\circ }\), the change in amplitude of the SIF \(K_{\mathrm {I}}\) and \(K_{\mathrm {II}}\) along the thickness direction first decreases and then increases as \(\varphi \) increases. When angle \(\varphi \approx 26^{\circ }\), the change in amplitude is minimum. When \(\theta =30^{\circ }, 45^{\circ }\) and \(60^{\circ }\), the change in amplitude of \(K_{\mathrm {I}}\) and \(K_{\mathrm {II}}\) along the thickness direction decreases as the angle \(\varphi \) increases. \(\theta =90^{\circ }\), the change in amplitude of \(K_{\mathrm {I}}\) along the thickness direction increases for increasing \(\varphi \). That of \(K_{\mathrm {II}}\) is just the opposite.

8.3 Transverse crack arbitrary growth

Crack growth predictions are carried out in this section for plates with an edge through crack and for plates with both an edge through crack and an semi-elliptical delamination. Both isotropic and composite plates are considered. The effects of the fibre angle on the growth angle are investigated.

8.3.1 Rectangular composite plates with edge through cracks

The isotropic plate employed in Sect. 8.1, see Fig. 5, is first considered. The initial crack length is 1.5 m and the crack angle \(\varphi \) is zero. The average crack growth angle is used to update the location of crack tip. Figure 21 shows the effect of the crack size on the \(K_{\mathrm {I}}\). The predicted growth angle is zero, which agrees with the analytical solution. As the crack grows, \(K_{\mathrm {I}}\) first increases slowly and then quickly. Moreover, the predicted SIF in all layers are graphically indistinguishable as noted in the figure.

Fig. 21
figure 21

Effect of the crack size on the SIF for the rectangular isotropic plates with an edge through crack

Full size image
Fig. 22
figure 22

Variation of SIF versus the crack size in different fibre angle for the rectangular composite plates with an edge crack

Full size image

The composite plate employed in Sect. 8.1, see Fig. 6, is then considered. The initial crack length is 3.5 m and the crack angle \(\varphi \) is zero. Again, the average crack growth angle is used to update the location of crack tip. The predicted \(K_{\mathrm {I}}\) and \(K_{\mathrm {II}}\) versus the crack size are shown in Fig. 22. Figure 23 shows the growth paths for different fibre angle. As the crack grows, \(K_{\mathrm {I}}\) increases whilst \(K_{\mathrm {II}}\) first increases and then decreases. If the fibre angle \(\theta =0^{\circ }\) and \(90^{\circ }\), the crack growth angle predicted by the present method is zero. From the existing solution [54], the crack growth angle varies approximately \(sin(2\theta )\) with the maximum and minimum growth angles occurring at \(\theta =35^{\circ }\) and \(\theta =135^{\circ }\), respectively. For the fibre angles considered in this numerical example, the maximum value of growth angle occurs when \(\theta =30^{\circ }\), which somehow agrees with the existing solution.

8.3.2 Rectangular composite plates with semi-elliptical delaminations

SIF and crack growth prediction are conducted for the rectangular composite plate with an elliptic delamination and an edge through crack shown in Fig. 6. The initial crack length is 3.02 mm, and the delamination is located at the mid-plane. A unit uniform load is imposed on the top and bottom surfaces of the delaminated region, and a unit tensile stress is applied to the upper and lower edges of the plate.

Fig. 23
figure 23

The crack growth path for different fibre angles

Full size image

The crack growth problem of the isotropic plate with delamination and crack is first considered. The material properties are \(E=52\, \mathrm {GPa}\), and \(\nu =0.3\). Figures 24 and 25 portray how the predicted SIF varies with the crack length and along the thickness direction. Figure 24 shows that \(K_{\mathrm {I}}\) increases as the crack size increases. Figure 24 shows that the SIF assumes its maximum value when the crack tip is very close to the delamination front as in the case of crack length equal to 3.1805 m. Otherwise, the maximum values occurs at the top/bottom surfaces. In other words, the delamination front significantly affects the crack tip stress field. \(K_{\mathrm {I}}\) and \(K_{\mathrm {II}}\) are symmetrical along the thickness direction with respect to the mid-plane. The displacement and stress contours are shown in Figs. 26 and 27, respectively. In the crack growing process, stress concentration appears at the transverse crack tip and delamination front. Stress concentrations of \(\sigma _{11}\) and \(\sigma _{22}\) are most significant along \(\omega =0^{\circ }\) and \(\omega =\pm 90^{\circ }\) which define the minor and major axis of the semi-elliptical delamination, respectively. Meanwhile, stress concentration of \(\sigma _{12}\) is most significant along \(\omega =\pm 45^{\circ }\).

Fig. 24
figure 24

Variation of SIF versus the crack size for the rectangular isotropic plates with an edge crack and elliptic delamination

Full size image
Fig. 25
figure 25

Distribution of SIF along the thickness direction as the crack growing for the rectangular isotropic plates with an edge crack and elliptic delamination

Full size image
Fig. 26
figure 26

Fringe of displacements for the rectangular isotropic plates with an edge crack and elliptic delamination a \(u_{1}\); b \(u_{2}\) and c \(u_{3}\)

Full size image
Fig. 27
figure 27

Fringe of stresses for the rectangular isotropic plates with an edge crack and elliptic delamination a \(\sigma _{11}\); b \(\sigma _{22}\) and c \(\sigma _{12}\)

Full size image

The material properties of the rectangular composite plate with delamination and transverse crack are the same as those given in Sect. 8.2.2. Three kinds of stacking sequences \([30]_{8}, [45]_{8}\) and \([60]_{8}\) are considered. The boundary condition and loads are the same as those of the isotropic plate. The elliptic delamination is located at the 4th interface, namely, \([\theta /\theta /\theta /\theta /\cap /\theta /\theta /\theta /\theta ]\).

Variation of SIF versus the crack size is shown in Fig. 28. The distributions of SIF along the thickness direction are shown in Fig. 29 as the crack grows. For fibre angle equal to \(45^{\circ }\). \(K_{\mathrm {I}}\) increases with the crack length. Meanwhile, \(K_{\mathrm {II}}\) first increases and then decreases as the crack grows. Similar to the isotropic plate, the delamination front significantly affects the crack tip stress field. Both \(K_{\mathrm {I}}\) and \(K_{\mathrm {II}}\) along the thickness direction are symmetrical with respect to the mid-plane. The changes in \(K_{\mathrm {I}}\) and \(K_{\mathrm {II}}\) along the thickness direction increase as the transverse crack tip approaches the delamination front.

Displacement and stress contours are shown in Figs. 30 and 31, respectively, which can illustrate the effect of fibre angle on the displacement and stress distributions with respect to those of the isotropic plate. Stress concentrations still appear at the transverse crack tip and delamination front. However, in the delamination front, the concentration area of \(\sigma _{11}\) is located at the directions \(\omega =-30^{\circ }\), the concentration area of \(\sigma _{22}\) is located at the directions \(\omega =-45^{\circ }\) and \(\omega =90^{\circ }\) and the concentration area of \(\sigma _{12}\) is located at region near the directions \(\omega =\pm 45^{\circ }\).

For three kinds of fibre angle (\(\theta =30^{\circ }, \theta =45^{\circ }\) and \(\theta =60^{\circ }\)), growth paths are shown in Fig. 32.

Fig. 28
figure 28

Variation of SIF versus the crack size for the rectangular composite plates with an edge crack and elliptic delamination

Full size image
Fig. 29
figure 29

Distribution of SIF along the thickness direction as the crack grows for the rectangular composite plate with an edge crack and an semi-elliptic delamination a \(K_{\mathrm {I}}\); b \(K_{\mathrm {II}}\)

Full size image
Fig. 30
figure 30

Fringe of displacements for the rectangular composite plates with an edge crack and an semi-elliptic delamination a \(u_{1}\); b \(u_{2}\) and c \(u_{3}\)

Full size image
Fig. 31
figure 31

Fringe of stresses for the rectangular composite plates with an edge crack and elliptic delamination a \(\sigma _{11}\); b \(\sigma _{22}\) and c \(\sigma _{12}\)

Full size image
Fig. 32
figure 32

Growth path for different fibre angle

Full size image

9 Conclusions

Using an improved layerwise displacement assumption and the extended finite element method (XFEM), a new analysis method is proposed for the laminated composite plates with transverse transverse cracks and/or multiple delaminations. The SIF and the crack growth are predicted by the interaction integral method and the maximum circumferential tensile criterion, respectively.

The extended layerwise method (XLWM) of laminated composite plates can not only describe the multiple delaminations together with through and non-through transverse cracks but also accurately predict the displacement and stress fields of the crack tip and delamination front. As the XLWM is quasi three dimensional and the transverse cracks of each single layer are independently described, the thickness distribution of the SIF can be calculated and the predict crack growth angle can be different for each mathematic layer. This is an important advantage compared with the existing shell elements enriched by XFEM. The XLWM extends the application of the XFEM in damage analysis and prediction to laminated composite structures.

The predicted static responses, SIF and crack growth are in excellent agreement to the analytical and the available solutions. From the numerical investigations, the following conclusions can be drawn:

  1. (1)

    Some nodes will be very close to the crack surface as the crack grows. The present local remeshing scheme can shift these nodes without scarifying the mesh quality.

  2. (2)

    For the static response, the present displacement prediction agrees well to that of the 3D elastic prediction of MSC.Nastran whilst the SIF and crack angle predictions are in excellent agreement with the analytical or other reference solutions.

  3. (3)

    The boundary and loading conditions are symmetric with respect to the mid-plane in the numerical example, the thickness distribution of \(K_{\mathrm {I}}\) follows. Furthermore, \(K_{\mathrm {I}}\) and \(K_{\mathrm {II}}\) are always equal to their respective average values along the thickness direction near \(z/H \approx 0.2\) and \(z/H \approx 0.8\).

  4. (4)

    The delamination front has a profound effect on the crack tip stress field. The changes in \(K_{\mathrm {I}}\) and \(K_{\mathrm {II}}\) along the thickness direction increase as the transverse crack tip gets closer to the delamination front.