A simple way to improved formulation of $\hbox {FE}^2$ analysis

Abstract

A new formulation of two-scale $\hbox {FE}^2$ analysis introduces symmetric stretch tensor as strain measure on macro level instead of asymmetric deformation gradient to determine boundary conditions on embedded microstructure. This significantly reduces computational cost of boundary conditions related sensitivity analysis of microstructure and with it the evaluation of local macroscopic stress tensors and tangent matrices. Various $\hbox {FE}^2$ formulations with isogeometric and standard finite element microanalysis are tested for consistency, accuracy and numerical efficiency on numerical homogenisation examples. Objective performance comparison of different $\hbox {FE}^2$ formulations is enabled with automation of all procedures in symbolic code generation system AceGen. The results obtained in numerical examples show reduced computational cost of the new $\hbox {FE}^2$ formulation without loss of accuracy and comparable numerical efficiency of higher order isogeometric and standard $\hbox {FE}^2$ formulations.

1 Introduction

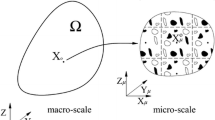
A two-scale $\hbox {FE}^2$ scheme is a well established computational homogenisation technique [1–7] for determination of material characteristics of multiphase materials. $\hbox {FE}^2$ method predicts the global response of microscopic heterogeneous materials (such as metal alloy systems, polymer blends, porous media, polycristaline materials and composites) by employing micromechanical models and transferring the microscale information to the macroscale analysis. The computational cost of $\hbox {FE}^2$ analysis is enormous since this nested finite element method framework simultaneously analyzes microstructure and macrostructure. This paper presents a new $\hbox {FE}^2$ formulation with reduced computational cost without altering the numerical model of multiphase material. At each Newton–Raphson iteration on macro level local tangent operator consistent with local macroscopic stress tensor is extracted from embedded microscale computation. A conventional way is based on the idea of condensing the microscale tangent information stored in the global finite element tangent matrix to a fourth-order local tangent operator at macroscopic integration point (see [2]). In case of complex microstructures this procedure inflicts too high memory allocation demands for standard workstations to handle (see [8, 9]). An alternative technique for tangent computation was presented by Lamut (see [8]) which determines local macroscopic tangent operator with sensitivity analysis of embedded microstructure with respect to boundary conditions (see [10]). Result of sensitivity analysis are partial derivatives of response function with respect to sensitivity parameters, which are independent components of the macro strain measure. Macro strain measure is in a conventional $\hbox {FE}^2$ procedure asymmetric macroscopic deformation gradient with nine independent components. A motivation for this paper was to reduce computational cost of sensitivity analysis with transition to symmetric stretch tensor as macro strain measure which reduces the number of sensitivity parameters from nine to six. For this study also various $\hbox {FE}^2$ formulations with isogeometric and standard finite element microanalysis were developed and compared on numerical homogenisation examples. To enable objective performance comparison of different $\hbox {FE}^2$ formulations are all considered procedures implemented in automatic code generator AceGen which provides uniformly automated $\hbox {FE}^2$ flowchart. Different $\hbox {FE}^2$ formulations are tested for consistency of micro–macro coupling, accuracy and numerical efficiency on numerical homogenisation examples with hyperelastic and linear elastic porous material. For accuracy validation in linear case a Nemat-Nassers analytical estimate of effective elastic tensor is calculated (see [11–13]) and compared to numerical solution. Findings of this study are summarized in conclusions at the end of this paper.

2 Specifics of proposed approach to $\hbox {FE}^2$ method

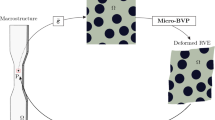
$\hbox {FE}^2$ homogenisation scheme simultaneously analyses heterogeneous multi-phase material on two nested scales of finite elements. On the outer loop of $\hbox {FE}^2$ procedure macrostructure is analyzed and discretized with finite elements. To each macroscopic integration point a representative volume element (RVE) is assigned, which represents the underlying microstructure. This research deals with hyperelastic multiphase materials and assumes that constitutive behavior of all microstructural constituents is known and defined by strain energy function. Contrary to conventional formulation which determines prescribed essential boundary conditions on RVE with local macroscopic deformation gradient $\varvec{F}_M$ (see [2]) this paper presents transition to symmetric tensor with the aim of reducing the computational cost of local macroscopic tangent matrix evaluation. The right polar decomposition of the deformation gradient $\varvec{F}_M$ into a product of an orthogonal tensor $\varvec{R}_M$ and a positive definite symmetric tensor $\varvec{U}_M$ (see [14]), is written as

$$\begin{aligned}&\varvec{F}_M = \varvec{R}_M \cdot \varvec{U}_M \,, \end{aligned}$$

(1)

where $\varvec{R}_M$ represents rigid rotation and $\varvec{U}_M$ the stretch tensor. Here and in the following the subscript “M” refers to macroscale quantity, while the subscript “m” will denote a microscopic quantity. The material characteristics of hyperelastic material depend only on stretch tensor $\varvec{U}_M$, since rigid body rotation does not alter the material volume or shape. Since local macroscopic Cauchy–Green tensor $\varvec{C}_M={\varvec{F}_M^T} \,\varvec{F}_M={\varvec{U}_M} \,\varvec{U}_M$ is symmetric and positive definite, $\varvec{U}_M$ is unique symmetric positive definite square root of $\varvec{C}_M$. The exact finite term expansion of matrix square root and and its first and second derivative was obtained by differentiating a scalar generating function of the eigenvalues of $\varvec{C}_M$ (see [15]) as

$$\begin{aligned}&\varvec{U}_M=\frac{2}{3} \,\frac{\partial \left( E_1^{3/2}+E_2^{3/2}+E_3^{3/2}\right) }{\partial \varvec{C}_M} \, , \end{aligned}$$

(2)

where $E_1$, $E_2$, $E_3$ are eigenvalues of $\varvec{C}_M$ determined with trigonometric functions (see [16, 17]). In case of multiple or almost equal eigenvalues in which general formulation exhibits ill-conditioning, asymptotic expansions presented in [17] are applied. The actual derivatives were obtained with use of backward mode automatic differentiation technique as described in [17]. In this way the usual evaluation of matrix square root function based on polar decomposition and associated numerical difficulties are avoided. Hence, prescribed boundary conditions can be formulated with $\varvec{U}_M$ instead of $\varvec{F}_M$ without prejudice to the generality of $\hbox {FE}^2$ method.

RVE is brick shaped and essential boundary conditions are assigned in each corner node on the RVE boundary as

$$\begin{aligned}&\bar{\mathbf{u}}=(\varvec{U}_M-\mathbf{I }) \, \mathbf{B}_c, \end{aligned}$$

(3)

where $\mathbf{B}_c$ are reference coordinates of a corner node in RVE. For the unconstrained boundary nodes microstructural periodicity assumption is adopted as justified by a number of authors [2, 9, 18]. The deformed position of all unconstrained nodes on RVE boundary is constrained with periodicity conditions written in general form as

$$\begin{aligned}&\mathbf{x}^+ -\mathbf{x}^-= \varvec{U}_M \, (\mathbf{X}^+ - \mathbf{X}^-)= \varvec{U}_M \, (\mathbf{B}_c^+ - \mathbf{B}_c^-), \end{aligned}$$

(4)

where $\mathbf{x}^+$ and $\mathbf{x}^-$ ($\mathbf{X}^+$ and $\mathbf{X}^-$) denote deformed (reference) position of nodes on opposite RVE boundary surfaces and $\mathbf{B}_c^+$ and $\mathbf{B}_c^-$ represent reference position of associated corner nodes. Periodic boundary conditions in (4) imply periodic deformation and stress field (see [11]). Thus, for boundary stress $\varvec{p}= \varvec{P}_m \cdot \varvec{n}$, where $\varvec{P}_m$ is the microscopic 1. Piola-Kirchhoff stress tensor and $\varvec{n}$ is the associated normal to the undeformed RVE boundary surface it holds true that $\varvec{p}^+=\varvec{p}^-$ on opposite boundary surfaces of RVE. Periodicity conditions (4) are added to microscale analysis as equality constraints for a given boundary problem which is then solved monolithically with the method of Lagrange multipliers. On the inner loop of $\hbox {FE}^2$ analysis RVE is discretized and analyzed with finite elements. Additional Lagrange finite elements link displacements of the constrained corner nodes $\mathbf{B}_c$ with those of unconstrained nodes on opposing boundary planes of RVE. The Lagrange finite elements are defined by augmented Lagrange multiplier potential,

$$\begin{aligned}&{\varXi }(\varvec{\lambda }_i)=\varvec{\lambda }_i (\mathbf{u}^+ -\mathbf{u}^-) + \rho \, (\mathbf{u}^+ -\mathbf{u}^-)^2, \end{aligned}$$

(5)

where $\varvec{\lambda }_i=\{ \lambda _1, \lambda _2, \lambda _3\}$ are the Lagrange multipliers of the i-th equality constraint and $\rho$ is arbitrary weight.

3 The proof of consistency of micro - macro coupling

The coupling between macroscopic and microscopic levels is based on averaging theorems [11, 19, 20]. The energy averaging theorem known as Hill–Mandel condition requires equality between volume average of virtual work performed by variation of microscopic deformations on RVE and virtual work performed by variation of macroscopic deformations in associated point on macro-scale,

$$\begin{aligned}&\frac{1}{V_0} \, \int _{V_0} \varvec{P}_m : \delta \varvec{F}_m^T \, dV=\varvec{P}_M : \delta \varvec{F}_M^T, \quad \forall \, \delta \varvec{x}, \end{aligned}$$

(6)

where $\varvec{P}_M$ is the 1st Piola–Krichhoff stress tensor associated with variation of work conjugate deformation gradient $\delta \varvec{F}_M$. Here it will be shown that the equality (6) holds true also in the case where only symmetric stretch tensor $\varvec{U}_M$ defines boundary conditions on RVE without the rotational part $\varvec{R}_M$ of the polar decomposition of deformation gradient $\varvec{F}_M$. The volume average of microstructural deformation gradient $\varvec{F}_m$ over RVE in case of periodic boundary conditions (4) equals

$$\begin{aligned} \frac{1}{V_0} \int _{V_0} \varvec{F}_m \, dV= & {} \frac{1}{V_0} \int _{V_0}(\nabla \varvec{x})^T\, dV=\frac{1}{V_0} \int _{{\varGamma }_0} \varvec{x}\, \varvec{n} \, d{\varGamma }\nonumber \\= & {} \frac{1}{V_0} \int _{{\varGamma }_0^+} (\varvec{x}^+ - \varvec{x}^- ) \, \varvec{n}^+ d{\varGamma }\nonumber \\= & {} \frac{1}{V_0}\, \varvec{U}^M\cdot \int _{{\varGamma }_0^+} (\varvec{X}^+ - \varvec{X}^- ) \, \varvec{n}^+ d{\varGamma }\nonumber \\= & {} \frac{1}{V_0}\, \varvec{U}^M\cdot \int _{{\varGamma }_0} \varvec{X}\, \varvec{n} \, d{\varGamma }\,\nonumber \\= & {} \frac{1}{V_0}\, \varvec{U}^M\cdot \int _{V_0} \nabla \varvec{X} \, dV\,=\varvec{U}^M, \end{aligned}$$

(7)

where equality $\nabla \varvec{X}=\mathbf{I }$ is taken into account and divergence theorem is used to transform the integral over undeformed volume $V_0$ of the RVE to an integral over undeformed boundary surface ${\varGamma }_0$ of the RVE with associated normal $\varvec{n}$ and vice versa. This yields the relation between macroscopic deformation gradient $\varvec{F}_M$ and the volume average of its microstructural counterpart $\varvec{F}_m$ as

$$\begin{aligned}&\varvec{F}_M= \varvec{R}_M \cdot \varvec{U}_M = \varvec{R}_M \cdot \frac{1}{V_0} \int _{V_0} \varvec{F}_m \, dV\, . \end{aligned}$$

(8)

Volume average of microstructural 1. Piola-Kirchhoff stress tensor $\varvec{P}_m$ resulting from boundary conditions (4) on RVE, equals

$$\begin{aligned}&\varvec{\hat{P}}= \frac{1}{V_0} \int _{V_0} \varvec{P}_m \, dV. \end{aligned}$$

(9)

Macroscopic 1. Piola-Kirchhoff stress tensor $\varvec{P}_M$ is obtained after the rotation tensor $\varvec{R}_M$ is superimposed upon deformed form caused by stretch tensor $\varvec{U}_M$, affecting the direction of stress field and leading to relation

$$\begin{aligned}&\varvec{P}_M= \varvec{R}_M \cdot \varvec{\hat{P}}. \end{aligned}$$

(10)

When the right side of Hill–Mandel condition (6), $\varvec{P}_M : \delta \varvec{F}_M$, is expressed in terms of Biot stress tensor $\varvec{T}_M$ and its work conjugate pair, the stretch tensor $\varvec{U}_M$, it can be seen that

$$\begin{aligned} \varvec{P}_M : \delta \varvec{F}_M^T= & {} \varvec{T}_M : \delta \varvec{U}_M\nonumber \\= & {} \frac{1}{2}\,(\varvec{R}_M^T \varvec{P}_M+\varvec{P}_M^T \varvec{R}_M) : \delta \varvec{U}_M \nonumber \\= & {} \frac{1}{2}\,(\varvec{R}_M^T \varvec{R}_M \, \varvec{\hat{P}}+(\varvec{R}_M \, \varvec{\hat{P}})^T \varvec{R}_M) : \delta \varvec{U}_M\nonumber \\= & {} \frac{1}{2} \,(\varvec{\hat{P}}+ \varvec{\hat{P}}^T) : \delta \varvec{U}_M \nonumber \\= & {} \varvec{\hat{P}} : \delta \varvec{U}_M, \end{aligned}$$

(11)

since $\varvec{\hat{P}} : \delta \varvec{U}_M=\mathrm {tr}(\varvec{\hat{P}}^T \, \delta \varvec{U}_M)=\mathrm {tr}(\varvec{\hat{P}} \, \delta \varvec{U}_M)=\varvec{\hat{P}}^T : \delta \varvec{U}_M$ and $\varvec{ R}_M$ is orthogonal tensor, thus $\varvec{ R}_M^T \, \varvec{R}_M=\varvec{I}$. When periodicity conditions (4) on RVE boundary ${\varGamma }_0$ are applied to the left side of the Hill–Mandel equality (6) and divergence theorem is put into use it can be expressed as

$$\begin{aligned}&\frac{1}{V_0} \, \int _{V_0} \varvec{P}_m : \delta \varvec{F}^T_m \, dV= \frac{1}{V_0} \, \int _{{\varGamma }_0} \varvec{p} \cdot \delta \varvec{x}\, d{\varGamma }\nonumber \\&\quad = \frac{1}{V_0} \, \int _{{\varGamma }_0^+} \varvec{p}^+ \, ( \varvec{X}^+ - \varvec{X}^- ) \, d{\varGamma }:\delta \varvec{U}_M \nonumber \\&\quad =\frac{1}{V_0}\, \int _{{\varGamma }_0} \varvec{p} \, \varvec{X} \, d{\varGamma }:\delta \varvec{U}_M \nonumber \\&\quad =\frac{1}{V_0}\, \int _{V_0} \varvec{P}_m \, dV :\delta \varvec{U}_M =\varvec{\hat{P}} : \delta \varvec{U}_M, \end{aligned}$$

(12)

where $\varvec{p}= \varvec{P}_m \cdot \varvec{n}$ (for more details see [21]). This proves the equality of the left and the right side of the Hill–Mandel macrohomogenity condition (6) for chosen boundary conditions (4).

4 Automatic differentiation based (ADB) notation

Multiscale $\hbox {FE}^2$ procedure is implemented in symbolic code generation system AceGen that combines the symbolic and algebraic capabilities of general computer algebra system Mathematica [22], automatic differentiation technique and simultaneous optimization of expressions (see [23, 24]). ADB method [25–27] is used for evaluation of the exact derivatives of any arbitrary complex function via chain rule and represents an alternative solution to the numerical differentiation and symbolic differentiation. ADB operator $\hat{\delta } f(\varvec{a})/ \hat{\delta } \varvec{a}$ represents partial differentiation of a function $f(\varvec{a})$ with respect to variables $\varvec{a}$. If for example an alternative or additional dependencies for variables $\varvec{b}$ have to be considered for differentiation, local ADB exception is indicated by the following formalism:

$$\begin{aligned} \left. \frac{{\hat{\delta }} f(\varvec{a},\varvec{b}) }{{\hat{\delta }} \varvec{a}} \right| _{ \genfrac{}{}{}1{D\varvec{b}}{D\varvec{a}} = \varvec{M}} \, , \end{aligned}$$

(13)

which indicates that during ADB procedure, the total derivatives of variables $\varvec{b}$ with respect to variables $\varvec{a}$ are set to be equal to matrix $\varvec{M}$. The ADB notation can be directly translated in the program code and is part of numerically efficient code automation. Further details regarding this notation can be found in [10].

5 Numerical formulation of proposed approach to $\hbox {FE}^2$ method

The response of each phase in heterogeneous RVE is defined by constitutive equation specified with a strain energy function ${\varPsi }(\varvec{F}_m)$. The neo-Hookean type of strain energy function used in numerical examples in Sect. 7 is chosen in a form

$$\begin{aligned} {\varPsi }(\varvec{F}_m)= & {} \frac{\mu }{2} \, \left( J_{F}^{-2/3} \, \hbox {tr}(\varvec{C}_m)-3 \right) \nonumber \\&+\frac{K}{\beta ^2} \, \left( J_{F}^{-\beta } -1+\beta \, \hbox {ln}{(J_{F}- 3 )} \right) , \end{aligned}$$

(14)

where $\varvec{C}_m$ is Cauchy–Green deformation tensor, $J_{F} = \det \varvec{F}_m$, $\mu$ is shear modulus, K is compression modulus and $\beta$ is dimensionless parameter. In RVE analysis is augmented Lagrange multiplier potential ${\varXi }$ defined in (5) added to elastic deformation energy $\int _{V_0} {\varPsi }\, dV$, yielding in the absence of external forces the system of nonlinear equations

$$\begin{aligned}&\mathbf{R}_m= \frac{\partial }{\partial \mathbf{p}} \left( {\varXi }(\mathbf{p})+ \int _{V_0} {\varPsi }(\varvec{F}_m) \, dV \right) = \varvec{0}, \quad \text {where}\nonumber \\&\quad \mathbf{p} =\mathbf{u} \cup \varvec{\lambda }, \end{aligned}$$

(15)

$\mathbf{p}$ is a vector of unknowns composed of nodal displacements $\mathbf{u}$ and Lagrange multipliers $\varvec{\lambda }$. Global residual vector $\mathbf{R}_m$ of micro problem assembled through integration domains as

(16)

where operator stands for standard FE assembly procedure through finite element domains e and Lagrange element domains le, $\mathbf{R}_{le}=\hat{\delta } {\varXi }/ \hat{\delta }\mathbf{p}_{le}$ is Lagrange element residual, g is Gauss point and $w_{mg}$, $J_{mg}$, $\mathbf{R}_{mg}=\hat{\delta } {\varPsi }/ \hat{\delta }\mathbf{p}_e$ are the corresponding Gauss point weight, Jacobian determinant and residual, respectively. System of equations (15) is solved numerically with standard Newton–Raphson method. The resulting microstress field is expressed as 1st Piola-Krichhoff stress tensor $\varvec{P}_m=\partial {\varPsi }(\varvec{F}_m)/ \partial \varvec{F}_m$, averaged over RVE volume and returned to macroscopic integration point as local macroscopic stress $\varvec{\hat{P}}$,

$$\begin{aligned}&\varvec{\hat{P}}= \frac{1 }{V_0}\sum _{e=1}^{n_e} \sum _{g=1}^{n_g}w_{mg}\; J_{mg}\; \varvec{P}_{mg}, \end{aligned}$$

(17)

where $V_0$ is RVE volume and $\varvec{P}_{mg}=\hat{\delta } {\varPsi }/ \hat{\delta } \varvec{F}_m$ is Gauss point stress tensor. Macroelement formulation is established in terms of a weak statement of static equilibrium of the body. Contribution of internal forces to global weak form is given as:

$$\begin{aligned}&\delta W_\mathrm{{int}} =\int _{V_M} \varvec{ P}_M : \delta \varvec{F}_M^T \, dV=\int _{V_M} \varvec{\hat{P}} : \delta \varvec{U}_M \, dV, \end{aligned}$$

(18)

where $\delta W_\mathrm{{int}}$ is the internal virtual work done by the stresses and $V_M$ is the volume of the body on macroscale (see [14]). The contribution of internal forces to residual of macro problem is obtained in the same manner as the residual of micro problem, i. e.

(19)

where $\mathbf{R}_{Mg}$ is Gauss point contribution given by

$$\begin{aligned} \mathbf{R}_{Mg}= \varvec{\hat{P}} : \frac{\partial \varvec{U}_M}{\partial \mathbf{u}_e} = \left. \frac{{\hat{\delta }} (\varvec{\hat{P}} : \varvec{U}_M) }{{\hat{\delta }} \mathbf{u}_e} \right| _{ \genfrac{}{}{}1{D\hat{\mathbf{P}}}{D\mathbf{u}_e} = \mathbf{0}} . \end{aligned}$$

(20)

The requirement that global residual be zero yields nonlinear system of equations which is solved numerically with standard Newton–Raphson method. Like global residual is macroscopic tangent operator $\mathbf{K}_M$ formed from Gauss point tangent operator $\mathbf{K}_{Mg}$ which is obtained via chain rule as

$$\begin{aligned} \mathbf{K}_{Mg}= & {} \frac{\partial \mathbf{R}_{Mg}}{\partial \mathbf{u}_e}+ \frac{\partial \mathbf{R}_{Mg}}{\partial \varvec{\hat{P}}} \frac{D \varvec{\hat{P}}}{D \varvec{U}_M} \frac{\partial \varvec{U}_M}{\partial \mathbf{u}_e}\nonumber \\= & {} \left. \frac{{\hat{\delta }} \mathbf{R}_{Mg} }{{\hat{\delta }} \mathbf{u}_e} \right| _{ \genfrac{}{}{}1{D\varvec{\hat{P}}}{D\varvec{U}_M} = D\varvec{\hat{P}}D\varvec{U}_M} . \end{aligned}$$

(21)

The first derivative $D\varvec{\hat{P}}/ D\varvec{U}_M$ of average stress tensor $\varvec{\hat{P}}$ with respect to symmetric stretch tensor $\varvec{U}_M$ in (21) is obtained from boundary conditions related sensitivity analysis of the microstructure (RVE).

5.1 Sensitivity analysis on RVE

Macroscopic stress tensor $\varvec{\hat{P}}$ is defined as averaged microstress over volume of the RVE (see (9)) so the total derivative $D\varvec{\hat{P}}/ D\varvec{U}_M$ can be written as

$$\begin{aligned}&\frac{D \varvec{\hat{P}}}{D \varvec{U}_M}=\frac{1}{V_0} \, \int _{V_0} \frac{D \varvec{ P}_m}{D \varvec{U}_M} \, dV. \end{aligned}$$

(22)

and evaluated on micro level as averaged sensitivity of microscopic 1. Piola-Kirchhoff stress tensor $\varvec{ P}_m$ on variation of sensitivity parameters, which are defined as the six independent components of the symmetric tensor $\varvec{U}_M$,

$$\begin{aligned}&{\varvec{\phi }} = \left\{ U_{11}, U_{12}, U_{13}, U_{22}, U_{23}, U_{33}\right\} . \end{aligned}$$

(23)

Sensitivity problem is in analogy with primal analysis defined by residual $\mathbf{R}_m$,

$$\begin{aligned}&\mathbf{R}_m(\mathbf{p}({\varvec{\phi }} ), \bar{\mathbf{u}}({\varvec{\phi }} ) )=\varvec{0}, \end{aligned}$$

(24)

where $\bar{\mathbf{u}}$ are prescribed essential boundary conditions and $\mathbf{p}$ is a vector of unknowns all defined as a function of sensitivity parameters ${\varvec{\phi }}$. The direct differentiation of time-independent residual (24) with respect to sensitivity parameters ${\varvec{\phi }}$ yields the following system of linear equations for response sensitivity $D \mathbf{p}/ D {\varvec{\phi }}$,

$$\begin{aligned}&\frac{\partial \mathbf{R}_m}{\partial \mathbf{p}} \,\frac{D \mathbf{p} }{ D {\varvec{\phi }}}=-\frac{\partial \mathbf{R}_m}{\partial \bar{\mathbf{u}} } \,\frac{D \bar{\mathbf{u}} }{ D{\varvec{\phi }}}, \end{aligned}$$

(25)

where $\partial \mathbf{R}_m/ \partial \mathbf{p}$ is exactly the independent tangent operator $\mathbf{K}_m$ of the primal problem on micro level. The global sensitivity problem is then rewritten as

$$\begin{aligned}&\mathbf{K}_m\,\frac{D \mathbf{p} }{ D {\varvec{\phi }}}= - \tilde{\mathbf{R}}_m, \end{aligned}$$

(26)

where $\tilde{\mathbf{R}}_m$ is sensitivity pseudo residual formed from Gauss point pseudo residual $\tilde{\mathbf{R}}_{mg}$ and Lagrange element pseudo residual $\tilde{\mathbf{R}}_{le}$ defined by

$$\begin{aligned}&\tilde{\mathbf{R}}_{mg}= \left. \frac{{\hat{\delta }} \mathbf{R}_{mg} }{{\hat{\delta }} {\varvec{\phi }}} \right| _{ \genfrac{}{}{}1{D\bar{\mathbf{u}}}{D{\varvec{\phi }}} = D \bar{\mathbf{u}} D {\varvec{\phi }}} \quad \text {and} \quad \tilde{\mathbf{R}}_{le}= \left. \frac{{\hat{\delta }} \mathbf{R}_{le} }{{\hat{\delta }} {\varvec{\phi }}} \right| _{ \genfrac{}{}{}1{D\bar{\mathbf{u}}}{D{\varvec{\phi }}} = D \bar{\mathbf{u}} D {\varvec{\phi }}} ,\nonumber \\ \end{aligned}$$

(27)

respectively, where $D \bar{\mathbf{u}} D {\varvec{\phi }}$ is boundary condition velocity field. $D \bar{\mathbf{u}} D {\varvec{\phi }}$ represents the derivatives of prescribed essential boundary conditions $\bar{\mathbf{u}}$ with respect to sensitivity parameters ${\varvec{\phi }}$ which is input data for microanalysis. Sensitivity problem (26) is solved after converged solution for primal problem is obtained. Then the average stress sensitivity $D \varvec{\hat{P}} / D \varvec{U}_M$ is calculated with direct differentiation as

$$\begin{aligned}&\frac{ D \varvec{\hat{P}}}{D \varvec{U}_M}= \frac{1 }{V_0}\sum _{e=1}^{n_e} \sum _{g=1}^{n_g}w_{mg}\; J_{mg}\; \left. \frac{{\hat{\delta }} \varvec{P}_{mg} }{{\hat{\delta }} {\varvec{\phi }}} \right| _{ \genfrac{}{}{}1{D\mathbf{p}_e}{D{\varvec{\phi }}} = D \mathbf{p}D {\varvec{\phi }}} \, , \end{aligned}$$

(28)

where $D \mathbf{p} D {\varvec{\phi }}$ is the result of sensitivity analysis.

6 Automation of $\hbox {FE}^2$ procedure

A pseudocode of automated displacement based $\hbox {FE}^2$ analysis is given in Algorithm 1 for the analysis on macro level and in Algorithm 2 for microanalysis. Flowchart for macroelement is applicable on arbitrary finite element formulated on virtual work principle as presented in Sect. 5. Local macroscopic stretch tensor $\varvec{U}_M$ determines essential boundary conditions on associated RVE (see (3), (4)). Lagrange finite elements are introduced to impose periodicity constraints on displacements of nodes on RVE boundary. Primal analysis of RVE is in Algorithm 2 augmented with boundary conditions related sensitivity analysis as explained in 5.1. Sensitivity of prescribed boundary conditions on variation of $\varvec{U}_M$ is defined on the input. When static equilibrium is achieved under given equality constraints, microanalysis returns to the macroscopic integration point average stress tensor $\varvec{\hat{P}}$ and its sensitivity $D \varvec{\hat{P}} D \varvec{U}_M$ on variation of $\varvec{U}_M$. Convergence of the iterative Newton–Raphson method has to be achieved simultaneously on micro and macro level on each load step for the overall convergence of the $\hbox {FE}^2$ method.

7 Accuracy and numerical efficiency of proposed $\hbox {FE}^2$ formulation

Various automated $\hbox {FE}^2$ formulations with isogeometric and standard finite element microanalysis are tested for consistency, accuracy and numerical efficiency consideration on chosen computational homogenisation examples. All numerical examples are performed with three-dimensional solid finite elements. Procedures of primal and sensitivity analyses shown in Algorithm 2 were obtained from [10]. Procedure of primal isogeometric analysis follows formulation presented in [28]. All calculations are executed without parallelization on 8 GB RAM and 2.8 GHz processor.

7.1 Test of consistency of micro–macro coupling

A test with homogeneous material was considered to show that the results of implemented $\hbox {FE}^2$ procedure are identical to those of single scale analysis in the case of homogeneous micro structure. A standard Cooke membrane is discretized with a mesh of $4 \times 1 \times 4$ standard linear Lagrange (H1) finite elements for single scale analysis and for macro level of two-scale $\hbox {FE}^2$ analysis. The system, load and material data are given in Fig. 1. A. For microscale analysis are standard linear and quadratic Lagrange (H1 and H2) finite elements and isogeometric finite elements with linear and quadratic Bezier splines (ISOB1 and ISOB2) chosen to show that in the case of homogeneous microstructure the results obtained with $\hbox {FE}^2$ analysis do not depend on the element formulation on micro level. Hence, homogeneous RVE was discretized with a $2 \times 2 \times 2$ finite elements mesh for linear formulations and with a single element mesh for quadratic formulations. Size of RVE does not affect the resulting microstress field or its derivatives in $\hbox {FE}^2$ analysis. The load was applied in ten equal load steps. The resulting displacements of point P (see Fig. 1) obtained with different $\hbox {FE}^2$ formulations are compared to the results of single scale analysis. The results presented in Table 1 show that in case of homogeneous microstructure all two-scale $\hbox {FE}^2$ analyses give numerically the same results as single scale analysis within machine precision accuracy.

Fig. 1

a Macrostructure: system, load and expected result. b Porous microstructure: geometry and material data

Table 1 Vertical displacement of point P in a homogeneous Cooke membrane test for single scale analysis and different two-scale $\hbox {FE}^2$ analyses

7.2 Numerical efficiency consideration of proposed $\hbox {FE}^2$ formulation

A computational homogenisation example of porous material is considered to justify the proposed $\hbox {FE}^2$ formulation in terms of numerical efficiency. Here the performance of conventional $\hbox {FE}^2$ formulation with asymmetric deformation gradient as strain measure is compared to proposed $\hbox {FE}^2$ formulation with symmetric stretch tensor as strain measure. Macrostructure is a Cooke membrane and microstructure is represented by a cubic RVE with spherical opening in its center. Volume fraction of spherical opening is $0.1~\%$. The system, load and material data are given in Fig. 1. Cooke membrane is on macro level discretized with a mesh of $4 \times 1 \times 4$ standard linear Lagrange (H1) finite elements. Computational model of cubic RVE is composed of six equal patches, each of them is associated to one RVE boundary plane and one sixth of spherical opening in the center of RVE (see Fig. 1). Each of these six equal patches is discretized with standard linear (H1) and quadratic (H2) Lagrange finite elements and quadratic isogeometric finite elements (ISOB2) and quadratic standard Lagrange finite elements (H2) for several mesh densities (see Table 2). The load was applied in ten equal load steps. The resulting vertical displacement of point P (see Fig. 1) obtained with conventional and new $\hbox {FE}^2$ formulation together with associated computational time per one Newton–Raphson iteration on macro level is shown in Table 2. When compared to conventional $\hbox {FE}^2$ formulation, the proposed $\hbox {FE}^2$ formulation makes an additional calculation and linearisation of a tensor square root in macroanalysis which increases evaluation time. On the other hand, less complex boundary conditions related sensitivity analysis of RVE in the proposed $\hbox {FE}^2$ formulation reduces global tangent matrix evaluation time. Obtained total reduction of average CPU time for this particular example varies between 17 and $27~\%$ for one Newton–Raphson iteration on macroscale (see Table 2). CPU time is most reduced in the case of isogeometric microanalysis, which also exhibits most favorable ratio between accuracy and computational cost (CPU time and memory) for the coarsest RVE mesh. Reduced amount of needed memory space is also noted (see Table 2).

Table 2 Vertical displacement of point P ($w_P$) and computational times for one Newton–Raphson iteration in a porous Cooke membrane test

The convergence of $\hbox {FE}^2$ analysis is then studied with mesh refinement on macro scale. RVE mesh has a fixed size of $6 \cdot (2 \times 2 \times 2)$ finite elements. Quadratic isogeometric finite elements (ISOB2) were used for microanalysis and quadratic standard Lagrange finite elements (H2) for macroanalysis. The convergence of the resulting macroscopic displacement $w_P$ is shown in Fig. 2 with regard to number of macroscopic degrees of freedom (DOF).

Fig. 2

Convergence of vertical displacement of point P ($w_P$) in a porous Cooke membrane test with increasing of macroscopic finite element mesh density (degrees of freedom—DOF)

Fig. 3

a Vertical displacement of point P ($w_P$) and b ratio (r) between maximal calculated microscopic and macroscopic Mises stress in a porous Cooke membrane test with regard to volume fraction of openings (f)

The effect of volume fraction of openings on resulting vertical displacement $w_P$ is presented next. The porosity was increased to the point where the first opening closes at maximal load (further increase of porosity was not possible since self contact was not considered in finite element formulation). Figure 3 shows that the resulting vertical displacement $w_P$ increases proportional to volume fraction of the openings while the ratio between maximal microscopic and maximal macroscopic Mises stress tends to increase exponentially. The point of maximal macroscopic Mises stress is approximately at maximal tension at the top of constrained end. Maximal microscopic Mises stress was located at the bottom of the Cooke’s membrane in nodes located from 24 mm to 27 mm away from constrained end and being closer to constrained end for higher values of f.

7.3 Agreement between numerical and analytical estimates for effective elastic stiffness tensor

Accuracy of the presented $\hbox {FE}^2$ procedure is tested on a computational homogenisation example of porous linear elastic material. Linear elastic material is chosen to stand comparison to known analytical solution for effective elastic stiffness tensor $\varvec{C}_{eff}$ estimate derived by Nemat-Nasser ([11–13]). Due to linear elasticity the presented $\hbox {FE}^2$ procedure is simplified. Instead of stretch tensor $\varvec{U}$ small strain deformation tensor $\varvec{E}=\frac{1}{2} \,(\varvec{H}+\varvec{H}^T)$ is applied and its six independent components are used for sensitivity analysis. Strain density function is given by $W(\varvec{E})= \frac{\lambda }{2}\,(\text {tr}(\varvec{E}))^2+\mu \,\text {tr}(\varvec{E}^2)$ and stress tensor is defined by $\mathbf{S}= \hat{\delta } W / \hat{\delta } \mathbf{E}\, .$ Macrostructure is a cube with dimensions 10 mm $\times$ 10 mm $\times$ 10 mm with fixed clamped end condition on one side and a prescribed uniform displacement $u=1$ mm on the opposite side. The microstructure is represented by a linear elastic cube (RVE) with spherical opening in its center. Volume fraction of spherical opening is $0.1~\%$. Geometry of RVE is given in Fig. 1. B. Macroscale analysis is preformed by one standard linear Lagrange (H1) finite element. On micro level, different element definitions and mesh densities are used for accuracy and efficiency comparison of the considered finite element formulations. An objective mesh of a sphere is composed of six equal patches, as described in example 7.2. The exact geometry of the considered quadratic surface can only be represented by quartic Bezier splines (see [29, 30]). Hence, the chosen isogeometric $\hbox {FE}^2$ procedure for this numerical homogenisation example performs microanalysis with isogeometric finite elements with quartic Bezier splines (ISOB4). The results were obtained also for standard $\hbox {FE}^2$ procedures that analyze microstructure with standard linear and quadratic Lagrange (H1 and H2) finite elements. The numerical solutions for components of effective elastic stiffnes tensor

$$\begin{aligned} \varvec{C}_{eff} =\left[ \begin{array}{llllll} \bar{C}_{1111} &{} \bar{C}_{1122} &{} \bar{C}_{1122} &{}\quad 0&{}\quad 0&{}\quad 0 \\ &{} \bar{C}_{1111} &{}\bar{C}_{1122} &{}\quad 0&{}\quad 0&{}\quad 0 \\ &{} &{} \bar{C}_{1111} &{}\quad 0&{}\quad 0&{}\quad 0 \\ &{} &{} &{} \bar{C}_{2323}&{}\quad 0&{}\quad 0 \\ &{} \text {symm.}&{} &{}&{} \quad \bar{C}_{2323}&{}\quad 0 \\ &{} &{} &{} &{} &{} \quad \bar{C}_{2323} \end{array} \right] \end{aligned}$$

(29)

of porous linear elastic material with associated computational time are given in Table 3 for various RVE mesh densities and all considered $\hbox {FE}^2$ formulations. One iteration of Newton–Raphson method returns converged solution with machine precision since it is a linear problem. $\hbox {FE}^2$ analysis converges to same solutions for all considered $\hbox {FE}^2$ formulations, where isogeometric $\hbox {FE}^2$ formulation exhibits highest convergence rate and superior numerical efficiency of $\hbox {FE}^2$ analysis in terms of most favorable ratio between solution accuracy and computational time. This result confirms that exact modeling of microstructure geometry produces superior results of numerical homogenisation procedure. The obtained numerical solutions are compared to Nemat-Nassers analytical solution for effective elastic stiffness tensor estimate $\varvec{C}_{eff}$ of periodic multiphase linear elastic materials (see [11]). Nemat-Nasser assumed in all directions infinite periodic, linear elastic and isotropic microstructure and derived a Fourier series expansion of displacement and stress fields. If RVE is a cube with boundary size a and spherical opening of radius b, effective elastic stiffness tensor $\varvec{C}_{eff}$ of periodic porous linear elastic material is estimated as

$$\begin{aligned}&\varvec{C}_{eff}=\varvec{C} \left( \varvec{1} - f\, ( \varvec{1}^{(4s)}-\varvec{S}^p )^{-1} \varvec{1}^{(4s)} \right) , \end{aligned}$$

(30)

where $\varvec{1}^{(4s)}$ is fourth order symmetric unit tensor and $\varvec{S}^p$ reference elastic stiffness tensor. Tensor $\varvec{S}^p$ has cubic symmetry like $\varvec{C}_{eff}$ (see (29)) and its nonzero components are written as

$$\begin{aligned}&\varvec{S}^p_{1111}=\sum \sum _{\varvec{v} \ne \varvec{0}} \sum f \, g(\varvec{v})^2 \, (v_1/|\varvec{v}|)^2, \nonumber \\&\quad \varvec{v} = \pi /a \,(v_1, v_2, v_3), \; v_i \in \mathbb {Z} \; \; \forall i \end{aligned}$$

(31)

$$\begin{aligned}&\varvec{S}^p_{1122}= \sum \sum _{\varvec{v} \ne \varvec{0}} \sum f \, g(\varvec{v})^2 \, (v_1/|\varvec{v}|)^4,\end{aligned}$$

(32)

$$\begin{aligned}&\varvec{S}^p_{2323}= \sum \sum _{\varvec{v} \ne \varvec{0}} \sum f \, g(\varvec{v})^2 \, (v_2/|\varvec{v}|)^2 (v_3/|\varvec{v}|)^2, \end{aligned}$$

(33)

where $|\varvec{v}|$ is Euclidian norm of vector $\varvec{v}$, f volume fraction of spherical opening and

$$\begin{aligned} g(\varvec{v} )=3 \, (\sin (b\, |\varvec{v} |) - b \, |\varvec{v} | \cos (b \, |\varvec{v} |) )/(b \, |\varvec{v} |)^3 \quad \text {for }|\varvec{v} | \ne 0. \end{aligned}$$

(34)

Analytical estimates for $\varvec{C}_{eff}$ of considered periodic porous linear elastic material are calculated for $v_i \in \{-n, n\} \; \; \forall i \in \{1,2,3\}$ and various values of n and presented in Table 4. All calculated numerical solutions in Table 3 and analytical estimates converge to same solution which validates the accuracy of the presented $\hbox {FE}^2$ implementation. The C code for evaluation of Nemat-Nassers $\varvec{C}_{eff}$ estimate is generated by AceGen so that computation time can be compared to the computation time of the presented $\hbox {FE}^2$ procedure. Evaluation of Nemat-Nassers analytical estimate gives solution with three correct digits in 237 seconds, whereas the standard $\hbox {FE}^2$ procedure that performs microanalysis with standard quadratic Lagrange element (H2) achieves this in 60 seconds and isogeometric $\hbox {FE}^2$ procedure in 66 seconds.

Table 3 Convergence of $\bar{C}_{ijkl}/ C_{ijkl}$ ratios for effective elastic stiffnes tensor $\varvec{C}_{eff}$ evaluated with isogeometric and standard $\hbox {FE}^2$ procedures and associated total computational time

Table 4 Convergence of $\bar{C}_{ijkl}/ C_{ijkl}$ ratios for Nemat-Nassers analytical estimate of $\varvec{C}_{eff}$ with associated computation time

8 Conclusions

This paper presents a new $\hbox {FE}^2$ formulation that significantly reduces the computational cost of two-scale $\hbox {FE}^2$ analysis, proves its compliance to energy averaging theorem and discusses its consistency, accuracy and numerical efficiency on numerical homogenisation examples. The new $\hbox {FE}^2$ formulation introduces symmetric stretch tensor as a macro strain measure instead of conventionally used asymmetric deformation gradient to determine the prescribed boundary conditions of underlying microstructure (RVE). This reduces the computational cost of boundary conditions related sensitivity analysis of RVE that is performed on micro level to evaluate the local macroscopic tangent operator. Stretch tensor is matrix square root of Cauchy–Green tensor which is evaluated together with its first and second derivatives with automatic differentiation of appropriate scalar generating function to avoid the difficulties associated with evaluation of matrix square root based on polar decomposition. The new two-scale $\hbox {FE}^2$ scheme was implemented in symbolic code generation system AceGen which automates derivation of quantities needed in primal and sensitivity analyses on micro level and primal analysis on macro level of $\hbox {FE}^2$ procedure and also simultaneously performs automatic differentiation and optimization of expressions. The $\hbox {FE}^2$ flowchart based on AceGen enables objective comparison of different $\hbox {FE}^2$ formulations. Various $\hbox {FE}^2$ formulations with isogeometric and standard finite element microanalysis were developed and tested on numerical homogenisation examples to study consistency, accuracy and numerical efficiency of $\hbox {FE}^2$ analysis. Consistency of micro–macro coupling is first tested on a homogeneous material. Results obtained with $\hbox {FE}^2$ analysis and single scale FEM analysis are numerically identical with machine precision for all considered $\hbox {FE}^2$ formulations. New $\hbox {FE}^2$ formulation was further tested on homogenisation of a porous hyperelastic material. Results obtained with conventional and new $\hbox {FE}^2$ formulation show that introduction of symmetric stretch tensor as a strain measure contributes to a total reduction of computation time between 17 and $27~\%$ depending on chosen finite element formulation for microanalysis. Reduced sensitivity analysis lowers also memory usage during calculation. Accuracy of the presented $\hbox {FE}^2$ formulation is further verified on numerical homogenisation of linear elastic porous material for which Nemat-Nasser (see [11]) derived an analytical estimate of effective elastic stiffness tensor. All considered isogeometric and standard $\hbox {FE}^2$ procedures converge in both numerical examples to same converged values and in latter example to Nemat-Nassers analytical estimate. The obtained results confirm better convergence rate regarding number of degrees of freedom for higher order isogeometric $\hbox {FE}^2$ analysis and show comparable numerical efficiency in terms of most favorable ratio between solution accuracy and computational time of higher order isogeometric $\hbox {FE}^2$ analysis when compared to standard $\hbox {FE}^2$ analysis with quadratic Lagrange finite elements.