Computational electro-chemo-mechanics of lithium-ion battery electrodes at finite strains

Abstract

A finite strain theory for electro-chemo-mechanics of lithium ion battery electrodes along with a monolithic and unconditionally stable finite element algorithm for the solution of the resulting equation systems is proposed. The chemical concentration and the displacement fields are introduced as independent variables for the formulation diffusion-mechanics coupling. The electrochemistry of the surface reaction kinetics is imposed at the boundary in terms of the Butler–Volmer kinetics. The intrinsic coupling arises from both stress-assisted diffusion in electrodes and ion mass flux induced volumetric deformation. We demonstrate the theoretical modeling aspects and algorithmic performance through representative initial boundary value problems. The proposed finite strain theory is especially well suited for electrode materials like silicon which exhibit large volume changes during lithium insertion/ extraction. We demonstrate the inadequacy of small-strain theories for diffusion-mechanics coupling in silicon based anode materials. The proposed numerical algorithm shows excellent performance, demonstrated for 2D and 3D representative numerical examples.

1 Introduction

In addition to being the leading energy storage systems in portable electronic devices, the advent of the electro vehicles (EVs) and hybrid electro vehicles (HEVs) has increased the popularity of lithium-ion batteries tremendously. Main challenge in the use of lithium ion batteries in EVs and HEVs is the limited lifetime along with need for high capacity electrode materials. The conventional batteries might perform up to around several hundred electro-chemical cycles which is far from being feasible for HEV and EV applications. In the recent years, silicon has emerged as a promising candidate for anode material in Li-ion batteries thanks to its highest capacity among all known anode materials and low discharge potential [15]. However, the theoretical capacity of silicon cannot be fully utilized due to the high volume changes along with concentration gradients, leading to cracking and pulverization during electro-chemical cycles [9].

A typical Li-ion battery consists of anode, cathode, separator, and current collectors as depicted in Fig. 1. The anode consists of graphite, silicon or carbon where the latter is usually embedded into polymer binder. The cathode is an oxide compound embedded in a PVDF binder which is continuously interconnected enabling electron transfer to the current collector. The separator consists of electrolyte, e.g. a lithium salt, and a porous polymer, e.g. polyolefin. During charging process, Li-ions are extracted from positive electrode material through oxidation reactions and travel from cathode to anode through the separator and intercalates into anode particles together with the electrons arriving through charging device connecting the current collectors. The reactions are reversed during the discharge process.

Fig. 1

Schematic of a charging process of a Li-ion battery, consisting of current collectors, anode, cathode and separator. a Onset of charging in the discharged state and b fully charged state. Li$^+$ ions are extracted from the metal-oxide and travel from the active cathode material to the anode through the electrolyte. The extraction of Li-ions from the cathode induces large volume shrinkage of the particles, causing highly inhomogeneous stress fields and fracture

The chemo-mechanical response of Li-ion batteries is critical in battery performance due to the complex interplay between mechanical degradation and electro-chemical performance [22]. Lithium insertion into and extraction from the electrode particles during the electrochemical cycles leads to volume changes. Stresses generated due to the gradients of lithium concentration under high insertion/extraction rates or under repeated cycles lead to micro-cracks resulting in comminution of compund oxide particles in the electrode particles. In LiMn$_2$O$_4$ (LMO) cathodes, volume change is around $6.5$ % whereas in negative electrode such as Si, this amount of swelling might be as high as $400$ %. We refer to the seminal work of Doyle, Fuller & Newman [17] for the description of intercalation kinetics of Li-ions into electrode particles. This theory is further advanced by Christensen & Newman [13, 14] and Zhang, Sastry & Shyy [33, 34], Christensen [12] to include diffusion mechanics coupling (DMC) at small strain setting. The chemo-mechanical coupling is based on the diffusion of lithium ions under concentration and pressure gradients where the mechanical deformation results from the volumetric strains induced from ion concentration change. In these contributions, the potentiodynamic surface ion flux kinetics is generally described in terms of Butler–Volmer-type reaction kinetics. Cheng & Verbrugge [10], Deshpande, Cheng & Verbrugge [16], and Golmon et al. [20] applied small strain DMC theories for the investigation of the effect of size, geometry and surface structure on the stress generation and stress based crack analysis during lithiation and delithiation. Du et al. [19] have employed a surrogate-based analysis by using the diffusion-mechanics coupling in order to investigate the influence of cycling rate, geometry and material parameters in order to maximize the battery performance. Seo et al. [27] simulated three dimensional realistic LMO particle geometries obtained from atomic force microscopy. An alternative approach for Li-ion intercalation-deintercalation kinetics is the use of Cahn–Hilliard-type [7, 8] phase-field models for electrode particles showing phase segregation. Cahn–Hilliard-type diffuse-interfaces approach has been applied to Li-ion electrodes by Bazant and co-workers [6, 31]. The extension of this approach to a thermodynamically consistent model of chemo-mechanics of Li-ion electrodes which accounts for swelling and phase segregation has been proposed by Anand [1]. For and alternative derivation of Cahn–Hilliard-type diffuse-interface approach in terms of microforce balance, we refer to Gurtin [21] and the recent work by Miehe, Hildebrand & Böger [24] on its variational structure. A framework of chemo-elasticity at finite strains, accounting standard and gradient-enhanced Cahn–Hilliard-type diffusion, was outlined recently by Miehe, Ulmer & Mauthe [25] based on a rigorous construction of variational potentials.

Understanding the mechanisms leading to capacity fade in silicon based negative electrodes and the microstructural design methodoligies accomodating large volume changes without pulverization is currently an active field of research [32]. The material suffers significantly from cracking resulting from large stresses generated during electro-chemical cycles. We refer to the excellent review of Kasavajjula et al. [23] on the methods adopted for reducing the capacity fade and improving durability in silicon-based anodes. Experimental measurements carried out by Sethuraman et al. [29] show significant stress-potential coupling in silicon which can be modeled by including stress dependence of chemical potential. The dependence of elastic constants on the concentration level have been quantified by Sethuraman et al. [28]. Also, significant plastic flows driven by deviatoric stresses occur during lithiation and delithiation of silicon [11, 30, 35]. The tailored design of battery structures from nano- to micro-scales is crucial for the commercialization of silicon based anode systems. Albeit tremendous efforts in the development of theories for coupled chemo-mechanics of battery electrodes, there is still a lack of rigorous finite strain theory for the canonical description of diffusion-mechanics coupling. Recently, Bower, Guduru & Sethuraman [5] have proposed a brief finite strain theory for a whole lithium-ion battery cell incorporating electrical, chemical and mechanical fields and inelastic phenomena. They applied the theory for the validation of stress potential coupling and plastic flow in silicon anode in 1D.

In this work, we formulate a thermodynamically consistent finite strain model for stress assisted diffusion and diffusion induced swelling phenomena in Li-ion battery electrodes, and construct details of its numerical implementation. To this end, we confine ourselves to the modeling of anodic and cathodic electrode particles and omit the thermal and electric fields in our treatments as well as rate-independent mechanical response. Furthermore, we focus on the description of nonlinear chemo-elasticity for the bulk response, and neglect at this stage inelastic effects and phase segregation phenomena. The global and the local forms of the balance equations and the dissipation inequality governing the coupled chemo-mechanics are introduced. On the numerical side, a robust and modular numerical scheme for the resulting partial differential equations is proposed. The electro-chemical reaction kinetics is incorporated into the model via Butler–Volmer-type surface flux. The proposed finite strain theory is especially well suited for electrode materials like silicon which exhibit large volume changes during lithium insertion/extraction. However, the proposed framework is general and can be applied to various anode/cathode particles. The small strain theory of Sastry et al. [33, 34] is recovered in the limiting case.

The paper is organized as follows: in Sect. 2, we start our investigations by introducing the primary fields governing the finite elasticity and the species diffusion. In Sect.  3, we introduce a particular set of constitutive relations describing the mechanical stresses and the mass flux of Li-ions in agreement with the postulates of the dissipation principle. The electro-chemistry of surface reactions in terms of Butler–Volmer kinetics is discussed in Sect. 4. Section 5 presents a compact recipe for the time–space discretization of the resulting partial differential equations and the solution based on Galerkin-type finite element formulation. We investigate Li$_{x}$Si anode and Li$_x$Mn$_2$O$_4$ cathode particles as benchmark examples in Sect. 6.

2 Finite elasticity coupled with species diffusion

2.1 The primary fields and their gradients

The boundary-value-problem for the modeling of diffusion in elastic solids is a coupled two-field problem, characterized by the deformation field of the solid and the concentration of the Li-ions which diffuse through the solid

$$\begin{aligned} {\varvec{\varphi }}: {\left\{ \begin{array}{ll} {\mathcal B}_0\times {\mathcal T}\rightarrow {\mathcal B}_t\subset {\mathcal R}^3 \\ ({\varvec{ X }},t) \mapsto {\varvec{ x }}={\varvec{\varphi }}({\varvec{ X }},t) \end{array}\right. } \quad c: {\left\{ \begin{array}{ll} {\mathcal B}_0\times {\mathcal T}\rightarrow {\mathcal R}\\ ({\varvec{ X }},t) \mapsto c({\varvec{ X }},t) \end{array}\right. } \end{aligned}$$

(1)

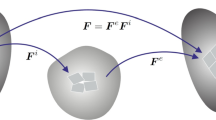
The deformation field ${\varvec{\varphi }}$ maps at time $t\in {\mathcal T}$ points ${\varvec{ X }}\in {\mathcal B}_0$ of the reference configuration ${\mathcal B}_0\subset {\mathcal R}^3$ onto points ${\varvec{ x }}\in {\mathcal B}_t$ of the current configuration ${\mathcal B}_t\subset {\mathcal R}^3$. The concentration field $c$ represents at a point of the solid the number of lithium ions with respect to the volume of the undeformed configuration, see Fig. 2. The gradients of these fields define the material deformation gradient and the material concentration gradient

(2)

respectively. The deformation gradient ${\varvec{ F }}$ itself, its cofactor $\mathop {\hbox {cof}}[{\varvec{ F }}]= \det [{\varvec{ F }}] {\varvec{ F }}^{-T}$ and its Jacobian $J{:}=\det [{\varvec{ F }}]$ characterize the deformation of infinitesimal line, area and volume elements

$$\begin{aligned} d{\varvec{ x }}= {\varvec{ F }}d{\varvec{ X }}\, , \quad d{\varvec{ a }}= \mathop {\hbox {cof}}[{\varvec{ F }}] d{\varvec{ A }}\, , \quad dv = \det [{\varvec{ F }}] dV \, . \end{aligned}$$

(3)

The deformation map ${\varvec{\varphi }}$ is constrained by the condition $J {:}= \det [{\varvec{ F }}] > 0$ in order to ensure non-penetrable deformations. Furthermore, let ${\varvec{ g }},{\varvec{ G }}\in Sym_+(3)$ be the standard metrics of the current and reference configurations ${\mathcal B}_0$ and ${\mathcal B}_t$. Then

$$\begin{aligned} {\varvec{ C }}:= {\varvec{ F }}^T {\varvec{ g }}{\varvec{ F }}\quad \quad \text{ and }\quad \quad {\varvec{ c }}:= {\varvec{ F }}^{-T} {\varvec{ G }}{\varvec{ F }}^{-1} \end{aligned}$$

(4)

are convected current and reference metrics, often denoted as right and left Cauchy–Green tensors, respectively. The spatial concentration gradient is obtained from a parametrization of the concentration field by the spatial coordinates ${\varvec{ x }}={\varvec{\varphi }}({\varvec{ X }},t)$, yielding the relationship

(5)

Fig. 2

Multifield initial boundary value problem of chemo-mechanics. The boundary $\partial {\mathcal B}_0$ of the solid is decomposed into Dirichlet and Neumann-type boundaries $\partial {\mathcal B}^\varphi _0\cup \partial {\mathcal B}^t_0$ for mechanical problem and $\partial {\mathcal B}^c_0\cup \partial {\mathcal B}^h_0$ for diffusion problem, respectively

2.2 Stress tensors, species flux vectors and chemical potential

2.2.1 Stress tensors

Consider a part ${\mathcal P}_0\subset {\mathcal B}_0$ cut out of the reference configuration ${\mathcal B}_0$ and its spatial counterpart ${\mathcal P}\subset {\mathcal B}_t$, with boundaries $\partial {\mathcal P}_0$ and $\partial {\mathcal P}_t$, respectively. The total stress vector ${\varvec{ t }}$ acts on the surface element $d{\varvec{ a }}\subset \partial {\mathcal P}_t$ on the deformed configuration and represents the force that the rest of the body ${\mathcal B}_t\setminus {\mathcal P}_t$ exerts on ${\mathcal P}_t$ through $\partial {\mathcal P}_t$. Cauchy’s stress theorem defines the traction to depend linearly on the outward surface normal

$$\begin{aligned} {\varvec{ t }}({\varvec{ x }},t;{\varvec{ n }}) := {\varvec{\sigma }}({\varvec{ x }},t){\varvec{ n }} \end{aligned}$$

(6)

through the total Cauchy stress tensor ${\varvec{\sigma }}$. Now consider the identity ${\varvec{ T }}dA ={\varvec{ t }}da$ by scaling the (true) spatial force ${\varvec{ t }}da$ by the reference area element $dA$. This induces the definition of the nominal stress tensor ${\varvec{ P }}$ by setting

$$\begin{aligned} {\varvec{ P }}d{\varvec{ A }}= {\varvec{\sigma }}d{\varvec{ a }}\quad \text{ with }\quad {\varvec{ P }}:= (J {\varvec{\sigma }}) {\varvec{ F }}^{-T} \, , \end{aligned}$$

(7)

where the area map (3)$_2$ was inserted. Here, $\tilde{{\varvec{\sigma }}} := J {\varvec{\sigma }}$ is denoted as the total Kirchhoff stress and ${\varvec{ S }}:= {\varvec{ F }}^{-1} \tilde{{\varvec{\sigma }}} {\varvec{ F }}^{-T}$ as the symmetric Lagrangian stress.

2.2.2 Species flux vectors

Consider a species outflux $h$ through the surface element $d{\varvec{ a }}$ of $\partial {\mathcal P}_t$ in the current configuration, that depends linearly on the outward normal

(8)

through the spatial species flux vector . A modified species flux $H$ is then defined by the identity $HdA = hda$, i.e. by scaling by the infinitesimal reference area $dA$. This induces the definition of the a material species flux by setting

(9)

where we made use of the area map (5)$_2$. In what follows, we denote as the Kirchhoff-type species flux.

2.2.3 Electrochemical potential

The flux of the species, i.e. the Li-ions, is driven by the gradient of a chemical potential field. It is a scalar field

$$\begin{aligned} \mu : {\left\{ \begin{array}{ll} {\mathcal B}_0\times {\mathcal T}\rightarrow {\mathcal R}\\ ({\varvec{ X }},t) \mapsto \mu ({\varvec{ X }},t) \end{array}\right. } \end{aligned}$$

(10)

parametrized by the material coordinates ${\varvec{ X }}\in {\mathcal B}_0$. Alternatively, we may parametrize the chemical potential by the spatial coordinates ${\varvec{ x }}={\varvec{\varphi }}({\varvec{ X }},t)$.

2.3 General equations in finite elasticity coupled with diffusion

2.3.1 Global equations

The general equations which drive the coupled deformation-diffusion problem are formulated as balances for a part ${\mathcal P}_t\subset {\mathcal B}_t$ of the deformed configuration. The diffusion of Li-ion species through the elastically deforming solid is a solid-species-mixture. No mass production due to chemical reactions is assumed. As a consequence, separate balances for the mass of the solid and the species may be formulated. The conservation of solid mass reads

$$\begin{aligned} \int _{{\mathcal P}_t} \rho \, dv = \int _{{\mathcal P}_0} \rho _0\, dV \, , \end{aligned}$$

(11)

where $\rho ({{\mathbf {x}}},t)$ and $\rho _0({\varvec{ X }})$ are the solid density fields of the current and the reference configurations, respectively. With regard to the transport of Li-ions, the part ${\mathcal P}_t\subset {\mathcal B}_t$ is considered as a control volume. The conservation of species then reads

$$\begin{aligned} \frac{d}{dt} \int _{{\mathcal P}_t} \rho c \,dv = - \int _{\partial {\mathcal P}_t} h \,da \end{aligned}$$

(12)

in terms of the Li-ion concentration $c({{\mathbf {x}}},t)$ defined in (1) and the spatial species out-flux $h({{\mathbf {x}}},t)$ introduced in (8). When neglecting inertia effects, the conservations of linear and angular momentum of the part ${\mathcal P}_t\subset {\mathcal B}_t$ degenerate to the equilibrium conditions

$$\begin{aligned}&\int _{\partial {\mathcal P}_t} {\varvec{ t }}\,da + \int _{{\mathcal P}_t} \rho {\varvec{\gamma }}\,dv = {\varvec{ 0 }}\quad \quad \text{ and }\quad \nonumber \\&\int _{\partial {\mathcal P}_t} {\varvec{ x }}\times {\varvec{ t }}\,da + \int _{{\mathcal P}_t} {\varvec{ x }}\times \rho {\varvec{\gamma }}\,dv = {\varvec{ 0 }}, \end{aligned}$$

(13)

where ${\varvec{\gamma }}({\varvec{ x }},t)$ is a given body force field.

2.3.2 Local equations

Pulling back these integrals to the reference configuration by using the volume map (3)${}_3$, inserting the definitions (6)–(9) for the traction ${\varvec{ t }}$ and the species out-flux $h$, using the Gauss theorem and the standard localization argument, we end up with the four conservation equations

(14)

defined on the reference configuration ${\mathcal B}_0$ for the quasi-static problem under consideration. Recall in this context the Piola transformations and $\hbox {Div} [{\varvec{ P }}] = J \hbox {div} [\tilde{{\varvec{\sigma }}}/J]$, which allow to express the above material divergence terms as spatial divergence terms of the Kirchhoff-type species flux and the Kirchhoff stress tensor $\tilde{{\varvec{\sigma }}} {:}= J {\varvec{\sigma }}$. Furthermore, note that the last equations simply states the symmetry of the Cauchy stress ${\varvec{\sigma }}$. Then, the conservation equations in the Eulerian setting read

(15)

per unit undeformed volume.

2.4 Principle of irreversibility and constitutive equations

2.4.1 Dissipation principle

The formulation of the constitutive equations must be consistent with a principle of irreversibility, consistent with the second axiom of thermodynamics. Let $\varPsi$ be the free energy density per unit mass stored at a spatial point ${\varvec{ x }}\in {\mathcal B}_t$ of the mixture, consisting of the solid and the Li-ion species. Then, if irreversible processes such as the Li-ion transport are involved, the evolution of the energy in the part ${\mathcal P}_t\subset {\mathcal B}_t$ must be less than the power of the chemo-mechanical external actions on ${\mathcal P}_t$. This is expressed by the global dissipation postulate

$$\begin{aligned} \frac{d}{dt} \int _{{\mathcal P}_t} \!\! \rho \varPsi \,dv \le \int _{\partial {\mathcal P}_t} \!\! {\varvec{ t }}\cdot {\varvec{ v }}\,da + \int _{{\mathcal P}_t} \rho {\varvec{\gamma }}\cdot {\varvec{ v }}\,dv - \int _{\partial {\mathcal P}_t} \!\! \mu h \,da \, . \end{aligned}$$

(16)

The first two terms on the right side is the mechanical power due to tractions and body forces, where ${\varvec{ v }}:= \dot{\varvec{\varphi }}\circ {\varvec{\varphi }}^{-1}$ is the spatial velocity field. The last term characterizes the out-flux of energy due to the Li-ion species transport, based on the chemical potential $\mu$ introduced in (10). Pulling back these integrals to the referece configuration with the volume map (3)$_3$, inserting the definitions (6)–(9) for the traction ${\varvec{ t }}$ and the species out-flux $h$, using the Gauss theorem, the standard localization argument and inserting the balance equations (14) gives the local dissipation postulate

(17)

For dissipative transport problems in elastic solids, this eqation can be splitted up into a part due to local actions and a part due to diffusion

(18)

where we introduced the negative material gradient of the chemical potential with spatial counterpart

(19)

in analogy to (5).

2.4.2 Objective free energy function

The constitutive equations are constructed such that the above dissipation conditions (17) are a priori satisfied for all processes. Assuming a local theory of the grade one, free energy is assumed to depend on the primary variables (1) and its first gradients

$$\begin{aligned} \varPsi = \widetilde{\varPsi }({\varvec{\varphi }}, \nabla {\varvec{\varphi }}, c, \nabla c; {\varvec{ X }}) \, . \end{aligned}$$

(20)

Demanding invariance of $\widetilde{\varPsi }$ with respect to rigid deformation superimposed on the current configuration ${\varvec{\varphi }}^+ = {\varvec{ Q }}{\varvec{\varphi }}+ {\varvec{ c }}$ for all translations ${\varvec{ c }}(t)$ and rotations ${\varvec{ Q }}(t)\in SO(3)$, as well as consistency with the dissipation principle (18)$_1$, we obtain the reduced form

$$\begin{aligned} \varPsi = \widehat{\varPsi }({\varvec{ C }}, c; {\varvec{ X }}) \end{aligned}$$

(21)

in terms of the right Cauchy–Green tensor ${\varvec{ C }}$ defined in (4). Note that within the framework of standard diffusion considered here, $\varPsi$ cannot be a function of $\nabla c$ due to (18)$_1$. Insertion into (17)$_1$ then gives the consitutive equations

$$\begin{aligned} \boxed { \begin{array}{rl@{\quad }l} 5.&{}\text{ Nominal } \text{ stresses } &{} {\varvec{ P }}= \rho _0\partial _{{\varvec{ F }}} \widehat{\varPsi }({\varvec{ C }}, c; {\varvec{ X }}) \\ 6.&{}\text{ Chemical } \text{ potential } &{} \mu = \partial _{c} \widehat{\varPsi }({\varvec{ C }}, c; {\varvec{ X }}) \end{array} } \end{aligned}$$

(22)

consistent with the dissipation principle (16).

2.4.3 Objective and convex dissipation potential

In order to prescribe the flux of the species, we define an objective dissipation potential that depends on the negative gradient of the chemical potential defined in (19)

(23)

at a given objective state $\{ {\varvec{ C }}, c \}$ of deformation and concentration. Then the species flux vector is defined by the constitutive equation

(24)

The dissipation inequality (18) is then satisfied if $\widehat{\varPhi }$ is a convex function with respect to the argument .

2.5 The boundary conditions for the coupled problem

In order to be able to solve the coupled system general and constitutive equations (14), (22) and (24) we have to postulate boundary conditions for the solid-species-mixture. To this end, the surface $\partial {\mathcal B}_0$ of the reference configuration is decomposed into mechanical and chemical parts

$$\begin{aligned} \partial {\mathcal B}_0 = \partial {\mathcal B}_0^{\varphi }\cup \partial {\mathcal B}_0^{t} \quad \text{ and }\quad \partial {\mathcal B}_0 = \partial {\mathcal B}_0^{c} \cup \partial {\mathcal B}_0^{h} \, , \end{aligned}$$

(25)

respectively, with $\partial {\mathcal B}_0^{\varphi } \cap \partial {\mathcal B}_0^{t} = \emptyset$ and $\partial {\mathcal B}_0^{c} \cap \partial {\mathcal B}_0^{h} = \emptyset$. We postulate Dirichlet- and Neumann-type boundary conditions for the mechanical problem

$$\begin{aligned} {\varvec{\varphi }}= \bar{\varvec{\varphi }}({\varvec{ X }},t) \ \mathrm on \ \partial {\mathcal B}_0^\varphi \quad \text{ and }\quad {\varvec{\sigma }}{\varvec{ n }}= \bar{\varvec{ t }}({\varvec{ x }},t) \ \mathrm on \ \partial {\mathcal B}_t^{t} \, , \end{aligned}$$

(26)

and for the chemical Li-ion diffusion problem

(27)

with prescribed deformation $\bar{\varvec{\varphi }}$, traction $\bar{\varvec{ t }}$, ion concentration $\bar{c}$ and species outflux $\bar{h}$, respectively. A particular role in the application to the Li-ion batteries is played by the Li-ion flux $\bar{h}$ on the surface ${\mathcal B}_t^h$ of the current configuration. It is constitutively described by Butler–Volmer-type surface flux and will be explained in Sect. 4.

3 Constitutive modeling of the coupled bulk response

In order to get a more compact notation, we drop in what follows the explicit dependence of the constitutive functions $\widehat{\varPsi }$ and $\widehat{\varPhi }$ on the position ${\varvec{ X }}\in {\mathcal B}_0$ and consider a homogeneous domain ${\mathcal B}_0$ of the solid. We outline in what follows a simple isotropic model for the coupled response of bulk. It is built onto the following ingredients.

3.1 The construction of an energy storage function

3.1.1 Contributions to the free energy

The free energy storage in the bulk is assumed to splitted up into a part due to elastic distortions and a part due to the Li-ion concentration. Hence, we split the function (21) into two parts

$$\begin{aligned} \widehat{\varPsi } ({\varvec{ C }}, c) = \widehat{\varPsi }_e({\varvec{ C }}, c) + \widehat{\varPsi }_c(c) \, , \end{aligned}$$

(28)

where $\widehat{\varPsi }_e$ governs the coupling effect caused by the swelling of the solid due to the concentration of Li-ions.

3.1.2 Multiplicative split of deformation gradient

In order to describe the swelling due to an increase of Li-ion concentration, we decompose the deformation gradient into a part ${\varvec{ F }}_c$ due to the swelling and a stress producing part ${\varvec{ F }}_e$. The latter is then defined by

$$\begin{aligned} {\varvec{ F }}_e {:=} {\varvec{ F }}{\varvec{ F }}_c^{-1} \quad \text{ with }\quad {\varvec{ F }}_{c} {:=} \widehat{J}^{1/3}_c(c) {\varvec{ 1 }}\end{aligned}$$

(29)

Hence, the swelling is assumed to be isotropic and assumed to be governed by the constitutive function for the volume expansion

$$\begin{aligned} J_c = \widehat{J}_c(c) = 1+ \varOmega (c - c_0) \end{aligned}$$

(30)

where the material parameter $\varOmega$ is the molar volume of the solute, i.e. the volume occupied by a mol of Li-ions. $c_0$ is the Li-ion concentration of a reference state. With this assumption at hand, the stress producing elastic right Cauchy–Green tensor ${\varvec{ C }}_e {:}= {\varvec{ F }}^T_e {{\mathbf {g}}} {\varvec{ F }}_e$ is a function

$$\begin{aligned} {\varvec{ C }}_e = \widehat{{\varvec{ C }}}_e({\varvec{ C }}, c) = \widehat{J}^{-2/3}_c(c) {\varvec{ C }}\end{aligned}$$

(31)

of the current metric tensor ${\varvec{ C }}$ and the concentration $c$.

3.1.3 Elastic stored free energy

With the definition of the elastic right Cauchy–Green tensor at hand, we assume the elastic stored energy function in (28) to have the specific form

$$\begin{aligned} \widehat{\varPsi }_e({\varvec{ C }}, c) = \widetilde{\varPsi }_e(\widehat{{\varvec{ C }}}_e({\varvec{ C }}, c)) \, , \end{aligned}$$

(32)

which is assumed to be isotropic i.e. $\widetilde{\varPsi }_e({\varvec{ Q }}{{\varvec{ C }}}_e{\varvec{ Q }}^T) = \widetilde{\varPsi }_e({{\varvec{ C }}}_e)$ for all ${\varvec{ Q }}\in SO(3)$. Hence, the function depends on the invariants of the elastic right Cauchy–Green tensor

$$\begin{aligned}&\widetilde{\varPsi }_e({\varvec{ C }}_e; {\varvec{ G }}) \!=\!\widetilde{\varPsi }_e(\hbox {tr}[({\varvec{ C }}_e{\varvec{ G }}^{-1})], \hbox {tr} [({\varvec{ C }}_e{\varvec{ G }}^{-1})^2], \hbox {tr} [({\varvec{ C }}_e{\varvec{ G }}^{-1})^3]),\nonumber \\ \end{aligned}$$

(33)

where the traces are taken with the standard metric ${\varvec{ G }}$ of the reference configuration. The last ground invariant $\hbox {tr} [({\varvec{ C }}_e{\varvec{ G }}^{-1})^3]$ is conveniently replaced by the Jacobian of the elastic deformation map $J_e {:}= \det {\varvec{ F }}_e = (\det {\varvec{ C }}_e)^{1/2}$. In order to make things concrete, we consider for the model problem a compressible Neo-Hookean function of the form

$$\begin{aligned} \rho _0\widetilde{\varPsi }_e({\varvec{ C }}_e; {\varvec{ G }}) \!=\! \frac{\lambda }{2} \ln ^2(J_e) \!+\! \frac{\mu }{2} [ \hbox {tr}[({\varvec{ C }}_e{\varvec{ G }}^{-1})] \! -\! 2 \ln J_e ] \end{aligned}$$

(34)

with the explicit representation of the elastic Jacobian

$$\begin{aligned} J_e = \widehat{J}_e(J,c) = J \widehat{J}^{-1}_c(c) \, . \end{aligned}$$

(35)

$\lambda$ and $\mu$ are related to the classical Lamé parameters of the linear theory of elasticity.

3.1.4 Chemical stored free energy

The chemical contribution to the stored energy (28) is assumed to have the simple form

$$\begin{aligned} \widehat{\varPsi }_c(c) = R \theta _0 c_{\text {max}} [\bar{c} \ln \bar{c} + (1-\bar{c}) \ln (1-\bar{c})] \, , \end{aligned}$$

(36)

where $\bar{c} =c/c_{\text {max}}$, is the normalized concentration, $c_{\text {max}}$ is the maximum concentration, $R$ is the gas constant and $\theta _0$ the absolute reference temperature.

3.1.5 Free energy of the mixture

The total free energy of the mixture for the model problem under consideration contains the elastic and chemical contributions (34) and (36), i.e.

$$\begin{aligned} \begin{array}{rcl} \rho _0 \widehat{\varPsi } &{}=&{} \displaystyle \frac{\lambda }{2} \ln ^2(\widehat{J}_e) + \frac{\mu }{2} [ \hbox {tr}[(\widehat{{\varvec{ C }}}_e{\varvec{ G }}^{-1})] - 2 \ln \widehat{J}_e ]\\ &{}&{} \displaystyle + \rho _0 R \theta _0 [ \bar{c} \ln \bar{c} + (1-\bar{c}) \ln (1-\bar{c}) ] \end{array} \end{aligned}$$

(37)

where the functions $\widehat{{\varvec{ C }}}_e ({\varvec{ C }},c)$ and $\widehat{J}_e (J,c)$ are given in (31) and (35).

3.2 The dissipation function for the species transport

What remains is the constitutive definition of the dissipative transport of Li-ions, i.e. the specification of the dissipation function $\widehat{\varPhi }$ in (14). We assume isotropic response for all ${\varvec{ Q }}\in SO(3)$ an assume the dependence on the coupled invariant of the negative material gradient of the chemical potential and the current metric in its representation ${\varvec{ C }}$ in the reference configuration

(38)

that models a transport law based on spatial gradient of the chemical potential. We assume the concrete function

(39)

which is quadratic with respect to the gradient . Here, the parameter $M$ is the mobility of the Li-ions. Thermodynamic consistency with the dissipation principle (16) is guaranteed if the potential $\widehat{\varPhi }$ is convex with respect to the gradient . This is achived for the thermodynamical restrictions

(40)

on the material parameter $M$ and the concentration field $c$, which are ensured in the subsequent treatments.

3.3 Summary of the constitutive equations

With the above two basic functions (37) and (39) for the free energy storage $\widehat{\varPsi }$ and the dissipation potential $\widehat{\varPhi }$ at hand, we may evaluate the constitutive functions (22) and (24) for the nominal stresses ${\varvec{ P }}$, the chemical potential $\mu$ and the ion flux . Taking into account the relationships

$$\begin{aligned}&2 \partial _{{\varvec{ C }}} \widehat{\varPsi }_e =J^{-2/3}_c (2\partial _{{\varvec{ C }}_e} \widehat{\varPsi }_e) \quad \quad \text{ and }\quad \nonumber \\&\partial _{c} \widehat{\varPsi }_e = - \varOmega J^{-1}_c \frac{1}{3}\hbox {tr}[ (2\partial _{{\varvec{ C }}} \widehat{\varPsi }_e){\varvec{ C }}], \end{aligned}$$

(41)

which account for the multiplicative decomposition, and using the standard derivative

$$\begin{aligned} \rho _o 2\partial _{{\varvec{ C }}_e} \widehat{\varPsi }_e = \lambda \ln J_e {\varvec{ C }}_e^{-1} + \mu ({\varvec{ G }}^{-1} - {\varvec{ C }}_e^{-1} ) \, , \end{aligned}$$

(42)

we find the closed-form constitutive expressions

(43)

with $p {:}= - \frac{1}{3}\hbox {tr}[ {\varvec{ P }}{\varvec{ F }}^T{\varvec{ g }}]$ for the model problem under consideration. Therein, the diffusion coefficient $D=MR\theta _0$ is introduced. Recalling the relationships $\tilde{{\varvec{\sigma }}} = {\varvec{ P }}{\varvec{ F }}^T$ and for the Kirchhoff stress and the Kirchhoff-type species flux, the above equations read in the Eulerian setting

(44)

Here $p := - \frac{1}{3}\hbox {tr}[ \tilde{{\varvec{\sigma }}}{\varvec{ g }}]$ is the Kirchhoff stress pressure and ${\varvec{ c }}^{-1} = {\varvec{ F }}{\varvec{ G }}^{-1} {\varvec{ F }}^T = {\varvec{ b }}$ is often denoted as the Finger tensor. These two equations give the most transparent insight in the constitutive response of bulk response. The stresses $\tilde{{\varvec{\sigma }}}$ are defined by a compressible Neo-Hookean function in terms of an elastic Jacobian defined in terms of the volume expansion $\widehat{J}_c$ due to swelling defined in (30). The transport is driven by the spatial gradient of the concentration $c$ and the pressure $p$ from their higher towards lower levels.

4 Constitutive modeling of the coupled surface response

In this section, we discuss the electrochemical surface reaction kinetics governing the Neumann-type surface flux of Li-ions. For more details on the derivations presented here, we refer to Doyle et al. [17] and Newmann & Thomas-Alyea [26]. The Lithium-ion flux through the boundary of the electrode particles is controlled by the kinetics of oxidation and reduction reactions on the surface of electrode particles. The redox reaction

$$\begin{aligned} \text{ Li } \text{ H } \Longleftrightarrow \text {Li}_{1-n}\text {H} + \text {nLi}^+ + \text {ne}^- \, . \end{aligned}$$

(45)

takes place in the electrode particles due to Li$^+$ insertion into the host material H, e.g., manganese oxide $\text {Mn}_2\text {O}_4$, cobalt oxide $\text {Co}\text {O}_2$, iron phosphate $\text {Fe}\text {PO}_4$ for cathode and silicon Si, and graphite C$_6$ for anode. The rates of anodic and cathodic chemical reactions are defined as the Arrhenius type energy activated equations

$$\begin{aligned} a_a&= k_a c_R \exp \Big ( -\frac{E_a}{RT} \Big ) \quad \text{ and }\quad \nonumber \\ a_c&= k_c c_O \exp \Big ( -\frac{E_c}{RT}\Big ) \, . \end{aligned}$$

(46)

Here, $k_a$ and $k_c$ are the reaction rate constant, whereas $c_R$ and $c_O$ are the concentrations of the anodic and cathodic reactants on the surface. The parameters $R$ and $T$ are the universal gas constant and absolute temperature. Defining the activation energies $E_a$ and $E_c$ in terms of the chemical potential $V$, the Faraday constant $F$, the transfer symmetry factor $\beta$ and the valence of Li-ions $n$

$$\begin{aligned} E_a = -(1-\beta )n F V \quad \text{ and }\quad E_c = \beta n F V \end{aligned}$$

(47)

and inserting them into (46) yields

$$\begin{aligned} \displaystyle a_a&= k_a c_R \exp \Big ( \frac{nF}{RT}\Big (1-\beta \Big )V \Big ) \quad \text{ and } \nonumber \\ a_c&= k_c c_O \exp \Big ( -\frac{nF}{RT}\beta V \Big ). \end{aligned}$$

(48)

The forward and backward electrochemical reactions occur simultaneously with net rate of reactions

$$\begin{aligned} a = a_a - a_c \, . \end{aligned}$$

(49)

At equilibrium state, the net rate of reaction vanishes. Evaluating $a=0$, one obtains a form of the Nernst equation, which relates the equilibrium potential $V_{eq}$ to the concentration of the reactants

$$\begin{aligned} V_{eq} = \frac{RT}{nF} \ln \Big ( \frac{k_c c_O}{k_a c_R} \Big ) \, . \end{aligned}$$

(50)

The chemical potential is decomposed into the equilibrium potential and a surface overpotential $\eta _s$

$$\begin{aligned} V = V_{eq} + \eta _s. \end{aligned}$$

(51)

By inserting (51) into (49) and by making use of (50), one obtains the reaction rates

$$\begin{aligned} a_a&= k_a c_R \Big ( \frac{k_c c_O}{k_a c_R} \Big )^{(1-\beta )} \exp \Big ( \frac{nF}{RT}\Big (1-\beta \Big )\eta _s \Big ) \quad \text{ and } \nonumber \\ a_c&= k_cc_O \Big ( \frac{k_c c_O}{k_a c_R} \Big )^{-\beta } \exp \Big ( -\frac{nF}{RT}\beta \eta _s \Big ). \end{aligned}$$

(52)

Furthermore, the concentrations $c_O = c_{amb}(c_{\text {max}}-c)$ and $c_R = c$ are introduced in terms of the Li-ion concentrations in the electrolyte $c_{amb}$ and the maximum Li-ion concentration in the electrode $c_{\text {max}}$. The net reaction rate reads

$$\begin{aligned} \begin{array}{rcl} a &{}=&{} k c_{amb}^{1-\beta }(c_{\text {max}}-c)^{1-\beta } c^\beta \\ &{}&{} \displaystyle \times \left( \exp \left( \frac{nF}{RT}(1-\beta )\eta _s \right) - \exp \left( -\frac{nF}{RT}\beta \eta _s \right) \right) \end{array} \end{aligned}$$

(53)

with $k=k_a^\beta k_c^{1-\beta }$. The net reaction is taken as the constitutive function for the surface flux boundary condition (8), i.e.

$$\begin{aligned} a := h({\varvec{ x }},t;{\varvec{ n }}) = h_1(c) \cdot h_2(\eta _s) \end{aligned}$$

(54)

which is decomposed into a concentration dependent

$$\begin{aligned} h_1(c) = k c_{amb}^{1-\beta }(c_{\text {max}}-c)^{1-\beta } c^\beta \end{aligned}$$

(55)

and a overpotential activated term

$$\begin{aligned} h_2(\eta _s) = \exp \Big ( \frac{nF}{RT}(1-\beta ) \eta _s \Big ) - \exp \Big ( -\frac{nF}{RT}\beta \eta _s \Big ) \end{aligned}$$

(56)

for the surface of a cathode particle. The sensitivity of $h_1$ and $h_2$ with respect to the symmetry factor $\beta$ is depicted in Fig. 3.

Fig. 3

The species flux density $h$ defined in (54) is decomposed into the a reaction rate dependent $h_1(c)$ and the b energy activated term $h_2(\eta _s)$ for various values of symmetry factor $\beta$

5 Time–space discretization and solution algorithms

5.1 Time-discrete field variables in incremental setting

We consider a finite time increment $[t_n, t_{n+1}]$, where $\tau _{n+1} := t_{n+1} - t_n > 0$ denotes the step length. All fields at time $t_n$ are assumed to be known. The goal then is to determine the fields at time $t_{n+1}$. In order to keep the notation compact, subsequently all variables without subscript are evaluated at time $t_{n+1}$. An algorithm for the update of the concentration field $c$ in the increment $[t_n, t_{n+1}]$ can be based on the time-discrete form of the balance equation (14)$_2$

(57)

in terms of the algorithmic expressions

(58)

Here, $\alpha \in [0,1]$ is an algorithmic parameter which gives for $\alpha = 1$ the backward Euler scheme and for $\alpha = 1/2$ the trapezoidal rule. Note carefully that these algorithmic expressions are functions of the deformation field ${\varvec{\varphi }}$ and the concentration field $c$ and its gradients at the disctrete time $t_{n+1}$. Observe, that the flux is a function of the second gradient of the deformation field as a consequence of its dependence on the gradient of the pressure $\nabla p$, see (43)$_3$. In order to avoid the difficulty of using higher-order finite element interpolations for the deformation field, we propose a semi-implicit scheme, see (68) below.

5.2 Weak form of the time-discrete equations

For the quasi-static problem under consideration, the update of the deformation and concentration field in a typical time increment is governed by the balance of momentum (14)$_3$, evaluated at the current time $t_{n+1}$, and the algorithmic form (57) for the balance of the Li ion species. Now define the two test functions fields ${\varvec{ X }}\mapsto \delta {\varvec{\varphi }}({\varvec{ X }})$ and ${\varvec{ X }}\mapsto \delta c({\varvec{ X }})$ for the deformation and the concentration fields on the reference domain ${\varvec{ X }}\in {\mathcal B}_0$, which satisfy the homogeneous form of the Dirichlet conditions

$$\begin{aligned}&\delta {\varvec{\varphi }}\in {\mathcal W}^\varphi _0 {:}= \{ \delta {\varvec{\varphi }}\,|\, \delta {\varvec{\varphi }}= 0 \text{ on } \partial {\mathcal B}^\varphi _0 \} \quad \text{ and } \nonumber \\&\delta c \in {\mathcal W}^c_0 {:}= \{ \delta c \,|\, \delta c = 0 \text{ on } \partial {\mathcal B}^c_0 \}. \end{aligned}$$

(59)

Then, a standard Galerkin procedure gives the weak forms of the two governing equations of the coupled deformation-diffusion problem

(60)

where the notation $\delta {\varvec{ F }}{:}=\nabla \delta {\varvec{\varphi }}$ and was used. Note that these two coupled weak forms are functions of the deformation ${\varvec{\varphi }}$ and concentration $c$ at the current time $t_{n+1}$.

5.3 Space–time-discrete finite element formulation

Now consider a standard finite element discretization of the spatial domain ${\mathcal B}_0$ of the reference configuration and Neumann surfaces $\partial {\mathcal B}^t_t$ and $\partial {\mathcal B}^h_t$ of the current configuration. We write

$$\begin{aligned} {\mathcal B}_0 = \bigcup _{e=1}^{N_e} {\mathcal B}^e_0 \, , \quad \partial {\mathcal B}^t_t = \bigcup _{s^t=1}^{N^t_s} \partial {\mathcal B}^{t\, s^t}_t \, , \quad \partial {\mathcal B}^h_t = \bigcup _{s^h=1}^{N^h_s} \partial {\mathcal B}^{h\, s^h}_t \end{aligned}$$

(61)

where $N_e$ is the number of bulk finite elements, $N^t_s$ and $N^h_s$ the numbers of surface finite elements for the mechanical tractions and the species flow, respectively. The discretization by bulk elements ${\mathcal B}^e_0\subset {\mathcal B}_0$ in the reference configuration is based on the finite element shapes

$$\begin{aligned} \begin{array}{l} {\varvec{\varphi }}^h({\varvec{ X }}) = {\varvec{ N }}^e_\varphi ({\varvec{ X }}) {\varvec{ d }}_\varphi \\ c^h({\varvec{ X }})= {\varvec{ N }}^e_c({\varvec{ X }}) {\varvec{ d }}_c \end{array} \quad \text{ and }\quad \begin{array}{l} \nabla {\varvec{\varphi }}^h({\varvec{ X }}) = {\varvec{ B }}^e_\varphi ({\varvec{ X }}){\varvec{ d }}_\varphi \\ \nabla c^h({\varvec{ X }}) = {\varvec{ B }}^e_c({\varvec{ X }}) {\varvec{ d }}_c \end{array} \end{aligned}$$

(62)

in terms of the matrices ${\varvec{ N }}^e_\varphi$ and ${\varvec{ N }}^e_c$ of bulk shape functions and their derivatives ${\varvec{ B }}^e_\varphi$ and ${\varvec{ B }}^e_c$. Here, ${\varvec{ d }}_\varphi$ and ${\varvec{ d }}_c$ are the space–time-discrete values of the deformation and the concentration at typical nodal points of the finite element mesh. The discretization of the Neumann surfaces by surface elements $\partial {\mathcal B}^{t\, s^t}_t \subset \partial {\mathcal B}^{t}_t$ and $\partial {\mathcal B}^{h\, s^h}_t \subset \partial {\mathcal B}^{h}_t$ is based on the finite element shapes

$$\begin{aligned} {\varvec{\varphi }}^h({\varvec{ x }}) = {\varvec{ N }}^s_\varphi ({\varvec{ x }}) {\varvec{ d }}_\varphi \quad \text{ and }\quad c^h({\varvec{ x }}) = {\varvec{ N }}^s_c({\varvec{ x }}) {\varvec{ d }}_c \end{aligned}$$

(63)

in terms of the matrices ${\varvec{ N }}^s_\varphi$ and ${\varvec{ N }}^s_c$ of surface shape functions. Insertion of shapes (62) and (63) into the time-discrete weak form (60) and applying standard arguments gives the coupled algebraic system

(64)

This is a coupled systems for the determination of the nodal deformation and concentration values ${\varvec{ d }}_\varphi$ and ${\varvec{ d }}_c$ at the current time $t_{n+1}$.¹

5.4 Solution of the coupled algebraic finite element system

The algebraic system (64) can be solved by standard methods for the solution of nonlinear equations. Introducing the compact notation for the global degrees and the residual of the finite element mesh

$$\begin{aligned} {\varvec{ d }}{:}= [ {\varvec{ d }}_\varphi \ {\varvec{ d }}_c ]^T \quad \text{ and }\quad {\varvec{ R }}{:}= [ {\varvec{ R }}_\varphi \ {\varvec{ R }}_c ]^T \, , \end{aligned}$$

(69)

we write the algebraic problem (64) in the form

$$\begin{aligned} {\varvec{ R }}({\varvec{ d }}) = {\varvec{ 0 }}\, . \end{aligned}$$

(70)

A canonical solver is the Newton-Raphson iterations based on the updates

$$\begin{aligned} {\varvec{ d }}\Leftarrow {\varvec{ d }}- [D {\varvec{ R }}({\varvec{ d }}) ]^{-1} {\varvec{ R }}\end{aligned}$$

(71)

until convergence is achieved in the sense $||{\varvec{ R }}||< tol$. It is based on a full linearization of the nonlinear algebraic system based on the monolithic tangent $D {\varvec{ R }}({\varvec{ d }})$.

6 Representative numerical examples

In this section, we apply the finite strain theory of diffusion-mechanics for Li-ion electrodes outlined in Sect. 3 to representative model problems. Two class of materials will be considered during the numerical investigations. In the first example we treat a silicon anode electrode particle Li$_{15}$Si$_4$, which is reported to show significant volume changes during intercalation. The second and the third examples will investigate deintercalation of LiMn$_2$O$_4$ cathode electrode particles of circular and ellipsoidal disk shapes and random geometries. Traction-free mechanical boundary conditions are assumed on the particle surfaces. The chemical boundary conditions at the particle surfaces follows the Butler–Volmer electro-chemical reaction kinetics as outlined in Sect. 4. The Li$^+$ intercalation into the anode and the deintercalation from the cathode correspond to the charging process of the battery.

6.1 Circular and elliptic disks under potentiodynamic control

6.1.1 Potentiodynamic charging process of Li$_{15}$Si$_{4}$ anode particle

Silicon anode electrodes are particularly attractive due to their high theoretical gravimetric and volumetric storage capacity, but suffer significantly from large stresses associated with concentration gradients. The conventional approaches to diffussion-mechanics coupling utilize small strain deformation theory Christensen & Newman [13, 14], Golmon et al. [20] and Seo et al. [27]. In order to justify the use of the finite strain theory for diffusion-mechanics coupling, a circular disk of radius $r = 5~\upmu$m is investigated. The equilibrium open circuit potential (OCP) curve

$$\begin{aligned} U_\mathrm{ocp }(c)&\cong -4.76(c/c_{\text {max}})^6 + 9.34(c/c_{\text {max}})^5\nonumber \\&-1.8(c/c_{\text {max}})^4 - 7.13(c/c_{\text {max}})^3 \nonumber \\&+5.8(c/c_{\text {max}})^2 - 1.94(c/c_{\text {max}}) + 0.62 \end{aligned}$$

(72)

for silicon is taken from Sethuraman et al. [29]. The approximation (72) to the OCP is depicted in Fig. 4a. The material parameters for silicon anode are given in Table 1, see also Golmon et al. [20] and Bower & Guduru [4]. The anode particle is initially in deintercalated state. A potentiodynamic loading with sweep rate $0.245$ mV/s is applied for $t=$2,000 s and the applied potential is kept constant, see Fig. 4b. No mechanical loading is applied during the charging process. The overpotential $\eta _s$ computed on the surface and the concentration profiles across the radius at various stages of the simulation are shown in Fig. 4c, d. During potentiodynamic charging process Li-ions intercalate into the electrode particles in anode which is described by the Butler–Volmer kinetics in the sense of Doyle et al. [17, 18] as outlined in Sect. 4. The competition between the time scales associated with intercalation kinetics and the diffusion kinetics determine the stress peaks. The higher the concentration gradient, the greater are the stresses generated. The normalized Li$^+$ concentrations contours on the deformed configuration of the circular disk at times $t=$1,000 s, $t=$2,000 s, $t=$3,000 s, and $t=$4,000 s are shown in Fig. 5. The undeformed configuration is also drawn with dotted lines in order to emphasize the large volumetric expansion associated with the intercalation process. Figs. 6 and 7 depict the radial and tangential stress profiles at times $t=$1,000 s, $t=$2,000 s, $t=$3,000 s, and $t=$4,000 s, respectively. The radial and the tangential components of the Cauchy stresses

$$\begin{aligned} \sigma _r ={\varvec{\sigma }}:{\varvec{ n }}\otimes {\varvec{ n }}\quad \text{ and }\quad \sigma _\theta = {\varvec{\sigma }}:{\varvec{ t }}\otimes {\varvec{ t }}\end{aligned}$$

(73)

are obtained by projecting the stresses in the normal ${\varvec{ n }}$ and tangential ${\varvec{ t }}$ directions. Similarly, the radial and tangential components of the first Piola Kirchoff stresses ${\varvec{ P }}=J{\varvec{\sigma }}{\varvec{ F }}^{-T}$ read

$$\begin{aligned} P_r ={\varvec{ P }}:{\varvec{ n }}\otimes {\varvec{ n }}\quad \text{ and }\quad P_\theta ={\varvec{ P }}:{\varvec{ t }}\otimes {\varvec{ t }}\, . \end{aligned}$$

(74)

The Cauchy stress and the first Piola–Kirchhoff stress show significant deviations from one another as the volume increases underlining the inadequacy of the small strain kinematics in the stress computations. This fact justifies the necessity of the proposed finite strain chemomechanics model for the analysis of electrode materials exhibiting large volume changes during intercalation and deintercalation cycles.

Fig. 4

a Open circuit potential for Si$_{15}$Li$_{4}$, b applied potential over time, c overpotential over time, and d normalized concentration profile across the radius

Fig. 5

Normalized Li-ion concentration $c/c_{max}$ on the deformed mesh at times a $t =$ 1,000 s, b $t =$ 2,000 s, c $t =$ 3,000 s, and d $t =$ 4,000 s. Dotted circle denotes the undeformed circular disk

Fig. 6

Radial Cauchy and first Piola Kirchhoff stresses across the cross-section at times a $t =$ 1,000 s, b $t =$ 2,000 s, c $t =$ 3,000 s, and d $t =$ 4,000 s

Fig. 7

Tangential Cauchy and first Piola Kirchhoff stresses across the cross-section at times a $t=$1,000 s, b $t =$ 2,000 s, c $t =$ 3,000 s, and d $t =$ 4,000 s

Table 1 Material parameters for Li$_{15}$Si$_{4}$

The variation of concentration, radial and tangential stresses over time at the points shown in Fig. 8a are depicted in Fig. 8b–d, respectively. One can clearly observe that he generated stresses relax under potentiostatic conditions. Hence, the applied sweep rate and the resulting overpotential are the determinant factors in the intercalation induced stresses generation. The computed radial and tangential stresses far beyond the theoretical strength for the the silicon. In reality, silicon shows significant plastic yielding and finaly cracking as reported in Bower & Guduru [4] and Baggetto et al. [2]. Further experimental data is necessary for the characterization of the material parameters governing the mechanical deformation and the diffusion process. The diffusion coefficient is taken to be constant, which might as well be taken as a function of the concentration level or the state of charge. However, the results shown qualitatively agree well with those presented in the literature.

Fig. 8

a Circular disk of radius $r=5~\upmu$m, b normalized concentration at depicted points over time, c radial Cauchy stress $\sigma _r$ at depicted points, and d tangential Cauchy stress $\sigma _\theta$ on the surface

6.1.2 Potentiodynamic charging process of LiMn$_{2}$O$_{4}$ cathode particle

The first example is reinvestigated for the deintercalation of Li$^+$ ions into Mn$_2$O$_4$ cathodic host material. We refer to Zhang et al. [33, 34] for similar investigations in the small strain setting. The investigation aims at the investigation of discrepancy between the small strain and finite strain approaches to diffusion-mechanics coupling phenomena. In order to study the deintercalation induced stress generation in LMO cathode particles, we devise a representative circular disk of radius $r=5~\upmu$m with initially in fully discharged state $c_0=0.996c_{\text {max}}$ is charged with a linear applied potential $V=vt$ with a constant sweep rate $v$, see Fig. 9b. The natural boundary conditions for ion outflux at the surface of the disk are modeled through the Butler–Volmer kinetics. The material parameters are taken from references Zhang et al. [33, 34] and are listed in Table 2. The OCP is approximated with the exponential function

$$\begin{aligned} U_\mathrm{ocp }(c)&\cong \sum _{i=1}^{6}U^{i}_\mathrm{ocp }(c) \quad \text{ with } \nonumber \\ U^{i}_\mathrm{ocp }(c)&= p(i,1) \exp ( - [ (c-p(i,2))/p(i,3)]^2 ) \, , \end{aligned}$$

(75)

where the parameters $p(i,j)$ with $i=\{1,6\}$ and $j=\{1,3\}$ are depicted in Table 3. The charging process in the cathode leads to deintercalation of Li-ions from the cathodic electrode. During potentiodynamic charging process Li-ions deintercalate from the electrode particles in cathode under following the Butler–Volmer kinetics. The competition between the time scales associated with deintercalation kinetics and the diffusion kinetics determine the stress peaks. The higher the concentration gradient, the greater are the stresses generated. The higher gradients are caused by the variation in the overpotential as depicted in Fig. 9c. Figure 10a depicts the tangential stress contours corresponding to the peak time $t=$1,236 s. The variation of concentration, radial stresses at the center, and the tangential stresses on the surface over time is shown in Fig. 10b–d. The radial and tangential stress profiles across the radius at the peak times $t=885$ s and $t=$1,236 s are shown in Fig. 11. The Cauchy and first Piola Kirchhoff stresses coincide which justifies the use of small strain theory for the diffusion-mechanics coupling in Li Mn$_2$O$_4$ cathode particles. The stress profiles obtained across the radius are similar to those obtained for silicon. It is to be mentioned that the sign of the radial and tangential stresses is reversed due to the reversal of the concentration gradients during deintercalation simulation.

Fig. 9

a Open circuit potential for Li Mn$_{2}$O$_{4}$, b applied potential over time, c overpotential over time, and d normalized concentration profile across the radius

Fig. 10

a Tangential stress contours at the peak time $t=$ 1,236 s. b Concentration versus time and c radial stress $\sigma _r$ versus time at the center and d tangential stress $\sigma _\theta$ versus time at the surface of the circular disk

Fig. 11

a, b Radial and c, d tangential components of the Cauchy and the first Piola Kirchhoff stresses across the cross-section at peak times a, c $t=885$s and b, d $t=$1,231 s

Table 2 Material parameters for Li Mn$_2$O$_4$

Table 3 Parameters $p(i,j)$ of open circuit potential function $U_\mathrm{ocp }$ for LMO

6.1.3 Optimization of elliptic electrode particles

In this example, we analyse an elliptic disk representing the Li$_x$Si and Li$_x$Mn$_2$O$_4$ electrode particles, respectively. The peak stress sensitivity with respect to (i) particle area, (ii) aspect ratio $\alpha =r_x/r_y$ of the elliptic disk for constant $r_x$, constant $r_y$ and constant disk area $A$ will be investigated, respectively. The circular disk of radius $r_0=5~\upmu$m considered in the previous example for LMO cathode is reinvestigated for various aspect ratios in the range $1\le \alpha \le 2$. The material parameters are taken to be identical to the previous example and are depicted in Tables 1 and 2 for silicon and LMO electrodes, respectively. The results obtained for silicon and LMO are depicted in Figs. 12 and 13, respectively. The sensitivity of the peak stresses with respect to particle volume and aspect ratio show the same trends for silicon anode and LMO cathode although the curves are obtained from intercalation simulation in the former case and from deintercalation simulaton in the latter case. The maximum radial stresses occur at the center of the ellipsoidal disk whereas the maximum tangential stresses occur at the oblate surface where the distance to the center is minimum. The maximum stresses are depicted at the peak time throughout the whole (de)intercalation process. For the circular disk the peak times are $t=$1,145 s (silicon) and $t=$1,236 s (LMO) and slightly vary as the aspect ratio changes. For constant $r_x=r_0$ the $r_y$ decreasas for increasing aspect ratio $\alpha$. The maximum radial stresses decrease monotonically with increasing aspect ratio, see Figs. 12 and 13a. The maximum tangential stresses, however, slightly increase with increasing aspect ratio followed by a monotonous decrease when $r_x$ is kept constant, see Figs. 12 and 13b. For constant $r_y=r_0$ the $r_x$ increases proportional to aspect ratio $\alpha$ and the maximum radial stresses first increase and then start to decrease monotonically after a peak at $\alpha \approx 1.2$. The maximum tangential stresses monotonically increase with increasing aspect ratio. For constant area $A=A_0$ the $r_x$ increases and $r_y$ decreases for increasing aspect ratio $\alpha$. The maximum radial stresses monotonically decrease with increasing aspect ratio. The maximum tangential stresses first increase, reach a maximum value around $\alpha =1.5$ and then monotonically decrease with increasing aspect ratio. In order to investigate the sensitivity of the peak stresseses with respect to particle size, we repeat our simulations for various surface area $A=nA_0$. As surface area $A$ increases/decreases, the maximum radial and tangential stresses also increase/decrease as depicted in Figs. 12 and 13c, d.

Fig. 12

Li$_x$Si anode: variation of maximum a, c tangential and b, d radial Cauchy stresses with respect to the aspect ratio $r_x/r_y$ for constant $r_x=r_0$, constant $r_y=r_0$ and constant area $A=n A_0$

Fig. 13

Li$_x$Mn$_2$O$_4$ cathode: variation of maximum a, c tangential and b, d radial Cauchy stresses with respect to the aspect ratio $r_x/r_y$ for constant $r_x=r_0$, constant $r_y=r_0$ and constant area $A=n A_0$

6.2 Simulation of a realistic electrode particle geometry

In the last example, we investigate a realistic two dimensional particle geometry taken from the SEM images of LMO battery cathode documented in Bohn [3, p. 78]. Due to the lack of information, we analyze the image in 2D under plane-strain assumption. The geometry and the mesh used for the simulation is depicted in Fig. 14a. We use 5,808 two-dimensional four node standard displacement elements and 303 one-dimensional line elements in order to impose the Butler–Volmer kinetics at the boundary. The normalized concentration contours and the maximumum in-plane principal stress contours are depicted at the peak time $t=$1,231 s in Fig. 14b,c. Compared to the ideal circular disk the maximum stresses at the surfaces are considerably higher in real particles due to surface irregularities and kinks. Although the area of the particle is slightly less than the circular disk investigated in Sect. 6.1.2, the maximum stresses computed at the surface kinks go upto twice as high as those measured on the surface of the circular disk. In Fig. 15a–c, the maximum stresses at surface kinks depicted on the mesh in Fig. 14a are plotted over time. Since the normalized concentrations on the surface are indifferent they have been depicted as a single curve in Fig. 15a.

Fig. 14

a Geometry and mesh of the particle, b normalized Li-ion concentration $c/c_{\text {max}}$ contours and c maximum principal stress $\sigma _\mathrm{max }$ corresponding to the peak at time $t=$1,231 s

Fig. 15

a Li-ion concentration versus time on the particle surface. b, c Maximum principal stress $\sigma _\mathrm{max }$ versus time at various points on the surface

6.3 Simulation of three-dimensional electrode particles

In this section, we analyze three-dimensional hollow cylinder and a hollow sphere. The geometry, boundary conditions and the finite element discretization for the hollow cylinder is depicted Fig. 16. The inner and outer surfaces are subjected to Neumann-type boundary conditions where the Butler–Volmer equation is applied at the outer surface and the inner surface is kept flux-free. Due to symmetry, one quarter of the hollow cylinder is discretized along with symmetry preserving Dirichlet-type boundary conditions at the intersection surfaces. No mechanical tractions are applied to the inner and outer surfaces. The initial relative concentration and the material parameters used for the problem are depicted in Table 1. The snapshots of the reference and deformed configurations at various times of intercalation process are given in Fig. 17. The tangential Cauchy stresses and the relative Li-ion concentration at the outer surface are depicted in Fig. 20a, b, respectively. The monolithic solution algorithm shows excellent performance thanks to the fully implicit global time integration. The hollow cylinder shows significantly less stresses compared to the full cylinder.

Fig. 16

Quarter of a hollow cylinder: Geometry, boundary conditions and finite element discretization

Fig. 17

Tangential Cauchy stresses (in MPa) developed in the hollow disk of silicon. Plots of the deformed mesh at times a $t = 0$s, b $t =$ 1,000 s, c $t =$ 1,500 s, and d $t =$ 2,000 s

Recently, Cui and coworkers [32] have proposed use of interconnected silicon hollow nanosphere as a candidate for commercial anode with long cycle life. They have achieved an initial capacity of 2,725 mA hg$^{-1}$ with less than 8 % capacity degradation every hundred cycles. In order to justify the use of hollow nanospheres as anodic particles, we have analyzed the chemomechanical behavior under potentiodynamic charging process. A hollow sphere with outer radius $r=1~\upmu$m, where the geometry, boundary conditions and the finite element discretization are depicted in Fig. 18, is investigated. The reference and the deformed configuration of the material are depicted at various stages of intercalation process in Fig. 19. The tangential Cauchy stresses and the relative Li-ion concentration at the outer surface are depicted in Fig. 20c,d, respectively. Three orders of reduction in the tangential stresses are quantified, which are well below the yielding or fracture stresses reported for lithium. The simulations carried out justify the use of tailored microstructures. In circumstances where the decrease in size is limited due to the problems associated with electrical conductivity and SEI formation, the presented theory shows promising results.

Fig. 18

Octant of a hollow sphere: Geometry, boundary conditions and finite element discretization

Fig. 19

Tangential Cauchy stresses (in MPa) developed in hollow sphere of silicon. Plots of the deformed mesh at times a $t = 0$s, b $t =$ 1,000 s, c $t =$ 1,500 s, and d $t =$ 2,000 s

Fig. 20

Hollow disk of silicon: a Maximum tangential stresses over time and b concentration profile. Hollow sphere of silicon: c Maximum tangential stresses over time and d concentration profile

7 Conclusion

We proposed a theoretical and computational framework for coupled diffusion-mechanics of Li-ion battery electrodes at finite strains. It is suitable for the analysis of diffusion of Li-ions during intercalation into and deintercalation from the electrode particles. A convenient semi-implicit finite element implementation for the proposed theory was developed. The framework is very well suited for electrode materials exhibiting large volume changes during charge-discharge cycles. The numerical investigations clearly demonstrated the necessity of the finite strain theory for the diffusion-mechanics coupling in Li-ion electrodes. The surface electro-chemistry governing the oxidation and reduction reaction kinetics was implemented through surface elements, utilizing Butler–Volmer kinetics in terms of nonlinear Neumann-type boundary conditions. The analysis carried out on silicon anode particles show significant deviations between the nominal and true stresses, justifying the necessity of the proposed finite-strain theory. The suggested semi-implicit finite element algorithm, where the pressure field is discretized as an independent field variable and the concentration and deformation fields are solved via a monolithic update scheme, is very robust. The representative boundary value examples show promising results towards future investigations on micro-structure optimization of silicon particles for more durable and high-performance silicon based anodes for EV applications. Future investigations will cover extensions to inelastic bulk response, phase segregation and fracture.