1 Introduction

Cell migration is a complex process which plays a critical role in a wide array of physio-pathological phenomena, among other cancer growth and development. For instance, solid tumors first undergo through a relatively simple, avascular stage of growth, with nutrient and growth factor supply by diffusion from the local microenvironment [1, 34, 57]. Then, the search of available quantities of critical substrates results in a subsequent aggressive phase, with the invasion of the surrounding tissue [1, 6]. In particular, a part of the malignant mass remains densely packed, while a number of isolated cells detach and begin to invade the neighboring spaces. These shed individuals, which are difficult to be clinically detected, have the greatest potential to invade the host and further metastasize. They display in fact an evident ability to wonder in the close proximity and to spread in the surrounding tissue. The scattered individuals, evading destruction by the immune system, may subsequently enter the host bloodstream or lymphatics, extravasate at a distant site, metastasize and establish secondary colonies with devastating consequences for the wellbeing of the patient, as the likelihood of success of therapeutic interventions strongly decreases. For these reasons, the analysis of the migratory properties of malignant individuals, as long as the discovery of the relative biomedical therapies, is a pivotal issue in cancer research and treatment.

The motile behavior of metastatic tumor cells is determined by a set of specific determinants of both the malignant individuals themselves and of the surrounding environment, whose basic component, in connective tissues, is the extracellular matrix (ECM). In particular, in vivo interstitial ECMs are heterogeneous in composition, density and organization, and are characterized by degree of alignment, width of pores and stiffness. Loose matrix regions are mainly composed of random collagenous fibers, which form gap and clefts with variable diameters, providing an optimal scaffold for cell adhesion, dissemination and movement. On the opposite, matrix regions of high density, constituted by tightly packed collagen fibers, result in physical barriers, adjacent to channel/track-like spaces, which, depending on their dimensionality, may either guide, hinder, or completely prevent cell movement [20, 60].

For instance, quantitative relations between micro-structural properties of fibrous ECMs and specific cell migration parameters, such as speed and persistence time, have been provided both experimentally [7, 13, 27, 61] and theoretically [45, 63, 64]. In particular, different studies have reported that tumor cells can achieve a significant displacement in highly constrained environments by localized pericellular proteolysis (via matrix metalloproteinases, MMPs) and/or by drastic morphological deformations, that require the substantial reorganization both of the cytoskeleton and of other organelles, in particular of the nucleus, the most voluminous and rigid intracellular compartment [11, 12, 41, 59].

At this regard, the most used cell migration assays used to analyze the different molecular mechanisms (i.e., MMP-dependent and MMP-independent) underlying cell migration in dense matrices is based on collagen lattices with well-controlled spatial characteristics [10, 20, 61]. In particular, in recent years, defined in vivo-like trails have been created by combining a fibrillar matrix random polymerization with laser microsurgery procedures, that are able to generate predefined tracks of defined width and length [22].

Such a type of experimental system is here reproduced and simulated by an extended cellular Potts model (CPM, [2, 14, 15, 17, 30, 44]). It is a grid-based Monte Carlo technique which employs a stochastic energy minimization principle to display the invasiveness of an individual cancer cell into a matrix environment characterized by specific topologies. In particular, in this paper, we will extend the series of models proposed by the Czirok’s group [51–55], by integrating them with the compartmentalization approach proposed in [44, 45]. As distinct features of the proposed approach, the migrating malignant cell will be in fact modeled as a discrete physical unit, compartmentalized into the nucleus and the cytosol, whereas its directional shape-dependent movement will be not imposed a priori, but it will be the result of the evolution of its polarity vector and of the relative asymmetric bias added to the minimization algorithm. Finally, for the first time in a CPM, the activity of the cell proteolytic machinery will be described taking into account the transition from a MMP-dependent to a MMP-independent sustained cell locomotion.

As outcomes of the model, we will focus on experimentally addressable characteristics of cell locomotion, i.e. overall displacement and velocity, predicting how these quantities are influenced by the specific geometrical feature of the matrix. In particular, we will analyze how the biophysical properties (i.e., nucleus elasticity/MMP activity) of the malignant cell determine its migratory phenotype and affect the directional component of its movement.

The remaining parts of this publication are organized as follows: in Sect. 2 (Mathematical Model), we clarify the assumptions on which our approach is based. The computational findings are then presented in Sect. 3 (Results), where we separate the analysis of the MMP-dependent and MMP-independent cell motion. Finally, the results are discussed in Sect. 4 (Discussion).

2 Mathematical model

The cell-matrix system is modeled at the mesoscopic level using an extended Cellular Potts Model, a grid-based stochastic approach, which realistically preserves the identity of the single cell-scale individuals and describes their behavior and interactions with the local microenvironment in energetic terms and constraints. The simulation domain is a two-dimensional regular lattice \(\Omega \,\,{\subset }\,\, R^{2}\), formed by identical closed grid sites that, with an abuse of notation, will be identified by their center \(\mathbf{x} \,\,{\in }\,\, R^2\). Each grid site is labeled by an integer number, \(\sigma (\mathbf{x}) \in N\), that can be interpreted as a degenerate spin originally coming from statistical physics [25, 37]. The border of a lattice site \(\mathbf{x}\) is identified as \(\partial \mathbf{x}\), one of its neighbors by \(\mathbf{x}'\), while its overall neighborhood by \(\Omega ^{'}_{\mathbf{x}}\), i.e. \(\Omega ^{'}_{\mathbf{x}}=\{\mathbf{x}' \in \Omega : \mathbf{x}'\) is a neighbor of \(\mathbf{x}\}\). Subdomains of contiguous sites with identical spin form discrete objects \(\Sigma _{\sigma }\) (i.e., \(\Sigma _{\overline{\sigma }}=\{\mathbf{x} \in \Omega : \sigma (\mathbf{x})=\overline{\sigma } \}\)) which have an associated type \(\tau (\Sigma _{\sigma })\).

Following the compartmentalization approach proposed in [44], the cancer cell, denoted by \(\eta \), is defined as a compartmentalized element, composed of two subregions which, in turn, are classical CPM objects \(\Sigma _{\sigma }\): the nucleus, a central cluster \(\Sigma _{\sigma =1}\) of type \(\tau =N\), and the surrounding cytosol, \(\Sigma _{\sigma =2}\) of type \(\tau =C\). Each cell compartment is obviously characterized, as an additional attribute, by the cluster id \(\eta \). The extracellular matrix environment is classically differentiated in a medium-like state, \(\tau =M\), and a polymeric-like state, \(\tau =P\), see also [3, 40, 45]. The medium-like state represents the mixture of soluble components, which, together with the water solvent, compose the interstitial fluid. It is assumed to be a single object \(\Sigma _{\sigma =0}\) isotropically distributed throughout the simulation domain, forming no large-scale structures. The polymeric state, given by an extended element \(\Sigma _{\sigma =3}\), represents instead the fixed structure of a dense collagen lattice, that is typically used for in vitro migration assays. Based on the re-assembly of monomeric collagen fibrils, such scaffolds are in fact able to mimic the structure of in vivo connective tissues, which provide barrier functions to moving cells [10, 61]. In particular, the spatial characteristics of the simulated matrix will be described in the next section.

Cell movement results from an iterative and stochastic series of elementary steps of a modified Metropolis method for Monte Carlo–Boltzmann dynamics [17, 32]. This algorithm is in fact able to implement the natural exploratory behavior of biological individuals. Procedurally, at each time step \(t\), called Monte Carlo Step (MCS, the basic unit of time of the model), a lattice site \(\mathbf{x}_{s}\) (s for source) belonging to a cell compartment \(\Sigma _{\sigma (\mathbf{x}_{s})}\) is selected at random and attempts to copy its spin, \(\sigma (\mathbf{x}_{s})\), into one of its unlike neighbors, \(\mathbf{x}_{t} \in \Omega ^{'}_{\mathbf{x}_{s}}: \mathbf{x}_{t} \notin \Sigma _{\sigma (\mathbf{x}_{s})}\) (t for target), also randomly selected. Such a trial spin update is accepted with a Boltzmann-like probability function \(P (\sigma (\mathbf{x}_{s}) \rightarrow \sigma (\mathbf{x}_{t}))\), that, as specified later, will involve both a symmetric minimization of a system free energy and two asymmetric biases relating to specific cell behavior.

For any given time \(t\), the system energy is defined with an hamiltonian functional, as:

$$\begin{aligned} H(t)= H_\mathrm{{shape}}(t) + H_\mathrm{{adhesion}}(t) + H_\mathrm{{persistence}}(t). \end{aligned}$$
(1)

\(H_\mathrm{{shape}}\) models the geometrical attributes of the subcellular compartments, which are written as non-dimensional relative deformations in the following quadratic form (see again [44] for a more detailed explanation):

$$\begin{aligned} \begin{aligned}&H_\mathrm{{shape}}(t)= H_\mathrm{{surface}}(t) + H_\mathrm{{perimeter}}(t)\\&\quad \!=\! \sum _{\Sigma _{\sigma }}\left[ \!\kappa _{\Sigma _{\sigma }} \left( \frac{s_{\Sigma _{\sigma }}\!-\! S_{\tau (\Sigma _{\sigma })}}{s_{\Sigma _{\sigma }}(t)}\right) ^{2} \!+\! \nu _{\Sigma _{\sigma }}\left( \frac{p_{\Sigma _{\sigma }} \!-\! P_{\tau (\Sigma _{\sigma })}}{p_{\Sigma _{\sigma }}}\right) ^{2} \!\right] \!, \end{aligned}\nonumber \\ \end{aligned}$$
(2)

which depend on the actual surface and perimeter of the subcellular units (we recall that here the model is two-bidimensional, but the 3D-extension is straightforward), \(s_{\Sigma _{\sigma }}(t)\) and \(p_{\Sigma _{\sigma }}(t)\), as well as on the same quantities in the relaxed state, \(S_{\tau (\Sigma _{\sigma })}\) and \(P_{\tau (\Sigma _{\sigma })}\), which correspond instead to their initial measures. \(\kappa _{\Sigma _{\sigma }}(t)\) and \(\nu _{\Sigma _{\sigma }}(t) \in R_{+}\) are mechanical moduli in units of energy: in particular, \(\kappa _{\Sigma _{\sigma }}(t)\) refer to surface changes, while \(\nu _{\Sigma _{\sigma }}(t)\) relate to the deformability/elasticity of the related subcellular compartment, i.e. the ease with which it is able to remodel changing its perimeter. Establishing that the tumor cell does not significantly grow during migration (which is consistent with the time-scale of the phenomenon of our interest), the fluctuations of its surface are kept negligible with high constant values \(\kappa _{\Sigma _{1}}=\kappa _{\Sigma _{2}}=\kappa \gg 1\).

Moreover, assuming that malignant cells moving in matrix environments are typically deformable, we set \(\nu _{\Sigma _{2}}=\nu _C <1\). In principle, cell nucleus is typically stiffer than the surrounding cytosolic region: however, intracellular cascades increasing its elasticity can be activated when the all the MMP activity is inhibited, as widely demonstrated in the recent experimental literature for different tumor cell lines [11, 12, 41, 59]. Following these considerations, we set

$$\begin{aligned} \nu _{\Sigma _{\sigma =1}}=\nu _N \left( \frac{1 + a\;\pi _m}{1+ b\; \pi _m}\right) , \end{aligned}$$
(3)

where \(a=2, b=1, \nu _N >> 1\) and \(\pi _m\) is the MMP production rate, that will be defined in Eq. (11). However, even if \(\pi _m=0\), we opt to maintain \(\nu _{\Sigma _{1}} > \nu _C\), since the cytoplasmic region of the cell remains typically softer than the nuclear cluster.

\(H_\mathrm{{adhesion}}\) is the general extension of Steinberg’s Differential Adhesion Hypothesis (DAH) [17, 49, 50]. In particular, it is differentiated in the contributions due to either the generalized contact tension between the nucleus and the cytoplasm within the cancer cell, or to the effective adhesion between the malignant individual and an extracellular component:

$$\begin{aligned} \begin{aligned}&H_\mathrm{{adhesion}} (t) = H^\mathrm{{int}}_\mathrm{{adhesion}} (t) + H^\mathrm{{ext}}_\mathrm{{adhesion}}(t)\\&\quad =\sum _{\mathop {(\partial \mathbf{x} \in \partial \Sigma _{1}) \cap }\limits _{(\partial \mathbf{x}' \in \partial \Sigma _{2})}} J^\mathrm{{int}}_{N,C}+ \sum _{\mathop {(\partial \mathbf{x} \in \partial \Sigma _{2}) \cap }\limits _{(\partial \mathbf{x}' \in \partial \Sigma _{0})}} J^\mathrm{{ext}}_{C,M}+\sum _{\mathop {(\partial \mathbf{x} \in \partial \Sigma _{2}) \cap }\limits _{(\partial \mathbf{x}' \in \partial \Sigma _{3})}} J^\mathrm{{ext}}_{C,P}, \end{aligned}\nonumber \\ \end{aligned}$$
(4)

where \(\mathbf{x}\) and \(\mathbf{x}'\) are two neighboring sites (i.e., \(\mathbf{x}' \in \Omega ^{'}_\mathbf{x}\)) and \(\Sigma _{\sigma (\mathbf x )}\) and \(\Sigma _{\sigma (\mathbf x ')}\) two neighboring elements (i.e., \(\partial \Sigma _{\sigma }\) is intended as the border of \(\Sigma _{\sigma }\)). The coefficients \(J\mathrm{s} \in R\) are binding forces per unit area, and are obviously symmetric w.r.t. the indices. In particular, \(J^\mathrm{{int}}_{N,C}\) implicitly models the forces exerted by intermediate actin filaments and microtubules to anchor the nucleus to the cell cytoskeleton, preventing the cell from fragmenting. \(J^\mathrm{{ext}}_{C,M}\) and \(J^\mathrm{{ext}}_{C,P}\) evaluate the heterophilic contact interactions between the cell and an extracellular component. On one hand, \(J^\mathrm{{ext}}_{C,M}\) accounts for the adhesiveness between the cell membrane and specific soluble ligands present in the medium. On the other hand, \(J^\mathrm{{ext}}_{C,P}\) measures the affinity between integrins complexes on the cell surface and the collagenous molecules forming the dense scaffold. In particular, given \(J^\mathrm{{int}}_{N,C} \ll 0\) to prevent cell splitting, we give null contribution to the adhesive interactions between the moving cell and an extracellular component (i.e., we assume \(J^\mathrm{{ext}}_{C,M} = J^\mathrm{{ext}}_{C,P} = 0\)). This choice, successfully used in another similar model of in vitro cell migration [42], is done to analyze the direct influence of cell deformability and/or proteolytic activity on its motile behavior, and is consistent with experimental literature, which widely demonstrates that most cell lines display sustained ameboid motility in confined environments in a poorly adhesive mode [18, 28, 39].

The Boltzmann probability function implemented in the model, whose specific form is commented in [44], reads as:

$$\begin{aligned} \begin{aligned}&P (\sigma (\mathbf{x}_{s}) \rightarrow \sigma (\mathbf{x}_{t})) (t)=\\ \displaystyle&\tanh (T_{\Sigma _{\sigma (\mathbf{x}_{s})}}(t)) \min \left\{ 1\; ,\; \exp \left( \frac{-\Delta H + \sum _{j} w_j}{T_{\Sigma _{\sigma (\mathbf{x}_{s})}}(t)}\right) \right\} . \end{aligned} \end{aligned}$$
(5)

\(\Delta H\) is the net difference of the system energy, which is defined by the hamiltonian \(H\), due to the proposed change of domain configuration. The \(w_i\)s are instead asymmetric biases describing specific mechanisms taken into account: their expression will be clarified below. Finally, \(T_{\Sigma _{\sigma (\mathbf{x}_{s})}}(t) \in R_{+}\) is a Boltzmann temperature, that measures the agitation rate of moving object \(\Sigma _{\sigma (\mathbf{x}_{s})}\). In particular, if \(\mathbf{x}_\mathrm{{source}} \in \Sigma _{\sigma =1}\), \(T_{\Sigma _{1}}=T_N\) gives the agitation rate of cell nucleus, while, for if \(\mathbf{x}_{s} \in \Sigma _{\sigma =2}\), \(T_{\Sigma _{2}}=T_C\) is a measure of the intrinsic motility of the overall malignant individual, as it gives the frequency of the ruffles of its cytosol (which, on a molecular level, are determined by polarization/depolarization processes of the actin cytoskeleton, refer to [33, 36, 38] and references therein). \(T_N\) is a low value, resulting in the passive motion of the nucleus, which, unable to have an autonomous movement, is dragged by the surrounding cytosol, characterized instead by a high \(T_C\) (see [42] for a more detailed mechanical explanation). The ECM polymeric components are instead assumed fixed and immutable, representing a restriction for cell movement. Only the activity of cell secreted proteolytic enzymes (i.e., MMPs) can degrade ECM-contained sites, opening space for cell locomotion.

The minimization of the hamiltonian allows to choose the system configurations which are energetically more convenient. However, as explained in details in [51–53], specific cellular behavior that directly influence cell movement can be implemented by introducing the relative bias (i.e., the terms \(w_i\)) to each elementary step. In particular, following [51, 53, 54], we here take into account the possible polarization of the moving tumor cell (i.e., its ability to differentiate in a leading and a trailing surface) and the resulting (1) persistent directional motility and (2) specific non-uniform membrane dynamics along the its perimeter. The inertial shape-dependent self-propulsion of the cell is modeled by altering the probability assigned to each spin update, as:

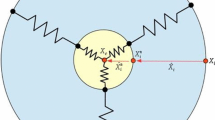
$$\begin{aligned} w_1(\sigma (\mathbf{x}_{s}) \rightarrow \sigma (\mathbf{x}_{t}))= P_\mathrm{{pers}} \frac{\mathbf{p}_{\eta }}{|\mathbf{p}_{\eta }|} (\mathbf{x}_{t}- \mathbf{x}_{s}), \end{aligned}$$
(6)

where \(P_\mathrm{{pers}}\) sets the magnitude of the cell autonomous motility and \(\mathbf{p}_{\eta }\) is the polarity vector of \(\eta \), see Fig. 1 (left panel), which, on a molecular level, may represent spatial differences in its biochemical state (see [47] and references therein). The coefficient \(P_\mathrm{{pers}}\) is here set constant in time: however, it may vary with the specific length of an individual or with the intracellular level of motile proteins. The cell polarity vector is then updated by considering a spontaneous decay and a reinforcement from cell displacements as, for each MCS,

$$\begin{aligned} \Delta \mathbf{p}_{\eta }= - \frac{1}{t_{\mathbf{p}}} \mathbf{p}_{\eta } + \Delta \mathbf{x}^{CM}_{\eta }, \end{aligned}$$
(7)

where \(t_{\mathbf{p}}\) is a characteristic memory length of the polarization vector, which can be also defined as the inverse of a rate of spontaneous decay, and \(\Delta \mathbf{x}^{CM}_{\eta }\) is the net displacement of the cell center of mass during the MCS considered. Relation (7) is introduced according to the statistical analysis of single cell motility data performed in [46]. The term \(w_1\) establishes a direct positive feedback loop involving cell movement and polarity [55], which corresponds to the molecular feedback regulation of the activation of rho GTPases and processes involved in cellular motility such as expansion of the cytosol and polymerization of cytoskeletal elements [8, 58].

Fig. 1
figure 1

Left panel geometrical characteristics of the moving tumor cell. \(\mathbf x ^{CM}_{\eta (\Sigma _{\sigma (\mathbf x _{s})})}\) indicates the center of mass of cell \(\eta \), whose site \(\mathbf x _{s}\) is attempting to move. The red vector \(\mathbf p _{\eta }\) represents the cell polarity vector, which forms the angle \(\phi \) with the direction of vector (\(\mathbf x _{s}- \mathbf x ^{CM}_{\eta }\)). The width of the leading edge is instead defined by the angle \(\psi \), which is formed by the segments connecting \(\mathbf x ^{CM}_{\eta }\) with extreme sites of the frontal part of the cell membrane, see also [53]. Right panel: MMP-production mechanism. Only a cell site located in the frontal part of the border of a cell can secrete proteolytic enzymes. In particular, the quantity of produced proteases is proportional to the quantity of ECM insoluble components in its first neighborhood. The bold black border indicate the membrane of the cell, the red dot its center of mass. We recall that label \(P\) stands for matrix polymeric-like state, whereas label \(M\) stands for matrix medium-like state. (Color figure online)

Full size image

The term \(w_2\), introduced in [53], models the fact that membrane dynamics (i.e., extensions/retractions of filopods and pseudopods) are more pronounced at the leading edge of a polarized cell, while they are almost poor at the sides and trailing edge [29]. Indeed, defined as \(\psi _{\eta }\) the width of the leading edge of cell \(\eta \), we set

$$\begin{aligned}&w_2(\sigma (\mathbf{x}_{s}) \rightarrow \sigma (\mathbf{x}_{t}))\nonumber \\&\quad = P_\mathrm{{dyn}} f\left( \frac{\psi _{\eta }}{2}- \phi (\mathbf{p}_{\eta }\;, \; \mathbf{x}_{s} - \mathbf{x}^{CM}_{\eta })\right) , \end{aligned}$$
(8)

where \(P_\mathrm{{dyn}}\) sets the magnitude of this effect. \(\phi (\; \cdot \; , \; \cdot \;)\) denotes the absolute value of the angle between vectors \(\mathbf{p}_{\eta }\) and \((\mathbf{x}_{s} - \mathbf{x}^{CM}_{\eta })\), see again Fig. 1 (left panel). Finally, \(f(\alpha ) = 2 \Theta (\alpha )-1\) is conveniently constructed using a Heaviside function \(\Theta (\alpha )\).

It is useful to emphasize that the asymmetric corrections \(w_i\) replace and are preferable to the standard \(H_\mathrm{{persistence}}\) contribution to the \(\textit{hamiltonian}\) typically used in other similar papers [42, 43], which only implicitly defines the polarization process of the moving cell as its ability to maintain the direction of the velocity characterizing its recent past movements. More in details, \(H_\mathrm{{persistence}}\) forces the moving individual to choose configurations that do not change its velocity, as it is a sort of “passive” term. In fact, a cell, once taken a direction of movement for a specific reason (i.e., due to chemical or geometrical stimuli), keeps such a path because it is energetically convenient. On the contrary, the biases \(w_i\) implement an “active” self-propulsion, since at each time step the cell reinforces its polarization with localized membrane fluctuations.

The matrix metalloproteinases secreted by the cancer cell to facilitate its locomotion are defined as \(m(\mathbf x ,t)\) and assumed to evolve following a standard reaction-diffusion equation:

$$\begin{aligned} \begin{aligned} \frac{\partial m(\mathbf x ,t)}{\partial t} =&\underbrace{P(\mathbf x , t)}_\mathrm{{production}} + \underbrace{D_m \nabla ^{2} m(\mathbf x ,t)}_\mathrm{{diffusion}}\\&- \underbrace{\lambda _m m(\mathbf x ,t)\delta (\tau (\Sigma _{\sigma (\mathbf x )}),M)}_\mathrm{{decay}}, \end{aligned} \end{aligned}$$
(9)

where \(\delta (\tau (\Sigma _{\sigma (\mathbf x )}),M)=1\) in the interstitial medium \(M\) and 0 elsewhere. \(\lambda _m\) and \(D_m\) are, respectively, the decay rate and the effective diffusion coefficient of proteolytic enzymes, constant and homogeneous in the whole extracellular environment. A low value of \(D_m\) is set to model a proteolytic mechanism strongly localized in the regions close to the cell membrane, in agreement with experimental evidence in [41, 60]. \(P(\mathbf x ,t)\) models the local production of proteases from the cell surface. In particular, using the above-introduced notation, it is possible to describe the MMP-secretion process only by i) the leading edge and ii) the neighboring parts of the lateral edges of the cell membrane, as widely demonstrated in literature both in general [1, 26] and in particular for vascular [48] and metastatic cells [56]:

$$\begin{aligned} P(\mathbf x ,t) = \left\{ \begin{array}{l} \displaystyle \sum _{\mathop {\partial \mathbf{x} \in \partial \Sigma _{\sigma =2} :}\limits _{\Sigma _{\sigma (\mathbf x ' \in \Omega '_\mathbf{x })}=\{0,3\}}} \Pi _m(\partial \mathbf x , t)\\ if\;\;\;\;\;\;\phi (\mathbf{p}_{\eta }\;, \; \mathbf{x} - \mathbf{x}^{CM}_{\eta }) \in (0, \frac{\pi }{2});\\ 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; else. \end{array}\right. \end{aligned}$$
(10)

Moreover, we set

$$\begin{aligned} \Pi _{m}(\partial \mathbf x ,t)= \pi _{m} \sum _\mathbf{x ' \in \Omega ^{'}_\mathbf{x }: \Sigma _{\sigma (\mathbf x ')= 3}} 1_{\mathbf{x}'}, \end{aligned}$$
(11)

where \(1_{\mathbf{x}'}\) is the indicator function, to allow MMP production only when it is really needed, i.e., only when the cell senses a matrix component in its close neighborhood, which indeed represents an obstacle for its movement, see the right panel of Fig. 1 for clarity. Summing up, the condition in Eq. (10) localizes the parts of the cell membrane where the MMP can be produced, whereas the condition in Eq. (11) establishes the effective quantity of secreted proteolytic enzymes (Table 1).

Table 1 Summary of the parameters used in the model. (\(*\)) indicates those that vary in the different sets of simulations
Full size table

Finally, to reproduce matrix degradation, a lattice grid site \(\mathbf x \) belonging to the polymeric part of the ECM becomes a generalized medium (fluid) site when the local level of MMPs (\(m(\mathbf x ,t)\)) is sufficiently high (in our simulations above \(2.5~\upmu \)M). This change is implemented by switching its type \(\tau \) from \(P\) to \(M\), as done in [16, 45].

3 Simulation characteristics and results

The simulation domain \(\Omega \subset R^{2}\) is a 400 \(\times \) 400 regular grid, with no flux conditions in both directions. The characteristic size of each grid site is 1 \(\upmu \)m. The lattice reproduces an in vitro dense collagenous matrix characterized by well-defined microtraks, which can be experimentally generated by laser ablation (see for instance [22] and references therein). In particular, the scaffold pattern consists of two perpendicular channels, which are equal in length (\(270~\upmu \)m) and width. In order to exploit different geometries, the diameter of the microtracks will be varied in the different sets of simulations, see Fig. 2. It is useful to remark that the smallest channel can be experimentally obtained only by the use of a single-line scan, as it represent a technical limit of laser-dissection procedures [22]. The temporal resolution of the model is, as seen, a MCS, which is set to correspond to 2 s in order to compare the simulated cellular dynamics with the relative experimental observations. To ensure the development of sufficiently long migration paths, the overall observation time is set equal to 16,200 MCS (\(\approx \)9 h). The PDE for the evolution of tumor MMPs is numerically solved with a finite difference scheme on a grid with the same spatial resolution as \(\Omega \), characterized by 30 diffusion steps per MCS. This temporal scale is sufficiently small to guarantee the stability of the numerical method.

Fig. 2
figure 2

The simulation domain \(\Omega \) reproduces a bidimensional dense collagenous lattice with microtracks of well-defined dimensions. In particular, we will analyze cell migration within channels (i) larger than the overall cell diameter, which is 30 \(\upmu \)m; (ii) smaller than the overall cell diameter but larger than the nuclear diameter, which is 16 \(\upmu \)m; and (iii) smaller than the nucleus size

Full size image

In all simulations, the tumor cell has an overall target area of 800 sites (\(\approx \)800 \(\upmu \mathrm{m}^2\)), which would correspond to a diameter of 30 \(\upmu \)m in a resting, un-polarized, morphology. The nucleus is instead a central and round cluster of 8 \(\upmu \)m (8 sites) of radius. These dimensions reflect the mean measures of typical cancer cells [1].

In all simulations, the cell is initially seeded just near the entrance of the vertical channel with an elliptical shape, as it and it is characterized by a polarity vector \(\mathbf p _{\eta }\) directed towards the vertical direction. This translates the assumption that the individual has already penetrated the microtrack and, chosen the direction of movement, it has accordingly organized its shape. Finally, 10 annealed MCS are run before each simulation in order to let the cell realistically arranges its body within the structure.

3.1 MMP-independent cell migration

In first set of simulations, we study the migration of a tumor cell with disrupted proteolytic machinery, obtained by imposing \(\pi _m=0\) in Eq. (11). The matrix structure represents indeed a fixed and undegradable barrier, whose walls delimit the space for cell locomotion. However, the inhibition of MMP activity activates intracellular signals resulting in the enhancement of nuclear elasticity, as modeled by Eq. (3).

In the case of the microtrack with the largest cross-section, the malignant cell quickly loses its initial polarization and turns back to a roundish shape. Then, in the absence of chemotactic (or other) cues, it starts to fluctuate and “rebound” between the channel walls, without displaying a significant penetration within the structure. The large microtrack does not in fact represent a significant geometrical contact guidance for the moving cell, which remains almost in the middle of the pattern in a resting, non-motile morphology, see Fig. 3a.

Fig. 3
figure 3

MMP-independent cell migratory behavior within different microchannels. a The widest channel does not provide a geometrical guidance for the tumor cell, which indeed assumes a stationary round morphology and display a short-range random movement. b–c In the case of both the middle and the small channel, the malignant individual maintains a polarized morphology and invades the vertical structures. Then, it autonomously remodels and changes direction, as it can not overcome the undegradable barrier represented by the matrix. In particular, the cancer cell is able to move within the smallest track by only compressing and squeezing its nuclear cluster. In all panels, the nucleus is manually encircled for the reader’s convenience

Full size image

At the intermediate channel width (i.e., smaller than cellular dimensions but bigger than nuclear dimensions), the cancer cell is able to maintain the polarized morphology and to undergo a persistent movement within the vertical microtrack. Such an inertial shape-dependent migration is actively reinforced at each MCS by the asymmetric biases added to the Boltzmann probability function. At the end of the vertical channel, the malignant individual spontaneously reorganizes and then turns the direction of motion, thereby invading the horizontal structure. From a modeling view point, the shape transition is driven by the evolution of the cell polarity vector: referring to Eq. (7), the cell center of mass in fact slowly displaces towards the open space on the right, as the cell can not overcome the vertical barrier. Once the cell has repolarized, the new direction of movement is finally established and maintained by the terms \(w_i\). In this case, the elasticity of the nucleus is not fundamental for the overall cell movement, since the track is large enough. However, it allows a more efficient deformation of the entire cell body in the angle between the channels, see indeed Fig. 3(b, third panel).

Finally, in the smallest track, both the cell and its nucleus adopt a cigar-like shape to invade the structure. With the inhibition of the proteolytic activity, the only way for the cell to move within such a confined space is in fact an ameboid motion, which requires the substantial deformation and squeezing also of its more voluminous compartment. In particular, the individual is again able to turn morphology and direction of movement, but it takes a longer time ( Fig. 3c). At the end of the observation time (i.e., at \(t =\) 9 h), the malignant cell still localizes in the central part of the channel, as it does not reach the opposite border of the scaffold. This is indicative of a slower velocity of migration (see below for a more detailed analysis).

The computational findings are consistent with the outcomes of similar models reproducing cell migration both in fibrous scaffolds and in microchannel devices [43, 45]. In particular, in [43], we analyzed in great detail the relation between the cell migratory ability within fixed subcellular and subnuclear structures and the elastic/mechanical properties of both the cell cytosol and of the nucleus. The same topic is also approached with a number of experimental models. In [4], glioma cell lines have been shown to squeeze through narrow locations in a brain model in vivo, thereby increasing their metastatic potential, by significantly compressing their nucleus upon recruitment of nonmuscle myosin II (NMMII). Moreover, very recently, Irimia et al. [23, 24] have provided that the directional persistence of cancer cells in microsized structures is mainly regulated by the steric hindrance due to the presence of a rigid and voluminous nucleus. In [5, 39], Panc-1 cells have instead been shown to overcome size exclusion in microchannels architectures upon treatments with bioactive SPC.

3.1.1 Migration velocities and turning time

In Fig. 4(left panel), we analyze the average velocity of the cancer cell, defined as the average velocity of its center of mass [31, 35, 42], within the different channel structures. This comparison allows to elucidate and to further quantify the differences between cell migratory phenotypes in specific geometric conditions. Cell migration in the largest channel is characterized by a low 0.65 \(\upmu \)m/min: this confirms that a structure whose dimension is greater than cellular measures does not represent a guidance cue, but rather behaves as an open space, where a cell undergoes a slow random movement. In the case of the intermediate channel, the malignant individual displays an approximately 2.5-fold increment in its migration speed (\(\approx \)1.65 \(\upmu \)m/min). Finally, in the case of the smallest channel, the cell average velocity slightly decreases again to nearly to 1.15 \(\upmu \)m/min. The explanation resides in the fact that although the nucleus is deformable, it is however stiffer (and less motile) than the surrounding cytoplasm and therefore takes more time to deform and move, slowering the overall individual.

Fig. 4
figure 4

MMP-independent cell migratory behavior within different microchannels. Left panel bimodal behavior of the average cell migration velocity within the different microtracks. Cell velocity in the larger channel is substantially low. Within the intermediate structure, it undergoes a more than two-fold increment. Cell speed decreases again within the subnuclear track. Right panel turning time vs. memory length of the cell polarity vector, \(t_\mathbf{p }\). Both in the middle and in the smallest channel, the time needed for the tumor cell to reorganize and to change direction is closely dependent to the value of \(t_\mathbf{p }\). In particular, in the subnuclear structure, the turning time is constantly higher because the nucleus, which has to to completely squeeze and remodel, is stiffer than the cytosolic region. All the values in the plots are represented as means \(\pm \) SD over 50 realizations

Full size image

Such a bimodal behavior of speeds allows to identify an optimal channel dimension for cell migration: smaller than the cellular diameter but larger than the nuclear diameter. In particular, the use of subcellular structures as a contact guidance, which results in a sustained cell locomotion, relies upon the deformation ability of the moving individual and, mainly, of its voluminous nucleus, which needs to adapt to the geometrical characteristic of the tracks.

The drastic differences in cell migration speeds due to the specific environment dimensionality, captured by the model, are consistent with recent studies performed on NIH-3T3 fibroblasts [9], leukocytes [28] and pancreatic cancer cells [39]. Analogous conclusions have been found also by different theoretical models. In [19], Hawkins et al. have reported that the migration of cells in a microsized channel strongly depends on partial pressure differences formed between the channel walls and either the leading or the rear edge of the individual. In [43], a compartmentalized CPM reveals two distinct migratory phenotypes, that are proposed to occur for cells placed either in open structures (i.e., 2D surfaces or large channels) or in confined architectures (i.e., channels smaller than cellular dimensions). In particular, the cell velocities measured in that model are surprisingly similar to those evaluated in the presented CPM, even if the persistent cell-dependent motion is, as already underlined, modeled with different approaches. This is indicative of the fact that both assumptions provide, although with different viewpoints, a realistic description of the directional locomotion of polarized cells.

We finally investigate the relation between the turning time of the tumor cell, i.e., the time needed to remodel and establish the new direction of movement, and the value given to the memory length of the polarity vector, \(t_\mathbf{p }\), see Fig. 4(right panel). For both the intermediate and the small channel, we observe that increments in \(t_\mathbf{p }\) correspond to increments in the cell turning time, until a saturation value. This is biologically realistic, as \(t_\mathbf{p }\) models the time needed to the intracellular machinery to resynchronize the polarity in the new direction of movement, i.e. to activate molecular pathways able to reinforce cytoskeletal actin polymerization towards the open space. The same graph also gives a further proof of the fact that a subnuclear structure represents a steric hindrance for cell movement, partially inhibiting its locomotion. In fact, although the malignant cell is able to compress and pull its nuclear region within the smallest tracks, it takes a significantly longer time to remodel and turn direction of motion.

3.2 MMP-dependent cell migration

In the previous section, we have demonstrated that a tumor cell is able to move within highly constrained matrix environments, that act as constraints, deforming both its overall body and its nucleus. However, as an additional mechanism to overcome limited spaces, it can activate proteolytic enzymes degrading the ECM structure [62]. As a result, barrier-free matrix spaces may be created resulting in longer distance traveling.

Given that the largest track does not represent a significative obstacle for cell migration, therefore not requiring MMP-activity, we first focus on the intermediate channel.

As reproduced in Fig. 5, the cancer cell maintains the polarity and easily invades the vertical track. In particular, the extracellular scaffold is not significantly altered by the proteolytic machinery, as the ECM structure does not represent a steric obstacle for cell persistent migration along the channel walls. The directional movement is then maintained despite the horizontal wall of the channel: the fully activated MMP activity is in fact able to generate a de novo vertical track, allowing the cell to maintain the polarity and the relative direction of motion.

Fig. 5
figure 5

MMP-dependent cell migration in the intermediate track. The proteolytic machinery is able to generate a de novo vertical channel, which allows the malignant cell to maintain the polarization and the relative directional movement. In all panels, the nucleus in manually encircled for the reader’s convenience

Full size image

The creation of secondary invasion zones by migrating malignant individuals has been described in details in the case both of mouse mammary tumor (MMT) cells [22] and of fibrosarcoma cells [60], placed in 3D collagenous scaffolds and organized in multicellular spheroids. It is useful to underline that, in these cases, cell movement is slowered by intercellular adhesive interactions, as the matrices are invaded by compact multicellular strands.

Interestingly, as soon as the MMP secretion rate slightly decreases, a well-defined de novo part of the vertical track is not longer generated, see Fig. 6. Consequently, the tumor cell loses its polarity, reverts back to a roundish morphology and starts wandering in the close proximity, while slowly degrading the surrounding matrix in a random-isotropic way. This behavior, which does not change after the observation time set for the representative simulations (not shown), is somewhat consistent for a large region of values assumed by \(\pi _m\), see again Fig. 5. An almost complete inhibition of the proteolytic machinery (i.e., \(\pi _m\) = \(10^{-5}\) s\(^{-1}\)) eventually results in an ameboid movement of the malignant cell. As done in the case of the MMP-independent migration, it in fact repolarizes and spontaneously turns direction of motion, following the contact cues provided by the undegraded matrix structure (refer to Fig. 3 and to the last panel of Fig. 6).

Fig. 6
figure 6

MMP-dependent cell migration in the intermediate track. A fully activated proteolytic machinery (i.e., \(\pi _m\) = 5 \(\cdot 10^{-3}\) s\(^{-1}\)) allows the tumor cell to create a de novo vertical track and therefore to maintain the direction of movement. For decreasing values of the MMP secretion rate (i.e., \(\pi _m\) = 10\(^{-3}\) s\(^{-1}\) and \(\pi _m\) = 10\(^{-4}\) s\(^{-1}\)), a new and well-defined vertical track is no longer created and the cell constantly reverts back to a round stationary morphology and starts a random fluctuation, while slowly degrading the surrounding matrix. Finally, an almost complete inhibition of the MMP activity (i.e., \(\pi _m\) = 10\(^{-5}\) s\(^{-1}\)) results in the above-described repolarization of the malignant individual, which turns direction of movement. In all panels, the nucleus in manually encircled for the reader’s convenience

Full size image

These results are biologically relevant, as they clearly demonstrate that the most efficient cell migration within a confined subcellular structure can be achieved

  1. 1.

    with the maximal activity of cell matrix-degrading enzymes, which for instance allow the malignant individual to maintain the predefined direction of movement (i.e., mesenchymal locomotion);

  2. 2.

    with an ameboid sustained locomotion, which allows the malignant individual to use the surrounding environment as a geometric guidance.

Analogous outcomes would be obtained by keeping fixed \(\pi _m\), while increasing the value of the amount of MMPs needed to degrade a matrix component (which is set equal to 2.5 \(\upmu \)M).

We finally analyze the MMP-dependent cell migration within the vertical subnuclear track. The entrance of the channel is widened to allow the entrance of the cell nucleus, which is characterized by a constant stiffness as the cell proteolytic machinery is activated (refer to Eq. 3). After the penetration of the cytosolic part of the cell, the subnuclear part of the track is laterally enlarged by the MMPs, so that the resulting space matches the diameter of the voluminous and rigid nuclear cluster. The tumor cell is then able to maintain the predefined direction of movement, see the left panels in Fig. 7. The velocity of migration of the cell in such a small channel increases with the MMP secretion rate, until a threshold value, which, interestingly, matches the speed of the MMP-deprived cell within the intermediate channel, see the plot in Fig. 7.

Fig. 7
figure 7

MMP-dependent cell migration in the subnuclear track. Left panels the proteolytic machinery generates a lateral widening of the microchannel, allowing the tumor cell to pull into its voluminous and rigid nucleus, which is manually encircled for the reader’s convenience. Right graph the velocity of migration increases with the value of the MMP secretion rate, \(\pi _m\), until a threshold limit. In particular, the speed of a cancer cell with fully activated MMPs nearly matches the one observed for the MMP-deprived cell moving within the intermediate channel. The numerical labels within the graph indicate the exact values assumed by \(\pi _m\). In each case, we represent means \(\pm \) SD over 50 realizations

Full size image

At the end of the vertical channel, only a cell with a fully active proteolytic machinery (i.e., \(\pi _m\) = 5 \(\times 10^{-3}\) s\(^{-1}\)) would be able to create a de novo track large enough to maintain its directional movement. In all the other cases, it would slowly lose the polarity and start an isotropic Brownian movement (these model outcomes are not explicitly shown since they are very similar to the case of the intermediate 25 \(\upmu \)m-channel).

Together with the results presented in the previous section, these observations show that the inhibition of both the proteolytic machinery and of the contractility of cell nucleus results in a significative disruption of malignant cell invasion within highly constrained extracellular matrices, such as those forming in vivo connective tissues.

4 Discussion

Due to the increasingly recognized importance of cell migration processes in cancer growth and development, and their exploitation for therapy and for tissue engineering, an increasing number of experimental models has been developed. These approaches analyze the relative importance of single and interrelated parameters to predict the migratory behavior of cancer cells in matrix scaffolds, which mimic in vivo connective tissues. In particular, new perspectives on this issue have been developed by in vitro assays that consist in micropatterned collagenous devices useful to study the migratory phenotype of tumor cells in predefined channel-like structures, as described in [22] and in the references therein.

We have here employed a specific version of the Cellular Potts Model to simulate such experimental systems. As a distinct feature of the proposed model, the cancer cell is represented as physical object compartmentalized into nucleus and cytoplasm. Cell movement is then driven by explicit interactions with the extracellular environment, which is in turn differentiated into the medium and in a collagenous dense and insoluble structure. Moreover, the polarization process of the malignant individual, as well as its directional shape-dependent locomotion is explicitly obtained by asymmetric biases added in the Metropolis algorithm, as done by Czirok and colleagues [51–55]. The integration of these two extensions of the basic CPM allows to have a realistic and detailed description of the MMP activity, which is not present in similar models.

The resulting model has been able to analyze both the MMP-dependent and the MMP-independent cell migration within different microtracks, which vary in width. In particular, a tumor cell moving in a structure larger than its overall diameter has been provided to lose its polarity and therefore the relative directional movement. This is consistent with the experimental observation that the predominant mechanism underlying cell migration in open spaces mainly depends on adhesive interactions and not on geometrical considerations, as steric hindrances have only a minor influence [9, 28].

On the opposite, cell migratory ability in subcellular channels closely depends on its proteolytic machinery. In particular, a full MMP activity has been shown to generate secondary paths which allow the malignant cell to disrupt steric barriers and maintain the direction of movement. An MMP-deprived cell is instead forced to switch to an ameboid migration, as its polarity and morphology follows the geometry of the open pattern.

Finally, a subnuclear track represents an obstacle for migration. In this case, the model has provided the fact that the cancer cell can achieved a sustained locomotion by either using a pericellular proteolysis or by dramatically deforming its nucleus.

Taken together, these considerations demonstrate the fact that the pathways which are able to control the switch between a mesenchymal MMP-dependent and an ameboid MMP-independent movement are fundamental promigratory factors for metastatic individuals.

As a clear advantage of a theoretical approach, we have been able to independently vary and modulate in a graded fashion both biophysical cell parameters and micro-structural properties of the matrix environment. However, the presented model has disregarded some other mechanisms underlying tumor cell motion in matrix environments such as (i) the additional matrix deposition of moving individuals, which leads to altered traction generation, adhesion and contact guidance; (ii) soluble or matrix-bound gradients of chemoattractants; (iii) molecular signals transmitted from the ECM to cells (outside-in signaling), thereby changing the activity of polarization or contractility-mediating proteins (Rac, Rho) [12]; (iv) a nonproteolytic displacement of the matrix interface, which results in secondary track widening. As shown in [22], despite inhibition of MMPs, invading individual can in fact employ an adaptive pressure-driven process that adjusts the geometry of a confined ECM (obviously, as far as the matrix elasticity permits). Such cell-derived compression of a fibrillar tissue may lead to scaffold condensation, thus locally increasing ECM tension and density, although the current literature does not permit to directly measure the pressure forces exerted by the cells for such a space enlargement.

It would be biologically relevant to adapt our approach to specific tumor cell lines, characterized by distinct biophysical phenotypes (i.e., intrinsic motility, elasticity, or proteases activity). This can be easily done by inheriting the model parameters from experimentally-measured quantities, characteristic of the selected cell population. It would be also interesting to analyze collective migrations of malignant cellular ensembles, which characterize different type of tumors, as commented in [16, 21]. A differentiation may also occur among individuals of the same aggregate, whereas competitions for nutrients or altered heterotypic interactions may significantly affect the migratory capacity of an entire cell lineage (for example, cancer cells of epithelial origin inhibit the motility and induce apoptosis in neighboring normal individuals). Obviously, in this case, it would be necessary to define in the model framework all cell types, with the relative phenotypic parameters and the rules for their behavior and mutual interactions.