Deforming-Spatial-Domain/Stabilized Space–Time (DSD/SST) method in computation of non-Newtonian fluid flow and heat transfer with moving boundaries

Abstract

This work presents an extension of the Deforming-Spatial-Domain/Stabilized Space–Time (DSD/SST) method to non-Newtonian fluid flow and heat transfer with moving boundaries. In this method, the variational formulation is written over the space–time domain. Three sets of stabilization parameters are used for the continuity, momentum and thermal energy equations. The more efficient solution for highly non-linear problems is achieved by using the Newton–Raphson iterative method for non-linear terms and the generalized minimal residual method for algebraic equations. This work makes the computations feasible with third-order accuracy in time, which is higher then most versions of the FEM. To validate this method, it is used to solve the well-known benchmark problems such as channel-confined flow, lid-driven cavity, flow around a cylinder, and flow in channel with wavy wall, where the non-Newtonian fluid rheological behaviour is incorporated. In particular, the results in terms of the Nusselt number, wall shear stress (WSS), vorticity fields and streamlines are discussed. It shows that the flow and heat transfer characteristics are quite different if the moving boundaries are taken into account. In summary, this work provides an effective extension of the DSD/SST method to hydrodynamics and heat transfer problems involving complex fluids and moving boundaries.

1 Introduction

Many substances encountered in industrial processes (polymer and melt solutions, pulp and paper, minerals, food, pastes and cosmetics processing, etc.) normally display non-Newtonian (i.e., shear-thinning, shear-thickening, yield-stress, visco-elastic and visco-plastic, etc.) fluid behaviours [1]. The rheological characteristics of such fluids can not be described by the Newton’s law of viscosity. The high viscosity levels in conjunction with the complexity in behaviour of the stress terms of momentum equations for non-Newtonian fluids generally pose the limitation of fluids processing under the laminar flow conditions. Due to the pragmatic significance of complex non-Newtonian fluids in the process industries, over the years, remarkable research efforts have been concentrated on the development of various computational tools and/or algorithms (see Refs. [2–8]) to explore the insights of the complex fluid flow and heat transfer phenomena.

Evidently, most of the notable research have presented the numerical methods based on the stationary boundaries. The difficulties associated with the numerical solution of complex fluid flow for the fixed (or stationary) boundary situations are very well appreciated in the literature  (see Refs. [1, 9–12]). It is also observed that many practically important flow processes involve the moving and/or deforming boundaries such as flexible interfaces, wavy channels, etc. The tractable level of complexities further enhances, even for the simple fluids, in obtaining the solution of flow problems influenced by the moving or deforming surfaces or interfaces. The available literature comprises several numerical simulation or computational fluid dynamics techniques such as finite difference [13–15], finite volume [16, 17], finite element [8, 18], Lattice Boltzmann [19–22], etc. This research work, however, mainly focuses on the finite element method (FEM). A recent study [7] has briefly reviewed the status of stabilized FEM for non-Newtonian fluid flow. The available literature  (see Refs. [3, 5–7, 23–26]) suggests that seldom efforts have been put into the development of numerical approaches for the simulation of the non-Newtonian fluid flow in conjunction with moving boundaries. The Deforming-Spatial-Domain/Stabilized Space–Time (DSD/SST) method [24, 25, 27–31], which was introduced in the context of incompressible flows, was also applied to coupled momentum and energy equations in the context of compressible flows [32–34] and to problems governed by the Navier–Stokes equations plus a scalar equation coupled to the Navier–Stokes equations (see the MITICT [35–37]) (and this is basically how the energy equation is coupled to the Navier–Stokes equations). Furthermore, in a paper on the space–time fluid–structure interaction method [29], a formulation for thermal coupling was added in the context of an ALE method, and extending that to the space–time method which consists of converting all the spatial integrations to space–time integrations and adding the jump term. Still, as far as known to us, the existing computational simulation approaches based on the FEMs do not account for the stabilized space–time FEM in conjunction with moving boundaries for the computations of the complex fluid flow and heat transfer. Thus, it constitutes the main motivation of this work. The present work, therefore, aims to present an extension of the DSD/SST method to computation of non-Newtonian fluid flow and heat transfer with the moving boundaries.

In this work, the stabilized space–time FEM considers the time as one of the dimensions. Thus, the proposed approach suitably handles the moving boundaries by the moving-mesh strategy. The finite element interpolation functions are continuous in the space. The interpolation is discontinuous in time and, in turn, the fully discrete equations are solved one space–time slab at a time. It makes the computations feasible with third-order accuracy in time, which is higher then most versions of the FEM. The more efficient solution for highly non-linear problems such as non-Newtonian fluids flow is achieved by using the Newton–Raphson iterative method for non-linear terms and the generalized minimal residual method (GMRES) for algebraic equations. Further, the designed stabilization strategy has been applied to the thermal energy equation, which is highly efficient for the coupled solution of the Navier–Stokes equations with thermal energy equation.

The organization of the present paper is as follows. The governing equations of the fluid and heat transfer are briefly described in Sect. 2. Section 3 presents the numerical approach. Several canonical examples are provided in Sect. 4 to validate the accuracy of the present method. The laminar flow in a channel with wavy wall is performed in Sect. 5 to demonstrate the rich phenomena beneath the non-Newtonian flow with moving boundaries. Final conclusions are given in Sect. 6.

2 Mathematical formulation

In this paper, we consider the two-dimensional, incompressible, non-Newtonian fluid flow and heat transfer involving the moving boundaries. The governing equations, namely, continuity, momentum and thermal energy equations [38–40], in the dimensional form (variables with $^*$ superscript) for the fluid flow in the spatial region ${\varOmega }_t^*$ and the temporal region $(0, T_0^*)$ are given as follow,

$$\begin{aligned}&\nabla ^*\cdot \mathbf{u}^* = 0 \quad \text{ on }\quad {\varOmega }_t^* \times (0,T_0^*),\end{aligned}$$

(1)

$$\begin{aligned}&\rho \left( \frac{\partial \mathbf{u}^*}{\partial t^*}+\mathbf{u}^*\cdot \nabla ^*\mathbf{u}^*\right) =\rho \mathbf{f}^*+\nabla ^*\cdot \mathbf{\sigma }^* \quad \text{ on }\quad {\varOmega }_t^* \times (0,T_0^*),\end{aligned}$$

(2)

$$\begin{aligned}&\rho c_p\left( \frac{\partial T^*}{\partial t^*}+\mathbf{u}^*\cdot \nabla ^* T^*\right) =\kappa \nabla ^{*2} T^* \quad \text{ on }\quad {\varOmega }_t^* \times (0,T_0^*), \end{aligned}$$

(3)

where $\rho$ is the fluid density, $\mathbf{u}^*=(u^*,v^*)$ is the velocity, $T^*$ is the temperature, $\mathbf{\sigma }^*$ is the stress, $c_p$ and $\kappa$ are the specific heat and thermal conductivity of the fluid, respectively. For the viscous fluids, $\mathbf{\sigma }^*$ is calculated by,

$$\begin{aligned} \mathbf{\sigma }^*=-p^*\mathbf{I}+2\eta ^*\mathbf{\epsilon }^* \end{aligned}$$

(4)

where $p^*$ is the pressure of the fluid, $\eta ^*$ is the viscosity, $\mathbf{I}$ denotes the identity tensor, and $\mathbf{\epsilon }^*$ is the rate of the strain tensor. Without loss of generality, the power-law fluid is taken as a representation of non-Newtonian fluids in the present paper. The rheological equation of state for power-law fluids [1] is defined by

$$\begin{aligned} \eta ^*=m\left( \frac{I_2^*}{2}\right) ^{(n-1)/2}, \end{aligned}$$

(5)

where $m$ is the power-law consistency index, $n$ is the power-law fluid behaviour index, and ${I}_2^*$ is the second invariant of rate of the strain tensor.

Both the Dirichlet and Neumann type boundary conditions are taken into account as shown below,

$$\begin{aligned}&\mathbf{u}^* = \mathbf{u}_g^* \quad \text {on}\quad \quad {\varGamma }_g^*,\end{aligned}$$

(6)

$$\begin{aligned}&\mathbf{n}\cdot \mathbf{\sigma }^* = \mathbf{h}^*\quad \text {on} \quad \quad {\varGamma }_h^*,\end{aligned}$$

(7)

$$\begin{aligned}&T^* = T_s^* \quad \text {on} \quad \quad {\varGamma }_{Tg}^*,\end{aligned}$$

(8)

$$\begin{aligned}&\nabla T^* = \mathbf{Q}^* \quad \text {on}\quad \quad {\varGamma }_{Th}^*, \end{aligned}$$

(9)

where ${\varGamma }_g^*$ (or ${\varGamma }_{Tg}^*$) and ${\varGamma }_h^*$ (or ${\varGamma }_{Th}^*$) are complementary subsets of the boundary ${\varGamma }_t$. The initial condition consists of a divergence-free velocity field, a uniform pressure field and a uniform temperature field specified over the entire initial domain, as shown below,

$$\begin{aligned}&\mathbf{u}^*(\mathbf{x}^*,0) = \mathbf{u}_0^*, \ \ \text {on}\quad {\varOmega }_0^*, \end{aligned}$$

(10)

$$\begin{aligned}&{p}^*(\mathbf{x}^*,0) = {p}_0^*, \ \ \text {on}\quad {\varOmega }_0^*, \end{aligned}$$

(11)

$$\begin{aligned}&{T}^*(\mathbf{x}^*,0) = {T}_0^* \ \ \text {on}\quad {\varOmega }_0^*. \end{aligned}$$

(12)

The governing equations (Eqs. 1–3), initial and boundary conditions are made dimensionless using the characteristic scaling variables $L, L/U_{\infty }, U_{\infty }, \rho U_{\infty }^2, \rho U_{\infty }^2, m(U_{\infty }/L)^n$, $U_{\infty }/L, m(U_{\infty }/L)^{n-1}$, and ($T_s-T_{\infty }$) for length ($\mathbf{x}^*$), time ($t^*$), velocity ($\mathbf{u}^*$), pressure ($p^*$), stress ($\mathbf{\sigma }^*$), strain ($\mathbf{\epsilon }^*$), viscosity ($\eta ^*$), and temperature ($T^*-T_{\infty }$), respectively. Therefore, the dimensionless form of the governing equations are rewritten as,

$$\begin{aligned}&\nabla \cdot \mathbf{u} = 0 \quad \text{ on }\quad {\varOmega }_t \times (0,T_0),\end{aligned}$$

(13)

$$\begin{aligned}&\frac{\partial \mathbf{u}}{\partial t}+\mathbf{u}\cdot \nabla \mathbf{u}= \mathbf{f}+\frac{2}{Re}\nabla \cdot (\eta \mathbf{\epsilon }) \quad \text{ on }\quad {\varOmega }_t \times (0,T_0),\end{aligned}$$

(14)

$$\begin{aligned}&\frac{\partial T}{\partial t}+\mathbf{u}\cdot \nabla T = \frac{1}{Pe} \nabla ^{2}T \quad \text{ on }\quad {\varOmega }_t \times (0,T_0), \end{aligned}$$

(15)

together with the non-dimensional version for initial and boundary conditions (Eqs. 6–12), where the superscript ‘$*$’ is dropped. The Reynolds ($Re$), Prandtl ($Pr$) and Peclet ($Pe$) numbers appearing in the above equations are defined as follows,

$$\begin{aligned}&Re = \frac{\rho L^n U_{\infty }^{2-n}}{m},\qquad Pr=\frac{c_p m(U_{\infty }/L)^{n-1}}{\kappa },\\&Pe = Pr\times Re=\frac{\rho c_pU_{\infty }L}{\kappa }. \end{aligned}$$

3 DSD/SST method

The DSD/SST method [24, 25, 27–31, 36, 41–48], a version of stabilized space–time FEM, is extended here in the present work to the computational simulation of the dimensionless form of the non-Newtonian fluid flow and thermal energy equations in conjunction with appropriate boundary conditions (Eqs. 13–15). Tezduyar et al. [24, 25, 27] first showed that the DSD/SST method, which allows the spatial domains at various time levels to vary, can be effectively applied to fluid dynamics computations involving moving boundaries and interfaces. The DSD/SST formulation for Newtonian fluid flow has been extensively used to simulate the problems involving moving boundaries and fluid–structure interaction. Some examples of these applications are animal swimming and flight [46, 49–54], flag flapping [42], spacecraft parachutes [55–62], cardiovascular fluid mechanics [63–66], and wind-turbine aerodynamics [67–69]. In this section, an extension of DSD/SST formulation for the non-Newtonian power-law fluid flow and heat transfer involving moving boundaries/interfaces is presented in detail.

The space–time domain (i.e. ${\varOmega }_t \times (0,T_0)$) is divided into time slab series $Q_n$ (as shown in Fig. 1), which is enclosed by ${\varOmega }_n$, ${\varOmega }_{n+1}$ and $P_n$, where $P_n$ is the lateral surface of $Q_n$ described by the boundary ${\varGamma }$ as $t$ traverses $I_n=(t_n,t_{n+1})$ ($0=t_0<t_1<\cdots <t_N=T_0$). As is the case with ${\varGamma }_t$, $P_n$ can be decomposed into $(P_n)_g$ (and $(P_n)_{Tg}$), and $(P_n)_h$ (and $(P_n)_{Th}$), with respect to the Dirichlet and Neumann boundary conditions being applied for the momentum (and heat transfer) equations. For each space–time slab, the finite element interpolation function spaces for the velocity, pressure and temperature are defined as follow,

$$\begin{aligned} (S_u^h)_n&= \{\mathbf{u}^h|\mathbf{u}^h\in (H_{1h})^{n_{sd}}(Q_n),\quad \mathbf{u}^h=\mathbf{g}^h \quad \text {on} \quad (P_n)_g\},\end{aligned}$$

(16)

$$\begin{aligned} (V_u^h)_n&= \{\mathbf{w}^h|\mathbf{w}^h\in (H_{1h})^{n_{sd}}(Q_n),\quad \mathbf{w}^h=0 \quad \text {on} \quad (P_n)_g\},\end{aligned}$$

(17)

$$\begin{aligned} (S_p^h)_n&= (V_p^h)_n=\{q^h|q^h\in H_{1h}(Q_n)\},\end{aligned}$$

(18)

$$\begin{aligned} (S_T^h)_n&= (V_T^h)_n=\{r^h|r^h\in H_{1h}(Q_n)\}, \end{aligned}$$

(19)

where $H_{1h}(Q_n)$ represents the finite dimensional function space over the space–time slab $Q_n$. Over the parent (element) domain, this space is formed by using first-order polynomials in both space and time. Globally, the interpolation functions are continuous in space while discontinuous in time [24, 25].

Fig. 1

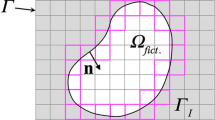
The space–time slab $Q_n$ for the DSD/SST [24, 27] formulation. The space–time domain (i.e. ${\varOmega }_t \times (0,T_0)$) is dived into time slab series $Q_n$ enclosed by ${\varOmega }_n$, ${\varOmega }_{n+1}$ and $P_n$, where $P_n$ is the lateral surface of $Q_n$ described by the boundary ${\varGamma }$ as $t$ traverses $I_n=(t_n,t_{n+1})$. The figure is from Refs. [24, 35]

The DSD/SST formulation for Eqs. (13)–(15) can be written as follows: Given $(\mathbf{u}^h)_n^-$ and $(T^h)_n^-$, find $\mathbf{u}^h\in \left( S_u^h\right) _n$, $p^h\in \left( S_p^h\right) _n$ and $T^h\in \left( S_T^h\right) _n$ such that $\forall \mathbf{w}^h\in \left( V_u^h\right) _n, \forall q^h\in \left( V_p^h\right) _n$ and $\forall r^h\in \left( V_T^h\right) _n$, the following variational formulation is satisfied

$$\begin{aligned}&\int _{Q_n}r^h\left( \frac{\partial T^h}{\partial t}+\mathbf{u}^h\cdot \nabla T^h\right) dQ+\int _{Q_n}\frac{1}{Pe}\nabla r^h\cdot \nabla T^hdQ \nonumber \\&\quad -\!\int _{(P_n)_{Th}}\!\frac{1}{Pe} r^h\mathbf{n}\cdot \mathbf{Q} dP\!+\!\int _{{\varOmega }_n}(r^h)_n^+\left( (T^h)_n^+\!-\!(T^h)_n^-\right) d{\varOmega }\nonumber \\&\quad +\sum _{e=1}^{nel}\int _{Q_n^e}\tau _T\left( \frac{\partial T^h}{\partial t}+\mathbf{u}^h\cdot \nabla T^h-\frac{1}{Pe}\nabla ^2 T^h\right) \nonumber \\&\quad \times \left( \frac{\partial r^h}{\partial t}+\mathbf{u}^h\cdot \nabla r^h-\frac{1}{Pe}\nabla ^2 r^h\right) dQ \nonumber \\&\quad +\int _{Q_n}\mathbf{w}^h\cdot \left( \frac{\partial \mathbf{u}^h}{\partial t}+\mathbf{u}^h\cdot \nabla \mathbf{u}^h-\mathbf{f}\right) dQ\nonumber \\&\qquad +\int _{Q_n}\mathbf{\epsilon } (\mathbf{w}^h):\mathbf{\sigma }^h dQ \nonumber \\&\quad -\int _{(P_n)_h}\mathbf{w}^h\cdot \mathbf{h} dP +\int _{Q_n}q^h\nabla \cdot \mathbf{u}^h dQ \nonumber \\&\quad +\sum _{e=1}^{nel}\int _{Q_n^e}\tau \left( \frac{\partial \mathbf{u}^h}{\partial t}+\mathbf{u}^h\cdot \nabla \mathbf{u}^h-\mathbf{f}-\frac{2}{Re}\nabla \cdot (\eta \mathbf{\epsilon }^h)\right) \nonumber \\&\quad \times \left( \frac{\partial \mathbf{w}^h}{\partial t}+\mathbf{u}^h\cdot \nabla \mathbf{w}^h-\frac{2}{Re}\nabla \cdot \left( \eta \mathbf{\epsilon }(\mathbf{w}^h)\right) \right) dQ \nonumber \\&\quad +\sum _{e=1}^{nel}\int _{Q_n^e}\delta (\nabla \cdot \mathbf{w}^h)(\nabla \cdot \mathbf{u}^h)dQ \nonumber \\&\quad +\int _{{\varOmega }_n}(\mathbf{w}^n)_n^+\cdot \left( (\mathbf{u}^h)_n^+-(\mathbf{u}^h)_n^-\right) d{\varOmega }=0, \end{aligned}$$

(20)

where the following notations are used,

$$\begin{aligned}&(\mathbf{u}_h)_n^{\pm } = \lim _{\varepsilon \rightarrow 0}\mathbf{u}(t_n\pm \varepsilon ), \end{aligned}$$

(21)

$$\begin{aligned}&\int _{Q_n}(\cdots )dQ = \int _{I_n}\int _{{\varOmega }_t^h}(\cdots )d{\varOmega } dt,\end{aligned}$$

(22)

$$\begin{aligned}&\int _{P_n}(\cdots )dP = \int _{I_n}\int _{{\varGamma }_t^h}(\cdots )d{\varGamma } dt. \end{aligned}$$

(23)

In Eq. (20), $\tau _T, \tau$ and $\delta$ are the stabilization parameters which determine the weight of the least-squares terms added to the Galerkin variational formulation to assure the numerical stability of the computations. In the present work, these stabilization parameters are defined by

$$\begin{aligned}&\tau _T = \frac{h}{2\sqrt{T^2}}\zeta (P_e^h), \end{aligned}$$

(24)

$$\begin{aligned}&\tau = \frac{h}{2\sqrt{u^2+v^2}}\zeta (R_e^h),\end{aligned}$$

(25)

$$\begin{aligned}&\delta = \frac{h\sqrt{u^2+v^2}}{2}\zeta (R_e^h), \end{aligned}$$

(26)

where $\zeta (z), P_e^h$ and $R_e^h$ are defined by

$$\begin{aligned}&\zeta (z) = \left\{ \begin{array}{cc} z, &{} \quad z\le 1, \\ 1, &{} \quad z>1, \end{array} \right. \end{aligned}$$

(27)

$$\begin{aligned}&P_e^h = \left( \frac{h \sqrt{T^2}}{12}\right) Pe,\end{aligned}$$

(28)

$$\begin{aligned}&R_e^h = \left( \frac{h \sqrt{u^2+v^2}}{12}\right) Re. \end{aligned}$$

(29)

In Eqs. (28) and (29), $P_e^h$ and $R_e^h$ are the element Peclet and Reynolds numbers. This type of stabilization is referred to as the Galerkin/least-squares procedure and is a generalization of the hybrid of streamlineupwind/Petrov–Galerkin [70] and pressure-stabilization/Petrov–Galerkin [71].

The process described in Eq. (20) is applied sequentially to all the space–time slabs $Q_0$, $Q_1, \ldots , Q_{N-1}$. The computations start with $(\mathbf{u}^h)_0=\mathbf{u}_0$ and $(T^h)_0=T_0$.

In the cases where the temporal accuracy is not important, Eq. (20) can be divided into two sub-steps given below,

$$\begin{aligned}&\nonumber \int _{Q_n}r^h\left( \frac{\partial T^h}{\partial t}+(\mathbf{u}^h)_n^-\cdot \nabla T^h\right) dQ+\int _{Q_n}\frac{1}{Pe}\nabla r^h\cdot \nabla T^hdQ\\&\quad \nonumber -\!\int _{(P_n)_{Th}}\!\frac{1}{Pe} r^h\mathbf{n}\cdot \mathbf{Q} dP\!+\!\int _{{\varOmega }_n}(r^h)_n^+\left( (T^h)_n^+\!-\!(T^h)_n^-\right) d{\varOmega }\\&\quad \nonumber +\sum _{e=1}^{nel}\int _{Q_n^e}\tau _T\left( \frac{\partial T^h}{\partial t}+(\mathbf{u}^h)_n^-\cdot \nabla T^h-\frac{1}{Pe}\nabla ^2 T^h\right) \\&\quad \times \left( \frac{\partial r^h}{\partial t}+(\mathbf{u}^h)_n^-\cdot \nabla r^h-\frac{1}{Pe}\nabla ^2 r^h\right) dQ=0,\end{aligned}$$

(30)

$$\begin{aligned}&\quad \int _{Q_n}\mathbf{w}^h\cdot \left( \frac{\partial \mathbf{u}^h}{\partial t}+\mathbf{u}^h\cdot \nabla \mathbf{u}^h-\mathbf{f}[(T^h)_n^-]\right) dQ\nonumber \\&\quad +\int _{Q_n}\mathbf{\epsilon } (\mathbf{w}^h):\mathbf{\sigma }^h dQ \!-\!\int _{(P_n)_h}\mathbf{w}^h\cdot \mathbf{h} dP +\int _{Q_n}q^h\nabla \cdot \mathbf{u}^h dQ\nonumber \\&\quad \nonumber +\sum _{e=1}^{nel}\,\int _{Q_n^e}\tau \left( \frac{\partial \mathbf{u}^h}{\partial t}+\mathbf{u}^h\cdot \nabla \mathbf{u}^h-\mathbf{f} [(T^h)_n^-]-\frac{2}{Re}\nabla \cdot (\eta \mathbf{\epsilon }^h)\right) \\&\quad \nonumber \times \left( \frac{\partial \mathbf{w}^h}{\partial t}+\mathbf{u}^h\cdot \nabla \mathbf{w}^h-\frac{2}{Re}\nabla \cdot \left( \eta \mathbf{\epsilon }(\mathbf{w}^h)\right) \right) dQ\\&\quad +\sum _{e=1}^{nel}\int _{Q_n^e}\delta (\nabla \cdot \mathbf{w}^h)(\nabla \cdot \mathbf{u}^h)dQ \nonumber \\&\quad +\int _{{\varOmega }_n}(\mathbf{w}^n)_n^+\cdot \left( (\mathbf{u}^h)_n^+-(\mathbf{u}^h)_n^-\right) d{\varOmega }=0. \end{aligned}$$

(31)

In this work, the moving mesh is handled by a simple method [72–74], namely the quasi-elastic method which takes advantages of minimizing the frequency of mesh regeneration to reduce the projection errors and minimizing the cost associated with mesh generation and parallelization setup [50, 73, 75–78]. In this method, the computational domain is modelled by a linear elastic body. The motion of the moving mesh is described by the elastic equilibrium equation which is solved with the boundary conditions, and consequently the mesh movement is obtained.

The present approach uses the equal-in-order basis functions for the velocity and pressure as in the original DSD/SST method, which are bilinear in space and linear in time [71]. The Gaussian quadrature is employed for numerical integration [79]. The non-linear equations resulting from the space–time finite-element discretization of the flow and heat transfer governing equations are solved by the Newton–Raphson method [80, 81] and the linear system of algebraic equations is solved by generalized minimal residual (GMRES) method with the preconditioning based on incomplete LU factorization technique, i.e., ILU(0) preconditioning [82, 83] to accelerate an iterative solution process. The ILU(0) preconditioning is based on a well-known factorization of the original matrix into a product of two triangular matrices: lower and upper triangular matrices. Usually, such decomposition leads to some fill-in in the resulting matrix structure in comparison with the original matrix. The distinctive feature of the ILU(0) preconditioning is that it preserves the structure of the original matrix in the result.

The computational algorithm is summarized as follow. Known $U^n$, set initial state as $k=0$ and $U_k=U^n$. The advance values of $U^{n+1}$ for the nonlinear system $F({U}^{n+1})=0$ are determined as,

• (1) Calculate $g_k=-F(U_k)$ and $J_k=\frac{\partial F(U_k)}{\partial U_k}$, so that establish the linear system $J_k\Delta U_k=g_k$;

• (2) Apply ILU(0), so that transfer the linear system to the form of $Ax=f$, where $A=(LU)^{-1}J_k$, $x=\Delta U_k$ and $f=(LU)^{-1}g_k$;

• (3) Choose $x_0$, compute $r_0=f-Ax_0$ and $v_1=r_0/\Vert r_0\Vert$;

• (4) For $j=1, 2, \ldots , m$ do: $h_{i,j}=(Av_j,v_i)$, for $i=1, 2, \ldots , j$, $\hat{v}_{j+1}=Av_j-\sum _{i=1}^jh_{i,j}v_i$, $h_{i+1,j}=\Vert \hat{v}_{j+1}\Vert$, $v_{j+1}=\hat{v}_{j+1}/h_{i+1,j}$;

• (5) Form the approximate solution:$x_m=x_0+V_m y_m$ where $y_m$ minimizes $\Vert \beta e_1-\bar{H}_m y\Vert$, $y\in R^m$;

• (6) Compute $r_m=f-Ax_m$ and check for the convergence. (a) If the specified convergence criteria is not satisfied, then compute $x_0=x_m$, $v_1=r_m/\Vert r_m\Vert$ and go to step 3; (b) If the specified convergence is achieved the go to step 7;

• (7) Compute $U_{k+1}=U_k+\Delta U_k$, check for the convergence status. (a) If the convergence is not achieved then $k=k+1$ and go to step 1; (b) If the convergence criteria is satisfied then compute $U^{n+1}=U_{k+1}$ and stop the computations.

In the present work, the above mentioned computational simulation algorithm is implemented in Fortran 90 programming language. The reliability and accuracy of the proposed numerical approach is ascertained in next section by comparing the present results with those of the standard benchmark problems in the computational fluid dynamics.

4 Validation of the numerical method

The numerical simulation approach discussed in the previous section has been validated thoroughly to establish the reliability and accuracy by comparing the present results with the following standard benchmark problems of non-Newtonian fluid flow and heat transfer: (1) channel confined flow at low Reynolds number, (2) lid-driven cavity flow, and (3) flow across a stationary cylinder. These benchmark problems cover large domain of computational fluid dynamics, i.e., steady flow, unsteady flow, heat transfer, stationary and moving boundaries, etc. The successful validation will provide support for our later study of non-Newtonian power-law fluid flow in a rectangular channel with wavy wall. Further applications of the space–time FEM for the Newtonian fluids can be found in our previous publications [45, 46, 74].

4.1 Developing flow of non-Newtonian power-law fluid in a channel

The developing flow through a confined channel is considered to be one of the benchmark problems to validate an in-house CFD solver. Consider the two-dimensional steady laminar developing flow of power-law fluid with a uniform incoming flow (dimensional uniform velocity, $U_{\infty }=1$) through a rectangular channel of height $h$ and length $L$, as shown in Fig. 2. The physically realistic initial and boundary conditions are given as,

$$\begin{aligned} u(x,y)&= 0,\quad v(x,y)=0,\quad p(x,y)=0 \quad t=0, (x,y)\in {\varOmega }_1,\\ u(x,y)&= 1,\quad v(x,y)=0 \qquad \qquad \qquad \qquad t>0, (x,y)\in \mathfrak I ,\\ u(x,y)&= 0, \quad v(x,y)=0 \qquad \qquad \qquad \quad t>0, (x,y)\in \partial {\varOmega }_1,\\ p(x,y)&= 0 \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad t>0, (x,y)\in \mathfrak R . \end{aligned}$$

The computations are performed with the dimensionless domain size ($L\times h$) of $15\times 1$ and computational mesh consisting of $6191$ nodes and $6000$ elements. The time step is chosen as $\Delta t= 10^{-2}$. The numerical results in terms of the fully developed velocity profiles are obtained for the Reynolds number of $10$ and for the power-index in the range of $0.2 \le n \le 2.0$. The simulations are performed for sufficiently long time so that the flow in the channel attains a steady state. The fully developed velocity profiles predicted by the numerical simulations are compared in Fig. 3 with the corresponding analytical solution for fully developed velocity profile [1, 11, 84] for power-law fluid flow in a channel which is given as

$$\begin{aligned} u_f(y,n)=\frac{2n+1}{n+1}\left( 1-\left| 1-\frac{2y}{h}\right| ^{(n+1)/n}\right) . \end{aligned}$$

(32)

Figure 3 shows an good agreement between the present numerical results and the analytical values for various values of power-law index. It is noted from Fig. 3 that the shear layer is thinned for $n<1$ and thickened for $n>1$ compared to the Newtonian fluid case ($n=1$). Thus, the power-law fluids of $n<1$ and $n>1$ are shear-thinning and shear-thickening type fluids, respectively [85, 86].

Fig. 2

Sketch of the power-law fluid flow in a channel

Fig. 3

Comparison of the present numerical results of the fully developed velocity profiles in a channel with the corresponding analytical profiles (Eq. 32) for Reynolds number of $Re=10$ and power-law index as $0.2<n<2$

Further, the maximum velocities of the fully developed flow in channel calculated by the numerical simulation are also compared in Table 1 with those predicted by analytical expression. It also shows an great correspondence (${<}{\pm }$0.1 %) between the numerical and analytical results. The excellent correspondence between the present and analytical results gives us a confidence in the reliability and accuracy of the present numerical solution procedure. Further attempts are also made to verify the efficacy of the present solver in the subsequent sections.

Table 1 The comparison of the maximum velocity in the fully developed flow of power-law fluids in a channel

4.2 Lid-driven square cavity flow of non-Newtonian power-law fluid

The lid-driven cavity flow is another standard test problem in computational fluid dynamics. Here we consider the two-dimensional incompressible flow of power-law fluids in a lid-driven square cavity. An schematics of square cavity with appropriate boundary conditions is shown in Fig. 4. The driving force for the flow in the cavity is the shear stress created by the top lid moving with uniform velocity ($u=1$ and $v=0$). The stationary conditions are prescribed on the other three boundaries while the hydrostatic pressure shift is eliminated by fixing the pressure value at a single grid node, as on the mid node at the bottom boundary. The computational mesh consists of $2601$ nodes and $2500$ elements. The time step is considered as $\Delta t=10^{-2}$. The computations are carried out for the Reynolds number of $Re=100$ and for the power-law index in the range of $0.25 \le n \le 1.5$ thereby covering both the shear-thinning ($n<1$) as well as shear-thickening ($n>1$) fluid behaviours.

Fig. 4

Schematic representation of a lid-driven square cavity flow with appropriate boundary conditions

Figure 5 shows the variations of centerline velocity profiles, i.e., $u(y,x=0.5)$ and $v(y=0.5,x)$, for different values of power-law index ($n$). The velocity profiles are seen to be consistent (qualitatively as well quantitatively) with those reported in Ref. [3]. The profiles show that the shear layer is thinned for $n<1$ and thickened for $n>1$ compared to the Newtonian fluid case ($n=1$).

Fig. 5

Centerline velocity profiles for the power-law fluid flow in a square cavity

Further, Table 2 compares the present results (i.e., maximum and minimum centerline velocities and their locations) with the available literature [3, 11]. The present results (as shown in Table 2) are seen to be in good agreement with the literature. The minor deviations observed in $u_{min}$ at $n=0.25$ and in $x$ of $v_{min}$ at $n=1.5$ are acceptable in numerical studies and arise due to the differences in the grid spacing, discretization schemes, numerical methods, etc.

Table 2 Comparison of the maximum and minimum centerline velocities and their location for the power-law fluid flow in a lid-driven square cavity

A moving cavity flow is designed to validate the accuracy of the moving-mesh strategy. This case was conducted also in Ref. [24] for Newtonian fluid flow. In the simulation, the cavity is moving with a velocity of $u=-0.2$, and the velocity of the sliding lid is $u=0.8$. A typical case ($Re=100$ and $n=0.75$) is used for the validation of the results. Figure 6 compares the centerline velocity profiles ($u$ at the vertical centerline and $v$ at the horizontal centerline) of the moving-mesh case with those of the stationary mesh case. The result shows that the profiles predicted by the moving-mesh strategy are in great agreement with those of the stationary mesh case. The excellent correspondence seen herein for the stationary boundary and moving boundary problems encourages the efficacy of the present numerical simulation method for non-Newtonian fluid flow with moving boundaries. Consequent attempts are made to validate the present simulation strategy with the classical problem in fluid mechanics, i.e., flow over a cylinder.

Fig. 6

Validation of moving-mesh strategy

4.3 Non-Newtonian power-law fluid flow and heat transfer from a stationary cylinder

Flow across a circular cylinder is considered to be one of the canonical examples in fluid mechanics for testing the accuracy of a numerical method. The two-dimensional uniform flow (with uniform free-stream velocity, $U_0$) of power-law fluid across a cylinder (of diameter $D$) is considered in this section. The computational domain is $33D\times 12D$. The mesh employed consists of $4558$ nodes and $4424$ elements, which are non-uniformly distributed. Special meshes of this design were extensively used in the literature  [24–26, 41]. The element size around the cylinder is approximately $0.005D$. Figure 7 represents the computational domain, computational mesh and the boundary conditions. Simulations are performed for $Pr=1$ and a wide range of Reynolds numbers ($Re = 10$, 20, 40, and 100) covering both the 2-D steady to unsteady flow regimes and for the different values of the power-law index ($n$) thereby covering both shear-thinning and shear-thickening fluid behaviours. The dimensionless parameters ($Re$ and $Pr$) herein is based on the free-stream velocity ($U_0$) and the diameter of the cylinder ($D$). In the simulations, the initial flow is prescribed as the potential flow around cylinder with a small perturbation. The computations are performed for sufficiently long time such that a steady (for the cases of $Re = 10$, 20 and 40) or periodic (for $Re=100$) flow is fully established.

Fig. 7

Schematic representation of computational domain, boundary conditions and computational mesh for non-Newtonian power-law flow over a stationary cylinder

The validation of results for the cylinder flow problem has been carried out in steps, i.e., steady flow over a cylinder, unsteady flow over a cylinder and heat transfer from a cylinder. Table 3 compares the present values (for both stationary and moving meshes) of individual and total drag coefficients ($C_{DP}, C_{DF}$ and $C_D$) for steady flow of non-Newtonian fluid flow around the cylinder with the available literature [12, 20, 87–89] for two values of the Reynolds number ($Re$ = 20 and 40) and for three values of the power-law index ($n$ = 0.6, 1 and 1.4). It can clearly be seen that the present results are well consistent with the available literature values. It should be pointed out that drag coefficient ($C_D$) value is larger than those reported in the literature [12, 87], and in several cases, such as $Re=40$ and $n=0.6$, $C_{DP}$ is much larger than the literature values. On the other hand, comparison of the present drag values for Newtonian fluid with the literature [20, 88, 89] are seen to be in the good agreement. It may noted that the computational domains in the present work is smaller than that used in Refs. [12, 87], which seems to be a justified explanation of deviations noted above. To further validate the efficiency and robustness of the moving-mesh strategy in the present code, the simulations are carried out for a cylinder moving with a velocity of $u=-1$. The velocity boundary conditions are shifted by a term of $(-1,0)$ and the stress boundary is the same as the previous series of simulations. The results of moving mesh for $Re=20$ and $n=0.6$, $1.0$ and $1.4$, are also shown in Table 3. It is observed that the results obtained in the moving-mesh method are the same as those in stationary mesh, which further demonstrates the efficiency of the moving-mesh strategy in the present work.

Table 3 Comparison of the individual and total drag coefficients for the steady flow over a cylinder

Further, the transient nature of the solver is thoroughly verified by increasing the Reynolds number as 100 at which the flow patterns show von-Kármán periodic vortex shedding behind the cylinder. The transient simulations for non-Newtonian power-law fluid flow over a cylinder are performed at a fixed value of the Reynolds number ($Re=100$) for a range of power-law index ($n=0.4$, 0.6, 1.0, 1.4 and 1.8). The present results for time-averaged drag coefficients ($\overline{C_D}$), maximum lift coefficient ($C_{L,max}$) and Strouhal number ($St$) are compared in Table 4 with the literature [20, 88–91]. It is observed that the drag coefficients in the present work are in good agreement with those reported in the literature. At lower values of power-law index, as $n\le 1$, the present $St$ is in a good agreement with references, while there is an obvious discrepancy at higher power-law index. Several additional results of Newtonian fluid are also listed in Table 4. One can see that even for the Newtonian fluid, the value of $St$ varies 5–6 % using different methods. Thus, the discrepancy of $St$ at high power-law index ($n$) is acceptable.

Table 4 Unsteady flow of non-Newtonian power-law fluid over a cylinder at Reynolds number of $Re=100$

Further attempts are made to validate both fluid flow and thermal solvers. It is done by considering the steady forced convection heat transfer from a heated cylinder to non-Newtonian power-law fluid. The simulations are performed for the following parameters: Prandtl number, $Pr=1.0$, Reynolds numbers, $Re=10$ and 20, power-law index, $n=0.8$, 1.0, 1.2 and 1.4. The results of the averaged Nusselt number ($\overline{Nu}$) are compared with the available literature data in Table 5. It shows that the present results are in close agreement ($\pm$5–6 %) with the literature values. It needs to be emphasized here that the deviations of this order as that seen in Table 5 are common in such numerical studies, as discussed in the Refs. [86, 90, 92, 93].

Table 5 Comparison of the averaged Nusselt number ($Nu$) for forced convection heat transfer from a cylinder to power-law fluids at Prandtl number, $Pr=1$

5 Laminar flow of non-Newtonian power-law fluid flow in a rectangular channel with wavy wall

The turbulence flow over a wavy surface has been studied extensively owing to the importance in fundamentals and applications [94–98]. On the other hand, laminar flow over wavy surfaces has received much less attention. As an application of the present numerical solution method, the non-Newtonian power-law fluid flow and heat transfer in a two-dimensional rectangular channel with wavy wall is considered, as shown in Fig. 8. In this work, the height $h$ of the channel is taken as the characteristic length. The length of the channel ranges from 0 to $16h$. The initial and the boundary conditions are set as,

$$\begin{aligned}&u(x,y)=U_{\infty }=1,\quad v(x,y)=p(x,y)=t(x,y)=0,\\&\quad (x,y)\in {\varOmega }_1,\quad t=0,\\&u(x,y)=U_{\infty }=1,\quad v(x,y)=0, T(x,y)=0,\\&\quad x,y)\in \mathfrak I ,\quad t>0,\\&u(x,y)=v(x,y)=T(x,y)=0,\quad (x,y)\in \partial {\varOmega }_1, \quad t>0,\\&\quad v(x,y)=2\pi \omega A\sin (2\pi k x)\cos (2\pi \omega t),\quad u(x,y)=0,\\&T(x,y)=1,\; (x,y)\in \partial {\varOmega }_2,t>0,\\&\quad p(x,y)=0,\quad (x,y)\in \mathfrak R ,\quad t>0. \end{aligned}$$

All the simulations are performed at Reynolds number of $Re=10$, Prandtl number $Pr=0.5, A=0.1, \omega =1.0$, and $k=0.5$ by varying the power-law index ($n$) from 0.2 to 1.8. To discuss the present results, the WSS is first defined herein [8],

$$\begin{aligned} \text {WSS}=\eta |\omega |/Re. \end{aligned}$$

(33)

The variations of surface Nusselt number ($Nu$) are shown in Fig. 9a, b for two instants in a period, i.e. $T/4$ and $2T/4$. Figure 9c presents the shape and the moving direction of the boundary at the corresponding two instants. It is found that $Nu$ is strongly dependent on the power-law index ($n$). On the other hand, $Nu$ of the fully developed channel flow for $A=0$ (stationary regular channel) is 1.0 and independent on power-law index. In addition, $Nu$ for larger power-law index is lower along the half wave moving upward and is reverse along the half wave moving downward. Finally, at $t=T/4$, $Nu$ near the peaks is larger than that near the troughs and $Nu$ at the higher power-law index is smaller near the peaks, and is reverse near the troughs.

Fig. 8

Schematics of non-Newtonian power-law flow in a channel with wavy wall

Fig. 9

The variation of Nusselt number ($Nu$) along the wavy surface for $Re=10, Pr=0.5$ and $k=0.5$. a $T/4$; b $2T/4$; c sketch of the wavy wall. In (a), the gray region denotes the half wave moving upward and the white region represents the other half wave moving downward. In (c), the vectors are the moving direction of the wall

Another important quantity is the WSS (Eq. 33), which has been linked to the pathogenesis of atherosclerosis. Vessel segments with low WSS appear to be at the highest risk for development of atherosclerosis [8, 99]. Similar theories could be applied to other engineering fluid transportation, such as oil and liquid chemical material transportation. Figure 10 shows the variations of the WSS along the wavy wall for four instants in a period. Further, the instantaneous variations of the vorticity contours and streamlines are shown in Fig. 11.

Fig. 10

The variations of the WSS along the wavy surface for $Re=10, Pr=0.5$ and $k=0.5$. a $T/4$ and b $2T/4$

Fig. 11

The vorticity contours and streamlines for $Re=10$, $Pr=0.5$ and $k=0.5$ at $2T/4$. a vorticity contours for $n=0.6$; b vorticity contours for $n=1.0$; c vorticity contours for $n=1.4$; d streamlines for $n=0.6$; e streamlines for $n=1.0$; f streamlines for $n=1.4$

From Fig. 10, one can see that for the zero velocity instants (i.e., $T/4$), the WSS for shear-thinning fluids ($n<1$) is less than one. This trend is similar to that of fully developed channel flow for $A=0$. Specifically, the WSS values of fully developed channel flow are 0.224, 0.600 and 1.429 for $n=0.2$, 1.0 and 1.8, respectively. At $2/4 T$, the trend is a little complex. For the cases that do not have positive vorticity near these points, the WSS is less than one. This trend is reverse for cases with positive vorticity near the junction points of half waves. To further demonstrate this point, the vorticity contours and streamlines (Fig. 11) show that the positive vorticity occurs near the junction points of half waves where the WSS is anomalous. In addition, the eddies are observed near the junction points of half waves at $2T/4$ for fluids of shear-thinning fluids ($n<1$), which is regarded to be related to the positive vorticity and further the anomalous WSS.

All in all, the results show that $Nu$, the WSS, vorticity field and flow structures are quite different when the moving boundaries are considered. Thus, it is suggested that many possibilities of new flow phenomena may be observed and new physical mechanisms could be uncovered by considering the moving boundaries. The research shall be further extended to explore the new dimensions of the physical phenomena in practical problems with the help of moving boundaries solver presented herein this work.

6 Conclusion

An extension of DSD/SST method is presented to simulate the non-Newtonian fluid flow and heat transfer in conjunction with moving boundaries. More specifically, three stabilization parameters are used in the finite element formulation for the thermal, momentum, and continuity equations. This work makes the computations feasible with third-order accuracy in time, which is higher then most versions of the FEM. The proposed methodology and developed solver has been validated with the well-documented standard benchmark problems in the computational fluid dynamics involving the non-Newtonian fluids flow, i.e., channel confined flow at low Reynolds number, lid-driven cavity flow, and cross flow and heat transfer from a stationary cylinder. The non-Newtonian fluid rheological behavior has been incorporated by using the shear-dependent power-law fluid viscosity model in these benchmark problems. As an application of the present method, the non-Newtonian power-law fluid flow and heat transfer in a channel with wavy wall is studied. Particularly, the Nusselt number, WSS, vorticity fields and streamlines are discussed in detail. It has been observed from the results that the flow and heat transfer characteristics are quite different if the moving boundaries are taken into account.

In summary, the overall analysis of the results suggests that the extension of the DSD/SST method provides an efficient method for solving the hydrodynamics and heat transfer problems involving the complex fluids by considering the moving boundaries to understand the complex flow phenomena and physical mechanisms. It shall be undertaken as an important topic for the research in the near future.