Some Results About Equichordal Convex Bodies

Abstract

Let K and L be two convex bodies in ${\mathbb {R}}^n$, $n\ge 2$, with $L\subset {{\,\textrm{int}\,}}K$. We say that L is an equichordal body for K if every chord of K tangent to L has length equal to a given fixed value $\lambda$. Barker and Larman (Discrete Math. 241(1–3), 79–96 (2001)) proved that if L is a ball, then K is a ball concentric with L. In this paper we prove that there exist an infinite number of closed curves, different from circles, which possess an equichordal convex body. If the dimension of the space is more than or equal to 3, then only Euclidean balls possess an equichordal convex body.

1 Introduction

Let K be a convex body in the plane, i.e., a compact and convex set with non-empty interior, and let x be a point in its interior. We say that x is an equichordal point if every chord of K through x have the same length. The famous Equichordal Problem, due to Blaschke et al. [2], and Fujiwara [5], asks about the existence of a convex body with two equichordal points. There are many false proofs about the non existence of such a body, however, Rychlik finally gave a complete proof about the non existence of a body with two equichordal points in [12]. It is worth mentioning that there are many convex bodies, different from the disc, which have exactly one equichordal point. Here we are interested in a generalization of the notion of equichordal point in the following way: Let K and L be two convex bodies in ${\mathbb {R}}^n$, $n\ge 2$, with $L\subset {{\,\textrm{int}\,}}K$. We say that L is an equichordal body for K if every chord of K tangent to L have length equal to a given fixed value $\lambda$. In [1], Barker and Larman proved that if K is a convex body that possesses an equichordal ball then it is also a ball. However, we wonder if there exist convex bodies different from balls which possess an equichordal convex body in its interior. It seems that bodies which float in equilibrium in every position provide examples of such bodies in the plane (see for instance [15]), however, it is not clear if the considered bodies K are convex or not.

In Sect. 3 we study convex bodies L for which the chords of one of its isoptic curves (defined in the following section), that are supporting L have length equal to a constant number $\lambda$. In Sect. 5 we also prove that in dimension 3 or higher, only Euclidean balls (or simply balls) possess an equichordal convex body in its interior.

2 Preliminary Concepts

We give first some definitions and notation. Let K be a given planar convex body; for every real number t we denote by $\ell (t)$ the supporting line of K with outward normal vector $u(t)=(\cos t,\sin t)$. The function $p:{\mathbb {R}}\rightarrow {\mathbb {R}}$, defined as $p(t)=\max _{x\in K}\langle u(t),x\rangle$, is known by the name of supporting function of K. When the origin O is contained in K, p(t) is nothing else than the distance from O to the support line $\ell (t)$. The distance between the support lines $\ell (t)$ and $\ell \hspace{0.33325pt}(t+\pi )$ is called the width of K in direction u(t) and it is denoted by w(t), in other words, $w(t)=p(t)+p\hspace{0.33325pt}(t+\pi )$. If w(t) is constant, independently of t, we say that K is a body of constant width. For any $\alpha \in (0,\pi )$, the $\alpha$-isoptic $K_\alpha$ of K is defined as the locus of points at which two tangent lines to K intersect at an angle $\alpha$. Using the support function, $\partial K$ is parameterized (see for instance [14]) by

$$\begin{aligned} \gamma (t)=p(t)\hspace{0.49988pt}u(t)+p'(t)\hspace{0.49988pt}u'(t),\quad \text {for}\ t\in [0,2\pi ]. \end{aligned}$$

The isoptic curve $K_\alpha$ can be parameterized by the same angle by the formula (see [4] or [9])

$$\begin{aligned} \gamma _\alpha (t)=p(t)\hspace{0.49988pt}u(t)+\biggl [p(t)\cot \alpha +\frac{p(t+\pi -\alpha )}{\sin \alpha }\biggr ]\hspace{0.55542pt}u'(t). \end{aligned}$$

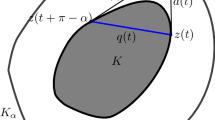
For any $t\in {\mathbb {R}}$ we define (see Fig. 1)

$$\begin{aligned} a(t)= & {} |\gamma _\alpha (t)-\gamma (t)|,\qquad b(t)=|\gamma _\alpha (t)-\gamma (t+\pi -\alpha )|,\\ c(t)= & {} |\gamma _\alpha (t)-\gamma _\alpha (t+\pi -\alpha )|=b(t)+a(t+\pi -\alpha ), \\ q(t)= & {} |\gamma (t)-\gamma \hspace{0.27771pt}(t+\pi -\alpha )|. \end{aligned}$$

Fig. 1

Parameters of the isoptic curve

By some tedious but simple calculations we can express the lengths of all these chords in terms of the support function of K:

$$\begin{aligned} a(t)&=\frac{p(t+\pi -\alpha )+p(t)\cos \alpha -p'(t)\sin \alpha }{\sin \alpha }\nonumber ,\\ b(t)&=\frac{p(t+\pi -\alpha )\cos \alpha +p'(t+\pi -\alpha )\sin \alpha +p(t)}{\sin \alpha },\nonumber \\ c(t)&=\frac{2p(t+\pi -\alpha )\cos \alpha +p(t)+p(t-2\alpha )}{\sin \alpha }. \end{aligned}$$

(1)

Finally, the support function of a strictly convex body, i.e., a convex body without segments in its boundary, is a periodic function, with period $2\pi$, and it is also absolutely continuous, indeed it is of class $C^2$. So we can consider its expansion in terms of the Fourier series (see [6, p. 139]), i.e.,

$$\begin{aligned} p(t)=a_0+\sum _{n=1}^\infty \hspace{0.83328pt}(a_n\cos nt+b_n\sin nt). \end{aligned}$$

The first and second derivatives of p are expressed as

$$\begin{aligned} p'(t)&=-\sum _{n=1}^\infty \hspace{0.83328pt}(na_n\sin nt-nb_n\cos nt),\\ p''(t)&=-n^2\sum _{n=1}^\infty \hspace{0.83328pt}(a_n\cos nt+b_n\sin nt). \nonumber \end{aligned}$$

(2)

3 Some Results About Equichordal Bodies in the Plane

In this section we present two results which give conditions under which a body (not necessarily convex) that possesses an equichordal convex body in its interior, is a disc. However, the question about whether there exists a convex body L, different from the disc, which possesses an equichordal convex body, remains open. Our first result is the following.

Theorem 3.1

Let K be a strictly convex body in the plane with differentiable boundary and let $\alpha \in (0,\pi )$ be a fixed angle such that $\alpha /\pi$ is an irrational number. Suppose $c(t)=c_0$, for every $t\in [0,2\pi ]$, for a positive number $c_0$. Then K is a disc.

Proof

Since $c(t)=c_0$ we have by (1) that

$$\begin{aligned} c(t)=\frac{2p(t+\pi -\alpha )\cos \alpha +p(t)+p(t-2\alpha )}{\sin \alpha }=c_0, \end{aligned}$$

it follows that

$$\begin{aligned} 2p'(t+\pi -\alpha )\cos \alpha +p'(t)+p'(t-2\alpha )=0. \end{aligned}$$

(3)

If we substitute the Fourier coefficients of p(t) in the differential equation (3), by (2) we have

$$\begin{aligned}&2\cos \alpha \sum _{n=1}^\infty \hspace{0.83328pt}(nb_n\cos n(t+\pi -\alpha )-na_n\sin n(t+\pi -\alpha ))\\&\qquad +\sum _{n=1}^\infty \hspace{0.83328pt}(nb_n\cos nt-na_n\sin nt)\\&\qquad +\sum _{n=1}^\infty \hspace{0.83328pt}(nb_n\cos n(t-2\alpha )-na_n\sin n(t-2\alpha ))=0. \end{aligned}$$

Since this holds for every real number t, we must have that for every n,

$$\begin{aligned}&\cos nt\cdot [-2na_n\sin n(\pi -\alpha )\cos \alpha \\&\qquad \qquad +na_n\sin 2n\alpha +2nb_n\cos n(\pi -\alpha )\cos \alpha +nb_n+nb_n\cos 2n\alpha ]\\&\quad +\sin nt\cdot [-2na_n\cos n(\pi -\alpha )\cos \alpha -na_n\\&\qquad \qquad \quad -na_n\cos 2n\alpha -2nb_n\sin n(\pi -\alpha )\cos \alpha +nb_n\sin 2n\alpha ]=0. \end{aligned}$$

The coefficients of $\cos nt$ and $\sin nt$ must be both equal to 0, hence we have that

$$\begin{aligned} \left[ \begin{array}{ll} -2\sin n(\pi -\alpha )\cos \alpha +\sin 2n\alpha &{}2\cos n(\pi -\alpha )\cos \alpha +1+\cos 2n\alpha \\ -2\cos n(\pi -\alpha )\cos \alpha -1-\cos 2n\alpha &{} \quad -2\sin n(\pi -\alpha )\cos \alpha +\sin 2n\alpha \end{array}\right] \cdot \left[ \begin{array}{l} a_n\\ b_n\end{array}\right] = \left[ \begin{array}{l} 0\\ 0\end{array}\right] . \end{aligned}$$

The determinant of the matrix above is given by

$$\begin{aligned} (-2\sin n(\pi -\alpha )\cos \alpha +\sin 2n\alpha )^2+(2\cos n(\pi -\alpha )\cos \alpha +1+\cos 2n\alpha )^2. \end{aligned}$$

This determinant is zero only if

$$\begin{aligned} -2\sin n(\pi -\alpha )\cos \alpha +\sin 2n\alpha =0 \end{aligned}$$

(4)

and

$$\begin{aligned} 2\cos n(\pi -\alpha )\cos \alpha +1+\cos 2n\alpha =0. \end{aligned}$$

(5)

Since $\alpha \in (0,\pi )$, for every $n\ge 2$ we have that none of (4) and (5) is satisfied if $\alpha /\pi$ is an irrational number. Hence, we have that the determinant is non zero and then $a_n=b_n=0$ for every $n\ge 2$. It follows that $p(t)=a_0+a_1\cos t+b_1\sin t$, i.e., p is the support function of a disc (see for instance [14]). $\square$

Remark 3.2

Theorem 3.1 can be also proved using a result due to Lumer [10] as soon as the isoptic curve $K_\alpha$ be a convex curve. However, in the proof given here we are not assuming that $K_\alpha$ is a convex curve.

If we impose the additional condition that q(t) is also constant, then K must be a disc.

Theorem 3.3

Let K be a strictly convex body in the plane with differentiable boundary $\partial K$, and let $\alpha \in (0,\pi )$ be a fixed angle. Suppose $c(t)=c_0$, and $q(t)=q_0$, for every $t\in [0,2\pi ]$, and for two positive numbers $c_0$ and $q_0$. Then K is a disc.

Proof

By some simple calculations we have that $|\gamma '_\alpha (t)|=q(t)/{\sin \alpha }$ (see e.g. [4]). Since $c(t)=c_0$ is also constant, we have

$$\begin{aligned}{} & {} \frac{d}{dt}\hspace{0.55542pt}(|\gamma _\alpha (t+\pi -\alpha )-\gamma _\alpha (t)|^2) \\ {}{} & {} \quad =\frac{d}{dt}\hspace{0.55542pt}(\langle \gamma _\alpha (t+\pi -\alpha )-\gamma _\alpha (t),\gamma _\alpha (t+\pi -\alpha ) -\gamma _\alpha (t)\rangle )=0, \end{aligned}$$

hence

$$\begin{aligned} \langle \gamma _\alpha (t+\pi -\alpha )-\gamma _\alpha (t),\gamma '_\alpha (t+\pi -\alpha )\rangle =\langle \gamma _\alpha (t+\pi -\alpha )-\gamma _\alpha (t),\gamma '_\alpha (t)\rangle . \end{aligned}$$

It follows that

$$\begin{aligned} c_0\cdot |\gamma '_\alpha (t+\pi -\alpha )|\cos \beta _1=c_0\cdot |\gamma '_\alpha (t)|\cos \beta _2, \end{aligned}$$

which implies that $\beta _1=\beta _2$, where $\beta _1$ is the angle between the vectors $\gamma _\alpha (t+\pi -\alpha )-\gamma _\alpha (t)$ and $\gamma '_\alpha (t+\pi -\alpha )$, and $\beta _2$ is the angle between the vectors $\gamma _\alpha (t+\pi -\alpha )-\gamma _\alpha (t)$ and $\gamma '_\alpha (t)$. It follows that the angles between the chord $[\gamma _\alpha (t+\pi -\alpha ),\gamma _\alpha (t)]$ and the tangent lines at $\gamma _\alpha (t)$ and $\gamma _\alpha (t+\pi -\alpha )$, are equal (see Fig. 2). Similarly, we obtain that the angles between the chord $[\gamma _\alpha (t-\pi +\alpha ),\gamma _\alpha (t)]$ and the tangent lines at $\gamma _\alpha (t)$ and $\gamma _\alpha (t-\pi +\alpha )$, are equal. Since the length of the tangent vector $\gamma '_\alpha (t)$ is constant for every t, and all the triangles $\triangle \gamma _\alpha (t-\pi +\alpha )\hspace{0.88882pt}\gamma _\alpha (t)\hspace{0.88882pt}\gamma _\alpha (t+\pi -\alpha )$ are congruent, we also have that the angles between the chord $[\gamma _\alpha (t-\pi +\alpha ),\gamma _\alpha (t+\pi -\alpha )]$ and the tangent lines at $\gamma _\alpha (t+\pi -\alpha )$ and $\gamma _\alpha (t-\pi +\alpha )$, are equal. By elementary geometry we have that the circle circumscribed to $\triangle \gamma _\alpha (t-\pi +\alpha )\hspace{0.88882pt}\gamma _\alpha (t)\hspace{0.88882pt}\gamma _\alpha (t+\pi -\alpha )$ and the body $K_\alpha$, share the tangent lines at the points $\gamma _\alpha (t-\pi +\alpha )$, $\gamma _\alpha (t)$, and $\gamma _\alpha (t+\pi -\alpha )$; under this condition it was proved in [7, Lemma 3.3] that $K_\alpha$ must be a disc. Now we use [8, Theorem 2(b)] and conclude that K is a disc. $\square$

Fig. 2

The angle between the chord $[\gamma _\alpha (t+\pi -\alpha ),\gamma _\alpha (t)]$ and the tangent lines are equal

4 Some Comments About Rotors in the Plane

Let K be a convex body in the plane and let ${\mathcal {P}}$ be a convex polygon. It is said that K is a rotor in ${\mathcal {P}}$ if for every rotation $\rho$, there is a translate of ${\mathcal {P}}$ that contains $\rho (K)$ and all sides of ${\mathcal {P}}$ are tangent to K. There are many results about rotors in regular polygons, see for instance [6], and for the particular case of rotors in equilateral triangles see [16]. The case of rotors in squares is well known, indeed, bodies of constant width are a very important topic in Convex Geometry and have many interesting properties and applications in mechanisms (see the quite nice book [11]).

In this section we give some words about how the results obtained in the previous section are related to rotors in polygons. Moreover, in all the examples shown below, if we fix the convex body and the circumscribed polygon is rotated, while maintained circumscribed to K, the vertices describe an isoptic curve of K.

When c(t) has constant value, using the Fourier series for the support function of p in the proof of Theorem 3.1 we arrived to the equations

$$\begin{aligned} -2\sin n(\pi -\alpha )\cos \alpha +\sin 2n\alpha&=0\qquad \text {and}\\ \quad 2\cos n(\pi -\alpha )\cos \alpha +1 +\cos 2n\alpha&=0. \end{aligned}$$

If n is even, then

$$\begin{aligned} \sin n\alpha \cdot (\cos n\alpha +\cos \alpha )&=0\qquad \text {and}\\ \quad \cos n\alpha \cdot (\cos n\alpha +\cos \alpha )&=0. \end{aligned}$$

Both of them are zero if $\cos n\alpha +\cos \alpha =0,$ or after some trigonometric transformations

$$\begin{aligned} \cos \frac{n\alpha +\alpha }{2}\cos \frac{n\alpha -\alpha }{2}=0. \end{aligned}$$

It follows that $\alpha =(2r+1)\hspace{0.49988pt}\pi /(n+1)$ or $\alpha =(2r+1)\hspace{0.49988pt}\pi /(n-1)$, where r is any integer number. In this case the determinant of the associated matrix is zero and we can choose the coefficients $a_n,b_n$ arbitrarily. For instance, for $n=4$ we select $\alpha =\pi /3$, $a_0=30$, $a_4=0$, $b_4=1$, and for any other natural number n we have that $a_n=b_n=0$, i.e., the support function of K is $p(t)=30+\sin 4t$ (see Fig. 3). The body K in this example is centrally symmetric.

Fig. 3

A centrally symmetric rotor in the equilateral triangle

If n is odd, then

$$\begin{aligned} \sin n\alpha \cdot (\cos n\alpha -\cos \alpha )&=0\qquad \text {and}\\ \cos n\alpha \cdot (\cos n\alpha -\cos \alpha )&=0. \end{aligned}$$

Both of them are zero if $\cos n\alpha -\cos \alpha =0,$ or after some trigonometric transformations

$$\begin{aligned} \sin \frac{n\alpha +\alpha }{2}\sin \frac{n\alpha -\alpha }{2}=0. \end{aligned}$$

It follows that $\alpha =2r\pi /(n+1)$ or $\alpha =2r\pi /(n-1)$, where r is any integer number. Notice that we can obtain an example for any angle of the form $\alpha =s\pi /q$, where s and q are integers such that $0<s<q$. We just use this case, since $\alpha =2s\pi /(2q)$, we select $r=s$ and $n=2q+1$ or $n=2q-1$. For instance, for $\alpha =2\pi \cdot \pi /3=4\pi \cdot \pi /6$, and then we select $n=7$. In Fig. 4 we show the body K with its isoptic $K_{2\pi /3}$, with the property that c(t) has a constant value. The support function for this example is $p(t)=80+\cos 7t$. The body in this example has constant width.

Fig. 4

A rotor with constant width in the regular hexagon

5 Some Results in Higher Dimensions

The following lemma is needed for some of the subsequent results.

Lemma 5.1

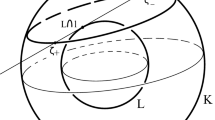
Let $K,L\subset {\mathbb {R}}^n$, $n\ge 3$, be convex bodies with $L\subset {{\,\textrm{int}\,}}K$ a strictly convex body, such that every $(n-1)$-dimensional section of K tangent to L is an $(n-1)$-dimensional ball, then K is a ball. If additionally, the centre of every tangent ball is at the point of contact with L, then K and L are concentric balls.

Proof

There are several ways to prove this lemma. Here we give the following proof. First note that if all the 3-dimensional sections of a convex body through a given point in its interior are 3-dimensional balls, then it is an n-dimensional ball. We consider any point in the interior of L for such a point and since the hypothesis of the theorem is inherited to every 3-dimensional section, we have that it is sufficient to prove the theorem in the 3-dimensional case.

Let x be any point in $\partial K$ and let $\ell$ be any line supporting K at x. Consider the two supporting planes of L which share the line $\ell$, to say $H_1$ and $H_2$. Let H be any other supporting plane of L through the point x. By hypothesis $H\cap K$ is a disc which intersects each one of the circles $H_1\cap \partial K$ and $H_2\cap \partial K$ at two points. The circle $H\cap \partial K$ passes through three points of the set $(H_1\cap \partial K)\cup (H_2\cap \partial K)$, and since there is a unique sphere which contains the two circles $H_1\cap \partial K$ and $H_2\cap \partial K$, it holds that this sphere contains $H\cap \partial K$. Since H is any supporting plane of L through x, we have that ${\mathcal {R}}_x=\{H\cap \partial K:H\ \text {is a support plane of}\ L\ \text {through}\ x\}$ is a closed subset of a sphere. Let $y\in \partial K$ be any point such that ${\mathcal {R}}_y\cap {\mathcal {R}}_x\ne \emptyset$, then ${\mathcal {R}}_y\cup {\mathcal {R}}_x$ is contained in the same sphere. Continuing in this way, since K is a compact set, we can prove that $\partial K$ is a sphere.

Now, let H be any hyperplane supporting L at a point z and suppose the centre of the $(n-1)$-dimensional ball $H\cap K$ is z. The line orthogonal to H through z passes through the centre of the ball K, this implies that indeed H is the tangent plane of L through z. Suppose to the contrary, that there exists another plane $H_1$ supporting L at z. In this case $H_1\cap K$ would be a circle centred at z and then the line orthogonal to $H_1$, through the point z, would pass through the centre of K. We would have that z must be the centre of the ball K. This can happen only for one point in $\partial L$, it follows that except at this point, $\partial L$ must be a differentiable surface. Since all the normal lines of $\partial L$ pass through the centre of K, we have that (see for instance [13]) $\partial L$ is a sphere with centre at the centre of K. We conclude that K and L are concentric balls. $\square$

The following result shows that in dimension 3 or higher, only Euclidean balls have an equichordal convex body.

Theorem 5.2

Let $K\subset {\mathbb {R}}^n$, $n\ge 3$, be a strictly convex body which possesses an equichordal convex body L in its interior. Then K and L are concentric balls.

Proof

Suppose the length of the chords of K tangent to L is $\lambda$. First we prove that L is strictly convex, i.e., L has no segments in its boundary. Suppose to the contrary that there is a segment $[a,b]\subset \partial L$ and consider any 2-dimensional plane H supporting L at [a, b]. By hypothesis, every chord of $H\cap K$ through a has length $\lambda$, and the same happens for every chord through b. This implies that $H\cap K$ has two equichordal points, but as was proved by Rychlik [12] this is not possible.

Now, let H be any 2-dimensional plane supporting L at a point x. We will prove that the diameter of $H\cap K$ is $\lambda$. Suppose this is not the case and there is a chord [a, b] of $H\cap K$ with $|a-b|>\lambda$. Clearly, $[a,b]\cap L=\emptyset$. Consider a 2-dimensional plane $\Pi$ that contains [a, b] and such that $\Pi \cap {{\,\textrm{int}\,}}L\ne \emptyset$. Let $c,d\in \partial \hspace{0.3888pt}(\Pi \cap L)$ such that the lines through c and d, respectively, that are parallel to [a, b] are supporting lines of $\Pi \cap L$. Since $|a-b|>\lambda$, we have that there exists a chord [e, f] of $\Pi \cap K$ that is separated from $\Pi \cap L$ by the chord [a, b] and $|e-f|=\lambda$. We have three chords of $\Pi \cap K$ parallel to [a, b] and with length $\lambda$. This contradicts that K is strictly convex, then the diameter of $H\cap K$ must be $\lambda$.

Every chord of $H\cap K$ through x has length equal to $\lambda$, then every chord of $H\cap K$ through x is a binormal of $H\cap K$; it follows that $H\cap K$ is a disc centred at x (see for instance [3]). Since this is true for every 2-dimensional plane H through x, we have that any $(n-1)$-dimensional section of K tangent to L at x is an $(n-1)$-dimensional sphere centred at x. This is also true for every $x\in \partial L$, so we apply Lemma 5.1 and conclude that K and L are concentric balls. $\square$

Corollary 5.3

Let $K,L\subset {\mathbb {R}}^n$, $n\ge 3$, be two convex bodies. Suppose that for every hyperplane H that intersects L it holds that $H\cap L$ is an equichordal body of $H\cap K$. Then K and L are concentric balls.

Proof

It is quite simple to prove that all the chords of K tangent to L have the same length. The conclusion follows applying Theorem 5.2. $\square$