Spherical Cap Discrepancy of the Diamond Ensemble

Abstract

In Beltrán and Etayo (J. Complexity 59, # 101471 (2020)) the authors presented a family of points on the sphere $\mathbb {S}^{2}$ depending on many parameters, called the Diamond ensemble. In this paper we compute the spherical cap discrepancy of the Diamond ensemble as well as some other quantities. We also define an area regular partition on the sphere where each region contains exactly one point of the set. For a concrete choice of parameters, we prove that the Diamond ensemble provides the best spherical cap discrepancy, known until now for a deterministic family of points.

1 Introduction and Main Results

Sets of points on the sphere $\mathbb {S}^{2}$ that are, in a sense, well distributed have been broadly studied in the literature, see for example [13, 18, 21]. We use the expression family of points to denote a sequence of configurations of points on the sphere $\mathbb {S}^{2}$, $(\omega _{N})_{N}$, where N is the number of points of the configuration. N does not necessarily run through every integer number, but an infinite subsequence of them. In order to ease the notation, we will use $\omega _{N}$ both for a family of points and a set of points, although the meaning should be clear from the context.

Let us consider a family of points $\omega _{N}\subset \mathbb {S}^{2}$ and let $\mu$ be the Lebesgue measure on the sphere $\mathbb {S}^{2}$. We recall that a Borel set $C\subset \mathbb {S}^{2}$ is $\mu$-continuous if $\mu (\partial C)=0$, where $\partial C$ is the boundary of C. Then we say that $\omega _{N}$ is asymptotically uniformly distributed if

$$\begin{aligned} \lim _{N\rightarrow \infty }\frac{\mu ( \mathbb {S}^{2}) }{N}\sum _{j=1}^{N}f(x_{j})=\int _{\mathbb {S}^{2}} f(x)\,d\mu (x), \end{aligned}$$

where, for a fixed N, $\omega _{N} = \{ x_{1},x_{2},\dots ,x_{N}\}$ and the equation is satisfied for all continuous functions $f:\mathbb {S}^{2} \rightarrow \mathbb {R}$. This definition is equivalent to the statement

$$\begin{aligned} \lim _{N\rightarrow \infty }\frac{\#\,(\omega _{N}\cap C)}{N}=\frac{\mu (C)}{\mu ( \mathbb {S}^{2})} \end{aligned}$$

(1)

for all $\mu$-continuous sets C. Asymptotical uniformity is one of the main conditions that one may ask a family of points in order to have an even distribution. This notion is described in a more general context in [17, Chapter 3].

In this article we work with the spherical distance on $\mathbb {S}^{2}$. Let us highlight, however, that the spherical distance and the Euclidean distance are equivalent for small quantities and so for all results presented here. The separation distance of a set of points $\omega _{N}$ is given by

$$\begin{aligned} \delta ( \omega _{N})=\min _{1\le i<j \le N}\Vert x_{i}-x_{j}\Vert , \end{aligned}$$

and a family of points $\omega _{N}$ is said to be well-separated if

$$\begin{aligned} \delta ( \omega _{N})\ge \frac{c}{\sqrt{N}} \end{aligned}$$

for some constant c not depending on N. The covering radius of a set of points on $\mathbb {S}^{2}$, also known as mesh norm, is defined as

$$\begin{aligned} \rho ( \omega _{N} )=\max _{y \in \mathbb {S}^{2}}\min _{1\le j \le N}\Vert y-x_{j} \Vert . \end{aligned}$$

A family of points $\omega _{N}$ is a good covering if

$$\begin{aligned} \rho ( \omega _{N})\le \frac{c}{\sqrt{N}} \end{aligned}$$

for some constant c not depending on N. The relation between the separation distance and the covering radius is usually referred to as the mesh-separation ratio

$$\begin{aligned} \gamma ( \omega _{N})=\frac{\rho ( \omega _{N})}{\delta ( \omega _{N})} \end{aligned}$$

and can be thought of as a condition number for approximation problems on the sphere.

1.1 Spherical Cap Discrepancy

Whenever we have a family of points that are asymptotically uniformly distributed, i.e., their limit distribution is the uniform measure on $\mathbb {S}^{2}$, we may ask what is the speed of convergence. From formula (1) we know that a family of points is asymptotically uniformly distributed if

$$\begin{aligned} \lim _{N\rightarrow \infty }\frac{\#\,(\omega _{N}\cap C)}{N}=\frac{\mu (C)}{\mu ( \mathbb {S}^{2})} \end{aligned}$$

for all $\mu$-continuous Borel sets $C\subset \mathbb {S}^{2}$. So, we want to study the rate at which

$$\begin{aligned} \biggl |\frac{\#\,(\omega _{N}\cap C)}{N}-\frac{\mu (C)}{\mu ( \mathbb {S}^{2})}\biggr | \end{aligned}$$

tends to 0 in some norm and for some suitable collection of test sets. This quantity is called discrepancy. The most classical discrepancy on the sphere is the so-called spherical cap discrepancy, where we consider the set of all the spherical caps and the norm is either the supremum or the $L^2$ norm. We denote by cap the set of all possible spherical caps on $\mathbb {S}^2$. Then the spherical cap discrepancy of a set of points $\omega _{N}$ is defined as

$$\begin{aligned} D_{sup ,cap } (\omega _{N})\,=\sup _{C \in cap }\,\biggl |\frac{\#\,(\omega _{N}\cap C)}{N}-\frac{\mu (C)}{\mu ( \mathbb {S}^{2})}\biggr |. \end{aligned}$$

(2)

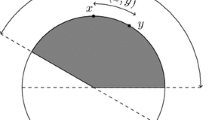
A spherical cap $C = C(z,t)$ centered at $z\in \mathbb {S}^{2}$ with height $t\in [-1,1]$ is the set

$$\begin{aligned} C(z,t) = \{ y\in \mathbb {S}^{2} : \langle z, y \rangle > t \}, \end{aligned}$$

where we denote by $\langle z, y \rangle$ the usual inner product in $\mathbb {R}^{3}$. If instead of the supremum norm the $\text {L}^{2}$ norm is considered, then the corresponding discrepancy is defined by

$$\begin{aligned} D_{\text {L}^{2},\text {cap}} (\omega _{N})=\Biggl (\int _{-1}^{1}\int _{\mathbb {S}^{2}}\,\biggl |\frac{\#\,(\omega _{N}\cap C(z,t))}{N}-\frac{\mu (C(z,t))}{\mu ( \mathbb {S}^{2})}\biggr |^{2}d\mu (z)\,dt\Biggr )^{\!{1}/{2}}. \end{aligned}$$

(3)

The Stolarsky invariance formula, stated in [23], establishes a relation between the sum of distances of the points from $\omega _{N}$ and the $\text {L}^{2}$ spherical cap discrepancy:

$$\begin{aligned} c_{d}\bigl (D_{\text {L}^{2},\text {cap}} (\omega _{N})\bigr )^{2}=\int _{\mathbb {S}^{d}}\int _{\mathbb {S}^{d}}\Vert x-y\Vert \,d\mu _{\mathbb {S}^{d}}(x)\,d\mu _{\mathbb {S}^{d}}(y)- \frac{1}{N^{2}}\sum _{i,j=1}^{N}\Vert x_{i} - x_{j}\Vert , \end{aligned}$$

where $c_{d}$ is a constant depending only on the dimension of the sphere and $\mu _{\mathbb {S}^{d}}$ is the Lebesgue measure on $\mathbb {S}^{d}$ normalized so that $\mu _{\mathbb {S}^{d}} (\mathbb {S}^{d}) = 1$. See also [9, 12] for more modern proofs of the Stolarsky invariance formula.

1.1.1 Minimal Spherical Cap Discrepancy

In [5] it was shown that there exists a constant $c>0$, independent of N, such that for any N-point set $\omega _{N}\subset \mathbb {S}^2$ we have

$$\begin{aligned} D_{sup ,cap }( \omega _{N})\ge cN^{{-3}/{4}}. \end{aligned}$$

On the other hand, using probabilistic methods, it has been shown in [4] that for all $N\ge 1$ there exists a point set $\omega _N$ in $\mathbb {S}^2$ satisfying

$$\begin{aligned} D_{sup ,cap }( \omega _{N})\le c'N^{{-3}/{4}}\sqrt{\log N}, \end{aligned}$$

where $c'>0$ is a constant independent of N. The proof of the last result is non-constructive.

1.1.2 Probabilistic Sets of Points

The spherical cap discrepancy of a random set of points coming from the uniform distribution on the sphere is of the order $N^{{-1}/{2}}$, see [1] for a proof. In the papers [3, 7], the authors define two determinantal point processes on the sphere $\mathbb {S}^{2}$ and compute the spherical cap discrepancy, obtaining

$$\begin{aligned} D_{sup ,cap }\bigl ( \omega _{N} \sim \mathfrak {X}_{*}^{(N)}\bigr )=O\bigl (N^{{-3}/{4}}\sqrt{\log N}\bigr ) \end{aligned}$$

with overwhelming probability for the spherical ensemble (see [3, Thm. 1.1]) and the same for the harmonic ensemble, see [7, Corollary 5]. Here, $\omega _{N}\sim \mathfrak {X}_{*}^{(N)}$ means a random set of N different points on $\mathbb {S}^{2}$ following the distribution given by $\mathfrak {X}_{*}^{(N)}$, the determinantal point process.

1.1.3 Deterministic Sets of Points

It is unknown how to construct a deterministic family of points with spherical cap discrepancy decaying like $N^{{-3}/{4}}\sqrt{\log N}$. The best bound given to date for a deterministic family of points can be found in the article [1], where the authors are able to bound the spherical cap discrepancy of the so-called spherical Fibonacci nodes by

$$\begin{aligned} D_{\text {sup},\text {cap}} ( \omega _{N} )\le 44\sqrt{8}N^{{-1}/{2}}. \end{aligned}$$

(4)

1.1.4 Riesz Potentials and Spherical Cap Discrepancy

Given $s\in (0,\infty )$, the Riesz potential or s-energy of a set of points $\omega _{N} = \{ x_{1}, \ldots ,x_{N} \}$ on the sphere $\mathbb {S}^{2}$ is

$$\begin{aligned} \mathscr {E}_{s}(\omega _{N}) =\sum _{i \ne j} \frac{1}{\Vert x_{i} - x_{j} \Vert ^{s}}. \end{aligned}$$

This energy has a physical interpretation for some particular values of s, i.e., for $s=1$ the Riesz energy is the Coulomb potential and for $s=0$ the energy is defined by

$$\begin{aligned} \mathscr {E}_{\log }(\omega _{N})= \frac{d\mathscr {E}_{s}(\omega _N)}{ds}\biggl |_{s=0} = \,\sum _{i \ne j} \log {\Vert x_{i} - x_{j} \Vert ^{-1} }. \end{aligned}$$

Finding quasiminimizers of the logarithmic energy is stated as the problem number 7 in the list of problems for the 21st century proposed by Smale, see [22].

There exist several results relating minimizers of the spherical cap discrepancy and minimizers of the Riesz energy. For example, minimizers of Riesz and logarithmic energy exhibit small spherical cap discrepancy; we refer to [13] and cites therein. The last word in this respect was given by Marzo and Mas who proved that any set of points that minimizes some Riesz energy with parameter $0\le s<2$ has spherical cap discrepancy bounded by

$$\begin{aligned} D_{sup ,cap } (\omega _{N})\le c_{s}N^{-({2-s})/({6-s})}, \end{aligned}$$

where $c_{s}$ is a constant depending only on s. See [20, Thm. 1.1] for the statement of the result in this full generality.

1.2 Main Results

In [8], the authors present a constructive family of points defined by: the North Pole, the South Pole, and sets of equispaced points located on several parallels. It is a parametrical model depending on the parallels chosen, the number of points chosen on each parallel, and the rotation angle of every parallel. The family is called the Diamond ensemble and it is denoted by $\diamond (N)$, where N is the number of points. This model is defined in full generality in Sect. 2.

Theorem 1.1

For any choice of parameters of the Diamond ensemble there exist two constants $c_{1}, c_{2} \in \mathbb {R}_{+}$, depending only on the parameters, such that

$$\begin{aligned} \frac{c_{1}}{\sqrt{N}}\le D_{sup ,cap }(\diamond (N))\le \frac{c_{2}}{\sqrt{N}}. \end{aligned}$$

Corollary 1.2

For any choice of parameters of the Diamond ensemble we have

$$\begin{aligned} D_{L ^2,cap }(\diamond (N))\le \frac{c_{2}}{\sqrt{N}} \end{aligned}$$

where $c_{2}\in \mathbb {R}_{+}$ is a fixed constant that depends on the concrete model.

Remark 1.3

Intuitively speaking, we tend to think that the $L ^{2}$ spherical cap discrepancy of a set of points coming from the Diamond ensemble is lower than the bound proposed in Corollary 1.2. There are $\sqrt{N}$ caps that present greater spherical cap discrepancy and that is where the supremum spherical cap discrepancy arises, but they should not influence that much when we average over all spherical caps.

Remark 1.4

The separation distances of the minimal logarithmic energy configurations on $\mathbb {S}^2$ have been proven to be of the good order: there exists a constant c such that the distance in between any pair of points from a concrete configuration is greater than $cN^{-1/2}$; for explicit values of the constant, we refer to [14, 21]. Since the logarithmic energy of the points coming from the Diamond ensemble is close to the minimal (see [8, Thm. 1.1]), their separation distance is expected to be of the right order. Then using Theorem 1.1 we could obtain a bound for the Riesz potential as it is done in [19, Thm. 5.2.1].

The constants $c_{1}$ and $c_{2}$ from Theorem 1.1 can be explicitly computed for any choice of parameters, and so, for the model presented in Sect. 3.3 we have the following statement.

Theorem 1.5

Let $\diamond (N)$ be the Diamond ensemble defined by $n=1$ and $r_j=4j$ for $1\le j\le M$. Then

$$\begin{aligned} \frac{1}{\sqrt{N}}+ o\biggl ( \frac{1}{\sqrt{N}} \biggr )\le D_{sup ,cap }(\diamond (N))<\frac{4+ 2\sqrt{2}}{\sqrt{N}}. \end{aligned}$$

Note that the choice of parameters in Theorem 1.5 is really simple and yet we obtain a bound for the discrepancy that is better than the best one known to date for a deterministic set of points, see formula (4). With better choices of parameters, for instance, with the ones proposed in [8], we should obtain better bounds.

1.2.1 Proof of Theorem 1.1

The proof of Theorem 1.1 follows from these two intermediate results.

Theorem 1.6

For any choice of parameters of the Diamond ensemble we have

$$\begin{aligned} D_{sup ,cap }{\diamond (N)}\le \frac{c_2}{\sqrt{N}}, \end{aligned}$$

where $c_2\in \mathbb {R}_{+}$ is a fixed number that depends on the concrete model.

The proof of Theorem 1.6 follows the classical argument of Beck for the upper bound on the discrepancy, see for example [6, Thm. 24D]. In order to prove it, we define an area regular partition on the sphere in Sect. 3 and we complete the proof in Sect. 4.

Theorem 1.7

For any choice of parameters of the Diamond ensemble we have

$$\begin{aligned} D_{sup ,cap }{\diamond (N)}\ge \frac{c_1}{\sqrt{N}}, \end{aligned}$$

where $c_1\in \mathbb {R}_{+}$ is a fixed number that depends on the concrete model.

For proving Theorem 1.7 it is enough to compute the value of

$$\begin{aligned} \biggl |\frac{\#\,(\diamond ( N ) \cap C)}{N}-\frac{\mu (C)}{\mu ( N)}\biggr | \end{aligned}$$

for a particular spherical cap C, as we do in Sect. 5.

1.3 Organization of the Paper

In Sect. 2 we recall the principal characteristics of the Diamond ensemble presented in [8] and prove some new results, essentially concerning the relation between the number of points on a given parallel and the total number of points. In Sect. 3 we present an area regular partition of the sphere coming from the Diamond ensemble and we prove some of its properties. We employ the rest of the sections in proving Theorems 1.5, 1.6, and 1.7.

2 The Diamond Ensemble

2.1 Definitions

In this section we follow [8]. Fix $z\in (-1,1)$, the parallel of height z in the sphere $\mathbb {S}^{2} \subset \mathbb {R}^{3}$ is simply the set of points $x\in \mathbb {S}^{2}$ such that $\langle x,(0,0,1)\rangle =z$. Then we define a general construction of points as follows:

• 1. Choose a positive integer p and $z_1,\ldots ,z_p \in \mathbb {R}$ such that $1> z_1> \ldots> z_p >-1$. Consider the p parallels with heights $z_1,\ldots ,z_p$.

• 2. For each j, $1\le j\le p$, choose a number $r_j$ of points to be allocated on parallel j (which is a circumference) by projecting the $r_j$ roots of unity onto the circumference and rotating them by a phase $\theta _j\in [0,2\pi ]$, that also has to be chosen.

• 3. To the already constructed collection of points, add the North and South Poles.

We denote this set by $\Omega (p,\{r_{j}\},\{z_{j}\},\{\theta _j\})$. Explicit formulas for this construction are easily produced: points in parallel of height $z_j$ are of the form

$$\begin{aligned} x = \Bigl ( {\sqrt{1 - z_{j}^{2}}} \cos \theta , {\sqrt{1 - z_{j}^{2}}} \sin \theta , z_{j} \Bigr ) \end{aligned}$$

for some $\theta \in [0,2\pi ]$, and thus the set $\Omega (p,\{r_{j}\},\{z_{j}\},\{\theta _j\})$ we have described is defined by

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathscr {N} = (0,0,1), \\ x_{j}^{i} = \biggl ( \sqrt{1-z_{j}^{2}}\cos {\biggl (\displaystyle \frac{2\pi i}{r_{j}} + \theta _{j}\biggr )}, \sqrt{1-z_{j}^{2}}\sin {\biggl ( \displaystyle \frac{2\pi i}{r_{j}} + \theta _{j}\biggr )}, z_{j} \biggr ),\\ \mathscr {S} = (0,0,-1). \end{array}\right. } \end{aligned}$$

We can rewrite $\Omega (p,\{r_{j}\},\{z_{j}\},\{\theta _j\})$ using spherical coordinates:

$$\begin{aligned} \Omega (p,\{r_{j}\},\{z_{j}\},\{\theta _j\}) ={\left\{ \begin{array}{ll} \mathscr {N} = (0,0), \\ x_{j}^{i} = \biggl (\displaystyle \frac{2\pi i}{r_{j}} + \theta _{j},\, \arccos z_{j}\!\biggr ),\\ \mathscr {S} = (0,\pi ), \end{array}\right. } \end{aligned}$$

where the first coordinate is an angle between 0 and $2\pi$ defined in the plane $z=0$ and the second coordinate is an angle between 0 and $\pi$ defined in the half-plane $x=0$, $y>0$. Note that since the points belong to the sphere, we do not write the coordinate correspondent to the radius, $r= 1$. We obtain different families of points from the Diamond ensemble giving values to the parameters p, $\theta _j$, $r_{j}$, and $z_{j}$ as in the following definition.

Definition 2.1

([8, Defn. 3.1]) Let p, M be two positive integers with $p=2M-1$ odd and let $r_{j}=r(j)$ where $r:[0,2M]\rightarrow \mathbb {R}$ is a continuous piecewise linear function satisfying $r(x)=r(2M-x)$ and

$$\begin{aligned} r(x)= {\left\{ \begin{array}{ll} \alpha _1+\beta _1 x&{} \text{ if } 0=t_0 \le x \le t_1 , \\ \vdots &{}\vdots \\ \alpha _n+\beta _n x &{} \text{ if } t_{n-1} \le x \le t_n=M. \end{array}\right. } \end{aligned}$$

Here, $[t_0,t_1,\ldots ,t_n]$ is some partition of [0, M] and all the $t_\ell , \alpha _\ell ,\beta _\ell$ are assumed to be integers. The further assumptions on the parameters are that $\alpha _1=0$, $\alpha _\ell ,\beta _\ell \ge 0$, $\beta _1>0$, and there exists a constant $A\ge 2$ not depending on M such that $\alpha _\ell \le AM$ and $\beta _\ell \le A$ for all $1\le \ell \le n$. We also assume that $t_1\ge cM$ for some $c>0$.

The final goal of defining the Diamond ensemble in [8] was to be able to compute its logarithmic energy. Authors could not reach this goal for any set $\Omega (p,\{r_{j}\},\{z_{j}\},\{\theta _j\})$, but they could compute the expected value of the logarithmic energy when the angles $\theta _{j}$ are taken randomly uniformly distributed in $[0,2\pi ]$. Moreover, this gives us some natural candidates for the $z_{j}$’s.

Proposition 2.2

([8, Prop. 2.5]) Given $\{ r_{1},\ldots ,r_{p} \}$ such that $r_{i} \in \mathbb {N}$, there exists a unique set of heights $\{z_{1},\ldots ,z_{p} \}$ such that $z_{1}> \ldots > z_{p}$ and

$$\begin{aligned} \mathrm{E}_{\theta _{1},\ldots ,\theta _{p} \in [0,2\pi ]^{p}}\left[ \mathscr {E}_{\log }(\Omega (p,\{r_{j}\},\{z_{j}\},\{\theta _j\}))\right] \end{aligned}$$

is minimized. The heights are:

$$\begin{aligned} z_{l}=\frac{\displaystyle \sum _{j=l+1}^{p}r_{j} - \displaystyle \sum _{j=1}^{l-1}r_{j}}{1 +\displaystyle \sum _{j=1}^{p}r_{j}}=1-\frac{1+r_l+2\displaystyle \sum _{j=1}^{l-1}r_j}{N-1}, \end{aligned}$$

where $N=2+\sum _{j=1}^{p}r_j$ is the total number of points.

From now on, let $z_{j}$ be as defined in Proposition 2.2.

Remark 2.3

Note that since $\beta _1>0$ and we have $\alpha _{\ell } + \beta _{\ell }t_{\ell } = \alpha _{\ell +1} + \beta _{\ell +1}t_{\ell }$, the function r(x) is non-decreasing on [0, M]; in other words, $r_{j} \ge r_{k}$ if $M> j > k$.

We call the family of points defined by the $r_j$’s given in Definition 2.1 and the $z_j$’s as in Proposition 2.2 the Diamond ensemble and we denote it by $\diamond (N)$, omitting in the notation the dependence on all the parameters n, $t_1,\ldots ,t_n$, $\alpha _1,\ldots ,\alpha _n$, $\beta _1,\ldots ,\beta _n$, $\theta _1,\ldots ,\theta _n$. We may not worry about the angle $\theta _j$, since the results presented here are valid for any choice of $\theta _j\in [0,2\pi ]$, so we denote $\Omega (p,\{r_{j}\},\{z_{j}\},\{\theta _j\})$ by $\Omega (p,\{r_{j}\},\{z_j\})$. The choice of parameters n, $t_{\ell }$, and $r_{\ell }$ for $1\le \ell \le n$ hence defines a sequence of configurations of points, where not all the integer numbers are taken but still the sequence goes to infinity as we make M cover the natural numbers.

Fig. 1

Models of the Diamond ensemble for different choices of parameters. Different colors for points correspond to different linear pieces defining r(x)

2.2 Some Extra Properties

The total number of points of $\diamond (N)$ is

$$\begin{aligned} N=2-(\alpha _n+\beta _nM)+2\sum _{\ell =1}^n\,\sum _{j=t_{\ell -1}+1}^{t_\ell }\!\!(\alpha _\ell +\beta _\ell j). \end{aligned}$$

We denote

$$\begin{aligned} N_j=1 + \sum _{k=1}^{j-1}r_k. \end{aligned}$$

(5)

Using the notation $N_{j}$ we can rewrite the value of $z_{j}$:

$$\begin{aligned} z_j=1-\frac{1+r_j+\displaystyle 2\sum _{k=1}^{j-1}r_k}{N-1}=1-\frac{2N_{j}}{N-1} - \frac{r_{j}-1}{N-1}. \end{aligned}$$

(6)

The following proposition shows the dependence of N on the number of parallels.

Lemma 2.4

There exist constants $a_{1},a_{2}\in \mathbb {R}_{+}$, depending only on the choice of parameters $n, t_{\ell }, \alpha _{\ell }, \beta _{\ell }$ for all $1\le \ell \le n$, such that

$$\begin{aligned} a_{1}M^2 \le N \le a_{2}M^2. \end{aligned}$$

Proof

From the properties of $\alpha _{\ell },\beta _{\ell }$ we have that

$$\begin{aligned} N&=2-(\alpha _n+\beta _nM)+2\sum _{\ell =1}^n\,\sum _{j=t_{\ell -1}+1}^{t_\ell }\!\!(\alpha _\ell +\beta _\ell j)\\&\le 2+2\sum _{\ell =1}^n\,\sum _{j=t_{\ell -1}+1}^{t_\ell }\!\!(AM+A j)\\&=2+ 2AM^2 + AM(M+1)=3AM^2 + AM + 2, \end{aligned}$$

where A is the constant from Definition 2.1. So it is enough to take $a_{2} = 4A$ for $M\ge 2$. For the other inequality, using again the properties from Definition 2.1, we have

$$\begin{aligned} N_{t_{1}}=1+\sum _{j=1}^{t_1-1}(\alpha _1+\beta _1 j)\ge 1+\sum _{j=1}^{cM-1} j=1+\frac{cM(cM-1)}{2}=\frac{c^2}{2} M^2 - \frac{cM}{2} + 1. \end{aligned}$$

We take $a_{1} = ({c^2-c})/{2}$ and conclude with

$$\begin{aligned} N \ge N_{t_{1}} \ge a_{1}M^{2}. \end{aligned}$$

(7)

$\square$

Lemma 2.5

There exist constants $k_{1},k_{2}\in \mathbb {R}_{+}$ depending only on the choice of parameters $n,t_{\ell },\alpha _{\ell },\beta _{\ell }$, $1\le \ell \le n$, such that for all $1 \le j \le M$ we have

$$\begin{aligned} k_{1} r_{j}^2\le N_{j}\le k_{2} r_{j}^2. \end{aligned}$$

Proof

For $1\le j \le t_{1}$ we have that $\alpha _{1} = 0$, and so

$$\begin{aligned} N_{j}=1 + \sum _{k=1}^{j-1}\beta _1 k=1 + \frac{\beta _{1}}{2}j(j-1)\quad \ \text{ and } \ \quad r_{j}^2=\beta _{1}^2j^2. \end{aligned}$$

It is immediate to check that if we take $\dot{k}_{2}=1$, then $N_{j} \le \dot{k}_{2} r_{j}^2$ for all $1\le j \le t_{1}$. We observe that both $N_{j}$ and $r_{j}^2$ are positive branches of parabolas in j. Let us consider the functions

$$\begin{aligned} r^2(x) = \beta _{1}^2x^2\quad \ \text { and }\ \quad N(x)=\frac{\beta _{1}}{2}x^2 - \frac{\beta _{1}}{2} x + 1. \end{aligned}$$

Then, if we take $\dot{k}_{1} =1/(2\beta _1^2)$, we have $\dot{k}_{1}r^{2}(1) = 1/{2}< N(1)$ and $\dot{k}_{1}(r^2(x))' \le N(x)'$ for all $x\in (1,t_{1})$ so we conclude that $\dot{k}_{1} r_{j}^2 \le N_{j}$ for all $1\le j \le t_{1}$. For $j > t_{1}$ we have

$$\begin{aligned} r_{j}^{2}=( \alpha _{\ell } + \beta _{\ell }j )^2\le ( AM + AM )^2= 4A^2M^2 \end{aligned}$$

and from (7)

$$\begin{aligned} N_{j}\ge N_{t_{1}}\ge a_{1} M^2. \end{aligned}$$

So it is enough to take $\tilde{k}_{1} = {a_{1}}/({4A^2})$. On the other hand, by Lemma 2.4 we have

$$\begin{aligned} N_{j}\le N\le a_{2}M^2 \end{aligned}$$

and, by the monotonicity of the function (see Remark 2.3),

$$\begin{aligned} r_{j}^2=(\alpha _{\ell } + \beta _{\ell }j )^2\ge t_{1}^{2}\ge c^2M^2. \end{aligned}$$

So it is enough to take $\tilde{k}_{2} = {a_{2}}/{c^2}$. We conclude by taking

$$\begin{aligned} k_{1} = \min {\{ \tilde{k}_{1}, \dot{k}_{1}\}} \quad \ \text { and }\quad \ k_{2} = \max {\{ \tilde{k}_{2}, \dot{k}_{2}\}}. \end{aligned}$$

$\square$

3 An Area Regular Partition Coming from the Diamond Ensemble

3.1 About Area Regular Partitions on the Sphere

In the literature we can find several references to area regular partitions on the sphere $\mathbb {S}^{2}$ but no so many explicit examples of them; we refer to [2, 11, 15, 23]. In [24] Zhou describes an area regular partition in $\mathbb {S}^{2}$ quite similar to the one that we present here. The same construction is explained in [21] and later in [16]. This construction was modified by Bondarenko et al. [10] to create a partition with geodesic boundaries in order to obtain well-separated spherical designs. In his PhD dissertation [19], Leopardi studied the construction of Zhou generalizing it to higher dimensional spheres. He also provided a code in Matlab available at http://eqsp.sourceforge.net/ where one can obtain an area regular partition in $\mathbb {S}^{d}$ for any given number of cells.

3.2 ARP for the Diamond Ensemble

Given a family of points coming from the Diamond ensemble, we define an area regular partition by taking two spherical caps, one centered at the North Pole and the other at the South Pole, and a collection of rectangular regions located in some collars, see Fig. 2. The partition of a collar into $r_{j}$ rectangular regions is made so that every point of the parallel $z_{j}$ is located on a different region of the collar.

Fig. 2

Example of an area regular partition coming from the Diamond ensemble

Definition 3.1

Let p, M be two positive integers with $p=2M-1$ and let us consider the following subsets of $\mathbb {S}^{2}$:

• A spherical cap centered at the North Pole with height $1 -h_{1}$, which we denote by $R_{N}$.

• The spherical rectangles on the Northern Hemisphere given in spherical coordinates on the sphere by

  $$\begin{aligned} R_{j}^{i}&= \biggl [\frac{2\pi i}{r_{j}} + \frac{\pi }{r_{j}} + \theta _{j}, \frac{2\pi (i+1)}{r_{j}} + \frac{\pi }{r_{j}} + \theta _{j}\biggr ]\times [{\arccos h_{j}},\arccos h_{j+1}]. \end{aligned}$$

• The spherical rectangles contained in a collar containing the equator:

  $$\begin{aligned} R_{M}^{i} \!=\! \biggl [ \frac{2\pi i}{r_{M}} \!+\! \frac{\pi }{r_{M}} \!+\! \theta _{M}, \frac{2\pi (i+1)}{r_{M}} \!+\! \frac{\pi }{r_{M}} \!+\! \theta _{M}\biggr ]\times [{\arccos h_{M}},\pi -\arccos h_{M}]. \end{aligned}$$

• The symmetrization of the Northern Hemisphere.

Let $h_{j}$ be defined by the following recurrence relation:

$$\begin{aligned} h_{1} = 1 - \frac{2}{N},\quad \ h_{j+1} = h_{j} - \frac{2r_{j}}{N}\qquad \text {for }1 \le j \le M, \end{aligned}$$

or, in an explicit formula, using the notation from equation (5), by

$$\begin{aligned} h_{j} = 1 - \frac{2N_{j}}{N}. \end{aligned}$$

Proposition 3.2

The partition defined in Definition 3.1 is an area regular partition.

Proof

From the definition, we can see that it is enough to compute the area of the North Pole region, one of the regions $R_{j}^{i}$ and one of the regions $R_{M}^{i}$. We start by computing the area of the region containing the North Pole:

$$\begin{aligned} A(R_{N})=2\pi (1 - h_{1})=2\pi \biggl ( 1 - 1 + \frac{2}{N}\biggr )=\frac{4\pi }{N}. \end{aligned}$$

Now we consider a rectangle $R_{j}^{i}$ and compute its area.

$$\begin{aligned} A(R_{j}^{i})&=\int _{{2\pi i}/{r_{j}} + {\pi }/{r_{j}} + \theta _{j}}^{{2\pi (i+1)}/{r_{j}} + {\pi }/{r_{j}} + \theta _{j}}\! \int _{\arccos h_{j}}^{\arccos h_{j+1}}\sin \theta \,d\theta \,d\phi \\&=\int _{{2\pi i}/{r_{j}} + {\pi }/{r_{j}} + \theta _{j}}^{{2\pi (i+1)}/{r_{j}} + {\pi }/{r_{j}} + \theta _{j}} d\phi \;\,\cdot \,\int _{\arccos h_{j}}^{\arccos h_{j+1}}\sin \theta \,d\theta \\&=\frac{2\pi }{r_{j}}(\cos \arccos h_{j}- \cos \arccos h_{j+1})=\frac{2\pi }{r_{j}}(h_{j} -h_{j+1}). \end{aligned}$$

By the recurrence relation defining $h_{j+1}$, we have

$$\begin{aligned} A(R_{j}^{i})=\frac{2\pi }{r_{j}}\biggl (h_{j} -h_{j} + \frac{2r_{j}}{N}\biggr )=\frac{4\pi }{N}. \end{aligned}$$

It remains to consider the case $R_{M}^{i}$. We compute the area of half of the region:

$$\begin{aligned} \frac{A( R_{M}^{i} )}{2}=\int _{{2\pi i}/{r_{M}} + {\pi }/{r_{M}} + \theta _{M}}^{{2\pi (i+1)}/{r_{M}} + {\pi }/{r_{M}} + \theta _{M}}\! \int _{\arccos h_{M}}^{{\pi }/{2}}\!\sin \theta \,d\theta \,d\phi =\frac{2\pi }{r_{M}}h_{M}. \end{aligned}$$

Using the explicit definition of $h_{M}$ we can write

$$\begin{aligned} \frac{A( R_{M}^{i})}{2}=\frac{2\pi }{r_{M}} \biggl ( 1 - \frac{2}{N} N_{M} \biggr )=\frac{2\pi }{N} \biggl ( \frac{N}{r_{M}} - \frac{2N_{M}}{r_{M}}\biggr )=\frac{2\pi }{N} . \end{aligned}$$

$\square$

Proposition 3.3

Every region of the partition defined in Definition 3.1 contains a unique point of the Diamond ensemble.

Proof

Since, given a collar, it is partitioned in such a way that every point belongs to a different region, it is enough to prove that

$$\begin{aligned} h_{j+1}<z_{j}<h_{j} \end{aligned}$$

for all $1\le j \le M-1$ and that $h_{M} >0$. We start by proving that $z_{j} < h_{j}$, which follows easily from these two facts:

$$\begin{aligned} \frac{2N_{j}}{N-1}>\frac{2N_{j}}{N}\qquad \text { and }\qquad \frac{r_{j} -1 }{N-1} \ge 0. \end{aligned}$$

If we take now the characterizations for $z_{j}$ and $h_{j}$ given in (6) and Definition 3.1 respectively, the proof is done. To prove that $h_{j+1} < z_{j}$ we use the same characterizations and the fact that $2N_{j} + r_{j} = 2N_{j+1} - r_{j}$; then

$$\begin{aligned} z_{j} - h_{j+1}=-\frac{2N_{j+1} - r_{j} - 1}{N-1} + \frac{2N_{j+1}}{N}=\frac{N(r_{j} + 1) - 2N_{j+1}}{N(N-1)}>0. \end{aligned}$$

We conclude with

$$\begin{aligned} h_{M}=1 - \frac{2N_{M}}{N}=1 - \frac{N-r_{M}}{N}=\frac{r_{M}}{N}>0. \end{aligned}$$

$\square$

We describe some properties of the area regular partition.

Proposition 3.4

The radius of the region $R_{N}$ is $2 \arcsin {({1}/\!{\sqrt{N}})} \approx {2}/\!{\sqrt{N}}$ for big N.

Proof

The proof consists of some trigonometric computations and is left to the reader. $\square$

Proposition 3.5

For every rectangular region $R_{j}^{i}$, the length of the horizontal sides (those parallel to the equator) is bounded as follows:

$$\begin{aligned} \frac{d_{1}}{\sqrt{N}}<\,\text {length of the horizontal sides of } R_{j}^{i}\,<\frac{d_{2}}{\sqrt{N}}, \end{aligned}$$

where $d_{1},d_{2} \in \mathbb {R}_{+}$ are fixed constants depending only on the choice of parameters $n, t_{\ell }, \alpha _{\ell }, \beta _{\ell }$, $1\le \ell \le n$.

Proof

By the symmetry of the model, we only work with the regions contained in the Northern Hemisphere and those containing the equator. Note that for every rectangular region of the Northern Hemisphere, the side parallel to the equator that is closer to the North Pole is shorter than the one that is closer to the equator, see Fig. 2. In the case $R_{M}^{i}$ they are equal. So it is enough to prove that

$$\begin{aligned} \frac{d_{1}}{\sqrt{N}}<\frac{2\pi \sqrt{1 - h_{j}^{2}}}{r_{j}}<\frac{d_{2}}{\sqrt{N}} \end{aligned}$$

for $1 \le j \le M$. We transform this expression:

$$\begin{aligned} \frac{2\pi \sqrt{1 - h_{j}^{2}}}{r_{j}}>\frac{d_{1}}{\sqrt{N}}\ \Leftrightarrow \ N(1 - h_{j}^{2})>\frac{d_{1}^2r_{j}^{2}}{4\pi ^2}\ \Leftrightarrow \ N_{j}\biggl (1 - \frac{N_{j}}{N}\biggr )>\frac{d_{1}^2r_{j}^{2}}{16\pi ^2} . \end{aligned}$$

Since $1 \le j \le M$, we have that ${1}/{2}< 1 - {N_{j}}/{N} < 1$. Applying Proposition 2.5 we have

$$\begin{aligned} N_{j}\biggl (1 - \frac{N_{j}}{N}\biggr )>\frac{N_{j}}{2}\ge \frac{k_{1}}{2} r_{j}^2 \end{aligned}$$

and so it is enough to take $d_{1} = 2\sqrt{2}\pi \sqrt{k_{1}}$. On the other hand,

$$\begin{aligned} N_{j}\biggl (1 - \frac{N_{j}}{N}\biggr )<N_{j}\le k_{2} r_{j}^2, \end{aligned}$$

and so we take $d_{2}=4\pi \sqrt{k_{2}}$. $\square$

Corollary 3.6

The heights of the rectangles $R_{j}^{i}$ for $1\le j\le M$ of the area regular partition are bounded from above by ${e}/\!{\sqrt{N}}$, where $e\in \mathbb {R}_{+}$ depends only on the choice of parameters $n, t_{\ell }, \alpha _{\ell }, \beta _{\ell }$, $1\le \ell \le n$.

Corollary 3.7

The diameters of the rectangles $R_{j}^{i}$ for $1\le j\le M$ of the area regular partition are bounded as follows:

$$\begin{aligned} \frac{g_{1}}{\sqrt{N}}<\,{\text {diam}} R_{j}^{i}<\frac{g_{2}}{\sqrt{N}}, \end{aligned}$$

where $g_{1}, g_{2}\in \mathbb {R}_{+}$ depend only on the choice of parameters $n, t_{\ell }, \alpha _{\ell }, \beta _{\ell }$, $1\le \ell \le n$.

Corollary 3.7 implies that the mesh norm of the Diamond ensemble is bounded by ${g_{2}}/\!\sqrt{N}$. So in particular we can state that the Diamond ensemble is a good covering.

3.3 A Concrete Example

We consider in this section the simple model defined in [8, Sect. 4.1] and compute explicitly all the constants presented in the previous section. Following the notation from Definition 2.1, we choose $n=1$ and $r_j=4j$ for $1\le j\le M$. Then, for all $j\in \{1,\ldots ,M\}$ we have

$$\begin{aligned} z_j=1-\frac{1+4j^2}{N-1}. \end{aligned}$$

The number of parallels is $2M-1$ and the number of points is

$$\begin{aligned} N=2 -4M+ 2\sum _{j=1}^{M} 4j=2 + 4M^2\quad \ \text { and }\ \quad N_{j}=1 + \sum _{k=1}^{j-1} 4k=2j^2 - 2j + 1. \end{aligned}$$

We consider the partition of $\mathbb {S}^{2}$ defined in Definition 3.1 where

$$\begin{aligned} h_{j}=1 - \frac{2}{N} - \frac{4j(j-1)}{N}=\frac{-4}{N} j^{2} + \frac{4}{N} j + \biggl ( 1 - \frac{2}{N} \biggr ), \end{aligned}$$

for $1\le j \le M$, and is given by the recurrence relation:

$$\begin{aligned} h_{j+1}=h_{j} - \frac{8j}{N}. \end{aligned}$$

We can obtain the same bound as in Proposition 3.5 with explicit constants $d_{1}$ and $d_{2}$.

Proposition 3.8

For every rectangular region $R_{j}^{i}$ from the area regular partition described above, the length of the horizontal sides (those parallel to the equator) is bounded as follows:

$$\begin{aligned} \frac{\pi }{\sqrt{2N}}<\,\text {length of the horizontal sides of }R_{j}^{i}\,<\frac{\pi \sqrt{2}}{\sqrt{N}}. \end{aligned}$$

Proof

As in the proof of Proposition 3.5, we consider the quantity

$$\begin{aligned} \frac{2\pi \sqrt{1 - h_{j}^{2}}}{r_{j}}=\frac{2\pi }{4j}\sqrt{\frac{4N_{j}}{N}\biggl ( 1 - \frac{N_{j}}{N}\biggr )}=\frac{\pi }{N} \sqrt{\frac{( 2j^2 - 2j + 1)( 4M^2 - 2j^2 + 2j + 1)}{j^2}}\,. \end{aligned}$$

First we bound

$$\begin{aligned} 1\le \frac{2j^2 - 2j + 1}{j^2}<2\quad \ \text { for all }\ 1\le j \le M. \end{aligned}$$

On the other hand,

$$\begin{aligned} 2M^2 + 2M + 1\le 4M^2 - 2j^2 + 2j + 1\le 4M^2 + 1\quad \ \text { for all }\ 1\le j \le M. \end{aligned}$$

Since all quantities are positive, we have

$$\begin{aligned} \sqrt{2M^2 + 2M + 1}\le \sqrt{(4M^2 - 2j^2 + 2j + 1)\frac{2j^2 - 2j + 1}{j^2}}<\sqrt{2(4M^2 + 1)}\,. \end{aligned}$$

We rewrite the expressions in terms of N:

$$\begin{aligned} \frac{\pi }{N}\sqrt{2M^2 + 2M + 1}=\frac{\pi }{N}\sqrt{\frac{N}{2} + \sqrt{N-2}}\ge \frac{\pi }{\sqrt{2}}\frac{1}{\sqrt{N}} \end{aligned}$$

and

$$\begin{aligned} \frac{\pi }{N}\sqrt{2(4M^2 + 1)}=\frac{\pi }{N}\sqrt{2N}=\frac{\pi \sqrt{2}}{\sqrt{N}}\,. \end{aligned}$$

$\square$

We can easily deduce bounds for the other quantities for this model as in Corollaries 3.6 and 3.7.

4 Proof of Theorem 1.6

As we mentioned before, to prove Theorem 1.6 we follow the general lines of the proof proposed in [6, Thm. 24D].

Given a family of points coming from the Diamond ensemble for some choice of parameters $n,t_{\ell },\alpha _{\ell },\beta _{\ell }$ for $1\le \ell \le n$, we consider the associated area regular partition given in Definition 3.1. Let us take a spherical cap on the sphere $\mathbb {S}^2$ and denote it by C. We can split

$$\begin{aligned} C = \tilde{C} \cup \dot{C} \end{aligned}$$

where $\dot{C}$ is the union of all the regions of the area regular partition that are completely contained in C. Therefore, $\tilde{C}$ is the union of all the regions of the area regular partition that are partially contained in C, intersected with C. Then we have

$$\begin{aligned} D_{sup ,cap } (\diamond ( N ))= & {} \sup _{C \in cap }\,\biggl |\frac{\#\,(\diamond ( N) \cap C) }{N}-\frac{\mu (C)}{4\pi }\biggr |\\= & {} \sup _{C \in cap }\,\biggl |\frac{\#\,(\diamond ( N ) \cap \tilde{C})}{N}+\frac{\#\,(\diamond ( N) \cap \dot{C})}{N}-\frac{\mu (\tilde{C})}{4\pi } -\frac{\mu (\dot{C})}{4\pi }\biggr |. \end{aligned}$$

Since we are taking an area regular partition, we have

$$\begin{aligned} \frac{\#\,(\diamond ( N) \cap \dot{C})}{N}=\frac{\mu (\dot{C})}{4\pi } \end{aligned}$$

and so

$$\begin{aligned} D_{sup ,cap } (\diamond ( N))=\sup _{C \in \text {cap}}\,\biggl |\frac{\#\,(\diamond ( N) \cap \tilde{C})}{N}-\frac{\mu (\tilde{C})}{4\pi }\biggr |. \end{aligned}$$

Now let us prove that the border of any spherical cap C passes through at most $k\sqrt{N}$ different regions of our partition, with $k\in \mathbb {R}_{+}$ depending only on the choice of parameters $n, t_{\ell }, \alpha _{\ell }, \beta _{\ell }$, $1\le \ell \le n$. In order to do so, we consider the intersection of the border of our spherical cap, which we will denote by $\mathscr {C}$, and a collar $Z_{j}=\bigcup _{i=1}^{r_{j}} R_{j}^{i}$. Let

$$\begin{aligned} \mathscr {L}_{j}=Z_{j}\cap \mathscr {C}, \end{aligned}$$

and we consider the length of $\mathscr {L}_{j}$, which we denote by $|\mathscr {L}_{j}|$. Note that $\mathscr {C}$ can pass through each $Z_{j}$ at most twice and at non-consecutive times, see Fig. 3 (a). Then the number of regions that $\mathscr {L}_{j}$ passes through, which we denote by $N(\mathscr {L}_{j})$, is bounded as follows:

$$\begin{aligned} N(\mathscr {L}_{j})\le 4+\frac{|\mathscr {L}_{j}|}{{d_{1}}/{\sqrt{N}}} \end{aligned}$$

with $d_{1}$ as in Proposition 3.5. So, the number of regions that the border of C passes through is bounded by

$$\begin{aligned} \sum _{j=1}^{2M-1}N(\mathscr {L}_{j})\le & {} \sum _{j=1}^{2M-1}\biggl (4+\frac{|\mathscr {L}_{j}|}{{d_{1}}/\!{\sqrt{N}}}\biggr )=4(2M-1) + \frac{\sqrt{N}}{d_{1}}\sum _{j=1}^{2M-1}|\mathscr {L}_{j}|\\\le & {} 4(2M-1) +\frac{2\pi }{d_{1}}\sqrt{N}\le \frac{8}{\sqrt{a_{1}}}\sqrt{N} - 4 +\frac{2\pi }{d_{1}}\sqrt{N}\\\le & {} \biggl (\frac{8}{\sqrt{a_{1}}} +\frac{2\pi }{d_{1}}\biggr )\sqrt{N}, \end{aligned}$$

where we have used Lemma 2.4 to bound M.

Fig. 3

Decomposition of the border of a spherical cap

Since every region has area ${4\pi }/{N}$, we conclude that

$$\begin{aligned} D_{sup ,cap } (\diamond ( N) )=\sup _{C \in cap }\,\biggl |\frac{\#\,(\diamond ( N) \cap \tilde{C})}{N} -\frac{\mu (\tilde{C})}{4\pi }\biggr |\le \biggl (\frac{8}{\sqrt{a_{1}}}+\frac{2\pi }{d_{1}}\biggr )\frac{1}{\sqrt{N}}. \end{aligned}$$

Note that we are not taking into account the regions containing the North or South Pole since they are meaningless for the asymptotics.

5 Proof of Theorem 1.7

For proving Theorem 1.7 we consider the very specific spherical cap consisting of the upper half semisphere containing the line of the equator. Then the expression

$$\begin{aligned} \biggl |\frac{\#\,(\diamond ( N) \cap C)}{N}-\frac{\mu (C)}{4\pi }\biggr | \end{aligned}$$

can be simplified. For the symmetry of the model,

$$\begin{aligned} \#\,(\diamond ( N) \cap C)=\frac{N}{2} + \frac{r_{M}}{2}, \end{aligned}$$

where by $r_{M}$ we denote the number of points that lie in the equator and ${\mu (C)}/({4\pi })={1}/{2}$. Then we have

$$\begin{aligned} \biggl |\frac{\#\,(\diamond ( N) \cap C)}{N}-\frac{\mu (C)}{4\pi }\biggr |=\biggl |\frac{{N}/{2} + {r_{M}}/{2}}{N}-\frac{1}{2}\biggr |= \biggl |\frac{1}{2}+\frac{r_{M}}{2N}-\frac{1}{2}\biggr |=\frac{r_{M}}{2N}. \end{aligned}$$

From Definition 2.1 we know that $r_{M}\ge r_{t_{1}}\ge cM$ and from Lemma 2.4 we have $N\le a_{2}M^2$. So,

$$\begin{aligned} \biggl |\frac{\#\,(\diamond ( N) \cap C)}{N}-\frac{\mu (C)}{4\pi }\biggr |=\frac{r_{M}}{2N}\ge \frac{cM}{2N}\ge \frac{c\sqrt{N}}{2\sqrt{a_{2}}N}= \frac{c}{2\sqrt{a_{2}}}\cdot \frac{1}{\sqrt{N}}. \end{aligned}$$

Then, it is enough to take $c_{1} = {c}/({2\sqrt{a_{2}}})$ to conclude that

$$\begin{aligned} D_{sup ,cap } (\diamond ( N))=\sup _{C \in cap }\,\biggl |\frac{\#\,(\diamond ( N) \cap C)}{N}-\frac{\mu (C)}{4\pi }\biggr |\ge \frac{c_{1}}{\sqrt{N}}. \end{aligned}$$

6 Proof of Theorem 1.5

As for Theorem 1.1, we split the proof of Theorem 1.5 into two lemmas.

Lemma 6.1

Let $\diamond (N)$ be the Diamond ensemble defined by $n=1$ and $r_j=4j$ for $1\le j\le M$. Then

$$\begin{aligned} D_{sup ,cap }(\diamond (N))<\frac{4+ 2\sqrt{2}}{\sqrt{N}}. \end{aligned}$$

Proof

We follow the proof from Theorem 1.6, then using the bounds given in Proposition 3.8 we have

$$\begin{aligned} \sum _{j=1}^{2M-1}N(\mathscr {L}_{j})< & {} \sum _{j=1}^{2M-1}\biggl (4+\frac{|\mathscr {L}_{j}|}{{\pi }/{\sqrt{2N}}}\biggr )=4(2M-1) +\frac{\sqrt{2}}{\pi }\sqrt{N}\sum _{j=1}^{2M-1}|\mathscr {L}_{j}|\\\le & {} 4\sqrt{N-2}-4 +2\sqrt{2N}<(4+ 2\sqrt{2})\sqrt{N}. \end{aligned}$$

Then, we have

$$\begin{aligned} D_{sup ,cap } (\diamond ( N))=\sup _{C \in cap }\,\biggl |\frac{\#\,(\diamond ( N) \cap \tilde{C})}{N}-\frac{\mu (\tilde{C})}{4\pi }\biggr |\le \frac{4+ 2\sqrt{2}}{\sqrt{N}}. \square \end{aligned}$$

Lemma 6.2

Let $\diamond (N)$ be the Diamond ensemble defined by $n=1$ and $r_j=4j$ for $1\le j\le M$. Then

$$\begin{aligned} D_{sup ,cap }(\diamond (N))\ge \frac{1}{\sqrt{N}}+ o\biggl ( \frac{1}{\sqrt{N}} \biggr ). \end{aligned}$$

Proof

We are going to consider a subfamily of spherical caps in $\mathbb {S}^2$ formed by the caps that are centered at the North Pole and whose border is one of the parallels where we have chosen the points, i.e., one of the parallels defined by the $z_{j}$’s. For the symmetry of the model, it is enough to consider $1\le j \le M$. The discrepancy for these particular caps reads

$$\begin{aligned} \sup _{1\le j \le M}\,\biggl |\frac{\#\,(\diamond ( N) \cap C)}{N}-\frac{\mu (C)}{4\pi }\biggr |&=\sup _{1\le j \le M}\,\biggl |\frac{N_{j+1}}{N}-\frac{2\pi (1-z_{j})}{4\pi }\biggr |\\&=\sup _{1\le j \le M}\,\biggl |\frac{N-2 - 4j^2 + 4j(N-1)}{2N(N-1)}\biggr |, \end{aligned}$$

where $N-2 - 4j^2 + 4(N-1)j>0$ for all $1\le j \le M$, and $f(x) = N-2 - 4x^2 + 4(N-1)x$ is an increasing function in the interval [1, M], so

$$\begin{aligned} \sup _{1\le j \le M}\biggl |\frac{\#\,(\diamond ( N) \cap C)}{N}-\frac{\mu (C)}{4\pi }\biggr |&=\frac{N-2 - 4M^2 + 4M(N-1)}{2N(N-1)}\\&=\frac{\sqrt{N-2}}{N}=\frac{1}{\sqrt{N}} + o\biggl ( \frac{1}{\sqrt{N}} \biggr ). \end{aligned}$$

$\square$