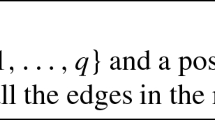1 Introduction

Given an input graph, to output an optimal subgraph satisfying some constraints is perhaps the most studied family of problems from an approximation perspective. Of late combinatorists have extensively studied such problems when the edges are colored, called Rainbow Subgraph problems. See [2, 10, 15, 25, 26] for a short representative list.

Our focus is arguably the simplest such computational problem, called the minimum rainbow subgraph (MRS) problem. The input to the problem is an n-vertex simple undirected graph, with each edge colored with one of p colors. The goal is to find a subgraph on a minimum number of vertices which has one induced edge of each color. It was introduced in [5] and has been studied from the approximation viewpoint by [5, 19, 23]. The problem is known to be NP-hard.

The motivation for this problem comes from the pure parsimony haplotyping (PPH) problem in computational biology, which was introduced by Gusfield in 2003 [14]. Input to the problem is a set \(\mathcal {G}\) of p genotypes (vectors of entries in \(\{0,1,2\}\)) corresponding to individuals in population, and a set of \(\mathcal {H}\) of haplotypes (vectors of entries in \(\{0,1\}\)). A genotype g is explained by two haplotypes \(h_1\) and \(h_2\), if for each i, either \(g[i]=h_1[i]=h_2[i]\), or \(g[i]=2\) and \(h_1[i]\ne h_2[i]\). The goal of the PPH problem is to find a minimum subset of haplotypes that explain every genotype in \(\mathcal {G}\). If the number of entries where \(g[i]=2\) is k, then the problem is called PPH(k). Camcho et al. [5] showed that if \(k = O(\log p)\), then PPH(k) can be reduced to the MRS problem.

There is a trivial \(O(\sqrt{n})\)-approximation algorithm for the MRS problem. Select one edge of each color and add its end points to the solution set. And this is the best known upper bound for this problem. The upper bound on the approximation ratio can be improved for bounded degree graphs. Camcho et al. [5] gave a \(\frac{5}{6}\Delta \)-approximation algorithm on graphs with maximum degree \(\Delta \), which was later improved by Katrenič et al. [19] to \(\left( \frac{1}{2}+\left( \frac{1}{2}+\epsilon \right) \Delta \right) \). Katrenič et al. [19] also present an exact algorithm for the MRS problem that has a running time of \(n^{O(1)}\cdot 2^p \cdot \Delta ^{2p}\). Hüffner et al. [18] study the parameterized complexity of the MRS problem with different parameters.

We observe that the approximation ratio for the MRS problem achieved by the trivial algorithm may not be beaten using natural LP and SDP relaxations (in Sect. 2). We give an \(\Omega (\sqrt{n})\) lower bound on the integrality gap for these natural relaxations. As the first idea towards an algorithm with an improved ratio, we define a new problem: the densest colored k-subgraph (DCkS) problem. The input to the DCkS problem consists of an undirected graph with each edge colored with one of p colors and a parameter k. The goal is to find a subgraph on k vertices which has the maximum number of edges with distinct colors. We show then that an f-approximation algorithm for the DCkS problem implies an \(O(f\log n)\)-approximation algorithm for the MRS problem.

Note that the well studied densest k-subgraph (DkS) problem is a special case of the DCkS problem, in which every edge is colored with a different color. In addition to being NP-hard, the DkS problem has been shown not to admit a PTAS under various complexity theoretic assumptions [12, 20]. Assuming the Small Set Expansion conjecture, Raghavendra et al. [24] rule out constant factor approximation for the DkS problem. The DkS problem is known to be notoriously hard to approximate. Breaking the \(O(\sqrt{n})\) barrier, Feige et al. [13] gave an \(O(n^{1/3-\epsilon })\)-approximation algorithm, for some \(\epsilon >0\). In a remarkable paper, Bhaskara et al. [3] improve this to \(O(n^{1/4+\epsilon })\), for any \(\epsilon >0\). There is a large gap between the known upper and lower bounds for the DkS problem. As evidence for the hardness of approximating the DkS problem within polynomial factors, a lower bound of \(\Omega (n^{1/4}/\log ^3n)\) on the integrality gap for \(\Omega (\log n/ \log \log n)\) rounds of the Sherali-Adams relaxation for the DkS problem is shown in [4].

The introduction of colors (in the DCkS problem) intuitively seems to increase the difficulty. One difficulty, for instance is that exactly one edge of each color is of importance. In this paper, we give an \(O(n^{1/3})\)-approximation algorithm for the DCkS problem. Our algorithm builds on the one for the DkS problem in [13].

The MRS problem falls in a class of problems with the known upper bound on the approximation ratio \(|I|^c\) where |I| is the input size and c a constant less than one, and with the known lower bounds being smaller growing functions. Prior to a breakthrough result by Charikar et al. [7], several papers reduced the Min-Rep [21] problem (defined in Sect. 3.7) to other problems in order to obtain hardness results. It was conjectured that the Min-Rep problem has a lower bound \(\Omega (\sqrt{n})\) on the approximation ratio, which was refuted by Charikar et al. [7]. They gave an LP-rounding algorithm with approximation ratio \(O(n^{1/3}\log ^{2/3}n)\). We observe that the Min-Rep problem is a special case of the MRS problem, and this gives a combinatorial \(O(n^{1/3}\log n)\)-approximation algorithm for Min-Rep. Note that an \(o(n^{1/3})\)-approximation algorithm for the MRS problem, implies an improved approximation ratio for the Min-Rep problem.

On the inapproximability side, a proof in [23] implies that it is quasi-NP-hard to approximate the MRS problem to within a factor of \(\log n\). Kortsarz [21] showed that it is quasi-NP-hard to approximate the Min-Rep problem to within a factor of \(2^{\log ^{1-\epsilon }n}\), for any \(\epsilon >0\). The same hardness result applies to the MRS problem.

We present a randomized approximation preserving reduction from the DkS problem to the MRS problem (in Sect. 4.1), and if we prove an \(O(n^{1/8-\epsilon })\)-approximation algorithm for MRS, then we will have better (than the current best known) approximation algorithm for the DkS problem. We also observe that there exist approximation preserving reductions from the MRS problem to three problems, namely, the red blue set cover (RBSC) problem, the power dominating set (PDS) problem, and the target set selection (TSS) problem (See Sect. 4 for problem definitions). So, if a polynomial approximation hardness result is proved for MRS, then a polynomial approximation hardness result applies to RBSC, PDS, and TSS problems.

We conclude the paper by observing the existence of a PTAS for the MRS problem on planar graphs, and in general on minor free graphs.

2 Large Integrality Gaps for Natural LPs and SDP

Consider the following Linear Programming relaxation LP1 (used in [23]) for the MRS problem:

figure a

here, \(v_i\) is a variable representing a choice of a vertex \(i\in V\), \(x_e\) is a variable representing a choice of an edge \(e\in E\), and \(e\rightsquigarrow i\) represents that the edge e is incident on vertex i. col(e) is a function that returns the color of the edge e. The first constraint says that every color needs to be covered. The second constraint says if an edge is chosen in the solution, then the vertices on which it is incident are also chosen. This Linear program has integrality gap of at least \((n-1)\). To see this, consider the complete graph \(K_n\) in which all the edges are colored the same. For each edge e, set \(x_e=\frac{2}{n(n-1)}\). And for each vertex i, set \(v_i=\frac{2}{{n(n-1)}}\). Hence \(OPT(LP1)\le \frac{2}{n-1}\). Whereas the integral optimal has size 2. This yields an integrality gap of at least \(n-1\).

Consider the following Linear Programming relaxation LP2 (used in [16]) for the MRS problem. This relaxation is stronger than LP1. The second constraint says that for every vertex i and color c pair, if there is an edge of color c incident on that vertex i in the solution, then the vertex i is also included in the solution.

figure b

Consider a complete bipartite graph \(K_{n,n}\). Color an edge (i, j) with color \((i+j)mod\ n\). Now, on any vertex, all the edges that are incident will have different colors. And there will be n edges of each color in the graph. Set \(x_e=1/n\) for each edge and \(v_i=1/n\). Thus, \(OPT(LP2)\le 2\). Whereas the minimum rainbow subgraph will have size at least \(2\sqrt{n}\). This is because, any n edge bipartite graph should have at least \(2\sqrt{n}\) vertices. Thus LP2 has an integrality gap of \(\Omega (\sqrt{n})\).

Consider the following SDP for MRS.

figure c

here, \(v_0\) is the handle vector, and every vertex i for which \(v_i\) is in the direction of \(v_0\) will be in the solution. The first constraint says that every color should be covered.

Again the same example as LP2 has integrality gap of \(\Omega (\sqrt{n})\). This can be seen as follows. Set \(v_0=(\frac{1}{\sqrt{n}},\dots , \frac{1}{\sqrt{n}})\), and \(v_i=(\frac{1}{\sqrt{n}},-\frac{1}{\sqrt{n}},\dots , -\frac{1}{\sqrt{n}})\) for each i. Clearly \(\frac{v_0\cdot v_i+1}{2} = 1/n\) for each i. It can be seen that the above values will satisfy both the SDP constraints. Thus, \(OPT(SDP)\le 1\). And hence, the integrality gap \(\Omega (\sqrt{n})\). In the paper [17], the authors give an \(O(\log n)\)-approximation algorithm for the Optimal Haplotype Inference problem, which is basically the MRS problem in disguise, using the above mentioned SDP relaxation. The integrality gap disproves their result.

3 An \(O(n^{1/3})\)-Approximation Algorithm for DCkS

Our algorithm follows the one in [13] to some extent. Some of the claims one can make in the uncolored case do not hold here and we need to overcome this. A major difficulty is that we do not know which colors appear in the optimum and hence are “important”. The basic idea in [13] is to pick the vertices in two phases. First pick a subset of vertices with a large number of edges incident on them and then to pick a subset with large number of edges incident on these and the first set.

Our algorithm A employs four different procedures, \(A_1\), \(A_2\), \(A_3\), and \(A_4\), each of which selects a dense colored subgraph. It returns the densest of the four colored subgraphs that are found.

3.1 Preliminaries

The color degree of a vertex is defined to be the number of distinct colors represented among edges incident on the vertex. The average color degree of the subgraph on a set \(S\subseteq V\) is the ratio of total number of distinct colors among the edges induced by the vertices in S to the size of S. For a set \(S\subseteq V\) and a vertex v, the color degree of v into S is the color degree of v in the graph induced by \(S\cup \{v\}\).

Let, for \(1\le i\le 4\), \(A_i(G,k)\) denote the average color degree of the subgraph selected by the algorithm \(A_i\).

One tool that we use repeatedly is the well known approximation algorithm for the unweighted maximum coverage problem. In this problem we are given a collection of subsets of a set and a positive integer k. The objective is to find k subsets which cover the maximum number of elements. This problem is known to be NP-hard. The greedy algorithm which chooses the subset which covers the most number of uncovered elements at each stage has an approximation ratio \(1-1/e\), and no algorithm can do better [11].

For instance if we wish to determine k vertices which have the maximum number of edges with distinct colors incident on them, we can use the same greedy strategy and get an approximation ratio of \(1-1/e\) on the maximum number of colors covered. We make the following Proposition for finding k vertices with maximum number of edges of distinct colors incident on them.

Proposition 1

The greedy algorithm to find k vertices with the maximum number of edges of distinct colors incident on them is \((1-1/e)\)-approximate.

Let \(G^*\) denote the optimum densest colored subgraph on k vertices. Although, more than one edge of a color could be present in the induced subgraph on \(V(G^*)\), we assume that only one edge of a color is present in \(G^*\). This helps us with the analysis of our algorithm, and even with this assumption \(G^*\) still remains the optimum densest colored subgraph on k vertices. Let the average color degree of \(G^*\) be \(d^*(G,k)\), or simply \(d^*\) when it is obvious from the context.

3.2 Procedure \(A_1\): A Trivial Procedure

Without loss of generality, we may assume that the graph G contains at least k / 2 edges of distinct colors.

figure d

Clearly, \(A_1(G,k)\ge 1/2\).

3.3 Procedure \(A_2\): A Greedy Procedure

Our next procedure is a two step procedure. We first, greedily select a subset T of k / 2 vertices to maximize the number of edges with distinct colors having at least one end-point in T. Later we again greedily pick k / 2 vertices \(T'\) to maximize the number of edges with distinct colors covered by \(T\cup T'\).

figure e

Let c(T) denote the number of distinct colors among edges incident on vertices in T. Let \(d_T= c(T)/(k/2)\).

Lemma 1

Procedure \(A_2\) returns a subgraph satisfying \(A_2(G,k)\ge c_1\frac{kd_T}{2n},\) for some constant \(c_1>0\).

Proof

Let \(m_1\) denote the number of distinct colors among edges, both of whose endpoints lie in T. Then the number of distinct colors with one end point in T is \(d_T |T|-m_1 = d_Tk/2-m_1 \ge 0\). The greedy strategy together with Proposition 1 ensures that at least \(\left( 1-\frac{1}{e}\right) |T'|/ |V(G)\setminus T| > \left( 1-\frac{1}{e}\right) \frac{k}{2n}\) fraction of these distinct colored edges are contained in \(T\cup T'\). Thus the total number of distinct colored edges in the subgraph induced by \(T\cup T'\) is at least

$$\begin{aligned} \left( \frac{d_Tk}{2}-m_1\right) \left( \left( 1-\frac{1}{e}\right) \frac{k}{2n}\right) + m_1 \ge c_1\frac{d_Tk^2}{n}. \end{aligned}$$

\(\square \)

The maximum number of distinct colored edges incident on any k / 2 vertices is at least \(\frac{1}{2}\cdot d^*k/2\). So, by Proposition 1, \(c(T) \ge \left( 1-\frac{1}{e}\right) d^*(G,k)\cdot k/4\). Hence, \(d_T \ge \left( 1-\frac{1}{e}\right) d^*(G,k)/2\). Thus, this greedy procedure approximates \(d^*(G,k)\) to within a ratio of at most \(O(\frac{n}{k})\).

3.4 Procedure \(A_3\): Colored Walks of Length 2

Our next procedure works when the color degree of vertices is small. Towards building intuition, consider \(G^*\), the optimum densest colored k-subgraph in G. Suppose there exists a vertex v in \(V(G^*)\) so that half the vertices in \(V(G^*)\) are at distance 2 from v. The idea is to look “greedily” in such neighborhoods. Suppose we knew this vertex v. (We try every vertex.) Then we try to find the densest colored k subgraph on vertices in G at distance at most 2 from v. Details follow.

figure f

Let \(cdeg^* ( v )\) denote the color degree of v in \(G^*\).

Lemma 2

Procedure \(A_3\) returns a subgraph satisfying

$$\begin{aligned} A_3(G,k)\ge c_2\frac{(d^*( G, k ))^2 }{ 2\max [k, 2\Delta _c( G ))]}, \end{aligned}$$

for some constant \(c_2>0\).

Proof

We now analyze the approximation ratio of this procedure. Let us first note that the number of colored length 2 walks within the optimum subgraph \(G^*\) is at least \(k(d^*( G, k))^2\). This is because each \(v\in V(G^*)\) contributes \((cdeg^* ( v ))^2\) to this sum, and \(\sum _{v\in V(G^*)} (cdeg^* ( v ))^2\ge k (d^* ( G, k ))^2\) by convexity.

It follows that there is a vertex v which is the endpoint of at least \(( d^* ( G, k ))^2\) colored length-2 walks in \(G^*\). This implies that there exists a subgraph on at most k vertices in the graph induced on \(N(v)\cup N_2(v)\), which has at least \(( d^* ( G, k ))^2\) edges of distinct colors. In P(v), we add k / 2 vertices from \(N_2(v)\) which have maximum number of distinct colored edges going into N(v). We use the greedy construction from Proposition 1 for the same. Therefore there are at least \(\left( 1-\frac{1}{e}\right) ( d^* ( G, k ))^2/ 2\) edges of distinct colors incident on vertices of P(v). There are at least \((1-1/e)( d^* ( G, k ))^2 / 2\) distinct colored edges between Q(v) and P(v) if \(cdeg(v)\le k/2\), and at least \((1-\frac{1}{e})^2( d^* ( G, k ))^2 k/ 4 cdeg( v )\) distinct colored edges between Q(v) and P(v) otherwise [by greedy construction of Q(v)]. Since we do not require P(v) and Q(v) to be disjoint, each edge may have been counted twice. Hence, altogether, H(v) contains at least \((1-\frac{1}{e})^2\min [ ( d^* ( G, k ))^2/ 4 , ( d^* ( G, k ))^2 k/ 8 \Delta _c( G ))]\) edges, where \(\Delta _c( G )\) denotes the maximum color degree in the graph.

This guarantees,

$$\begin{aligned} A_3(G,k)\ge \left( 1-\frac{1}{e}\right) ^2\frac{(d^*( G, k ))^2 }{ 2\max [k, 2\Delta _c( G ))]}. \end{aligned}$$

\(\square \)

3.5 Procedure \(A_4\): Another Greedy Procedure

This procedure is the key to handling colors. This complements Procedure \(A_3\). In this procedure, we will pick a candidate subgraph with the following guarantee. Either the vertices in this subgraph will have high color degree, or the graph left after removing this subgraph has only vertices of low color degree.

So this procedure works in conjunction with Procedure \(A_3\). In the uncolored case, a procedure like Procedure \(A_2\) is enough to achieve this result. In this case it is tricky, and we need to get the algorithm just right. Details follow.

figure g

Let \(d_U\) denote the color degree of last vertex added to U.

Lemma 3

If \(k^2\ge 4n\), then \( A_4(G,k) \ge c_3\frac{d_U}{k}\), for some constant \(c_3>0\). Else, \( A_4(G,k) \ge c_4\frac{d_Uk}{n}\), for some constant \(c_4>0\). Also, if half the edges in \(G^*\) are incident on U, then the average color degree of the subgraph induced on \(U\cup V'\) is \(c_5d^*\), for some constant \(c_5>0\).

Proof

The total number of edges incident on the vertices U is at least \(kd_U/2\). Let the total number of colors covered after picking the ith vertex in V be \(f_i\). So, the total number of colors covered, after picking k / 2 vertices in V, in the subgraph induced on \(U\cup V\) is at least \(f_{k/2}\), and the average color degree is at least \(f_{k/2}/k\).

After i vertices have been picked in V, the number of edges incident on vertices of U which are colored with one of these \(f_i\) colors is at most \(kf_i/2\). This is because every vertex in U can have one edge of same color incident on it. Hence the total number of edges incident on vertices in U colored with uncovered colors is at least \(kd_U/2 - kf_i/2\). Hence, the next vertex added to V will cover at least \((kd_U/2 - kf_i/2)/n\) colors. Hence, \(f_{i+1} \ge f_i + (kd_U/2 - kf_i/2)/n = (1-k/2n)f_i +kd_U/2n\). We use induction to prove that the total number of colors covered in the subgraph induced on \(U\cup V\) is \(f_{\frac{k}{2}} \ge d_U \left( 1- \left( 1-\frac{k}{2n}\right) ^{\frac{k}{2}}\right) \). Suppose, \(f_i \ge d_U \left( 1- \left( 1-\frac{k}{2n}\right) ^i\right) \), then we can show that

$$\begin{aligned} f_{i+1}&\ge (1-k/2n)f_i +kd_U/2n \\&\ge (1-k/2n)\cdot d_U \left( 1- \left( 1-\frac{k}{2n}\right) ^i\right) +kd_U/2n\\&= d_U -kd_U/2n - d_U \left( 1-\frac{k}{2n}\right) ^{i+1} +kd_U/2n\\&=d_U \left( 1- \left( 1-\frac{k}{2n}\right) ^{i+1}\right) . \end{aligned}$$

Now, if \(k^2\ge 4n\),

$$\begin{aligned} f_{\frac{k}{2}} \ge d_U \left( 1- \left( \frac{1}{e}\right) ^{\frac{k^2}{4n}}\right) \ge d_U \left( 1-\frac{1}{e}\right) . \end{aligned}$$

Else,

$$\begin{aligned} f_{\frac{k}{2}} \ge d_U \left( 1- \left( 1-\left( {\begin{array}{c}k/2\\ 1\end{array}}\right) \frac{k}{2n} +\left( {\begin{array}{c}k/2\\ 2\end{array}}\right) \left( \frac{k}{2n}\right) ^2\right) \right) \ge d_U \cdot \frac{k^2}{4n}. \end{aligned}$$

If half the edges in \(G^*\) are incident on U, then there exist k / 2 vertices from which at least half of these distinct colored edges go to U. In \(V'\), we pick k / 2 vertices greedily which have the maximum number of uncovered colored edges going into U. So, by Proposition 1, the average color degree of the subgraph induced on \(U\cup V'\) will be \(c_5d^*\), for some constant \(c_5>0\). \(\square \)

3.6 Algorithm A

Algorithm A applies Procedures \(A_1\), \(A_2\), and \(A_4\), on the graph G, and Procedure \(A_3\) on the subgraph induced on \(G_l=G\setminus U\), where U is the set of k / 2 vertices chosen by Procedure \(A_4\), and returns the densest colored subgraph of these.

Let an \(\alpha \) fraction of the edges in \(G^*\) be incident on the vertices of U. If \(\alpha \ge 1/2\), then \(A_4\) returns constant-approximation, and hence we may assume that \(\alpha < 1/2\), and then clearly \(G_l\) has a densest colored k-subgraph with average color degree \(\Omega (d^*)\).

The performance guarantee of algorithm A is at least the geometric mean of the performance guarantee of any three of the Procedures \(A_1\), \(A_2\), \(A_3\), and \(A_4\). We look at three different cases.

  1. 1.

    If \(k\ge d_U\), then \(\Delta _c(G_l)\le \frac{k}{2} + d_U \le 2k\). Thus,

    $$\begin{aligned} A(G,k)&\ge \max \left[ A_1(G,k), A_2(G,k), A_3(G_l,k)\right] \\&\ge \left( \frac{1}{2}\cdot c_1\frac{kd_T}{2n} \cdot c_2\frac{(d^*(G,k))^2}{2\max [k,2\Delta _c]}\right) ^{1/3} \ge \frac{d^*(G,k)}{cn^{1/3}}, \end{aligned}$$

    for some \(c>0\). Here the last inequality follows from the fact that \(d_T\ge (1-\frac{1}{e}) d^*(G,k)/2\). For the remaining cases, we may assume \(\Delta _c(G_l)\le 2d_U\) , because \(d_U>k\).

  2. 2.

    If \(k^2\ge 4n\), then

    $$\begin{aligned} A(G,k)&\ge \max \left[ A_2(G,k), A_4(G,k), A_3(G_l,k)\right] \\&\ge \left( c_1\frac{kd_T}{2n} \cdot c_4\frac{d_U}{k} \cdot c_2\frac{(d^*(G,k))^2}{8d_U}\right) ^{1/3} \ge \frac{d^*(G,k)}{cn^{1/3}}, \end{aligned}$$

    for some \(c>0\). Here the last inequality follows from the fact that \(d_T\ge (1-\frac{1}{e}) d^*(G,k)/2\).

  3. 3.

    If \(k^2 < 4n\), then

    $$\begin{aligned} A(G,k)&\ge \max \left[ A_1(G,k), A_4(G,k), A_3(G_l,k)\right] \\&\ge \left( \frac{1}{2} \cdot c_4\frac{d_Uk}{n} \cdot c_2\frac{(d^*(G,k))^2}{8d_U}\right) ^{1/3}\ge \frac{d^*(G,k)}{cn^{1/3}}, \end{aligned}$$

    for some \(c>0\). Here the last inequality follows from the fact that \(k\ge d^*(G,k)\) (this is because \(d^*(G,k)\) is the average color degree of a subgraph with k vertices).

This completes the proof for an \(O(n^{1/3})\)-approximation algorithm for the DCkS problem. The following theorem implies an \(O(n^{1/3}\log n)\)-approximation algorithm for the MRS problem.

Theorem 1

If there is an f-approximation algorithm for the DCkS problem then there is an \(O(f\log n)\)-approximation algorithm for the MRS problem.

Proof

Suppose the minimum rainbow subgraph has size k. It will contain edges of all the p colors. If we run the f-approximation algorithm for DCkS on this instance, then it will return a subgraph on k vertices with edges of at least p / f colors. Remove edges of these colors from the input graph and repeat the same procedure till edges of all the colors are covered. Take a union of all these subgraphs, and output it.

Let \(L_i\) be the number of uncovered colors after ith iteration. Then, \(L_0=p\), and \(L_i \le p \left( 1-\frac{1}{f}\right) ^i\). Let j be the number of iterations after which the number of uncovered colors is less than 1. If \(j=2f\log n\), then clearly \(L_j< 1\). Thus total number of vertices in the output is at most \(2kf\log n\). \(\square \)

3.7 An Algorithm for MIN-REP

The Min-Rep problem is a minimization version of the label cover problem [21]. The input consists of a bipartite graph \(G=(A,B,E)\), where \(|A|=|B|=n\), and equitable partitions of A and B into k sets of same size \(q=n/k\). The bipartite graph and the partitions of A and B induce a “supergraph” H in the following way—the vertices of graph H are the equitable partitions of set A and B. Two vertices corresponding to sets \(A_i\) and \(B_j\) are adjacent by a “superedge” in H if and only if there exist \(a_i \in A_i\) and \(b_i \in B_i\) which are adjacent in G. The goal is to choose \({A^\prime } \subset A\) and \({B^\prime } \subset B\) such that the pairs (a, b) , \(a\in A'\) and \(b\in B'\), cover all the superedges of H, while minimizing \(|A^\prime |+|B^\prime |\).

Charikar et al. [7] gave an \(O(n^{1/3}\log ^{2/3}n)\)-approximation algorithm for the Min-Rep problem using LP rounding. We observe that the Min-Rep problem is indeed a special case of the MRS problem. Consider an instance of the Min-Rep problem. Color all the edges between vertices of \(A_i\) and \(B_j\) with same color. Use different color for every pair \(A_i\) and \(B_j\). Clearly, an f-approximation algorithm for the MRS problem implies an f-approximation algorithm for the Min-Rep problem (Note that the algorithm for Min-Rep [7] uses a Linear Programming relaxation similar to LP2 in Sect. 2. Such a LP based algorithm will not give a better approximation ratio for the MRS problem. This is evident from the \(\Omega (\sqrt{n})\) integrality gap shown in Sect. 2 for LP2).

4 Related Problems

We present an approximation preserving randomized reduction from the densest k-subgraph problem to the MRS problem, and also observe the existence of approximation preserving reductions from the MRS problem to three other problems. All these reductions involve at most a polynomial sized blow-up, and thus the hardness of approximation ratios are polynomially related.

4.1 Reduction from the Densest k-Subgraph Problem

The densest k-subgraph (DkS) problem is a well studied problem [3, 4, 13]. Given a simple undirected graph, the goal is to output a subgraph on k vertices which has maximum number of edges. Feige [12] and Khot [20] prove that the DkS problem does not have a PTAS. Feige proves the result assuming random 3-SAT formulas are hard to refute and Khot proves it assuming NP does not have randomized algorithms that run in subexponential time [i.e. that NP \(\nsubseteq \cap _{\epsilon >0}\) BPTIME(\(2^{n^{\epsilon }}\))]. Assuming the Small Set Expansion conjecture, Raghavendra et al. [24] rule out constant factor approximation algorithm for the DkS problem. It is widely believed that the DkS problem has a lower bound on approximation ratio within a factor of \(n^c\), for some \(c>0\).

Theorem 2

If there is an f-approximation algorithm for the MRS problem, then there is a randomized \(O(f^2\cdot \log n)\)-approximation algorithm for the DkS problem.

Proof

We exhibit a randomized reduction from the DkS problem to the MRS problem. Consider an instance of the DkS problem. Assume that this graph G has a subgraph on k vertices with t edges such that t is maximum. Assume that t is known. This is a kosher assumption, since one can run the algorithm for each possible value of t. Pick an edge, which has not yet been colored, arbitrarily, and color it with one chosen uniformly at random from \(t/(c\log t)\) colors, for some constant \(c>0\). Repeat the same until all edges have been colored. Let X be a random variable that denotes the number of edges needed to cover all the colors.

We use the Coupon Collector argument to calculate the expected number of edges needed to cover all the color, which says – Given n coupons, the expected number of coupons you need to draw with replacement before having drawn each coupon at least once grows as \(\Theta ( n \log n)\). Similarly, the expected number of edges needed to cover all the colors is

$$\begin{aligned} c'\cdot \left( \frac{t}{c\log t}\right) \cdot \log \left( \frac{t}{c\log t}\right) \le \frac{t}{c''} \end{aligned}$$

Then by Markov’s inequality,

$$\begin{aligned} Pr(X>t) \le \frac{\mathbb {E}[X]}{t} \le \frac{1}{c''} \end{aligned}$$

If c is chosen appropriately, then this probability will be small. The probability that the first t edges picked will cover all the colors is the same as the probability that the t edges in the k vertex subgraph will have an edge of each of \(t/(c\log t)\) colors. Suppose there exists an f-approximation algorithm for the MRS problem. This algorithm will give a subgraph on at most \(f\cdot k\) vertices and at least \(t/(c\log t)\) edges. The density of this subgraph is at least \(\left( \frac{t}{c\log t}\cdot \frac{1}{fk}\right) \). Select k / 2 vertices of highest degree from this subgraph. Call this set U. So, total number of edges incident on vertices of U will be at least \(\frac{k}{2}\cdot \left( \frac{t}{c\log t}\cdot \frac{1}{fk}\right) \). Find k / 2 vertices of highest degree into U from this subgraph. Call this set V. The subgraph induced on \(U\cup V\) will have at least \(\frac{k/2}{fk}\cdot \frac{k}{2}\cdot \left( \frac{t}{c\log t}\cdot \frac{1}{fk}\right) =\frac{tk}{c_1f^2\log t}\) edges, for some constant \(c_1>0\). The subgraph induced on \(U\cup V\) will have density at least \(\frac{t}{c_1f^2\log t}\). Thus, an f-approximation algorithm for the MRS problem implies a randomized \(O(f^2\cdot \log n)\)-approximation algorithm for the DkS problem. \(\square \)

4.2 Red Blue Set Cover

The red blue set cover (RBSC) problem was introduced by Carr et al. [6]. Given a finite set of “red” elements R, a finite set of “blue” elements B and a family \(\mathcal {S}\subseteq 2^{R\uplus B}\), the red blue set cover problem is to find a subfamily \(C\subseteq \mathcal {S}\) which covers all blue elements, but which covers the minimum possible number of red elements. Carr et al. [6] gave a \(2\sqrt{n}\)-approximation algorithm for the restricted case in which every set contains only one blue element, and an \(O((kn)^{1-\frac{1}{k}}\log n)\)-approximation algorithm when each set has a maximum of k red elements. Peleg [22] gave a \(2\sqrt{n\log \beta }\)-approximation algorithm, where n is the number of sets and \(\beta \) is the number of blue elements. Even the restriction when every set contains one blue element and two red elements has a lower bound \(\Omega (2^{\log ^{1-1/\log \log ^cn}n})\) on the approximation ratio assuming P \(\ne \) NP, where \(c<\frac{1}{2}\) [6].

The MRS problem is easily seen to be a special case of RBSC – let each edge represent a set, its color represent a blue element in the set, and its each end point represent a red element in the set. Now, this instance is a special case of RBSC in which each set contains two red elements and one blue element. Finding the minimum rainbow subgraph is equivalent to finding the set cover which covers all blue elements and minimum number of red elements.

4.3 Power Dominating Set

The power dominating set (PDS) problem may be considered as an extension of the well-known Dominating Set problem. Power domination [1] is defined by two rules; the first rule is the same as the rule for the Dominating Set problem, but the second rule allows a type of indirect propagation. More precisely, given a set of vertices S, the set of vertices that are power dominated by S, denoted \(P_S\), is obtained as follows.

  • Rule 1 if vertex v is in S, then v and all of its neighbors are in \(P_S\);

  • Rule 2 (propagation) if vertex v is in \(P_S\), one of its neighbors w is not in \(P_S\), and all other neighbors of v are in \(P_S\), then w is inserted into \(P_S\).

The set \(P_S\) is independent of the sequence in which vertices are inserted by Rule 2. Otherwise, there is a minimal counter example with two maximal sequences of insertions and an “earliest” vertex that occurs in one sequence but not the other; this is not possible. The PDS problem is to find a vertex set S of minimum size that power dominates all vertices (i.e., find \(S \subseteq V\) with |S| minimum such that \(P_S = V\)). Note, \(n=|V|\). Aazami and Stilp [1] give an \(O(\sqrt{n})\)-approximation algorithm for planar graphs and prove that it is quasi-NP-hard to approximate PDS to within a factor of \(2^{\log ^{1-\epsilon }n}\), for any \(\epsilon >0\). They prove the lower bound by reduction from the Min-Rep problem. We observe that essentially the same reduction works for the MRS problem, and make the following proposition.

Proposition 2

If there is an f(n)-approximation algorithm for the PDS problem, then there is an f(N)-approximation algorithm for the MRS problem, where \(n=O(N^2)\).

Thus, if polynomial approximation hardness result is proved for the MRS problem, then it would imply a polynomial approximation hardness result for the PDS problem. Note that although the reduction is same as the one from Min-Rep, MRS could possibly have a better approximation hardness result than Min-Rep (which is a special case of MRS), and hence could improve the approximation hardness result for PDS.

4.4 Target Set Selection

The target set selection (TSS) problem is defined in [8]. Given a connected undirected graph \(G = (V, E)\), let d(v) be the degree of \(v \in V\). For each \(v \in V\), there is a threshold value \(t(v)\in \mathbb {N}\), where \(1 \le t(v) \le d(v)\). Initially, the states of all vertices are inactive. We pick a subset of vertices, the target set, and set their state to be active. After that, in each discrete time step, the states of vertices are updated according to following rule: an inactive vertex v becomes active if at least t(v) of its neighbors are active. The process runs until either all vertices are active or no additional vertices can update states from inactive to active (it is easy to verify the process runs at most \(n - 1\) rounds, where \(n = |V|\) is the number of vertices in the graph). The process we consider is progressive, i.e. a vertex can only become active from inactive but not vice versa.

The following optimization problem is of interest, which is called target set selection: which subset of vertices should be targeted at the beginning such that all (or a fixed fraction of) vertices in the graph are active at the end? Observe that a trivial solution is to target all vertices in the graph. The goal is to minimize the size of the target set. Chen [8] proves that it is quasi-NP-hard to approximate the TSS problem to within a factor of \(2^{\log ^{1-\epsilon }n}\), for any \(\epsilon >0\). They do this by reduction from the Min-Rep problem. We observe that essentially the same reduction works for the MRS problem, and make the following proposition.

Theorem 3

If there is an f(n)-approximation algorithm for the TSS problem, then there is an f(N)-approximation algorithm for the MRS problem, where \(n=O(N^6)\).

Thus, if polynomial approximation hardness result is proved for the MRS problem, then it would imply a polynomial approximation hardness result for the TSS problem. Note that although the reduction is same as the one from Min-Rep, MRS could possibly have a better approximation hardness result than Min-Rep (which is a special case of MRS), and hence could improve the approximation hardness result for PDS.

5 PTAS for Minor Free Graphs

Dawar et al. [9] prove the following theorem on planar graphs, and in general, on minor free families of graphs.

Theorem 4

Let \(\varphi (X)\) be a first-order formula in the language of graphs that is positive in a set variable X, and let \(\mathcal {C}\) be a class of graphs with an excluded minor. Then MIN\(_{\varphi (X)}(\mathcal {C})\) has a PTAS.

The minimum rainbow subgraph problem can be described as MIN\(_{\varphi (X)} (\mathcal {C})\) for the formula \(\varphi (X) = \forall c \exists x \exists y (Xx\wedge Xy \wedge Cxyc)\). Here, X is a set variable that represents a set of vertices \(X'\), and Xx is true if the vertex \(x\in X'\). The function C checks if the edge between vertices x and y, has color c. The formula \(\varphi (X)\) checks if the induced subgraph on \(X'\) is a rainbow subgraph, i.e. if there is an edge of every color induced on the vertices of \(X'\). MIN\(_{\varphi (X)}\) represents the minimum rainbow subgraph. From the above mentioned theorem, the minimum rainbow subgraph problem has a PTAS for minor free graphs.