Compact Navigation and Distance Oracles for Graphs with Small Treewidth

Abstract

Given an unlabeled, unweighted, and undirected graph with n vertices and small (but not necessarily constant) treewidth k, we consider the problem of preprocessing the graph to build space-efficient encodings (oracles) to perform various queries efficiently. We assume the word RAM model where the size of a word is Ω(logn) bits.

The first oracle, we present, is the navigation oracle which facilitates primitive navigation operations of adjacency, neighborhood, and degree queries. By way of an enumeration argument, which is of interest in its own right, we show the space requirement of the oracle is optimal to within lower order terms for all graphs with n vertices and treewidth k. The oracle supports the mentioned queries all in constant worst-case time. The second oracle, we present, is an exact distance oracle which facilitates distance queries between any pair of vertices (i.e., an all-pairs shortest-path oracle). The space requirement of the oracle is also optimal to within lower order terms. Moreover, the distance queries perform in O(k ³log³ k) time. Particularly, for the class of graphs of popular interest, graphs of bounded treewidth (where k is constant), the distances are reported in constant worst-case time.

1 Introduction

Graphs are arguably one of the most relevant structures to model relationships among entities. With the ever-growing number of entities in objects to model, the corresponding graphs increase in size. As a result, compact representation of graphs has always been of interest. In addition to compression of graphs, one ought to be able to use the graph in its compressed form. In this paper, we consider the problem of representing graphs compactly while allowing efficient access and utilization of the graph by way of efficient support for navigation and distance queries.

Random graphs are highly incompressible [4]. Fortunately, graphs that arise in practice are not random and often have particular combinatorial structures. Therefore, researchers have considered graphs with various combinatorial structures for the purpose of space-efficient representation: these combinatorial properties include but are not limited to: bounded arboricity, decomposability [35], separability [4, 5], planarity [16, 36, 38, 45], triconnected and/or triangulated planarity [14].

In this paper, we are interested in compact representation of graphs with small treewidth (to be defined in Sect. 2). Graphs of bounded treewidth are of interest since many NP-hard problems on general graphs are solvable in polynomial time on graphs with bounded treewidth. These graphs include such prevalent families of graphs as trees (treewidth 1), series-parallel graphs (treewidth 2), outerplanar graphs (treewidth 2), Halin graphs (treewidth 3). Graphs arising in various practical applications tend to have small treewidth. Flow graphs of structured programs have treewidth at most six [43]. In addition, many problems in practical applications require the treewidth of input graphs to be small, therefore the input graphs are necessarily of small treewidth: for instance, an algorithm that calculates the resistance in electrical networks requires that the graph is of treewidth at most three [8]. The gate matrix layout problem in VLSI layout design suggests that graphs corresponding to well-shaped circuits have small treewidth [18]. A good evolution tree in the perfect phylogeny problem in evolution theory corresponds to a graph of small treewidth [11]. Graphs with small treewidth occur in numerous more real-world applications [9, 17].

We assume the standard word RAM model where a word is Ω(lgn) bits wide and n is the number of vertices (lg denotes log₂). This is a realistic assumption commonly made in word RAM algorithms and succinct data structures [27, 37]; we essentially assume that a word of RAM is wide enough so that a vertex can be distinguished by a label that fits in a word and can be read in constant time. Note that the graphs we consider are unlabelled. However, there is an implicit labeling of vertices in oracles’ encoding which enables us to distinguish vertices in order to refer them in queries.

1.1 Contribution

In Sect. 4, we describe a data structure that encodes a given undirected and unlabeled graph with n vertices and of treewidth k in k(n+o(n)−k/2)+O(n) bits and supports degree, adjacency, and neighborhood queries in constant time. Degree query is to report the degree of a vertex. Adjacency query is, given two vertices u,w, to determine if edge (u,v) exists. Neighborhood queries are to report all neighbors of a given vertex in constant time per neighbor. These three queries constitute the set of primitive navigational queries often required in a graph [4, 5, 24].

Space-efficient encoding of trees (graphs with treewidth k=1) is a well-studied topic in the context of succinct representations [23, 25, 32–34, 38, 42]. An implicit representation of graphs of treewidth k exists which requires n(lgn+O(klglg(n/k))) bits [29], and this is not optimal. Although it is not explicitly mentioned, the succinct representation of separable graphs given in [5] yields an optimal navigation oracle for graphs of bounded treewidth where treewidth k=O(1). This is since graphs with constant treewidth are also separable (roughly speaking, a graph is separable if all its subgraphs can be partitioned into two approximately equally sized parts by removing a relatively small number of vertices [4]). The storage requirement of the oracle for separable graphs is optimal to within lower order terms, and the previously-mentioned navigation queries perform in constant time. In this paper, we extend the result to graphs with treewidth k=Ω(1).

Moreover, we show that the storage requirement of the oracle is optimal for all values of k by proving that k(n−o(n)−k/2)+δn bits are required to encode graphs with n vertices and of treewidth k where δ is a positive constant. Our proof works by way of a counting argument which is of independent interest as to the best of our knowledge there existed no such enumerative result for graphs with a given treewidth. Previously an analogous lower bound of kn−o(kn)¹ was given [28] for graphs with page-number k: a family of graphs which include graphs with treewidth smaller than k [20]. The navigation oracle adopts the encoding of [5] for values k=O(1) and the encoding outlined in this paper for k=Ω(1). Since the storage requirement of the oracle matches the lower bound for constant values of k and our lower bound for non-constant values of k, both the space of the oracle and the lower bound are tight. Throughout the paper, we interchangeably use the terms ‘lower bound’ and ‘entropy bound’. We follow the convention of referring lower bounds as entropy bounds (e.g., see [1, 2]). For constant values of k, some entropy bounds are known: for instance, for trees (k=1) of size n, the entropy is about 1.56n bits [39] and for series-parallel graphs (k=2) of size n, the entropy at least 3.18n bits [6].

In the second part of the paper, we give distance oracles for undirected, unlabeled, and unweighted graphs with n vertices and of treewidth k. For all values of k, the oracle requires the entropy bound number of bits to within lower order terms. These are exact oracles that report the distance of two given vertices precisely. The distance queries perform in time O(k ³lg³ k). We note that for graphs of bounded treewidth where k is constant (the family of graphs of our interest), this query time becomes constant.

The topic of distance queries for graphs is a well-studied area [46]. There is a large volume of work on approximate distance oracles where the reported distance between two given vertices can be a multiplicative factor term away from the actual distance [44]. For unweighted undirected graphs (the class that we consider in this paper), it is known that with subquadratic preprocessing time, approximate distance oracles can be generated that require superlinear space and report distances in constant time [3]. The superlinear space bound is strongly conjectured to be a lower bound [44]. Exact distance oracles for unweighted undirected graph require Ω(n ²) bits and there exists such an oracle with a space of about 0.79n ² bits [26]. Hence, we show that for graphs with bounded treewidth, these results can be significantly improved as there is a linear-size exact distance oracle. It was previously known that for trees, there exists an oracle with the entropy space bound to within lower order terms that answers distance queries in constant time [23]. Therefore in a sense, we also extend this result from trees to all tree-like graphs (graphs of constant treewidth).

The time to construct the oracles depends heavily on the time to compute the treewidth of the given graph and compute the tree decomposition correspondingly. Determining the treewidth of a graph is NP-hard [12]. Fortunately however, for graphs with constant treewidth, the treewidth and the corresponding tree decomposition can be determined in linear time [10]. Moreover, for graphs with treewidth k=ω(1), there exists a polynomial time algorithm that approximates the treewidth within O(logk) factor and generates the corresponding tree decomposition [13]. All other aspects of navigation oracles can be constructed in O(kn) time where k is the determined treewidth and n is the number of vertices. For the distance oracle, the other computational bottleneck is that we pre-compute distances between every pairs of vertices at the initial stage, and this can be accomplished in o(kn ²) time [15].

2 Tree Decompositions and Variations

In this section, we illustrate the notion of tree decomposition and treewidth which are the basis of our constructions. Intuitively, “the treewidth of a graph measures the ‘tree-likeness’ of the graph, while a tree decomposition is the mapping of the graph into a tree depicting such tree-like structure [19]”. More precisely, a tree decomposition of a graph G is a tree T so that each node of the tree, also called a bag, includes a subset of vertices of G. Each edge of G should find its both endpoints in at least one same bag. Also, each vertex should appear in a set of bags which form a connected subtree of the tree decomposition. These properties imply a locality property for a tree decomposition, i.e., if we remove the vertices of a bag, the resulted graph will be disconnected. This provides many useful properties for tree decompositions. Before going to these properties, we present a formal definition of a tree decomposition.

Definition 1

[9] A tree decomposition of a graph G=(V,E) of treewidth k is a pair ({X _i ∥i∈I},T) where {X _i } is a family of subsets of V (bags), and T is a rooted tree whose nodes are the subsets X _i such that

• ⋃ _i∈I X _i =V and max _i∈I |X _i |=k+1.

• for all edges (v,w)∈E, there exists an i∈I with v∈X _i and w∈X _i .

• for all i,j,k∈I: if X _j is on the path from X _i to X _k in T, then X _i ∩X _k ⊆X _j .

We say a vertex v∈V is introduced in node X _i (i∈I) of the tree, if v is in bag X _i (v∈X _i ) but not in that of the parent of X _i . All vertices at the bag of the root node are introduced by definition.

So, the treewidth of a tree decomposition is the maximum number of vertices in any bag of the tree, and the treewidth of a graph is the minimum treewidth of any tree decomposition of the graph. For example, a tree has a tree decomposition with two vertices in each bag, i.e., treewidth 1. A tree with a single node which includes all vertices is a valid tree decomposition for any graph; however such tree decomposition does not carry any information about the structure of the graph. In contrast, a tree decomposition with small treewidth enables us to efficiently store information about the structure of the graph to perform navigation queries. To yield this, instead of encoding the structure of the graph as a whole, we encode the tree decomposition of the graph. The simple tree-structure of a tree decomposition enables us to efficiently encode it. Moreover, we store additional information to separate graphs with the same tree decomposition. Note that a single tree decomposition can be associated with many graphs, depending on which edges exist in the graph. By the definition of tree decomposition, there can be an edge between any two vertices in the same bag. A (full) k-tree is a graph with treewidth k in which all these potential edges exist. A partial k-tree is a subgraph of a full k-tree in which a subset of the potential edges are missing. To encode a graph, beside the structure of the tree decomposition, we store additional information to distinct the graph from other partial k-trees. The details of such construction are presented in Sect. 4.

To provide an efficient distance oracle, we use a property of tree decomposition which enables us to locate some intermediate vertices on the shortest path between any pair of vertices. This property is elaborated in the following lemma.

Lemma 1

Let T be a tree decomposition of a graph G. Also, let x and y be two vertices of G and P=(x=p ₀,p ₁,…p _l−1,y=p _l ) be the shortest path between x and y. Let X and Y be two bags in T which respectively contain x and y. Any node on the unique path between X and Y on T includes at least one node p _i (0≤i≤l) of P.

Proof

By the definition of tree decomposition, each vertex v of G is listed in the bags of a contiguous subtree T _v of T. Consider two vertices p _i and p _i+1 in P. Since p _i and p _i+1 are neighbors, there is a bag in T which contains both of them. So the union of subtrees $T_{p_{i}}$ and $T_{p_{i+1}}$ forms a contiguous subtree of T. With a similar argument, the union of all subtrees of the nodes p ₀,…,p _l forms a contiguous subtree in T. Such subtree includes X and Y and hence any bag on the path between them. So any bag between X and Y includes at least one vertex p _i of P. □

Instead of storing the distance between any pair for vertices, we can store the distance between any vertex and the vertices which appear in ancestor nodes of that vertex in the tree decomposition. Moreover, the tree structure of the decomposition enables us to divide it into smaller subtrees and reduce the global distance queries into local distance queries in smaller graphs. The details of these constructions can be found in Sect. 5.

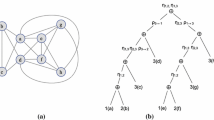
We introduce two specially adapted types of tree decomposition, each used for one of the oracles. For the navigation oracle, we use standard tree decompositions, in which each bag contains exactly k+1 vertices, and two neighboring nodes share exactly k vertices, i.e., each node introduces one vertex. A standard tree decomposition of a graph is depicted in Fig. 1. It is known that a tree decomposition can be transformed into a standard tree decomposition in linear time [7].

Fig. 1

A graph with treewidth k=2 and its standard tree decomposition. The graph edges are depicted in solid black, while the shaded edges complete the graph into a (full) 2-tree. Underlined labels in the tree decomposition correspond to vertices that are introduced in the bags

To design distance oracles, we use height-restricted tree decompositions, which we define as those whose height is logarithmic in the number of vertices, i.e., height(T)=O(logn). A tree decomposition can be transformed into a height-restricted tree decomposition by the following lemma:

Lemma 2

Given a tree decomposition with treewidth k of a graph with n vertices, one can obtain, in linear time, a height-restricted tree decomposition with n nodes and width at most 3k+2.

Proof

There exists a transformation [7] that given a tree decomposition with width k, gives a binary tree decomposition with O(n) nodes and width at most 3k+2. The transformation is a parallel algorithm in NC¹, however it is not hard to observe that the algorithm can be simulated sequentially in linear time.

To reduce the number of nodes to exactly n, it suffices to observe that there are at most n introductions of vertices in bags (a vertex v is introduced in a bag if the parent bag does not contain v). Hence if the number of bags is larger than n, there are bags whose associated set of vertices is a subset of that of the parent bag. We eliminate such bags by making their children, direct children of their grandparents. It is easy to verify that the resulting tree is a valid tree decomposition with n bags. Furthermore, the elimination process is performed in linear time. □

3 Lower Bound

To the best of our knowledge, there exists no enumerative result for the number of unlabeled graphs with a given number of vertices and of treewidth k. We prove such a result in this section. We use the concept of asymmetric trees (also known as identity trees) first introduced by Erdös and Rényi in [21]. These are trees in which the only automorphism is the identity. An automorphism of a tree is a permutation p of its nodes such that there is an edge between nodes u and v if and only if there is an edge between p(u) and p(v). The identity permutation is obviously an automorphism. An asymmetric tree is a tree for which there is no other automorphism, i.e., each node can be uniquely distinguished from others.

Harary et al. showed the total number of asymmetric trees on n nodes is u(n)∼cn ^−5/2 μ ⁻ⁿ in which c and μ are positive constants roughly equal to 0.299388 and 0.397213, respectively [31]. We use this result to count asymmetric k-graphs as a family of graphs with treewidth k.

Definition 2

An asymmetric k-graph on n vertices is a graph which has an asymmetric tree of size n−k as an induced subgraph. The vertices of this subgraph are called tree vertices. Among the other k vertices, there is one vertex, called center, which is connected to all other k−1 non-tree vertices and is not connected to any of the n−k tree vertices (Fig. 2).

Fig. 2

Two different understanding of tree vertices in an asymmetric 4-graph. Filled-in vertices are tree vertices

Lemma 3

Any asymmetric k-graph has a tree decomposition of width at most k.

Proof

Consider a tree decomposition of the asymmetric tree, which has at most two vertices in each bag. We include all other vertices except the center in all bags. Now each bag contains 2+(k−1) vertices. We create a new bag of size k involving all non-tree vertices (including center) and attach it to an arbitrary position in the tree decomposition (Fig. 3). The result is a legitimate tree decomposition of width k (at most k+1 vertices in each bag).

Fig. 3

An asymmetric 4-graph and a tree decomposition of width 4. The labels are added for the illustration of the tree decomposition

 □

To get a lower bound on the number of graphs of treewidth k, we count the asymmetric k-graphs, which form a proper subset of the family of all k-treewidth graphs.

Theorem 1

The number of asymmetric k-graphs with n vertices is at least $x_{n} \sim c 2^{ (k + \delta)n -(k^{2}+(3+2\delta)k-2)/2} \times(n - k)^{-5/2}/(n(k - 1)!)$ where c and δ are constants roughly equal to 0.299388 and 0.332015, respectively.

Proof

We count the number of partially labeled asymmetric k-graphs in which the center is fixed and its neighbors are labeled from 1 to k−1. We note that there are at most n(k−1)! ways to get such labeling for the same graph as there are at most n ways to fix the center and (k−1)! ways to label the neighbors of the center. Also, in the partially labeled graphs, non-tree vertices are distinct from the tree vertices, since they form the neighbors of the center. There are u _n−k ways to build an asymmetric tree on n−k tree vertices, where u _n−k is given by [31]. Now, assume the tree is fixed (Fig. 4). There are $2^{\genfrac {(}{)}{0pt}{}{ k-1}{2}}$ ways to fix a structure on the non-tree vertices (it can be any labeled graph on k−1 vertices). A tree vertex can be connected to any subset of non-tree vertices, hence there are 2^k−1 options for each tree vertex, giving a total number of 2^{(n−k)(k−1)} options for all tree vertices. Since there is no isomorphism between tree vertices and non-tree vertices are labelled, we are not double counting. Therefore, the number of partially labeled graphs is $\alpha= u_{n-k} 2^{\genfrac {(}{)}{0pt}{}{ k-1}{2}} \times2^{(n-k)(k-1)}$. As mentioned above, at most n(k−1)! of these partially labeled graph represent the same unlabeled graph. Therefore, there are at least x _n =α/(n(k−1)!) asymmetric k-graphs on n vertices. Replacing u _n−k with c(n−k)^−5/2 μ ^−(n−k) (as proved in [31]), and also applying δ=−(lgμ+1) completes the proof.

Fig. 4

A partially labeled graph, associated with graph of Fig. 2

 □

Since we match the bound with an encoding, the exponent is tight to within lower order terms.

Corollary 1

At least k(n−o(n)−k/2)+δn bits are required to represent a graph of treewidth k with n vertices, where δ is a constant roughly equal to 0.332015.

4 Navigation Oracles

In this section, we provide a compact representation of graphs of size n and treewidth k which supports adjacency, neighborhood, and degree queries in constant time in the lgn-bits word RAM model. The representation requires k(n+o(n)−k/2)+O(n) bits, which is optimal by Corollary 1.

4.1 Auxiliary Structures

Like most other succinct encodings, our oracles make use of some existing data structures which we elaborate in this section.

4.1.1 Succinct Rank/Select Structures

For a binary sequence S, access _S (i) reports the content of the i’th position of S, rank _S (i,c) reports the number of occurrences of c before position i, and select _S (i,c) reports the index of the i’th occurrence of c in S (c∈{0,1}). There are data structures which represent a binary sequence of length n using n+o(n) bits and support access, rank, select in constant time. Moreover, for sequences with m ones (m≪n), the space can be reduced to $\lg{ \genfrac {(}{)}{0pt}{}{n}{m}} + n / \lg n + \tilde {O}(n^{3/4})$ bits to support the queries in constant time [40].

4.1.2 Balanced Parenthesis and Multiple Parenthesis

A balanced parenthesis sequence of size 2n, which is equivalent to an ordered tree of size n, can be represented in 2n+o(n) bits, with support of access(v), rank(v,‘(’), select(v,‘(’), findmatch(v), and child(i,v) in constant time [32]; where access, rank, and select are defined as before, findmatch(v) finds the position of the parenthesis matching the parenthesis at position v, and child(v,q) finds the position of the q’th child of node v [42].

A multiple parenthesis sequence is an extension of balanced parenthesis in which there are k types of parenthesis. An open parenthesis of type i, denoted by ( _i , is matched by a closed parenthesis of the same type, denoted by ) _i .

Lemma 4

[2]

A multiple parenthesis sequence with 2n parentheses of k types, in which the parentheses of any given type are balanced, can be represented using (2+ϵ)nlgk+o(nlgk)+O(n) bits to support m_access, m_rank, m_select, m_findmatch and m_enclose in O(1) time, for any constant ϵ such that 0<ϵ<1; all operations are defined as before, m_enclose(v,i) gives the position of the tightest open parenthesis of type i which encloses v.

Compact Tables

Given a binary matrix M of size k×n, we are interested in a compact representation of M which supports the following queries: access(i,j) which gives the content of M[i,j], r_successor(i,j) which gives the index of the column that contains the next ‘1’ after column j in row i, and c_successor(i,j) which is defined identically on columns. For our purpose, we need to represent matrices in which k≤n, and the first k columns form a triangular submatrix.

Lemma 5

A k×n matrix, in which the first k columns form an upper triangular submatrix (k≤n), can be represented using kn−k ²/2+o(kn) bits to support access and successor queries in constant time.

Proof

It is known that a binary matrix of size n×n can be represented using n ²+o(n ²) to support access(i,j), r_successor(i,j), and c_successor(i,j) in constant time [24]. It is not hard to verify their approach works for the case where the matrix is rectangular and of size k×n.

Moreover, we claim k ²/2+o(k ²) bits are sufficient to store a triangular matrix of size k×k to support the same queries in constant time. Assume A is a k×k upper triangular matrix (by symmetry we can extend the result to lower triangular matrix). Let B denote the k/2×k/2 submatrix formed by the nonzero elements of the last k/2 rows of A. Then transpose of B is a lower triangular matrix, which can replace the empty part of the first ⌈k/2⌉ rows of A (Fig. 5). The result would be a matrix C of size ⌈k/2⌉×k, which can be stored using k ²/2+o(k ²) bits to support access and successor queries in constant time. It is easy to observe the queries on A can be translated to a constant number of queries on C, and vice versa. For example, for i≤j, access _A (i,j) is the same as access _C (i,j) if i≤⌈k/2⌉, and equal to access _C (j−⌈k/2⌉+1,i−⌈k/2⌉) if i>⌈k/2⌉. To get c_successor _A (i,j) when i≤⌈k/2⌉, we apply c_successor _C (i,j). If there is no such successor in C and j>⌈k/2⌉, we scan the (j−⌈k/2⌉+1)th row in C using r_successor _C (j−⌈k/2⌉+1,1). Moreover, to get c_successor _A (i,j) when i>⌈k/2⌉, we use r_successor _C (j−⌈k/2⌉+1,i−⌈k/2⌉) and report the result only if it is at most j−⌈k/2⌉ (otherwise there is no such successor). The r_successor query on A can be translated to queries in C by a symmetric argument. Note that for successor queries, we need to map the answer in C into A in constant time to get appropriate row/column (this is the inverse of the access query described previously).

Fig. 5

A triangular matrix of size k×k (matrix A) can be stored as a regular matrix of size ⌈k/2⌉×k (matrix C). The dark spots form matrix B mentioned in the text

To represent a k×n matrix M, in which the first k columns form an upper triangular submatrix (k≤n), we store the triangular submatrix A using k ²/2+o(k ²) bits, and the other component A′ using k×(n−k)+o(kn) bits. The total space is kn−k ²/2+o(kn) bits. The queries on M can be translated to a constant number of queries on A or A′. For instance access _M (i,j) is equal to access _A (i,j) if j≤k and access _A′(i,j−k) if j>k; the c_successor queries get translated similarly. For row successor queries, if j≤k, r_successor _M (i,j) is r_successor _A (i,j) and if it fails to give a successor in A we use r_successor _A′(i,1)+k to find the next successor in A′. In case j>k, r_successor _M (i,j) is simply r_successor _A′(i,j−k)+k. □

4.2 Encoding the Graph

To introduce a navigation oracle for a graph G, we store a standard tree decomposition of G, as well as additional information to distinct G from other graphs with the same tree decomposition. These graphs are the partial k-trees which are subgraphs of the (full) k-tree associated with the encoded tree decomposition. To encode a tree decomposition, we will show that a standard tree decomposition is equivalent to an ordered labeled tree, which can be stored as a multiple parenthesis sequence in o(kn) bits. The additional information for separating the partial k-trees is stored in a compact table using k(n+o(n)−k/2) bits. Beside these, additional auxiliary structures are stored in O(n)+o(kn) to perform navigation queries in constant time. The rest of this section elaborates the details of these constructions.

Assume for a given graph G=(V,E), a tree decomposition τ of width k is given in the standard form. Recall that in a standard tree decomposition, each node (except the root) introduces exactly one vertex, i.e., a node is different from its ancestor node by exactly one vertex. We assign types to all vertices in a top-down manner: for the vertices in the root, we fix an arbitrary ordering 1,2,…,k+1 and give a vertex type i iff it has index i in this ordering. For a vertex v introduced in a bag X, we define type(v)=j, where j is the type of the vertex in the parent of X which has been replaced by v. Note that the only information associated with each bag is the type of the vertex it introduces. Hence, we can represent the tree decomposition τ as an ordered tree with a single label, of value at most k+1, on each bag. We assume the root introduces k+1 vertices of different types, and to make representation easier separate them in a path of bags, with labels 1 to k+1 (see Fig. 6).

Fig. 6

A standard tree decomposition, an ordered labeled tree, and a multiple parenthesis are all equivalent

To represent τ efficiently, we use the multiple parenthesis structure of Lemma 4. Assuming a preorder traversal of τ, we open a parenthesis of type i (i≤k) whenever we enter a bag with label i, and close it when we leave the bag. The result would be a balanced sequence of 2n parentheses of k+1 types. Using Lemma 4, this can be represented using (2+ϵ)nlgk+o(nlgk)+O(n) bits. We call this sequence the MP sequence and label every vertex by the index of its corresponding opening parenthesis in this sequence. This labeling is implicit and is used only to refer to the vertices in navigation queries.

The MP sequence provides a complete image of a tree decomposition. To represent a graph, besides the tree decomposition, we also need to store which edges are indeed present in each bag. Consider a tree decomposition of width k of a graph, in which a new vertex is introduced in a bag X. Such vertex can be connected to any subset of the other k vertices in X. These vertices all have distinct types since they all appear in the same bag.

Assume the graph vertices are arranged in the order they are introduced in the preorder walk of the tree decomposition. For each vertex v introduced in bag X, let l _v be a bitmap of size k+1, such that l _v (j) indicates whether there is an edge between v and u _j , where u _j is the unique vertex of type j in bag X. Let all l _v ’s form the columns of a table M, which we refer to as the ‘big table’, in which the vertices are arranged in preorder. So, M is a matrix of size (k+1)×n and M[j,v]=l _v (j) (see Fig. 7). Since two vertices of the same type cannot be connected, for any vertex v we have M[type(v),v]=0 (in Fig. 7 these entries are labeled as ‘*’). Also the first k columns of M are associated with the vertices introduced in the root and form a triangular submatrix. We apply Lemma 5 to store matrix M in kn−k ²/2+o(kn) bits to support access and successor queries in constant time.

Fig. 7

The big table associated with graph of Fig. 1. In the big table the vertices are arranged in the order they are introduced in the preorder walk of the tree decomposition, and there is an entry for each type and vertex. Consider a vertex like L which has type 3 and is introduced in a bag which also includes A and E with types 1 and 2, respectively. The entry associated with L in the first row is 0. So L is not connected to the vertex of type 1 which comes before it, i.e. A. With a same argument, the entry in the second row implies that L is connected to E

In order to perform navigation queries, we need to check both MP sequence and the big table. As mentioned earlier, we refer to each vertex by its index in the MP sequence. We describe how to find the index of a vertex v in the preorder walk to access the associated entries in the big table. We use a map structure as follows: create a binary sequence S of size 2n with ‘1’ at position i if the i’th element is an open parenthesis (of any type) and ‘0’ otherwise. We store this sequence using 2n+o(n) bits to support rank and select in constant time [41]. Now rank _S (v,1) gives the index of v in the preorder walk, and select _S (i,1) retrieves the i’th vertex in the preorder walk. This enables us to interchangeably refer to a vertex by its position in the preorder walk (the big table index) or its position in the MP sequence. Now consider we are given a range R in the MP sequence, which is represented by its starting and ending indices (these endpoints are not necessarily open parentheses). Note that each open parenthesis in range R represents a vertex of the graph and the set of such vertices maps to a range R′ of vertices in the preorder walk. To perform navigation queries, we need to retrieve the preorder range R′ from R. If both endpoints of R are open parentheses, we simply map them into preorder indices as discussed. If R starts (ends) with a closed parenthesis, we need to find the next (previous) open parenthesis of any type in the MP sequence. We can use the map structure S to find the index of next (previous) open parenthesis as select _S (rank _S (i,1)±1).

The MP sequence and the big table are sufficient to represent a graph of treewidth k. The other structures used in the rest of this section are auxiliary structures maintained to support navigation queries in constant time.

4.3 Supporting Adjacency Queries

Given two vertices u and v we need to know if there is an edge between them. By the definition of tree decomposition, the necessary condition for having an edge between u and v is to have at least one bag which includes both. If such a bag exists, we say there is a potential edge between u and v. A (full) k-tree is indeed a graph which includes all potential edges and partial k-trees are subgraphs of such (full) k-tree. To check the adjacency between u and v, our algorithm first checks if there is a potential edge between u and v by looking at the MP sequence.

Lemma 6

Let u and v be two vertices of a graph G so that u is introduced before v in the preorder traversal of the standard tree decomposition T of G. Then u and v appear in the same bag (i.e., there is a potential edge between them) iff they have distinct types and the open parenthesis associated with u is the tightest parenthesis of its type to enclose that of v.

Proof

First, note that two vertices of the same type cannot appear in the same bag. Let U and V be two bags of T which respectively introduce u and v. Also, let T _u and T _v be the subtrees of T respectively rooted at U and V. By the definition of tree decomposition, u can only appear in bags of T _u and similarly v can only appear in bags of T _v . In the MP sequence, T _u is mapped to the substring started by the open parenthesis associated to u and its matching closed parenthesis (similar statement holds for v). So, the intersection of T _u and T _v is nonempty iff their substrings in the MP sequence intersect. Since the MP sequence is balanced, the open parenthesis of u should enclose that of v. Moreover u does not necessarily appear in all bag of T _u ; it might be overwritten by another vertex w which is introduced in a bag W∈T _u . In this case, w has the same type as u, and u does not appear in nodes of subtree T _w (the subtree of T rooted at W). So if the open parenthesis associated with w in the MP sequence also encloses that of v, then u and v do not appear in the same bag. As a result u and v appear in the same bag iff the open parenthesis of u is the tightest parenthesis of its kind to enclose v. □

The above lemma helps to check, in constant time, if u and v appear in the same bag. We can determine types of u and v from the MP sequence in constant time using m_access. Assume u proceeds v in preorder walk. Using Lemma 4 we can also find the tightest parenthesis of the same type as u which encloses v by calling m_enclose(v,j), where j denotes the type of u. Hence we can see if there is a potential edge between u and v in constant time.

If there is a potential edge between u and v, we have to check the big table to see if there is an actual edge between them. Note that if u is introduced before v, it appears in the bag V which introduces v. Let j denote the type of u. The entry in the jth row of the column associated with v in the big table determines if there is an edge between v and the vertex of type j in V, which is u. By Lemma 5, we can check the content of this entry using access _M (j,v) in constant time.

To summarize, to check if there is an edge between two vertices u and v, the algorithm uses m_access and m_enclose to see if there is a bag of the tree decomposition which includes both. If such a bag does not exists, there is no edge between u and v. If there is a bag which includes both u and v, the algorithm uses access _M to return the content of the entry associated with the type of u in the column associated with v. Figure 8 illustrates the algorithm by an example.

Fig. 8

The MP sequence and the big table associated with the graph of Fig. 7. Assume we need to know if there is an edge between vertices A and L. Note that the vertices are referred by the indices of their opening parenthesis in the preorder walk, i.e., 1 and 18 for A and L, respectively. First, the algorithm checks the types of the vertices using m_access(1) and m_access(18) in the MP sequence to get types 1 and 3 for A and L. Since L comes after A in the preorder walk, the algorithm calls m_enclose(18,1) to get the tightest parenthesis of type 1 (type of A) which encloses L. Since the output is A (index 1), there is a potential edge between A and L. Next, the algorithm checks the column associated with L in the big table. Using the map sequence S, this will be rank _S (18,1)=12’th column in the table. To see if there is an edge between L and the vertex of type 1 in the bag introducing L, the algorithm uses access _M (1,12) which gives 0, meaning that there is no edge between A and L

4.4 Supporting Neighborhood Queries

Given a vertex v, we need to report its neighbors in constant time per neighbor. First, we show how to report the neighbors which come before v in the preorder walk. Recall that a vertex u is a potential neighbor of v if there exists a bag containing both vertices. The column representing v in the big table distinguishes the actual neighbors of v among the potential neighbors preceding v in preorder. We successively apply c_successor on the big table M to visit all ‘1’s in the column of v. An entry M[j,v]=1 implies that v is connected to the vertex of type j in the bag which introduces v. By Lemma 4.3 such vertex is associated with the parenthesis of type j which encloses v, and can be reported in constant time using m_enclose(v,j).

Next, we show how to report the neighbors that come after v in the preorder. We start by showing how to detect the potential neighbors of v. Using the MP sequence, we can find the potential neighbors of v in constant time per potential neighbor as follows. We scan the sequence from the position of v and report every vertex (open parenthesis) until we observe the first open parenthesis of the same type as v. Let w be such parenthesis, we jump to the matching parenthesis of w using m_findmatch _MP (w) in constant time, and continue this process until we see the closed parenthesis matching v. Therefore, in the tree decomposition, we skip the subtrees in which v has been overwritten.

In fact, to report potential neighbors, we report a ‘segment’ of consecutive potential neighbors and jump to the next segment when v is overwritten by a vertex of the same type. There are two sources of difficulty to report the actual neighbors in this manner. First, in a given segment there may be a non-constant number of undesired potential neighbors between two consecutive actual neighbors (by undesired potential neighbor we mean a potential neighbor which is not an actual neighbor). Second, there may be a non-constant number of ‘trivial’ segments which do not include any actual neighbor. In what follows, we describe how to resolve these issues.

As mentioned, the potential neighbors of a vertex form segments of consecutive vertices in the preorder walk. A segment of type i is a range of elements in the MP sequence bordered by two parenthesis of type i. The bordering parenthesis can be open or closed, and their segment can be empty if they are adjacent in the MP sequence (Fig. 9(a)). Each segment is associated to exactly one vertex, which is the nearest vertex of the same type which encloses it. By this definition, the vertices which are introduced in a segment associated with a vertex v, will have v in the bags that introduce them (i.e., v will be the unique vertex of its type in these bags). To report the actual neighbors in a given segment associated with vertex v, we use the map structure to find the range of the segment in the big table, and successively apply r_successor _M on the row of the same type as v in the big table to find all 1’s in the range of the segment. Hence inside a segment, we can report the neighbors in constant time per neighbor.

Fig. 9

The MP sequence and the contracted parenthesis of type 1 for the graph of Fig. 7. Assume we need to report the neighbors of vertex A. The ignore sequence for vertex A (Ig _A ) is 100100, i.e., the first and fourth segments are non-trivial and need to be checked. Note that the third segment which includes vertices L and M is trivial since A is not connected to any of them. To report neighbors in the 4th segment associated with A in the MP sequence, we find the 3rd child of A in the contracted parenthesis of type 1 (the starred vertex in (b)); its matching parenthesis and the one after (arrowed ones) are the representative boundaries of the segment in the contracted sequence, which can be mapped to the MP sequence. The vertices in the segment are O, P, and Q, and the entries in the big table associated with type 1 (type of A) and these are respectively 0, 1, and 1 (these entries are shadowed in Fig. 8). Using r_successor operations in the big table, the algorithm skips O and reports P and Q

We also need to address how to select the appropriate segments. We say a segment is nontrivial if it includes at least one actual neighbor of v, and it is trivial otherwise. The main issue is that there may be a non-constant number of trivial segments associated with a vertex, and we cannot afford to probe all of them. To resolve this issue, we store two auxiliary structures: one is to distinguish nontrivial segments among all segments associated to each vertex, and the other is to locate the nontrivial segments in the preorder sequence.

For each vertex v, we define a bitmap Ig _v where Ig _v (i) determines whether the ith segment associated with v is nontrivial (‘1’) or trivial (‘0’). We store an ignore sequence IG as follows: read vertices in preorder, for each vertex v write down a ‘2’ followed by the sequence Ig _v . The result would be a sequence of length 3n−(k+1) on alphabet {0,1,2}. This sequence can be stored using O(n) bits to support select in constant time [30]. To see why the size of IG is 3n−(k+1), we observe that there are 2n _i −1 segments of type i where n _i is the number of vertices of type i; therefore there are 2n−(k+1) segments in total. Since each segment is associated with exactly one vertex, the size of IG is 2n−(k+1)+n. Ig _v is precisely the subsequence beginning at position select _IG (i,2)+1 and ending at position select _IG (i+1,2), in which i is the index of v in the preorder walk.

Using the ignore sequence, we can distinguish the indices of non-trivial segments among all segments associated with a vertex v. We also need to locate these segments in the MP sequence and subsequently use the map structure to locate the range of the segment in the big table. For each type i, we store a contracted parenthesis of type i, denoted by C _i , as a copy of the MP sequence in which all parenthesis except those of type i are removed. The result would be a balanced parenthesis sequence, or equivalently an ordered tree, for each type. The total size of these trees is equal to n and we need 2n+o(n) bits to represent them.

Now we demonstrate how to locate the t’th segment of vertex v in the MP sequence. If t=1, the desired segment starts with the parenthesis representing v and ends with the next parenthesis of the same type, which can be located in constant time. If t>1, we locate the segment in the contracted parenthesis sequence and map it into the MP sequence as follows. Let i be the type of v. First we locate v in the contracted parenthesis, using $v_{c} = \mathit{select}_{C_{i}}(x,` ( \mbox{'})$ where x is the rank of v among vertices of the same type, i.e., x=rank <sub>MP</sub> (v,`( _i ’). Observe that the t’th segment of v starts after the closed parenthesis matching the open parenthesis representing the t’th child of v in the contracted parenthesis (Fig. 9(b)). We apply $\alpha= \mathit{child}_{C_{i}}(v_{c},t)$ and $\beta = \mathit{findmatch}_{C_{i}}(\alpha)$ to find β,β+1 as the two neighboring parenthesis of type i which bound segment t in the contracted parenthesis. Using rank and select, respectively on C _i and MP, we can locate these parentheses in the MP sequence (see Fig. 9).

To summarize, to report neighbors of vertex v which come after v in preorder, we use the ignore sequence to find the indices of nontrivial segments among all segments associated to v. We use the contracted parenthesis to find the actual positions of nontrivial segments in the MP sequence, and use the map structure to find the range of the segments in the big table. Using r_successor operation in the big table we can report neighbors in constant time per neighbor.

The additional space used for supporting neighbor report are due to the ignore sequence and the contracted parenthesis, which require O(n) bits.

4.5 Supporting Degree Queries

To support degree queries, we observe that a graph of treewidth k on n vertices has at most kn−k(k−3)/2 edges, which is the number of edges in a (full) k-tree of the same size. This is true since in a standard decomposition of a k-tree, the root introduces exactly $\genfrac {(}{)}{0pt}{}{k}{2}$ edges, and the other n−1 bags each introduce exactly k edges which sums up to kn−k(k−3)/2 edges.

We create the following degree sequence D. Considering vertices in preorder, we store the degree of vertices in unary format, i.e., for each vertex v of degree d(v), write down d(v) ‘1’s followed by a ‘0’. The resulting sequence D has n zeros and 2m ones, where m is the number of edges in the graph. We represent degree sequence using $\lg{ \genfrac {(}{)}{0pt}{}{n+2m}{n}} + (n+2m) / \lg(n+2m) + \tilde{O}(n+2m)^{3/4} \leq n \lg((n+2m)e/n) + o(n+2m)$ bits, to support rank and select queries in constant time [40]. As mentioned previously, m≤kn, and hence the size of the sequence is nlgk+o(kn) bits, which is O(n) when k=O(1), and o(kn) for non-constant values of k.² To retrieve the degree of a vertex v, we simply compute rank _D (i+1,0)−rank _D (i,0)−1 in constant time, where i is the index of v in preorder.

The size of the auxiliary structures for supporting neighbor request is O(n) bits, and there is no additional index for adjacency queries (Sect. 4.3). Together with the main structures (the MP sequence, the big table, and the map sequence), the size of the oracle would be k(n+o(n)−k/2)+O(n) bits.

Theorem 2

Given a graph of size n and treewidth k, an oracle is constructed to answer degree, adjacency, and neighborhood queries in constant time. The storage requirement of the oracle is optimal to within lower order terms.

5 Distance Oracles

In this section we introduce a distance oracle which outputs the distance of two given vertices of a graph of treewidth k in time O(k ³lg³ k). The storage requirement of this oracle is asymptotically optimal to within lower order terms.

First we illustrate a simple idea which provides the basis of our constructions. Let x and y be two vertices of a graph G, and X and Y be two nodes of a tree decomposition T of G which respectively introduce x and y. Also, let Z be the least common ancestor of X and Y in T. Lemma 1 implies that any node in the path between X and Y in T includes at least one vertex in the shortest path between x and y. Hence, there is at least one vertex in Z which belongs to the shortest path between x and y. As a result, to find the distance between x and y, it suffices to find the minimum value of d(x,z)+d(z,y) for all vertices like z in Z. A simple distance oracle is hence achieved by explicitly storing the distance between any vertex x and all ancestor vertices of x, where ancestor vertices of x are the vertices which belong to an ancestor node of the node introducing x in the tree decomposition. In a tree decomposition of width k and height h, there are at most h(k+1) ancestor vertices for each vertex. Hence, our simple oracle requires nh(k+1)lgn bits to answer distance queries in time O(k). If we apply Lemma 2 to achieve a height-restricted tree decomposition, the storage requirement of the oracle will be O(nklg² n). In what follows, we apply a recursion technique for decomposing the tree decomposition into smaller trees. This improves the storage complexity of the oracle to the entropy bound within lower order terms. The recursion allows us to reduce the distance queries in a large graph into queries in smaller graphs. Depending on the relation between k and n, the time complexities of the resulted oracles change. For graph with small treewidth where we have lgk=O((lglglgn)³), the query time is O(k ²). For larger values of k the query time is O(k ³lg³ k).

In the rest of this section, we consider the height-restricted tree decomposition T as defined in Sect. 2, and obtained using Lemma 2. Let k′ denote the maximum number of vertices in a node of T. Since by Lemma 2 treewidth of T is at most 3k+2, we have k′≤3k+3.

We define the weight of a node as the number of vertices introduced in (the bag of) that node. Correspondingly, we define the weight of a subtree as the sum of the weights of nodes in the subtree. There are three recursive decompositions of G into smaller subgraphs based on its height-restricted tree decomposition T using the following lemma:

Lemma 7

For any parameter 1≤L≤n, a tree with n nodes and node weights at most k′ can be decomposed into Θ(n/L) subtrees of weight at most 2k′L which are pairwise disjoint aside from their roots. Furthermore, other than edges stemming from the component root nodes, there is at most one edge leaving a node of a component to its child in another component.

Proof

The lemma is essentially the weighted version of and follows trivially from the following lemma by observing that a subtree of size at most 2L has weight at most 2k′L:

Lemma 8

[22, 23]

For any parameter 1≤L≤n, a tree with n nodes can be decomposed into Θ(n/L) subtrees of size at most 2L which are pairwise disjoint aside from their roots. Furthermore, aside from edges stemming from the component root nodes, there is at most one edge leaving a node of a component to its child in another component (Fig. 10). □

Fig. 10

Decomposition of a tree into subtree for value L=5. Subtrees have weight at most 2L=10, and other than edges stemming from roots of subtrees, each subtree has at most one other edge leaving the subtree to another subtree. The highlighted nodes are those which are connected to other subtrees (portal nodes)

5.1 Decomposition into Subgraphs

In the first decomposition phase, the height-restricted tree decomposition T is decomposed into smaller subtrees T ₁,T ₂,… using Lemma 7 with parameter L ₁=k′lg³ n (and skipping the phase entirely where L ₁≥n). By the lemma, we obtain n/(k′lg³ n) such subtrees, each corresponding to at most 2k′²lg³ n graph vertices. Let V _i be the set of such graph vertices that occur in a node in subtree T _i . We define G _i as the subgraph of G induced on V _i .

Lemma 7 guarantees that there are at most two nodes of each subtree T _i that are connected via a tree edge to other subtrees; we refer to these tree nodes as portal nodes (dark nodes in Fig. 10). These nodes correspond to at most 2k′ vertices in each subgraph. We refer to these vertices as the portal vertices of G _i , and denote this set of vertices by P _i .

Lemma 1 implies that the shortest path between a vertex x inside G _x and a vertex y outside G _x passes through at least one portal vertex of G _x . So, to find the distance between x and y, it suffices to have the distance between x and all portal vertices $p^{x}_{1} \ldots p^{x}_{2k'}$ of G _x , the distance between y and all portal vertices $p^{y}_{1} \ldots p^{y}_{2k'}$ of G _x , and the distance between the portal vertices of x and those of y. Note that the shortest path between a portal vertex $v \in\{ p^{x}_{1} , \ldots, p^{x}_{2k'} \}$ and $w \in\{ p^{y}_{1} , \ldots, p^{y}_{2k'} \}$ passes through at least one vertex in the common ancestor of any two bags which include them (see Fig. 11). We explicitly store the distance from each portal vertex to all vertices that occur in an ancestor node of the corresponding portal node. Namely, for each vertex v∈P _i in a portal tree node V and vertex u in an ancestor node of V, we explicitly store the distance between v and u. Since the height of the tree is O(lgn), there are O(k′lgn) such vertices as u. The storage requirement of this list is $O(\frac{n}{k'\lg^{3} n}{k'} (k'\lg n){\lg n }) = o(kn)$ bits.

Fig. 11

The shortest path between two vertices x and y passes through at least one vertex of any bag on the path between the bags which introduce x and y. In particular, at least one portal vertex of the graphs associated with x and y belongs to the shortest path. Also, at least one vertex of the bag L is on the shortest path between x and y, where L is the lowest common ancestor of portal nodes of trees associated with x and y

We construct a portal tree T _P which is essentially the projection of tree T on portal nodes. Nodes of T _P correspond to portal nodes of T, and there exist an edge between two nodes of T _P iff the path between the corresponding nodes in T does not contain another portal node. The projected tree T _P has O(n/(k′lg³ n)) nodes. We preprocess and store the tree (in O(n/(k′lg³ n)) bits) to be able to answer lowest common ancestor queries in constant time [32].

5.2 Vertex Labels

Before going to the further details of the distance oracle, we describe how to refer to the graph vertices in such oracle. Note that the original graph is unlabelled and we need to label the vertices suitably for our purposes. Such labelling should be in a way that we can determine the subgraphs associated with each vertex (and the portal vertices associated with them) in constant time. The labeling of the vertices is a recursive procedure according to the recursive decomposition of the graph into subgraphs. At the first level of recursion, we ensure that the labels of vertices of an individual subgraph G _i form a consecutive sequence of numbers. We store an index of O(lgn) bits for each sequence of numbers to associate it with the corresponding subgraph. These indices together with a rank/select structure enable us to look-up the corresponding subgraph of a given vertex in constant time. The labeling of vertices within an individual subgraph G _i is determined recursively in the same manner: the subgraph is decomposed into smaller subgraphs and vertex labels of each such small subgraph correspond to a consecutive subsequence of the sequence of G _i , and so on. At the deepest level of recursion, the labeling is set according to the method we use to produce distance oracles.

Some vertices are duplicated in more than one subgraph G _i and this can also happen in lower levels of recursion. These vertices are a subset of the portal vertices. Therefore, the numbers we assign as labels can exceed n. However, we need a distinct unique label for each vertex to refer to it. To resolve this issue, at each level of recursion, we maintain rank/select data structures (as in [5]) to identify duplicates. The genuine label of each vertex is an integer from 1 to n and is the rank of that vertex in the duplicate-eliminated list of labels. The rank/select data structure allows us to translate between the unique label and the original label in constant time. As there are O(k′) portal vertices per subgraph per level of recursion the space requirement of such rank/select structures remain o(kn) bits.

5.3 Reduction to the Subgraphs

We now show one can reduce the problem of generating distance oracles to within G _i ’s with an additional O(k ²) term in time and o(kn) term in space. Assume we have an oracle that answers the following two queries in any G _i in time O(t). The first query is a regular distance query that asks for the local distances between any two vertices u,v∈G _i . The second query, called portal query, asks for the distances from any vertex w∈G _i to all portal vertices of G _i . Note that this query needs to report up to 2k′ distance, hence we have t=Ω(k). Provided with a distance oracles which answers these queries in time O(t) in any G _i , we can determine distances globally between any two vertices in time O(t+k ²).

Given two vertices x,y, we first determine the subgraphs G _x ,G _y they belong in as previously mentioned. We query the local oracles for the distances from x to portal vertices $p^{x}_{1}, \ldots, p^{x}_{2k'}$ in G _x and analogously for the distances from y to the portal vertices $p^{y}_{1}, \ldots, p^{y}_{2k'}$ of G _y (see Fig. 12). Let T _x and T _y be the subtrees corresponding to G _x ,G _y . We determine in constant time the lowest common ancestor L of the roots of T _x and T _y in portal tree T _P . Portal vertices have their distances to vertices introduced in their ancestors explicitly stored. Therefore, $p^{x}_{1}, \ldots, p^{x}_{2k'}$ and also $p^{y}_{1}, \ldots, p^{y}_{2k'}$ have their distances to vertices l ₁,…,l _2k′ in the bag of node L stored.

Fig. 12

Distance oracle: computing the distance between x and y

Depending on whether L is indeed either of T _x ,T _y or not, two cases are possible. In the former case where L is either T _x or T _y (say T _x ), the root node of T _x is an ancestor of T _y . The latter case is where L is different than both T _x and T _y . This case is depicted in Fig. 12.

In the former case, the distances from $p^{y}_{i}$’s to $p^{x}_{i}$’s are explicitly stored and therefore one can easily compute the distance from x to y (i.e. d(x,y)) by determining the minimum value of $d(y,p^{y}_{i}) + d(p^{y}_{i}, p^{x}_{j}) + d(p^{x}_{j}, x)$ for all i,j∈[2k′]. This process requires O(t+k ²) time. In the latter case, the distances $d(p^{x}_{i}, l_{j})$ for all i,j are explicitly stored. Therefore, one can compute the distances d(x,l _i ) for all i’s as $\min_{j} \{d(x, p^{x}_{j}) + d(p^{x}_{j}, l_{i})\}$ in O(t+k ²) time. Analogously, one can compute the distances from y to l _i ’s in O(t+k ²) time. Thus, the distance between x and y can be determined as d(x,y)=min _i {d(x,l _i )+d(y,l _i )} in O(t+k ²) time.

5.4 Further Decompositions of the Subgraphs

To answer global distance queries, we need to answer local distance queries in each G _i . Recall that local queries include regular and portal queries. We decompose each G _i further into yet smaller subgraphs $G'_{j}$’s. The decomposition of each subgraph is analogous to that of the original graph G into subgraphs G _i ’s. Namely, given T _i , the tree decomposition of G _i , we use Lemma 2 to obtain a height-restricted tree decomposition $T'_{i}$ of width k′≤3k+2. We decompose $T'_{i}$ using Lemma 7 with parameter L ₂=k′lg²(k′)(lglg(n))³ to obtain smaller subtrees and correspondingly smaller subgraphs $G'_{i}$, each of which has at most 2k′²lg² k′(lglgn)³ vertices.

As in the previous level of decomposition, we explicitly store the distances between portal vertices corresponding to two portal nodes where one is an ancestor of the other. The number of bits required to store these distances is

$$O\biggl(\frac{n}{k'\lg^2 k' (\lg\lg n )^3} k' \bigl(k' \lg \bigl(k'^2 \lg^3 n\bigr) \bigr) { \lg \bigl(k'^2 \lg^3 n \bigr)}\biggr) = o(kn). $$

Additionally, to answer portal queries, we store the distance between each second-level portal vertex and all first-level portal vertices contained in the same subgraph G _i . This structure allows us to produce distances from any vertex $v\in G'_{i}$ to all portal vertices of the containing subgraph G _j efficiently. More precisely, if distances from any vertex to all portals of $G'_{i}$ can be produced in O(t) time, then distances from the vertex to all portals of the containing subgraph G _j can be produced in time O(k ²+t) time. The storage requirement of this additional vector of distances in number of bits is:

$$O\biggl(\frac{n}{k'\lg^2(k') (\lg\lg(n))^3} k'\times k' { \lg \bigl(k'^2 \lg^3(n)\bigr)}\biggr) = o(kn). $$

Hence, the problem has essentially been reduced further to within the smaller subgraphs $G'_{i}$. For one last time, we recursively decompose smaller subgraphs $G'_{i}$s into tiny subgraphs $G''_{i}$’s. We repeat the same set of steps and use Lemma 7 with parameter L ₃=k′lg²(k′)(lglglg(n))³ to obtain tiny subgraphs $G''_{i}$. Analogously, one can reduce the problem to within these tiny subgraphs.

5.5 Distance Oracles for the Tiny Subgraphs

At the bottommost level of recursion, we give compact distance oracles for tiny subgraphs $G''_{i}$ that support reporting the distance between two given vertices (i.e., regular queries) and also reporting the distances from a given vertex to all (third-level) portal vertices of $G''_{i}$ (i.e., portal queries) in O(k ³lg³ k) time.

As $G''_{i}$’s are subgraphs of the original graph, their treewidth is at most k. The corresponding tree decomposition for these graphs can be obtained trivially by projecting from the tree decomposition of the original graph. Hence, genuine treewidths of $G''_{i}$’s are k (and not k′).

We distinguish two cases according to the value of k relative to n. For smaller range of values of k where lgk=O((lglglgn)³), the size of a third-level subgraph $G''_{i}$ is O(k′²lg²(k′)(lglglg(n))³), which is o(lg(n)/k). Therefore, we can have a look-up table that catalogs all graphs with p vertices and treewidth k−1 where p<lg(n)/(4k). The representation of Sect. 4 bounds the number of such graphs to at most p×2^{kp+o(kp)+O(p)}=o(n ^3/4lgn). We exhaustively list answers to all distance queries together with each graph. Consequently the size of the table is O(n ^3/4lgnp ²)=o(n) (note that for constant values of k, we have $G''_{i} = O (\lg \lg \lg n)^{3}$ and it is sufficient to have p=lglgn). A subgraph $G''_{i}=(V''_{i},E''_{i})$ is represented by an index to within the look-up table and therefore, the space requirement of each $G''_{i}$ matches the entropy of graphs with |V″| vertices and of treewidth k. Since $\sum_{i} |V''_{i}| = n +o(n)$, the total space of distance oracles for tiny subgraphs requires space which matches the entropy of graphs with treewidth k to within lower order terms. Distances in $G''_{i}$ are read in constant time from the table and there is an additive overhead of O(k ²) for each level of recursion. Thus, the total distance query time is O(k ²). As a corollary, we have that where k=O(1), the distance query performs in constant time.

For larger values of k, where lgk=ω((lglglgn)³), we simply store a third-level graph $G''_{i} =(V''_{i},E''_{i})$ using the navigation oracle representation of Sect. 4 to store each $G''_{i}$ in $k(|V''_{i}|+o(| V''_{i}|)-k/2)+O(|V''_{i}|)$ bits. Since $\sum_{i} |V''_{i}| = n +o(n)$, the total storage requirement for the distance oracle in this case is k(n+o(n)−k/2)+O(n). In order to determine the distance of a vertex in $G''_{i}$ to another vertex or to the third-level portals of $G''_{i}$, we simply perform a breadth first search (BFS). The time of performing a BFS is asymptotically the number of edges of such graphs which is O(k ³lg²(k)(lglglg(n))³). In the given range of values of k, this time calculates to O(k ³lg³(k)). This dominates the overhead of O(k ²) from higher recursion levels, and hence distance queries perform in O(k ³lg³ k) time.

Theorem 3

Given an unlabeled, undirected, and unweighted graph with n vertices and of treewidth k, an exact distance oracle is constructed to answer distance queries in time O(k ³lg³ k). The storage requirement of the oracle is optimal to within lower order terms.

6 Conclusion

We considered the problem of preprocessing a graph with small treewidth to construct space-efficient oracles that answer a variety of queries efficiently. We presented a navigation oracle that answers navigation queries of adjacency, neighborhood, and degree queries in constant time. We also proposed a distance query which reports the distances of any pair of vertices in O(k ³log³ k) where k is the (determined) treewidth. By way of an enumerative result, we showed the space requirements of the oracles are optimal to within lower order terms. For future work, we consider improving the distance oracle, so that it can recover the shortest path between queried vertices in time proportional to the size of the path. We also leave the problem of space-efficient oracles for weighted graphs of small treewidth as future work.