The distribution of overlaps between eigenvectors of Ginibre matrices

Abstract

We study the overlaps between eigenvectors of nonnormal matrices. They quantify the stability of the spectrum, and characterize the joint eigenvalues increments under Dyson-type dynamics. Well known work by Chalker and Mehlig calculated the expectation of these overlaps for complex Ginibre matrices. For the same model, we extend their results by deriving the distribution of diagonal overlaps (the condition numbers), and their correlations. We prove: (i) convergence of condition numbers for bulk eigenvalues to an inverse Gamma distribution; more generally, we decompose the quenched overlap (i.e. conditioned on eigenvalues) as a product of independent random variables; (ii) asymptotic expectation of off-diagonal overlaps, both for microscopic or mesoscopic separation of the corresponding eigenvalues; (iii) decorrelation of condition numbers associated to eigenvalues at mesoscopic distance, at polynomial speed in the dimension; (iv) second moment asymptotics to identify the fluctuations order for off-diagonal overlaps, when the related eigenvalues are separated by any mesoscopic scale; (v) a new formula for the correlation between overlaps for eigenvalues at microscopic distance, both diagonal and off-diagonal. These results imply estimates on the extreme condition numbers, the volume of the pseudospectrum and the diffusive evolution of eigenvalues under Dyson-type dynamics, at equilibrium.

1 Introduction

1.1 The Ginibre ensemble

Throughout this article we will consider a complex Ginibre matrix $G_N =(G_{ij})_{i,j=1}^N$ where the $G_{ij}$’s are independent and identically distributed complex Gaussian random variables, with distribution $\mu =\mu ^{(N)}$:

$$\begin{aligned} G_{ij} {\mathop {=}\limits ^{\mathrm{(d)}}} {\mathscr {N}}_{{\mathbb {C}}} \Big (0, \frac{1}{2N} \mathrm {Id} \Big ), \qquad \mu (\mathrm {d}\lambda ) = \frac{N}{\pi } e^{- N|\lambda |^2} \mathrm {d}m(\lambda ), \end{aligned}$$

(1.1)

where m is the Lebesgue measure on ${\mathbb {C}}$. As proved in [28], the eigenvalues of $G_N$ have joint distribution

$$\begin{aligned} \rho _{N} (\lambda _1, \dots , \lambda _N) m^{\otimes N}(\mathrm{d}{\varvec{\lambda }})= \frac{1}{Z_N} \prod _{j<k} |\lambda _j - \lambda _k|^2 \prod _{k=1}^N\mu (\mathrm{d}\lambda _k), \end{aligned}$$

(1.2)

where $Z_N=N^{-N(N-1)/2}\prod _{j=1}^N j!$. The above measure is written ${\mathbb {P}}_N$, with corresponding expectation ${\mathbb {E}}_N$. The limiting empirical spectral measure converges to the circular law, i.e. $\frac{1}{N}\sum \delta _{\lambda _i}\rightarrow \frac{1}{\pi }\mathbb {1}_{|\lambda |<1}\mathrm{d}m(\lambda )$.

The statistics of eigenvalues of Ginibre matrices have been studied in great details, and other non-Hermitian matrix models are known to be integrable, see e.g. [23, 37]. Much less is known about the statistical properties of eigenvectors of non-Hermitian ensembles.

1.2 Overlaps

Almost surely, the eigenvalues of a Ginibre matrix are distinct and G can be diagonalized with left eigenvectors denoted $(L_i)_{i=1}^N$, right eigenvectors $(R_i)_{i=1}^N$, defined by $G R_i=\lambda _iR_i$, $L_i^{\mathrm{t}}G=\lambda _i L_i^{\mathrm{t}}$ (for a column vector $\mathbf{{x}}$, we write $\mathbf{{x}}^{\mathrm{t}}=(x_1,\dots ,x_n)$, $\mathbf{{x}}^{*}=(\overline{x_1},\dots ,\overline{x_n})$ and $\Vert \mathbf{{x}}\Vert =(\mathbf{{x}}^*\mathbf{{x}})^{1/2}$). Right and left eigenvectors are biorthogonal basis sets, normalized by

$$\begin{aligned} L_i^tR_j=\delta _{ij}. \end{aligned}$$

(1.3)

In other words, defining X with ith column $R_i$, we have $G= X \Delta X^{-1}$ with $\Delta =\mathrm{diag}(\lambda _1,\dots ,\lambda _N)$, and $L_i^{\mathrm{t}}$ is the ith row of $Y=X^{-1}$. Because of the normalization (1.3), the first interesting statistics to quantify non-orthogonality of the eigenbasis is

$$\begin{aligned} {\mathscr {O}}_{ij}= (R_j^* R_i)(L_j^* L_i). \end{aligned}$$

(1.4)

These overlaps are invariant under the rescaling $R_i\rightarrow c_iR_i$, $L_i\rightarrow c_i^{-1} L_i$ and the diagonal overlaps ${\mathscr {O}}_{ii}= \Vert R_i \Vert ^2 \Vert L_i \Vert ^2$ directly quantify the stability of the spectrum. Indeed, if we assume all eigenvalues of G are distinct and denote $\lambda _i(t)$ the eigenvalues of $G+tE$, standard perturbation theory yields (in this paper $\Vert M\Vert =\sup _{\Vert \mathbf{{x}}\Vert _2=1}\Vert M \mathbf{{x}}\Vert _2$)

$$\begin{aligned} {\mathscr {O}}_{ii}^{1/2}=\lim _{t\rightarrow 0}\sup _{\Vert E\Vert =1}t^{-1}|\lambda _i(t)-\lambda _i|, \end{aligned}$$

so that the ${\mathscr {O}}_{ii}^{1/2}$’s are also called condition numbers. They also naturally appear through the formulas ${\mathscr {O}}_{ii}^{1/2}=\Vert R_iL_i^{\mathrm{t}}\Vert$ or ${\mathscr {O}}_{ii}^{1/2}=\limsup _{z\rightarrow \lambda _i} \Vert (z-G)^{-1}\Vert \cdot |z-\lambda _i|$. We refer to [52, Sects. 35 and 52] for further discussion and references about the relevance of condition numbers to the perturbative theory of eigenvalues, and to estimates of the pseudospectrum.

Eigenvector overlaps also play a fundamental role in non perturbative dynamical settings. First, the large off-diagonal ${\mathscr {O}}_{ij}$’s appear when G is the generator of evolution in real or imaginary time, see [13, Appendix B]. More generally, eigenvector correlations are as relevant as eigenvalue distributions in determining evolution at intermediate times, a well known fact in hydrodynamic stability theory [53]. Second, the overlaps also fully characterize the eigenvalue increments when all matrix entries undergo independent Brownian motions, as shown in “Appendix A”, for any deterministic initial condition. For the Dyson Brownian motion on Hermitian matrices, the eigenvalues evolution is autonomous and coincides with Langevin dynamics for a one-dimensional log-gas. On the contrary, in the nonnormal setting, the Dyson and Langevin dynamics strongly differ. More about the Dyson-type dynamics in the context of the Ginibre ensemble can be found in [11, 30], and the Langevin equation related to (1.2) is studied in [7].

1.3 Overlaps statistics

The statistical study of overlaps started with the seminal work of Chalker and Mehlig [12, 13, 43]. They estimated the large N limit of the expectation of diagonal and off-diagonal overlaps, for the complex Ginibre ensemble: for any $|z_1|, |z_2|<1$,

$$\begin{aligned}&{\mathbb {E}}\left( {\mathscr {O}}_{11}\mid \lambda _1=z_1\right) \underset{N\rightarrow \infty }{\sim }N(1-|z_1|^2), \end{aligned}$$

(1.5)

$$\begin{aligned}&{\mathbb {E}}\left( {\mathscr {O}}_{12}\mid \lambda _1=z_1,\lambda _2=z_2\right) \nonumber \\&\quad \underset{N\rightarrow \infty }{\sim }-\frac{1}{N}\frac{1-z_1\overline{z_2}}{|z_1-z_2|^4} \frac{1-(1+N|z_1-z_2|^2)e^{-N|z_1-z_2|^2}}{1-e^{-N|z_1-z_2|^2}}, \end{aligned}$$

(1.6)

with (1.6) uniformly in $|z_1-z_2|$ from the macroscopic up to the microscopic $N^{-1/2}$ scale.¹ In [13], (1.5) and (1.6) were rigorously established for $z_1=0$, and convincing heuristics extended them anywhere in the bulk of the spectrum. From (1.5), one readily quantifies the instability of the spectrum, an order N greater than for normal matrices in the bulk, and more stable closer to the edge.

An increasing interest in the statistical properties of overlaps for nonnormal matrices followed in theoretical physics [5, 29, 33, 48, 50], often with interest in calculating overlaps averages beyond the Ginibre ensemble. For example, eigenvector overlaps appear to describe resonance shift if one perturbs a scattering system [25,26,27]. This was experimentally verified [31]. Remarkably, the exact statistics (1.6) appeared very recently in an experiment from [15] for microscopic separation of eigenvalues, suggesting some universality of this formula. Unfortunately, many of the models considered in the physics literature are perturbative, and most of the examined statistics are limited to expectations.

In the mathematics community, the overlaps were recently studied in [54]. Walters and Starr extended (1.5) to any $z_1$ in the bulk, established asymptotics for $z_1$ at the edge of the spectrum, and suggested an approach towards a proof of (1.6). They also studied the connection between overlaps and mixed matrix moments. Concentration for such moments for more general matrix models was established in [21], together with applications to coupled differential equations with random coefficients. We continue the rigorous analysis of overlaps by deriving the full distribution of the condition numbers for bulk eigenvalues of the complex Ginibre ensembles. We also establish (1.6) and an explicit formula for the correlation between diagonal and off-diagonal overlaps, on any scale including microscopic. These formulas have consequences on the volume of the pseudospectrum and eigenvalues dynamics.

Motivated by our explicit distribution for the overlaps, Fyodorov [24] recently derived the distribution of diagonal overlaps for real eigenvalues of real Ginibre matrices, as well as an alternative proof for the distribution of diagonal overlaps for the complex Ginibre ensemble. Fyodorov’s method relies on the supersymmetry approach in random matrix theory, while our technique is probabilistic, as described below.

1.4 Main results

Equation (1.5) suggests that the overlaps have typical size of order N. For the complex Ginibre ensemble, we confirm that this is indeed the typical behavior, identifying the limiting distribution of ${\mathscr {O}}_{11}$. We recall that a Gamma random variable $\gamma _{\alpha }$ has density $\frac{1}{\Gamma (\alpha )}x^{\alpha -1}e^{-x}$ on ${\mathbb {R}}_+$.

Theorem 1.1

(Limiting distribution of diagonal overlaps) Let $\kappa >0$ be an arbitrarily constant. Uniformly² in $|z|<1-N^{-\frac{1}{2}+\kappa }$, the following holds. Conditionally on $\lambda _1=z$, the rescaled diagonal overlap ${\mathscr {O}}_{11}$ converges in distribution to an inverse Gamma random variable with parameter 2 as $N\rightarrow \infty$, namely

$$\begin{aligned} \frac{{\mathscr {O}}_{11}}{N(1-|z|^2)} \overset{(\mathrm d)}{\rightarrow } \frac{1}{\gamma _2}. \end{aligned}$$

(1.7)

Our proof also gives convergence of the expectation, in the complex Ginibre case, so that it extends (1.5). Equation (1.7) means that for any continuous bounded function f we have

$$\begin{aligned} {\mathbb {E}}\left( f\left( \frac{ {\mathscr {O}}_{11}}{N(1-|z|^2)}\right) \mid \lambda _1=z\right) \rightarrow \int _0^\infty f(t)\, \frac{e^{-\frac{1}{t}}}{t^3} \mathrm{d}t. \end{aligned}$$

(1.8)

This $t^{-3}$ asymptotic density was calculated for $N=2$ in [13, Sect. V.A.2], where this heavy tail was suggested to remain in the large N limit.

Theorem 1.1 requires integrating over all the randomness of the Ginibre ensemble, in this sense this is an annealed result. It derives from a quenched result, when conditioning on all eigenvalues: the overlap ${\mathscr {O}}_{11}$ can then be decomposed as a product of independent random variables, see Theorem 2.2. Very similar results have been recently established for the Quaternionic Ginibre Ensemble [19], as well as for the Spherical and Truncated Unitary Ensembles [20].

We observe that the limiting density in (1.8) vanishes exponentially fast at 0, so that it is extremely unlikely to find any bulk overlap of polynomial order smaller than N: the spectrum is uniformly unstable. This is confirmed by the following bound on the extremes of condition numbers.

Corollary 1.2

(Bounds on the condition numbers) Let $\kappa ,{\varepsilon }>0$, $\kappa <\kappa _0\leqslant 1/2$ be fixed and $\Omega _N\subset \{1-N^{-\frac{1}{2}+\kappa _0}\leqslant |z|<1-N^{-\frac{1}{2}+\kappa }\}$ be deterministic, measurable. Then with probability tending to 1 as $N\rightarrow \infty$, the following event holds: for any $\lambda _i\in \Omega _N$,

$$\begin{aligned} N^{\frac{1}{2}+\kappa -{\varepsilon }} \leqslant {\mathscr {O}}_{ii}\leqslant N^{1+\kappa _0+{\varepsilon }}m(\Omega _N)^{1/2}. \end{aligned}$$

In particular, all bulk overlaps are in $[N^{1-{\varepsilon }},N^{3/2+{\varepsilon }}]$ with large probability. In terms of polynomial scales in N, the above lower bound is clearly optimal, and we believe the upper bound is also the best possible.

The next result is a rigorous proof of (1.6) in the bulk of the spectrum. It answers Conjecture 4.5 in [54] and gives firm grounds to the heuristic arguments of Chalker and Mehlig [13]. Different heuristics towards Theorem 1.3 for more general ensembles recently appeared in [46], based on diagrammatics. Another recent approach [14] allows to compute the conditional expectation of more general multi-index overlaps when eigenvalues are conditioned to be at macroscopic distance.

Theorem 1.3

(Expectation of off-diagonal overlaps, microscopic and mesoscopic scales) For any $\kappa \in (0,1/2)$, any ${\varepsilon }>0$ and $C>0$ the following holds. Uniformly in $z_1,z_2$ such that $|z_1|<1-N^{-\frac{1}{2}+\kappa }$, $\omega =\sqrt{N}|z_1-z_2|\in [N^{-C},N^{\kappa -{\varepsilon }}]$, we have

$$\begin{aligned} {\mathbb {E}}\left( {\mathscr {O}}_{12}\mid \lambda _1=z_1,\lambda _2=z_2\right)&=-N\frac{1-z_1\overline{z_2}}{|\omega |^4}\frac{1-(1+|\omega |^2)e^{-|\omega |^2}}{1-e^{-|\omega |^2}} \left( 1+{{\,\mathrm{O}\,}}(N^{-2\kappa +{\varepsilon }})\right) . \end{aligned}$$

(1.9)

In particular, under the same hypothesis, in the mesoscopic regime $|w|\rightarrow \infty$, Eq. (1.9) simplifies to

$$\begin{aligned} {\mathbb {E}}\left( {\mathscr {O}}_{12}\mid \lambda _1=z_1,\lambda _2=z_2\right) =-\frac{1-z_1\overline{z_2}}{N|z_1-z_2|^4}(1+{{\,\mathrm{o}\,}}(1)), \end{aligned}$$

(1.10)

showing that the expectation of off-diagonal overlaps decreases with the separation of eigenvalues. Our next result, about second moments at any scale, allows to identify the natural size of off-diagonal overlaps, and gives polynomial decay of correlations between condition numbers.

Theorem 1.4

(Correlations of overlaps: microscopic and mesoscopic scales) Let $\kappa \in (0,1/2)$ and $\sigma \in (0,\kappa )$. Let ${\varepsilon }>0$. Then uniformly in $z_1,z_2$ such that $|z_1|<1-N^{-\frac{1}{2}+\kappa }$, $\omega =\sqrt{N}|z_1-z_2|\in [N^{-\frac{\kappa }{2}+{\varepsilon }},N^{\sigma }]$, we have

$$\begin{aligned}&{\mathbb {E}}\left( |{\mathscr {O}}_{12}|^2\mid \lambda _1=z_1,\lambda _2=z_2\right) = \frac{N^2(1-|z_1|^2)(1-|z_2|^2)}{|\omega |^4} \left( 1+{{\,\mathrm{O}\,}}(N^{2(\sigma -\kappa )+{\varepsilon }})\right) , \end{aligned}$$

(1.11)

$$\begin{aligned}&{\mathbb {E}}\left( {\mathscr {O}}_{11}{\mathscr {O}}_{22}\mid \lambda _1=z_1,\lambda _2=z_2\right) \nonumber \\&\quad = \frac{N^2(1-|z_1|^2)(1-|z_2|^2)}{|\omega |^4}\frac{1+|\omega |^4- e^{-|\omega |^2}}{1-e^{-|\omega |^2}}\left( 1 +{{\,\mathrm{O}\,}}(N^{2(\sigma -\kappa )+{\varepsilon }})\right) . \end{aligned}$$

(1.12)

For the mesoscopic scales $|w|\rightarrow \infty$, the above asymptotics become

$$\begin{aligned} {\mathbb {E}}\left( |{\mathscr {O}}_{12}|^2\mid \lambda _1=z_1,\lambda _2=z_2\right)&\sim \frac{(1-|z_1|^2)(1-|z_2|^2)}{|z_1-z_2|^4}, \end{aligned}$$

(1.13)

$$\begin{aligned} {\mathbb {E}}\left( {\mathscr {O}}_{11}{\mathscr {O}}_{22}\mid \lambda _1=z_1,\lambda _2=z_2\right)&\sim {\mathbb {E}}\left( {\mathscr {O}}_{11}\mid \lambda _1=z_1\right) {\mathbb {E}}\left( {\mathscr {O}}_{22}\mid \lambda _2=z_2\right) . \end{aligned}$$

(1.14)

Equations (1.10) and (1.13) suggest that for any mesoscopic separation of eigenvalues, ${\mathscr {O}}_{12}$ does not concentrate, because ${\mathbb {E}}(|{\mathscr {O}}_{12}|^2)$ is of larger order than ${\mathbb {E}}({\mathscr {O}}_{12})^2$. Contrary to (1.6), (1.13) therefore identifies the size of off-diagonal overlaps, at mesoscopic scales.

The covariance bounds from Theorem 1.4 yield effective estimates on the volume of the pseudospectrum, defined through $\sigma _{\varepsilon }(G)=\left\{ z: \Vert z-G\Vert ^{-1}>{\varepsilon }^{-1}\right\}$. We state the result when the pseudospectrum is intersected with a mesoscopic ball, although it clearly holds on any domain within the bulk that is regular enough.

Corollary 1.5

(Volume of the pseudospectrum) Let $\kappa>a>0$ be any constants and ${\mathscr {B}}_N\subset \{|z|<1-N^{-\frac{1}{2}+\kappa }\}$ be a ball with radius at least $N^{-\frac{1}{2}+a}$, at most $N^{-\frac{1}{2}+\kappa -a}$. Then the volume of the pseudospectrum in ${\mathscr {B}}_N$ is deterministic at first order: for any $c>0$,

$$\begin{aligned} \lim _{N \rightarrow \infty } \lim _{{\varepsilon }\rightarrow 0}{\mathbb {P}}\left( 1-c<\frac{m\left( \sigma _{{\varepsilon }}(G)\cap {\mathscr {B}}_N\right) }{{\varepsilon }^2N^2 {\int _{{\mathscr {B}}_N}} (1-|z|^2)\mathrm{d}m(z)}<1+c\right) = 1. \end{aligned}$$

(1.15)

Finally, we remark that our results shed some light on natural matrix dynamics on nonnormal matrices, the Dyson-type evolution where all matrix entries follow independent complex Ornstein-Uhlenbeck processes. Under this evolution, the eigenvalues follow the dynamics (see Proposition A.1)

$$\begin{aligned} \mathrm {d}\lambda _k(t) = \mathrm{d}M_k(t) - \frac{1}{2} \lambda _k(t)\mathrm {d}t \end{aligned}$$

where the martingales $(M_k)_{1\leqslant k\leqslant N}$ have brackets $\langle M_i,M_j\rangle =0$ and $\mathrm{d}\langle M_i,\overline{M_j}\rangle _t={\mathscr {O}}_{ij}(t)\frac{\mathrm{d}t}{N}.$ Based on this observation, Theorem 1.1, Theorem 1.3 and some bound from [24], we show that the eigenvalues propagate with diffusive scaling, at equilibrium, but slower when close to the boundary.

Corollary 1.6

(Diffusive exponent for eigenvalues dynamics) Let $c,a>0$ be arbitrarily. Consider the matrix dynamics (A.1) with initial condition G(0) distributed as (1.1). Let ${\mathscr {B}}\subset \{|z|<1-c\}$ be a ball, and $t<N^{-c}$. Then as $N\rightarrow \infty$ we have

$$\begin{aligned}&{\mathbb {E}}(|\lambda _1(t)-\lambda _1(0)|^2\mathbb {1}_{\lambda _1(0)\in {\mathscr {B}}})=t\int _{{\mathscr {B}}}(1-|z|^2)\frac{\mathrm{d}m(z)}{\pi }(1+{{\,\mathrm{o}\,}}(1)), \end{aligned}$$

(1.16)

$$\begin{aligned}&{\mathbb {E}}\left( (\lambda _1(t)-\lambda _1(0))\overline{(\lambda _2(t) -\lambda _2(0))}\mathbb {1}_{\{\lambda _1(0)\in {\mathscr {B}}\}\cap \{|\lambda _1(0)-\lambda _2(0)|<N^{-a}\}}\right) ={{\,\mathrm{o}\,}}(tN^{-2a}). \end{aligned}$$

(1.17)

Given the time scale in (1.16), we expect that, conditionally on $\{\lambda _i(0)=z\}$, the process

$$\begin{aligned} \frac{(\lambda _i(ts)-z)_{0\leqslant s\leqslant 1}}{\sqrt{t(1-|z|^2)}} \end{aligned}$$

converges in distribution to a normalized complex Brownian motion as $N\rightarrow \infty$ (t is any scale $N^{-1+c}<t<N^{-c}$), i.e. $\frac{1}{\sqrt{2}}(B_s^{(i)}+\mathrm {i}\widetilde{B}_s^{(i)})_{0\leqslant s\leqslant 1}$ with $B^{(i)}$ and $\widetilde{B}^{(i)}$ independent standard Brownian motions. Moreover, from (1.17), we expect that these limiting processes associated to different eigenvalues are independent.

1.5 About the proofs

Our analysis of the condition numbers starts with the observation of Chalker and Mehlig: the overlaps coincide with those of the Schur form of the original operator, a particularly simple decomposition when the input is a Ginibre matrix. We refer the reader to (2.2) for this key structure at the source of our inductions.

In Sect. 2 our method to prove Theorem 1.1 follows from a simple, remarkable identity in law: the quenched overlap (i.e. conditionally on eigenvalues and integrating only over the complementary randomness of the Ginibre ensemble) is a product of $N-1$ independent random variables, see Theorem 2.2. In the specific case $\lambda _1=0$, for the complex Ginibre ensemble, this split of the distribution of ${\mathscr {O}}_{11}$ remains in the annealed setting, as a consequence of a theorem of Kostlan: the radii of eigenvalues of complex Ginibre matrices are independent random variables. For the Ginibre ensemble with conditioned eigenvalue, we give the extension of Kostlan’s theorem in Sect. 5. This concludes a short probabilistic proof of Theorem 1.1 in the case $\lambda _1=0$.

The extension to general $\lambda _1$ in the bulk proceeds by decomposition of ${\mathscr {O}}_{11}$ into a long-range factor, which gives the deterministic $1-|z|^2$ coefficient, and a short-range factor, responsible for the $\gamma _2^{-1}$ fluctuations. Concentration of the long-range contribution relies on rigidity results for eigenvalues, from [9, 10]. To prove that the short-range contribution is independent of the position of $\lambda _1$, we need strong form of invariance for our measure, around the conditioned point $\lambda _1$. While translation invariance for ${\mathbb {P}}$ follows easily from the explicit form of the Ginibre determinantal kernel, the invariance of the conditioned measure requires more involved tools such as the negative association property for determinantal point processes, see Sect. 4. Corollary 1.2 directly follows from our estimates on the speed of convergence to the inverse Gamma distribution, as explained in Sect. 2.

The proof of Theorems 1.3 and 1.4 in Sect. 3 follows the same scheme: first a quenched identity, then an explicit formula obtained for $z_1=0$ and a localization procedure to isolate the short and long-range contributions. The main difference with the proof of Theorem 1.1 concerns the special case $z_1=0$, the other step being more robust. Due to conditioning on $z_2$, rotational invariance of the remaining eigenvalues is broken and there is no analogue of Kostlan’s theorem to obtain the explicit joint distribution of ${\mathscr {O}}_{12}, {\mathscr {O}}_{11}$ and ${\mathscr {O}}_{22}$. Despite this lack of rotational invariance, Chalker and Mehlig had already obtained a closed-form formula for ${\mathbb {E}}({\mathscr {O}}_{12})$ when $z_1=0$. Remarkably, the second moments are also explicit (although considerably more involved) even for finite N, see Proposition 3.6. Our correlation estimates on overlaps imply Corollary 1.5 by a second moment method. It is plausible yet unclear that Theorem 1.4 admits generalizations to joint moments with an arbitrary number of conditioned eigenvalues. In fact, our second moment calculation involves a P-recursive sequence [see (3.23)], for which explicit solutions are not expected in general. We hope to address the general study of relevant holonomic sequences in future work.

In “Appendix A”, we consider eigenvalues dynamics. After deriving the relevant stochastic differential equations in Proposition A.1, we show that Corollary 1.6 follows from Theorem 1.1 and Theorem 1.3. The diagonal overlaps dictates the eigenvalues quadratic variation, the off-diagonal overlaps their correlations.

Finally, although this article focuses on the eigenvalues condition numbers, the Schur decomposition technique also readily answers the natural question of angles between normalized Ginibre eigenvectors, as explained in “Appendix B”.

1.6 Numerical test for universality of the distribution of overlaps

Universality of eigenvector statistics recently attracted a lot of attention for random Hermitian matrices. For the Gaussian orthogonal and unitary ensembles, the eigenvectors basis is Haar distributed on the corresponding unitary group. As a consequence, projections of eigenvectors on deterministic directions are asymptotically normal, as the projection of the uniform measure on high dimensional spheres (a result due to Lévy and Borel). These eigenvector statistics are now known to be universal [8, 39, 51], holding for generalized Wigner matrices.

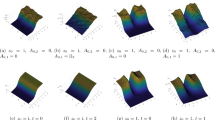
The situation is quite different for eigenvectors of dense random non Hermitian matrices: orders of magnitude such as delocalization are known [49] , but universality seems out of reach with current techniques. In Fig. 1, we numerically investigate whether the inverse Gamma distribution from Theorem 1.1 describes the typical behavior of condition numbers. This leads us to conjecture that for any complex random matrix with i.i.d. entries with substantial real and imaginary parts, the normalized condition numbers converge to the inverse Gamma distribution with parameter two.

Fig. 1

The histogram of the overlaps $\frac{{\mathscr {O}}_{ii}}{N(1-|\lambda _i|^2)}$ associated to bulk eigenvalues for different densities of the matrix entries. The average is performed over all bulk eigenvalues of a $600\times 600$ matrix, sampled 100 times. The curve gives the density of the inverse Gamma distribution with parameter 2

1.7 Notations and conventions

The partial sums of the exponential are written

$$\begin{aligned} e_k^{(\ell )}(x)= \sum _{i=k}^{\ell } {x^i \over i!} \end{aligned}$$

(1.18)

and we abbreviate $e_k=e_k^{(\infty )}$, $e^{(N)}=e_0^{(N)}$. Throughout the paper, $0 \leqslant \chi \leqslant 1$ is a smooth cut-off function on ${\mathbb {R}}_+$ such that $\chi (x)=1$ for $x<1/2$ and 0 for $x>1$. We write $f={{\,\mathrm{O}\,}}(\phi )$ if $|f|<C|\phi |$ for some $C>0$ which does not depend on N, and $f={{\,\mathrm{o}\,}}(\phi )$ if $|f|/|\phi |\rightarrow 0$ as $N\rightarrow \infty$. Along this work, the constants C and c are some universal (resp. typically large and small) constants that may vary from line to line.

2 Diagonal overlaps

This section first gives a remarkable identity in law for the diagonal overlap conditioned on the eigenvalues, Theorem 2.2. Eigenvalues are then integrated, first for $\lambda _1$ at the center of the spectrum thanks to a variant of Kostlan’s theorem, then anywhere in the bulk.

2.1 The quenched diagonal overlap

For all $i\ne j$ we denote $\alpha _{ij} = \frac{1}{\lambda _i - \lambda _j},$ and $\alpha _{ii}=0$. These numbers satisfy

$$\begin{aligned} \alpha _{ij} + \alpha _{ji} =0,\ \alpha _{ij} + \alpha _{jk} =\frac{ \alpha _{ij} \alpha _{jk}}{\alpha _{ik}}. \end{aligned}$$

(2.1)

We first recall the analysis of the overlaps given by Chalker and Mehlig, and include the short proof for completeness.

Proposition 2.1

(From [12, 13, 43]) The following joint equality in distribution holds:

$$\begin{aligned} {\mathscr {O}}_{11} = \sum _{i=1}^N |b_i|^2, \qquad {\mathscr {O}}_{12}= - \overline{b_2} \sum _{i=2}^N b_i \overline{d_i}, \qquad {\mathscr {O}}_{22} = (1+|b_2|^2) \sum _{i=2}^N |d_i|^2, \end{aligned}$$

where $b_1= d_2=1$, $d_1=0$, and the next terms are defined by the recurrence

$$\begin{aligned} b_i =\alpha _{1i} \sum _{k=1}^{i-1} b_k T_{ki}\ \mathrm{for}\ i\geqslant 2,\ \ d_i =\alpha _{2i}\sum _{k=1}^{i-1} d_k T_{ki}\ \mathrm{for}\ i\geqslant 3. \end{aligned}$$

The $T_{ij}$ are independent complex Gaussian variables, centered and with variance $N^{-1}$.

Proof

The overlaps are unchanged by an unitary change of basis, and therefore we can study directly the overlaps of the matrix T. As proved in [44, Appendix 35], this Schur transform T has the eigenvalues of G as diagonal entries, and independently the upper triangle consists in uncorrelated Gaussian random variables, $T_{ij} {\mathop {=}\limits ^{\mathrm{(d)}}} G_{ij}$:

$$\begin{aligned} T= \left( \begin{array}{cccc} \lambda _1 &{} T_{12} &{} \dots &{} T_{1N} \\ 0 &{} \lambda _2 &{} \dots &{} T_{2N} \\ \vdots &{} \ddots &{} \ddots &{} \vdots \\ 0 &{} \dots &{} 0 &{} \lambda _N \\ \end{array} \right) . \end{aligned}$$

(2.2)

For T, the right eigenvectors are of type

$$\begin{aligned} R_1=(1,0, \dots , 0)^t, \qquad R_2=(a,1,0,\dots , 0)^t, \end{aligned}$$

and the left eigenvectors are denoted

$$\begin{aligned} L_1=(b_1, \dots , b_N)^t, \qquad L_2=(d_1,\dots , d_N)^t. \end{aligned}$$

Biorthogonality relations give $b_1=1$, $d_1=0$, $d_2=1$ and $a=- b_2$. The formulas given for the overlaps follow, and the recurrence formulas proceed from the definition of the eigenvectors, i.e. $L_j^t T = \lambda _j L_j^t$. $\square$

Proposition 2.1 shows that the eigenvectors, and thus the overlaps, are obtained according to a very straightforward random process. Indeed, let us consider the sequences of column vectors:

$$\begin{aligned} B_k&= (1, b_2,\dots ,b_k)^{\mathrm{t}} \qquad \text {so that } L_1=B_N, \\ D_k&= (0, 1, d_3,\dots , d_k)^{\mathrm{t}} \qquad \text {so that } L_2=D_N, \\ T_k&= (T_{1,k+1},\dots ,T_{k,k+1})^{\mathrm{t}} \qquad \text {(subset of the }k+1\text { th column of }T). \end{aligned}$$

For any k, $T_k$ is a k-dimensional centered Gaussian vector with independent coordinates and variance 1 / N. We denote the corresponding $\sigma$-algebras

$$\begin{aligned} {\mathcal {F}}_n=\sigma \left( T_k,1\leqslant k\leqslant n\right) =\sigma \left( T_{i,j+1},1\leqslant i\leqslant j\leqslant n\right) . \end{aligned}$$

In particular, $b_2=\frac{T_{12}}{\lambda _1-\lambda _2}\in {\mathcal {F}}_1$. The recurrence formula from Proposition 2.1 becomes

$$\begin{aligned} b_{n+1} = \alpha _{1,n+1}\, B_n^{\mathrm{t}} T_n,\ d_{n+1} = \alpha _{2, n+1}\, D_n^{\mathrm{t}} T_n,\ n\geqslant 1. \end{aligned}$$

(2.3)

Theorem 2.2

The following equality in law holds conditionally on $\{\lambda _1,\dots ,\lambda _N\}$:

$$\begin{aligned} {\mathscr {O}}_{11} \overset{(\mathrm d)}{=} \prod _{n=2}^{N} \Big (1 + {|X_n|^2 \over N |\lambda _1-\lambda _n |^2}\Big ) \end{aligned}$$

where the $X_n$’s are independent standard complex Gaussian random variables ($X_n{\mathop {=}\limits ^{\mathrm{(d)}}} \frac{1}{\sqrt{2}}({\mathscr {N}}_1+\mathrm {i}{\mathscr {N}}_2)$ with standard real Gaussians ${\mathscr {N}}_1$, ${\mathscr {N}}_2$).

Remark 2.3

In particular

$$\begin{aligned} {\mathbb {E}}_T ({\mathscr {O}}_{11}) = \prod _{n=2}^{N} \Big (1 + \frac{1}{ N |\lambda _1-\lambda _n |^2}\Big ), \end{aligned}$$

(2.4)

where ${\mathbb {E}}_T$ is partial integration in the upper-diagonal variables $(T_{ij})_{j>i}$. We therefore recover the result by Chalker and Mehlig [12, 13, 43].

Proof

For fixed N and $1\leqslant n\leqslant N$ we shall use the notations

$$\begin{aligned} {\mathscr {O}}_{11}^{(n)} = \Vert B_n \Vert ^2,\ {\mathscr {O}}_{12}^{(n)} = - \overline{b_2}\, B_n^{\mathrm{t}} {\bar{D}}_n,\ {\mathscr {O}}_{22}^{(n)} = (1+|b_2|^2) \Vert D_n \Vert ^2. \end{aligned}$$

(2.5)

Note that

$$\begin{aligned} {\mathscr {O}}_{11}^{(1)} =1,\ {\mathscr {O}}_{11}^{(2)} = 1+ |b_2|^2 = 1 + \Big | {T_{12} \over \lambda _1 - \lambda _2} \Big |^2 \end{aligned}$$

and, with (2.3),

$$\begin{aligned} {\mathscr {O}}_{11}^{(n+1)}= & {} \Vert B_{n+1} \Vert ^2 = \Vert B_n \Vert ^2 + |b_{n+1}|^2 = \Vert B_n \Vert ^2 \Big ( 1+ { | \alpha _{1,n+1}\,B_n^{\mathrm{t}} T_n |^2 \over \Vert B_n \Vert ^2} \Big ) \\= & {} {\mathscr {O}}_{11}^{(n)} \Big ( 1+ {|X_{n+1}|^2 \over N | \lambda _1 - \lambda _{n+1}|^2} \Big ), \end{aligned}$$

where $X_{n+1}:= \sqrt{N} {B_n^{\mathrm{t}}T_n \over \Vert B_n \Vert }$ is a ${\mathcal {F}}_{n}$-measurable Gaussian with variance 1, independent of ${\mathcal {F}}_{n-1}$. We have therefore proved the expected factorization with independent $X_n$’s, by an immediate induction. $\square$

2.2 The annealed diagonal overlap at the origin

We recall that a Gamma random variable $\gamma _{\alpha }$ has density $\frac{1}{\Gamma (\alpha )}x^{\alpha -1}e^{-x}$ on ${\mathbb {R}}_+$, and a Beta random variable $\beta _{a,b}$ has density $\frac{\Gamma (a+b)}{\Gamma (a)\Gamma (b)}x^{a-1}(1-x)^{b-1} \mathbb {1}_{[0,1]}(x)$.

Proposition 2.4

Conditionally on $\{ \lambda _1 =0 \}$, the following equality in distribution holds:

$$\begin{aligned} {\mathscr {O}}_{11} \overset{(\mathrm d)}{=} \frac{1}{\beta _{2,N-1}}. \end{aligned}$$

(2.6)

In particular, ${\mathbb {E}}\left( {\mathscr {O}}_{11}\mid \lambda _1=0 \right) =N$ and $N^{-1} {\mathscr {O}}_{11}$ converges weakly to $\gamma _2^{-1}$.

Proof

With the notations from Theorem 2.2, we have $(|X_2|^2,\dots ,|X_N|^2) \overset{(\mathrm d)}{=} (\gamma _1^{(2)},\dots \gamma _1^{(N)})$, a collection of $N-1$ independent Gamma random variables with parameter 1. Moreover, still conditionally on $\lambda _1=0$, from Corollary 5.6 we have $\{N |\lambda _2|^2,\dots , N |\lambda _N|^2\}\overset{(\mathrm d)}{=}\{\gamma _2,\dots ,\gamma _N\}$, a set of independent Gamma random variables with corresponding parameters. Theorem 2.2 therefore yields, conditionally on $\lambda _1=0$,

$$\begin{aligned} {\mathscr {O}}_{11}\overset{(\mathrm d)}{=} \prod _{j=2}^N \left( 1 + { \gamma _1^{(j)} \over \gamma _j}\right) , \end{aligned}$$

where all random variable are independent. Equation (2.6) then follows immediately from Lemma 2.5 below. This readily implies

$$\begin{aligned} {\mathbb {E}}\left( {\mathscr {O}}_{11}\mid \lambda _1=0 \right) = {\mathbb {E}}\left( \beta _{2,N-1}^{-1}\right) = {\Gamma (1) \Gamma (N+1) \over \Gamma (2) \Gamma (N) }=N. \end{aligned}$$

(2.7)

The convergence in distribution follows from a simple change of variables: for any bounded test function f,

$$\begin{aligned} {\mathbb {E}}\left( f\left( \frac{1}{N\beta _{2,N-1}}\right) \right)= & {} \int _0^1f\left( \frac{1}{Nx}\right) \frac{N!}{(N-2)!}x(1-x)^{N-2}\mathrm{d}x\nonumber \\= & {} \int _{N^{-1}}^\infty f\left( t\right) \frac{N-1}{N}\left( 1-\frac{1}{Nt}\right) ^{N-2}\frac{\mathrm{d}t}{t^3}, \end{aligned}$$

(2.8)

which clearly converges to the right hand side of (1.8) as $N\rightarrow \infty$. $\square$

Lemma 2.5

The following equalities in distribution hold, where all random variables with different indexes are independent:

$$\begin{aligned}&{\gamma _a \over \gamma _a + \gamma _b} \overset{(\mathrm d)}{=} \beta _{a,b}, \end{aligned}$$

(2.9)

$$\begin{aligned}&\prod _{j=2}^{N} \beta _{j,1} \overset{(\mathrm d)}{=} \beta _{2,N-1}. \end{aligned}$$

(2.10)

Proof

Equation (2.9) is standard, see e.g. [34, Chapter 25]. The equality (2.10) follows by immediate induction from the following property [17]: if $\beta _{p,q}$ and $\beta _{p+q,r}$ are independent, their product has distribution $\beta _{p,q+r}$. $\square$

2.3 The annealed diagonal overlap in the bulk

With the following theorem, we first recall how the expectation of diagonal overlaps is accessible, following [12, 13, 43, 54]. We then prove Theorem 1.1.

The following was proved by Chalker and Mehlig for $z=0$. They gave convincing arguments for any z in the bulk, a result then proved by Walters and Starr. Explicit formulae have also been recently obtained in [1] for the conditional expectation of diagonal and off-diagonal overlaps with respect to any number of eigenvalues. We include the following statement and its short proof for the sake of completeness.

Theorem 2.6

(From [12, 13, 43, 54]) For any $z \in {\mathbb {D}}$, we have

$$\begin{aligned}&{\mathbb {E}}\left( {\mathscr {O}}_{11}\mid \lambda _1=z \right) = N (1-|z|^2) + {{\,\mathrm{O}\,}}\left( \sqrt{N}\frac{e^{- c(z) N }}{1-|z|^2}\right) \\&\qquad \text {where} \ c(z)= |z|^2-1- \log (|z|^2)>0. \end{aligned}$$

Proof

From (2.4), we can write

$$\begin{aligned} {\mathbb {E}}\left( {\mathscr {O}}_{11}\mid \lambda _1=z\right) = {\mathbb {E}}\left( \prod _{k=2}^{N} \left( 1+\frac{1}{ N| z - \lambda _k|^2} \right) \mid \lambda _1= z\right) . \end{aligned}$$

Theorem 5.3 with $g(\lambda ) =1+\frac{1}{ N|z - \lambda |^2}$ then gives

$$\begin{aligned}&{\mathbb {E}}\left( \prod _{k=2}^{N} g (\lambda _k) \mid \lambda _1 = z \right) = {\det (f_{ij})_{1\leqslant i,j\leqslant N-1} \over Z_N^{(z)}} \ \text {where} \ f_{ij} \\&\quad = \frac{1}{ i!} \int \lambda ^{i-1} {\bar{\lambda }}^{j-1} \left( \frac{1}{N}+ |z -\lambda |^2 \right) \mu (\mathrm {d}\lambda ). \end{aligned}$$

This is the determinant of a tridiagonal matrix, with entries [we use (5.1)]

$$\begin{aligned} f_{ii}=\frac{1}{N^i}+\frac{N^{-1}+|z|^2}{iN^{i-1}},\ f_{i,i+1}=-\frac{{\overline{z}}}{N^i},\ f_{i,i-1}=- \frac{z}{i N^{i-1}}. \end{aligned}$$

Denoting $x=N |z|^2$ and $d_k=\det ((M_{ij})_{1\leqslant i,j\leqslant k})$, with the convention $d_0=1$ we have

$$\begin{aligned} d_1&=\frac{x+2}{N},\\ d_k&=\left( 1+\frac{x+1}{k}\right) \frac{1}{N^k}d_{k-1} -\frac{x}{k}\frac{1}{N^{2k-1}}d_{k-2}, \end{aligned}$$

so that $a_k=d_k N^{\frac{k(k+1)}{2}}$ satisfies $a_0=1$, $a_1=x+2$,

$$\begin{aligned} a_k=\left( 1+\frac{x+1}{k}\right) a_{k-1}-\frac{x}{k}a_{k-2}. \end{aligned}$$

This gives $a_k=(k+1)e^{(k+1)}(x)-x e^{(k)}(x)$ by an immediate induction. Thus, we conclude

$$\begin{aligned} {\mathbb {E}}\left( {\mathscr {O}}_{11}\mid \lambda _1=z\right) = N\frac{e^{(N)}(x)}{e^{(N-1)}(x)}-x. \end{aligned}$$

(2.11)

From the asymptotics

$$\begin{aligned}&e^{(N)}(x)=e^x-\sum _{\ell >N}\frac{x^\ell }{\ell !}=e^x+{{\,\mathrm{O}\,}}\left( \frac{x^N}{N!(1-|z|^2)}\right) \\&\quad =e^x\left( 1 +{{\,\mathrm{O}\,}}\left( \frac{e^{N(1-|z|^2+\log |z|^2)}}{\sqrt{2\pi N}(1-|z|^2)}\right) \right) , \end{aligned}$$

the expected formula follows. $\square$

The following proofs make use of special integrability when the conditioned particle is at the center, together with a separation of the short-range and long-range eigenvalues. This separation of scales idea is already present in [13], though not rigorous. To illustrate the main ideas, we first give an alternative proof of Theorem 2.6 (with deteriorated error estimate) which does not rely on explicit formulas, but rather on rigidity and translation invariance. We then prove the main result of this section, Theorem 1.1.

Proof

(Alternative proof of Theorem 2.6) We denote $\nu _z$ the measure (1.2) conditioned to $\lambda _1=z$. Note that $\nu _z$ is a determinantal measure as it has density $\prod _{2\leqslant i<j\leqslant N}|\lambda _i-\lambda _j|^2e^{-\sum _2^NV(\lambda _i)}$ for some external potential V (which depends on z). With a slight abuse of language, we will abbreviate ${\mathbb {E}}_{\nu _z}(X)={\mathbb {E}}(X\mid \lambda _1=z)$ even for X a function of the overlaps.

The proof consists in three steps: we first show that we can afford a small cutoff of our test function around the singularity, then we decompose our product into smooth long-range and a short-range parts. The long range concentrates, and the short range is invariant by translation.

${\textit{First step: small cutoff}}$ Let $g_z(\lambda )=1+ \frac{1}{N|z-\lambda |^2}$. Remember that from (2.4), ${\mathbb {E}}_{\nu _z}({\mathscr {O}}_{11}) = {\mathbb {E}}_{\nu _z}\left( \prod _{i=2}^{N} g_z(\lambda _i)\right) .$ We denote $h_z(\lambda )=g_z(\lambda ) \mathbb {1}_{{|z-\lambda |}>N^{-A}}$, with $A=A(\kappa )$ a large enough chosen constant, and first prove the following elementary equality:

$$\begin{aligned} {\mathbb {E}}_{\nu _z}\left( \prod _{i=2}^{N} g_z(\lambda _i)\right) = {\mathbb {E}}_{\nu _z}\left( \prod _{i=2}^{N} h_z(\lambda _i)\right) +{{\,\mathrm{O}\,}}(N^{-3}). \end{aligned}$$

(2.12)

Note that the exponent $N^{-3}$ here is just chosen for the sake of concreteness. The left hand side coincides with ${\mathbb {E}}_{N-1}\left( \prod _{i=2}^N(|z{-}\lambda _i|^2{+}N^{-1})\right) \left( {\mathbb {E}}_{N-1}\left( \prod _{i=2}^N(|z{-}\lambda _i|^2)\right) \right) ^{-1},$ so that (2.12) follows if we can prove

$$\begin{aligned}&{\mathbb {E}}_{N-1}\left( \prod _{i=2}^N(|z-\lambda _i|^2+N^{-1})e^{-N(|z|^2-1)}) \right) \nonumber \\&\quad - {\mathbb {E}}_{N-1}\left( \prod _{i=2}^N(|z-\lambda _i|^2+N^{-1} \mathbb {1}_{|z-\lambda _i|>N^{-A}})e^{-N(|z|^2-1)}\right) ={{\,\mathrm{O}\,}}(N^{-B}), \end{aligned}$$

(2.13)

$$\begin{aligned}&{\mathbb {E}}_{N-1}\left( \prod _{i=2}^N(|z-\lambda _i|^2)e^{-N(|z|^2-1)}\right) \geqslant N^{-C}, \end{aligned}$$

(2.14)

for a constant B sufficiently larger than C. Equation (2.14) follows from Lemma 2.11. For equation (2.13), note that the left hand side has size order

$$\begin{aligned}&{\mathbb {E}}_{N-1}\left( \prod _{i=2}^N(|z-\lambda _i|^2+N^{-1})e^{-N(|z|^2-1)}) \mathbb {1}_{\exists i: |\lambda _i-z|<N^{-A}}\right) \\&\quad ={{\,\mathrm{O}\,}}(N^{-A/10}){\mathbb {E}}_{N-1}\left( \prod _{i=2}^N(|z -\lambda _i|^2+N^{-1})^2e^{-2N(|z|^2-1)}\right) ^{1/2}, \end{aligned}$$

by Cauchy–Schwarz inequality, union bound, and considering that A can be taken as large as needed. This last expectation is bounded by Lemma 2.11, which concludes the proof of (2.12) by choosing A large enough.

Second step: the long-range contribution concentrates We smoothly separate the short-range from a long-range contributions on the right hand side of (2.12). For this, we define:

$$\begin{aligned} \chi _{z,\delta } (\lambda )&= \chi \Big (N^{\frac{1}{2}-\delta }|z-\lambda | \Big ) \quad \text {with} \quad \delta \in (0, \kappa ) \end{aligned}$$

(2.15)

$$\begin{aligned} f^{\ell }_z(\lambda )&=\frac{1}{ N |z - \lambda |^2} (1 - \chi _{z,\delta } (\lambda )) \end{aligned}$$

(2.16)

$$\begin{aligned} {\bar{f}}_z&=(N-1)\int _{{\mathbb {D}}} {1 - \chi _{z,\delta } (\lambda ) \over N|z - \lambda |^2} \frac{\mathrm {d}m(\lambda )}{\pi } \end{aligned}$$

(2.17)

$$\begin{aligned} h_z(\lambda )&=e^{h_z^{s}(\lambda )+h_z^{\ell }(\lambda )},\nonumber \\ h_z^{s}(\lambda )&= \log \Big ( 1 + \frac{1}{ N |z - \lambda |^2}\mathbb {1}_{{|z-\lambda |}>N^{-A}} \Big ) \chi _{z,\delta } (\lambda ),\nonumber \\ h_z^{\ell }(\lambda )&= \log \Big ( 1 + \frac{1}{ N |z - \lambda |^2} \Big ) (1 - \chi _{z,\delta } (\lambda )), \end{aligned}$$

(2.18)

Note that

$$\begin{aligned} \left| \sum _{i=2}^Nh^\ell _z(\lambda _i)-{\bar{f}}_z\right| \leqslant \left| \sum _{i=2}^Nf^\ell _z(\lambda _i)-\bar{f}_z\right| +\sum _{i=2}^N\frac{1}{N^2|z-\lambda _i|^4}(1 - \chi _{z,\delta } (\lambda _i)). \end{aligned}$$

(2.19)

To bound the first term on the right hand side, we rely on [10, Lemma 3.2]: for any $\alpha$ such that $\alpha \Vert f^{\ell }_z\Vert _\infty <1/3$ (in practice $\Vert f^{\ell }_z\Vert _\infty <N^{-2\delta }$ so that we will choose $\alpha =c N^{2\delta }$ for some fixed small c), we have

$$\begin{aligned} {\mathbb {E}}_{\nu _z}\left( e^{\alpha \left( \sum _{i=2}^Nf^\ell _z(\lambda _i) -{\mathbb {E}}_{\nu _z}\left( \sum _{i=2}^Nf^\ell _z(\lambda _i)\right) \right) }\right) \leqslant e^{C\alpha ^2 {\mathrm{Var}}_{\nu _z}\left( \sum _{i=2}^N f^\ell _z(\lambda _i)\right) } \end{aligned}$$

(2.20)

for some C which does not depend on N. We first bound the above variance. Introduce a partition of type $1=\chi +\sum _{k\geqslant 1}\xi (2^{-k}x)$ for any $x>0$, with $\xi$ smooth, compactly supported. Let $f^{\ell }_{z,k}(\lambda )=f^{\ell }_{z}(\lambda )\xi (2^{-k}N^ {1/2-\delta }|z-\lambda |)$ and $K=\min \{k\geqslant 1:2^kN^{-1/2+\delta }>C\}$ where C and therefore K only depend on $\xi$. Then $\sum _if^{\ell }_z(\lambda _i)=\sum _{k=1}^{K}\sum _if^{\ell }_{z,k}(\lambda _i)$ with probability $1-e^{-cN}$ (here we use that there are no eigenvalues $|\lambda _k|>1+{\varepsilon }$ with probability $1-e^{-c({\varepsilon })N}$, thanks to the Corollary 5.5). Moreover, from [9, Theorem 1.2], for any ${\varepsilon }>0$ and $D>0$, there exists $N_0>0$ such that for any $N\geqslant N_0$, $|z|<1$ and $1\leqslant k\leqslant K$ we have

$$\begin{aligned} {\mathbb {P}}_{N-1}\left( \left| \sum f^{\ell }_{z,k}(\lambda _i)-(N-1)\int _{|\lambda |<1} f^{\ell }_{z,k}\right| >N^{-2\delta +{\varepsilon }} \right) \leqslant N^{-D}. \end{aligned}$$

This implies the same estimate for the conditioned measure by a simple Cauchy–Schwarz inequality:

$$\begin{aligned}&{\mathbb {P}}_{\nu _z}\left( \left| \sum f^{\ell }_{z,k}(\lambda _i)-(N-1)\int _{|z|<1} f^{\ell }_{z,k}\right|>N^{-2\delta +{\varepsilon }} \right) \\&\quad \leqslant N^C {\mathbb {P}}_{N-1}\left( \left| \sum f^{\ell }_{z,k}(\lambda _i)-(N-1)\int _{|z|<1} f^{\ell }_{z,k}\right| >N^{-2\delta +{\varepsilon }} \right) ^{1/2}\\&\quad {\mathbb {E}}_{N-1}\left( \prod _{i=2}^N|z-\lambda _i|^4e^{-2N (|z|^2-1)}\right) ^{1/2}\leqslant N^{-\frac{D}{2}+2C}. \end{aligned}$$

where we used Lemma 2.11. We conclude that for any ${\varepsilon }>0$ and D we have

$$\begin{aligned} {\mathbb {P}}_{\nu _z}\left( |\sum f^{\ell }_z(\lambda _i)-\bar{f}_z|>N^{-2\delta +{\varepsilon }} \right) \leqslant N^{-D}, \end{aligned}$$

so that ${\mathrm{Var}}_{\nu _z}(\sum _{i=2}^N f_z^\ell (\lambda _i))={{\,\mathrm{O}\,}}(N^{-4\delta +{\varepsilon }})$ and ${\mathbb {E}}_{\nu _z}(\sum _{i=2}^N f_z^\ell (\lambda _i))=\bar{f}_z+{{\,\mathrm{O}\,}}(N^{-2\delta +{\varepsilon }})$. As a consequence, (2.20) becomes

$$\begin{aligned} {\mathbb {E}}_{\nu _z}\left( e^{\alpha \left( \sum _{i=2}^Nf^\ell _z(\lambda _i)-\bar{f}_z\right) }\right) \leqslant e^{C\alpha ^2 N^{-4\delta +{\varepsilon }}+C|\alpha | N^{-2\delta +{\varepsilon }}}. \end{aligned}$$

(2.21)

The same reasoning yields

$$\begin{aligned} {\mathbb {E}}_{\nu _z}\left( e^{\alpha \sum _{i=2}^N\frac{1}{N^2|z -\lambda _i|^4}(1-\chi _{z,\delta }(\lambda _i))}\right) \leqslant e^{C\alpha ^2 N^{-8\delta +{\varepsilon }}+C|\alpha | N^{-2\delta +{\varepsilon }}}. \end{aligned}$$

(2.22)

The choice $\alpha =\pm c N^{2\delta }$ in (2.21), (2.22) together with (2.19) implies

$$\begin{aligned} {\mathbb {P}}_{\nu _z}(A)<e^{-c N^{{\varepsilon }}},\ \text{ where }\ A=\left\{ \left| \sum _{i=2}^Nh^\ell _z(\lambda _i)-{\bar{f}}_z \right| >N^{-2\delta +{\varepsilon }} \right\} . \end{aligned}$$

This yields, for some $p=1+c(\kappa )$, $c(\kappa )>0$ and some $q,r>1$,

$$\begin{aligned}&{\mathbb {E}}_{\nu _z}\left( e^{\sum _i(h^s_z(\lambda _i) +h^\ell _z(\lambda _i))}\mathbb {1}_{A}\right) \nonumber \\&\quad \leqslant {\mathbb {E}}_{\nu _z}\left( e^{p\sum _ih^s_z(\lambda _i)}\right) ^{1/p} {\mathbb {E}}_{\nu _z}\left( e^{q\sum _i h^\ell _z(\lambda _i)}\right) ^{1/q} {\mathbb {P}}_{\nu _z}(A)^{1/r}\leqslant e^{-c N^{\varepsilon }}. \end{aligned}$$

(2.23)

Here we used that the third term has size order $e^{-c N^{{\varepsilon }}}$, the second one is of order $e^{q{\bar{f}}_z}={{\,\mathrm{O}\,}}(N^{C})$ from (2.21), (2.22), and so is the first one from Lemma 2.9 (we needed the initial small cutoff changing g into h in order to apply this Lemma). Moreover,

$$\begin{aligned} {\mathbb {E}}_{\nu _z}\left( e^{\sum _i(h^s_z(\lambda _i) +h^\ell _z(\lambda _i))}\mathbb {1}_{A^c}\right)= & {} (1+{{\,\mathrm{O}\,}}(N^{-2\delta +{\varepsilon }})){\mathbb {E}}_{\nu _z} \left( e^{\sum _ih^s_z(\lambda _i)+{\bar{f}}_z}\right) \\&-(1+{{\,\mathrm{O}\,}}(N^{-2\delta +{\varepsilon }})){\mathbb {E}}_{\nu _z}\left( e^{\sum _ih^s_z (\lambda _i)+{\bar{f}}_z}\mathbb {1}_{A}\right) , \end{aligned}$$

and this last expectation is of order $e^{-c N^{{\varepsilon }}}$ for the same reason as (2.23). To summarize, with the previous two equations we have proved (up to exponentially small error terms)

$$\begin{aligned} {\mathbb {E}}_{\nu _z}\left( \prod _{i=2}^Nh_z(\lambda _i)\right) = (1+{{\,\mathrm{O}\,}}(N^{-2\delta +{\varepsilon }}))e^{{\bar{f}}_z}\ {\mathbb {E}}_{\nu _z}\left( e^{\sum _ih^s_z(\lambda _i)}\right) . \end{aligned}$$

Third step: the local part is invariant. With $p=1$ in (2.33), we have

$$\begin{aligned} {\mathbb {E}}_{\nu _z}\left( e^{\sum _ih_z^s(\lambda _i)}\right) ={\mathbb {E}}_{\nu _0}\left( e^{\sum _ih_0^s(\lambda _i)} \right) +{{\,\mathrm{O}\,}}\left( e^{-c N^{2\kappa }}\right) . \end{aligned}$$

This yields

$$\begin{aligned} {\mathbb {E}}_{\nu _z}\left( \prod _{i=2}^Nh_z(\lambda _i)\right) = (1+{{\,\mathrm{O}\,}}(N^{-2\delta +{\varepsilon }}))e^{{\bar{f}}_z-{\bar{f}}_0}\ {\mathbb {E}}_{\nu _0}\left( \prod _{i=2}^Nh_0(\lambda _i)\right) . \end{aligned}$$

From Lemma 2.8, $e^{{\bar{f}}_z-{\bar{f}}_0}=1-|z|^2$, and from (2.7), (2.12) we have ${\mathbb {E}}_{\nu _0}\left( \prod _{i=2}^Nh_0 (\lambda _i)\right) =N+{{\,\mathrm{O}\,}}(N^{-2})$. This concludes the proof. $\square$

Proof of Theorem 1.1

We follow the same method as in the previous proof, except that we won’t need a small a priori cutoff: we are interested in convergence in distribution, not in ${\mathrm{L}}^1$.

First step: the long-range contribution concentrates We smoothly separate the short-range from a long-range contributions in Theorem 2.2:

$$\begin{aligned} {\mathscr {O}}_{11}&\overset{(\mathrm d)}{=}e^{\sum _2^N g^s_z(\lambda _i,X_i)+\sum _2^N g^\ell _z(\lambda _i,X_i)},\nonumber \\ g_z^{s}(\lambda ,x)&= \log \Big ( 1 + {|x|^2 \over N |z - \lambda |^2} \Big ) \chi _{z,\delta } (\lambda ),\nonumber \\ g_z^{\ell }(\lambda ,x)&= \log \Big ( 1 + {|x|^2 \over N |z - \lambda |^2} \Big ) (1 - \chi _{z,\delta } (\lambda )), \end{aligned}$$

(2.24)

For the convenience of the reader we recall the notations defined above :

$$\begin{aligned} \chi _{z,\delta } (\lambda )&= \chi \Big (N^{\frac{1}{2}-\delta }|z-\lambda | \Big ) \quad \text {with} \quad \delta \in (0, \kappa ) \\ f^{\ell }_z(\lambda ,x)&={|x|^2 \over N |z - \lambda |^2} (1 - \chi _{z,\delta } (\lambda )) \\ {\bar{f}}_z&=(N-1)\int _{{\mathbb {D}}} {1 - \chi _{z,\delta } (\lambda ) \over N|z - \lambda |^2} \frac{\mathrm {d}m(\lambda )}{\pi } \end{aligned}$$

Let ${\mathcal {G}}$ be the distribution of $(X_2,\dots ,X_N)$. For any ${\varepsilon }>0$, by Gaussian tail we have

$$\begin{aligned} {\mathcal {G}}(B)\geqslant 1-e^{-cN^{{\varepsilon }/10}},\ \text{ where }\ B=\{|X_i|^2\leqslant N^{{\varepsilon }/10}\ \text{ for } \text{ all }\ 2\leqslant i\leqslant N\}. \end{aligned}$$

Moreover,

$$\begin{aligned}&|\sum _{i=2}^Ng^\ell _z(\lambda _i,X_i)-{\bar{f}}_z|\mathbb {1}_{B}\nonumber \\&\quad \leqslant |\sum _{i=2}^Nf^\ell _z(\lambda _i,X_i)-{\bar{f}}_z|+C N^{{\varepsilon }/2}\sum _{i=2}^N\frac{1}{N^2|z-\lambda _i|^4}(1 - \chi _{z,\delta } (\lambda _i)). \end{aligned}$$

(2.25)

To bound the first term on the right hand side, we first integrate over the Gaussian variables:

$$\begin{aligned}&{\mathbb {E}}_{\nu _z\times {\mathcal {G}}}\left( e^{\alpha \left( \sum _{i=2}^N f_z^{\ell }(\lambda _i,X_i)-{\bar{f}}_z\right) } \right) \\&\quad = {\mathbb {E}}_{\nu _z}\left( \prod _{i=2}^N \frac{1}{1-\alpha \frac{1-\chi _{z,\delta }(\lambda _i)}{N|z-\lambda _i|^2}} e^{-\alpha {\bar{f}}_z} \right) \\&\quad \leqslant {\mathbb {E}}_{\nu _z}\left( e^{\alpha \left( \sum _{i=2}^N f_z^{\ell }(\lambda _i)-\bar{f}_z\right) +C\alpha ^2\sum _{i=2}^N\frac{1}{N^2|z-\lambda _i|^4}(1 - \chi _{z,\delta } (\lambda _i))^2} \right) \\&\quad \leqslant e^{C\alpha ^2 N^{-4\delta +{\varepsilon }}+C\alpha N^{-2\delta +{\varepsilon }}}, \end{aligned}$$

where, for the last inequality, we used (2.21) and (2.22) together with the Cauchy–Schwarz inequality, with $\alpha =c N^{2\delta }$ for some fixed small enough c being admissible. With (2.25), we obtain

$$\begin{aligned} {\mathbb {P}}_{\nu _z\times {\mathcal {G}}}(A)<e^{-c N^{{\varepsilon }}},\ \text{ where }\ A=\left\{ \left| \sum _{i=2}^N g_z^{\ell }(\lambda _i,X_i)-{\bar{f}}_z \right| >N^{-2\delta +{\varepsilon }} \right\} . \end{aligned}$$

(2.26)

Let $\xi \in {\mathbb {R}}$ be fixed. From the above bound we have

$$\begin{aligned}&{\mathbb {E}}\left( \left( \frac{{\mathscr {O}}_{11}}{N(1-|z|^2)} \right) ^{\mathrm {i}\xi }\mid \lambda _1=z\right) \\&\quad = {\mathbb {E}}_{\nu _z\times {\mathcal {G}}}\left( \left( \frac{e^{\sum _2^N g^s_z(\lambda _i,X_i)+\sum _2^N g^\ell _z(\lambda _i,X_i)}}{N(1-|z|^2)}\right) ^{\mathrm {i}\xi } \mathbb {1}_{A^c}\right) +{{\,\mathrm{O}\,}}(e^{-c N^{{\varepsilon }}})\\&\quad = {\mathbb {E}}_{\nu _z\times {\mathcal {G}}}\left( \left( \frac{e^{\sum _2^N g^s_z(\lambda _i,X_i)+\bar{f}_z}}{N(1-|z|^2)}\right) ^{\mathrm {i}\xi } \mathbb {1}_{A^c}\right) +{{\,\mathrm{O}\,}}\left( |\xi | N^{-2\delta +{\varepsilon }}\right) \\&\quad ={\mathbb {E}}_{\nu _z\times {\mathcal {G}}}\left( \left( \frac{e^{\sum _2^N g^s_z(\lambda _i,X_i)+{\bar{f}}_0}}{N}\right) ^{\mathrm {i}\xi } \right) +{{\,\mathrm{O}\,}}(|\xi | N^{-2\delta +{\varepsilon }}), \end{aligned}$$

where we used $e^{{\bar{f}}_z}/(1-|z|^2)=e^{{\bar{f}}_0}$, from Lemma 2.8.

We now define the function $a_z$ (omitting the dependence in $\xi$ in the notation) through

$$\begin{aligned} e^{a_z(\lambda )}={\mathbb {E}}_{{\mathcal {G}}}\left( e^{\mathrm {i}\xi g_z^s(\lambda ,X_i)}\right) . \end{aligned}$$

Note that $a_z$ does not depend on i because the $X_i$’s are identically distributed. We want to apply Lemma 4.3. Note that $a_z$ is supported on $|z-\lambda |<C N^{-\frac{1}{2}+\delta }$ and ${{\,\mathrm{Re}\,}}(a_z)\leqslant 0$, so that (4.3) and (4.4) are automatically satisfied and $(N\Vert \nu \Vert _1)^r\leqslant C N^{2r\delta }$, hence (4.2) holds for the choice $r=3$, $\delta =\kappa /10$. For this choice of $\delta$, we therefore have

$$\begin{aligned} {\mathbb {E}}_{\nu _z}\left( e^{\sum _{i=2}^N a_z(\lambda _i)}\right) = {\mathbb {E}}_{\nu _0}\left( e^{\sum _{i=2}^N a_0(\lambda _i)}\right) +{{\,\mathrm{O}\,}}\left( e^{-cN^{2\kappa }}\right) \end{aligned}$$

(2.27)

uniformly in $\xi$. This proves

$$\begin{aligned}&{\mathbb {E}}\left( \left( \frac{{\mathscr {O}}_{11}}{N(1-|z|^2)} \right) ^{\mathrm {i}\xi }\mid \lambda _1=z\right) \nonumber \\&\quad = {\mathbb {E}}_{\nu _0\times {\mathcal {G}}}\left( \left( \frac{e^{\sum _2^N g^s_0(\lambda _i,X_i)+\bar{f}_0}}{N}\right) ^{\mathrm {i}\xi } \right) +{{\,\mathrm{O}\,}}(|\xi | N^{-2\delta +{\varepsilon }})\nonumber \\&\quad ={\mathbb {E}}\left( \left( \frac{{\mathscr {O}}_{11}}{N}\right) ^{\mathrm {i}\xi }\mid \lambda _1=0\right) +{{\,\mathrm{O}\,}}(|\xi | N^{-2\delta +{\varepsilon }}). \end{aligned}$$

(2.28)

Together with Proposition 2.4, this concludes the proof of Theorem 1.1. $\square$

Proof of Corollary 1.2

We start with the lower bound. From (2.26) we have

$$\begin{aligned} {\mathbb {P}}\left( \frac{{\mathscr {O}}_{11}}{1-|z|^2}<N^{1-{\varepsilon }}\mid \lambda _1=z \right) \leqslant {\mathbb {P}}_{\nu _z\times {\mathcal {G}}}\left( e^{\sum _2^N g^s_z(\lambda _i,X_i)+{\bar{f}}_0} <N^{1-\frac{{\varepsilon }}{2}} \right) +{{\,\mathrm{O}\,}}(e^{-c N^{\varepsilon }}). \end{aligned}$$

We now apply Lemma 2.10 to justify that z can essentially be replaced by $z=0$ in the above left hand side. From (2.27), the Fourier transforms of $g_z,g_0$ are exponentially close uniformly in the Fourier parameter $\xi$. By choosing in Lemma 2.10$R=T=e^{N^{{\varepsilon }/10}}$ and F smooth bounded equal to 1 on the interval $(-\infty ,(1-{\varepsilon }/2\log N-{\bar{f}}_0)]$, 0 on $[(1-{\varepsilon }/2\log N-\bar{f}_0+1,\infty )$, we have

$$\begin{aligned}&{\mathbb {P}}_{\nu _z\times {\mathcal {G}}}\left( e^{\sum _2^N g^s_z(\lambda _i,X_i)+{\bar{f}}_0}<N^{1-\frac{{\varepsilon }}{2}} \right) \nonumber \\&\quad \leqslant {\mathbb {P}}_{\nu _0\times {\mathcal {G}}}\left( e^{\sum _2^N g^s_0(\lambda _i,X_i)+{\bar{f}}_0}<N^{1-\frac{{\varepsilon }}{4}} \right) +{{\,\mathrm{O}\,}}(e^{-N^{{\varepsilon }/10}})\nonumber \\&\quad \leqslant {\mathbb {P}}\left( {\mathscr {O}}_{11}<N^{1-{\varepsilon }/8}\mid \lambda _1=0 \right) +{{\,\mathrm{O}\,}}(e^{-N^{{\varepsilon }/10}})={{\,\mathrm{O}\,}}(e^{-N^{{\varepsilon }/10}}), \end{aligned}$$

(2.29)

where this last probability was estimated thanks to Proposition 2.4. For $|z|<1-N^{-\frac{1}{2}+\kappa }$, this yields

$$\begin{aligned} {\mathbb {P}}\left( {\mathscr {O}}_{11}<N^{-\frac{1}{2}+\kappa }N^{1-{\varepsilon }}\mid \lambda _1=z \right) ={{\,\mathrm{O}\,}}(e^{-N^{{\varepsilon }/10}}), \end{aligned}$$

and we conclude by a union bound (an error bound ${{\,\mathrm{o}\,}}(N^{-1})$ above would be enough). For the upper estimate, in the same way as previously, for any $x>0$ we obtain

$$\begin{aligned} {\mathbb {P}}\left( \frac{{\mathscr {O}}_{11}}{1-|z|^2}>x\mid \lambda _1=z \right) \leqslant {\mathbb {P}}\left( {\mathscr {O}}_{11}>x/2\mid \lambda _1=0 \right) +{{\,\mathrm{O}\,}}(e^{-N^{{\varepsilon }/10}}). \end{aligned}$$

(2.30)

For $x\gg N$, the following is easy to justify:

$$\begin{aligned}&{\mathbb {P}}\left( {\mathscr {O}}_{11}>x\mid \lambda _1=0 \right) = N(N-1)\int _0^{1/x}u(1-u)^{N-2} \mathrm{d}u \\&\quad = \frac{N-1}{N}\int _{x/N}^\infty \left( 1-\frac{1}{Nt}\right) ^{N-2}\frac{\mathrm{d}t}{t^3} \sim \int _{x/N}^\infty \frac{\mathrm{d}t}{t^3}=\frac{N^2}{2 x^2}. \end{aligned}$$

We obtained

$$\begin{aligned}&\sum _{i=1}^N{\mathbb {P}}\left( \lambda _i\in \Omega _N,{\mathscr {O}}_{ii}\geqslant N^{1+\kappa _0+{\varepsilon }}m(\Omega _N)^{1/2}\right) \\&\quad =N{\mathbb {P}}\left( \lambda _i\in \Omega _N\right) {\mathbb {P}}\left( {\mathscr {O}}_{11}\geqslant N^{1+\kappa _0+{\varepsilon }}m(\Omega _N)^{1/2}\mid \lambda _1\in \Omega _N\right) \\&\quad \leqslant N{\mathbb {P}}\left( \lambda _i\in \Omega _N\right) {\mathbb {P}}\left( \frac{{\mathscr {O}}_{11}}{1-|\lambda _1|^2}\geqslant N^{\frac{3}{2}+{\varepsilon }}m(\Omega _N)^{1/2}\mid \lambda _1\in \Omega _N\right) \\&\quad \leqslant N m(\Omega _N)\frac{N^2}{(N^{\frac{3}{2}+{\varepsilon }}m(\Omega _N)^{1/2})^2}\leqslant N^{-2{\varepsilon }}, \end{aligned}$$

which concludes the proof by a union bound. $\square$

Remark 2.7

One may wonder about the true asymptotics of the greatest overlap over the whole spectrum. The above bounds could easily be refined to prove that for any $C>0$ and $N\ll x\ll N^C$,

$$\begin{aligned} \sum _{i=1}^N{\mathbb {P}}\left( {\mathscr {O}}_{ii}\geqslant x\right) \sim N\int _{{\mathbb {D}}}\frac{N^2(1-|z|^2)^2}{2 x^2}\frac{\mathrm{d}m(z)}{\pi }=\frac{N^3}{6 x^2}. \end{aligned}$$

If the overlaps are sufficiently independent (a fact suggested by (1.14)), this hints towards convergence of the maximum to a Fréchet distribution: for any fixed $y>0$, as $N\rightarrow \infty$

$$\begin{aligned} {\mathbb {P}}\left( \max _{1\leqslant i\leqslant N}\frac{{\mathscr {O}}_{ii}}{N^{3/2}}<y\right) \rightarrow e^{-\frac{1}{6y^2}}. \end{aligned}$$

Remember that $0 \leqslant \chi \leqslant 1$ is a smooth cut-off function on ${\mathbb {R}}_+$ such that $\chi (x)=1$ for $x<1/2$ and 0 for $x>1$, and we denote

$$\begin{aligned} \chi _{z,\delta } (\lambda )= \chi \Big ( N^{\frac{1}{2}-\delta }|z-\lambda |\Big ). \end{aligned}$$

The following three lemmas were used in the previous proofs.

Lemma 2.8

There exists a constant $c(\chi )$ such that for any $|z|<1-N^{-\frac{1}{2}+\delta }$ we have

$$\begin{aligned} \frac{1}{ \pi } \int _{{\mathbb {D}}} {1 - \chi _{z,\delta } (\lambda ) \over |z - \lambda |^2} \mathrm {d}m(\lambda ) = (1- 2 \delta ) \log (N) + \log (1 - |z|^2 ) + c(\chi ). \end{aligned}$$

Proof

For $z=0$, this is an elementary calculation in polar coordinates, so that we only need to show that for any given $0<{\varepsilon }<1-|z|$ we have (here ${\mathbb {D}}_a$ is the disk with center a, radius ${\varepsilon }$)

$$\begin{aligned} \frac{1}{ \pi } \int _{{\mathbb {D}}-{\mathbb {D}}_z} {1 \over |z - \lambda |^2} \mathrm {d}m(\lambda ) - \frac{1}{ \pi } \int _{{\mathbb {D}}-{\mathbb {D}}_0} {1 \over |\lambda |^2} \mathrm {d}m(\lambda ) =\log (1-|z|^2). \end{aligned}$$

(2.31)

Denote $x+\mathrm {i}y=r e^{\mathrm {i}\theta }$ and $a=|z|$. Note that $\frac{1}{r^2}=\partial _x(x\frac{\log r}{r^2})+\partial _y(y\frac{\log r}{r^2})$, so that by Green’s theorem we have

$$\begin{aligned} \frac{1}{ \pi } \int _{{\mathbb {D}}-{\mathbb {D}}_z} {1 \over |z - \lambda |^2} \mathrm {d}m(\lambda )=\frac{1}{ \pi } \left( \int _{\partial {\mathbb {D}}}-\int _{\partial {\mathbb {D}}_z}\right) \frac{\log |re^{\mathrm {i}\theta }-a|}{|re^{\mathrm {i}\theta }-a|^2}\left( (x-a)\mathrm{d}y-y\mathrm{d}x\right) . \end{aligned}$$

The second integral clearly does not depend on a. The first integral can be split into

$$\begin{aligned} \frac{1}{ \pi } \int _{\partial {\mathbb {D}}}\frac{\log |re^{\mathrm {i}\theta }-a|}{|e^{\mathrm {i}\theta }-a|^2}\mathrm{d}\theta - \frac{a}{ 2\pi } \int _{\partial {\mathbb {D}}}\frac{\log |re^{\mathrm {i}\theta }-a|}{|e^{\mathrm {i}\theta }-a|^2}(e^{\mathrm {i}\theta }+e^{-\mathrm {i}\theta })\mathrm{d}\theta . \end{aligned}$$

To calculate the first integral above, we expand $\log |e^{\mathrm {i}\theta }-a|=\mathfrak {R}\sum _{p\geqslant 1}\frac{1}{p}(ae^{-\mathrm {i}\theta })^p$, $|e^{\mathrm {i}\theta }-a|^{-2}=\sum _{k,\ell \geqslant 0}a^{k+\ell }e^{\mathrm {i}(k-\ell )\theta },$ and obtain

$$\begin{aligned} \frac{1}{ \pi } \int _{\partial {\mathbb {D}}}\frac{\log |re^{\mathrm {i}\theta }-a|}{|e^{\mathrm {i}\theta }-a|^2}\mathrm{d}\theta =2\sum _{p\geqslant 1,k=p+\ell }\frac{a^{p+k+\ell }}{p}=2\frac{\log (1-a^2)}{1-a^2}. \end{aligned}$$

In the same way, we have

$$\begin{aligned}&\frac{a}{ 2\pi } \int _{\partial {\mathbb {D}}}\frac{\log |re^{\mathrm {i}\theta }-a|}{|e^{\mathrm {i}\theta }-a|^2}(e^{\mathrm {i}\theta }+e^{-\mathrm {i}\theta })\mathrm{d}\theta \\&\quad = a\left( \sum _{p\geqslant 1,k+1=p+\ell }+\sum _{p\geqslant 1,k-1=p+\ell }\right) \frac{a^{k+\ell +p}}{p} = \frac{\log (1-a^2)}{1-a^2}+a^2\frac{\log (1-a^2)}{1-a^2} \end{aligned}$$

To summarize we have proved that

$$\begin{aligned} \frac{1}{ \pi } \int _{{\mathbb {D}}-{\mathbb {D}}_z} {1 \over |z - \lambda |^2} \mathrm {d}m(\lambda )=\log (1-a^2)+c \end{aligned}$$

where c does not depend on z, and (2.31) follows. $\square$

Lemma 2.9

Let $h_z^s$ be given by (2.18). For any $\kappa \in (0,1/2)$, there exists $c(\kappa ),\, C(\kappa )>0$ such that for any $|z|<1-N^{-\frac{1}{2}+\kappa }$ and $p\in [1,1+c(\kappa )]$, we have

$$\begin{aligned} {\mathbb {E}}_{\nu _z}\left( e^{p\sum _2^N h_z^s(\lambda _i)}\right) \leqslant N^{C(\kappa )}. \end{aligned}$$

Proof

First, the result is true for $z=0$. Indeed,

$$\begin{aligned} {\mathbb {E}}_{\nu _0}\left( e^{p\sum _2^N h_0^s(\lambda _i)}\right) \leqslant {\mathbb {E}}_{\nu _0}\left( \prod _{i=2}^N\left( 1+\frac{1}{N|\lambda _i|}\right) ^p\right) =\prod _{k=2}^N{\mathbb {E}}\left( \left( 1+\frac{1}{\gamma _k}\right) ^p\right) ={{\,\mathrm{O}\,}}(N^{C}), \end{aligned}$$

(2.32)

where we used Corollary 5.6.

We want to apply Lemma 4.3 to conclude the proof. For this we need to check conditions (4.2), (4.3) and (4.4) for our function $f=ph^s_z$, and $\nu =e^f-1$. First note that $\Vert \nu \Vert _1\leqslant C\int _{N^{-A}<|\lambda |<1}\frac{1}{(N|\lambda ^2|)^p}\leqslant C N^{-p}N^{A(2p-2)}$, so that (4.2) holds by choosing $p=1+c(\kappa )$ with $c(\kappa )$ small enough. To prove (4.3) and (4.4), we rely on Lemma 4.2:

$$\begin{aligned}&{\mathbb {E}}_{\nu _z}\left( e^{p\sum _{i=2}^Nh^s_z(\lambda _i)}\right) = {\mathbb {E}}_{\nu _z}\left( e^{p\sum _{i=2}^Nh^s_0(\lambda _i)}\right) (1+{{\,\mathrm{o}\,}}(1))\\&\quad \leqslant {\mathbb {E}}\left( \left( 1+\frac{\mathbb {1}_{\gamma _1>N^{-A}}}{\gamma _1} \right) ^p \right) \prod _{k=2}^N{\mathbb {E}}\left( \left( 1+\frac{1}{\gamma _k}\right) ^p\right) \leqslant N^C \end{aligned}$$

where we used (4.2) for the first equation, and the calculation $\int _{N^{-A}}^{\infty } \frac{1}{x^p}e^{-x}\leqslant N^C.$ We therefore obtained

$$\begin{aligned} {\mathbb {E}}_{\nu _z}\left( e^{p\sum _2^N h_z^s(\lambda _i)}\right) = {\mathbb {E}}_{\nu _0}\left( e^{p\sum _2^N h_z^s(\lambda _i)}\right) +{{\,\mathrm{O}\,}}\left( e^{-c N^{2\kappa }}\right) \end{aligned}$$

(2.33)

for any $1\leqslant p\leqslant 1+c(\kappa )$ with $c(\kappa )$ small enough. Equations (2.32) and (2.33) conclude the proof. $\square$

To quantitatively invert the Fourier transform, we use the following crude bound, see [4, Lemma 2.6] following from [6, Corollary 11.5].

Lemma 2.10

There exists a constant c such that if $\mu$ and $\nu$ are probability measures on ${\mathbb {R}}$ with Fourier transforms ${\hat{\mu }}\left( {t}\right) =\int e^{\mathrm {i}{t}{x}}\mu \left( \mathrm{d}x\right)$ and ${\hat{\nu }}\left( {t}\right) =\int e^{\mathrm {i}{t}{x}}\nu \left( { d}x\right)$, then for any $R,T>0$ and any function $f:{\mathbb {R}}\rightarrow {\mathbb {R}}$ with Lipschitz constant C,

$$\begin{aligned} \left| \mu \left( f\right) -\nu \left( f\right) \right|\leqslant & {} c\frac{C}{T}+c\Vert f\Vert _{\infty }\left\{ RT\Vert \mathbb {1}_{\left( -T,T\right) }\left( {\hat{\mu }}-{\hat{\nu }} \right) \Vert _{\infty }\right. \nonumber \\&\left. +\,\mu \left( [-R,R]^{c}\right) +\nu \left( [-R,R]^{c}\right) \right\} . \end{aligned}$$

(2.34)

The following crude a priori estimates are used in this paper. Note that for z strictly in the bulk of the spectrum ($|z|<1-{\varepsilon }$ for fixed ${\varepsilon }>0$), the first statement is a simple consequence of the main result in [55].

Lemma 2.11

For any $p,\kappa >0$, there exists $C>0$ such that, for large enough N, uniformly in $|z_1|, |z_2|<1-N^{-\frac{1}{2}+\kappa }$ we have

$$\begin{aligned} N^{-C}&\leqslant {\mathbb {E}}_N\left( \prod _{i=1}^N |z_1-\lambda _i|^{2p}e^{-pN(|z_1|^2-1)}\right) \leqslant N^{C}, \end{aligned}$$

(2.35)

$$\begin{aligned} N^{-C}&\leqslant {\mathbb {E}}_N\left( \prod _{i=1}^N \left( |z_1-\lambda _i|^{2}+\frac{1}{N}\right) ^pe^{-pN(|z_1|^2-1)}\right) \leqslant N^{C}, \end{aligned}$$

(2.36)

$$\begin{aligned} N^{-C}&\leqslant {\mathbb {E}}_N\left( \prod _{i=1}^N |z_1-\lambda _i|^2 |z_2-\lambda _i|^2e^{-N(|z_1|^2-1)}e^{-N(|z_2|^2-1)}\right) \leqslant N^{C}. \end{aligned}$$

(2.37)

Proof

We start with the lower bounds, which are elementary: as ${\mathbb {E}}(e^X)>e^{{\mathbb {E}}(X)}$, we have

$$\begin{aligned}&{\mathbb {E}}_N\left( \prod _{i=1}^N |z_1-\lambda _i|^{2p}e^{-pN(|z_1|^2-1)}\right) \\&\quad \geqslant \exp \left( 2pN\int \log (|z_1-\lambda |)\left( \rho _1^N(\lambda ) -\frac{\mathbb {1}_{|\lambda |<1}}{\pi }\right) \mathrm{d}m(z)\right) \geqslant \exp ({{\,\mathrm{O}\,}}(1)), \end{aligned}$$

where for the last inequality we used that the density of states for the Ginibre ensemble is close to the uniform measure on the disk with high accuracy (see e.g. [9, Lemma 4.5]). This proves the lower bounds in (2.35) and the lower bounds for (2.36), (2.37) hold by the same argument.

For the upper bounds, we only need to prove (2.36), as (2.35) will follow by monotonicity, and (2.37) by the Cauchy–Schwarz inequality from (2.35). Remember the notation (2.15) and abbreviate $\log _N(x)=\log (|x|^2+1/N)$. We can bound

$$\begin{aligned}&{\mathbb {E}}_N\left( \prod _{i=1}^N \left( |z_1-\lambda _i|^{2}+\frac{1}{N}\right) ^pe^{-pN(|z_1|^2-1)}\right) \nonumber \\&\quad \leqslant {\mathbb {E}}_N\left( e^{2p\sum \log _N(z_1-\lambda _i)\chi _{z_1,\delta }(\lambda _i)-2pN\int \log |z_1-\lambda |\chi _{z_1,\delta }(\lambda )} \right) ^{\frac{1}{2}} \nonumber \\&\qquad \times {\mathbb {E}}_N\left( e^{2p\sum \log _N(z_1-\lambda _i)(1-\chi _{z_1,\delta }(\lambda _i))-2pN\int \log |z_1-\lambda |(1-\chi _{z_1,\delta }(\lambda ))}. \right) ^{\frac{1}{2}} \end{aligned}$$

(2.38)

For the first expectation corresponding to the short range, we apply Lemma 4.2, observing that $N\Vert \nu \Vert _1={{\,\mathrm{O}\,}}(N^{2\delta })$ is negligible for $\delta$ small enough. We obtain that this first expectation is equivalent to

$$\begin{aligned} {\mathbb {E}}_N\left( e^{2p\sum \log _N(\lambda _i)\chi _{0,\delta }(\lambda _i)-2pN\int \log |\lambda |\chi _{0,\delta }(\lambda )} \right) \leqslant N^C, \end{aligned}$$

where the above inequality follows from Corollary 5.5.

The second expectation in (2.38) is the Laplace transform of smooth linear statistics, so that the loop equations techniques apply to prove it is of polynomial order, see [40, Theorem 1.3]. More precisely, [40] applies to the smooth function $(1-\chi _{z_1,\delta })\log$ instead of $(1-\chi _{z_1,\delta })\log _N$, but we can decompose $\log _N(\lambda )=2\log |\lambda |+\log (1+\frac{1}{N|\lambda ^2|})$. With the Cauchy–Schwarz inequality we separate contribution from these two functions, then the analogue (for the unconditioned measure) of (2.21) shows the Laplace transform of linear statistics of $(1-\chi _{z_1,\delta })\log (1+\frac{1}{N|\lambda ^2|})$ is ${{\,\mathrm{O}\,}}(1)$, and finally [40, Theorem 1.3] bounds the contribution of $(1-\chi _{z_1,\delta })\log |\lambda |$ by ${{\,\mathrm{O}\,}}(N^C)$. $\square$

3 Off-diagonal overlaps

In this section we consider the distribution of N Ginibre points conditioned to $\{ \lambda _1 = z_1, \lambda _2 = z_2\}$. We will successively prove identities for the quenched off-diagonal overlaps, for all $z_1,z_2$, and then get explicit relations for $z_1=0$ in the annealed setting. Finally, these new correlation identities are extended to any $z_1, z_2$ in the bulk of the spectrum by a decomposition of short and long range contributions.

3.1 The quenched off-diagonal overlap

Contrary to the diagonal overlap, the factorization here doesn’t involve independent variables.

Proposition 3.1

The following equality in law holds, conditionally on $\{ \lambda _1, \dots , \lambda _N\}$:

$$\begin{aligned} {\mathscr {O}}_{12}&\overset{(\mathrm{d})}{=} - \Big | {T_{12} \over \lambda _1 - \lambda _2} \Big |^2\prod _{n=3}^N \Big (1 + {Z_{n} \over N (\lambda _1-\lambda _{n}) (\overline{\lambda _2 - \lambda _{n}})} \Big ), \end{aligned}$$

where, conditionally on ${\mathcal {F}}_{n-2}$, $Z_n$ is a product of two (correlated) complex Gaussian random variables, and ${\mathbb {E}}(Z_{n}\mid {\mathcal {F}}_{n-2})=1$.

Proof

As for the diagonal overlap, we simply compute, with the notation (2.5),

$$\begin{aligned} {\mathscr {O}}_{12}^{(2)} = - |b_2|^2 = - \Big | {T_{12} \over \lambda _1 - \lambda _2} \Big |^2 \end{aligned}$$

and

$$\begin{aligned} {\mathscr {O}}_{12}^{(n+1)}= & {} - \overline{b_2}\, B_{n+1}^{\mathrm{t}} \bar{D}_{n+1} = - \overline{b_2} ( B_{n}^{\mathrm{t}} {\bar{D}}_{n} + b_{n+1} \overline{d_{n+1}}) \\= & {} - \overline{b_2} (B_{n}^{\mathrm{t}} {\bar{D}}_{n} + \alpha _{1,n+1} B_n^{\mathrm{t}}T_n \overline{\alpha _{2, n+1} D_n^{\mathrm{t}} T_n}) \\= & {} - \overline{b_2} B_{n}^{\mathrm{t}} {\bar{D}}_{n} \Big ( 1+ \alpha _{1,n+1} \overline{\alpha _{2, n+1}} { B_n^{\mathrm{t}} T_n \overline{D_n^{\mathrm{t}} T_n} \over B_{n}^{\mathrm{t}} {\bar{D}}_{n}} \Big )\\= & {} {\mathscr {O}}_{12}^{(n)} \Big ( 1+ {Z_{n+1} \over N (\lambda _1 - \lambda _{n+1}) \overline{( \lambda _2 - \lambda _{n+1})}} \Big ), \end{aligned}$$

where

$$\begin{aligned} Z_{n+1}=N {B_n^{\mathrm{t}} T_n\, \overline{D_n^{\mathrm{t}} T_n} \over B_{n}^{\mathrm{t}} {\bar{D}}_{n}}. \end{aligned}$$

(3.1)

Clearly, conditionally on ${\mathcal {F}}_{n-1}$, $Z_{n+1}$ is a product of two complex Gaussian random variables, a distribution which depends on ${\mathscr {O}}_{12}^{(n)}$. Moreover, $B_n,D_n\in {\mathcal {F}}_{n-1}$ and $T_n$ is independent of ${\mathcal {F}}_{n-1}$, so that ${\mathbb {E}}(Z_{n+1}\mid {\mathcal {F}}_{n-1})=1$. $\square$

Remark 3.2

By successive conditional expectations with respect to ${\mathcal {F}}_{n-2},\dots ,{\mathcal {F}}_1$, Proposition 3.1 implies

$$\begin{aligned} {\mathbb {E}}_T\left( {\mathscr {O}}_{12}\right) = - \frac{1}{ N |\lambda _1-\lambda _2|^2} \prod _{k=3}^{N} \Big (1 + \frac{1}{ N (\lambda _1-\lambda _k) (\overline{\lambda _2 - \lambda _k})} \Big ), \end{aligned}$$

(3.2)

an important fact already proved in [12, 13, 43].

3.2 The annealed off-diagonal overlap: expectation

Remarkably, the works [12, 13, 43] also explicitly integrated the random variable (3.2) over $\lambda _3,\dots ,\lambda _N$, in the specific case $\lambda _1=0$. We state the resulting asymptotics and add the proof from Chalker and Mehlig, for completeness.

Corollary 3.3

(Chalker, Mehlig [12, 13, 43]) For any ${\varepsilon }>0$, there exists $c>0$ such that uniformly in $|z|<N^{-{\varepsilon }}$,

$$\begin{aligned} {\mathbb {E}}\left( {\mathscr {O}}_{12}\mid \lambda _1=0, \lambda _2=z \right) =-\frac{1}{ N |z|^4} \frac{1 - (1 + N |z|^2) e^{-N |z|^2}}{1-e^{-N|z|^2}} + {{\,\mathrm{O}\,}}(e^{-c N}). \end{aligned}$$

Proof

From (3.2), we want to evaluate

$$\begin{aligned} {\mathbb {E}}\left( {\mathscr {O}}_{12}\mid \lambda _1=0, \lambda _2=z \right) = - \frac{1}{ N|z|^2} {\mathbb {E}}\left( \prod _{k=3}^{N} \Big (1 - \frac{1}{ N \lambda _k (\overline{z - \lambda _k})} \Big ) \mid \lambda _1=0, \lambda _2= z \right) \end{aligned}$$

From Theorem 5.4 with $g (\lambda ) =1 - \frac{1}{ N\lambda ( \overline{z - \lambda })}$, we find that

$$\begin{aligned} {\mathbb {E}}\left( \prod _{k=2}^{N} g (\lambda _k) \mid \lambda _1=0, \lambda _2 = z\right)&= \frac{1}{Z_N^{(0,z)}}\det (f_{i,j})_{i,j = 1}^{N-2} \end{aligned}$$

where

$$\begin{aligned} f_{i,j}= & {} \frac{1}{ (i+1)!} \int \lambda ^{i-1} {\bar{\lambda }}^{j-1} |\lambda |^2 |z - \lambda |^2 g (\lambda ) \mu (\mathrm {d}\lambda )\\= & {} \frac{1}{ (i+1)!} \int \lambda ^{i-1} {\bar{\lambda }}^{j-1} \Big ( |\lambda |^2 |z-\lambda |^2 -\frac{1}{N} {\overline{\lambda }} (z - \lambda ) \Big ) \mu (\mathrm {d}\lambda ). \end{aligned}$$

This matrix is tridiagonal with entries

$$\begin{aligned} f_{ii}=\frac{1}{N^{i+1}}+\frac{|z|^2}{(i+1) N^i}+\frac{1}{(i+1) N^{i+1}},\ f_{i,i+1}=-\frac{{\overline{z}}}{N^{i+1}},\ f_{i,i-1}=- \frac{z}{iN^{i}}. \end{aligned}$$

Let $d_k=\det (f_{i,j})_{i,j = 1}^{k}$ and $x= N|z|^2$. With the convention $d_0=1$ we have

$$\begin{aligned} d_1&=\frac{1}{N^2}\left( \frac{3}{2}+\frac{x}{2}\right) ,\\ d_k&=\left( 1+\frac{x+1}{k+1}\right) \frac{1}{N^{k+1}}d_{k-1} -\frac{x}{k}\frac{1}{N^{2k+1}}d_{k-2}. \end{aligned}$$

so that $a_k=d_k N^{\frac{k(k+3)}{2}}$ satisfies $a_0=1$, $a_1=3/2+x/2$,

$$\begin{aligned} a_k=\left( 1+\frac{x+1}{k+1}\right) a_{k-1}-\frac{x}{k}a_{k-2}. \end{aligned}$$

An immediate induction gives $a_k=(k+2)x^{-2}e_2^{(k+2)}(x)$. Thus, we conclude

$$\begin{aligned} {\mathbb {E}}\left( {\mathscr {O}}_{12} \mid \ \lambda _1=0, \lambda _2=z \right) = - \frac{N}{x^2}\frac{e_2^{(N)}(x)}{e_1^{(N)}(x)}. \end{aligned}$$

The proof is then concluded by standard asymptotics. $\square$

With Corollary 3.3, the expectation of ${\mathscr {O}}_{12}$ is known for $\lambda _1=0$. To extend the result to anywhere in the bulk of the spectrum, we mimic the alternative proof of Theorem 2.6, from Sect. 2.3.

Proof of Theorem 1.3

We denote $\nu _{z_1,z_2}$ the measure (1.2) conditioned to $\lambda _1=z_1,\lambda _2=z_2$. Note that $\nu _{z_1,z_2}$ is a determinantal measure. With a slight abuse of language, we will abbreviate ${\mathbb {E}}_{\nu _{z_1,z_2}}(X)={\mathbb {E}}(X\mid \lambda _1=z_1,\lambda _2=z_2)$ even for X a function of the overlaps.

We follow the same three steps as in the alternative proof of Theorem 2.6. Strictly speaking, if we were to impose $|z_1-z_2|>N^{-C}$ for some fixed C, we would not need the first step below, as the singularity 1 / |z| is integrable, contrary to our previous singularity $1/|z|^2$. However, in Theorem 1.3 we allow $z_1$ and $z_2$ to be arbitrarily close, so we first perform an initial small cutoff.

First step: small cutoff  Let $g_{z_1,z_2}(\lambda )= 1+\frac{1}{N(z_1-\lambda )(\overline{z_2-\lambda })}$. Remember that, from (3.2)

$$\begin{aligned} {\mathbb {E}}_{\nu _{z_1,z_2}}({\mathscr {O}}_{12}) =-\frac{1}{N|z_1-z_2|^2} {\mathbb {E}}_{\nu _{z_1,z_2}}\left( \prod _{n=3}^{N} g_{z_1,z_2}(\lambda _i)\right) . \end{aligned}$$

We denote $h_{z_1,z_2}(\lambda )=g_{z_1,z_2}(\lambda ) \mathbb {1}_{\lambda \not \in {\mathscr {B}}}$ where ${\mathscr {B}}=\{|\lambda -z_1|<N^{-A}\}\cup \{|\lambda -z_2|<N^{-A}\}$. For A a large enough constant, the analogue of (2.12) holds:

$$\begin{aligned} {\mathbb {E}}_{\nu _{z_1,z_2}}\left( \prod _{i=3}^{N} g_{z_1,z_2}(\lambda _i)\right) = {\mathbb {E}}_{\nu _{z_1,z_2}}\left( \prod _{i=3}^{N} h_{z_1,z_2}(\lambda _i)\right) +{{\,\mathrm{O}\,}}(N^{-3}). \end{aligned}$$

(3.3)

Indeed, by making explicit the above conditional measures, (3.3) follows from

$$\begin{aligned}&{\mathbb {E}}_{N-2}\left( \prod _{i=3}^N(|z_1-\lambda _i|^2|z_2 -\lambda _i|^2+N^{-1}\overline{(z_1-\lambda _i)}(z_2-\lambda _i)) e^{-N(|z_1|^2-1)-N(|z_2|^2-1)}\right) \nonumber \\&\quad - {\mathbb {E}}_{N-2}\left( \prod _{i=3}^N(|z_1-\lambda _i|^2|z_2 -\lambda _i|^2+\,N^{-1}\overline{(z_1-\lambda _i)}(z_2-\lambda _i)) \mathbb {1}_{\lambda _i\not \in {\mathscr {B}}}e^{-N(|z_1|^2-1) -N(|z_2|^2-1)}\right) ={{\,\mathrm{O}\,}}(N^{-B}),\nonumber \\ \end{aligned}$$

(3.4)

and

$$\begin{aligned} {\mathbb {E}}_{N-2}\left( \prod _{i=3}^N(|z_1-\lambda _i|^2|z_2 -\lambda _i|^2)e^{-N(|z_1|^2-1)-N(|z_2|^2-1)}\right) \geqslant N^{-C_1}. \end{aligned}$$

(3.5)

with B much larger than $C_1$. Lemma 2.11 gives (3.5). The left hand side of (3.4) has size order

$$\begin{aligned}&{\mathbb {E}}_{N-2}\left( \prod _{i=3}^N(|z_1-\lambda _i|^2+N^{-1}) (|z_2-\lambda _i|^2+N^{-1})e^{-N(|z_1|^2-1)-N(|z_2|^2-1)}\mathbb {1}_{\exists i: \lambda _i\in {\mathscr {B}}}\right) \\&\quad ={{\,\mathrm{O}\,}}(N^{-A+C_2}) \end{aligned}$$

by the Cauchy–Schwarz inequality and Lemma 2.11, for some $C_2$ which does not depend on A. This concludes the proof of (3.3) by choosing A large enough.

Second step: the long-range contribution concentrates We smoothly separate the short-range from a long-range contributions on the right hand side of (3.3):

$$\begin{aligned} h_{z_1,z_2}(\lambda )&=e^{h_{z_1,z_2}^{s}(\lambda ) +h_{z_1,z_2}^{\ell }(\lambda )},\\ h_{z_1,z_2}^{s}(\lambda )&= \log \Big ( 1 + \frac{1}{N (z_1 - \lambda )\overline{(z_2-\lambda )}}\mathbb {1}_{ \lambda \not \in {\mathscr {B}}} \Big ) \chi _{z,\delta } (\lambda ),\\ h_{z_1,z_2}^{\ell }(\lambda )&= \log \Big ( 1 + \frac{1}{N (z_1 - \lambda )\overline{(z_2-\lambda )}} \Big ) (1 - \chi _{z,\delta } (\lambda )), \end{aligned}$$

and we denote $z=(z_1+z_2)/2$, recall $|z_1-z_2|<N^{-\frac{1}{2}+\kappa -{\varepsilon }}$, $\chi _{z,\delta } (\lambda )= \chi \Big (N^{\frac{1}{2}-\delta }|z-\lambda | \Big )$, and choose $\delta \in (\kappa -{\varepsilon }, \kappa )$. In the definition of $h_{z_1,z_2}^{s}$, we can choose any branch for the logarithm, this won’t have any impact on the rest of the proof. In the long-range contribution $h^{\ell }_{z_1,z_2}$, the logarithm is defined by continuity from $\log (1)=0$. Let $f^{\ell }_{z_1,z_2}(\lambda )= \frac{1}{N (z_1 - \lambda )\overline{(z_2-\lambda )}} (1 - \chi _{z,\delta } (\lambda ))$ and $\bar{f}_{z_1,z_2}=\frac{N-2}{N}\frac{1}{ \pi } \int _{{\mathbb {D}}} {1 - \chi _{z,\delta } (\lambda ) \over (z_1-\lambda )\overline{(z_2-\lambda )}} \mathrm {d}m(\lambda )$. Note that

$$\begin{aligned}&|\sum _{i=3}^Nh^\ell _{z_1,z_2}(\lambda _i)-{\bar{f}}_{z_1,z_2}|\leqslant |\sum _{i=3}^Nf^\ell _{z_1,z_2}(\lambda _i)-\bar{f}_{z_1,z_2}|+\frac{1}{2}\nonumber \\&\quad \left( \sum _{i=3}^N\frac{1}{N^2|z_1-\lambda _i|^4}(1 - \chi _{z,\delta } (\lambda _i))+ \sum _{i=3}^N\frac{1}{N^2|z_2-\lambda _i|^4}(1 - \chi _{z,\delta } (\lambda _i)) \right) .\qquad \end{aligned}$$

(3.6)

The last two sums are bounded as in (2.22). For the first term on the right hand side, we bound the real and imaginary parts separately: similarly to (2.20), we have

$$\begin{aligned}&{\mathbb {E}}_{\nu _{z_1,z_2}}\left( e^{\alpha \left( \sum _{i=3}^N \mathrm{Re}f^\ell _{z_1,z_2}(\lambda _i)-{\mathbb {E}}_{\nu _{z_1,z_2}}\left( \sum _{i=3}^N\mathrm{Re} f^\ell _{z_1,z_2}(\lambda _i)\right) \right) }\right) \nonumber \\&\quad \leqslant e^{C\alpha ^2 {\mathrm{Var}}_{\nu _{z_1,z_2}}\left( \sum _{i=3}^N \mathrm{Re}f^\ell _{z_1,z_2}(\lambda _i)\right) } \end{aligned}$$

(3.7)

where $\alpha =c N^{2\delta }$ for some fixed c and C which does not depend on N. We first bound the above variance. Remember we have a partition of type $1=\chi +\sum _{k\geqslant 1}\xi (2^{-k}x)$ for any $x>0$, with $\xi$ smooth, compactly supported. Let $f^{\ell }_{z_1,z_2,k}(\lambda )=f^{\ell }_{z_1,z_2}(\lambda )\xi (2^{-k}N^{1/2-\delta }|z-\lambda |)$ and $K=\min \{k\geqslant 1:2^kN^{-1/2+\delta }>10\}$. Then $\sum _if^{\ell }_z(\lambda _i)=\sum _{k=1}^{K}\sum _if^{\ell }_{z,k}(\lambda _i)$ with probability $1-e^{-cN}$, and with [9, Theorem 1.2], for any ${\varepsilon }>0$ and $D>0$, there exists $N_0>0$ such that for any $N\geqslant N_0$ and $1\leqslant k\leqslant K$ we have (we now omit to write the real part, being understanding that f is either $\mathrm{Re} f$ or $\mathrm{Im} f$)

$$\begin{aligned} {\mathbb {P}}_{N-2}\left( \left| \sum f^{\ell }_{z_1,z_2,k}(\lambda _i)-(N-2)\int _{|z|<1} f^{\ell }_{z_1,z_2,k}\right| >N^{-2\delta +{\varepsilon }} \right) \leqslant N^{-D}. \end{aligned}$$

The same estimate holds for the conditioned measure by the Cauchy–Schwarz inequality:

$$\begin{aligned}&{\mathbb {P}}_{\nu _{z_1,z_2}}\left( |\sum f^{\ell }_{z_1,z_2,k}(\lambda _i)-(N-2)\int _{|z|<1} f^{\ell }_{z_1,z_2,k}|>N^{-2\delta +{\varepsilon }} \right) \\&\quad \leqslant {\mathbb {P}}_{N-2}\left( |\sum f^{\ell }_{z_1,z_2,k}(\lambda _i)-(N-2)\int _{|z|<1} f^{\ell }_{z_1,z_2,k}|>N^{-2\delta +{\varepsilon }} \right) ^{1/2}N^C\\&\quad {\mathbb {E}}_{N-2}\left( \prod _{i=2}^N|z_1-\lambda _i|^4e^{-2N (|z_1|^2-1)}\prod _{i=2}^N|z_2-\lambda _i|^4e^{-2N(|z_2|^2-1)}\right) ^{1/2} \leqslant N^{-\frac{D}{2}+2C}. \end{aligned}$$

for some C which only depends on $\kappa$, where we used Lemma 2.11. We conclude that for any small ${\varepsilon }>0$ and D we have

$$\begin{aligned} {\mathbb {P}}_{\nu _{z_1,z_2}}\left( |\sum f^{\ell }_{z_1,z_2}(\lambda _i)-{\bar{f}}_{z_1,z_2}|>N^{-2\delta +{\varepsilon }} \right) \leqslant N^{-D}, \end{aligned}$$

so that ${\mathrm{Var}}_{\nu _{z_1,z_2}}(\sum _{i=3}^N f_{z_1,z_2}^\ell (\lambda _i))={{\,\mathrm{O}\,}}(N^{-4\delta +{\varepsilon }})$ and ${\mathbb {E}}_{\nu _{z_1,z_2}}(\sum _{i=3}^N f_{z_1,z_2}^\ell (\lambda _i))=\bar{f}_{z_1,z_2}+{{\,\mathrm{O}\,}}(N^{-2\delta +{\varepsilon }})$. As a consequence, (3.7) becomes

$$\begin{aligned} {\mathbb {E}}_{\nu _{z_1,z_2}}\left( e^{\alpha \left( \sum _{i=3}^Nf^\ell _{z_1,z_2} (\lambda _i)-{\bar{f}}_{z_1,z_2}\right) }\right) \leqslant e^{C\alpha ^2 N^{-4\delta +{\varepsilon }}+C\alpha N^{-2\delta +{\varepsilon }}}. \end{aligned}$$

(3.8)

With $\alpha =c N^{2\delta }$, we obtain

$$\begin{aligned} {\mathbb {P}}_{\nu _{z_1,z_2}}(A)<e^{-c N^{{\varepsilon }}},\ \text{ where }\ A=\left\{ \left| \sum _{i=2}^Nh^\ell _{z_1,z_2}(\lambda _i)-{\bar{f}}_{z_1,z_2} \right| >N^{-2\delta +{\varepsilon }} \right\} . \end{aligned}$$

This yields, for some $p=1+c(\kappa )$, $c(\kappa )>0$ and some $q,r>1$,

$$\begin{aligned}&{\mathbb {E}}_{\nu _{z_1,z_2}}\left( e^{\sum _i(h^s_{z_1,z_2} (\lambda _i)+h^\ell _{z_1,z_2}(\lambda _i))}\mathbb {1}_{A}\right) \nonumber \\&\quad \leqslant {\mathbb {E}}_{\nu _{z_1,z_2}}\left( e^{p\sum _ih^s_{z_1,z_2} (\lambda _i)}\right) ^{1/p} {\mathbb {E}}_{\nu _{z_1,z_2}}\left( e^{q\sum _i h^\ell _{z_1,z_2}(\lambda _i)}\right) ^{1/q} {\mathbb {P}}(A)^{1/r}\leqslant e^{-c N^{\varepsilon }}. \end{aligned}$$

(3.9)

Here we used that the third term has size order $e^{-c N^{{\varepsilon }}}$, the second one is of order $e^{q{\bar{f}}_{z_1,z_2}}={{\,\mathrm{O}\,}}(N^{C})$, and so is the first one from Lemma 3.8 and $|1+\frac{1}{(z_1-\lambda )\overline{(z_2-\lambda )}}|\leqslant (1+\frac{1}{N|z_1-\lambda |^2})(1+\frac{1}{N|z_2-\lambda |^2})$. Moreover,

$$\begin{aligned}&{\mathbb {E}}_{\nu _{z_1,z_2}}\left( e^{\sum _i(h^s_{z_1,z_2} (\lambda _i)+h^\ell _{z_1,z_2}(\lambda _i))}\mathbb {1}_{A^c}\right) \nonumber \\&\quad =(1+{{\,\mathrm{O}\,}}(N^{-2\delta +{\varepsilon }})){\mathbb {E}}_{\nu _{z_1,z_2}} \left( e^{\sum _ih^s_{z_1,z_2}(\lambda _i)+\bar{f}_{z_1,z_2}}\right) \nonumber \\&\qquad -\, (1+{{\,\mathrm{O}\,}}(N^{-2\delta +{\varepsilon }})){\mathbb {E}}_{\nu _{z_1,z_2}} \left( e^{\sum _ih^s_{z_1,z_2}(\lambda _i)+\bar{f}_{z_1,z_2}}\mathbb {1}_{A^c}\right) , \end{aligned}$$

(3.10)

and this last expectation is of order $e^{-c N^{{\varepsilon }}}$ for the same reason as (3.9). To summarize, with the previous two equations we have proved (up to exponentially small additive error terms)

$$\begin{aligned} {\mathbb {E}}_{\nu _{z_1,z_2}}\left( \prod _{i=3}^Nh_{z_1,z_2}(\lambda _i)\right) = (1+{{\,\mathrm{O}\,}}(N^{-2\delta +{\varepsilon }}))e^{{\bar{f}}_{z_1,z_2}}\ {\mathbb {E}}_{\nu _{z_1,z_2}}\left( e^{\sum _ih^s_{z_1,z_2}(\lambda _i)}\right) . \end{aligned}$$

Third step: the local part is invariant. For our test function $h^s_{z_1,z_2}$, the reader can easily check the conditions of Lemma 4.4, so that

$$\begin{aligned} {\mathbb {E}}_{\nu _{z_1,z_2}}\left( e^{\sum _ih_{z_1,z_2}^s (\lambda _i)}\right) ={\mathbb {E}}_{\nu _{0,z_2-z_1}} \left( e^{\sum _ih_{0,z_2-z_1}^s(\lambda _i)}\right) +{{\,\mathrm{O}\,}}\left( e^{-c N^{2\kappa }}\right) . \end{aligned}$$

This yields

$$\begin{aligned}&{\mathbb {E}}_{\nu _{z_1,z_2}}\left( \prod _{i=3}^Nh_{z_1,z_2}(\lambda _i)\right) \\&\quad = (1+{{\,\mathrm{O}\,}}(N^{-2\delta +{\varepsilon }}))e^{{\bar{f}}_{z_1,z_2}-\bar{f}_{0,z_2-z_1}}\ {\mathbb {E}}_{\nu _{0,z_2-z_1}}\left( \prod _{i=3}^Nh_{0,z_2-z_1} (\lambda _i)\right) . \end{aligned}$$

From Lemma 3.4, $e^{{\bar{f}}_{z_1,z_2}-\bar{f}_{0,z_2-z_1}}=(1-z_1\overline{z_2})^{\frac{N-2}{N}}$. Together with Corollary 3.3, this concludes the proof. $\square$

Lemma 3.4

For any $\lambda _1, \lambda _2 \in {\mathbb {D}}$,

$$\begin{aligned} \frac{1}{ \pi } \int _{{\mathbb {D}}} \frac{1}{ ( \lambda _1 - z) (\overline{\lambda _2 - z}) } \mathrm {d}m(z) = \log \Big ({ 1 - \lambda _1 \overline{\lambda _2} \over |\lambda _1-\lambda _2|^2} \Big ). \end{aligned}$$

Proof

We consider the following domains, assuming $0< |\lambda _1|< |\lambda _2| <1$ and $\varepsilon >0$ is small enough. The following computation still holds if $|\lambda _1| = |\lambda _2|$, as long as $\lambda _1 \ne \lambda _2$. Integrability is clear, as the poles are simple and isolated. Moreover, under these conditions, the integral cancels on the disks $D_1$ and $D_2$.

$$\begin{aligned}&\frac{1}{ \pi } \int _{D_0} \frac{1}{ ( \lambda _1 - z) (\overline{\lambda _2 - z})} \mathrm {d}m(z) \nonumber \\&\quad = \frac{1}{ \pi } \iint _{r=0}^{|\lambda _1|- \varepsilon } \frac{1}{ \lambda _1 \overline{\lambda _2}} {r \mathrm {d}r \mathrm {d}\theta \over \left( 1 - {r e^{i \theta } \over \lambda _1}\right) \left( 1- \overline{r e^{i \theta } \over \lambda _2 }\right) } = 2 \int _{r=0}^{|\lambda _1|- \varepsilon } \frac{1}{ \lambda _1 \overline{\lambda _2}} \sum _k \Big ( {r^2 \over \lambda _1 \overline{\lambda _2}} \Big )^k r \mathrm {d}r \nonumber \\&\quad = \int _{r=0}^{|\lambda _1|- \varepsilon } {2 r \over \lambda _1 \overline{\lambda _2}-r^2} \mathrm {d}r = \log (\lambda _1 \overline{\lambda _2}) - \log (\lambda _1 \overline{\lambda _2} - (|\lambda _1|- \varepsilon )^2). \end{aligned}$$

(3.11)

The same type of expansion shows that the integral over $R_2$ vanishes and the contribution from $R_4$ is

$$\begin{aligned} \frac{1}{ \pi } \int _{R_4} \frac{1}{ ( \lambda _1 - z) (\overline{\lambda _2 - z})} \mathrm {d}m(z) = \log (1 - \lambda _1 \overline{\lambda _2}) - \log ((|\lambda _2|+\varepsilon )^2 - \lambda _1 \overline{\lambda _2}). \end{aligned}$$

(3.12)

As the expression is integrable, on the domains $R_1, R_3$ there is no contribution as $\varepsilon \rightarrow 0$. Summing (3.11) and (3.12) gives the result. $\square$

3.3 The quenched off-diagonal overlap: second moments

The main result of this subsection is the following lemma, which gives the expectation of second moments of overlaps conditionally on the eigenvalues positions. For this, we define

$$\begin{aligned} X_n= & {} \left( \begin{array}{c} |B_{n}^{\mathrm{t}} {\bar{D}}_{n}|^2 \\ \Vert B_n\Vert ^2 \Vert D_n\Vert ^2 \end{array} \right) ,\nonumber \\ \gamma _{ij}= & {} \frac{\alpha _{i,j}}{\sqrt{N}},\ A_n = \left( \begin{array}{cc} |1 + \gamma _{1,n} \overline{\gamma _{2,n}} |^2&{}|\gamma _{1,n} \gamma _{2,n}|^2 \\ |\gamma _{1,n} \gamma _{2,n}|^2&{}(1+|\gamma _{1,n}|^2) (1+|\gamma _{2,n}|^2 ) \end{array} \right) . \end{aligned}$$

(3.13)

Lemma 3.5

For any $2\leqslant n\leqslant N-1$ we have

$$\begin{aligned} {\mathbb {E}}\left( X_{n+1} \mid {\mathcal {F}}_{n-1}\right) = A_{n+1} X_{n}. \end{aligned}$$

(3.14)

In particular,

$$\begin{aligned} \left( \begin{array}{c} {\mathbb {E}}_T(|{\mathscr {O}}_{12}|^2\mid {\mathcal {F}}_1)\\ {\mathbb {E}}_T( {\mathscr {O}}_{11}{\mathscr {O}}_{22} \mid {\mathcal {F}}_1) \end{array} \right) = \left( \begin{array}{cc} |b_2|^2&{}0\\ 0&{}1+|b_2|^2\\ \end{array} \right) \left( \prod _{i=3}^n A_i\right) \left( \begin{array}{cc} |b_2|^2&{}0\\ 0&{}1+|b_2|^2\\ \end{array} \right) \left( \begin{array}{c} 1\\ 1 \end{array} \right) . \end{aligned}$$

(3.15)

Proof

We recall the notation (3.1) and the property ${\mathbb {E}}(Z_{n+1}\mid {\mathcal {F}}_{n-1})=1$. A short calculation also gives ${\mathbb {E}}(|Z_{n+1}|^2\mid {\mathcal {F}}_{n-1})=1+\frac{\Vert B_n\Vert ^2\Vert D_n\Vert ^2}{|B_n^{\mathrm{t}} \bar{D}_n|^2}$. Abbreviating $\gamma _k=\gamma _{k,n+1}$, this gives

$$\begin{aligned}&{\mathbb {E}}\left( |B_{n+1}^{\mathrm{t}}{\bar{D}}_{n+1}|^2\mid {\mathcal {F}}_{n-1}\right) \nonumber \\&\quad = {\mathbb {E}}\left( | B_n^{\mathrm{t}} {\bar{D}}_n|^2 | 1+ \gamma _1 \overline{\gamma _2} Z_{n+1}|^2 \mid {\mathcal {F}}_{n-1} \right) \nonumber \\&\quad = |B_n^{\mathrm{t}} {\bar{D}}_n|^2 {\mathbb {E}}\left( 1+ \gamma _1 \overline{\gamma _2} Z_{n+1} + \overline{\gamma _1} {\gamma _2} \overline{Z_{n+1}} + |\gamma _1 {\gamma _2} Z_{n+1}|^2\mid {\mathcal {F}}_{n-1}\right) \nonumber \\&\quad = | 1+ \gamma _1 \overline{\gamma _2}|^2 |B_n^{\mathrm{t}} {\bar{D}}_n|^2 + |\gamma _1 {\gamma _2} |^2 \Vert B_n\Vert ^2 \Vert D_n\Vert ^2. \end{aligned}$$

(3.16)

We now denote $X=X_{n+1}= \sqrt{N} {B_n^{\mathrm{t}}T_n \over \Vert B_n \Vert }$, $Y=Y_{n+1}= \sqrt{N}{D_n^{\mathrm{t}}T_n \over \Vert D_n \Vert }$, so that ${\mathbb {E}}(|X_{n+1}|^2 \mid {\mathcal {F}}_{n-1})={\mathbb {E}}(|Y_{n+1}|^2 \mid {\mathcal {F}}_{n-1})=1$ and ${\mathbb {E}}(|X_{n+1}Y_{n+1}|^2 \mid {\mathcal {F}}_{n-1})=1+\frac{|B_n^{\mathrm{t}} \bar{D}_n|^2}{\Vert B_n\Vert ^2\Vert D_n\Vert ^2}$. This yields

$$\begin{aligned}&{\mathbb {E}}\left( \Vert B_{n+1} \Vert ^2 \Vert D_{n+1} \Vert ^2 \mid {\mathcal {F}}_{n-1}\right) \nonumber \\&\quad = {\mathbb {E}}\left( \Vert B_n\Vert ^2 \Vert D_n\Vert ^2 \big ( 1+ |\gamma _1 X|^2\big ) \big ( 1+ |\gamma _2 Y|^2\big )\mid {\mathcal {F}}_{n-1}\right) \nonumber \\&\quad = \Vert B_n\Vert ^2 \Vert D_n\Vert ^2 {\mathbb {E}}\left( 1+ |\gamma _1 X|^2 + |{\gamma _2}Y|^2 + |\gamma _1 {\gamma _2} XY |^2\mid {\mathcal {F}}_{n-1}\right) \nonumber \\&\quad = \big ( 1+ |\gamma _1|^2 \big ) \big (1 + |\gamma _2|^2 \big ) \Vert B_n\Vert ^2 \Vert D_n\Vert ^2+ |\gamma _1 {\gamma _2} |^2|B_n^{\mathrm{t}} \bar{D}_n|^2. \end{aligned}$$

(3.17)

Equations (3.16) and (3.17) together conclude the proof of (3.14). Denoting $Y_n={\mathbb {E}}_{T}(X_n\mid {\mathcal {F}}_1)$, we obtain

$$\begin{aligned} Y_n=\left( \prod _{i=3}^n A_i\right) Y_2=\left( \prod _{i=3}^n A_i\right) {\mathbb {E}}\left( \left( \begin{array}{c} |B_2^{\mathrm{t}} {\bar{D}}_2|^2\\ \Vert B_2\Vert ^2\Vert D_2\Vert ^2 \end{array} \right) \mid {\mathcal {F}}_1\right) = \left( \prod _{i=3}^n A_i\right) \left( \begin{array}{c} |b_2|^2\\ 1+|b_2|^2 \end{array} \right) \end{aligned}$$

and (3.15) immediately follows. $\square$

3.4 The annealed off-diagonal overlap: second moments for $\lambda _1=0$

We now want to integrate (3.15) over the eigenvalues $\lambda _3,\dots ,\lambda _N$, first in the special case $\lambda _1=0$. This requires some new notations. We abbreviate

$$\begin{aligned} \delta = N | \lambda _{1} - \lambda _{2} |^2, \ \ a= \frac{\delta }{2} + \sqrt{1 + \frac{\delta ^2}{4}},\ \ b=-a^{-1}=\frac{\delta }{2} - \sqrt{1 + \frac{\delta ^2}{4}} \end{aligned}$$

and will often use the property

$$\begin{aligned} \delta = a-\frac{1}{a}=b-\frac{1}{b}. \end{aligned}$$

(3.18)

We also define the following rational fractions of x

$$\begin{aligned} u_k(x)&=1- {1-x^{-1} \over k+3}, \nonumber \\ d_k(x,\delta )&= \frac{ (k+2) (k+3)}{e_1^{(k+1)}(\delta )} \nonumber \\&\quad \left( u_k(x) \frac{1}{(x-1)^2}e_3^{(k)}(\delta )-\frac{\delta u_k(x)}{2 x}\nonumber \right. \\&\qquad \left. +\, \frac{1}{(x-1)^2}\frac{x^2+(k+2)x+ (k+1)(k+3)}{(k+3)!}\delta ^{k+1} \right) . \end{aligned}$$

(3.19)

We can now state the following main proposition on which Theorem 1.4 depends. The reason why such formulas exist relies on two algebraic facts.

• (i) The $A_n$’s from (3.13) are diagonalizable in the same basis, see (3.20). Their commutation was expected, our choice of eigenvalues ordering being arbitrary, while the left hand side of (3.15) is intrinsic.

• (ii) More surprisingly, the obtained holonomic sequence (3.23) is exactly solvable.

Proposition 3.6

Conditionally on $\{\lambda _1=0,\lambda _2=z\}$, we have

$$\begin{aligned} {\mathbb {E}}(|{\mathscr {O}}_{12}|^2)&=\frac{1}{1+a^2}\left( \frac{a^2}{(a+1)^2}d_{N-2}(a,\delta )+\frac{a^2}{(a-1)^2}d_{N-2}(b,\delta )\right) ,\\ {\mathbb {E}}({\mathscr {O}}_{11}{\mathscr {O}}_{22})&=\frac{1}{1+a^2} \left( \frac{1}{(a+1)^2}d_{N-2}(a,\delta )+\frac{a^4}{(a-1)^2}d_{N-2}(b,\delta )\right) . \end{aligned}$$

Proof

Importantly, the matrices $A_n, 3\leqslant n\leqslant N$, can be diagonalized in the same basis: from (3.13) an elementary calculation based on (2.1) gives

$$\begin{aligned} A_n = (1+|\gamma _{1,n}|^2) (1+|\gamma _{2,n}|^2 ) \mathrm{I}_2 + |\gamma _{1,n} \gamma _{2,n}|^2 \left( \begin{array}{cc} - N | \lambda _{1} - \lambda _{2} |^2 &{} 1 \\ 1 &{} 0 \end{array} \right) , \end{aligned}$$

(3.20)

so that its eigenvectors clearly do not depend on n. With these notations, the eigenvalues of $A_n$ are

$$\begin{aligned} \lambda _+(n)&=(1+|\gamma _{1,n}|^2) (1+|\gamma _{2,n}|^2 ) - |\gamma _{1,n} \gamma _{2,n}|^2 a \\ \lambda _-(n)&= (1+|\gamma _{1,n}|^2) (1+|\gamma _{2,n}|^2 ) - |\gamma _{1,n} \gamma _{2,n}|^2 b, \end{aligned}$$

and the orthogonal basis

$$\begin{aligned} U=\frac{1}{\sqrt{1+a^2}} \left( \begin{array}{cc} a &{} -1 \\ 1 &{} a \end{array} \right) \end{aligned}$$

diagonalizes all $A_n$’s simultaneously: $UA_nU^{t}={{\,\mathrm{diag}\,}}(\lambda _+(n),\lambda _-(n))$. Then (3.15), together with the codiagonalization of the $A_n$’s, ${\mathbb {E}}|T|^2=1$ and ${\mathbb {E}}(|T|^4)=2$, yields the following simple expression:

$$\begin{aligned}&\left( \begin{array}{c} {\mathbb {E}}_T(|{\mathscr {O}}_{12}|^2)\\ {\mathbb {E}}_T({\mathscr {O}}_{11}{\mathscr {O}}_{22}) \end{array} \right) = \frac{1}{1+a^2} \left( \begin{array}{c} \frac{a^2}{(a+1)^2}d_++\frac{a^2}{(a-1)^2}d_-\\ \frac{1}{(a+1)^2}d_++\frac{a^4}{(a-1)^2}d_- \end{array} \right) , \end{aligned}$$

(3.21)

$$\begin{aligned}&d_+=\prod _{n=3}^N\lambda _+(n),\ d_-=\prod _{i=3}^N\lambda _-(n). \end{aligned}$$

(3.22)

Note that we have not yet used $z_1=0$: the above formula holds for any given $z_1,z_2$.

The remarkable fact is that in the specific case $z_1=0$, ${\mathbb {E}}(d_+)$ and ${\mathbb {E}}(d_-)$ can be calculated, as shown below (here ${\mathbb {E}}$ denotes integration over all variables except $\lambda _1,\lambda _2$). We start with ${\mathbb {E}}(d_+)$. From Theorem 5.4, the following representation holds:

$$\begin{aligned} {\mathbb {E}}\left( \prod _{n=3}^{N} \lambda _{+}(n) \mid \lambda _1=0, \lambda _2=z\right) = \frac{ \det (f_{i,j})_{1\leqslant i,j\leqslant N-2} }{Z_N^{(0,z)}} \end{aligned}$$

where $Z_N^{(0,z)}$ is given by (5.2) and

$$\begin{aligned} f_{i,j}&= \frac{1}{ {( i+1)}! } \int \lambda ^{i-1} {\bar{\lambda }}^{j-1} |\lambda |^2 |z-\lambda |^2 \lambda _+(\lambda ) \mu ( \mathrm {d}\lambda )\\&= \frac{1}{ {( i+1)}! } \\&\quad \int \lambda ^{i-1} {\bar{\lambda }}^{j-1}( |\lambda |^2 |z-\lambda |^2 +N^{-1} |\lambda |^2 + N^{-1}|z-\lambda |^2 -N^{-2}(a-1)) \mu ( \mathrm {d}\lambda ). \end{aligned}$$

We expand $|\lambda -z|^2 = |\lambda |^2 + |z|^2 - {\bar{z}} \lambda - z {\bar{\lambda }}$. The resulting matrix is thus tridiagonal with

$$\begin{aligned} f_{i,i-1}&= {-z }\frac{1}{iN^i},\\ f_{i,i}&= \frac{1}{N^{i+1}}+\frac{2N^{-1}+|z|^2}{(i+1)N^i} +\frac{N^{-1}|z|^2-N^{-2}(a-1)}{i(i+1)N^{i-1}},\\ f_{i,i+1}&= -{\bar{z}}\frac{i+2}{(i+1)N^{i+1}}. \end{aligned}$$

With the notation $d_k=\det (f_{ij})_{1\leqslant i,j\leqslant k}$, the recurrence $d_{k} = f_{k,k} d_{k-1} - f_{k,k-1} f_{k-1,k} d_{k-2}$ holds, so that defining $a_k=d_k N^{\frac{k(k+3)}{2}}$ we have

$$\begin{aligned} a_k=\left( 1+\frac{2+\delta }{k+1}+\frac{1-a^{-1}}{k(k+1)}\right) a_{k-1} - \delta \frac{k+1}{k^2} a_{k-2}, \end{aligned}$$

with the convention $a_0=1$ and $a_1=2+\frac{\delta }{2}+\frac{1-a^{-1}}{2}.$ Note that for $z=0$ we have $\delta =0$ and $a=1$, hence

$$\begin{aligned} a_{k}^{0}:= a_k (z=0) = 2\prod _{j=2}^{k}\left( 1+\frac{2}{j+1}\right) =\frac{(k+2)(k+3)}{6}. \end{aligned}$$

As a consequence, $g_k = {a_k \over a_{k}^{0} }$ satisfies $g_0=1$, $g_1=1+\frac{\delta }{4}+\frac{1-a^{-1}}{4}$, and

$$\begin{aligned} g_{k}&=m_1(k,a) g_{k-1} -m_2(k,a) g_{k-2},\nonumber \\ m_1(k,a)&=1+\frac{\delta }{k+3}+\frac{1-a^{-1}}{k(k+3)},\nonumber \\ m_2(k,a)&=\delta \frac{(k+1)^2}{k(k+2)(k+3)}. \end{aligned}$$

(3.23)

We cannot see an a priori reason why this equation could be solved, but it can be. We remark that the function $u_k=u_k(a)$ from (3.19) also satisfies the induction

$$\begin{aligned} u_{k}=m_1(k,a) u_{k-1} -m_2(k,a) u_{k-2}. \end{aligned}$$

(3.24)

The reader who would like to check the above equation can substitute $\delta =a-\frac{1}{a}$ and verify that the Laurent series in a on both sides of (3.24) coincide. This equation implies

$$\begin{aligned} g_{k-1} { u_{k} \over u_{k-1}} = m_1(k,a) g_{k-1} - m_2 (k,a) g_{k-1} { u_{k-2} \over u_{k-1}} \end{aligned}$$

(3.25)

Subtracting (3.25) from (3.23) gives

$$\begin{aligned} \delta _{k}:= g_{k}- g_{k-1} { u_{k}\over u_{k-1}} = - m_2 (k,a) \Big ( g_{k-2} - g_{k-1} { u_{k-2} \over u_{k-1}} \Big ) = m_2(k,a) { u_{k-2} \over u_{k-1}} \delta _{k-1}, \end{aligned}$$

which yields

$$\begin{aligned} \delta _k = \left( \prod _{j=2}^{k} m_2(j,a) { u_{j-2}\over u_{j-1}}\right) \delta _{1}=36 \frac{1}{ (k+3)!} {k+1 \over k+2} \delta ^{k-1} {u_0 \over u_{k-1}} \delta _{1}. \end{aligned}$$

(3.26)

Together with ${g_k \over u_k} = {g_{k-1} \over u_{k-1}}+ {\delta _k \over u_k}$, from (3.26) we obtain

$$\begin{aligned} {g_k \over u_k}=36\sum _{j=1}^k \frac{1}{ (j+3)!} {j+1 \over j+2} \delta ^{j-1} {u_0 \over u_{j-1}u_j} \delta _{1}+\frac{g_0}{u_0}. \end{aligned}$$

A calculation gives $u_0\delta _1=\frac{1}{6}(a-a^{-1})(1+a^{-1})$, so that

$$\begin{aligned} {g_k \over u_k}=6(1+a^{-1})\sum _{j=1}^k \frac{1}{ (j+3)!} {j+1 \over j+2} \delta ^{j} \frac{1}{ u_{j-1}u_j}+\frac{1}{u_0}. \end{aligned}$$

(3.27)

Note that

$$\begin{aligned} \frac{1}{u_{j-1}u_j}=\frac{(j+2)(j+3)}{1-a^{-1}} \left( \frac{1}{u_{j-1}}-\frac{1}{u_j}\right) , \end{aligned}$$

which simplifies (3.27) into

$$\begin{aligned} {g_k \over u_k}&=6\frac{1+a^{-1}}{1-a^{-1}}\sum _{j=1}^k \frac{1}{ j!(j+2)}\left( \frac{1}{u_{j-1}}-\frac{1}{u_j}\right) \delta ^{j}+\frac{1}{u_0}\\&=6\frac{1+a^{-1}}{1-a^{-1}}\left( \sum _{j=1}^{k-1}\frac{1}{u_j}\left( \frac{\delta }{(j+1)!(j+3)} -\frac{1}{j!(j+2)}\right) \delta ^{j} -\frac{1}{k!(k+2)}\frac{\delta ^k}{u_k}+\frac{\delta }{3u_0} \right) +\frac{1}{u_0}\\&=6\frac{a+1}{a-1}\left( \sum _{j=1}^{k-1} \left( \frac{a}{(j+2)!}-\frac{1}{(j+1)!}\right) \delta ^{j} -\frac{1}{k!(k+2)}\frac{\delta ^k}{u_k}+\frac{\delta }{3u_0} \right) +\frac{1}{u_0}\\&= 6\frac{a+1}{a-1}\left( \frac{1}{a\delta ^2}\sum _{j=3}^k\frac{\delta ^j}{j!}+ \frac{a\delta ^{k-1}}{(k+1)!}-\frac{\delta }{2} -\frac{1}{k!(k+2)}\frac{\delta ^k}{u_k}+\frac{\delta }{3u_0} \right) +\frac{1}{u_0} \end{aligned}$$

where we used $\delta =a-a^{-1}$ and (3.19) at several steps. The above formula can be written in terms of (1.18) and further simplified as

$$\begin{aligned} g_k=6u_k\frac{a+1}{a-1}\frac{1}{a\delta ^2}e_3^{(k)}(\delta )-\frac{3u_k}{a} + 6\frac{a+1}{a-1} \frac{a+(k+2)+a^{-1}(k+1)(k+3)}{(k+3)!}\delta ^{k-1}. \end{aligned}$$

By definition of $g_k$, $a_k = g_k a_{k}^{0}$, that is

$$\begin{aligned} a_k= & {} u_k\frac{1}{(a-1)^2 \delta } (k+2) (k+3)e_3^{(k)}(\delta )-\frac{u_k}{2a} (k+2) (k+3) \\&+ \frac{a+1}{a-1} \frac{a+(k+2)+a^{-1}(k+1)(k+3)}{(k+1)!}\delta ^{k-1}. \end{aligned}$$

Then, using the normalizing constant (5.2), we obtain

$$\begin{aligned} {\mathbb {E}}(d_+)= \frac{d_{N-2}}{Z_N^{(0,z)}} = \frac{a_{N-2}}{Z_N^{(0,z)} N^{\frac{(N-2) (N+1)}{2}}} = \frac{ \delta a_{N-2} }{ e_{1}^{(N-1)} (\delta )} \end{aligned}$$

as $\delta =N|z|^2$. We find

$$\begin{aligned}&{\mathbb {E}}(d_+) = \frac{ N (N+1)}{e_1^{(N-1)}(\delta )} \nonumber \\&\quad \left( \frac{u_{N-2}(a)}{(a-1)^2} e_3^{(N-2)}(\delta )-\frac{ \delta u_{N-2}(a)}{2 a} \right. \nonumber \\&\left. +\, \frac{1}{(a-1)^2}\frac{ a^2+ Na + (N-1)(N+1)}{(N+1)!}\delta ^{N-1} \right) \end{aligned}$$

(3.28)

which has been defined as $d_{N-2}(a, \delta )$. The formula for ${\mathbb {E}}(d_-)$ is obtained in the exact same way, with the only difference that a is replaced by b. Finally, conditionally on $\{\lambda _1=0,\lambda _2=z\}$, (3.21) gives

$$\begin{aligned} \left( \begin{array}{c} {\mathbb {E}}(|{\mathscr {O}}_{12}|^2)\\ {\mathbb {E}}({\mathscr {O}}_{11}{\mathscr {O}}_{22}) \end{array} \right) = \frac{1}{1+a^2} \left( \begin{array}{c} \frac{a^2}{(a+1)^2}{\mathbb {E}}(d_+) + \frac{a^2}{(a-1)^2} {\mathbb {E}}(d_-)\\ \frac{1}{(a+1)^2}{\mathbb {E}}(d_+) + \frac{a^4}{(a-1)^2} {\mathbb {E}}(d_-) \end{array} \right) . \end{aligned}$$

We can replace ${\mathbb {E}}(d_+)$ and ${\mathbb {E}}(d_-)$ by their exact expressions to obtain the claimed formula. $\square$

Proposition 3.7

Let $\sigma \in (0,1/2)$. Denoting $\omega =\sqrt{N}|z|$, uniformly in $|z|\in [0,N^{-\frac{1}{2}+\sigma }]$ we have

$$\begin{aligned} {\mathbb {E}}\left( |{\mathscr {O}}_{12}|^2\mid \lambda _1=0,\lambda _2=z\right)&= \frac{N^2}{|\omega |^4}\left( 1+{{\,\mathrm{O}\,}}(N^{2\sigma -1})\right) , \end{aligned}$$

(3.29)

$$\begin{aligned} {\mathbb {E}}\left( {\mathscr {O}}_{11}{\mathscr {O}}_{22}\mid \lambda _1=0,\lambda _2=z\right)&= \frac{N^2}{|\omega |^4}\frac{1+|\omega |^4- e^{-|\omega |^2}}{1-e^{-|\omega |^2}}\left( 1+{{\,\mathrm{O}\,}}(N^{2\sigma -1})\right) . \end{aligned}$$

(3.30)

Proof

We consider asymptotics in Proposition 3.6. First, the term $\frac{\delta ^{N-1}}{(N+1)!}$ is obviously negligible. Second, we always have $a\geqslant 1$ and $|b|\geqslant c/\delta \geqslant N^{-2\sigma }$, so that $u_{N-2}(a)= 1 + {{\,\mathrm{O}\,}}(N^{-1})$, $u_{N-2}(b) = 1 + {{\,\mathrm{O}\,}}(N^{2\sigma -1})$. Moreover,

$$\begin{aligned} e_1^{(N-1)}(\delta )= & {} (e^{\delta } -1) \left( 1 + {{\,\mathrm{O}\,}}(N^{-1})\right) ,\\ e_3^{(N-2)}(\delta )= & {} \left( e^{\delta } -1- \delta - \frac{\delta ^2}{2}\right) \left( 1 + {{\,\mathrm{O}\,}}(N^{-1})\right) . \end{aligned}$$

From (3.18), we have $\frac{a^2}{(1+a)^2 (1-a)^2} = \frac{b^2}{(1+b)^2 (1-b)^2} = \frac{1}{\delta ^2},$ so that (3.28) and its analogue for $d_-$ give

$$\begin{aligned} \frac{a^2}{(a+1)^2}{\mathbb {E}}(d_+)&= \frac{ N^2 }{ \delta ^2 (e^{\delta } -1)} \left( e^{\delta } -1- \delta - \frac{\delta ^2}{2} - \frac{ \delta (a-1)^2}{2a} \right) \nonumber \\&\quad \left( 1 + {{\,\mathrm{O}\,}}(N^{-1})\right) , \end{aligned}$$

(3.31)

$$\begin{aligned} \frac{a^2}{(a-1)^2}{\mathbb {E}}(d_-)&= \frac{ N^2 }{\delta ^2 (e^{\delta } -1)} \left( a^2\left( e^{\delta } -1- \delta - \frac{\delta ^2}{2}\right) + \frac{\delta a}{2}(a+1)^2 \right) \nonumber \\&\quad \left( 1 + {{\,\mathrm{O}\,}}(N^{2\sigma -1})\right) . \end{aligned}$$

(3.32)

We observe that

$$\begin{aligned} \frac{1}{a^2+1}\left( - \frac{ \delta (a-1)^2}{2a} + \frac{\delta a}{2}(a+1)^2 \right) =\delta +\frac{\delta ^2}{2}, \end{aligned}$$

and the previous three equations give

$$\begin{aligned}&{\mathbb {E}}(|{\mathscr {O}}_{12}|^2\mid \lambda _1=0,\lambda _2=x) = \frac{1}{1+a^2} \left( \frac{a^2}{(a+1)^2}{\mathbb {E}}(d_+) + \frac{a^2}{(a-1)^2} {\mathbb {E}}(d_-) \right) \\&\quad = \frac{ N^2 }{ \delta ^2 (e^{\delta } -1)} \left( e^{\delta } -1- \delta - \frac{\delta ^2}{2} + \delta + \frac{\delta ^2}{2} \right) \left( 1 + {{\,\mathrm{O}\,}}(N^{2\sigma -1})\right) \\&\quad = \frac{ N^2 }{ |\omega |^4} \left( 1 + {{\,\mathrm{O}\,}}(N^{2\sigma -1})\right) . \end{aligned}$$

The similar computation for ${\mathbb {E}}({\mathscr {O}}_{11} {\mathscr {O}}_{22}\mid \lambda _1=0,\lambda _2=z)$ involves the two terms

$$\begin{aligned}&\frac{1}{(a+1)^2}{\mathbb {E}}(d_+) = \frac{ N^2 }{ e^{\delta } -1} \\&\quad \left( \frac{1}{(a-1)^2 (a+1)^2} \left( e^{\delta } -1- \delta - \frac{\delta ^2}{2} \right) - \frac{ \delta }{2 a (a+1)^2} \right) \left( 1 + {{\,\mathrm{O}\,}}(N^{-1})\right) , \\&\frac{a^4}{(a-1)^2}{\mathbb {E}}(d_-) = \frac{ N^2 }{ e^{\delta } -1} \\&\quad \left( \frac{a^6}{(a-1)^2 (a+1)^2} \left( e^{\delta } -1- \delta - \frac{\delta ^2}{2} \right) + \frac{ \delta a^5 }{2 (a-1)^2} \right) \left( 1 + {{\,\mathrm{O}\,}}(N^{2\sigma -1})\right) . \end{aligned}$$

Moreover, some algebra gives

$$\begin{aligned}&\frac{1}{1+a^2} \left( \frac{1}{(a-1)^2 (a+1)^2} + \frac{a^6}{(a-1)^2 (a+1)^2} \right) = \frac{1 + \delta ^2}{\delta ^2},\\&\frac{1}{1+a^2} \left( \frac{ \delta a^5 }{2 (a-1)^2} - \frac{ \delta }{2 a (a+1)^2} \right) = \frac{ (\delta +1)( \delta ^2 + \delta +2) }{ 2 \delta }. \end{aligned}$$

Once combined, these four equations yield

$$\begin{aligned}&{\mathbb {E}}\left( {\mathscr {O}}_{11}{\mathscr {O}}_{22}\mid \lambda _1=0,\lambda _2=z\right) \\&\quad = \frac{1}{1+a^2} \left( \frac{1}{(a+1)^2}{\mathbb {E}}(d_+) + \frac{a^4}{(a-1)^2} {\mathbb {E}}(d_-) \right) \\&\quad = \frac{ N^2 }{ e^{\delta } -1} \left( \frac{1 + \delta ^2}{\delta ^2} \left( e^{\delta } -1- \delta - \frac{\delta ^2}{2} \right) + \frac{ (\delta +1)( \delta ^2 + \delta +2) }{ 2 \delta } \right) \left( 1 + {{\,\mathrm{O}\,}}(N^{2 \sigma -1})\right) \\&\quad = \frac{ N^2 }{ |\omega |^4} \frac{1+ |\omega |^4 - e^{- |\omega |^2}}{1-e^{-|\omega |^2} } \left( 1 +{{\,\mathrm{O}\,}}(N^{2\sigma -1})\right) , \end{aligned}$$

which concludes the proof. $\square$

3.5 The annealed off-diagonal overlap: second moments in the general case

We can now prove Theorem 1.4. We closely follow the method developed first in our alternative proof of Theorem 2.6, in Sect. 2.3, then in our proof of Theorem 1.3 in Sect. 3.2. In particular, following the proof of Theorem 1.3, we denote $\nu _{z_1,z_2}$ the measure (1.2) conditioned to $\lambda _1=z_1,\lambda _2=z_2$.

Proof of Theorem 1.4

Remember the notation (3.22). Assume we can prove (under the hypothesis of Theorem 1.4) that

$$\begin{aligned} {\mathbb {E}}_{\nu _{z_1,z_2}}(d_+)&=(1-|z_1|^2)(1-|z_2|^2) {\mathbb {E}}_{\nu _{0,z_2-z_1}}(d_+)\left( 1+{{\,\mathrm{O}\,}}(N^{-2\kappa +{\varepsilon }})\right) , \end{aligned}$$

(3.33)

$$\begin{aligned} {\mathbb {E}}_{\nu _{z_1,z_2}}(d_-)&=(1-|z_1|^2)(1-|z_2|^2) {\mathbb {E}}_{\nu _{0,z_2-z_1}}(d_-)\left( 1+{{\,\mathrm{O}\,}}(N^{-2\kappa +{\varepsilon }})\right) . \end{aligned}$$

(3.34)

From (3.31) and (3.32), a calculation gives ${\mathbb {E}}_{\nu _{0,z_2-z_1}}(d_+)>0$, ${\mathbb {E}}_{\nu _{0,z_2-z_1}}(d_-)>0$, so that (3.33), (3.34) together with (3.21) give

$$\begin{aligned} \left( \begin{array}{c} {\mathbb {E}}_{\nu _{z_1,z_2}}(|{\mathscr {O}}_{12}|^2)\\ {\mathbb {E}}_{\nu _{z_1,z_2}}({\mathscr {O}}_{11}{\mathscr {O}}_{22}) \end{array} \right) =(1-|z_1|^2)(1-|z_2|^2) \left( \begin{array}{c} {\mathbb {E}}_{\nu _{0,z_2-z_1}}(|{\mathscr {O}}_{12}|^2)\\ {\mathbb {E}}_{\nu _{0,z_2-z_1}}({\mathscr {O}}_{11}{\mathscr {O}}_{22}) \end{array} \right) \left( 1+{{\,\mathrm{O}\,}}(N^{-2\kappa +{\varepsilon }})\right) . \end{aligned}$$

Together with Proposition 3.7, this concludes the proof. We therefore only need to show (3.33). The proof for (3.34) is identical up to trivial adjustments.

First step: small cutoff  Our test function of interest and its short-range cut version are

$$\begin{aligned} g_{z_1,z_2}(\lambda )&=\left( 1+\frac{1}{N|z_1-\lambda |^2} \right) \left( 1+\frac{1}{N|z_2-\lambda |^2}\right) \nonumber \\&\quad -\frac{a}{N^2}\frac{1}{|z_1-\lambda |^2|z_2-\lambda |^2} \end{aligned}$$

(3.35)

$$\begin{aligned} h_{z_1,z_2}(\lambda )&=\left( 1+\frac{1}{N|z_1-\lambda |^2} \mathbb {1}_{\lambda \not \in {\mathscr {B}}}\right) \left( 1+\frac{1}{N|z_2 -\lambda |^2}\mathbb {1}_{\lambda \not \in {\mathscr {B}}}\right) \nonumber \\&\quad -\frac{a}{N^2}\frac{1}{|z_1-\lambda |^2|z_2-\lambda |^2} \mathbb {1}_{\lambda \not \in {\mathscr {B}}} \end{aligned}$$

(3.36)

where ${\mathscr {B}}=\{|\lambda -z_1|<N^{-A}\}\cup \{|\lambda -z_2|<N^{-A}\}$. We first prove (3.3) for our new definition of $g_{z_1,z_2},\, h_{z_1,z_2}$. It follows from

$$\begin{aligned}&{\mathbb {E}}_{N-2}\left( \prod _{i=3}^N\left( \left( |z_1-\lambda _i|^2 +\frac{1}{N}\right) \left( |z_2-\lambda _i|^2 +\frac{1}{N}\right) -\frac{a}{N^2}\right) e^{-N(|z_1|^2-1)-N(|z_2|^2-1)}\right) \end{aligned}$$

(3.37)

$$\begin{aligned}&- {\mathbb {E}}_{N-2}\left( \prod _{i=3}^N\left( \left( |z_1-\lambda _i|^2 +\frac{\mathbb {1}_{\lambda _i\not \in {\mathscr {B}}}}{N}\right) \left( |z_2-\lambda _i|^2 +\frac{\mathbb {1}_{\lambda _i\not \in {\mathscr {B}}}}{N}\right) \right. \right. \nonumber \\&\qquad \qquad \qquad \left. \left. -\,\frac{a}{N^2} \mathbb {1}_{\lambda _i\not \in {\mathscr {B}}}\right) e^{-N(|z_1|^2-1)-N(|z_2|^2-1)}\right) ={{\,\mathrm{O}\,}}(N^{-A/2+C}), \end{aligned}$$

(3.38)

and (3.5), for some C which does not depend on A. Equation (3.38) holds as the left hand side is bounded by

$$\begin{aligned}&{\mathbb {E}}_{N-2} \left( \prod _{i=3}^N\left( \left( |z_1-\lambda _i|^2 +\frac{1}{N}\right) \right) \left( |z_2-\lambda _i|^2 +\frac{1}{N}\right) \right. \nonumber \\&\qquad \qquad \qquad \left. \left( 1-\prod _3^N\mathbb {1}_{\lambda _i\not \in {\mathscr {B}}}\right) e^{-N(|z_1|^2-1)-N(|z_2|^2-1)}\right) \nonumber \\&\quad ={{\,\mathrm{O}\,}}(N^{-A/2}){\mathbb {E}}_{N-2}\left( \prod _{i=3}^N\left( \left( |z_1-\lambda _i|^2 +\frac{1}{N}\right) ^2\right. \right. \nonumber \\&\qquad \qquad \left. \left. \left( |z_2 -\lambda _i|^2 +\frac{1}{N}\right) \right) ^2e^{-2N(|z_1|^2-1) -2N(|z_2|^2-1)}\right) ^{1/2}, \end{aligned}$$

(3.39)

where we used the Cauchy–Schwarz inequality and

$$\begin{aligned}&\left| \left( |z_1-\lambda _i|^2 +\frac{1}{N}\right) \left( |z_2-\lambda _i|^2 +\frac{1}{N}\right) -\frac{a}{N^2}\right| \\&\quad \leqslant \left( |z_1-\lambda _i|^2 +\frac{1}{N}\right) \left( |z_2-\lambda _i|^2 +\frac{1}{N}\right) . \end{aligned}$$

Indeed, after rescaling and shifting and introducing z so that $|z|^2=\delta$, the above bound follows from

$$\begin{aligned}&2(1+|\lambda |^2)(1+|z-\lambda |^2)-a\\&\quad = ((1+|\lambda |^2)(1+|z-\lambda |^2)-\delta )\\&\qquad +\,(1+|\lambda |^2)(1+|z-\lambda |^2)\\&\qquad +\,(\delta -a)\geqslant 1+\delta -a=1-\frac{1}{a}\geqslant 0. \end{aligned}$$

We used $(1+|\lambda |^2)(1+|z-\lambda |^2)\geqslant \delta$, as proved by a simple optimization. The last expectation in (3.39) has size order at most $N^{C}$ from Lemma 2.11, which concludes the proof of our initial short-range cutoff by choosing A large enough.

Second step: the long-range contribution concentrates We smoothly separate the short-range from a long-range contributions in (3.36):

$$\begin{aligned} h_{z_1,z_2}(\lambda )&=e^{h_{z_1,z_2}^{s}(\lambda ) +h_{z_1,z_2}^{\ell }(\lambda )},\\ h_{z_1,z_2}^{s}(\lambda )&= (\log h_{z_1,z_2}(\lambda )) \chi _{z,\delta } (\lambda ),\\ h_{z_1,z_2}^{\ell }(\lambda )&= (\log h_{z_1,z_2}(\lambda )) (1 - \chi _{z,\delta } (\lambda )), \end{aligned}$$

and, as earlier in this article, we denote $z=(z_1+z_2)/2$, recall $|z_1-z_2|<N^{-\frac{1}{2}+\sigma }$, $\chi _{z,\delta } (\lambda )= \chi \Big (N^{\frac{1}{2}-\delta }|z-\lambda | \Big )$, and choose $\delta \in (\sigma , \kappa )$. Note that our notation $\delta$ in this step of the proof is unrelated to $\delta = N | \lambda _{1} - \lambda _{2} |^2$ in the previous step. We define $f^{\ell }_{z_1,z_2}(\lambda )= (\frac{1}{N |z_1 - \lambda |^2}+\frac{1}{N |z_1 - \lambda |^2})(1 - \chi _{z,\delta } (\lambda ))$ and ${\bar{f}}_{z_1,z_2}=(N-2)\frac{1}{ \pi } \int _{{\mathbb {D}}} f^{\ell }_{z_1,z_2}(\lambda ) \mathrm {d}m(\lambda )$. Note that

$$\begin{aligned}&\left| \sum _{i=3}^Nh^\ell _{z_1,z_2}(\lambda _i)-\bar{f}_{z_1,z_2}\right| \leqslant \left| \sum _{i=3}^Nf^\ell _{z_1,z_2}(\lambda _i)-\bar{f}_{z_1,z_2}\right| \\&\quad +\left( \sum _{i=3}^N\frac{N^{2\sigma }}{N^2|z_1-\lambda _i|^4}(1 - \chi _{z,\delta } (\lambda _i)) + \sum _{i=3}^N\frac{N^{2\sigma }}{N^2|z_2-\lambda _i|^4}(1 - \chi _{z,\delta } (\lambda _i)) \right) , \end{aligned}$$

where we used $a\leqslant N^{2\sigma }$.

With the exact same reasoning as from (2.20) to (2.21) (with $\nu _z$ replaced by $\nu _{z_1,z_2}$), we obtain that $\sum _{i=3}^Nf^\ell _{z_1,z_2}(\lambda _i)-\bar{f}_{z_1,z_2}$ is exponentially concentrated on scale $N^{-2\delta +{\varepsilon }}$. Moreover, similarly, to (2.22), we now have

$$\begin{aligned} {\mathbb {E}}_{\nu _{z_1,z_2}}\left( e^{\alpha \sum _{i=2}^N\frac{N^{2\sigma }}{N^2|z_1-\lambda _i|^4}(1-\chi _{z,\delta }(\lambda _i))}\right) \leqslant e^{C\alpha ^2 N^{4\sigma -8\delta +{\varepsilon }}+C\alpha N^{2\sigma -2\delta +{\varepsilon }}}. \end{aligned}$$

With $\alpha =c N^{2\delta }$, we therefore obtain

$$\begin{aligned} {\mathbb {P}}_{\nu _{z_1,z_2}}(A)<e^{-c N^{{\varepsilon }}},\ \text{ where }\ A=\left\{ \left| \sum _{i=2}^Nh^\ell _{z_1,z_2}(\lambda _i)-\bar{f}_{z_1,z_2} \right| >N^{2\sigma -2\delta +{\varepsilon }} \right\} . \end{aligned}$$

This yields, for some $p=1+c(\kappa )$, $c(\kappa )>0$ and some $q,r>1$,

$$\begin{aligned}&{\mathbb {E}}_{\nu _{z_1,z_2}}\left( e^{\sum _i(h^s_{z_1,z_2} (\lambda _i)+h^\ell _{z_1,z_2}(\lambda _i))}\mathbb {1}_{A}\right) \nonumber \\&\quad \leqslant {\mathbb {E}}_{\nu _{z_1,z_2}}\left( e^{p\sum _ih^s_{z_1,z_2} (\lambda _i)}\right) ^{1/p} {\mathbb {E}}_{\nu _{z_1,z_2}}\left( e^{q\sum _i h^\ell _{z_1,z_2}(\lambda _i)}\right) ^{1/q} {\mathbb {P}}(A)^{1/r}\leqslant e^{-c N^{\varepsilon }}.\nonumber \\ \end{aligned}$$

(3.40)

Here we used that the third term has size order $e^{-c N^{{\varepsilon }}}$, the second one is of order $e^{q{\bar{f}}_{z_1,z_2}}={{\,\mathrm{O}\,}}(N^{C})$, and so is the first one from Lemma 3.8. Moreover,

$$\begin{aligned}&{\mathbb {E}}_{\nu _{z_1,z_2}}\left( e^{\sum _i(h^s_{z_1,z_2} (\lambda _i)+h^\ell _{z_1,z_2}(\lambda _i))}\mathbb {1}_{A^c}\right) \\&\quad = (1+{{\,\mathrm{O}\,}}(N^{2\sigma -2\delta +{\varepsilon }})){\mathbb {E}}_{\nu _{z_1,z_2}} \left( e^{\sum _ih^s_{z_1,z_2}(\lambda _i)+{\bar{f}}_{z_1,z_2}}\right) \\&\qquad -\,(1+{{\,\mathrm{O}\,}}(N^{2\sigma -2\delta +{\varepsilon }})){\mathbb {E}}_{\nu _{z_1,z_2}} \left( e^{\sum _ih^s_{z_1,z_2}(\lambda _i)+\bar{f}_{z_1,z_2}}\mathbb {1}_{A^c}\right) , \end{aligned}$$

Following similar arguments as (3.9), (3.10), still relying on Lemma 3.8, we finally obtain

$$\begin{aligned} {\mathbb {E}}_{\nu _{z_1,z_2}}\left( \prod _{i=3}^Nh_{z_1,z_2}(\lambda _i)\right) = (1+{{\,\mathrm{O}\,}}(N^{2\sigma -2\delta +{\varepsilon }}))e^{{\bar{f}}_{z_1,z_2}}\ {\mathbb {E}}_{\nu _{z_1,z_2}}\left( e^{\sum _ih^s_{z_1,z_2}(\lambda _i)}\right) . \end{aligned}$$

Third step: the local part is invariant. For our test function $h^s_{z_1,z_2}$, the reader can easily check the conditions of Lemma 4.4: the only new ingredient is

$$\begin{aligned} \int _{{\mathscr {B}}^c} \frac{\mathrm{d}m(\lambda )}{|z_1-\lambda |^2|z_2-\lambda |^2}\leqslant \frac{\log N}{|z_1-z_2|^2}, \end{aligned}$$

so that in this setting, the existence of $r>2$, $d<\kappa$ such that $(N\Vert \nu \Vert _1)^r\leqslant N^{d}$ means that there exists ${\varepsilon }>0$ such that $\left( \frac{\log N}{N|z_1-z_2|^2}\right) ^{2+{\varepsilon }}\leqslant N^{2\kappa -{\varepsilon }},$ i.e. $|z_1-z_2|\geqslant N^{-\frac{1}{2}-\frac{\kappa }{2}+{\varepsilon }},$ as we assumed by hypothesis. This gives

$$\begin{aligned} {\mathbb {E}}_{\nu _{z_1,z_2}}\left( e^{\sum _ih_{z_1,z_2}^s (\lambda _i)}\right) ={\mathbb {E}}_{\nu _{0,z_2-z_1}} \left( e^{\sum _ih_{0,z_2-z_1}^s(\lambda _i)}\right) +{{\,\mathrm{O}\,}}\left( e^{-c N^{2\kappa }}\right) . \end{aligned}$$

This yields

$$\begin{aligned}&{\mathbb {E}}_{\nu _{z_1,z_2}}\left( \prod _{i=3}^Nh_{z_1,z_2}(\lambda _i)\right) \\&\quad = (1+{{\,\mathrm{O}\,}}(N^{2\sigma -2\delta +{\varepsilon }}))e^{{\bar{f}}_{z_1,z_2}-\bar{f}_{0,z_2-z_1}}\ {\mathbb {E}}_{\nu _{0,z_2-z_1}}\left( \prod _{i=3}^Nh_{0,z_2-z_1} (\lambda _i)\right) . \end{aligned}$$

From Lemma 2.8, $e^{{\bar{f}}_{z_1,z_2}-\bar{f}_{0,z_2-z_1}}=(1-|z_1|^2)(1-|z_2|^2)$. With Proposition 3.7, this concludes the proof. $\square$

Lemma 3.8

For any $0<\sigma<d<\kappa <1/2$, there exists $p>1$, $C>0$ such that for any $|z_1|<1-N^{-1/2+\kappa },|z_1-z_2|<N^{-\frac{1}{2}+\sigma }$, $z=(z_1+z_2)/2$, we have

$$\begin{aligned} {\mathbb {E}}_{\nu _{z_1,z_2}}\left( \prod _{k=3}^N\left( \left( 1 +\frac{1}{N|\lambda _k-z_1|^2}\right) \left( 1+\frac{1}{N|\lambda _k-z_2|^2}\right) \right) ^{p\chi _{z, \delta }(\lambda _k)} \right) \leqslant N^C. \end{aligned}$$

Proof

The above left hand side is at most

$$\begin{aligned} \frac{{\mathbb {E}}\left( \prod _{k=3}^N\left( \left( 1+\frac{1}{N|\lambda _k-z_1|^2}\right) \left( 1+\frac{1}{N|\lambda _k-z_2|^2}\right) \right) ^{(p-1) \chi _{z,\delta }(\lambda _k)} (|z_1-\lambda _k|^2+\frac{1}{N})(|z_2-\lambda _k|^2+\frac{1}{N}) e^{-N(|z_1|^2-1)-N(|z_2|^2-1)} \right) }{ {\mathbb {E}}\left( \prod _{k=3}^N|z_1-\lambda _k|^2|z_2-\lambda _k|^2e^{-N(|z_1|^2-1) -N(|z_2|^2-1)}\right) } \end{aligned}$$

With Lemma 2.11 and the Cauchy–Schwarz inequality, we therefore just need to prove that

$$\begin{aligned} {\mathbb {E}}_{N-2}\left( \prod _{k=3}^N\left( \left( 1+\frac{1}{N| \lambda _k-z_1|^2}\right) ^{4(p-1)\chi _{z,\delta } (\lambda _k)}\right) \right) \leqslant N^C. \end{aligned}$$

We can apply Lemma 4.2 (for p small enough we have $N\Vert \nu \Vert _1={{\,\mathrm{O}\,}}(1)$) to compare it to the case $z_1=0$, which is easily shown to be ${{\,\mathrm{O}\,}}(N^C)$ by Corollary 5.6. $\square$

3.6 Proof of Corollary 1.5

Following a notation from [52], let $\kappa (\lambda _j)={\mathscr {O}}_{jj}^{1/2}$ be the condition number associated to $\lambda _j$. As the spectrum of a G is almost surely simple, from [52, Equation (52.11)] we know that

$$\begin{aligned} \Vert (z-G)^{-1}\Vert =\frac{\kappa (\lambda _j)}{|z-\lambda _j|}+{{\,\mathrm{O}\,}}\left( \sum _{k\ne j}\frac{\kappa (\lambda _k)}{|z-\lambda _k|}\right) \end{aligned}$$

as $z\rightarrow \lambda _j$. Together with $\sigma _{\varepsilon }(G)=\left\{ z: \Vert z-G\Vert ^{-1}>{\varepsilon }^{-1}\right\}$, this gives the following almost sure asymptotics:

$$\begin{aligned} m(\sigma _{\varepsilon }(G)\cap {\mathscr {B}}_N)\underset{{\varepsilon }\rightarrow 0}{\sim }\sum _{\lambda _j\in {\mathscr {B}}_N}\pi (\kappa (\lambda _j){\varepsilon })^2. \end{aligned}$$

Denoting $c_N=N^2\int _{{\mathscr {B}}_N} (1-|z|^2)\frac{\mathrm{d}m(z)}{\pi }$, we therefore have

$$\begin{aligned} \lim _{{\varepsilon }\rightarrow 0}{\mathbb {P}}\left( 1-c<\frac{m(\sigma _{{\varepsilon }}(G)\cap {\mathscr {B}}_N)}{\pi {\varepsilon }^2 c_N}<1+c\right) = {\mathbb {P}}\left( \left| \frac{\sum _{\lambda _j\in {\mathscr {B}}_n} {\mathscr {O}}_{jj}}{c_N}-1\right| <c\right) . \end{aligned}$$

From Corollary 1.2,

$$\begin{aligned} {\mathbb {P}}(\exists i: \lambda _i\in {\mathscr {B}}_N: |{\mathscr {O}}_{ii}|>N^{10})={{\,\mathrm{o}\,}}(1), \end{aligned}$$

hence we only need to prove

$$\begin{aligned} {\mathbb {P}}\left( \left| \frac{\sum _{\lambda _j\in {\mathscr {B}}_n} {\mathscr {O}}_{jj}}{c_N}-1\right| <c, {\mathscr {O}}_{ii}\leqslant N^{10}\ \mathrm{for\ all}\ \lambda _i\in {\mathscr {B}}_N\right) \rightarrow 1. \end{aligned}$$

(3.41)

We proceed by bounding the second moment

$$\begin{aligned}&{\mathbb {E}}\left( \left| \sum _{\lambda _j\in {\mathscr {B}}_n}{\mathscr {O}}_{jj} -c_N\right| ^2\prod _{i=1}^N\mathbb {1}_{{\mathscr {O}}_{ii}\leqslant N^{10}}\right) \nonumber \\&\quad \leqslant {\mathbb {E}}\left( \sum _{\lambda _j\in {\mathscr {B}}_n}{\mathscr {O}}_{jj}^2 \mathbb {1}_{{\mathscr {O}}_{jj}\leqslant N^{10}}\right) \end{aligned}$$

(3.42)

$$\begin{aligned}&\qquad +\,{\mathbb {E}}\left( \sum _{\lambda _i,\lambda _j\in {\mathscr {B}}_n,i\ne j}{\mathscr {O}}_{ii}{\mathscr {O}}_{jj}\mathbb {1}_{{\mathscr {O}}_{ii}, {\mathscr {O}}_{jj}\leqslant N^{10}}\right) \end{aligned}$$

(3.43)

$$\begin{aligned}&\qquad +\,c_N^2-2c_N{\mathbb {E}}\left( \sum _{\lambda _i\in {\mathscr {B}}_n} {\mathscr {O}}_{ii}\right) +2c_N{\mathbb {E}}\left( \sum _{\lambda _i\in {\mathscr {B}}_n}{\mathscr {O}}_{ii}\mathbb {1}_{\exists \lambda _j\in {\mathscr {B}}_N:{\mathscr {O}}_{jj}\geqslant N^{10}}\right) \end{aligned}$$

(3.44)

To bound the first term, note that

$$\begin{aligned} {\mathbb {E}}\left( {\mathscr {O}}_{jj}^2\mathbb {1}_{\lambda _j\in {\mathscr {B}}_N,{\mathscr {O}}_{jj}\leqslant N^{10}}\right) \leqslant C\int _{{\mathscr {B}}_N}\int _{0}^{N^{10}} x\,{\mathbb {P}}({\mathscr {O}}_{jj}\geqslant x\mid \lambda _j=z)\mathrm{d}x\mathrm{d}m(z). \end{aligned}$$

Following the same reasoning as (2.29), we have

$$\begin{aligned}&{\mathbb {P}}\left( {\mathscr {O}}_{jj}\geqslant x\mid \lambda _j=z\right) \leqslant {\mathbb {P}}({\mathscr {O}}_{jj}\geqslant x N^{-{\varepsilon }}(1-|z|^2)^{-1}\mid \lambda _j=0)+{{\,\mathrm{O}\,}}(e^{-N^{{\varepsilon }}}) \\&\quad \leqslant \frac{C N^{2+2{\varepsilon }}(1-|z|^2)^2}{x^2}+{{\,\mathrm{O}\,}}(e^{-N^{\varepsilon }}), \end{aligned}$$

where we used Proposition 2.4. Denoting a the center of ${\mathscr {B}}_N$, we therefore bounded the right hand side of (3.42) by $N^{{3+3{\varepsilon }}} (1-|a|^2)^2 m({\mathscr {B}}_N)\ll c_N^2$ because $m({\mathscr {B}}_N)\geqslant N^{-1+2a}$ and ${\varepsilon }$ is arbitrary.

To bound (3.43), we first consider close eigenvalues and bound ${\mathscr {O}}_{ii}{\mathscr {O}}_{jj}\leqslant \frac{1}{2}({\mathscr {O}}_{ii}^2+{\mathscr {O}}_{jj}^2)$:

$$\begin{aligned}&{\mathbb {E}}\left( \sum _{\lambda _i,\lambda _j\in {\mathscr {B}}_n,i\ne j}{\mathscr {O}}_{ii}{\mathscr {O}}_{jj}\mathbb {1}_{{\mathscr {O}}_{ii}, {\mathscr {O}}_{jj}\leqslant N^{10},|\lambda _i-\lambda _j|<N^{-\frac{1}{2}+{\varepsilon }}}\right) \\&\quad \leqslant C N {\mathbb {E}}\left( {\mathscr {O}}_{11}^2\mathbb {1}_{{\mathscr {O}}_{11} \leqslant N^{10},\lambda _1\in {\mathscr {B}}_N}|\left\{ j:|\lambda _j-\lambda _1| \leqslant N^{-\frac{1}{2}+{\varepsilon }}\right\} |\right) \nonumber \\&\quad \leqslant C N^{1+2{\varepsilon }}{\mathbb {E}}\left( {\mathscr {O}}_{11}^2 \mathbb {1}_{{\mathscr {O}}_{11}\leqslant N^{10},\lambda _1\in {\mathscr {B}}_N}\right) m({\mathscr {B}}_N) \leqslant C N^{3+4{\varepsilon }}(1-|a|^2)^2\ll c_N^2. \end{aligned}$$

In the second estimate, we used the local law for Ginibre matrices: from [9, Theorem 4.1] the above number of close eigenvalues is at most $C N^{2{\varepsilon }}$ for some large C, with probability at least $1-N^{-D}$ for arbitrarily large D. The third estimate was obtained in the same way we bounded (3.42).

For eigenvalues at mesoscopic distance in $[N^{-\frac{1}{2}+{\varepsilon }},N^{-\frac{1}{2}+\kappa -a}]$, the contribution of (3.43) is obtained thanks to (1.12):

$$\begin{aligned}&{\mathbb {E}}\left( \sum _{\lambda _i,\lambda _j\in {\mathscr {B}}_n,N^{-\frac{1}{2} +{\varepsilon }}<|\lambda _i-\lambda _j|}{\mathscr {O}}_{ii}{\mathscr {O}}_{jj}\right) \\&\quad =N(N-1){\mathbb {E}}\left( {\mathscr {O}}_{11}{\mathscr {O}}_{22} \mathbb {1}_{\lambda _1,\lambda _2\in {\mathscr {B}}_N,N^{-\frac{1}{2} +{\varepsilon }}<|\lambda _1-\lambda _2|}\right) \\&\quad = N(N-1)\int _{{\mathscr {B}}_N^2\cap \left\{ |z_1-z_2|>N^{-\frac{1}{2} +{\varepsilon }}\right\} }{\mathbb {E}}\left( {\mathscr {O}}_{11}{\mathscr {O}}_{22}\mid \lambda _1 =z_1\lambda _2=z_2\right) \frac{\mathrm{d}m(z_1)}{\pi }\frac{\mathrm{d}m(z_2)}{\pi } + {{\,\mathrm{O}\,}}(e^{-c N^{{\varepsilon }}})\\&\quad = N(N-1)\int _{{\mathscr {B}}_N^2\cap \left\{ |z_1-z_2|>N^{-\frac{1}{2} +{\varepsilon }}\right\} }N^2(1-|z_1|^2)(1-|z_2|^2)(1+{{\,\mathrm{O}\,}}(N^{-{\varepsilon }}))\frac{\mathrm{d}m(z_1)}{\pi } \frac{\mathrm{d}m(z_2)}{\pi } + {{\,\mathrm{O}\,}}(e^{-c N^{{\varepsilon }}})\\&\quad =c_N^2(1+{{\,\mathrm{O}\,}}(N^{-{\varepsilon }})). \end{aligned}$$

Finally, the line (3.44) is easily shown to be of order $-c_N^2(1+N^{-\varepsilon })$ thanks to (1.5) and (2.30). We conclude that the left hand side of (3.42) is at most $N^{-{\varepsilon }}c_N^2$, which concludes the proof of (3.41) by Markov’s inequality.

4 Translation invariance for conditioned measures

Recall that the Ginibre kernel is

$$\begin{aligned} K_N(z,w)=\frac{N}{\pi }e^{-N\left( \frac{|z|^2}{2} +\frac{|w|^2}{2}\right) }\sum _{k=0}^{N-1}\frac{(Nz{\bar{w}})^k}{k!}. \end{aligned}$$

We also denote its bulk limit as $k_N(z,w)=\frac{N}{\pi }e^{-N(\frac{|z|^2}{2}+\frac{|w|^2}{2}-z\bar{w})}$.

Lemma 4.1

Let $\kappa >0$. There exists $c=c(\kappa )>0$ such that for any $|z|,|w|\leqslant 1-N^{-\frac{1}{2}+\kappa }$, we have

$$\begin{aligned} K_N(z,w)=k_N(z,w)+{{\,\mathrm{O}\,}}(e^{-cN^{2\kappa }}) \end{aligned}$$

Proof

This is a straightforward adaptation of the proof of [9, Lemma 4.2]. $\square$

We denote ${\mathscr {B}}_{a,\delta }$ the ball with center a and radius $N^{-\frac{1}{2}+\delta }$.

Lemma 4.2

Let $0<\delta<\kappa <1/2$ be fixed constants. Consider any ${\mathbb {C}}$-valued measurable function f supported on ${\mathscr {B}}_{0,\delta }$, $|a|\leqslant 1-N^{-\frac{1}{2}+\kappa }$, and $\nu (z)=e^{f(z)}-1$. For any $r>2$ there exists $c, C>0$ depending only on $\kappa ,\delta ,r$ such that

$$\begin{aligned} {\mathbb {E}}\left( e^{\sum _{i=1}^N f(\lambda _i-a)}\right) = {\mathbb {E}}\left( e^{\sum _{i=1}^N f(\lambda _i)}\right) +{{\,\mathrm{O}\,}}\left( e^{-cN^{2\kappa }} e^{C(N\Vert \nu \Vert _1)^r}\right) . \end{aligned}$$

Proof

Let $K_N^{(a)}(z,w)=K_N(z-a,w-a)$. We define $\Vert K\Vert =\sup _{z,w\in \mathrm{supp}(\nu )}|K(z,w)|$. We successively compare linear statistics for $K_N^{(a)},k_N^{(a)},k_N$ and $K_N$. First note that $k_N$ is the kernel of a translation invariant point process, so that comparison between $k_N^{(a)}$ and $k_N$ is trivial. For the other steps, we use [2, Lemma 3.4.5] and obtain

$$\begin{aligned}&\left| {\mathbb {E}}\left( e^{\sum _{i=1}^N f(\lambda _i-a)}\right) -{\mathbb {E}}\left( e^{\sum _{i=1}^N f(\lambda _i)}\right) \right| \nonumber \\&\quad \leqslant \sum _{n=1}^\infty \frac{n^{1+\frac{n}{2}}}{n!}\Vert \nu \Vert _1^n \left( \max (\Vert K_N^{(a)}\Vert ,\Vert k_N^{(a)}\Vert )^{n-1}\Vert K_N^{(a)}-k_N^{(a)}\Vert \right. \nonumber \\&\qquad \left. +\, \max (\Vert K_N\Vert ,\Vert k_N\Vert )^{n-1}\Vert K_N-k_N\Vert \right) . \end{aligned}$$

(4.1)

Clearly, $\Vert K_N\Vert \leqslant \frac{N}{\pi }$ and we bound $\Vert K_N^{(a)}-K_N\Vert$ with Lemma 4.1. We conclude that for a universal large enough C, and $1/r+1/s=1$, we have

$$\begin{aligned}&\left| {\mathbb {E}}\left( e^{\sum _{i=1}^N f(\lambda _i-a)}\right) -{\mathbb {E}}\left( e^{\sum _{i=1}^N f(\lambda _i)}\right) \right| \\&\quad \leqslant e^{-cN^{2\kappa }}\sum _{n=1}^\infty \frac{n^{1+\frac{n}{2}}}{(n!)^{1/s}}\frac{1}{(n!)^{1/r}}\left( \frac{N}{\pi }\Vert \nu \Vert _1\right) ^n \leqslant Ce^{-cN^{2\kappa }} e^{C(N\Vert \nu \Vert _1)^r}, \end{aligned}$$

where in the last inequality we used Hölder’s inequality and $r>2$. $\square$

Lemma 4.3

Remember $\nu (z)=e^{f(z)}-1$ and ${\mathscr {B}}_{a,\delta }$ is the ball with center a and radius $N^{-\frac{1}{2}+\delta }$. Let $0<\delta<\kappa <1/2$ be fixed constants. Consider any ${\mathbb {C}}$-valued measurable function f supported on ${\mathscr {B}}_{0,\delta }$, and $|a|\leqslant 1-N^{-\frac{1}{2}+\kappa }$. Assume also that either (i) or (ii) below holds:

• (i) $\mathrm{Re}(f)=0$;

• (ii) there exist $d>0$, $p>1$ and $r>2$ such that $rd<2\kappa$, $f=0$ on $|z|<e^{-N^{d}}$, and ($f_+=\max (\mathrm{Re} f,0)$)

  $$\begin{aligned}&(N\Vert \nu \Vert _1)^r\leqslant N^{d}, \end{aligned}$$

  (4.2)
  $$\begin{aligned}&\log \Vert e^{\sum _{i=2}^Nf_+(\lambda _i-a)}\Vert _{{\mathrm{L}}^p} \leqslant N^d, \end{aligned}$$

  (4.3)
  $$\begin{aligned}&\log \Vert e^{\sum _{i=2}^Nf_+(\lambda _i)}\Vert _{{\mathrm{L}}^p} \leqslant N^d. \end{aligned}$$

  (4.4)

  where the $L^p$ norm is taken with respect to ${\mathbb {E}}_{N-1}$.

Then for any $q<2\kappa$, uniformly in f satisfying the above hypothese, we have

$$\begin{aligned}&{\mathbb {E}}\left( e^{\sum _{i=2}^N f(\lambda _i-a)}\mid \lambda _1=a\right) \\&\quad ={\mathbb {E}} \left( e^{\sum _{i=2}^N f(\lambda _i)}\mid \lambda _1=0\right) \left( 1+{{\,\mathrm{O}\,}}\left( e^{-cN^{q}}\right) \right) +{{\,\mathrm{O}\,}}\left( e^{-cN^{q}}\right) . \end{aligned}$$

Proof

In this proof we first consider the most difficult case (ii), and we will finally mention the simple modifications required for (i). We start with

$$\begin{aligned} {\mathbb {E}}_{N}\left( e^{\sum _{i=2}^N f(\lambda _i-a)}\mid \lambda _1=a\right) = \frac{{\mathbb {E}}_{N-1}\left( e^{\sum _{i=2}^N f(\lambda _i-a)}\prod _{i=2}^{N}|\lambda _i-a|^2e^{-N(|a|^2-1)}\right) }{{\mathbb {E}}_{N-1}\left( \prod _{i=2}^{N}|\lambda _i-a|^2e^{-N(|a|^2-1)}\right) }. \end{aligned}$$

(4.5)

Fix some constants $\kappa _1, \kappa _2$ such that $d<q<\kappa _2<\kappa _1<2\kappa$ and define $\chi ^a_j(\lambda )=\mathbb {1}_{|\lambda -a|<e^{-N^{\kappa _j}}}$, $j=1, 2$. We first show we can afford imposing $\chi ^a_2(\lambda _i)=0$: for some positive q, r such that $p^{-1}+q^{-1}+r^{-1}=1$, we have

$$\begin{aligned}&{\mathbb {E}}_{N-1}\left( e^{\sum _{i=2}^N f(\lambda _i-a)}\left( 1-\prod _{i=2}^N(1-\chi ^a_2(\lambda _i)) \right) \prod _{i=2}^{N}|\lambda _i-a|^2e^{-N(|a|^2-1)}\right) \nonumber \\&\quad \leqslant \left\| e^{\sum _{i=2}^N f(\lambda _i-a)}\right\| _{{\mathrm{L}}^p} \left\| 1-\prod _{i=2}^N(1-\chi ^a_2(\lambda _i))\right\| _{{\mathrm{L}}^q} \left\| \prod _{i=2}^{N}|\lambda _i-a|^2e^{-N(|a|^2-1)}\right\| _{{\mathrm{L}}^r} \end{aligned}$$

(4.6)

where ${\mathrm{L}}^p={\mathrm{L}}^p({\mathbb {P}}_{N-1})$. By hypotheses (4.3) and (4.4), the first norm is at most $e^{c N^d}$. The second is at most $N{\mathbb {P}}_{N-1}(|\lambda _2|\leqslant e^{-N^{\kappa _2}})\leqslant e^{-cN^{\kappa _2}}$. The third norm is at most $N^{C}$, as a simple consequence of Lemma 2.11. These estimates also hold for $f=0$, so that we proved

$$\begin{aligned}&{\mathbb {E}}_{N}\left( e^{\sum _{i=2}^N f(\lambda _i-a)}\mid \lambda _1=a\right) \nonumber \\&\quad = \frac{{\mathbb {E}}_{N-1}\left( e^{\sum _{i=2}^N f(\lambda _i-a)}\prod _{i=2}^{N}(1-\chi ^a_2(\lambda _i))|\lambda _i-a |^2e^{-N(|a|^2-1)}\right) +{{\,\mathrm{O}\,}}(e^{-c N^{\kappa _2}})}{{\mathbb {E}}_{N-1}\left( \prod _{i=2}^{N}(1- \chi ^a_2(\lambda _i))|\lambda _i-a|^2e^{-N(|a|^2-1)}\right) +{{\,\mathrm{O}\,}}(e^{-c N^{\kappa _2}})}.\nonumber \\ \end{aligned}$$

(4.7)

If $|\lambda _1-a|<e^{-N^{\kappa _1}}$ and $|\lambda _i-a|>e^{-N^{\kappa _2}}$, $2\leqslant i\leqslant N$, we have

$$\begin{aligned} \prod _{i=2}^N|\lambda _i-a|= & {} \left( 1+{{\,\mathrm{O}\,}}\left( e^{-cN^{\kappa _1}} \right) \right) \prod _{i=2}^N|\lambda _i-\lambda _1|,\\ e^{-N|a|^2}= & {} \left( 1+{{\,\mathrm{O}\,}}\left( e^{-cN^{\kappa _1}}\right) \right) e^{-N|\lambda _1|^2}. \end{aligned}$$

The expectation in the numerator of (4.7) is therefore (in the first equation below $\lambda _1$ has distribution U, the uniform measure on the unit disk with center a and radius $e^{-N^{\kappa _1}}$, with volume $b_N=\pi (e^{-2N^{\kappa _1}})$):

$$\begin{aligned}&{\mathbb {E}}_{{\mathbb {P}}_{N-1}\times U}\left( e^{\sum _{i=2}^N f(\lambda _i-a)}\prod _{i=2}^{N}(1-\chi ^a_2(\lambda _i))|\lambda _i -\lambda _1|^2e^{-N(|\lambda _1|^2-1)}\right) \left( 1+{{\,\mathrm{O}\,}}\left( e^{-cN^{\kappa _1}}\right) \right) \nonumber \\&\quad = \frac{e^N Z_N}{Z_{N-1}} \frac{1}{b_N}{\mathbb {E}}_{{N}} \left( e^{\sum _{i=2}^N f(\lambda _i-a)}\prod _{i=2}^{N}(1-\chi ^a_2(\lambda _i)) \chi ^a_1(\lambda _1)\right) \left( 1+{{\,\mathrm{O}\,}}\left( e^{-cN^{\kappa _1}}\right) \right) \end{aligned}$$

(4.8)

We now want to remove the constraint on $(\lambda _i)_{i=2}^N$, i.e. prove

$$\begin{aligned}&\frac{1}{b_N}{\mathbb {E}}_{{N}}\left( e^{\sum _{i=2}^N f(\lambda _i-a)}\prod _{i=2}^{N}(1-\chi ^a_2(\lambda _i))\chi ^a_1(\lambda _1)\right) \nonumber \\&\quad = \frac{1}{b_N}{\mathbb {E}}_{{N}}\left( e^{\sum _{i=2}^N f(\lambda _i-a)}\chi ^a_1(\lambda _1)\right) +{{\,\mathrm{O}\,}}(e^{-cN^{\kappa _2}}). \end{aligned}$$

(4.9)

This requires a longer argument. Let ${\mathscr {B}}^a_{i}=\{|z-a|\leqslant e^{-N^{\kappa _i}}\}$, $i=1$ or 2, $\xi =\sum _{1}^N\delta _{\lambda _i}$, $\widetilde{\xi }=\sum _{2}^N\delta _{\lambda _i}$. Then,

$$\begin{aligned}&\left| e^{\sum _{i=2}^N f(\lambda _i-a)}(1-\prod _{i=2}^{N}(1-\chi ^a_2(\lambda _i)))\chi ^a_1(\lambda _1)\right| \nonumber \\&\quad \leqslant e^{\sum _{i=2}^N\mathrm{Re}f(\lambda _i)}\widetilde{\xi }({\mathscr {B}}^a_{2})\chi ^a_1(\lambda _1)\nonumber \\&\quad \leqslant e^{\sum _{i=2}^N\mathrm{Re}f(\lambda _i)}\xi ({\mathscr {B}}^a_{2}-{\mathscr {B}}^a_{1})\chi ^a_1(\lambda _1) + e^{\sum _{i=2}^N\mathrm{Re}f(\lambda _i)}\widetilde{\xi }({\mathscr {B}}^a_{1})\chi ^a_1(\lambda _1). \end{aligned}$$

(4.10)

To bound the first term, we use the negative association property of determinantal point processes for disjoint sets (see e.g. [42]), using $f_+\geqslant 0$ and $f=0$ on ${\mathscr {B}}^a_{2}$:

$$\begin{aligned}&{\mathbb {E}}_N\left( e^{\sum _{i=2}^N\mathrm{Re}f(\lambda _i)} \xi ({\mathscr {B}}^a_{2}-{\mathscr {B}}^a_{1}) \xi ({\mathscr {B}}^a_{1})\right) \nonumber \\&\quad \leqslant {\mathbb {E}}_N\left( e^{\sum _{i=2}^Nf_+(\lambda _i)}\right) {\mathbb {E}}_N\left( \xi ({\mathscr {B}}^a_{2}-{\mathscr {B}}^a_{1})\right) {\mathbb {E}}_N\left( \xi ({\mathscr {B}}^a_{1})\right) . \end{aligned}$$

(4.11)

By (4.3) and (4.4), the first expectation above has size order at most $e^{cN^{d}}$. The second is of order $e^{-cN^{\kappa _2}}$ and the third one is bounded by $Nb_N(1+{{\,\mathrm{o}\,}}(1))$, so that the first term in (4.10) gives an error ${{\,\mathrm{O}\,}}(b_N e^{-c N^{\kappa _2}})$.

For the second term in (4.10), we also use the negative association property and $f=0$ on ${\mathscr {B}}^a_{2}$:

$$\begin{aligned}&{\mathbb {E}}_N\left( e^{\sum _{i=2}^N\mathrm{Re}f(\lambda _i)}\widetilde{\xi }({\mathscr {B}}^a_{1})\chi ^a_1(\lambda _1)\right) \\&\quad \leqslant {\mathbb {E}}_N\left( e^{\sum _{i=2}^Nf_+(\lambda _i)}\right) {\mathbb {E}}_N \left( \widetilde{\xi }({\mathscr {B}}^a_{1})\chi ^a_1(\lambda _1)\right) \leqslant e^{N^d}{\mathbb {E}}_N\left( \widetilde{\xi }({\mathscr {B}}^a_{1})\chi ^a_1(\lambda _1)\right) . \end{aligned}$$

Together with

$$\begin{aligned} {\mathbb {E}}\left( \widetilde{\xi }({\mathscr {B}}^a_{1})\chi ^a_1(\lambda _1)\right) \leqslant {\mathbb {E}}\left( \xi ({\mathscr {B}}^a_{1})(\xi ({\mathscr {B}}^a_{1})-1)\right) = \int _{({\mathscr {B}}^a_{1})^2} |K_N(z_1,z_2)|^2\leqslant N^2 b_N^2, \end{aligned}$$

(4.12)

we have proved that the second term in (4.10) gives an error ${{\,\mathrm{O}\,}}(b_N e^{-c N^{\kappa _2}})$. This concludes the proof of (4.9), so that the numerator in (4.7) is

$$\begin{aligned}&\frac{e^N Z_N}{Z_{N-1}} \left( \frac{1}{b_N}{\mathbb {E}}_{{N}}\left( e^{\sum _{i=2}^N f(\lambda _i-a)}\chi ^a_1(\lambda _1)\right) \right. \\&\qquad \qquad \left. \left( 1 +{{\,\mathrm{O}\,}}\left( e^{-cN^{q}}\right) \right) +{{\,\mathrm{O}\,}}\left( e^{-cN^{q}}\right) \right) +{{\,\mathrm{O}\,}}\left( e^{-cN^{q}}\right) \\&\quad =\frac{e^N Z_N}{Z_{N-1}} \left( \frac{1}{b_N}{\mathbb {E}}_{{N}}\left( e^{\sum _{i=2}^N f(\lambda _i-a)}\chi ^a_1(\lambda _1)\right) \left( 1 +{{\,\mathrm{O}\,}}\left( e^{-cN^{q}}\right) \right) +{{\,\mathrm{O}\,}}\left( e^{-cN^{q}}\right) \right) , \end{aligned}$$

where we used $\frac{e^N Z_N}{Z_{N-1}}\sim c_1 N^{c_2}$ for some $c_1,c_2$, as obtained from (1.2). In the same way, the denominator in (4.7) is $\frac{e^N Z_N}{Z_{N-1}} \left( 1+{{\,\mathrm{O}\,}}\left( e^{-cN^{\kappa _2}}\right) \right)$, so that we obtained

$$\begin{aligned}&{\mathbb {E}}_{N}\left( e^{\sum _{i=2}^N f(\lambda _i-a)}\mid \lambda _1=a\right) \nonumber \\&\quad =\frac{1}{b_N}{\mathbb {E}}_{N}\left( e^{\sum _{i=2}^N f(\lambda _i-a)}\chi ^a_1(\lambda _1)\right) \left( 1+{{\,\mathrm{O}\,}}\left( e^{-cN^{q}}\right) \right) +{{\,\mathrm{O}\,}}(e^{-cN^{q}})\nonumber \\&\quad =\frac{1}{b_N}{\mathbb {E}}_{N}\left( e^{\sum _{i=1}^N f(\lambda _i-a)}\chi ^a_1(\lambda _1)\right) \left( 1+{{\,\mathrm{O}\,}}\left( e^{-cN^{q}}\right) \right) +{{\,\mathrm{O}\,}}(e^{-cN^{q}})\nonumber \\&\quad =\frac{1}{Nb_N}{\mathbb {E}}_{N}\left( e^{\sum _{i=1}^N f(\lambda _i-a)}\xi ({\mathscr {B}}^a_1)\right) \left( 1+{{\,\mathrm{O}\,}}\left( e^{-cN^{q}}\right) \right) +{{\,\mathrm{O}\,}}(e^{-cN^{q}}), \end{aligned}$$

(4.13)

where we successively used that fact that f vanishes on ${\mathscr {B}}_1^a$ and symmetrized.

To conclude the proof, we therefore just need

$$\begin{aligned} f_a'(0)=f_0'(0)+{{\,\mathrm{O}\,}}(e^{-cN^{{2\kappa }}}),\ \mathrm{where}\ f_a(w)=\frac{1}{Nb_N}{\mathbb {E}}_{N}\left( e^{\sum _{i=1}^N f(\lambda _i-a)+w \xi ({\mathscr {B}}_1^a)}\right) . \end{aligned}$$

(4.14)

From Lemma 4.2 we know that uniformly on $|w|<1$ we have

$$\begin{aligned} f_a(w)=f_0(w)+ {{\,\mathrm{O}\,}}(e^{-N^{2\kappa }}), \end{aligned}$$

which proves (4.14) by Cauchy’s theorem, and therefore the lemma in case (ii).

Under the assumption (i), up to (4.13) the results hold and the reasoning is simplified as all $L^p$ norms related to f can be bounded by 1. To justify an analogue of (4.13) and the end of the reasoning, we first replace f by $\widetilde{f}=f\mathbb {1}_{({\mathscr {B}}_1^a)^c}$ and note that

$$\begin{aligned}&\left| \frac{1}{b_N}{\mathbb {E}}_{N}\left( \left( e^{\sum _{i=2}^N f(\lambda _i-a)}-e^{\sum _{i=2}^N \widetilde{f}(\lambda _i-a)}\right) \chi ^a_1(\lambda _1)\right) \right| \\&\quad \leqslant \frac{2}{b_N} {\mathbb {E}}_N(\xi ({\mathscr {B}}_1^a)(\xi ({\mathscr {B}}_1^a)-1))={{\,\mathrm{O}\,}}(N^2 b_N), \end{aligned}$$

so that by symmetrizing we now obtain

$$\begin{aligned} {\mathbb {E}}_{N}\left( e^{\sum _{i=2}^N f(\lambda _i-a)}\mid \lambda _1=a\right) = \frac{1}{Nb_N}{\mathbb {E}}_{N}\left( e^{\sum _{i=1}^N \widetilde{f}(\lambda _i-a)}\xi ({\mathscr {B}}^a_1)\right) +{{\,\mathrm{O}\,}}(e^{-cN^{\kappa _2}}). \end{aligned}$$

The rest of the proof is identical to case (i). $\square$

We now state and prove an analogue of Lemma 4.3 when conditioning on two points. We will only need case (ii), as we are interested in expectations in Sect. 3, not in convergence in distribution.

Lemma 4.4

Let $0<\delta<\kappa <1/2$ be fixed constants and $C>0$ fixed, arbitrarily large. Consider any ${\mathbb {C}}$-valued measurable function f supported on ${\mathscr {B}}_{0,\delta }$, $|a|,|b|\leqslant 1-N^{-\frac{1}{2}+\kappa }$, and $N^{-C}<|b-a|<N^{-1/2+d}$. Assume that there exists $d<2\kappa$, $p>1$ and $r>2$ such that $f=0$ on $|z|<e^{-N^{d}}$, on $|z-(b-a)|<e^{-N^{d}}$, and (4.2), (4.3) and (4.4) hold. Then for any $q<2\kappa$ we have

$$\begin{aligned}&{\mathbb {E}}_{N}\left( e^{\sum _{i=3}^N f(\lambda _i-a)}\mid \lambda _1=a,\lambda _2=b \right) \\&\quad = {\mathbb {E}}_{N}\left( e^{\sum _{i=3}^N f(\lambda _i)}\mid \lambda _1=0,\lambda _2=b-a\right) \left( 1+{{\,\mathrm{O}\,}}\left( e^{-cN^{q}} \right) \right) +{{\,\mathrm{O}\,}}\left( e^{-cN^{q}}\right) . \end{aligned}$$

Proof

We start similarly to the proof of Lemma 4.3, by writing

$$\begin{aligned}&{\mathbb {E}}_{N}\left( e^{\sum _{i=2}^N f(\lambda _i-a)}\mid \lambda _1=a,\lambda _2=b\right) \nonumber \\&\quad = \frac{{\mathbb {E}}_{N-2}\left( e^{\sum _{i=3}^N f(\lambda _i-a)}\prod _{i=3}^{N}|\lambda _i-a|^2e^{-N(|a|^2-1)} \prod _{i=3}^{N}|\lambda _i-b|^2e^{-N(|b|^2-1)}\right) }{{\mathbb {E}}_{N-2}\left( \prod _{i=3}^{N}|\lambda _i-a|^2e^{-N(|a|^2-1)} \prod _{i=3}^{N}|\lambda _i-b|^2e^{-N(|b|^2-1)}\right) }.\nonumber \\ \end{aligned}$$

(4.15)

Again, we fix some constants $\kappa _1, \kappa _2$ such that $d<\kappa _2<\kappa _1<2\kappa$ and define $\chi ^x_j(\lambda )=\mathbb {1}_{|\lambda -a|<e^{-N^{\kappa _j}}}$, $j=1, 2$, $x=a,b$. The strict analogue of (4.6) holds, so that the left hand side of (4.15) can be written

$$\begin{aligned} \frac{{\mathbb {E}}_{N-2}\left( e^{\sum _{i=3}^N f(\lambda _i-a)}\prod _{i=3}^{N}(1-\chi ^a_2(\lambda _i))|\lambda _i-a |^2e^{-N(|a|^2-1)}\prod _{i=3}^{N}(1-\chi ^b_2(\lambda _i)) |\lambda _i-b|^2e^{-N(|b|^2-1)}\right) +{{\,\mathrm{O}\,}}(e^{-c N^{\kappa _2}})}{{\mathbb {E}}_{N-2}\left( \prod _{i=3}^{N}(1-\chi ^a_2(\lambda _i)) |\lambda _i-a|^2e^{-N(|a|^2-1)}\prod _{i=3}^{N}(1-\chi ^b_2(\lambda _i)) |\lambda _i-b|^2e^{-N(|b|^2-1)}\right) +{{\,\mathrm{O}\,}}(e^{-c N^{\kappa _2}})}. \end{aligned}$$

(4.16)

The analogue of (4.8) then holds exactly in the same way: the expectation in the numerator of (4.16) is

$$\begin{aligned}&\frac{e^{2N} Z_N}{|a-b|^2Z_{N-2}} \frac{1}{b_N^2}{\mathbb {E}}_{{N}}\\&\quad \left( e^{\sum _{i=3}^N f(\lambda _i-a)}\prod _{i=3}^{N}(1-\chi ^a_2(\lambda _i)) (1-\chi ^b_2(\lambda _i))\chi ^a_1(\lambda _1)\chi ^b_1(\lambda _2)\right) \left( 1+{{\,\mathrm{O}\,}}\left( e^{-cN^{\kappa _1}}\right) \right) . \end{aligned}$$

Again, we want to remove the constraint on $(\lambda _i)_{i=3}^N$, i.e. prove

$$\begin{aligned}&\frac{1}{b_N^2}{\mathbb {E}}_{{N}}\left( e^{\sum _{i=3}^N f(\lambda _i-a)}\prod _{i=3}^{N}(1-\chi ^a_2(\lambda _i)) (1-\chi ^b_2(\lambda _i))\chi ^a_1(\lambda _1)\chi ^b_1(\lambda _2)\right) \\&\qquad \qquad =\frac{1}{b_N^2}{\mathbb {E}}_{{N}}\left( e^{\sum _{i=3}^N f(\lambda _i-a)}\chi ^a_1(\lambda _1)\chi ^b_1(\lambda _2)\right) +{{\,\mathrm{O}\,}}(e^{-cN^{\kappa _2}}). \end{aligned}$$

With the negative association property, the strict analogues of Eqs. (4.10), (4.11) and (4.12) hold, so that the numerator in (4.16) is

$$\begin{aligned}&\frac{e^{2N} Z_N}{|a-b|^2Z_{N-2}} \left( \frac{1}{b_N^2} {\mathbb {E}}_{{N}}\left( e^{\sum _{i=3}^N f(\lambda _i-a)}\chi ^a_1(\lambda _1)\chi ^b_1(\lambda _2)\right) +{{\,\mathrm{O}\,}}\left( e^{-cN^{\kappa _2}}\right) \right) \\&\qquad +\,{{\,\mathrm{O}\,}}\left( e^{-cN^{\kappa _2}}\right) \\&\quad =\frac{e^{2N} Z_N}{|a-b|^2Z_{N-2}} \left( \frac{1}{b_N^2}{\mathbb {E}}_{{N}}\left( e^{\sum _{i=3}^N f(\lambda _i-a)}\chi ^a_1(\lambda _1)\chi ^b_1(\lambda _2)\right) +{{\,\mathrm{O}\,}}\left( e^{-cN^{\kappa _2}}\right) \right) \end{aligned}$$

where we used $\frac{e^{2N} Z_N}{Z_{N-2}}\sim c_1 N^{c_2}$ for some $c_1,c_2$, as obtained from (1.2). In the same way, the denominator in (4.16) is $\frac{e^{2N} Z_N}{|a-b|^2Z_{N-2}} \left( 1+{{\,\mathrm{O}\,}}\left( e^{-cN^{\kappa _2}}\right) \right)$, giving

$$\begin{aligned}&{\mathbb {E}}_{N}\left( e^{\sum _{i=3}^N f(\lambda _i-a)}\mid \lambda _1=a,\lambda _2=b\right) \nonumber \\&\quad =\frac{1}{b_N^2}{\mathbb {E}}_{N}\left( e^{\sum _{i=3}^N f(\lambda _i-a)}\chi ^a_1(\lambda _1)\chi ^b_1(\lambda _2)\right) \left( 1+{{\,\mathrm{O}\,}}(e^{-cN^{q}})\right) +{{\,\mathrm{O}\,}}(e^{-cN^{q}})\nonumber \\&\quad =\frac{1}{b_N^2}{\mathbb {E}}_{N}\left( e^{\sum _{i=1}^N f(\lambda _i-a)}\chi ^a_1(\lambda _1)\chi ^b_1(\lambda _2)\right) \left( 1+{{\,\mathrm{O}\,}}(e^{-cN^{q}})\right) +{{\,\mathrm{O}\,}}(e^{-cN^{q}})\nonumber \\&\quad =\frac{1}{N(N-1)b_N^2}{\mathbb {E}}_{N}\left( e^{\sum _{i=1}^N f(\lambda _i-a)}\xi ({\mathscr {B}}^a_1)\xi ({\mathscr {B}}^b_1)\right) \left( 1+{{\,\mathrm{O}\,}}(e^{-cN^{q}})\right) +{{\,\mathrm{O}\,}}(e^{-cN^{q}}), \end{aligned}$$

(4.17)

where we successively used that fact that f vanishes on ${\mathscr {B}}_1^a\cup {\mathscr {B}}_1^b$, ${\mathscr {B}}_1^a\cap {\mathscr {B}}_1^b=\varnothing$ (this holds because $|a-b|>N^{-C}$) and symmetrized. To conclude the proof, we therefore just need $\partial _{z_1z_2}f_{a,b}(0,0)=\partial _{z_1z_2} f_{0,b-a}(0,0)+{{\,\mathrm{O}\,}}(e^{-cN^{{q}}})$, where

$$\begin{aligned} f_{a,b}(z_1,z_2)=\frac{1}{N(N-1)b_N^2}{\mathbb {E}}_{N}\left( e^{\sum _{i=1}^N f(\lambda _i-a)+z_1 \xi ({\mathscr {B}}_1^a)+z_2 \xi ({\mathscr {B}}_1^b)})\right) \end{aligned}$$

(4.18)

This follows from Lemma 4.2 and Cauchy’s Theorem, similarly to the end of the proof of Lemma 4.3. $\square$

5 Andréief’s identity and Kostlan’s theorem

This section gives applications of Andréief’s identity to the conditioned measures of interest in this work. In particular, it proves some slight extensions of Kostlan’s theorem (Corollary 5.5), following a method from [18]. The common main tool will be the following classical Lemma, by Andréief [3] (see [16] for a short proof). Note that the original proof of Kostlan’s theorem [38] and some of its extensions [32] were based on different arguments.

Lemma 5.1

(Andréief’s identity) On a measured space $(E, {\mathcal {E}}, \mu )$ For any functions $(\phi _i, \psi _i)_{i=1}^N \in L_2(\mu )^{2N}$,

$$\begin{aligned}&\frac{1}{ N! } \int _{E^N} \det \left( \phi _i(\lambda _j) \right) \ \det \left( \psi _i (\lambda _j) \right) \ \mu (\mathrm {d}\lambda _1) \dots \mu ( \mathrm {d}\lambda _N ) = \det \left( f_{i,j}\right) \\&\quad \text {where} \ f_{i,j} = \int _E \phi _i(\lambda ) \psi _j(\lambda ) \mu (\mathrm {d}\lambda ). \end{aligned}$$

Theorem 5.2

Let $E={\mathbb {C}}$, $g \in L_2(\mu )$, and $\{ \lambda _1, \dots , \lambda _N\}$ eigenvalues from the Ginibre ensemble. Then

$$\begin{aligned}&{\mathbb {E}}\left( \prod _{k=1}^N g (\lambda _k)\right) = N^{\frac{N(N-1)}{2}}\det (f_{i,j})_{i,j = 1}^{N} \quad \\&\text {where}\; f_{i,j} = \frac{1}{ (j-1)!} \int \lambda ^{i-1} {\bar{\lambda }}^{j-1} g(\lambda ) \mu (\mathrm {d}\lambda ). \end{aligned}$$

Proof

The following is elementary:

$$\begin{aligned} \int |\lambda |^{2i}\mathrm{d}\mu (\lambda )=\frac{i!}{N^i}. \end{aligned}$$

(5.1)

The proof then follows from Andréief’s identity. $\square$

Theorem 5.3

We have (remember $\mu =\mu ^{(N)}$)

$$\begin{aligned}&{\mathbb {E}}\left( \prod _{k=2}^{N} g (\lambda _k) \mid \lambda _1 = z\right) = \frac{1}{Z_N^{(z)}} \det (f_{i,j})_{i,j = 1}^{N-1} \\&\quad \text {where} f_{i,j} = \frac{1}{ j!} \int \lambda ^{i-1} {\bar{\lambda }}^{j-1} |z -\lambda |^2 g (\lambda ) \mu (\mathrm {d}\lambda ) \end{aligned}$$

and

$$\begin{aligned} Z_N^{(z)}= N^{-\frac{N(N-1)}{2}}e^{(N-1)}\left( N|z|^2\right) . \end{aligned}$$

Proof

Using Andréief’s identity with $\phi _i(\lambda ) = \lambda ^{i-1} g(\lambda ) |z - \lambda |^2$, $\psi _j(\lambda )= \lambda ^{j-1}$, we find

$$\begin{aligned} {\mathbb {E}}\left( \prod _{k=2}^{N} g (\lambda _k)\mid \lambda _1 = z\right) = \frac{1}{Z_N^{(z)}} \det (f_{i,j})_{i,j = 1}^{N-1} \end{aligned}$$

where

$$\begin{aligned} Z_N^{(z)}=\det (M_{ij})_{i,j = 1}^{N-1},\ \ M_{ij}=\frac{1}{ i !} \int \lambda ^{i-1} {\bar{\lambda }}^{j-1} |z - \lambda |^2 \mu (\mathrm {d}\lambda ). \end{aligned}$$

By expanding $|z- \lambda |^2 = |z|^2 + |\lambda |^2 - z {\overline{\lambda }} - {\overline{z}} \lambda$, we see that that M is tridiagonal, with entries (remember (5.1))

$$\begin{aligned} M_{ii}=\frac{1}{N^i}+\frac{|z|^2}{iN^{i-1}},\ M_{i,i+1}=-\frac{{\overline{z}}}{N^i},\ M_{i,i-1}=- \frac{z}{i N^{i-1}}. \end{aligned}$$

Denoting $x=N |z|^2$ and $d_k=\det ((M_{ij})_{1\leqslant i,j\leqslant k})$, with the convention $d_0=1$ we have

$$\begin{aligned} d_1&=\frac{1+x}{N}\\ d_k&=\left( 1+\frac{x}{k}\right) \frac{1}{N^k}d_{k-1} -\frac{x}{k}\frac{1}{N^{2k-1}}d_{k-2} \end{aligned}$$

so that $a_k=d_k N^{\frac{k(k+1)}{2}}$ satisfies $a_0=1$, $a_1=1+x$,

$$\begin{aligned} a_k=\left( 1+\frac{x}{k}\right) a_{k-1}-\frac{x}{k}a_{k-2}. \end{aligned}$$

This gives $a_k=e^{(k)}(x)$ by an immediate induction. $\square$

Theorem 5.4

We have

$$\begin{aligned}&{\mathbb {E}}\left( \prod _{k=3}^{N} g(\lambda _k) \mid \lambda _1 = 0, \lambda _2 = z\right) = \frac{1}{Z_N^{(0,z)}}\det (f_{i,j})_{i,j = 1}^{N-2} \quad \text {where} \\&\quad f_{i,j} = \frac{1}{ (i+1)!} \int \lambda ^{i-1} {\bar{\lambda }}^{j-1} |\lambda |^2 |z - \lambda |^2 g (\lambda ) \mu (\mathrm {d}\lambda ) \end{aligned}$$

and

$$\begin{aligned} Z_N^{(0,z)}=N^{-\frac{(N-2)(N+1)}{2}}\frac{e_1^{(N-1)}(N|z|^2)}{N|z|^2}. \end{aligned}$$

(5.2)

Proof

By Andréief’s identity, the result holds with

$$\begin{aligned} Z_N^{(0,z)} = \det (M_{ij})_{i,j = 1}^{N-2},\ M_{ij}=\frac{1}{ (i+1) !} \int \lambda ^{i-1} {\bar{\lambda }}^{j-1} |\lambda |^2 |z - \lambda |^2 \mu (\mathrm {d}\lambda ). \end{aligned}$$

Expanding $|z - \lambda |^2 = |z|^2 + |\lambda |^2 - z {\overline{\lambda }} - {\overline{z}} \lambda$, we see that M is tridiagonal with entries

$$\begin{aligned} M_{ii}=\frac{1}{N^{i+1}}+\frac{|z|^2}{(i+1) N^i},\ M_{i,i+1}=-\frac{{\overline{z}}}{N^{i+1}},\ M_{i,i-1}=- \frac{z}{(i+1)N^{i}}. \end{aligned}$$

Denoting $x=N |z|^2$ and $d_k=\det ((M_{ij})_{1\leqslant i,j\leqslant k})$, with the convention $d_0=1$ we have

$$\begin{aligned} d_1&=\frac{2+x}{2N^2},\\ d_k&=\left( 1+\frac{x}{k+1}\right) \frac{1}{N^{k+1}} d_{k-1}-\frac{x}{k+1}\frac{1}{N^{2k+1}}d_{k-2}. \end{aligned}$$

so that $a_k=d_k N^{\frac{k(k+3)}{2}}$ satisfies $a_0=1$, $a_1=1+x/2$,

$$\begin{aligned} a_k=\left( 1+\frac{x}{k+1}\right) a_{k-1}-\frac{x}{k+1}a_{k-2}. \end{aligned}$$

This gives the expected result by an immediate induction. $\square$

Kostlan’s theorem now comes as a corollary, as well as a similar property for the Ginibre ensemble conditioned on $\lambda _1 =0$.

Corollary 5.5

(Kostlan) The set $N\{ |\lambda _1|^2, \dots , |\lambda _N|^2 \}$ is distributed as $\{\gamma _1,\dots ,\gamma _N\}$, a set of (unordered) independent Gamma variables of parameters $1,2, \dots , N$.

Proof

Let $g \in {\mathbb {C}}[X]$ and use Theorem 5.2 with the radially symmetric function $g(|\cdot |^2)$. The relevant matrix is then diagonal, with coefficients

$$\begin{aligned} f_{i,i}= & {} \frac{1}{ (i-1)!} \int |\lambda |^{2i-2} g(|\lambda |^2) \mu (\mathrm {d}\lambda ) \\= & {} {N^{-(i-1)} \over (i-1)!} \int _{r=0}^{\infty } r^{i-1} g(r/N) e^{-r} \mathrm {d}r = N^{-(i-1)}{\mathbb {E}}(g(\gamma _i/N)). \end{aligned}$$

In other words,

$$\begin{aligned} {\mathbb {E}}\left( \prod _{i=1}^N g(|\lambda _i|^2)\right) ={\mathbb {E}}\left( \prod _{i=1}^N g(\gamma _{i}/N)\right) . \end{aligned}$$

Note that these statistics characterize the distribution of a set of unordered points, as such expressions with polynomial g generate all symmetric polynomials, as stated in Lemma 5.7, and the gamma distributions are characterized by their moments. For more details, see [18]. We conclude that $N\{ |\lambda _1|^2, \dots , |\lambda _N|^2 \} {\mathop {=}\limits ^{d}} \{ \gamma _1, \dots , \gamma _N\}$. $\square$

Corollary 5.6

Conditioned on $\{ \lambda _1 =0\}$, $\{ N |\lambda _2|^2, \dots , N |\lambda _N|^2 \}$ is distributed as $\{\gamma _2,\dots \gamma _N\}$, a set of (unordered) independent Gamma variables of parameters $2,3, \dots , N$.

Proof

Similarly to the proof of Corollary 5.5, we take $g \in {\mathbb {C}}[X]$ and the radially symmetric function $g(|\cdot |^2)$. In Theorem 5.3, we have

$$\begin{aligned} f_{i,i} = \frac{1}{ i!} \int |\lambda |^{2i} g(|\lambda |^2) \mu (\mathrm {d}\lambda ) = {N^{-i} \over i!} \int _{r=0}^{\infty } r^{i} g(r/N) e^{-r} \mathrm {d}r = N^{-i}{\mathbb {E}}\big [ g(\gamma _{i+1}/N) \big ]. \end{aligned}$$

This together with our expression for $Z_N^{(z=0)}$ in Theorem 5.3 yields

$$\begin{aligned} {\mathbb {E}}\left( \prod _{i=2}^N g(|\lambda _i|^2) \mid \lambda _1=0\right) = {\mathbb {E}}\left( \prod _{i=2}^N g(\gamma _{i})\right) \end{aligned}$$

and we conclude in the same way that $N\{ |\lambda _2|^2, \dots , |\lambda _N|^2 \} {\mathop {=}\limits ^{d}} \{ \gamma _2, \dots , \gamma _N\}$. $\square$

For the proof of the following lemma, we refer to [18]. We define the product symmetric polynomials as the symmetric polynomials given by products of polynomials in one variable:

$$\begin{aligned} \mathrm {PS}_{{\mathbb {C}}}(N) = \left\{ \ \prod _{i=1}^N P(X_i) \ | \ P \in {\mathbb {C}} [X] \ \right\} \end{aligned}$$

Lemma 5.7

$\mathrm {PS}_{{\mathbb {C}}}(N)$ spans the vector space of symmetric polynomials of N variables.

Appendices

Appendix A: Eigenvalues dynamics

This Appendix derives the Dyson-type dynamics for eigenvalues of nonnormal matrices. More precisely, we consider the Ornstein-Uhlenbeck version so that the equilibrium measure is the (real or complex) Ginibre ensemble. These dynamics take a particularly simple form in the case of complex Gaussian addition, where the drift term shows no interaction between eigenvalues: only the correlation of martingale terms is responsible for eigenvalues repulsion.

We also describe natural dynamics with equilibrium measure given by the real Ginibre ensemble. Then, the eigenvalues evolution is more intricate.

It was already noted in [11] that eigenvectors impact the eigenvalues dynamics for nonnormal matrices, and the full dynamics in the complex case have been written down in [30].

1.1 Complex Ginibre dynamics

Let G(0) be a complex matrix of size N, assumed to be diagonalized as $YGX = \Delta = \mathrm {Diag}(\lambda _1,\dots ,\lambda _N)$, where X, Y are the matrices of the right- and left-eigenvectors of G(0). We also assume that G(0) has simple spectrum, and X, Y invertible. The right eigenvectors $(x_i)$ are the columns of X, and the left-eigenvectors $(y_j)$ are the rows of Y. They are chosen uniquely such that $XY=I$ and, for any $1\leqslant k\leqslant N$, $X_{kk}=1$.

We now consider the complex Dyson-type dynamics: for any $1\leqslant i,j\leqslant N$,

$$\begin{aligned} \mathrm{d}G_{ij}(t)=\frac{\mathrm{d}B_{ij}(t)}{\sqrt{N}}-\frac{1}{2}G_{ij}(t)\mathrm{d}t, \end{aligned}$$

(A.1)

where the $B_{ij}$’s are independent standard complex Brownian motions: $\sqrt{2}{{\,\mathrm{Re}\,}}(B_{ij})$ and $\sqrt{2}{{\,\mathrm{Im}\,}}(B_{ij})$ are standard real Brownian motions. One can easily check that G(t) converges to the Ginibre ensemble as $t\rightarrow \infty$, with normalization (1.1).

In the following, the bracket of two complex martingales M, N is defined by bilinearity: $\langle M,N\rangle =\langle {{\,\mathrm{Re}\,}}M,{{\,\mathrm{Re}\,}}N\rangle -\langle {{\,\mathrm{Im}\,}}M,{{\,\mathrm{Im}\,}}N\rangle +\mathrm {i}\langle {{\,\mathrm{Re}\,}}M,{{\,\mathrm{Im}\,}}N\rangle +\mathrm {i}\langle {{\,\mathrm{Im}\,}}M,{{\,\mathrm{Re}\,}}N\rangle$.

Proposition A.1

The spectrum $(\lambda _1(t),\dots , \lambda _n(t))$ is a semimartingale satisfying the system of equations

$$\begin{aligned} \mathrm {d}\lambda _k(t) = \mathrm{d}M_k(t) - \frac{1}{2} \lambda _k(t)\mathrm {d}t \end{aligned}$$

where the martingales $(M_k)_{1\leqslant k\leqslant N}$ have brackets $\langle M_i,M_j\rangle =0$ and

$$\begin{aligned} \mathrm{d}\langle M_i,\overline{M_j}\rangle _t={\mathscr {O}}_{ij}(t)\frac{\mathrm{d}t}{N}. \end{aligned}$$

Remark A.2

As explained below, this equation (in particular the off-diagonal brackets) is coherent with the eigenvalues repulsion observed in (1.2). Contrary to the Hermitian Dyson Brownian motion, all eigenvalues are martingales (up to the Ornstein Uhlenbeck drift term), so that their repulsion is not due to direct mutual interaction, but to correlations between these martingales at the microscopic scale.

For example, assume that G(0) is already at equilibrium. Using physics conventions, for any bulk eigenvalues $\lambda _1,\lambda _2$ satisfying $w={{\,\mathrm{O}\,}}(1)$ (remember $w=\sqrt{N}(\lambda _1-\lambda _2)$), Proposition A.1 and Theorem 1.4 imply

$$\begin{aligned}&{\mathbb {E}}\left( \mathrm{d}\lambda _1\mathrm{d}\overline{\lambda _2}\mid \lambda _1=z_1,\lambda _2=z_2\right) \sim {\mathbb {E}}({\mathscr {O}}_{12}\mid \lambda _1=z_1,\lambda _2=z_2)\\&\quad \frac{\mathrm{d}t}{N}\sim -(1-|z_1|^2)\frac{1}{|w|^4}\frac{1- (1+|\omega |^2)e^{-|\omega |^2}}{1-e^{-|\omega |^2}}\mathrm{d}t \end{aligned}$$

in the bulk. By considering the real part in this equation and denoting $\mathrm{d}\lambda _1=\mathrm{d}x_1+\mathrm {i}\mathrm{d}y_1$, $\mathrm{d}\lambda _2=\mathrm{d}x_2+\mathrm {i}\mathrm{d}y_2$, we have in particular ${\mathbb {E}}(\mathrm{d}x_1\mathrm{d}x_2+\mathrm{d}y_1\mathrm{d}y_2)<0$, and this negative correlation is responsible for repulsion: the eigenvalues tend to move in opposite directions. Moreover, as eigenvalues get closer on the microscopic scale, $w\rightarrow 0$ and the repulsion gets stronger:

$$\begin{aligned} {\mathbb {E}}\left( \mathrm{d}\lambda _1\mathrm{d}\overline{\lambda _2}\mid \lambda _1=z_1,\lambda _2=z_2\right) \sim -\frac{1-|z_1|^2}{|w|^2}\mathrm{d}t. \end{aligned}$$

On the other hand, for mesoscopic scale $N^{-1/2}\ll |\lambda _1-\lambda _2|$, Proposition A.1 and Theorem 1.4 give ${\mathbb {E}}\left( \mathrm{d}\lambda _1\mathrm{d}\overline{\lambda _2}\right) \sim -\frac{(1-|\lambda _1|^2)}{N^2|\lambda _1-\lambda _2|^4}\mathrm{d}t={{\,\mathrm{o}\,}}(\mathrm{d}t)$, so that increments are uncorrelated for large N.

For a given differential operator $f\mapsto f'$, we introduce the matrix $C=X^{-1}X'$. Along the following lemmas, all eigenvalues are assumed to be distinct. In our application, this spectrum simplicity will hold almost surely for any $t\geqslant 0$ as G(0) has simple spectrum.

Lemma A.3

We have $X'=XC$ and $Y'=-CY$.

Proof

The first equality is the definition of C. For the second one, $XY=I$ gives $XY'+X'Y=0$, hence $Y' = - X^{-1} X' Y = -CY.$$\square$

Lemma A.4

The first order perturbation of eigenvalues is given by $\lambda _k ' = y_k G' x_k$.

Proof

We have $\Delta ' = (YGX)' = Y'GX + YG'X + YGX' = YG'X + YGXC - C YGX = YG'X + \Delta C - C \Delta = YG'X + [\Delta ,C]$. Therefore $\lambda _k' = (YG'X)_{kk} + [\Delta ,C]_{kk} = y_k G' x_k$. $\square$

Lemma A.5

For any $i \ne j$, $C_{ij} = {y_i G' x_j \over \lambda _j - \lambda _i}$.

Proof

For such i, j, $\Delta '_{ij} = 0$. With the same computation as in the previous lemma, this gives $(YG'X)_{ij} + [\Delta ,C]_{ij}=0$. Thus $(\lambda _i - \lambda _j) C_{ij} = - (YG'X)_{ij} = - y_i G' x_j$, from which the result follows. $\square$

Lemma A.6

For any $1\leqslant k\leqslant N$, $C_{kk} = - \sum _{l \ne k} X_{kl} {y_l G' x_k \over \lambda _k - \lambda _l}$.

Proof

We use the assumption $X_{kk}=1$. From this, and the definition of C, we get

$$\begin{aligned} X'_{kk}=0=(XC)_{kk} = \sum _{l=1}^n X_{kl} C_{lk} = X_{kk} C_{kk} + \sum _{l \ne k} X_{kl} C_{lk}. \end{aligned}$$

As a consequence, $C_{kk} = - \sum _{l \ne k} X_{kl} C_{lk}$ and we obtain the result thanks to the previous lemma. $\square$

From now on the differential operator will be either $\partial _{{{\,\mathrm{Re}\,}}G_{ab}}$ ($G' = E_{ab}= \{ \delta _{ia} \delta _{jb} \}_{1\leqslant i,j\leqslant N}$), or $\partial _{{{\,\mathrm{Im}\,}}G_{ab}}$, ($G' = \mathrm {i}E_{ab})$. In both cases, $G''=0$. We denote $C^{{{\,\mathrm{Re}\,}}}$ and $C^{{{\,\mathrm{Im}\,}}}$ accordingly. In particular, for any k and $i\ne j$ the following holds:

$$\begin{aligned}&\partial _{{{\,\mathrm{Re}\,}}G_{ab}} \lambda _k = Y_{ka} X_{b,k},\ \partial _{{{\,\mathrm{Im}\,}}G_{ab}}\lambda _k = \mathrm {i}Y_{ka} X_{b,k} \nonumber \\&C_{ij}^{{{\,\mathrm{Re}\,}}} = {Y_{ia} X_{bj} \over \lambda _j - \lambda _i},\ C_{kk}^{{{\,\mathrm{Re}\,}}} = - \sum _{l \ne k} X_{kl} { Y_{la} X_{b,k} \over \lambda _k - \lambda _l}, \nonumber \\&C_{ij}^{{{\,\mathrm{Im}\,}}} = \mathrm {i}{Y_{ia} X_{bj} \over \lambda _j - \lambda _i}, \ C_{kk}^{{{\,\mathrm{Im}\,}}} = - \mathrm {i}\sum _{l \ne k} X_{kl} { Y_{la} X_{b,k} \over \lambda _k - \lambda _l}. \end{aligned}$$

(A.2)

Lemma A.7

We have

$$\begin{aligned} \partial _{{{\,\mathrm{Re}\,}}G_{ab}} X_{ij}&= \sum _{l \ne j} (X_{il}- X_{ij} X_{jl} ) {Y_{la} X_{bj} \over \lambda _j - \lambda _l},\\ \partial _{{{\,\mathrm{Im}\,}}G_{ab}} X_{ij}&= \mathrm {i}\sum _{l \ne j} (X_{il}- X_{ij} X_{jl} ) {Y_{la} X_{bj} \over \lambda _j - \lambda _l}. \\ \partial _{{{\,\mathrm{Re}\,}}G_{ab}} Y_{ij}&= \sum _{l \ne i} \frac{1}{ \lambda _i - \lambda _l} (X_{il} Y_{la} X_{b,i} Y_{ij} + Y_{ia} X_{bl} Y_{lj}),\\ \partial _{{{\,\mathrm{Im}\,}}G_{ab}} Y_{ij}&= \mathrm {i}\sum _{l \ne i} \frac{1}{ \lambda _i - \lambda _l} (X_{il} Y_{la} X_{b,i} Y_{ij} + Y_{ia} X_{bl} Y_{lj}). \end{aligned}$$

Proof

Below is the computation for $\partial _{{{\,\mathrm{Re}\,}}G_{ab}}X_{ij}$. We use $X'=XC$ and (A.2):

$$\begin{aligned} X'_{ij}= & {} (XC)_{ij} = \sum _{l=1}^n X_{il} C_{lj} = \sum _{l \ne j} X_{il} {Y_{la} X_{bj} \over \lambda _j - \lambda _l} \\&- X_{ij} \sum _{l \ne j} X_{jl} { Y_{la} X_{bj} \over \lambda _j - \lambda _l} = \sum _{l \ne j} (X_{il}- X_{ij} X_{jl} ) {Y_{la} X_{bj} \over \lambda _j - \lambda _l}. \end{aligned}$$

The case $\partial _{{{\,\mathrm{Im}\,}}G_{ab}}X_{ij}$ is obtained similarly, as are the formulas for Y. $\square$

Lemma A.8

The second order perturbation of eigenvalues is given by

$$\begin{aligned} \partial _{{{\,\mathrm{Re}\,}}G_{ab}}^2 \lambda _k = 2 \sum _{l \ne k} { Y_{ka} X_{bl} Y_{la} X_{b,k} \over \lambda _k - \lambda _l},\ \ \partial _{{{\,\mathrm{Im}\,}}G_{ab}}^2 \lambda _k = -2 \sum _{l \ne k} { Y_{ka} X_{bl} Y_{la} X_{b,k} \over \lambda _k - \lambda _l}. \end{aligned}$$

Proof

We compute the perturbation for $\partial _{{{\,\mathrm{Re}\,}}G_{ab}}$. Differentiating $\lambda$ a second time gives

$$\begin{aligned} \lambda _k'' = y_k' G' x_k + y_k G'' x_k+ y_k G' x_k' = Y_{ka}' X_{b,k} + Y_{ka} X_{b,k}'. \end{aligned}$$

Replacing $X'$ and $Y'$ with their expressions yields

$$\begin{aligned} \lambda _k''&= \sum _{l \ne k} \frac{1}{ \lambda _k - \lambda _l} (X_{kl} Y_{la} X_{b,k} Y_{ka} + Y_{ka} X_{bl} Y_{la}) X_{b,k} \\&\quad +\, Y_{ka} \sum _{l \ne j} (X_{bl}- X_{b,k} X_{kl} ) {Y_{la} X_{b,k} \over \lambda _k - \lambda _l} \\&= \sum _{l \ne k} \frac{1}{ \lambda _k - \lambda _l} (X_{kl} Y_{la} X_{b,k} Y_{ka} X_{b,k} + Y_{ka} X_{bl} Y_{la} X_{b,k}\\&\quad + Y_{ka} X_{bl} Y_{la} X_{b,k}- Y_{ka}X_{b,k} X_{kl} Y_{la} X_{b,k}) \\&= 2 \sum _{l \ne k} { Y_{ka} X_{bl} Y_{la} X_{b,k} \over \lambda _k - \lambda _l}, \end{aligned}$$

which concludes the proof, the other cases being similar. $\square$

For the proof of Proposition A.1, we need the following elementary lemma.

Lemma A.9

Let $\tau =\inf \{t\geqslant 0:\exists i\ne j, \lambda _i(t)=\lambda _j(t)\}$. Then $\tau =\infty$ almost surely.

Proof

The set of matrices G with Jordan form of type

$$\begin{aligned} \lambda _1\oplus \dots \oplus \lambda _{N-2}\oplus \left( \begin{array}{cc} \lambda _{N-1}&{}1\\ 0&{}\lambda _{N-1}\end{array}\right) (\mathrm{respectively}\ \lambda _1\oplus \dots \oplus \lambda _{N-2}\oplus \lambda _{N-1}\oplus \lambda _{N-1}) \end{aligned}$$

is a submanifold ${\mathcal {M}}_1$ (resp. ${\mathcal {M}}_2$) of ${\mathbb {C}}^{N^2}$ with complex codimension 1 (resp. 3), see e.g. [36, 47]. Therefore, almost surely, a Brownian motion in ${\mathbb {C}}^{N^2}$ starting from a diagonalizable matrix with simple spectrum will not hit ${\mathcal {M}}_1$ or ${\mathcal {M}}_2$. This concludes the proof. $\square$

All derivatives can therefore be calculated, as eigenvalues and eigenvectors are analytic functions of the matrix entries (see [35]).

Proof of Proposition A.1

In our context,the Itô formula will take the following form: for a function f from ${\mathbb {C}}^n$ to ${\mathbb {C}}$ of class $C^2$, where $B_t=(B_t^1,\dots ,B_t^n)$ is made of independent standard complex Brownian motions, we have

$$\begin{aligned} \mathrm {d}f (B_t)= & {} \sum _{i=1}^n \Bigg ({\partial f \over \partial {{\,\mathrm{Re}\,}}z_i } \mathrm {d}{{\,\mathrm{Re}\,}}B_t^{i} + {\partial f \over \partial {{\,\mathrm{Im}\,}}z_i} \mathrm {d}{{\,\mathrm{Im}\,}}B_t^{i} \Bigg )\nonumber \\&+ \frac{1}{ 2} \Bigg (\sum _{i=1}^n {\partial ^2 f \over \partial {{\,\mathrm{Re}\,}}{z_i}^2 } + {\partial ^2 f \over \partial {{{\,\mathrm{Im}\,}}z_i}^2 } \Bigg ) \mathrm {d}t. \end{aligned}$$

(A.3)

For any given $0<{\varepsilon }<\min \{|\lambda _i(0)-\lambda _j(0)|,i\ne j\}$, let

$$\begin{aligned} \tau _{{\varepsilon }}=\inf \{t\geqslant 0:\exists i\ne j, |\lambda _i(t)-\lambda _j(t)|<{\varepsilon }\}. \end{aligned}$$

(A.4)

Eigenvalues are smooth functions of the matrix coefficients on the domain $\cap _{i<j}\{|\lambda _i-\lambda _j|>{\varepsilon }\}$, so that Eq. (A.3) together with Lemmas A.4 and A.8 gives the following equality of stochastic integrals, with substantial cancellations of the drift term:

$$\begin{aligned} \mathrm {d}\lambda _k(t\wedge \tau _{{\varepsilon }})= & {} \sum _{i,j=1}^n Y_{ki} X_{jk} \left( \frac{\mathrm {d}B_{ij}(t\wedge \tau _{{\varepsilon }})}{\sqrt{N}} - \frac{G_{ij} }{2}\mathrm {d}(t\wedge \tau _{\varepsilon })\right) \\&+ \frac{1}{N} \sum _{i,j,\ell \ne k}\Bigg ( { Y_{ki} X_{jl} Y_{li} X_{jk} \over \lambda _k - \lambda _l} - { Y_{ki} X_{jl} Y_{li} X_{jk} \over \lambda _k - \lambda _l} \Bigg ) \mathrm {d}(t\wedge \tau _{{\varepsilon }})\\= & {} \sum _{i,j=1}^n Y_{ki} X_{jk} \frac{\mathrm {d}B_{ij}(t\wedge \tau _{{\varepsilon }})}{\sqrt{N}} -\frac{1}{2} \sum _{i,j=1}^n Y_{ki} G_{ij} X_{jk} \mathrm {d}(t\wedge \tau _{{\varepsilon }})\\= & {} \sum _{i,j=1}^n Y_{ki} X_{jk} \frac{\mathrm {d}B_{ij}(t\wedge \tau _{{\varepsilon }})}{\sqrt{N}} -\frac{1}{2} \lambda _k \mathrm {d}(t\wedge \tau _{{\varepsilon }}). \end{aligned}$$

Taking ${\varepsilon }\rightarrow 0$ in the above equation together with Lemma A.9 yields

$$\begin{aligned} \mathrm {d}\lambda _k(t)= \sum _{i,j=1}^n Y_{ki} X_{jk} \frac{\mathrm {d}B_{ij}(t)}{\sqrt{N}} -\frac{1}{2} \lambda _k \mathrm {d}t. \end{aligned}$$

The eigenvalues martingales terms are correlated. Their brackets are

$$\begin{aligned}&\mathrm {d}\langle \lambda _i, {{\bar{\lambda }}}_j \rangle _t = \frac{1}{N} \sum _{a,b,c,d=1}^n Y_{ia} X_{b,i} \overline{Y_{jc} X_{d,j}} \mathrm {d}\langle B_{ab}, \overline{ \mathrm {d}B_{cd}}\rangle _t \nonumber \\&\quad = (X^{\mathrm{t}}{\overline{X}})_{ij} (Y Y^*)_{ij} \frac{\mathrm {d}t}{N} = {\mathscr {O}}_{ij}(t) \frac{\mathrm {d}t}{N}, \end{aligned}$$

(A.5)

$$\begin{aligned}&\mathrm {d}\langle \lambda _i, \lambda _j \rangle _t=0. \end{aligned}$$

(A.6)

This concludes the proof. $\square$

1.2 Proof of Corollary 1.6

Let $A_{t,{\varepsilon }}=\{\sup _{0\leqslant s\leqslant t}|\lambda _1(s)-\lambda _1(0)|<N^{\varepsilon }t^{1/2}\}$. We start by proving that

$$\begin{aligned} {\mathbb {P}}(A_{t,{\varepsilon }})=1-{{\,\mathrm{o}\,}}(1). \end{aligned}$$

(A.7)

From Proposition A.1 and Itô’s formula, we have

$$\begin{aligned} e^{\frac{t}{2}}\lambda _1(t)-\lambda _1(0)=\int _0^te^{\frac{s}{2}}\mathrm{d}M_1(s), \end{aligned}$$

(A.8)

which is a local martingale. It is an actual martingale because

$$\begin{aligned} {\mathbb {E}}\left( \langle \int _0^{\cdot }e^{\frac{s}{2}}\mathrm{d}M_1(s)\rangle _t\right) =\int _0^t{\mathbb {E}}\left( e^{\frac{s}{2}} \frac{{\mathscr {O}}_{11}(s)}{N}\mathrm{d}s\right) ={{\,\mathrm{O}\,}}(t)<\infty , \end{aligned}$$

(A.9)

where in the last equality we used ${\mathbb {E}}({\mathscr {O}}_{11}(s))={{\,\mathrm{O}\,}}(N)$, which follows from (2.11). The estimate (A.7) follows by Doob’s and Markov’s inequalities.

For (1.16), we start with

$$\begin{aligned} |e^{\frac{t}{2}}\lambda _1(t)-\lambda _1(0)|^2=2\mathrm{Re}\int _0^t\overline{e^{\frac{s}{2}}\lambda _1(s)-\lambda _1(0)}e^{\frac{s}{2}}\mathrm{d}M_1(s) +\int _0^te^s\frac{{\mathscr {O}}_{11}(s)}{N}\mathrm{d}s. \end{aligned}$$

(A.10)

This implies

$$\begin{aligned} {\mathbb {E}}\left( e^t|\lambda _1(t)-\lambda _1(0)|^2 \mathbb {1}_{\{\lambda _1(0)\in {\mathscr {B}}\}}\right) = \int _0^t{\mathbb {E}}\left( e^s\frac{{\mathscr {O}}_{11}(s)}{N} \mathbb {1}_{\{\lambda _1(0)\in {\mathscr {B}}\}}\right) \mathrm{d}s+{{\,\mathrm{o}\,}}(t). \end{aligned}$$

(A.11)

Here, we used that $(\mathrm{Re}\int _0^t\overline{e^{\frac{s}{2}}\lambda _1(s)-\lambda _1(0)}e^{\frac{s}{2}}\mathrm{d}M_1(s) )_t$ is an actual martingale, because the expectation of its bracket is

$$\begin{aligned}&\int _0^te^{s}{\mathbb {E}}\left( |e^{\frac{s}{2}}\lambda _1(s) -\lambda _1(0)|^2\frac{{\mathscr {O}}_{11}(s)}{N}\mathbb {1}_{\{\lambda _1(0)\in {\mathscr {B}}\}}\mathrm{d}s\right) \\&\quad \leqslant 2\int _0^te^{2s}{\mathbb {E}}\left( |\lambda _1(s)|^2+1) \frac{{\mathscr {O}}_{11}(s)}{N}\mathrm{d}s\right) <\infty , \end{aligned}$$

where for the last inequality we used (2.11).

To evaluate the right hand side of (A.11), we would like to change $\lambda _1(0)\in {\mathscr {B}}$ into $\lambda _1(s)\in {\mathscr {B}}$. First,

$$\begin{aligned}&\left| {\mathbb {E}}\left( \frac{{\mathscr {O}}_{11}(s)}{N} \mathbb {1}_{A_{t,{\varepsilon }}}\left( \mathbb {1}_{\lambda _1(0)\in {\mathscr {B}}}-\mathbb {1}_{\lambda _1(s)\in {\mathscr {B}}}\right) \right) \right| \nonumber \\&\quad \leqslant {\mathbb {E}}\left( \frac{{\mathscr {O}}_{11}(s)}{N} \mathbb {1}_{\mathrm{dist}(\lambda _1(s),\partial {\mathscr {B}})\leqslant N^{\varepsilon }t^{1/2}}\right) ={{\,\mathrm{O}\,}}(N^{\varepsilon }t^{1/2}), \end{aligned}$$

(A.12)

where for the last inequality we used (2.11), again. Moreover, if $1/p+1/q=1$ with $p<2$. we have

$$\begin{aligned} {\mathbb {E}}\left( \frac{{\mathscr {O}}_{11}(s)}{N} \mathbb {1}_{(A_{t,{\varepsilon }})^c}\right) \leqslant {\mathbb {E}}\left( \left( \frac{{\mathscr {O}}_{11}(s)}{N}\right) ^p\right) ^{1/p} {\mathbb {P}}\left( (A^{(1)}_{t,{\varepsilon }})^c\right) ^{1/q}={{\,\mathrm{o}\,}}(1), \end{aligned}$$

(A.13)

where we used [24, Theorem 2.3] to obtain that uniformly in the complex plane and in N, ${\mathscr {O}}_{11}/N$ has finite moment of order $p<2$. Equations (A.11), (A.12) and (A.13) imply

$$\begin{aligned} {\mathbb {E}}\left( |\lambda _1(t)-\lambda _1(0)|^2 \mathbb {1}_{\lambda _1(0)\in {\mathscr {B}}}\right) = \int _0^t{\mathbb {E}}\left( \frac{{\mathscr {O}}_{11}(s)}{N} \mathbb {1}_{\{\lambda _1(s)\in {\mathscr {B}}\}}\right) \mathrm{d}s+{{\,\mathrm{o}\,}}(t), \end{aligned}$$

and one concludes the proof of (1.16) with (2.11).

The proof of (1.17) is identical, except that we rely on the off-diagonal bracket $\mathrm{d}\langle \lambda _1,\bar{\lambda }_2\rangle _s={\mathscr {O}}_{12}(s)\frac{\mathrm{d}s}{N}$, the estimate (1.9), and the elementary inequality

$$\begin{aligned} |{\mathscr {O}}_{12}|=|(R_j^* R_i)(L_j^* L_i)|\leqslant & {} \Vert R_j\Vert \Vert R_i\Vert \Vert L_j\Vert \Vert L_i\Vert \\\leqslant & {} \frac{1}{2}\left( \Vert R_i\Vert ^2 \Vert L_i\Vert ^2+\Vert R_j\Vert ^2\Vert L_j\Vert ^2\right) =\frac{1}{2} \left( {\mathscr {O}}_{11}+{\mathscr {O}}_{22}\right) \end{aligned}$$

to bound the (first and p-th) moment of ${\mathscr {O}}_{12}$ in the whole complex plane based on those of ${\mathscr {O}}_{11}$, ${\mathscr {O}}_{22}$.

1.3 Real Ginibre dynamics

We now consider G(0) a real matrix of size N, again assumed to be diagonalized as $YGX = \Delta = \mathrm {Diag}(\lambda _1,\dots ,\lambda _N)$, where X, Y are the matrices of the right- and left-eigenvectors of G(0). We also assume that G(0) has simple spectrum, and X, Y invertible. We keep the same notations for the right eigenvectors $(x_i)$, columns of X, and the left-eigenvectors $(y_j)$, rows of Y. They are again chosen such that $XY=I$ and, for any $1\leqslant k\leqslant N$, $X_{kk}=1$.

In this subsection, the real Dyson-type dynamics are ($1\leqslant i,j\leqslant N$),

$$\begin{aligned} \mathrm{d}G_{ij}(t)=\frac{\mathrm{d}B_{ij}(t)}{\sqrt{N}}-\frac{1}{2}G_{ij}(t)\mathrm{d}t, \end{aligned}$$

(A.14)

where the $B_{ij}$’s are independent standard Brownian motions. One can easily check that G(t) converges to the real Ginibre ensemble as $t\rightarrow \infty$.

Note that the real analogue of Lemma A.9 gives weaker repulsion: the set of real matrices with Jordan form of type

$$\begin{aligned} \lambda _1\oplus \dots \oplus \lambda _{N-2}\oplus \left( \begin{array}{cc} \lambda _{N-1}&{}1\\ 0&{}\lambda _{N-1}\end{array}\right) \end{aligned}$$

is a submanifold ${\mathcal {M}}_1$ of ${\mathbb {R}}^{N^2}$, supported on $\lambda _{N-1}\in {\mathbb {R}}$, with real codimension 1 (as proved by a straightforward adaptation of [36, Theorem 7]). Denoting $\tau =\inf \{t\geqslant 0:\exists i\ne j, \lambda _i(t)=\lambda _j(t)\}$, under the dynamics (A.14) for any $t>0$ we therefore have

$$\begin{aligned} {\mathbb {P}}(\tau <t)>0, \end{aligned}$$

so that we can only state the real version of Proposition A.1 up to time $\tau$. In fact, collisions occur transforming pairs of real eigenvalues into pairs of complex conjugate eigenvalues, a mechanism coherent with the random number of real eigenvalues in the real Ginibre ensemble [22, 41].

The overlaps (1.4) are enough to describe the complex Ginibre dynamics, and so are they for the real Ginibre ensemble, up to the introduction of the following notation: we define $\bar{i}\in \llbracket 1,N\rrbracket$ through $\lambda _{\bar{i}}=\overline{\lambda _i}$, i.e. ${\bar{i}}$ is the index of the conjugate eigenvalue to $\lambda _i$. Note that ${\bar{i}}=i$ if $\lambda _i\in {\mathbb {R}}$. For real matrices, if $L_j,R_j$ are eigenvectors associated to $\lambda _j$, ${\bar{L}}_j,{\bar{R}}_j$ are eigenvectors for ${{\bar{\lambda }}}_j$, so that

$$\begin{aligned} {\mathscr {O}}_{i{\bar{j}}}=({\bar{R}}_j^* R_i)({\bar{L}}_j^* L_i)=(R_j^{\mathrm{t}} R_i)(L_j^{\mathrm{t}} L_i). \end{aligned}$$

Proposition A.10

The spectrum $(\lambda _1(t),\dots , \lambda _n(t))$ evolves according to the following stochastic equations, up to the first collision:

$$\begin{aligned} \mathrm {d}\lambda _k(t\wedge \tau ) = \mathrm{d}M_k(t\wedge \tau )+ \left( \sum _{l\ne k}\frac{ {{\mathscr {O}}}_{k\bar{l}}}{\lambda _k-\lambda _\ell } -\frac{1}{2} \lambda _k\right) \mathrm {d}(t\wedge \tau ) \end{aligned}$$

where the martingales $(M_k)_{1\leqslant k\leqslant N}$ have brackets

$$\begin{aligned} \mathrm{d}\langle M_i,M_j\rangle _{t\wedge \tau }={{\mathscr {O}}}_{i\bar{j}}(t)\frac{\mathrm{d}(t\wedge \tau )}{N},\ \ \mathrm{d}\langle M_i,\overline{M_j}\rangle _{t\wedge \tau }={\mathscr {O}}_{ij}(t)\frac{\mathrm{d}(t\wedge \tau )}{N}. \end{aligned}$$

Note that the real eigenvalues have associated real eigenvectors. For those, ${{\mathscr {O}}}_{k{\bar{l}}}={\mathscr {O}}_{kl}$, and the variation is real: real eigenvalues remain real as long as they do not collide.

Remark A.11

Proposition A.10 is coherent with the attraction between conjugate eigenvalues exhibited in [45]. In fact, if $\eta ={{\,\mathrm{Im}\,}}(\lambda _k)>0$, the drift interaction term with $\bar{\lambda }_k$ is ${\mathscr {O}}_{kk}/(\lambda _k-{{\bar{\lambda }}}_k)=-\mathrm {i}{\mathscr {O}}_{kk}/(2\eta )$, so that these eigenvalues attract each other stronger as they approach the real axis.

For the proof, we omit the details and only mention the differences with respect to Proposition A.1. We apply the Itô formula for a ${\mathscr {C}}^2$ function f from ${\mathbb {R}}^n$ to ${\mathbb {C}}$, with argument $U_t=(U_t^1,\dots ,U_t^n)$ is made of independent Ornstein-Uhlenbeck processes. Together with the perturbation formulas for $\lambda _k$, Lemmas A.4 and A.8 , we obtain (remember the notation (A.4))

$$\begin{aligned} \mathrm {d}\lambda _k(t\wedge \tau _{{\varepsilon }})= & {} \sum _{i,j=1}^n Y_{ki} X_{jk} \left( \frac{\mathrm {d}B_{ij}(t\wedge \tau _{{\varepsilon }})}{\sqrt{N}} - \frac{1}{2}G_{ij} \mathrm {d}(t\wedge \tau _{\varepsilon }\right) \\&+ \sum _{i,j} \sum _{l \ne k} { Y_{ki} X_{jl} Y_{li} X_{jk} \over \lambda _k - \lambda _l} \mathrm {d}(t\wedge \tau _{{\varepsilon }}) \\= & {} \sum _{i,j=1}^n Y_{ki} X_{jk} \frac{\mathrm {d}B_{ij}(t\wedge \tau _{{\varepsilon }})}{\sqrt{N}}\\&+\left( \sum _{l\ne k}\frac{ (X^tX)_{lk} (YY^t)_{kl}}{\lambda _k-\lambda _\ell } -\frac{1}{2} \lambda _k \right) \mathrm {d}(t\wedge \tau _{{\varepsilon }}). \end{aligned}$$

We can take ${\varepsilon }\rightarrow 0$ in the above formulas and the brackets are calculated as follows, concluding the proof:

$$\begin{aligned}&\mathrm {d}\langle \lambda _i, {{\bar{\lambda }}}_j \rangle _{t\wedge \tau } = \frac{1}{N} \sum _{a,b,c,d=1}^n Y_{ia} X_{b,i} \overline{Y_{jc} X_{d,j}} \mathrm {d}\langle B_{ab}, \overline{ \mathrm {d}B_{cd}}\rangle _{t\wedge \tau }\nonumber \\&\quad = (X^{\mathrm{t}}{\overline{X}})_{ij} (Y Y^*)_{ij} \frac{\mathrm {d}(t\wedge \tau )}{N} = {\mathscr {O}}_{ij}(t) \frac{\mathrm {d}(t\wedge \tau )}{N}, \end{aligned}$$

(A.15)

$$\begin{aligned}&\mathrm {d}\langle \lambda _i, \lambda _j \rangle _{t\wedge \tau }= \frac{1}{N} \sum _{a,b,c,d=1}^n Y_{ia} X_{b,i} {Y_{jc} X_{d,j}} \mathrm {d}\langle B_{ab},{ \mathrm {d}B_{cd}}\rangle _{t\wedge \tau }\nonumber \\&\quad = (X^{\mathrm{t}}{X})_{ij} (Y Y^{\mathrm{t}})_{ij} \frac{\mathrm {d}(t\wedge \tau )}{N} = {\mathscr {O}}_{i{\bar{j}}}(t) \frac{\mathrm {d}(t\wedge \tau )}{N}. \end{aligned}$$

(A.16)

Appendix B: Normalized eigenvectors

This paper focuses on the condition numbers and off-diagonal overlaps, but the Schur decomposition also easily gives information about other statistics such as the angles between eigenvectors. We include these results for the sake of completeness. We denote the complex angle as

$$\begin{aligned} \arg (\lambda _1,\lambda _2)={R_1^{*} R_2 \over \Vert R_1 \Vert \Vert R_2 \Vert }, \end{aligned}$$

where the phases of $R_1(1)$ and $R_2(1)$ can be chosen independent uniform on $[0,2\pi )$. We also define

$$\begin{aligned} \Phi (z) = {z \over \sqrt{1+|z|^2} }. \end{aligned}$$

Proposition B.1

Conditionally on $\lambda _1=z_1,\lambda _2=z_2$, we have

$$\begin{aligned} \arg (\lambda _1,\lambda _2) \overset{(\mathrm d)}{=}\Phi \left( {X\over \sqrt{N} |z_1 - z_2| }\right) \end{aligned}$$

where $X \sim {\mathscr {N}}_{{\mathbb {C}}}(0,\frac{1}{2} \mathrm{Id})$.

In particular, for $\lambda _1, \lambda _2$ at mesoscopic distance, the complex angle converges in distribution to a Dirac mass at 0. Therefore in such a setting eigenvectors strongly tend to be orthogonal: matrices sampled from the Ginibre ensemble are not far from normal, when only considering eigenvectors angles. The limit distribution becomes non trivial in the microscopic scaling $|\lambda _1 - \lambda _2| \sim N^{-1/2}$, it is the pushforward of a complex Gaussian measure by $\Phi$.

Proof

From Proposition 2.1 we know that $R_1^*R_2=R_{T,1}^*R_{T,2}$, $\Vert R_1\Vert =\Vert R_{T,1}\Vert$ and $\Vert R_2\Vert =\Vert R_{T,2}\Vert$, where $R_{T,i}$ (and $L_{T,i}$) are the normalized bi-orthogonal bases of right and left eigenvectors for T, defined as (2.2). The first eigenvectors are written $R_{T,1}=(1,0,\dots ,0)$ and $R_{T,2}=(a,1,0\dots ,0)$ where $a=-\bar{b}_2=-\frac{T_{12}}{\lambda _1-\lambda _2}$, with $T_{12}$ complex Gaussian ${\mathscr {N}}\left( 0,\frac{1}{2N}\mathrm{Id}\right)$, independent of $\lambda _1$ and $\lambda _2$. This gives

$$\begin{aligned} \arg (\lambda _1,\lambda _2) =-\frac{{\bar{b}}_2}{\sqrt{1+|b_2|^2}} \end{aligned}$$

and concludes the proof. $\square$

From Proposition B.1, the distribution of the angle for fixed $\lambda _1$ and random $\lambda _2$ can easily be inferred. For example, if $\lambda _2$ is chosen uniformly among eigenvalues in a macroscopic domain $\Omega \subset \{|z|<1\}$ with nonempty interior, we obtain the convergence in distribution ($X_\Omega$ is uniform on $\Omega$, independent of ${\mathscr {N}}$)

$$\begin{aligned} N | \arg (\lambda _1 ,\lambda _2) |^2 \underset{N\rightarrow \infty }{\rightarrow }\frac{|{\mathscr {N}}|^2}{|z_1-X_\Omega |^2}. \end{aligned}$$

When $z_1=0$ and $z_2$ is free, the following gives a more precise distribution, for finite N and in the limit.

Corollary B.2

Conditionally on $\{ \lambda _1 =0 \}$ we have

$$\begin{aligned} N | \arg (\lambda _1 ,\lambda _2) |^2 \overset{(\mathrm d)}{=} N\beta _{1,U_N}\overset{(\mathrm d)}{\longrightarrow }X \end{aligned}$$

where $U_N$ is an independent random variable uniform on $\{ 2,\dots ,N\}$, and X has density ${1 - (1+t) e^{-t} \over t^2} {\mathbf {1}}_{{\mathbb {R}}_+} (t).$

Proof

From Corollary 5.6, $N |\lambda _2|^2 \sim \gamma _{U_N}$. Together with Lemma 2.5, this gives

$$\begin{aligned} | \arg (\lambda _1 ,\lambda _2) |^2 = { {|{\mathscr {N}}|^2 \over N | \lambda _2|^2 } \over 1+ {|{\mathscr {N}}|^2 \over N | \lambda _2|^2 } } \overset{(\mathrm d)}{=} {\gamma _1 \over \gamma _1 + \gamma _{U_N}} \overset{(\mathrm d)}{=} \beta _{1,U_N}. \end{aligned}$$

The limiting density then follows from the explicit distribution of $\beta$ random variables. $\square$