Abstract
The Brownian motion \((U^N_t)_{t\ge 0}\) on the unitary group converges, as a process, to the free unitary Brownian motion \((u_t)_{t\ge 0}\) as \(N\rightarrow \infty \). In this paper, we prove that it converges strongly as a process: not only in distribution but also in operator norm. In particular, for a fixed time \(t>0\), we prove that the unitary Brownian motion has a spectral edge: there are no outlier eigenvalues in the limit. We also prove an extension theorem: any strongly convergent collection of random matrix ensembles independent from a unitary Brownian motion also converge strongly jointly with the Brownian motion. We give an application of this strong convergence to the Jacobi process.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
This paper is concerned with convergence of the noncommutative distribution of the standard Brownian motion on unitary groups. Let \(\mathbb {M}_N\) denote the space of \(N\times N\) complex matrices, and let \(\mathrm {Tr}(A) = \sum _{j=1}^N A_{jj}\) denote the (usual) trace. It will be convenient throughout to use the normalized trace, and so we use the symbol \(\mathrm {tr}= \frac{1}{N}\mathrm {Tr}\) (with a lower-case \(\mathrm {t}\)) for this purpose. We denote the unitary group in \(\mathbb {M}_N\) as \(\mathbb {U}_N\). The Brownian motion on \(\mathbb {U}_N\) is the diffusion process \((U^N_t)_{t\ge 0}\) started at the identity with infinitesimal generator \(\frac{1}{2}\Delta _{\mathbb {U}_N}\), where \(\Delta _{\mathbb {U}_N}\) is the left-invariant Laplacian on \(\mathbb {U}_N\). (This is uniquely defined up to a choice of N-dependent scale; see Sect. 2.1 for precise definitions, notation, and discussion.)
For each fixed \(t\ge 0, U^N_t\) is a random unitary matrix, whose spectrum \(\mathrm {spec}(U^N_t)\) consists of N eigenvalues \(\lambda _1(U^N_t),\ldots ,\lambda _N(U^N_t)\). The empirical spectral distribution, also known as the empirical law of eigenvalues, of \(U^N_t\) (for a fixed \(t\ge 0\)) is the random probability measure \(\mathrm {Law}_{U^N_t}\) on the unit circle \(\mathbb {U}_1\) that puts equal mass on each eigenvalue (counted according to multiplicity):
In other words: \(\mathrm {Law}_{\mathbb {U}^N_t}\) is the random measure determined by the characterization that its integral against a test function \(f\in C(\mathbb {U}_1)\) is given by
It is customary to realize all of the processes \(\{U_t^N:N\in {\mathbb {N}}\}\) on a single probability space in order to talk about almost sure convergence of \(\mathrm {Law}_{U^N_t}\) as \(N\rightarrow \infty \). The standard realization is to declare that \(U_t^N\) and \(U_s^M\) are independent for all \(s,t\ge 0\) and all \(N\ne M\). (To be clear, though, none of the results stated below depend on this particular realization, and indeed hold for any coupling.)
In [4], Biane showed that the random measure \(\mathrm {Law}_{U^N_t}\) converges weakly almost surely to a deterministic limit probability measure \(\nu _t\),
The measure \(\nu _t\) can be described as the spectral measure of a free unitary Brownian motion (cf. Sect. 2.3). For \(t>0, \nu _t\) possesses a continuous density that is symmetric about \(1\in \mathbb {U}_1\), and is supported on an arc strictly contained in the circle for \(0<t<4\); for \(t\ge 4, \mathrm {supp}\,\nu _t = \mathbb {U}_1\).
The result of (1.2) is a bulk result: it does not constrain the behavior of eigenvalues near the edge. The additive counterpart is the classical Wigner’s semicircle law. Let \(X^N\) be a Gaussian unitary ensemble (\(\mathrm {GUE}^N\)), meaning that the joint density of entries of \(X^N\) is proportional to \(\exp (-\frac{N}{2}\mathrm {Tr}(X^2))\). Alternatively, \(X^N\) may be described as a Gaussian Wigner matrix, meaning it is Hermitian, and otherwise has i.i.d. centered Gaussian entries of variance \(\frac{1}{N}\). Wigner’s law states that the empirical spectral distribution converges weakly almost surely to a limit: the semicircle distribution \(\frac{1}{2\pi }\sqrt{(4-x^2)_+}\,dx\), supported on \([-2,2]\) (cf. [50]). This holds for all Wigner matrices, independent of the distribution of the entries, cf. [2]. But this does not imply that the spectrum of \(X^N\) converges almost surely to \([-2,2]\); indeed, it is known that this spectral edge phenomenon occurs iff the fourth moments of the entries of \(X^N\) are finite (cf. [3]).
Our first major theorem is a spectral edge result for the empirical law of eigenvalues of the Brownian motion \(U^N_t\). Since the spectrum is contained in the circle \(\mathbb {U}_1\), instead of discussing the ill-defined “largest” eigenvalue, we characterize convergence in terms of Hausdorff distance \(d_H\): the Hausdorff distance between two compact subsets A, B of a metric space is defined to be
where \(A_\epsilon \) is the set of points within distance \(\epsilon \) of A. It is easy to check that the spectral edge theorem for Wigner ensembles is equivalent to the statement that \(d_H(\mathrm {spec}(X^N),[-2,2])\rightarrow 0 \; a.s.\) as \(N\rightarrow \infty \); for a related discussion, see Corollary 3.3 and Remark 3.4 below.
Theorem 1.1
Let \(N\in {\mathbb {N}},\) and let \((U^N_t)_{t\ge 0}\) be a Brownian motion on \(\mathbb {U}_N\). Fix \(t\ge 0\). Denote by \(\nu _t\) the law of the free unitary Brownian motion, cf. Theorem 2.5. Then
Remark 1.2
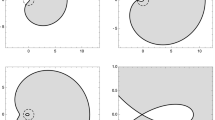
When \(t\ge 4, \mathrm {supp}\,\nu _t = \mathbb {U}_1\), and Theorem 1.1 is immediate; the content here is that, for \(0\le t<4\), for large N all the eigenvalues are very close to the arc defined in (2.7) (Fig. 1).
The spectrum of the unitary Brownian motion \(U^N_t\) with \(N=400\) and \(t=1\). These figures were produced from 1000 trials. On the left is a plot of the eigenvalues, while on the right is a 1000-bin histogram of their complex arguments. The argument range of the data is \([-1.9392,1.9291]\), as compared to the predicted large-N limit range (to four digits) \([-1.9132,1.9132]\), cf. (2.7)
To prove Theorem 1.1, our method is to prove sufficiently tight estimates on the rate of convergence of the moments of \(U^N_t\). We record the main estimate here, since it is of independent interest.
Theorem 1.3
Let \(N,n\in {\mathbb {N}},\) and fix \(t\ge 0\). Then
Theorems 1.1 and 1.3 are proved in Sect. 3.
The second half of this paper is devoted to a multi-time, multi-matrix extension of this result. Biane’s main theorem in [4] states that the process \((U^N_t)_{t\ge 0}\) converges (in the sense of finite-dimensional noncommutative distributions) to a free unitary Brownian motion \((u_t)_{t\ge 0}\). To be precise: for any \(k\in {\mathbb {N}}\) and times \(t_1,\ldots ,t_k\ge 0\), and any noncommutative polynomial \(P\in {\mathbb {C}}\langle X_1,\ldots ,X_{2k}\rangle \) in 2k indeterminates, the random trace moments of \((U^N_{t_j})_{1\le j\le k}\) converge almost surely to the corresponding trace moments of \((u_{t_j})_{1\le j\le k}\):
(Here \(\tau \) is the tracial state on the noncommutative probability space where \((u_t)_{t\ge 0}\) lives; cf. Sect. 2.3.) This is the noncommutative extension of a.s. weak convergence of the empirical spectral distribution. The corresponding strengthening to the level of the spectral edge is strong convergence: instead of measuring moments with the linear functionals \(\mathrm {tr}\) and \(\tau \), we insist on a.s. convergence of polynomials in operator norm. See Sect. 2.2 for a full definition and history.
Theorem 1.1 can be rephrased to say that, for any fixed \(t\ge 0, U^N_t\) converges strongly to \(u_t\) (cf. Corollary 3.3). Our second main theorem is the extension of this to any finite collection of times. In fact, we prove a more general extension theorem, as follows.
Theorem 1.4
For each N, let \((U^N_t)_{t\ge 0}\) be a Brownian motion on \(\mathbb {U}_N\). Let \(A^N_1,\ldots ,A^N_n\) be random matrix ensembles in \(\mathbb {M}_N\) all independent from \((U^N_t)_{t\ge 0},\) and suppose that \((A^N_1,\ldots ,A^N_n)\) converges strongly to \((a_1,\ldots ,a_n)\). Let \((u_t)_{t\ge 0}\) be a free unitary Brownian motion freely independent from \(\{a_1,\ldots ,a_n\}\). Then, for any \(k\in {\mathbb {N}},\) and any \(t_1,\ldots ,t_k\ge 0,\)
Theorem 1.4 is proved in Sect. 4.
We conclude the paper with an application of these strong convergence results to the empirical spectral distribution of the Jacobi process, in Theorem 5.7. We proceed now with Sect. 2, laying out the basic concepts, preceding results, and notation we will use throughout.
2 Background
Here we set notation and briefly recall some main ideas and results we will need to prove our main results. Section 2.1 introduces the Brownian motion \((U^N_t)_{t\ge 0}\) on \(\mathbb {U}_N\). Section 2.2 discusses noncommutative distributions (which generalize empirical spectral distributions to collections of noncommuting random matrix ensembles, and beyond) and associated notions of convergence, including strong convergence. Finally, Sect. 2.3 reviews key ideas from free probability and free stochastic calculus, leading up to the definition of free unitary Brownian motion and its spectral measure \(\nu _t\).
2.1 Brownian motion on \(\mathbb {U}_N\)
Throughout, \(\mathbb {U}_N\) denotes the unitary group of rank N; its Lie algebra \(\mathrm {Lie}(\mathbb {U}_N) = \mathfrak {u}_N\) consists of the skew-Hermitian matrices in \(\mathbb {M}_N, \mathfrak {u}_N = \{X\in \mathbb {M}_N:X^*=-X\}\). We define a real inner product on \(\mathfrak {u}_N\) by scaling the Hilbert–Schmidt inner product
As explained in [20], this is the unique scaling that gives a meaningful limit as \(N\rightarrow \infty \).
Any vector \(X\in \mathfrak {u}_N\) gives rise to a unique left-invariant vector field on \(\mathbb {U}_N\); we denote this vector field as \(\partial _X\) (it is more commonly called \({\widetilde{X}}\) in the geometry literature). That is: \(\partial _X\) is a left-invariant derivation on \(C^\infty (\mathbb {U}_N)\) whose action is
where \(e^{tX}\) denotes the usual matrix exponential (which is the exponential map for the matrix Lie group \(\mathbb {U}_N\); in particular \(e^{tX}\in \mathbb {U}_N\) whenever \(X\in \mathfrak {u}_N\)). The Laplacian \(\Delta _{\mathbb {U}_N}\) on \(\mathbb {U}_N\) (determined by the metric \(\langle \cdot ,\cdot \rangle _N\)) is the second-order differential operator
where \(\beta _N\) is any orthonormal basis for \(\mathfrak {u}_N\); the operator does not depend on which orthonormal basis is used. The Laplacian is a negative definite elliptic operator; it is essentially self-adjoint in \(L^2(\mathbb {U}_N)\) taken with respect to the Haar measure (cf. [41, 45]).
The unitary Brownian motion \(U^N = (U^N_t)_{t\ge 0}\) is the Markov diffusion process on \(\mathbb {U}_N\) with generator \(\frac{1}{2}\Delta _{\mathbb {U}_N}\), with \(U^N_0=I_N\). In particular, this means that the law of \(U^N_t\) at any fixed time \(t\ge 0\) is the heat kernel measure on \(\mathbb {U}_N\). This is essentially by definition: the heat kernel measure \(\rho ^N_t\) is defined weakly by
We mention here the fact that the heat kernel measure is symmetric: it is invariant under \(U\mapsto U^{-1}\) (this is true on any Lie group).
There are (at least) two more constructive ways to understand the Brownian motion \(U^N\) directly. The first is as a Lévy process: \(U^N\) is uniquely defined by the following properties.
-
Continuity: The paths \(t\mapsto U^N_t\) are a.s. continuous.
-
Independent Multiplicative Increments: For \(0\le s\le t\), the multiplicative increment \((U_s^N)^{-1}U_t^N\) is independent from the filtration up to time s (i.e. from all random variables measurable with respect to the entires of \(U_r^N\) for \(0\le r\le s\)).
-
Stationary Heat-Kernel Distributed Increments: For \(0\le s\le t\), the multiplicative increment \((U_s^N)^{-1}U_t^N\) has the distribution \(\rho ^N_{t-s}\).
In particular, since \(U^N_t\) is distributed according to \(\rho ^N_t\), we typically write expectations of functions on \(\mathbb {U}_N\) with respect to \(\rho ^N_t\) as
For the purpose of computations, the best representation of \(U^N\) is as the solution to a stochastic differential equation. Let \(X^N\) be a \(\mathrm {GUE}^N\)-valued Brownian motion: that is, \(X^N\) is Hermitian where the random variables \([X^N]_{jj}, \mathrm {Re}[X^N]_{jk}, \mathrm {Im}[X^N]_{jk}\) for \(1\le j<k\le N\) are all independent Brownian motions (of variance t / N on the main diagonal and t / 2N above it). Then \(U^N\) is the solution of the Itô stochastic differential equation
We will use this latter definition of \(U^N_t\), via the SDE in terms of \(\mathrm {GUE}^N\)-valued Brownian motion, almost exclusively throughout this paper.
2.2 Noncommutative distributions and convergence
Let \(({\mathscr {A}},\tau )\) be a \(W^*\)-probability space: a von Neumann algebra \({\mathscr {A}}\) equipped with a faithful, normal, tracial state \(\tau \). Elements \(a\in {\mathscr {A}}\) are referred to as (noncommutative) random variables. The noncommutative distribution of any finite collection \(a_1,\ldots ,a_k\in A\) is the linear functional \(\mu _{(a_1,\ldots ,a_k)}\) on noncommutative polynomials defined by
Some authors explicitly include moments in \(a_j,a_j^*\) in the definition of the distribution; we will instead refer to the \(*\)-distribution as the noncommutative distribution \(\mu _{(a_1,a_1^*,\ldots ,a_k,a_k^*)}\) explicitly when needed. Note, when \(a\in {\mathscr {A}}\) is normal, \(\mu _{a,a^*}\) is determined by a unique probability measure \(\mathrm {Law}_a\), the spectral measure of a, on \({\mathbb {C}}\) in the usual way:
(i.e. when normal it suffices to restrict the noncommutative distribution to ordinary commuting polynomials). In this case, the support \(\mathrm {supp}\,\mathrm {Law}_a\) is equal to the spectrum \(\mathrm {spec}(a)\). If \(u\in {\mathscr {A}}\) is unitary, \(\mathrm {Law}_u\) is supported in the unit circle \(\mathbb {U}_1\). For example: a Haar unitary is a unitary operator in \(({\mathscr {A}},\tau )\) whose spectral measure is the uniform probability measure on \(\mathbb {U}_1\) (equivalently \(\tau (u^n) = \delta _{n0}\) for \(n\in {\mathbb {Z}}\)). In general, however, for a collection of elements \(a_1,\ldots ,a_k\) (normal or not) that do not commute, the noncommutative distribution is not determined by any measure on \({\mathbb {C}}\).
As a prominent example, let \(A^N\) be a normal random matrix ensemble in \(\mathbb {M}_N\): i.e. \(A^N\) is a random variable defined on some probability space \((\Omega ,{\mathscr {F}},{\mathbb {P}})\), taking values in \(\mathbb {M}_N\). The distribution of \(A^N\) as a random variable is a measure on \(\mathbb {M}_N\); but for each instance \(\omega \in \Omega \), the matrix \(A^N(\omega )\) is a noncommutative random variable in the \(W^*\)-probability space \(\mathbb {M}_N\), whose unique tracial state is \(\mathrm {tr}\). In this interpretation, the law \(\mathrm {Law}_{A^N(\omega )}\) determined by its noncommutative distribution is precisely the empirical spectral distribution
where \(\lambda _1(A^N(\omega )),\ldots ,\lambda _n(A^N(\omega ))\) are the (random) eigenvalues of \(A^N\).
Let \((A^N_1,\ldots ,A^N_n)\) be a collection of random matrix ensembles, viewed as (random) noncommutative random variables in \((\mathbb {M}_N,\mathrm {tr})\). We will assume that the entries of \(A^N\) are in \(L^{\infty -}(\Omega ,{\mathscr {F}},{\mathbb {P}})\), meaning that they have finite moments of all orders. The noncommutative distribution \(\mu _{(A^N_1,\ldots ,A^N_n)}\) is thus a random linear functional \({\mathbb {C}}\langle X_1,\ldots ,X_n\rangle \rightarrow {\mathbb {C}}\); its value on a polynomial P is the (classical) random variable \(\mathrm {tr}(P(A^N_1,\ldots ,A^N_n))\), cf. (2.3). Now, let \(({\mathscr {A}},\tau )\) be a \(W^*\)-probability space, and let \(a_1,\ldots ,a_n\in {\mathscr {A}}\). Say that \((A^N_1,\ldots ,A^N_n)\) converges in noncommutative distribution to \(a_1,\ldots ,a_n\) almost surely if \(\mu _{(A^N_1,\ldots ,A^N_n)}\longrightarrow \mu _{(a_1,\ldots ,a_n)}\) almost surely in the topology of pointwise convergence. That is to say: convergence in noncommutative distribution means that all (random) mixed \(\mathrm {tr}\) moments of the ensembles \(A^N_j\) converge a.s. to the same mixed \(\tau \) moments of the \(a_j\). Later, a stronger notion of convergence emerged.
Definition 2.1
Let \(\mathbf {A}^N = (A^N_1,\ldots ,A^N_n)\) be random matrix ensembles in \((\mathbb {M}_N,\mathrm {tr})\), and let \(\mathbf {a}=(a_1,\ldots ,a_n)\) be random variables in a \(W^*\)-probability space \(({\mathscr {A}},\tau )\). Say that \(\mathbf {A}^N\) converges strongly to \(\mathbf {a}\) if \(\mathbf {A}^N\) converges to \(\mathbf {a}\) almost surely in noncommutative distribution, and additionally
(Here \(\Vert \cdot \Vert _{\mathbb {M}_N}\)denotes the usual operator norm on \(\mathbb {M}_N\), and \(\Vert \cdot \Vert _{{\mathscr {A}}}\) denotes the operator norm on \({\mathscr {A}}\).)
This notion first appeared in the seminal paper [24] of Haagerup and Thorbjørnsen, where they showed that if \(X^N_1,\ldots ,X^N_n\) are independent \(\mathrm {GUE}^N\) random matrices, then they converge strongly to free semicircular random variables \((x_1,\ldots ,x_n)\). The notion was formalized into Definition 2.1 in the dissertation of Male (cf. [35]).
Remark 2.2
It should be noted that the choice of terminology strong convergence is at odds with the standard notion of strong topology in functional analysis, which certainly does not involve the operator norm! While this may be jarring to some readers, the terminology is now standard in free probability circles.
Male’s paper [35] also proved the following generalization: an extension property of strong convergence).
Theorem 2.3
(Male [35]) Let \(\mathbf {A}^N = (A^N_1,\ldots ,A^N_n)\) be a collection of random matrix ensembles that converges strongly to some \(\mathbf {a}=(a_1,\ldots ,a_n)\) in a \(W^*\)-probability space \(({\mathscr {A}},\tau )\). Let \(\mathbf {X}^N = (X^N_1,\ldots ,X^N_k)\) be independent Gaussian unitary ensembles independent from \(\mathbf {A}^N,\) and let \(\mathbf {x} = (x_1,\ldots ,x_k)\) be freely independent semicircular random variables in \({\mathscr {A}}\) all free from \(\mathbf {a}\). Then \((\mathbf {A}^N,\mathbf {X}^N)\) converges strongly to \((\mathbf {a},\mathbf {x})\).
(For a brief definition and discussion of free independence, see Sect. 2.3 below.) Later, together with the present first author in [13], Male proved a strong convergence result for Haar distributed random unitary matrices (which can be realized as \(\lim _{t\rightarrow \infty } U^N_t\)).
Theorem 2.4
(Collins and Male [13]) Let \(\mathbf {A}^N = (A^N_1,\ldots ,A^N_n)\) be a collection of random matrix ensembles that converges strongly to some \(\mathbf {a}=(a_1,\ldots ,a_n)\) in a \(W^*\)-probability space \(({\mathscr {A}},\tau )\). Let \(U^N\) be a Haar-distributed random unitary matrix independent from \(\mathbf {A}^N,\) and let u be a Haar unitary operator in \({\mathscr {A}}\) freely independent from \(\mathbf {a}\). Then \((\mathbf {A}^N,U^N,(U^N)^*)\) converges strongly to \((\mathbf {a},u,u^*)\).
(The convergence in distribution in Theorem 2.4 is originally due to Voiculescu [47]; a simpler proof of this result was given in [10].) Note that, for any matrix \(A\in \mathbb {M}_N\) and any operator \(a\in {\mathscr {A}}\),
These hold because the states \(\mathrm {tr}\) and \(\tau \) are faithful. These are the noncommutative \(L^p\)-norms on \(L^p(\mathbb {M}_N,\mathrm {tr})\) and \(L^p({\mathscr {A}},\tau )\) respectively. The norm-convergence statement of strong convergence can thus be rephrased as an almost sure interchange of limits: if \(\mathbf {A}^N\) converges a.s. to \(\mathbf {a}\) in noncommutative distribution, then \(\mathbf {A}^N\) converges to \(\mathbf {a}\) strongly if and only if
If we fix p instead of sending \(p\rightarrow \infty \), the corresponding notion of “\(L^p\)-strong convergence” of the unitary Brownian motion \((U^N_t)_{t\ge 0}\) to the free unitary Brownian motion \((u_t)_{t\ge 0}\) was proved in the third author’s paper [30]. This weaker notion of strong convergence does not have the same important applications as strong convergence, however. As a demonstration of the power of true strong convergence, we give an application to the eigenvalues of the Jacobi process in Sect. 5: the principal angles between subspaces randomly rotated by \(U^N_t\) evolve a.s. with finite speed for all large N.
2.3 Free probability, free stochastics, and free unitary Brownian motion
We briefly recall basic definitions and constructions here, mostly for the sake of fixing notation. The uninitiated reader is referred to the monographs [38, 49], and the introductions of the authors’ previous papers [12, 30, 32] for more details.
Let \(({\mathscr {A}},\tau )\) be a \(W^*\)-probability space. Unital subalgebras \({\mathscr {A}}_1,\ldots ,{\mathscr {A}}_m\subset {\mathscr {A}}\) are called free or freely independent if the following property holds: given any sequence of indices \(k_1,\ldots ,k_n\in \{1,\ldots ,m\}\) that are consecutively-distinct (meaning \(k_{j-1}\ne k_j\) for \(1<j\le n\)) and random variables \(a_j\in {\mathscr {A}}_{k_j}\), if \(\tau (a_j)=0\) for \(1\le j\le n\) then \(\tau (a_1\cdots a_n)=0\). We say random variables \(a_1,\ldots ,a_m\) are freely independent if the unital \(*\)-subalgebras \({\mathscr {A}}_j\equiv \langle a_j,a_j^*\rangle \subset {\mathscr {A}}\) they generate are freely independent. Freeness is a moment factorization property: by centering random variables \(a\rightarrow a-\tau (a)1_{\mathscr {A}}\), freeness allows the (recursive) computation of any joint moment in free variables as a polynomial in the moments of the separate random variables. In other words: the distribution \(\mu _{(a_1,\ldots ,a_k)}\) of a collection of free random variables is determined by the distributions \(\mu _{a_1},\ldots ,\mu _{a_k}\) separately.
A noncommutative stochastic process is simply a one-parameter family \(a=(a_t)_{t\ge 0}\) of random variables in some \(W^*\)-probability space \(({\mathscr {A}},\tau )\). It defines a filtration: an increasing (by inclusion) collection \({\mathscr {A}}_t\) of subalgebras of \({\mathscr {A}}\) defined by \({\mathscr {A}}_t \equiv W^*(a_s:0\le s\le t)\), the von Neumann algebras generated by all the random variables \(a_s\) for \(s\le t\). Given such a filtration \(({\mathscr {A}}_t)_{t\ge 0}\), we call a process \(b=(b_t)_{t\ge 0}\) adapted if \(b_t\in {\mathscr {A}}_t\) for all \(t\ge 0\).
A free additive Brownian motion is a selfadjoint noncommutative stochastic process \(x=(x_t)_{t\ge 0}\) in a \(W^*\)-probability space \(({\mathscr {A}},\tau )\) with the following properties:
-
Continuity: The map \({\mathbb {R}}_+\rightarrow {\mathscr {A}}:t\mapsto x_t\) is weak\(^*\)-continuous.
-
Free Increments: For \(0\le s\le t\), the additive increment \(x_t-x_s\) is freely independent from \({\mathscr {A}}_s\) (the filtration generated by x up to time s).
-
Stationary Increments: For \(0\le s\le t, \mu _{x_t-x_s} = \mu _{x_{t-s}}\).
It follows from the free central limit theorem that the increments must have the semicircular distribution: \(\mathrm {Law}_{x_t} = \frac{1}{2\pi t}\sqrt{(4t-x^2)_+}\,dx\). Voiculescu (cf. [46, 47, 49]) showed that free additive Brownian motions exist: they can be constructed in any \(W^*\)-probability space rich enough to contain an infinite sequence of freely independent semicircular random variables (where x can be constructed in the usual way as an isonormal process).
In pioneering work of Biane and Speicher [6, 7] (and many subsequent works such as the third author’s joint paper with Nourdin, Peccati, and Speicher [32]), a theory of stochastic analysis built on x was developed. Free stochastic integrals with respect to x are defined precisely as in the classical setting: as \(L^2({\mathscr {A}},\tau )\)-limits of integrals of simple processes, where for constant \(a\in {\mathscr {A}}, \int _0^t {\mathbbm {1}}_{[t_-,t_+]}(s)a\,dx_s\) is defined to be \(a\cdot (x_{t_+}-x_{t_-})\). Using the standard Picard iteration techniques, it is known that free stochastic integral equations of the form
have unique adapted solutions for drift \(\phi \) and diffusion \(\sigma \) coefficient functions that are globally Lipschitz. Note: due to the noncommutativity, the kinds of processes one should really use in the stochastic integral are biprocesses: \(\beta _t\in {\mathscr {A}}\otimes {\mathscr {A}}\). The stochastic integral against a single free Brownian motion \(x_t\) is then denoted \(\beta _t\# dx_t\), where this is defined so that, if \(\beta _t = a_t\otimes b_t\) is a pure tensor state, then \(\beta _t\# dx_t = a_t dx_t b_t\), allowing the process to act on both sides of the Brownian motion. (See [6, 32] for details.) A one-sided process like the one in (2.5) is typically not self-adjoint, which limits \(\phi ,\sigma \) to be polynomials, and ergo linear polynomials due to the Lipschitz constraint. That will suffice for our present purposes.) Equations like (2.5) are often written in “stochastic differential” form as
Given a free additive Brownian motion x, the associated free unitary Brownian motion \(u=(u_t)_{t\ge 0}\) is the solution to the free SDE
This precisely mirrors the (classical) Itô SDE (2.2) that determines the Brownian motion \((U^N_t)_{t\ge 0}\) on \(\mathbb {U}_N\).
The free unitary Brownian motion \((u_t)_{t\ge 0}\) was introduced by Biane in [4] via the above definition. In that paper, with more details in Biane’s subsequent [5], together with independent statements of the same type in [40], \(\mathrm {Law}_{u_t}\) was computed. Since \(u_t\) is unitary, this distribution is determined by a measure \(\nu _t\) that is supported on the unit circle \(\mathbb {U}_1\). This measure is described as follows.
Theorem 2.5
(Biane [5, Proposition 10 and Lemma 11]) For \(t>0, \nu _t\) has a continuous density \(\varrho _t\) with respect to the normalized Haar measure on \(\mathbb {U}_1\). For \(0<t<4,\) its support is the connected arc
while \(\mathrm {supp}\,\nu _t=\mathbb {U}_1\) for \(t\ge 4\). The density \(\varrho _t\) is real analytic on the interior of the arc. It is symmetric about 1, and is determined by \(\varrho _t(e^{i\theta }) = \mathrm {Re}\, \kappa _t(e^{i\theta })\) where \(z=\kappa _t(e^{i\theta })\) is the unique solution (with positive real part) to
Note that the arc (2.7) is the spectrum \(\mathrm {spec}(u_t)\) for \(0<t<4\); for \(t\ge 4, \mathrm {spec}(u_t) = \mathbb {U}_1\).
With this description, one can also give a characterization of the free unitary Brownian motion similar to the invariant characterization of the Brownian motion \((U^N_t)_{t\ge 0}\) on page 5. That is, \((u_t)_{t\ge 0}\) is the unique unitary-valued process that satisfies:
-
Continuity: The map \({\mathbb {R}}_+\rightarrow {\mathscr {A}}:t\mapsto u_t\) is weak\(^*\) continuous.
-
Freely Independent Multiplicative Increments: For \(0\le s\le t\), the multiplicative increment \(u_s^{-1}u_t\) is independent from the filtration up to time s (i.e. from the von Neumann algebra \({\mathscr {A}}_s\) generated by \(\{u_r:0\le r\le s\}\)).
-
Stationary Increments with Distribution \(\nu \): For \(0\le s\le t\), the multiplicative increment \(u_s^{-1}u_t\) has distribution given by the law \(\nu _{t-s}\).
3 The edge of the spectrum
This section is devoted to the proof of our spectral edge theorem for a single time marginal \(U^N_t\). We begin by showing how Theorem 1.1 follows from Theorem 1.3, and recast the conclusion as a strong convergence statement in Corollary 3.3. Section 3.2 is then devoted to the proof of the moment growth bound of Theorem 1.3.
3.1 Strong convergence and the proof of Theorem 1.1
We begin by briefly recalling some basic Fourier analysis on the circle \(\mathbb {U}_1\). For \(f\in L^2(\mathbb {U}_1)\), its Fourier expansion is
where dw is the normalized Lebesgue measure on \(\mathbb {U}_1\). For \(p>0\), the Sobolev space \(H_p(\mathbb {U}_1)\) is defined to be
If \(\ell >k\ge 1\) are integers, and \(\ell \ge p \ge k+\frac{1}{2}\), then \(C^\ell (\mathbb {U}_1)\subset H_p(\mathbb {U})\subset C^k(\mathbb {U}_1)\); it follows that \(H_\infty (\mathbb {U}_1)\equiv \bigcap _{p\ge 0} H_p(\mathbb {U}_1) = C^\infty (\mathbb {U}_1)\). These are standard Sobolev imbedding theorems (that hold for smooth manifolds); for reference, see [22, Chapter 5.6] and [42, Chapter 3.2].
Theorem 1.3 yields the following estimate on moment growth tested against Sobolev functions disjoint from the limit support.
Proposition 3.1
Fix \(0\le t<4\). Let \(f\in H_5(\mathbb {U}_1)\) have support disjoint from \(\mathrm {supp}\,\nu _t\). There is a constant \(C(f)>0\) such that, for all \(N\in {\mathbb {N}},\)
Proof
Denote by \(\nu ^N_t(n) {\,\equiv \,} {\mathbb {E}}\mathrm {tr}[(U^N_t)^n]\) and \(\nu _t(n) {\,\equiv } \int _{\mathbb {U}_1} w^n\,\nu _t(dw) {\,=\,} \lim _{N\rightarrow \infty } \nu _t^N(n)\). Expanding f as a Fourier series, we have
By the assumption that \(\mathrm {supp}\,f\) is disjoint from \(\mathrm {supp}\,\nu _t\), we have
Combining (3.3) and (3.4) with Theorem 1.3 yields
By assumption \(f\in H_5(\mathbb {U}_1)\), and so
Taking \(C(f) = \frac{\pi }{\sqrt{3}}\Vert f\Vert _{H_5}\) concludes the proof. \(\square \)
We now use Proposition 3.1 to give an improved variance estimate related to [34, Propositions 6.1, 6.2].
Proposition 3.2
Fix \(0\le t<4\). Let \(f\in C^6(\mathbb {U}_1)\) with support disjoint from \(\mathrm {supp}\,\nu _t\). There is a constant \(C'(f)>0\) such that, for all \(N\in {\mathbb {N}},\)
Proof
In the proof of [34, Proposition 3.1] (on p. 3179), and also in [9, Proposition 4.2 & Corollary 4.5], the desired variance is shown to have the form
where \(U^N,V^N,W^N\) are three independent Brownian motions on \(\mathbb {U}_N\). For fixed \(s\in [0,t]\), we apply the Cauchy–Schwarz inequality twice and use the equidistribution of \(U_s^NV_{t-s}^N\) and \(U_s^NW_{t-s}^N\) to yield
Since \(U^N\) and \(V^N\) are independent, \((U^N_s,V^N_{t-s})\) has the same distribution as \((U^N_s,(U^N_s)^{-1}U^N_t)\) (as the increments are independent and stationary). Thus \({\mathbb {E}}\mathrm {tr}[f'(U_s^NV_{t-s}^N)^2] = {\mathbb {E}}\mathrm {tr}[f'(U^N_t)^2]\), and so, integrating, we find
Since \(f\in C^6(\mathbb {U}_1)\), the function \((f')^2\) is \(C^5\subset H_5\), and the result now follows from Proposition 3.1, with \(C'(f) = C((f')^2)\). \(\square \)
This brings us to the proof of the spectral edge theorem.
Proof of Theorem 1.1 assuming Theorem 1.3
Fix a closed arc \(\alpha \subset \mathbb {U}_1\) that is disjoint from \(\mathrm {supp}\,\nu _t\). Let f be a \(C^\infty \) bump function with values in [0, 1] such that \(\left. f\right| _\alpha = 1\) and \(\mathrm {supp}\,f\cap \mathrm {supp}\,\nu _t=\varnothing \). Then
We now apply Chebyshev’s inequality, in the following form: let \(Y=\mathrm {Tr}[f(U^N_t)]\). Then, assuming \(1-{\mathbb {E}}(Y)>0\), we have
In our case, we have \(|{\mathbb {E}}(Y)| = |{\mathbb {E}}\mathrm {Tr}[f(U^N_t)]| = N|{\mathbb {E}}\mathrm {tr}[f(U^N_t)]| \le \frac{t^2C(f)}{N}\) by Proposition 3.1. Thus, there is \(N_0\) (depending only on f and t) so that \((1-{\mathbb {E}}\mathrm {Tr}[f(U^N_t)])^2\ge \frac{1}{2}\) for \(N\ge N_0\). Combining this with (3.7) yields
Now invoking Proposition 3.2, we find that this is \(\le \frac{2t^3 C'(f)}{N^2}\) whenever \(N\ge N_0\). It thus follows from the Borel–Cantelli lemma that the probability that \(\mathrm {spec}(U^N_t)\cap \alpha \ne \varnothing \) for infinitely many N is 0; i.e. with probability 1, for all sufficiently large \(N, U^N_t\) has no eigenvalues in \(\alpha \).
Thus, we have shown that, for any closed arc \(\alpha \) disjoint from \(\mathrm {supp}\,\nu _t\), with probability \(1, \mathrm {spec}(U^N_t)\) is contained in \(\mathbb {U}_1{\setminus }\alpha \) for all large N. In particular, fixing any open arc \(\beta \subset \mathbb {U}_1\) containing \(\mathrm {supp}\,\nu _t\), this applies to \(\alpha = \mathbb {U}_1{\setminus }\beta \). I.e. \(\mathrm {spec}(U^N_t)\) is a.s. contained in any neighborhood of \(\mathrm {supp}\,\nu _t\) for all sufficiently large N. This suffices to prove the theorem: because \(\mathrm {Law}_{U^N_t}\) converges weakly almost surely to the measure \(\nu _t\) which possesses a strictly positive continuous density on its support, any neighborhood of the spectrum of \(U^N_t\) eventually covers \(\mathrm {supp}\,\nu _t\). \(\square \)
Thus, we have proved Theorem 1.1 under the assumption that Theorem 1.3 is true. Before turning to the proof of this latter result, let us recast Theorem 1.1 in the language of strong convergence, as we will proceed to generalize this to the fully noncommutative setting in Sect. 4.
Corollary 3.3
For \(N\in {\mathbb {N}},\) let \((U^N_t)_{t\ge 0}\) be a Brownian motion on \(\mathbb {U}_N\). Let \((u_t)_{t\ge 0}\) be a free unitary Brownian motion. Then for any fixed \(t\ge 0, (U^N_t,(U^N_t)^*)\) converges strongly to \((u_t,u_t^*)\).
Proof
Since \(U^N_t\rightarrow u_t\) in noncommutative distribution, strong convergence is the statement that
in operator norms. Fix a noncommutative polynomial P in two variables, and let p be the unique Laurent polynomial in one variable so that \(P(U,U^*) = p(U)\) for every unitary operator U. Since \(U_t^N\) is normal, \(\Vert p(U_t^N)\Vert = \max \{|\lambda |:\lambda \in p(\mathrm {spec}(U^N_t))\}\); similarly, \(\Vert p(u_t)\Vert = \max \{|\lambda |:\lambda \in p(\mathrm {supp}\,\nu _t)\}\) where \(\mathrm {supp}\,\nu _t\) is the arc in (2.7).
Let \(\Lambda _p^N = |p|(\mathrm {spec}(U^N_t))\), and let \(\Lambda _p = |p|(\mathrm {supp}\,\nu _t)\). (Here |p| denotes the modulus of the polynomial function, \(|p|(u) = |p(u)|\).) Since \(\mathrm {spec}(U^N_t)\) converges to \(\mathrm {supp}\,\nu _t\) in Hausdorff distance and all the sets are compact, it follows easily from the continuity of |p| (on the unit circle) that \(\Lambda _p^N\) converges to \(\Lambda _p\) in Hausdorff distance as well. In particular, for any \(\epsilon >0\), there is some \(N_0\in {\mathbb {N}}\) so that, for all \(N\ge N_0, (\Lambda _p^N)_\epsilon \subseteq \Lambda _p\) and \((\Lambda _p)_\epsilon \subseteq \Lambda _p^N\). It follows that \(\max \Lambda _p -\epsilon \le \max \Lambda _p^N \le \max \Lambda _p+\epsilon \). This shows that \(\Vert p(U_t^N)\Vert = \max \Lambda _p^N \rightarrow \max \Lambda _p = \Vert p(u_t)\Vert \), as desired. \(\square \)
Remark 3.4
In fact, the converse of Corollary 3.3 also holds: strong convergence of \(U^N_t\rightarrow u_t\) (for a fixed \(t<4\)) implies convergence of the spectrum in Hausdorff distance. Indeed, suppose we know strong convergence. In particular, taking the polynomial \(P(U) = U-1\), we then have \(\Vert U_t^N-I_N\Vert \rightarrow \Vert u_t-1\Vert \). Since the spectrum of \(u_t\) is an arc symmetric about \(1, \mathrm {spec}(u_t) = B_{\Vert u_t-1\Vert }(1)\cap \mathbb {U}_1\) (here \(B_R(1)\) denotes the ball \(\{z\in {\mathbb {C}}:|z-1|<R\}\) ). Note that \(\Vert U_t^N-I_N\Vert = \max _k \Vert \lambda _k(t)-1\Vert \); this shows that all eigenvalues \(\lambda _k(t)\) are in an arc very close to \(\mathrm {spec}(u_t)\) for large N. This shows that \(\mathrm {spec}(U^N_t)\) is eventually contained in any neighborhood of \(\mathrm {supp}\,\nu _t\); the other half of the convergence in Hausdorff distance follows from the convergence in distribution (and strict positivity of the limit density \(\nu _t\) on \(\mathrm {supp}\,\nu _t\)).
When \(t\ge 4, \mathrm {supp}\,\nu _t =\mathbb {U}_1\), and strong convergence becomes vacuously equivalent to the known convergence in distribution.
3.2 The proof of Theorem 1.3
This section is devoted to the proof of the main moment growth bound, i.e. (1.3). Before proceeding with our proof which is quite involved, it is worth noting a key feature. The bound (1.3) on the speed of convergence \(\nu ^N_t(n)\rightarrow \nu _t(n)\) depends polynomially on n; this is crucial to the proof of Theorem 1.1. If one only requires the \(O(\frac{1}{N^2})\) bound of this estimate without much regard for the dependence on n, a much simpler (though still nontrivial) approach can be found in the third author’s paper [30, Section 3.3], which provides a bound of the form \(K(t,n)/N^2\), where \(K(t,n) \sim \frac{tn^2}{2}\exp (\frac{tn^2}{2})\). This growth in n is much too large to get control over test functions that are only in a Sobolev space, or even in \(C^\infty (\mathbb {U}_1)\); the largest class of functions for which this Fourier series is summable is an ultra-analytic Gevrey class. That blunter estimate does not suffice for our present purposes; showing polynomial dependence on n turns out to require very careful analysis so as not to ignore the many cancellations in the complicated expansions for the moments.
Remark 3.5
We note that the blunter bound in [30] was proved not only for \(U^N\), but for a family of diffusions on \(\mathbb {GL}_N\) including both \(U^N\) and the Brownian motion on \(\mathbb {GL}_N\). It remains open whether a polynomial bound like (1.3) holds for this wider class of diffusions.
The proof of the weaker bound described above relied on an explicit decomposition of the Laplacian on \(\mathbb {U}_N\) in the form \(D+\frac{1}{N^2}L\), which was exploited in the third author’s papers [30, 31] and joint work with Driver and Hall [20] (and Cébron’s independent work [8]), in the complementary work of the second author [14] and preceding paper of T. Lévy [33], and in some form also in the preceding work of Rains [40], Sengupta [43], and others. In that approach, the idea was to decompose the relevant space of functions (polynomials in traces of powers of the matrix) into a nested family of finite-dimensional subspaces all invariant under the Laplacian, and then appropriately estimate the distortion between the norm of \(\exp (D)\) and \(\exp (D+\frac{1}{N^2}L)\) on each such space. While an approach of that nature might conceivably yield bounds similar to (1.3), our present approach is quite different.
To begin: we will actually prove the following Cauchy sequence growth estimate. We again use the notation \(\nu ^N_t(n) = {\mathbb {E}}[\mathrm {tr}(U^N_t)^n]\).
Proposition 3.6
Let \(N,n\in {\mathbb {N}},\) and fix \(t\ge 0\). Then
This is the main technical result of the first part of the paper, and its proof will occupy most of this section. Let us first show how Theorem 1.3 follows from Proposition 3.6.
Proof of Theorem 1.3 assuming Proposition 3.6
Since \(\lim _{N\rightarrow \infty } \nu ^N_t(n) = \nu _t(n)\), we have the following convergent telescoping series:
Now apply (3.8) with N replaced by \(N2^k\), we find
Summing the geometric series proves the theorem. \(\square \)
3.2.1 Outline of the proof of Proposition 3.6
The proposition requires comparison of a moment \(\nu _t^N(n)\) of an \(N\times N\) unitary Brownian motion with a moment \(\nu _t^{2N}(n)\) of a \(2N\times 2N\) unitary Brownian motion. To compare them, we need to choose a coupling between the two processes in different spaces. As such, fix a Brownian motion \(U^{2N}\) on \(\mathbb {U}_{2N}\), along with two Brownian motions \(U^{N,1},U^{N,2}\) on \(\mathbb {U}_N\), so that the processes \(U^{2N},U^{N,1},U^{N,2}\) are all independent. For \(t\ge 0\), let \(B^{2N}_t\in \mathbb {U}_{2N}\) denote the block diagonal random matrix
We will hold t fixed through; let us fix the notation
This process will be used very often in what follows.
Setting \(s=0\), we have \(A^{2N}_0 = U_t^{2N}\); on the other hand, setting \(s=t\), we have \(A^{2N}_t = B^{2N}_t\). Hence
Therefore, setting
we see that the quantity \(\nu _t^N(n)-\nu _t^{2N}(n)\) to be estimated in Proposition 3.6 is equal to
The main approach of the proof will be to show that \(F\in C^1[0,t]\), so that the Fundamental Theorem of Calculus allows us to express
and then appropriately estimate \(|F'(s)|\) to achieve the desired bound of (3.8).
Due to the nonlinearity (for \(n>1\)) of the trace moment \(F(s) = {\mathbb {E}}\mathrm {tr}[(A_s^{2N})^n]\) as a function of \(A_s^{2N}\), it is useful to multilinearize this quantity in what follows. To do so, we will work in the n-fold tensor product of \(\mathbb {M}_{2N}\), essentially replacing a power \(A^n\) with a tensor power \(A^{\otimes n} = A\otimes A \otimes \cdots \otimes A \in (\mathbb {M}_{2N})^{\otimes n}\); since we could identify this space with \(\mathbb {M}_{2Nn}\), we will still refer to such tensor product operators as matrices. To recover the original quantity (in terms of the trace of \(A^n\)), we cannot simply take the trace of \(A^{\otimes n}\) (which would produce \([\mathrm {Tr}(A)]^n\)); instead, we must involve an action of the symmetric group \(S_n\). To any permutation \(\sigma \in S_n\), we associate a matrix \([\sigma ]\in (\mathbb {M}_{2N})^{\otimes n}\) by permuting the tensor indices: for any vector \(v_1\otimes \cdots \otimes v_n \in ({\mathbb {C}}^{2N})^{\otimes n}\),
Remark 3.7
This representation of \(S_n\) on \(({\mathbb {C}}^{2N})^{\otimes n}\) is sometimes called the Schur–Weyl representation. In general, for any vector space V, the Schur–Weyl representation of \(S_n\) on \(V^{\otimes n}\) is faithful whenever \(\mathrm {dim} V\ge n\), and since we hold n fixed and send \(N\rightarrow \infty \), we may always safely assume the representation is faithful; i.e. the map \(\sigma \mapsto [\sigma ]\) may be assumed to be one-to-one.
This representation is dual to the standard representation of \(\mathrm {GL}(V)\) on \(V^{\otimes n}\)—\(G\cdot v_1\otimes \cdots \otimes v_n = (Gv_1)\otimes \cdots \otimes (Gv_n)\)—in the sense that the two representations commute and are in fact mutual centralizers in \(\mathrm {End}(V^{\otimes n})\). This is the so-called Schur–Weyl duality, which allows for a lot of useful computations by interchanging the two representations back and forth. The Schur–Weyl duality plays a central role in T. Lévy’s approach to the heat kernel on unitary groups, cf. [33]; we will not need much of that detailed approach here, but we are motivated by it in our present constructions.
We may readily verify that, if \(\sigma \in S_n\) and has cycle decomposition \(\sigma = c_1\cdots c_r\) with \(c_k = (i^k_1 \cdots i^k_{\ell _k})\), then for \(A_1,\ldots ,A_n\in \mathbb {M}_{2N}\),
where we have (in this one instance only) emphasized over which space each trace is taken. Note, in particular, that if \(\sigma = (i_1\cdots i_n)\) is a cycle, then \(\mathrm {Tr}([\sigma ]A_1\otimes \cdots \otimes A_n) = \mathrm {Tr}(A_{i_n}\cdots A_{i_1})\) is a single trace. Hence
where \((1\cdots n)\) denotes the standard full cycle in \(S_n\).
Interchanging the trace and expectation, we can now work with the following simpler tensor-valued function:
Then we have \(F(s) = \frac{1}{N}\mathrm {Tr}\left( [(1\cdots n)]G(s)\right) \), and hence to prove F is \(C^1\), it suffices to prove that G is \(C^1\). Computing this derivative is greatly aided by the independence of the processes \(U^{2N}\) and \(B^{2N}\): by definition \((A_s^{2N})^{\otimes n} = (U_{t-s}^{2N}B_s^{2N})^{\otimes n} = (U_{t-s}^{2N})^{\otimes n}(B_s^{2N})^{\otimes n}\), and by independence we have
To concretely express the derivative of G, we introduce a little more notation. First, due to the block structure of the matrix \(B^{2N}_s\), the two projections
will play a role in all of what follows. Because the diffusion term in the SDE (2.2) governing \(U^{2N}_s\) depends linearly on \(U^{2N}_s\), there is mixing that can be expressed as a combination of all transpositions in the Schur–Weyl representation. Hence, we introduce the following notation: for any \(A,B\in \mathbb {M}_{2N}\) and \(1\le i<j\le n\), denote by \([A\otimes B]_{i,j}\) the following matrix in \((\mathbb {M}_{2N})^{\otimes n}\):
where \(I=I_{2N}\) is the identity matrix in \(\mathbb {M}_{2N}\).
With this notation in hand, we can now show that \(G\in C^1[0,t]\), and compute that its derivative is given by
where \([(i\,j)]\) denotes the Schur-Weyl representation of the transposition in \(S_n\), cf. (3.11). This is proved in Lemma 3.8 in Sect. 3.2.2 below. The computation begins by writing down SDEs for \((U_s^{2N})^{\otimes n}\) and\((B_s^{2N})^{\otimes n}\) (following from (2.2)), and then using the product rule in conjunction with (3.15).
Since F is a linear functional of G, this shows that F is also \(C^1[0,t]\). The next step in the proof is to plug (3.18) into (3.13) to derive an expression for the derivative \(F'(s)\). The derivative \(G'(s)\) is a sum of \(\left( {\begin{array}{c}n\\ 2\end{array}}\right) \) terms, but after contracting them in the trace, the derivative \(F'(s)\) can be written as a sum of \(n-1\) similar terms:
where
This is proved in Lemma 3.9 below. Combining this with (3.10), we therefore have
It now behooves us to estimate the terms \(H_{p,n-p}(s)\), cf. (3.19). These terms have an explicit \(\frac{1}{N^2}\) factor, which appears to be good news for the desired estimate of Proposition 3.6. Note, however, that (3.19) involves expectations of products of pairs of unnormalized traces of powers of \(A^{2N}_s\). Since \(A^{2N}_s\) possesses a large-N limit noncommutative distribution in terms of normalized traces, the leading order contribution of the first term in \(H_{p,n-p}(s)\) is O(1). In fact, there are many cancellations between the two terms; this is the key observation of the whole proof. The way we will encapsulate the cancellations is by first re-expressing \(H_{p,q}(s)\) as a combination of covariances:
This is proved in Lemma 3.10, and is a fairly straightforward computation: the \(P_1\) and \(P_2\) terms can be combined due to the rotational-invariance of the process \(A_s^{2N}\), and the remaining product terms cancel between the two covariances.
While the two expectation terms in the expression for \(N^2H_{p,q}(s)\) in (3.19) are each \(O(N^2)\), once the cancellations between them have been taken into account to produce the covariance expression of (3.21), we find that \(N^2H_{p,q}(s) = O(1)\). In fact, each of the covariance terms in (3.21) is O(1): the precise estimates are
for \(0\le s\le t\). From here, the remainder of the proof is routine: (3.21) shows that \(|H_{p,n-p}(s)|\le \frac{5p(n-p)(t+3s)}{4N^2}\); summing \(0\le p\le n\), and integrating \(s\in [0,t]\) gives a cubic in n times a linear factor in t times \(\frac{1}{N^2}\), and then (3.20) completes the proof. These details are written out more explicitly at the end of Sect. 3.2.2.
Thus, the proof is completed by proving the covariance estimates (3.22). This is the most technically challenging part of the proof, and requires several involved steps, which we outline here.
-
1.
Multilinearize the covariances: as we did in replacing the moment F(s) with the tensor-valued function G(s), we compute that both covariances in (3.21) can be expressed as certain contractions of a common covariance tensor \(\mathcal {C}_{p,n-p}(s)\), defined by
$$\begin{aligned} \mathcal {C}_{p,n-p}(s) \equiv {\mathbb {E}}((A_s^{2N})^{\otimes n})-{\mathbb {E}}((A_s^{2N})^{\otimes p})\otimes {\mathbb {E}}((A_s^{2N})^{\otimes (n-p)}). \end{aligned}$$(3.23)The two covariance terms in (3.21) can be expressed in terms of \(\mathcal {C}_{p,n-p}(s)\) by tracing against certain p-dependent permutation and projection matrices. This computation is the content of Lemma 3.11.
-
2.
Explicitly compute the covariance tensor \(\mathcal {C}_{p,n-p}(s)\): using the tensorized SDE for the unitary Brownian motion (following from (2.2), as used in the computation (3.18) of \(G'(s)\)) and taking expectations, we compute two explicit matrices \(\Phi _p,\Psi _p\in (\mathbb {M}_{2N})^{\otimes n}\) for \(0\le p\le n\) such that
$$\begin{aligned} \mathcal {C}_{p,n-p}(s) = e^{-\frac{nt}{2}}[e^{(t-s)\Phi _n}e^{s\Psi _n}-e^{(t-s)\Phi _p}e^{s\Psi _p}]. \end{aligned}$$The matrices \(\Phi _p\) and \(\Psi _p\) are given by certain p-restricted sums of transposition matrices \([(i\,j)]\) and the tensorized projection matrices \([P_\ell \otimes P_\ell ]_{i,j}\), and are explicitly defined below in (3.36). These computations are done in Lemma 3.12 and Corollary 3.13.
-
3.
Use Duhamel’s formula to produce more cancellations: for any complex matrices X and Y, Duhamel’s formula asserts that
$$\begin{aligned} e^X-e^Y = \int _0^1 e^{(1-u)X}(X-Y)e^{uY}\,du. \end{aligned}$$(3.24)Applying this in telescoping fashion to the above expression for \(\mathcal {C}_{p,n-p}(s)\) and simplifying yields the expression
$$\begin{aligned} \mathcal {C}_{p,n-p}(s)= & {} \int _0^{t-s} e^{(t-s-u)\Phi _n}(\Phi _n-\Phi _p) e^{u\Phi _p}e^{s\Psi _n}\,du \\&+ \int _0^s e^{(t-s)\Phi _p}e^{(s-u)\Psi _n}(\Psi _n-\Psi _p)e^{u\Psi _p}\,du. \end{aligned}$$This is helpful because \(\Phi _n-\Phi _p\) and \(\Psi _n-\Psi _p\) yield yet more cancellations. The resulting expression for \(\mathcal {C}_{p,n-p}(s)\) is given in Lemma 3.14.
-
4.
Reinterpret the terms as expectations of products of unitary and projection matrices: since the matrices \(\Phi _p\) and \(\Psi _p\) generate (via exponential) the expectations of tensor powers of \(U^{2N}\) and \(B^{2N}\), it is possible to reinterpret the preceding expression for \(\mathcal {C}_{p,n-p}(s)\) as a sum of expected traces of matrices that are tensor products of independent copies of \(U^{2N}\) and \(B^{2N}\) mixed with certain permutation matrices and projection matrices (given in the definition (3.36) of \(\Phi _p\) and \(\Psi _p\)).
To be more precise, for \(0\le p\le n\) and i, j with \(1\le i\le p\) and \(p<j\le n\), there are random matrices \(R^p_{i,j}(u;t,s),Q^p_{i,j}(u;t,s)\in (\mathbb {M}_{2N})^{\otimes n}\) such that
$$\begin{aligned} \mathcal {C}_{p,n-p}(s) = \frac{1}{2N} \sum _{1\le i\le p<j\le n} \left( \int _0^{t-s} {\mathbb {E}}[R^p_{i,j}(u;t,s)]\,du + \int _0^s {\mathbb {E}}[Q^p_{i,j}(u;t,s)]\,du\right) . \end{aligned}$$The matrices \(R^p_{i,j}(u;t,s)\) and \(Q^p_{i,j}(u;t,s)\) are defined in (3.45) and (3.46); each is a pure tensor product of matrices built out of independent copies of the processes \(U^{2N}\) and \(B^{2N}\), together with permutation and projection matrices. This is proved in Lemma 3.15.
-
5.
Contract \(\mathcal {C}_{p,n-p}(s)\) to yield expressions for the desired covariance terms, and use soft estimates to prove (3.22): the desired covariance terms are related to \(\mathcal {C}_{p,n-p}(s)\) via contraction against certain permutation and projection matrices, as explained in Step 1. Performing these contractions with the integrand expressions in Step 4 yield a sum of terms all of which are given as an expected (unnormalized) trace \(\mathrm {Tr}\) of a product of unitary and projection matrices. In particular, as each is a contraction, the modulus of the trace is bounded by 2N (by the Schatten–Hölder inequality), which cancels the \(\frac{1}{2N}\) factor before the sum in the final expression for \(\mathcal {C}_{p,n-p}(s)\). Integrating and summing then yields the desired estimates (3.22) to complete the proof. The calculations are performed in Lemmas 3.16 and 3.17.
3.2.2 Proof of Proposition 3.6
We now proceed to fill in the details of the proof outline given in the previous section. We succinctly restate terminology and notation throughout to make the proof more readable. We begin with the computation of the derivative of the tensor-valued function G.
Lemma 3.8
Fix \(t>0\) and \(N,n\in {\mathbb {N}},\) and let \(G:[0,t]\rightarrow (\mathbb {M}_{2N})^{\otimes n}\) denote the function \(G(s) = {\mathbb {E}}[(A^{2N}_s)^{\otimes n}]\). Then \(G\in C^1[0,t],\) and its derivative is given by (3.18):
Proof
To begin, note that \(U^{2N}\) and \(B^{2N}\) are independent, and so following (3.15) we have
where both factors \(G_1,G_2\) are continuous (since they are expectations of polynomials in diffusions). Using the SDE (2.2) and applying Itô’s formula to the diffusion \(B^{2N}\) shows that there is an \(L^2\)-martingale \((M^{2N}_s)_{s\ge 0}\) such that
where \(E_{c,d}\in \mathbb {M}_{2N}\) is the standard matrix unit (all 0 entries except a 1 in entry (c, d)) with indices written modulo 2N. Using the projection matrices \(P_1\) and \(P_2\) of (3.16) and notation (3.17), we can write this SDE in the form
It follows that \(G_2\in C^1[0,t]\), and
At the same time, a similar calculation with Itô’s formula applied with (2.2) shows that there is an \(L^2\)-martingale \(({\widetilde{M}}^{2N}_s)_{s\ge 0}\) such that
which, changing \(s\mapsto t-s\), implies that \(G_1\) is \(C^1[0,t]\) and
Combining (3.27) and (3.29), the product rule \(G'(s) = G_1(s)G_2'(s) + G_2(s)G_1'(s)\) shows that \(G\in C^1[0,t]\). Using \(G=G_1\cdot G_2\) again when recombining, we see that the \(\frac{n}{2}\) terms cancel; moreover, the same recombination due to independence yields
Finally, in the first term, notice that \([(i\,j)](B^{2N}_s)^{\otimes n}=(B^{2N}_s)^{\otimes n}[(i\,j)]\) (since the Schur-Weyl representation of any permutation commutes with any matrix of the form \(B^{\otimes n}\)). Hence, we have
Similarly factoring out the G(s) from the second term yields the result. \(\square \)
This allows us to compute the derivative of \(F(s) = \frac{1}{N}\mathrm {Tr}\left( [(1\cdots n)]G(s)\right) \), in terms of the auxiliary functions \(H_{p,q}(s)\) defined in (3.19).
Lemma 3.9
For \(0\le s\le t,\)
where
Proof
Applying (3.18), we have
We now use the trace property in the first term to cyclically reorder the matrices; thus we must compute \([(i\,j)][(1\cdots n)] = [(i\,j)(1\cdots n)]\). Noting that \((i\,j)(1\,\cdots \,n) = (1,\ldots ,i-1,j,\ldots ,n)(i\cdots j-1)\), it follows from (3.12) that
A similar calculation shows that
Thus, we have
The terms inside the overall summation depend on (i, j) only through \(j-i\); in other words, the overall sum has the form
for a function \(h:\{1,\ldots ,n-1\}^2\rightarrow {\mathbb {C}}\) which is symmetric in its two variables. For such a sum in general we have
since the number of (i, j) with \(1\le i<j\le n\) and \(j-i=p\) is \((n-p)\). Now using the symmetry and reindexing by \(q=n-p\) we have
Applying this with the above summations yields the result. \(\square \)
Having now expressed the desired quantities in terms of \(H_{p,q}(s)\), we proceed to encapsulate the many cancellations by re-expressing \(H_{p,q}(s)\) as a linear combination of covariances.
Lemma 3.10
For \(s\ge 0\) and \(p,q\in {\mathbb {N}}, H_{p,q}(s)\) is given by the linear combination of covariances in (3.21):
Proof
From (3.19), \(N^2 H_{p,q}(s)\) is a difference of two terms. The first is
The second term is a sum
Let R be the block rotation matrix of \({\mathbb {C}}^{2N}\) by \(\frac{\pi }{2}\) in each factor of \({\mathbb {C}}^N\), so that \(RP_1R^*= P_2\). Since the distribution of \(A^{2N}_s\) is invariant under rotations, it follows that
do not depend on \(\ell \) (as each is a conjugation-invariant polynomial function in \(A_s^{2N}\)). In particular, the two terms in the \(\ell \)-sum are equal, and so the second term in \(H_{p,q}(s)\) is
Moreover, since \({\mathbb {E}}[\mathrm {Tr}((A^{2N}_s)^pP_1)] = {\mathbb {E}}[\mathrm {Tr}((A^{2N}_s)^pP_2)]\) and \(P_1+P_2 = I\), we have \({\mathbb {E}}[\mathrm {Tr}((A^{2N}_s)^pP_1)] = \frac{1}{2}{\mathbb {E}}[\mathrm {Tr}((A^{2N}_s)^p)]\). Thus, the last term in (3.32) is \(-\frac{1}{4}{\mathbb {E}}[\mathrm {Tr}((A^{2N}_s)^p)]{\mathbb {E}}[\mathrm {Tr}((A^{2N}_s)^q)]\). Combining this with (3.31) then yields the result. \(\square \)
Now, to begin the process of estimating these covariances, we re-express them using the Schur–Weyl representation, in terms of the two-cycle permutation
(For present notational convenience, we de-emphasize the role of n, letting \(q=n-p\).)
Lemma 3.11
Let \(\mathcal {C}_{p,q}(s)\) denote the covariance tensor of (3.23),
Then the two covariance terms in (3.21) are given by
Proof
To begin, observe that for any matrix A, (3.12) yields
For notational convenience in this proof, denote the full cycle \((1\cdots p)\in S_p\) by \(\gamma _p\), so that \(\mathrm {Tr}(A^p) = \mathrm {Tr}\left( A^{\otimes p}[\gamma _p]\right) \). It follows that
thus proving (3.33). At the same time, using the fact that the projection \(P_1\) is diagonal, we have for any matrix \(A\in \mathbb {M}_{2N}\)
where we remind the reader that \([P_\ell \otimes P_\ell ]_{i,j}\) references notation (3.17); here \(i=p\) and \(j=p+q\) (the final tensor factor). The derivation of (3.34) follows from here analogously to the above computations. \(\square \)
Thus, from (3.21), (3.33), and (3.34), to estimate \(H_{p,n-p}(s)\) we must understand the covariance tensor \(\mathcal {C}_{p,n-p}(s)\). To that end, we introduce some notation. For \(1\le i<j\le n\), define the matrix \(T_{i,j}\in (\mathbb {M}_{2N})^{\otimes n}\) by
Additionally, for \(1\le p\le n\), we introduce \(\Phi _p,\Psi _p\in (\mathbb {M}_{2N})^{\otimes n}\) as follows:
with the understanding that, when \(p=n\), the sum is simply over \(1\le i<j\le n\).
Lemma 3.12
Let \(p\in \{1,\ldots ,n\},\) and let \(0\le s\le t\). Then
where, in the case \(p=n,\) we interpret the 0-fold tensor product as the identity as usual.
Proof
Returning to the SDEs (3.26) and (3.28), taking expectations we find that
Since the processes \(B^{2N}\) and \(U^{2N}\) start at the identity, it is then immediate to verify that the solutions to these ODEs are
Now, for the tensor product, we decompose
We can express these expectations as in (3.40), provided we note that \((i\,j)\) now refers (alternatively) to the action of \(S_p\) or \(S_{n-p}\) on \((\mathbb {M}_{2N})^{\otimes n} = (\mathbb {M}_{2N})^{\otimes p}\otimes (\mathbb {M}_{2N})^{\otimes (n-p)}\), either trivially in the first factor or the second. The result is that
Note that all the \((i\,j)\) terms in the first sum commute with all the \((i'\,j')\) terms in the second sum (since \(i<j<i'<j'\)) and taking the product, we can combine to yield
verifying (3.37). An entirely analogous analysis proves (3.38).
Finally, using independence as in (3.25) to factor
and substituting \(s\mapsto t-s\) in (3.37), (3.39) follows from (3.38) and (3.42). \(\square \)
Corollary 3.13
For \(0\le p\le n\) and \(0\le s\le t,\)
Proof
From (3.39), we have
for \(0\le p\le n\). In particular, taking \(p=n\) (in which case the second factor is trivial and omitted) we have
Subtracting these two and using the definition (3.23) of \(\mathcal {C}_{p,n-p}(s)\) yields the result. \(\square \)
The next technical lemma uses Duhamel’s formula to rewrite the expression in (3.43) in a more complicated, but more computationally useful, way.
Lemma 3.14
For \(0\le s\le t,\)
Proof
We begin by using Duhamel’s formula (3.24), applied to (3.43) by adding and subtracting the mixed term \(e^{(t-s)\Phi _p}e^{s\Psi _n}\):
where we have made the substitution \(u\mapsto (t-s)u\) in the first integral and \(u\mapsto su\) in the second. Now, from the definition (3.36) of \(\Phi _p\) and \(\Psi _p\), we have
Substituting these into (3.44) yields the result. \(\square \)
We now reinterpret the exponentials in the integrals as expectations of the processes \(U^{2N}\) and \(B^{2N}\), using (3.37) and (3.38). The first integrand is
By definition \(U^{2N}\) and \(B^{2N}\) are independent. Let us introduce two more copies \(V^{2N},W^{2N}\) of \(U^{2N}\) so the \(\{U^{2N},V^{2N},W^{2N},B^{2N}\}\) are all independent. Then this product may be expressed as the expectation of
Similarly, if we introduce independent copies \(C^{2N}\) and \(D^{2N}\) of \(B^{2N}\) so that all the processes \(U^{2N}, V^{2N}, W^{2N}, B^{2N}, C^{2N}, D^{2N}\) are independent, the second integrand can be expressed as the expectation of
To summarize, we have computed the following.
Lemma 3.15
Let \(0\le s\le t\) and \(p\in \{1,\ldots ,n\}\). Then
We will now use this, together with (3.21), (3.33), and (3.34), to estimate \(H_{p,n-p}(s)\). We estimate each of the two covariance terms separately, in the following two lemmas.
Lemma 3.16
For \(p\in \{1,\ldots ,n\}\) and \(0\le s\le t,\)
Proof
From (3.47) together with (3.33), the quantity whose modulus we wish to estimate is
For the first term, we note \((U_{t-s-u}^{2N})^{\otimes n}[\gamma _{p,n-p}] = [\gamma _{p,n-p}](U_{t-s-u}^{2N})^{\otimes n}\) (the Schur-Weyl representation of any permutation in \(S_n\) commutes with a matrix of the form \(M^{\otimes n}\)). It follows from the trace property that
Since \(i\le p<j\), the permutation \(\gamma _{p,n-p}(i\,j)\) is a single cycle. Thus, by (3.12), the \(\otimes n\)-fold trace reduces to a trace of some p, n, i, j-dependent word in \(V_u^{2N}, W_u^{2N}, B_s^{2N}\), and \(U^{2N}_{t-s-u}\). This word is a random element of \(\mathbb {U}_{2N}\), and hence
Hence, the first integral is
For the second term, the fact that \(T_{i,j} = 2[(i\,j)][P_1\otimes P_1 + P_2\otimes P_2]_{i,j}\) only acts non-trivially in the i, j factors, and \(i\le p<j\), shows that (as above) \(T_{i,j}\) commutes with \((C^{2N}_u)^{\otimes p}\otimes (D_u^{2N})^{\otimes (n-p)}\). Hence, we can express the second integrand as
where we have used the fact that \([\gamma _{p,n-p}]\) commutes with any matrix of the form \(C^{\otimes p}\otimes D^{\otimes (n-p)}\) in the second equality, and then the trace property in the third equality. As above, each of these terms reduces to a trace of a word, this time of the form
where \(\mathcal {U}\) and \(\mathcal {V}\) are random matrices in \(\mathbb {U}_{2N}\) (depending on p, n, i, j). Since \(\Vert P_\ell \Vert \le 1\), the modulus of each term is \(\le 2N\), giving an overall factor of \(\le 8N\). Combining with the \(\frac{1}{2N}\) in the integral, this gives
Hence, from (3.49) and (3.51), the modulus of the desired covariance is bounded by
yielding (3.48). \(\square \)
Lemma 3.17
For \(p\in \{1,\ldots ,n\}\) and \(0\le s\le t,\)
Proof
From (3.47) together with (3.34), the quantity whose modulus we wish to estimate is
For the first term, we expand the integrand, commuting \([(i\,j)]\) past \((U^{2N}_{t-s-u})^{\otimes n}\) as in the proof of Lemma 3.16, to give
As above, since \(\gamma _{p,n-p}\cdot (i,j)\) is a single cycle, this trace reduces to a trace over \({\mathbb {C}}^{2N}\), of the form
where \(\mathcal {U}'\) and \(\mathcal {V}'\) are random unitary matrices in \(\mathbb {U}_{2N}\) composed of certain i, j, p, n-dependent words in \(U^{2N}_{t-s-u}, V^{2N}_u, W^{2N}_u\), and \(B^{2N}_s\). As \(\Vert P_1\Vert \le 1\), it follows that this normalized trace is \(\le 1\), and so the first integral in (3.53) is \(\le (t-s)\) in modulus, as in (3.49).
Similarly, we expand the second term as in (3.50), which gives the sum over \(\ell \in \{1,2\}\) of the expected normalized trace of
As in the above cases, since \(\gamma _{p,n-p}(i,j)\) is a single cycle, this is equal to a single trace \(\mathrm {Tr}(A_1\cdots A_n)\) where \(A_1,\ldots ,A_n\) belong to the set \(\{V_{t-s}^{2N},W_{t-s}^{2N},B^{2N}_{s-u},C^{2N}_u,D^{2N}_u, P_\ell ,P_1\}\). As each of these is either a random unitary matrix or a projection, it follows that the expected normalized trace has modulus \(\le 1\), and so the \(\frac{1}{N}\)-weighted sum of 2 terms, each of modulus \(\le 2N\), gives a contribution no bigger than 4. The remainder of the proof is exactly as the end of the proof of Lemma 3.16. \(\square \)
Finally, we are ready to conclude this section.
Proof of Proposition 3.6
From (3.20), we have
Lemma 3.10 then gives
Combining this with (3.48) and (3.52) therefore yields
Integration then gives
The sum over p has the exact value \(\frac{1}{6}(n^3-n) \le \frac{n^3}{6}\). The blunt estimate \(\frac{25}{96}<\frac{3}{4}\) yields the result. \(\square \)
4 Strong convergence
In this section, we prove Theorem 1.4. We begin by showing (in Sect. 4.1) that the eigenvalues of the unitary Brownian motion at a fixed time converge to their “classical locations”, and we use this to prove that the unitary Brownian motion can be uniformly approximated by a function of a Gaussian unitary ensemble (for time \(t<4\)). We then use this, together with Male’s Theorem 2.3, to prove Theorem 1.4.
4.1 Marginals of unitary Brownian motion and approximation by \(\mathrm {GUE}^N\)
We begin with the following general result on convergence of empirical measures. As usual, for a probability measure \(\mu \) on \({\mathbb {R}}\), the cumulative distribution function \(F_\mu \) is the nondecreasing function \(F_\mu (x) = \mu ((-\infty ,x])\) and its right-inverse is the left-continuous nondecreasing function
with \(F_{\mu }^{-1}(0)=-\infty .\) If \(\mu \) has a density \(\rho \), we may abuse notation and write \(F_\mu = F_\rho \).
Proposition 4.1
For each \(N\in {\mathbb {N}},\) let \((x^N_k)_{k=1}^N\) be points in \({\mathbb {R}}\) with \(x^N_1\le \cdots \le x^N_N\). Let \(\mu ^N = \frac{1}{N}\sum _{k=1}^N \delta _{x^N_k}\) be the associated empirical measures. Suppose the following hold true.
-
1.
There is a compact interval \([a_-,a_+]\) and a continuous probability density \(\rho \) with \(\mathrm {supp}\,\rho = [a_-,a_+]\) so that, with \(\mu (dx) = \rho (x)\,dx,\) we have \(\mu ^N\rightharpoonup \mu \) weakly as \(N\rightarrow \infty \).
-
2.
\(x^N_1 \rightarrow a_-\) and \(x^N_N\rightarrow a_+\) as \(N\rightarrow \infty \).
For \(r\in [0,1],\) define \(x^*(r) =F_\mu ^{-1}(r)\) if \(r\in (0,1),\) and \(x^*(0)=a_-, x^*(1) = a_+\). Then, as \(N\rightarrow \infty ,\)
Proof
For any N, the right-inverse of \(F_{\mu _N}\) satisfies
for any \(k\in \{1,\ldots , N\}\) and \(r\in (\frac{k-1}{N},\frac{k}{N}].\) Since \(\mu ^N\) converges weakly towards \(\mu \) and \(F_\mu \) is continuous, the sequence \(F_{\mu ^N}\) converges pointwise towards \(F_\mu \). What is more, using that \(\mu \) is compactly supported, a variant of Dini’s theorem (cf. [39, Problem 127 Chapter II]) implies further that \(F_{\mu ^N}\rightarrow F\) uniformly on \({\mathbb {R}}\). Let us consider \(\Psi : [0,1]\rightarrow [a_-, a_+],\) the continuous inverse of the one-to-one map \(F_{\mu }: [a_-,a_+]\rightarrow [0,1].\) It satisfies \(\Psi (r)=F_{\mu }^{-1}(r),\) for any \(r\in (0,1]\) and \(\Psi (F_{\mu }(x))= \max (a_-, \min (a_+, x)),\) for any \(x\in {\mathbb {R}}\). Combining this latter equality with (4.1), and using the uniform continuity of \(\Psi \) and the uniform convergence of \(F_{\mu _N}\) towards \(F_{\mu }\), implies that \(\max (a_{-}, \min (a_{+}, F_{\mu _N}^{-1}))\) converges uniformly towards \(\Psi \) on (0, 1]. The first equality of (4.1) together with the assumption (2) yield then the claim. \(\square \)
For example, if \((x^N_k)_{k=1}^N\) are the ordered eigenvalues of a \(\mathrm {GUE}^N\), then Wigner’s law (and the corresponding spectral edge theorem) show that the empirical spectral distribution satisfies the conditions of Proposition 4.1 almost surely, where the limit measure is the semicircle law \(\mu =\sigma _1\equiv \frac{1}{2\pi }\sqrt{(4-x^2)_+}\,dx\). In particular, when \(\frac{k(N)}{N}\rightarrow r\), we have \(x^N_{k(N)} \rightarrow F_{\sigma _1}^{-1}(r)\). These values are sometimes called the classical locations of the eigenvalues. In the case of a \(\mathrm {GUE}^N\), much more is known; for example, [23] showed that the eigenvalues have variance of \(O(\frac{\log N}{N^2})\) in the bulk and \(O(N^{-4/3})\) at the edge, and further standardizing them, their limit distribution is Gaussian in the bulk and Tracy–Widom at the edge. For our purposes, the macroscopic statement of Proposition 4.1 will suffice.
Now, fix \(t\in [0,4)\). From Theorem 2.5, the law \(\nu _t\) of the free unitary Brownian motion \(u_t\) has an analytic density \(\varrho _t\) supported on a closed arc strictly contained in \(\mathbb {U}_1\), and has the form \(\varrho _t(e^{ix}) = \rho _t(x)\) for some strictly positive continuous probability density function \(\rho _t:(-\pi ,\pi )\rightarrow {\mathbb {R}}\) which is symmetric about 0 and supported in a symmetric interval \([-a(t),a(t)]\) where \(a(t) = \frac{1}{2}\sqrt{t(4-t)}+\arccos (1-t/2)\); cf. (2.7). For \(0< r< 1\), define that classical locations \(\upsilon ^*(t,r)\) of the eigenvalues of unitary Brownian motion as follows:
and also set \(\upsilon ^*(t,0) = e^{-ia(t)}\) and \(\upsilon ^*(t,1) = e^{ia(t)}\).
Corollary 4.2
Let \(0\le t<4,\) and let \(V_t^N\) be a random unitary matrix distributed according to the heat kernel on \(\mathbb {U}_N\) at time t (i.e. equal in distribution to the t-marginal of the unitary Brownian motion \(U_t^N).\) Enumerate the eigenvalues of \(V_t^N\) as \(\upsilon ^N_1(t),\ldots ,\upsilon ^N_N(t),\) in increasing order of complex argument in \((-\pi ,\pi )\). Then,
Proof
Let \(x^N_k(t) = -i\log \upsilon ^N_k(t)\), where we use the branch of the logarithm cut along the negative real axis. Note: by Theorem 1.1, for sufficiently large \(N, \upsilon ^N_k(t)\) are outside a t-dependent neighborhood of \(-1\), and so the log function is continuous. The empirical law of \(\{\upsilon ^N_k(t):1\le k\le N<\infty \}\) converges weakly a.s. to \(\nu _t\) (cf. (1.2)), and so by continuity, the empirical measure of \(\{x^N_k(t):1\le k\le N<\infty \}\) converges a.s. to the measure with density \(\rho _t\). Moreover, Theorem 1.1 shows that \(\upsilon ^N_1(t)\rightarrow e^{-ia(t)}\) and \(\upsilon ^N_N(t)\rightarrow e^{ia(t)}\) a.s., and so \(x^N_1(t)\rightarrow -a(t)\) while \(x^N_N(t)\rightarrow a(t)\) a.s. Hence, by Proposition 4.1, \(\max _{1\le k\le N} |x_k^N(t)- F^{-1}_{\rho _t}(\frac{k}{N}) |\rightarrow 0 \). Taking \(\exp (i\cdot )\) of these statements yields the corollary. \(\square \)
Now, let us combine this result with the comparable one for the \(\mathrm {GUE}^N\). Let \(g_t:{\mathbb {R}}\rightarrow {\mathbb {R}}\) be given by \(g_t = F_{\rho _t}^{-1}\circ F_{\sigma _1}\); this is an increasing, continuous map that pushes \(\sigma _1\) forward to \(\rho _t\). Define \(f_t:{\mathbb {R}}\rightarrow \mathbb {U}_1\) by
The main result of this section is that, rather than just pushing the semicircle law forward to the law of free unitary Brownian motion, \(g_t\) in fact pushes a \(\mathrm {GUE}^N\) forward, asymptotically, to \(V_t^N\) (for fixed \(t\in [0,4)\)).
Proposition 4.3
Let \(0\le t<4,\) and let \(V_t^N\) be a random unitary matrix distributed according to the heat kernel on \(\mathbb {U}_N\) at time t (i.e. equal in distribution to the t-marginal of the unitary Brownian motion \(U_t^N).\) There exists a self-adjoint random matrix \(X^N\) with the following properties :
-
1.
\(X^N\) is a \(\mathrm {GUE}^N\).
-
2.
The eigenvalues of \(X^N\) are independent from \(V_t^N,\) and \(\{V^N_t, X^N\}\) have the same eigenvectors.
-
3.
\(\Vert f_t(X^N)-V^N_t\Vert _{\mathbb {M}_N}\rightarrow 0 \;\; a.s.\) as \(N\rightarrow \infty \).
Proof
Let \((\upsilon _k^N(t))_{k=1}^N\) denote the eigenvalues of \(V^N_t\) in order of increasing argument in \((-\pi ,\pi )\), as in Corollary 4.2. It is almost surely true that \(\mathrm {arg}(\upsilon _1^N(t))<\cdots <\mathrm {arg}(\upsilon _N^N(t))\), and so we work in this event only. Let \({\mathscr {E}}_k^N\) denote the eigenspace of the eigenvalue \(\upsilon _k^N(t)\). This space has complex dimension 1 a.s., and so we may select a unit length vector \(E_k^N\) from this space, with phase chosen uniformly at random in \(\mathbb {U}_1\), independently for each of \(E_1^N,\ldots ,E_N^N\). Then, by orthogonality of distinct eigenspaces, the random matrix \(E^N = [{\begin{matrix} E^N_1&\cdots&E^N_N \end{matrix}}]\) is in \(\mathbb {U}_N\); what’s more, since the distribution of \(V_t^N\) is invariant under conjugation by unitaries, we may further assume that \(E^N\) is Haar distributed on \(\mathbb {U}_N\). Now, for each N, fix a random vector \(\varvec{\mu }^N = (\mu _1^N,\ldots ,\mu _N^N)\) independent from \(V_t^N\) with joint density \(f_{\varvec{\mu }^N}(x_1,\ldots ,x_N)\) equal to the known joint density of eigenvalues of a \(\mathrm {GUE}^N\), i.e. proportional to
Then we define
It is well known (cf. [1, 37]) that the distribution of \(X^N\) is the \(\mathrm {GUE}^N\), verifying item (1). Item (2) holds by construction of \(X^N\). It remains to see that (3) holds true. Note, since operator norm is invariant under unitary conjugation, we simply have
But for any \(k\in \{1,\ldots ,N\}, v^{*}(t,\frac{k}{N})=f_t(\mu _k^N)\) and Corollary 4.2 yields the result. \(\square \)
4.2 Strong convergence of the process \((U^N_t)_{t\ge 0}\)
Since the Gaussian unitary ensemble is selfadjoint, we may extend Male’s Theorem 2.3 to continuous functions in independent \(\mathrm {GUE}^N\)s.
Lemma 4.4
Let \(\mathbf {A}^N = (A^N_1,\ldots ,A^N_n)\) be a collection of random matrix ensembles that converges strongly to some \(\mathbf {a}=(a_1,\ldots ,a_n)\) in a \(W^*\)-probability space \(({\mathscr {A}},\tau )\). Let \(\mathbf {X}^N = (X^N_1,\ldots ,X^N_k)\) be independent Gaussian unitary ensembles independent from \(\mathbf {A}^N,\) and let \(\mathbf {x} = (x_1,\ldots ,x_k)\) be freely independent semicircular random variables in \({\mathscr {A}}\) all free from \(\mathbf {a}\). Let \(\mathbf {f}=(f_1,\ldots ,f_k):{\mathbb {R}}\rightarrow {\mathbb {C}}^k\) be continuous functions, and let \(\mathbf {f}(\mathbf {X}^N) = (f_1(X^N_1),\ldots ,f_k(X^N_k))\) and \(\mathbf {f}(\mathbf {x}) = (f_1(x_1),\ldots ,f_k(x_k))\). Then \((\mathbf {A}^N,\mathbf {f}(\mathbf {X}^N))\) converges strongly to \((\mathbf {a},\mathbf {f}(\mathbf {x}))\).
Proof
We begin with the case \(k=1\). If p is any polynomial, by Theorem 2.3, \((\mathbf {A}^N,p(X^N_1))\) converges strongly to \((\mathbf {a},p(x_1))\) by definition. Now, let \(\epsilon >0\), and fix a noncommutative polynomial P in \(n+1\) indeterminates. Then \(P(\mathbf {a},y)\) is a finite sum of monomials, each of the form
for some noncommutative polynomials \(Q_0,\ldots ,Q_d\) and nonnegative integers d. Let \(d_P\) be the “degree” of P: the maximum number of \(Q_k(\mathbf {a})\) terms that appears in any monomial in the above expansion of \(P(\mathbf {a},y)\). Let \(M = 1+ \) the sum of all the products \(\Vert Q_0(\mathbf {a})\Vert \cdots \Vert Q_d(\mathbf {a})\Vert \) over all monomial terms appearing in P. Given a fixed \(\kappa >2,\) by the Weierstrass approximation theorem, for any \(\epsilon >0\), there is a polynomial p in one indeterminate so that
It follows that, for small enough \(\epsilon >0\), we also have \(\Vert p\Vert _{L^\infty [-\kappa ,\kappa ]} \le 1+\Vert f_1\Vert _{L^\infty [-\kappa ,\kappa ]}\). Now we break up the difference in the usual manner,
By the known strong convergence of \((\mathbf {A}^N,p(X_1^N))\) to \((\mathbf {a},p(x_1))\), the middle term is \(<\frac{\epsilon }{4}\) for all sufficiently large N. For the first and third terms, we use the reverse triangle inequality; in the third term this gives
Let \(y=p(x_1)\) and \(z=f_1(x_1)\). We may estimate the norm of the difference using the triangle inequality summing over all monomial terms; then we have a sum of terms of the form
By introducing intermediate mixed terms of the form \(Q_0(\mathbf {a})y\cdots Q_{k-1}(\mathbf {a})yQ_k(\mathbf {a})z\cdots Q_{d-1}(\mathbf {a})zQ_d(\mathbf {a})\) to give a telescoping sum, we can estimate the term in (4.6) by
Since \(\Vert y\Vert =\Vert p(x_1)\Vert = \Vert p\Vert _{L^\infty [-\kappa ,\kappa ]} \le 1+\Vert f_1\Vert _{L^\infty [-\kappa ,\kappa ]}\) and \(\Vert z\Vert = \Vert f_1(x_1)\Vert \le 1+\Vert f_1\Vert _{L^\infty [-\kappa ,\kappa ]}\), each term in the previous sum is bounded by
Since \(\Vert y-z\Vert = \Vert p-f_1\Vert _{L^\infty [-\kappa ,\kappa ]}\), combining this with (4.4) shows that the third term in (4.5) is \(<\frac{\epsilon }{4}\) for all large N.
The first term in (4.5) is handled in an analogous fashion, with the caveat that the prefactor in (4.7) is replaced by \(\Vert Q_0(\mathbf {A}^N)\Vert \cdots \Vert Q_d(\mathbf {A}^N)\Vert \). Here we use the fact that \(X_1^N\) converges strongly towards \(x_1\) to ensure that almost surely, for N large enough,
together with the assumption of strong convergence of \(\mathbf {A}^N\rightarrow \mathbf {a}\) to show that, for all sufficiently large N,
Then we see that the first term in (4.5) is \(<\frac{\epsilon }{2}\) for all large N, and so we have bounded the sum \(<\epsilon \) for all large N, concluding the proof of the lemma in the case \(k=1\).
Now suppose we have verified the conclusion of the lemma for a given k. We proceed by induction. Taking \((\mathbf {A}^N,f_1(X^N_1),\ldots ,f_k(X^N_k))\) as our new input vector, since \(f_{k+1}(X^N_{k+1})\) is independent from all previous terms, the induction hypothesis and the preceding argument in the case \(k=1\) give strong convergence of the augmented vector \((\mathbf {A}^N,f_1(X^N_1),\ldots ,f_k(X^N_k),f_{k+1}(X^N_{k+1}))\) as well. Hence, the proof is complete by induction. \(\square \)
This finally brings us to the proof of Theorem 1.4.
Proof of Theorem 1.4
As above, let \(\mathbf {A}^N = (A^N_1,\ldots ,A^N_n)\) and let \(\mathbf {a} = (a_1,\ldots ,a_n)\) be the strong limit. By reindexing the order of the variables in the noncommutative polynomial P appearing in the definition of strong convergence, it suffices to prove the theorem in the case of time-ordered entries: \(U^N_{t_1},\ldots ,U^N_{t_k}\) with \(t_1\le t_2\le \cdots \le t_k\). What’s more, we may assume without loss of generality that the time increments \(s_1=t_1,s_2=t_2-t_1,\ldots ,s_k=t_k-t_{k-1}\) are all in [0, 4). Indeed, if we know the theorem holds in this case, then for a list of ordered times with some gaps 4 or larger, we may introduce intermediate times until all gaps are \(<4\); then the restricted theorem implies strong convergence for this longer list of marginals, which trivially implies strong convergence for the original list.
Now, set \(V_{s_1}^N = U^N_{t_1}\), and \(V_{s_j}^N = (U^N_{t_{j-1}})^*U^N_{t_j}\) for \(2\le j\le k\). As discussed in Sect. 2.1, these increments of the process are independent, and \(V_{s_j}^N\) has the same distribution as \(U_{s_j}^N\). Hence, by Proposition 4.3, there are k independent \(\mathrm {GUE}^N\)s \(X^N_1,\ldots ,X^N_k\), and continuous functions \(f_{s_j}:{\mathbb {R}}\rightarrow {\mathbb {C}}\), so that \(\Vert f_{s_j}(X^N_j) - V^N_{s_j}\Vert _{\mathbb {M}_N}\rightarrow 0\) as \(N\rightarrow \infty \). Since the \(V_{s_j}^N\) are all independent from \(\mathbf {A}^N\), so are the \(X^N_j\). Hence, by Lemma 4.4, taking \(x_1,\ldots ,x_k\) freely independent semicircular random variables all free from \(\mathbf {a}\), it follows that
By the definition of the mapping \(f_s\) (cf. (4.2)), \(f_{s_j}(x_j)\) has distribution \(\nu _{s_j}\), and as all variables in sight are free, \((\mathbf {a},f_{s_1}(x_1),\ldots ,f_{s_k}(x_k))\) has the same distribution as \((\mathbf {a},v_{s_1},\ldots ,v_{s_k})\) where \((v_s)_{s\ge 0}\) is a free unitary Brownian motion, freely independent from \(\mathbf {a}\).
It now follows, since \(\Vert f_{s_j}(X_j^N)-V_{s_j}^N\Vert _{\mathbb {M}_N}\rightarrow 0\), that
(The proof is very similar to the proof of Lemma 4.4.) Finally, we can recover the original variables \(U^N_{t_j} = V^N_{s_1}V^N_{s_2}\cdots V^N_{s_j}\). Therefore
The discussion at the end of Sect. 2.3 shows that \((v_{s_1},v_{s_1}v_{s_2},\ldots ,v_{s_1}v_{s_2}\cdots v_{s_k})\) has the same distribution as \((u_{t_1},u_{t_2},\ldots ,u_{t_k})\) where \((u_t)_{t\ge 0}\) is a free unitary Brownian motion in the \(W^*\)-algebra generated by \((v_s)_{s\ge 0}\), and is therefore freely independent from \(\mathbf {a}\). This concludes the proof. \(\square \)
5 Application to the Jacobi process
In this final section we combine our main Theorem 1.4 with some of the results of the first and third authors’ earlier paper [12], to show that the Jacobi process (cf. (5.1) and (5.2)) has spectral edges that evolve with finite propagation speed.
There are three classical Hermitian Gaussian ensembles that have been well studied. The first is the Gaussian Unitary Ensemble described in detail above, whose analysis was initiated by Wigner [50] and began random matrix theory. The second is the Wishart Ensemble, also known (through its applications in statistics) as a sample covariance matrix. Let \(a\ge 1\), and let \(X=X^N\) be an \(N\times \lceil aN \rceil \) matrix all of whose entries are independent normal random variables of variance \(\frac{1}{N}\); then \(W = XX^*\) is a Wishart ensemble with parameter a. As \(N\rightarrow \infty \), its empirical spectral distribution converges almost surely to a law known as the Marchenko–Pastur distribution; this was proved in [36]. As with the Gaussian Unitary Ensemble, it also has a spectral edge, and the largest eigenvalue when properly renormalized has the Tracy-Widom law.
The third Hermitian Gaussian ensemble is the Jacobi Ensemble. Let \(W_a\) and \(W_b'\) be independent Wishart ensembles of parameters \(a,b\ge 1\). Then it is known that \(W_a+W_b'\) is a Wishart ensemble of parameter \(a+b\), and is a.s. invertible (cf. [11, Lemma 2.1]). The associated Jacobi Ensemble is
Such matrices have been studied in the statistics literature for over thirty years; they play a key role in MANOVA (multivariate analysis of variance) and are sometimes simply called MANOVA matrices. The joint law of eigenvalues is explicitly known, but the large-N limit is notoriously harder than the Gaussian Unitary and Wishart Ensembles. In [11], the present first author made the following discovery which led to a new approach to the asymptotics of the ensemble: its joint law can be described by a product of randomly rotated projections, as follows. (For the sake of making the statement simpler, we assume a, b are such that aN and bN are integers.)
Theorem 5.1
[11, Theorem 2.2]. Let \(J_{a,b}=J_{a,b}^N\) be an \(N\times N\) Jacobi ensemble with parameters \(a,b\ge 1\). Let \(P,Q\in \mathbb {M}_{(a+b)N}\) be (deterministic) orthogonal projections with \(\mathrm {rank}(P) = bN\) and \(\mathrm {rank}(Q) = N\). Let \(U\in \mathbb {U}_{(a+b)N}\) be a random unitary matrix sampled from the Haar measure. Then \(Q U^*PU Q,\) viewed as a random matrix in \(\mathbb {M}_N\) via the unitary isomorphism \(\mathbb {M}_N \cong Q\mathbb {M}_{(a+b)N}Q,\) has the same distribution as \(J_{a,b}\).
Given two closed subspaces \(\mathbb {V},\mathbb {W}\) of a Hilbert space \(\mathbb {H}\), if \(P:\mathbb {H}\rightarrow \mathbb {V}\) and \(Q:\mathbb {H}\rightarrow \mathbb {W}\) are the orthogonal projections, then the operator QPQ is known as the operator valued angle between the two subspaces. (Indeed, in the finite-dimensional setting, the eigenvalues of QPQ are trigonometric polynomials in the principal angles between the subspaces \(\mathbb {V}\) and \(\mathbb {W}\).) Thus, the law of the Jacobi ensemble records all the remaining information about the angles between two uniformly randomly rotated subspaces of fixed ranks. These observations were used to make significant progress in understanding the Jacobi Ensemble in statistical applications (cf. [29]), and to generalize many of these results to the full expected universality class (beyond Gaussian entries) in the limit (cf. [21]).
In terms of the large-N limit: letting \(\alpha = \frac{b}{a+b}\) and \(\beta = \frac{1}{a+b}\), we have \(\mathrm {tr}P = \alpha \) and \(\mathrm {tr}Q = \beta \) fixed as N grows, and therefore there are limit projections p, q of these same traces. The chosen Haar distributed unitary matrices converge in noncommutative distribution to a Haar unitary operator u freely independent from p, q, and so the empirical spectral distribution of \(J_{a,b}\) converges to the law of \(qu^*p u q\), which was explicitly computed in [49] as an elementary example of free multiplicative convolution:
where \(r_{\pm } = \alpha +\beta -2\alpha \beta \pm 2\sqrt{\alpha \beta (1-\alpha )(1-\beta )}\). Furthermore, it was shown in [29] that the Jacobi Ensemble has a spectral edge, the rate of convergence of the largest eigenvalue is \(N^{-2/3}\) (as with the Gaussian Unitary and Wishart Ensembles), and the rescaled limit distribution of the largest eigenvalue is the Tracy–Widom law of [44].
Simultaneously to these developments, Voiculescu [48] introduced free liberation. Given two subalgebras A, B of a \(W^*\)-probability space \(({\mathscr {A}},\tau )\) and a Haar unitary operator \(u\in {\mathscr {A}}\) that is freely independent from A, B, the rotated subalgebra \(u^*A u\) is freely independent from B. If \((u_t)_{t\ge 0}\) is a free unitary Brownian motion freely independent from A, B, it is not generally true that \(u_t^*A u_t\) is free from B for any finite t (in particular when \(t=0\) we just have A, B), but since the (strong operator) limit as \(t\rightarrow \infty \) of \(u_t\) is a Haar unitary, this process “liberates” A and B. This concept was used to define several important regularized versions of measures associated to free entropy and free information theory, and to this days plays an important role in free probability theory. The special case that A, B are algebras generated by two projections has been extensively studied [15,16,17,18,19, 25,26,27], as the best special case where one can hope to compute all quantities fairly explicitly.
In the first and third authors’ paper [12, Section 3.2], the following was proved.
Theorem 5.2
[12, Lemmas 3.2–3.6] Let p, q be orthogonal projections with traces \(\alpha ,\beta ,\) and let \((u_t)_{t\ge 0}\) be a free unitary Brownian motion freely independent from p, q. Let \(\mu _t = \mathrm {Law}_{qu_t^*p u_t q}\). Then
where \({\widetilde{\mu }}_t\) is a positive measure (of mass \(\min \{\alpha ,\beta \}-\max \{\alpha +\beta -1,0\}).\) Let \(I_1,I_2\) be two disjoint open subintervals of (0, 1). If \(\mathrm {supp}\,{\widetilde{\mu }}_{t_0}\subset I_1\sqcup I_2\) for some \(t_0\ge 0,\) then \(\mathrm {supp}\,{\widetilde{\mu }}_t\subset I_1\sqcup I_2\) for \(|t-t_0|\) sufficiently small; moreover, \({\widetilde{\mu }}_t(I_1)\) and \({\widetilde{\mu }}_t(I_2)\) do not vary with t close to \(t_0\).
If \({\widetilde{\mu }}_t\) has a continuous density on (0, 1) for \(t>0,\) and \(x_{t_0}\in (0,1)\) is a boundary point of \(\mathrm {supp}\,{\widetilde{\mu }}_{t_0},\) then for \(|t-t_0|\) sufficiently small there is a \(C^1\) function \(t\mapsto x(t)\) with \(x(t_0) = x_{t_0}\) so that x(t) is a boundary point of \(\mathrm {supp}\,{\widetilde{\mu }}_{t_0}\).
Finally, in the special case \(\alpha =\beta =\frac{1}{2},\) for all \(t>0, {\widetilde{\mu }}_t\) possesses a continuous density which is analytic on the interior of its support.
Remark 5.3
-
1.
It is expected that the final statement, regarding the existence of a continuous density, holds true for all \(\alpha ,\beta \in (0,1)\); at present time, this is only known for \(\alpha =\beta =\frac{1}{2}\). Nevertheless, the “islands stay separated” result holds in general.
-
2.
Our method of proof of the regularity of \({\widetilde{\mu }}_t\) involved a combination of free probability, complex analysis, and PDE techniques. In [28], Izumi and Ueda partly extended this framework beyond the \(\alpha =\beta =\frac{1}{2}\) case; but they were still not able to prove continuity of the measure. They did, however, give a much simpler proof of the result in the case \(\alpha =\beta =\frac{1}{2}\): here, \({\widetilde{\mu }}_t\) can be described as the so-called Szegő transform (from the unit circle to the unit interval) of the law of \(v_0u_t\), where \(v_0\) is determined by the law of qpq. Via this description, the regularity result is an immediate consequence of Theorem 2.5 above.
-
3.
Let us note that \(\alpha =\beta =\frac{1}{2}\) corresponds to \(a=b=1\), meaning the “square” Jacobi ensemble. This is, of course, the case that is least interesting to statisticians: in MANOVA problems the data sets are typically time series, where there are many more samples than detection sites, meaning that \(a,b\ggg 1\). In fact, it is generally questioned whether the Jacobi Ensemble is a realistic regime for real world applications, rather than building the Wishart Ensembles out of \(N\times M\) Gaussian matrices where \(\frac{M}{N}\rightarrow \infty \).
Thus, it is natural to consider the corresponding finite-t deformation of the Jacobi Ensemble. The matrix Jacobi process \(J_t^N\) associated to the projections \(P^N,Q^N\in \mathbb {M}_N\), is given by
where \((U^N_t)_{t\ge 0}\) is a Brownian motion in \(\mathbb {U}_N\). (Typically \(P^N,Q^N\) are deterministic; they may also be chosen randomly, in which case \(U^N_t\) must be chosen independent from them.) This is a diffusion process in \(\mathbb {M}_N^{[0,1]}\): it lives a.s. in the space of matrices \(M\in \mathbb {M}_N\) with \(0\le M\le 1\) (i.e. M is self-adjoint and has eigenvalues in [0, 1]). Note that the initial value is \(J_0^N = Q^NP^NQ^N\), the operator-valued angle between the subspaces in the images of \(P^N,Q^N\). In particular, the Jacobi process records (through its eigenvalues) the evolution of the principal angles between two subspaces as they are continuously rotated by a unitary Brownian motion.
In the case \(N=1\), the process (5.2) precisely corresponds to what is classically known as the Jacobi process: the Markov process on [0, 1] with generator \({\mathscr {L}} = x(x-1)\frac{\partial ^2}{\partial x^2} - (cx+d)\frac{\partial }{\partial x}\), where \(c=2\min \{\alpha ,\beta \}-1, d=|\alpha -\beta |\). This is where the name comes from, as the orthogonal polynomials associated to this Markov process are the Jacobi polynomials, cf. [19].
Remark 5.4
Comparing to Theorem 5.1, we have now compressed the projections and the Brownian motion into \(\mathbb {M}_N\) from the start. We could instead formulate the process as in that theorem by choosing projections and Brownian motion in a larger space, which would have the effect of using a “corner” of a higher-dimensional Brownian motion instead of \(U^N_t\). While this makes a difference for the finite-dimensional distribution, it does not affect the large-N behavior.
This brings us to our main application. First note that, from our main Theorem 1.4, the Jacobi process converges strongly.
Corollary 5.5
Let \(P^N,Q^N\) be deterministic orthogonal projections in \(\mathbb {M}_N\), and suppose \(\{P^N,Q^N\}\) converges strongly to \(\{p,q\}\). Let \((u_t)_{t\ge 0}\) be a free unitary Brownian motion freely independent from p, q. Then for each \(t\ge 0\) the Jacobi process marginal \(J^N_t\) converges strongly to \(j_t = qu_t^*p u_t q\). What’s more, if \(f\in C[0,1]\) is any continuous test function, then \(\Vert f(J^N_t)\Vert \rightarrow \Vert f(j_t)\Vert \) a.s. as \(N\rightarrow \infty \).
Proof
The strong convergence statement is an immediate corollary to Theorem 1.4, with \(A^N_1 = P^N, A^N_2 = Q^N\), and \(n=2,k=1\). The extension to continuous test functions beyond polynomials is then an elementary Weierstrass approximation argument. \(\square \)
Example 5.6
For fixed \(k\in {\mathbb {N}}\), select two orthogonal projections \(P,Q\in \mathbb {M}_k\). Then define \(P^N,Q^N\in \mathbb {M}_{kN}\) by \(P^N = P\otimes I^N\) and \(Q^N = Q\otimes I^N\). (Here we are identifying \(\mathbb {M}_k\otimes \mathbb {M}_N\cong \mathbb {M}_{kN}\) via the Kronecker product.) If F is a noncommutative polynomial in two indeterminates, then
and it follows immediately that \(\{P^N,Q^N\}\) converges strongly to \(\{P,Q\}\) (i.e. the \(W^*\)-probability space can be taken to be \((\mathbb {M}_k,\mathrm {tr})\)). Expanding this space to include a free unitary Brownian motion freely independent from \(\{P,Q\}\) and setting \(j_t = Qu_t^*P u_t Q\), Corollary 5.5 yields that the Jacobi process \(J^{kN}_t\) with initial value \(Q^NP^NQ^N\) converges strongly to \(j_t\).
Figure 2 illustrates the eigenvalues of \(J^{kN}_t\) with \(k=4, N=100\), and initial projections given by
which have been selected so that the initial operator-valued angle QPQ has non-trivial eigenvalues 0.2 and 0.8; this therefore holds as well for \(Q^NP^NQ^N\) for all N. This implies that the subspaces \(P^N({\mathbb {C}}^{kN})\) and \(Q^N({\mathbb {C}}^{kN})\) have precisely two distinct principal angles.
The spectral distribution of the Jacobi process \(J^{kN}_t\) of Example 5.6 with \(k=4, N=100\) and times \(t=0.01\) (on the left) and \(t=0.25\) (on the right). The histograms were made with 1000 trials each, yielding \(4\times 10^5\) eigenvalues sorted into 1000 bins
As is plainly visible in Fig. 2, for small time, the eigenvalues (which are fixed trigonometric polynomials in the principal angles) stay close to their initial values. That is: despite the fact that the diffusion’s measure is fully supported on \(\mathbb {M}_N^{[0,1]}\) for every \(t,N>0\), the eigenvalues move with finite speed for all large N. That is our final theorem.
Theorem 5.7
For each \(N\ge 1,\) let \((U^N_t)_{t\ge 0}\) be a Brownian motion on \(\mathbb {U}_N,\) let \(\mathbb {V}^N\) and \(\mathbb {W}^N\) be subspaces of \({\mathbb {C}}^N,\) and suppose that the orthogonal projections onto these subspaces converge jointly strongly as \(N\rightarrow \infty \). Suppose there is a fixed finite set \(\varvec{\theta } = \{\theta _1,\ldots ,\theta _k\}\) of angles so that all principal angles between \(\mathbb {V}^N\) and \(\mathbb {W}^N\) are in \(\varvec{\theta }\) for all N. Fix any open neighborhood \({\mathscr {O}}\) of \(\varvec{\theta }\). Then there exists some \(T>0\) so that, for all \(t\in [0,T],\) with probability 1, all principal angles between \(U^N_t(\mathbb {V}^N)\) and \(\mathbb {W}^N\) are in \({\mathscr {O}}\) for all sufficiently large N.
Proof
Let \(P^N\) and \(Q^N\) be the projections onto \(\mathbb {V}^N\) and \(\mathbb {W}^N\). Then there is a fixed list \(\varvec{\lambda } = \{\lambda _1,\ldots ,\lambda _k\}\) in [0, 1] so that all eigenvalues of \(Q^NP^NQ^N\) are in \(\varvec{\lambda }\). (The eigenvalues \(\lambda _j\) are certain fixed trigonometric polynomials in \(\varvec{\theta }\)). Let \(J^N_t\) be the Jacobi process associated to \(P^N,Q^N\), and let \(j_t\) be the associated large-N limit. By Corollary 5.5, for any \(t\ge 0\) and any \(f\in C[0,1], \Vert f(J^N_t)\Vert \rightarrow \Vert f(j_t)\Vert \) a.s. as \(N\rightarrow \infty \).
Applying this at time \(t=0\), let \(\lambda _i,\lambda _j\in \varvec{\lambda }\) with \(\lambda _i<\lambda _j\) such that no elements of \(\varvec{\lambda }\) are in the interval \((\lambda _i,\lambda _j)\). Now let f be a continuous bump function supported in \((\lambda _i,\lambda _j)\). Then \(f(J^N_0) = 0\), and it therefore follows that \(\Vert f(j_0)\Vert =0\). As this holds for all bump function supported in \((\lambda _i,\lambda _j)\), it follows that \(\mathrm {spec}(j_0)\) does not intersect \((\lambda _i,\lambda _j)\). Thus \(j_0\) has pure point spectrum precisely equal to \(\varvec{\lambda }\).
Now, fix any \(\epsilon >0\); by (induction on) Theorem 5.2, for sufficiently small \(t>0, \mathrm {spec}(j_t)\) is contained in \(\varvec{\lambda }_\epsilon \) (the union of \(\epsilon \)-balls centered at the points of \(\varvec{\lambda }\)). Now, suppose (for a contradiction) that, for some \(N_0, J^{N_0}_t\) possesses an eigenvalue \(\lambda \in (0,1){\setminus }\varvec{\lambda }_\epsilon \). Let g be a bump function supported in \((0,1){\setminus }\varvec{\lambda }_\epsilon \) that is equal to 1 on a neighborhood of \(\lambda \); then \(\Vert g(J^{N_0}_t)\Vert \ge 1\). But, by Corollary 5.5, we know \(\Vert g(J^N_t)\Vert \rightarrow \Vert g(j_t)\Vert = 0\) a.s. as \(N\rightarrow \infty \). Thus, for all sufficiently large \(N, \Vert g(J^N_t)\Vert <1\), which implies that \(\lambda \) is not an eigenvalue. As this holds for any point in \((0,1){\setminus }\varvec{\lambda }_\epsilon \), it follows that \(\mathrm {spec}(J^N_t)\) is almost surely contained in \(\varvec{\lambda }_\epsilon \) for all sufficiently large N.
The result now follows from the fact that the principal angles between \(U^N_t(\mathbb {V})\) and \(\mathbb {W}\) are fixed continuous functions (trigonometric polynomials) in the eigenvalues of \(J^N_t\). \(\square \)
References
Anderson, G.W., Guionnet, A., Zeitouni, O.: An Introduction to Random Matrices, vol. 118. Cambridge Studies in Advanced Mathematics. Cambridge University Press, Cambridge (2010)
Bai, Z. D.: Methodologies in spectral analysis of large-dimensional random matrices, a review. Stat. Sin. 9(3), 611–677 (1999). With comments by G. J. Rodgers and Jack W. Silverstein; and a rejoinder by the author
Bai, Z.D., Yin, Y.Q.: Necessary and sufficient conditions for almost sure convergence of the largest eigenvalue of a Wigner matrix. Ann. Probab. 16(4), 1729–1741 (1988)
Biane, P.: Free Brownian motion, free stochastic calculus and random matrices. Free Probability Theory (Waterloo, ON, 1995). Fields Institute Communications, vol. 12, pp. 1–19. American Mathematical Society, Providence (1997)
Biane, P.: Segal-Bargmann transform, functional calculus on matrix spaces and the theory of semi-circular and circular systems. J. Funct. Anal. 144(1), 232–286 (1997)
Biane, P., Speicher, R.: Stochastic calculus with respect to free Brownian motion and analysis on Wigner space. Probab. Theory Relat. Fields 112(3), 373–409 (1998)
Biane, P., Speicher, R.: Free diffusions, free entropy and free Fisher information. Ann. Inst. H. Poincaré Probab. Stat. 37(5), 581–606 (2001)
Cébron, G.: Free convolution operators and free Hall transform. J. Funct. Anal. 265(11), 2645–2708 (2013)
Cébron, G., Kemp, T.: Fluctuations of Brownian motions on \({\mathbb{G}L}_N\) (2014). arXiv:1409.5624
Collins, B.: Moments and cumulants of polynomial random variables on unitary groups, the Itzykson–Zuber integral, and free probability. Int. Math. Res. Not. 17, 953–982 (2003)
Collins, B.: Product of random projections, Jacobi ensembles and universality problems arising from free probability. Probab. Theory Relat. Fields 133(3), 315–344 (2005)
Collins, B., Kemp, T.: Liberation of projections. J. Funct. Anal. 266(4), 1988–2052 (2014)
Collins, B., Male, C.: The strong asymptotic freeness of Haar and deterministic matrices. Ann. Sci. Éc. Norm. Supér. (4) 47 1, 147–163 (2014)
Dahlqvist, A.: Integration formula for Brownian motion on classical compact Lie groups. Ann. Inst. H. Poincaré Probab. Stat. (to appear)
Demni, N.: Free Jacobi process. J. Theor. Probab. 21(1), 118–143 (2008)
Demni, N.: Free Jacobi process associated with one projection: local inverse of the flow (2015). arXiv:1502.00013
Demni, N., Hamdi, T., Hmidi, T.: Spectral distribution of the free Jacobi process. Indiana Univ. Math. J. 61(3), 1351–1368 (2012)
Demni, N., Hmidi, T.: Spectral distribution of the free Jacobi process associated with one projection. Colloq. Math. 137(2), 271–296 (2014)
Demni, N., Zani, M.: Large deviations for statistics of the Jacobi process. Stoch. Process. Appl. 119(2), 518–533 (2009)
Driver, B.K., Hall, B.C., Kemp, T.: The large-\(N\) limit of the Segal–Bargmann transform on \(\mathbb{U}_N\). J. Funct. Anal. 265(11), 2585–2644 (2013)
Erdős, L., Farrell, B.: Local eigenvalue density for general MANOVA matrices. J. Stat. Phys. 152(6), 1003–1032 (2013)
Evans, L.C.: Partial Differential Equations, vol. 19, 2nd edn. Graduate Studies in Mathematics. American Mathematical Society, Providence (2010)
Gustavsson, J.: Gaussian fluctuations of eigenvalues in the GUE. Ann. Inst. H. Poincaré Probab. Stat. 41(2), 151–178 (2005)
Haagerup, U., Thorbjørnsen, S.: A new application of random matrices: \({\rm Ext}(C^*_{\rm red}(F_2))\) is not a group. Ann. Math. (2) 162(2), 711–775 (2005)
Hiai, F., Miyamoto, T., Ueda, Y.: Orbital approach to microstate free entropy. Int. J. Math. 20(2), 227–273 (2009)
Hiai, F., Ueda, Y.: Notes on microstate free entropy of projections. Publ. Res. Inst. Math. Sci. 44(1), 49–89 (2008)
Hiai, F., Ueda, Y.: A log-Sobolev type inequality for free entropy of two projections. Ann. Inst. Henri Poincaré Probab. Stat. 45(1), 239–249 (2009)
Izumi, M., Ueda, Y.: Remarks on free mutual information and orbital free entropy. Nagoya Math. J. 220, 45–66 (2015)
Johnstone, I.M.: Multivariate analysis and Jacobi ensembles: largest eigenvalue, Tracy–Widom limits and rates of convergence. Ann. Stat. 36(6), 2638–2716 (2008)
Kemp, T.: Heat kernel empirical Laws on \({\mathbb{U}}_N\) and \({\mathbb{G}}{\mathbb{L}}_N\). J. Theor. Probab. (2015, to appear)
Kemp, T.: The large-\(N\) limits of Brownian motions on \({\mathbb{G}L}_N\). Int. Math. Res. Not. 2016(13), 4012–4057 (2016)
Kemp, T., Nourdin, I., Peccati, G., Speicher, R.: Wigner chaos and the fourth moment. Ann. Probab. 40(4), 1577–1635 (2012)
Lévy, T.: Schur–Weyl duality and the heat kernel measure on the unitary group. Adv. Math. 218(2), 537–575 (2008)
Lévy, T., Maïda, M.: Central limit theorem for the heat kernel measure on the unitary group. J. Funct. Anal. 259(12), 3163–3204 (2010)
Male, C.: The norm of polynomials in large random and deterministic matrices. Probab. Theory Relat. Fields 154(3–4), 477–532 (2012). With an appendix by Dimitri Shlyakhtenko
Marchenko, V.A., Pastur, L.A.: Distribution of eigenvalues in certain sets of random matrices. Mat. Sb. (N.S.) 72(114), 507–536 (1967)
Mehta, M.L.: Random Matrices, vol. 142, 3rd edn. Pure and Applied Mathematics (Amsterdam). Elsevier/Academic Press, Amsterdam (2004)
Nica, A., Speicher, R.: Lectures on the Combinatorics of Free Probability, vol. 335. London Mathematical Society Lecture Note Series. Cambridge University Press, Cambridge (2006)
Pólya, G., Szegő, G.: Problems and Theorems in Analysis. I. Classics in Mathematics. Springer, Berlin (1998). Series, integral calculus, theory of functions, Translated from the German by Dorothee Aeppli, Reprint of the 1978 English translation
Rains, E.M.: Combinatorial properties of Brownian motion on the compact classical groups. J. Theor. Probab. 10(3), 659–679 (1997)
Robinson, D.W.: Elliptic Operators and Lie Groups. Oxford Mathematical Monographs. The Clarendon Press, Oxford University Press/Oxford Science Publications, New York (1991)
Saloff-Coste, L.: Aspects of Sobolev-Type Inequalities. London Mathematical Society Lecture Note Series, vol. 289. Cambridge University Press, Cambridge (2002)
Sengupta, A.: Traces in Two-Dimensional QCD: The Large \(N\)-Limit. Aspects of Mathematics, E38. Friedrich Vieweg & Sohn, Wiesbaden (2008)
Tracy, C.A., Widom, H.: Level-spacing distributions and the Airy kernel. Commun. Math. Phys. 159(1), 151–174 (1994)
Varopoulos, N.T., Saloff-Coste, L., Coulhon, T.: Analysis and Geometry on Groups, vol. 100. Cambridge Tracts in Mathematics. Cambridge University Press, Cambridge (1992)
Voiculescu, D.: Limit laws for random matrices and free products. Invent. Math. 104(1), 201–220 (1991)
Voiculescu, D.: A strengthened asymptotic freeness result for random matrices with applications to free entropy. Int. Math. Res. Not. 1, 41–63 (1998)
Voiculescu, D.: The analogues of entropy and of Fisher’s information measure in free probability theory. VI. Liberation and mutual free information. Adv. Math. 146(2), 101–166 (1999)
Voiculescu, D.V., Dykema, K.J., Nica, A.: Free Random Variables. CRM Monograph Series, vol. 1. American Mathematical Society, Providence (1992). A noncommutative probability approach to free products with applications to random matrices, operator algebras and harmonic analysis on free groups
Wigner, E.P.: On the distribution of the roots of certain symmetric matrices. Ann. Math. 2(67), 325–327 (1958)
Acknowledgements
This paper was initiated during a research visit of BC to TK in late 2012; substantial subsequent progress was made during a one-month visit of AD to BC at AIMR, Sendai during the fall of 2013. We would like to express our great thanks to UC San Diego and AIMR for their warm hospitality, fruitful work environments, and financial support that aided in the completion of this work. We would like to thank Ioana Dumitriu for helping to design the simulations that produced the figures. Finally, we express our gratitude to the anonymous referees whose careful reading and detailed comments significantly improved the presentation of this manuscript (particularly in Sect. 3.2).
Author information
Authors and Affiliations
Corresponding author
Additional information
B. Collins was supported in part by Kakenhi, an NSERC discovery grant, Ontario’s ERA and ANR-14-CE25-0003.
A. Dahlqvist was supported in part by RTG 1845 and EPSRC Grant EP/I03372X/1.
T. Kemp was supported in part by NSF CAREER Award DMS-1254807.
Rights and permissions
About this article
Cite this article
Collins, B., Dahlqvist, A. & Kemp, T. The spectral edge of unitary Brownian motion. Probab. Theory Relat. Fields 170, 49–93 (2018). https://doi.org/10.1007/s00440-016-0753-x
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00440-016-0753-x