Compact Brownian surfaces I: Brownian disks

Abstract

We show that, under certain natural assumptions, large random plane bipartite maps with a boundary converge after rescaling to a one-parameter family $(\mathrm {BD}_L,\, 0<L<\infty )$ of random metric spaces homeomorphic to the closed unit disk of $\mathbb {R}^2$, the space $\mathrm {BD}_L$ being called the Brownian disk of perimeter L and unit area. These results can be seen as an extension of the convergence of uniform plane quadrangulations to the Brownian map, which intuitively corresponds to the limit case where $L=0$. Similar results are obtained for maps following a Boltzmann distribution, in which the perimeter is fixed but the area is random.

1 Introduction

1.1 Motivation

Random maps are a natural discrete version of random surfaces. It has been shown in recent years that their scaling limits can provide “canonical” models of random metric spaces homeomorphic to a surface of a given topology. More precisely, given a random map M, one can consider it as a random finite metric space by endowing its vertex set with the usual graph metric, and multiply this graph metric by a suitable renormalizing factor that converges to 0 as the size of the map M is sent to infinity. One is then interested in the convergence in distribution of the resulting sequence of rescaled maps, in the Gromov–Hausdorff topology [23] (or pointed Gromov–Hausdorff topology if one is interested in non-compact topologies), to some limiting random metric space.

Until now, the topology for which this program has been carried out completely is that of the sphere, for a large (and still growing) family of different random maps models, see [1, 2, 7, 12, 30, 38], including for instance the case of uniform triangulations of the sphere with n faces, or uniform random maps of the sphere with n edges. The limiting metric space, called the Brownian map, turns out not only to have the topology of the sphere [32, 37], as can be expected, but also to be independent (up to a scale constant) of the model of random maps that one chooses, provided it is, in some sense, “reasonable.” See however [3, 31] for natural models of random maps that converge to qualitatively different metric spaces. These two facts indeed qualify the Brownian map as being a canonical random geometry on the sphere. Note that a non-compact variant of the Brownian map, called the Brownian plane, has been introduced in [21] and shown to be the scaling limit of some natural models of random quadrangulations.

However, for other topologies allowing higher genera and boundary components, only partial results are known [8,9,10,11]. Although subsequential convergence results have been obtained for rescaled random maps in general topologies, it has not been shown that the limit is uniquely defined and independent of the choice of the extraction. The goal of this paper and its companion [13] is to fill in this gap by showing convergence of a natural model of random maps on a given compact surface S to a random metric space with same topology, which one naturally can call the “Brownian S.”

This paper will focus exclusively on the particular case of the disk topology, which requires quite specific arguments, and indeed serves as a building block to construct the boundaries of general compact Brownian surfaces in [13].

1.2 Maps

To state our results, let us recall some important definitions and set some notation. We first define the objects that will serve as discrete models for a metric space with the disk topology.

A plane map is an embedding of a finite connected multigraph into the 2-dimensional sphere, and considered up to orientation-preserving homeomorphisms of the latter. The faces of the map are the connected components of the complement of edges, and can be then shown to be homeomorphic to 2-dimensional open disks. For every oriented edge e, with origin vertex v, we can consider the oriented edge $e'$ that follows e in counterclockwise order around v, and define the corner incident to e as a small open angular sector between e and $e'$. It does not matter how we choose these regions as long as they are pairwise disjoint. The number of corners contained in a given face f is called the degree of that face; equivalently, it is the number of oriented edges to the left of which f lies—we say that f is incident to these oriented edges, or to the corresponding corners. We let $\mathbf {V}(\mathbf {m})$, $\mathbf {E}(\mathbf {m})$, $\mathbf {F}(\mathbf {m})$ denote the sets of vertices, edges and faces of a map $\mathbf {m}$, or simply $\mathbf {V}$, $\mathbf {E}$, $\mathbf {F}$ when the mention of $\mathbf {m}$ is clear from the context.

If $\mathbf {m}$ is a map, we can view it as a metric space $(\mathbf {V}(\mathbf {m}),d_{\mathbf {m}})$, where $d_\mathbf {m}$ is the graph metric on the set $\mathbf {V}(\mathbf {m})$ of vertices of $\mathbf {m}$. For simplicity, we will sometimes denote this metric space by $\mathbf {m}$ as well and, if $a>0$, we denote by $a\mathbf {m}$ the metric space $(\mathbf {V}(\mathbf {m}),ad_{\mathbf {m}})$.

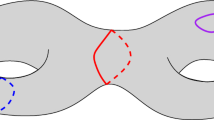
For technical reasons, the maps we consider will always implicitly be rooted, which means that one of the corners (equivalently, one of the oriented edges) is distinguished and called the root. The face $f_*$ incident to the root is called the root face. Since we want to consider objects with the topology of a disk, we insist that the root face is an external face to the map, whose incident edges forms the boundary of the map, and call its degree the perimeter of the map. By contrast, the non-root faces are called internal faces. Note that the boundary of the external face is in general not a simple curve (see Fig. 1). As a result, the topological space obtained by removing the external face from the surface in which the map is embedded is not necessarily a surface with a boundary, in the sense that every point does not have a neighborhood homeomorphic to some open set of $\mathbb {R}\times \mathbb {R}_+$. However, removing any Jordan domain from the external face does of course result in a surface with a boundary, which is homeomorphic to the 2-dimensional disk.

1.3 The case of quadrangulations

The first part of the paper is concerned exclusively with a particular family of maps, for which the results are the simplest to obtain and to state. A quadrangulation with a boundary is a rooted plane map whose internal faces all have degree 4. It is a simple exercise to see that this implies in fact that the perimeter is necessarily an even number. For l, $n\in \mathbb {N}$, we let $\mathbf{Q}_{l,n}$ be the set of quadrangulations with a boundary having n internal faces and perimeter 2l.

Fig. 1

A quadrangulation from $\mathbf{Q}_{23,19}$. The root is the corner indicated by the red arrow (color figure online)

Our main result in the context of random quadrangulations is the following.

Theorem 1

Let $L\in [0,\infty )$ be fixed, and $(l_n,n\ge 1)$ be a sequence of integers such that $l_n/{\sqrt{2n}} \rightarrow L$ as $n\rightarrow \infty$. Let $Q_n$ be uniformly distributed over $\mathbf{Q}_{l_n,n}$. There exists a random compact metric space $\mathrm {BD}_L$ such that

where the convergence holds in distribution for the Gromov–Hausdorff topology.

The random metric space $\mathrm {BD}_L$ is called the Brownian disk with perimeter L and unit area. We will give in Sect. 2 an explicit description of $\mathrm {BD}_L$ (as well as versions $\mathrm {BD}_{L,A}$ with general areas $A>0$, see also Sect. 1.5) in terms of certain stochastic processes, and the convention for the scaling constant $(9/8)^{1/4}$ is here to make the description of these processes simpler. We note that from the construction, $\mathrm {BD}_{L,A}$ comes naturally with a distinguished point $x_*$, as well as a natural “uniform” measure, such that $x_*$ can be seen as a random point chosen according to this measure. See Lemma 21 for a precise statement. We will in fact prove that Theorem 1 holds in the pointed Gromov–Hausdorff space, when $Q_n$ is equipped with a uniformly chosen random vertex $v_*$ and when $\mathrm {BD}_L$ is equipped with $x_*$; see the comment before Proposition 16 below.

The main properties of $\mathrm {BD}_L$ are the following; they follow from [10, Theorems 1–3].

Proposition 2

Let $L>0$ be fixed. Almost surely, the space $\mathrm {BD}_L$ is homeomorphic to the closed unit disk of $\mathbb {R}^2$. Moreover, almost surely, the Hausdorff dimension of $\mathrm {BD}_L$ is 4, while that of its boundary $\partial \mathrm {BD}_L$ is 2.

We stress that the case $L=0$, corresponding to the situation where $l_n=o(\sqrt{n})$, is the statement of [10, Theorem 4], which says that $\mathrm {BD}_0$ is the so-called Brownian map. Since the Brownian map is a.s. homeomorphic to the sphere [32], this means that the boundaries of the approximating random maps are too small to be seen in the limit. This particular case generalizes the convergence of uniform random quadrangulations, obtained in [30, 38], corresponding to the case where $l_n=2$ for every $n\ge 1$.

The case where $l_n/\sqrt{n}\rightarrow \infty$ is also of interest, and is the object of [10, Theorem 5], showing that, in this case, $(2l_n)^{-1/2}Q_n$ converges to the so-called Brownian Continuum Random Tree [4, 5]. This means that the boundary takes over the planar geometry and folds the map into a tree-shaped object.

We will prove our result by using the already studied case of plane maps without boundary, together with some surgical methods. Heuristically, we will cut $Q_n$ along certain geodesics into elementary pieces of planar topology, to which we can apply a variant of the convergence of random spherical quadrangulations to the Brownian map. The idea of cutting into slices quadrangulations with a boundary along geodesics appears in Bouttier and Guitter [16, 17]. The use of these slices (also called maps with a piecewise geodesic boundary) plays an important role in Le Gall’s approach [30] to the uniqueness of the Brownian map in the planar case, which requires to introduce the scaling limits of these slices. The previously cited works are influential to our approach. It however requires to glue an infinite number of metric spaces along geodesic boundaries, which could create potential problems when passing to the limit.

1.4 Universal aspects of the limit

Another important aspect is that of universality of the spaces $\mathrm {BD}_L$. Indeed, we expect these spaces to be the scaling limit of many other models of random maps with a boundary, as in the case of the Brownian map, which corresponds to $L=0$. In the latter case, it has indeed been proved, starting in Le Gall’s work [30], that the Brownian map is the unique scaling limit for a large family of natural models of discrete random maps, see [1, 2, 7, 12]. The now classical approach to universality developed in [30] can be generalized to our context, as we illustrate in the case of critical bipartite Boltzmann maps.

1.4.1 Boltzmann random maps

Let $\mathbf {B}$ be the set of bipartite rooted plane maps, that is, the set of rooted plane maps with faces all having even degrees (equivalently, this is the set of maps whose internal faces all have even degrees). For $l\in \mathbb {Z}_+$, let $\mathbf {B}_l$ be the set of bipartite maps $\mathbf {m}\in \mathbf {B}$ with perimeter¹ 2l. Note that when $l=1$, meaning that the root face has degree 2, there is a natural bijection between $\mathbf {B}_1$ and $\mathbf {B}{\setminus } \mathbf {B}_0$, consisting in gluing together the two edges of the root face into one edge.

Let $q=(q_1,q_2,\ldots )$ be a sequence of non-negative weights. We assume throughout that $q_i>0$ for at least one index $i\ge 2$. The Boltzmann measure associated with the sequence q is the measure $W(q;\cdot )$ on $\mathbf {B}$ defined by

$$\begin{aligned} W(q;\mathbf {m})=\prod _{f\in \mathbf {F}(\mathbf {m}){\setminus }\{f_*\}}q_{\deg (f)/2}. \end{aligned}$$

This defines a non-negative, $\sigma$-finite measure, and by convention the vertex-map receives a weight $W(q,\circ )=1$. In what follows, the weight sequence q is considered fixed and its mention will be implicit, so that we denote for example $W(\mathbf {m})=W(q;\mathbf {m})$, and likewise for the variants of W to be defined below.

We aim at understanding various probability measures obtained by conditioning W with respect to certain specific subsets of $\mathbf {B}$. It is a simple exercise to check that $W(\mathbf {B}_l)$ is non-zero for every $l\in \mathbb {N}$ (because $\mathbf {B}_l$ contains all rooted plane trees with l edges, which all receive a weight 1), and that $W(\mathbf {B}_l)$ is finite for one value of $l>0$ if and only if it is finite for all values of $l>0$. To see this, pick $i\ge 2$ so that $q_i>0$, and let A be a map composed of k degree 2i-faces arranged into some annulus and two other faces (the boundary components of the annulus) of degree 2l and $2l'$. Gluing A to the boundary of a map with perimeter $2l'$ turns it into a map with perimeter 2l. This shows that $q_i^k W(\mathbf {B}_{l'})\le W(\mathbf {B}_l)$.

If $W(\mathbf {B}_l)<\infty$, which we will assume throughout the paper, it makes sense to define the Boltzmann probability measures

$$\begin{aligned} \mathbb {W}_l=W(\cdot \, | \, \mathbf {B}_l)=\frac{W(\cdot \cap \mathbf {B}_l)}{W(\mathbf {B}_l)},\qquad l\ge 0. \end{aligned}$$

A random map with distribution $\mathbb {W}_l$ has a root face of fixed degree 2l, but a random number of vertices, edges and faces.

Likewise, we can consider conditioned versions of W given both the perimeter and the “size” of the map, where the size can be alternatively the number of vertices, edges or internal faces.² We let $\mathbf {B}^{\mathbf {V}}_{l,n}$, $\mathbf {B}^{\mathbf {E}}_{l,n}$, $\mathbf {B}^{\mathbf {F}}_{l,n}$ be the subsets of $\mathbf {B}_l$ consisting of maps with respectively $n+1$ vertices, n edges and n internal faces. (The choice of $n+1$ vertices instead of a more natural choice of n vertices is technical and will make the statements simpler.)

In all the statements involving a given weight sequence q and a symbol $\mathbf {S}\in \{\mathbf {V},\mathbf {E},\mathbf {F}\}$ (for “size”), it will always be tacitly imposed that (l, n) belongs to the set

$$\begin{aligned} \mathcal {E}^\mathbf {S}(q)=\left\{ (l,n)\in \mathbb {Z}_+^2:W\left( \mathbf {B}^\mathbf {S}_{l,n}\right) >0\right\} . \end{aligned}$$

Note that for $(l,n)\in \mathcal {E}^\mathbf {S}(q)$, it holds that $W(\mathbf {B}^{\mathbf {S}}_{l,n})<\infty$ since $W(\mathbf {B}_l)<\infty$. In this way, we can define the distribution

$$\begin{aligned} \mathbb {W}^{\mathbf {S}}_{l,n}(\cdot )=W\left( \cdot \, |\, \mathbf {B}^{\mathbf {S}}_{l,n}\right) . \end{aligned}$$

It will be useful in the following to know what the set $\mathcal {E}^\mathbf {S}(q)$ looks like. More precisely, let

$$\begin{aligned} \mathcal {E}^\mathbf {S}_l(q)=\{n\ge 0:(l,n)\in \mathcal {E}^\mathbf {S}(q)\}. \end{aligned}$$

(1)

As above, when the weight sequence q is unequivocally fixed, we will drop the mention of it from the notation and write $\mathcal {E}^\mathbf {S}$ and $\mathcal {E}^\mathbf {S}_l$.

Define three numbers $h^\mathbf {V}$, $h^\mathbf {E}$, $h^\mathbf {F}$ by

$$\begin{aligned} h^\mathbf {V}=\mathrm {gcd}(\{n\ge 1:q_{n+1}>0\}),\qquad h^\mathbf {E}=\mathrm {gcd}(\{n\ge 1:q_{n}>0\}),\qquad h^\mathbf {F}=1\,. \end{aligned}$$

(2)

Then we have the following lemma, which is a slight generalization of [42, Lemma 6.1].

Lemma 3

Let q be a weight sequence, and let $\mathbf {S}$ be one of the three symbols $\mathbf {V}$, $\mathbf {E}$, $\mathbf {F}$. There exists an integer $\beta ^\mathbf {S}\ge 0$ such that for every $l\ge 1$, there exists a set $R^\mathbf {S}_l\subseteq \{0,1,\ldots ,l\beta ^\mathbf {S}-1\}$ such that

$$\begin{aligned} \mathcal {E}^\mathbf {S}_l(q)=R^\mathbf {S}_l\cup \left( l\beta ^\mathbf {S}+h^\mathbf {S}\mathbb {Z}_+\right) . \end{aligned}$$

In fact, note that $\mathcal {E}^\mathbf {F}_l(q)=\mathbb {Z}_+$, which amounts to the fact that, for any q and any $n\ge 0$, $l\ge 1$, there is at least one map $\mathbf {m}$ with n internal faces and perimeter 2l such that $W(q;\mathbf {m})>0$. As a consequence, we can always take $\beta ^\mathbf {F}=0$. We will prove this lemma later in Sect. 6.2.

1.4.2 Admissible, regular critical weight sequences

Let us introduce some terminology taken from [34]. Let

$$\begin{aligned} f_q(x)=\sum _{k\ge 0}x^k\left( {\begin{array}{c}2k+1\\ k\end{array}}\right) q_{k+1},\qquad x\ge 0. \end{aligned}$$

This defines a totally monotone function with values in $[0,\infty ]$.

Definition 4

We say that q is admissible if the equation

$$\begin{aligned} f_q(z)=1-\frac{1}{z} \end{aligned}$$

(3)

admits a solution $z>1$. We also say that q is regular critical if moreover this solution satisfies

$$\begin{aligned} z^2 f_q'(z)=1 \end{aligned}$$

and if there exists $\varepsilon >0$ such that $f_q(z+\varepsilon )<\infty$.

Note that q being regular critical means that the graphs of $f_q$ and of $x\mapsto 1-1/x$ are tangent at the point of abscissa z, and in particular, by convexity of $f_q$, the solution z to (3) is unique. We denote by

$$\begin{aligned} \mathcal {Z}_q=z \end{aligned}$$

this solution, which will play an important role in the discussion to come.

To give a little more insight into this definition, let us introduce at this point a measure on maps that might look less natural at first sight than the Boltzmann measure $\mathbb {W}_l$, but which will turn out to be better-behaved from the bijective point of view on which this work relies. Let $\mathbf {B}^\bullet$ be the set of pairs $(\mathbf {m},v_*)$ where $\mathbf {m}\in \mathbf {B}$ is a rooted bipartite map and $v_*\in \mathbf {V}(\mathbf {m})$ is a distinguished vertex. We also let $\mathbf {B}^\bullet _l$ be the subset of $\mathbf {B}^\bullet$ consisting of the maps having perimeter 2l. We let $W^{\bullet }(q;\cdot )$ be the measure on $\mathbf {B}^\bullet$ defined by

$$\begin{aligned} W^{\bullet }(q;\{(\mathbf {m},v_*)\})=W(\mathbf {m}),\qquad (\mathbf {m},v_*)\in \mathbf {B}^\bullet , \end{aligned}$$

(4)

as well as the probability measures $\mathbb {W}^{\bullet }_l$, defined by conditioning $W^{\bullet }$ (we will usually omit the mention of q) on $\mathbf {B}^{\bullet }_l$, whenever this makes sense. Similarly to the above, for $\mathbf {S}\in \{\mathbf {V},\mathbf {E},\mathbf {F}\}$, we let $\mathbf {B}^{\bullet ,\mathbf {S}}_{l,n}$ be the set of pointed maps $(\mathbf {m},v_*)\in \mathbf {B}^\bullet$ such that $\mathbf {m}\in \mathbf {B}^{\mathbf {S}}_{l,n}$ and, when $0<W^\bullet (\mathbf {B}^{\bullet ,\mathbf {S}}_{l,n})<\infty$ we define

$$\begin{aligned} \mathbb {W}^{\bullet ,\mathbf {S}}_{l,n}=W^\bullet \left( \cdot \, \big |\, \mathbf {B}^{\bullet ,\mathbf {S}}_{l,n}\right) . \end{aligned}$$

(5)

Note that, if $\phi (\mathbf {m},v_*)=\mathbf {m}$ denotes the map from $\mathbf {B}^\bullet$ to $\mathbf {B}$ that forgets the marked vertex, then $\mathbb {W}_l$ is absolutely continuous with respect to $\phi _*\mathbb {W}^\bullet _l$, with density function given by

$$\begin{aligned} \mathrm {d}\mathbb {W}_l(\mathbf {m})=\frac{K_l}{|\mathbf {V}|} \mathrm {d}(\phi _*\mathbb {W}^{\bullet }_l)(\mathbf {m}), \end{aligned}$$

(6)

where $|\mathbf {V}|$ should be understood as the random variable $\mathbf {m}\mapsto |\mathbf {V}(\mathbf {m})|$ giving the number of vertices of the map, and $K_l=\mathbb {W}^\bullet _l[1/|\mathbf {V}|]^{-1}$. This fact will be useful later.

Proposition 1 in [34] shows that the sequence q of non-negative weights is admissible if and only if $W^\bullet (q;\mathbf {B}^\bullet _1)<\infty$ (this is in fact the defining condition of admissibility in [34]). We see that this clearly implies that $W(q;\mathbf {B}_1)<\infty$, and even that $W^\bullet (q;\mathbf {B}^\bullet _l)<\infty$ and $W(q;\mathbf {B}_l)<\infty$ for every $l\ge 1$, by the same trick as in Sect. 1.4.1 of gluing an annular map to a (pointed) map with perimeter 2l to turn it into a map with perimeter 2. Moreover, in this case, the constant $\mathcal {Z}_q$ has a nice interpretation in terms of the pointed measures. Namely, it holds that

$$\begin{aligned} \mathcal {Z}_q=1+W^\bullet (\mathbf {B}^{\bullet }_1)/2. \end{aligned}$$

(7)

From now on, our attention will be exclusively focused on regular critical weight sequences. It is not obvious at this point how to interpret the definition, which will become clearer when we see how to code maps with decorated trees. However, let us explain now in which context this property typically intervenes, and refer the reader to the upcoming Sect. 1.4.3 for two applications. For instance, if one wants to study uniform random quadrangulations with a boundary and with n faces as we did in the first part of this paper, it is natural to consider the sequence $q^\circ =\delta _{2}=(0,1,0,0,\ldots )$ and to note that $\mathbb {W}^{\mathbf {F}}_{l,n}(q^\circ ;\cdot )$ is the uniform distribution on $\mathbf{Q}_{l,n}$. Here, note that the sequence $q^\circ$ is not admissible, but the probability measure $\mathbb {W}^{\mathbf {F}}_{l,n}(q^\circ ;\cdot )$ does make sense because $0<W(\mathbf {B}^{\mathbf {F}}_{l,n})<\infty$, due to the fact that there are finitely many quadrangulations with a boundary of perimeter 2l, and with n internal faces. Now, it can be checked that $q=12^{-1}q^\circ$ is admissible and regular critical, and that $\mathbb {W}^{\mathbf {F}}_{l,n}(q;\cdot )=\mathbb {W}^{\mathbf {F}}_{l,n}(q^\circ ;\cdot )$ is still the uniform distribution on $\mathbf{Q}_{l,n}$. This way of transforming a “naturally given” weight sequence $q^\circ$ into a regular weight sequence while leaving $\mathbb {W}^{\mathbf {S}}_{l,n}$ invariant is common and very useful.

The main result is the following. Let q be a regular critical weight sequence. Define $\rho _q=2+\mathcal {Z}_q^3f''_q(\mathcal {Z}_q)$ and let ${\sigma _{\mathbf {E}}}$, ${\sigma _{\mathbf {V}}}$, ${\sigma _{\mathbf {F}}}$ be the non-negative numbers with squares

$$\begin{aligned} {\sigma _{\mathbf {E}}}^2=\frac{\rho _q}{\mathcal {Z}_q},\quad {\sigma _{\mathbf {V}}}^2=\rho _q,\quad {\sigma _{\mathbf {F}}}^2=\frac{\rho _q}{\mathcal {Z}_q-1}\,. \end{aligned}$$

(8)

For $L>0$, we denote by $\mathscr {S}^\mathbf {S}_L$ the set of sequences $(l_k,n_k)_{k\ge 0}\in (\mathcal {E}^\mathbf {S})^\mathbb {N}$ such that $l_k$, $n_k\rightarrow \infty$ with $l_k\sim L{\sigma _{\mathbf {S}}}\sqrt{n_k}$ as $k\rightarrow \infty$.

Theorem 5

Let q be a regular critical weight sequence. Let $\mathbf {S}$ denote one of the symbols $\mathbf {V}$, $\mathbf {E}$, $\mathbf {F}$, and $(l_k,n_k)_{k\ge 0}\in \mathscr {S}^\mathbf {S}_L$ for some $L>0$. For $k\ge 0$, denote by $M_k$ a random map with distribution $\mathbb {W}^{\mathbf {S}}_{l_k,n_k}$. Then

in distribution for the Gromov–Hausdorff topology. Similarly, if $M_k^\bullet$ denotes a pointed random map with distribution $\mathbb {W}^{\bullet ,\mathbf {S}}_{l_k,n_k}$, then

in distribution for the pointed Gromov–Hausdorff topology, if $\mathrm {BD}_L$ is equipped with the distinguished point $x_*$.

Remark 1

The intuitive meaning for these renormalization constants is the following: in a large random map with Boltzmann distribution, it can be checked that the numbers $|\mathbf {V}|$ and $|\mathbf {F}|$ of vertices and faces are of order $|\mathbf {E}|/\mathcal {Z}_q$ and $|\mathbf {E}|(1-1/\mathcal {Z}_q)$ respectively, where $|\mathbf {E}|$ is the number of edges, and that conditioning on having n edges is asymptotically the same as conditioning on having (approximately) $n/\mathcal {Z}_q$ vertices, or $n\,(1-1/\mathcal {Z}_q)$ faces.

Remark 2

In fact, the above result is also valid in the case where $L=0$, with the interpretation that $\mathrm {BD}_0$ is the Brownian map. The proof of this claim can be obtained by following ideas similar to [10, Section 6.1]. However, a full proof requires the convergence of a map with law $\mathbb {W}_{1,n}^\mathbf {S}$, rescaled by $(4{\sigma _{\mathbf {S}}}^2n/9)^{1/4}$, to the Brownian map, and this has been explicitly done only in the case where $\mathbf {S}=\mathbf {V}$ in [30, Section 9]. In fact, building on the existing literature [34, 36], it is easy to adapt the argument to work for $\mathbf {S}=\mathbf {F}$ in the same way, while the case $\mathbf {S}=\mathbf {E}$, which is slightly different, can be tackled by the methods of [1]. Writing all the details would add a consequent number of pages to this already lengthy paper, so we will omit the proof.

1.4.3 Applications

Let us give two interesting specializations of Theorem 5. If $p\ge 2$ is an integer, a 2p-angulation with a boundary is a map whose internal faces all have degree 2p. The computations of the various constants appearing in the statement of Theorem 5 have been performed in Section 1.5.1 of [34]. These show that the weight sequence

$$\begin{aligned} q=\frac{(p-1)^{p-1}}{p^p\left( {\begin{array}{c}2p-1\\ p\end{array}}\right) }\delta _p \end{aligned}$$

is regular critical, that $\mathbb {W}^{\mathbf {F}}_{l,n}$ is the uniform law on the set of 2p-angulations with n faces and perimeter 2l in this case, and that the constants are

$$\begin{aligned} \mathcal {Z}_q=\frac{p}{p-1},\quad \rho _q=p,\quad {\sigma _{\mathbf {E}}}^2=p-1,\quad {\sigma _{\mathbf {V}}}^2=p,\quad {\sigma _{\mathbf {F}}}^2=p(p-1). \end{aligned}$$

Therefore, in this situation, Theorem 5 for $\mathbf {S}=\mathbf {F}$ gives the following result, that clearly generalizes Theorem 1.

Corollary 6

Let $L\in (0,\infty )$ be fixed, $(l_n,n\ge 1)$ be a sequence of integers such that $l_n\sim L\sqrt{p(p-1)n}$ as $n\rightarrow \infty$, and $M_n$ be uniformly distributed over the set of 2p-angulations with n internal faces and with perimeter $2l_n$. Then the following convergence holds in distribution for the Gromov–Hausdorff topology:

Next, consider the case where $q_k=a^{-k}$, $k\ge 1$ for some $a>0$. In this case, for every $\mathbf {m}\in \mathbf {B}$, a simple computation shows that

$$\begin{aligned} W(\mathbf {m})=a^{-|\mathbf {E}(\mathbf {m})|+l} \end{aligned}$$

so that $\mathbb {W}^{\mathbf {E}}_{l,n}$ is the uniform distribution over bipartite maps with n edges and a perimeter 2l. It was shown in [34, Section 1.5.2] (and implicitly recovered in [1, Proposition 2]) that choosing $a=1/8$ makes q regular critical and that, in this case,

$$\begin{aligned} \mathcal {Z}_q=\frac{3}{2},\qquad \rho _q=\frac{27}{4},\qquad {\sigma _{\mathbf {E}}}^2=\frac{9}{2}. \end{aligned}$$

Thus, one deduces the following statement, that should be compared to [1, Theorem 1].

Corollary 7

Let $M_n$ be a uniform random bipartite map with n edges and with perimeter $2l_n$, where $l_n\sim 3L\sqrt{n/2}$ for some $L>0$. Then the following convergence holds in distribution for the Gromov–Hausdorff topology:

1.5 Convergence of Boltzmann maps

The models we have presented so far consist in taking a random map with a fixed size and perimeter and letting both these quantities go to infinity in an appropriate regime. However, it is legitimate to ask about the behavior of a typical random map with law $\mathbb {W}_l$ or $\mathbb {W}^\bullet _l$ when $l\rightarrow \infty$, so that the perimeter is fixed and large, while the total size is left free.

For every $L\ge 0$ and $A>0$, we define a random metric space $\mathrm {BD}_{L,A}$, which we interpret as the Brownian disk with area A and perimeter L. The definition is postponed to Sect. 2.3 but, for concreteness, we can note the important scaling property stating that the space $\mathrm {BD}_{L,A}$ has same distribution as $A^{1/4}\,\mathrm {BD}_{A^{-1/2}L}$. This property is a simple consequence of the definition, but can also be derived from Theorem 1 by noting that $\mathrm {BD}_{L,1}$ has same distribution as $\mathrm {BD}_L$ and that, if $Q_n$ is a uniform random element in $\mathbf{Q}_{\lfloor L\sqrt{2n}\rfloor , \lfloor An\rfloor }$, then $(8n/9)^{-1/4}Q_n$ converges in distribution for the Gromov–Hausdorff topology to $\mathrm {BD}_{L,A}$, by virtue of Theorem 1. See also Remark 3 in Sect. 2.3 below.

Let $\mathcal {A}^\bullet$ be a stable random variable with index 1 / 2, with distribution given by

$$\begin{aligned} \mathbb {P}(\mathcal {A}^\bullet \in \mathrm {d}A)=\frac{1}{\sqrt{2\pi A^3}}\exp \left( -\frac{1}{2 A}\right) \mathrm {d}A\, \mathbf {1}_{\{A>0\}}. \end{aligned}$$

Note that $\mathbb {E}[1/\mathcal {A}^\bullet ]=1$, so that the formula

$$\begin{aligned} \frac{\mathbb {P}(\mathcal {A}^\bullet \in \mathrm {d}A)}{ A}=\frac{1}{\sqrt{2\pi A^5}}\exp \left( -\frac{1}{2A}\right) \mathrm {d}A\, \mathbf {1}_{\{A>0\}} \end{aligned}$$

also defines a probability distribution, and we let $\mathcal {A}$ be a random variable with this distribution. We define the free Brownian disk with perimeter 1 to be a space with same law as $\mathrm {BD}_{1,\mathcal {A}}$, where this notation means that conditionally given $\mathcal {A}=A$, it has same distribution as $\mathrm {BD}_{1,A}$. Likewise, the free pointed Brownian disk with perimeter 1 has same distribution as $\mathrm {BD}_{1,\mathcal {A}^\bullet }$, and, as the name suggests, it is seen as a pointed metric space by distinguishing the point $x_*$.

For future reference, for $L>0$, it is natural to define the law of the free Brownian disk (resp. free pointed Brownian disk) with perimeter L by scaling, setting it to be the law of $\sqrt{L}\,\mathrm {BD}_{1,\mathcal {A}}$ or equivalently of $\mathrm {BD}_{L,L^2\mathcal {A}}$ (resp. $\sqrt{L}\,\mathrm {BD}_{1,\mathcal {A}^\bullet }=^{(d)}\mathrm {BD}_{L,L^2\mathcal {A}^\bullet }$). We let $\mathrm {FBD}_L$ (resp. $\mathrm {FBD}^\bullet _L$) stand for the free Brownian disk (resp. free pointed Brownian disk) with perimeter L.

Theorem 8

Let q be a regular critical weight sequence. For $l\in \mathbb {N}$, let $B_l$ (resp. $B^\bullet _l$) be distributed according to $\mathbb {W}_l(q;\cdot )$ (resp. $\mathbb {W}^\bullet _l(q;\cdot )$). Then

in distribution for the Gromov–Hausdorff topology, and respectively

in distribution for the pointed Gromov–Hausdorff topology.

It is remarkable that the renormalization in this theorem does not involve q whatsoever!

1.6 Further comments and organization of the paper

The very recent preprint [39] by Miller and Sheffield aims at providing an axiomatic characterization of the Brownian map in terms of elementary properties. In this work, certain measures on random disks play a central role. We expect that these measures, denoted by $\mu _{\mathrm {DISK}}^{k,L}$ for $k\in \{0,1\}$ and $L>0$, are respectively the laws of the free Brownian disk ($k=0$) and the pointed free Brownian disk ($k=1$) with perimeter $L>0$. Miller and Sheffield define these measures directly in terms of the metric balls in certain versions of the Brownian map, and it is not immediate, though it is arguably very likely, that this definition matches the one given in the present paper. Establishing such a connection would be interesting from the perspective of [39] since, for example, it is not established that $\mu _{\mathrm {DISK}}^{k,L}$ is supported on compact metric spaces, due to the possibly wild behavior of the boundary from a metric point of view. We hope to address such questions in future work.

Note also that [39] introduces another measure on metric spaces, called $\mu _{\mathrm {MET}}^L$, which intuitively corresponds to the law of a variant of a metric ball in the Brownian map, with a given boundary length. A description of this measure in terms of slices is given in [39], which is very much similar to the one we describe in the current work. However, there is a fundamental difference, which is that $\mu _{\mathrm {MET}}^L$ does not satisfy the invariance under re-rooting that is essential to our study of random disks. In a few words, in a random disk with distribution $\mu _{\mathrm {MET}}^L$, all points of the boundary are equidistant from some special point (the center of the ball), while it is very likely that no such point exists a.s. in $\mathrm {BD}_{L,A}$, or under the law $\mu _{\mathrm {DISK}}^{k,L}$.

It would be natural to consider the operation that consists in gluing Brownian disks, say with same perimeter, along their boundaries, hence constructing what should intuitively be a random sphere with a self-avoiding loop. However, this operation is in general badly behaved from a metric point of view (in the sense of [18, Chapter 3] say), and it is not clear that the resulting space has the same topology as the topological gluing. The reason for this difficulty is that we require to glue along curves that are not Lipschitz, since the boundaries of the spaces $\mathrm {BD}_L$ have Hausdorff dimension 2 (by contrast, the gluings considered in Sect. 5 of the present paper are all along geodesics.) At present, such questions remain to be investigated.³

The rest of the paper is organized as follows. In Sect. 2, we give a self-standing definition of the limiting objects. As in many papers on random maps, we rely on bijective tools, and Sect. 3 introduces these tools. Section 4 gives a technical result of convergence of slices, which are the elementary pieces from which the Brownian disks are constructed. Section 5 is dedicated to the proof of Theorem 1. In Sects. 6–8, we address the question of universality and prove Theorems 5 and 8.

2 Definition of Brownian disks

Recall that the Brownian map $\mathrm {BD}_0$ is defined ([28], see also [35] and Sect. 4.1 below) in terms of a certain stochastic process called the normalized Brownian snake. Likewise, the spaces $\mathrm {BD}_L$, $L>0$ of Theorem 1 are defined in terms of stochastic processes, as we now discuss.

2.1 First-passage bridges and random continuum forests

The first building blocks of the Brownian disks are first-passage bridges of Brownian motion. Informally, given A, $L>0$, the first-passage bridge at level $-L$ and time A is a Brownian motion conditioned to first hit $-L$ at time A. To be more precise, let us introduce some notation. We let X be the canonical continuous process, and $\mathcal {G}_s=\sigma (X_u,u\le s)$ be the associated canonical filtration. Denote by $\mathbb {P}$ the law of standard Brownian motion, and by $\mathbb {P}^A$ the law of standard Brownian motion killed at time $A>0$. For $L\ge 0$, let $T_L=\inf \{s\ge 0:X_s=-L\}$ be the first hitting time of $-L$. We denote the density function of its law by

$$\begin{aligned} j_L(A)=\frac{\mathbb {P}(T_L\in \mathrm {d}A)}{\mathrm {d}A}=\frac{L}{\sqrt{2\pi A^3}}\exp \left( -\frac{L^2}{2A}\right) . \end{aligned}$$

(9)

With this notation, the law $\mathbb {F}^A_L$ of the first-passage bridge at level $-L$ and at time A can informally be seen as $\mathbb {P}^A(\,\cdot \, |\, T_L=A)$. It is best defined by an absolute continuity relation with respect to $\mathbb {P}^A$. Namely, for every $s\in (0,A)$ and every non-negative random variable G that is measurable with respect to $\mathcal {G}_s$, we let

$$\begin{aligned} \mathbb {F}^A_L(G)=\mathbb {P}^A\left[ G\,\mathbf {1}_{\{T_L>s\}}\frac{j_{L+X_s}(A-s)}{j_L(A)}\right] . \end{aligned}$$

(10)

It can be seen [19] that this definition is consistent and uniquely extends to a law $\mathbb {F}^A_L$ on $\mathcal {G}_A$, such that $\mathbb {F}^A_L(T_L=A)=1$.

An alternative description of first-passage bridges, which will be useful to us later, is the following.

Proposition 9

Let A, $L>0$. Then for every $y\in (0,L)$ and for every non-negative random variable G that is measurable with respect to $\mathcal {G}_{T_y}$, we have

$$\begin{aligned} \mathbb {F}^A_L[G]=\mathbb {P}^A\left[ G\,\mathbf {1}_{\{T_y<A\}}\frac{j_{L-y}(A-T_y)}{j_L(A)}\right] . \end{aligned}$$

(11)

Moreover, this property characterizes $\mathbb {F}^A_L$ among all measures on $\mathcal {G}_A$.

Proof

The consistency of (10) as s varies implies that the process $\mathcal {M}=(\mathbf {1}_{\{T_L>s\}}j_{L+X_s}(A-s)/j_L(A),\,0\le s<A)$ is a $(\mathcal {G}_s,\,0\le s<A)$-martingale under $\mathbb {P}^A$. Therefore, for every stopping time T such that $T<A$ a.s. under $\mathbb {F}^A_L$, and for every $E\in \mathcal {G}_T$, we have

$$\begin{aligned} \mathbb {F}_L^A(E)= & {} \lim _{s\uparrow A}\mathbb {P}^A[\mathbf {1}_{E\cap \{T\le s\}}\mathcal {M}_s]= \lim _{s\uparrow A}\mathbb {P}^A[\mathbf {1}_{E\cap \{T\le s\}}\mathbb {P}^A[\mathcal {M}_s\,|\,\mathcal {G}_T]] \\= & {} \lim _{s\uparrow A}\mathbb {P}^A[\mathbf {1}_{E\cap \{T\le s\}}\mathcal {M}_T], \end{aligned}$$

and this is equal to $\mathbb {P}^A[\mathbf {1}_{E}\mathcal {M}_T]$. The formula is obtained by applying this result to $T=T_y$.

The fact that $\mathbb {F}^A_L$ is characterized by these formulas comes from the following observation. Suppose $\tilde{\mathbb {F}}^A_L$ is a probability measure on $\mathcal {G}_A$ for which (11) holds for every $y\in (0,L)$. Then for every $s<A$, $\tilde{\mathbb {F}}^A_L(T_y<s)=\mathbb {P}^A[\mathbf {1}_{\{T_y<s\}}j_{L-y}(A-T_y)/j_L(A)]$, and this clearly converges to 0 as $y\uparrow L$. Therefore, $T_y$ converges $\tilde{\mathbb {F}}^A_L$-a.s. to A as $y\uparrow L$. Then for every $s<A$ and $E\in \mathcal {G}_s$, similar manipulations to the above ones show that

$$\begin{aligned} \tilde{\mathbb {F}}^A_L(E)= & {} \lim _{y\uparrow L}\tilde{\mathbb {F}}^A_L(E\cap \{T_y>s\})=\lim _{y\uparrow L}\mathbb {P}^A\left[ \mathbf {1}_{E\cap \{T_y>s\}}\mathcal {M}_{T_y}\right] \\= & {} \lim _{y\uparrow L}\mathbb {P}^A\left[ \mathbf {1}_{E\cap \{T_y>s\}}\mathcal {M}_{s}\right] \end{aligned}$$

and this is $\lim _{y\uparrow L}\mathbb {F}^A_L(E\cap \{T_y>s\})=\mathbb {F}^A_L(E)$. This implies that $\tilde{\mathbb {F}}^A_L$ and $\mathbb {F}^A_L$ have the same finite-dimensional marginal distributions, so that they are equal. $\square$

It is convenient to view a first-passage bridge as encoding a random continuum forest. This is a classical construction that can be summarized as follows, see for instance [40]. Here we work under $\mathbb F^A_L$. For $0\le s\le s'\le A$, define $\underline{X}_{s,s'}=\inf \{X_u:s\le u\le s'\}$ and let

$$\begin{aligned} d_X(s,s')=X_s+X_{s'}-2\underline{X}_{s\wedge s',s\vee s'}\qquad s,s'\in [0,A]. \end{aligned}$$

(12)

The function $d_X$ on $[0,A]^2$ is a pseudo-metric, to which one can associate a random metric space $\mathcal {F}^A_L=[0,A]/\{d_X=0\}$, endowed with the quotient metric induced from $d_X$. This metric space is a.s. a compact $\mathbb {R}$-tree, that is, a compact geodesic metric space into which $\mathbb {S}^1$ cannot be embedded. It comes with a distinguished geodesic of length L, which is the image of the first hitting times $\{T_y,0\le y\le L\}$ under the canonical projection $p_X:[0,A]\rightarrow \mathcal {F}^A_L$. It is convenient to view this segment as the floor of a forest of $\mathbb {R}$-trees, these trees being exactly of the form $\mathcal {T}_y=p_X((T_{y-},T_y])$, corresponding to the excursions of X above its past infimum. One should imagine that the $\mathbb {R}$-tree $\mathcal {T}_y$ is grafted at the point $p_X(T_y)$ of the floor lying at distance y from $p_X(0)$.

2.2 Snakes

We now enrich the random “real forest” described above by assigning labels to it. Informally speaking, the trees of the forest are labeled by independent Brownian snakes [22, 27], while the floor of the forest is labeled by a Brownian bridge with variance factor 3.

More precisely, let X be a first-passage bridge with law $\mathbb {F}^A_L$. Conditionally given X, we let $(Z^{\mathbf 0}_s,0\le s\le A)$ be a centered Gaussian process with covariance function

$$\begin{aligned} \mathrm{Cov\,}\left( Z^{\mathbf 0}_s,Z^{\mathbf 0}_{s'}\right) =\inf _{u\in [s\wedge s',s\vee s']}(X_u-\underline{X}_u)\qquad s,s'\in [0,A], \end{aligned}$$

(13)

where $\underline{X}_u=\inf _{0\le v\le u}X_v$ is the past infimum of X. Note in particular that $Z^{\mathbf 0}_s$ and $Z^{\mathbf 0}_{s'}$ are independent if s, $s'$ belong to two different excursion intervals of X above $\underline{X}$. It is classical [27] that $Z^{\mathbf 0}$ admits a continuous modification, see also [8] for a discussion in the current context. For this modification, we a.s. have $Z^{\mathbf 0}_{T_y}=0$ for every $y\in [0,L]$ (for a given y, this comes directly from the variance formula). The process $Z^{\mathbf 0}$ is sometimes called the head of the Brownian snake driven by the process $X-\underline{X}$, the reason being that it can be obtained as a specialization of a path-valued Markov process called the Brownian snake [27] driven by $X-\underline{X}$. The process $Z^{\mathbf 0}$ itself is not Markov.

Independently of $Z^{\mathbf 0}$, let also $\mathrm {b}$ be a standard Brownian bridge of duration L, so that

$$\begin{aligned} \mathrm{Cov\,}(\mathrm {b}_y,\mathrm {b}_{y'})=\frac{y(L-y')}{L},\qquad 0\le y\le y'\le L. \end{aligned}$$

We define the process Z to be

$$\begin{aligned} Z_s=Z^{\mathbf 0}_s+\sqrt{3}\,\mathrm {b}_{-\underline{X}_s},\qquad 0\le s\le A. \end{aligned}$$

(14)

We abuse notation and still denote by $\mathbb {F}^A_L$ the law of the pair (X, Z) thus defined, so that $\mathbb {F}^A_L$ is seen as a probability distribution on the space $\mathcal {C}([0,A],\mathbb {R})^2$. In the same spirit, we will still denote by $\mathcal {G}_t$ the natural filtration $\sigma (\{(X_s,Z_s),\,0\le s\le t\})$. We use a similar extended notation for $\mathbb {P}^A$, defining Z in the same way under this probability measure. Note that the absolute continuity relations (10) and (11) are still valid verbatim with these extended notation and, in particular, the density function involves only X and not Z.

It is classical that a.s. under $\mathbb {F}^A_L$, Z is a class function on [0, A] for the equivalence relation $\{d_X=0\}$, so that Z can also be seen as a function on the forest $\mathcal {F}^A_L$. Note that $-\underline{X}_{T_y}=y$ for every $0\le y\le L$, which corresponds to the fact that, in the above depiction of the random forest, the point $p_X(T_y)$ receives label $\sqrt{3}\,\mathrm {b}_y$.

It is a simple exercise to check that the above definition of Z is equivalent to the following quicker (but more obscure) one. Conditionally given X, we have that Z is Gaussian, centered, with covariance function

$$\begin{aligned} \mathrm{Cov\,}(Z_s,Z_{s'})=\underline{X}_{s,s'}-\underline{X}_{s'}-3 \underline{X}_{s}(L+\underline{X}_{s'})/L\qquad 0\le s\le s'\le A\,. \end{aligned}$$

Similarly as (12), we define a pseudo-metric using the process Z instead of X, but with an extra twist. As above, let $\underline{Z}_{s,s'}=\inf \{Z_u:u\in [s,s']\}$ for $0\le s\le s' \le A$, and this time we extend the definition to $0\le s'<s\le A$ by setting

$$\begin{aligned} \underline{Z}_{s,s'}=\inf \{Z_u:u\in [s,A]\cup [0,s']\}=\underline{Z}_{s,A}\wedge \underline{Z}_{0,s'}, \end{aligned}$$

so if we see [0, A] as a circle by identifying 0 with A, $\underline{Z}_{s,s'}$ is the minimum of Z on the directed arc from s to $s'$. We let

$$\begin{aligned} d_Z(s,s')=Z_s+Z_{s'}-2\max (\underline{Z}_{s,s'},\underline{Z}_{s',s})\qquad s,s'\in [0,A]\,. \end{aligned}$$

(15)

2.3 Brownian disks

We are now ready to give the definition of Brownian disks. Consider the (random) set $\mathcal {D}$ of all pseudo-metrics d on [0, A] satisfying the two properties

$$\begin{aligned} {\left\{ \begin{array}{ll} \{d_X=0\}\subseteq \{d=0\}\,;\\ d\le d_Z. \end{array}\right. } \end{aligned}$$

(16)

The set $\mathcal {D}$ is nonempty (it contains the zero pseudo-metric) and contains a maximal element $D^*$ defined by

$$\begin{aligned}&D^*(s,s')\nonumber \\&\quad =\inf \left\{ \sum _{i=1}^kd_Z(s_i,t_i):\begin{array}{l}k\ge 1,\quad t_1,s_2,t_2,\ldots ,s_k\in [0,A],\, s_1=s,\,t_k=s' ,\\ d_X(t_i,s_{i+1})=0\, \text{ for } \text{ every } i\in \{1,\ldots , k-1\}\, \end{array} \right\} ,\nonumber \\ \end{aligned}$$

(17)

see [18, Chapter 3]. The Brownian disk $\mathrm {BD}_{L,A}$ with area A and perimeter L is the quotient set $[0,A]/\{D^*=0\}$, endowed with the quotient metric induced from $D^*$ (which we still denote by $D^*$ for simplicity), and considered under the law $\mathbb {F}^A_L$. In the case $A=1$, we drop the second subscript and write $\mathrm {BD}_L=\mathrm {BD}_{L,1}$.

Finally, we let $x_*=\mathbf {p}^*(s_*)$, where $\mathbf {p}^*:[0,A]\rightarrow [0,A]/\{D^*=0\}$ is the canonical projection, and $s_*$ is the (a.s. unique [10, Lemma 11]) point in [0, 1] at which Z reaches its global minimum. The point $x_*$ is the naturally distinguished point that was alluded to in the introduction.

Remark 3

Observe that, by usual scaling properties of Gaussian random variables, under the law $\mathbb {F}^A_L$, the scaled pair $((\lambda ^{1/2}X_{s/\lambda },\, 0\le s\le \lambda A ),(\lambda ^{1/4}Z_{s/\lambda },\, 0\le s\le \lambda A))$ has law $\mathbb {F}^{\lambda A}_{\lambda ^{1/2} L}$, from which we deduce that the random metric space $\lambda ^{-1/4} \mathrm {BD}_{\lambda ^{1/2}\,L,\lambda A}$ has the same distribution as $\mathrm {BD}_{L,A}$.

The reason why we say that $\mathrm {BD}_{L,A}$ has “area” A is that it naturally comes with a non-negative measure of total mass A, which is the image of the Lebesgue measure on [0, A] by the canonical projection $\mathbf {p}:[0,A]\rightarrow \mathrm {BD}_{L,A}$. It will be justified later that $\mathrm {BD}_{L,A}$ is a.s. homeomorphic to the closed unit disk, so that the term area makes more sense in this context. Furthermore, the boundary $\partial \mathrm {BD}_{L,A}$ will be shown to be equal to $\mathbf {p}(\{T_y:0\le y\le L\})$, so that it can be endowed with a natural non-negative measure with total mass L, which is the image of the Lebesgue measure on [0, L] by $y\mapsto \mathbf {p}(T_y)$. This justifies the term “perimeter.”

3 The Schaeffer bijection and two variants

This work strongly relies on powerful encodings of discrete maps by trees and related objects. In this section we present the encodings we will need: the original Cori–Vauquelin–Schaeffer bijection [20, 41], a variant for so-called slices [30] and a variant for plane quadrangulations with a boundary (particular case of [15]). We only give the constructions from the encoding objects to the considered maps and refer the reader to the aforementioned works for converse constructions and proofs.

3.1 The original Cori–Vauquelin–Schaeffer bijection

Let $(\mathbf {t},\ell )$ be a well-labeled tree with n edges. Recall that this means that $\mathbf {t}$ is a rooted plane tree with n edges, and $\ell :\mathbf {V}(\mathbf {t})\rightarrow \mathbb {Z}$ is a labeling function such that $\ell (u)-\ell (v)\in \{-1,0,1\}$ whenever u and v are neighboring vertices in $\mathbf {t}$. It is usual to “normalize” $\ell$ in such a way that the root vertex of $\mathbf {t}$ gets label 0, but we will also consider different conventions: in fact, all our discussion really deals with the function $\ell$ up to addition of a constant. For simplicity, in the following, we let $\ell _*=\min \{\ell (v):v\in \mathbf {V}(\mathbf {t})\}-1$.

Note

Throughout this paper, whenever a function f is defined at a vertex v, we extend its definition to any corner c incident to v by setting $f(c)=f(v)$. In particular, the label $\ell (c)$ of a corner is understood as the label of the incident vertex.

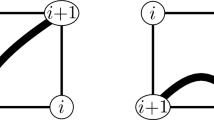
Let $c_0$, $c_1$, ..., $c_{2n-1}$ be the sequence of corners of $\mathbf {t}$ in contour order, starting from the root corner. We extend the list of corners by periodicity, setting $c_{2n+i}=c_i$ for every $i\ge 0$, and adding one corner $c_\infty$ incident to a vertex $v_*$ not belonging to $\mathbf {t}$, with label $\ell (c_\infty )=\ell (v_*)=\ell _*$. Once this is done, we define the successor functions by setting

$$\begin{aligned} s(i)=\inf \{j>i:\ell (c_j)=\ell (c_i)-1\}\in \mathbb {Z}_+\cup \{\infty \},\qquad i\in \{0,1,\ldots ,2n-1\}, \end{aligned}$$

and $s(c_i)=c_{s(i)}$. The Cori–Vauquelin–Schaeffer construction consists in linking $c_i$ with $s(c_i)$ by an arc, in a non-crossing fashion, for every $i\in \{0,1,\ldots ,2n-1\}$. The embedded graph $\mathbf {q}$ with vertex set $\mathbf {V}(\mathbf {t})\,\cup \,\{v_*\}$ and edge set the set of arcs (excluding the edges of $\mathbf {t}$) is then a quadrangulation, which is rooted according to some convention (we omit details here as this point is not important for our purposes), and is naturally pointed at $v_*$. Moreover, the labels on $\mathbf {V}(\mathbf {q})$ inherited from those on $\mathbf {t}$ (and still denoted by $\ell$) are exactly the relative distances to $v_*$ in $\mathbf {q}$:

$$\begin{aligned} d_\mathbf {q}(v,v_*)=\ell (v)-\ell _*,\qquad v\in \mathbf {V}(\mathbf {q}). \end{aligned}$$

(This entirely determines $\ell$ as soon as the value $\ell (v_0)$ is known for some specific $v_0$, but recall that in general we do not want to fix the normalization of $\ell$.) See Fig. 2 for an example of the construction.

For every corner c of $\mathbf {t}$, there is an associated path in $\mathbf {q}$ that follows the arcs between the consecutive successors c, s(c), s(s(c)), ..., $c_\infty$. This path is a geodesic path between the vertex incident to c and $v_*$, it is called the maximal geodesic from c to $v_*$, it can be seen as the geodesic path to $v_*$, with first step the arc from c to s(c), and that turns as much as possible to the left.

Following these paths provides a very useful upper-bound for distances in $\mathbf {q}$. Let us denote by $v_i$ the vertex incident to the corner $c_i$, and let $\ell (i)=\ell (v_i)$ to simplify notation. Let $\check{\ell }(i,j)$ is the minimal value of $\ell (r)$ for r between i and j in cyclic order modulo 2n, that is

$$\begin{aligned} \check{\ell }(i,j)=\left\{ \begin{array}{ll} \min \{\ell (r),r\in [i,j]\} &{}\quad \text{ if } i\le j\\ \min \{\ell (r),r\in [i,2n]\cup [0,j]\} &{}\quad \text{ otherwise. } \end{array}\right. \end{aligned}$$

Then it holds that

$$\begin{aligned} d_\mathbf {q}(v_i,v_j)\le \ell (i)+\ell (j)-2\max \{\check{\ell }(i, j),\check{\ell }( j, i)\}+2. \end{aligned}$$

(18)

The interpretation of this is as follows. Consider the maximal geodesics from the corners $c_{i}$ and $c_{j}$ to $v_*$. These two geodesics coalesce at a first corner $c_k$, and the upper bound is given by the length of the concatenation of the geodesic from $c_i$ to $c_k$ with the segment of the geodesic from $c_k$ to $c_j$. This path will be called the maximal wedge path from $c_i$ to $c_j$.

Fig. 2

The Cori–Vauquelin–Schaeffer bijection. There are two possible rootings of $\mathbf {q}$: they are indicated with question marks. The maximal geodesic from the corner $c_0$ to $v_*$ has been magnified

3.2 Slices

We now follow [30] and describe a modification of the previous construction that, roughly speaking, cuts open the maximal geodesic of $\mathbf {q}$ from $c_0$ to $v_*$. See Fig. 3 for an example, and compare with Fig. 2.

Fig. 3

A map with geodesic boundary is associated with a well-labeled tree via the modified Schaeffer bijection. The maximal geodesic is represented in red on the left and the shuttle is the green chain on the right (color figure online)

Rather than appending to $\mathbf {t}$ a single corner $c_\infty$ incident to a vertex $v_*$, we add a sequence of vertices incident to corners $c'_1$, $c'_2$, ..., $c'_{\ell (c_0)-\ell _*-1}$, $c'_{\ell (c_0)-\ell _*}=c_\infty$, and set labels $\ell (c'_i)=\ell (c_0)-i$ so, in particular, this is consistent with the label we already set for $c_\infty$. Also, instead of extending the sequence $c_0$, $c_1$, ..., $c_{2n-1}$ by periodicity, we add an extra corner $c_{2n}$ to the right of $c_0$ and we let $c_{2n+i}=c'_i$ for $i\in \{1,2,\ldots , \ell (c_0)-\ell _*\}$. The definition of the successor

$$\begin{aligned} s(i)=\inf \{j>i:\ell (c_j)=\ell (c_i)-1\},\qquad s(c_i)=c_{s(i)} \end{aligned}$$

(19)

then makes sense for $i\in \{0,1,\ldots ,2n+\ell (c_0)-\ell _*-1\}$, and we can draw the arcs from $c_i$ to $s(c_i)$ for every $i\in \{0,1,\ldots ,2n+\ell (c_0)-\ell _*-1\}$. In particular, note that the arcs link $c_{2n}$ with $c'_1$, $c'_2$, ..., $c'_{\ell (c_0)-\ell _*-1}$, $c_\infty$ into a chain, which we call shuttle, and to which are connected the arcs $c_i\rightarrow s(c_i)$ with $i\le 2n-1$ and $s(i)>2n-1$. Let $\tilde{\mathbf {q}}$ be the map obtained by this construction. It is called the slice coded by $(\mathbf {t},\ell )$.

This map contains two distinguished geodesic chains, which are, on the one hand, the maximal geodesic from $c_0$ to $v_*$ made of arcs between consecutive successors $c_0$, $s(c_0)$, $s(s(c_0))$, ..., $c_\infty$ and, on the other hand, the shuttle linking $c_{2n}$, $c'_1$, $c'_2$, ..., $c'_{\ell (c_0)-\ell _*-1}$, $c_\infty$. Note that both chains indeed have the same length (number of edges), equal to $\ell (c_0)-\ell _*$. In particular, we have $d_{\tilde{\mathbf {q}}}(c_0,c_\infty )=d_\mathbf {q}(c_0,c_\infty )=\ell (c_0)-\ell _*$, where $\mathbf {q}$ is the quadrangulation from the previous section, constructed from the same well-labeled tree $(\mathbf {t},\ell )$. These two chains are incident to a face of $\tilde{\mathbf {q}}$ of degree $2d_\mathbf {q}(c_0,c_\infty )$, and all other faces have degree 4. Observe that the maximal geodesic and the shuttle only intersect at the root vertex of the tree and $v_*$; as a result, the boundary of the degree $2d_\mathbf {q}(c_0,c_\infty )$-face is a simple curve.

Finally, the quadrangulation $\mathbf {q}$ can then be obtained from $\tilde{\mathbf {q}}$ by identifying one by one the edges of the maximal geodesic with the edges of the shuttle, in the same order. More precisely, we note that there is a natural projection p from $E(\tilde{\mathbf {q}})$ to $E(\mathbf {q})$ defined by $p(e)=e$ for every edge e that is not an edge of the shuttle, and $p(e'_i)=e_i$ if $e_i$ is the i-th edge on the maximal geodesic, and $e'_i$ is the i-th edge of the shuttle, starting from $c_0$. In particular, $p^{-1}(e)$ contains two edges of $\tilde{\mathbf {q}}$ if and only if e is an edge of the maximal geodesic of $\mathbf {q}$. The projection p induces also a projection, still denoted by p, from $V(\tilde{\mathbf {q}})$ onto $V(\mathbf {q})$ such that, if u, v are the extremities of e, then p(u), p(v) are the extremities of p(e). For this reason, any path in $\tilde{\mathbf {q}}$ projects into a path in $\mathbf {q}$ via p, and the graph distances satisfy the inequality

$$\begin{aligned}d_{\mathbf {q}}(p(u),p(v))\le d_{\tilde{\mathbf {q}}}(u,v),\qquad u,v\in V(\tilde{\mathbf {q}}). \end{aligned}$$

Using the same idea as in the preceding section, we obtain another useful bound for distances in $\tilde{\mathbf {q}}$, as follows. Again, let $v_i$ be the vertex incident to the corner $c_i$, and $\ell (i)=\ell (v_i)$. Then

$$\begin{aligned} d_{\tilde{\mathbf {q}}}(v_i,v_j)\le \ell (i)+\ell (j)-2\check{\ell }(i\wedge j,i\vee j)+2, \end{aligned}$$

(20)

where $\check{\ell }(i,j)$ is again defined as the minimal value of $\ell$ between i and j. Again, this upper bound corresponds to the length of a concatenation of maximal geodesics from $c_i$, $c_j$ to $v_*$ up to the point where they coalesce. In words, the difference is that by taking systematically $\check{\ell }(i\wedge j,i\vee j)$ in the definition rather than the maximum of $\{\check{\ell }(i,j),\check{\ell }(j,i)\}$, we do not allow to “jump” from the shuttle to the maximal geodesic boundary (or vice-versa), which would result in a path present in $\mathbf {q}$ but not in $\tilde{\mathbf {q}}$.

3.3 Plane quadrangulations with a boundary

We now present the variant for plane quadrangulations with a boundary, which is a particular case of the Bouttier–Di Francesco–Guitter bijection [15]. We rather use the presentation of [11], better fitted to our situation.

Fig. 4

The bijection for a plane quadrangulation with a boundary. The l edges we added to $\mathbf {f}$ are represented by dotted lines and the root edge of $\mathbf {q}$ is represented in red. Note that we used for $\ell$ the normalization given by $\ell (\rho _1)=0$ (color figure online)

The encoding object of a plane quadrangulation with a boundary having n internal faces and perimeter 2l is a forest $\mathbf {f}=(\mathbf {t}_1, \dots , \mathbf {t}_l)$ of l trees with n edges in total, together with a labeling function $\ell :\mathbf {V}(\mathbf {f})=\bigsqcup _i \mathbf {V}(\mathbf {t}_i)\rightarrow \mathbb {Z}$ satisfying the following:

• for $1\le i \le l$, the tree $\mathbf {t}_i$ equipped with the restriction of $\ell$ to $V(\mathbf {t}_i)$ is a well-labeled tree;

• for $1\le i \le l$, we have $\ell (\rho _{i+1})\ge \ell (\rho _{i})-1$, where $\rho _i$ denotes the root vertex of $\mathbf {t}_i$ and setting $\ell (\rho _{l+1})=\ell (\rho _1)$ by convention.

Note that the condition on the labels of the root vertices is different from the condition on the labels of neighboring vertices of a given tree. The reader familiar with the Bouttier–Di Francesco–Guitter bijection may recognize the label condition for faces of even degree more than 4. We will come back to this during Sect. 6.

Here and later, it will be convenient to normalize $\ell$ by asking that $\ell (\rho _1)=0$. As before, we define $\ell _*=\min \{\ell (v):v\in \mathbf {V}(\mathbf {f})\}-1$. We identify $\mathbf {f}$ with the map obtained by adding l edges linking the roots $\rho _1$, $\rho _2$, ..., $\rho _l$ of the successive trees in a cycle. This map has two faces, one of degree $2n +l$ (the bounded one on Fig. 4) and one of degree l (the unbounded one on Fig. 4). We then follow a procedure similar to that of Sect. 3.1. We let $c_0$, $c_1$, ..., $c_{2n+l-1}$ be the sequence of corners of the face of degree $2n+l$ in contour order, starting from the root corner of $\mathbf {t}_1$. We extend this list by periodicity and add one corner $c_\infty$ incident to a vertex $v_*$ lying inside the face of degree $2n+l$, with label $\ell (c_\infty )=\ell (v_*)=\ell _*$. We define the successor functions by (19) and draw an arc from $c_i$ to $s(c_i)$ for every $i\in \{0,1,\ldots ,2n+l-1\}$, in such a way that this arc does not cross the edges of $\mathbf {f}$, or other arcs.

The embedded graph $\mathbf {q}$ with vertex set $\mathbf {V}(\mathbf {f})\cup \{v_*\}$ and edge set given by the added arcs is a plane quadrangulation with a boundary, whose external face is the degree-2l face corresponding to the face of degree l. It is rooted at the corner of the unbounded face that is incident to the root vertex of $\mathbf {t}_1$, and it is naturally pointed at $v_*$. See Fig. 4.

The above mapping is a bijection between previously described labeled forests and the set of pointed plane quadrangulations $(\mathbf {q},v_*)$ with a boundary having n internal faces and perimeter 2l that further satisfy the property that $d_\mathbf {q}(e_*^+,v_*)=d_\mathbf {q}(e_*^-,v_*)+1$, where $e_*$ denotes the root edge of $\mathbf {q}$, that is, the oriented edge incident to the root face that directly precedes the root corner in the contour order (see Fig. 4). In words, the pointed quadrangulations that are in the image of the above mapping are those whose root edge points away from the distinguished vertex $v_*$.

The requirement that the root edge is directed away from the distinguished vertex is not a serious issue, as we can dispose of this constraint simply by re-rooting along the boundary:

Lemma 10

Let $(Q,v_*)$ be uniformly distributed in the set $\mathbf{Q}_{l,n}^{\bullet ,+}$ of rooted and pointed quadrangulations such that $Q\in \mathbf{Q}_{l,n}$ and such that the root edge $e_*$ points away from $v_*$. Let $c'$ be a uniformly chosen random corner incident to the root face of Q, and let $Q'$ be the map Q re-rooted at $c'$. Then $Q'$ is a uniform random element of $\mathbf{Q}_{l,n}$.

Proof

The probability that $Q'$ is a given rooted map $\mathbf {q}'$ is equal

$$\begin{aligned} \mathbb {P}(Q'=\mathbf {q}')=\frac{1}{2l}\sum _{v\in \mathbf {V}(\mathbf {q}')}\sum ^+_{c}\mathbb {P}((Q,v_*)=(\mathbf {q},v))=\frac{1}{2l}\sum _{v\in \mathbf {V}(\mathbf {q}')}\sum ^+_{c}\frac{1}{|\mathbf{Q}_{l,n}^{\bullet ,+}|}, \end{aligned}$$

where the factor 1 / 2l is the probability that $c'$ is chosen to be the root corner of $\mathbf {q}'$, the symbol $\sum ^+_c$ stands for the sum over all corners incident to the root face of $\mathbf {q}'$ that point away from v, and $\mathbf {q}$ is the map $\mathbf {q}'$ re-rooted at the corner c.

Now fix the vertex $v\in \mathbf {V}(\mathbf {q}')$. Due to the bipartite nature of $\mathbf {q}'$, among the 2l oriented edges incident to the root face, l are pointing away from v, and l are pointing toward v. Indeed, let $\tilde{c}_0$ be the root corner of Q, and $\tilde{c}_1$, $\tilde{c}_2$, ..., $\tilde{c}_{2l-1}$, $\tilde{c}_{2l}=\tilde{c}_0$ be the corners incident to the root face in cyclic order. The sequence $(d_{\mathbf {q}'}(\tilde{c}_i,v_*),\, 0\le i\le 2l)$ takes integer values, varies by $\pm 1$ at every step as $\mathbf {q}'$ is bipartite, and takes the same value at times 0 and 2l. This means that l of its increments are equal to $+1$ and l are equal to $-1$, respectively corresponding to edges that point away from v and toward v.

Therefore, the sum $\sum ^+_c$ contains exactly l elements. Noting that every map in $\mathbf{Q}_{l,n}$ has $n+l+1$ vertices, by the Euler characteristic formula, this gives

$$\begin{aligned} \mathbb {P}(Q'=\mathbf {q}')=\frac{n+l+1}{2\,|\mathbf{Q}_{l,n}^{\bullet ,+}|}, \end{aligned}$$

which depends only on n, l and not on the particular choice of $\mathbf {q}'$. $\square$

4 Scaling limit of slices

In this section, we elaborate on Proposition 3.3 and Proposition 9.2 in [30], by showing that uniform random slices converge after rescaling to a limiting metric space, which can be called the Brownian map with a geodesic boundary. Such a property was indeed shown in [30], but with a description of the limit that is different from the one we will need.

4.1 Subsequential convergence

Let $(T_n,\ell _n)$ be a random variable that is uniformly distributed over the set of well-labeled trees with n edges. With this random variable, we can associate two pointed and rooted random maps $(Q_n,v_*)$ and $(\tilde{Q}_n,v_*)$ by the constructions of Sects. 3.1 and 3.2 respectively. We use the same notation for the distinguished vertex $v_*$ since $Q_n$ and $\tilde{Q}_n$ share naturally the same vertex set, except for the extra vertices on the shuttle of $\tilde{Q}_n$.

Let $c_0$, $c_1$, ..., $c_{2n-1}$, $c_{2n}=c_0$ be the sequence of corners of $T_n$ in contour order starting from the root corner, and let $v_i^n$ be the vertex incident to $c_i$ in $T_n$. We let $C_n(i)$ be the distance in $T_n$ between the vertices $v^n_0$ and $v^n_i$, so that $C_n(i)$ can be seen as the height of $v^n_i$ in the tree $T_n$ rooted at $c_0$. The process $(C_n(i),0\le i\le 2n)$, extended to a continuous random function on [0, 2n] by linear interpolation between integer values, is called the contour process of $T_n$. Similarly, we let $\ell _n(i)=\ell _n(v^n_i)$ and call the process $(\ell _n(i),0\le i\le 2n)$, which we also extend to [0, 2n] in a similar fashion, the label process of $(T_n,\ell _n)$.

For $0\le i,j\le 2n$, let $D_n(i,j)=d_{Q_n}(v^n_i,v^n_j)$ and $\tilde{D}_n(i,j)=d_{\tilde{Q}_n}(i,j)$. We extend $D_n$, $\tilde{D}_n$ to continuous functions on $[0,2n]^2$ by “bilinear interpolation,” writing $\{s\}=s-\lfloor s\rfloor$ for the fractional part of s and then setting

$$\begin{aligned} D_n(s,t)&=(1-\{s\}) (1-\{t\}) D_n(\lfloor s\rfloor ,\lfloor t\rfloor )+\{s\}(1-\{t\}) D_n(\lfloor s\rfloor +1,\lfloor t\rfloor ) \nonumber \\&\quad + (1-\{s\})\{t\}D_n(\lfloor s\rfloor ,\lfloor t\rfloor +1)+\{s\}\{t\} D_n(\lfloor s\rfloor +1,\lfloor t\rfloor +1), \end{aligned}$$

(21)

and similarly for $\tilde{D}_n$. We define the renormalized versions of $C_n$, $\ell _n$, $D_n$ and $\tilde{D_n}$ by

$$\begin{aligned} C_{(n)}(s)=\frac{C_n(2ns)}{\sqrt{2n}},\quad \ell _{(n)}(s)=\left( \frac{9}{8n}\right) ^{1/4}\ell _n(2ns), \end{aligned}$$

and

$$\begin{aligned} D_{(n)}(s,t)=\left( \frac{9}{8n}\right) ^{1/4}D_n \left( 2ns, 2nt \right) ,\qquad \tilde{D}_{(n)}(s,t)=\left( \frac{9}{8n}\right) ^{1/4}\tilde{D}_n \left( 2ns, 2nt \right) \end{aligned}$$

for every s, $t\in [0,1]$.

From [30, Proposition 3.1], it holds that up to extraction, one has the joint convergence

(22)

where $\mathbf {e}$ is the normalized Brownian excursion, Z is the head of the snake driven by $\mathbf {e}$ (which is defined as the process $Z^{\mathbf 0}$ around (13), with $\mathbf {e}$ in place of X) and D, $\tilde{D}$ are two random pseudo-metrics on [0, 1] such that $D\le \tilde{D}$. In the rest of this section, we are going to fix one extraction along which this convergence holds, and always assume that the values of n that we consider belong to this particular extraction. Moreover, by a use of the Skorokhod representation theorem, we may and will assume that the convergence holds in fact in the a.s. sense.

For s, $s'\in [0,1]$, define $d_\mathbf {e}(s,s')=\mathbf {e}_s+\mathbf {e}_{s'}-2\inf _{s\wedge s'\le u\le s\vee s'}\mathbf {e}_u$, $d_Z(s,s')$ as in formula (15) (with $A=1$), and let

$$\begin{aligned} \tilde{d}_Z(s,s')=Z_s+Z_{s'}-2\underline{Z}_{s\wedge s',s\vee s'}, \end{aligned}$$

so that clearly one has $d_Z\le \tilde{d}_Z$. The quotient space $S=[0,1]/\{D=0\}$ endowed with the distance induced by D (and still denoted by D), is the so-called Brownian map. Likewise, we set $\tilde{S}=[0,1]/\{\tilde{D}=0\}$ and endow it with the induced distance still denoted by $\tilde{D}$. We let $\mathbf {p}:[0,1]\rightarrow S$, $\tilde{\mathbf {p}}:[0,1]\rightarrow \tilde{S}$ denote the canonical projections, which are continuous since D, $\tilde{D}$ are continuous functions on $[0,1]^2$. Note that, since $D\le \tilde{D}$, there exists a unique continuous (even 1-Lipschitz) projection $\pi :\tilde{S}\rightarrow S$ such that $\mathbf {p}=\pi \circ \tilde{\mathbf {p}}$.

The main result of [30, 38] states that a.s., for every s, $t\in [0,1]$, D(s, t) is given by the explicit formula

$$\begin{aligned} D(s,t)= \inf \left\{ \sum _{j=1}^kd_Z(s_j,t_j):\begin{array}{l}k\ge 1,\quad t_1,s_2,t_2,\ldots ,s_k\in [0,1],\, s_1=s,\,t_k=t ,\\ d_\mathbf {e}(t_j,s_{j+1})=0\, \quad \text{ for } \text{ every } j\in \{1,\ldots , k-1\} \end{array} \right\} .\nonumber \\ \end{aligned}$$

(23)

The main goal of this section is to show that the following analog formula holds for $\tilde{D}$. First, we recall from [30] that $\tilde{D}\le \tilde{d}_Z$ and that $\{d_\mathbf {e}=0\}\subseteq \{\tilde{D}=0\}$. Note that the first of these two properties results from a simple passage to the limit in the bound (20). We let $\tilde{D}^*$ be the largest pseudo-metric on [0, 1] such that these two facts are verified, that is,

$$\begin{aligned} \tilde{D}^*(s,t)=\inf \left\{ \sum _{j=1}^k\tilde{d}_Z(s_j,t_j):\begin{array}{l}k\ge 1,\quad t_1,s_2,t_2,\ldots ,s_k\in [0,1],\, s_1=s,\,t_k=t ,\\ d_\mathbf {e}(t_j,s_{j+1})=0\,\quad \text{ for } \text{ every } j\in \{1,\ldots , k-1\}\, \end{array} \right\} . \end{aligned}$$

In particular, $\tilde{D}\le \tilde{D}^*$. We will show that $\tilde{D}=\tilde{D}^*$ a.s., and in particular, the convergence in (22) holds without having to extract a subsequence. Results by Le Gall [30, Propositions 3.3 and 9.2] provide yet another formula for $\tilde{D}$, which is expressed in terms of cutting the space (S, D) along a certain distinguished geodesic. However, it is not clear that this formula is equivalent to $\tilde{D}=\tilde{D}^*$.

Theorem 11

Almost surely, it holds that for every s, $t\in [0,1]$, $\tilde{D}(s,t)=\tilde{D}^*(s,t)$.

Moreover, we have for every x, $y\in \tilde{S}$,

$$\begin{aligned} \tilde{D}(x,y)=\inf \left\{ \mathrm {length}_D (\pi \circ \gamma ):\begin{array}{c} \gamma :[0,1]\rightarrow \tilde{S} \text{ continuous }\\ \gamma (0)=x,\gamma (1)=y \end{array} \right\} \end{aligned}$$

where $\tilde{S}$ is endowed with the quotient topology of $[0,1]/\{\tilde{D}=0\}$.

Here, the length function is defined as follows. If (M, d) is a metric space (or a pseudo-metric space), and $\gamma :[0,1]\rightarrow M$ is a continuous path, we let

$$\begin{aligned} \mathrm {length}_d(\gamma )=\sup \sum _{i=1}^kd \left( \gamma (r_{i-1}),\gamma (r_i) \right) , \end{aligned}$$

where the supremum is taken over all partitions $0=r_0<r_1<\cdots<r_{k-1}<r_k=1$ of [0, 1]. We invite the reader to compare the last formula for $\tilde{D}(x,y)$ with Proposition 3.3 in [30], which describes with some care a space isometric to $(\tilde{S},\tilde{D})$. Our formulation avoids describing more explicitly the topology on $\tilde{S}$.

4.2 Basic properties of the limit spaces

We will need some more properties of the distances D, $\tilde{D}$, $\tilde{D}^*$. An important fact that we will need is the following identification of the sets $\{D=0\}$, $\{\tilde{D}=0\}$, $\{\tilde{D}^*=0\}$, which is a reformulation of [28, Theorem 4.2], [32, Lemma 3.2] and [30, Proposition 3.1] in our setting. Point (iii) comes from [33, Proposition 2.5] and [30, Proposition 3.2].

Lemma 12

(i) Almost surely, for every s, $t\in [0,1]$ such that $s\ne t$, it holds that $D(s,t)=0$ if and only if either $d_\mathbf {e}(s,t)=0$ or $d_Z(s,t)=0$, these two cases being mutually exclusive, with the only exception of $\{s,t\}=\{0,1\}$.

(ii) Likewise, almost surely, for every s, $t\in [0,1]$ such that $s\ne t$, it holds that $\tilde{D}(s,t)=0$ if and only if either $d_\mathbf {e}(s,t)=0$ or $\tilde{d}_Z(s,t)=0$, and these two cases are mutually exclusive.

(iii) There is only one time $s_*\in [0,1]$ such that $Z_{s_*}=\inf _{[0,1]}Z$. Moreover, $D(0,s_*)=\tilde{D}(0,s_*)=-Z_{s_*}$.

This implies that the equivalence relations $\{\tilde{D}=0\}$ and $\{\tilde{D}^*=0\}$ coincide, since $\tilde{D}\le \tilde{D}^*\le \tilde{d}_Z$ and $\{d_\mathbf {e}=0\}\subseteq \{\tilde{D}^*=0\}$ by definition. In particular, we see that $\tilde{S}=[0,1]/\{\tilde{D}^*=0\}$ endowed with the induced metric $\tilde{D}^*$ is homeomorphic to $(\tilde{S},\tilde{D})$.

Note that (i) and (ii) in the last statement are very closely related. One sees that the points $s<t$ such that $D(s,t)=0$ but $\tilde{D}(s,t)\ne 0$ are exactly the points such that

$$\begin{aligned} Z_s=\inf _{[0,s]}Z=\inf _{[t,1]}Z=Z_t\quad \text {and}\quad (s,t)\ne (0,1). \end{aligned}$$

Indeed, the previous equalities imply that $d_Z(s,t)=0$ and that $\inf _{[s,t]}Z<Z_s$, by (iii), so that $\tilde{d}_Z(s,t)>0$; furthermore, $d_Z(s,t)=0$ and $(s,t)\ne (0,1)$ imply by (i) that $d_\mathbf {e}(s,t)>0$. This entails that, for $s<t$ of this form, one has that $x=\mathbf {p}(s)=\mathbf {p}(t)\in S$ has two preimages $\pi ^{-1}(x)=\{\tilde{\mathbf {p}}(s),\tilde{\mathbf {p}}(t)\}\in \tilde{S}$, while for any other point $x\in S$, $\pi ^{-1}(x)$ is a singleton.

More precisely, let $\Delta =D(0,s_*)=\tilde{D}(0,s_*)$ and, for $r\in [0,\Delta ]$, let

$$\begin{aligned} \Gamma _0(r)=\inf \{s\ge 0:Z_s=-r\},\quad \text{ and }\quad \Gamma _1(r)=\sup \{s\ge 0:Z_s=-r\}. \end{aligned}$$

We also let $\gamma _i(r)=\tilde{\mathbf {p}}(\Gamma _i(r))$ for $i\in \{0,1\}$ and $r\in [0,\Delta ]$, and $\gamma (r)=\mathbf {p}(\Gamma _0(r))=\mathbf {p}(\Gamma _1(r))$. We let $\overset{\circ }{\gamma }_0=\gamma _0((0,\Delta ))$ and we define $\overset{\circ }{\gamma }_1$ and $\overset{\circ }{\gamma }$ in a similar fashion.

Corollary 13

It holds that $\overset{\circ }{\gamma }_0\cap \overset{\circ }{\gamma }_1=\varnothing$. Moreover, the projection $\pi$ is one-to-one from $\tilde{S}{\setminus }(\overset{\circ }{\gamma }_0\cup \overset{\circ }{\gamma }_1)$ onto $S{\setminus } \overset{\circ }{\gamma }$, while $\pi ^{-1}(\gamma (r))=\{\gamma _0(r),\gamma _1(r)\}$ for every $r\in [0,\Delta ]$, and the latter is a singleton if and only if $r\in \{0,\Delta \}$.

Next, we say that a metric space (M, d) is a length space if for every x, $y\in M$, $d(x,y)=\inf \mathrm {length}_d(\gamma )$ where the infimum is taken over all continuous paths $\gamma :[0,1]\rightarrow M$ with $\gamma (0)=x$ and $\gamma (1)=y$. A path $\gamma$ for which the infimum is attained is called a geodesic, and a geodesic metric space is a length space (M, d) such that every pair of points is joined by a geodesic. A compact length space is a geodesic space by [18, Theorem 2.5.23].

Lemma 14

The spaces (S, D), $(\tilde{S},\tilde{D})$ and $(\tilde{S},\tilde{D}^*)$ are compact geodesic metric spaces.

Proof

We only sketch the proof of this lemma. Recall that the property of being a compact geodesic metric space is preserved by taking Gromov–Hausdorff limits, by [18, Theorem 7.5.1]. Now, we use the fact that (S, D), $(\tilde{S},\tilde{D})$ are Gromov–Hausdorff limits of the metric spaces $(V(Q_n),(9/8n)^{1/4}d_{Q_n})$ and $(V(\tilde{Q}_n),(9/8n)^{1/4}d_{\tilde{Q}_n})$, which in turn are at distance less than $(9/8n)^{1/4}$ from metric graphs obtained by linking any two adjacent vertices by an edge of length $(9/8n)^{1/4}$, the latter being geodesic metric spaces. For $(\tilde{S},\tilde{D}^*)$, this comes from the fact that $\tilde{D}^*$ is a quotient pseudo-metric of the space $([0,1]/\{\tilde{d}_Z=0\},\tilde{d}_Z)$ with respect to the equivalence relation induced on $[0,1]/\{\tilde{d}_Z=0\}$ by $\{d_\mathbf {e}=0\}$. Since $([0,1]/\{\tilde{d}_Z=0\},\tilde{d}_Z)$ is a length space (it is indeed an $\mathbb {R}$-tree), the quotient pseudo-metric $(\tilde{S},\tilde{D}^*)$ is also a length space, hence a geodesic space since it is compact. See the discussion after Exercise 3.1.13 in [18].   $\square$

We conclude by mentioning that the mappings $r\mapsto \gamma _0(r)$ and $r\mapsto \gamma _1(r)$ are geodesics in $(\tilde{S},\tilde{D})$ and that $r\mapsto \gamma (r)$ is a geodesic in (S, D). This follows easily from approximations ($\gamma _0$ is the continuum counterpart to the maximal geodesic in Sect. 3.2, and $\gamma _1$ to the shuttle) and is discussed in [30].

4.3 Local isometries between $\tilde{S}$ and S

In the following, if (M, d) is a metric space or a pseudo-metric space, and if $x\in M$, $A\subseteq M$, we let $d(x,A)=\inf \{d(x,y):y\in A\}$. For $i\in \{0,1\}$, we also use the shorthand $\Gamma _i$, $\gamma _i$ to designate the image sets $\{\Gamma _i(r),0\le r\le \Delta \}$ and $\{\gamma _i(r),0\le r\le \Delta \}$.

Lemma 15

The following holds almost surely. Fix $\varepsilon >0$, $i\in \{0,1\}$, and let s, $t\in [0,1]$ be such that $\tilde{D}(s,\Gamma _i)\wedge \tilde{D}(t,\Gamma _i)> \varepsilon$ and $\tilde{D}(s,t)<\varepsilon /2$. Then, it holds that $\tilde{D}(s,t)=D(s,t)=\tilde{D}^*(s,t)$.

Proof

Assume that $i=0$. Let $i_n$, $j_n\in \{0,1,\ldots ,2n\}$ be such that $i_n/2n\rightarrow s$ and $j_n/2n\rightarrow t$ as $n\rightarrow \infty$. Recall that, throughout this section, we have fixed an extraction along which (22) holds and that $n\rightarrow \infty$ is understood along this extraction. Then,

From the fact that $\tilde{D}(s,\Gamma _0)>\varepsilon$ we deduce that for every n large enough, the vertex $v^n_{i_n}$ is at $d_{\tilde{Q}_n}$-distance at least $(8n/9)^{1/4}\varepsilon$ from the maximal geodesic in $\tilde{Q}_n$. Indeed, if this were not the case, then for infinitely many values of n, we could find a vertex $v^n_{k_n}$ of the maximal geodesic with $d_{\tilde{Q}_n}(v^n_{k_n},v^n_{i_n})\le (8n/9)^{1/4}\varepsilon$. By definition of the maximal geodesic, it must hold that $\ell _n(k_n)=\inf \{\ell _n(i):0\le i\le k_n\}$, and by passing to the limit up to further extraction, we may assume that $k_n/2n$ converges to some u such that $Z_u=\inf \{Z_s,0\le s\le u\}$, so that $\tilde{\mathbf {p}}(u)\in \gamma _0$ and $\tilde{D}(u,s)\le \varepsilon$, a contradiction with the fact that $\tilde{D}(s,\Gamma _0)>\varepsilon$.

Fix $\eta >0$. By (23), there exist $s=s_1$, $t_1$, ..., $s_k$, $t_k=t$ such that $d_\mathbf {e}(t_m,s_{m+1})=0$ for $1\le m\le k-1$, and

$$\begin{aligned} D(s,t)\ge \sum _{m=1}^k d_Z(s_m,t_m)-\eta . \end{aligned}$$

Then, we can choose integers $i_n(m)$, $j_n(m)$, $1\le m\le k$ such that $i_n(m)/2n\rightarrow s_m$ and $j_n(m)/2n\rightarrow t_m$ as $n\rightarrow \infty$, and we can also require that $v^n_{j_n(m)}=v^n_{i_n(m+1)}$ for all $m\in \{1,\ldots ,k-1\}$. Indeed, this last property amounts to the fact that $C_n(j_n(m))=C_n(i_n(m+1))$ and that $C_n$ is greater than or equal to this common value on $[j_n(m)\wedge i_n(m+1),j_n(m)\vee i_n(m+1)]$; we can require this as a simple consequence of the fact that $d_\mathbf {e}(t_m,s_{m+1})=0$ and of the convergence of $C_{(n)}$ to $\mathbf {e}$. For every $m\in \{1,\ldots ,k\}$, let $g_{n,m}$ be the maximal wedge path in $Q_n$ from $c_{i_n(m)}$ to $c_{j_n(m)}$, as defined at the end of Sect. 3.1. The length of this path is given by the upper-bound of (18) for $\ell =\ell _n$, $i=i_n(m)$ and $j=j_n(m)$ and, after renormalization by $(8n/9)^{1/4}$, this length converges to $d_Z(s_m,t_m)$. Therefore, if we let $g_n$ be the concatenation of the paths $g_{n,1}$, $g_{n,2}$, ..., $g_{n,k}$, then the length of $g_n$ is asymptotically $(8n/9)^{1/4}\sum _{1\le m\le k}d_Z(s_m,t_m)\le (8n/9)^{1/4}(D(s,t)+\eta )$.

If $g_n$ does not intersect the maximal geodesic from the root $c_0$ to $v_*$ in $Q_n$, then $g_n$ is also a path in $\tilde{Q}_n$ (meaning that it can be lifted via the projection p from $\tilde{Q}_n$ to $Q_n$, as defined in Sect. 3.2). In this case, this also means that the maximal wedge paths $g_{n,m}$ are also paths in $\tilde{Q}_n$, entailing that their lengths are given by the upper-bounds in (20). If, for infinitely many n’s, $g_n$ does not intersect the maximal geodesic from the root $c_0$ to $v_*$ in $Q_n$ then, by passing to the limit, we obtain $d_Z(s_m,t_m)=\tilde{d}_Z(s_m,t_m)$. We immediately get

$$\begin{aligned} \tilde{D}(s,t)\le \tilde{D}^*(s,t)\le \sum _{m=1}^k \tilde{d}_Z(s_m,t_m)=\sum _{m=1}^k d_Z(s_m,t_m)\le D(s,t)+\eta . \end{aligned}$$

Since $\eta$ was arbitrary we obtain $\tilde{D}(s,t)\le \tilde{D}^*(s,t)\le D(s,t)$, but since $D\le \tilde{D}$, we conclude that this must be an equality all along.

Suppose now that, for infinitely many n’s, the path $g_n$ does intersect the maximal geodesic from $c_0$ to $v_*$ in $Q_n$. For such an n fixed, let a, b be the minimal and maximal integers such that $g_n(a)$, $g_n(b)$ belong to this path. Clearly, we can modify the path $g_n$ by replacing it if necessary by the arc of the maximal geodesic between $g_n(a)$ and $g_n(b)$ without increasing its length. Now, the vertices $g_n(0),g_n(1),\ldots ,g_n(a-1)$ are vertices of $Q_n$ that are not in the maximal geodesic, so they lift via the projection p to a path in $\tilde{Q}_n$, with same length. The edge between $g_n(a-1)$ and $g_n(a)$ also lifts into an edge of $\tilde{Q}_n$, and it arrives at a point $g'_n(a)\in p^{-1}(g_n(a))$ which is either on the maximal geodesic or on the shuttle of $\tilde{Q}_n$. However, the first case is impossible for large n’s, since the maximal geodesic is at $d_{\tilde{Q}_n}$-distance at least $(8n/9)^{1/4}\varepsilon$ from $v^n_{i_n}=g_n(0)$ and $d_{\tilde{Q}_n}(g_n(0),g'_n(a))\le d_{\tilde{Q}_n}(v^n_{i_n},v^n_{j_n})\le (8n/9)^{1/4}\varepsilon /2$. The same argument applies to the path $g_n(b)$, $g_n(b+1)$, ..., $v^n_{j_n}$, which can be viewed as a path in $\tilde{Q}_n$ leaving the vertex $g'_n(b)$ of the shuttle and going to $v^n_{j_n}$. Moreover, since the shuttle projects to a geodesic path in $Q_n$, the length $b-a$ of $g_n(a)$, $g_n(a+1)$, ..., $g_n(b-1)$, $g_n(b)$ is not smaller than the length of the segment of the shuttle between the vertices $g_n'(a)$ and $g_n'(b)$.

Therefore, we see that, if $g_n$ intersects the maximal geodesic from $c_0$ to $v_*$ in $Q_n$, we can construct from it a path in $\tilde{Q}_n$ with same length, going from $v^n_{i_n}$ to $g'_n(a)$, then taking the segment of the shuttle from $g'_n(a)$ to $g'_n(b)$, then going from $g'_n(b)$ to $v^n_{j_n}$. This path is still a concatenation of maximal wedge paths that are now in $\tilde{Q}_n$, so by a new passage to the limit (possibly up to a new extraction), we can find $k'\le k$ and $s=s'_1$, $t'_1$, ..., $s'_{k'}$, $t'_{k'}=t$ such that, for every m,

$$\begin{aligned} \tilde{d}_Z\left( s'_m,t'_m\right) =d_Z\left( s'_m,t'_m\right) ,\qquad d_\mathbf {e}\left( t'_m,s'_{m+1}\right) =0, \end{aligned}$$

and such that

$$\begin{aligned}&D(s,t)+\eta \ge \sum _{m=1}^kd_Z(s_m,t_m)\ge \sum _{m=1}^{k'}d_Z\left( s'_m,t'_m\right) \\&\quad =\sum _{m=1}^{k'}\tilde{d}_Z\left( s'_m,t'_m\right) \ge \tilde{D}^*(s,t)\ge \tilde{D}(s,t). \end{aligned}$$

Again, since $\eta$ was arbitrary, this yields $D(s,t)=\tilde{D}^*(s,t)=\tilde{D}(s,t)$.

We obtain the same result with $\Gamma _1$ replaced by $\Gamma _0$ by a similar reasoning. $\square$

4.4 Proof of Theorem 11

We now turn the “local” lemma that we just proved into a “global” result, which is the content of Theorem 11.

Proof of Theorem 11

Fix two points x, $y\in \tilde{S}$, and a continuous, injective path $f:[0,1]\rightarrow \tilde{S}$ going from x to y.

For every $r\in [0,1]$, let $F(r)\in [0,1]$ be an arbitrary point such that $\tilde{\mathbf {p}}(F(r))=f(r)$. Suppose first that f does not visit the points $\tilde{\mathbf {p}}(0)$ and $\tilde{\mathbf {p}}(s_*)$. Then for every $r\in [0,1]$, $\tilde{\mathbf {p}}(F(r))$ is either not in $\gamma _0$, or not in $\gamma _1$. Assume for the moment that we are in the first case. It means that we can find a neighborhood $V_r$ of r in [0, 1] and $\varepsilon _r>0$ such that $\tilde{D}(F(r'),F(r))<\varepsilon _r/2$ and $\tilde{D}(F(r'),\Gamma _0)>\varepsilon _r$ for every $r'\in V_r$. In the second case, a similar property holds with $\Gamma _1$ instead of $\Gamma _0$. By taking a finite subcover, and applying Lemma 15, we obtain the existence of $\varepsilon >0$ depending on f such that for every r, $r'\in [0,1]$, $|r-r'|\le \varepsilon$ implies

$$\begin{aligned} \tilde{D}\left( F(r),F(r') \right) =\tilde{D}^* \left( F(r),F(r') \right) =D \left( F(r),F(r') \right) . \end{aligned}$$

Hence, for every partition $0=r_0<r_1<\cdots <r_k=1$ such that $|r_{i+1}-r_i|<\varepsilon$ for every $i\in \{0,\ldots ,k-1\}$,

$$\begin{aligned} \sum _{i=0}^{k-1}\tilde{D} \left( F(r_i),F(r_{i+1}) \right) =\sum _{i=0}^{k-1}\tilde{D}^* \left( F(r_i),F(r_{i+1}) \right) =\sum _{i=0}^{k-1}D \left( F(r_i),F(r_{i+1}) \right) , \end{aligned}$$

which implies that

$$\begin{aligned} \mathrm {length}_{\tilde{D}}(f)=\mathrm {length}_{\tilde{D}^*}(f)=\mathrm {length}_{D}(\pi \circ f). \end{aligned}$$

(24)

We now use the easy fact that for any metric space (M, d) and every continuous path $\gamma :[0,1]\rightarrow M$, the function $r\mapsto \mathrm {length}_d(\gamma |_{[0,r]})$ is a non-decreasing, left-continuous function from [0, 1] to $[0,\infty ]$. Moreover, the length function is additive in the sense that $\mathrm {length}_d(\gamma )=\mathrm {length}_d(\gamma |_{[0,r]})+\mathrm {length}_d(\gamma |_{[r,1]})$ for every $r\in [0,1]$. These two properties together clearly imply that (24) is still valid if the injective, continuous path f is allowed to visit $\tilde{\mathbf {p}}(0)$, $\tilde{\mathbf {p}}(s_*)$, or both. Taking the infimum over all such functions from a point x to y, and using Lemma 14, we finally get $\tilde{D}(x,y)=\tilde{D}^*(x,y)$, and that this quantity is the infimum of $\mathrm {length}_D(\pi \circ f)$ over all injective continuous paths from x to y in $\tilde{S}$, hence over all continuous paths from x to y in $\tilde{S}$, not necessarily injective. This last fact follows from the fact that a path-connected (separable) space is also arc-connected, see e.g. Section 31 in [43]. $\square$

5 Proof of Theorem 1

5.1 Subsequential convergence

We now move to quadrangulations with boundaries, which are our main object of interest. Recall the construction of Sect. 3.3 and consider an encoding labeled forest $(\mathbf {f},\ell )$ for a quadrangulation with a boundary. As in the preceding section, we will further encode it by a pair of real-valued functions. Before we proceed, it will be convenient to add an extra vertex-tree $\rho _{l+1}$ with label $\ell (\rho _{l+1})=\ell (\rho _1)$ to the forest. This extra vertex does not really play a part but its introduction will make the presentation simpler. We also add l edges between $\rho _i$ and $\rho _{i+1}$, for $1\le i \le l$. See Fig. 5.

We let $c_0$, $c_1$, ..., $c_{2n+l-1}$ be as in Sect. 3.3 and we add to this list the corner $c_{2n+l}$ incident to the extra vertex-tree $\rho _{l+1}$. We define the contour and label processes on $[0,2n+l]$ by

$$\begin{aligned} C(j)=d_{\mathbf {f}}(c_j,\rho _{l+1})-l\quad \text { and }\quad \ell (j)=\ell (c_j),\qquad 0\le j\le 2n+l \end{aligned}$$

and by linear interpolation between integer values.

Fig. 5

The contour and label processes associated with the labeled forest of Fig. 4. The extra vertex-tree $\rho _7$ and the edges linking the roots are represented with a dashed line. Note that the normalization we chose for the labels is equivalent to imposing $\ell (0)=0$

Let us fix $L\in (0,\infty )$ and a sequence $(l_n,n\ge 1)$ such that $l_n\sim L\sqrt{2n}$ as $n\rightarrow \infty$. We let $(F_n,\ell _n)$ be uniformly distributed over the set of labeled forests of $l_n$ trees with n edges in total, and let $(Q_n,v_*)$ be the random pointed quadrangulation⁴ associated with $F_n$ via the bijection of Sect. 3.3. Note that up to re-rooting $Q_n$ at a uniform corner incident to the root face, we may assume that $Q_n$ is uniform in $\mathbf{Q}_{l_n,n}$ by Lemma 10.

We let $C_n$, $\ell _n$ be the associated contour and label processes, and we define their renormalized versions

$$\begin{aligned} C_{(n)}(s)=\frac{C_n \left( (2n+{l_n})s \right) }{\sqrt{2n}},\qquad \ell _{(n)}(s)=\left( \frac{9}{8n}\right) ^{1/4}\ell _n \left( (2n+{l_n})s \right) ,\qquad 0\le s\le 1. \end{aligned}$$

We let $D_n(i,j)$ be the distance in $Q_n$ between the vertices incident to the i-th and j-th corner of $F_n$, for $i,j\in \{0,1,\ldots ,2n+{l_n}\}$. We extend $D_n$ to a continuous function on $[0,2n+{l_n}]^2$ by the exact same formula as (21), and we finally define its renormalized version

$$\begin{aligned} D_{(n)}(s,t)=\left( \frac{9}{8n}\right) ^{1/4}D_n \left( (2n+{l_n})\,s, (2n+{l_n})\,t \right) ,\qquad 0\le s,t\le 1. \end{aligned}$$

(25)

It is shown in [10] that, from every increasing family of positive numbers, one can extract a further subsequence along which

(26)

in distribution in the space $\mathcal {C}([0,1])\times \mathcal {C}([0,1])\times \mathcal {C}([0,1]^2)$. (At this moment, the need of extracting a subsequence is caused by the last coordinate $D_{(n)}$ and the convergence without extraction holds if one drops this coordinate.) Here, D is a random pseudo-metric on [0, 1] and (X, Z) has law⁵ $\mathbb {F}^1_L$ defined in Sect. 2, so that X is a first-passage bridge, attaining level $-L$ for the first time at time 1, and Z is the associated snake process.

Proposition 16

[10] Almost surely, the space $\mathbf {D}=[0,1]/\{D=0\}$ is a topological disk whose boundary $\partial \mathbf {D}$ satisfies

$$\begin{aligned} \mathbf {p}^{-1}(\partial \mathbf {D})=\{s\in [0,1]:X_s=\underline{X}_s\}, \end{aligned}$$

(27)

where $\mathbf {p}:[0,1]\rightarrow \mathbf {D}$ is the canonical projection. Almost surely, the Hausdorff dimension of $\mathbf {D}$ is 4, and that of $\partial \mathbf {D}$ is 2.

Recall definition (16) of the set $\mathcal D$, as well as the definition of $s_*$, the unique element of [0, 1] at which Z reaches its minimum. The following is classical, see e.g. Equation (11) and Section 4.2 in [10].

Lemma 17

The following properties hold almost surely.

• $D\in \mathcal D$.

• $D(s,s_*)=Z_s-Z_{s_*}$ for every $s\in [0,1]$.

Let now $x_*=\mathbf {p}(s_*)$. Note that the definition is different from that in Sect. 2.3: for now we have to use this definition, but we will see in a moment, in Theorem 20 that $D=D^*$ so that the two definitions do coincide. Recall that $v_*$ is a uniform random vertex in $Q_n$, conditionally given the latter. From this observation, we obtain an invariance under re-rooting property of $(\mathbf {D},D,x_*)$, along the same lines as [29].

Lemma 18

Let U, V be uniform random variables in [0, 1], independent of (X, Z, D). Then the two doubly pointed spaces $(\mathbf {D},D,\mathbf {p}(U),\mathbf {p}(V))$ and $(\mathbf {D},D,x_*,\mathbf {p}(U))$ have the same distribution.

Finally, the following lemma is an easy consequence of the study of geodesics done in [11].

Lemma 19

Almost surely, for every $x\in \mathbf {D}{\setminus } \partial \mathbf {D}$, each geodesic from x to $x_*$ does not intersect $\partial \mathbf {D}$. Moreover, there is only one geodesic from x to $x_*$ for $\mu$-almost every $x\in \mathbf {D}$, where $\mu =\mathbf {p}_*(\mathrm {Leb}_{[0,1]})$.

Proof

For $s\in [0,1]$, we define the path $\Phi _s: [0, D(s_*,s)]\rightarrow \mathbf {D}$ by

$$\begin{aligned} \Phi _s(w)= \mathbf {p}\left( \sup \left\{ r\, :\, \underline{Z}_{r,s} = Z_{s_*}+ w\right\} \right) ,\qquad 0\le w\le D(s_*,s)=Z_s-Z_{s_*}. \end{aligned}$$

It is shown in [11, Proposition 23] that the path $\Phi _s$ is a geodesic from $x_*$ to $\mathbf {p}(s)$ in $\mathbf {D}$ and that a.s. all the geodesics from $x_*$ are of this form. We call increase point of a function a point t such that the function is greater than its value at t on a small interval of the form $[t-\varepsilon ,t]$ or $[t, t+\varepsilon ]$ for some $\varepsilon >0$. Clearly, for $0\le w < D(s_*,s)$, the point $\sup \left\{ r\, :\, \underline{Z}_{r,s} = Z_{s_*}+ w\right\}$ is an increase point of the process Z, which is furthermore different from 0. On the other hand, the expression (27) shows that $\mathbf {p}^{-1}(\partial \mathbf {D})$ is made only of increase points of X, together with the point 0. Moreover, [11, Lemma 18] states that, a.s., the processes X and Z do not share any increase points. As a consequence, $\Phi _s$ may only intersect $\partial \mathbf {D}$ at its endpoint $\mathbf {p}(s)$ and the first statement follows.

In addition, [11, Proposition 17] entails that, for $0\le s\le t\le 1$, $D(s,t)=0$ if and only if one of the following occurs:

$$\begin{aligned} X_s= & {} X_t=\underline{X}_{s,t} \hbox { or, equivalently, } d_X(s,t)=0; \end{aligned}$$

(28a)

$$\begin{aligned} Z_s= & {} Z_t=\underline{Z}_{s,t} \hbox { or }Z_s=Z_t=\underline{Z}_{t,s}\hbox { or, equivalently, }d_Z(s,t)=0. \end{aligned}$$

(28b)

Moreover, for $s\ne t$, only one of the previous situations can happen. In some sense, this can be thought of as a continuous version of the bijection from Sect. 3.3: point (28a) constructs the continuous random forest and drawing an arc between a corner and its successor becomes, in the limit, identifying points with the same label and such that the labels visited in between in the contour order are all larger (point (28b)). Standard properties of the process Z then allow us to conclude that $\mathrm {Leb}_{[0,1]}(\{s:\,\exists t\ne s:\, D(s,t)=0\})=0$, so that, for $\mu$-almost every $x\in \mathbf {D}$, the set $\mathbf {p}^{-1}(x)$ is a singleton $\{s\}$ and the only geodesic from $x_*$ to x is thus $\Phi _{s}$. $\square$

Combining Lemmas 18 and 19, we see that the conclusion of the latter is still valid if $x_*$ is replaced by a uniformly chosen point in $\mathbf {D}$, that is, a random point of the form $\mathbf {p}(U)$ as in the first lemma.

5.2 Identification of the limit

Recall the notation $D^*$ from Sect. 2.3 (here we are interested in the case $A=1$). In this section, we show the following analog to the first part of Theorem 11.

Theorem 20

Almost surely, it holds that $D=D^*$.

Theorem 1 is an immediate consequence of this. Indeed, since $D^*$ is a measurable function of (X, Z), this shows that $D^*$ is the only possible subsequential limit of $D_{(n)}$. This, combined with the tightness of the sequence $(D_{(n)},n\ge 1)$ that we alluded to above, implies that $D_{(n)}$ converges in distribution to $D^*$.

In turn, this convergence implies that of $(9/8n)^{1/4}Q_n$ to $\mathrm {BD}_{L}=(\mathbf {D},D^*)$ in the Gromov–Hausdorff sense and even that of the pointed space $((9/8n)^{1/4}Q_n,v_*)$ to $(\mathrm {BD}_L,x_*)$. Let us recall how to prove this fact. First, one can assume that the convergence of $(C_{(n)},\ell _{(n)},D_{(n)})$ to $(X,Z,D^*)$ is almost-sure, by using Skorokhod’s representation theorem. Then we define a correspondence $\mathcal {R}_n$ between $Q_n$ and $\mathrm {BD}_L$ by

$$\begin{aligned} \mathcal {R}_n=\left\{ \left( v^n_{\lfloor (2n+l_n)s\rfloor },\mathbf {p}(s)\right) :s\in [0,1]\right\} \cup \{(v_*,\mathbf {p}(s_*))\}, \end{aligned}$$

where, as before, $v^n_i$ is the vertex of $Q_n$ incident to the i-th corner $c_i$. It is elementary to see from the uniform convergence of $D_{(n)}$ to $D^*$ that the distortion of $\mathcal {R}_n$ with respect to the metrics $(9/8n)^{1/4}d_{Q_n}$ and $D^*$ converges to 0 as $n\rightarrow \infty$.

Combined with Lemma 18, Theorem 20 immediately yields the following corollary.

Corollary 21

Let U, V be uniform random variables in [0, 1], independent of (X, Z). Then the random variables $D^*(s_*,U)$ and $D^*(U,V)$ have the same distribution.

This corollary will play a very important part in the proof of the invariance principle (Sect. 8). It is the analog in our setting to Le Gall’s observation at the heart of his proof of the universality of the Brownian map [30, Sections 8.3 and 9.1].

Recall that [a, b] is an excursion interval of X above $\underline{X}$ if $a<b$ and $X_a=X_b=\underline{X}_b$. Let us arrange the excursion intervals of X above $\underline{X}$ as $[a_i,b_i]$, $i\ge 1$ in decreasing order of length. For a given i, the excursion interval $[a_i,b_i]$ encodes a slice in the sense of Sect. 4. Namely, for s, $t\in [a_i,b_i]$, let $d_Z^i(s,t)=Z_s+Z_t-2\underline{Z}_{s\wedge t,s\vee t}$, and

$$\begin{aligned} \tilde{D}^{i}(s,t)=\inf \left\{ \sum _{j=1}^kd^i_Z(s_j,t_j): \begin{array}{l} k\ge 1,\quad t_1,s_2,t_2,\ldots ,s_k\in [a_i,b_i],\, s_1=s,\,t_k=t ,\\ d_X(t_j,s_{j+1})=0\, \text{ for } \text{ every } j\in \{1,\ldots , k-1\}\, \end{array} \right\} . \end{aligned}$$

We also extend $\tilde{D}^{i}$ by the formula $\tilde{D}^{i}(s,t)=\tilde{D}^{i}((s\vee a_i)\wedge b_i,(t\vee a_i)\wedge b_i)$ into a continuous function on $[0,1]^2$. By simple scaling properties and excursion theory, conditionally given the excursion lengths $(b_i-a_i)$, $i\ge 1$, the spaces ${S}^i=[a_i,b_i]/\{\tilde{D}^{i}=0\}$, equipped with the induced distance, still denoted by $\tilde{D}^{i}$, are independent versions of the Brownian slices of Sect. 4, with distances rescaled by $(b_i-a_i)^{1/4}$ respectively. The next key lemma states that the distance D can be identified as a metric gluing of these slices along their boundaries. This guides the intuition of its proof, which will partly consist in going back to the discrete slices that compose the quadrangulations with a boundary of which we took the limit. For convenience, we set for s, $t\in [0,1]$,

$$\begin{aligned} \tilde{D}^{\lozenge }(s,t)={\left\{ \begin{array}{ll} \tilde{D}^{i}(s,t) &{}\quad \text { if } s,t\in [a_i,b_i] \text { for some } i\ge 1\,;\\ \infty &{}\quad \text { otherwise}. \end{array}\right. } \end{aligned}$$

Lemma 22

For almost every $(s,t)\in [0,1]^2$ with respect to the Lebesgue measure, it holds that

$$\begin{aligned} D(s,t)=\inf \left\{ \sum _{j=1}^k\tilde{D}^{\lozenge }(s_j,t_j): \begin{array}{l} k\ge 1,\quad t_1,s_2,t_2,\ldots ,s_k \in [0,1],\, s_1=s,\,t_k=t ,\\ d_Z(t_j,s_{j+1})=0\, \text{ for } \text{ every } j\in \{1,\ldots , k-1\}\, \end{array} \right\} \end{aligned}$$

and, moreover, that the above infimum is in fact a minimum.

Proof

Clearly, $D(s,t)\le d_Z(s,t)\le d_Z^i(s,t)$ whenever s, $t\in [a_i,b_i]$, so that $D(s,t)\le \tilde{D}^{\lozenge }(s,t)$ for any s, $t\in [0,1]$ and, as a consequence, the left-hand side is smaller than the right-hand side for every s, $t\in [0,1]$. We then only need to prove the converse inequality for almost every s, t in [0, 1]. To this end, by Fubini’s theorem, it suffices to show the claimed formula when s, t are replaced by two independent uniform random variables U, V in [0, 1], independent of the other random variables considered so far.

Let $\gamma :[0, D(U,V)]\rightarrow \mathbf D$ be the geodesic in $(\mathbf {D},D)$ from $\mathbf {p}(U)$ to $\mathbf {p}(V)$, which by Lemmas 18 and 19 is unique and does not intersect $\partial \mathbf {D}$, a.s. Let also $\mathrm {Im}(\gamma )=\gamma ([0,D(U,V)])$ denote its image and define

$$\begin{aligned} I(U,V)= \left\{ i\ge 1:\mathbf {p}^{-1}(\mathrm {Im}(\gamma ))\cap [a_i,b_i]\ne \varnothing \right\} \end{aligned}$$

the set of indices of the slices that $\gamma$ visits. We invite the reader to use Fig. 6 as a visual aid for the remaining of the proof.

Claim 1

The set I(U, V) is almost surely finite.

Proof

Let us argue by contradiction, assuming that I(U, V) is infinite with positive probability. Then it holds that, still with positive probability, there is an increasing integer sequence $(i_n)_{n\ge 1}$ and a sequence $(r_n)_{n\ge 1}$ with values in [0, D(U, V)] such that $\gamma (r_n)\in \mathbf {p}([a_{i_n},b_{i_n}])$. Then, up to extraction, the sequence $(r_n)$ converges to some limit r, and if $s_n\in [a_{i_n},b_{i_n}]$ is a choice of a given element in $\mathbf {p}^{-1}(\gamma (r_n))$, then, again up to possibly further extraction, $(s_n)$ converges to a limit s with $\mathbf {p}(s)=\gamma (r)$. By construction, s is not in $\bigcup _{i\ge 1}(a_i,b_i)$, since the intervals in this union are pairwise disjoint. This implies that $X_s=\underline{X}_s$, meaning that $\gamma (r)=\mathbf {p}(s)\in \partial \mathbf {D}$, which is the contradiction we were looking for. $\square$

Fig. 6

The geodesic $\gamma$ from $\mathbf {p}(U)$ to $\mathbf {p}(V)$ only visits a finite number of slices (Claim 1), and every piece of slice boundary that is visited is visited during a connected interval of times (Claims 2 and 3). It can thus be broken down to small segments satisfying (31a) or (31b)

Let $\wp ^i_l$, $\wp ^i_r$ denote the left and right “geodesic boundaries” of the space $([a_i,b_i]/d_Z^i,d_Z^i)$, defined by

$$\begin{aligned} \wp ^i_l(t)&=\mathbf {p}\left( \inf \{s\in [ a_i,b_i]:Z_s=Z_{a_i}-t\} \right) , \end{aligned}$$

(29)

$$\begin{aligned} \wp ^i_r(t)&=\mathbf {p}\left( \sup \{s\in [a_i,b_i]:Z_s=Z_{a_i}-t\} \right) , \end{aligned}$$

(30)

where t ranges over $[0,Z_{a_i}-\underline{Z}_{a_i,b_i}]$ (recall that $Z_{a_i}=Z_{b_i}$). Those are geodesic paths in $(\mathbf {D},D)$ from $\mathbf {p}(a_i)$ to $\mathbf {p}(s_i^*)$, where $s_i^*$ is the (a.s. unique [33]) time in $[a_i,b_i]$ at which Z attains its infimum on that same interval. Alternatively, these paths are parts of the geodesics $\Phi _{a_i}$ and $\Phi _{b_i}$ introduced earlier. Note also that $\mathrm {Im}(\wp ^i_l)\cap \mathrm {Im}(\wp ^i_r)$ is not necessarily reduced to $\{\mathbf {p}(a_i),\mathbf {p}(s_i^*)\}$. In fact, on the interval $[a_i,b_i]\ni s_*$, this intersection contains a whole segment of $\mathrm {Im}(\wp ^i_l)$ near $x_*$.

Claim 2

It is not possible to find $r_1<r_2<r_3$ and some $i\ge 1$ such that $\gamma (r_1),\gamma (r_3)\in \mathrm {Im}(\wp ^i_l)$ and $\gamma (r_2)\notin \mathrm {Im}(\wp ^i_l)$. The same statement is valid for $\wp ^i_r$ instead of $\wp ^i_l$.

Proof

Indeed, such a situation would clearly violate the uniqueness of the geodesic $\gamma$, since we could replace it between times $r_1$ and $r_3$ by the arc of $\wp ^i_l$ from $\gamma (r_1)$ to $\gamma (r_3)$, and still obtain a geodesic from $\mathbf {p}(U)$ to $\mathbf {p}(V)$, distinct from $\gamma$. $\square$

Claim 3

Almost surely, for every $i\ge 1$, the topological boundary of $\mathbf {p}([a_i,b_i])$ in $(\mathbf {D},D)$ is included in $\mathrm {Im}(\wp _l^i)\cup \mathrm {Im}(\wp ^i_r)$.

Proof

This statement is relatively obvious with the interpretation that $([a_i,b_i]/\{\tilde{D}^{i}=0\},\tilde{D}^{i})$ is a space with geodesic boundaries given by $\wp _l^i$, $\wp _r^i$, but since we are not referring explicitly to these spaces, let us give a complete proof. In fact, the topological boundary of $\mathbf {p}([s,t])$ for any $a_i\le s\le t\le b_i$ is given by [11, Lemma 21] but, as the proof is quite short, we restate the arguments here. Note that $\mathbf {p}([a_i,b_i])$ is closed so that every point in $\partial \mathbf {p}([a_i,b_i])$ is of the form $\mathbf {p}(s')$ for some $s'\in [a_i,b_i]$ and is a limit of a sequence of points of the form $\mathbf {p}(s_n)$, $n\ge 1$, where $s_n\notin [a_i,b_i]$ for every $n\ge 1$. Up to extraction, $(s_n)$ converges to a limit $s\notin (a_i,b_i)$ such that $D(s,s')=0$. If $s\in \{a_i,b_i\}$ then the claim follows immediately. Otherwise, $s\ne s'$ and, as mentioned during the proof of Lemma 19, this implies $d_X(s,s')=0$ (28a) or $d_Z(s,s')=0$ (28b). It cannot hold that $d_X(s,s')=0$ because $s'\in [a_i,b_i]$ while $s\notin [a_i,b_i]$, so necessarily $d_Z(s,s')=0$. Assuming for instance that $Z_s=Z_{s'}=\underline{Z}_{s,s'}$, so that $Z_u\ge Z_{s'}$ for every $u\in [a_i,s']$, this implies that $d_Z(s,\inf \{u\in [a_i,b_i]:Z_u=Z_s)=0$. Finally, we get that $\mathbf {p}(s)=\wp _l^i(Z_{a_i}-Z_s)\in \mathrm {Im}(\wp ^i_l)$. Similarly, if $Z_s=Z_{s'}=\underline{Z}_{s',s}$, we obtain that $\mathbf {p}(s)\in \mathrm {Im}(\wp ^i_r)$. $\square$

From the three claims above, we obtain that there exists a finite number of pairwise distinct points $x_1$, $x_2$, ..., $x_{k+1}\in \mathbf D$ and integers $i_1$, ..., $i_k$ with $x_1=\mathbf {p}(U)$, $x_{k+1}=\mathbf {p}(V)$, such that $\gamma$ visits the points $x_1$, $x_2$, ..., $x_{k+1}$ in this order, and such that the segment of $\gamma$ between $x_j$ and $x_{j+1}$ is

$$\begin{aligned}&\hbox {either included in }\mathrm {Im}(\wp ^{i_j}_l)\hbox { or included in }\mathrm {Im}(\wp ^{i_j}_r) \end{aligned}$$

(31a)

$$\begin{aligned}&\quad \hbox {or included in }\mathbf {p}([a_{i_j},b_{i_j}])\hbox { and such that its intersection with }\mathrm {Im}\nonumber \\&\quad \left( \wp ^{i_j}_l\right) \cup \,\mathrm {Im}(\wp ^{i_j}_r)\hbox { is a subset of } \{x_j,x_{j+1}\}. \end{aligned}$$

(31b)

Indeed, Claims 1 and 2 entail that $\mathrm {Im}(\gamma )\cap (\bigcup _i \mathrm {Im}(\wp ^{i}_l)\cup \mathrm {Im}(\wp ^{i}_r))$ is a finite union of segments satisfying (31a) and the arcs of $\gamma$ linking two successive such segments satisfy (31b), by Claim 3. Note that, in (31b), we cannot impose that the intersection with $\mathrm {Im}(\wp ^{i_j}_l)\cup \mathrm {Im}(\wp ^{i_j}_r)$ be equal to $\{x_j,x_{j+1}\}$ as the extremities ($x_1$ and $x_{k+1}$) of $\gamma$ are a priori not included in $\bigcup _i \mathrm {Im}(\wp ^{i}_l)\cup \mathrm {Im}(\wp ^{i}_r)$.

For $j\in \{1,\ldots , k\}$, since the segment of $\gamma$ between $x_j$ and $x_{j+1}$ is included in $\mathbf {p}([a_{i_j},b_{i_j}])$ in either case, we may choose $s_j$, $t_j\in [a_{i_j},b_{i_j}]$ such that $x_j=\mathbf {p}(s_j)$ and $x_{j+1}=\mathbf {p}(t_j)$. For any such choice,

$$\begin{aligned} D(U,V)=\sum _{j=1}^{k} D(s_j,t_j). \end{aligned}$$

We will soon justify that a.s. we can choose such $s_j$, $t_j$ satisfying the extra property that $D(s_j,t_j)=\tilde{D}^{i_j}(s_j,t_j)$. For convenience, we set $s_0=U$, $t_0=s_1$, $s_{k+1}=t_k$ and $t_{k+1}=V$. By definition, for any $0\le j\le k$, we have $\mathbf {p}(t_j)=\mathbf {p}(s_{j+1})$, which entails that $d_X(t_j,s_{j+1})=0$ (28a) or $d_Z(t_j,s_{j+1})=0$ (28b). The former case implies that $\tilde{D}^{\lozenge }(t_j,s_{j+1})=0$ so that, by the triangle inequality, $\tilde{D}^{\lozenge }(s_j,t_j) + \tilde{D}^{\lozenge }(s_{j+1},t_{j+1}) \ge \tilde{D}^{\lozenge }(s_j,t_{j+1})$. We remove the pairs $(t_j,s_{j+1})$ for which $d_X(t_j,s_{j+1})=0$ from the list $s_0$, $t_0$, $s_1$, $t_1$, ..., $s_{k+1}$, $t_{k+1}$ and rewrite the resulting list as $s'_1$, $t'_1$, ..., $s'_{p}$, $t'_{p}$. We obtain that D(U, V) is bounded from below by the sum $\sum _{j=1}^p \tilde{D}^{\lozenge }(s'_j,t'_j)$, where we now have $d_Z(t'_j,s'_{j+1})=0$ for every $j\in \{1,\ldots ,p-1\}$. This shows that D(U, V) is greater than or equal to the infimum appearing in the statement of Lemma 22 for $s=U$ and $t=V$. As mentioned at the beginning of the proof, D(U, V) is also smaller than this quantity so that equality actually holds, and the infimum is in fact a minimum. This concludes the proof of Lemma 22, provided we can justify the possibility of choosing $s_j$, $t_j$ as claimed.

To this end, note that if the segment of $\gamma$ between $x_j$ and $x_{j+1}$ satisfies (31a), then we may impose that $s_j$ and $t_j$ are both of the form appearing in the argument of $\mathbf {p}$ in (29) or both of the form appearing in the argument of $\mathbf {p}$ in (30), as $x_j$ and $x_{j+1}$ both belong to $\mathrm {Im}(\wp ^{i_j}_l)$ or both belong to $\mathrm {Im}(\wp ^{i_j}_r)$. The claim then readily follows from Lemma 17, as

$$\begin{aligned} D(s_j,t_j)\ge |D(s_j,s_*)-D(t_j,s_*)|=|Z_{s_j}-Z_{t_j}|= d^{i_j}_Z(s_j,t_j) \ge \tilde{D}^{i_j}(s_j,t_j) \end{aligned}$$

and the converse inequality always holds.

It remains to deal with the situation where the segment of $\gamma$ between $x_j$ and $x_{j+1}$ satisfies (31b). At this point we need to go back to the discrete setting, and, in particular, to define the discrete analogs to the functions $\tilde{D}^{i}$. We consider the i-th largest tree $\mathbf {t}$ of $F_n$ and we suppose that it is visited between times $a_i^n$ and $b_i^n$ in the contour order of $F_n$. For j, $k\in \{a_i^n,\ldots ,b_i^n\}$, we let $\tilde{D}^i_n(j,k)$ be the distance in the slice corresponding to $\mathbf {t}$ between the vertices $v^n_j$ and $v^n_k$ incident to the j-th and k-th corner of $F_n$. In other words, $\tilde{D}^i_n(j,k)$ is the length of a shortest path linking $v^n_j$ to $v^n_k$ and that does not “traverse” the images in $Q_n$ of the maximal geodesic and shuttle of the aforementioned slice. We then extend $\tilde{D}^i_n$ to a continuous function on $[a_i^n,b_i^n]^2$ by bilinear interpolation, and then to a continuous function on $[0,2n+l_n]^2$ by the formula $\tilde{D}^i_n(s,t)=\tilde{D}^i_n((s\vee a_i^n)\wedge b_i^n,(t\vee a_i^n)\wedge b_i^n)$. Finally we define its renormalized version $\tilde{D}^{i}_{(n)}$ on $[0,1]^2$ by the analog of (25). We define $\tilde{D}^i_{(n)}$ arbitrarily for $i>l_n$.

As a simple consequence of Theorem 11 and of the convergence (22), reformulated in the context of the excursion intervals $[a_i^n,b_i^n]$, we obtain the joint convergence in distribution of $(C_{(n)},\ell _{(n)},(\tilde{D}^i_{(n)})_{i\ge 1})$ to $(X,Z,(\tilde{D}^{i})_{i\ge 1})$. Together with (26), we conclude that

$$\begin{aligned} \left( C_{(n)},\ell _{(n)},D_{(n),}\left( \tilde{D}^i_{(n)} \right) _{i\ge 1}\right) \xrightarrow [n\rightarrow \infty ]{}\left( X,Z,D, \left( \tilde{D}^{i} \right) _{i\ge 1}\right) \end{aligned}$$

(32)

in distribution in the space $\mathcal {C}([0,1])\times \mathcal {C}([0,1])\times \mathcal {C}([0,1]^2) \times \mathcal {C}([0,1]^2)^\mathbb {N}$, and along an appropriate extraction (due to the third coordinate). Applying Skorokhod’s representation theorem, we also assume from now on that this convergence holds in the almost sure sense.

For $y\in \{0,1/(2n+l_n),\ldots ,1\}$, we denote by $c_n(y)$ the $(2n+l_n)y$-th corner of $F_n$. In what follows, whenever we use the notation $c_n(y)$ it will be implicit that y is chosen in the set for which this notation makes sense. We let $a_{i_j}^n$ and $b_{i_j}^n$ be such that $c_n(a_{i_j}^n)$ and $c_n(b_{i_j}^n)$ are the first and last corners of the $i_j$-th largest tree of $F_n$. Standard properties of Brownian motion and the convergence $C_{(n)}\rightarrow X$ entail that $a_{i_j}^n\rightarrow a_{i_j}$ and $b_{i_j}^n\rightarrow b_{i_j}$.

Now recall that we are assuming that the segment of $\gamma$ between $x_j$ and $x_{j+1}$ satisfies (31b) and that we aim to justify the existence of $s_j$, $t_j$ satisfying $x_j=\mathbf {p}(s_j)$, $x_{j+1}=\mathbf {p}(t_j)$ and $D(s_j,t_j)=\tilde{D}^{i_j}(s_j,t_j)$. We first take $s'_j$, $t'_j\in [a_{i_j},b_{i_j}]$ such that $x_j=\mathbf {p}(s'_j)$ and $x_{j+1}=\mathbf {p}(t'_j)$.

Choose two sequences of numbers $s^n_j$, $t^n_j\in [a_{i_j}^n,b_{i_j}^n]\cap \{0,1/(2n+l_n),\ldots ,1\}$ indexed by n such that $s^n_j\rightarrow s'_j$ and $t^n_j\rightarrow t'_j$, and denote by $u_j^n$ and $w_j^n$ the vertices incident respectively to $c_n(s^n_j)$ and $c_n(t^n_j)$. We let $\gamma _j^n$ be a geodesic in $Q_n$ from $u_j^n$ to $w_j^n$, and denote by $\gamma _j^n(0)=u_j^n$, $\gamma _j^n(1)$, ..., $\gamma _j^n(d_{Q_n}(u_j^n,w_j^n))=w_j^n$ the subsequent vertices it visits.

We also let $\mathbf {V}^n_j$ be the set of vertices of $i_j$-th largest tree of $F_n$ that do not belong to the maximal geodesic of the slice corresponding to this tree, seen as a subset of $\mathbf {V}(Q_n)$. As the portion of $\gamma$ we consider satisfies (31b), it is intuitive that $\gamma _j^n$, which should be a discrete approximation of this portion, is such that $\mathrm {Im}(\gamma _j^n)$ is “mostly included” in $\mathbf {V}^n_j$. More precisely, we claim that, for any fixed $\varepsilon \in (0,1/2)$, the vertices visited by $\gamma _j^n$ between $\gamma _j^n(\lfloor \varepsilon \, d_{Q_n}(u_j^n,w_j^n)\rfloor )$ and $\gamma _j^n(\lfloor (1-\varepsilon )\, d_{Q_n}(u_j^n,w_j^n)\rfloor )$ all belong to $\mathbf {V}^n_j$ for large n. Indeed, let us argue by contradiction and assume otherwise. Then, for infinitely many values of n, we can find real numbers $z_n\notin [a_{i_j}^n,b_{i_j}^n]$ such that $c_n(z_n)$ is at $d_{Q_n}$-distance at most 1 from one of the vertices visited by $\gamma _j^n$ between $\gamma _j^n(\lfloor \varepsilon \, d_{Q_n}(u_j^n,w_j^n)\rfloor )$ and $\gamma _j^n(\lfloor (1-\varepsilon )\, d_{Q_n}(u_j^n,w_j^n)\rfloor )$. (The “at most 1” is here because $\gamma _j^n$ may exit $\mathbf {V}_j^n$ by visiting the maximal geodesic, whose vertices are encoded by corners of $[a_{i_j}^n,b_{i_j}^n]$ but are at $d_{Q_n}$-distance 1 from vertices encoded by corners outside of $[a_{i_j}^n,b_{i_j}^n]$.) Up to further extraction, we may suppose that $z_n\rightarrow z\notin (a_{i_j},b_{i_j})$, so that $\mathbf {p}(z)$ does not belong to the interior of $\mathbf {p}([a_{i_j},b_{i_j}])$. As $\gamma _j^n$ is a geodesic, we have $D_{(n)}(s_j^n,z_n)+D_{(n)}(z_n,t_j^n)=D_{(n)}(s_j^n,t_j^n)+O(n^{-1/4})$, which yields $D(s'_j,z)+D(z,t'_j)=D(s'_j,t'_j)$. This means that $\mathbf {p}(z)$ lies on a geodesic between $x_j$ and $x_{j+1}$, hence on the portion of $\gamma$ between $x_j$ and $x_{j+1}$, which is the only geodesic path between these points, by Lemma 19. By (31b), $\mathbf {p}(z)$ belongs to $\mathbf {p}([a_{i_j},b_{i_j}])$, and thus to the topological boundary of this set, which is included in $\mathrm {Im}(\wp _l^{i_j})\cup \mathrm {Im}(\wp ^{i_j}_r)$ by Claim 3. Finally, this forces $\mathbf {p}(z)\in \{x_j,x_{j+1}\}$, by (31b). This is in contradiction with the fact that $D_{(n)}(s_j^n,z_n)\wedge D_{(n)}(z_n,t_j^n)\ge \varepsilon D_{(n)}(s_j^n,t_j^n)+O(n^{-1/4})$, which yields $D(s'_j,z)\wedge D(z,t'_j)\ge \varepsilon D(s'_j,t'_j)>0$.

We construct an increasing subsequence $(n_m)_m$ of the sequence of values of n we considered so far, in such a way that $n_m$ satisfies the above condition for $\varepsilon =1/m$. Let $s_{j,m}^{n_m}\in [a_{i_j}^{n_m},b_{i_j}^{n_m}]$ be such that $c_{n_m}(s_{j,m}^{n_m})$ is incident to $\gamma _j^{n_m}(\lfloor d_{Q_{n_m}}(u_j^{n_m},w_j^{n_m})/m\rfloor )$ and $t_{j,m}^{n_m}\in [a_{i_j}^{n_m},b_{i_j}^{n_m}]$ be such that $c_{n_m}(t_{j,m}^{n_m})$ is incident to $\gamma _j^{n_m}(\lfloor (1-1/m)\, d_{Q_{n_m}}(u_j^{n_m},w_j^{n_m})\rfloor )$. We extract from $(s_{j,m}^{n_m})_m$ and $(t_{j,m}^{n_m})_m$ two subsequences along which $s_{j,m}^{n_m}\rightarrow s_j\in [a_{i_j},b_{i_j}]$ and $t_{j,m}^{n_m}\rightarrow t_j\in [a_{i_j},b_{i_j}]$ as $m\rightarrow \infty$. Let us see that $s_j$ and $t_j$ are as desired.

First, by definition, $D_{({n_m})}(s_j^{n_m},s_{j,m}^{n_m})= D_{({n_m})}(s_j^{n_m},t_j^{n_m})/m+O({n_m}^{-1/4})$, which yields $D(s'_j, s_j)=0$, so that $x_j=\mathbf {p}(s_j)$. Similarly, $x_{j+1}=\mathbf {p}(t_j)$. Finally, as the portion of $\gamma _j^{n_m}$ between $\gamma _j^{n_m}(\lfloor d_{Q_{n_m}}(u_j^{n_m},w_j^{n_m})/m_n\rfloor )$ and $\gamma _j^{n_m}(\lfloor (1-1/m)\, d_{Q_{n_m}}(u_j^{n_m},w_j^{n_m})\rfloor )$ is completely included inside $\mathbf {V}^{n_m}_j$, this path also exists in the corresponding slice of $Q_{n_m}$ (recall that $\mathbf {V}_j^{n_m}$ does not contain the maximal geodesic). As a result, $D_{({n_m})}(s^{n_m}_{j,m},t^{n_m}_{j,m})=\tilde{D}_{({n_m})}^{i_j}(s^{n_m}_{j,m},t^{n_m}_{j,m})$ and we obtain $D(s_j, t_j)=\tilde{D}^{i_j}(s_j,t_j)$ by (32), as wanted. This concludes the proof of Lemma 22. $\square$

Remark that, in the previous proof, it is possible that $D(s'_j, t'_j)\ne \tilde{D}^{i_j}(s'_j,t'_j)$ as we may have $\tilde{D}^{i_j}(s'_j,s_j)>0$ if $[a_{i_j},b_{i_j}]$ is the excursion containing $s_*$ and $x_j\in \mathrm {Im}(\wp ^{i_j}_l)\cap \mathrm {Im}(\wp ^{i_j}_r)$.

We now conclude the proof of Theorem 20. First, from the definition of $D^*$, it holds that $D^*\le \tilde{D}^{\lozenge }$. From this, together with Lemma 22 and the fact that $D^*\le d_Z$, we deduce that $D(s,t)\ge D^*(s,t)$ for Lebesgue-almost every s, $t\in [0,1]$, so that equality holds since $D\le D^*$ by Lemma 17. Since $D^*\le d_Z$, which is continuous on $[0,1]^2$ and null on the diagonal, we immediately deduce that the pseudo-metrics D, $D^*$ are continuous when seen as functions on $[0,1]^2$, and by density we get that $D=D^*$. This proves Theorem 20, and hence also Theorem 1.

6 Boltzmann random maps and well-labeled mobiles

6.1 The Bouttier–Di Francesco–Guitter bijection

There is a well-known extension of the Cori–Vauquelin–Schaeffer bijection to general maps. This extension, due to Bouttier, Di Francesco and Guitter [15], can roughly be described in the following way. Any bipartite map can be coded by an object called a well-labeled mobile. Namely, a mobile is a rooted plane tree $\mathbf {t}$ (we usually call $e_0$ its root edge) together with a bicoloration of its vertices into “white vertices” and “black vertices.” We denote by $\mathbf {V}_\circ (\mathbf {t})$, $\mathbf {V}_\bullet (\mathbf {t})$ the corresponding sets of vertices, and ask that any two neighboring vertices carry different colors, and that $e_0^-\in \mathbf {V}_\circ (\mathbf {t})$, meaning that mobiles are rooted at a white vertex.

Moreover, the set $\mathbf {V}_\circ (\mathbf {t})$ carries a label function $\ell :\mathbf {V}_\circ (\mathbf {t})\rightarrow \mathbb {Z}$, that satisfies the following property: if $v'\in \mathbf {V}_\bullet (\mathbf {t})$ is a black vertex, and if $v'_0$, $v'_1$, ..., $v'_{k-1}\in \mathbf {V}_\circ (\mathbf {t})$ denote the neighbors of $v'$ arranged in clockwise order around $v'$ induced by the planar structure of $\mathbf {t}$ (so that $k=\deg _\mathbf {t}(v')$), it holds that

$$\begin{aligned} \ell \left( v'_{i+1}\right) -\ell \left( v'_{i}\right) \ge -1,\qquad \forall \, i\in \{0,1,\ldots ,k-1\}, \end{aligned}$$

with the convention that $v'_k=v'_0$. A simple counting argument shows that, as soon as one of the labels, say $\ell (v'_0)$, is fixed, there are exactly $\left( {\begin{array}{c}2k-1\\ k\end{array}}\right)$ possible choices for the other labels $\ell (v'_1)$, ..., $\ell (v'_{k-1})$. At this point of the discussion, we do not insist that the label of any given vertex is fixed, so we really view $\ell$ as a function defined up an additive constant, as we did in Sect. 3. We will fix a normalization in the next section.

In our context of maps with a boundary, we use the following conventions. The objects encoding the bipartite maps with perimeter 2l (maps of $\mathbf {B}_l$) are forests $\mathbf {f}=(\mathbf {t}_1, \dots , \mathbf {t}_l)$ of l mobiles, together with a labeling function $\ell :\mathbf {V}_\circ (\mathbf {f})=\bigsqcup _i \mathbf {V}_\circ (\mathbf {t}_i)\rightarrow \mathbb {Z}$ satisfying the following:

• for $1\le i \le l$, the mobile $\mathbf {t}_i$ equipped with the restriction of $\ell$ to $\mathbf {V}_\circ (\mathbf {t}_i)$ is a well-labeled mobile;

• for $1\le i \le l$, we have $\ell (\rho _{i+1})\ge \ell (\rho _{i})-1$, where $\rho _i$ denotes the root vertex of $\mathbf {t}_i$ and $\ell (\rho _{l+1})=\ell (\rho _1)$.

Remark 4

These forests are in simple bijection with the set of mobiles rooted (unusually) at a black vertex of degree l. But since the external face really plays a different role from the other faces, we prefer indeed to view those as forests of individual mobiles, rather than one single mobile.

The BDG bijection is very similar to the construction presented in Sect. 3.3. We consider a forest $\mathbf {f}=(\mathbf {t}_1, \dots , \mathbf {t}_l)$ of l mobiles, labeled by $\ell$ as above and we set $\ell _*=\min \{\ell (v):v\in \mathbf {V}_\circ (\mathbf {f})\}-1$. We let $N^\mathbf {V}$ be its number of white vertices, $N^\mathbf {F}$ be its number of black vertices, and $N^\mathbf {E}=N^\mathbf {V}+N^\mathbf {F}$ be its total number of vertices. (The reason for this notation will become clear in a short moment.)

We identify $\mathbf {f}$ with the map obtained by adding l edges linking the roots $\rho _1$, $\rho _2$, ..., $\rho _l$ of the successive trees in a cycle. This map has one face of degree l incident to the l added edges and another face f of degree $2N^\mathbf {E}-l$, incident to the l added edges as well as all the mobiles. It is also a simple exercise to see that $N^\mathbf {E}$ of the corners of the face f are incident to white vertices, and we denote by $c_0$, $c_1$, ..., $c_{N^\mathbf {E}-1}$these corners, listed in contour order, and starting from the root corner of $\mathbf {t}_1$. We extend this list by periodicity and add one corner $c_\infty$ incident to a vertex $v_*$ lying inside the face f, with label $\ell (c_\infty )=\ell (v_*)=\ell _*$. We define the successor functions by (19) and draw arcs in a non-crossing fashion from $c_i$ to $s(c_i)$ for every $i\in \{0,1,\ldots ,N^\mathbf {E}-1\}$. We root the resulting map at the corner of the face that is incident to the root vertex of $\mathbf {t}_1$; note that this face turns out to have degree 2l. We obtain a rooted bipartite map $\mathbf {m}$ with perimeter 2l, with vertex set $\mathbf {V}_\circ (\mathbf {t})\cup \{v_*\}$, which is naturally pointed at $v_*$, and such that the root edge points away from $v_*$.

As in Sect. 3.3, the fact that the root edge necessarily points away from $v_*$ is a bit unfortunate and we use the same trick in order to overcome this technicality. More precisely, we consider the map obtained from $\mathbf {m}$ by forgetting its root and re-rooting it at a corner chosen uniformly at random among the 2l corners of the root face.

A noticeable fact about the BDG bijection is that the black vertices of the forest are in bijection with the internal faces of the map. More precisely, if $v\in \mathbf {V}_\bullet (\mathbf {f})$ corresponds to the face f of $\mathbf {m}$, then $\deg _\mathbf {m}(f)=2\deg _\mathbf {f}(v)$. Furthermore, the white vertices are bijectively associated with $\mathbf {V}(\mathbf {m}){\setminus }\{v_*\}$ (so that we can naturally identify these two sets), in such a way that the label function $\ell$ gives distances to $v_*$ via the formula

$$\begin{aligned} d_\mathbf {m}(v,v_*)=\ell (v)-\ell _*. \end{aligned}$$

(33)

As a result (and with the help of the Euler characteristic formula), note that $N^\mathbf {V}+1$, $N^\mathbf {F}$ and $N^\mathbf {E}$ respectively correspond to the number of vertices, internal faces, and edges of $\mathbf {m}$—this explains the notation.

6.2 Random mobiles

We now show how to represent the pointed Boltzmann measures $\mathbb {W}^\bullet _l$ of Sect. 1.4.2 in terms of random trees, via the BDG bijection. Let $\mu _\circ$ be the geometric distribution with parameter $1/\mathcal {Z}_q$, given by

$$\begin{aligned} \mu _\circ (k)=\frac{1}{\mathcal {Z}_q}\left( 1-\frac{1}{\mathcal {Z}_q}\right) ^k,\qquad k\ge 0. \end{aligned}$$

Let also

$$\begin{aligned} \mu _\bullet (k)=\frac{\mathcal {Z}_q^k\left( {\begin{array}{c}2k+1\\ k\end{array}}\right) \,q_{k+1}}{f_q(\mathcal {Z}_q)}\, \qquad k\ge 0. \end{aligned}$$

Let $\mathbb {M}_l$ be the law of a two-type Bienaymé–Galton–Watson forest, with l independent tree components, and in which even generations (white vertices) use the offspring distribution $\mu _\circ$, while odd generations (black vertices) use the offspring distribution $\mu _\bullet$. Formally, we let $\mathbb {M}_l=(\mathbb {M}_1)^{\otimes l}$ where $\mathbb {M}_1$ is defined by

$$\begin{aligned} \mathbb {M}_1(\{\mathbf {t}\})=\prod _{u\in \mathbf {V}_\circ (\mathbf {t})}\mu _\circ (k_u(\mathbf {t}))\prod _{u\in \mathbf {V}_\bullet (\mathbf {t})}\mu _\bullet (k_u(\mathbf {t}))\, \end{aligned}$$

for every tree $\mathbf {t}$, where $k_u(\mathbf {t})$ is the number of children of u in $\mathbf {t}$. Next, let $\xi _1$, $\xi _2$, ...be a sequence of i.i.d. random variables with shifted geometric(1 / 2) distribution

$$\begin{aligned} \mathbb {P}(\xi _i=r)=2^{-r-2}, \qquad r\ge -1,\ i\ge 1, \end{aligned}$$

(34)

and let $(0,Y_1,\ldots ,Y_{k-1})$ be distributed as the partial sums $(0,\xi _1,\xi _1+\xi _2,\ldots ,\xi _1+\cdots +\xi _{k-1})$ conditionally given $\xi _1+\cdots +\xi _{k}=0$. We say that $(0,Y_1,\ldots ,Y_{k-1})$ is a discrete bridge with shifted geometric steps, and we let $\nu _k$ be the law of this random vector. It is simple to see that, if $\nu _k^0$ is the uniform distribution on

$$\begin{aligned} \left\{ (x_1,\ldots ,x_k)\in \{-1,0,1,2,\ldots \}^{k}\, :\, \sum _{i=1}^{k}x_i=0\right\} , \end{aligned}$$

then $\nu _k$ is the image measure of $\nu _k^0$ under $(x_1,\ldots ,x_{k})\mapsto (\sum _{i=1}^jx_j,\,0\le j\le k-1)$.

Finally, the white vertices of a forest with law $\mathbb {M}_l$ carry random integer labels with the following law. Conditionally given the forest, if u is a black vertex with parent $u_0$ and children $u_1$, $u_2$, ..., $u_k$, then the law of the label differences $(\ell (u_i)-\ell (u_0),\,1\le i\le k)$ is given by $\nu _k$, while those label differences are independent as u ranges over all black vertices of the forest. The labels of the roots $\rho _1$, ..., $\rho _l$ of the forest have same law as $(0,Y_1,\ldots ,Y_{l-1})$, where $(Y_1,\ldots ,Y_{l-1})$ has law $\nu _{l}$. These specify entirely the law of the labels, and in fact, one sees that labels are uniform among all admissible labelings of the forest, in which the root $\rho _1$ of the first tree carries label 0. For simplicity, we still denote by $\mathbb {M}_l$ the law of the forest of well-labeled mobiles thus obtained.

Recall the definitions (4) and (5) of the pointed measures $W^\bullet$ and $\mathbb {W}^{\bullet ,\mathbf {S}}_{l,n}$.

Proposition 23

Let q be an admissible sequence, and $l\ge 1$. Then the image of $\mathbb {M}_l$ under the Bouttier–Di Francesco–Guitter bijection is, after uniform re-rooting on the boundary, the probability measure $\mathbb {W}^{\bullet }_l$.

For $\mathbf {S}\in \{\mathbf {V},\mathbf {E},\mathbf {F}\}$ and a pair (l, n) such that $\mathbb {M}_l(N^\mathbf {S}=n)>0$, the same statement holds if we replace both $\mathbb {M}_l$ with $\mathbb {M}_l(\,\cdot \,|\, N^\mathbf {S}=n)$ and $\mathbb {W}^{\bullet }_l$ with $\mathbb {W}^{\bullet ,\mathbf {S}}_{l,n}$.

This is proved by following the same steps as in [34, Proposition 7] and by applying a straightforward analog of Lemma 10; we omit the details. At this point, we can prove Lemma 3, which describes the set $\mathcal {E}^\mathbf {S}(q)$ of pairs (l, n) such that $\mathbb {W}(\mathbf {B}^\mathbf {S}_{l,n})>0$ or, equivalently, such that $\mathbb {M}_l(N^\mathbf {S}=n) >0$.

Proof of Lemma 3

Let us fix the symbol $\mathbf {S}$. By Proposition 2.2 in [42], under the law $\mathbb {M}_1$, there exist two constants $\alpha$, h such that the support of $N^\mathbf {S}$ is included in $\alpha +h\mathbb {Z}_+$, and moreover, for every m large enough, $\mathbb {M}_1(N^\mathbf {S}=\alpha +hm)>0$. In particular, there exists $\beta \in \alpha +h\mathbb {Z}_+$ such that $\mathbb {M}_1(N^\mathbf {S}=\beta +hm)>0$ for every $m\ge 0$. This means that the support of the law of $N^\mathbf {S}$ under $\mathbb {M}_1$ is equal to $R\cup (\beta +h\mathbb {Z}_+)$, for some $R\subseteq \{0,1,\ldots ,\beta -1\}\cap (\alpha +h\mathbb {Z}_+)$. From this, we immediately deduce the similar result for forests under the distribution $\mathbb {M}_l$. Namely, the support of $N^\mathbf {S}$ under $\mathbb {M}_l$ is equal to $R_l\cup (\beta l+h\mathbb {Z}_+)$, for some $R_l\subseteq \{0,1,\ldots ,\beta l-1\}$. From this observation and Proposition 23, using the remark at the end of the preceding section that the image of $N^\mathbf {S}$ under the BDG bijection is $|\mathbf {S}| - \mathbf {1}_{\{\mathbf {S}=\mathbf {V}\}}$, we obtain that the support of the law of $|\mathbf {S}(\mathbf {m})|-\mathbf {1}_{\{\mathbf {S}=\mathbf {V}\}}$ under $\mathbb {W}_l^\bullet$ (or under $\mathbb {W}_l$ by the absolute continuity relation (6)) is equal to

$$\begin{aligned} R_l\cup (\beta l+h\mathbb {Z}_+). \end{aligned}$$

The result follows immediately from this, since the explicit form of h was computed in Lemma 6.1 of [42]. $\square$

Again, in all the following, when considering pairs (l, n) where l corresponds to the boundary length of a map, and n to its size (measured with respect to the symbol $\mathbf {S}$), it will always be implicitly assumed that $(l,n)\in \mathcal {E}^\mathbf {S}(q)$, which by Lemma 3 means that, up to finitely many exceptions,

$$\begin{aligned} n=\beta ^\mathbf {S}l\quad [\mathrm {mod }\, h^\mathbf {S}]. \end{aligned}$$

7 Convergence of the encoding processes

In this section, it will be convenient to consider possibly infinite forests $\mathbf {f}=(\mathbf {t}_1,\mathbf {t}_2,\ldots )$ equipped with a label function $\ell$, rather than finite forests only. Let $(\mathbf {f},\ell )$ be either a finite or such an infinite labeled forest.

With it, we associate several exploration processes. Let $v_0$, $v_1$, $v_2$... denote the vertices of $\mathbf {f}$ (black or white), listed in depth-first order, tree by tree. Let H be the so-called height process associated with $\mathbf {f}$, that is, H(i) denotes the distance between the vertex $v_i$ and the root $\rho _{(i)}$ of the tree to which it belongs. If the forest $\mathbf {f}$ is finite, this process is defined for $0\le i\le N^\mathbf {E}-1$, and we extend it one step further by letting $H(N^\mathbf {E})=0$. For $0\le i\le N^\mathbf {E}\in \mathbb {N}\cup \{\infty \}$, we set $\hat{\ell }(i)=\ell (v_i)$, as well as $\hat{\ell }^{\mathbf {0}}(i)=\hat{\ell }(i)-\ell (\rho _{(i)})$. Note that this notion of label process differs from the one introduced during Sect. 5; we use the notation with a hat in order to avoid confusion. Next, let $\Upsilon (i)$ be the number of fully explored trees at time i, that is, $\Upsilon (i)+1=p$ whenever $v_i$ belongs to the p-th tree of $\mathbf {f}$, that is $\rho _{(i)}=\rho _p$. We also let

$$\begin{aligned} \tau _l=\inf \{i\ge 0:\Upsilon (i)=l\} \end{aligned}$$

be the number of (black or white) vertices in the first l trees of the forest. Note for instance that, with the notation of Sect. 6.1, one has $N^\mathbf {E}=\tau _l$ if $\mathbf {f}$ has l trees. Finally, we extend the definitions of H, $\hat{\ell }^{\mathbf {0}}$, $\hat{\ell }$ and $\Upsilon$ to $\mathbb {R}_+$ by linear interpolation.

Let us now consider an infinite random labeled forest $(F,\ell )$ with distribution $\mathbb {M}_\infty =(\mathbb {M}_1)^{\otimes \mathbb {N}}$. Under this law, the random labels are defined as explained before Proposition 23, except that the root labels are all set to 0, so that $\hat{\ell }=\hat{\ell }^{\mathbf {0}}$ in this context. In fact, the process $\hat{\ell }$ will only be of interest under $\mathbb {M}_l$; we will focus on it later.

7.1 Convergence for an infinite forest

A key result is the following. Recall that $\mathcal {Z}_q$ is given by (7) and $\rho _q=2+\mathcal {Z}_q^3f_q''(\mathcal {Z}_q)$. Define

$$\begin{aligned} \sigma _q^2=\frac{\mathcal {Z}_q \rho _q}{4},\qquad {\sigma _{\mathbf {E}}}^2=\frac{\rho _q}{\mathcal {Z}_q}. \end{aligned}$$

Proposition 24

The following joint convergence holds in distribution in $\mathcal {C}(\mathbb {R}_+,\mathbb {R}^3)$ under $\mathbb {M}_\infty$:

where $(X_t,t\ge 0)$ is a standard Brownian motion, $\underline{X}_t=\inf _{0\le s\le t}X_s$ and $Z^{\mathbf 0}$ is the Brownian snake with driving process $X-\underline{X}$, introduced in Sect. 2.2.

Proof

We note that the two-type branching process with offspring distributions $\mu _\circ$, $\mu _\bullet$ and alternating types is a critical branching process, in which the offspring distributions have small exponential moments (this is the place where we use the fact that q is regular critical), as discussed in Proposition 7 of [34]. Furthermore, the spatial displacements with distribution $\nu _k$ are centered and carried by $[-k,k]^k$ respectively. In particular, they have moments of all orders, which grow at most polynomially, in the sense that for every $a>0$,

$$\begin{aligned} \langle \nu _k,|\cdot |^a\rangle =O(k^{a}), \end{aligned}$$

where $|\cdot |$ is the Euclidean norm in $\mathbb {R}^k$. This is exactly what is needed to apply Theorems 1 and 3 in [36], which in our particular context stipulate that

where the constants $\sigma$, $b_\circ$ and $\Sigma$ are defined in the following way. The mean matrix of the two-type Galton–Watson process under consideration is given by

$$\begin{aligned} \left( \begin{array}{cc} 0 &{}\quad m_\circ \\ m_\bullet &{}\quad 0 \end{array} \right) , \end{aligned}$$

where $m_\circ$ is the mean of $\mu _\circ$, and $m_\bullet$ is the mean of $\mu _\bullet$. Note that $m_\bullet =m_\circ ^{-1}$ as an immediate consequence of the fact that q is regular critical. This matrix admits a left invariant vector $\mathbf {a}=(a_\circ ,a_\bullet )$ normalized to be a probability, namely $a_\circ =(1+m_\circ )^{-1}$ and $a_\bullet =(1+m_\bullet )^{-1}$, and a right invariant $\mathbf {b}=(b_\circ ,b_\bullet )$ normalized in such a way that the scalar product $\mathbf {a}\cdot \mathbf {b}=1$, namely $b_\circ =(1+m_\circ )/2$ and $b_\bullet =(1+m_\bullet )/2$. Finally, with $(\mu _\circ ,\mu _\bullet )$, one can associate a quadratic function $\mathbf{Q}:\mathbb {R}^2\rightarrow \mathbb {R}^2$ given by

$$\begin{aligned} \mathbf{Q}(x_\circ ,x_\bullet )=((\sigma _\circ ^2+m_\circ (m_\circ -1))\,x_\bullet ^2, (\sigma _\bullet ^2+m_\bullet (m_\bullet -1))\,x_\circ ^2), \end{aligned}$$

where $\sigma _\circ ^2$ and $\sigma _\bullet ^2$ are the variances of $\mu _\circ$ and $\mu _\bullet$. Then $\sigma ^2$ is given by the scalar product

$$\begin{aligned} \sigma ^2=\mathbf {a}\cdot \mathbf {Q}(\mathbf {b}). \end{aligned}$$

Finally, $\Sigma ^2$ is given by the formula

$$\begin{aligned} \Sigma ^2=\frac{1}{2}\sum _{k\ge 1}\frac{\mu _\bullet (k)}{m_\bullet }(\Sigma _\bullet ^k)^2 \end{aligned}$$

where $(\Sigma _\bullet ^k)^2=\langle \nu _k,|\cdot |^2\rangle =k(k+1)/3$, as can be checked in [34]. After computations, which have been performed in Section 3.2 of [34], one obtains in particular

$$\begin{aligned} m_\circ =\mathcal {Z}_q-1,\quad b_\circ =\frac{\mathcal {Z}_q}{2},\quad \sigma ^2=\frac{\mathcal {Z}_q\rho _q}{4},\quad \Sigma ^2=\frac{\rho _q}{6}. \end{aligned}$$

The conclusion follows. $\square$

We are also going to need the following fact. For every $m\ge 1$, let

$$\begin{aligned} \begin{aligned} \Lambda ^\mathbf {V}(m)=\left| \left\{ i\in \{0,1,\ldots ,m-1\}:v_i\in \mathbf {V}_\circ (\mathbf {f})\right\} \right| ,\\ \Lambda ^\mathbf {F}(m)=\left| \left\{ i\in \{0,1,\ldots ,m-1\}:v_i\in \mathbf {V}_\bullet (\mathbf {f}) \right\} \right| , \end{aligned} \end{aligned}$$

(35)

be respectively the number of white vertices and the number of black vertices among the first m vertices of F in depth-first order. For convenience, we also let $\Lambda ^\mathbf {E}(m)=m$ (the number of vertices of either type), so that $\Lambda ^\mathbf {S}$ makes sense for every $\mathbf {S}\in \{\mathbf {V},\mathbf {E},\mathbf {F}\}$. Define

$$\begin{aligned} a_\mathbf {V}=\mathcal {Z}_q^{-1},\qquad a_\mathbf {F}=1-\mathcal {Z}_q^{-1},\qquad a_{\mathbf {E}}=1\,. \end{aligned}$$

(36)

The first two quantities are the ones that appeared in the proof of Proposition 24, under the notation $a_\mathbf {V}=a_\circ$ and $a_\mathbf {F}=a_\bullet$. (Recall that, through the BDG bijection, $\mathbf {V}$ correspond essentially to white vertices, $\mathbf {F}$ to black vertices and $\mathbf {E}$ to edges of the mobile, which are in direct bijection with the set of vertices of both colors.)

In the following statement and later, the notation $\mathrm {oe}(n)$ stands for a quantity that is bounded from above by $c\exp (-c'n^{c''})$ for three positive constants c, $c'$, $c''$, uniformly in n.

Proposition 25

Fix $\mathbf {S}\in \{\mathbf {V},\mathbf {E},\mathbf {F}\}$. Then it holds that

in probability under $\mathbb {M}_\infty$ for the uniform topology over compact subintervals of $\mathbb {R}_+$. More precisely, for every $K>0$, one has the concentration result

$$\begin{aligned} \mathbb {M}_\infty \left( \max _{0\le k\le Km}|\Lambda ^\mathbf {S}(k) - a_\mathbf {S}\, k|>m^{3/4}\right) =\mathrm {oe}(m)\,. \end{aligned}$$

Proof

The result is obvious for $\mathbf {S}=\mathbf {E}$, so that we suppose $\mathbf {S}\in \{\mathbf {V},\mathbf {F}\}$. We first note that, since $\Lambda ^\mathbf {S}(k)\le k$, it suffices to prove the same bound with the maximum restricted over indices $k\in [m^{1/2},Km]$. Now [36, Proposition 6 (ii)] shows that, if $G_x^\mathbf {S}$ denotes the number of vertices in depth-first order (of either type) that have been visited before the $\lfloor x\rfloor$-th vertex of type $\mathbf {S}$ (white if $\mathbf {S}=\mathbf {V}$, black if $\mathbf {S}=\mathbf {F}$), then $\mathbb {M}_\infty (|G_k^\mathbf {S}- a_\mathbf {S}^{-1}\, k|>k^{3/4})=\mathrm {oe}(k)$. Now $|\Lambda ^\mathbf {S}(k)-a_\mathbf {S}\, k|>m^{3/4}$ implies that $G^\mathbf {S}_{a_\mathbf {S}k+m^{3/4}}\le k$ or $G^\mathbf {S}_{(a_\mathbf {S}k-m^{3/4})_+}\ge k$, the probability of which is bounded from above by

$$\begin{aligned}&\mathbb {M}_\infty \left( |G^\mathbf {S}_{a_\mathbf {S}k+m^{3/4}}-a_\mathbf {S}^{-1}(a_\mathbf {S}\, k+m^{3/4})|\ge a_\mathbf {S}^{-1}m^{3/4} \right) \\&\quad +\mathbb {M}_\infty \left( |G^\mathbf {S}_{(a_\mathbf {S}k-m^{3/4})_+}-a_\mathbf {S}^{-1}(a_\mathbf {S}\, k-m^{3/4})_+|\ge a_\mathbf {S}^{-1}m^{3/4} \right) . \end{aligned}$$

Taking the maximum over all $k\in [m^{1/2},Km]\cap \mathbb {Z}$, we see that this quantity is $\mathrm {oe}(m)$, as claimed. $\square$

7.2 Convergence for a conditioned forest

We now want a conditioned version of Proposition 25. We are going to need the following estimates. Recall the definition (2) of $h^\mathbf {S}$, the definition (9) of $j_L(A)$, and define $Q^\mathbf {S}(l,n)=\mathbb {M}_l(N^\mathbf {S}=n)$. We will also need the notation

$$\begin{aligned} \tau ^\mathbf {S}_l=\Lambda ^\mathbf {S}(\tau _l)\,. \end{aligned}$$

In words, $\tau ^\mathbf {E}_l=\tau _l$ is the number of vertices in the l first trees of the forest, while $\tau ^\mathbf {V}_l$ (resp. $\tau ^\mathbf {F}_l$) is the number of white (resp. black) vertices in these trees.

Lemma 26

Let $\mathbf {S}\in \{\mathbf {V},\mathbf {E},\mathbf {F}\}$. Then

Proof

Suppose first that $\mathbf {S}=\mathbf {E}$. In this case, a consequence of the convergence of the second component in Proposition 24 is that

where we recall that $T_{1/{\sigma _{\mathbf {E}}}}=\inf \{t\ge 0:\underline{X}_t=-1/{\sigma _{\mathbf {E}}}\}$ is a.s. a continuous function of X under the Wiener measure, due to the fact that $\underline{X}_{(T_{1/{\sigma _{\mathbf {E}}}}-\varepsilon )_+}>-1/{\sigma _{\mathbf {E}}}>\underline{X}_{T_{1/{\sigma _{\mathbf {E}}}}+\varepsilon }$ a.s. for every $\varepsilon >0$. Moreover, $\tau _l$ under $\mathbb {M}_\infty$ is the sum of l i.i.d. random variables with same law as $\tau _1$: these are given by the number of vertices of the first l trees in the infinite forest of independent random mobiles. Since it is well known that $T_{1/{\sigma _{\mathbf {E}}}}$ follows a stable distribution with index 1 / 2, with a density given by $j_{1/{\sigma _{\mathbf {E}}}}$, we conclude that $\tau _1$ under $\mathbb {M}_\infty$ is in the domain of attraction of this law. The statement is then a consequence of the local limit theorem for stable random variables [14, Theorem 8.4.1].

The remaining two cases $\mathbf {S}\in \{\mathbf {V},\mathbf {F}\}$ are now direct consequences of the case $\mathbf {S}=\mathbf {E}$ and of Proposition 25, which together imply that we have

$$\begin{aligned} \frac{\tau _l^\mathbf {S}}{l^2}=\frac{\Lambda ^\mathbf {S}(\tau _l)}{l^2}=\frac{a_\mathbf {S}\,\tau _l\,(1+o_\mathbb {P}(1))}{l^2}, \end{aligned}$$

(37)

where $o_\mathbb {P}(1)$ denotes a quantity that converges to 0 in probability. This yields that

as can be checked using (8) and (36). The conclusion follows by the same arguments as in the case $\mathbf {S}=\mathbf {E}$. $\square$

In this section, it is convenient to consider processes whose total duration is not fixed. We let $\mathcal {W}$ be the set of real-valued continuous functions f defined on an interval of the form $[0,\zeta ]$ for some $\zeta =\zeta (f)\in [0,\infty )$. This set is endowed with the distance

$$\begin{aligned} \mathrm {dist}(f,g)=\Vert f(\cdot \wedge \zeta (f))-g(\cdot \wedge \zeta (g))\Vert _\infty +|\zeta (f)-\zeta (g)|\, \end{aligned}$$

which makes it a complete separable metric space. For instance, the height process H under the law $\mathbb {M}_l$ is defined as before, by letting H(i) be the distance of the $i+1$-th visited vertex $v_i$ to the root of the tree to which it belongs, for $0\le i\le \tau _l-1$, and with the convention that $H(\tau _l)=0$. After interpolation between integer values, H is an element of $\mathcal {W}$ with duration $\zeta (H)=\tau _l=N^\mathbf {E}$.

Recall the definition of $\mathscr {S}^\mathbf {S}_L$ given right after (8).

Proposition 27

Let $\mathbf {S}\in \{\mathbf {V},\mathbf {E},\mathbf {F}\}$ and $(l_k,n_k)_{k\ge 0}\in \mathscr {S}^\mathbf {S}_L$ for some $L>0$. Then, under $\mathbb {M}_{l_k}(\,\cdot \, |\, N^\mathbf {S}=n_k)$, it holds that

in distribution in the space $\mathcal {W}^3$ where, in the limit, X, $Z^{\mathbf 0}$ are understood under the law $\mathbb {F}^1_L$ defined in Sect. 2.2. Note that, on the left-hand side above, all three processes have duration $a_\mathbf {S}\tau _{l_k}/n_k$.

Proof

For simplicity, let $\Xi _k$ denote the triple appearing in the left-hand side of the convergence. Denote by $\mathcal {F}_{p}$ the $\sigma$-field generated by the p first trees of the generic (canonical process) infinite forest $\mathbf {f}=(\mathbf {t}_1,\mathbf {t}_2,\ldots )$, together with their labels. Let G be measurable with respect to $\mathcal {F}_{l_k'}$, with $l_k'< l_k$. Then, by independence of the trees under $\mathbb {M}_{l_k}$, we have

$$\begin{aligned} \mathbb {M}_{l_k}\left[ G\, \big |\, N^\mathbf {S}=n_k\right] =\mathbb {M}_\infty \left[ G \, \frac{Q^\mathbf {S}\left( l_k-l'_k,n_k-\tau ^\mathbf {S}_{l_k'}\right) }{Q^\mathbf {S}(l_k,n_k)}\right] , \end{aligned}$$

(38)

where it should be understood that the quantity in the expectation is 0 whenever $\tau ^\mathbf {S}_{l_k'}> n_k$. Note that this is the place where we have to consider the label process $\hat{\ell }^{\mathbf {0}}$ rather than $\hat{\ell }$, which amounts to setting the root labels to zero, in order to be able to use the claimed independence of the labeled trees.

Now, we impose that $G=\Phi (\Xi _k')$ is a continuous, bounded function of the triple of processes

$$\begin{aligned} \Xi _k'=\left( \frac{H\left( a_\mathbf {S}^{-1}n_k\cdot \wedge \tau _{l'_k}\right) }{\sqrt{n_k}},\frac{\Upsilon \left( {a_\mathbf {S}^{-1}n_k\cdot \wedge \tau _{l'_k}}\right) }{\sqrt{n_k}},\frac{{\hat{\ell }}^{\mathbf {0}}\left( {a_\mathbf {S}^{-1}n_k\cdot \wedge \tau _{l'_k}}\right) }{n_k^{1/4}}\right) , \end{aligned}$$

where we assume that $l'_k\sim L'{\sigma _{\mathbf {S}}}\sqrt{n_k}$ for some $0<L'<L$. Proposition 24 shows the convergence in distribution

where the limit is understood under the law $\mathbb {P}$. Using the convergence of the second component, the asymptotic behavior of $l'_k$ and the fact that $a_\mathbf {S}{\sigma _{\mathbf {S}}}^2={\sigma _{\mathbf {E}}}^2$, it follows that

and that this convergence holds jointly with the previous one. From this, it follows that $\Xi _k'$ converges in distribution under $\mathbb {M}_\infty$ to the triple

$$\begin{aligned} \Xi _\infty '=\left( \frac{2}{\sqrt{a_\mathbf {S}}\,\sigma _q}(X-\underline{X})_{\,\cdot \,\wedge T_{L'}},-{\sigma _{\mathbf {S}}}\,\underline{X}_{\,\cdot \,\wedge T_{L'}},\sqrt{\frac{2{\sigma _{\mathbf {S}}}}{3}}Z^{\mathbf 0}_{\,\cdot \,\wedge T_{L'}}\right) \end{aligned}$$

and an application of (37) implies that $\tau ^\mathbf {S}_{l_k'}/{n_k}\rightarrow T_{L'}$ jointly with the above convergence. By the Skorokhod representation theorem, we may assume that the probability space is chosen in such a way that these convergences hold in the almost-sure sense, and then (38) together with Lemma 26 implies that

and the limit can be re-expressed as

$$\begin{aligned} \mathbb {E}\left[ \Phi (\Xi '_\infty )\,\frac{j_{L-{L'}}(1-T_{L'})}{j_L(1)}\right] =\mathbb {F}^1_L[\Phi (\Xi '_\infty )]. \end{aligned}$$

In other words, under $\mathbb {M}_{l_k}(\,\cdot \, |\, N^\mathbf {S}=n_k)$, the vector $\Xi '_k$ converges in distribution to $\Xi '_\infty$, where, in the limit, X, $Z^{\mathbf 0}$ are understood under $\mathbb {F}^1_L$. By definition, $\Phi (\Xi '_\infty )$ is $\mathcal {G}_{T_{L'}}$-measurable and, by Galmarino’s test, we have $\mathcal {G}_{T_{L'}}=\sigma (X_{\cdot \,\wedge T_{L'}},Z^{\mathbf 0}_{\,\cdot \,\wedge T_{L'}})$, so that, if it exists, the limit of the triple considered in the statement of the proposition necessarily has the claimed law, by virtue of Proposition 9.

To conclude the proof, it remains to prove that the laws of the processes under consideration are tight in $\mathcal {W}^3$. We can argue as follows. Let f be a continuous function defined on an interval I, and $J\subseteq I$ be a subinterval of I. Denote by

$$\begin{aligned} \omega (f,\delta ,J)=\sup _{s,t\in J,\, |t-s|\le \delta }|f(t)-f(s)| \end{aligned}$$

the modulus of continuity of f restricted to J, and let $\omega (f,\delta )=\omega (f,\delta ,I)$.

Here, let $Y_k$ denote either of the coordinates of $\Xi _k$. Then, under $\mathbb {M}_{l_k}(\,\cdot \, |\, N^\mathbf {S}={n_k})$,

$$\begin{aligned} \omega (Y_k,\delta ) \le \omega \left( Y_k,\delta ,[0,a_\mathbf {S}\tau _{l'_k}/{n_k}] \right) + \omega \left( Y_k,\delta ,[a_\mathbf {S}\tau _{l'_k}/{n_k},a_\mathbf {S}\tau _{l_k}/{n_k}] \right) \end{aligned}$$

while the second component has same distribution as

$$\begin{aligned} \omega \left( Y_k,\delta ,[0,a_\mathbf {S}\tau _{l_k-l_k'}/{n_k}] \right) \end{aligned}$$

by a symmetry argument (the $l_k$ trees of the labeled forest are exchangeable). Choosing $l'_k\sim l_k/2$, we obtain from the convergence of $\Xi _k'$ (for ${L'}=L/2$) that

$$\begin{aligned}&\limsup _{k\rightarrow \infty }\mathbb {M}_{l_k} \left( \omega (Y_k,\delta )\ge \varepsilon \, \big |\, N^\mathbf {S}={n_k} \right) \\&\quad \le \limsup _{k\rightarrow \infty } \left( \mathbb {M}_{l_k}\left( \omega \left( Y_k,\delta ,[0,a_\mathbf {S}\tau _{l_k'}/{n_k}] \right) \ge \varepsilon /2\, \big |\, N^\mathbf {S}={n_k} \right) \right. \\&\qquad \left. +\mathbb {M}_{l_k} \left( \omega \left( Y_k,\delta ,[0,a_\mathbf {S}\tau _{l_k-l_k'}/{n_k}] \right) \ge \varepsilon /2\, \big |\, N^\mathbf {S}={n_k} \right) \right) \\&\quad \le 2\,\mathbb {F}^1_L \left( \omega \left( Y_\infty ,\delta ,[0,T_{L/2}] \right) \ge \varepsilon /2 \right) , \end{aligned}$$

where $Y_\infty$ is the coordinate of the limiting vector of the statement that corresponds to $Y_k$ (for instance $Y_\infty =2(X-\underline{X})/\sqrt{a_\mathbf {S}}\,\sigma _q$ if $Y_k$ is the first component of $\Xi _k$). This quantity converges to 0 as $\delta \rightarrow 0$, for any fixed $\varepsilon >0$. A similar yet simpler reasoning gives that the total durations $a_\mathbf {S}\tau _{l_k}/n_k$, $k\ge 0$ considered respectively under $\mathbb {M}_{l_k}(\cdot \, |\, N^\mathbf {S}=n_k)$, $k\ge 0$ form a tight family. From this, it is an immediate consequence of the Ascoli–Arzela theorem that the laws of $\Xi _k$, $k\ge 1$ are relatively compact in $\mathcal {W}^3$.

$\square$

We are now in position to consider the root labels under $\mathbb {M}_l$, that is, to look at the convergence of the label process $\hat{\ell }$ rather than $\hat{\ell }^{\mathbf {0}}$.

Corollary 28

Let $\mathbf {S}\in \{\mathbf {V},\mathbf {E},\mathbf {F}\}$ and $(l_k,n_k)_{k\ge 0}\in \mathscr {S}^\mathbf {S}_L$ for some $L>0$. Then, under $\mathbb {M}_{l_k}(\,\cdot \, |\, N^\mathbf {S}=n_k)$, it holds that

in distribution in the space $\mathcal {W}^3$ where, in the limit, X, Z are understood under the law $\mathbb {F}^1_L$, defined in Sect. 2.2.

Proof

It suffices to apply the preceding proposition, noting that one can get the following representation for the label process $\hat{\ell }$ in terms of $\hat{\ell }^{\mathbf {0}}$:

$$\begin{aligned} \hat{\ell }(i)=\hat{\ell }^{\mathbf {0}}(i)+\mathrm {B}({\Upsilon (i)}), \end{aligned}$$

where $\mathrm {B}$ is a discrete bridge with shifted geometric step, with law $\nu _{l_k}$ defined in Sect. 6.2, and independent of H, $\Upsilon$, $\hat{\ell }^{\mathbf {0}}$. It holds that, under our hypotheses, $\mathrm {B}({{\sigma _{\mathbf {S}}}\sqrt{n_k}\,\cdot })/\sqrt{2{\sigma _{\mathbf {S}}}}n_k^{1/4}$ converges in distribution to a Brownian bridge $\mathrm {b}$ with duration L (see [10, Proposition 7]). Putting things together, we obtain that

$$\begin{aligned} \frac{\hat{\ell }\left( {a_\mathbf {S}^{-1}{n_k}\,\cdot }\right) }{{n_k}^{1/4}}=\frac{\hat{\ell }^{\mathbf {0}}\left( {a_\mathbf {S}^{-1}{n_k}\,\cdot }\right) }{{n_k}^{1/4}}+\frac{\mathrm {B}\left( {{\sigma _{\mathbf {S}}}\sqrt{{n_k}}\, (\Upsilon ({a_\mathbf {S}^{-1}{n_k}\,\cdot })/{\sigma _{\mathbf {S}}}\sqrt{{n_k}})} \right) }{{n_k}^{1/4}}, \end{aligned}$$

which converges in distribution to $s\mapsto \sqrt{2{\sigma _{\mathbf {S}}}/3}\,Z^{\mathbf 0}_s+\sqrt{2{\sigma _{\mathbf {S}}}}\,\mathrm {b}_{-\underline{X}_s}$, jointly with the rescaled processes H and $\Upsilon$, with $\mathrm {b}$ independent of X, $Z^{\mathbf 0}$. By definition (14), this yields the result. $\square$

Finally, we note that the convergence of $\Lambda ^\mathbf {S}$ stated in Proposition 25 still holds for conditioned forests. Indeed, since the conditioning event $\{N^\mathbf {S}=n_k\}$ has a probability $Q^\mathbf {S}(l_k,n_k)=\Theta (l_k^{-2})=\Theta (n_k^{-1})$ by Lemma 26, we obtain that for any $c'>0$,

$$\begin{aligned}&\mathbb {M}_{l_k}\left( \max _{0\le i\le N^\mathbf {E}}|\Lambda ^\mathbf {S}(i)-a_\mathbf {S}\,i|>n_k^{3/4}\, |\, N^\mathbf {S}=n_k\right) \\&\quad \le cn_k\,\mathbb {M}_\infty \left( \max _{0\le i\le c'n_k}|\Lambda ^\mathbf {S}(i)-a_\mathbf {S}\,i|>n_k^{3/4}\right) +\mathbb {M}_{l_k}(N^\mathbf {E}>c'n_k\, |\, N^\mathbf {S}=n_k). \end{aligned}$$

for some constant $c>0$. The first term is $\mathrm {oe}(n_k)$ by Proposition 25. The second term is equal to 0 if $\mathbf {S}=\mathbf {E}$ and $c'>1$. If $\mathbf {S}=\mathbf {V}$, it can be bounded by

$$\begin{aligned} cn_k\,\mathbb {M}_\infty (\Lambda ^\mathbf {V}(c'n_k)\le n_k)=\mathrm {oe}(n_k), \end{aligned}$$

as soon as $c'$ is chosen strictly larger than $a_\mathbf {V}^{-1}$, again by Proposition 25. The argument is the same if $\mathbf {S}=\mathbf {F}$. In particular, as $\Lambda ^\mathbf {S}(N^\mathbf {E})=N^\mathbf {S}$, this implies that, under $\mathbb {M}_{l_k}(\,\cdot \, |\, N^\mathbf {S}=n_k)$, one has

$$\begin{aligned} \frac{N^\mathbf {S}}{N^\mathbf {E}}\longrightarrow a_\mathbf {S}\end{aligned}$$

in probability as $k\rightarrow \infty$. This implies the following reformulation and refinement of the preceding corollary.

Corollary 29

Let $\mathbf {S}\in \{\mathbf {V},\mathbf {E},\mathbf {F}\}$ and $(l_k,n_k)_{k\ge 0}\in \mathscr {S}^\mathbf {S}_L$ for some $L>0$. Then, under $\mathbb {M}_{l_k}(\,\cdot \, |\, N^\mathbf {S}=n_k)$, it holds that

in distribution in the space $\mathcal {W}^3$, where, in the limit, X, Z are understood under the law $\mathbb {F}^1_L$. Moreover, one has, still under $\mathbb {M}_{l_k}(\,\cdot \, |\, N^\mathbf {S}=n_k)$,

in probability.

7.3 Convergence of the white contour and label processes

Finally, we consider a variant of the latest corollary where the height process is replaced by the slightly more convenient contour processes. First, given the forest F with possibly infinitely many trees, we let $\bar{C}$ be its contour process, defined as follows. We first add edges linking the roots of consecutive trees as we did before (see for instance the left part of Fig. 5). We then let $c_0$, $c_1$... be the list of corners of the trees, arranged in contour order. The purpose of the added edges linking the roots is to “split in two” the root corners of the trees: a tree with p edges will thus have 2p+1 corners. Finally, we let $\bar{C}(i)$ be the distance between $c_i$ and the root of the tree to which it belongs. Note that there is slight difference with the contour function C defined in Sect. 5.1, where a downstep was separating the contours of successive trees, instead of the horizontal step we have here. It is a standard fact, proved in [22, Chapter 2.4], that the contour and height process of a forest are asymptotically similar in the following sense. First, let $f(i)+1$ be the number of distinct vertices incident to the corners $c_0$, $c_1$, ..., $c_i$ (these vertices being $v_0$, ..., $v_{f(i)}$). Then it holds that $f(i)\le i$ for every $i\ge 0$, and for every $m\ge 0$, one has

$$\begin{aligned} \sup _{0\le i\le m} \left| \bar{C}(i)-H(f(i)) \right| \le 1+\sup _{0\le i\le m} \left| H(i+1)-H(i) \right| \end{aligned}$$

and

$$\begin{aligned} \max _{0\le i\le m}\left| f(i)-\frac{i}{2}\right| \le 1+\frac{1}{2}\max _{0\le i\le m}H_i. \end{aligned}$$

(39)

From this, and the convergence of the rescaled height process stated in Corollary 29, it follows easily that under the same hypotheses,

where X is understood under $\mathbb {F}^1_L$. Now, we want to consider the white contour process $\bar{C}^\circ$, defined as follows. We let $c^\circ _0$, $c^\circ _1$, ..., $c^\circ _{N^\mathbf {E}-1}$ be the list of corners that are incident to white vertices, arranged in contour order as above. Then 2$\bar{C}^\circ (i)$ is the distance between $c^\circ _i$ and the root of the tree to which it belongs (note that this number is even). In the contour process, white vertices are visited once in every pair of steps, except at times when one of the trees has been fully explored. The number of such exceptions is $l_k=O(\sqrt{n_k})$, so clearly the preceding convergence implies

where the limit is understood under $\mathbb {F}^1_L$. Define $\Upsilon ^\circ (i)$ to be the number of completely explored trees when visiting $c^\circ _i$, as well as $\ell ^\circ (i)$ to be the label of $c^\circ _i$. Beware that the definitions of $\bar{C}^\circ$, $\Upsilon ^\circ$ and $\ell ^\circ$ involve corners listed in contour order, instead of vertices listed in depth-first order, as in the definitions of H, $\Upsilon$ and $\hat{\ell }$. Similar arguments entail the following joint convergence.

Corollary 30

Let $\mathbf {S}\in \{\mathbf {V},\mathbf {E},\mathbf {F}\}$ and $(l_k,n_k)_{k\ge 0}\in \mathscr {S}^\mathbf {S}_L$ for some $L>0$. Then, under $\mathbb {M}_{l_k}(\,\cdot \, |\, N^\mathbf {S}=n_k)$, it holds that

in distribution in the space $\mathcal {W}^3$, where, in the limit, X, Z are understood under the law $\mathbb {F}^1_L$.

8 Proof of the invariance principle

In this section, we prove Theorems 5 and 8. The arguments, originating in [30, Section 8], are now very standard, and have been applied successfully in [1, 2, 7, 12] in particular. Our approach is an easy adaptation of the arguments that can be found in either of these papers, so here we will be a bit sketchy. Let q be a regular critical sequence as in the previous section.

8.1 Convergence of conditioned pointed maps

The goal of this subsection is to prove the second statement of Theorem 5, dealing with the laws $\mathbb {W}^{\bullet ,\mathbf {S}}_{l,n}$, defined by (5).

Fix $\mathbf {S}\in \{\mathbf {V},\mathbf {E},\mathbf {F}\}$ and $(l_k,n_k)_{k\ge 0}\in \mathscr {S}^\mathbf {S}_L$ for some $L>0$. For every $k\ge 0$, consider a forest $(F,\ell )$ of labeled mobiles with law $\mathbb {M}_{l_k}(\,\cdot \, |\, N^\mathbf {S}=n_k)$, and let $M_k^\bullet$ be the pointed random map with distribution $\mathbb {W}^{\bullet ,\mathbf {S}}_{l_k,n_k}$ which is the image of $(F,\ell )$ under the Bouttier–Di Francesco–Guitter bijection, uniformly re-rooted on the boundary, as in Proposition 23.

Recall that we want to show the convergence in distribution for the pointed Gromov–Hausdorff topology

(40)

where $\mathrm {BD}_L$ is pointed at $x_*$. The proof follows closely in spirit that of [30, Section 8]. Let

$$\begin{aligned} D'_k(i,j)=d_{M_k^\bullet }\left( c^\circ _i,c^\circ _j\right) ,\qquad 0\le i,j\le N^\mathbf {E}\end{aligned}$$

(with the convention that $c^\circ _{N^\mathbf {E}}=c^\circ _0$) and extend $D'_k$ to a continuous function on $[0,N^\mathbf {E}]^2$ by a formula similar to (21). In this way, $D'_k$ satisfies the triangle inequality, and one has

$$\begin{aligned} D'_k(i,j)\le \ell ^\circ (i)+\ell ^\circ (j)-2\max \left( \min _{[i\wedge j,i\vee j]} \ell ^\circ ,\min _{[i\vee j,N^\mathbf {E}]\cup [0,i\wedge j]}\ell ^\circ \right) +2, \end{aligned}$$

(41)

see for instance [28, Lemma 3.1] for the special case of p-mobiles (in which black vertices all have degree p, which corresponds to 2p-angulations via the BDG bijection), but the proof in this general context is the same. Clearly, it also holds that, if $c^\circ _i$ and $c^\circ _j$ are incident to the same vertex, which means that $\bar{C}^\circ (i)=\bar{C}^\circ (j)=\min _{r\in [i\wedge j,i\vee j]} \bar{C}^\circ (r)$ and $\Upsilon ^\circ (i)=\Upsilon ^\circ (j)$ then $D'_k(i,j)=0$. This generalizes to all s, $t\in [0,N^\mathbf {E}]$ rather than just integer values.

Now for s, $t\in [0,1]$ let $D'_{(k)}(s,t)=(4{\sigma _{\mathbf {S}}}^2 n_k/9)^{-1/4}D'_k(N^\mathbf {E}s,N^\mathbf {E}t)$. The same proof as [28, Proposition 3.2] (the key ingredients being (41) and the convergence of the rescaled labeled process $\ell ^\circ$, established in Corollary 30) shows that, under $\mathbb {M}_{l_k}$, the laws of $D'_{(k)}$ are tight in the space $\mathcal {C}([0,1]^2,\mathbb {R})$. Therefore, from any extraction, one can further extract a subsequence along which one has the following joint convergence in distribution under $\mathbb {M}_{l_k}(\cdot \, |\, N^\mathbf {S}=n_k)$,

(42)

where $D'$ is some random continuous function on $[0,1]^2$, and (X, Z) is the snake process under the law $\mathbb {F}^1_L$ introduced in Sect. 2.2. Recall the definition of the set $\mathcal {D}$ in Sect. 2.3, as well as the definition of $s_*$, the a.s. unique time in [0, 1] such that $Z_{s_*}=\inf Z$. We have the following result, which follows from a simple limiting argument, based on (41) and the discussion above, as well as (33) for the last point.

Lemma 31

Almost-surely, it holds that

• the random function $D'$ is a pseudo-metric on [0, 1], such that $D'\in \mathcal {D}$, and

• for every $s\in [0,1]$, $D'(s,s_*)=Z_s-Z_{s_*}$.

Let $D^*$ be the Brownian disk distance defined from the process (X, Z) by (17). By definition, it holds that $D'\le D^*$. The conclusion will follow from the following re-rooting property.

Lemma 32

Let U, V be two independent uniform random variables in [0, 1], independent of the other random variables under consideration. Then $D'(U,V)$ and $D'(s_*,U)$ have the same distribution.

Proof

This is again obtained by a limiting argument. The idea is to couple the random variables U and V with two uniformly chosen vertices of $M_k^\bullet$.

For $i\in \{1,2,\ldots ,N^\mathbf {V}\}$, let g(i) be the first time j such that $c^\circ _j$ is the i-th white vertex in depth-first order. We also let $g(0)=0$ and extend by linear interpolation g into a continuous increasing function on $[0,N^\mathbf {V}]$. Recall the definition (35) of $\Lambda ^\mathbf {V}(i)$ (for $0\le i\le N^\mathbf {E}$), the number of white vertices among $v_0$, ..., $v_i$, where $v_0$, $v_1$... are listed in depth-first order. For $i\in \{1,2,\ldots ,N^\mathbf {V}\}$, let

$$\begin{aligned} K(i)=\inf \{j\in \{0,1,\ldots ,N^\mathbf {E}\}: \Lambda ^\mathbf {V}(j)=i\}, \end{aligned}$$

so by definition, $v_{K(i)}$ is the i-th visited white vertex in depth-first order. Recall also from Sect. 7.3 that $f(j)+1$ is the number of distinct vertices incident to the corners $c_0$, ..., $c_j$. We let

$$\begin{aligned} K'(i)=\inf \{j\ge 0:f(j)=i\} \end{aligned}$$

be the first time of visit of the vertex $v_i$ in contour order. Consequently, $K'(K(i))$ is the first time of visit, in the contour sequence $c_0$, $c_1$..., of $v_{K(i)}$. Finally, since g(i) is the first index j such that $c^\circ _j$ is incident to $v_{K(i)}$, we have that

$$\begin{aligned} g(i)=K'(K(i))/2+R_k(i) \end{aligned}$$

(43)

where the error term satisfies $\sup _{1\le i\le N^\mathbf {V}}|R_k(i)|\le l_k=O(\sqrt{n_k})$, recalling the discussion of Sect. 7.3.

It follows from the last part of Corollary 29 and from (39) respectively that

in probability under $\mathbb {M}_{l_k}(\,\cdot \, |\, N^\mathbf {S}=n_k)$. From this and (43), we conclude that

(44)

still in the same sense.

Now, if I is a uniform random variable on $\{1,2,\ldots ,N^\mathbf {V}\}$ independent of the rest, then $v_{K(I)}$ is uniformly distributed among the white vertices of the forest, that is, among the vertices of the map $M_k^\bullet$ distinct from the distinguished vertex $v_*$. Therefore, if we let $v_{(1)}=v_{K(\lceil N^\mathbf {V}U\rceil )}$ and $v_{(2)}=v_{K(\lceil N^\mathbf {V}V\rceil )}$, then $v_{(1)}$, $v_{(2)}$ can be coupled with two independent uniform vertices $v'_{(1)}$, $v'_{(2)}$ of $M_k^\bullet$ in such a way that the conditional probability given $M_k^\bullet$ that $v_{(i)}\ne v'_{(i)}$, $i\in \{1,2\}$, is at most $1/|\mathbf {V}(M_k^\bullet )|$. The latter quantity, also equal to $1/(N^\mathbf {V}+1)$, converges to 0 in probability under $\mathbb {M}_{l_k}(\,\cdot \, |\, N^\mathbf {S}=n_k)$ as $k\rightarrow \infty$.

Since $v_*$ is a uniform random vertex of $M_k^\bullet$, we obtain that

Due to the above discussion, outside a set of vanishing probability, we may assume that $v'_{(1)}=v_{(1)}$ and $v'_{(2)}=v_{(2)}$.

Now note that, by (33),

$$\begin{aligned} d_{M_k^\bullet }(v_*,v_{(1)})=\ell ^\circ \left( g(\lceil N^\mathbf {V}U\rceil ) \right) -\inf \ell ^\circ +1, \end{aligned}$$

and, by definition of $D'_k$,

$$\begin{aligned} d_{M_k^\bullet }(v_{(1)},v_{(2)})=D'_k \left( g(\lceil N^\mathbf {V}U\rceil ),g(\lceil N^\mathbf {V}V\rceil ) \right) . \end{aligned}$$

Using (44), we conclude that

while

It follows that $D'(U,V)$ and $D'(s_*,U)$ have same distribution, as claimed. $\square$

To conclude the proof of (40), we note that, by Lemma 32,

$$\begin{aligned} E[D'(U,V)]=E[D'(s_*,U)]=E[Z_U-\inf Z]=E[D^*(s_*,U)]=E[D^*(U,V)], \end{aligned}$$

whence it follows that $D'(U,V)=D^*(U,V)$ a.s. since $D'\le D^*$. The last equality comes from Corollary 21; this is in fact the only place where we use the specific study of Sects. 3 and 5.

This implies, by Fubini’s theorem, that a.s. $D'(s,t)=D^*(s,t)$ for a.e. s, $t\in [0,1]$, so that $D'=D^*$ a.s. by a density argument. This identifies $D'$ uniquely, and shows that the convergence of $D'_{(k)}$ to $D'=D^*$ holds without having to pass to a subsequence. From there, showing the pointed Gromov–Hausdorff convergence of $(4{\sigma _{\mathbf {S}}}^2n_k/9)^{-1/4}M_k^\bullet$ under $\mathbb {W}^{\bullet , \mathbf {S}}_{l_k,n_k}$ to $\mathrm {BD}_{L}$ (pointed at $x_*$) is routine, and similar to the beginning of Sect. 5.2 or [10, Section 3.2].

8.2 De-pointing

Here we show how to dispose of the pointing that intervenes in (40), to obtain the first statement of Theorem 5. The argument closely follows the last section of [1], see also [12] for a similar situation.

Similarly to the absolute continuity relation (6), for $\mathbf {S}\in \{\mathbf {V},\mathbf {E},\mathbf {F}\}$, we have

$$\begin{aligned} \mathrm {d}\mathbb {W}^\mathbf {S}_{l,n}(\mathbf {m})=\frac{K^\mathbf {S}_{l,n}}{|\mathbf {V}|}\mathrm {d}\left( \phi _*\mathbb {W}^{\bullet ,\mathbf {S}}_{l,n}\right) (\mathbf {m}) \end{aligned}$$

(45)

where $K^{\mathbf {S}}_{l,n}=\mathbb {W}^{\bullet ,\mathbf {S}}_{l,n}[1/|\mathbf {V}|]^{-1}$ and $\phi :\mathbf {B}^\bullet \rightarrow \mathbf {B}$ is the function defined before (6) that forgets the distinguished vertex. In particular, $\mathbb {W}^{\mathbf {V}}_{l,n}=\phi _*\mathbb {W}^{\bullet ,\mathbf {V}}_{l,n}$ for every l, n, so in the case $\mathbf {S}=\mathbf {V}$, the statement of Theorem 5 follows from (40).

Now suppose that $\mathbf {S}\in \{\mathbf {E},\mathbf {F}\}$. Then, by Propositions 23 and 25, it holds that, for every $\varepsilon >0$,

$$\begin{aligned} \mathbb {W}^{\bullet ,\mathbf {S}}_{l_k,{n_k}}\left( \left| |\mathbf {V}|-\frac{a_\mathbf {V}}{a_\mathbf {S}}\, {n_k}\right|>\varepsilon {n_k}\right)= & {} \mathbb {M}_{l_k}\left( \left| N^\mathbf {V}+1-\frac{a_\mathbf {V}}{a_\mathbf {S}}\, {n_k}\right| >\varepsilon {n_k}\, \Bigg |\, N^\mathbf {S}={n_k}\right) \\= & {} \mathrm {oe}({n_k})\,. \end{aligned}$$

(Note that a bound of the form $o(1/{n_k})$ would suffice for the argument to work.) From this and the fact that $1/|\mathbf {V}|\le 1$, we obtain that, for every $\delta >0$,

$$\begin{aligned} \mathbb {W}^{\bullet ,\mathbf {S}}_{l_k,{n_k}}\left[ \left| \frac{{a_\mathbf {V}}\, {n_k}}{{a_\mathbf {S}}\,|\mathbf {V}|}-1\right| \right]\le & {} \delta +\left( \frac{a_\mathbf {V}}{a_\mathbf {S}}\, {n_k}+1 \right) \mathbb {W}^{\bullet ,\mathbf {S}}_{l_k,{n_k}} \left( \left| \frac{a_\mathbf {V}}{a_\mathbf {S}}\, {n_k}-|\mathbf {V}|\right| >\delta \,|\mathbf {V}|\right) \\= & {} \delta + \mathrm {oe}({n_k}), \end{aligned}$$

since

$$\begin{aligned} \mathbb {W}^{\bullet ,\mathbf {S}}_{l_k,{n_k}} \left( \left| \frac{a_\mathbf {V}}{a_\mathbf {S}}\, {n_k}-|\mathbf {V}|\right|>\delta \,|\mathbf {V}| \right)&\le \mathbb {W}^{\bullet ,\mathbf {S}}_{l_k,{n_k}}\left( |\mathbf {V}|\le \frac{a_\mathbf {V}}{a_\mathbf {S}}\frac{{n_k}}{2} \right) \\&\quad + \mathbb {W}^{\bullet ,\mathbf {S}}_{l_k,{n_k}} \left( \left| \frac{a_\mathbf {V}}{a_\mathbf {S}}\, {n_k}-|\mathbf {V}| \right| >\delta \frac{a_\mathbf {V}}{a_\mathbf {S}}\frac{{n_k}}{2} \right) =\mathrm {oe}({n_k}). \end{aligned}$$

From this it follows that $K^\mathbf {S}_{l_k,{n_k}}= \frac{a_\mathbf {V}}{a_\mathbf {S}} {n_k} (1+o(1))$ as $k\rightarrow \infty$, and then that

From this and (45), we obtain the following result.

Lemma 33

For every $\mathbf {S}\in \{\mathbf {E},\mathbf {F}\}$, and every $(l_k,n_k)_{k\ge 0}\in \mathscr {S}^\mathbf {S}_L$, one has

where $\Vert \cdot \Vert$ is the total variation norm.

Theorem 5 is now a direct consequence of this statement combined with (40).

8.3 Proof of the convergence of Boltzmann maps

This section is dedicated to the proof of Theorem 8. As in the proof of Theorem 5, we first focus on random maps with distribution $\mathbb {W}^\bullet _l$, which are easier to handle, since they are directly related by Proposition 23 to random labeled forests with law $\mathbb {M}_l$.

The result follows from the fact that, for any measurable and bounded function $\Phi$,

$$\begin{aligned} \mathbb {W}_l^\bullet [\Phi ]&=\sum _{n\in \mathcal {E}^\mathbf {V}_l}\mathbb {W}_l^\bullet \left( |\mathbf {V}|=n+1 \right) \,\mathbb {W}_{l,n}^{\bullet ,\mathbf {V}}[\Phi ] \nonumber \\&=\sum _{n\in \mathcal {E}^\mathbf {V}_l}\mathbb {M}_l \left( N^\mathbf {V}=n \right) \,\mathbb {W}_{l,n}^{\bullet ,\mathbf {V}}[\Phi ]. \end{aligned}$$

(46)

At this point, recall from Lemma 3 that $\mathcal {E}^\mathbf {V}_l= R^\mathbf {V}_l \cup (\beta ^\mathbf {V}l+h^\mathbf {V}\mathbb {Z}_+)$, where $\beta ^\mathbf {V}\ge 1$ and $R^\mathbf {V}_l\subseteq \{0,1,\ldots ,\beta ^\mathbf {V}l-1\}$. For simplicity, let us use the notation $\beta =\beta ^\mathbf {V}$ and $h=h^\mathbf {V}$. Therefore,

$$\begin{aligned} \mathbb {W}_l^\bullet [\Phi ]&=\sum _{n\ge 0}\mathbb {M}_l \left( N^\mathbf {V}=\beta l+h n \right) \,\mathbb {W}_{l,\beta l+h n}^{\bullet ,\mathbf {V}}[\Phi ] +\mathcal {R}_l\\&=\int _{\mathbb {R}_+}l^2Q^\mathbf {V}\left( l,\beta l+h\lfloor l^2A\rfloor \right) \, \mathbb {W}_{l,\beta l+h\lfloor l^2 A\rfloor }^{\bullet ,\mathbf {V}}[\Phi ]\,\mathrm {d}A +\mathcal {R}_l \end{aligned}$$

where $|\mathcal {R}_l|\le \Vert \Phi \Vert _\infty \mathbb {W}_l^\bullet (|\mathbf {V}|\le \beta l)$. Recall that, by Proposition 23 and definition of $\mathbb {M}_l$, under $\mathbb {W}_l^\bullet$, the random variable $|\mathbf {V}|-1$ has same distribution as a sum of l i.i.d. random variables with distribution $Q^\mathbf {V}(1,\cdot )$. The proof of Lemma 26 yields that, under $\mathbb {W}_l^\bullet$

where $\mathcal {A}^\bullet$ is a stable random variable with density $j_1$. Clearly, this implies that $\mathcal {R}_l \rightarrow 0$ as $l\rightarrow \infty$. Now assume that $\Phi =\varphi ((2l/3)^{-1/2}M)$ where $\varphi$ is a continuous and bounded function on the pointed Gromov–Hausdorff space. Then one has, by Theorem 5,

where the last equality follows from Remark 3. At this point, we apply Lemma 26, which implies that for every $A>0$,

The Scheffé Lemma (in fact a slight generalization, since the functions on the left-hand side are only sub-probability densities) implies that the latter convergence holds in fact in $L^1(\mathrm {d}A)$, and we conclude that

$$\begin{aligned} \lim _{l\rightarrow \infty }\mathbb {W}_l^\bullet \left[ \varphi \left( (2l/3)^{-1/2}M \right) \right]&= \int _{\mathbb {R}_+}h{\sigma _{\mathbf {V}}}^2j_1 \left( h{\sigma _{\mathbf {V}}}^2 A \right) \, \mathbb {E}\left[ \varphi \left( \mathrm {BD}_{1,h{\sigma _{\mathbf {V}}}^2 A} \right) \right] \, \mathrm {d}A\\&= \int _{\mathbb {R}_+} j_1(A)\mathbb {E}[\varphi (\mathrm {BD}_{1,A})]\,\mathrm {d}A \end{aligned}$$

and this is equal to $\mathbb {E}[\varphi (\mathrm {FBD}^\bullet _1)]$. The second part of Theorem 8 follows.

To obtain the result under $\mathbb {W}_l$ instead of $\mathbb {W}_l^\bullet$, note that (6) implies

$$\begin{aligned} \mathbb {W}_l(|\mathbf {V}|=n+1)=K_l\, \frac{\mathbb {W}^\bullet _l(|\mathbf {V}|=n+1)}{n+1} \end{aligned}$$

(47)

where $K_l=\mathbb {W}^\bullet _l[1/|\mathbf {V}|]^{-1}$. We then use the following lemma, which is certainly known, but for which we did not find a proper reference.

Lemma 34

Let $X_1$, $X_2$...be a sequence of i.i.d. r.v.s with values in $\{1,2,3,\ldots \}$, and such that

for some constants $c\in (0,\infty )$ and $\alpha \in (0,1)$. Then

where S is the limit in distribution of $(X_1+\cdots +X_l)/l^{1/\alpha }$ as $l\rightarrow \infty$ (so that S is a stable distribution of index $\alpha$).

Proof

By hypothesis and standard facts on stable domains of attractions [14, Chapter 8], our hypotheses imply that as $s\uparrow 1$,

$$\begin{aligned} \mathbb {E}[s^{X_1}]=1-c'(1-s)^\alpha (1+o(1)) \end{aligned}$$

for some constant $c'\in (0,\infty )$ depending only on c and $\alpha$. Applying this to $s=\exp (-\lambda )$ for $\lambda \ge 0$ implies that

$$\begin{aligned} \mathbb {E}[\exp (-\lambda X_1)]=1-c'\lambda ^\alpha (1+o(1)) \end{aligned}$$

as $\lambda \downarrow 0$, so that there exists $c''\in (0,\infty )$ such that for every $\lambda \in [0,1]$, one has

$$\begin{aligned} \mathbb {E}[\exp (-\lambda X_1)]&\le 1-c''\lambda ^\alpha \nonumber \\&\le \exp (-c''\lambda ^\alpha ). \end{aligned}$$

(48)

On the other hand, the assumption that $X_1\ge 1$ a.s. implies that $\mathbb {E}[\exp (-\lambda X_1)]\le \exp (-\lambda )$ for every $\lambda \ge 0$. This implies that, possibly by choosing $c''$ smaller, one can assume that (48) is valid for every $\lambda \ge 0$, as we supposed $\alpha \le 1$.

Now note that, for every $x>0$, one has (using the inequality $\mathbf {1}_{[0,1]}(u)\le e\, \exp (-u)$ in the first step)

$$\begin{aligned} \mathbb {P}\left( X_1+\cdots +X_l \le xl^{1/\alpha } \right)&\le e\, \mathbb {E}\left[ \exp \left( -(X_1+\cdots +X_l)/(xl^{1/\alpha }) \right) \right] \\&\le e\, \mathbb {E}\left[ \exp \left( -X_1/(xl^{1/\alpha }) \right) \right] ^l\\&\le e\, \exp (-c''x^{-\alpha }), \end{aligned}$$

where we used the version of (48) valid for all $\lambda$ at the last step. This stretched-exponential tail bound is uniform in l and clearly implies the convergence of all negative moments. $\square$

Since, as we observed, $|\mathbf {V}|-1$ under $\mathbb {W}^\bullet _l$ is distributed as a sum of l i.i.d. random variables satisfying the hypotheses of Lemma 34 with $\alpha =1/2$ (by Lemma 26), this entails that

$$\begin{aligned} \lim _{l\rightarrow \infty }\frac{K_l}{l^2}=\mathbb {E}\left[ \frac{{\sigma _{\mathbf {V}}}^2}{\mathcal {A}^\bullet }\right] ^{-1}=\frac{1}{{\sigma _{\mathbf {V}}}^2}. \end{aligned}$$

Repeating the previous argument, only changing $\mathbb {W}_l^\bullet (|\mathbf {V}|=n+1)$ by $\mathbb {W}_l(|\mathbf {V}|=n+1)$ in (46) and applying (47), and then performing the same steps using the asymptotics we obtained for $K_l$, we obtain that for $\phi$ a continuous bounded function on the (non-pointed) Gromov–Hausdorff space,

$$\begin{aligned} \lim _{l\rightarrow \infty }\mathbb {W}_l\left[ \varphi \left( (2l/3)^{-1/2}M \right) \right] = \int _{\mathbb {R}_+}\frac{h{\sigma _{\mathbf {V}}}^2}{h{\sigma _{\mathbf {V}}}^2 A} j_1 \left( h{\sigma _{\mathbf {V}}}^2 A \right) \, \mathbb {E}\left[ \varphi \left( \mathrm {BD}_{1,h{\sigma _{\mathbf {V}}}^2 A} \right) \right] \, \mathrm {d}A \end{aligned}$$

and this is $\mathbb {E}[\varphi (\mathrm {FBD_1})]$, as wanted.