Extremal eigenvalues and eigenvectors of deformed Wigner matrices

Abstract

We consider random matrices of the form $H = W + \lambda V, \lambda \in {\mathbb {R}}^+$, where $W$ is a real symmetric or complex Hermitian Wigner matrix of size $N$ and $V$ is a real bounded diagonal random matrix of size $N$ with i.i.d. entries that are independent of $W$. We assume subexponential decay of the distribution of the matrix entries of $W$ and we choose $\lambda \sim 1$, so that the eigenvalues of $W$ and $\lambda V$ are typically of the same order. Further, we assume that the density of the entries of $V$ is supported on a single interval and is convex near the edges of its support. In this paper we prove that there is $\lambda _+\in {\mathbb {R}}^+$ such that the largest eigenvalues of $H$ are in the limit of large $N$ determined by the order statistics of $V$ for $\lambda >\lambda _+$. In particular, the largest eigenvalue of $H$ has a Weibull distribution in the limit $N\rightarrow \infty$ if $\lambda >\lambda _+$. Moreover, for $N$ sufficiently large, we show that the eigenvectors associated to the largest eigenvalues are partially localized for $\lambda >\lambda _+$, while they are completely delocalized for $\lambda <\lambda _+$. Similar results hold for the lowest eigenvalues.

1 Introduction

The universality of random matrices is usually divided into bulk and edge universalities. Edge universality concerns the distribution of the extreme eigenvalues. It is known that the extreme eigenvalues of a large class of Wigner matrices exhibit universal limiting behavior. The limiting distribution of the largest eigenvalue was first identified by Tracy and Widom [48, 49] for the Gaussian ensembles. Edge universality for Wigner matrices has first been proved by Soshnikov [45] (see also [44]) for real symmetric and complex Hermitian ensembles with symmetric distributions. The symmetry assumption on the entries’ distribution was partially removed in [39, 40]. Edge universality without any symmetry assumption was proved in [47] under the condition that the distribution of the matrix elements has subexponential decay and its first three moments match those of the Gaussian distribution. For Wigner matrices with arbitrary symmetry class, edge universality was proven in [15] under the assumption that the entries have $12+\epsilon$ moments. Recently, a necessary and sufficient condition for the edge universality of Wigner matrices was given in [33].

The distribution of the largest eigenvalues of a random diagonal matrix $V$ whose entries $(v_i)$ are i.i.d. real random variables is given by the order statistics of $(v_i)$. The Fisher–Tippett–Gnedenko theorem (see e.g. [27]) thus implies that the limiting distribution of the largest eigenvalue of $V$ belongs either to the Gumbel, Fréchet or Weibull family.

In this paper, we consider the interpolation between Wigner matrices and real diagonal random matrices. Let $W$ be an $N\times N$ real symmetric or complex Hermitian Wigner matrix whose centered entries have variance $N^{-1}$ and subexponential decay. Let $V$ be an $N\times N$ real diagonal random matrix whose entries are bounded i.i.d. random variables. For $\lambda \in {\mathbb {R}}^+$ we set

$$\begin{aligned} H = (h_{ij}) \mathrel {\mathop :}=\lambda V + W,\quad (1\le i,j\le N). \end{aligned}$$

(1.1)

The matrices $V$ and $W$ are normalized in the sense that the eigenvalues of $V$ and $W$ are of order one.

If $W$ belongs to the Gaussian Unitary ensemble (GUE), the model (1.1) is called the deformed GUE. It was shown in [29, 43] that the edge eigenvalues of the deformed GUE are governed by the Tracy–Widom distribution for $\lambda \ll N^{-1/6}$. At $\lambda \sim N^{-1/6}$ the fluctuations of the edge eigenvalues change from the Tracy–Widom to a Gaussian distribution. More precisely, Johansson showed in [29] that the limiting distribution of the edge eigenvalues for $\lambda ={\alpha }{N^{-1/6}}$ is given by the convolution of the Tracy–Widom and the centered Gaussian distribution, with variance depending on $\alpha$. These results have not been established for the Gaussian orthogonal ensemble (GOE) or for general Wigner matrices.

In the present paper, we consider the edge behavior of the deformed model (1.1) in the regime $\lambda \sim 1$ with $W$ a real symmetric or complex Hermitian matrix. We show that there is, for certain $V$, yet another transition for the limiting behavior of the largest eigenvalues of $H$ as $\lambda$ varies. For simplicity, we assume that the distribution of the entries of $V$ is centered and given by the density

$$\begin{aligned} \mu (v)\mathrel {\mathop :}=Z^{-1} (1+v)^{\mathrm {a}}(1-v)^{\mathrm {b}} d(v){\mathbb {1}}_{[-1, 1]}(v), \end{aligned}$$

(1.2)

where $-1\le \mathrm {a}, \mathrm {b}<\infty$, $d$ is a strictly positive $C^1$-function and $Z$ is a normalization constant. We primarily focus on the choices $\mathrm {a},\mathrm {b}>1$. From our first main result, Theorem 2.7, it follows that there are $N$-independent constants $\lambda _+\equiv \lambda _{+}(\mu )>1$ and $L_+\equiv L_+(\mu ,\lambda )>2$, such that, for $\mathrm {b}>1$ and $\lambda > \lambda _+$, the largest eigenvalue $\mu _1$ of $H$ satisfies

$$\begin{aligned} \lim _{N\rightarrow \infty }\mathbb {P}( N^{1/(\mathrm {b}+1)} (L_+-\mu _1) \le x)=G_{\mathrm {b}+1}(x)\,,\qquad \mathrm {b}>1\,,\quad \lambda >\lambda _+, \end{aligned}$$

(1.3)

where $G_{\mathrm {b}+1}$ is a Weibull distribution with parameter $\mathrm {b}+1$; see (2.19).

However, if $\lambda <\lambda _+$, then there are $N$-independent constants $L_+\equiv L_+(\mu ,\lambda )$ and $c\equiv c(\mu ,\lambda )$, such that

$$\begin{aligned} \lim _{N\rightarrow \infty }\mathbb {P}( N^{1/2}( L_+ -\mu _1) \le x)=\Phi _c(x)\,,\qquad \mathrm {b}>1\,,\quad \lambda <\lambda _+, \end{aligned}$$

(1.4)

where $\Phi _c$ denotes the cumulative distribution function of the centered Gaussian distribution with variance $c$; see Sect. 4.3. In this case, i.e., for $\lambda <\lambda _+$, the location of the largest eigenvalue depends on the collective behavior of the random variables $(v_i)$, while it is determined by the largest $v_i$, for $\lambda >\lambda _+$; see Sect. 5. We remark that neither (1.3) nor (1.4) depend on the symmetry type of the Wigner matrix $W$.

The appearance of the Weibull distribution in the model (1.1) is indeed expected when $\lambda$ grows sufficiently fast with $N$, since in this case the diagonal matrix dominates the spectral properties of $H$. However, it is quite surprising that the Weibull distribution already appears for $\lambda$ order one, since the local behavior of the eigenvalues in the bulk of the deformed model mainly stems from the Wigner part, and the contribution from the random diagonal part is limited to mesoscopic fluctuations of the eigenvalues; see [31].

Having identified two possible limiting distributions of the largest eigenvalues, it is natural to ask about the behavior of the associated eigenvectors. Before considering the deformed model, we recall that the eigenvectors of Wigner matrices with subexponential decay are completely delocalized, as was proved by Erdős et al. [20, 21].

For deformed Wigner matrices we show that the eigenvectors of the largest eigenvalues are partially localized in the regime where the edge behavior (1.3) holds. More precisely, we prove that one component of the ($\ell ^2$-normalized) eigenvectors associated with eigenvalues at the extreme edge carries a weight of order one, while the other components each carry a weight of order $o(1)$; see Theorem 2.10. If, however, the edge behavior (1.4) holds, all eigenvectors are completely delocalized. Although we do not prove it explicitly, we claim that the bulk eigenvectors of the model (1.1) with (1.2) for the choice of $\mu$, are completely delocalized (for any choice of $\lambda \sim 1$). This can be proved with the very same methods as in [31]. To understand the transition from partial localization to delocalization, further efforts are required. Finally, we remark that there are some results on bulk universality for the deformed model (1.1); see [32, 36, 42].

The phenomenology described above is reminiscent of the one for heavy-tailed Wigner matrices. For instance, consider real symmetric Wigner matrices whose entries’ distribution function decays as a power law, i.e.,

$$\begin{aligned} {\mathbb {P}}(|h_{ij}| > x) = L(x) x^{-\alpha }\,,\qquad (1\le i,j\le N), \end{aligned}$$

(1.5)

for some slowly varying function $L(x)$. It was proved by Soshnikov [46] that the linear statistics of the largest eigenvalues are Poissonian for $\alpha < 2$; in particular, the largest eigenvalue has a Fréchet limit distribution. Later, Auffinger et al. [3] showed that the same conclusions hold for $2 \le \alpha < 4$ as well. Recently, it was proved by Bordenave and Guionnet [8] that the eigenvectors of models satisfying (1.5) are weakly delocalized for $1 < \alpha < 2$. For $0<\alpha <1$, it is conjectured [10] that there is a sharp “metal-insulator” transition. In [8] it is proved that the eigenvectors of sufficiently large eigenvalues are weakly localized for $0<\alpha <2/3$.

To clarify the terminology “partial localization” we remark that it is quite different from the usual notion of localization for random Schrödinger operators. The telltale signature of localization for random Schrödinger operators is an exponential decay of off-diagonal Green function entries, which implies the absence of diffusion, spectral localization etc. For the Anderson model in dimensions $d\ge 3$ such an exponential decay was first obtained by Fröhlich and Spencer [26] using a multiscale analysis. Later, a similar bound was presented by Aizenman and Molchanov [1] using fractional moments. Due to the mean-field nature of the Wigner matrix $W$, there is no notion of distance for the deformed model (1.1). Instead, our localization result states that most of the mass of the eigenvectors is concentrated on a few sites, whose locations are independent and uniformly distributed. This result agrees with the predictions of formal perturbation theory.

We also mention that the localization result we prove in this paper also differs from that for random band matrices, where all the eigenvectors are localized, even in the bulk. We refer to [13, 16, 41] for more details on the localization/delocalization for random band matrices.

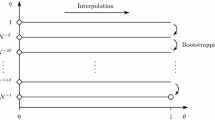
Next, we outline the proofs of our main results. It was first shown by Pastur [37] that the empirical eigenvalue distribution of the deformed model (1.1) converges to a deterministic distribution in the limit $N\rightarrow \infty$ under some weak assumption on $\lambda V$. However, this limiting eigenvalue distribution, referred to as the deformed semicircle law in the following, is in general different from Wigner’s semicircle law and depends on the limiting distribution of $\lambda V$. The deformed semicircle law can be defined in terms of a functional equation for the Stieltjes transforms of the limiting eigenvalue distributions of $\lambda V$ and $W$ [37]. Restricting the discussion to the special case when the entries of $V$ follow the centered Jacobi distribution in (1.2) with $\mathrm {b}>1$, we showed in [31] that the deformed semicircle law, henceforth denoted by $\mu _{fc}$, is supported on a single interval and shows either of the following behavior close to the upper edge:

$$\begin{aligned} \mu _{fc}(E)\sim {\left\{ \begin{array}{ll} \sqrt{\kappa _E}\,,\quad &{}\mathrm for \,\lambda <\lambda _+,\\ (\kappa _E)^{\mathrm {b}}\,,&{}\mathrm for \, \lambda >\lambda _+, \end{array}\right. } \end{aligned}$$

(1.6)

for $E\in {{\mathrm{supp}}}\mu _{fc}$, $E\ge 0$, where $\kappa _E$ denotes the distance from $E$ to the upper endpoint of the support of $\mu _{fc}$; see Lemma 2.3 below. In case the square root behavior prevails, we are going to show that the largest eigenvalue of $H$ satisfies (1.4), whereas in case we have a “convex decay” with $\mathrm {b}>1$, (1.3) is satisfied.

In a first step, we derive a local law for the empirical eigenvalue density: Under some moment conditions the convergence of the empirical eigenvalue distribution to the semicircle law also holds on very small scales. Denoting by $G(z)=(H-z)^{-1}$, $z\in {\mathbb {C}}^+$, the Green function or resolvent of $H$, convergence of the empirical eigenvalue distribution on scale $\eta$ around an energy $E\in {\mathbb {R}}$ is equivalent to the convergence of the averaged Green function $m(z)=N^{-1}{{\mathrm{Tr}}}G(z)$, $z=E+\mathrm {i}\eta$. In a series of papers [20–22] Erdős, Schlein and Yau showed that the semicircle law for Wigner matrices also holds down to the optimal scale $1/N$, up to logarithmic corrections. In [24] a “fluctuation average lemma” was introduced that yielded optimal bounds on the convergence of $m(z)$ for Wigner matrices in the bulk [24] and up to the edge [25] on scales $\eta \gg N^{-1}$. Below this scale the eigenvalue density remains fluctuating even for large $N$. In [25] the Green function $G(z)$ and its average $m(z)$ have been used to prove edge universality for generalized Wigner matrices. In [31] we derived a local deformed semicircle law for the deformed ensemble (1.1) under the assumption that $\mu _{fc}$ has a square root behavior at the endpoints. In the present paper, we derive a local law at the extreme edge in case $\mu _{fc}$ shows a convex decay at the edge. We propose, however, a slightly different path than the one taken in [31]: We condition on the random variables $(v_i)$ and show that $m(z)$ converges, for “typical” realizations of $(v_i)$, on scale $\sim N^{-1/2}$; see Proposition 5.1. In particular, we show that the typical eigenvalue spacing at the extreme edge is of order $N^{-1/(\mathrm {b}+1)}\gg N^{-1/2}$; as is suggested by the convex decay in (1.6). Similar to the Wigner case, see e.g., [25], this is accomplished by deriving a self-consistent equation for $m(z)$. However, the analysis of the self-consistent equation is quite different from the Wigner case, due to the absence of the usual stability bound; see [31].

In a second step, we can use the self-averaging property of the Wigner matrix $W$, to show that the imaginary part of $m$ can be controlled on scales much smaller than $N^{-1/2}$: the technical input here is the “fluctuation averaging lemma” [17, 18, 25]. Our proof relies on the basic strategy of [17]. However, in our setup the diagonal entries of $G$ are not uniformly bounded, which requires several changes to previous arguments. To complete the proof of our first main result, Theorem 2.10, we note that the imaginary part of $m$ can be written as

$$\begin{aligned} {\mathrm {Im }}\,m(E+\mathrm {i}\eta )=\frac{1}{N}\sum _{\alpha =1}^N\frac{\eta }{(\mu _\alpha -E)^2+\eta ^2}\,,\quad \qquad (E\in {\mathbb {R}}\,,\eta >0), \end{aligned}$$

(1.7)

where $(\mu _\alpha )$ are the eigenvalues of $H$. Thus, having control on the left side for $\eta \ll N^{-1/2}$ allows tracking the individual eigenvalues at the extreme edge, where their typical spacing much bigger than $N^{-1/2}$.

Finally, we point out the main steps in the proof of the partial localization of eigenvectors; see Theorem 2.10 for precise results. It is well-known that information on the averaged Green function $m(z)$ can be translated via the Helffer–Sjöstrand formula to information on the density of states; see, e.g., [19]. Since the typical eigenvalue spacing at the edge is, for the case at hand, much larger than $N^{-1/2}$, the Helffer–Sjöstrand formula also allows to translate information on the diagonal Green function entries $(G_{ii}(z))$ into information on the eigenvectors at the edge. Relying on estimates on the Green function, we can then prove “partial localization” of the eigenvectors at the edge.

The paper is organized as follows: In Sect. 2, we introduce the precise definition of the model and state the main results of the paper. In Sect. 3, we collect basic notations and identities for the resolvent of $H$. In Sect. 4, we prove the first main result of the paper, Theorem 2.7, using estimates on the Stieltjes transform of the deformed semicircle measure. (See also Corollary 4.6.) In Sects. 5 and 6, we prove important lemmas on the location of the extreme eigenvalues, including the local law, which have crucial roles in the proof of Theorem 2.7. In Sect. 7, we prove the second main result of the paper, Theorem 2.10, on the partial localization of the eigenvectors at the edge. Proofs of some technical lemmas are collected in the Appendices A, B and C.

2 Definition and results

In this section, we define our model and state our main results.

2.1 Deformed semicircle law

For a (probability) measure, $\omega$, on ${\mathbb {R}}$, we define its Stieltjes transform by

$$\begin{aligned} m_{\omega }(z)\mathrel {\mathop :}=\int _{{\mathbb {R}}}\frac{\mathrm {d}\omega (x)}{x-z},\quad (z\in {\mathbb {C}}^+). \end{aligned}$$

(2.1)

Note that $m_{\omega }(z)$ is an analytic function in the upper half plane, satisfying ${\mathrm {Im }}\,m_{\omega }(z)\ge 0$, $z\in {\mathbb {C}}^+$.

As first shown in [37], the Stieltjes transform of the limiting spectral distribution of the interpolating model (1.1) satisfies the equation

$$\begin{aligned} m_{fc}(z)=\int _{\mathbb {R}}\frac{\mathrm {d}\mu (v)}{\lambda v-z-m_{fc}(z)},\quad {\mathrm {Im }}\,m_{fc}(z)\ge 0,\qquad \quad (z\in {\mathbb {C}}^+), \end{aligned}$$

(2.2)

where $\mu$ is the distribution of the i.i.d. random variables $(v_i)$. Equation (2.2) is often called the Pastur relation. It is shown in [7, 37] that (2.2) has a unique solution. Moreover, it is easy to check that $\limsup _{\eta \searrow 0} {\mathrm {Im }}\,m_{fc}(E+\mathrm {i}\eta )<\infty$, thus $m_{fc}(z)$ determines an absolutely continuous probability measure on ${\mathbb {R}}$, whose density, $\mu _{fc}$, is given by

$$\begin{aligned} \mu _{fc}(E)=\frac{1}{\pi }\lim _{\eta \searrow 0} {\mathrm {Im }}\,m_{fc}(E+\mathrm {i}\eta ),\quad \quad (E\in {\mathbb {R}}). \end{aligned}$$

(2.3)

The measure $\mu _{fc}$ has been studied in details in [7]; for example, it was shown that the function $m_{fc}$, a priori defined on ${\mathbb {C}}^+$, has a continuous extension to ${\mathbb {C}}^+\cup {\mathbb {R}}$ and that $\mu _{fc}$ is an analytic function inside its support. Below we use the notation $m_{fc}(E)=\lim _{\eta \searrow 0} m_{fc}(E+\mathrm {i}\eta )$, $E\in {\mathbb {R}}$. Finally, note that $\mu _{fc}$ converges weakly to the standard semicircle law, $\mu _{sc}$, as $\lambda \rightarrow 0$.

Remark 2.1

The measure $\mu _{fc}$ is often called the additive free convolution of the semicircular law and the measure $\mu$ (up to the scaling by $\lambda$). More generally, the additive free convolution of two (probability) measures $\omega _1$ and $\omega _2$, usually denoted by $\omega _1\boxplus \omega _2$, is defined as the distribution of the sum of two freely independent non-commutative random variables, having distributions $\omega _1$, $\omega _2$ respectively; we refer to [2, 28, 34, 50]. Similarly to (2.2), the free convolution measure $\omega _1\boxplus \omega _2$ can be described in terms of a set of functional equations for the Stieltjes transforms; see [5, 11, 38]. For a discussion of regularity properties of $\omega _1\boxplus \omega _2$ we refer to [4].

Free probability theory turned out to be a natural setting for studying global laws for such ensembles; see, e.g., [2, 50]. For more recent treatments, including local laws, we refer to [6, 9, 30].

2.2 Definition of the model

Definition 2.2

Let $W$ be an $N\times N$ random matrix, whose entries, $(w_{ij})$, are independent, up to the symmetry constraint $w_{ij}=\overline{w_{ji}}$, centered, real (complex) random variables with variance $N^{-1}$ and with subexponential decay, i.e.,

$$\begin{aligned} {\mathbb {P}}{\left( \sqrt{N} |w_{ij}|>x \right) } \le C_0 {\mathrm {e}}^{-x^{1/\theta }}, \end{aligned}$$

(2.4)

for some positive constants $C_0$ and $\theta >1$. In particular, if $(w_{ij})$ are complex random variables,

$$\begin{aligned}&{\mathbb {E}}w_{ij}=0,\qquad \quad {\mathbb {E}}|w_{ij}|^2 = \frac{1}{N}, \qquad \quad {\mathbb {E}}w_{ij}^2 = 0,\nonumber \\&{\mathbb {E}}|w_{ij}|^p \le C \frac{(\theta p)^{\theta p}}{N^{p/2}}, \qquad (p \ge 3); \end{aligned}$$

(2.5)

if $(w_{ij})$ are real random variables,

$$\begin{aligned} {\mathbb {E}}w_{ij}=0,\qquad \quad {\mathbb {E}}w_{ij}^2 = \frac{1+\delta _{ij}}{N}, \qquad \quad {\mathbb {E}}|w_{ij}|^p \le C \frac{(\theta p)^{\theta p}}{N^{p/2}},\qquad (p \ge 3). \end{aligned}$$

(2.6)

Let $V$ be an $N\times N$ diagonal random matrix, whose entries $(v_i)$ are real, centered, i.i.d. random variables, independent of $W=(w_{ij})$, with law $\mu$. More assumptions on $\mu$ will be stated below. Without loss of generality, we assume that the entries of $V$ are ordered,

$$\begin{aligned} v_1 \ge v_2 \ge \dots \ge v_N. \end{aligned}$$

(2.7)

For $\lambda \in {\mathbb {R}}^+$, we consider the random matrix

$$\begin{aligned} H = (h_{ij}) \mathrel {\mathop :}=\lambda V + W. \end{aligned}$$

(2.8)

We choose $\mu$ as a Jacobi measure, i.e., $\mu$ is described in terms of its density

$$\begin{aligned} \mu (v)= Z^{-1} (1+v)^{\mathrm {a}}(1-v)^{\mathrm {b}} d(v){\mathbb {1}}_{[-1, 1]}(v), \end{aligned}$$

(2.9)

where $\mathrm {a},\mathrm {b}>-1$, $d\in C^1 ([-1, 1])$ such that $d(v)>0$, $v \in [-1, 1]$, and $Z$ is an appropriately chosen normalization constant. We assume, for simplicity of the arguments, that $\mu$ is centered, but this condition can easily be relaxed. We remark that the measure $\mu$ has support $[-1,1]$, but we observe that varying $\lambda$ is equivalent to changing the support of $\mu$. Since $\mu$ is absolutely continuous, we may assume that (2.7) holds with strict inequalities.

2.3 Edge behavior of $\mu _{fc}$

Properties of $\mu _{fc}$ with the special choice (2.9) for $\mu$ and with $\lambda \sim 1$, have been studied in [31]; see also [7, 43]. For example, the support of $\mu _{fc}$ consists of a single interval. For $E\in {\mathbb {R}}$, we denote by $\kappa _E$ the distance to the endpoints support of $\mu _{fc}$, i.e.,

$$\begin{aligned} \kappa _E\mathrel {\mathop :}=\min \{|E-L_-|,|E-L_+|\},\qquad {{\mathrm{supp}}}\,\mu _{fc} =[L_-,L_+],\quad \qquad (E\in {\mathbb {R}}). \end{aligned}$$

(2.10)

In the following we will often abbreviate $\kappa \equiv \kappa _E$.

In the present paper, we are mainly interested in the limiting behavior of the largest, respectively smallest, eigenvalues of the interpolating matrix (2.8), for $\lambda \sim 1$. For concreteness, we focus on the upper edge and comment on the lower edge in Remark 2.6. The following lemma is taken from [31]; see also [7, 35, 43] for statement (1).

Lemma 2.3

Let $\mu$ be a centered Jacobi measure defined in (2.9) with $\mathrm {b}>1$. Define

$$\begin{aligned} \lambda _+ \mathrel {\mathop :}={\left( \int _{-1}^1 \frac{\mu (v)\mathrm {d}v}{(1-v)^2}\right) }^{1/2}, \qquad \quad \tau _+ \mathrel {\mathop :}=\int _{-1}^1 \frac{\mu (v) \mathrm {d}v}{1-v}. \end{aligned}$$

(2.11)

Then, there exist $L_- < 0 <L_+$ such that the support of $\mu _{fc}$ is $[L_-,L_+]$. Moreover,

• (1) if $\lambda <\lambda _+$, then for $0 \le \kappa \le L_+$,

  $$\begin{aligned} C^{-1}\sqrt{\kappa } \le \mu _{fc}(L_+-\kappa ) \le C \sqrt{\kappa }, \end{aligned}$$

  (2.12)

  for some $C \ge 1$;

• (2) if $\lambda >\lambda _+$, then $L_+ = \lambda +(\tau _+/\lambda )$ and, for $0 \le \kappa \le L_+$,

  $$\begin{aligned} C^{-1}{\kappa }^{\mathrm {b}} \le \mu _{fc}(L_+-\kappa ) \le C \kappa ^{\mathrm {b}}, \end{aligned}$$

  (2.13)

  for some $C \ge 1$. Moreover, $L_+$ satisfies $L_++m_{fc}(L_+)=\lambda$.

Remark 2.4

Since

$$\begin{aligned} \tau _+ =\int _{-1}^1 \frac{\mu (v) \mathrm {d}v}{1-v} > \int _{-1}^1 (1+v) \mu (v) \mathrm {d}v = 1, \end{aligned}$$

(2.14)

we find that $L_+ > \lambda + (1/\lambda ) \ge 2$. Similarly, we also have that $L_- \le -2$.

Remark 2.5

When $-1 < \mathrm {a}, \mathrm {b}\le 1$, there exist, for any $\lambda \in {\mathbb {R}}^+, L_-<0<L_+$ such that ${{\mathrm{supp}}}\,\mu _{fc}=[L_-,L_+]$. In fact, for $\mathrm {b}\le 1$, the first integral in (2.11) diverges and for any $\lambda <\infty$ there exists $C\ge 1$ such that

$$\begin{aligned} C^{-1}\sqrt{\kappa _E}\le \mu _{fc}(E)\le C\sqrt{\kappa _E}\,,\quad \quad E\in [L_-,L_+]. \end{aligned}$$

(2.15)

For $\mathrm {b}>1$ the first integral in (2.11) is finite and we have $\lambda _+<\infty$. Either way, for $\lambda <\lambda _+$, the square root behavior of $\mu _{fc}$ follows from the “stability bound” $|\lambda -z-m_{fc}(z)|\ge c$, for some $c>0$. In particular, the integrand on the right side of (2.2) is non-singular and the main contributions to the integral come from the bulk. However, for $\lambda >\lambda _+$, $|\lambda -z-m_{fc}(z)|$ is not bounded uniformly away from zero, for $z$ close to the edge, and the integral on the right side of (2.2) is sensible to the specific decay of $\mu$ for such $z$: Setting $\tau \mathrel {\mathop :}=z+m_{fc}(z)$, we find that the leading contribution to the integral, for $z$ close to $L_+$, is roughly $(\tau -1)^{\mathrm {b}}$. We hence expect that ${\mathrm {Im }}\,m_{fc}(z)\sim \kappa ^\mathrm {b}+\eta$, for $z$ close to $L_+$. For more details, we refer to [31].

If $\mathrm {a}\le 1 < \mathrm {b}$ or $\mathrm {b}\le 1 < \mathrm {a}$, the analogous statement to (2.15) holds only at the lower edge or at the upper edge, respectively. These results can be proved using the methods of [43]; see [31] for more details.

Remark 2.6

For $\mathrm {a}>1$, the analogue statements to Lemma 2.3 hold for the lower endpoint $L_-$ of the support of $\mu _{fc}$, with $\lambda _+$ and $\tau _+$ replaced by

$$\begin{aligned} \lambda _- \mathrel {\mathop :}={\left( \int _{-1}^1 \frac{\mu (v)\mathrm {d}v}{(1+v)^2}\right) }^{1/2}\,,\qquad \tau _- \mathrel {\mathop :}=\int _{-1}^1 \frac{\mu (v) \mathrm {d}v}{1+v}. \end{aligned}$$

(2.16)

In [31], spectral properties of the interpolating matrix (2.8) were analyzed in detail under the assumption that (2.15) holds, i.e., it was assumed that either $\lambda$ is sufficiently small or $\mathrm {a},\mathrm {b}\le 1$.

2.4 Main results

Denote by $(\mu _i)$ the ordered eigenvalues of the matrix $H=\lambda V+W$,

$$\begin{aligned} \mu _1 \ge \mu _2 \ge \dots \ge \mu _N. \end{aligned}$$

In the following, we fix some $n_0\in {\mathbb {N}}$, independent of $N$, and consider the largest eigenvalues $(\mu _i)_{i=1}^{n_0}$ of $H$. All our results also apply mutatis mutandis to the smallest eigenvalues $(\mu _i)_{i=N-n_0}^N$ of $H$ as can readily be checked.

2.4.1 Eigenvalue statistics

The first main result of the paper shows that the locations of the extreme eigenvalues are determined by the order statistics of the diagonal elements $(v_i)$. Recall that we denote by $\mu$ the distribution of the (unordered) centered random variables $(v_i)$.

Theorem 2.7

Let $W$ be a real symmetric or complex Hermitian Wigner matrix, satisfying the assumptions in Definition 2.2. Assume that the distribution $\mu$ is given by (2.9) with $b>1$ and fix some $\lambda >\lambda _+$; see (2.11). Let $n_0>10$ be a fixed constant independent of $N$, denote by $\mu _i$ the $i$-th largest eigenvalue of $H=\lambda V+W$ and let $1\le k<n_0$. Then the joint distribution function of the $k$ largest rescaled eigenvalues,

$$\begin{aligned}&{\mathbb {P}}{\left( N^{1/(\mathrm {b}+1)} (L_+ - \mu _1)\le s_1,\, N^{1/(\mathrm {b}+1)} (L_+ - \mu _2)\right. }\nonumber \\&{\left. \quad \le s_2,\, \ldots ,\, N^{1/(\mathrm {b}+1)} (L_+ - \mu _k)\le s_k\right) }, \end{aligned}$$

(2.17)

converges to the joint distribution function of the $k$ largest rescaled order statistics of $(v_i)$,

$$\begin{aligned}&{\mathbb {P}}{\left( C_\lambda N^{1/(\mathrm {b}+1)} (1-v_1)\le s_1,\,C_\lambda N^{1/(\mathrm {b}+1)} (1-v_2)\right. }\nonumber \\&{\left. \quad \le s_2,\, \ldots ,\,C_\lambda N^{1/(\mathrm {b}+1)} (1-v_k)\le s_k\right) }, \end{aligned}$$

(2.18)

as $N \rightarrow \infty$, where $C_\lambda = \frac{\lambda ^2 - \lambda _+^2}{\lambda }$. In particular, the cumulative distribution function of the rescaled largest eigenvalue $N^{1/(\mathrm {b}+1)} (L_+ - \mu _1)$ converges to the cumulative distribution function of the Weibull distribution,

$$\begin{aligned} G_{\mathrm {b}+1}(s)\mathrel {\mathop :}=1 - \exp {\left( -\frac{C_{\mu } s^{\mathrm {b}+1}}{(\mathrm {b}+1)}\right) }, \end{aligned}$$

(2.19)

where

$$\begin{aligned} C_{\mu } \mathrel {\mathop :}={\left( \frac{\lambda }{\lambda ^2 - \lambda _+^2}\right) }^{\mathrm {b}+1} \lim _{v \rightarrow 1} \frac{\mu (v)}{(1-v)^{\mathrm {b}}}. \end{aligned}$$

In Sect. 5 we obtain estimates on the speed of convergence of (2.17); see Corollary 4.6.

Remark 2.8

For $\lambda >\lambda _+$, the typical size of the fluctuations of the largest eigenvalues is of order $N^{-1/(\mathrm {b}+1)}$ (with $\mathrm {b}>1$) as we can see from Theorem 2.7. For $\lambda < \lambda _+$, on the other hand, the fluctuations for the largest eigenvalue become, in the limit $N\rightarrow \infty$, Gaussian with standard deviation of order $N^{-1/2}$; see Sect. 4.3 for more detail.

Remark 2.9

Theorem 2.7 shows that the extreme eigenvalues of $H$ become, for $\lambda >\lambda _+$, uncorrelated in the limit $N\rightarrow \infty$. In fact, extending the methods presented in this paper (by choosing $n_0\lesssim N^{1/(\mathrm {b}+1)}$), one can show that the point process defined by the (unordered) rescaled extreme eigenvalues of $H$ converges in distribution to an inhomogeneous Poisson point process on ${\mathbb {R}}^+$ with intensity function determined by $\lambda$ and $\mu$.

2.4.2 Eigenvectors behavior

Our second main result asserts that the eigenvectors associated with the largest eigenvalues are “partially localized” for $\lambda >\lambda _+$. We denote by $(u_k(j))_{j=1}^N$ the components of the eigenvector $u_k$ associated to the eigenvalue $\mu _k$. All eigenvectors are normalized as $\sum _{j=1}^N|u_k(j)|^2=\Vert u_k\Vert _2^2=1$.

Theorem 2.10

Let $W$ be a real symmetric or complex Hermitian Wigner matrix satisfying the assumptions in Definition 2.2. Assume that the distribution $\mu$ is given by (2.9) with $b>1$ and fix some $\lambda >\lambda _+$; see (2.11). Let $n_0>10$ be a fixed constant independent of $N$. Then there exist constants $\delta , \delta ',\sigma >0$, depending only on $\mathrm {b}$, $\lambda$ and $\mu$, such that

$$\begin{aligned} {\mathbb {P}}{\left( \left| |u_k (k)|^2 - \frac{\lambda ^2 - \lambda _+^2}{\lambda ^2}\right| > N^{-\delta }\right) }\le N^{-\sigma }\,,\quad \qquad (1\le k\le n_0-1), \end{aligned}$$

(2.20)

and

$$\begin{aligned} {\mathbb {P}}{\left( |u_k (j)|^2 > \frac{N^{\delta '}}{N^{}} \frac{1}{\lambda ^2 |v_k - v_j|^2}\right) }\le N^{-\sigma }\,,\quad \qquad (1\!\le \! j\!\le \! N\,,1\!\le \! k\!\le \! n_0\!-\!1, j\ne k). \end{aligned}$$

(2.21)

In Sect. 7 we obtain explicit expressions for the constants $\delta , \delta ',\sigma >0$.

Remark 2.11

In the preceding paper [31], we proved that all eigenvectors are completely delocalized when $\lambda < \lambda _+$. This shows the existence of a sharp transition from the partial localization to the complete delocalization regime. We say that an eigenvalue $\mu _i$ is in the bulk of the spectrum of $H$ if $i\in [\epsilon N,(1-\epsilon )N]$, for any (small) $\epsilon >0$ and sufficiently large $N$. Following the proof in [31], can prove that the eigenvectors associated to eigenvalues in the bulk are completely delocalized if $\lambda > \lambda _+$.

Assuming that $\mu$ is given by (2.9) with $\mathrm {b}\le 1$ (and $\mathrm {a}\le 1$), we showed in [31] that all eigenvectors of $H$ are completely delocalized up to the edge.

Remark 2.12

Theorems 2.7 and 2.10 remain valid for deterministic potentials $V$, provided the entries $(v_i)$ satisfy some suitable assumptions; see Definition 3.5 in Sect. 4 for details.

Remark 2.13

From (2.20) we find

$$\begin{aligned} \sum _{j:j \ne k}^N |u_k (j)|^2 = \frac{\lambda _+^2}{\lambda ^2} + o(1),\qquad (1\le k \le n_0-1), \end{aligned}$$

which is in accordance with the fact that (2.21) holds and that, typically,

$$\begin{aligned} \frac{1}{N} \sum _{j:j \ne k}^N \frac{1}{\lambda ^2 |v_k - v_j|^2} = \frac{\lambda _+^2}{\lambda ^2} + o(1),\qquad (1\le k \le n_0-1), \end{aligned}$$

where we used (2.18).

In the remaining sections, we prove Theorems 2.7 and 2.10. We state our proofs for complex Hermitian matrices. The real symmetric case can be dealt with in the same way.

3 Preliminaries

In this section, we collect basic notations and identities.

3.1 Notations

For high probability estimates we use two parameters $\xi \equiv \xi _N$ and $\varphi \equiv \varphi _N$: We let

$$\begin{aligned} \xi = 10 \log \log N\,, \qquad \varphi =(\log N)^C, \end{aligned}$$

(3.1)

for some fixed constant $C \ge 1$.

Definition 3.1

We say an event $\Omega$ has $(\xi ,\nu )$-high probability, if

$$\begin{aligned} {\mathbb {P}}(\Omega ^c) \le {\mathrm {e}}^{-\nu (\log N)^{\xi }}, \end{aligned}$$

for $N$ sufficiently large. Similarly, for a given event $\Omega _0$ we say an event $\Omega$ holds with $(\xi ,\nu )$-high probability on $\Omega _0$, if

$$\begin{aligned} {\mathbb {P}}(\Omega _0\cap \Omega ^c) \le {\mathrm {e}}^{-\nu (\log N)^{\xi }}, \end{aligned}$$

for $N$ sufficiently large.

For brevity, we occasionally say an event holds with high probability, when we mean with $(\xi ,\nu )$-high probability. We do not keep track of the explicit value of $\nu$ in the following, allowing $\nu$ to decrease from line to line such that $\nu >0$. From our proof it becomes apparent that such reductions occur only finitely many times.

We define the resolvent, or Green function, $G(z)$, and the averaged Green function, $m(z)$, of $H$ by

$$\begin{aligned} G(z) = (G_{ij}(z)) \mathrel {\mathop :}=\frac{1}{H-z} = \frac{1}{\lambda V+W-z},\quad m(z) \mathrel {\mathop :}=\frac{1}{N} {{\mathrm{Tr}}}G(z), \quad \quad (z \in {\mathbb {C}}^{+}). \end{aligned}$$

(3.2)

Frequently, we abbreviate $G \equiv G(z)$, $m\equiv m(z)$, etc. We refer to $z$ as spectral parameter and often write $z=E+\mathrm {i}\eta$, $E\in {\mathbb {R}}$, $\eta >0$.

We will use double brackets to denote the index set, i.e., for $n_1, n_2 \in {\mathbb {R}}$,

$$\begin{aligned}{}[\![n_1, n_2 ]\!]\mathrel {\mathop :}=[n_1, n_2] \cap {\mathbb {Z}}. \end{aligned}$$

We use the symbols ${\mathcal {O}}(\,\cdot \,)$ and $o(\,\cdot \,)$ for the standard big-O and little-o notation. The notations ${\mathcal {O}}$, $o$, $\ll$, $\gg$, refer to the limit $N \rightarrow \infty$ unless otherwise stated, where the notation $a \ll b$ means $a=o(b)$. We use $c$ and $C$ to denote positive constants that do not depend on $N$. Their value may change from line to line. Finally, we write $a \sim b$, if there is $C \ge 1$ such that $C^{-1}|b| \le |a| \le C |b|$, and, occasionally, we write for $N$-dependent quantities $a_N \lesssim b_N$, if there exist constants $C, c >0$ such that $|a_N| \le C(\varphi _N)^{c\xi }|b_N|$.

3.2 Minors

Let ${\mathbb {T}}\subset [\![1, N ]\!]$. Then we define $H^{({\mathbb {T}})}$ as the $(N-|{\mathbb {T}}|)\times (N-|{\mathbb {T}}|)$ minor of $H$ obtained by removing all columns and rows of $H$ indexed by $i\in {\mathbb {T}}$. Note that we do not change the names of the indices of $H$ when defining $H^{({\mathbb {T}})}$. More specifically, we define an operation $\pi _i$, $i\in [\![1, N ]\!]$, on the probability space by

$$\begin{aligned} (\pi _i(H))_{kl}\mathrel {\mathop :}={\mathbb {1}}(k\not =i){\mathbb {1}}(l\not =i)h_{kl}. \end{aligned}$$

(3.3)

Then, for ${\mathbb {T}}\subset [\![1, N ]\!]$, we set $\pi _{{\mathbb {T}}}\mathrel {\mathop :}=\prod _{i\in {\mathbb {T}}}\pi _i$ and define

$$\begin{aligned} H^{({\mathbb {T}})}\mathrel {\mathop :}=((\pi _{{\mathbb {T}}}(H)_{ij})_{i,j\not \in {\mathbb {T}}}. \end{aligned}$$

(3.4)

The Green functions $G^{({\mathbb {T}})}$, are defined in an obvious way using $H^{({\mathbb {T}})}$. Moreover, we use the shorthand notation

$$\begin{aligned} \sum _{i}^{({\mathbb {T}})}\mathrel {\mathop :}=\sum _{\begin{array}{c} i=1\\ i\not \in {\mathbb {T}} \end{array}}^N\,\,,\qquad \qquad \sum _{i\not =j}^{({\mathbb {T}})}\mathrel {\mathop :}=\sum _{\begin{array}{c} i=1,\, j=1\\ i\not =j\,,\,i,j\not \in {\mathbb {T}} \end{array}}^N, \end{aligned}$$

(3.5)

abbreviate $(i)=(\{i\}), ({\mathbb {T}}i)=({\mathbb {T}}\cup \{i\})$ and use the convention $({\mathbb {T}}\backslash i)= ({\mathbb {T}}\backslash \{i\})$, if $i\in {\mathbb {T}}$, $({\mathbb {T}}\backslash i)=({\mathbb {T}})$, else. In Green function entries $(G_{ij}^{({\mathbb {T}})})$ we refer to $\{i,j\}$ as lower indices and to ${\mathbb {T}}$ as upper indices.

Finally, we set

$$\begin{aligned} m^{({\mathbb {T}})}\mathrel {\mathop :}=\frac{1}{N}\sum _{i}^{({\mathbb {T}})}G_{ii}^{({\mathbb {T}})}. \end{aligned}$$

(3.6)

Here, we use the normalization $N^{-1}$, instead $(N-|{\mathbb {T}}|)^{-1}$, since it is more convenient for our computations.

3.3 Resolvent identities

The next lemma collects identities between resolvent matrix elements of $H$ and $H^{({\mathbb {T}})}$.

Lemma 3.2

Let $H=H^*$ be an $N\times N$ matrix. Consider the Green function $G(z)\equiv G\mathrel {\mathop :}=(H-z)^{-1}$, $z\in {\mathbb {C}}^+$. Then, for $i,j,k,l\in [\![1,N]\!]$, the following identities hold:

• Schur complement/Feshbach formula: For any $i$,

  $$\begin{aligned} G_{ii}=\frac{1}{h_{ii}-z-\sum _{k,l}^{(i)}{h_{ik} G_{kl}^{(i)}}h_{li}}. \end{aligned}$$

  (3.7)

• For $i\not =j$,

  $$\begin{aligned} G_{ij}=-G_{ii}G_{jj}^{(i)}{\left( h_{ij}-\sum _{k,l}^{(ij)}h_{ik} G_{kl}^{(ij)}h_{lj}\right) }. \end{aligned}$$

  (3.8)

• For $i\not =j$,

  $$\begin{aligned} G_{ij}=-G_{ii}\sum _{k}^{(i)}h_{ik}G_{kj}^{(i)}=-G_{jj}\sum _{k}^{(j)} G_{ik}^{(j)} h_{kj}. \end{aligned}$$

  (3.9)

• For $i,j\not =k$,

  $$\begin{aligned} G_{ij}=G_{ij}^{(k)}+\frac{G_{ik}G_{kj}}{G_{kk}}. \end{aligned}$$

  (3.10)

• Ward identity: For any $i$,

  $$\begin{aligned} \sum _{j=1}^N|G_{ij}|^2=\frac{1}{\eta }{\mathrm {Im }}\,G_{ii}, \end{aligned}$$

  (3.11)

  where $\eta ={\mathrm {Im }}\,z$.

For a proof we refer to, e.g., [14].

Lemma 3.3

There is a constant $C$ such that, for any $z \in {\mathbb {C}}^+$, $i\in [\![1,N]\!]$, we have

$$\begin{aligned} |m(z)-m^{(i)}(z)|\le \frac{C}{N\eta }. \end{aligned}$$

(3.12)

The lemma follows from Cauchy’s interlacing property of eigenvalues of $H$ and its minor $H^{(i)}$. For a detailed proof we refer to [12]. For ${\mathbb {T}}\subset [\![1,N]\!]$, with, say, $|{\mathbb {T}}|\le 10$, we obtain $|m-m^{({\mathbb {T}})}|\le \frac{C}{N\eta }$.

3.4 Large deviation estimates

We collect here some useful large deviation estimates for random variables with slowly decaying moments.

Lemma 3.4

Let $(a_i)$ and $(b_i)$ be centered and independent complex random variables with variance $\sigma ^2$ and having subexponential decay

$$\begin{aligned} \mathbb {P}{\left( |a_i|\ge x\sigma \right) }\le C_0\, \mathrm {e}^{-x^{1/\theta }}\,,\qquad \mathbb {P}{\left( |b_i|\ge x\sigma \right) }\le C_0\,\mathrm {e}^{-x^{1/\theta }}, \end{aligned}$$

(3.13)

for some positive constants $C_0$ and $\theta >1$. For $i,j\in [\![1,N]\!]$, let $A_i\in {\mathbb {C}}$ and $B_{ij}\in {\mathbb {C}}$. Then there exists a constant $c_0$, depending only on $\theta$ and $C_0$, such that for $1<\xi \le 10\log \log N$ and $\varphi _N=(\log N)^{c_0}$ the following estimates hold.

• (1)
  $$\begin{aligned}&\displaystyle \mathbb {P}\left( \left| \sum _{i=1}^N A_ia_i\right| \ge (\varphi _N)^{\xi } \sigma \left( \sum _{i=1}^N|A_i|^2\right) ^{1/2}\right) \le \mathrm {e}^{- (\log N)^{\xi }},\end{aligned}$$

  (3.14)
  $$\begin{aligned}&\displaystyle \mathbb {P}\left( \left| \sum _{i=1}^N\overline{a}_i B_{ii}a_i-\sum _{i= 1}^N \sigma ^2 B_{ii}\right| \ge (\varphi _N)^{\xi }\sigma ^2\left( \sum _{i =1}^N|B_{ii}|^2\right) ^{1/2}\right) \le \mathrm {e}^{-(\log N)^{\xi }},\nonumber \\ \end{aligned}$$

  (3.15)
  $$\begin{aligned}&\displaystyle \mathbb {P}\left( \left| \sum _{i\not =j}^N\overline{a}_i B_{ij}a_j\right| \ge (\varphi _N)^{2\xi }\sigma ^2\left( \sum _{i\not =j}|B_{ij}|^2 \right) ^{1/2}\right) \le \mathrm {e}^{-(\log N)^{\xi }}, \end{aligned}$$

  (3.16)

  for $N$ sufficiently large;

• (2)
  $$\begin{aligned} \mathbb {P}\left( \left| \sum _{i,j} \overline{a}_i B_{ij}b_j\right| \ge (\varphi _N)^{2\xi }\sigma ^2\left( \sum _{i,j}|B_{ij}|^2\right) ^{1/2}\right) \le \mathrm {e}^{-(\log N)^{\xi }}, \end{aligned}$$

  (3.17)

  for $N$ sufficiently large.

For a proof we refer to [23]. We now choose $C$ in (3.1) such that $C\ge c_0$.

Finally, we point out the difference between the random variables $(w_{ij})$ and $(v_i)$: From (2.4), we obtain

$$\begin{aligned} |w_{ij}|\le \frac{(\varphi _N)^{\xi }}{\sqrt{N}}, \end{aligned}$$

(3.18)

with $(\xi ,\nu )$-high probability, whereas $v_i\in [-1,1]$, almost surely.

3.5 Definition of $\Omega _V$

In this subsection we define an event $\Omega _V$, on which the random variables $(v_i)$ exhibit “typical” behavior. For this purpose we need some more notation: Denote by ${\varpi _{\mathrm{b}}}$ the constant

$$\begin{aligned} {\varpi _{\mathrm{b}}}\mathrel {\mathop :}=\frac{1}{2} - \frac{1}{\mathrm {b}+1} = \frac{\mathrm {b}-1}{2(\mathrm {b}+ 1)} = \frac{\mathrm {b}}{\mathrm {b}+1} - \frac{1}{2}\,, \end{aligned}$$

(3.19)

which only depends on $\mathrm {b}$. Fix some small $\epsilon > 0$ satisfying

$$\begin{aligned} \epsilon < \left( 10 + \frac{\mathrm {b}+1}{\mathrm {b}-1} \right) {\varpi _{\mathrm{b}}}, \end{aligned}$$

(3.20)

and define the domain, ${\mathcal {D}}_{\epsilon }$, of the spectral parameter $z$ by

$$\begin{aligned} {\mathcal {D}}_{\epsilon } \mathrel {\mathop :}=\{z = E + \mathrm {i}\eta \in {\mathbb {C}}^+\, :\, -3 - \lambda \le E \le 3 + \lambda , \; N^{-1/2 - \epsilon } \le \eta \le N^{-1/(\mathrm {b}+1) + \epsilon }\}. \end{aligned}$$

(3.21)

Using spectral perturbation theory, we find that the following a priori bound

$$\begin{aligned} |\mu _k| \le \Vert H \Vert \le \Vert W \Vert + \lambda \Vert V \Vert \le 2+\lambda +(\varphi _N)^{c\xi }N^{-2/3}\,,\quad \qquad (k\in [\![1,N]\!]), \end{aligned}$$

(3.22)

holds with high probability; see, e.g., Theorem 2.1. in [25].

Further, we define $N$-dependent constants $\kappa _0$ and $\eta _0$ by

$$\begin{aligned} \kappa _0 \mathrel {\mathop :}=N^{-1/(\mathrm {b}+1)},\quad \eta _0 \mathrel {\mathop :}=\frac{N^{-\epsilon }}{\sqrt{N}}. \end{aligned}$$

(3.23)

In the following, typical choices for $z \equiv L_+ - \kappa + \mathrm {i}\eta$ will be such that $\kappa$ and $\eta$ satisfy $\kappa \lesssim \kappa _0$ and $\eta \ge \eta _0$.

We are now prepared to give a definition of the “good” event $\Omega _V$:

Definition 3.5

Let $n_0 > 10$ be a fixed positive integer independent of $N$. We define $\Omega _V$ to be the event on which the following conditions hold for any $k \in [\![1, n_0 -1 ]\!]$:

• (1) The $k$-th largest random variable $v_k$ satisfies, for all $j\in [\![1,N]\!]$ with $j \ne k$,

  $$\begin{aligned} N^{-\epsilon } \kappa _0 < |v_j - v_k| < (\log N) \kappa _0. \end{aligned}$$

  (3.24)

  In addition, for $k=1$, we have

  $$\begin{aligned} N^{-\epsilon } \kappa _0 < |1 - v_1| < (\log N) \kappa _0. \end{aligned}$$

  (3.25)

• (2) There exists a constant $\mathfrak {c} <1$ independent of $N$ such that, for any $z \in {\mathcal {D}}_{\epsilon }$ satisfying

  $$\begin{aligned} \min _{i \in [\![1, N ]\!]} |{\mathrm {Re }}\,(z + m_{fc}(z)) - \lambda v_i| = |{\mathrm {Re }}\,(z + m_{fc}(z)) - \lambda v_k|, \end{aligned}$$

  (3.26)

  we have

  $$\begin{aligned} \frac{1}{N} \sum _{i}^{(k)} \frac{1}{|\lambda v_i - z - m_{fc}(z)|^2} <\mathfrak {c} < 1. \end{aligned}$$

  (3.27)

  We remark that, together with (3.24) and (3.25), (3.26) implies

  $$\begin{aligned} |{\mathrm {Re }}\,(z + m_{fc}(z)) - \lambda v_i| > \frac{N^{-\epsilon } \kappa _0}{2}, \end{aligned}$$

  (3.28)

  for all $i \ne k$.

• (3) There exists a constant $C>0$ such that, for any $z \in {\mathcal {D}}_{\epsilon }$, we have

  $$\begin{aligned} \left| \frac{1}{N} \sum _{i=1}^N \frac{1}{\lambda v_i - z - m_{fc}(z)} - \int \frac{\mathrm {d}\mu (v)}{\lambda v - z - m_{fc}(z)} \right| \le \frac{C N^{3\epsilon /2}}{\sqrt{N}}. \end{aligned}$$

  (3.29)

In the Appendix A we show that

$$\begin{aligned} {\mathbb {P}}(\Omega _V) \ge 1 - C (\log N)^{1 + 2\mathrm {b}} N^{-\epsilon }, \end{aligned}$$

(3.30)

thus $(\Omega _V)^c$ is indeed a rare event.

3.6 Definition of $\widehat{m}_{fc}$

Let $\widehat{\mu }$ be the empirical measure defined by

$$\begin{aligned} \widehat{\mu } \mathrel {\mathop :}=\frac{1}{N} \sum _{i=1}^N \delta _{\lambda v_i}. \end{aligned}$$

(3.31)

We define a random measure $\widehat{\mu }_{fc}$ by setting $\widehat{\mu }_{fc} \mathrel {\mathop :}=\widehat{\mu }\boxplus \mu _{sc}$, i.e., $\widehat{\mu }_{fc}$ is the additive free convolution of the empirical measure $\widehat{\mu }$ and the semicircular measure $\mu _{sc}$. As in the case of $m_{fc}$, the Stieltjes transform $\widehat{m}_{fc}$ of the measure $\widehat{\mu }_{fc}$ is a solution to the equation

$$\begin{aligned} \widehat{m}_{fc}(z) = \frac{1}{N} \sum _{i=1}^N \frac{1}{\lambda v_i - z - \widehat{m}_{fc}(z)}\,,\qquad {\mathrm {Im }}\,\widehat{m}_{fc}(z)\ge 0\,,\quad (z\in {\mathbb {C}}^+), \end{aligned}$$

(3.32)

and we obtain $\widehat{\mu }_{fc}$ trough the Stieltjes inversion formula from $\widehat{m}_{fc}(z)$, c.f., (2.3).

To estimate the difference $|\widehat{m}_{fc} - m_{fc}|$, we consider the following subset of ${\mathcal {D}}_{\epsilon }$.

Definition 3.6

Let $A\mathrel {\mathop :}=[\![n_0,N]\!]$. We define the domain ${\mathcal {D}}_{\epsilon }'$ of the spectral parameter $z$ as

$$\begin{aligned} {\mathcal {D}}_{\epsilon }'=\left\{ z\in {\mathcal {D}}_{\epsilon }\,:\, |\lambda v_a-z-{m}_{fc}(z)| > \frac{1}{2} N^{-1 / (\mathrm {b}+ 1)-\epsilon },\,\forall a\in A\right\} . \end{aligned}$$

(3.33)

Eventually, we are going to show that $\mu _k + \mathrm {i}\eta _0 \in {\mathcal {D}}_{\epsilon }'$, $k\in [\![1,n_0-1]\!]$, with high probability on $\Omega _V$; see Remark 4.4.

Recall that we assume that $v_1 > v_2 > \dots > v_N$. Assuming that $\Omega _V$ holds, i.e., $(v_i)$ are fixed and satisfy the conditions in Definition 3.5, we have the following lemma, which shows that $\widehat{m}_{fc}(z)$ is a good approximation of $m_{fc}(z)$ for $z \in {\mathcal {D}}_{\epsilon }'$.

Lemma 3.7

For any $z \in {\mathcal {D}}_{\epsilon }'$, we have on $\Omega _V$ that

$$\begin{aligned} |\widehat{m}_{fc} (z)-m_{fc}(z) | \le \frac{N^{2\epsilon }}{\sqrt{N}}. \end{aligned}$$

(3.34)

Proof

Assume that $\Omega _V$ holds. For given $z \in {\mathcal {D}}_{\epsilon }'$, choose $k \in [\![1, n_0 -1 ]\!]$ satisfying (3.26), i.e., among $(\lambda v_i)$, $\lambda v_k$ is closest to ${\mathrm {Re }}\,(z + m_{fc}(z))$. Suppose that (3.34) does not hold. Using the definitions of $m_{fc}$ and $\widehat{m}_{fc}$, we obtain the following self-consistent equation for $(\widehat{m}_{fc} - m_{fc})$:

$$\begin{aligned} \widehat{m}_{fc}-m_{fc} =&\frac{1}{N}\sum _{i=1}^N\left( \frac{1}{\lambda v_i - z - \widehat{m}_{fc}} - m_{fc}\right) \nonumber \\ =&\frac{1}{N}\sum _{i=1}^N \left( \frac{1}{\lambda v_i - z - \widehat{m}_{fc}} - \frac{1}{\lambda v_i - z - m_{fc}}\right) \nonumber \\&+ \left( \frac{1}{N} \sum _{i=1}^N \frac{1}{\lambda v_i - z - m_{fc}} - \int \frac{\mathrm {d}\mu (v)}{\lambda v - z - m_{fc}} \right) \nonumber \\ =&\frac{1}{N} \sum _{i=1}^N \frac{\widehat{m}_{fc} - m_{fc}}{(\lambda v_i - z - \widehat{m}_{fc})(\lambda v_i - z - m_{fc})}\nonumber \\&+ \left( \frac{1}{N} \sum _{i=1}^N \frac{1}{\lambda v_i - z - m_{fc}} - \int \frac{\mathrm {d}\mu (v)}{\lambda v - z - m_{fc}}\right) . \end{aligned}$$

(3.35)

From the assumption (3.29), we find that the second term in the right hand side of (3.35) is bounded by $N^{-1/2 + 3\epsilon /2}$.

Next, we estimate the first term in the right hand side of (3.35). For $i=k$, we have

$$\begin{aligned} |\lambda v_k - z - \widehat{m}_{fc}| + |\lambda v_k - z - m_{fc}| \ge |\widehat{m}_{fc} (z) - m_{fc} (z)| > \frac{N^{2\epsilon }}{\sqrt{N}}, \end{aligned}$$

which shows that either

$$\begin{aligned} |\lambda v_k - z - \widehat{m}_{fc}| \ge \frac{N^{2\epsilon }}{2\sqrt{N}} \qquad \text {or} \qquad |\lambda v_k - z - m_{fc}| \ge \frac{N^{2\epsilon }}{2\sqrt{N}}. \end{aligned}$$

In either case, by considering the imaginary part, we find

$$\begin{aligned} \frac{1}{N} \left| \frac{1}{(\lambda v_k - z - \widehat{m}_{fc}) (\lambda v_k - z - m_{fc})} \right| \le \frac{1}{N} \frac{2\sqrt{N}}{N^{2\epsilon }} \frac{1}{\eta } \le C N^{-\epsilon }\,,\quad (z\in {\mathcal {D}}_{\epsilon }'). \end{aligned}$$

For the other terms, we use

$$\begin{aligned}&\frac{1}{N} \left| \sum _{i}^{(k)}\frac{1}{(\lambda v_i - z - \widehat{m}_{fc})(\lambda v_i - z - m_{fc})}\right| \nonumber \\&\quad \le \frac{1}{2N} \sum _{i}^{(k)} \left( \frac{1}{|\lambda v_i - z - \widehat{m}_{fc}|^2} + \frac{1}{|\lambda v_i - z - m_{fc}|^2}\right) . \end{aligned}$$

(3.36)

From (3.32), we have that

$$\begin{aligned} \frac{1}{N} \sum _{i=1}^N \frac{1}{|\lambda v_i - z - \widehat{m}_{fc}|^2} = \frac{{\mathrm {Im }}\,\widehat{m}_{fc}}{\eta + {\mathrm {Im }}\,\widehat{m}_{fc}} < 1. \end{aligned}$$

(3.37)

We also assume in the assumption (3.27) that

$$\begin{aligned} \frac{1}{N} \sum _{i}^{(k)} \frac{1}{|\lambda v_i - z - m_{fc}|^2} < \mathfrak {c} < 1, \end{aligned}$$

(3.38)

for some constant $\mathfrak {c}$. Thus, we get

$$\begin{aligned} |\widehat{m}_{fc} (z) - m_{fc} (z)| < \frac{1+\mathfrak {c}}{2} |\widehat{m}_{fc} (z) - m_{fc} (z)| + N^{-1/2 + 3\epsilon /2}\,,\quad (z\in {\mathcal {D}}_{\epsilon }')\,, \end{aligned}$$

(3.39)

which implies that

$$\begin{aligned} |\widehat{m}_{fc} (z) - m_{fc} (z)| < C N^{-1/2 + 3\epsilon /2}\,,\quad (z\in {\mathcal {D}}_{\epsilon }'). \end{aligned}$$

Since this contradicts the assumption that (3.34) does not hold, it proves the desired lemma. $\square$

4 Proof of Theorem 2.7

In this section, we outline the proof of Theorem 2.7. We first fix the diagonal random entries $(v_i)$ and consider $\widehat{\mu }_{fc}$ near the edge $L_+$, where the largest eigenvalues are located as we can see from Proposition 4.3. The main tools we use in the proof are Lemma 4.1 below, where we obtain a linear approximation of $m_{fc}$, and Lemma 3.7, which estimates the difference between $m_{fc}$ and $\widehat{m}_{fc}$. Using Proposition 4.3 that estimates the eigenvalue locations in terms of $\widehat{m}_{fc}$, we prove Theorem 2.7.

4.1 Properties of $m_{fc}$ and $\widehat{m}_{fc}$

Recall the definitions of $m_{fc}$ and $\widehat{m}_{fc}$. Let

$$\begin{aligned} R_2 (z)&\mathrel {\mathop :}= \int \frac{\mathrm {d}\mu (v)}{|\lambda v - z - m_{fc}(z)|^2},\nonumber \\ \widehat{R}_2 (z)&\mathrel {\mathop :}= \frac{1}{N} \sum _{i=1}^N \frac{1}{|\lambda v_i - z - \widehat{m}_{fc}(z)|^2}\,,\quad (z\in {\mathbb {C}}^+). \end{aligned}$$

(4.1)

Since

$$\begin{aligned} {\mathrm {Im }}\,m_{fc}(z) = \int \frac{{\mathrm {Im }}\,z + {\mathrm {Im }}\,m_{fc}(z)}{|\lambda v - z - m_{fc}(z)|^2}\, \mathrm {d}\mu (v), \end{aligned}$$

we have that

$$\begin{aligned} R_2 (z) = \frac{{\mathrm {Im }}\,m_{fc}(z)}{{\mathrm {Im }}\,z + {\mathrm {Im }}\,m_{fc}(z)} < 1,\quad (z\in {\mathbb {C}}^+). \end{aligned}$$

Similarly, we also find that $\widehat{R}_2 (z) < 1$.

The following lemma shows that $m_{fc}$ is approximately a linear function near the spectral edge.

Lemma 4.1

Let $z = L_+ - \kappa + \mathrm {i}\eta \in {\mathcal {D}}_{\epsilon }$. Then,

$$\begin{aligned} z+m_{fc}(z)=\lambda -\frac{\lambda ^2}{\lambda ^2-\lambda _+^2}(L_+-z) + {\mathcal {O}}\left( (\log N) (\kappa + \eta )^{\min \{\mathrm {b}, 2\}}\right) . \end{aligned}$$

(4.2)

Similarly, if $z, z' \in {\mathcal {D}}_{\epsilon }$, then

$$\begin{aligned} m_{fc}(z) \!-\! m_{fc}(z') = \frac{\lambda _+^2}{\lambda ^2 - \lambda _+^2} (z-z') + {\mathcal {O}}\left( (\log N)^2 (N^{-1/(\mathrm {b}+1)})^{\min \{\mathrm {b}-1, 1\}}|z-z'|\right) . \end{aligned}$$

(4.3)

Proof

We only prove the first part of the lemma; the second part is proved analogously. Since $L_+ + m_{fc}(L_+) = \lambda$, see Lemma 2.3, we can write

$$\begin{aligned} m_{fc}(z) - m_{fc}(L_+)&= \int \frac{\mathrm {d}\mu (v)}{\lambda v - z - m_{fc}(z)} - \int \frac{\mathrm {d}\mu (v)}{\lambda v - L_+ - m_{fc}(L_+)}\nonumber \\&= \int \frac{m_{fc}(z) - m_{fc}(L_+) + (z-L_+)}{(\lambda v - z - m_{fc}(z))(\lambda v - \lambda )} \mathrm {d}\mu (v). \end{aligned}$$

(4.4)

Setting

$$\begin{aligned} T(z) \mathrel {\mathop :}=\int \frac{\mathrm {d}\mu (v)}{(\lambda v - z - m_{fc}(z))(\lambda v - \lambda )}, \end{aligned}$$

(4.5)

we find

$$\begin{aligned} |T(z)| \le \left( \int \frac{\mathrm {d}\mu (v)}{|\lambda v - z \!-\! m_{fc}(z)|^2} \right) ^{1/2} \left( \int \frac{\mathrm {d}\mu (v)}{|\lambda v - \lambda |^2}\right) ^{1/2}\!\le \!\sqrt{R_2(z)}\frac{\lambda _+}{\lambda } < \frac{\lambda _+}{\lambda } < 1. \end{aligned}$$

(4.6)

Hence, for $z \in {\mathcal {D}}_{\epsilon }$, we have

$$\begin{aligned} m_{fc}(z) - m_{fc}(L_+) = \frac{T(z)}{1-T(z)} (z - L_+), \end{aligned}$$

(4.7)

which shows that

$$\begin{aligned} z + m_{fc}(z) = \lambda - \frac{1}{1-T(z)} (L_+ - z). \end{aligned}$$

(4.8)

We thus obtain from (4.6) and (4.8) that

$$\begin{aligned} |z + m_{fc}(z) - \lambda | \le \frac{\lambda }{\lambda - \lambda _+} |L_+ -z|. \end{aligned}$$

We now estimate the difference $T(z)-{\lambda ^2_+}/{\lambda ^2}\,$: Let $\tau \mathrel {\mathop :}=z + m_{fc}(z)$. We have

$$\begin{aligned} T(z) - \frac{\lambda _+^2}{\lambda ^2}&= \int \frac{\mathrm {d}\mu (v)}{(\lambda v - \tau )(\lambda v - \lambda )} - \int \frac{\mathrm {d}\mu (v)}{(\lambda v - \lambda )^2}\nonumber \\&= (\tau - \lambda ) \int \frac{\mathrm {d}\mu (v)}{(\lambda v - \tau )(\lambda v - \lambda )^2}. \end{aligned}$$

(4.9)

In order to find an upper bound on the integral on the very right side, we consider the following cases:

• (1) When $\mathrm {b}\ge 2$, we have

  $$\begin{aligned} \left| \int \frac{\mathrm {d}\mu (v)}{(\lambda v - \tau )(\lambda v - \lambda )^2} \right| \le C \int _{-1}^1 \frac{\mathrm {d}v}{|\lambda v - \tau |} \le C \log N. \end{aligned}$$

  (4.10)

• (2) When $\mathrm {b}< 2$, define a set $B \subset [-1, 1]$ by

  $$\begin{aligned} B \mathrel {\mathop :}=\{v \in [-1, 1] : \lambda v < -\lambda + 2 \, {\mathrm {Re }}\,\tau \}, \end{aligned}$$

  and $B^c\equiv [-1, 1] \backslash B$. Estimating the integral in (4.9) on $B$ we find

  $$\begin{aligned} \left| \int _{B} \frac{\mathrm {d}\mu (v)}{(\lambda v - \tau )(\lambda v - \lambda )^2} \right| \le C \int _{B} \frac{\mathrm {d}\mu (v)}{|\lambda v - \lambda |^3} \le C |\lambda - \tau |^{\mathrm {b}-2}, \end{aligned}$$

  (4.11)

  where we have used that, for $v \in B$,

  $$\begin{aligned} |\lambda v - \tau | > |{\mathrm {Re }}\,\tau - \lambda v| > \frac{1}{2} (\lambda - \lambda v). \end{aligned}$$

  On the set $B^c$, we have

  $$\begin{aligned} \left| \int _{B^c} \frac{\mathrm {d}\mu (v)}{(\lambda v - \tau )(\lambda v - \lambda )} \right| \le C \int _{B^c} \frac{|\lambda - \lambda v|^{\mathrm {b}-1}}{|\lambda v - \tau |} \mathrm {d}v \le C |\lambda - \tau |^{\mathrm {b}-1} \log N, \end{aligned}$$

  (4.12)

  where we have used that, for $v \in B^c$,

  $$\begin{aligned} |\lambda - \lambda v| \le 2 (\lambda - {\mathrm {Re }}\,\tau ) \le 2 |\lambda - \tau |. \end{aligned}$$

  We also have

  $$\begin{aligned} \left| \int _{B^c} \frac{\mathrm {d}\mu (v)}{(\lambda v - \lambda )^2}\right| \le C \int _{B^c} |\lambda v - \lambda |^{\mathrm {b}-2} \mathrm {d}v \le C |\lambda - \tau |^{\mathrm {b}-1}. \end{aligned}$$

  (4.13)

  Thus, we obtain from (4.9), (4.12) and (4.13) that

  $$\begin{aligned} \left| \int \frac{\mathrm {d}\mu (v)}{(\lambda v - \tau )(\lambda v - \lambda )^2} \right| \le C |\lambda - \tau |^{\mathrm {b}-2} \log N. \end{aligned}$$

  (4.14)

Since $T(z)$ is continuous and ${\mathcal {D}}_\epsilon$ is compact, we can choose the constants uniform in $z$. We thus have proved that

$$\begin{aligned} T(z) = \frac{\lambda _+^2}{\lambda ^2} + {\mathcal {O}}\left( (\log N)|L_+ - z|^{\min \{\mathrm {b}-1, 1\} } \right) , \end{aligned}$$

(4.15)

which, combined with (4.8), proves the desired lemma. $\square$

Remark 4.2

Choosing in Lemma 4.1 $z=z_k$, where $z_k \mathrel {\mathop :}=L_+ - \kappa _k + \mathrm {i}\eta \in {\mathcal {D}}_{\epsilon }$ with

$$\begin{aligned} \kappa _k = \frac{\lambda ^2 - \lambda _+^2}{\lambda } (1-v_k), \end{aligned}$$

we obtain

$$\begin{aligned} z_k + m_{fc}(z_k) = \lambda v_k + \frac{\lambda ^2}{\lambda ^2 - \lambda _+^2} \eta + {\mathcal {O}}\left( (\log N) N^{-\min \{\mathrm {b}, 2\} / (\mathrm {b}+1) + 2 \epsilon }\right) . \end{aligned}$$

(4.16)

4.2 Proof of Theorem 2.7

The main result of this subsection is Proposition 4.5, which will imply Theorem 2.7. The key ingredient of the proof of Proposition 4.5 is an implicit equation for the largest eigenvalues $(\mu _k)$ of $H$. This equation, Eq. (4.17) in Proposition 4.3 below, involves the Stieltjes transform $\widehat{m}_{fc}$ and the random variables $(v_k)$. Using the information on $\widehat{m}_{fc}$ gathered in the previous subsections, we can approximately solve Eq. (4.17) for $(\mu _k)$. The proof of Proposition 4.3 is postponed to Sect. 5.

Proposition 4.3

Let $n_0>10$ be a fixed integer independent of $N$. Let $\mu _k$ be the $k$-th largest eigenvalue of $H$, $k\in [\![1, n_0-1]\!]$. Suppose that the assumptions in Theorem 2.7 hold. Then, the following holds with $(\xi -2,\nu )$-high probability on $\Omega _V$:

$$\begin{aligned} \mu _k + {\mathrm {Re }}\,\widehat{m}_{fc} (\mu _k + \mathrm {i}\eta _0) = \lambda v_k + {\mathcal {O}}(N^{-1/2 + 3\epsilon }), \end{aligned}$$

(4.17)

where $\eta _0$ is defined in (3.23).

Remark 4.4

Since $|\lambda v_i - \lambda v_k| \ge N^{-\epsilon } \kappa _0 \gg N^{-1/2 + 3\epsilon }$, for all $i \ne k$, on $\Omega _V$, we obtain from Proposition 4.3 that

$$\begin{aligned}&|\mu _k + \mathrm {i}\eta _0 + {\mathrm {Re }}\,\widehat{m}_{fc}(\mu _k + \mathrm {i}\eta _0) - \lambda v_i| \ge |\lambda v_i - \lambda v_k| - |\mu _k + \mathrm {i}\eta _0\\&\quad + {\mathrm {Re }}\,\widehat{m}_{fc}(\mu _k + \mathrm {i}\eta _0) - \lambda v_k| \ge \frac{N^{-\epsilon } \kappa _0}{2}, \end{aligned}$$

on $\Omega _V$. Hence, we find that $\mu _k + \mathrm {i}\eta _0 \in {\mathcal {D}}_{\epsilon }'$, $k\in [\![1,n_0-1]\!]$, with high probability on $\Omega _V$.

Combining the tools developed in the previous subsection, we now prove the main result on the eigenvalue locations.

Proposition 4.5

Let $n_0>10$ be a fixed integer independent of $N$. Let $\mu _k$ be the $k$-th largest eigenvalue of $H=\lambda V+W$, where $k \in [\![1, n_0 -1 ]\!]$. Then, there exist constants $C$ and $\nu >0$ such that we have

$$\begin{aligned} \left| \mu _k - \left( L_+ - \frac{\lambda ^2 - \lambda _+^2}{\lambda } (1-v_k) \right) \right| \le C \frac{1}{N^{1/(\mathrm {b}+1)}} \left( \frac{N^{3\epsilon }}{ N^{{\varpi _{\mathrm{b}}}}} + \frac{(\log N)^2}{N^{1/(\mathrm {b}+1)}}\right) , \end{aligned}$$

(4.18)

with $(\xi -2,\nu )$-high probability on $\Omega _V$.

Proof of Theorem 2.7 and Proposition 4.5

It suffices to prove Proposition 4.5. Let $k\in [\![1,n_0-1]\!]$. From Lemma 3.7 and Proposition 4.3, we find that, with high probability on $\Omega _V$,

$$\begin{aligned} \mu _k + {\mathrm {Re }}\,m_{fc} (\mu _k + \mathrm {i}\eta _0) = \lambda v_k + {\mathcal {O}}(N^{-1/2 + 3\epsilon }). \end{aligned}$$

(4.19)

In Lemma 4.1, we showed that

$$\begin{aligned} \mu _k + \mathrm {i}\eta _0 + m_{fc} (\mu _k + \mathrm {i}\eta _0)&= \lambda - \frac{\lambda ^2}{\lambda ^2 - \lambda _+^2} (L_+ - \mu _k) + \mathrm {i}C \eta _0 \nonumber \\&\quad + {\mathcal {O}}\left( \kappa _0^{\min \{\mathrm {b}, 2\}} (\log N)^2\right) . \end{aligned}$$

(4.20)

Thus, we obtain

$$\begin{aligned} \mu _k + {\mathrm {Re }}\,m_{fc} (\mu _k + \mathrm {i}\eta _0) = \lambda - \frac{\lambda ^2}{\lambda ^2 - \lambda _+^2} (L_+ - \mu _k) + {\mathcal {O}}\left( \kappa _0^{\min \{\mathrm {b}, 2\}}(\log N)^2\right) . \end{aligned}$$

(4.21)

Therefore, we have with high probability on $\Omega _V$ that

$$\begin{aligned} \mu _k = L_+ - \frac{\lambda ^2 - \lambda _+^2}{\lambda } (1-v_k) + {\mathcal {O}}\left( \kappa _0^{\min \{\mathrm {b}, 2\}} (\log N)^2 \right) + {\mathcal {O}}(N^{-1/2 + 3\epsilon }), \end{aligned}$$

(4.22)

completing the proof of Proposition 4.5. $\square$

Recalling that ${\mathbb {P}}(\Omega _V) \ge 1 - C (\log N)^{1 + 2\mathrm {b}} N^{-\epsilon }$, we obtain from Proposition 4.5 the following corollary.

Corollary 4.6

Let $n_0$ be a fixed constant independent of $N$. Let $\mu _k$ be the $k$-th largest eigenvalue of $H=\lambda V+W$, where $1 \le k < n_0$. Then, there exists a constant $C_1 > 0$ such that for $s\in {\mathbb {R}}^+$ we have

$$\begin{aligned}&{\mathbb {P}}\left( N^{1/(\mathrm {b}+1)} \frac{\lambda ^2 - \lambda _+^2}{\lambda } (1-v_k) \le s - C_1 \left( \frac{N^{3\epsilon }}{N^{{\varpi _{\mathrm{b}}}}} + \frac{(\log N)^2}{N^{1/(\mathrm {b}+1)}} \right) \right) - C_1 \frac{(\log N)^{1+2\mathrm {b}}}{N^{\epsilon }} \nonumber \\&\quad \le {\mathbb {P}}\left( N^{1/(\mathrm {b}+1)} (L_+ - \mu _k) \le s\right) \nonumber \\&\quad \le {\mathbb {P}}\left( N^{1/(\mathrm {b}+1)} \frac{\lambda ^2 - \lambda _+^2}{\lambda } (1-v_k) \le s + C_1 \left( \frac{N^{3\epsilon }}{N^{{\varpi _{\mathrm{b}}}}} + \frac{(\log N)^2}{N^{1/ (\mathrm {b}+1)}}\right) \right) \nonumber \\ {}&\qquad + C_1 \frac{(\log N)^{1+2\mathrm {b}}}{N^{\epsilon }}, \end{aligned}$$

(4.23)

for $N$ sufficiently large.

Remark 4.7

The constants in Proposition 4.5 and Corollary 4.6 depend only on $\lambda$, the distribution $\mu$ and the constants $C_0$ and $\theta$ in (2.4), but are otherwise independent of the detailed structure of the Wigner matrix $W$.

4.3 Gaussian fluctuation for the regime $\lambda < \lambda _+$

In this subsection, we consider the setup $\lambda < \lambda _+$. Recall that $\widehat{\mu }_{fc} = \widehat{\mu } \boxplus \mu _{sc}$ denotes the free convolution measure of the empirical measure $\widehat{\mu }$, which is defined in (3.31), and the semicircular measure $\mu _{sc}$. Also recall that we denote by $L_{\pm }$ the endpoints of the support of the measure $\mu _{fc}$.

Lemma 4.8

Let $\mu$ be a centered Jacobi measure defined in (2.9) with $\mathrm {b}> 1$. Let ${{\mathrm{supp}}}\widehat{\mu }_{fc} = [\widehat{L}_-, \widehat{L}_+]$, where $\widehat{L}_-$ and $\widehat{L}_+$ are random variables depending on $(v_i)$. Then, if $\lambda < \lambda _+$, the rescaled fluctuation $N^{1/2} (\widehat{L}_+ - L_+)$ converges to a Gaussian random variable with mean 0 and variance $(1 - [m_{fc} (L_+)]^2)$ in distribution, as $N \rightarrow \infty$.

Remark 4.9

When $\mathrm {a}> 1$, the analogous statement to Lemma 4.8 holds at the lower edge. See also Remark 2.6.

Proof

Following the proof in [31, 43], we find that $\widehat{L}_+$ is the solution to the equations

$$\begin{aligned} \widehat{m}_{fc} (\widehat{L}_+) \!= \!\frac{1}{N} \sum _{j=1}^N \frac{1}{\lambda v_j - \widehat{L}_+ - \widehat{m}_{fc}(\widehat{L}_+)}\,, \quad \frac{1}{N} \sum _{j=1}^N \frac{1}{(\lambda v_j - \widehat{L}_+ - \widehat{m}_{fc} (\widehat{L}_+))^2} = 1. \end{aligned}$$

(4.24)

Similarly, we find that $L_+$ is the solution to the equations

$$\begin{aligned} m_{fc} (L_+) =\int \frac{\mathrm {d}\mu (v)}{\lambda v - L_+ - m_{fc}(L_+)}\,, \qquad \int \frac{\mathrm {d}\mu (v)}{(\lambda v - L_+ - m_{fc}(L_+))^2} = 1. \end{aligned}$$

(4.25)

Let

$$\begin{aligned} \tau \mathrel {\mathop :}=L_+ + m_{fc}(L_+), \qquad \widehat{\tau } \mathrel {\mathop :}=\widehat{L}_+ + \widehat{m}_{fc}(\widehat{L}_+). \end{aligned}$$

Since $\lambda < \lambda _+$, we may assume that

$$\begin{aligned} \int \frac{\mathrm {d}\mu (v)}{(\lambda v - \lambda )^2} > 1 + \delta , \qquad \frac{1}{N} \sum _{j=1}^N \frac{1}{(\lambda v_j - \lambda )^2} > 1 + \delta , \end{aligned}$$

(4.26)

for some $\delta > 0$. Notice that the second inequality holds with high probability on $\Omega _V$. From the assumption, we also find that $\tau , \widehat{\tau } > \lambda$. Thus we get

$$\begin{aligned} 0&= \frac{1}{N} \sum _{j=1}^N \frac{1}{(\lambda v_j - \widehat{\tau })^2} - 1 = \frac{1}{N} \sum _{j=1}^N \frac{1}{(\lambda v_j - \widehat{\tau })^2}\nonumber \\&\quad - \frac{1}{N} \sum _{j=1}^N \frac{1}{(\lambda v_j -\tau )^2}+ {\mathcal {O}}((\varphi _N)^{\xi } N^{-1/2}) \nonumber \\&= \frac{1}{N} \sum _{j=1}^N \frac{(-2 \lambda v_j + \tau + \widehat{\tau })(\tau - \widehat{\tau })}{(\lambda v_j - \tau )^2 (\lambda v_j - \widehat{\tau })^2} + {\mathcal {O}}((\varphi _N)^{\xi } N^{-1/2}), \end{aligned}$$

(4.27)

which holds with high probability. Since $\tau , \widehat{\tau } > \lambda$, we have

$$\begin{aligned} -2 \lambda v_j + \tau + \widehat{\tau } \ge 0. \end{aligned}$$

Moreover, with high probability, $|\{v_j : v_j < 0 \}| > cN$ for some constant $c > 0$, independent of $N$. In particular,

$$\begin{aligned} \frac{1}{N} \sum _{j=1}^N \frac{-2 \lambda v_j + \tau + \widehat{\tau }}{(\lambda v_j - \tau )^2 (\lambda v_j - \widehat{\tau })^2} > c' > 0, \end{aligned}$$

for some constant $c'$ independent of $N$. This shows together with (4.27) that

$$\begin{aligned} \tau - \widehat{\tau } = {\mathcal {O}}((\varphi _N)^{\xi } N^{-1/2}), \end{aligned}$$

with high probability on $\Omega _V$.

We can thus write

$$\begin{aligned} \widehat{m}_{fc}(L_+) = \widehat{\tau } - \widehat{L}_+&= \frac{1}{N} \sum _{j=1}^N \frac{1}{\lambda v_j - \widehat{\tau }} = \frac{1}{N} \sum _{j=1}^N \frac{1}{\lambda v_j - \tau }\nonumber \\&\quad + \frac{1}{N} \sum _{j=1}^N \frac{\widehat{\tau } - \tau }{(\lambda v_j - \tau )^2} + {\mathcal {O}}((\varphi _N)^{2\xi } N^{-1})\nonumber \\&= m_{fc}(L_+) + X + (\widehat{\tau } - \tau ) + {\mathcal {O}}((\varphi _N)^{2\xi } N^{-1}), \end{aligned}$$

(4.28)

with high probability, where we define the random variable $X$ by

$$\begin{aligned} X \mathrel {\mathop :}=\frac{1}{N} \sum _{j=1}^N \frac{1}{\lambda v_j - \tau } - \int \frac{\mathrm {d}\mu (v)}{\lambda v - \tau } = \frac{1}{N} \sum _{j=1}^N \left( \frac{1}{\lambda v_j -\tau } - {\mathbb {E}}\left[ \frac{1}{\lambda v_j - \tau }\right] \right) . \end{aligned}$$

(4.29)

Notice that, by the central limit theorem, $X$ converges to a Gaussian random variable with mean 0 and variance $N^{-1} (1 - (m_{fc} (L_+))^2)$. Since,

$$\begin{aligned} L_+ - \widehat{L}_+ = X + {\mathcal {O}}((\varphi _N)^{2\xi } N^{-1}), \end{aligned}$$

(4.30)

with high probability, the desired lemma follows. $\square$

When $(v_i)$ are fixed, we may follow the proof of Theorem 2.21 in [31] to get

$$\begin{aligned} |L_+ - \mu _1| \le (\varphi _N)^{C \xi } N^{-2/3} \end{aligned}$$

(4.31)

with high probability. Since $|\widehat{L}_+ - L_+| \sim N^{-1/2}$, we find that the leading fluctuation of the largest eigenvalue comes from the Gaussian fluctuation obtained in Lemma 4.8. This also shows that there is a sharp transition in the distribution of the largest eigenvalue from a Gaussian law to a Weibull distribution as $\lambda$ crosses $\lambda _+$.

5 Estimates on the location of the eigenvalues

In this section, we prove Proposition 4.3. Recall the definition of $\eta _0$ in (3.23). For $k\in [\![1,n_0-1]\!]$, let $\widehat{E}_k\in {\mathbb {R}}$ be a solution $E=\widehat{E}_k$ to the equation

$$\begin{aligned} E + {\mathrm {Re }}\,\widehat{m}_{fc} (E+\mathrm {i}\eta _0 ) = \lambda v_k,\qquad \quad (E\in {\mathbb {R}}), \end{aligned}$$

(5.1)

and set $\widehat{z}_k \mathrel {\mathop :}=\widehat{E}_k+\mathrm {i}\eta _0$. The existence of such $\widehat{E}_k$ is easy to see from Lemmas 4.1 and 3.7. If there are two or more solutions to (5.1), we choose $\widehat{E}_k$ to be the largest one among these solutions.

The key observation used in the proof of Proposition 4.3 is that ${\mathrm {Im }}\,m(z)$, the imaginary part of the averaged Green function, has a sharp peak if and only if the imaginary part of

$$\begin{aligned} g_{k}(z)\mathrel {\mathop :}=\frac{1}{\lambda v_k - z - \widehat{m}_{fc} (z)}\,,\quad (z\in {\mathbb {C}}^+), \end{aligned}$$

(5.2)

becomes sufficiently large for some $k\in [\![1,n_0-1]\!]$. We remark that this phenomenon occurs only when the deformed semicircle measure $\mu _{fc}$ has a convex decay; when the square root behavior prevails, we have the stability bound

$$\begin{aligned} |\lambda - z - \widehat{m}_{fc} (z)| > c, \end{aligned}$$

(5.3)

for some constant $c>0$, near the edge of the spectrum. Hence the location of the peak of

$$\begin{aligned} {\mathrm {Im }}\,\widehat{m}_{fc}(z) = \frac{1}{N} \sum _{k=1}^N g_k (z) \end{aligned}$$

is not solely determined by a behavior of single $v_k$, but affected by all $(v_k)$.

Since $z\mapsto {\mathrm {Im }}\,g_k(z)$ has a sharp peak near $\widehat{z}_k$, we then conclude that $z\mapsto {\mathrm {Im }}\,m(z)$ also has a peak near $\widehat{z}_k$. From the spectral decomposition

$$\begin{aligned} {\mathrm {Im }}\,m(E + \mathrm {i}\eta _0) = \frac{1}{N} \sum _{\alpha =1}^N \frac{\eta _0}{(\mu _{\alpha } - E)^2 + \eta _0^2}, \end{aligned}$$

we also observe that the positions of the peaks of ${\mathrm {Im }}\,m(z)$ correspond to the locations of the eigenvalues. This will enable us to estimate the location of the $k$-th largest eigenvalue in terms of $v_k$, yielding a proof of Proposition 4.3.

This section is organized as follows. In Sect. , we establish a local law for $m(z)$ with $z\in {\mathcal {D}}_{\epsilon }'$, i.e., for $z$ close to the upper edge; see Proposition 5.1 below. In the Sects. 5.2 and 5.3 we establish further estimates that will be used in the proof of Proposition 4.3. The estimates in Sect. 5.3 are rather straightforward, while the estimates of Sect. 5.3 rely on the “fluctuation average lemma” whose proof is postponed to Sect. 6. The proof of Proposition 4.3 is then completed in Sect. 5.4.

5.1 Properties of $\widehat{m}_{fc}$ and $m$

In the proof of Proposition 4.3, we will use the following local law as an a priori estimate. Recall the constant $\epsilon >0$ in (3.20) and the definition of the domain ${\mathcal {D}}_{\epsilon }'$ in (3.33).

Proposition 5.1

(Local law near the edge) We have with $(\xi ,\nu )$-high probability on $\Omega _V$ that

$$\begin{aligned} |m(z)-\widehat{m}_{fc}(z)| \le \frac{N^{2\epsilon }}{\sqrt{N}}, \end{aligned}$$

(5.4)

for all $z \in {\mathcal {D}}_{\epsilon }'$.

We remark that Proposition 5.1 also holds if $\mu _{fc}$ has a square root behavior at the edge, since we have in that case the stronger bound $|m(z)-\widehat{m}_{fc}(z)| \le N^{\epsilon } (N \eta )^{-1}$, which holds with $(\xi ,\nu )$-high probability on $\Omega _V$; see Theorem 2.12 in [31].

The proof of Proposition 5.1 is the content of the rest of this subsection.

Recall the definitions of $(\widehat{z}_k)$ in (5.1). We begin by deriving a basic property of $\widehat{m}_{fc}(z)$ near $(\widehat{z}_k)$. Recall the definition of $\eta _0$ in (3.23).

Lemma 5.2

For $z = E + \mathrm {i}\eta _0 \in {\mathcal {D}}_{\epsilon }'$, the following hold on $\Omega _V$:

• (1) if $|z- \widehat{z}_j| \ge N^{-1/2 + 3\epsilon }$ for all $j \in [\![1,n_0-1]\!]$, then there exists a constant $C >1$ such that

  $$\begin{aligned} C^{-1} \eta _0 \le {\mathrm {Im }}\,\widehat{m}_{fc} (z) \le C \eta _0; \end{aligned}$$

• (2) if $z= \widehat{z}_k$ for some $k \in [\![1,n_0-1]\!]$, then there exists a constant $C >1$ such that

  $$\begin{aligned} C^{-1} N^{-1/2} \le {\mathrm {Im }}\,\widehat{m}_{fc} (z) \le C N^{-1/2}. \end{aligned}$$

Remark 5.3

We remark that Lemma 5.2 does not hold when $\lambda < \lambda _+$. In this case, we have near the edge that

$$\begin{aligned} \frac{{\mathrm {Im }}\,m_{fc}(z)}{{\mathrm {Im }}\,m_{fc}(z) + \eta } = 1 + o(1), \end{aligned}$$

(5.5)

which implies that ${\mathrm {Im }}\,m_{fc}(z) \gg \eta$. We may apply a similar argument to show that ${\mathrm {Im }}\,\widehat{m}_{fc}(z) \gg \eta$ as well. See Lemma A.5 in [31] for more detail.

Proof of 5.2

Recall that

$$\begin{aligned} \widehat{R}_2 (z) = \frac{{\mathrm {Im }}\,\widehat{m}_{fc}(z)}{\eta _0 + {\mathrm {Im }}\,\widehat{m}_{fc}(z)} = \frac{1}{N} \sum _{i=1}^N \frac{1}{|\lambda v_i - z - \widehat{m}_{fc}(z)|^2}<1,\quad ( z\in {\mathbb {C}}^+), \end{aligned}$$

(5.6)

c.f., (4.1). For given $z \in {\mathcal {D}}_{\epsilon }'$ with ${\mathrm {Im }}\,z=\eta _0$, choose $k \in [\![1, n_0 -1 ]\!]$ such that (3.26) is satisfied. In the first case, where $|z- \widehat{z}_k| \gg N^{-1/2 + 2\epsilon }$, we find from Lemmas 4.1 and 3.7 that

$$\begin{aligned} |\lambda v_k - {\mathrm {Re }}\,(z + \widehat{m}_{fc}(z))| \gg N^{-1/2 + 2\epsilon }. \end{aligned}$$

(5.7)

Since $z=E+\mathrm {i}\eta _0$ satisfies (3.26), we also find that

$$\begin{aligned} \widehat{R}_2^{(k)}(z)&\mathrel {\mathop :}= \frac{1}{N} \sum _{i}^{(k)} \frac{1}{|\lambda v_i - z - \widehat{m}_{fc}(z)|^2} \nonumber \\&= \frac{1}{N} \sum _{i}^{(k)} \frac{1}{|\lambda v_i - z - m_{fc}(z)|^2} + o(1) < c < 1, \end{aligned}$$

(5.8)

for some constant $c$. Thus,

$$\begin{aligned} \widehat{R}_2(z) = \frac{1}{N} \frac{1}{|\lambda v_k - z - \widehat{m}_{fc}(z)|^2} + \frac{1}{N} \sum _{i}^{(k)} \frac{1}{|\lambda v_i - z - \widehat{m}_{fc}(z)|^2} < c' < 1, \end{aligned}$$

(5.9)

for some constant $c'$. Recalling that

$$\begin{aligned} {\mathrm {Im }}\,\widehat{m}_{fc}(z) = \frac{\widehat{R}_2(z)}{1 - \widehat{R}_2(z)} \eta _0, \end{aligned}$$

statement $(1)$ of the lemma follows.

Next, we consider the second case: $z=\widehat{z}_k=\widehat{E}_k +\mathrm {i}\eta _0$, for some $k\in [\![1,n_0-1]\!]$. We have

$$\begin{aligned} {\mathrm {Im }}\,\widehat{m}_{fc}(\widehat{z}_k) =&\frac{1}{N} \sum _{i=1}^N \frac{\eta _0 + {\mathrm {Im }}\,\widehat{m}_{fc}(\widehat{z}_k)}{|\lambda v_i - \widehat{z}_k - \widehat{m}_{fc}(\widehat{z}_k)|^2} = \frac{1}{N} \frac{1}{\eta _0 + {\mathrm {Im }}\,\widehat{m}_{fc}(\widehat{z}_k)}\nonumber \\&+ \frac{1}{N} \sum _{i}^{(k)} \frac{\eta _0 + {\mathrm {Im }}\,\widehat{m}_{fc} (\widehat{z}_k)}{|\lambda v_i - \widehat{z}_k - \widehat{m}_{fc}(\widehat{z}_k)|^2}, \end{aligned}$$

(5.10)

hence

$$\begin{aligned} \left( 1 \!-\! \widehat{R}_2^{(k)}(\widehat{z}_k)\right) \left( {\mathrm {Im }}\,\widehat{m}_{fc} (\widehat{z}_k)\right) ^2 \!+\! \left( 1 - 2\widehat{R}_2^{(k)}(\widehat{z}_k)\right) \eta _0 \,{\mathrm {Im }}\,\widehat{m}_{fc}(\widehat{z}_k) \!=\! \frac{1}{N} + \widehat{R}_2^{(k)}(\widehat{z}_k) \eta _0^2. \end{aligned}$$

Solving the quadratic equation above for ${\mathrm {Im }}\,\widehat{m}_{fc} (\widehat{z}_k)$, we find

$$\begin{aligned} C^{-1} N^{-1/2} \le {\mathrm {Im }}\,\widehat{m}_{fc} (\widehat{z}_k) \le C N^{-1/2}, \end{aligned}$$

completing the proof of the lemma. $\square$

Remark 5.4

For any $z = E + \mathrm {i}\eta _0 \in {\mathcal {D}}_{\epsilon }'$, we have, similarly to (5.10), that

$$\begin{aligned} {\mathrm {Im }}\,\widehat{m}_{fc}(z) \le \frac{1}{N} \frac{1}{\eta _0 + {\mathrm {Im }}\,\widehat{m}_{fc}(z)} + \frac{1}{N} \sum _{i}^{(k)} \frac{\eta _0 + {\mathrm {Im }}\,\widehat{m}_{fc}(z)}{|\lambda v_i - z - \widehat{m}_{fc}(z)|^2}. \end{aligned}$$

(5.11)

Solving this inequality for ${\mathrm {Im }}\,\widehat{m}_{fc}(z)$, we find that ${\mathrm {Im }}\,\widehat{m}_{fc} (z) \le C N^{-1/2}$.

Recall that by Schur’s complement formula we have, for all $i\in [\![1,N]\!]$,

$$\begin{aligned} G_{ii} = \frac{1}{\lambda v_i + w_{ii} - z - \sum _{s, t}^{(i)} {h_{is} G_{st}^{(i)} h_{ti}}}; \end{aligned}$$

see (3.7). Define ${\mathbb {E}}_i$ to be the partial expectation with respect to the $i$-th column/row of $W$ and set

$$\begin{aligned} Z_i \mathrel {\mathop :}=({\mathbb {1}}-{\mathbb {E}}_i) \sum _{s, t}^{(i)} {h_{is} G_{st}^{(i)} h_{ti}} = \sum _{s}^{(i)} \left( |w_{is}|^2 - \frac{1}{N}\right) G_{ss}^{(i)} + \sum _{s \ne t}^{(i)} w_{is} G_{st}^{(i)} w_{ti}. \end{aligned}$$

(5.12)

Using $Z_i$, we can rewrite $G_{ii}$ as

$$\begin{aligned} G_{ii} = \frac{1}{\lambda v_i + w_{ii} - z - m^{(i)} - Z_i}. \end{aligned}$$

(5.13)

The following lemma states an a priori bound on ${\mathrm {Im }}\,m$, the imaginary part of $m=N^{-1}{{\mathrm{Tr}}}G$.

Lemma 5.5

We have with $(\xi ,\nu )$-high probability on $\Omega _V$ that, for all $z = E + \mathrm {i}\eta _0 \in {\mathcal {D}}_{\epsilon }'$,

$$\begin{aligned} {\mathrm {Im }}\,m(z) \le \frac{N^{2\epsilon }}{\sqrt{N}}. \end{aligned}$$

(5.14)

Proof

Fix $\eta = \eta _0$. For given $z=E+\mathrm {i}\eta _0 \in {\mathcal {D}}_{\epsilon }'$, choose $k \in [\![1, n_0 -1 ]\!]$ such that (3.26) is satisfied. Suppose that ${\mathrm {Im }}\,m(z) > N^{-1/2 + 5\epsilon /3}$. Reasoning as in the proof of Lemma 3.7, we find the following equation for $(m -\widehat{m}_{fc})$:

$$\begin{aligned} m - \widehat{m}_{fc}&= \frac{1}{N} \sum _{i=1}^N \left( \frac{1}{\lambda v_i + w_{ii} - z - m^{(i)} - Z_i} - \frac{1}{\lambda v_i - z - \widehat{m}_{fc}}\right) \nonumber \\&= \frac{1}{N} \sum _{i=1}^N \frac{m^{(i)} - \widehat{m}_{fc} + Z_i - w_{ii}}{(\lambda v_i + w_{ii} - z - m^{(i)} - Z_i) (\lambda v_i - z - \widehat{m}_{fc})}. \end{aligned}$$

(5.15)

Abbreviate

$$\begin{aligned} T_m\equiv T_m(z) \mathrel {\mathop :}=\frac{1}{N} \sum _{i=1}^N \left| \frac{1}{(\lambda v_i + w_{ii} - z - m^{(i)} - Z_i) (\lambda v_i - z - \widehat{m}_{fc})}\right| . \end{aligned}$$

(5.16)

We are going to show that $T_m<c<1$: We define events $\Omega _Z$ and $\Omega _W$ by

$$\begin{aligned} \Omega _Z(z)\equiv \Omega _Z\mathrel {\mathop :}=\bigcap _{i=1}^N\left\{ |Z_i|\le (\varphi _N)^{\xi } \sqrt{ \frac{{\mathrm {Im }}\,m^{(i)}}{N \eta }}\right\} \,, \qquad \Omega ^W \mathrel {\mathop :}=\bigcap _{i=1}^N\left\{ |w_{ii}|\le \frac{(\varphi _N)^{\xi }}{\sqrt{N}}\right\} . \end{aligned}$$

(5.17)

We notice that, by the large deviation estimates in Lemma 3.4 and the subexponential decay of $|w_{ii}|$, $\Omega _Z$ and $\Omega _W$ both hold with high probability. Suppose now that $\Omega _Z$ and $\Omega _W$ hold. Then, we have

$$\begin{aligned} |Z_i| \le (\varphi _N)^{\xi } \sqrt{\frac{{\mathrm {Im }}\,m^{(i)}}{N \eta }} \le (\varphi _N)^{-\xi } {\mathrm {Im }}\,m^{(i)} + C \frac{(\varphi _N)^{2\xi }}{N \eta } \ll {\mathrm {Im }}\,m, \end{aligned}$$

where we have used $|m - m^{(i)}| \le C (N \eta )^{-1} \ll {\mathrm {Im }}\,m$. We also have from $\eta \ll {\mathrm {Im }}\,m$ that

$$\begin{aligned} {\mathrm {Im }}\,m^{(i)} + \eta + {\mathrm {Im }}\,Z_i = (1 + o(1)) {\mathrm {Im }}\,m. \end{aligned}$$

Thus,

$$\begin{aligned} \begin{aligned} \frac{1}{N} \sum _{i=1}^N \frac{1}{|\lambda v_i + w_{ii} - z - m^{(i)} - Z_i|^2}&= \frac{1}{N} \sum _{i=1}^N \frac{{\mathrm {Im }}\,G_{ii}}{{\mathrm {Im }}\,m^{(i)} + \eta + {\mathrm {Im }}\,Z_i}\\&= \frac{1}{N} \sum _{i=1}^N \frac{ {\mathrm {Im }}\,G_{ii}}{{\mathrm {Im }}\,m}(1 + o(1)) = 1 + o(1). \end{aligned} \end{aligned}$$

(5.18)

We get from Lemma 3.7 that, on $\Omega _V$,

$$\begin{aligned} \frac{1}{N} \sum _i^{(k)} \frac{1}{|\lambda v_i - z - \widehat{m}_{fc}|^2} = \frac{1}{N} \sum _i^{(k)} \frac{1 + o(1)}{|\lambda v_i - z - m_{fc}|^2} < c < 1, \end{aligned}$$

for some constant $c > 0$, and

$$\begin{aligned} \frac{1}{N} \left| \frac{1}{(\lambda v_k + w_{kk} - z - m^{(k)} - Z_k) (\lambda v_k - z - \widehat{m}_{fc})} \right| \!\le \! C \frac{1}{N} \frac{1}{N^{-1/2 + 5\epsilon /3} \eta } \le N^{-2\epsilon /3}. \end{aligned}$$

Hence, we find that $T_m < c' < 1$ for some constant $c'$. Notice that the assumption ${\mathrm {Im }}\,m > N^{-1/2 + 5\epsilon /3}$ also implies that

$$\begin{aligned} |m - \widehat{m}_{fc}| \ge |{\mathrm {Im }}\,m - {\mathrm {Im }}\,\widehat{m}_{fc}| > C N^{-1/2 + 5\epsilon /3}\,, \end{aligned}$$

as we can see from Remark 5.4. Now, if we let

$$\begin{aligned} M \mathrel {\mathop :}=\max _i |m^{(i)} - m + Z_i - w_{ii}|, \end{aligned}$$

then $M \ll |m - \widehat{m}_{fc}|$. Thus, taking absolute value on both sides of (5.15), we get

$$\begin{aligned} |m - \widehat{m}_{fc}| \le T_m (|m - \widehat{m}_{fc}| + M) = \left( T_m + o(1)\right) |m - \widehat{m}_{fc}|, \end{aligned}$$

contradicting $T_m < c' < 1$.

We have thus shown that for fixed $z\in {\mathcal {D}}_\epsilon '$,

$$\begin{aligned} {\mathrm {Im }}\,m(z) \le N^{-1/2 + 5\epsilon /3}, \end{aligned}$$

with high probability on $\Omega _V$.

In order to prove that the desired bound holds uniformly on $z$, we consider a lattice ${\mathcal {L}}$ such that, for any $z$ satisfying the assumption of the lemma, there exists $z' = E' + \mathrm {i}\eta _0 \in {\mathcal {L}}$ with $|z - z'| \le N^{-3}$. We have already seen that the uniform bound holds for all points in ${\mathcal {L}}$. For a point $z \notin {\mathcal {L}}$, we have $|m(z) - m(z')| \le \eta _0^2 |z-z'| \le N^{-1}$, for $z' \in {\mathcal {L}}$ with $|z - z'| \le N^{-3}$. This proves the desired lemma. $\square$

As a corollary of Lemma 5.5 we obtain:

Corollary 5.6

We have with $(\xi ,\nu )$-high probability on $\Omega _V$ that, for all $z = E + \mathrm {i}\eta _0 \in {\mathcal {D}}_{\epsilon }'$,

$$\begin{aligned} \max _i |Z_i(z)| \le \frac{N^{2\epsilon }}{\sqrt{N}}\,, \qquad \max _i |Z_i^{(k)}(z)| \le \frac{N^{2\epsilon }}{\sqrt{N}}\,,\qquad \quad (k\in [\![1,N]\!]). \end{aligned}$$

(5.19)

Next, we prove an estimate for the difference $\Lambda (z)\mathrel {\mathop :}=|m(z)-\widehat{m}_{fc}(z)|$. We first show the bound on $\Lambda (z)$ in Proposition 5.1 holds for large $\eta$; see Lemma 5.7 below. Then, using the self-consistent equation (5.15), we show that if, for some $z\in {\mathcal {D}}_{\epsilon }', \Lambda (z)\le N^{-1/2+3\epsilon }$, then we must have $\Lambda (z)\le N^{-1/2+2\epsilon }$ with high probability; see Lemma 5.8. Thus, using the Lipschitz continuity of the Green function $G$ and of the Stieltjes transform $\widehat{m}_{fc}$, we can conclude that if $\Lambda (z)\le N^{-1/2+2\epsilon }$, we also have $\Lambda (z')\le N^{-1/2+2\epsilon }$, with high probability, for $z'$ in a sufficiently small neighborhood of $z$. Repeated use this argument yields a proof of Proposition 5.1 at the end of this subsection.

Recall that we have set $\kappa _0=N^{-1/(\mathrm {b}+1)}$; see (3.23).

Lemma 5.7

We have with high probability on $\Omega _V$ that, for all $z = E + \mathrm {i}\eta \in {\mathcal {D}}_{\epsilon }'$ with $N^{-1/2 + \epsilon } \le \eta \le N^{\epsilon } \kappa _0$,

$$\begin{aligned} |m(z)-\widehat{m}_{fc}(z)|\le \frac{N^{2\epsilon }}{\sqrt{N}}. \end{aligned}$$

(5.20)

Proof

The proof closely follows the proof of Lemma 5.5. Fix $z\in {\mathcal {D}}_{\epsilon }'$. Suppose that $|m(z)-\widehat{m}_{fc}(z) | > N^{-1/2 + 5\epsilon /3}$. Consider the self-consistent equation (5.15) and define $T_m$ as in (5.16).

Since ${\mathrm {Im }}\,m(E+\mathrm {i}\eta )\ge C\eta$, for $z\in {\mathcal {D}}_{\epsilon }'$, with high probability on $\Omega _V$, we obtain that

$$\begin{aligned} {\mathrm {Im }}\,m^{(i)} + \eta + {\mathrm {Im }}\,Z_i = (1 + o(1)) {\mathrm {Im }}\,m, \end{aligned}$$

with high probability on $\Omega _V$, as in the proof of Lemma 5.5. This implies that $T_m < c < 1$. If we let

$$\begin{aligned} M = \max _i |m^{(i)} - m + Z_i - w_{ii}|, \end{aligned}$$

it then follows that $M \ll |m - \widehat{m}_{fc}|$ with high probability on $\Omega _V$. Taking absolute values on both sides of (5.15), we obtain a contradiction to the assumption $|m(z)-\widehat{m}_{fc}(z)| > N^{-1/2 + 5\epsilon /3}$. In order to attain a uniform bound, we again use the lattice argument as in the proof of Lemma 5.5. This completes the proof of the lemma. $\square$

Lemma 5.8

Let $z \in {\mathcal {D}}_{\epsilon }'$. If $|m(z)-\widehat{m}_{fc}(z)| \le N^{-1/2 + 3\epsilon }$, then we have with $(\xi ,\nu )$-high probability on $\Omega _V$ that $|m(z)-\widehat{m}_{fc}(z) | \le N^{-1/2 + 2\epsilon }$.

Proof

Since the proof closely follows the proof of Lemma 5.5, we only check the main steps here. Fix $z\in {\mathcal {D}}_{\epsilon }'$ and choose $k \in [\![1, n_0 -1 ]\!]$ such that (3.26) is satisfied. Assume that $N^{-1/2 + 5\epsilon /3} < |m(z)-\widehat{m}_{fc}(z)| \le N^{-1/2 + 3\epsilon }$. We consider the self-consistent equation (5.15) and define $T_m$ as in (5.16). We now estimate $T_m$. For $i \ne k$, $i\in [\![1,N]\!]$, we have

$$\begin{aligned} \frac{1}{(\lambda v_i + w_{ii} - z - m^{(i)} - Z_i) (\lambda v_i - z - \widehat{m}_{fc})} = \frac{1}{(\lambda v_i - z - \widehat{m}_{fc})^2} + o(1), \end{aligned}$$

where we have used that

$$\begin{aligned} |w_{ii} - m^{(i)} - Z_i + \widehat{m}_{fc}|&\le |w_{ii}| + |m - m^{(i)}| + |m - \widehat{m}_{fc}| + |Z_i|\nonumber \\&\le \frac{N^{\epsilon }}{\sqrt{N}} + \frac{C}{N \eta } + N^{-1/2 + 3\epsilon } + C (\varphi _N)^{\xi } \sqrt{\frac{{\mathrm {Im }}\,m^{(i)}}{N \eta }}\nonumber \\&\ll |v_i - v_k|, \end{aligned}$$

(5.21)

which holds with high probability on $\Omega _V$. For $i=k$, we have

$$\begin{aligned}&|\lambda v_k + w_{kk} - z - m^{(k)} - Z_k| + |\lambda v_k - z - \widehat{m}_{fc}| \nonumber \\&\quad \ge |m - \widehat{m}_{fc}| - |w_{kk}| - |m - m^{(k)}| - |Z_k|\nonumber \\&\quad \ge \frac{1}{2} N^{-1/2 + 2\epsilon }, \end{aligned}$$

(5.22)

thus, as in the proofs of Lemmas 3.7 and 5.5,

$$\begin{aligned} \frac{1}{N} \left| \frac{1}{(\lambda v_k + w_{kk} - z - m^{(k)} - Z_k) (\lambda v_k - z - \widehat{m}_{fc})}\right| \le C N^{-2\epsilon /3}, \end{aligned}$$

where we used that $|G_{kk}|\,,|g_k|\le \eta ^{-1}$.

We now have that

$$\begin{aligned} T_m = \widehat{R}_2^{(k)} + o(1) = R_2 + o(1), \end{aligned}$$

(5.23)

and, in particular, $T_m < c < 1$, with high probability on $\Omega _V$. We again let $M \mathrel {\mathop :}=\max _i |m^{(i)} - m + Z_i - w_{ii}|$ and find that $M \ll |m - \widehat{m}_{fc}|$ with high probability on $\Omega _V$, which contradicts the assumption. Therefore, if $|m(z)-\widehat{m}_{fc}(z) | \le N^{-1/2 + 3\epsilon }$, then $|m(z)-\widehat{m}_{fc}(z)| \le N^{-1/2 + 5\epsilon /3}$ with high probability on $\Omega _V$. In order to attain a uniform bound, we use the lattice argument as in the proof of Lemma 5.5. This proves the desired lemma. $\square$

We now prove Proposition 5.1 using a discrete continuity argument.

Proof of Proposition 5.1

Fix $E$ such that $z=E+\mathrm {i}\eta _0\in {\mathcal {D}}_{\epsilon }'$. Consider a sequence $(\eta _j)$ defined by $\eta _{j=0} = \eta _0$ and $\eta _j = \eta _{j-1} + N^{-2}$. Let $K$ be the smallest positive integer such that $\eta _K \ge N^{-1/2 + \epsilon }$. We prove by induction that, for $z_j = E + \mathrm {i}\eta _j$, we have with high probability on $\Omega _V$ that

$$\begin{aligned} |m(z_j)-\widehat{m}_{fc}(z_j)|\le \frac{N^{2\epsilon }}{\sqrt{N}}. \end{aligned}$$

(5.24)

The case $j=K$ is already proved in Lemma 5.7. For any $z = E + \mathrm {i}\eta$, with $\eta _{j-1} \le \eta \le \eta _j$, we have

$$\begin{aligned} |m(z_j) - m(z)| \le \frac{|z_j - z|}{\eta _{j-1}^2} \le \frac{N^{2 \epsilon }}{N}, \qquad \quad |\widehat{m}_{fc}(z_j) - \widehat{m}_{fc}(z)| \le \frac{|z_j - z|}{\eta _{j-1}^2} \le \frac{N^{2 \epsilon }}{N}. \end{aligned}$$

Thus, we find that if $|\widehat{m}_{fc}(z_j) - m(z_j)| \le N^{-1/2 + 2\epsilon }$ then

$$\begin{aligned} |m(z)-\widehat{m}_{fc}(z)|\le N^{-1/2 + 2\epsilon } + \frac{2 N^{2 \epsilon }}{N} \ll N^{-1/2 + 3\epsilon }. \end{aligned}$$

We now invoke Lemma 5.8 to obtain that $|m(z)-\widehat{m}_{fc}(z)|\le N^{-1/2 + 2\epsilon }$. This proves the desired lemma for any $z = E + \mathrm {i}\eta$, with $\eta _{j-1} \le \eta \le \eta _j$. The desired lemma can now be proved by induction on $j$. Uniformity can now be obtained using a lattice argument. $\square$

5.2 Estimates on $|m - m^{(i)}|$

In order to derive a more accurate estimate on the difference $|{\mathrm {Im }}\,m(z) - {\mathrm {Im }}\,\widehat{m}_{fc}(z)|$, as the one obtained in Proposition 5.1, we establish detailed estimates on $|m - m^{(i)}|$ and $N^{-1}\sum Z_i$. We first prove the following bound on the difference $|m - m^{(i)}|$.

Lemma 5.9

There exists a constant $C > 1$ such that the following bound holds with $(\xi ,\nu )$-high probability on $\Omega _V$ for all $z = E + \mathrm {i}\eta _0 \in {\mathcal {D}}_{\epsilon }'$: For given $z$, choose $k \in [\![1, n_0 -1 ]\!]$ such that (3.26) is satisfied. Then, for any $i \ne k$, $i\in [\![1,N]\!]$,

$$\begin{aligned} |m(z) - m^{(i)}(z)| \le C N^{1/(\mathrm {b}+1)} \frac{N^{4\epsilon }}{N} \end{aligned}$$

(5.25)

and

$$\begin{aligned} |m^{(k)}(z)-m^{(ki)}(z)|\le CN^{1/(\mathrm {b}+1)} \frac{N^{4\epsilon }}{N}. \end{aligned}$$

(5.26)

Proof

Let $\eta = \eta _0$. Since

$$\begin{aligned} G_{ij} = - G_{ii} \left( \sum _s^{(i)} w_{is} G_{sj}^{(i)}\right) , \end{aligned}$$

we find from the large deviation estimates in Lemma 3.4 and the Ward identity (3.11) that

$$\begin{aligned} |G_{jj} - G_{jj}^{(i)}| = \left| \frac{G_{ij} G_{ji}}{G_{ii}}\right| \le (\varphi _N)^{2\xi } |G_{ii}| \frac{{\mathrm {Im }}\,G_{jj}^{(i)}}{N \eta }, \end{aligned}$$

with high probability on $\Omega _V$. For $i \ne k$, we have

$$\begin{aligned} |G_{ii}| = \frac{1}{|\lambda v_i + w_{ii} - z - m^{(i)} - Z_i|} \le \frac{C}{|\lambda v_i - z - \widehat{m}_{fc}|} \le C N^{\epsilon } \kappa _0^{-1}, \end{aligned}$$

with high probability on $\Omega _V$. Thus, we obtain

$$\begin{aligned} |m(z) - m^{(i)}(z)|&\le \frac{|G_{ii}|}{N} + \frac{1}{N} \sum _{j}^{(i)}|G_{jj} - G_{jj}^{(i)}| \le \frac{|G_{ii}|}{N} \nonumber \\ {}&\quad + C (\varphi _N)^{2\xi } \frac{N^{\epsilon } \kappa _0^{-1}}{N} \sum _{j}^{(i)} \frac{{\mathrm {Im }}\,G_{jj}^{(i)}}{N \eta } \nonumber \\&\le \frac{N^{\epsilon } \kappa _0^{-1}}{N} + C (\varphi _N)^{2\xi } \frac{N^{\epsilon } \kappa _0^{-1}}{N \eta } {\mathrm {Im }}\,m^{(i)} \le C N^{1/(\mathrm {b}+1)} \frac{N^{4\epsilon }}{N}, \end{aligned}$$

(5.27)

with high probability on $\Omega _V$. Together with the usual lattice argument, this proves the first part of the lemma. The second part of the lemma can be proved in a similar manner. $\square$

5.3 Estimates on $N^{-1}\sum Z_i$

Recall that $n_0>10$ is an integer independent of $N$. In the next lemma, we control the fluctuation average $\frac{1}{N} \sum _{i=n_0}^N Z_i$ and other related quantities. Here, we aim to use cancellations in the averaging over $i$, but note that $(Z_i)$ are not independent.

Lemma 5.10

There is a constant $c$, such that, for all $z\in {\mathcal {D}}_\epsilon '$, the following bounds hold with $(\xi -2,\nu )$-high probability on $\Omega _V$:

$$\begin{aligned} \left| \frac{1}{N} \sum _{i=n_0}^N Z_i(z)\right| \le (\varphi _N)^{c\xi } N^{-1/2-{\varpi _{\mathrm{b}}}/2+4\epsilon }, \end{aligned}$$

(5.28)

and, for $k\in [\![1,n_0-1]\!]$,

$$\begin{aligned} \left| \frac{1}{N} \sum _{\begin{array}{c} i=n_0\\ i\not =k \end{array}}^N Z_i^{(k)}(z)\right| \le (\varphi _N)^{c\xi }N^{-1/2-{\varpi _{\mathrm{b}}}/2+4\epsilon }. \end{aligned}$$

(5.29)

Corollary 5.11

There is a constant $c$, such that, for all $z\in {\mathcal {D}}_\epsilon '$, the following bounds hold with $(\xi -2,\nu )$-high probability on $\Omega _V$:

$$\begin{aligned} \left| \frac{1}{N} \sum _{i=n_0}^N \frac{w_{ii} - Z_i(z)}{(\lambda v_i - z - \widehat{m}_{fc}(z))^2}\right| \le (\varphi _N)^{c\xi }N^{-1/2-{\varpi _{\mathrm{b}}}/2+4\epsilon }, \end{aligned}$$

(5.30)

and, for $k\in [\![1,n_0-1]\!]$,

$$\begin{aligned} \left| \frac{1}{N} \sum _{\begin{array}{c} i=n_0\\ i\not =k \end{array}}^N \frac{w_{ii} - Z_i^{(k)}(z)}{(\lambda v_i - z - \widehat{m}_{fc}(z))^2} \right| \le (\varphi _N)^{c\xi }N^{-1/2-{\varpi _{\mathrm{b}}}/2+4\epsilon }. \end{aligned}$$

(5.31)

Remark 5.12

The bounds we obtained in Lemmas 5.9, 5.10, and Corollary 5.11 are $o(\eta )$. This will be used on several occasions in the next subsection.

Lemma 5.10 and Corollary 5.11 are proved in Sect. 6.

5.4 Proof of Proposition 5.1

Recall the definition of $(\widehat{z}_k)$ in (5.1). We first estimate ${\mathrm {Im }}\,m(z)$ for $z = E + \mathrm {i}\eta _0$ satisfying $|z - \widehat{z}_k| \ge N^{-1/2 + 3\epsilon }$, for all $k \in [\![1, n_0 -1 ]\!]$.

Lemma 5.13

There exists a constant $C > 1$ such that the following bound holds with $(\xi -2,\nu$)-high probability on $\Omega _V$: For any $z = E + \mathrm {i}\eta _0 \in {\mathcal {D}}_{\epsilon }'$, satisfying $|z - \widehat{z}_k| \ge N^{-1/2 + 3\epsilon }$ for all $k \in [\![1, n_0 -1 ]\!]$, we have

$$\begin{aligned} C^{-1} \eta \le {\mathrm {Im }}\,m(z) \le C \eta . \end{aligned}$$

(5.32)

Proof

Let $z\in {\mathcal {D}}_{\epsilon }'$ with $\eta =\eta _0$ and choose $k \in [\![1, n_0 -1 ]\!]$ such that (3.26) is satisfied. Consider

$$\begin{aligned} m = \frac{G_{kk}}{N} + \frac{1}{N} \sum _{i}^{(k)} \frac{1}{\lambda v_i + w_{ii} - z - m^{(i)} - Z_i}. \end{aligned}$$

(5.33)

From the assumption in (3.26), Corollary 5.6, and Proposition 5.1, we find that, with high probability on $\Omega _V$,

$$\begin{aligned} \begin{aligned}&{\left| \frac{1}{N} \sum _{i}^{(k)} {\left( \frac{1}{\lambda v_i + w_{ii} - z - m^{(i)} - Z_i} \!-\! \frac{1}{\lambda v_i - z - \widehat{m}_{fc}}\! -\! \frac{m^{(i)} - \widehat{m}_{fc} + Z_i - w_{ii}}{(\lambda v_i - z - \widehat{m}_{fc})^2}\right) }\right| } \\&\le \frac{C}{N} \sum _{i}^{(k)} \frac{N^{-1 + 4\epsilon }}{|\lambda v_i - z - \widehat{m}_{fc}|^3} \le C \frac{N^{4 \epsilon }}{N} N^{\epsilon } N^{1/(\mathrm {b}+1)} \frac{1}{N} \sum _{i}^{(k)} \frac{1}{|\lambda v_i - z - \widehat{m}_{fc}|^2} \ll \eta . \end{aligned} \end{aligned}$$

(5.34)

We also observe that

$$\begin{aligned} \left| \frac{1}{N} \sum _{\begin{array}{c} i=1\\ i \ne k \end{array}}^{n_0} \frac{w_{ii} - Z_i}{(\lambda v_i - z - \widehat{m}_{fc}(z))^2} \right| \le C N^{-1} N^{-1/2 + 2\epsilon } N^{1/(\mathrm {b}+1)} \ll N^{-1} \ll \eta . \end{aligned}$$

Thus, from Lemma 5.9 and Corollary 5.11, we find with high probability on $\Omega _V$ that

$$\begin{aligned} \frac{1}{N} \sum _{i}^{(k)} \frac{m^{(i)} - \widehat{m}_{fc} + Z_i - w_{ii}}{(\lambda v_i - z - \widehat{m}_{fc})^2} = \frac{1}{N} \sum _{i}^{(k)} \frac{m - \widehat{m}_{fc}}{(\lambda v_i - z - \widehat{m}_{fc})^2} + o(\eta ). \end{aligned}$$

(5.35)

Recalling (5.7), i.e.,

$$\begin{aligned} |\lambda v_k - {\mathrm {Re }}\,(z + \widehat{m}_{fc}(z))| \gg N^{-1/2 + 2\epsilon }, \end{aligned}$$

we get $|G_{kk}| \le N^{1/2 - 2\epsilon }$. We thus obtain from (5.33), (5.34), and (5.35) that, with high probability on $\Omega _V$,

$$\begin{aligned} m = \frac{1}{N} \sum _{i}^{(k)} \left( \frac{1}{\lambda v_i - z - \widehat{m}_{fc}} + \frac{m - \widehat{m}_{fc}}{(\lambda v_i - z - \widehat{m}_{fc})^2} \right) + o(\eta ). \end{aligned}$$

(5.36)

We also notice that, with high probability on $\Omega _V$,

$$\begin{aligned} \frac{1}{N} \sum _{i}^{(k)} \frac{1}{\lambda v_i - z - m} =&\frac{1}{N} \sum _{i}^{(k)} \left( \frac{1}{\lambda v_i - z - \widehat{m}_{fc}} + \frac{m - \widehat{m}_{fc}}{(\lambda v_i - z - \widehat{m}_{fc})^2}\right) \nonumber \\&+ {\mathcal {O}}\left( \frac{1}{N} \sum _{i}^{(k)} \frac{N^{-1 + 4\epsilon }}{|\lambda v_i - z - \widehat{m}_{fc}|^3}\right) , \end{aligned}$$

(5.37)

and following the estimate in (5.34), we find that

$$\begin{aligned} \frac{1}{N} \sum _{i}^{(k)} \frac{1}{\lambda v_i - z - m} =&\frac{1}{N} \sum _{i}^{(k)} \left( \frac{1}{\lambda v_i - z - \widehat{m}_{fc}}+ \frac{m - \widehat{m}_{fc}}{(\lambda v_i - z - \widehat{m}_{fc})^2}\right) \nonumber \\&+ o(\eta ) = m + o(\eta ). \end{aligned}$$

(5.38)

Taking imaginary parts, we get

$$\begin{aligned} {\mathrm {Im }}\,m = \frac{1}{N} \sum _{i}^{(k)} \frac{\eta + {\mathrm {Im }}\,m}{|\lambda v_i - z - m|^2} + o(\eta ). \end{aligned}$$

Since

$$\begin{aligned} \frac{1}{N} \sum _{i}^{(k)} \frac{1}{|\lambda v_i - z - m|^2} = \frac{1}{N} \sum _{i}^{(k)} \frac{1}{|\lambda v_i - z - m_{fc}|^2} + o(1) < c < 1, \end{aligned}$$

for some constant $c$, we can conclude that $C^{-1} \eta \le {\mathrm {Im }}\,m \le C \eta$ with high probability for some $C > 1$. This proves the desired lemma. $\square$

As a next step, we prove that there exists $\widetilde{z}_k = \widetilde{E}_k + \mathrm {i}\eta _0$ near $\widehat{z}_k$ such that ${\mathrm {Im }}\,m(\widetilde{z}_k) \gg \eta$. Before proving this, we first show that ${\mathrm {Im }}\,m^{(k)} (z) \sim \eta$ even if $z$ is near $\widehat{z}_k$.

Lemma 5.14

There exists a constant $C > 1$ such that the following bound holds with $(\xi -2,\nu )$-high probability on $\Omega _V$, for all $z = E + \mathrm {i}\eta _0 \in {\mathcal {D}}_{\epsilon }'$: For given $z$, choose $k \in [\![1, n_0 -1 ]\!]$ such that (3.26) is satisfied. Then, we have

$$\begin{aligned} C^{-1} \eta _0 \le {\mathrm {Im }}\,m^{(k)}(z) \le C \eta _0. \end{aligned}$$

(5.39)

Proof

Reasoning as in the proof of Lemma 5.13, we find from Proposition 5.1, Corollary 5.6, Lemma 5.9, and Corollary 5.11 that, with high probability on $\Omega _V$,

$$\begin{aligned} m^{(k)} =&\frac{1}{N} \sum _i^{(k)} \left( \frac{1}{\lambda v_i - z - \widehat{m}_{fc}} + \frac{m^{(k)} - \widehat{m}_{fc}}{(\lambda v_i - z - \widehat{m}_{fc})^2}\right) + o(\eta _0)\nonumber \\ =&\frac{1}{N} \sum _i^{(k)} \frac{1}{\lambda v_i - z -m^{(k)}} + o(\eta _0). \end{aligned}$$

(5.40)

Considering the imaginary part, we can prove the desired lemma as in the proof of Lemma 5.13. $\square$

Corollary 5.15

There exists a constant $C > 1$ such that the following bound holds with $(\xi -2,\nu )$-high probability on $\Omega _V$, for all $z = E + \mathrm {i}\eta _0 \in {\mathcal {D}}_{\epsilon }'$: For given $z$, choose $k \in [\![1, n_0 -1 ]\!]$ such that (3.26) is satisfied. Then, we have

$$\begin{aligned} |Z_k| \le C \frac{(\varphi _N)^{\xi }}{\sqrt{N}}. \end{aligned}$$

(5.41)

We are now ready to locate the points $z\in {\mathcal {D}}_{\epsilon }'$ for which ${\mathrm {Im }}\,m(z) \gg \eta _0$.

Lemma 5.16

For any $k \in [\![1, n_0-1 ]\!]$, there exists $\widetilde{E}_k\in {\mathbb {R}}$ such that the following holds with $(\xi -2,\nu )$-high probability on $\Omega _V$: If we let $\widetilde{z}_k\mathrel {\mathop :}=\widetilde{E}_k + \mathrm {i}\eta _0$, then $|\widetilde{z}_k - \widehat{z}_k| \le N^{-1/2 + 3\epsilon }$ and ${\mathrm {Im }}\,m(\widetilde{z}_k) \gg \eta _0$.

Proof

We first notice that the condition $|z - \widehat{z}_k| \ge N^{-1/2 + 3\epsilon }$ has not been used in the derivation of (5.34) and (5.35), hence, even though $|z - \widehat{z}_k| \le N^{-1/2 + 3\epsilon }$, we still attain that

$$\begin{aligned} m =&\frac{G_{kk}}{N} + \frac{1}{N} \sum _i^{(k)} \frac{1}{\lambda v_i + w_{ii} - z - m^{(i)} - Z_i} = \frac{G_{kk}}{N}\nonumber \\&+ \frac{1}{N} \sum _i^{(k)} \frac{1}{\lambda v_i - z - m} + o(\eta _0), \end{aligned}$$

(5.42)

with high probability on $\Omega _V$. Consider

$$\begin{aligned} \frac{1}{G_{kk}} = \lambda v_k + w_{kk} - z - m^{(k)} - Z_k. \end{aligned}$$

Setting $z_k^+ \mathrel {\mathop :}=\widehat{z}_k + N^{-1/2 + 3\epsilon }$, Lemma 4.1 shows that

$$\begin{aligned} {\mathrm {Re }}\,(z_k^+ + m_{fc}(z_k^+)) - {\mathrm {Re }}\,(\widehat{z}_k + m_{fc}(\widehat{z}_k)) \ge C N^{-1/2 + 3\epsilon }, \end{aligned}$$

on $\Omega _V$. Thus, from Lemma 3.7 and the definition of $\widehat{z}_k$, we find that

$$\begin{aligned} \lambda v_k - {\mathrm {Re }}\,(z_k^+ + \widehat{m}_{fc}(z_k^+)) \le -C N^{-1/2 + 3\epsilon }, \end{aligned}$$

on $\Omega _V$. Similarly, if we let $z_k^- \mathrel {\mathop :}=\widehat{z}_k - N^{-1/2 + 3\epsilon }$, we have that

$$\begin{aligned} \lambda v_k - {\mathrm {Re }}\,(z_k^- + \widehat{m}_{fc}(z_k^-)) \ge C N^{-1/2 + 3\epsilon }, \end{aligned}$$

on $\Omega _V$. Since

$$\begin{aligned} |w_{kk} + \widehat{m}_{fc} - m^{(k)} - Z_k| \le |w_{kk}| + |m-\widehat{m}_{fc}| + |m^{(k)}-m| + |Z_k| \ll N^{-1/2 + 3\epsilon }, \end{aligned}$$

with high probability on $\Omega _V$, we find that there exists $\widetilde{z}_k = \widetilde{E}_k + \mathrm {i}\eta _0$, with $\widetilde{E}_k \in (\widehat{E}_k - N^{-1/2 + 3\epsilon }, \widehat{E}_k + N^{-1/2 + 3\epsilon })$, such that ${\mathrm {Re }}\,G_{kk}(\widetilde{z}_k) = 0$. When $z = \widetilde{z}_k$, we have from Lemma 5.14 and Corollary 5.15 that, with high probability on $\Omega _V$,

$$\begin{aligned} |{\mathrm {Im }}\,G_{kk}(\widetilde{z}_k)| \!=\! \frac{1}{|{\mathrm {Im }}\,\widetilde{z}_k + {\mathrm {Im }}\,m^{(k)}(\widetilde{z}_k) + {\mathrm {Im }}\,Z_k(\widetilde{z}_k)|} \ge C (\varphi _N)^{-\xi } N^{1/2},\quad {\mathrm {Re }}\,G_{kk}(\widetilde{z}_k)\!=\!0. \end{aligned}$$

(5.43)

From (5.42), we obtain that

$$\begin{aligned} {\mathrm {Im }}\,m(\widetilde{z}_k) = \frac{{{\mathrm {Im }}\,G_{kk}(\widetilde{z}_k)}}{N} + \frac{1}{N} \sum _i^{(k)} \frac{\eta _0 + {\mathrm {Im }}\,m(\widetilde{z}_k)}{|\lambda v_i - \widetilde{z}_k - m(\widetilde{z}_k)|^2} + o(\eta _0). \end{aligned}$$

(5.44)

Since

$$\begin{aligned} \sum _i^{(k)} \frac{1}{|\lambda v_i - \widetilde{z}_k - m(\widetilde{z}_k)|^2} < c < 1, \end{aligned}$$

with high probability on $\Omega _V$, for some constant $c$, we get

$$\begin{aligned} {\mathrm {Im }}\,m(\widetilde{z}_k) \ge C (\varphi _N)^{-\xi } N^{-1/2} + C \eta _0 \gg \eta _0, \end{aligned}$$

(5.45)

with high probability on $\Omega _V$, which was to be proved. $\square$

We now turn to the proof of Proposition 4.3. Recall that we denote by $\mu _k$ the $k$-th largest eigenvalue of $H$, $k\in [\![1,n_0-1]\!]$. Also recall that $\kappa _0=N^{-1/(\mathrm {b}+1)}$; see (3.23).

Proof of Proposition 4.3

We first consider the case $k=1$. From the spectral decomposition of $H$, we have

$$\begin{aligned} {\mathrm {Im }}\,m(E + \mathrm {i}\eta _0) = \frac{1}{N} \sum _{\alpha =1}^N \frac{\eta _0}{(\mu _{\alpha } - E)^2 + \eta _0^2}, \end{aligned}$$

(5.46)

and in particular, ${\mathrm {Im }}\,m(\mu _1 + \mathrm {i}\eta _0) \ge (N \eta _0)^{-1} \gg \eta _0$. Recall that $\mu _1 \le 3 + \lambda$ with high probability as discussed in (3.22). Recall the definition of  $\widehat{z}_1=\widehat{E}_1+\mathrm {i}\eta _0$ in (5.1). Since, with high probability on $\Omega _V$, ${\mathrm {Im }}\,m(z) \sim \eta _0$ for $z \in {\mathcal {D}}_{\epsilon }'$ satisfying $|z - \widehat{z}_1| \ge N^{-1/2 + 3\epsilon }$, as we proved in Lemma 5.16, we obtain that $\mu _1 < \widehat{E}_1 + N^{-1/2 + 3\epsilon }$.

Recall the definitions for $\widehat{z}_1$ and $z_1^-$ in the proof of Lemma 5.16. Assume that $\mu _1 < \widehat{E}_1 - N^{-1/2 + 3\epsilon }$. Then, on the interval $(\widehat{E}_1 - N^{-1/2 + 3\epsilon }, \widehat{E}_1 + N^{-1/2 + 3\epsilon })$, ${\mathrm {Im }}\,m(E + \mathrm {i}\eta _0)$ is a decreasing function of $E$. However, we already showed in Lemmas 5.13 and 5.16 that, with $(\xi -2,\nu )$-high probability, ${\mathrm {Im }}\,m(\widetilde{z}_1) \gg \eta _0$, ${\mathrm {Im }}\,m(z_1^-) \sim \eta _0$, and ${\mathrm {Re }}\,\widetilde{z}_1 > {\mathrm {Re }}\,z_1^-$. Thus, $\mu _1 \ge \widehat{E}_1 - N^{-1/2 + 3\epsilon }$. We now use Lemmas 4.1 and 3.7, together with Remark 5.4, to conclude that

$$\begin{aligned} \mu _1 + \mathrm {i}\eta _0 + \widehat{m}_{fc} (\mu _1 + \mathrm {i}\eta _0) = \widehat{z}_1 + \widehat{m}_{fc} (\widehat{z}_1) + {\mathcal {O}}(N^{-1/2 + 3\epsilon })\! =\! \lambda v_1 + {\mathcal {O}}(N^{-1/2 + 3\epsilon }), \end{aligned}$$

(5.47)

which proves the proposition for the special choice $k=1$.

Next, we consider the case $k=2$; the general case can be proved in a similar manner by induction. Consider $H^{(1)}$, the minor of $H$ obtained by removing the first column and the first row. If we denote by $\mu _1^{(1)}$ the largest eigenvalue of $H^{(1)}$, then the Cauchy interlacing property yields $\mu _2 \le \mu _1^{(1)}$. We now follow the first part of the proof to estimate $\mu _1^{(1)}$, which gives us

$$\begin{aligned} \widehat{E}_2 - N^{-1/2 + 3\epsilon } \le \mu _1^{(1)} \le \widehat{E}_2 + N^{-1/2 + 3\epsilon }, \end{aligned}$$

(5.48)

where we let $\widehat{z}_2 = \widehat{E}_2 + \mathrm {i}\eta _0$ be a solution to the equation

$$\begin{aligned} {\mathrm {Re }}\,\left( \widehat{z}_2 + \widehat{m}_{fc} (\widehat{z}_2)\right) = \lambda v_2. \end{aligned}$$

This, in particular, shows that

$$\begin{aligned} \mu _2 \le \widehat{E}_2 + N^{-1/2 + 3\epsilon }. \end{aligned}$$

(5.49)

To prove the lower bound, we may follow the arguments we used in the first part of the proof. Recall that we have proved in Lemmas 5.13 and 5.16 that, with $(\xi -2,\nu )$-high probability on $\Omega _V$,

• (1) for $z = \widehat{z}_2 - N^{-1/2 + 3\epsilon }$, we have ${\mathrm {Im }}\,m(z) \le C \eta _0$;

• (2) there exists $\widetilde{z}_2 = \widetilde{E}_2 + \mathrm {i}\eta _0$, satisfying $|\widetilde{z}_2 - \widehat{z}_2| \le N^{-1/2 + 3\epsilon }$, such that ${\mathrm {Im }}\,m(\widetilde{z}_2) \gg \eta _0$.

If $\mu _2 < \widehat{E}_2 - N^{-1/2 + 3\epsilon }$, then

$$\begin{aligned} {\mathrm {Im }}\,m(E + \mathrm {i}\eta _0) - \frac{1}{N} \frac{\eta _0}{(\mu _1 - E)^2 + \eta _0^2} = \frac{1}{N} \sum _{\alpha =2}^N\frac{\eta _0}{(\mu _{\alpha } - E)^2 + \eta _0^2} \end{aligned}$$

is a decreasing function of $E$. Since we know that, with $(\xi -2,\nu )$-high probability on $\Omega _V$,

$$\begin{aligned} \frac{1}{N} \frac{\eta _0}{(\mu _1 - \widehat{E}_2)^2 + \eta _0^2} \le \frac{1}{N}\frac{C \eta _0}{ N^{-2\epsilon } \kappa _0^2} \ll \eta _0, \end{aligned}$$

we have that ${\mathrm {Im }}\,m(\widetilde{z}_2) \le C \eta _0$, which contradicts the definition of $\widetilde{z}_2$. Thus, we find that $\mu _2 \ge \widehat{E}_2 - N^{-1/2 + 3\epsilon }$, with $(\xi -2,\nu )$-high probability on $\Omega _V$.

We now proceed as above to conclude that, with $(\xi -2,\nu )$-high probability on $\Omega _V$,

$$\begin{aligned} \mu _2 + \mathrm {i}\eta _0 + \widehat{m}_{fc} (\mu _2 + \mathrm {i}\eta _0) = \widehat{z}_2 + \widehat{m}_{fc} (\widehat{z}_2) + {\mathcal {O}}(N^{-1/2 + 3\epsilon })\! =\! \lambda v_2 + {\mathcal {O}}(N^{-1/2 + 3\epsilon }), \end{aligned}$$

(5.50)

which proves the proposition for $k=2$. The general case is proven in the same way. $\square$

6 Fluctuation average lemma

In this section we prove Lemma 5.10 and Corollary 5.11. Recall that we denote by ${\mathbb {E}}_i$ the partial expectation with respect to the $i$-th column/row of $W$. Set $Q_i\mathrel {\mathop :}={\mathbb {1}}-{\mathbb {E}}_i$.

We are interested in bounding the fluctuation average

$$\begin{aligned} \frac{1}{N}\sum _{a=n_0}^NZ_a(z), \end{aligned}$$

(6.1)

where $n_0$ is an $N$-independent fixed integer. We first note that, using Schur’s complement formula, we can write

$$\begin{aligned} \frac{1}{N}\sum _{a=n_0}^{N}Q_a\left( \frac{1}{G_{aa}}\right)&= \frac{1}{N}\sum _{a=n_0}^Nw_{aa}-\frac{1}{N}\sum _{a=n_0}^NQ_a \sum _{k,l}^{(a)}w_{ak}G_{kl}^{(a)}w_{la}\nonumber \\&=-\frac{1}{N}\sum _{a=n_0}^N Z_a+{\mathcal {O}}\left( \frac{(\varphi _N)^{c \xi }}{N}\right) , \end{aligned}$$

(6.2)

with high probability, where we used the large deviation estimate (3.14). The main result of this section, Lemma 6.6, asserts that

$$\begin{aligned} \left| \frac{1}{N}\sum _{a=n_0}^{N}Q_a\left( \frac{1}{G_{aa}(z)}\right) \right| \le (\varphi _N)^{c\xi } N^{-1/2-{\varpi _{\mathrm{b}}}/2+4\epsilon }, \end{aligned}$$

(6.3)

with $(\xi -2,\nu )$-high probability, provided that $z$ satisfies $|\lambda v_a-{\mathrm {Re }}\,{m}_{fc}(z)-{\mathrm {Re }}\,z|\ge \frac{1}{2} N^{-1/(b+1)+\epsilon }$, for all $a\ge n_0$. (Note that we reduced here $\xi$ to $\xi -2$).

Fluctuation averages of the form (6.1) (with $n_0=1$) and more general fluctuation averages have been studied in [18], see also [17], for generalized Wigner ensembles and random band matrices. In [31], these ideas have been applied to the deformed Wigner ensemble, under the assumptions that the limiting eigenvalue distribution has a square root behavior at the spectral edge. In these studies, it was assumed that there is a deterministic control parameter $\Lambda _o\equiv \Lambda _o(z)$, such that $G_{ij}(z)$ and $Z_i(z)$ satisfy $\max _{i,j} |G_{ij}|\le C\Lambda _o+C\delta _{ij}$, $|G_{ii}(z)|\ge c$, and $\max _i|Z_i|\le C\Lambda _o$, with high probability, and $\Lambda _o$ satisfies $\Lambda _o\ll 1$, for ${\mathrm {Im }}\,z\gg N^{-1}$.

Under the assumption of Lemma 5.10, the Green function entries $(G_{ij}(z))$ can become large, e.g., $|G_{11}(z)|\gg 1$, if $\eta \sim N^{-1/2}$ and $E$ is close to the spectral edge. Further, it is also possible to have $|G_{1j}(z)|\gg 1$ for such $z$ and some $j > 1$ as one can see from the resolvent identity (3.9). However, resolvent fractions of the form $G_{ab}(z)/G_{bb}(z)$ and $G_{ab}(z)/G_{aa}(z)G_{bb}(z)$ ($a,b\ge n_0$), are small (see Lemma 6.2 below for a precise statement). Using this observation, we adapt the methods of [17] to control the fluctuation average (6.1).

6.1 Preliminaries

Let $a,b\in [\![1,N]\!]$ and ${\mathbb {T}},{\mathbb {T}}'\subset [\![1,N]\!]$, with $a,b\not \in {\mathbb {T}}$, $b\not \in {\mathbb {T}}'$, $a\not =b$, then we set

$$\begin{aligned} F_{ab}^{({\mathbb {T}},{\mathbb {T}}')}(z)\mathrel {\mathop :}=\frac{G_{ab}^{({\mathbb {T}})}(z)}{G_{bb}^{({\mathbb {T}}')}(z)},\qquad \quad (z\in {\mathbb {C}}^+), \end{aligned}$$

(6.4)

and we often abbreviate $F_{ab}^{({\mathbb {T}},{\mathbb {T}}')}\equiv F_{ab}^{({\mathbb {T}},{\mathbb {T}}')}(z)$. In case ${\mathbb {T}}={\mathbb {T}}'=\emptyset$, we simply write $F_{ab}\equiv F_{ab}^{({\mathbb {T}},{\mathbb {T}}')}$. Below we will always implicitly assume that $\{a,b\}$ and ${\mathbb {T}},{\mathbb {T}}'$ are compatible in the sense that $a\not =b$, $a,b\not \in {\mathbb {T}}$, $b\not \in {\mathbb {T}}'$.

Starting from (3.10), simple algebra yields the following relations among the $\lbrace F_{ab}^{({\mathbb {T}},{\mathbb {T}}')}\rbrace$.

Lemma 6.1

Let $a,b,c\in [\![1,N]\!]$, all distinct, and let ${\mathbb {T}},{\mathbb {T}}'\subset [\![1,N]\!]$. Then,

• (1) for $c\not \in {\mathbb {T}}\cup {\mathbb {T}}'$,

  $$\begin{aligned} F_{ab}^{({\mathbb {T}},{\mathbb {T}}')}=F_{ab}^{({\mathbb {T}}c,{\mathbb {T}}')}+F_{ac}^{({\mathbb {T}},{\mathbb {T}}')} F_{cb}^{({\mathbb {T}},{\mathbb {T}}')}; \end{aligned}$$

  (6.5)

• (2) for $c\not \in {\mathbb {T}}\cup {\mathbb {T}}'$,

  $$\begin{aligned} F_{ab}^{({\mathbb {T}},{\mathbb {T}}')}=F_{ab}^{({\mathbb {T}},{\mathbb {T}}'c)}-F_{ab}^{({\mathbb {T}},{\mathbb {T}}'c)}F_{bc}^{({\mathbb {T}}, {\mathbb {T}}')}F_{cb}^{({\mathbb {T}},{\mathbb {T}}')}; \end{aligned}$$

  (6.6)

• (3) for $c\not \in {\mathbb {T}}$,

  $$\begin{aligned} \frac{1}{G_{aa}^{({\mathbb {T}})}}=\frac{1}{G_{aa}^{({\mathbb {T}}c)}}\left( 1- F_{ac}^{({\mathbb {T}},{\mathbb {T}})}F_{ca}^{({\mathbb {T}},{\mathbb {T}})}\right) . \end{aligned}$$

  (6.7)

6.2 The fluctuation average lemma

Recall the definition of the domain ${\mathcal {D}}_{\epsilon }'$ of the spectral parameter in (3.33) and of the constant ${\varpi _{\mathrm{b}}}>0$ in (3.19). Set $A\mathrel {\mathop :}=[\![n_0,N]\!]$. To start with, we bound $F_{ab}$ and $F_{ab}^{(\emptyset ,a)}/G_{aa}$ on the domain ${\mathcal {D}}_{\epsilon }'$.

Lemma 6.2

Assume that, for all $z\in {\mathcal {D}}_{\epsilon }'$, the estimates

$$\begin{aligned} |m(z)-\widehat{m}_{fc}(z)|\le N^{-1/2+2\epsilon },\qquad {\mathrm {Im }}\,m(z)\le N^{-1/2+2\epsilon }, \end{aligned}$$

(6.8)

hold with $(\xi ,\nu )$-high probability on $\Omega _V$.

Then, there exists a constant $c$, such that for all $z\in {\mathcal {D}}_{\epsilon }'$,

$$\begin{aligned} \max _{\begin{array}{c} a,b\in A\\ a\not =b \end{array}}|F_{ab}(z)|\le (\varphi _N)^{c \xi }N^{-{\varpi _{\mathrm{b}}}/2}N^{\epsilon },\quad (z\in {\mathcal {D}}_{\epsilon }'), \end{aligned}$$

(6.9)

and

$$\begin{aligned} \max _{\begin{array}{c} a,b\in A\\ a\not =b \end{array}}\left| \frac{F_{ab}^{(\emptyset , a)}(z)}{G_{aa}(z)}\right| \le (\varphi _N)^{c\xi } N^{-1/2}N^{2\epsilon },\quad ( z\in {\mathcal {D}}_{\epsilon }'), \end{aligned}$$

(6.10)

with $(\xi ,\nu )$-high probability on $\Omega _V$.

Proof

Dropping the $z$-dependence from the notation, we first note that by Schur’s complement formula (3.7) and Inequality (6.8), we have with high probability on $\Omega _V$, for $z\in {\mathcal {D}}_{\epsilon }'$,

$$\begin{aligned} \frac{1}{G^{(b)}_{aa}}=\lambda v_a-z-\widehat{m}_{fc}+{\mathcal {O}}(|m- m^{(ab)}|)+{\mathcal {O}}(N^{-1/2+2\epsilon }), \end{aligned}$$

(6.11)

for all $a \in A$, $b\in [\![1,N]\!]$, $a\not =b$. Thus, for $z\in {\mathcal {D}}_{\epsilon }'$, Lemma 3.3 yields

$$\begin{aligned} |G^{(b)}_{aa}|\le C(\varphi _N)^{\xi }N^{1/{(\mathrm {b}+1)}}N^{\epsilon }, \end{aligned}$$

(6.12)

with high probability on $\Omega _V$. Further, from the resolvent formula (3.9) we obtain

$$\begin{aligned} F_{ab}=-\sum _{k}^{(b)} G_{ak}^{( b)}h_{kb}, \end{aligned}$$

(6.13)

for $a,b\in A$, $a\not = b$. From the large deviation estimate (3.14) we infer that

$$\begin{aligned} \left| \sum _{k}^{(b)} G_{ak}^{(b)}h_{kb}\right| \le (\varphi _N)^{\xi } \left( \frac{{\mathrm {Im }}\,G^{(b)}_{aa}}{N\eta }\right) ^{1/2}, \end{aligned}$$

(6.14)

with high probability, and hence conclude by (6.12) that

$$\begin{aligned} |F_{ab}|\le C(\varphi _N)^{2\xi }N^{-{\varpi _{\mathrm{b}}}/2}N^{\epsilon }, \end{aligned}$$

(6.15)

with high probability on $\Omega _V$.

To prove the second claim, we recall that, for $a\not =b$, the resolvent formula (3.8) gives

$$\begin{aligned} \frac{F_{ab}^{(\emptyset , a)}}{G_{aa}}= -h_{ab}+\sum _{k,l}^{(ab)} h_{ak}G_{kl}^{(ab)}h_{lb}, \end{aligned}$$

(6.16)

and we conclude from the large deviation estimates (3.17) and (3.18) that

$$\begin{aligned} \left| \frac{F_{ab}^{(\emptyset , a)}}{G_{aa}}\right| \le \frac{(\varphi _N)^{\xi }}{\sqrt{N}}+(\varphi _N)^{\xi }\sqrt{\frac{{\mathrm {Im }}\,m^{(ab)}}{N\eta }}, \end{aligned}$$

(6.17)

with high probability. Since $|m-m^{(ab)}|\le CN^{-1/2+\epsilon }$ on ${\mathcal {D}}_{\epsilon }'$, by Lemma 3.3, we obtain using (6.8) that

$$\begin{aligned} \left| \frac{F_{ab}^{(\emptyset ,a)}}{G_{aa}}\right| \le (\varphi _N)^{c \xi }N^{-1/2}N^{2\epsilon }, \end{aligned}$$

(6.18)

with high probability on $\Omega _V$. $\square$

Definition 6.3

Let $\Xi$ be an event defined by requiring that the following holds on it: $(1)$ there exists a constant $c$, such that for all $z\in {\mathcal {D}}_{\epsilon }'$, (6.8), (6.9) and (6.10) hold; $(2)$ there exists a constant $c$ such that, for all $z\in {\mathcal {D}}_{\epsilon }'$ and $a\in A$,

$$\begin{aligned} \left| Q_{a}\left( \frac{1}{G_{aa}}\right) \right| \le (\varphi _N)^{c\xi } N^{-1/2+2\epsilon }; \end{aligned}$$

(6.19)

and $(3)$, for all $i,j\in [\![1,N]\!]$,

$$\begin{aligned} \max _{ij}|w_{ij}|\le \frac{(\varphi _N)^{c\xi }}{\sqrt{N}}. \end{aligned}$$

(6.20)

By Lemma 6.2, Lemma 5.8, Corollary 5.6, Lemma 5.5 and Inequality (3.18), we know that $\Xi$ holds with $(\xi ,\nu )$-high probability on $\Omega _V$.

Corollary 6.4

For $p\le (\log N)^{\xi }$, there exists a constant $c$, such that the following holds. For all ${\mathbb {T}},{\mathbb {T}}',{\mathbb {T}}''\subset A$, with $|{\mathbb {T}}|\,,|{\mathbb {T}}'|\,,|{\mathbb {T}}''|\le p$, for all $a,b\in A$, $a\not =b$, and, for all $z\in {\mathcal {D}}_{\epsilon }'$, we have

$$\begin{aligned}&{\mathbb {1}}(\Xi )\left| {F^{({\mathbb {T}},{\mathbb {T}}')}_{ab}(z)}\right| \le (\varphi _N)^{c\xi } N^{-{\varpi _{\mathrm{b}}}/2}N^{\epsilon },\end{aligned}$$

(6.21)

$$\begin{aligned}&{\mathbb {1}}(\Xi )\left| \frac{F_{ab}^{({\mathbb {T}}',{\mathbb {T}}'')}(z)}{G_{aa}^{({\mathbb {T}})}(z)}\right| \le (\varphi _N)^{c\xi } N^{-1/2}N^{2\epsilon }, \end{aligned}$$

(6.22)

and

$$\begin{aligned} {\mathbb {1}}(\Xi )\left| Q_{a}\left( \frac{1}{G_{aa}^{({\mathbb {T}})}}\right) \right| \le (\varphi _N)^{c\xi } N^{-1/2}N^{2\epsilon }, \end{aligned}$$

(6.23)

on $\Omega _V$, for $N$ sufficiently large.

The proof of this corollary is given in Appendix B.

Before we state the next lemma, we remark that in this section we use the symbol ${\mathbb {E}}^W$ for the partial expectation with respect to the random variables $(w_{ij})$ with $(v_i)$ kept fixed, i.e., ${\mathbb {E}}^W[\,\cdot \,]\equiv {\mathbb {E}}[\,\cdot \,| (v_i)]$.

Lemma 6.5

Let $p\in {\mathbb {N}}$ satisfy $p\le (\log N)^{\xi -3/2}$. Let $q\in [\![0,p]\!]$ and consider random variables $({\mathcal {X}}_{i}) \equiv ({\mathcal {X}}_{i}(H))$ and $({\mathcal {Y}}_{i})\equiv ({\mathcal {Y}}_{i}(H))$, $i\in [\![1,p]\!]$, satisfying

$$\begin{aligned}&{\mathbb {1}}(\Xi )|{\mathcal {X}}_{i}|\le C(\varphi _N)^{c\xi d_{i}}N^{-1/2+2\epsilon } N^{-(d_{i}-1)({\varpi _{\mathrm{b}}}/2-\epsilon )},\nonumber \\&{\mathbb {1}}(\Xi )|Q_{i}{\mathcal {Y}}_{i}|\le C(\varphi _N)^{c\xi }N^{-1/2}N^{2\epsilon }, \end{aligned}$$

(6.24)

where $d_{i}\in {\mathbb {N}}_0$ satisfy $0\le s=\sum _{i=1}^q (d_{i}-1)\le p+2$. Assume moreover that there are constants $C'$ and $K$, such that

$$\begin{aligned} {\mathbb {E}}^W |{\mathcal {X}}_{i}|^{r}\le (C'N)^{K(d_{i}+1) r},\qquad {\mathbb {E}}^W| {\mathcal {Y}}_{i}|^{r}\le (C'N)^{Kr}, \end{aligned}$$

(6.25)

for any $r\in {\mathbb {N}}$, with $r\le 10 p$. Finally, assume that the event $\Xi$ holds with $(\xi ,\nu )$-high probability.

Then, there is a constant $c_0$, depending only on $C,C',c,K$ in (6.24) and (6.25), and on $\xi$ and $\nu$, such that

$$\begin{aligned} \left| {\mathbb {E}}^W\prod _{i=1}^qQ_{i}({\mathcal {X}}_{i})\prod _{i=q+1}^pQ_{i}({\mathcal {Y}}_{i}) \right| \le (\varphi _N)^{c_0\xi p}N^{-p/2-s{\varpi _{\mathrm{b}}}/2}N^{(2p+s)\epsilon }. \end{aligned}$$

(6.26)

(Here, we use the convention that, for $q=0$, the first product is set to one, and, similarly, for $q=p$, the second product is set to one.)

Lemma 6.5 is proved in Appendix B.

Next, we state the main result of this section:

Lemma 6.6

(Fluctuation Average Lemma) Let $A\mathrel {\mathop :}=[\![n_0,N]\!]$. Recall the definition of the domain ${\mathcal {D}}_{\epsilon }'$ in (3.33). Let $\Xi$ denote the event in Definition 6.3 and assume it has $(\xi ,\nu )$-high probability. Then there exist constants $C, c, c_0$, such that for $p=2r, r\in {\mathbb {N}}, p\le (\log N)^{\xi -3/2}$, we have

$$\begin{aligned} {\mathbb {E}}^W\left| \frac{1}{N}\sum _{a\in A}Q_{a}\left( \frac{1}{G_{aa}(z)} \right) \right| ^{p}\le (Cp)^{cp}(\varphi _N)^{c_0p\xi } N^{-p/2-p {\varpi _{\mathrm{b}}}/2}N^{3p\epsilon }, \end{aligned}$$

(6.27)

for all $z\in {\mathcal {D}}_{\epsilon }'$, on $\Omega _V$.

Proof

Fix $z\in {\mathcal {D}}_{\epsilon }'$. For simplicity we drop the $z$-dependence from our notation and we always work on $\Omega _V$. We explain the idea of the proof for the simple case $p=2$. First, we note that

$$\begin{aligned} \frac{1}{N^2}\sum _{a\in A}{\mathbb {E}}^W\,\left| Q_{a}\left( \frac{1}{G_{aa}} \right) \right| ^2\le C(\varphi _N)^{2c_0\xi }\frac{N^{4\epsilon }}{N^2}, \end{aligned}$$

(6.28)

where we used (6.23) and (6.26) (with $p=2$, $q=0$, ${\mathcal {Y}}_{1}=(\overline{G_{aa}})^{-1}$, ${\mathcal {Y}}_{2}={({G_{aa}})^{-1}}$). Here, we also used that ${\mathbb {E}}^W |G_{aa}|^{-r}\le (CN)^{Kr}$, for some $K>0$, $r\in {\mathbb {N}}$, (see Remark 6.10 below) to ensure (6.25). It thus suffices to consider

$$\begin{aligned} \frac{1}{N^2}\sum _{\begin{array}{c} a_1\in A,a_2\in A\\ a_1\not =a_2 \end{array}}{\mathbb {E}}^W\, Q_{a_1}\overline{\left( \frac{1}{G_{a_1a_1}}\right) } Q_{a_2}\left( \frac{1}{G_{a_2a_2}} \right) . \end{aligned}$$

(6.29)

Applying the formula

$$\begin{aligned} \frac{1}{G_{aa}}=\frac{1}{G_{aa}^{(b)}}\left( 1-F_{ab}F_{ba}\right) \,, \qquad (a\not =b), \end{aligned}$$

(6.30)

twice, we obtain

$$\begin{aligned} {\mathbb {E}}^W\, Q_{a_1}\overline{\left( \frac{1}{G_{a_1a_1}}\right) } Q_{a_2}\left( \frac{1}{G_{a_2a_2}} \right)&={\mathbb {E}}^W\, Q_{a_1} \overline{\left( {\frac{1}{G_{a_1a_1}^{(a_2)}}\left( 1-F_{a_1 a_2}F_{a_2a_1}\right) }\right) }\nonumber \\&\quad \times Q_{a_2}\left( {\frac{1}{G_{a_2a_2}^{(a_1)}}\left( 1-F_{a_2a_1} F_{a_1a_2}\right) }\right) \nonumber \\&={\mathbb {E}}^W\, Q_{a_1}\overline{\left( {\frac{1}{G_{a_1a_1}^{(a_2)}} F_{a_1a_2}F_{a_2a_1}}\right) }\nonumber \\&\quad \times Q_{a_2}\left( {\frac{1}{G_{a_2 a_2}^{(a_1)}}F_{a_2 a_1}F_{a_1a_2}}\right) , \end{aligned}$$

(6.31)

where we used that $G_{aa}^{(b)}$, $a\not =b$, is independent of the entries in the $b$-th column/row of $W$, and that, for general random variables $A=A(W)$ and $B=B(W)$, ${\mathbb {E}}^W[ (Q_{b}A) B]={\mathbb {E}}^W[B {\mathbb {E}}_{b}Q_{b} A]=0$ if $B$ is independent of the variables in the ${b}$-th column/row of $W$.

By Corollary 6.4, we have

$$\begin{aligned} {\mathbb {1}}(\Xi )\left| \frac{F_{a_2a_1}}{G_{a_1a_1}^{(a_2)}}F_{a_1a_2}\right| \le C N^{-1/2-{\varpi _{\mathrm{b}}}/2}N^{3\epsilon }, \end{aligned}$$

(6.32)

with high probability, and a similar bound holds for the second term in (6.31). Since

$$\begin{aligned} {\mathbb {E}}^W \left| \frac{F_{a_2a_1}}{G_{a_1a_1}^{(a_2)}}F_{a_1a_2}\right| ^r \le (CN)^{4Kr}, \end{aligned}$$

(6.33)

for $r\le 10p$, for some $K$, as can be easily checked (c.f., Remark 6.10 below), Lemma 6.5 implies that

$$\begin{aligned} \left| \frac{1}{N^2}\sum _{a_1\in A, a_2\in A}{\mathbb {E}}^W\, Q_{a_1}\overline{\left( \frac{1}{G_{a_1a_1}}\right) } Q_{a_2}\left( \frac{1}{G_{a_2a_2}} \right) \right| \le C(\varphi _N)^{2c_0\xi } N^{-1-{\varpi _{\mathrm{b}}}}N^{6\epsilon }, \end{aligned}$$

(6.34)

and we obtain the claim in the sense of second moment bounds.

To deal with higher moments, we abbreviate $\mathbf {a}\equiv (a_1,\ldots ,a_p)$ and write, for $p=2r$ satisfying $p\le (\log N)^{\xi -3/2}$,

$$\begin{aligned} {\mathbb {E}}^W\left| \frac{1}{N}\sum _{a\in A} Q_a\left( \frac{1}{G_{aa}} \right) \right| ^{2r}&=\frac{1}{N^{2r}}\sum _{a_1\in A,\ldots , a_{2r}\in A}{\mathbb {E}}^W \overline{X}_{a_1}\cdots \overline{X}_{a_r} X_{a_{r+1}}\cdots X_{a_{2r}}\nonumber \\&=\frac{1}{N^{2r}}\sum _{a_1\in A,\ldots , a_{2r}\in A}{\mathbb {E}}^W {X}_\mathbf {a} \end{aligned}$$

(6.35)

where $X_{a}\mathrel {\mathop :}=Q_{a}(G_{aa})^{-1}$ and $X_\mathbf {a}\mathrel {\mathop :}=\overline{X}_{a_1} \cdots \overline{X}_{a_r}X_{a_{r+1}}\cdots X_{a_{2r}}$.

To cope with (6.35) efficiently, we need some more notation. Let $\mathbf {L},\mathbf {U}\subset [\![1,N]\!]$. We denote by ${\mathcal {F}}(\mathbf {L}, \mathbf {U})$ the set of all “off-diagonal resolvent fractions” $F_{ab}^{({\mathbb {T}},{\mathbb {T}}')}$, $a\not =b$, $a,b\in \mathbf {L}$ and ${\mathbb {T}},{\mathbb {T}}'\subset \mathbf {U}$, with $a,b\not \in {\mathbb {T}}$, $b\not \in {\mathbb {T}}'$. Further, we denote by ${\mathcal {G}}(\mathbf {L}, \mathbf {U})$ the set of “diagonal resolvent entries” having lower indices in $\mathbf {L}$ and upper indices in $\mathbf {U}$; more precisely, ${\mathcal {G}}(\mathbf {L}, \mathbf {U})\mathrel {\mathop :}=\{G_{aa}^{({\mathbb {T}})}\,:\, a\in \mathbf L, {\mathbb {T}}\subset \mathbf {U}\,, a\not \in {\mathbb {T}}\}$. Finally, we denote by $\widetilde{{\mathcal {F}}}(\mathbf {L}, \mathbf {U})$ the set of monomials of the form ${\mathbb {C}}G_d^{-1}F_1F_2\cdots F_n$, with $G_d\in {\mathcal {G}}(\mathbf {L}, \mathbf {U})$, $F_i\in {\mathcal {F}}(\mathbf {L}, \mathbf {U})$, $n\in {\mathbb {N}}_0$.

Following [17], we call $F_{ab}^{({\mathbb {T}},{\mathbb {T}}')}\in {\mathcal {F}}(\mathbf {L}, \mathbf {U})$, maximally expanded (in $\mathbf {U}$), if $\{a,b\}\cup {\mathbb {T}}\supset \mathbf {L}$ and $\{b\}\cup {\mathbb {T}}'\supset \ \mathbf {L}$. Similarly, $G_{aa}^{({\mathbb {T}})}$, is maximally expanded if $\{a\}\cup {\mathbb {T}}\supset \mathbf {L}$, and we call a monomial in $\widetilde{\mathcal {F}}(\mathbf {L},\mathbf {U})$ maximally expanded if all its factors are maximally expanded. The degree of $F\in \widetilde{{\mathcal {F}}}(\mathbf {L},\mathbf {U})$ is defined as the number of factors of $F_{ab}^{({\mathbb {T}},{\mathbb {T}}')}$ in $F$ (with $a\not =b$).

Next, we define a recursive procedure that, given $F\in \widetilde{{\mathcal {F}}}(\mathbf {L},\mathbf {U})$, successively adds upper indices from the set $\mathbf {U}$ to $F$, at the expense of generating terms of higher degree. This procedure is iterated until either all generated terms are maximally expanded or their degree is sufficiently large, so that they can be neglected.

Given $F\in \widetilde{{\mathcal {F}}}(\mathbf {L},\mathbf {U})$ the recursive procedure is as follows:

• (A) Stopping rules: If the degree of $F$ is bigger equal $p+1$ or if $F$ is maximally expanded in $\mathbf {U}$, we stop the procedure.

• (B) Iteration: Else, we choose an arbitrary non-maximally expanded factor $F_{ab}^{({\mathbb {T}},{\mathbb {T}}')}$ or ${1/G_{aa}^{({\mathbb {T}})}}$ of $F$ and split it using, for the former choice, either

  $$\begin{aligned} F_{ab}^{({\mathbb {T}},{\mathbb {T}}')}&={F_{ab}^{({\mathbb {T}}c,{\mathbb {T}}')}}+{F_{ac}^{({\mathbb {T}},{\mathbb {T}}')} F_{cb}^{({\mathbb {T}},{\mathbb {T}}')}}, \end{aligned}$$

  (6.36)

  for the smallest $c\in \mathbf {U}\backslash ({\mathbb {T}}ab)$, or

  $$\begin{aligned} F_{ab}^{({\mathbb {T}},{\mathbb {T}}')}=F_{ab}^{({\mathbb {T}},{\mathbb {T}}'c)}- F_{ab}^{({\mathbb {T}},{\mathbb {T}}'c)} F_{bc}^{({\mathbb {T}},{\mathbb {T}}')}F_{cb}^{({\mathbb {T}},{\mathbb {T}}')}, \end{aligned}$$

  (6.37)

  for the smallest $c\in \mathbf {U}\backslash ({\mathbb {T}}' b)$, respectively,

  $$\begin{aligned} \frac{1}{G_{aa}^{({\mathbb {T}})}}=\frac{1}{G_{aa}^{({\mathbb {T}}c)}}\left( 1-F_{ac}^{({\mathbb {T}},{\mathbb {T}})}F_{ca}^{({\mathbb {T}},{\mathbb {T}})}\right) , \end{aligned}$$

  (6.38)

  for the smallest $c\in \mathbf {U}\backslash ({\mathbb {T}}a)$, for the latter choice. Then, we start over with $F$ being one of the generated monomials.

We remark that a similar algorithm (expanding the resolvent entries $G_{ij}^{({\mathbb {T}})}$ instead of $F_{ij}^{({\mathbb {T}},{\mathbb {T}}')}$) appeared first in [18]; see also [17].

Remark 6.7

This recursive procedure contains some arbitrariness, e.g., in the specific choice of $F_{ab}^{({\mathbb {T}},{\mathbb {T}}')}$ in (6.36), (6.37) or (6.38). This arbitrariness does not affect the argument and we thus choose not to remove it.

We now use the above algorithm to expand the right side of (6.35): Denote by ${\mathcal {P}}_{2r}$ the set of partitions of $[\![1,2r]\!]$ and let $\Gamma (\mathbf {a})\in {\mathcal {P}}_{2r}$ be the partition induced by the equivalence relation $i\sim j$, if and only if $a_i=a_j$, $i,j\in [\![1,2r]\!]$. Then we can write

$$\begin{aligned} {\mathbb {E}}^W\left| \frac{1}{N}\sum _{a\in A}Q_a\left( \frac{1}{G_{aa}}\right) \right| ^{2r}=\frac{1}{N^{2r}}\sum _{\Gamma \in {\mathcal {P}}_{2r}}\sum _{a_1\in A,\ldots ,a_{2r}\in A}{\mathbb {1}}(\Gamma =\Gamma (\mathbf {a}))\,{\mathbb {E}}^W X_{\mathbf {a}}. \end{aligned}$$

(6.39)

Given $\mathbf {a}=(a_i)$, denote by $\Gamma \mathrel {\mathop :}=\Gamma (\mathbf {a})$, the partition induced by the equivalence relation $\sim$. For a label $i\in [\![1,2r]\!]$, we denote by $[i]$ the block of $i$ in $\Gamma$. Let $S(\Gamma )\mathrel {\mathop :}=\{ i\,:\ |[i]|=1\}\subset [\![1,2r]\!]$ denote the set of singletons or single labels and abbreviate by $s\mathrel {\mathop :}=|S(\Gamma )|$ its cardinality. We denote by $\mathbf {A}_S\equiv \mathbf {A}_{S(\Gamma )} \mathrel {\mathop :}=\{a_i\}_{i\in S}$, the summation indices associated with single labels. Notice that if $i$ is a single label (for some $\Gamma$), then there is exactly one $Q_{a_i}$ on the right side of (6.39). However, if $i$ is not a single label (for some $\Gamma$), $Q_{a_i}$ appears more than once on the right side of (6.39).

We now choose $\mathbf {L}=\mathbf {A}_\Gamma \equiv \{a_i\}_{i}$ and $\mathbf {U}=\mathbf {A}_{S(\Gamma )}\equiv \mathbf {A}_S$ and apply the algorithm $(A)$–$(B)$ to $X_{a_i}$: In the first step, we get

$$\begin{aligned} X_{a_i}=Q_{a_i}\left( \frac{1}{G_{a_ia_i}^{(b_1)}}\right) -Q_{a_i} \left( \frac{1}{G_{a_ia_i}} F_{a_ib_1}F_{b_1a_i}\right) , \end{aligned}$$

(6.40)

for some $b_1\in \varvec{A}_S\backslash \{a_i\}$. Since neither of the two terms is maximally expanded nor has degree bigger than $p+1$, we apply step $(B)$ to, e.g., $F_{b_1a_i}$, to get

$$\begin{aligned} X_{a_i}=Q_{a_i}\left( \frac{1}{G_{a_ia_i}^{(b_1)}}\right) -Q_{a_i} \left( \frac{1}{G_{a_ia_i}}F_{a_ib_1}F_{b_1a_i}^{(b_2,\emptyset )}\right) -Q_{a_i}\left( \frac{1}{G_{a_ia_i}}F_{a_ib_1}F_{b_1b_2}F_{b_2a_i}\right) , \end{aligned}$$

for some $b_2\in \varvec{A}_S\backslash \{a_i,b_1\}$. Continuing in this way, we eventually trigger the stopping rules $(A)$, and we obtain the following expansion of $X_{a_i}$:

$$\begin{aligned}&X_{a_i}=X_{a_i}^{(\mathbf {A}_S\backslash a_i)}+Q_{a_i}M_{a_i} (\mathbf {A}_\Gamma ,\mathbf {A}_S)+Q_{a_i}R_{a_i}(\mathbf {A}_\Gamma , \mathbf {A}_S),\nonumber \\&\quad X_{a_i}^{(\mathbf {A}_S\backslash a_i)}\mathrel {\mathop :}=Q_{a_i}\left( \frac{1}{G_{a_ia_i}^{(\mathbf {A}_S\backslash a_i)}}\right) , \end{aligned}$$

(6.41)

where $M_{a_i}(\mathbf {A}_\Gamma ,\mathbf {A}_S)$ and $R_{a_i}(\mathbf {A}_\Gamma ,\mathbf {A}_S)$ are sums of elements in $\widetilde{{\mathcal {F}}}(\mathbf {A}_{\Gamma },\mathbf {A}_{S})$, such that each term in $M_{a_i}(\mathbf {A}_\Gamma ,\mathbf {A}_S)$ is maximally expanded in $\mathbf {A}_S$ and each summand in $R_{a_i}(\mathbf {A}_\Gamma ,\mathbf {A}_S)$ is of degree $p+1$ or higher.

Remark 6.8

The stopping rules $(A)$ ensure that the procedure stops after a finite number of steps when applied to $X_{a_i}$.

Indeed, the procedure described above generates a rooted binary tree, whose vertices are labeled by binary strings: Starting from $X_{a_i}$ step $(B)$ yields the decomposition $X_{a_i}=(X_{a_i})_0+(X_{a_i})_1$ corresponding to the splitting on the right side of (6.40). Here the subscript $0$ indicates that we have added one upper index to a Green function entry (first term on the right side of (6.40)) and the subscript $1$ indicates that we have generated additional off-diagonal resolvent entries [second term on the right side of (6.40)]. Applying step $(B)$ once more to $(X_{a_i})_0$, respectively $(X_{a_i})_1$, we obtain

$$\begin{aligned} (X_{a_i})_0=(X_{a_i})_{00}+( X_{a_i})_{01}\,,\qquad (X_{a_i})_1=(X_{a_i})_{10}+( X_{a_i})_{11}, \end{aligned}$$

(where the precise choices of the index and of the resolvent fractions used in step $(B)$ are unimportant). Continuing, we generate terms that are labeled by binary strings and that may be arranged in a rooted binary tree. Each application of step $(B)$ induces a splitting of the form $( X_{a_i})_\sigma =(X_{a_i})_{\sigma 0}+( X_{a_i})_{\sigma 1}$, $\sigma$ a binary string, where $\sigma 0$, $\sigma 1$ denote the strings obtained by concatenating $\sigma$ and $0$, $1$.

By the stopping rules $(A)$, each term generated by the above procedure, i.e., each term on the right side of (6.41), corresponds to a leaf node of the tree. Thus to get an upper bound on the number of terms in (6.41), it is enough to estimate the depth of the tree.

To estimate the depth of the tree, we estimate the maximal length of a generated string $\sigma$. We first observe that the number of off-diagonal resolvent fractions is raised by one or two under the operation $\sigma \mapsto \sigma 1$. Note that in the first step we always generate two off-diagonal resolvent fractions. Hence, by the stopping rules $(A)$, the leaf nodes are labeled by strings with $p$ or less ones in it. Also note that the operation $\sigma \mapsto \sigma 0$ does not change the number of off-diagonal resolvent fractions. Hence, a bound on the number of upper indices for a vertex is $(p+1)p$. In other words, a string labeling a vertex has at most $(p+1)p$ zeros. Thus a string labeling a leaf node has a most $(p+1)p$ zeros and $p$ ones, therefore has length at most $p^2+2p$ and we conclude that the number of leaf nodes of the tree is bounded by

$$\begin{aligned} \sum _{q=0}^{p+1}\left( {\begin{array}{c}p^2+2p\\ q\end{array}}\right) \le (p+2) \frac{(p^2+2p)^{p}}{(p+1)!} \le (Cp)^{2cp}, \end{aligned}$$

for some constants $c$ and $C$, independent of $p$.

For more details we refer to, e.g., [17, page 54].

Remark 6.9

Ignoring for the moment the upper indices, we observe that each summand in $M_{a_i}(\mathbf {A}_\Gamma ,\mathbf {A}_S)$ or $R_{a_i}(\mathbf {A}_\Gamma ,\mathbf {A}_S)$ is of the form

$$\begin{aligned} \frac{F^{\#}_{a_ib_1}}{G_{a_ia_i}^{\#}}\cdot F^{\#}_{b_1b_2} F^{\#}_{b_2b_3}\cdots F^{\#}_{b_na_i}, \end{aligned}$$

(6.42)

for some $(b_1,\ldots , b_n)\in \mathbf {A}_S^n$, with $1\le n\le p+1$, satisfying $b_1\not =a_i$, $b_k\not =b_{k+1}$, ($k\in [\![1,n-1]\!]$), $b_n\not =a_1$. Here $\#$ stands for some appropriate $({\mathbb {T}},{\mathbb {T}}')$, with $|{\mathbb {T}}|\le p-2$, $|{\mathbb {T}}'|\le p-1$. Indeed, when applying the recursive procedure to $1/G_{a_ia_i}$, the first step yields

$$\begin{aligned} \frac{1}{G_{a_ia_i}}=\frac{1}{G_{a_ia_i}^{(b_1)}}\left( 1-F_{a_i b_1}F_{b_1a_i}\right) , \end{aligned}$$

(6.43)

for some $b_1\in \ \mathbf {A}_S\backslash \{a_i\}$, which is of the claimed form. Applying (6.36), (6.37) or (6.38) to a factor in (6.43) yields again two terms of the form (6.42), etc. The claim then follows by noticing that the stopping rules ensure that each summand is of degree less equal $p+2$.

Using (6.21) $n$ times and (6.22) once, we obtain

$$\begin{aligned} {\mathbb {1}}(\Xi ) \left| \frac{F^{\#}_{a_ib_1}}{G_{a_ia_i}^{\#}}\cdot F^{\#}_{b_1b_2}F^{\#}_{b_2b_3}\cdots F^{\#}_{b_na_i}\right| \le C^{n+1}(\varphi _N)^{c\xi (n+1)} N^{-1/2} N^{-n{\varpi _{\mathrm{b}}}/2}N^{(n+2)\epsilon }, \end{aligned}$$

(6.44)

irrespective of the choice of the upper indices (recall that $\#$ stands for some $({\mathbb {T}},{\mathbb {T}}')$ satisfying $|{\mathbb {T}}|,|{\mathbb {T}}'|\le (\log N)^{\xi }$). For $n=0$, the analogous bound to (6.44) reads

$$\begin{aligned} {\mathbb {1}}(\Xi )\left| Q_{a_i}\left( \frac{1}{G_{a_ia_i}^{\#}}\right) \right| \le C(\varphi _N)^{c\xi } N^{-1/2}N^{2\epsilon }; \end{aligned}$$

(6.45)

see (6.23).

Remark 6.10

Still ignoring the upper indices, we remark that in order to apply Lemma 6.5, we need to check that

$$\begin{aligned} {\mathbb {E}}^W\left| \frac{F^{\#}_{a_ib_1}}{G_{a_ia_i}^{\#}}\cdot F^{\#}_{b_1 b_2}F^{\#}_{b_2b_3}\cdots F^{\#}_{b_na_i}\right| ^r\le (CN)^{Kr(n+1)}, \end{aligned}$$

(6.46)

for some constants $C$ and $K$, for all $r\le 10 p$. To verify (6.46), we first use Hölder’s inequality to obtain

$$\begin{aligned} {\mathbb {E}}^W\left| \frac{F^{\#}_{a_ib_1}}{G_{a_ia_i}^{\#}}\!\cdot \! F^{\#}_{b_1b_2} F^{\#}_{b_2b_3}\cdots F^{\#}_{b_na_i}\right| ^r \!\!\le \!\left\| \frac{F^{\#}_{a_ib_1}}{G_{a_ia_i}^{\#}} \right\| _{r(n+1)}^r\,\prod _{i=1}^n \left\| F_{b_ib_{i+1}}^\# \right\| _{r(n+1)}^r,\,\,\, (b_{n+1}\!=\!a_i). \end{aligned}$$

Next, using Schur’s formula

$$\begin{aligned} \frac{1}{G_{aa}^{({\mathbb {T}})}}=\lambda v_a+w_{aa}-z-\sum _{k,l}^{({\mathbb {T}}a)}w_{ak}G^{(a{\mathbb {T}})}_{kl}w_{la}\,,\quad (a\not \in {\mathbb {T}}), \end{aligned}$$

and the trivial bounds $|G_{ab}^{({\mathbb {T}})}|\le \eta ^{-1}\le N$, ${\mathbb {E}}^W |w_{ij}|^{q}\le C (\theta q)^{\theta q}N^{-q/2}$ and $|\lambda v_i|^q\le C^q$, and the boundedness of ${\mathcal {D}}_\epsilon '$, we get

$$\begin{aligned} \Vert F^{\#}_{b_ib_{i+1}}\Vert _{r(n+1)}&\le \frac{1}{\eta } \left\| \frac{1}{G_{b_{i+1}b_{i+1}}^{\#}}\right\| _{r(n+1)}\\&\le N\left( C+\sum _{k,l}^{(\# b_{i+1})}\left\| w_{b_{i+1}k}G^{(\# b_{i+1})}_{kl}w_{lb_{i+1}}\right\| _{r(n+1)}\right) \ \le N^3 {Cr(n+1)}. \end{aligned}$$

Similarly, we obtain

$$\begin{aligned} \left\| \frac{F^{\#}_{a_ib_1}}{G_{a_ia_i}^{\#}} \right\| _{r(n+1)}\le N^4 Cr(n+1). \end{aligned}$$

(6.47)

Thus

$$\begin{aligned} \left\| \frac{F^{\#}_{a_ib_1}}{G_{a_ia_i}^{\#}} \right\| _{r(n+1)}^r\prod _{i=1}^n \left\| F_{b_ib_{i+1}}^\# \right\| _{r(n+1)}^r\le (Cr(n+1))^{r(n+1)}N^{4r+3rn}. \end{aligned}$$

(6.48)

Recalling that $1\le n\le p+1$, $r\le 10p$ and $p\le (\log N)^{\xi -3/2}$, we have $C r(n+1)\ll N$. Thus (6.46) holds with, e.g., $K=4$, $C=1$.

Combining Remarks 6.8 and 6.9 we obtain a bound on the remainder term $R_{a_i}(\mathbf {A}_\Gamma ,\mathbf {A}_S)$,

$$\begin{aligned} {\mathbb {1}}(\Xi )|R_{a_i}(\mathbf {A}_\Gamma ,\mathbf {A}_S)|\le (Cp)^{2p}(\varphi _N)^{c\xi p} N^{-1/2}N^{-p{\varpi _{\mathrm{b}}}/2}N^{(p+2)\epsilon }. \end{aligned}$$

(6.49)

To condense the notation slightly, we abbreviate $M_{a_i}\equiv M_{a_i}(\mathbf {A}_\Gamma ,\mathbf {A}_S)$, $R_{a_i}\equiv R_{a_i}(\mathbf {A}_\Gamma ,\mathbf {A}_S)$ and set

$$\begin{aligned} M'_{a_i}\mathrel {\mathop :}=(G_{a_ia_i}^{(\mathbf {A}_S\backslash a_i)})^{-1}+M_{a_i}. \end{aligned}$$

(6.50)

Returning to (6.39) and choosing $i=1$, we can write

$$\begin{aligned} {\mathbb {E}}^W X_{\mathbf {a}}={\mathbb {E}}^W Q_{a_1}{(\overline{M'}_{a_1}})\, \overline{X}_{a_2}\cdots X_{a_{2r}}+{\mathcal {R}}_{a_1}\,, \end{aligned}$$

(6.51)

where we have set ${\mathcal {R}}_{a_1}\mathrel {\mathop :}={\mathbb {E}}^W Q_{a_1}{\left( \overline{R}_{a_1}\right) } \,\overline{X}_{a_2} \cdots X_{a_p}$. By the bound (6.49) and the bounds in Remark 6.10, Lemma 6.5 yields

$$\begin{aligned} |{\mathcal {R}}_{a_1}|\le (Cp)^{cp}(\varphi _N)^{c_0\xi p}N^{-p/2-p{\varpi _{\mathrm{b}}}/2+3p\epsilon }. \end{aligned}$$

(6.52)

Before we expand in a next step $X_{a_2}$ in (6.39), we make the following observation.

Remark 6.11

Let $F\in \widetilde{F}(\mathbf {A}_\Gamma ,\mathbf {A}_S)$ be a maximally expanded monomial of degree $d=n+1$. From Remark 6.9, we know that $F$ is of the form (6.42). Since $F$ is maximally expanded, the lower indices in each factor in (6.42) also determine its upper indices. Thus, a summand $F\in \widetilde{{\mathcal {F}}}(\mathbf {A}_\Gamma ,\mathbf {A}_S)$ in $M_{a_i}$ can be labeled by a sequence $\mathbf {b}=(b_1,\ldots , b_n)\in \mathbf {A}_S^n$, satisfying $b_1\not =a_i$, $b_k\not =b_{k+1}$, $(k\in [\![1,n-1]\!]$), $b_n\not =a_i$. Here $d=n+1$, $n\ge 1$, is the degree of $F$. In the following we write $F\equiv F_{a_i,\mathbf {b}}\in \widetilde{{\mathcal {F}}}(\mathbf {A}_\Gamma ,\mathbf {A}_S)$. Denoting by $\mathbf {B}(a_i,n)$ the set of such labeling sequences of length $n$, we can write

$$\begin{aligned} M_{a_i}=\sum _{n=1}^{p}\sum _{\mathbf {b}\in \mathbf {C}(a_i,n)}F_{a_i,\mathbf {b}}, \end{aligned}$$

(6.53)

where $\mathbf {C}(a_i,n)$ is some subset of $\mathbf {B}(a_i,n)$. For later purposes, we note the following crude upper bound on the cardinality of $\mathbf {B}(a_i,n)$:

$$\begin{aligned} |\mathbf {B}(a_i,n)|\le |\mathbf {A}_S|^n\le p^n\le p^p\,,\qquad (n\ge 1). \end{aligned}$$

(6.54)

For $n=0$, we set $F_{a_i,(0)}\mathrel {\mathop :}=(G_{a_ia_i}^{(\mathbf {A}_S \backslash a_i)})^{-1}$ and $\mathbf {B}(a_i,0)\mathrel {\mathop :}=\{(0)\}$.

Using Remark 6.11, we can write, for $X_\mathbf {a}$ as in (6.39),

$$\begin{aligned} {\mathbb {E}}^W X_{\mathbf {a}}=\sum _{n_1=0}^p \sum _{\mathbf {b_1}\in \mathbf {C}(a_1,n_1)}{\mathbb {E}}^W\,Q_{a_1}{(\overline{{F}}_{a_1,\mathbf {b_1}})}\, \overline{X}_{a_2}\cdots {X}_{a_{p}}+{\mathcal {R}}_{a_1}, \end{aligned}$$

(6.55)

where the $n_1=0$ term in the sum is understood as ${\mathbb {E}}^W \, Q_{a_1}{(\overline{F}_{a_1,(0)})}\,\overline{X}_{a_2}\cdots {X}_{a_{p}}$.

Next, we expand $X_{a_2}$ in each summand

$$\begin{aligned} {\mathbb {E}}^W\, Q_{a_1}{(\overline{F}_{a_1,\mathbf {b_1}})}\,{\overline{X}_{a_2}} \cdots {X}_{a_{p}}, \end{aligned}$$

(6.56)

using the algorithm $(A)$–$(B)$, however, we stop expanding a term (generated from $X_{a_2}$), if its degree is bigger than $p+1-n_1$, or if it is maximally expanded. Note that we do not expand the rest term ${\mathcal {R}}_{a_1}$ any further. With this modified stopping rule, we arrive at

$$\begin{aligned} {\mathbb {E}}^W X_{\mathbf {a}}=&\sum _{n_1=0}^p\sum _{n_2=0}^{p} \sum _{\mathbf {b_1}\in \mathbf {C}(a_1,n_1)}\sum _{\mathbf {b_2}\in \mathbf {C}(a_2,n_2)}{\mathbb {1}}(n_1+n_2\le p) {\mathbb {E}}^W\, Q_{a_1}{(\overline{F}_{a_1,\mathbf {b_1}})}\nonumber \\&\times Q_{a_2}{(\overline{F}_{a_2, \mathbf {b}_2})}\cdots {X}_{a_{p}}+{\mathcal {R}}_{a_1}+{\mathcal {R}}_{a_2}, \end{aligned}$$

(6.57)

for some sets of labeling sequences $\mathbf {C}(a_1,n_1)$ and $\mathbf {C}(a_2,n_2)$. It is easy to check that the rest term ${\mathcal {R}}_{a_2}$ satisfies the same bound (with possibly slightly larger constants) as ${\mathcal {R}}_{a_1}$. This is checked in the same way as before. To estimate the number of summands in $R_{a_2}$, we note that we apply the algorithm $|\mathbf {C}(a_1,n_1)|$ times and each application yields no more than $(Cp)^{cp}$ terms; see Remark 6.8. Thus the number of summands in ${\mathcal {R}}_{a_2}$ is bounded by $(Cp)^{c'p}$, $c'>c$.

We continue expanding the remaining $X_{a_k}$, $k\ge 3$, in (6.57) using the algorithm $(A)$–$(B)$, but while expanding $X_{a_k}$, we stop the expansion as soon as the degree of a generated term exceeds $p+1-\sum _{i=1}^{k-1} n_i$. This leads to,

$$\begin{aligned} {\mathbb {E}}^W X_{\mathbf {a}}\!=&\!\sum _{n_1,\ldots ,n_p=0}^p\,\,&\sum _{\mathbf {b_1} \in \mathbf {C}(a_1,n_1)}\!\cdots \!\sum _{\mathbf {b_p}\in \mathbf {C}(a_p,n_p)} {\mathbb {1}}\left( \sum _{i=1}^pn_i\!\le \! p\right) \,{\mathbb {E}}^WY(\mathbf {a},\mathbf {b_1},\dots , \mathbf {b_p})\nonumber \\&+\sum _{i=1}^p{\mathcal {R}}_{a_i}, \end{aligned}$$

(6.58)

where $(\mathbf {C}(a_i,n_i))$ are subsets of $(\mathbf {B}(a_i, n_i))$, and where we have abbreviated

$$\begin{aligned} Y(\mathbf {a},\mathbf {b_1},\dots ,\mathbf {b_p})\mathrel {\mathop :}=\prod _{i=1}^r Q_{a_i}{(\overline{F}_{a_i,\mathbf {b_i}})}\,\prod _{i=r+1}^{2r} Q_{a_i}(F_{a_i,\mathbf {b}_i}). \end{aligned}$$

(6.59)

The remainder terms $({\mathcal {R}}_{a_i})$ clearly satisfy

$$\begin{aligned} |{\mathcal {R}}_{a_i}|\le (Cp)^{cp}(\varphi _N)^{c_0\xi p}N^{-p/2- p{\varpi _{\mathrm{b}}}/2}N^{3p}, \end{aligned}$$

(6.60)

for all $i\in [\![1,p]\!]$. It thus suffices to bound the first term on the right side of (6.58).

Following [17], we pick a term $Y\equiv Y(\mathbf {a},\mathbf {b_1},\dots ,\mathbf {b_p})$ of the form (6.59) that has a non-vanishing expectation, ${\mathbb {E}}^W Y\not =0$. Considering a single label $i\in S\equiv S(\Gamma )$, we know that there exists a label $j\in S\backslash \{i\}$, such that the monomial $F_{a_j,\mathbf {b_j}}\in \widetilde{{\mathcal {F}}} (\mathbf {A}_\Gamma ,\mathbf {A}_S)$ in (6.59) contains a factor $F\in {\mathcal {F}}(\mathbf {A}_\Gamma ,\mathbf {A}_{S})$, having $a_i$ as a lower index (otherwise the expectation of $Y$ has to vanish due to the presence of the $Q_{a_i}$). It follows from Remark 6.9 that $F_{a_j,\mathbf {b_j}}$ is of the form (6.42), with $n\ge 1$ and $b_k=a_i$, for some $k\in [\![1,n]\!]$. Note that we use here that all indices in $\mathbf {A}_S$ are distinct.

We write $j=\mathfrak {l}(i)$, if a label $j$ is linked to a label $i$ in the sense of the previous paragraph. Denoting by $l_j\mathrel {\mathop :}=|\mathfrak {l}^{(-1)}(\{j\})|$, the number of times the label $j$ has been chosen to be linked in the above sense to some other label, we obtain

$$\begin{aligned} {\mathbb {1}}(\Xi )|F_{a_j,\mathbf {b}_j}|\le C^p(\varphi _N)^{c\xi p}N^{-1/2}N^{-l_j{\varpi _{\mathrm{b}}}/2}N^{2p\epsilon +l_j\epsilon }, \end{aligned}$$

(6.61)

as follows from (6.44).

Finally, using $\sum _{j\in S}l_j\ge |S|=s$, we get

$$\begin{aligned} {\mathbb {1}}(\Xi )| Y|\le C^p(\varphi _N)^{c\xi p} N^{-p/2}N^{-s{\varpi _{\mathrm{b}}}/2} N^{2p\epsilon +s\epsilon }, \end{aligned}$$

(6.62)

for $Y$ as in (6.59), with ${\mathbb {E}}^W Y\not =0$. Lemma 6.5 thus gives

$$\begin{aligned} |{\mathbb {E}}^WY|\le C^p(\varphi _N)^{c_0\xi p} N^{-p/2-s{\varpi _{\mathrm{b}}}/2}N^{2p\epsilon +s\epsilon }. \end{aligned}$$

(6.63)

To bound the right side of (6.58), it remains to bound the number of summands in the first term. Using (6.54), we obtain

$$\begin{aligned}&\sum _{n_1,\ldots , n_p=0}^p\,\, \sum _{\mathbf {b_1}\in \mathbf {C}(a_1, n_1)}\cdots \sum _{\mathbf {b_p}\in \mathbf {C}(a_p,n_p)}{\mathbb {1}}\left( \sum _{i=1}^pn_i\le p\right) \nonumber \\&\quad \le \sum _{n_1,\ldots , n_p=0}^p{\mathbb {1}}\left( \sum _{i=1}^pn_i\le p\right) \prod _{i=1}^p p^{n_i}\nonumber \\&\quad \le \sum _{n_1,\ldots , n_p=0}^p p^{p} \le (Cp)^{2p}, \end{aligned}$$

(6.64)

and we can bound (6.58) by

$$\begin{aligned} |{\mathbb {E}}^WX_{\mathbf {a}}|\le (Cp)^{cp}(\varphi _N)^{c_0\xi p} N^{-p/2-s{\varpi _{\mathrm{b}}}/2+3p\epsilon +s\epsilon }. \end{aligned}$$

(6.65)

We now return to (6.39). We perform the summation by first fixing a partition $\Gamma \in {\mathcal {P}}_{2r}$. Then we observe that

$$\begin{aligned} \frac{1}{N^{2r}}\sum _{\mathbf {a}}{\mathbb {1}}(\Gamma =\Gamma (\mathbf {a}))\le \left( \frac{1}{N}\right) ^{2r-|\Gamma |}\le \left( \frac{1}{\sqrt{N}}\right) ^{2r-s}, \end{aligned}$$

(6.66)

since any block in the partition $\Gamma$ that is not associated to a single label consists of at least two elements. Thus $|\Gamma |\le (2r+s)/2=r+s/2$. Using $N^{-1/2}\ll N^{-{\varpi _{\mathrm{b}}}}$ we find

$$\begin{aligned} {\mathbb {E}}^W\left| \frac{1}{N}\sum _{a\in A}Q_{a}\left( \frac{1}{G_{aa}}\right) \right| ^{2r}\le (Cp)^{cp}(\varphi _N)^{c\xi p}\sum _{\Gamma \in {\mathcal {P}}_{2r}}N^{-p/2-p{\varpi _{\mathrm{b}}}/2}N^{3p\epsilon }. \end{aligned}$$

(6.67)

Recalling that the number of partitions of $p$ elements is bounded by $(Cp)^{2p}$, we thus get

$$\begin{aligned} {\mathbb {E}}^W\left| \frac{1}{N}\sum _{a\in A}Q_{a}\left( \frac{1}{G_{aa}(z)} \right) \right| ^{2r}\le (Cp)^{cp}(\varphi _N)^{c_0\xi p}N^{-p/2-p{\varpi _{\mathrm{b}}}/2}N^{3p\epsilon }, \end{aligned}$$

(6.68)

for some constants $C$ and $c$. Finally, we note that the constants can be chosen uniformly in $z\in {\mathcal {D}}_\epsilon '$, since all estimates used are uniform in $z$. $\square$

Next, we prove Lemma 5.10.

Proof of Lemma 5.10

Recalling the remark after Definition 6.3, we know that the event $\Xi$ has $(\xi ,\nu )$-high probability. Choosing $p$ as the largest integer smaller than $\nu (\log N)^{\xi -2}$, Markov’s inequality and the moment bound (6.27) yield, for some constant $c$,

$$\begin{aligned} \frac{1}{N}\left| \sum _{a=n_0}^N Z_{a}(z)\right| \le (\varphi _N)^{c\xi }N^{-1/2-{\varpi _{\mathrm{b}}}/2+4\epsilon }, \end{aligned}$$

(6.69)

with $(\xi -2,\nu )$-high probability on $\Omega _V$, uniformly for $z\in {\mathcal {D}}_\epsilon '$. This finishes the proof of (5.28).

To prove (5.29), it suffices to replace $(G_{aa})$ in (6.2), by $(G_{aa}^{(k)}\,:\,a\not = k)$. Using (6.7) and the bounds (6.21) and (6.22), the claim (5.29), follows from (5.28). We leave the details aside. $\square$

Next, we prove Corollary 5.11. Define, for $a\in A$,

$$\begin{aligned} g_a(z)\mathrel {\mathop :}=\frac{1}{\lambda v_a-z-\widehat{m}_{fc} {(z)}}\,,\qquad \quad ( z\in {\mathbb {C}}^{+}). \end{aligned}$$

(6.70)

Note that for $z\in {\mathcal {D}}_{\epsilon }'$, we have $|g_a(z)|\le C N^{1/(\mathrm {b}+1)}N^{\epsilon }$ on $\Omega _V$.

Lemma 6.12

Let $A=[\![n_0,N]\!]$. Recall the definition of the domain ${\mathcal {D}}_{\epsilon }'$ in (3.33). Let $\Xi$ denote the event in Definition 6.3 and assume it has $(\xi ,\nu )$-high probability. Then there exist constants $C$, $c$, $c_0$, such that for $p=2r$, $r\in {\mathbb {N}}$, $p\le (\log N)^{\xi -3/2}$, we have

$$\begin{aligned} {\mathbb {E}}^W\left| \frac{1}{N}\sum _{a\in A}(g_{a}(z))^2Q_{a} \left( \frac{1}{G_{aa}(z)}\right) \right| ^{p}\le (Cp)^{cp}(\varphi _N)^{c_0\xi p} N^{-p/2-p{\varpi _{\mathrm{b}}}/2}N^{3p\epsilon }, \end{aligned}$$

(6.71)

on $\Omega _V$, for all $z\in {\mathcal {D}}_\epsilon '$.

Proof

First, we note that $g_{a}Q_{b}=Q_{b} g_{a}$, $a,b\in [\![1,N]\!]$, since the $(g_a)$ are independent of the random variables $(w_{ij})$. Similar to (6.35), we are led to consider

$$\begin{aligned} {\mathbb {E}}^W\left| \frac{1}{N}\sum _{a\in A}g_a^2 Q_a\left( \frac{1}{G_{aa}} \right) \right| ^{2r}&=\frac{1}{N^{2r}}\sum _{a_1\in A,\ldots , a_{2r} \in A}g_{\mathbf {a}}^2\,{\mathbb {E}}^W{X}_\mathbf {a}, \end{aligned}$$

(6.72)

where we have set $g_\mathbf {a}\mathrel {\mathop :}=\overline{g}_{a_1}\cdots \overline{g}_{a_r}g_{a_{r+1}}\cdots g_{a_{2r}}$.

Following the lines of the proof of Lemma 6.6, we write (6.72) as

$$\begin{aligned} {\mathbb {E}}^W\left| \frac{1}{N}\sum _{a\in A} g_a^2 Q_a\left( \frac{1}{G_{aa}}\right) \right| ^{2r}=\frac{1}{N^{2r}}\sum _{\Gamma \in {\mathcal {P}}_{2r}}\sum _{a_1\in A,\ldots ,a_{2r}\in A}{\mathbb {1}}(\Gamma =\Gamma (\mathbf {a}))g^2_{\mathbf {a}}\,{\mathbb {E}}^W X_{\mathbf {a}}. \end{aligned}$$

(6.73)

As in the proof of Lemma 6.6, we fix $\mathbf {a}$ and denote by $\Gamma \mathrel {\mathop :}=\Gamma (\mathbf {a})$, the partition induced by the equivalence relation $\sim$. Since ${\mathbb {E}}^W X_{\mathbf {a}}$ with $\mathbf {a}\equiv \mathbf {a}_\Gamma$ has already been bounded in the proof of Lemma 6.6, with a bound that only depends on $s\equiv |S(\Gamma )|$ [see (6.65)], it suffices to control

$$\begin{aligned} \frac{1}{N^{2r}}\sum _{a_1\in A,\ldots ,a_{2r}\in A}{\mathbb {1}}(\Gamma = \Gamma (\mathbf {a}))g^2_{\mathbf {a}}. \end{aligned}$$

(6.74)

Recall that

$$\begin{aligned} \frac{1}{N}\sum _{i=1}^N\frac{1}{|\lambda v_i-z-\widehat{m}_{fc} (z)|^2}=\widehat{R}_2(z)<1, \quad (z\in {\mathcal {D}}_{\epsilon }'); \end{aligned}$$

(6.75)

see, e.g., (3.37). Applying (6.75) $|\Gamma |$ times, we obtain

$$\begin{aligned} \frac{1}{N^{2r}}\sum _{a_1\in A,\ldots ,a_{2r}\in A}{\mathbb {1}}(\Gamma = \Gamma (\mathbf {a}))|g_{\mathbf {a}}|^2\le C^{2r}\left( \frac{N^{2/ (\mathrm {b}+1)}N^{2\epsilon }}{N}\right) ^{2r-|\Gamma |}. \end{aligned}$$

(6.76)

Here $|\Gamma |$ denotes the number of blocks of the partition $\Gamma$, and $s$ denotes the number of single labels in $\mathbf {a}$. Since every block of $\Gamma$ that is not associated with a single label consists of at least two elements, we have $|\Gamma |\le (2r+s)/2=r+s/2$, thus $2r-|\Gamma |\ge r-s/2$, and we obtain,

$$\begin{aligned} \frac{1}{N^{2r}}\sum _{a_1\in A,\ldots ,a_{2r}\in A}{\mathbb {1}}(\Gamma = \Gamma (\mathbf {a}))|g_{\mathbf {a}}|^2&\le C^{2r}\left( \frac{N^{2 /(\mathrm {b}+1)}N^{2\epsilon }}{N}\right) ^{r-s/2}\nonumber \\&=C^{2r}\left( \frac{N^{1/(\mathrm {b}+1)}N^{\epsilon }}{\sqrt{N}} \right) ^{2r-s}\nonumber \\&\le C^{2r}\left( N^{-{\varpi _{\mathrm{b}}}}\right) ^{2r-s}N^{(2r-s)\epsilon }. \end{aligned}$$

(6.77)

The proof of Lemma 6.12 is now completed as the proof of Lemma 6.6. $\square$

Proof of Corollary 5.11

Recalling (6.2), Corollary 5.11 can be proven in the same way as Lemma 5.10 above. $\square$

7 Proof of Theorem 2.10

In this section, we prove Theorem 2.10. The proof of (2.20) is based on an analysis of $(G_{jj}(z))$, for $z$ close to the eigenvalues $\mu _k$, $k\in [\![1, n_0-1]\!]$, using the Helffer–Sjöstrand formula (7.10) below. The Helffer–Sjöstrand calculus has been applied in [19] to $m(z)$, the averaged Green function, respectively to the empirical eigenvalue counting function, to obtain rigidity estimates on the eigenvalue locations. In Sect. 7.2, we apply the Helffer–Sjöstrand formula to $(G_{jj}(z))$, respectively, to a weighted empirical eigenvalue counting function; see (7.6).

In Sect. 7.3, we prove (2.21) following the argument given in [23] for generalized Wigner matrices.

7.1 Preliminaries

To start with, we claim that, for $z$ close to the spectral edge, $z+\widehat{m}_{fc}(z)$ is well approximated by a linear function.

Lemma 7.1

On $\Omega _V$, we have for all $z\in {\mathcal {D}}_{\epsilon }'$ that

$$\begin{aligned} z+\widehat{m}_{fc}(z)=\lambda -\frac{\lambda ^2}{\lambda _+^2-\lambda ^2} (z-L_+)+{\mathcal {O}}\left( (\varphi _N)^{\xi }(\kappa +\eta )^{\min \{\mathrm {b},2\}}\right) +{\mathcal {O}}(N^{-1/2+2\epsilon }). \end{aligned}$$

(7.1)

Proof

The lemma follows readily by combining Lemmas 4.1 and 3.7. $\square$

Remark 7.2

Combining Lemma 7.1 and Proposition 4.5, we obtain, for $j\le n_0-1$,

$$\begin{aligned}&\lambda v_j-z-\widehat{m}_{fc}(z)=\frac{\lambda ^2}{\lambda ^2- \lambda _+^2}(\mu _j-z)+{\mathcal {O}}\left( (\varphi _N)^{2\xi }N^{-2/(\mathrm {b}+1)}\right) \nonumber \\&\quad +{\mathcal {O}}\left( N^{-1/2+3\epsilon }\right) +{\mathcal {O}}\left( (\varphi _N)^{\xi }(\kappa +\eta )^{\min \{\mathrm {b},2\}}\right) , \end{aligned}$$

(7.2)

with $(\xi ,\nu )$-high probability, for all $z\in {\mathcal {D}}_{\epsilon }'$.

To state the next lemma, it is convenient to abbreviate

$$\begin{aligned} g_j^\circ (z)\mathrel {\mathop :}=\frac{\lambda ^2-\lambda _+^2}{\lambda ^2}\frac{1}{\mu _j-z}\,, \qquad G^{\Delta }_{jj}(z)\mathrel {\mathop :}=G_{jj}(z)-g_j^\circ (z)\,, \qquad \quad (z\in {\mathbb {C}}^+). \end{aligned}$$

(7.3)

We have the following estimate on $G^{\Delta }_{jj}(z)$.

Lemma 7.3

There are constants $C$ and $c$, such that, for all $z\in {\mathcal {D}}_{\epsilon }'$, and all $j\le n_0-1$,

$$\begin{aligned} |G^{\Delta }_{jj}(z)|\le C(\varphi _N)^{2\xi }|g^\circ _j(z)|\left( \frac{1}{N^{2/(\mathrm {b}+1)}\eta }+\frac{N^{3\epsilon }}{N^{1/2}\eta }+ \frac{(\kappa +\eta )^{\min \{\mathrm {b},2\}}}{\eta }\right) , \end{aligned}$$

(7.4)

with $(\xi ,\nu )$-high probability on $\Omega _V$.

Proof

For $z\in {\mathcal {D}}_{\epsilon }'$, we have $(G_{jj}(z))^{-1}={\lambda v_j-z-\widehat{m}_{fc}(z)+{\mathcal {O}}(N^{-1/2+2\epsilon })}$, with high probability on $\Omega _V$; see Lemma 5.1. We thus obtain from (7.2) that

$$\begin{aligned} G_{jj}(z)&\!=\!g_j^\circ (z)\!+\!g_j^\circ (z)G_{jj}(z){\mathcal {O}}\left( (\varphi _N)^{2 \xi }\frac{1}{N^{2/(\mathrm {b}+1)}}\!+\!\frac{N^{3\epsilon }}{N^{1/2}}\!+\!(\varphi _N)^{\xi } (\kappa \!+\!\eta )^{\min \{\mathrm {b},2\}}\right) , \end{aligned}$$

(7.5)

with high probability on $\Omega _V$. Applying the trivial bound $|G_{jj}(z)|\le \eta ^{-1}$, Inequality (7.4) follows. $\square$

7.2 Proof of Theorem 2.10: inequality (2.20)

For $j\in [\![1,N]\!]$, we define a weighted empirical eigenvalue counting measure, $\rho _j$, by

$$\begin{aligned} \rho _j\mathrel {\mathop :}=\sum _{k=1}^N |u_{k}(j)|^2\delta _{\mu _{k}}, \end{aligned}$$

(7.6)

where $(\mu _{k})$ are the eigenvalues of $H$ and $(u_{k}(j))$ the components of the associated eigenvectors. For $k\in [\![1,n_0-1]\!]$, let $f_k(x)\ge 0$ be a smooth test function satisfying

$$\begin{aligned} f_k(x)\!=\! {\left\{ \begin{array}{ll} 1\,, &{} \mathrm if |x-\mu _k|\le N^{-1/(\mathrm {b}+1)-\epsilon '}\\ 0\,, &{} \mathrm if |x-\mu _k|\ge 2 N^{-1/(\mathrm {b}+1)-\epsilon '} \end{array}\right. }, \quad |f_k'(x)|\le C N^{1/(\mathrm {b}+1)}N^{\epsilon '}\,,\quad |f_k''(x)|\le C N^{2/(\mathrm {b}+1)}N^{2\epsilon '}, \end{aligned}$$

(7.7)

for some $\epsilon '>\epsilon$. By Proposition 4.5, we know that the eigenvalues $(\mu _k)$ satisfy

$$\begin{aligned} \min _{1 \le k\le n_0-1}( \mu _{k+1}-\mu _k)\ge C N^{-1/(\mathrm {b}+1)-\epsilon }, \end{aligned}$$

(7.8)

for some constant $C$, with high probability on $\Omega _V$. Since we chose $\epsilon '>\epsilon$, we conclude that the following formula holds with high probability on $\Omega _V$, for all $k\le n_0-1$,

$$\begin{aligned} |u_{k}(j)|^2=\int f_k(w)\mathrm {d}\rho _j(w). \end{aligned}$$

(7.9)

Using the Helffer–Sjöstrand formula, we may represent $f_k(w)$ as

$$\begin{aligned} f_k(w)=\frac{1}{2\pi } \int _{{\mathbb {R}}^2}\mathrm {d}x\,\mathrm {d}y\,\frac{\widetilde{f_k}(x+\mathrm {i}y)}{w-x-\mathrm {i}y}, \end{aligned}$$

(7.10)

where

$$\begin{aligned} \widetilde{f_k}(x+\mathrm {i}y)\mathrel {\mathop :}=\mathrm {i}y f_k''(x)\chi (y)+\mathrm {i}(f_k(x)+\mathrm {i}y f_k'(x))\chi '(y)\,,\quad ( x,y\in {\mathbb {R}}), \end{aligned}$$

(7.11)

with $\chi \ge 0$ a smooth test function satisfying

$$\begin{aligned} \chi (y)= {\left\{ \begin{array}{ll} 1\,, &{} \mathrm if y\in [-{\mathcal {E}},{\mathcal {E}}]\\ 0\,, &{}\mathrm if y\in [-2{\mathcal {E}},2{\mathcal {E}}]^{c} \end{array}\right. }, \quad |\chi '(y)|\le \frac{C}{{\mathcal {E}}}, \end{aligned}$$

(7.12)

where we have set ${\mathcal {E}}\mathrel {\mathop :}=N^{-1/(\mathrm {b}+1)}$.

Combining (7.9) with (7.10), we obtain the following representation for $|u_{k}(j)|$, with $k\in [\![1,n_0-1]\!]$, $j\in [\![1,N]\!]$,

$$\begin{aligned} |u_{k}(j)|^2=&\frac{1}{2\pi }\int _{{\mathbb {R}}^2}\mathrm {d}x\,\mathrm {d}y\,\widetilde{f_k} (x+\mathrm {i}y) g_j^\circ (x+\mathrm {i}y)\nonumber \\&+\frac{1}{2\pi }\int _{{\mathbb {R}}^2}\mathrm {d}x\,\mathrm {d}y\,\widetilde{f_k}(x+\mathrm {i}y)G^{\Delta }_{jj}(x+\mathrm {i}y), \end{aligned}$$

(7.13)

which holds with high probability on $\Omega _V$. The first term on the right side of (7.13) can be computed explicitly as

$$\begin{aligned} \frac{1}{2\pi }\int _{{\mathbb {R}}^2}\mathrm {d}x\,\mathrm {d}y\,\widetilde{f_k}(x\!+\!\mathrm {i}y) g_j^\circ (x\!+\!\mathrm {i}y)&\!=\!\frac{\lambda ^2-\lambda _+^2}{2\pi \lambda ^2} \int _{{\mathbb {R}}^2}\frac{\widetilde{f_k}(x+\mathrm {i}y)}{\mu _j-(x+\mathrm {i}y)} \!=\!\frac{\lambda ^2\!-\!\lambda _+^2}{\lambda ^2}f_k(\mu _j). \end{aligned}$$

(7.14)

Recalling (7.7), we conclude by Proposition 4.5 that, for $j,k\le n_0-1$, with high probability on $\Omega _V$,

$$\begin{aligned} \frac{1}{2\pi }\int _{{\mathbb {R}}^2}\mathrm {d}x\,\mathrm {d}y\,\widetilde{f_k}(x+\mathrm {i}y) g_j^\circ (x+\mathrm {i}y)=\frac{\lambda ^2-\lambda _+^2}{\lambda ^2}\delta _{jk}. \end{aligned}$$

(7.15)

To complete the proof of (2.20), it hence suffices to show that the second term on the right side of (7.13) is negligible compared to (7.15), provided $\epsilon '>\epsilon$. For concreteness we set $\epsilon '=2\epsilon$ in the following.

Lemma 7.4

Let $\widetilde{f}_k$ be defined as in (7.11) and set $\epsilon '=2\epsilon$. Then there are constants $C$ and $c$ such that, for $j,k\le n_0-1$,

$$\begin{aligned} \left| \int _{{\mathbb {R}}^2}\mathrm {d}x\,\mathrm {d}y\,\widetilde{f_k}(x+\mathrm {i}y) G^{\Delta }_{jj}(x+\mathrm {i}y)\right| \le C(\varphi _N)^{c\xi } \left( N^{-1/(\mathrm {b}+1)+3\epsilon }+N^{-{\varpi _{\mathrm{b}}}+5\epsilon }\right) , \end{aligned}$$

(7.16)

with $(\xi ,\nu$)-high probability on $\Omega _V$.

Proof

We set $\eta \mathrel {\mathop :}=\frac{1}{\sqrt{N}}$. Using $G^{\Delta }_{jj} (\overline{z}) =\overline{G^{\Delta }_{jj}(z)}$, $(z\in {\mathbb {C}}^+)$, we obtain,

$$\begin{aligned}&{\left| \int _{{\mathbb {R}}^2}\mathrm {d}x\,\mathrm {d}y\,\widetilde{f_k}(x+\mathrm {i}y) G^{\Delta }_{jj}(x+\mathrm {i}y)\right| }\le C\int \mathrm {d}x\int _0^{\infty } {\mathrm {d}y}|f_k(x)|\,|\chi '(y)|\, |G^{\Delta }_{jj}(x+\mathrm {i}y)|\nonumber \\&\quad + C\int \mathrm {d}x\int _0^{\infty } {\mathrm {d}y}\,y\, |f_k'(x)|\,| \chi '(y)|\, |G^{\Delta }_{jj}(x+\mathrm {i}y)|\nonumber \\&\quad +C{\left| \int \mathrm {d}x\int _0^{\eta }\mathrm {d}y f_k''(x)\chi (y) y\,{\mathrm {Im }}\,G^{\Delta }_{jj}(x+\mathrm {i}y) \right| }\nonumber \\&\quad +C{\left| \int \mathrm {d}x\int _{\eta }^{\infty }\mathrm {d}y f_k''(x) \chi (y) y\,{\mathrm {Im }}\,G^{\Delta }_{jj}(x+\mathrm {i}y)\right| }. \end{aligned}$$

(7.17)

The first term on the right side of (7.17) can be bounded by using (7.4): Bounding in (7.4) $\kappa \equiv \kappa _x$ by $\kappa \le N^{-1/(\mathrm {b}+1)+\epsilon /2}$ and $g_j^\circ$ by $|g_{j}^\circ (x+\mathrm {i}y)|\le Cy^{-1}$, we obtain

$$\begin{aligned}&\int \mathrm {d}x\int _0^{\infty } \mathrm {d}y \,|f_k(x)||\chi '(y)| |G^{\Delta }_{jj}(x+\mathrm {i}y)| \le \frac{C}{{\mathcal {E}}}\int \mathrm {d}x\,|f_k(x)|\,\int _{{\mathcal {E}}}^{2{\mathcal {E}}}\mathrm {d}y\, |G^{\Delta }_{jj}(x+\mathrm {i}y)|\nonumber \\&\quad \le C(\varphi _N)^{2\xi }\frac{N^{-1/(\mathrm {b}+1)-\epsilon '}}{{\mathcal {E}}^2} {\left( N^{-2/(\mathrm {b}+1)}+N^{-1/2+3\epsilon }+(N^{-1/(\mathrm {b}+1)+\epsilon / 2})^{\min \{\mathrm {b},2\}}\right) }\nonumber \\&\quad \le C(\varphi _N)^{2\xi }{\left( N^{-1/(\mathrm {b}+1)-\epsilon '+\epsilon } +N^{-{\varpi _{\mathrm{b}}}-\epsilon '+3\epsilon }\right) }, \end{aligned}$$

(7.18)

with high probability on $\Omega _V$.

Similarly, we bound the second term on the right side of (7.17):

$$\begin{aligned}&\int \mathrm {d}x\int _0^{\infty } \mathrm {d}y \, y\, |f_k'(x)|\,|\chi '(y)|| G^{\Delta }_{jj}(x+\mathrm {i}y)|\end{aligned}$$

(7.19)

$$\begin{aligned}&\quad \le \frac{C}{{\mathcal {E}}}\,\int \mathrm {d}x\,|f_k'(x)|\,\int _{{\mathcal {E}}}^{2{\mathcal {E}}}\mathrm {d}y\,{y}|G^{\Delta }_{jj}(x+\mathrm {i}y)|\nonumber \\&\quad \le \frac{C(\varphi _N)^{2\xi }}{{\mathcal {E}}}|\log {\mathcal {E}}|\left( N^{-2/(\mathrm {b}+1)} +N^{-1/2+3\epsilon }+(N^{-1/(\mathrm {b}+1)+\epsilon /2})^{\min \{\mathrm {b},2\}} \right) \nonumber \\&\quad \le C(\varphi _N)^{c\xi }\left( N^{-1/(\mathrm {b}+1)+\epsilon }+N^{-{\varpi _{\mathrm{b}}}+ 3\epsilon }\right) . \end{aligned}$$

(7.20)

To bound the third term on the right side of (7.17), we use that $|y\, {\mathrm {Im }}\,G^{\Delta }_{jj}(x+\mathrm {i}y)|\le C$, for all $y>0$, and we obtain

$$\begin{aligned} \left| \int \mathrm {d}x\int _0^{\eta }\mathrm {d}y f_k''(x)\chi (y) y\,{\mathrm {Im }}\,G^{\Delta }_{jj}(x+\mathrm {i}y) \right|&\le C\eta \int \mathrm {d}x\, |f_k''(x)| \le C N^{-{\varpi _{\mathrm{b}}}+\epsilon '}. \end{aligned}$$

(7.21)

To bound the fourth term in (7.17), we integrate by parts, first in $x$ then in $y$ to find the bound

$$\begin{aligned}&C\left| \int \mathrm {d}xf_k'(x)\eta \, {\mathrm {Re }}\,G^{\Delta }_{jj}(x+\mathrm {i}\eta ) \right| +C\left| \int \mathrm {d}x\int _{\eta }^{\infty }\mathrm {d}y f_k'(x)\chi '(y) { y}\, {\mathrm {Re }}\,G^{\Delta }_{jj} (x+\mathrm {i}y)\right| \nonumber \\&\quad + C\left| \int \mathrm {d}x \int _{\eta }^{\infty }\mathrm {d}y f_k'(x)\chi (y)\,{\mathrm {Re }}\,G^{\Delta }_{jj}(x+\mathrm {i}y)\right| . \end{aligned}$$

(7.22)

The first term in (7.22) can be bounded using (7.4): Since $f_k'(x)=0$, if $|x-\mu _k|\le N^{-1/(\mathrm {b}+1)-\epsilon '}$, we can bound $|f'_k(x) g_j^\circ (x+\mathrm {i}y)|\le C N^{2/(\mathrm {b}+1)+2\epsilon '}$, and we obtain

$$\begin{aligned}&{\left| \int \mathrm {d}xf_k'(x)\eta \, {\mathrm {Re }}\,G^{\Delta }_{jj}(x+\mathrm {i}\eta )\right| }\nonumber \\&\quad \le C(\varphi _N)^{2\xi }{N^{1/(\mathrm {b}+1)+\epsilon '}}\eta {\left( \frac{1}{N^{2/(\mathrm {b}+1)}\eta }+\frac{N^{3\epsilon }}{N^{1/2} \eta }+\frac{(N^{-1/(\mathrm {b}+1)+\epsilon /2})^{\min \{\mathrm {b},2\}})}{\eta } \right) }\nonumber \\&\quad \le C(\varphi _N)^{2\xi }{\left( N^{-1/(\mathrm {b}+1)+\epsilon '+ \epsilon }+N^{-{\varpi _{\mathrm{b}}}+\epsilon '+3\epsilon }\right) }, \end{aligned}$$

(7.23)

with high probability on $\Omega _V$.

Similarly for the second term in (7.22), using (7.4) we obtain

$$\begin{aligned}&\bigg |\int \mathrm {d}x\int _{\eta }^{\infty }\mathrm {d}y f_k'(x)\chi '(y) {y}\, {\mathrm {Re }}\,G^{\Delta }_{jj} (x+\mathrm {i}y)\bigg |\nonumber \\&\quad \le C(\varphi _N)^{2\xi }\left( N^{-1/(\mathrm {b}+1)+\epsilon '+ \epsilon }+N^{-{\varpi _{\mathrm{b}}}+\epsilon '+3\epsilon }\right) . \end{aligned}$$

(7.24)

The third term in (7.22) can be bounded using (7.4) as

$$\begin{aligned}&\bigg |\int \mathrm {d}x \int _{\eta }^{\infty }\mathrm {d}y f_k'(x)\chi (y){\mathrm {Re }}\,G^{\Delta }_{jj}(x+\mathrm {i}y)\bigg | \nonumber \\&\quad \le \! C(\varphi _N)^{2\xi }{N^{1/(\mathrm {b}+1)+\epsilon '}} \!\int _{\eta }^{2 {\mathcal {E}}}\!\mathrm {d}y\left( \frac{1}{N^{2/(\mathrm {b}+1)}y}+\frac{N^{3\epsilon }}{N^{1/2} y}\!+\!\frac{(N^{-1/(\mathrm {b}+1)\!+\!\epsilon /2})^{\min \{\mathrm {b},2\}})}{y}\right) \nonumber \\&\quad \le C|\log \eta |(\varphi _N)^{2\xi }\left( N^{-1/(\mathrm {b}+1)+\epsilon '+ \epsilon }+N^{-{\varpi _{\mathrm{b}}}+\epsilon '+3\epsilon }\right) . \end{aligned}$$

(7.25)

Thus combining (7.18), (7.21), (7.23), (7.24) and (7.25), we obtain, upon choosing $\epsilon '=2\epsilon$,

$$\begin{aligned} \left| \int \mathrm {d}x\,\mathrm {d}y\, \widetilde{f_k}(x+\mathrm {i}y)G^{\Delta }_{ii} (x+\mathrm {i}y)\right|&\le C(\varphi _N)^{c\xi }\left( N^{-1/(\mathrm {b}+1)+3 \epsilon }+N^{-{\varpi _{\mathrm{b}}}+5\epsilon }\right) , \end{aligned}$$

(7.26)

with high probability on $\Omega _V$. $\square$

Proof of Theorem 2.7: Equation (2.20)

Combining (7.13), (7.15) and (7.16), we obtain, for $j,k\le n_0-1$,

$$\begin{aligned} |u_k(j)|^2=\frac{\lambda ^2-\lambda _+^2}{\lambda ^2}\delta _{jk}+ {\mathcal {O}}\left( (\varphi _N)^{c\xi }N^{-1/(\mathrm {b}+1)+3\epsilon }+(\varphi _N)^{c\xi } N^{-{\varpi _{\mathrm{b}}}+5\epsilon }\right) , \end{aligned}$$

(7.27)

with high probability on $\Omega _V$. Choosing $k=j$, Eq. (2.20) follows. $\square$

7.3 Proof of Theorem 2.10: inequality (2.21)

In this subsection we prove the second part of Theorem 2.10. To prove (2.21), we follow the traditional path of [20–22]. Presumably, the same result can be obtained by a more detailed analysis of $G_{jj}^{\Delta }$ than the one carried out in the previous subsection.

Recall that we have set $\eta _0\mathrel {\mathop :}=N^{-1/2-\epsilon }$.

Lemma 7.5

There is a constant $C$, such that for $k\in [\![1,n_0-1]\!]$, $j\in [\![1,N]\!]$, ($k\not =j$),

$$\begin{aligned} {\mathrm {Im }}\,G_{jj}(\mu _k+\mathrm {i}\eta _0)\le \frac{C}{(\lambda v_j-\lambda v_{k})^2}N^{-1/2+3\epsilon }, \end{aligned}$$

(7.28)

with $(\xi ,\nu )$-high probability, on $\Omega _V$.

Proof

For $z\in {\mathcal {D}}_{\epsilon }'$, we have

$$\begin{aligned} (G_{jj}(z))^{-1}={\lambda v_j-z-\widehat{m}_{fc}(z)+{\mathcal {O}}(N^{-1 /2+2\epsilon })}, \end{aligned}$$

(7.29)

with high probability on $\Omega _V$; see Lemma 5.1. Next, recall from Proposition 4.3, we have with high probability on $\Omega _V$ that

$$\begin{aligned} \mu _k + {\mathrm {Re }}\,\widehat{m}_{fc} (\mu _k + \mathrm {i}\eta _0) = \lambda v_k + {\mathcal {O}}(N^{-1/2 + 3\epsilon }). \end{aligned}$$

Also recall the high probability estimate ${\mathrm {Im }}\,m(z) \le \frac{N^{2\epsilon }}{\sqrt{N}}$, for $z\in {\mathcal {D}}_{\epsilon }'$, on $\Omega _V$; see Lemma 5.5. Thus, choosing $z=\mu _k+\mathrm {i}\eta _0$, with $k\in [\![1,n_0-1]\!]$ and $k\not =j$, in (7.29) we obtain

$$\begin{aligned} ({G_{jj}(\mu _k+\mathrm {i}\eta _0)})^{-1}&={\lambda v_j-\mu _k-\mathrm {i}\eta _0- \widehat{m}_{fc}(\mu _k+\mathrm {i}\eta _o)+{\mathcal {O}}(N^{-1/2+2\epsilon })}\\&={\lambda v_j-\lambda v_k+{\mathcal {O}}(N^{-1/2+3\epsilon })}, \end{aligned}$$

with high probability on $\Omega _V$. Since $|v_j-v_k|\ge C N^{-1/(\mathrm {b}+1)-\epsilon }$, $j\not =k$, on $\Omega _V$, we obtain

$$\begin{aligned} {\mathrm {Im }}\,G_{jj}(\mu _k+\mathrm {i}\eta _0)\le \frac{C}{(\lambda v_j-\lambda v_k)^2}N^{-1/2+3\epsilon }, \end{aligned}$$

(7.30)

with high probability on $\Omega _V$, for some constant $C$. $\square$

Proof of Theorem 2.10: Inequality (2.21)

From the spectral decomposition of the resolvent of $H$, we obtain

$$\begin{aligned} {\mathrm {Im }}\,G_{jj}(\mu _k+\mathrm {i}\eta _0)&=\sum _{\alpha =1}^N\frac{|u_\alpha (j)|^2 \eta _0}{(\mu _{\alpha }-\mu _k)^2+\eta _0^2}\ge \frac{1}{\eta _0}|u_k(j)|^2, \end{aligned}$$

thus, using the bound (7.28), we conclude that

$$\begin{aligned} |u_k(j)|^2&\le C\frac{\eta _0}{(\lambda v_k-\lambda v_j)^2} N^{-1/2+3\epsilon }\le C\frac{1}{(\lambda v_k-\lambda v_j)^2}N^{-1+2\epsilon }, \end{aligned}$$

with high probability on $\Omega _V$, for $k\in [\![1, n_0-1]\!]$, $j\in [\![1,N]\!]$, $(j\not =k)$. This completes the proof of Theorem 2.10. $\square$

Appendices

Appendix A

In this appendix, we estimate the probabilities for the events $1.$–$3.$ in the definition of $\Omega _V$; see Definition 3.5. Recall the definition of the constants $\epsilon$ in (3.20) and $\kappa _0$ in (3.23). In the following, we denote, unlike in the rest of the paper, by $(v_i)_{i=1}^N$ (unordered) sample points distributed according to the measure $\mu$, (with $\mathrm {b}>1$). We denote by $(v_{(i)})$ the order statistics of $(v_i)$ with the convention $v_{(1)}\ge v_{(2)}\ge \dots \ge v_{(N)}$.

Lemma 8.1

Let $(v_{(i)})$ be the order statistics of sample points $(v_i)$ under the probability distribution $\mu$ with $\mathrm {b}>1$. Let $n_0 > 10$ be a fixed positive integer independent of $N$. Then, for any $k \in [\![1, n_0-1 ]\!]$ and for any sufficiently small $\epsilon > 0$, we have

$$\begin{aligned} {\mathbb {P}}\left( N^{-\epsilon } \kappa _0 < |v_{(k)} - v_{(j)}| < (\log N) \kappa _0\,, \forall j \ne k \right) \ge 1 - C (\log N)^{1+2\mathrm {b}} N^{-\epsilon }. \end{aligned}$$

(8.1)

In addition, for $k=1$, we have

$$\begin{aligned} {\mathbb {P}}\left( N^{-\epsilon } \kappa _0 < |1 - v_{(1)}| < (\log N) \kappa _0\right) \ge 1 - C N^{-\epsilon (\mathrm {b}+1)}. \end{aligned}$$

(8.2)

Proof

Consider the following claims:

• (1) There exists a constant $C > 0$ such that

  $$\begin{aligned} {\mathbb {P}}\left( |1 - v_{(1)}| > N^{-\epsilon } \kappa _0\right) \ge 1 - C N^{-\epsilon (\mathrm {b}+1)}. \end{aligned}$$

• (2) There exists a constant $c > 0$ such that

  $$\begin{aligned} {\mathbb {P}}\left( |1 - v_{(n_0)}| > (\log N) \kappa _0\right) \le e^{-c (\log N)^{\mathrm {b}+1}}. \end{aligned}$$

• (3) There exists a constant $C > 0$ such that, for any $k \in [\![1, n_0-1 ]\!]$,

  $$\begin{aligned} {\mathbb {P}}\left( |v_{(k)} - v_{(k+1)}| \le N^{-\epsilon } \kappa _0 \right) \le C (\log N)^{1+2\mathrm {b}} N^{-\epsilon }. \end{aligned}$$

Assuming the claims $(1)$–$(3)$, it is easy to see that the desired lemma holds.

For a random variables $v$ with law $\mu$ as in (2.9), we have for any $x \ge 0$,

$$\begin{aligned} C^{-1} x^{\mathrm {b}+1} \le {\mathbb {P}}(1 - v \le x) \le C x^{\mathrm {b}+1}, \end{aligned}$$

(8.3)

for some constant $C > 1$. Thus, we obtain for the first order statistics of $(v_i)$ that

$$\begin{aligned} {\mathbb {P}}(|1 - v_{(1)}| >&N^{-\epsilon } \kappa _0) = {\left( 1 - {\mathbb {P}}(1 - v \le N^{-\epsilon } \kappa _0)\right) }^N\nonumber \\ \ge&{\left( 1 - C N^{-\epsilon (\mathrm {b}+1)} N^{-1}\right) }^N \ge 1 - C N^{-\epsilon (\mathrm {b}+1)}, \end{aligned}$$

(8.4)

proving claim $(1)$.

Similarly, we have

$$\begin{aligned} \begin{aligned}&{\mathbb {P}}\left( |1 - v_{(n_0)}| > (\log N) \kappa _0\right) \le \left( {\begin{array}{c}N\\ n_0\end{array}}\right) \left( 1 - {\mathbb {P}}\left( 1 - v \le (\log N) \kappa _0\right) \right) ^{N-n_0} \\&\quad \le N^{n_0} \left( 1 - C^{-1} (\log N)^{\mathrm {b}+1} N^{-1} \right) ^{N-n_0} \le C N^{n_0} e^{-c (\log N)^{\mathrm {b}+1}} \le e^{-c'(\log N)^{\mathrm {b}+1}}, \end{aligned} \end{aligned}$$

(8.5)

for some constant $c, c' > 0$, proving claim $(2)$.

To prove claim $(3)$, we assume that $N^{-\epsilon } \kappa _0 < |1 - v_{(1)}| \le |1 - v_{(n_0)}| \le (\log N) \kappa _0$, which holds with probability higher than $1 - C N^{-\epsilon (\mathrm {b}+1)}$. Let

$$\begin{aligned} I_j \mathrel {\mathop :}=\left[ 1 - (j+1) N^{-\epsilon } \kappa _0, 1 - (j-1) N^{-\epsilon } \kappa _0 \right] ,\quad (j\in [\![1, (\log N) N^{\epsilon }]\!]). \end{aligned}$$

Then, it can easily be seen that if $|v_{(k)} - v_{(k+1)}| > N^{-\epsilon } \kappa _0$, then $v_{(k)}, v_{(k+1)} \in I_j$ for some $j\in [\![1, (\log N) N^{\epsilon }]\!]$. Letting $p_j \mathrel {\mathop :}={\mathbb {P}}( v \in I_j )$, we have that

$$\begin{aligned}&{\mathbb {P}}(|\{i \in [\![1, N ]\!]: v_i \in I_j\}| = 0) = (1- p_j)^N,\\&{\mathbb {P}}(|\{ i \in [\![1, N ]\!]: v_i \in I_j\}| = 1) = N p_j (1- p_j)^{N-1}, \end{aligned}$$

hence,

$$\begin{aligned} {\mathbb {P}}(v_{(k)}, v_{(k+1)} \in I_j)&\le {\mathbb {P}}(|\{i \in [\![1, N ]\!]: v_i \in I_j\}| = 2)\nonumber \\&\le 1 - (1-p_j)^N - Np_j (1-p_j)^{N-1} \le N^2 p_j^2. \end{aligned}$$

(8.6)

Since

$$\begin{aligned} p_j \le C N^{-\epsilon } \kappa _0 \left( (\log N) \kappa _0\right) ^{\mathrm {b}} = C (\log N)^{\mathrm {b}} N^{-1 -\epsilon }, \end{aligned}$$

we have

$$\begin{aligned} {\mathbb {P}}(|v_{(k)} - v_{(k+1)}| \le N^{-\epsilon } \kappa _0) \le \sum _{j\in [\![1,(\log N) N^{\epsilon }]\!]}^{} N^2 p_j^2\le C (\log N)^{1+2\mathrm {b}} N^{-\epsilon }. \end{aligned}$$

(8.7)

This proves the third part of the claim and completes the proof of the lemma. $\square$

Next, we estimate the probability of condition $(2)$ in Definition 3.5 to hold.

Lemma 8.2

Assume the conditions in Lemma 8.1. Recall the definition of  ${\mathcal {D}}_{\epsilon }$ in (3.21). Then, for any fixed $\ell >0$, there exists a constant $C_{\ell }$ (independent of $N$) such that

$$\begin{aligned} {\mathbb {P}}\left( \bigcup _{z \in {\mathcal {D}}_{\epsilon }} \ \left\{ \left| \frac{1}{N} \sum _{i=1}^N \frac{1}{\lambda v_i - z - m_{fc}(z)} \!-\! \int \frac{\mathrm {d}\mu (v)}{\lambda v - z - m_{fc}(z)}\right| \!>\! \frac{N^{3\epsilon /2}}{\sqrt{N}}\right\} \right) \!\le \! C_{\ell } N^{-\ell }. \end{aligned}$$

(8.8)

Proof

Fix $z \in {\mathcal {D}}_{\epsilon }$. For $i\in [\![1,N]\!]$, let $X_i \equiv X_i(z)$ be the random variable

$$\begin{aligned} X_i \mathrel {\mathop :}=\frac{1}{\lambda v_i - z - m_{fc}(z)} - m_{fc}(z) = \frac{1}{\lambda v_i - z - m_{fc}(z)} - \int \frac{\mathrm {d}\mu (v)}{\lambda v - z - m_{fc}(z)}. \end{aligned}$$

By definition, ${\mathbb {E}}X_i = 0$. Moreover, we have

$$\begin{aligned} {\mathbb {E}}|X_i|^2 \le \int \frac{\mathrm {d}\mu (v)}{|\lambda v - z - m_{fc}(z)|^2} = \frac{{\mathrm {Im }}\,m_{fc}((z)}{\eta + {\mathrm {Im }}\,m_{fc}(z)} < 1,\quad (z\in {\mathbb {C}}^+), \end{aligned}$$

and, for any positive integer $p \ge 2$,

$$\begin{aligned} {\mathbb {E}}|X_i|^{p} \le \frac{1}{\eta ^{p-2}} {\mathbb {E}}|X_i|^2 \le N^{(1/2 +\epsilon ) (p-2)}\,,\quad (z\in {\mathcal {D}}_{\epsilon }). \end{aligned}$$

We now consider

$$\begin{aligned} {\mathbb {E}}\left| \frac{1}{N} \sum _{i=1}^N X_i \right| ^{2p} = \frac{1}{N^{2p}} \sum _{i_1, i_2, \ldots , i_{2p}=1}^N {\mathbb {E}}\prod _{j=1}^p X_{i_j} \prod _{k=p+1}^{2p} \overline{X}_{i_k}. \end{aligned}$$

(8.9)

For fixed $i_1, i_2, \ldots , i_{2p}$, define

$$\begin{aligned} d_i \mathrel {\mathop :}=\sum _{j=1}^{2p} \mathbb {1} (i_j = i), \end{aligned}$$

for $i\in [\![1,N]\!]$.

We first estimate the summand in the right side of (8.9) when $d_1 \ge d_2 \ge \dots \ge d_r \ge 1$ and $d_{r+1} = d_{r+2} = \dots = d_N = 0$, for some $r\in [\![1, 2p ]\!]$. Since $(X_i)$ are independent and centered, we have

$$\begin{aligned} {\mathbb {E}}\prod _{j=1}^p X_{i_j} \prod _{k=p+1}^{2p} \overline{X}_{i_k} = 0, \end{aligned}$$

if $d_i = 1$, for some $i$, which shows that we may assume $r \le p$ and $d_r \ge 2$. When $d_r \ge 2$, we obtain that

$$\begin{aligned} \left| {\mathbb {E}}\prod _{j=1}^p X_{i_j} \prod _{k=p+1}^{2p} \overline{X}_{i_k} \right| \le {\mathbb {E}}\prod _{k=1}^r |X_k|^{d_k} \le \prod _{k=1}^r N^{(1/2 + \epsilon )(d_k -2)} \le N^{(1/2 + \epsilon )(2p -2r)}. \end{aligned}$$

Next, using the estimate obtained above, we can bound

$$\begin{aligned} \begin{aligned}&\sum _{i_1, i_2, \ldots , i_{2p}} {\mathbb {E}}\prod _{j=1}^p X_{i_j} \prod _{k=p+1}^{2p} \overline{X}_{i_k} \\&\qquad \le \sum _{r=1}^p r! \left( {\begin{array}{c}N\\ r\end{array}}\right) N^{(1/2 + \epsilon ) (2p -2r)} \le p! \sum _{r=1}^p N^r N^{(1/2 +\epsilon ) (2p-2r)} \le (p+1)! N^p N^{2 \epsilon p}. \end{aligned} \end{aligned}$$

(8.10)

Hence, by Markov’s inequality, we obtain that

$$\begin{aligned} {\mathbb {P}}\left( \left| \frac{1}{N} \sum _{i=1}^N X_i\right| \ge \frac{N^{3\epsilon /2}}{2 \sqrt{N}} \right) \!\le \! \left( \frac{1}{2} N^{3\epsilon /2} \right) ^{-2p} N^p {\mathbb {E}}\left| \frac{1}{N} \sum _{i=1}^N X_i \right| ^{2p} \le 4^p (p+1)! N^{-\epsilon p}. \end{aligned}$$

(8.11)

To obtain the uniform bound on ${\mathcal {D}}_{\epsilon }$, we choose a lattice ${\mathcal {L}}$ in ${\mathcal {D}}_{\epsilon }$ such that for any $z \in {\mathcal {D}}_{\epsilon }$ there exists $z' \in {\mathcal {L}}$ satisfying $|z - z'| \le N^{-2}$. Since, for $z \in {\mathcal {D}}_{\epsilon }$ and $z' \in {\mathcal {L}}$,

$$\begin{aligned} \left| \frac{1}{\lambda v - z - m_{fc}(z)} - \frac{1}{\lambda v - z' - m_{fc}(z')} \right| \le C \frac{1}{\eta _0^2} |z-z'| \le C N^{-1 + 2\epsilon }, \end{aligned}$$

we find that

$$\begin{aligned}&{\mathbb {P}}\left( \bigcup _{z \in {\mathcal {D}}_{\epsilon }} \ \left\{ \left| \frac{1}{N} \sum _{i=1}^N \frac{1}{\lambda v_i - z - m_{fc}(z)} -m_{fc}(z)\right| > \frac{N^{3\epsilon /2}}{\sqrt{N}}\right\} \right) \nonumber \\&\quad \le |{\mathcal {L}}| 4^p (p+1)! N^{-\epsilon p}\nonumber \\&\quad \le C N^4 4^p (p+1)! N^{-\epsilon p}. \end{aligned}$$

Setting $p = (\ell + 4) / \epsilon$, we obtain the desired lemma. $\square$

To estimate the probability for the third condition in Definition 3.5, we need the following two auxiliary lemmas. Recall the definition of $R_2$ in (4.1).

Lemma 8.3

If $0 < C^{-1} \eta \le {\mathrm {Im }}\,m_{fc}(z) \le C\,\eta$, $z=E+\mathrm {i}\eta$, for some constant $C \ge 1$, then we have

$$\begin{aligned} \frac{1}{1+ C} \le R_2 (z) \le \frac{C}{1+ C}. \end{aligned}$$

(8.12)

Proof

Since

$$\begin{aligned} {\mathrm {Im }}\,m_{fc} (z) = \int \frac{{\mathrm {Im }}\,z + {\mathrm {Im }}\,m_{fc}(z)}{|\lambda v - z - m_{fc}(z)|^2} \mathrm {d}\mu (v), \end{aligned}$$

we have that

$$\begin{aligned} \frac{C^{-1}}{1+ C^{-1}} \le R_2 (z) = \frac{{\mathrm {Im }}\,m_{fc}(z)}{{\mathrm {Im }}\,z + {\mathrm {Im }}\,m_{fc}(z)} \le \frac{C}{1+ C}. \end{aligned}$$

$\square$

The imaginary part of $m_{fc}(z)$ can be estimated using the following lemma.

Lemma 8.4

Assume that $\mu _{fc}$ has support $[L_-, L_+]$ and there exists a constant $C>1$ such that

$$\begin{aligned} C^{-1} \kappa ^{\mathrm {b}} \le \mu _{fc} (z) \le C \kappa ^{\mathrm {b}}, \end{aligned}$$

(8.13)

for any $0 \le \kappa \le L_+$. Then,

$(1)$ :

for $z = L_+ - \kappa + i \eta$ with $0 \le \kappa \le L_+$ and $0 < \eta \le 3$, there exists a constant $C>1$ such that

$$\begin{aligned} C^{-1} (\kappa ^{\mathrm {b}} + \eta ) \le {\mathrm {Im }}\,m_{fc} (z) \le C (\kappa ^{\mathrm {b}} + \eta ); \end{aligned}$$

(8.14)

$(2)$ :

for $z = L_+ + \kappa + i \eta$ with $0 \le \kappa \le 1$ and $0 < \eta \le 3$, there exists a constant $C>1$ such that

$$\begin{aligned} C^{-1} \eta \le {\mathrm {Im }}\,m_{fc} (z) \le C \eta . \end{aligned}$$

(8.15)

Remark 8.5

Lemma 8.4 shows that there exists a constant $C_{\mathrm {b}} > 1$ such that

$$\begin{aligned} C_{\mathrm {b}}^{-1} \eta \le {\mathrm {Im }}\,m_{fc} (z) \le C_{\mathrm {b}} \eta , \end{aligned}$$

(8.16)

for all $z \in {\mathcal {D}}_{\epsilon }$ satisfying $L_+ - {\mathrm {Re }}\,z \le N^{\epsilon } \kappa _0$.

Assuming Lemma 8.4, we have the following estimate. Recall that ${\mathcal {D}}_{\epsilon }$ is defined in (3.21).

Lemma 8.6

Assume the conditions in Lemma 8.1. Then, there exist constants $\mathfrak {c} < 1$ and $C > 0$, independent of $N$, such that, for any $z = E + \mathrm {i}\eta \in {\mathcal {D}}_{\epsilon }$ satisfying

$$\begin{aligned} \min _{i \in [\![1, N ]\!]} |{\mathrm {Re }}\,(z + m_{fc}(z)) - \lambda v_{(i)}| = |{\mathrm {Re }}\,(z + m_{fc}(z)) - \lambda v_{(k)}|, \end{aligned}$$

(8.17)

for some $k \in [\![1, n_0 -1 ]\!]$, we have

$$\begin{aligned} {\mathbb {P}}\left( \frac{1}{N} \sum _{i:i \ne k}^N \frac{1}{|\lambda v_{(i)} - z - m_{fc}(z)|^2} < \mathfrak {c} \right) \ge 1 - C (\log N)^{1+2\mathrm {b}} N^{-\epsilon }. \end{aligned}$$

(8.18)

Proof

Without loss of generality, we only prove the case $k=1$; the general case can easily be shown by using the same argument. In the following, we assume that $N^{-\epsilon } \kappa _0 < |1 - v_{(1)}| < (\log N) \kappa _0$, and $|v_{(1)} - v_{(2)}| > N^{-\epsilon } \kappa _0$.

Recall the definition of $R_2$ in (4.1). For $i\in [\![1,N]\!]$, let $Y_i \equiv Y_i(z)$ be the random variable

$$\begin{aligned} Y_i(z) \mathrel {\mathop :}=\frac{1}{|\lambda v_i - z - m_{fc}(z)|^2}\,, \quad (z\in {\mathbb {C}}^+), \end{aligned}$$

and observe that ${\mathbb {E}}Y_i = R_2 < 1$, ($z\in {\mathbb {C}}^+$). Moreover, combining Lemmas 8.3 and 8.4, we find that there exists a constant $c < 1$, independent of $N$, such that $R_2 (z) < c$ uniformly for all $z \in {\mathcal {D}}_{\epsilon }$ satisfying (8.17). Since ${\mathrm {Im }}\,(z + m_{fc}(z)) \ge \eta$, we also have that $Y_i(z) \le \eta ^{-2}$.

We first consider the special choice $E = L_+$. Let $\widetilde{Y}_i$ be the truncated random variable defined by

$$\begin{aligned} \widetilde{Y}_i \mathrel {\mathop :}={\left\{ \begin{array}{ll} Y_i\,, &{} \text { if } Y_i < N^{2\epsilon } \kappa _0^{-2}, \\ N^{2\epsilon } \kappa _0^{-2}\,, &{} \text { if } Y_i \ge N^{2\epsilon } \kappa _0^{-2}. \end{array}\right. } \end{aligned}$$

Notice that, using the estimate (8.3), we have for $z = L_+ + \mathrm {i}\eta \in {\mathcal {D}}_{\epsilon }$ that

$$\begin{aligned} {\mathbb {P}}(Y_i \ne \widetilde{Y}_i) \le C N^{-1 - (\mathrm {b}+1)\epsilon }. \end{aligned}$$

Let

$$\begin{aligned} S_N \mathrel {\mathop :}=\sum _{i=1}^N Y_i\,, \qquad \widetilde{S}_N \mathrel {\mathop :}=\sum _{i=1}^N \widetilde{Y}_i. \end{aligned}$$

Then,

$$\begin{aligned} {\mathbb {P}}(S_N \ne \widetilde{S}_N) \le C N^{- (\mathrm {b}+1)\epsilon }. \end{aligned}$$

(8.19)

We now estimate the mean and variance of $\widetilde{Y}_i$. From the trivial estimate ${\mathbb {P}}(Y_i \ge x) \le {\mathbb {P}}(Y_i \ne \widetilde{Y}_i)$ for $x \ge N^{2\epsilon } \kappa _0^{-2}$, we find that

$$\begin{aligned} {\mathbb {E}}Y_i - {\mathbb {E}}\widetilde{Y}_i \le \int _{N^{2\epsilon } \kappa _0^{-2}}^{\eta ^{-2}} {\mathbb {P}}(Y_i \ne \widetilde{Y}_i) \mathrm {d}x \le C' N^{-(\mathrm {b}-1)\epsilon }, \end{aligned}$$

(8.20)

for some $C' > 0$. Hence, we get

$$\begin{aligned} {\mathbb {E}}\widetilde{Y}_i^2 \le N^{2\epsilon } \kappa _0^{-2} {\mathbb {E}}\widetilde{Y}_i \le N^{2\epsilon } \kappa _0^{-2} {\mathbb {E}}Y_i \le N^{2\epsilon } \kappa _0^{-2}. \end{aligned}$$

(8.21)

We thus obtain that

$$\begin{aligned}&{\mathbb {P}}\left( \left| \frac{S_N}{N} - {\mathbb {E}}Y_i \right| \ge C' N^{-(\mathrm {b}-1) \epsilon } + N^{-\epsilon } \right) \!\le \! {\mathbb {P}}\left( \left| \frac{\widetilde{S}_N}{N} - {\mathbb {E}}\widetilde{Y}_i \right| \ge N^{-\epsilon } \right) \!+\! {\mathbb {P}}(S_N \ne \widetilde{S}_N) \nonumber \\&\quad \le \frac{N^{2\epsilon } {\mathbb {E}}\widetilde{Y}_i^2}{N} + C N^{- (\mathrm {b}+1)\epsilon } \le C N^{-\frac{\mathrm {b}-1}{\mathrm {b}+1} + 4\epsilon } = C N^{-2{\varpi _{\mathrm{b}}}+ 4\epsilon }, \end{aligned}$$

(8.22)

hence, for a constant $c$ satisfying $R_2 + C' N^{-(\mathrm {b}-1)\epsilon } + N^{-\epsilon } < c < 1$,

$$\begin{aligned} {\mathbb {P}}\left( \frac{1}{N} \sum _{i=1}^N \frac{1}{|\lambda v_i - z - m_{fc}(z)|^2} < c \right)&\ge 1\! -\! {\mathbb {P}}\left( \left| \frac{S_N}{N} - {\mathbb {E}}Y_i \right| \! \ge \! C' N^{-(\mathrm {b}-1)\epsilon } + N^{-\epsilon }\right) \\&\ge 1 - C N^{-2{\varpi _{\mathrm{b}}}+ 4\epsilon }. \end{aligned}$$

This proves the desired lemma for $E = L_+$.

Before we extend the result to general $z \in {\mathcal {D}}_{\epsilon }$, we estimate the probabilities for some typical events we want to assume. Consider the set

$$\begin{aligned} \Sigma _{\epsilon } \mathrel {\mathop :}=\{v_i : |1 - v_i| \le N^{3\epsilon } \kappa _0\}, \end{aligned}$$

and the event

$$\begin{aligned} \Omega _{\epsilon } \mathrel {\mathop :}=\{|\Sigma _{\epsilon }| < N^{3\epsilon (\mathrm {b}+2)}\}. \end{aligned}$$

Since we have from the estimate (8.3) that

$$\begin{aligned} {\mathbb {P}}(|1 - v_i| \ge N^{3\epsilon } \kappa _0) \le C N^{-1 + 3(\mathrm {b}+1)\epsilon }, \end{aligned}$$

we find, using a Chernoff bound, that

$$\begin{aligned} {\mathbb {P}}(\Omega _{\epsilon }^c) \le \exp \left( -C \epsilon (\log N) N^{3\epsilon } N^{3(\mathrm {b}+1) \epsilon }\right) , \end{aligned}$$

for some constant $C$. Notice that we have, for $v_i \notin \Sigma _{\epsilon }$,

$$\begin{aligned} L_++{\mathrm {Re }}\,m_{fc}(L_++\mathrm {i}\eta )-\lambda v_i > N^{3\epsilon } \kappa _0 \gg \eta + {\mathrm {Im }}\,m_{fc}(L_+ + \mathrm {i}\eta ), \end{aligned}$$

(8.23)

where we used Lemma 4.1, i.e., $|L_+ + \mathrm {i}\eta + m_{fc}(L_+ +\mathrm {i}\eta ) - \lambda | = {\mathcal {O}}(\eta )$, and that $\lambda >1$. We now assume that $\Omega _{\epsilon }$ holds and that

$$\begin{aligned} \frac{1}{N} \sum _{ i=1}^N \frac{1}{|\lambda v_i - (L_+ + \mathrm {i}\eta ) - m_{fc}(L_+ + \mathrm {i}\eta ) |^2} < c < 1. \end{aligned}$$

Further, we recall that the condition (8.17) implies

$$\begin{aligned} {\mathrm {Re }}\,(z + m_{fc}(z)) \ge \lambda v_{(n_0)}, \end{aligned}$$

which yields, together with Lemmas 4.1 and 8.1, that $E \ge L_+ - N^{\epsilon } \kappa _0$ with probability higher than $1 - C (\log N)^{1+2\mathrm {b}} N^{-\epsilon }$. We therefore assume in the following that $E \ge L_+-N^{\epsilon }\kappa _0$.

Consider the following two choices for such energies $E$:

• (1) When $L_+ - N^{\epsilon } \kappa _0 \le E \le L_+ + N^{2\epsilon } \kappa _0$, we have that

  $$\begin{aligned} |\lambda v_i - z - m_{fc}(z)| = |\lambda v_i - (L_+ + \mathrm {i}\eta ) - m_{fc}(L_+ + \mathrm {i}\eta )| + {\mathcal {O}}(N^{2\epsilon } \kappa _0), \end{aligned}$$

  where we used Lemma 4.1. Hence, using (8.23), we obtain for $v_i \notin \Sigma _{\epsilon }$ that

  $$\begin{aligned} \frac{1}{|\lambda v_i - z - m_{fc}(z)|^2}&\le \frac{1}{|\lambda v_i - (L_+ + \mathrm {i}\eta ) - m_{fc}(L_+ + \mathrm {i}\eta )|^2}\nonumber \\&\quad + \frac{N^{2\epsilon } \kappa _0}{|\lambda v_i - (L_+ + \mathrm {i}\eta ) - m_{fc}(L_+ + \mathrm {i}\eta )|^3} \nonumber \\&\le \frac{1 + C N^{-\epsilon }}{|\lambda v_i - (L_+ + \mathrm {i}\eta ) - m_{fc}(L_+ + \mathrm {i}\eta )|^2}. \end{aligned}$$

  (8.24)

  We thus have that

  $$\begin{aligned}&\frac{1}{N} \sum _{i=2}^N \frac{1}{|\lambda v_{(i)} - z - m_{fc}(z)|^2} \nonumber \\&\quad \le \frac{N^{3\epsilon (\mathrm {b}+2)}}{N} \frac{1}{(N^{-\epsilon } \kappa _0)^2} + \frac{1}{N} \sum _{i: v_i \notin \Sigma _{\epsilon }} \frac{1 + C N^{-\epsilon }}{|\lambda v_i - (L_+ + \mathrm {i}\eta ) - m_{fc}(L_+ + \mathrm {i}\eta )|^2} \nonumber \\&\quad \le N^{-\epsilon } + \frac{1}{N} \sum _{i=1}^N \frac{1 + C N^{-\epsilon }}{|\lambda v_i - (L_+ + \mathrm {i}\eta ) - m_{fc}(L_+ + \mathrm {i}\eta )|^2} < c < 1, \end{aligned}$$

  (8.25)

  where we also used the assumption that $|v_{(2)}-v_{(1)}|\ge N^{-\epsilon } \kappa _0$.

• (2) When $E > L_+ + N^{2\epsilon } \kappa _0$, we have

  $$\begin{aligned} (E - L_+) + \left( {\mathrm {Re }}\,m_{fc}(E + \mathrm {i}\eta ) - {\mathrm {Re }}\,m_{fc}(L_+ + \mathrm {i}\eta ) \right) \gg \eta + {\mathrm {Im }}\,m_{fc}(E + \mathrm {i}\eta ), \end{aligned}$$

  where we again used Lemma 4.1, hence, from (8.23) we obtain that

  $$\begin{aligned} |\lambda v_i - z - m_{fc}(z)| \ge |\lambda v_i - (L_+ + \mathrm {i}\eta ) - m_{fc}(L_+ + \mathrm {i}\eta )|. \end{aligned}$$

  We may now proceed as in $(1)$ to find that

  $$\begin{aligned}&\frac{1}{N} \sum _{i=1}^N \frac{1}{|\lambda v_i - z - m_{fc}(z)|^2} \nonumber \\&\quad \le N^{-\epsilon } + \frac{1}{N} \sum _{i=1}^N \frac{1}{|\lambda v_i - (L_+ + \mathrm {i}\eta ) - m_{fc}(L_+ + \mathrm {i}\eta )|^2} < c < 1. \end{aligned}$$

  (8.26)

Since we proved in Lemma 8.1 that the assumptions $N^{-\epsilon } \kappa _0 < |1 - v_{(1)}| < (\log N) \kappa _0$ and $|v_{(1)} - v_{(2)}| > N^{-\epsilon } \kappa _0$ hold with probability higher than $1 - C (\log N)^{1+2\mathrm {b}} N^{-\epsilon }$, we find that the desired lemma holds for any $z\in {\mathcal {D}}_{\epsilon }'$. $\square$

To conclude this appendix, we prove Lemma 8.4.

Proof of Lemma 8.4

We start with the claim $(1)$: Notice that

$$\begin{aligned} {\mathrm {Im }}\,m_{fc}(z) = {\mathrm {Im }}\,\int \frac{\mathrm {d}\mu _{fc}(x)}{x-z} = \eta \int \frac{\mathrm {d}\mu _{fc}(x)}{(x-L_++\kappa )^2 + \eta ^2}. \end{aligned}$$

(8.27)

When $\eta \ge 1/2$, we may use the trivial bound

$$\begin{aligned} {\mathrm {Im }}\,m_{fc}(z) \sim \eta \int \frac{\mathrm {d}\mu _{fc}(x)}{\eta ^2} = \eta ^{-1} \sim 1 \sim (\kappa ^{\mathrm {b}} + \eta ). \end{aligned}$$

When $\kappa \ge 1/2$, we can easily see from (8.27) that ${\mathrm {Im }}\,m_{fc}(z) \sim 1 \sim (\kappa ^{\mathrm {b}} + \eta )$. Thus, in the following, we only consider the case $\kappa , \eta < 1/2$.

To prove the lower bound, we notice that

$$\begin{aligned} {\mathrm {Im }}\,m_{fc}(z)&\ge \eta \int _{L_+ - \kappa - 2\eta }^{L_+ - \kappa - \eta } \frac{\mathrm {d}\mu _{fc}(x) }{(x-L_++\kappa )^2 + \eta ^2}\\&\ge C \eta \int _{L_+ - \kappa - 2\eta }^{L_+ - \kappa - \eta } \frac{(\kappa +\eta )^{\mathrm {b}} \mathrm {d}x}{\eta ^2} \ge C (\kappa +\eta )^{\mathrm {b}} \ge C \kappa ^{\mathrm {b}}. \end{aligned}$$

We also have that

$$\begin{aligned} {\mathrm {Im }}\,m_{fc}(z) \ge \eta \int _{0}^{1} \frac{\mathrm {d}\mu _{fc}(x)}{(x-L_+ +\kappa )^2 + \eta ^2} \ge C \eta \int _{0}^{1} \mathrm {d}x \ge C \eta . \end{aligned}$$

Thus, we find that ${\mathrm {Im }}\,m_{fc}(z) \ge C(\kappa ^{\mathrm {b}} + \eta )$.

For the upper bound, we first consider the case $\kappa \ge \eta$, where we have

$$\begin{aligned} \begin{aligned} {\mathrm {Im }}\,m_{fc}(z)&\le C \eta \int _{L_-}^{L_+ - \kappa - \eta } \frac{(L_+ -x)^{\mathrm {b}} \mathrm {d}x}{(x-L_++\kappa )^2} + C \eta \int _{L_+ - \kappa - \eta }^{L_+ - \kappa + \eta } \frac{(\kappa +\eta )^{\mathrm {b}} \mathrm {d}x}{\eta ^2}\\&\quad + C \eta \int _{L_+-\kappa +\eta }^{L_+ } \frac{\kappa ^{\mathrm {b}} \mathrm {d}x}{(x-L_++\kappa )^2} \\&\le C \eta \int _{\eta }^{L_+ - L_- - \kappa } \frac{(y+\kappa )^{\mathrm {b}} \mathrm {d}y}{y^2} + C (\kappa +\eta )^{\mathrm {b}} + C \eta \int _{\eta }^{\kappa } \frac{\kappa ^{\mathrm {b}}}{y^2} \mathrm {d}y\\&\le C (\kappa +\eta )^{\mathrm {b}} + C \eta \\ {}&\le C(\kappa ^{\mathrm {b}} + \eta ). \end{aligned} \end{aligned}$$

Here, we used that $(y+\kappa )^{\mathrm {b}} \le C(y^{\mathrm {b}} + \kappa ^{\mathrm {b}})$. The calculation for the case $\kappa < \eta$ is similar, in fact, easier.

We now prove the claim $(2)$. As in the proof of the statement $(1)$, we only consider the case $\kappa , \eta < 1/2$. We have, for the lower bound, that

$$\begin{aligned} {\mathrm {Im }}\,m_{fc}(z) \ge \eta \int _{0}^{1} \frac{\mathrm {d}\mu _{fc}(x) }{(x-L_+ -\kappa )^2 + \eta ^2} \ge C \eta \int _{0}^{1} \mathrm {d}x \ge C \eta , \end{aligned}$$

and, for the upper bound,

$$\begin{aligned} {\mathrm {Im }}\,m_{fc}(z) \le C \eta \int _{L_-}^{L_+} \frac{(L_+ -x)^{\mathrm {b}} \mathrm {d}x}{(x-L_+-\kappa )^2} \le C \eta \int _{\kappa }^{L_+ -L_- +\kappa } \frac{y^{\mathrm {b}}}{y^2} \mathrm {d}y \le C \eta . \end{aligned}$$

This completes proof of the desired lemma. $\square$

Appendix B

In this appendix, we prove Lemmas 6.4 and 6.5.

Proof of Lemma 6.4

Set for $l,l'\in [\![0, p]\!]$ and for $A=[\![n_0,N]\!]$,

$$\begin{aligned} \Gamma _{l,l'}(z)\!\equiv \!\Gamma _{l,l'}\!\mathrel {\mathop :}=\max \{|F_{ab}^{({\mathbb {T}},{\mathbb {T}}')} (z)|\,:\, a,b\in A,\,a\!\not =\!b, {\mathbb {T}},{\mathbb {T}}'\!\subset \! A,\,|{\mathbb {T}}|\!\le \! l,\,|{\mathbb {T}}'|\le l'\}. \end{aligned}$$

(9.1)

For simplicity we drop the $z$-dependence from the notation and always work on $\Omega _V$. We first consider $\Gamma _{l,0}$, i.e., we set ${\mathbb {T}}' =\emptyset$. Recalling that ${\mathbb {1}}(\Xi )|F_{ab}(z)|\le (\varphi _N)^{c\xi }N^{-{\varpi _{\mathrm{b}}}}N^{\epsilon }$, we obtain $p\,\Gamma _{0,0}\le p(\varphi _N)^{c\xi }N^{-{\varpi _{\mathrm{b}}}+\epsilon }\ll 1$ on $\Xi$. From (6.5), we get, for $c\in A$,

$$\begin{aligned} F_{ab}^{({\mathbb {T}}c,\emptyset )}=F_{ab}^{({\mathbb {T}},\emptyset )}-F_{ac}^{({\mathbb {T}}, \emptyset )}F_{cb}^{({\mathbb {T}},\emptyset )}, \end{aligned}$$

(9.2)

and we obtain on $\Xi$,

$$\begin{aligned} \Gamma _{l+1,0}\le \Gamma _{l,0}+\Gamma _{l,0}^2. \end{aligned}$$

(9.3)

Iterating (9.3), we obtain

$$\begin{aligned} \Gamma _{l+1,0}\le \Gamma _{0,0}+\sum _{i=0}^l {\Gamma _{i,0}^2} \le \Gamma _{0,0}+(l \Gamma _{l,0})\Gamma _{l+1,0}. \end{aligned}$$

(9.4)

Thus as long as $l\Gamma _{0,0}\le 1/4$, we obtain by induction on $l$, $\Gamma _{l+1,0}\le 2\Gamma _{0,0}$, on $\Xi$, proving (6.21) for the special case ${\mathbb {T}}'=\emptyset$. To prove the claim for ${\mathbb {T}}'\not =\emptyset$, we fix $l=|{\mathbb {T}}|$ and observe that (6.5), together with the assumption $\Gamma _{l,l'}\ll 1$, implies

$$\begin{aligned} \Gamma _{l,l'+1}\le \Gamma _{l,l'}+C\Gamma _{l,l'}^2, \end{aligned}$$

(9.5)

for some numerical constant $C$. Iterating, we find

$$\begin{aligned} \Gamma _{l,l'+1}\le \Gamma _{l,0}+C\sum _{i'=0}^{l'}\Gamma _{l,i'}^2 {\le \Gamma _{l,l'} + C l \Gamma _{l, l'} \Gamma _{l, l'+1}.} \end{aligned}$$

(9.6)

Thus as long as $Cl'\Gamma _{l,l'}\le 1/4$, we obtain on $\Xi$ that $\Gamma _{l,l'+1} \le 2\Gamma _{l,0} \le 4\Gamma _{0,0}$, where we used that $\Gamma _{l,0}\le 2\Gamma _{0,0} (\le N^{-{\varpi _{\mathrm{b}}}})$. This proves (6.21).

To prove (6.22), we define, for $l\in [\![1,p]\!]$,

$$\begin{aligned} \widetilde{\Gamma }_l\mathrel {\mathop :}=\max \left\{ \left| \frac{F_{ab}^{(\emptyset , a)}}{G_{aa}^{({\mathbb {T}})}}\right| \,:\,a,b\in A,\,a\not =b,\,{\mathbb {T}}\subset A,\, a\not \in {\mathbb {T}},\,|{\mathbb {T}}|\le l\right\} . \end{aligned}$$

(9.7)

Note that $\widetilde{\Gamma }_0\le (\varphi _N)^{c\xi }N^{-1/2+ 2\epsilon }$, on $\Xi$. From (6.7), we have on $\Xi$

$$\begin{aligned} \widetilde{\Gamma }_{l+1}\le \widetilde{\Gamma }_l+ C\widetilde{\Gamma }_l \Gamma _{l,l}^2, \end{aligned}$$

(9.8)

for a numerical constant $C$. Iterating as above, we find

$$\begin{aligned} \widetilde{\Gamma }_{l+1}\le \widetilde{\Gamma }_0+C\sum _{i=0}^l \widetilde{\Gamma }_i\Gamma _{i,i}^2\le \widetilde{\Gamma }_0+ {8} C\Gamma _{0,0}^2\sum _{i=0}^l\widetilde{\Gamma }_i. \end{aligned}$$

(9.9)

Since ${8}Cl\Gamma _{0,0}^2\le 1/4$, on $\Xi$, we obtain $\widetilde{\Gamma }_{l+1}\le 2\widetilde{\Gamma }_0$, on $\Xi$. Upon using (6.21) to bound $|F_{ab}^{(\emptyset ,a)}-F_{ab}^{({\mathbb {T}}',{\mathbb {T}}'')}|$, this proves (6.22).

The proof of (6.23) is similar to the proof of (6.22) but easier. $\square$

Proof of Lemma 6.5

First, we observe that for a random variables ${\mathcal {X}}\equiv {\mathcal {X}}(H)$,

$$\begin{aligned} {\mathbb {E}}^W|Q_b {\mathcal {X}}|^p= {\mathbb {E}}^W|{\mathcal {X}}-{\mathbb {E}}_b {\mathcal {X}}|^p\le 2^{p-1}{\mathbb {E}}^W|{\mathcal {X}}|^p+2^{p-1}{\mathbb {E}}^W|{\mathbb {E}}_b {\mathcal {X}}|^p. \end{aligned}$$

(9.10)

From Jensen’s inequality for the partial expectation ${\mathbb {E}}_b$, we hence obtain

$$\begin{aligned} {\mathbb {E}}^W|Q_b{\mathcal {X}}|^p\le 2^p{\mathbb {E}}^W|{\mathcal {X}}|^p. \end{aligned}$$

(9.11)

Next, let $h_i\mathrel {\mathop :}=2\lceil \frac{2+p}{1+d_{i}} \rceil$, $i\in [\![1,p]\!]$. One checks that $\sum _{i=1}^ph_i^{-1}\le 1$, $2\le h_{i}\le 2p+4$ and $h_i(d_{i}+1)\le 2p+4$. Thus Hölder’s inequality gives

$$\begin{aligned} \left| {\mathbb {E}}^W\prod _{i=1}^q Q_{i}{\mathcal {X}}_{i}\prod _{i=q+1}^p Q_{i}{\mathcal {Y}}_{i}\right| \le 2^q\prod _{i=1}^q\left( {\mathbb {E}}^W |{\mathcal {X}}_{i}|^{h_{i}}|\right) ^{1/{h_{i}}}\prod _{i=q+1}^p \left( {\mathbb {E}}^W|Q_{i}{\mathcal {Y}}_{i}|^{h_{i}}\right) ^{1/{h_{i}}}, \end{aligned}$$

(9.12)

where we used (9.11). By assumption, we have

$$\begin{aligned} {\mathbb {E}}^W\left[ |{\mathcal {X}}_{i}|^{h_{i}}{\mathbb {1}}(\Xi ^c)\right] \!\le \!({\mathbb {E}}^W |{\mathcal {X}}_{i}|^{2h_{i}})^{1/2}\mathbb {P}(\Xi ^c)^{1/2}\le N^{2K h_i (d_{i}+1)}\mathbb {P}(\Xi ^c)^{1/2}&\!\ll \! \mathrm {e}^{-c(\log N)^{\xi }}. \end{aligned}$$

(9.13)

Observing that $\frac{1}{h_{i}}\ge \frac{1+d_{i}}{4p}$, we thus get

$$\begin{aligned} ({\mathbb {E}}^W |{\mathcal {X}}_{i}|^{h_{i}}{\mathbb {1}}(\Xi ^c))^{1/h_{i}}&\le \mathrm {e}^{-c\frac{1+d_{i}}{4p}(\log N)^{\xi }}\\&\le \left( \mathrm {e}^{-c (\log N)^{3/2}}\right) ^{1+d_{i}} \ll N^{-(1+d_{i})}, \end{aligned}$$

where we used that $p^{-1}\ge (\log N)^{-\xi +3/2}$. In a similar way, one establishes

$$\begin{aligned} ({\mathbb {E}}^W |{\mathcal {Y}}_{i}|^{h_{i}}{\mathbb {1}}(\Xi ^c))^{1/h_{i}} \ll N^{-1}. \end{aligned}$$

Together with the estimates (6.24), valid on the event $\Xi$, we obtain

$$\begin{aligned} \left| {\mathbb {E}}^W\prod _{i=1}^q Q_{i}{\mathcal {X}}_{i}\prod _{i=q+1}^p Q_{i}{\mathcal {Y}}_{i}\right| \le (\varphi _N)^{c_0\xi p} N^{-\sum _{i=1}^q (d_{i}-1)({\varpi _{\mathrm{b}}}/2-\epsilon )}N^{2p\epsilon }. \end{aligned}$$

(9.14)

Recalling that we have set $\sum _{i=1}^qd_{i}-1= s$, the claim follows. $\square$