Introduction

The two-parameter model for critical power (\(\dot{w}_{\text{cr}}\)) was developed from the study of the relationship between applied mechanical power and the corresponding time to exhaustion (t lim) (Monod and Scherrer 1965). This relationship was treated as a translated hyperbola, wherein the power asymptote corresponds to \(\dot{w}_{\text{cr}}\), the curvature represents the work that can be done above \(\dot{w}_{\text{cr}}\), from here on defined as W′TOT, and the time asymptote was set equal to 0 s. Application of the two-parameter model to the analysis of incremental tests, whether with linear (Morton 1994, 2011), or stepwise (Adami et al. 2013) power increment, led to the demonstration that W′TOT is independent of the mean ramp slope (S).

Any incremental exercise, however, can also be divided into m segments of duration equal to t lim m−1, interspersed with n recovery time intervals (t r), so that the exercise becomes intermittent and consists of n exercise-recovery cycles plus a final exercise bout. In fact, an incremental exercise prolonged to t lim, without recovery intervals in between represents a particular case of intermittent exercise in which t r = 0 s.

Morton and Billat (2004) applied the two-parameter model of \(\dot{w}_{\text{cr}}\) to the analysis of intermittent exercise at constant running speed above \(\dot{w}_{\text{cr}}\) (critical running speed). The equations presented in their Appendix suggest an increase in “anaerobic capacity” (actually a distance, in running) and an unchanged critical running speed during intermittent as compared with continuous exercise. Their results showed that this was not so; indeed, they found no significant increases in anaerobic capacity, but significantly lower critical running speed values in the former than in the latter case. Thus, they invited to take those results with caution in view of the limited number of investigated subjects and concluded that a much larger comparative study would be necessary to resolve the issue.

We hypothesized that the introduction of recovery intervals also during incremental stepwise tests, for instance, at the end of each constant-power step, should lead to a positive dependence of W′TOT on t r. This hypothesis relies on the kinetics of replenishment of anaerobic energy stores (E an) during recovery, thus to the payment of the oxygen deficit. For any given number of recovery intervals, E an, and thus W′TOT, ought to be larger the longer is t r and the greater is the oxygen deficit, at least when t r < 300 s (di Prampero 1981; Poole and Jones 2012; Ferretti 2015). As a consequence, since the peak power (\(\dot{w}_{\text{peak}}\)) attained at the end of an incremental exercise depends on W′TOT, higher \(\dot{w}_{\text{peak}}\) values ought to be found the longer is t r, for any given S.

The aim of this study was to test the hypothesis that W′TOT is higher the longer is t r to analyse the quantitative characteristics of the relation between S, t r, and W′TOT and to investigate the ensuing effects on \(\dot{w}_{\text{peak}}\) and \(\dot{w}_{\text{cr}}\). To this aim, we determined W′TOT, \(\dot{w}_{\text{peak}}\), and \(\dot{w}_{\text{cr}}\) during incremental stepwise exercise of different S, prolonged to subject’s exhaustion, in which recovery intervals of varying duration were introduced at the end of each step.

Methods

Subjects

Seven healthy, moderately active subjects (6 males, 1 female), all non-smokers, volunteered for this study. They were, as determined on the first experimental session, 25.7 ± 4.7 years, 70.4 ± 8.3 kg heavy, and 1.75 ± 0.09 m tall. They were asked to abstain from exercise and from alcohol on the 24 h before each experiment and to have a light meal without coffee intake at least 2 h before reporting to the laboratory. They were informed about the aims, the procedures, and risks associated with the tests and they signed an informed consent form. The study conformed to the Declaration of Helsinki and was approved by the local ethical committee.

Protocols

The subjects performed incremental stepwise exercises until volitional exhaustion with invariant power increments (\(\Delta \dot{w}\) = 25 W). Step duration (t s) was 30, 60, 90, 120, and 300 s; investigated t r were 0 (continuous incremental stepwise exercise, Adami et al. 2013), 60, and 180 s (discontinuous incremental stepwise exercise). Therefore, each subject performed a total of 15 experimental sessions (five step durations time three recovery intervals), which were administered in random order. Successive tests were separated by at least 48 h. Subjects were asked to pedal at a preferred frequency between 60 and 90 rpm, to maintain that frequency invariant throughout each test by visual feedback, and to use the same pedalling frequency in all tests. Normally, each subject performed at least one experimental session per week, so that she/he completed the entire protocol within four months. During this period, subjects were instructed to maintain the training workload invariant.

Measurements and calculations

Exercise was performed on an electromagnetic cycle ergometer (Ergometrics er800S, Ergoline, Jaeger, Germany). Respiratory gas flows and ventilation were continuously measured breath-by-breath, at the mouth, using a metabolic unit (Quark b2, Cosmed, Italy), consisting of a zirconium O2 analyser, an infrared CO2 meter, and a turbine flowmeter. The gas analysers were calibrated with ambient air and with a mixture of known gases (O2 16%, CO2 5%, and N2 as balance), and the turbine by means of a 3-l syringe. Beat-by-beat heart rate (HR) was continuously monitored by cardiotachography (Cosmed, Italy). Capillary blood lactate concentration ([La]b) was measured on 10 µl blood samples taken from an earlobe, by an electro-enzymatic method (Lactate Pro, Arkray, Kyoto, Japan). Capillary blood samples for peak [La]b determination were taken at rest and at min 1, 3, and 5 during recovery after the last and highest power, to assess the peak [La]b.

S was calculated as the ratio between the power increment (25 W, invariant in this study) and t s, independent of t r. Investigated S where then 0.83, 0.42, 0.28, 0.21, and 0.08 W s−1. The highest 10-s-average oxygen consumption (\(\dot{V}{\text{O}}_{2} )\) and HR value were calculated and retained as the peak \(\dot{V}{\text{O}}_{2}\) and HR. The highest workload sustained for at least 10 s was retained as \(\dot{w}_{\text{peak}}\). \(\dot{w}_{\text{cr}}\) and W′TOT were calculated as described by Adami et al. (2013), on the basis of Morton’s model for ramp exercise (Morton 1994).

Statistics

Values are reported as mean ± standard deviation (±SD). A two-way ANOVA was used to compare results from the various protocols. A post hoc pairwise comparison with the Bonferroni adjustment was then applied to locate significant differences. Linear regressions were calculated by means of least square methods, with the constraint that parameters must be greater than 0. \(\dot{w}_{\text{cr}}\) and W′TOT were obtained from the parameters of the regression equations. A one-way ANOVA for repeated measures was used to compare the parameters of linear regression equations, again using the Bonferroni adjustment for post hoc analysis. The level of significance was set at p < 0.05. The statistical package Prism 6 (Version 6.01, GraphPad Software Inc., La Jolla, CA, USA) was used.

Results

The mean values of all measured variables for each protocol are reported in Table 1. In all tests, except the discontinuous exercises with the shorter t s (30 s), peak \(\dot{V}{\text{O}}_{2}\) was independent of t s and t r, thus representative of the subjects’ maximum (\(\dot{V}{\text{O}}_{{2{\text{max}}}}\)) . Peak HR also depended on t s in the same way as peak \(\dot{V}{\text{O}}_{2}\). Peak [La]b values at any t r were independent of t s. \(\dot{w}_{\text{peak}}\) was significantly affected by both t r and t s: post hoc analysis showed that it systematically increased with increasing t r and decreasing t s.

Fig. 1
figure 1

Graphical representation of Eq. (5), whereby the peak powers (\(\dot{w}_{\text{peak}}\)) of the five continuous (circles) and discontinuous incremental protocols (squares and triangles) are plotted as a function of the square root of the ramp slope (\(\sqrt S\)). The regression line was calculated on the ensemble of the individual data. Discontinuous incremental exercises have a significantly lower y-axis intercept and a significantly higher angular coefficient. Data are presented as mean ± SD. Circles t r = 0 s; squares t r = 60 s; triangles t r = 180 s

Full size image
Table 1 Summary of the physiological data obtained in the 15 tests
Full size table

The \(\dot{w}_{\text{peak}}\) values observed in each subject for the three investigated t r (0, 60, and 180 s) were plotted as a function of \(\sqrt S\) in Fig. 1, as proposed by Adami et al. (2013). The parameters of the individual linear regression analysis for t r = 0 s, corresponding to \(\dot{w}_{\text{cr}}\) and W′TOT, are reported in Table 2A. The mean value of the individual coefficients of determination (R 2) was 0.953 ± 0.056. Conversely, for t r = 60 s and t r = 180 s, the \(\dot{w}_{\text{cr}}\) and W′TOT values computed by linear regression analysis, also given in Table 2A, turned out significantly lower and higher, respectively, than the corresponding values for t r = 0 s, despite the mean value of the individual R 2 was 0.976 ± 0.014 and 0.981 ± 0.007 for t r = 60 and 180 s, respectively.

Table 2 Summary of the parameters derived from linear (A, Eq. 5) and quadratic (B, Eq. 6) regression analysis of the \(\dot{w}_{\text{peak}}\) versus \(\sqrt S\) relationship and from the linear regression analysis of the \(\Delta \dot{w}_{\text{peak}}\) versus S relationship (C, Eq. 8)
Full size table

Discussion

For t r = 0 s, the \(\dot{w}_{\text{cr}}\) and W′TOT values, as obtained by the linear regression of the relationship between \(\dot{w}_{\text{peak}}\) and \(\sqrt S\) (Fig. 1), were in line with previous data (Morton 1994; Adami et al. 2013). When the linear relationships between \(\dot{w}_{\text{peak}}\) and \(\sqrt S\) were constructed for intermittent incremental tests (t r > 0 s), they provided higher W′TOT values the longer was t r, as hypothesized, but also \(\dot{w}_{\text{cr}}\) values by far lower than those for t r = 0 s, in apparent contradiction with the concept that \(\dot{w}_{\text{cr}}\) is independent of W′TOT (Morton 1994; Jones et al. 2010; Adami et al. 2013; Ferretti 2015). Moreover, it is noteworthy that the difference between maximal aerobic power and \(\dot{w}_{\text{cr}}\) is a constant (Adami et al. 2013). Thus, since \(\dot{V}{\text{O}}_{{2{\text{max}}}}\) is invariant in all conditions (see Table 1), if we express \(\dot{w}_{\text{cr}}\) in terms of metabolic rate (\(\dot{V}{\text{O}}_{{2{\text{cr}}}}\)), we should note an inconsistency between the measured \(\dot{V}{\text{O}}_{{2{\text{max}}}}\) and the apparent changes in \(\dot{V}{\text{O}}_{{2{\text{cr}}}}\) (see Table 2A). This means that the model applied in Fig. 1 for the analysis of intermittent stepwise tests is inadequate when t r > 0 s and thus is to be refined.

The introduction of recovery intervals implies restoration of at least part of the anaerobic energy that is used for the contraction of the oxygen deficit at each step. The parallelism between recovery of the energy store component (W′) and muscle phosphocreatine resynthesis was recently demonstrated experimentally during single-leg extension exercise (Skiba et al. 2015). The amount of energy that is restored in the anaerobic energy reservoir at the end of the ith recovery is equal to

$$E_{{{\text{an}}(i)}} = \mathop \int \limits_{0}^{{t_{\text{r}} }} \dot{V}{\text{O}}_{{2(t_{\text{s}} , i)}}{\text{ }}{\text{e}}^{{ - t{\text{ }}\tau^{ - 1} }} {\text{d}}t = \dot{V}{\text{O}}_{{2(t_{\text{s}} , i)}}{\text{ }}\tau{\text{ }}(1 - {\text{e}}^{{ - t_{\text{r}} \tau^{ - 1} }} )$$
(1)

where \(\dot{V}{\text{O}}_{{2(t_{\text{s}} , i)}}\) is the net \(\dot{V}{\text{O}}_{2}\) (i.e., \(\dot{V}{\text{O}}_{2}\) above resting), either theoretical or actual (di Prampero et al. 2015), attained at the end of the ith exercise step, and τ is the time constant of the negative exponential equation describing the \(\dot{V}{\text{O}}_{2}\) versus time (t) relationship during the ith-recovery. When t r = 0 s, E an(i) = 0 J; when t r > 0 s, E an(i) is higher the longer is t r, at least within the investigated t r range. The E an(i) data provided by Eq. (1) may, however, be slightly overestimated for supramaximal exercise steps, due to the impossibility of overcoming \(\dot{V}{\text{O}}_{{2{\text{max}}}}\).

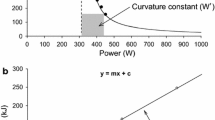
Since W′ concerns only the work done above \(\dot{w}_{\text{cr}}\), the contraction of the oxygen deficit and its payment during the recovery periods do not affect W′ below \(\dot{w}_{\text{cr}}\), but only above \(\dot{w}_{\text{cr}}\). In the latter case, the prediction of the oxygen deficit accumulated at the end of the ith exercise step becomes highly complex, since we need to account also for the progressive slowing of τ, the early lactate accumulation (Cerretelli et al. 1979), the differences in \(\tau\) between the on- and the off-exercise transient, and the reaching of \(\dot{V}{\text{O}}_{{2{\text{max}}}}\). In fact, W′ erosion represents not only the depletion of anaerobic energy stores (Jones et al. 2010), or the fraction of oxygen consumption occurring in uneven aerobic conditions (Ferretti 2015), but also the accumulation of intramuscular fatigue-related metabolites—e.g. H+, K+, Ca++ (Jones et al. 2010; Kent-Braun et al. 2012). These phenomena occur at a rate proportional to the difference between step power output and \(\dot{w}_{\text{cr}}\). They have strong impact on time to exhaustion and thus on the performable mechanical work above \(\dot{w}_{\text{cr}}\). In this situation, all oxygen deficit accumulated (and payed) below \(\dot{w}_{\text{cr}}\) is excluded from the computation of W′ (Fig. 2). Therefore, the concept of “W′ deficit” contraction and payment can be used as a surrogate. In fact, the portion of W′ that is utilized at the end of an ith exercise step (W′ out(i)) is

Fig. 2
figure 2

Balance between W′ erosion (W′ out(i)) and reconstitution (W′ in(i)) during the ith exercise step above critical power and the ensuing ith recovery, divided by the appropriate mechanical efficiency (η) to obtain its metabolic counterpart. \(\eta^{ - 1}{\text{ }}i{\text{ }}\Delta \dot{w}\), exercise step overall metabolic power; \(\dot{E}\), metabolic power; ω, non-W′ oxygen deficit; t, time; \(\dot{V}{\text{O}}_{{2{\text{cr}}}}\), critical metabolic power; \(\dot{V}{\text{O}}_{{2{\text{max}}}}\), maximal aerobic power

Full size image
$$W_{{{\text{out}}(i)}}^{'} = t_{\text{s}} (i{\text{ }}\Delta \dot{w} - \dot{w}_{\text{cr}} )$$
(2)

where \(i \Delta \dot{w}\) is the step power output (step ordinal number times power increment). W′ out(i) is slightly higher than the step’s oxygen deficit (see Fig. 2), except for very low step durations. The overestimation may derive from the additional time (and perhaps energy) for metabolite clearance during recovery (and perhaps already during exercise), although it does not contribute to E an depletion. In this setting, E an(i) can be seen as the payment of the total W′ deficit accumulated at the end of an ith step (\(W_{{{\text{def}}(t_{\text{s}} ,i)}}^{'}\)), which must decrease during recovery following a negative exponential kinetics, in line with Eq. (1) and with experimental data from the literature (Ferguson et al. 2010):

$$W_{{{\text{def}}(t_{\text{s}} ,i)}}^{'} - E_{{{\text{an}}(i)}} \cong W_{{{\text{def}}(t_{\text{s}} ,i)}}^{'} {\text{e}}^{{ - t_{\text{r}}{\text{ }}\tau^{ - 1} }} .$$
(3)

Equation (3) does not take into account the progressive slowing of τ with increasing power output and t s (Cerretelli et al. 1979), slightly overestimating the velocity of the payment at higher \(W_{{{\text{def}}(t_{\text{s}} ,i)}}^{'}\). However, we can assume τ as the mean value of all recoveries from \(\dot{w}_{\text{cr}}\) to \(\dot{w}_{\text{peak}}\).

When we expand Morton’s model to include recovery intervals, Eq. (1) cannot be neglected in the computation of W′ TOT. Therefore, in the expanded model, we have

$$W_{\text{TOT}}^{'} = W^{'} + \eta \mathop \sum \limits_{{i = i_{\text{cr}} }}^{n} E_{{{\text{an(}}i )}} = W^{'} + \eta \alpha$$
(4)

where W′ corresponds to the W′TOT that would occur in absence of energy store refilling, and α is the cumulative amount of energy restored at the end of the nth recovery period and η is the appropriate mechanical efficiency of exercise (an invariant during exercise on the cycle ergometer, see Gaesser and Brooks 1975; Girardis et al. 1999). For t r = 0 s, α = 0 J, and thus, W′TOT = W′, so that the critical power equation reported by Adami et al. (2013) for incremental exercise, that is

$$\dot{w}_{\text{peak}} = \dot{w}_{\text{cr}} + \sqrt {2 W_{\text{TOT}}^{'} S}$$
(5)

provides a complete description of the work performed above \(\dot{w}_{\text{cr}}\). However, when recovery intervals are introduced, i.e., when t r > 0 s, α is higher than 0 J and depends on η and n. Equation (4) shows that the total work performed above \(\dot{w}_{\text{cr}}\) is not an invariant, being independent only of \(\dot{w}_{\text{cr}}\), the only invariant term in this equation.

Starting from the definitions given in Eqs. (2) and (3), \(W^{'}_{{{\text{def}}(t_{\text{s}} ,i)}}\) can be calculated as a geometric progression (see “Appendix” for detailed analysis). When \(W_{{{\text{def}}(t_{\text{s}} ,i)}}^{'} = W^{'}\), the test will be interrupted because of exhaustion. The algebraic developments reported in the “Appendix” provide the formal demonstration that the y-axis intercepts shown in Fig. 1 for t r > 0 s are not representative of the subject’s \(\dot{w}_{\text{cr}}\). It is also demonstrated that the relationship between \(\dot{w}_{\text{peak}}\) and \(\sqrt S\) for intermittent exercise is the sum of a quadratic and an exponential function, the former being predominant in our investigated t r range. This being so, the relationship between \(\dot{w}_{\text{peak}}\) and \(\sqrt S\) for intermittent exercise can be simplified into the following quadratic equation:

$$\dot{w}_{\text{peak}} = \dot{w}_{\text{cr}} + \sqrt {2W^{'} S} + a S$$
(6)

where a is a lumped constant that includes t r, τ, W,′ and \(\Delta \dot{w}\). Thus, when t r = 0 s, \(\dot{w}_{\text{peak}} = \sqrt {2W^{'} S}\); instead, because of Eq. (4), when t r > 0 s, \(\dot{w}_{\text{peak}} > \sqrt {2W^{'} S}\). Furthermore, W′TOT becomes a function of S:

$$W_{\text{TOT}}^{'} = \frac{1}{2}(\dot{w}_{\text{peak}} - \dot{w}_{\text{cr}} )^{2} S^{ - 1} = W^{'} + \frac{1}{2}a^{2} S + a\sqrt {2W^{'} S} .$$
(7)

If Eq. (6) holds true, then we will expect that in discontinuous incremental exercise, the gain in \(\dot{w}_{\text{peak}}\) with respect to t r = 0 (\(\Delta \dot{w}_{\text{peak}}\)) will increase linearly with the first power of S, with a null y-axis intercept and an angular coefficient depending on t r:

$$\Delta \dot{w}_{\text{peak}} = \dot{w}_{\text{cr}} + \sqrt {2W^{'} S} + a S - \dot{w}_{\text{cr}} - \sqrt {2W^{'} S} = a S.$$
(8)

As reported in Fig. 3, this is the case indeed: from individual linear regression analysis, respectively, for t r = 60 s and t r = 180 s, we obtained an angular coefficient a of 199 ± 64 and 252 ± 39 s and the y-axis intercept −1 ± 18 and 1 ± 10 W, with an individual R 2 of 0.941 ± 0.071 and 0.965 ± 0.026. For t r = 0 s, \(\Delta \dot{w}_{\text{peak}}\) is obviously always equal to 0 W, and thus, a is null. There was a significant effect of t r on coefficient a (Table 2C), while y-axis intercepts were not significantly different from 0 W.

Fig. 3
figure 3

Gain in \(\dot{w}_{\text{peak}}\) with respect to the value obtained for t r = 0 s (\(\Delta \dot{w}_{\text{peak}}\)) is plotted against the ramp slope (S), instead of \(\sqrt S\). Regression lines and coefficients of determination (R 2) were calculated on the ensemble of the individual data. Lines have a y-axis intercept that does not differ from 0 W and an angular coefficient that is greater the greater t r. For t r = 0 s, \(\Delta \dot{w}_{\text{peak}}\) is obviously always equal to 0 W, and thus, the angular coefficient is nil. Data are presented as mean ± SD. Circles t r = 0 s; squares t r = 60 s; triangles t r = 180 s

Full size image

With these premises, the relationship between \(\dot{w}_{\text{peak}}\) and \(\sqrt S\) was re-analysed according to Eq. (6) (Fig. 4). With the individual quadratic regression analysis, for t r = 0 s, we obtained the same results, as shown in Fig. 1 (see Table 2B), with a = 0.0 s and an individual R 2 of 0.953 ± 0.056. For t r = 60 and 180 s, the obtained \(\dot{w}_{\text{cr}}\), W′, and a values are also reported in Table 2B; the individual R 2 were 0.991 ± 0.007 and 0.994 ± 0.007, respectively. An effect of t r was found on coefficient a (Table 2B), but not on \(\dot{w}_{\text{cr}}\) and W′. Equivalent values of coefficient a were obtained from quadratic Eq. (6) (Table 2B) and from simplified linear Eq. (8) (see Table 2C). Figure 4 supports essentially the tested hypothesis, as long as it shows that, for any given ramp, W′TOT is greater the longer t r. However, the non-linearity of the relationship between \(\dot{w}_{\text{peak}}\) and \(\sqrt S\) for t r > 0 s implies an increase in W′TOT also with the ramp slope: the steeper the ramp, the larger the number of exercise-recovery cycles.

Fig. 4
figure 4

Parabola of Eq. (6) was fitted through the ensemble of the individual data for all exercise conditions. Isopleths of the total work performed above critical power (W′ TOT) are added. For continuous ramps (circles), W′ TOT is invariant and equal to the energy store component (i.e., the constant W′). For discontinuous ramps (squares and triangles), the experimental points shift toward isopleths of higher W′ TOT. Data are presented as mean ± SD. Circles t r = 0 s; squares t r = 60 s; triangles t r = 180 s

Full size image

Current models of critical power imply a hyperbolic relationship between power and exhaustion time, the curvature of which corresponds to W′, which, therefore, is an invariant (Morton 1994; Adami et al. 2013). Equation (2) is a consequence of this statement that can be taken as the critical power axiom. Equations (4) and (7), however, admit variance of W′ TOT, which in principle implies distortion of the relationship between power and exhaustion time from the hyperbolic model, with values falling on different hyperbolas, depending on t r and n. We speculate, however, that, if all the factors affecting W′ are maintained invariant in a series of constant-power exercises at various powers higher than \(\dot{w}_{\text{cr}}\), we should still find hyperbolic power versus exhaustion time relations, yet with curvatures that are greater (higher W′ TOT), the higher are t r and n. Conversely, no changes in the two asymptotes are to be expected, as long as they are independent of the curvature.

In conclusion, Morton’s model for ramp exercise cannot be directly generalised to discontinuous incremental exercise; indeed, it represents a particular case, with a linear relationship between \(\dot{w}_{\text{peak}}\) and \(\sqrt S\), of a more general model accounting also for the recovery of E an due to the payment of the oxygen deficit during recovery. This appears to be a function of t r,\(\tau\), W′, \(\Delta \dot{w}\), t s, and, consequently, S (see “Appendix”). The basic principles of this more general model of critical power during incremental exercise are set in this study. Its rigorous quantitative characterisation, however, requires further more systematic investigations.