Introduction

The maximal oxygen consumption (\(\dot{V}{\text{O}}_{{ 2 {\text{max}}}}\)) is “an important determinant of the endurance performance, which represents a true parametric measure of cardiorespiratory capacity” (Levine 2008). A variety of incremental exercise test protocols, either continuous or discontinuous, have been proposed in the last decades to measure \(\dot{V}{\text{O}}_{{ 2 {\text{max}}}}\). The most classical protocol for \(\dot{V}{\text{O}}_{{ 2 {\text{max}}}}\) testing is the incremental intermittent Åstrand-type test (IIAT) (Åstrand et al. 2003). With IIAT \(\dot{V}{\text{O}}_{{ 2 {\text{max}}}}\) was identified as the plateau attained by the relationship between O2 consumption (\(\dot{V}{\text{O}}_{ 2}\)) and power, whence the concept of maximal aerobic mechanical power (\(\dot{w}_{\hbox{max} }\)) was defined as the power at which the plateau was attained (Åstrand et al. 2003; di Prampero 1981; Howley et al. 1995; Taylor et al. 1955). According to di Prampero (1981), \(\dot{w}_{\hbox{max} }\) represents the power that can be sustained by the active muscle mass with a rate of energy expenditure equivalent to \(\dot{V}{\text{O}}_{{ 2 {\text{max}}}}\). Subsequently, the introduction of commercial breath-by-breath metabolic carts (Myers and Bellin 2000) and the development of electro-magnetically braked cycle ergometers lead to the replacement of the IIAT by the incremental stepwise ramp tests (ISRT). ISRT provide the same \(\dot{V}{\text{O}}_{{ 2 {\text{max}}}}\) values as the IIAT (Duncan et al. 1997; Maksud and Coutts 1971; McArdle et al. 1973), but higher peak powers at the end of the tests (\(\dot{w}_{\text{peak}}\)) the greater is the mean slope of the ramp (Amann et al. 2004; Fairshter et al. 1983; Morton et al. 1997; Zhang et al. 1991).

On this basis, Whipp (1994) proposed a theoretical analysis of \(\dot{w}_{\text{peak}}\), whereby he assumed that, if one considers ISRT protocols with fixed power increments between two successive steps and variable step duration, there must be an inverse relationship between \(\dot{w}_{\text{peak}}\) and step duration, with asymptote equal to \(\dot{w}_{\hbox{max} }\). Starting from these concepts, Morton (2011) proposed a more detailed model that included critical power (CP) and anaerobic capacity as constants and the mean ramp slope (S) as variable. He validated his model by means of data taken from a previous study with continuous linear increases in S (Morton et al. 1997). Yet most of the ISRT do not foresee continuous linear power increments with time (i.e. power increases at each second) but stepwise power increments, in which power is increased by a given amount at a given fixed time, which may vary from 15 to 300 s. We do not know yet whether and how the data obtained with such a procedure fit into Morton’s model. Our hypothesis is that \(\dot{w}_{\text{peak}}\) depends only on S, and therefore that Morton’s model of ramp tests has a general validity, independent of the type of ISRT applied. If this is so, Morton’s model should account for differences in \(\dot{w}_{\text{peak}}\) obtained with both continuous ramps and ramps characterised by stepwise power increments. The aim of this study was to test this hypothesis by validating Morton’s model of \(\dot{w}_{\text{peak}}\) with a series of ISRT tests, in which the power increase was kept invariant and S was varied by changing only the step duration.

Methods

Subjects

Sixteen healthy, moderately active male subjects, all non-smokers, volunteered for this study. The subjects’ anthropometric characteristics, which were determined on the first experimental session, were as follows (mean ± SD): age 22 ± 1.7 years, body mass 73.5 ± 8.2 kg, height 1.78 ± 0.4 m. They were asked not to train and to abstain from alcohol on the 24 h before each experiment, and to have a light meal without coffee intake at least 2 h before reporting to the laboratory. They were informed about the aims, the procedures and risks associated with the tests and they signed an informed consent form. The study conformed to the Declaration of Helsinki and was approved by the local ethical committee.

Experimental design and methods

Six ISRT protocols and one IIAT protocol were administered in random order. All tests were performed on a cycle ergometer (Ergometrics er800S, Ergoline, Jaeger, Germany) to volitional exhaustion. Successive tests were separated by at least 72 h. The entire protocol was completed within 1 month, during which subjects were instructed to maintain constant the training workload and to refrain from competition. Subjects were asked to pedal at a frequency between 60 and 90 rpm. Each of them maintained his own pedalling frequency invariant by visual feedback and used the same pedalling frequency in all tests.

Respiratory gas flows and ventilation were continuously measured breath-by-breath, at the mouth, using a metabolic unit (Quark b 2, Cosmed, Italy), consisting of a Zirconium Oxygen analyser, an infrared CO2 meter and a turbine flowmeter. The gas analysers were calibrated with ambient air and with a mixture of known gases (O2 16 %, CO2 5 %, N2 as balance), and the turbine by means of a 3-l syringe. Beat-by-beat heart rate (HR) was continuously monitored by cardiotachography (Polar RS 800 CX, Polar, Finland). Blood lactate concentration ([La]b) was measured on 10 μl blood samples taken from an earlobe, by an electro-enzymatic method (Biosen C_line, EKF Diagnostic, Germany).

ISRT protocols

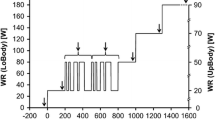
After 3 min at rest, the subjects pedalled at 50 W for 5 min as warm-up. Then the workload was progressively increased in a ladder-like way by 25 W step, occurring at the end of the selected step duration. As indeed, the six ISRT protocols differed among them only for the step duration, which was: 15, 30, 60, 90, 120 and 180 s. Subjects were encouraged verbally to carry the tests on until exhaustion. \(\dot{V}{\text{O}}_{ 2}\), expired ventilation and HR were averaged in the last 10 s of each workload for all ramps, including those with step duration of 120 and 180 s, after demonstration that the 10-s, 20-s and the 30-s average provided the same \(\dot{V}{\text{O}}_{ 2}\) values. The highest \(\dot{V}{\text{O}}_{ 2}\) value was retained as the individual \(\dot{V}{\text{O}}_{{ 2 {\text{max}}}}\), and the corresponding workload as the individual \(\dot{w}_{\text{peak}}\). Blood samples for [La]b determination were taken at rest and at 1, 3 and 5 min during recovery, in order to assess the peak [La]b at the end of the test (di Prampero 1981).

IIAT protocol

After 3 min at rest, the first workload was set at 50 W. Each successive load was 50 W higher than the immediately preceding one. This step increase in power was reduced to 25 W, as the expected maximal HR was approached. Each workload lasted 5 min. Successive workloads were separated by 6 min recovery intervals. The test was terminated at subject’s voluntary exhaustion.

\(\dot{V}{\text{O}}_{ 2}\), expired ventilation and HR were obtained as the mean value over the 5th min of each workload. Individual \(\dot{V}{\text{O}}_{{ 2 {\text{max}}}}\) was established from the plateau in the \(\dot{V}{\text{O}}_{ 2}\) versus power relationship. In case of absence of a plateau, the highest measured \(\dot{V}{\text{O}}_{ 2}\) was retained as \(\dot{V}{\text{O}}_{{ 2 {\text{max}}}}\) if at least two of the following conditions were met: (i) a lack of increase in HR between successive workloads; (ii) respiratory exchange ratio (RER) value ≥1.1; (iii) [La]b value higher than 10 mM at maximal exercise.

\(\dot{W}_{\hbox{max} }\) was determined as the power at the intersection between the \(\dot{V}{\text{O}}_{ 2}\) plateau and the line describing the relationship between \(\dot{V}{\text{O}}_{ 2}\) and power. In absence of a plateau, the power corresponding to the highest measured \(\dot{V}{\text{O}}_{ 2}\) was retained. The \(\dot{w}_{\hbox{max} }\) values provided by the IIAT were used to validate the predictions of Whipp’s model (see below).

Morton’s model

In Morton’s model (Morton 1994, 2011), the power (\(\dot{w}\)) in an ISRT is admitted to increase continuously with time (t) at a constant rate, so that there is a linear relationship between \(\dot{w}\) and t whose angular coefficient is the ramp slope (S):

$$\dot{w} = S \cdot t$$
(1)

The total mechanical work performed (W M) is equal to the triangular area under the \(\dot{w}\) versus t line (see Fig. 1), which is equal to:

Fig. 1
figure 1

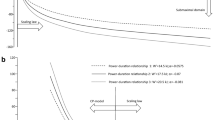
Geometric representation of Eq. 3. The linear relationship between power (\(\dot{w}\)) and time (t) is shown, which angular coefficient coincides with the ramp slope (S). The straight bold line represents the increment of power. CP indicates the critical power, and T the time to exhaustion. The area of triangle α is equal to \(\frac{1}{2}{\text{CP}}^{2} \cdot S^{ - 1}\) (first term of right branch of Eq. 3, while that of rectangle β is equal to \({\text{CP}} \cdot (T - {\text{CP}} \cdot S^{ - 1} )\)(second term of right branch of Eq. 3), and that of triangle γ is equal to \(\frac{1}{2}(\dot{w}{}_{\text{peak}} - {\text{CP}})(T - {\text{CP}} \cdot S^{ - 1} )\). Morton (2011) indentified γ area as the anaerobic work capacity (W’ in his notation, striped area in this figure). The sum of areas α + β + γ corresponds to the total mechanical work performed (\(\frac{1}{2} \cdot \dot{w}_{\text{peak}} \cdot T\))

Full size image
$$W_{\text{M}} = \int\limits_{0}^{T} {\dot{w}{\text{d}}t = \frac{1}{2}T \cdot \dot{w}_{\text{peak}} = \frac{1}{2}} S \cdot T^{2}$$
(2)

where T is the time to exhaustion. Eq. 2 has the following geometric solution:

$$\frac{1}{2}T \cdot \dot{w}_{\text{peak}} = \frac{1}{2}{\text{CP}}^{2} \cdot S^{ - 1} + {\text{CP}} \cdot (T - {\text{CP}} \cdot S^{ - 1} ) + \frac{1}{2}(\dot{w}{}_{\text{peak}} - {\text{CP}})(T - {\text{CP}} \cdot S^{ - 1} )$$
(3)

where CP is the critical power. Each of the three terms of the right branch of Eq. 3 represents a fraction of W M, indicated in Fig. 1 with Greek letters α, β and γ, respectively. The third of these terms (γ in Fig. 1) represents the amount of work carried out to sustain the power above CP, which Morton set equal to the anaerobic work capacity (\(W\prime\) in his notation), i.e. the amount of mechanical work carried out with anaerobic energy sources. In fact the metabolic energy supporting \(W\prime\) consists of a mixture of aerobic and anaerobic energy sources (see di Prampero 1981 for a discussion of this issue). A simplified version of Eq. 3 can be obtained by summing the terms corresponding to areas α and β (Fig. 1), and inserting \(W\prime\):

$$\frac{1}{2}T \cdot \dot{w}_{\text{peak}} = {\text{CP}} \cdot T - \frac{1}{2}{\text{CP}}^{2} \cdot S^{ - 1} + W\prime$$
(4)

whose trigonometric solution for T is given by (Morton 1994):

$$T = {\text{CP}} \cdot S^{ - 1} + \sqrt {\frac{2W\prime }{S}}$$
(5)

If we then multiply Eq. 5 by S, we get:

$$S \cdot T = \dot{w}_{\text{peak}} = {\text{CP}} + \sqrt {2W\prime S}$$
(6)

Eq. 6 tells that, if we plot \(\dot{w}_{\text{peak}}\) as a function of \(\sqrt S\) we obtain linear relationships with slope equal to \(\sqrt {2W\prime }\) and y-intercept equal to CP. This equation was tested by using the results of the six ISRT, with S corresponding to the mean ramp slope.

Whipp’s model

A simpler, concurrent model for the analysis of \(\dot{w}_{\text{peak}}\) was previously proposed by Whipp (1994) for ISRT protocols characterised by discrete ramps with the steps of different duration. This model predicted an inverse relationship between \(\dot{w}_{\text{peak}}\) and step duration, described by a translated equilateral hyperbola of this form:

$$T_{\text{S}} \cdot (\dot{w}_{\text{peak}} - b) = a$$
(7)

where T S is the step duration. According to Whipp (1994), constant b is equivalent to \(\dot{w}_{\hbox{max} }\) and constant a to the anaerobic work. Thus, Eq. 7 can be linearized as:

$$\dot{w}_{\text{peak}} = \frac{a}{{T_{\text{S}} }} + b$$
(8)

Statistics

Values are reported as mean and standard deviation (SD). A one-way ANOVA for repeated measurements was used to compare results from the various protocols. A Tukey post hoc test was then applied to locate significant differences. The level of significance was set at P < 0.05. Linear regressions were calculated by means of least square methods. The statistical package Prism 6 (Version 6.0b, GraphPad Software Inc., La Jolla, CA, USA) was used.

Results

The mean values of all measured variables for each maximal incremental test are reported in Table 1. No significant difference appeared for \(\dot{V}{\text{O}}_{{ 2 {\text{max}}}}\) and maximal expired ventilation (\(\dot{V}_{E_{\; \hbox{max} }}\)) among the protocols. In contrast, the ISRT \(\dot{w}_{\text{peak}}\) was lower the longer the step duration, with differences being significant among all step durations. Moreover, all \(\dot{w}_{\text{peak}}\) obtained in the various ISRT were significantly different from the \(\dot{w}_{\hbox{max} }\) reached at the end of IIAT. Consistently, maximal RER slightly decreased with increasing the ramp step duration. At the end of the test, no differences were observed for HR, except for the two shortest protocols (15 and 30 s ISRT), during which a significantly lower HR was reached compared with the two longest tests (180 s ISRT and IIAT). No differences were found for the peak [La]b values among the various ISRT. However, a few peak [La]b values were significantly different from the peak [La]b of IIAT, for a few low values in ISRT.

Table 1 Maximal O2 uptakes and powers, together with associated physiological variables obtained with the seven protocols
Full size table

Only the six ISRT \(\dot{w}_{\text{peak}}\) values were analysed with respect to Morton’s model in Fig. 2, where \(\dot{w}_{\text{peak}}\) was plotted as a function of \(\sqrt S\) (see Eq. 6). From individual linear regression analysis, mean CP turned out equal to 198.08 ± 37.46 W, i.e. 74.2 % of assessed \(\dot{w}_{\hbox{max} }\), and \(W\prime\) resulted equal to 16.82 ± 5.69 kJ. The mean value of the individual regression coefficients was 0.981 ± 0.016. The overall regression line on all individual data, reported in Fig. 2, is described by the following equation: \(\dot{w}_{\text{peak}}\) = 180.95 \(\sqrt S\) + 198.04; the correlation coefficient is equal to 0.819, reflecting inter-subject variability.

Fig. 2
figure 2

A graphical representation of Eq. 5, whereby peak power (\(\dot{w}_{\text{peak}}\)) is plotted as a function of the square root of the mean ramp slope (\(\sqrt S\)). Data are presented as mean ± SD. The regression line was calculated on the ensemble of the individual data

Full size image

On Fig. 3 we reported a theoretical solution of Eq. 8, obtained by setting a = \(W\prime\) (from Fig. 2) and b = \(\dot{w}_{\hbox{max} }\) (from Table 1, IIAT column). The present experimental data were also reported on the same figure. The equation provided by linear regression analysis on the latter data was y = 2612x + 263.5, r = 0.976, indicative of a \(\dot{w}_{\hbox{max} }\) of 264 W.

Fig. 3
figure 3

ISRT peak powers as a function of the reciprocal of the step duration. Empty dots: ISRT experimental data. Continuous line: regression line on experimental data. Dashed line: theoretical line assuming y-intercept equal to maximal aerobic power and slope equal to Morton’s constant \(W'\)

Full size image

Discussion

The \(\dot{V}{\text{O}}_{{ 2 {\text{max}}}}\) observed in the present study was the same in all performed tests, independent of the protocol used and, thus, independent of the step duration applied on an ISRT, in agreement with previous reports (Amann et al. 2004; Bentley et al. 2007; Bishop et al. 1998; Duncan et al. 1997; Hughson et al. 2000; Maksud and Coutts 1971; McArdle et al. 1973; McNaughton et al. 2005; Morton et al. 1997). As a consequence, both ISRT and IIAT can be conveniently used to determine \(\dot{V}{\text{O}}_{{ 2 {\text{max}}}}\). This result is coherent with the conclusions already arrived at by Howley et al. (1995) after having compared \(\dot{V}{\text{O}}_{{ 2 {\text{max}}}}\) values obtained with continuous or discontinuous exercise testing protocols, from different sources in the literature. In spite of this, the \(\dot{w}_{\text{peak}}\) values attained in ISRT were significantly different among them and from the \(\dot{w}_{\hbox{max} }\) attained in IIAT.

Morton et al. (1997) using continuous linear ramp increments of different slope, obtained similar results. Figure 2 shows excellent fitting of present results with Morton’s model. Since our data were obtained using stepwise power increments, with duration of constant-load steps ranging from 15 to 180 s, the present study extends the domain of utilisation of Morton’s model ideally to any type of ramp protocol. If this is so, only the mean ramp slope would determine the \(\dot{w}_{\text{peak}}\) that a given subject would attain at the end of an ISRT. In fact the area described by the power increments in our ISRT protocols is not a triangle, as is the case for true ramps (see Fig. 1), but is equivalent to that of the triangle described by the line connecting the midpoints of each step. This may explain the remarkable compliance of Morton’s model to our ISRT trials. We are nevertheless aware of the fact that the stepwise procedures utilised in this study are only approximation of a true ramp model defined by Morton et al. (1997). However, these data show that Morton’s model cannot be confined to the analysis of true (continuous) ramp protocols but its use can be expanded to include all protocols in which there is no interruption between successive steps. A further expansion would result from an inclusion also of Morton and Billat (2004) model of intermittent protocols, starting from the consideration that ISRT can be approximated to intermittent tests with recovery between successive steps equal to 0 s.

Recently, Morton (Morton 2011) expanded the original CP model (Monod and Scherrer 1965) to include an analysis of maximal ramp tests by means of a new model. Fig. 2 presents a linearized analytical form of that model, based on Eq. 5. The line’s slope, according to this equation, is equal to \(\sqrt {2W\prime }\). Morton (2011) stated that \(W\prime\) corresponds to the subjects’ anaerobic capacity, yet we think this is an oversimplification. An analysis of the energy balance at exercise intensity between CP and \(\dot{w}_{\text{peak}}\) shows that \(W\prime\) includes at least two terms: (i) the energy derived from anaerobic lactic energy sources, and (ii) the energy provided by the further increase in \(\dot{V}{\text{O}}_{ 2}\) at powers above CP. As a consequence, contrary to Morton’s prediction, \(W\prime\) is larger than anaerobic capacity.

On the other hand, the predictions resulting from application of Whipp’s model (Fig. 3), indicated that (i) the y-intercept of 264 W was indeed very close to the measured \(\dot{w}_{\hbox{max} }\) that we obtained during the IIAT (267 W, see Table 1), as predicted by Whipp (1994); whereas (ii) the regression slope a, which corresponded to 2.61 kJ, was about 1/7 of \(W\prime\). We suggest that the latter discrepancy may depend on the different meaning of a and \(W\prime\). Whereas a is the energy from anaerobic sources used to sustain powers above \(\dot{w}_{\hbox{max} }\), \(W\prime\) which includes a, is the energy (aerobic and anaerobic) sustaining all the work carried out above CP. We can therefore state that Eqs. 5 and 7 are equally good tools for the description of the \(\dot{w}_{\text{peak}}\) attained in ISRT.

The solutions of Eqs. 6 and 8 for \(\dot{w}_{\text{peak}}\) must be equivalent, so that they can be combined as follows:

$$\frac{a}{{T_{\text{S}} }} + \dot{w}_{\hbox{max} } = {\text{CP}} + \sqrt {2W 'S}$$
(9)

Rearrangement of Eq. 9 provides:

$$\sqrt {2W\prime S} = \frac{a}{{T_{\text{S}} }} + (\dot{w}_{ \hbox{max} } - {\text{CP}})$$
(10)

Equation 10 tells that \(\sqrt {2W'S}\) varies linearly with \(\frac{1}{{T_{\text{S}} }}\), with y-intercept equal to \(\left( {\dot{w}_{\hbox{max} } - {\text{CP}}} \right)\) and slope equal to a. This implies that (i) the difference between \(\dot{w}_{\hbox{max} }\) and CP is a constant that is independent of anaerobic capacity, step duration and ramp slope; (ii) \(\dot{w}_{\hbox{max} }\) and CP are bound to vary together, and by the same absolute amount; and (iii) their ratio becomes higher the higher is \(\dot{w}_{\hbox{max} }\), and therefore there is no fix CP/\(\dot{w}_{\hbox{max} }\) ratio. In practice, Eq. 10 explains why (i) CP is a higher fraction of \(\dot{w}_{\hbox{max} }\) in athletes with elevated \(\dot{V}{\text{O}}_{{ 2 {\text{max}}}}\) (Heubert et al. 2005) than in subjects with low \(\dot{V}{\text{O}}_{{ 2 {\text{max}}}}\), as the present ones; and (ii) the CP/\(\dot{w}_{\hbox{max} }\) ratio may vary with aerobic training (Heubert et al. 2003), and perhaps, we speculate, may differ according to muscle fibre composition. Since CP is strongly related to the so-called anaerobic threshold, a concept widely used in sport science, Eq. 10 also explains why intense aerobic training improves both \(\dot{w}_{\hbox{max} }\) and the anaerobic threshold, or the sustainable fraction of \(\dot{V}{\text{O}}_{{ 2 {\text{max}}}}\) (di Prampero 1986; Tam et al. 2012).

Conclusions

In conclusion, the quantitative analysis illustrated in this study demonstrated that Morton’s model well describes the evolution of \(\dot{w}_{\text{peak}}\) with any type of ramp, underlying once more that its magnitude is protocol-dependent. Moreover, a practical consideration emerges: performing a series of multiple (minimum three) ISRTs, varying in slope but not in power increment, allows the computation of the two other important physiological parameters highlighted in this study: \(\dot{w}_{\hbox{max} }\) and CP. The application of our analysis ensures an adequate methodology to correctly determine these parameters that are bound to vary together, by the same absolute amount, so that their ratio will result higher the higher is \(\dot{V}{\text{O}}_{{ 2 {\text{max}}}}\). The simultaneous knowledge of \(\dot{V}{\text{O}}_{{ 2 {\text{max}}}}\), \(\dot{w}_{\hbox{max} }\), and CP improves our ability of defining correct training programmes.