1 Introduction

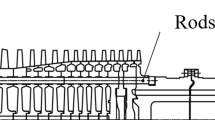
The rod fastening rotor (RFR) is the core component of gas turbines and some aero engines, of which the vibration characteristics have a great impact on the operating performance and safety of the whole machine. As shown in Fig. 1, all the disks (compressor end or turbine end) of a classic gas turbine are compacted together by a series of rods (bolts) with locknuts under sufficient preloads. In terms of application, RFRs have been widely employed in heavy-duty gas turbines and aero engines due to their good stiffness-to-weight properties, fast-startup characteristics and the ease of maintenance, as compared to conventional integral forged rotors. Under these high-speed and heavy-load conditions, oil-film bearings are usually used as supporting components, making the vibration response more complex and highly nonlinear.

Fig. 1
figure 1

Schematic diagram of a typical gas turbine rotor

Full size image

Undoubtedly, the structural discontinuity of RFR reduces the overall stiffness of the system, thus affecting the dynamic characteristics of the rotor. Furthermore, RFRs also exist internal damping effects, which further lead to the dynamic behaviors of RFRs different from that of the general rotors. For these high-speed RFRs, it is no longer suitable to conduct the rotor dynamics design according to the dynamic rule and experience from the integral forged rotor. Wrong dynamics design can easily lead to nonlinear vibration failures and even cause serious accidents, such as shaft fracture. Therefore, relatively accurate dynamic analyses and response predictions are of great importance before manufacturing.

The contact interface in the RFR causes the connection to be nonlinear. In view of the discontinuous nature of the RFR in structure, the contact characteristics between disks have been studied by many scholars. On the basis of Hertz contact theory, Gao et al. [1] calculated the bending stiffness under the coupling action of bending moment and preloading force. The results show that the natural frequency of the bending mode increases with the increase of the preload, and adequate pre-tightening force should be imposed to balance the external load. Zhang et al. [2] determined the normal contact stiffness between the disks by using FE method and modal experiment. Zhou et al. [3] compared the difference between the micro-asperity method and the finite element method in calculating the contact stiffness, of which two methods have little difference on the rotor dynamics of the RFR. With the contact stiffness simulated by a linear spring model, Liu et al. [4] studied the stability and bifurcation sequence of RFRs and observed period-doubling bifurcation phenomena and chaotic motion. Liu et al. [5] developed the bi-fractal model to conduct a modal analysis of the RFR considering the contact effect. Zhu et al. [6] also used a fractal contact model to establish the rough surface between the disks. It is well known that contact interfaces can influence the dynamic performance of RFR to some extent. Xia et al. [7] studied the influence of contact interface on torsional vibration characteristics of a heavy-duty gas turbine generator set, in which the torsional stiffness was defined as piecewise bilinear. In order to better consider the contact effect, Yuan et al. [8] improved the traditional two-dimensional finite element model with the contact interface simulated by an element with equivalent bending stiffness. Zhao et al. [9] established the dynamic model of a rod-fastened rotor considering manufacturing tolerances. The research shows that the vibration can be reduced by optimizing assembly angles.

As for high-speed rotating machines, various faults will gradually appear in the rotor during operation. In the case of non-standard detection, these faults can lead to catastrophic failure of RFRs. It is also very important to investigate the dynamic characteristics of a faulty rotor. Li et al. [10] studied the dynamics of RFR with bolt loosening fault. It has demonstrated that the rod loosening can yield a significant different behavior compared to the normal rotor. He et al. [11] conducted experimental study on the critical speeds of RFRs with the variation of tighten force. Chen et al. [12] revealed the bi-stable jump phenomena of RFR, and the contact interface was modeled by a nonlinear bending spring without mass. Li [13] and Liu [14] simplified the rod as a massless spring, while the contact stiffness between the disks was calculated by the method of microelement volume with the help of three-dimensional CAE software. Wang et al. [15] revealed the stability and bifurcation characteristics of the RFR with a transverse open crack fault. Hu et al. [16,17,18] studied the nonlinear dynamic response of the RFR with rub-impact and initial bow faults. Associated result shows the big radial stiffness of stator can simplify the motion status to some extent. Using the RFR similar to Hu [17], Hei et al. [19,20,21] modeled the dynamic model of the rotor supported by fixed-tilting pad bearings or hydrodynamic journal bearings. On the basis of this model, the nonlinear dynamic behavior and bifurcation phenomena were studied, and the results show that the motion of RFR is more stable compared with the integral rotor. Li et al. [22] studied the nonlinear dynamic behavior of the RFR under the support of ball bearings. Wang et al. [23] presented a numerical continuation method for periodic solutions of local nonlinear systems. By applying the methodology to a rod-fastened rolling bearing rotor system, it is shown that numerical continuation can be employed to calculate periodic solutions efficiently and robustly. In addition, Liu et al. [24] modeled a three-dimensional RFR-bearing system to investigate the nonlinear dynamic characteristics. To improve the vibration performance of RFR, Zhao et al. [25] optimized the combination of the initial bending and the unbalance. Based upon the transfer matrix method, Yang et al. [26] established a gas turbine blade-disk rotor system model, in which the connection characteristics were ignored.

The above research mainly focused on the contact characteristics of the rough surface between the disks, the variation of natural frequency under different pre-tightening forces and the nonlinear dynamic response under different faults. Apart from the interface contact stiffness that needs to be considered in the modeling, internal damping also affects the vibration response of RFR, which may exhibit different dynamic behaviors. At present, the works on the dynamic response of RFR with internal damping are not sufficient, and most of the modeling using the lumped mass method without considering the gyroscopic effect. The complex structure of the RFR and the nonlinearity of oil-film make the whirling motion of combined rotors complex and variable with dynamic parameters. Different from pure synchronous vibration (spin/whirl speed = 1), under the complex whirl modes, internal damping will inevitably affect the nonlinear dynamic response and stability of RFRs. There is no doubt that the internal damping should be taken into account in the modeling and analysis when the nonlinear dynamic behavior of the combined rotor is studied at high speed. In this paper, a mathematical model of RFR-bearing system with internal damping, considering the gyroscopic effect, contact characteristics, nonlinear oil-film force and residual unbalance force, is presented to investigate the nonlinear dynamic response and stability. The bifurcation diagram, Lyapunov stability, waterfall plot, shaft orbit, spectrum, time-domain waveform and Poincaré map are used to illustrate the difference between integral forged rotors and RFRs, the nonlinear dynamic characteristics and the internal damping effect on the RFR system. This work is helpful to provide new guidance for fault diagnosis and suppression of subsynchronous vibration of RFRs. In the meantime, the study contributes to provide an insight into the nonlinear dynamics for the RFR considering internal damping.

2 Mathematical model of RFR system with internal damping

The RFR is the core component of aero engines and heavy-duty gas turbines, in which the dynamic characteristics of the rotor directly affect the operating performance of the whole machine. The rotor is composed of multiple sets of tie rods (long bolts), nuts and disks, which are embedded on a single shaft with two bearings. As a typical combined rotor, it is different from the integral forged rotor that the wheel disks are compressed together through a series of tie rods and nuts, such that the rod is subjected to tension while the disk subjected to pressure.

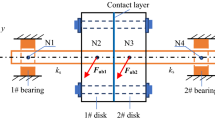
According to the distribution of the tie rod, rod-fastened rotor can be divided into two categories: One is the circumferential RFR and the other is the central RFR. In order to transmit force and torque, the disk to disk of the first type of rotor is connected by the annular plane, while the disk to disk of the second one is jointed by the curving coupling. Obviously, compared with the annular planar jointing structure, the curving coupling jointing structure requires higher manufacturing accuracy as well as cost. Thus, the application of the RFR with annular plane jointing structure is more extensive. Due to the existence of multi-rods and the discontinuity of interface contact, the dynamic characteristics of combined rotors are very complicated, and nonlinear phenomena such as bifurcation and response jump may show up under certain working conditions. Furthermore, in such RFR cases, the internal damping effect of the rotor is prominent and should also be taken into consideration when modeling. In order to guide the design more effectively and accurately predict the vibration response, it is urgent to know and reveal the nonlinear dynamic characteristics of the RFR considering the internal damping. As shown in Fig. 2, the circumferential RFR with a ring-shaped contact interface between two disks is studied to explore its rich dynamic characteristics and internal damping effects.

Fig. 2
figure 2

Schematic diagram of the RFR with journal bearings

Full size image

In order to effectively study the nonlinear dynamic characteristics and stability of the RFR system with internal damping, the torsional and axial vibrations of the RFR system are ignored. On this basis, the Timoshenko beam element equation is used to establish a dynamic model of four nodes connected by three flexible shaft segments.

2.1 Internal damping force

The nonlinearity of the connection and the bearing itself causes the whirling mode of the combined rotor to be complex and changeable over working conditions, such as rotational speed. The complex whirl motion is composed of synchronous motion and subsynchronous motion due to the excitation of nonlinear force. Different from pure synchronous vibration (spin/whirl speed = 1), internal damping will inevitably affect the nonlinear dynamic response and stability of RFR, such that the internal damping effect should be considered in modeling when studying the nonlinear dynamic behavior of combined rotors. The internal damping force in material is proportional to the velocity of the disk relative to the rotation axis (z) in the rotating reference frame and can be expressed as:

$$\left( \begin{gathered} F_{{xi^{\prime}}} \hfill \\ F_{{yi^{\prime}}} \hfill \\ \end{gathered} \right) = \left[ {\begin{array}{*{20}c} {c_{i} } & 0 \\ 0 & {c_{i} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\dot{x}^{\prime}} \\ {\dot{y}^{\prime}} \\ \end{array} } \right].$$
(1)

The coordinate transformation for the translational displacements between the fixed coordinate system (Fig. 3) and the rotating coordinate system is

$${\varvec{q}} = \user2{R\tilde{q},}$$
(2)

where

$${\varvec{q}} = \left[ \begin{gathered} x \hfill \\ y \hfill \\ \end{gathered} \right] \, \user2{R = }\left[ {\begin{array}{*{20}c} {\cos \omega t} & { - \sin \omega t} \\ {\sin \omega t} & {\cos \omega t} \\ \end{array} } \right] \, \tilde{\user2{q}} = \left[ \begin{gathered} {x^{\prime}} \hfill \\ {y^{\prime}} \hfill \\ \end{gathered} \right].$$
(3)
Fig. 3
figure 3

Fixed coordinate system (Oxyz) and rotating coordinate system (Ox′y′z)

Full size image

The first-time derivative of Eq. (2) is in the form:

$$\dot{\user2{q}} = \user2{R\dot{\tilde{q}} + \dot{R}\tilde{q}}\user2{.}$$
(4)

By using the coordinate transformation formula, the expression of internal damping forces in the fixed reference frame can be derived as

$$\left( \begin{gathered} F_{xi} \hfill \\ F_{yi} \hfill \\ \end{gathered} \right) = \left[ {\begin{array}{*{20}c} {c_{i} } & 0 \\ 0 & {c_{i} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\dot{x}} \\ {\dot{y}} \\ \end{array} } \right]{ + }\left[ {\begin{array}{*{20}c} 0 & {c_{i} \omega } \\ { - c_{i} \omega } & 0 \\ \end{array} } \right]\left( {\begin{array}{*{20}c} x \\ y \\ \end{array} } \right).$$
(5)

Considering a classical Laval–Jeffcott rotor-bearing system, the forces acting upon the disk include elastic restoring force, unbalance force, as well as both external and internal damping forces. The motion equations of the disk in the fixed reference frame are:

$$\left[ {\begin{array}{*{20}c} m & 0 \\ 0 & m \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\ddot{x}} \\ {\ddot{y}} \\ \end{array} } \right]{ + }\left[ {\begin{array}{*{20}c} {c_{e} + c_{i} } & 0 \\ 0 & {c_{e} + c_{i} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\dot{x}} \\ {\dot{y}} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} k & {c_{i} \Omega } \\ { - c_{i} \Omega } & k \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} x \\ y \\ \end{array} } \right] = me\Omega^{2} \left[ {\begin{array}{*{20}c} {\cos \Omega t} \\ {\sin \Omega t} \\ \end{array} } \right].$$
(6)

At the onset of instability, the shaft spinning speed is Ω0 and one eigenvalue has zero real part. At the instability threshold, the corresponding frequency (ω0) is referred to as unstable whirl frequency. In this case, the characteristic equation becomes:

$$- m\omega_{0}^{2} + j\left( {c_{e} + c_{i} } \right)\omega_{0} + \left( {k - j\Omega_{0} c_{i} } \right) = 0.$$
(7)

The forces acting on the disk, at the instability threshold, can be obtained by multiplying the displacement r with Eq. (7) and are shown in Fig. 4. It shows that the unstable motion caused by the internal damping force is a forward precession.

Fig. 4
figure 4

Force balance at instability threshold

Full size image

2.2 System governing equations of RFR-bearing system

In order to investigate the nonlinear dynamic behaviors of the rod fastening rotor considering internal damping, a real heavy-duty gas turbine rotor depicted in Fig. 1 is simplified into a classical RFR with single interface (Fig. 1a), which retains major structural characteristics of gas turbine rotors. The relevant model parameters of the RFR-bearing system are listed in Table 1. In order to conduct simulations, as shown in Fig. 2, the rotor is discretized by using the FE method based upon the Timoshenko beam theory, and corresponding mass and inertial moment are concentrated into the corresponding nodes. Disk 1 and Disk 2 are regarded as rigid bodies, while the properties are, respectively, lumped on Nodes 2 and 3. Finally, the RFR is simulated by a total of four nodes that include three beam elements. Each node of the beam element owns four degrees of freedom (DOFs), i.e., two translational DOFs and two rotational DOFs, as shown in Fig. 5.

Table 1 Parameters of the RFR-bearing system
Full size table
Fig. 5
figure 5

Timoshenko beam element model

Full size image

According to the Timoshenko beam element theory [27, 28], (4 × 4) element stiffness matrices due to shaft bending, in the xoz plane and the yoz plane, can be expressed as follows:

$${\varvec{K}}_{xoz}^{\text{e}} = \frac{EI}{{l^{3} }}\left[ {\begin{array}{*{20}c} {12} & {6l} & { - 12} & {6l} \\ {6l} & {4l^{2} } & { - 6l} & {2l^{2} } \\ { - 12} & { - 6l} & {12} & { - 6l} \\ {6l} & {2l^{2} } & { - 6l} & {4l^{2} } \\ \end{array} } \right],$$
(8)
$${\varvec{K}}_{yoz}^{\text{e}} = \frac{EI}{{l^{3} }}\left[ {\begin{array}{*{20}c} {12} & { - 6l} & { - 12} & { - 6l} \\ { - 6l} & {4l^{2} } & {6l} & {2l^{2} } \\ { - 12} & {6l} & {12} & {6l} \\ { - 6l} & {2l^{2} } & {6l} & {4l^{2} } \\ \end{array} } \right],$$
(9)

where E is the elastic modulus, I denotes the area moment of inertia and l represents the length of the beam element.

Motion equations of the beam elements are assembled together to form the global matrices of the RFR system. The schematic diagram of matrix assembly is shown in Fig. 6.

Fig. 6
figure 6

Assembly schematic diagram of rotor total matrices

Full size image

Then, the global motion equation of the RFR-bearing system with 16 DOFs can be derived as:

$${\varvec{M}}_{{\text{r}}} \user2{\ddot{q}} + ({\varvec{C}}_{{\text{r}}} + \omega {\varvec{G}}_{{\text{r}}} )\user2{\dot{q} + K}_{{\text{r}}} \user2{q = F}_{\text{u}} + {\varvec{F}}_{\text{b}} + {\varvec{F}}_{{{\text{c}}x}} - {\varvec{F}}_{g},$$
(10)

where q = [x1, θy1, …, x4, θy4, y1, θx1, …, y4, θx4]T is the generalized displacement vector of the RFR system to be solved. (xn, yn) and (θy, θx) are the translational and rotational displacements at the nth node (n = 1, 2, 3, 4), respectively. Mr, Gr and Kr are mass, gyroscopic and stiffness matrices of the RFR system with internal damping, which are, respectively, expressed as:

$${\varvec{M}}_{{\text{r}}} { = }\left[ {\begin{array}{*{20}c} {{\varvec{M}}_{x} } & {\mathbf{0}} \\ {\mathbf{0}} & {{\varvec{M}}_{y} } \\ \end{array} } \right],$$
(11)
$${\varvec{M}}_{x} = {\varvec{M}}_{y} = {diag([}m_{1} ,I_{{\text{d}1}} {,}m_{2} ,I_{{\text{d2}}} {,}m_{3} ,I_{{\text{d3}}} {,}m_{4} ,I_{{\text{d4}}} \text{]),}$$
(12)
$${\varvec{G}}_{{\text{r}}} { = }\left[ {\begin{array}{*{20}c} {\mathbf{0}} & { - {\varvec{G}}_{1} } \\ {{\varvec{G}}_{1} } & {\mathbf{0}} \\ \end{array} } \right],$$
(13)
$${\varvec{G}}_{{1}} = {\rm diag}([0,I_{{\text{p}1}} {,}0,I_{{\text{p2}}} {,}0,I_{{\text{p3}}} {,}0,I_{{\text{p4}}} \text{]),}$$
(14)
$${\varvec{K}}_{{\text{r}}} { = }\left[ {\begin{array}{*{20}c} {{\varvec{K}}_{x} } & {\mathbf{0}} \\ {\mathbf{0}} & {{\varvec{K}}_{y} } \\ \end{array} } \right] + {\varvec{K}}_{{\text{i}}} ,$$
(15)
$${\varvec{K}}_{x} = \left[ {\begin{array}{*{20}c} {\frac{{{12}EI_{\text{s}} }}{{L_{{1}}^{{3}} }}} & {\frac{{{6}EI_{\text{s}} }}{{L_{{1}}^{{2}} }}} & { - \frac{{{12}EI_{\text{s}} }}{{L_{{1}}^{{3}} }}} & {\frac{{{6}EI_{\text{s}} }}{{L_{{1}}^{{2}} }}} & {0} & {0} & {0} & {0} \\ {\frac{{{6}EI_{\text{s}} }}{{L_{{1}}^{{2}} }}} & {\frac{{{4}EI_{\text{s}} }}{{L_{1} }}} & { - \frac{{{6}EI_{\text{s}} }}{{L_{{1}}^{{2}} }}} & {\frac{{{2}EI_{\text{s}} }}{{L_{1} }}} & {0} & {0} & {0} & {0} \\ { - \frac{{{12}EI_{\text{s}} }}{{L_{{1}}^{{3}} }}} & { - \frac{{{6}EI_{\text{s}} }}{{L_{{1}}^{{2}} }}} & {\frac{{{12}EI_{\text{s}} }}{{L_{{1}}^{{3}} }} + \frac{{{12}E_{\text{c}} I_{\text{c}} }}{{L_{2}^{{3}} }}} & { - \frac{{{6}EI_{\text{s}} }}{{L_{{1}}^{{2}} }} + \frac{{{6}E_{\text{c}} I_{\text{c}} }}{{L_{{2}}^{{2}} }}} & { - \frac{{{12}E_{\text{c}} I_{\text{c}} }}{{L_{{2}}^{{3}} }}} & {\frac{{{6}E_{\text{c}} I_{\text{c}} }}{{L_{{2}}^{{2}} }}} & {0} & {0} \\ {\frac{{{6}EI_{\text{s}} }}{{L_{{1}}^{{2}} }}} & {\frac{{{2}EI_{\text{s}} }}{{L_{1} }}} & { - \frac{{{6}EI_{\text{s}} }}{{L_{{1}}^{{2}} }} + \frac{{{6}E_{\text{c}} I_{\text{c}} }}{{L_{{2}}^{{2}} }}} & {\frac{{{4}EI_{\text{s}} }}{{L_{1} }} + \frac{{{4}E_{\text{c}} I_{\text{c}} }}{{L_{2} }}} & { - \frac{{{6}E_{\text{c}} I_{\text{c}} }}{{L_{{2}}^{{2}} }}} & {\frac{{{2}E_{\text{c}} I_{\text{c}} }}{{L_{2} }}} & {0} & {0} \\ {0} & {0} & { - \frac{{{12}E_{\text{c}} I_{\text{c}} }}{{L_{{2}}^{{3}} }}} & { - \frac{{{6}E_{\text{c}} I_{\text{c}} }}{{L_{{2}}^{{2}} }}} & {\frac{{{12}E_{\text{c}} I_{\text{c}} }}{{L_{{2}}^{{3}} }} + \frac{{{12}EI_{\text{s}} }}{{L_{3}^{{3}} }}} & { - \frac{{{6}E_{\text{c}} I_{\text{c}} }}{{L_{{2}}^{{2}} }} + \frac{{{6}EI_{\text{s}} }}{{L_{{3}}^{{2}} }}} & { - \frac{{{12}EI_{\text{s}} }}{{L_{{3}}^{{3}} }}} & {\frac{{{6}EI_{\text{s}} }}{{L_{{3}}^{{2}} }}} \\ {0} & {0} & {\frac{{{6}E_{\text{c}} I_{\text{c}} }}{{L_{{2}}^{{2}} }}} & {\frac{{{2}E_{\text{c}} I_{\text{c}} }}{{L_{2} }}} & { - \frac{{{6}E_{\text{c}} I_{\text{c}} }}{{L_{{2}}^{{2}} }} + \frac{{{6}EI_{\text{s}} }}{{L_{{3}}^{{2}} }}} & {\frac{{{4}E_{\text{c}} I_{\text{c}} }}{{L_{2} }} + \frac{{{4}EI_{\text{s}} }}{{L_{3} }}} & { - \frac{{{6}EI_{\text{s}} }}{{L_{{3}}^{{2}} }}} & {\frac{{{2}EI_{\text{s}} }}{{L_{3} }}} \\ {0} & {0} & {0} & {0} & { - \frac{{{12}EI_{\text{s}} }}{{L_{{3}}^{{3}} }}} & { - \frac{{{6}EI_{\text{s}} }}{{L_{{3}}^{{2}} }}} & {\frac{{{12}EI_{\text{s}} }}{{L_{{3}}^{{3}} }}} & { - \frac{{{6}EI_{\text{s}} }}{{L_{3}^{{2}} }}} \\ {0} & {0} & {0} & {0} & {\frac{{{6}EI_{\text{s}} }}{{L_{{3}}^{{2}} }}} & {\frac{{{2}EI_{\text{s}} }}{{L_{3} }}} & { - \frac{{{6}EI_{\text{s}} }}{{L_{{3}}^{{2}} }}} & {\frac{{{4}EI_{\text{s}} }}{{L_{3} }}} \\ \end{array} } \right],$$
(16)
$${\varvec{K}}_{y} = \left[ {\begin{array}{*{20}c} {\frac{{{12}EI_{\text{s}} }}{L}} & { - \frac{{{6}EI_{\text{s}} }}{{L_{{1}}^{{2}} }}} & { - \frac{{{12}EI_{\text{s}} }}{{L_{{1}}^{{3}} }}} & { - \frac{{{6}EI_{\text{s}} }}{{L_{{1}}^{{2}} }}} & {0} & {0} & {0} & {0} \\ \\ { - \frac{{{6}EI_{\text{s}} }}{{L_{{1}}^{{2}} }}} & {\frac{{{4}EI_{\text{s}} }}{{L_{1} }}} & {\frac{{{6}EI_{\text{s}} }}{{L_{{1}}^{{2}} }}} & {\frac{{{2}EI_{\text{s}} }}{{L_{1} }}} & {0} & {0} & {0} & {0} \\ { - \frac{{{12}EI_{\text{s}} }}{{L_{{1}}^{{3}} }}} & {\frac{{{6}EI_{\text{s}} }}{{L_{{1}}^{{2}} }}} & {\frac{{{12}EI_{\text{s}} }}{{L_{{1}}^{{3}} }} + \frac{{{12}E_{\text{c}} I_{\text{c}} }}{{L_{2}^{{3}} }}} & {\frac{{{6}EI_{\text{s}} }}{{L_{{1}}^{{2}} }} - \frac{{{6}E_{\text{c}} I_{\text{c}} }}{{L_{{2}}^{{2}} }}} & { - \frac{{{12}E_{\text{c}} I_{\text{c}} }}{{L_{{2}}^{{3}} }}} & { - \frac{{{6}E_{\text{c}} I_{\text{c}} }}{{L_{{2}}^{{2}} }}} & {0} & {0} \\ { - \frac{{{6}EI_{\text{s}} }}{{L_{{1}}^{{2}} }}} & {\frac{{{2}EI_{\text{s}} }}{{L_{1} }}} & {\frac{{{6}EI_{\text{s}} }}{{L_{{1}}^{{2}} }} - \frac{{{6}E_{\text{c}} I_{\text{c}} }}{{L_{{2}}^{{2}} }}} & {\frac{{{4}EI_{\text{s}} }}{{L_{1} }} + \frac{{{4}E_{\text{c}} I_{\text{c}} }}{{L_{2} }}} & {\frac{{{6}E_{\text{c}} I_{\text{c}} }}{{L_{{2}}^{{2}} }}} & {\frac{{{2}E_{\text{c}} I_{\text{c}} }}{{L_{2} }}} & {0} & {0} \\ {0} & {0} & { - \frac{{{12}E_{\text{c}} I_{\text{c}} }}{{L_{{2}}^{{3}} }}} & {\frac{{{6}E_{\text{c}} I_{\text{c}} }}{{L_{{2}}^{{2}} }}} & {\frac{{{12}E_{\text{c}} I_{\text{c}} }}{{L_{{2}}^{{3}} }} + \frac{{{12}EI_{\text{s}} }}{{L_{3}^{{3}} }}} & {\frac{{{6}E_{\text{c}} I_{\text{c}} }}{{L_{{2}}^{{2}} }} - \frac{{{6}EI_{\text{s}} }}{{L_{{3}}^{{2}} }}} & { - \frac{{{12}EI_{\text{s}} }}{{L_{{3}}^{{3}} }}} & { - \frac{{{6}EI_{\text{s}} }}{{L_{{3}}^{{2}} }}} \\ {0} & {0} & { - \frac{{{6}E_{\text{c}} I_{\text{c}} }}{{L_{{2}}^{{2}} }}} & {\frac{{{2}E_{\text{c}} I_{\text{c}} }}{{L_{2} }}} & {\frac{{{6}E_{\text{c}} I_{\text{c}} }}{{L_{{2}}^{{2}} }} - \frac{{{6}EI_{\text{s}} }}{{L_{{3}}^{{2}} }}} & {\frac{{{4}E_{\text{c}} I_{\text{c}} }}{{L_{2} }} + \frac{{{4}EI_{\text{s}} }}{{L_{3} }}} & {\frac{{{6}EI_{\text{s}} }}{{L_{{3}}^{{2}} }}} & {\frac{{{2}EI_{\text{s}} }}{{L_{3} }}} \\ {0} & {0} & {0} & {0} & { - \frac{{{12}EI_{\text{s}} }}{{L_{{3}}^{{3}} }}} & {\frac{{{6}EI_{\text{s}} }}{{L_{{3}}^{{2}} }}} & {\frac{{{12}EI_{\text{s}} }}{{L_{{3}}^{{3}} }}} & {\frac{{{6}EI_{\text{s}} }}{{L_{3}^{{2}} }}} \\ {0} & {0} & {0} & {0} & { - \frac{{{6}EI_{\text{s}} }}{{L_{{3}}^{{2}} }}} & {\frac{{{2}EI_{\text{s}} }}{{L_{3} }}} & {\frac{{{6}EI_{\text{s}} }}{{L_{{3}}^{{2}} }}} & {\frac{{{4}EI_{\text{s}} }}{{L_{3} }}} \\ \end{array} } \right],$$
(17)
$${\varvec{K}}_{{\text{i}}} = {\text{d}}\text{iag(}\left[ {0,0,c_{{\text{i}}} \omega ,0,c_{{\text{i}}} \omega ,0,0,0} \right],8) + {diag(}\left[ {0,0, - c_{{\text{i}}} \omega ,0, - c_{{\text{i}}} \omega ,0,0,0} \right], - 8),$$
(18)

where mn, Idn and Ipn (n = 1, 2, 3, 4) are the mass, the polar moment of inertia and the diametral moment of inertia, respectively. Es and Ec are the elastic modulus of the shaft and the contact section, respectively. Is and Ic are the area moments of inertia of the shaft and the contact section, respectively. L1 = l1, L2 = l3, and L3 = l5.

The coupling damping equation of structural damping with rotor internal damping is

$${\varvec{C}}_{{\text{r}}} = {\varvec{C}}_{{\text{s}}} { + }{\varvec{C}}_{{\text{i}}} ,$$
(19)
$${\varvec{C}}_{{\text{i}}} = {diag(}\left[ {0,0,c_{{\text{i}}} ,0,c_{{\text{i}}} ,0,0,0,0,0,c_{{\text{i}}} ,0,c_{{\text{i}}} ,0,0,0} \right]).$$
(20)

In this paper, Rayleigh damping theory is adopted to obtain the global structure damping matrix (Cs) of the RFR system and it can be expressed as follows [29, 30]:

$${\varvec{C}}_{{\text{s}}} = \alpha {\varvec{M}}_{\text{r}} + \beta \left[ {\begin{array}{*{20}c} {{\varvec{K}}_{x} } & {\mathbf{0}} \\ {\mathbf{0}} & {{\varvec{K}}_{y} } \\ \end{array} } \right],$$
(21)
$$\left. \begin{gathered} \alpha = \frac{{4\pi \omega_{{\text{n}1}} \omega_{{\text{n2}}} (\xi_{1} \omega_{{\text{n2}}} - \xi_{2} \omega_{{\text{n1}}} )}}{{(\omega_{n2}^{2} - \omega_{n1}^{2} )}} \hfill \\ \beta = \frac{{\xi_{2} \omega_{{\text{n2}}} - \xi_{1} \omega_{{\text{n1}}} }}{{\pi (\omega_{n2}^{2} - \omega_{n1}^{2} )}} \hfill \\ \end{gathered} \right\},$$
(22)

where ωn1 and ωn2 are the first two natural frequency in Hz and ξ1 and ξ2 represent the first two modal damping ratios. Assuming that the same spring model with a stiffness of 2 × 108 N/m is applied to simulate the two bearings, the first and second natural frequencies of the RFR system are calculated to be 22.28 Hz and 69.80 Hz, respectively.

For the sake of analysis and solution, defining the dimensionless displacement parameters (p = q/c, X = x/c, Y = y/c), and the dimensionless time parameter (τ = ωt), then, \(\dot{x} = \omega \frac{dX}{{d\tau }}\) and \(\ddot{x} = \omega^{2} \frac{{d^{2} X}}{{d\tau^{2} }}\). Subsequently, let \(X^{\prime} = \frac{dX}{{d\tau }}\), \(Y^{\prime} = \frac{dY}{{d\tau }}\), and \(X^{\prime\prime}{ = }\frac{{d^{2} X}}{{d\tau^{2} }}\), \(Y^{\prime\prime}{ = }\frac{{d^{2} Y}}{{d\tau^{2} }}\). Substituting the above dimensionless transformations into Eq. (10), the dimensionless mathematical model can be deduced as:

$$\omega^{{2}} \user2{Mp^{\prime\prime}}\text{ + (}{\varvec{C}}_{\text{r}} \user2{ + }\omega {\varvec{G}}_{\text{r}} \text{)}\omega \user2{p^{\prime}}{ + }{\varvec{K}}_{\text{r}} \user2{p = }\frac{{{\varvec{F}}_{\text{u}} + {\varvec{F}}_{\text{b}} - {\varvec{F}}_{{\text{c}x}} - {\varvec{F}}_{g} }}{c},$$
(23)

where Fu, Fg and Fcx are, respectively, the unbalance force vector, the gravity vector and the nonlinear restoring force vector [31] caused by the rod and contact section, and the expressions are

$$\begin{gathered} {\varvec{F}}_{\text{u}} = [0,0,m_{2} e_{1} \omega^{2} \cos (\tau ),0,m_{3} e_{2} \omega^{2} \cos (\tau + \phi ),0,0,0, \hfill \\ \quad \quad \quad \, \, 0,0,m_{2} e_{1} \omega^{2} \sin (\tau ),0,m_{3} e_{2} \omega^{2} \sin (\tau + \phi ),0,0,0]^{\text{T}} , \hfill \\ \end{gathered}$$
(24)
$${\varvec{F}}_{g} = [0,0,0,0,0,0,0,0,m_{1} g,0,m_{2} g,0,m_{3} g,0,m_{4} g,0]^{\text{T}} ,$$
(25)
$${\varvec{F}}_{{{\text{c}}x}} = [0,0,F_{{{\text{c}}x{1}}} ,0,F_{{{\text{c}}x\text{2}}} ,0,0,0,0,0,F_{{{\text{c}}y{1}}} ,0,F_{{{\text{c}}y\text{2}}} ,0,0,0]^{\text{T}} ,$$
(26)
$$\left[ \begin{gathered} F_{cx1} \hfill \\ F_{cy1} \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} - F_{cx2} \hfill \\ - F_{cy2} \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} k_{1} c\left( {X_{2} - X_{3} } \right) + k_{1}^{^{\prime}} c\left( {X_{2} - X_{3} } \right)^{3} \hfill \\ k_{1} c\left( {Y_{2} - Y_{3} } \right) + k_{1}^{^{\prime}} c\left( {Y_{2} - Y_{3} } \right)^{3} \hfill \\ \end{gathered} \right],$$
(27)

where e1 and e2 are the unbalance eccentric distance of disk 1 and disk 2; ϕ is the relatively initial phase for these two disks; g represents the gravity constant; k1 is the linear stiffness; and k'1 is the nonlinear stiffness.

Fb is the nonlinear oil-film force vector based on the short bearing theory. According to the Capone model [32, 33], the nonlinear oil-film forces acting on Nodes 1 and 4 are determined as follows:

$$\begin{gathered} {\varvec{F}}_{{\text{b}}} = [F_{{{\text{b}}x}} (X_{1} ,Y_{1} ,\dot{X}_{1} ,\dot{Y}_{1} ),0,0,0,0,0,F_{{{\text{b}}x}} (X_{4} ,Y_{4} ,\dot{X}_{4} ,\dot{Y}_{4} ),0, \hfill \\ \quad \quad \quad \, \, F_{{{\text{b}}y}} (X_{1} ,Y_{1} ,\dot{X}_{1} ,\dot{Y}_{1} ),0,0,0,0,0,F_{{{\text{b}}y}} (X_{4} ,Y_{4} ,\dot{X}_{4} ,\dot{Y}_{4} ),0]^{\text{T}} , \hfill \\ \end{gathered}$$
(28)
$$\left( \begin{gathered} F_{{{\text{b}}x}} \hfill \\ F_{{{\text{b}}y}} \hfill \\ \end{gathered} \right) = - sW\frac{{\sqrt {(X - 2\dot{Y})^{2} + (Y + 2\dot{X})^{2} } }}{{1 - X^{2} - Y^{2} }} \times \left( \begin{gathered} 3X \times V(X,Y,\varphi ) - \sin \varphi \times G(X,Y,\varphi ) - 2\cos \varphi \times S(X,Y,\varphi ) \hfill \\ 3Y \times V(X,Y,\varphi ) + \cos \varphi \times G(X,Y,\varphi ) - 2\sin \varphi \times S(X,Y,\varphi ) \hfill \\ \end{gathered} \right),$$
(29)
$$V(X,Y,\varphi ) = \frac{2 + (Y\cos \varphi - X\sin \varphi ) \times G(X,Y,\varphi )}{{1 - X^{2} - Y^{2} }},$$
(30)
$$S(X,Y,\varphi ) = \frac{X\cos \varphi + Y\sin \varphi }{{1 - (X\cos \varphi + Y\sin \varphi )^{{2}} }},$$
(31)
$$G(X,Y,\varphi ) = \frac{2}{{\sqrt {1 - X^{2} - Y^{2} } }} \times \left( {\frac{\pi }{2} + \text{arctan}\frac{Y\cos \varphi - X\sin \varphi }{{\sqrt {1 - X^{2} - Y^{2} } }}} \right),$$
(32)
$$\varphi = \arctan \frac{{Y + 2\dot{X}}}{{X - 2\dot{Y}}} - \frac{\pi }{2}\text{sign}\frac{{Y + 2\dot{X}}}{{X - 2\dot{Y}}} - \frac{\pi }{2}\text{sign}(Y + 2\dot{X}),$$
(33)

where \(s = \frac{\eta \omega RL}{W}\left( \frac{R}{c} \right)^{2} \left( \frac{L}{2R} \right)^{2}\) is the Sommerfeld coefficient, η denotes the oil-film viscosity and W represents the bearing load.

3 Numerical results and discussion

In this section, a numerical study of nonlinear dynamic behaviors is done on the RFR-bearing system considering internal damping. The sliding bearings on both sides have the same structural parameters and lubrication conditions. The nonlinear differential equation of Eq. (23) is solved numerically by using the Newmark-beta method, which is a computationally efficient algorithm and satisfies the simulation purpose. The numerical integration step size is set to 2π/500. For each speed, the first 450 revolutions of the rotor response were calculated with all elements in the displacement vector, velocity vector and acceleration vector which are assumed to be 0.1 at the start of the numerical integration. The steady-state response of bearing 1 in the x direction was assumed to be achieved after neglecting the first 300 revolutions. Taking the rotational speed, contact characteristics and internal damping as control parameters in the performed simulations, the bifurcation diagram, Lyapunov index, 3D spectrum (waterfall plot), Poincaré map, rotor orbit, vibration time-domain waveform and response displacement are used to analyze the nonlinear dynamic characteristics and internal damping mechanism of the RFR system. It should be noted in the frequency spectrum that 1× represents the synchronous vibration (fundamental frequency) component corresponding to the precession speed equal to the spinning speed of rotor, 0.5× denotes the whirl speed approximately equal to half of rotor spinning speed, and so on.

As can be seen from the following, the obtained results systematically reveal the nonlinear dynamic behavior of the RFR system considering internal damping. In the performed simulations, some interesting and distinct phenomena in internal damping effects and bistable features, which have not been reported before, will be shown.

3.1 Validation

To validate the mathematical model and solution process developed in this paper, the responses are solved and compared with the results for a similar rotor in Ref. [34] in which the disk contact section is replaced by a thin shaft. In the calculation, the same parameters in the literature are used to perform simulation. The time-domain waveforms of the rotor system at 2800, 4400 and 6800 rpm are shown in Fig. 7. It is clearly shown that the results of the literature and the present have a good consistence and similarity, which validate the mathematical formulation and computation code proposed in this work.

Fig. 7
figure 7

Comparison of vibration responses of two rotors with similar structures: a results in Ref. [34], b results in this paper

Full size image

3.2 Nonlinear dynamics comparison between integral rotor and RFR

The RFR is discontinuous in nature in comparison with an integral forged rotor. In engineering or classical rotor dynamic studies, however, in order to facilitate analysis and save computation time, the modeling of RFRs is usually treated as the integral rotor, ignoring the interface contact stiffness. However, for more accurate rotor dynamics prediction, the contact characteristics should be considered in modeling.

Fig. 8
figure 8

Bifurcation diagrams of dimensionless displacement X1 for the rotor without considering internal damping

Full size image
Fig. 9
figure 9

Waterfall plots of dimensionless displacement X1 for the rotor without considering internal damping

Full size image

To know the difference between the integral forged rotor and RFR in dynamic behaviors, under no internal damping conditions, a comparison of bifurcation sequences of dimensionless displacement X1 between the integral rotor and RFR is shown in Fig. 8. Associated waterfall plots and vibration waveforms in time domain are depicted in Figs. 9 and 10, respectively. By comparing the results from two types of modeling methods in the speed range considered, i.e., the vibration characteristics of integral rotor and the RFR, it can be seen that the bifurcating trend is basically the same except few speed points. The reason for this phenomenon is that the analysis is based on the rod fastening rotor under the preloaded saturation state. At rotational speeds lower than 5800 rpm, both rotors exhibit stable period-1 motion (P-1), and only 1× frequency is observed in Fig. 9, which means that the rotor performs purely synchronous vibration around the static equilibrium position. The mass unbalance force dominates the system motion with single 1× frequency component at this speed region. Obviously, the system motion is stable and simple for this P-1 motion, which is an ideal motion state in engineering. Meaningfully, the instability threshold (6000 rpm) of integral rotor is slightly larger than that of the RFR (5800 rpm). Since then, the oil film becomes unstable and the system response enters into period-2 mode through a period-doubling bifurcation. With the increase in rotational speed, the vibration amplitude caused by half-frequency oil whirl increases rapidly and dominates the system motion. Although the response obtained by the two modeling methods is not much different under the preload saturation state, when the preload force drops or the preload force design is unreasonable, the combined rotor modeling method must be adopted. It is not suitable to simulate the RFR as an integral rotor in analyzing the nonlinear dynamic response of the system at the instability threshold.

Fig. 10
figure 10

Time-domain waveforms of X1 for the rotor without considering internal damping

Full size image

3.3 Internal damping effects on the RFR

The internal damping which makes the rotor motion more complicated is one of the factors of rotor instability. For complex rotor structures, such as RFRs, internal damping should be considered in the modeling to research vibration characteristics. Figure 11 shows the waterfall plots for the RFR with internal damping, and Figs. 12 and 13, respectively, depict the bifurcation diagram and waterfall plots of dimensionless displacement X1 for the RFR model with or without considering internal damping. Note that in Fig. 12 the points with pink color represent the case of system model without considering internal damping and the points with blue color depict the one considering internal damping. It clearly shows that internal damping is a key parameter that affects the nonlinear bifurcation characteristics of the RFR-bearing system. In the absence of internal damping, the half-frequency (0.5×) whirl instability appears at speeds range from 5800 to 8000 rpm (Figs. 9b and 13a). However, when internal damping is considered in the dynamic model, there is no pure half-frequency instability, which means that there is no double bifurcation phenomenon occurred in the RFR system model with internal damping. Besides, the onset speed of instability moves forward to 4400 rpm, which is reduced by 24.14% compared to the case without internal damping. Furthermore, when the system becomes unstable, the system performs quasi-period. Obviously, the motion of the system is much more complex than that of the model without considering the internal damping, at that special speeds range from 4400 to 8000 rpm. The above-mentioned differences of bifurcation sequences for the system with or without considering internal damping can also be verified in time-domain waveforms, shaft orbits, frequency spectrum and Poincaré maps, as shown in Figs. 14–17. In addition, the internal damping makes the frequency components more complex. These complex frequency components observed in the spectrum are 0.5 × , 1 × , fn1, fn2, fn3, fn1 + fn2 and 0.5fr-fn3, as shown in Figs. 11 and 13.

Fig. 11
figure 11

Waterfall plots of X1 for the RFR with internal damping

Full size image
Fig. 12
figure 12

Bifurcation diagram of dimensionless X1 for the RFR with or without internal damping

Full size image
Fig. 13
figure 13

2D frequency spectrum plots of dimensionless X1: a without internal damping and b with internal damping

Full size image
Fig. 14
figure 14

Time-domain response of RFR system with or without internal damping

Full size image
Fig. 15
figure 15

Orbits of RFR system with or without internal damping

Full size image
Fig. 16
figure 16

Poincaré maps of RFR system with or without internal damping

Full size image
Fig. 17
figure 17

Frequency spectrum of RFR system with or without internal damping

Full size image

In order to reveal the effect of internal damping on the nonlinear vibration response of rotor-bearing system, the root-mean-square (RMS) level and the single peak value (SPV) of amplitude are depicted in Fig. 18. When the rotational speed is below 4400 rpm, internal damping can suppress the vibration amplitude to some extent, but the efficiency is limited. The reason for this is that 1 × frequency vibration component dominates the system motion with simple P–1. Interestingly, when the speed is larger than 4400 rpm, there are big response differences between two cases with or without internal damping. The internal damping makes the system even more unstable at high speeds. That is, internal damping reduces the instability threshold. When the speed is higher, the response amplitude of two cases has little differences because the system response of these both cases is dominated by oil whip generated from nonlinear oil-film force. It can be clearly seen from Fig. 18 that the amplitude of oil whip is much larger than the amplitude of synchronous vibration. In summary, the internal damping also has a dual effect (low-speed attenuation and high-speed amplification) on the system response displacement. Therefore, the internal damping should be strictly considered for that complicated rotor structure, such as RFR under investigation.

Fig. 18
figure 18

Vibration response of RFR system with or without internal damping

Full size image

4 Conclusions

The dynamic model of the RFR system with internal damping and nonlinear oil-film forces is developed by using the FE method based upon the Timoshenko beam theory, considering the gyroscopic effects. On the basis of the established dynamic model, the rotational speed, contact characteristics and internal damping are taken as control parameters in the performed simulations. The nonlinear dynamic response and the internal damping effect on the RFR-bearing system are investigated in detail. The bifurcation diagram, Lyapunov index, 3D waterfall plot, Poincaré map, shaft orbit, time-domain waveform, spectrum and response amplitude are adopted to illustrate the rich-nonlinear dynamic characteristics of the RFR under investigation. The results show that the contact effects mainly affect the motion pattern of system at a certain high-speed region. It is not suitable to simulate the RFR as an integral rotor in analyzing the nonlinear dynamic response of the system at the instability threshold. Besides, some meaningful phenomena, such as complicated frequency spectrum characteristics and the special dual effect of internal damping, have been observed in the study. The double effect of internal damping on the RFR response is that the vibration amplitude is reduced to some extent at low speeds, but amplified significantly at high speeds. For those complicated rotors, the internal damping should be strictly considered. This work can provide a guidance for fault diagnosis and vibration reduction and contribute to further understanding of the nonlinear dynamic characteristics for the RFR.