Size effect on double-K fracture parameters of concrete based on fracture extreme theory

Abstract

Based on fracture extreme theory (FET), the size effect on initial fracture toughness $K_{\mathrm{I}}^{\mathrm{ini}}$ and unstable fracture toughness $K_{\mathrm{I}}^{\mathrm{un}}$ of concrete for three-point bending beam was investigated. Nine groups of geometrically similar specimen were simulated to obtain peak load and critical crack mouth opening displacement, of which specimen depth was from 200 to 1000 mm and initial crack length-to-depth ratios were from 0.1 to 0.6. The $K_{\mathrm{I}}^{\mathrm{ini}}$ and $K_{\mathrm{I}}^{\mathrm{un}}$ were calculated by FET and double-K method, in which FET adopted the linear, bilinear, and trilinear cohesive stress distribution assumptions and double-K method only used the linear cohesive stress distribution assumption. With linear cohesive stress distribution assumption, $K_{\mathrm{I}}^{\mathrm{ini}}$ and $K_{\mathrm{I}}^{\mathrm{un}}$ determined by FET and double- K method were compared. Then, the influence of specimen depth on $K_{\mathrm{I}}^{\mathrm{ini}}$ and $K_{\mathrm{I}}^{\mathrm{un}}$ was discussed. In addition, $K_{\mathrm{I}}^{\mathrm{ini}}/K_{\mathrm{I}}^{\mathrm{un}}$ calculated via FET using different cohesive stress distribution assumptions were analyzed.

1 Introduction

The fracture process zone (FPZ) exists at the crack tip in the crack propagation of concrete, which leads to the size effect of fracture parameters [1]. The linear elastic fracture mechanics (LEFM) is not applicable for quasi-brittle materials if the FPZ is not sufficiently small compared with the specimen size. Hence, various nonlinear fracture models considering the FPZ were proposed in determining fracture parameters of quasi-brittle materials [2,3,4,5,6,7,8]. The fictitious crack model (FCM) [2] regards the FPZ as a fictitious crack which can transfer cohesive stress. The tensile softening curve can describe the relationship between the cohesive stress and crack opening displacement, in which the cohesive stress decreases as the crack opening displacement increases.

The fracture process of concrete can be divided into three main stages, i.e., crack initiation, stable crack propagation, and unstable crack propagation, which has been verified by several studies [8, 9]. Xu and Reinhardt [8] proposed the double-K fracture model using initial fracture toughness $K_{\mathrm{I}}^{\mathrm{ini}}$ and unstable fracture toughness $K_{\mathrm{I}}^{\mathrm{un}}$ to characterize these three stages. A simplified method of determining $K_{\mathrm{I}}^{\mathrm{ini}}$ and $K_{\mathrm{I}}^{\mathrm{un}}$ of concrete for three-point bending beams was developed [9]. The determination of double-K fracture parameters requires experimental peak load $P_{\mathrm{max}}$ and critical crack mouth opening displacement $\hbox {CMOD}_{\mathrm{c}}$. To further simplify the calculation, Kumar and Barai [10, 11] utilized the weight function method to determine the stress intensity factor caused by cohesive stress $K_{\mathrm{I}}^{\mathrm{C}}$ and double-K fracture parameters of concrete. Furthermore, Qing et al. [12,13,14] proposed the fracture extreme theory (FET) to obtain $K_{\mathrm{I}}^{\mathrm{ini}}$ of concrete for wedge splitting and compact tension specimens [12], three-point bending beams [13], central notched cube, and cylinder split-tension specimens [14]. It should be noted that only the $P_{\mathrm{max}}$ of one specimen is required and measurement of $\hbox {CMOD}_{\mathrm{c}}$ is avoided in FET.

The size effect is a key problem that deserves to be extensively studied. Bažant pointed out that the main physical mechanism that causes the size effect is the crack front blunting of any type [3, 5]. Alexander and Blight [15] tested notched beams with depths varying from 100 mm to 800 mm and found that fracture toughness increases as the depth of the beams increases. Issa et al. [16] performed a lot of investigations on size effects in concrete fracture, which pointed out that the growth rate of fracture toughness increases with both specimen size and maximum aggregate size. Nallthambi et al. [17] proposed an expression for fracture toughness in terms of material properties, specimen size, notch depth, and maximum aggregate size. Perdikaris et al. [18] observed size effect on the fracture toughness in the static and fatigue tests and suggested that fracture toughness cannot be considered to be material parameters. The presence of FPZ ahead of the crack in concrete affects the fracture parameters based on assumed linear behavior. Kumar and Barai [19] followed the methodology of Planas and Elices [20] to compare the size effect predictions of double-K fracture model with that of FCM. It was found that FCM and double-K fracture model predict almost the same fracture behavior for laboratory size three-point bending beam. Choubey et al. [21] compared the $K_{\mathrm{I}}^{\mathrm{ini}}$ and $K_{\mathrm{I}}^{\mathrm{un}}$ determined by FET and weight function method for laboratory size specimens. Comparably, relatively limited studies on size effect analysis of $K_{\mathrm{I}}^{\mathrm{ini}}$ and $K_{\mathrm{I}}^{\mathrm{un}}$, and the corresponding relationship between $K_{\mathrm{I}}^{\mathrm{ini}}$ and $K_{\mathrm{I}}^{\mathrm{un}}$ for large size range are available.

In this study, nine groups of geometrically similar three-point bending concrete beam were used to investigate the size effect on initial fracture toughness $K_{\mathrm{I}}^{\mathrm{ini}}$ and unstable fracture toughness $K_{\mathrm{I}}^{\mathrm{un}}$. The specimen depths were from 200 to 1000 mm, and the crack length-to-depth ratios $a_{0}/D$ vary from 0.1 to 0.6 in each group. Then, the peak load $P_{\mathrm{max}}$ and critical crack mouth opening displacement $\hbox {CMOD}_{\mathrm{c}}$ were obtained by simulation. The corresponding $K_{\mathrm{I}}^{\mathrm{ini}}$ and $K_{\mathrm{I}}^{\mathrm{un}}$ of concrete were calculated by FET and double-K method. Linear, bilinear, and trilinear cohesive stress distribution assumptions were adopted in FET, while double-K method only used linear cohesive stress distribution assumption. The comparison of $K_{\mathrm{I}}^{\mathrm{ini}}$ and $K_{\mathrm{I}}^{\mathrm{un}}$ determined by FET and double-K method with linear cohesive stress distribution assumption was carried out. Finally, the $K_{\mathrm{I}}^{\mathrm{ini}}/K_{\mathrm{I}}^{\mathrm{un}}$ obtained by FET with three cohesive stress distribution assumptions were analyzed.

2 Fracture extreme theory of concrete

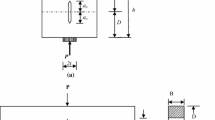
Figure 1 shows a typical $P - a/D$ curve of concrete [13], where $a_{0}$, a, D, and P represent the initial crack length, the effective crack length, the specimen depth, and the external load, respectively. The crack starts to propagate when P reaches the initial fracture load $P_{\mathrm{ini}}$, and then, P increases nonlinearly with a. When P reaches the peak load $P_{\mathrm{max}}$, a reaches its critical value $a_{\mathrm{c}}$. Subsequently, P decreases with the increase of a. According to the assumption of FET, the partial derivative of P to a at $P = P_{\mathrm{max}}$ is continuous, and the extreme point of the $P-a/D$ curve can be described by Eq. (1) [13]

$$\begin{aligned} \frac{\partial P}{\partial a}\bigg |_{a=a_{\mathrm{c}}}=0 \end{aligned}$$

(1)

Fig. 1

A typical $P-a/D$ curve of concrete [13]

3 The cohesive stress distribution assumption

The real cohesive stress distribution and the linear, bilinear, and trilinear cohesive stress distribution assumptions in FPZ are shown in Fig. 2, respectively. In Fig. 2, the kink point $a_{\mathrm{s}}$ is defined as the middle point of $a_{0}$ and a in the bilinear cohesive stress distribution assumption, i.e., $a_{\mathrm{s}} =(a_{0} +a)/2$. The kink points $a_{\mathrm{s}1}$ and $a_{\mathrm{s}2}$ are defined as the three equal points of $a_{0}$ and a in the trilinear cohesive stress distribution assumption, i.e., $a_{\mathrm{s}1} =2a_{0}/3 + a/3$, $a_{\mathrm{s}2} = a_{0}/3+ 2a/3$.

The nonlinear tensile softening curve [22] is adopted to describe the relationship between the cohesive stress and crack opening displacement, in which the cohesive stress at crack tip $\sigma _{\mathrm{s}}$(CTOD) as well as the cohesive stress at the kink points $\sigma _{\mathrm{s}}(\omega _{\mathrm{s}})$, $\sigma _{\mathrm{s}}(\omega _{\mathrm{s}1})$, and $\sigma _{\mathrm{s}}(\omega _{\mathrm{s}2})$ all can be expressed by Eq. (2). The crack opening displacement $\omega$ of the effective crack can be expressed by Eq. (3) [4]. Comparably, except for the cohesive stress and crack opening displacement at the points $a_{0}$ and $a_{\mathrm{c}}$ satisfy the tensile softening curve in those three cohesive stress distribution assumptions, and the cohesive stress and crack opening displacement at kink points $a_{\mathrm{s}}$, $a_{\mathrm{s}1}$, and $a_{\mathrm{s}2}$ also satisfy the tensile softening curve.

Fig. 2

Cohesive stress distribution in FPZ

$$\begin{aligned} \sigma _{\mathrm{s}} (\omega )=f_{\mathrm{t}} \left\{ {\left[ {1+\left( {\frac{c_{1} \omega }{\omega _{0} }} \right) ^{3}} \right] \hbox {e}^{\frac{-c_{2} \omega }{\omega _{0} }}-\frac{\omega }{\omega _{0} }\left( {1+c_{1}^{3}} \right) \hbox {e}^{-c_{2} }} \right\} \end{aligned}$$

(2)

where $c_{1}$, $c_{2}$, and $\omega _{0}$ are material parameters.

$$\begin{aligned} \omega =\hbox {CMOD}\left\{ {\left( {1-\frac{a_{{i}} }{a}} \right) ^{2} +\left( {-1.149\frac{a}{D}+1.081} \right) \left[ {\frac{a_{{i}} }{a} -\left( {\frac{a_{{i}} }{a}} \right) ^{2}} \right] } \right\} ^{1/2} \end{aligned}$$

(3)

where the crack mouth opening displacement CMOD is expressed by the following equation [23]:

$$\begin{aligned} \hbox {CMOD}=\frac{24Pa}{BDE}\left[ {\text{0 }.76-2.28\frac{a}{D}+3.87 \left( {\frac{a}{D}} \right) ^{2}-2.04\left( {\frac{a}{D}}\right) ^{3} +\frac{0.66}{\left( {1-a/D} \right) ^{2}}} \right] \end{aligned}$$

(4)

where B is the width of the specimen and E is the elastic modulus.

The expression of stress intensity factor caused by cohesive stress $K_{\mathrm{I}}^{\mathrm{C}}$ can be expressed as follows:

$$\begin{aligned} K_{\mathrm{I}}^{\mathrm{C}} =\sqrt{\frac{2}{\pi a}} g(a) \end{aligned}$$

(5)

where g(a) is calculated by four-term weight function [11]. Taking the bilinear cohesive stress distribution as an example, g(a) can be obtained by superimposing red shadow parts of (1)–(3) in Fig. 3.

Fig. 3

Calculating g(a) of bilinear cohesive stress distribution assumption

$$\begin{aligned} g(a)=g_{1} (a)+g_{2} (a)-g_{3} (a) \end{aligned}$$

(6)

where

$$\begin{aligned} g_{{i}} (a)= & {} A_{1}^{{i}} a \left( {2s_{{i}}^{\mathrm{1/2}} +M_{1} s_{{i}} +\frac{2}{3}M_{2} s_{{i}}^{3/2}+\frac{1}{2}M_{3} s_{{i}}^{2}} \right) \nonumber \\&+A_{2}^{{i}} a^{2}\left[ {\frac{4}{3}s_{{i}} ^{3/2}+\frac{M_{1} }{2}s_{{i}}^{2}+\frac{4}{15}M_{2} s_{{i}}^{5/2}\text{+ }\frac{M_{3} }{6} \left\{ {1-\left( {\frac{a_{{i}}}{a}} \right) ^{3} -3s_{{i}} \frac{a_{{i}} }{a}}\right\} } \right] \end{aligned}$$

(7)

when $i=1$, 3, $a_{{i}}=a_{\mathrm{s}}$; when $i=2$, $a_{{i}}=a_{0}$.

where

$$\begin{aligned}&s_{1} =s_{3} =1-a_{\mathrm{s}} /a \end{aligned}$$

(8)

$$\begin{aligned}&s_{2} =1-a_{0} /a \end{aligned}$$

(9)

$$\begin{aligned}&A_{1}^{1} =\sigma _{\mathrm{s}} (\omega _{\mathrm{s}} ) \end{aligned}$$

(10)

$$\begin{aligned}&A_{2}^{1} =\left( {f_{\mathrm{t}} -\sigma _{\mathrm{s}} (\omega _{\mathrm{s}} )}\right) /(a-a_{\mathrm{s}} ) \end{aligned}$$

(11)

$$\begin{aligned}&A_{1}^{2} =\sigma _{\mathrm{s}} (\mathrm{CTOD}) \end{aligned}$$

(12)

$$\begin{aligned}&A_{2}^{2} =\left( {\sigma _{\mathrm{s}} (\omega _{\mathrm{t}} ) -\sigma _{\mathrm{s}} (\mathrm{CTOD})} \right) /(a-a_{0} ) \end{aligned}$$

(13)

$$\begin{aligned}&A_{1}^{3} =\sigma _{\mathrm{s}} (\omega _{\mathrm{s}} ) \end{aligned}$$

(14)

$$\begin{aligned}&A_{2}^{3} =\left( {\sigma _{\mathrm{s}} (\omega _{\mathrm{t}} ) -\sigma _{\mathrm{s}} (\omega _{\mathrm{s}} )} \right) /(a-a_{\mathrm{s}} ) \end{aligned}$$

(15)

$\sigma _{\mathrm{s}}(\omega _{\mathrm{t}})$ is the cohesive stress corresponding to the effective crack length a on the linear extended line of $\sigma _{\mathrm{s}}$ (CTOD) and $\sigma _{\mathrm{s}}(\omega _{\mathrm{s}})$.

$$\begin{aligned} \sigma _{\mathrm{s}} (\omega _{\mathrm{t}} )=2\times \sigma _{\mathrm{s}} (\omega _{\mathrm{s}} )-\sigma _{\mathrm{s}} (\hbox {CTOD}) \end{aligned}$$

(16)

The expressions of $M_{1}$, $M_{2}$, and $M_{3}$ are shown as follows:

When $j=1$ or 3,

$$\begin{aligned} M_{{j}} =\frac{1}{\left( {1-\frac{a}{D}} \right) ^{3/2}} \left[ a_{{j}} +b_{{j}}\frac{a}{D}+c_{{j}} \left( {\frac{a}{D}} \right) ^{2}+d_{{j}} \left( {\frac{a}{D}}\right) ^{3} +e_{{j}} \left( {\frac{a}{D}} \right) ^{4} +f_{{j}} \left( {\frac{a}{D}} \right) ^{5} \right] \end{aligned}$$

(17)

When $j=2$,

$$\begin{aligned} M_{{j}} =a_{{j}} +b_{{j}} \frac{a}{D} \end{aligned}$$

(18)

The coefficients in Eqs. (17) and (18) are listed in Table 1.

Table 1 Values of coefficients in $M_{{j}}$ [11]

4 Calculating the fracture parameters using FET

Based on the initial fracture toughness criterion [24], the external load of three-point bending beams can be expressed as follows [13]:

$$\begin{aligned} P=\frac{2BD^{2}}{3S\sqrt{a} k\left( \alpha \right) } \left[ {K_{\mathrm{I}}^{\mathrm{C}} +K_{\mathrm{I}}^{\mathrm{ini}} } \right] -\frac{W}{2} \end{aligned}$$

(19)

where S is the span of the specimen, W is the weight of the specimen, $\alpha =a/D$, $K_{\mathrm{I}}^{\mathrm{C}}$ is calculated by Eq. (5). $k(\alpha )$ is shown as follows [23]:

$$\begin{aligned} k\left( \alpha \right) =\frac{1.99-\alpha \left( {1-\alpha } \right) \left[ {2.15-3.93\alpha +2.7\left( \alpha \right) ^{2}} \right] }{\left( {1+2\alpha }\right) \left( {1-\alpha } \right) ^{3/2}} \end{aligned}$$

(20)

Thus, the $\partial P/\partial a$ in Eq. (1) can be expressed as follows:

$$\begin{aligned} \frac{\partial P}{\partial a}=\zeta ^{'}(a)+\eta ^{'}(a)K_{\mathrm{I}}^{\mathrm{ini}} \end{aligned}$$

(21)

where

$$\begin{aligned} \zeta ^{'}(a)= & {} \frac{4BD^{2}}{3\sqrt{2\pi } S}\frac{g^{'}(a) k(\alpha )a-g(a)[k^{'}(\alpha )a+k(\alpha )]}{k^{2}(\alpha )a^{2}} \end{aligned}$$

(22)

$$\begin{aligned} \eta ^{'}(a)= & {} -\frac{2BD^{2}}{3S}\left[ {\frac{a^{-1/2}k(\alpha ) +a^{1/2}k^{'}(\alpha )}{2ak^{2}(\alpha )}} \right] \end{aligned}$$

(23)

where $g\prime (a)$ and $k\prime (\alpha )$ are shown in “Appendix.”

Combining Eqs. (1) and (21), the critical effective crack length $a_{\mathrm{c}}$ can be obtained. Substituting $a = a_{\mathrm{c}}$, $P =P_{\mathrm{max}}$ into Eq. (19), the initial fracture toughness $K_{\mathrm{I}}^{\mathrm{ini}}$ can be obtained.

$$\begin{aligned} K_{\mathrm{I}}^{\mathrm{ini}} =\frac{3S\left( {2P_{\max } +W} \right) \sqrt{a_{\mathrm{c}} } k\left( {\alpha _{\mathrm{c}} }\right) }{4BD^{2}} -\frac{2}{\sqrt{2\pi a_{\mathrm{c}} } }g\left( {a_{\mathrm{c}}}\right) \end{aligned}$$

(24)

The first term on the right side in Eq. (24) is $K_{\mathrm{I}}^{\mathrm{un}}$.

$$\begin{aligned} K_{\mathrm{I}}^{\mathrm{un}} =\frac{3S\left( {2P_{\max } +W}\right) }{4BD^{2}} \sqrt{a_{\mathrm{c}} } k\left( {\alpha _{\mathrm{c}}}\right) \end{aligned}$$

(25)

Finally, $K_{\mathrm{I}}^{\mathrm{ini }}$ and $K_{\mathrm{I}}^{\mathrm{un}}$ can be determined using FET with three different cohesive stress distribution assumptions.

5 Numerical simulation

Nine groups of geometrically similar three-point bending concrete beams with depths from 200 to 1000 mm were simulated to obtained peak load$P_{\mathrm{max}}$ and critical crack mouth opening displacement $\hbox {CMOD}_{\mathrm{c}}$. The $a_{0}/D$ in each group ranges from 0.1 to 0.6. Figure 4 shows the loading and boundary conditions for three-point bending beam, where D, B, and S are the depth, width, and span of the specimen and $S = 4D$.

The whole fracture processes of three-point bending beams were simulated with the finite element program of ABAQUS. The loading and boundary conditions of the model are applied according to the particularities of the test setup. The cohesive element technique of finite element analysis [25] was adopted to model the cracking region in the middle of the bending beam in the study, which has been verified by comparing the simulation results with the experimental data in Refai and Swartz [26]. Table 2 represents the model parameters used in the simulation. The finite element model is shown in Fig. 5 in which the Lagrange eight-node solid elements with different dimensions are used.

Fig. 4

Numerical model of three-point bending beam (Unit: mm)

Table 2 Concrete properties used in the numerical simulation

Fig. 5

Finite element model with three-dimensional mesh

Fig. 6

$P{-}\hbox {CMOD}$ curves for three-point bending beams

Table 3 Calculated results of the fracture parameters

6 Calculated results and discussions

Figure 6 shows the simulated load–crack mouth opening displacement ($P{-}\hbox {CMOD}$) curves of the geometrically similar three-point bending beams. The simulated values of $P_{\mathrm{max}}$ and $\hbox {CMOD}_{\mathrm{c}}$ as well as the double-K fracture parameters calculated by FET and double-K method are listed in Table 3. The double-K fracture parameters determined by FET with linear, bilinear, and trilinear cohesive stress distribution assumptions are denoted by the superscript L, B, and T. For instance, $K_{\mathrm{I}}^{\mathrm{ini-L}}$, $K_{\mathrm{I}}^{\mathrm{ini-B}}$, and $K_{\mathrm{I}}^{\mathrm{ini-T}}$ denote the initial fracture toughness obtained by three cohesive stress distribution assumptions in FET, respectively. The $K_{\mathrm{I}}^{\mathrm{ini-WF}}$ represents the initial fracture toughness determined by double-K method using the four-term weight function with linear cohesive stress distribution [11]. It should be pointed out that only the simulated $P_{\mathrm{max}}$ was required in FET, while both simulated $P_{\mathrm{max}}$ and $\hbox {CMOD}_{\mathrm{c}}$ are needed in double-K method.

Figures 7 and 8 show the comparisons of $K_{\mathrm{C}}/K_{\mathrm{I}}^{\mathrm{ini}}$ and $K_{\mathrm{C}}/K_{\mathrm{I}}^{\mathrm{un}}$ with $l_{\mathrm{ch}}/D$ calculated by FET and double-K method using linear cohesive stress distribution assumption, respectively, where the characteristic length $l_{\mathrm{ch}} =\textit{EG}_{\mathrm{F}}/f_{\mathrm{t}}^{2}$ and the critical value of stress intensity factor $K_{\mathrm{C}} =\sqrt{G_\mathrm{F} E}$ are proposed in FCM. It can be seen from Fig. 7, $K_{\mathrm{C}}/K_{\mathrm{I}}^{\mathrm{ini}}$ determined by FET are closed to those obtained by double-K method with the same $a_{0}/D$ and scarcely changed with $l_{\mathrm{ch}}/D$. In Fig. 8, $K_{\mathrm{C}}/K_{\mathrm{I}}^{\mathrm{un}}$ determined by FET increase with $l_{\mathrm{ch}}/D$ while those determined by double-K method almost not change with $l_{\mathrm{ch}}/D$. Besides, when $a_{0}/D$ in the region of 0.1 to 0.4 and $l_{\mathrm{ch}}/D$ are smaller than 0.6, i.e., specimen depths exceed 600 mm, $K_{\mathrm{C}}/K_{\mathrm{I}}^{\mathrm{un}}$ determined by FET were smaller than those obtained by double-K method. As $a_{0}/D = 0.5$ and 0.6, $K_{\mathrm{C}}/K_{\mathrm{I}}^{\mathrm{un}}$ determined by FET were generally larger than those obtained by double-K method. The possible reason is that FET adopts only the peak load $P_{\mathrm{max}}$ in determining $K_{\mathrm{I}}^{\mathrm{un}}$, and the double-K method is affected by both the peak load $P_{\mathrm{max}}$ and the critical crack mouth opening displacement $\hbox {CMOD}_{\mathrm{c}}$. The measurement error of $\hbox {CMOD}_{\mathrm{c}}$ would influence the calculated results, which is avoided in FET.

Fig. 7

Comparisons of $K_{\mathrm{C}}/K_{\mathrm{I}}^{\mathrm{ini}}$ obtained by FET and double-K method with linear cohesive stress distribution assumption

Fig. 8

Comparisons of $K_{\mathrm{C}}/K_{\mathrm{I}}^{\mathrm{un}}$ obtained by FET and double-K method with linear cohesive stress distribution assumption

Fig. 9

Comparisons of $K_{\mathrm{I}}^{\mathrm{ini}}/K_{\mathrm{I}}^{\mathrm{un}}$ obtained by FET with different cohesive stress distribution assumptions

Figure 9 compares $K_{\mathrm{I}}^{\mathrm{ini}}/K_{\mathrm{I}}^{\mathrm{un}}$ obtained by FET with different cohesive stress distribution assumptions. With bilinear and trilinear cohesive stress distribution assumptions, $K_{\mathrm{I}}^{\mathrm{ini}}/K_{\mathrm{I}}^{\mathrm{un}}$ slightly fluctuates around 0.5 and hardly affected by $l_{\mathrm{ch}}/D$, which is same as the conclusion drawn by Jenq and Shah [4] and Yon et al. [27] by the empirical estimation. While $K_{\mathrm{I}}^{\mathrm{ini}}/K_{\mathrm{I}}^{\mathrm{un}}$ calculated using linear cohesive stress distribution assumption are smaller than 0.5. Results show that the specimen depth has no obvious effect on $K_{\mathrm{I}}^{\mathrm{ini}}/K_{\mathrm{I}}^{\mathrm{un}}$ in FET with bilinear and trilinear cohesive stress distribution assumptions.

Table 3 shows that when the same specimen depth and $a_{0}/D$ were adopted, the initial fracture toughness determined by FET using linear cohesive stress distribution assumption $K_{\mathrm{I}}^{\mathrm{ini-L}}$ is slightly smaller than those determined with bilinear and trilinear cohesive stress distribution    assumptions ($K_{\mathrm{I}}^{\mathrm{ini-B}}$ and $K_{\mathrm{I}}^{\mathrm{ini-T}})$, the values of $K_{\mathrm{I}}^{\mathrm{un-B}}$ and $K_{\mathrm{I}}^{\mathrm{un-T}}$ obtained with bilinear and trilinear cohesive stress distribution assumptions are smaller than those obtained with linear cohesive stress distribution assumption ($K_{\mathrm{I}}^{\mathrm{un-L}})$, and the difference between $K_{\mathrm{I}}^{\mathrm{ini-B}}$ and $K_{\mathrm{I}}^{\mathrm{ini-T}}$ as well as $K_{\mathrm{I}}^{\mathrm{un-B}}$ and $K_{\mathrm{I}}^{\mathrm{un-T}}$ is small. The same phenomenon can be observed in Ref. [28] for the laboratory size specimens. However, the linear cohesive stress distribution assumption leads to an overestimation of $K_{\mathrm{I}}^{\mathrm{C}}$ as shown in Fig. 2. Therefore, accurate double-K fracture parameters can be obtained using the bilinear cohesive stress distribution assumption.

7 Conclusion

The size effect on double-K fracture parameters was theoretically investigated in this study. Nine groups of similar concrete three-point bending beams with specimen depths from 200 to 1000 mm and $a_{0}/D$ from 0.1 to 0.6 were established. The initial fracture toughness $K_{\mathrm{I}}^{\mathrm{ini}}$ and unstable fracture toughness $K_{\mathrm{I}}^{\mathrm{un}}$ were calculated by FET and double-K method. The linear, bilinear, and trilinear cohesive stress distribution assumptions were used in FET; the double-K method only adopted the linear cohesive stress distribution assumption. The following conclusions can be drawn from this study:

• (1) The $K_{\mathrm{C}}/K_{\mathrm{I}}^{\mathrm{ini}}$ determined by FET with linear cohesive stress distribution assumption were close to those obtained by double-K method, which were almost not affected by specimen depth.

• (2) With linear cohesive stress distribution assumption, $K_{\mathrm{C}}/K_{\mathrm{I}}^{\mathrm{un}}$ determined by FET increased with $l_{\mathrm{ch}}/D$, while, $K_{\mathrm{C}}/K_{\mathrm{I}}^{\mathrm{un}}$ obtained via double-K method slightly changed with $l_{\mathrm{ch}}/D$.

• (3) When bilinear and trilinear cohesive stress distribution assumptions were adopted in FET, the difference between $K_{\mathrm{C}}/K_{\mathrm{I}}^{\mathrm{ini}}$ and $K_{\mathrm{C}}/K_{\mathrm{I}}^{\mathrm{un}}$ is not obvious, and the $K_{\mathrm{I}}^{\mathrm{ini}}/K_{\mathrm{I}}^{\mathrm{un}}$ is stable and slightly fluctuates around 0.5

• (4) Based on FET, the bilinear cohesive stress distribution assumption was recommended to determine the double-K fracture parameters. The linear cohesive stress distribution assumption overestimated $K_{\mathrm{I}}^{\mathrm{C}}$, while the bilinear cohesive stress distribution assumption can effectively avoid and has relatively small computational complexity.

Appendix

The $g\prime (a)$ and $k\prime (\alpha )$ in Eq. (22) are shown as follows:

$$\begin{aligned} k^{'}\left( \alpha \right)= & {} \frac{\text{1 }}{D(1+2\alpha ^{2})(1-\alpha )^{3}} \times \left\{ {\left( {-2.15+12.16\alpha -19.89\alpha ^{2} +10.8\alpha ^{3}} \right) } \right. \times \left( {1+2\alpha } \right) \left( {1-\alpha }\right) ^{3/2} \nonumber \\&-\left( {1.99-2.15\alpha +6.08\alpha ^{2}-6.63\alpha ^{3}+2.7\alpha ^{4}}\right) \left. {\times \left[ {2(1-\alpha )^{3/2}-\frac{3}{2}(1+2\alpha ) (1-\alpha )^{1/2}} \right] } \right\} \qquad \end{aligned}$$

(A1)

$$\begin{aligned} {g}'(a)= & {} {g}'_{1} (a)+{g}'_{2} (a)-{g}'_{3} (a) \end{aligned}$$

(A2)

where

$$\begin{aligned} {g}'_{{i}} (a)= & {} \left( {A_{1}^{{i}}+{A_{1}^{{i}}}'a} \right) \left( {2s_{{i}}^{\mathrm{1/2}} +M_{1} s_{{i}} +\frac{2}{3}M_{2} s_{{i}}^{3/2} +\frac{1}{2}M_{3} s_{{i}}^{2} } \right) +A_{1}^{{i}}a\left[ {s_{{i}}^{\mathrm{-1/2}} s_{{i}}'+M_{1} s_{{i}} '+M_{2}'s_{{i}} +M_{3} s_{{i}} ^{1/2}s_{{i}}'} \right] \nonumber \\&+\,A_{1}^{{i}}a\left[ {\frac{2}{3}M_{2}'s_{{i}} ^{3/2}+M_{3} s_{{i}} s_{{i}}'+\frac{1}{2}M_{3}' s_{{i}}^{2}} \right] +A_{2}^{{i}}a^{2}\left[ {2s_{{i}} ^{1/2}s_{{i}}'+M_{1} s_{{i}} s_{{i}}' +\frac{M_{1}'}{2}s_{{i}}^{2}+\frac{2}{3}M_{2} s_{{i}}^{\mathrm{3/2}} s_{{i}}'} \right] \nonumber \\&+\,A_{2}^{{i}}a^{2}\left[ {\frac{4}{15}M_{2}' s_{{i}}^{\mathrm{5/2}} +\frac{M_{3}'}{6} \left[ {1-\left( {\frac{a_{{i}} }{a}} \right) ^{3}-3s_{{i}} \frac{a_{{i}} }{a}} \right] } \right] +A_{2}^{{i}} a^{2}f_{{i}}(a) \nonumber \\&+\,\left( {2A_{2}^{{i}}a+A_{2}'a^{2}} \right) \times \left[ {\frac{4}{3}s_{{i}}^{\mathrm{3/2}} +\frac{M_{1}}{2}s_{{i}}^{2} +\frac{4}{15}M_{2} s_{{i}}^{\mathrm{5/2}} +\frac{M_{3} }{6}\left\{ {1-\left( {\frac{a_{{i}} }{a}} \right) ^{3}-3s_{1} \frac{a_{{i}} }{a }} \right\} } \right] \end{aligned}$$

(A3)

when $i =1$, 3, $a_{{i}} = a_{\mathrm{s}}$; when $i =2$, $a_{{i}} = a_{0}$.

$$\begin{aligned} f_{1,3} (a)= & {} \frac{M_{3} }{2}\left( {-\left( {\frac{a_{\mathrm{s}} }{a}} \right) ^{2}\frac{a-2a_{\mathrm{s}} }{2a^{2}}-s_{{i}}' \frac{a_{\mathrm{s}} }{a}-s_{{i}} \frac{a-2a_{\mathrm{s}} }{2a^{2}}}\right) \end{aligned}$$

(A4)

$$\begin{aligned} f_{2} (a)= & {} \frac{M_{3} }{2}\left( {\frac{a_{0}^{3}}{a^{4} }-s_{{i}} '\frac{a_{0} }{a}+s_{{i}} \frac{a_{0} }{a^{2}}} \right) \end{aligned}$$

(A5)

where

$$\begin{aligned}&{s}'_{1,3} =-\frac{a-2a_{\mathrm{s}} }{2a^{2}} \end{aligned}$$

(A6)

$$\begin{aligned}&{s}'_{2} =\frac{a_{0} }{a^{2}} \end{aligned}$$

(A7)

$$\begin{aligned}&{A_{1}^{1}}'=\frac{\partial \sigma _{\mathrm{s}} \left( {\omega _{\mathrm{s}} } \right) }{\partial a}=\frac{\partial \sigma _{\mathrm{s}} \left( {\omega _{\mathrm{s}} } \right) }{\partial \omega _{\mathrm{s}} } \frac{\partial \omega _{\mathrm{s}} }{\partial a} \end{aligned}$$

(A8)

$$\begin{aligned}&{A_{2}^{1}}'=-\frac{{A_{1}^{2}}' \left( {a-a_{\mathrm{s}} } \right) +\left( {f_{\mathrm{t}} -A_{1}^{2} } \right) /2}{\left( {a-a_{\mathrm{s}} } \right) ^{2}} \end{aligned}$$

(A9)

$$\begin{aligned}&{A_{1}^{2}}'=\frac{\partial \sigma _{\mathrm{s}} \left( {\hbox {CTOD}} \right) }{\partial a}=\frac{\partial \sigma _{\mathrm{s}} \left( {\hbox {CTOD}} \right) }{\partial \hbox {CTOD}}\frac{\partial \hbox {CTOD}}{\partial a} \end{aligned}$$

(A10)

$$\begin{aligned}&{A_{2}^{2}}'=\frac{\left( {{\sigma }'_{\mathrm{s}} (\omega _{\mathrm{t}} ) -{A_{1}^{2}}'} \right) \left( {a-a_{0} } \right) -\left( {\sigma _{\mathrm{s}} (\omega _{\mathrm{t}} )-A_{1}^{2} } \right) }{\left( {a-a_{0} } \right) ^{2}} \end{aligned}$$

(A11)

$$\begin{aligned}&{A_{1}^{3}}'= {A_{1}^{1}}' \end{aligned}$$

(A12)

$$\begin{aligned}&{A_{2}^{3}}'=\frac{\left( {{\sigma }'_{\mathrm{s}} (\omega _{\mathrm{t}}) -{A_{1}^{1}}'} \right) \left( {a-a_{\mathrm{s}} }\right) -\left( {\sigma _{\mathrm{s}} (\omega _{\mathrm{t}}) -A_{1}^{1} } \right) /2}{\left( {a-a_{\mathrm{s}} }\right) ^{2}} \end{aligned}$$

(A13)

where

$$\begin{aligned}&\frac{\partial \sigma _{\mathrm{s}} \left( \omega \right) }{\partial \omega } =f_{\mathrm{t}} \left[ {\exp \left( {-\frac{c_{2} \omega }{w_{0} }} \right) } \right. \left. {\left[ {\frac{3c_{1} }{w_{0} } \left( {\frac{c_{1} \omega }{w_{0} }} \right) ^{2} -\frac{c_{2} }{w_{0} }\left( {1+\left( {\frac{c_{1} \omega }{w_{0} }} \right) ^{3}} \right) } \right] -\frac{1}{w_{0} } \left( {1+c_{1}^{3} } \right) \exp \left( {-c_{2} } \right) } \right] \qquad \end{aligned}$$

(A14)

$$\begin{aligned}&\frac{\partial \hbox {CTOD}}{\partial a}=\left\{ {\frac{6PS}{BD^{2}E}} \right. \times \left. {\left[ {0.76-4.56\alpha +11.61\alpha ^{2}-8.16\alpha ^{3} +\frac{0.66}{\left( {1-\alpha } \right) ^{2}}+\frac{1.32\alpha }{\left( {1-\alpha } \right) ^{3}}} \right] } \right\} \nonumber \\&\qquad \qquad \qquad \times \, \left\{ {\left( {1-\frac{a_{0} }{a}} \right) ^{2} +\left( {1.081-1.149\alpha } \right) \left[ {\frac{a_{0} }{a} -\left( {\frac{a_{0}}{a}} \right) ^{2}} \right] } \right\} ^{1/2} \nonumber \\&\qquad \qquad \qquad +\,\frac{3PSa}{BD^{2}E}\times \left( {0.76-2.28\alpha +3.87\alpha ^{2} -2.04\alpha ^{3}+\frac{0.66}{\left( {1-\alpha } \right) ^{2}}} \right) \nonumber \\&\qquad \qquad \qquad \times \, \left\{ {\left( {1-\frac{a_{0} }{a}} \right) ^{2} +\left( {1.081-1.149\alpha } \right) \left[ {\frac{a_{0} }{a} -\left( {\frac{a_{0}}{a}} \right) ^{2}} \right] } \right\} ^{-1/2} \nonumber \\&\qquad \qquad \qquad \times \, \left\{ {2\left( {1-\frac{a_{0} }{a}} \right) \frac{a_{0}}{a^{2}} -\frac{1.149}{D}\left[ {\frac{a_{0} }{a}-\left( {\frac{a_{0} }{a}} \right) ^{2}} \right] } \right. -\left. {\left( {1.081-1.149\alpha } \right) \left( {\frac{a_{0} }{a^{2}}-2\frac{a_{0}^{2} }{a^{3}}} \right) }\right\} \end{aligned}$$

(A15)

$$\begin{aligned}&\frac{\partial \omega _{\mathrm{s}} }{\partial a} =\left\{ {\frac{6PS}{BD^{2}E}} \right. \times \left. {\left[ {0.76-4.56\alpha +11.61\alpha ^{2}-8.16\alpha ^{3}\text{+ }\frac{0.66}{\left( {1-\alpha } \right) ^{2}}+\frac{1.32\alpha }{\left( {1-\alpha } \right) ^{3}}} \right] }\right\} \nonumber \\&\qquad \quad \times \, \left\{ {\left( {1-\frac{a_{\mathrm{s}} }{a}} \right) ^{2} +\left( {1.081-1.149\alpha } \right) \left( {\frac{a_{\mathrm{s}} }{a} -\left( {\frac{a_{\mathrm{s}} }{a}} \right) ^{2}} \right) } \right\} ^{\frac{1}{2}} \nonumber \\&\qquad \quad +\,\frac{3PSa}{BD^{2}E}\times \left( {0.76-2.28\alpha +3.87\alpha ^{2} -2.04\alpha ^{3}\text{+ }\frac{0.66}{\left( {1-\alpha } \right) ^{2}}}\right) \nonumber \\&\qquad \quad \times \, \left( {\left( {1-\frac{a_{\mathrm{s}} }{a}} \right) ^{2}}\right. +\left( {1.081-1.149\alpha } \right) \left( {\frac{a_{\mathrm{s}}}{a} -\left( {\frac{a_{\mathrm{s}} }{a}} \right) ^{2}} \right) ^{-\frac{1}{2}} \nonumber \\&\qquad \quad \times \, \left\{ {2\left( {1-\frac{a_{\mathrm{s}} }{a}} \right) \frac{a_{0}}{2a^{2}}} \right. +\left( {-\frac{1.149}{D}} \right) \left[ {\frac{a_{\mathrm{s}} }{a}-\left( {\frac{a_{\mathrm{s}} }{a}} \right) ^{2}}\right] -\left. {\left( {1.081-1.149\alpha } \right) \left[ {\frac{a_{0}}{2a^{2}} -\frac{a_{0} a_{\mathrm{s}} }{a^{3}}} \right] } \right\} \qquad \quad \end{aligned}$$

(A16)

$$\begin{aligned}&{\sigma }'_{\mathrm{s}} (\omega _{\mathrm{t}})= 2{A_{1}^{1}}'- {A_{3}^{1}}' \end{aligned}$$

(A17)

The partial derivatives of $M_{{j}}$ to a are expressed as follows:

when $j = 1$ or 3,

$$\begin{aligned} M_{{j}}'= & {} \frac{1}{\left( {1-a/D} \right) ^{3/2}}\times \left[ {\frac{b_{{j}} }{D}+2c_{{j}} \frac{a}{D^{2}}+3d_{{j}} \frac{a^{2}}{D^{3}}+4e_{{j}} \frac{a^{3}}{D^{4}}+5f_{{j}} \frac{a^{4}}{D^{5}}} \right] \nonumber \\&+\,\frac{3}{2D}\left( {1-\frac{a}{D}} \right) ^{-5/2}\times \left[ {a_{{j}} +b_{{j}} \frac{a}{D}+c_{{j}} \left( {\frac{a}{D}} \right) ^{2}+d_{{j}} \left( {\frac{a}{D}} \right) ^{3}+e_{{j}} \left( {\frac{a}{D}} \right) ^{4}+f_{{j}} \left( {\frac{a}{D}}\right) ^{5}} \right] \end{aligned}$$

(A18)

when $j \quad =$ 2,

$$\begin{aligned} M_{{j}}'=\frac{b_{{j}} }{D} \end{aligned}$$

(A19)