Effect of rotating unbalance and engine excitations on the nonlinear dynamic response of turbocharger flexible rotor system supported on floating ring bearings

Abstract

In practical conditions, turbochargers are supported by floating ring bearings and mounted on engines. In this paper, the effect of rotating unbalance and engine excitations on turbocharger is studied. The finite element model of turbocharger system is developed considering flexible rotor, using Timoshenko beam elements. The nonlinear fluid film forces generated in floating ring bearings are derived analytically in dimensional form using short bearing approximation. A new $\hbox {MATLAB}^{{\circledR }}$ code has been constructed to solve the governing differential equations of motion of system using implicit Newmark-$\upbeta$ numerical integration scheme along with Newton–Raphson convergence method, and dynamic response of the system is computed. The orbital plots, Poincare maps, and frequency spectrum are developed to show the nonlinear behaviour of the turbocharger system. At low rotor speeds, the system exhibits chaotic behaviour and has a wide range of sub-synchronous vibrations. As the speed of turbocharger increases, the forces due to unbalance dominate over engine excitations and nonlinear bearing forces and frequency spectrum become narrow. The behaviour of compressor and turbine disc centre is governed by their respective bearing nodes.

1 Introduction

Nowadays, around 70% of diesel fuel is consumed by transportation vehicles based on IC engines. In case of high-speed vehicles, there should be higher air–fuel ratio to increase the fuel efficiency of the engine. To achieve this, a turbocharger is incorporated into the engine to supply extra compressed air. The automotive turbocharger usually runs at very high speed compared to other turbo-machinery. Due to such high speed, even small unbalance or small manufacturing defects can cause large vibrations. To resolve such problems, analytical understanding of dynamic behaviour of the turbocharger rotor-bearing system (RBS) is required considering various nonlinearities. Researchers have devised several fault diagnosis methods based on nonlinear dynamic simulations for rotating machinery [1, 2].

Hydrodynamic bearings have better damping behaviour as compared to roller or ball bearings. In case of high-speed turbochargers running at around 180K rpm, instability and high friction losses in single fluid film bearings are the major issues. Therefore, floating ring bearings (FRB), i.e. full floating/semi-floating, are used which provide better damping effects and less friction losses than hydrodynamic bearings. As compared to simple hydrodynamic bearings, floating ring bearings show typical fluid film instability and chaotic behaviour [3]. Adiletta [4] used the Capone’s model and derived the nonlinear fluid film forces developed in journal bearing using short bearing approximations. Nguyen-Schäfer [5] linearized the nonlinear fluid film forces using Taylor’s series expansion.

Because of nonlinear elastic and damping forces arising from two fluid films in floating ring bearings of a turbocharger, its dynamic behaviour becomes quite intricate. The main advantage of full floating ring bearing is better performance in oil-contaminated environment and improved robustness as compared to semi-floating ring bearing, but the disadvantage of FRB is its stability behaviour which sometimes reaches to total instability. Tanaka and Hori [6] found the superior stability characteristics of the floating ring bearing as compared to conventional cylindrical journal bearing, using short bearing approximation. Few researchers [7,8,9,10,11,12] investigated the nonlinear stability analysis of floating ring bearings using Hopf bifurcation theory and other linear and nonlinear analysis methods.

The turbocharger rotor shaft can be modelled using different theories. Nelson and McVaugh [13] used Euler–Bernoulli (EB) beam element theory to describe the finite element modelling of the rotor shaft, whereas some researchers [14, 15] had been used Timoshenko beam element theory to develop the finite element model of flexible rotor shaft and got better results as compared to Euler–Bernoulli beam theory.

Different numerical integration schemes had been used to solve the nonlinear equations of motion of turbocharger rotor-bearing system. Bonello [16] analysed the nonlinear dynamic behaviour of floating ring bearings by transient modal analysis of TC FRB system with nonlinear fluid film forces. Tian [17] used $\hbox {MATLAB}^{\circledR }$ routine ode15s for turbocharger rotor system supported on floating ring bearings and investigated the dynamic response and synchronous and sub-synchronous vibrations. Schweizer [18, 19] analysed the occurrence of total instability phenomena for a flexible turbocharger FRB system using standard multibody dynamics software. Due to the presence of various nonlinearities in equations of motion of rotor-bearing systems, highly accurate and unconditionally stable implicit Newmark-$\upbeta$ numerical integration techniques along with Newton–Raphson convergence method have been preferred to get dynamic response of the system [20].

Many studies had been explained the effects of rotating unbalance on the dynamic behaviour of the rotor-bearing system. Nakagawa and Aoki [21] theoretically discussed the influence of unbalance on the symmetrical overhung rotor FRB system and also derived the approximate analytical solution of steady- and dynamic-state properties. Tian [22] used run-up and run-down simulations for turbocharger FRB system with rotating unbalance presented on both compressor and turbine discs and showed the nonlinear effects of unbalance on the dynamic response of the system.

The engine-induced vibrations caused rich sub-synchronous vibrations and tremendously influenced the rotor orbit shapes at lower rotor speeds. These engine-induced vibrations are generally treated as foundation excitations or base excitations. A lot of experimental work for turbochargers situated on engine has been studied by many researchers to investigate the vibration behaviour, jump phenomena and path trajectories of bearings and also compressor and turbine ends [23,24,25,26]. Maruyama [27] used engine excitations as base excitations and investigated nonlinear forced response oscillations by simulation using standard software. The simulation results obtained were compared to the test data. Ying [28] developed a dynamic model of turbocharger rotor supported on hydrodynamic bearings with foundation excitations considering these to be harmonic. Orbital plots and Poincare maps for the motion of disc (representing compressor and turbine) centre were plotted to investigate the effect of foundation excitations on rotor dynamic behaviour of a turbocharger.

In the present paper, the turbocharger rotor shaft is considered flexible, and both compressor and turbine disc are taken as rigid. The FE model is formulated by using Timoshenko beam element theory. Dimensional fluid film forces for floating ring bearing are calculated using short bearing approximation and half Sommerfeld condition. In operating conditions, the turbocharger system is attached on the engine. So, the engine vibrations are taken as base excitations in sinusoidal form. Along with base excitations, the rotating in-phase unbalance on both compressor and turbine disc is also considered. A new $\hbox {MATLAB}^{{\circledR }}$ has been constructed to solve the equations of motion of turbocharger FRB system along with the combined effect of unbalance and base excitations using unconditionally stable implicit Newmark-$\upbeta$ numerical integration scheme with Newton–Raphson convergence method. The orbital plots, Poincare maps and FFT plots are drawn to describe the nonlinear dynamic behaviour of the turbocharger system.

2 Model description

2.1 Turbocharger rotor modelling

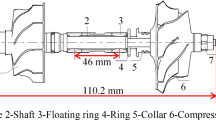
The turbocharger rotor shaft is considered to be flexible and discretized into three elements, and the compressor and turbine discs are taken as rigid bodies. The schematic diagram of FE modelling is shown in Fig. 1. The discs and bearing locations are taken as nodes for FE modelling. The motion in the axial direction is not considered. Thus, four degrees of freedom for each node have been taken, and elements are idealized by Timoshenko beam element [15, 29]. The dimensions and specification of the FE model of turbocharger are given in Table 1.

Fig. 1

Finite element model of turbocharger

The shape functions are derived for the Timoshenko beam element, from the exact solution of homogeneous form of differential equations of motion. Using Lagrange’s equation, the governing differential equation of motion of the turbocharger system is written as follows:

$$\begin{aligned} {[}{M_\mathrm{s}}{]}\{\ddot{{q}}_\mathrm{s} \}+[{\varOmega _j.G_\mathrm{s}}]\,\{\dot{q}_\mathrm{s}\}+[K_\mathrm{s}] \{q_\mathrm{s}\}=\{F_\mathrm{bi}\}+\{F_\mathrm{ub}\}+\{F_\mathrm{g}\} \end{aligned}$$

(1)

where $\{{q_s}\}^{T}=\{x_i \,y_i\,\theta _{{\textit{xi}}}\, \theta _{{\textit{yi}}}\}$ is displacement vector and $i=1,2,3,4$.

In Eq. (1), [$M_{\mathrm{S}}$] is mass matrix, [$G_{\mathrm{S}}$] is gyroscopic matrix and [$K_{\mathrm{S}}$] is stiffness matrix of the turbocharger rotor shaft and discs. The material damping of the system is not considered. $\{F_{\mathrm{bi}}\}, \{F_{\mathrm{ub}}\}$ and $\{{F}_{\mathrm{g}}\}$ are inner fluid film forces, unbalance forces and gravity force vector, respectively.

The governing differential equation for both rings is as follows:

$$\begin{aligned}{}[{m_r}]\{{\ddot{q}}_{r} \}=\{{F_{\mathrm{ring}}}\} \end{aligned}$$

(2)

where $[{m_r}]=\hbox {diag}( {[ {m_{r1}\,m_{r1} \,I_{r1} \,m_{r2} \,m_{r2} \,I_{r2}}]})$ is mass matrix for both rings.

Table 1 Parametric details of turbocharger system

$\{{\ddot{q}}\}_{r} =\{ {\ddot{X}}_{r1}\,{\ddot{Y}}_{r1} \,\dot{\omega }_{r1}\,{\ddot{X}}_{r2}\,\ddot{Y}_{r2}\,\dot{\omega }_{r2}\}^{T}$ is acceleration vector and $\{{F_{\mathrm{ring}}}\}$ represents force vector consisting of fluid film forces acting on both rings.

$$\begin{aligned} \{{F_{\mathrm{ring}}}\}=\{{F_{1x\_o} -F_{1x\_i} F_{1y\_o} -F_{1y\_i}\,T_{1\_i} -T_{1\_o}\,F_{2x\_o} -F_{2x\_i} F_{2y\_o} -F_{2y\_i}\,\tau _{2\_i} -\tau _{2\_o} }\}. \end{aligned}$$

The expression for fluid film forces in the dimensional form is derived and explained in detail in Sect. 2.2.

2.2 Floating ring bearing modelling

There are two fluid films (i.e. inner and outer) which are developed in a floating ring bearing, as shown in Fig. 2. The inner fluid film is formed between the journal and the floating ring, whereas the outer film is between floating ring and bearing housing. The nonlinear fluid film forces generated in floating ring bearing are derived in dimensional form using the Capone’s model [4]. While deriving the expression for fluid film forces, few assumptions have been made, which are as follows:

• (a) The fluid flow inside bearing is considered laminar and is iso-viscous Newtonian.

• (b) The bearing oil feeding mechanism is not considered.

Fig. 2

FRB model

Two separate Reynolds equations [6] have been used for different fluid films. After applying infinite short bearing approximation theory and integrating the Reynolds equations twice, the expression for pressure distribution is obtained as follows [17]:

$$\begin{aligned} P_\mathrm{i}= & {} \frac{3\mu _i}{h_i^3}\left( {Z_i^2 -\frac{L_i^2}{4}} \right) \left\{ {\left[ {\left( {\omega _j +\omega _r } \right) x_j -2{\dot{y}}_{j}}\right] }-\left[ (\omega _{j}+\omega _{r})y_{j}+2\dot{x}_j\right] \right\} \end{aligned}$$

(3)

$$\begin{aligned} P_\mathrm{o}= & {} \frac{3\mu _o }{h_o^3 }\left( {Z_o^2 -\frac{L_o^2 }{4}} \right) \left[ {\left( {\omega _r X_r -2{\dot{Y}}_{r}}\right) }-\left( \omega _{r}Y_{r}+2{\dot{X}}_{r}\right) \right] \end{aligned}$$

(4)

where $h_\mathrm{i} =C_1 -x_j \cos \vartheta _i -y_j \sin \vartheta _i$ and $h_\mathrm{o} =C_2 -X_r \cos \vartheta _o -Y_r \sin \vartheta _o$ represent the oil film thickness of the inner and outer film, respectively. Equations (3) and (4) can also be written as:

$$\begin{aligned} P_\mathrm{i}= & {} \frac{3\mu _i }{h_i^3 }\left( {Z_i^2 -\frac{L_i^2 }{4}} \right) \left[ {A\cdot \cos \alpha _1 \cdot \sin \vartheta _i -A\cdot \sin \alpha _1 \cdot \cos \vartheta _i } \right] , \end{aligned}$$

(5)

$$\begin{aligned} P_\mathrm{o}= & {} \frac{3\mu _o }{h_o^3 }\left( {Z_o^2 -\frac{L_o^2 }{4}} \right) \left[ {B\cdot \cos \alpha _2 \cdot \sin \vartheta _o -B\cdot \sin \alpha _2 \cdot \cos \vartheta _o } \right] . \end{aligned}$$

(6)

Here,

$$\begin{aligned} A= & {} \sqrt{\left[ {\left( {\omega _j +\omega _r } \right) x_{j} -2{\dot{y}}}_{j}\right] ^2+\left[ \left( \omega _{j}+\omega _{r}\right) y_j+2{\dot{x}}_{j}\right] ^{2}},\\ B= & {} \sqrt{\left( {\omega _r X_r -2{\dot{Y}}_{r}} \right) ^{2}+\left( \omega _{r}Y_{r}+2{\dot{X}}_{r}\right) ^{2}},\\ \alpha _1= & {} \tan ^{-1}\left( \frac{\left( \omega _j +\omega _r \right) y_j +2{\dot{x}}_{j}}{(\omega _j+\omega _r)x_j-2{\dot{y}}_{j}}\right) \quad \hbox {and}\quad \alpha _2=\tan ^{{-1}}\left( \frac{\omega _{r}Y_{r}+2{\dot{X}}_{r}}{\omega _{r}X_{r}+2{\dot{Y}}_{r}}\right) . \end{aligned}$$

The inner and outer fluid film forces are obtained by integrating the fluid film pressure Eqs. (5) and (6) as:

$$\begin{aligned} \left\{ {{\begin{array}{l} {F_{xi}} \\ {F_{yi}} \\ \end{array} }} \right\}= & {} \int \limits _{{\alpha _{1}}}^{{\pi +\alpha _1}}\int \limits _{-\frac{L_1}{2}}^{\frac{L_1}{2}}\,P_i \cdot R_j \cdot \left\{ {{\begin{array}{l} {\cos \vartheta _i} \\ {\sin \vartheta _i} \\ \end{array}}}\right\} \mathrm{d}z\cdot \mathrm{d}\vartheta _i, \end{aligned}$$

(7)

$$\begin{aligned} \left\{ {{\begin{array}{l} {F_{xo} } \\ {F_{yo} } \\ \end{array} }} \right\}= & {} \int \limits _{{\alpha _{2}}}^{{\pi +\alpha _{2}}}\int \limits _{-\frac{L_2}{2}}^{\frac{L_2 }{2}} P_o \cdot R_{ro} \cdot \left\{ {{\begin{array}{l} {\cos \vartheta _0 } \\ {\sin \vartheta _0 } \\ \end{array} }} \right\} \mathrm{d}z\cdot \mathrm{d}\vartheta _0. \end{aligned}$$

(8)

After integrating over the axial length and re-arranging the terms, Eqs. (7)–(8) become:

$$\begin{aligned} \left\{ {{\begin{array}{ll} F_{xi} \\ F_{yi} \\ \end{array}}} \right\}= & {} -\frac{\mu _{i}\cdot A\cdot L_1^3 \cdot R_j }{4}\left[ {\cos \alpha _1 \cdot \left\{ {{\begin{array}{ll} {\frac{\partial ^{2}G_1 }{\partial x_j \cdot \partial y_j }} \\ {\frac{\partial ^{2}G_1 }{\partial y_j^2 }} \\ \end{array} }} \right\} -\sin \alpha _1 \cdot \left\{ {{\begin{array}{ll} {\frac{\partial ^{2}G_1 }{\partial x_j^2 }} \\ {\frac{\partial ^{2}G_1 }{\partial x_j \cdot \partial y_j }} \\ \end{array} }} \right\} } \right] , \end{aligned}$$

(9)

$$\begin{aligned} \left\{ {{\begin{array}{l} {F_{xo} } \\ {F_{yo} } \\ \end{array} }} \right\}= & {} -\frac{\mu _{o}\cdot B\cdot L_2^3 \cdot R_{ro} }{4}\left[ {\cos \alpha _2 \cdot \left\{ {{\begin{array}{l} {\frac{\partial ^{2}G_2 }{\partial X_r \cdot \partial Y_r }} \\ {\frac{\partial ^{2}G_2 }{\partial Y_r^2 }} \\ \end{array} }} \right\} -\sin \alpha _2 \cdot \left\{ {{\begin{array}{ll} {\frac{\partial ^{2}G_2 }{\partial X_r^2 }} \\ {\frac{\partial ^{2}G_2 }{\partial X_r \cdot \partial Y_r }} \\ \end{array} }} \right\} } \right] . \end{aligned}$$

(10)

Here,

$$\begin{aligned} G_1= & {} \int \limits _{\alpha _1 }^{\pi +\alpha _1 } \frac{d\vartheta _i }{h_i }=\left. {\frac{2\tanh ^{-1}\left[ {\frac{y_j -\left( {C_1 +x_j } \right) .\tan \left( {\frac{\vartheta _i }{2}} \right) }{\sqrt{-C_1^2 +x_j^2 +y_j^2 }}} \right] }{\sqrt{-C_1^2 +x_j^2 +y_j^2 }}} \right| _{\alpha _1 }^{\pi +\alpha _1 }, \end{aligned}$$

(11)

$$\begin{aligned} G_2= & {} \int \limits _{\alpha _2 }^{\pi +\alpha _2 } \frac{d\vartheta _o }{h_o}=\left. {\frac{2 \tanh ^{-1}\left[ {\frac{Y_r -\left( {C_2 +X_r } \right) \cdot \tan \left( {\frac{\vartheta _o }{2}} \right) }{\sqrt{-C_2^2 +X_r^2 +Y_r^2 }}} \right] }{\sqrt{-C_2^2 +X_r^2 +Y_r^2 }}} \right| _{\alpha _2 }^{\pi +\alpha _2 }. \end{aligned}$$

(12)

Then,

$$\begin{aligned} G_1= & {} \frac{2}{\sqrt{C_1^2 -x_j^2 -y_j^2 }}\cdot \left[ {\frac{\pi }{2}+\tan ^{-1}\left( {\frac{y_j \cdot \cos \alpha _1 -x_j \cdot \sin \alpha _1 }{\sqrt{C_1^2 -x_j^2 -y_j^2 }}} \right) } \right] , \end{aligned}$$

(13)

$$\begin{aligned} G_2= & {} \frac{2}{\sqrt{C_2^2 -X_r^2 -Y_r^2 }}\cdot \left[ {\frac{\pi }{2}+\tan ^{-1}\left( {\frac{Y_r \cdot \cos \alpha _2 -X_r \cdot \sin \alpha _2 }{\sqrt{C_2^2 -X_r^2 -Y_r^2 }}} \right) } \right] . \end{aligned}$$

(14)

The expression for second derivative terms of $G_{1}$ and $G_{2}$ is shown in “Appendix A.”

The torque applied on the floating rings due to inner and outer fluid films is denoted by $\tau _\mathrm{i}$ and $\tau _\mathrm{o}$, respectively, and can be written as follows [3]:

$$\begin{aligned} \tau _\mathrm{i}= & {} 2\pi \frac{\mu _i R_{ri}^3 L_i \left( {\omega _j -\omega _r } \right) }{\sqrt{C_1^2 -x_j^2 -y_j^2 }}+\frac{\left( {x_j F_{yi} -y_j F_{xi} } \right) }{2},\end{aligned}$$

(15)

$$\begin{aligned} \tau _\mathrm{o}= & {} 2\pi \frac{\mu _o R_{ro}^3 L_o \omega _r }{\sqrt{C_2^2 -X_r^2 -Y_r^2 }}+\frac{\left( {X_r F_{yo} -Y_r F_{xo} } \right) }{2}. \end{aligned}$$

(16)

2.3 Newmark-$\beta$ Newton–Raphson techniques

The governing differential equation of turbocharger rotor shaft (i.e. Eq. (1)) and floating ring bearings (i.e. Eq. (2)) is combined to form the equation of system for the turbocharger system. The formed nonlinear governing differential equations of motion of system are solved to compute the dynamic response using implicit Newmark-$\upbeta$ time integration scheme with Newton–Raphson method. The combined equation is shown as:

$$\begin{aligned} \left[ {{\begin{array}{ll} {[{M_s}]}&{}\quad {0_{16*6} } \\ {0_{6*16} }&{} \quad {\left[ {m_r } \right] } \\ \end{array} }} \right] \left\{ {\ddot{q}} \right\} + \left[ {{\begin{array}{ll} {\left[ {\varOmega _j .G_s } \right] }&{}\quad {0_{16*6} } \\ {0_{6*16} }&{}\quad {0_{6*6} } \\ \end{array} }} \right] \left\{ {\dot{q}}\right\} +\left[ {{\begin{array}{ll} {\left[ {K_s } \right] }&{} \quad {0_{16*6} } \\ {0_{6*16} }&{}\quad {0_{6*6}} \\ \end{array} }} \right] \,\left\{ q\right\} =\left\{ R \right\} \end{aligned}$$

(17)

where $\{q\}^{T}=\left\{ {x_i \,y_i \,\theta _{xi} \,\theta _{yi} \ldots \,X_{rk} \,Y_{rk} \,\theta _{rk} \ldots } \right\} \quad \hbox {and}\,i=1,\ldots ,4;k=1,2$. And $\{R\}$ is combined force vector.

Equation (17) can be written in the generalized form at time $t+\Delta t$,

$$\begin{aligned}{}[M]_{t+\Delta t} \left\{ \ddot{q} \right\} _{t+\Delta t} + [ C ]_{t+\Delta t} \left\{ {\dot{q}} \right\} _{t+\Delta t} +[K ]_{t+\Delta t} \{ q \}_{t+\Delta t} =\{ R\}_{t+\Delta t}. \end{aligned}$$

(18)

To solve the above equation, the implicit average acceleration Newmark-$\upbeta$ numerical integration technique is used. This technique is highly accurate and unconditionally stable [20]. The basic equations that have been used for this scheme are:

$$\begin{aligned} \{{\dot{q}}\}_{t+\Delta t}= & {} \{{\dot{q}}\}_t +[{({1-\gamma })\{{\ddot{q}}\}_{t} +\gamma \,\{{\ddot{q}}\} _{t+\Delta t}} ]\Delta t, \end{aligned}$$

(19a)

$$\begin{aligned} \{q\}_{t+\Delta t}= & {} \{q\}_t +\{{\dot{q}}\}_t \Delta t+[(1/2-\beta )\{{\ddot{q}}\}_t +\beta \{{\ddot{q}}\}_{t+\Delta t} ]\Delta t^{2}. \end{aligned}$$

(19b)

Fig. 3

A flowchart for dynamic response of turbocharger FRB system

The parameters $\beta$ and $\upgamma$ are taken equal to 1/4 and 1/2, respectively. Substituting Eqs. (19a) and (19b) into Eq. (18) yields the following equation:

$$\begin{aligned} ( {[ K ]+a_0 [ M ]+a_1 [ C ]} )\{ q \}_{t+\Delta t} =\{ R \}_{t+\Delta t} +\{ F \}_{t}. \end{aligned}$$

(20)

Here, $\{F\}_t =\{{[M]({a_{0} \{ q \}_t +a_2 \{ {\dot{q}} \}_t +a_3 \{ {\ddot{q}}\}_t} )} \}+\{ {[ C ]( {a_1 \{ q \}_t +a_4 \{ {\dot{q}} \}_t +a_5 \{ {\ddot{q}}\}_t} )}\}$.

And, $[ K ]+a_0 [ M ]+a_1 [C]=\widehat{{K}}$ is effective stiffness matrix.

To apply the Newton–Raphson technique, Eq. (20) is written in the form of implicit function.

$$\begin{aligned} g(q^{*})=0=\{ R \}_{t+\Delta t} +\{ F \}_t -\widehat{{K}}\{q\}_{t+\Delta t}. \end{aligned}$$

(21)

Expanding Eq. (21) by Taylor’s series and the solution for ith iteration at any time step $t+\Delta t$ is given by

$$\begin{aligned} \Delta q^{i}=N^{-1}\cdot Q \end{aligned}$$

(22)

where $N=\left( {\frac{\partial g}{\partial q}} \right) _{i-1}^{t+\Delta t}$ and $Q=-\{ R \}_{t+\Delta t}^{i-1} -\{F\}_t +{\widehat{K}}\{q\}_{t+\Delta t}^{i-1}$

The constants used in the above integration method are defined as follows:

$$\begin{aligned} a_0 =\frac{1}{\beta \Delta t^{2}}\quad , \quad a_1 =\frac{\gamma }{\beta \cdot \Delta t}, \quad a_2 =\frac{1}{\beta \cdot \Delta t}, \quad a_3 =\left( {\frac{1}{2\beta }} \right) -1, \quad a_4 =\left( {\frac{\gamma }{\beta }} \right) -1, \quad a_5 =\left( {\frac{\Delta t}{2}} \right) . \end{aligned}$$

A brief flowchart of the algorithm to compute the dynamic response of turbocharger rotor-bearing system, which combines implicit Newmark-$\upbeta$ integration scheme with Newton–Raphson convergence technique, is shown in Fig. 3.

3 Results and discussion

In this section, a new $\hbox {MATLAB}^{{\circledR }}$ code has been developed for the nonlinear dynamic analysis of the turbocharger FRB system. The equations of motion of the system have been solved using the implicit Newmark-$\upbeta$ numerical integration scheme along with Newton–Raphson convergence method, and nonlinear dynamic response is computed. The specifications and dimensions of the system are taken from the literature [16] and are listed in Table 1. Relative error tolerance of 1E-12 has been taken to perform the simulations. Simulation has been performed at different rotor speeds using an appropriate set of initial conditions and considering zero cavitation pressure. The dynamic response is computed for the first 1000 rotations, and the steady state is found to be present for last 200 rotations. So the nonlinear response data of both journal centres and ring centres are collected for the last 200 rotations, and orbital and Poincare maps are plotted to show the nonlinear dynamic behaviour of the system.

3.1 Validation

To validate the FE modelling, simulation technique and $\hbox {MATLAB}^{{\circledR }}$ code presented in the current paper, the orbital plots of journal centres for a perfectly balanced turbocharger rotor system have been plotted at different speeds. The results are then compared with the results available in the literature, as shown in Fig. 4. A satisfactory similarity is found between the results that validate the mathematical formulation and $\hbox {MATLAB}^{{\circledR }}$ code presented in this study.

Fig. 4

Comparison of results

3.2 Effect of in-phase rotating unbalance at both ends and engine excitations

In the present paper, the simulations are performed for a turbocharger system having rotating in-phase unbalance on both discs and also encountered with engine excitations. This unbalance may be occurred due to manufacturing errors, due to adhesion of oil/dust on turbine or due to erosion of the impeller part. The rotating unbalance in automotive turbochargers is observed in the range of 0.1 to 1 gm-mm. In the present paper, an in-phase unbalance of 0.236 and 0.652 gm-mm is taken on compressor disc and turbine disc, respectively. Due to high running speed of the turbocharger rotor shaft, the inertia force produced due to unbalance becomes very high.

Fig. 5

Orbits and Poincare maps for journal and ring centre at low rotor speeds

In practice, the turbocharger rotor system has rigid housing made up of heat-resistant cast steel which is mounted on internal combustion engines. The vibrations transmitted from engine to turbocharger are modelled as a case of base excitations. These base excitations affect the turbocharger rotor responses significantly. In actual working condition, engine induces the vibrations in translational as well as rotational directions. But for simplicity, only translational vibrations perpendicular to the axis of shaft, i.e. X- and Y-directions, are considered in this research work. In case of engine-induced vibrations, the outer and inner fluid film thickness both will be affected. Based on the experimental results available in the literature, the base excitation of harmonic nature is a function of engine rotational speed $\omega _e$ which is given as follows [27, 28]:

$$\begin{aligned} X_e =( {\cos ( {\omega _e t} )+2\cos ( {2\omega _e t} )+\cos ( {3\omega _e t} )+3\hbox {cos}( {4\omega _e t} )} )\times 10^{-6}\,\hbox {m}\\ Y_e =( {3\sin ( {\omega _e t} )+6\sin ( {2\omega _e t} )+5\sin ( {3\omega _e t} )+2\hbox {sin}( {4\omega _e t} )} )\times 10^{-6}\,\hbox {m} \end{aligned}$$

where $(X_e ,Y_e)$ represent the displacement components of base excitation in x- and y-directions, respectively. It should be noted that the displacement amplitude component of $2\omega _e$ and $4\omega _e$ dominates in x-direction, whereas in y-direction, the amplitude of $2\omega _e$ and $3\omega _e$ dominates. The crank rotating speed is taken to be 3600 rpm. In actual working conditions, turbocharger rotor speed will depend on the engine rotating speed, and the amplitude of excitation parameters will vary according to the engine rotating speed. So, to completely understand the behaviour of turbocharger rotor, floating ring bearings, and compressor end, as well as turbine end, simulation has been performed at varying turbocharger rotor speeds. The response of turbocharger rotor and floating ring relative to housing is studied by orbital plots. The Poincare maps have also been plotted to understand nonlinear characteristics such as chaotic and quasi-periodic for the turbocharger system.

3.2.1 Dynamic analysis of turbocharger system at low rotor speeds

The orbit plots at 6000 rpm, as shown in Fig. 5i, for journal and floating ring centres at node two are close to the centre of bearing housing, whereas at node three, motion of both journal and ring centre relative to housing is in the fourth quadrant. The points distributed in Poincare maps at such speed appear to be in form of different rings. As the speed of rotor increased, the shape of orbit plots continuously changed and points in Poincare maps distributed irregularly, which shows the chaotic behaviour of turbocharger system as shown in Fig. 5ii. The radius of orbits increases with increased speed.

Fig. 6

Frequency spectrum of journal and ring at FRB1 and FRB2 at low turbocharger rotor speed

The FFT plots for the x-directional displacement of both journal and ring centre for speed range of 6000 and 12,000 rpm are shown in Fig. 6. The frequency spectrum shows the sub-synchronous vibrations of high amplitudes which occur due to the presence of oil whirl phenomenon. However, these high amplitude vibrations are synchronous to the engine speed (i.e. 3600 rpm). The amplitude of these vibrations increases with an increase in rotor speed and always has higher-amplitude vibrations for both journal and ring centre at node three as compared to node 2.

Figure 7 shows the orbits and Poincare maps of compressor and turbine ends at rotor speeds 6000 and 12,000 rpm. At rotor speed of 6000 rpm, the compressor end centre revolves in second quadrant of inertia frame, whereas the turbine end revolves in the fourth quadrant. The Poincare maps for both ends are formed in the shape of different rings. Upon increasing the rotor speed at 12,000 rpm, the orbital shapes became more complex, and the Poincare maps have irregular distribution of points that represents the chaotic behaviour of the turbocharger system.

Fig. 7

Orbits and Poincare maps for compressor and turbine ends at low rotor speeds

3.2.2 Dynamic analysis of turbocharger system at medium rotor speeds

At TC rotor speed of 24k, the orbit shapes altered dramatically, as shown in Fig. 8i, and turbocharger rotor run in complex chaotic state. As the speed of rotor increases up to 6000 rpm, the diameter of journal and ring centre orbit at FRB2 becomes large than the orbit of journal and ring centre at FRB1 that revolves in the form of circular orbits, as shown in Fig. 8ii. The oil whirl/whip phenomena play a significant role in motion of journal and ring centre for both bearing nodes, but the system remains in chaotic state as explained by Poincare maps.

Figure 9 shows the widespread components of the frequency spectrum of journal and ring centre for both bearing nodes at rotor speeds of 24,000 and 60,000 rpm. At 24,000 rpm rotor speed, the amplitude of 0.12$\times$ sub-synchronous vibrations is high, compared to other sub-synchronous vibrations. The sub-synchronous vibrations occur at FRB2 and always have high amplitude than vibrations occurring at FRB1 node. This can happen due to the presence of large rotating unbalance force on turbine end. At increased speed of 60,000 rpm, journal centre at FRB1 node experiences sub-synchronous vibrations at 0.02$\times$ and 0.12$\times$ of rotor frequency, and for FRB2 node, the sub-synchronous vibrations occur at 0.12$\times$ rotor frequency, as shown in Fig. 9ii.

Fig. 8

Orbits and Poincare maps for journal and ring centre at medium rotor speeds

The orbital and Poincare maps of compressor and turbine end for rotor speeds 24,000 and 60,000 rpm, as shown in Fig. 10. At 24,000 rpm of rotor speed, both compressor and turbine disc centres revolve intricately and the Poincare maps show chaotic behaviour of system, as shown in Fig. 10i. As the speed of turbocharger increases up to 60,000 rpm, the compressor end orbit becomes in shape of torus and turbine end orbits in the form of ring shape, but the system remains in chaotic state, as shown in Fig. 10ii.

Fig. 9

Frequency spectrum of journal and ring at FRB1 and FRB2 at medium turbocharger rotor speeds

Fig. 10

Orbits and Poincare maps for compressor and turbine ends at medium rotor speeds

3.2.3 Dynamic analysis of turbocharger system at high rotor speeds

At rotor speed of 90,000 rpm, the orbit plot for journal and ring centre relative to housing at node 2 shows complex shape, whereas at node 3, both journal and ring centre almost revolve in the form of circular orbits as shown in Fig. 11i. The Poincare maps at speed 90,000 rpm represent the chaotic behaviour of the journal and floating ring centres for both bearing nodes. Upon increasing the rotor speeds (i.e. 180,000 rpm), the orbital trajectory for journal and ring centre for both bearing nodes tends to form almost circular shape as shown in Fig. 11ii, but the Poincare maps of journal and ring at node 2 show chaotic behaviour and the Poincare maps for node 3 represent the transformation of chaotic to quasi-periodic state.

Fig. 11

Orbits and Poincare maps for journal and ring centre at high rotor speeds

Figure 12 shows the frequency spectrum of the journal and ring centre responses for both bearing nodes at rotor speeds of 90000 and 180,000 rpm. At 90,000 rpm speed, there are several peaks of sub-synchronous vibrations for FRB1, as shown in Fig. 12i, whereas for FRB2, there is only one peak present which has amplitude, four times to the maximum amplitude obtained for FRB1. Upon increasing the rotor speed up to 180,000 rpm, the magnitude of sub-synchronous vibrations decreases, and the range of the spectrum is also becoming thin, as shown in Fig. 12ii. This happens because at higher speeds, the inertia forces generated due to unbalance dominate over the engine excitations and bearing forces and diminish the sub-synchronous vibrations produce due engine excitations.

Fig. 12

The frequency spectrum of journal and ring at FRB1 and FRB2 at high turbocharger rotor speed

Fig. 13

Orbits and Poincare maps for compressor and turbine ends at high rotor speeds

The orbit and Poincare maps for compressor and turbine ends at high rotor speeds are shown in Fig. 13. At 90,000 rpm, both compressor and turbine disc centres revolve in circular shapes, but the Poincare maps show the system will be in chaotic state, as shown in Fig. 13i. Upon increasing the speed up to 180,000 rpm, the compressor disc node remains in chaotic state, whereas turbine end shifts to a quasi-periodic state of motion, as shown in Fig. 13ii.

The conclusion drawn from Fig. 14 is that the behaviour of turbocharger rotor ends is greatly affected by engine-induced vibrations at low speeds, and upon increasing the speed of TC rotor, the sub-synchronous vibrations suppress the engine-induced vibrations, whereas, at higher speeds (i.e. 148,000 and 180,000 rpm), the forces generated due to unbalance dominate the bearing forces and engine excitations. Therefore, the effect of engine excitations should not be neglected in the testing phase as well as the actual working state.

Fig. 14

Displacement versus time plot for rotor ends at different speeds for turbocharger rotor-bearing system

4 Conclusions

The governing differential equation of motion for turbocharger flexible rotor system is developed by finite element modelling using Timoshenko beam elements. The expression for nonlinear fluid film forces generated in floating ring bearings is derived in the dimensional form directly, using short bearing approximation and half Sommerfeld condition. Thus, there is no requirement to convert the pressure and other parameters from dimensional to non-dimensional form and then from non-dimensional to dimensional form. The equation of motion for rotor and floating ring bearings is combined and formed a single set of governing differential equations. For solving the differential equations of motion, a new $\hbox {MATLAB}^{{\circledR }}$ code is constructed using implicit Newmark-$\upbeta$ integration scheme along with Newton–Raphson convergence method, and dynamic response is computed. The effect of rotating unbalance and engine excitation on the behaviour of the turbocharger system is analysed by orbital plots, Poincare maps and frequency spectrum plots. At low rotor speeds, the centres of journal and rings for both bearing nodes follow a complex trajectory, and the system shows chaotic behaviour. The frequency spectrum shows a wide range of sub-synchronous vibrations. Upon increasing the rotor speed, the phenomenon of oil whirl comes into play, and the amplitude of sub-synchronous vibrations changes continuously with respect to change in rotor speed. But at higher turbocharger rotor speeds, the inertia force produced due to rotating unbalance dominates over the nonlinear bearing forces and engine excitations and thus diminishes the sub-synchronous vibrations. The journal and ring centre at FRB1 exhibits chaotic behaviour, whereas the journal and ring centre at FRB2 shows a transition of chaotic to quasi-periodic state of motion. Thus, rotating unbalance and engine excitations play a very significant role in working turbochargers.

Appendix A

For the inner fluid film,

$$\begin{aligned}&\frac{\partial ^{2}G_1 }{\partial x_j \cdot \partial y_j }=\frac{3\cdot x_j \cdot y_j \cdot G_1 }{A_1^2 }+\frac{4\cdot x_j \cdot \cos \alpha _1 }{A_1 \cdot A_4 }+\frac{6\cdot x_j \cdot y_j \cdot A_2 }{A_1^2 \cdot A_4 }-\frac{4\cdot \sin ^{2}\alpha _1 \cdot A_3 }{A_4^2 }+\frac{4\cdot x_j \cdot \sin \alpha _1 \cdot A_2 \cdot A_3 }{A_1 \cdot A_4^2 }\\&\frac{\partial ^{2}G_1 }{\partial x_j^2 }=\frac{G_1 }{A_1 }+\frac{3\cdot x_j^2 \cdot G_1 }{A_1^2 }+\frac{A_5 }{A_1 \cdot A_4 }+\frac{6\cdot x_j^2 \cdot A_2 }{A_1^2 \cdot A_4 }-\frac{4\cdot \sin \alpha _1 \cdot \cos \alpha _1 \cdot A_3 }{A_4^2 }+\frac{4\cdot x_j \cdot \cos \alpha _1 \cdot A_2 \cdot A_3 }{A_1 \cdot A_4^2 }\\&\frac{\partial ^{2}G_1 }{\partial y_j^2 }=\frac{G_1 }{A_1 }+\frac{3\cdot y_j^2 \cdot G_1 }{A_1^2 }+\frac{A_6 }{A_1 \cdot A_4 }+\frac{6\cdot y_j^2 \cdot A_2 }{A_1^2 \cdot A_4 }-\frac{4\cdot \sin \alpha _1 \cdot \cos \alpha _1 \cdot A_3 }{A_4^2 }+\frac{4\cdot y_j \cdot \sin \alpha _1 \cdot A_2 \cdot A_3 }{A_1 \cdot A_4^2 }. \end{aligned}$$

For the outer fluid film,

$$\begin{aligned}&\frac{\partial ^{2}G_2 }{\partial X_r \cdot \partial Y_r }=\frac{3\cdot X_r \cdot Y_r \cdot G_2 }{B_1^2 }+\frac{4\cdot X_r \cdot \cos \alpha _2 }{B_1 \cdot B_4 }+\frac{6\cdot X_r \cdot Y_r \cdot B_2 }{B_1^2 \cdot B_4 }-\frac{4\cdot \sin ^{2}\alpha _2 \cdot B_3 }{B_4^2 }+\frac{4\cdot X_r \cdot \sin \alpha _2 \cdot B_2 \cdot B_3 }{B_1 \cdot B_4^2 }\\&\frac{\partial ^{2}G_2 }{\partial X_r^2 }=\frac{G_2 }{B_1 }+\frac{3\cdot X_r^2 \cdot G_2 }{B_1^2 }+\frac{B_5 }{B_1 \cdot B_4 }+\frac{6\cdot X_r^2 \cdot B_2 }{B_1^2 \cdot B_4 }-\frac{4\cdot \sin \alpha _2 \cdot \cos \alpha _2 \cdot B_3 }{B_4^2 }+\frac{4\cdot X_r \cdot \cos \alpha _2 \cdot B_2 \cdot B_3 }{B_1 \cdot B_4^2 }\\&\frac{\partial ^{2}G_2 }{\partial Y_r^2 }=\frac{G_2 }{B_1 }+\frac{3\cdot Y_r^2 \cdot G_2 }{B_1^2 }+\frac{B_6 }{B_1 \cdot B_4 }+\frac{6\cdot Y_r^2 \cdot B_2 }{B_1^2 \cdot B_4 }-\frac{4\cdot \sin \alpha _2 \cdot \cos \alpha _2 \cdot B_3 }{B_4^2 }+\frac{4\cdot Y_r \cdot \sin \alpha _2 \cdot B_2 \cdot B_3 }{B_1 \cdot B_4^2 }. \end{aligned}$$

Here, $A_1 =C_1^2 -x_j^2 -y_j^2$

$$\begin{aligned} A_2= & {} y_j \cdot \cos \alpha _1 -x_j \cdot \sin \alpha _1,\\ A_3= & {} x_j \cdot \cos \alpha _1 +y_j \cdot \sin \alpha _1,\\ A_4= & {} C_1^2 -A_3^2,\\ A_5= & {} \left( {2\cdot y_j \cdot \cos \alpha _1 -6\cdot x_j \cdot \sin \alpha _1 } \right) ,\\ A_6= & {} \left( {6\cdot y_j \cdot \cos \alpha _1 -2\cdot x_j \cdot \sin \alpha _1 } \right) ,\\ B_1= & {} C_2^2 -X_r^2 -Y_r^2, \\ B_2= & {} Y_r \cdot \cos \alpha _2 -X_r \cdot \sin \alpha _2,\\ B_3= & {} X_r \cdot \cos \alpha _2 +Y_r \cdot \sin \alpha _2,\\ B_4= & {} C_2^2 -B_3^2,\\ B_5= & {} \left( {2\cdot Y_r \cdot \cos \alpha _2 -6\cdot X_r \cdot \sin \alpha _2 } \right) ,\\ B_6= & {} \left( {6\cdot Y_r \cdot \cos \alpha _2 -2\cdot X_r \cdot \sin \alpha _2 } \right) . \end{aligned}$$