Bending of beams with bisymmetrical cross sections under non-uniformly distributed load: analytical and numerical-FEM studies

Abstract

The paper is devoted to simply supported beams subjected to non-uniformly distributed loads. Shapes of bisymmetrical cross sections of the beams are expressed by special functions. The analytical model of the beams is formulated with consideration of the shear effect. A nonlinear hypothesis of deformation of a planar cross section of beams is assumed. The bending moment and the shear transverse force are formulated. Moreover, numerical-FEM models of the beams are developed. Deflections are calculated with the use of two methods for an exemplary beam family. The results of the studies are presented in tables.

1 Introduction

The problem of the shear effect occurring in homogeneous beams was described by Timoshenko in 1921. This effect has been considered in studies of the structures in further decades, until to-day. Wang et al. [17] presented a review of the theories that arose in the twentieth century with a view to explain the behaviour of the beams and plates with consideration of the shear effect. The works dealing with this subject have been supported only on the classical Euler–Bernoulli/Kirchhoff approach. Nevertheless, in deep beams and thick plates the effect of transverse shear strains is so meaningful, that the classical way gives no correct results. The authors proposed the shear deformation theories providing more accurate solutions.

Schardt [13] presented a general theory of thin-walled beam with open cross sections. The problem was solved with the use of deformation functions describing the bending, torsion and distortion of the beams. The differential equations derived based on the second-order generalized beam theory provided satisfactory solutions considering the coupling effects between various mode- and load cases.

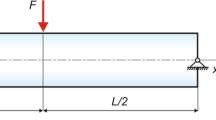
Hutchinson [4] considered the effects of shear deformation and rotary inertia on dynamic response of slender beams. These effects are modelled by the shear coefficients included in the Timoshenko beam theory. The author derived new formulae for these coefficients in the cases of various beam cross sections. Song et al. [16] dealt with analytical solutions of the static behaviour of an anisotropic composite I-beam subjected to a force applied to its free end. They used the theory of composite thin-walled beams considering two main coupling mechanisms. The authors demonstrated the effects of directional structure of the composite material and the transverse shear on static response of the beam. The thin-walled open-profile composite beams have been analysed by Jung and Lee [5]. The effects of elastic coupling, wall thickness, transverse shear and warping have been considered, using the Reissner’s energy functional to find the beam force–displacement relations. The static results of the composite I-beams have been validated based on finite element computation. Sapoutzakis and Mokos [12] developed a model of a plate stiffened by parallel beams, including the shear effect. The model takes into consideration the second-order effects. The plate is analysed based on Reissner’s theory. The problem of nonlinearly coupled plate and beams is solved with the use of iterative numerical methods. Several numerical examples of significant practical meaning are presented in the paper. Reddy [11] used the Eringen’s and von Kármán’s differential constitutive relationships of nonlinear strains in order to rewrite the theories of classical and shear deformation of beams and plates. The author derived the equations of equilibrium and developed a finite element model. The theoretical approach proposed in the paper enabled to obtain the finite element results and evaluate the effect of the geometric nonlinearity on the bending of beams and plates. Shi and Voyiadjis [14] presented a new beam theory using the sixth-order differential equilibrium equations with a view to analyse the shear deformable beams. Three classical beam bending problems have been solved with the use of the proposed theory, showing good agreement with the elasticity solutions, as opposed to the fourth-order Timoshenko beam theory giving worse results. Blaauwendraad [2] evaluated accuracy and applicability of the Haringx’s and Engesser’s theories for buckling prediction of structures. It turned out that the Engesser hypothesis gives larger critical buckling load and better predicts the sandwich behaviour, than the Haringx hypothesis. In conclusion, the Haringx’s approach should be avoided and, instead, the Engesser hypothesis is recommended in examining the stability of the structural members. Kim [6] developed a shear deformable beam element designed for analysis of thin-walled composite I-beams with doubly- and mono-symmetric cross sections. The equations and force–displacement relationships are formulated based on the principle of minimum total potential energy. The stiffness matrix of the element is formulated with consideration of the force–displacement relations. Accuracy and the effectiveness of the new beam element is estimated with the use of the ABAQUS shell elements and based on the solutions achieved by other researchers. Shi and Wang [15] made attempts to improve the third-order shear deformation theories of isotropic plates. The authors demonstrated that the proper displacement field should be consistent with the transverse shear strain energy, apart from the conditions on plate surfaces. This condition imposed on the assumed displacement fields agrees with Love’s criterion related to the strain energy, taking into account the transverse shear strain energy. The paper indicates that the various displacement fields using simple third-order shear deformations are identical, provided that consistence of the transverse shear strain energy is enforced. Rajagopal and Hodges [10] used the variational asymptotic method (VAM) in order to develop a beam theory considering a cross section being oblique to the beam reference line. Such a theory is more suitable for aeroelastic analysis of structures, enabling to find the 3D elasticity solutions of solid, prismatic, and cylindrical beams made of homogeneous, isotropic material. Greim et al. [3] proposed an original finite element suitable for modelling of the beams of more complex geometry. The new degrees of freedom of the element allow to consider the unit deflection shape at each node, thus enabling to avoid the use of volume elements that would be necessary to reflect the beam behaviour. Transformation of the unknowns reduces the number of the degrees of freedom and allows to solve the problem based on a 2D finite element mesh. Adámek [1] provided a discussion on possible application of classical Timoshenko beam theory, supplemented by the shear coefficient, to the problems of three-layered elastic beams of symmetrical structure. The research included three common types of the beams: a beam composed of two thick and stiff faces joint with a thin soft core, a soft-core sandwich beam and a sandwich beam with a core stiffer than the faces. It was demonstrated that the theory gives accurate results in the above cases; however in case of the soft-core sandwiches, the results are questionable. Magnucki and Lewinski [7] focused on an analytical model of an I-beam based on the sandwich beam theory, with consideration of the shear effect. A nonlinear hypothesis of the deformation of the beam cross section allowed to determine the beam displacements and strains. The principle of stationarity of the total potential energy served as a basis for formulation of the governing differential equations of the beam. The analytical solution was positively verified by FEM numerical computation. Magnucki et al. [8] dealt with the problem of the bending and free vibration of porous beams, taking into account the shear effect. Mechanical properties of the beam varied in the thickness direction, remaining symmetrical with respect to the neutral axis. Variability of the material properties was controlled by a specific function allowing to model the homogeneous, nonlinear variable and sandwich structures. The analytical results were verified by similar FEM models. Magnucki [9] considered symmetrical simply supported sandwich beams and I-beams subjected to three-point bending or uniformly distributed load. The principle of stationarity of the total potential energy allowed to formulate the differential equations of the beam equilibrium. The system of the above-mentioned equations was solved for exemplary beams taking into account the shear effect. The subject of the study are simply supported beams of length L with bisymmetrical cross section carrying the non-uniformly distributed load (Fig. 1). The beam is situated in the Cartesian coordinate system xyz.

Fig. 1

Scheme of the beam with the non-uniformly distributed load

The intensity of the non-uniformly distributed load is formulated in the following form

$$\begin{aligned} q\left( x \right) =\frac{k_F }{2\tan \mathrm{h} \left( {{k_F }/2} \right) }\frac{1}{\cos \mathrm{h} ^{2}\left[ {k_F \left( {\xi -\frac{1}{2}} \right) } \right] }\frac{F}{L}, \end{aligned}$$

(1)

where $k_{F}$—dimensionless parameter, $\xi =x/L$—dimensionless coordinate ($0\le \xi \le 1$).

The total transverse load

$$\begin{aligned} F=L\mathop {\int }\limits _0^1 {q\left( \xi \right) } \mathrm{d}\xi . \end{aligned}$$

(2)

The examples of various load distributions corresponding to selected $k_{F}$ values are shown in Fig. 4.

What distinguishes the present paper as compared to the works of other authors lies in generalization of the beam load distribution, achieved by means of a function developed for this purpose. Moreover, the novelty of the presented approach consists in formulation of an original analytical function allowing for free shaping of the beam cross section.

2 Analytical model and calculations

The bisymmetrical cross section of depth h and maximum width b of the considered beams is shown in Fig. 2.

The width of the cross section symmetrically varies in the depth direction as follows

$$\begin{aligned} b\left( y \right) =bf_b \left( \eta \right) , \end{aligned}$$

(3)

where $f_b \left( \eta \right) =\beta _0 +\left( {1-\beta _0 } \right) \left( {6\eta ^{2}-32\eta ^{6}} \right) ^{k_c }$—dimensionless function, $\beta _0 =\frac{b_0 }{b}$—parameter, $\eta =\frac{y}{h}$—dimensionless coordinate ($-\frac{1}{2}\le \eta \le \frac{1}{2})$, $k_{c}$—exponent (real number).

Fig. 2

Scheme of a bisymmetrical cross section of the beams

Values of the parameter $\beta _{0}$ and $k_{c}$ exponent are decisive for the shape of the cross section (Fig. 2) and are assumed for selected exemplary beam cross sections.

A planar cross section (a straight normal line) before the bending is deformed into a curve after bending of the beam (Fig. 3).

Fig. 3

Scheme of the deformed planar cross section after bending of the beam

Based on the above scheme, the hypothesis of the displacement in the x-direction is formulated in the following form

$$\begin{aligned} u\left( {x,y} \right) =-h\left[ {\eta \frac{\mathrm{d}v}{\mathrm{d}x}-f_d \left( \eta \right) \psi \left( x \right) } \right] , \end{aligned}$$

(4)

where $f_d \left( \eta \right) =\frac{1}{1-\beta }\left[ {1-\beta \left( {3\eta -4\eta ^{3}} \right) ^{k_s }} \right] \left( {3\eta -4\eta ^{3}} \right) , \psi \left( x \right) =\frac{u_1 \left( x \right) }{h}$—dimensionless functions, $\beta =\frac{1}{1+k_s }$—parameter, $k_{s}$—even exponent ($k_{s}=2, 4, \ldots$), v(x)—deflection.

The $k_{s}$ value is calculated based on maximization of the shear effect of the bent beam (14).

This polynomial hypothesis is similar to the trigonometric hypothesis presented by Magnucki et al. [8] and Magnucki [9].

The strains

$$\begin{aligned} \varepsilon _x \left( {x,y} \right) =\frac{\partial u}{\partial x}=-h\left[ {\eta \frac{\mathrm{d}^{2}v}{\mathrm{d}x^{2}}-f_d \left( \eta \right) \frac{\mathrm{d}\psi }{\mathrm{d}x}} \right] , \quad \gamma _{xy} \left( {x,y} \right) =\frac{\partial u}{\partial y}+\frac{\mathrm{d}v}{\mathrm{d}x}=\frac{\mathrm{d}f_d }{\mathrm{d}\eta }\psi \left( x \right) , \end{aligned}$$

(5)

where

$$\begin{aligned} \frac{\mathrm{d}f_d }{\mathrm{d}\eta }=\frac{3}{1-\beta }\left[ {1-\left( {3\eta -4\eta ^{3}} \right) ^{k_s }} \right] \left( {1-4\eta ^{2}} \right) . \end{aligned}$$

Taking into account the Hooke’s law, the bending moment and transverse shear force take the following form

$$\begin{aligned} M_b \left( x \right) =E\mathop {\int }\limits _A {y\varepsilon _x \left( {x,y} \right) \mathrm{d}A} , \quad T\left( x \right) =\frac{E}{2\left( {1+\nu } \right) }\mathop {\int }\limits _A {\gamma _{xy} \left( {x,y} \right) } \mathrm{d}A. \end{aligned}$$

(6)

Substitution of the expressions (5) into these equations and simple transformation provide

$$\begin{aligned}&{\tilde{J}}_z \frac{\mathrm{d}^{2}v}{\mathrm{d}x^{2}}-C_{v\psi } \frac{\mathrm{d}\psi }{\mathrm{d}x}=-\frac{M_b \left( x \right) }{Ebh^{3}}, \end{aligned}$$

(7)

$$\begin{aligned}&\psi \left( x \right) =2\frac{1+\nu }{C_\psi }\frac{T\left( x \right) }{Ebh}, \end{aligned}$$

(8)

where ${\tilde{J}}_z =\mathop {\int }\limits _{-1/2}^{1/2} {\eta ^{2}f_b \left( \eta \right) } \mathrm{d}\eta$—dimensionless inertia moment of the cross section, $C_{v\psi } =\mathop {\int }\limits _{-1/2}^{1/2} {\eta f_b } \left( \eta \right) f_d \left( \eta \right) \mathrm{d}\eta , C_\psi =\mathop {\int }\limits _{-1/2}^{1/2} {f_b \left( \eta \right) } \frac{\mathrm{d}f_d }{\mathrm{d}\eta }\mathrm{d}\eta$—dimensionless coefficients.

Taking into account the intensity of the non-uniformly distributed load (1) and the basic relations for beams $q\left( x \right) ={\mathrm{d}T}/{\mathrm{d}x}$, $T\left( x \right) ={\mathrm{d}M_b }/{\mathrm{d}x}$, the transverse shear force and bending moment read:

$$\begin{aligned} T\left( x \right)= & {} -\frac{1}{2\tan \mathrm{h} \left( {{k_F }/2} \right) }\tan \mathrm{h} \left[ {k_F \left( {\xi -\frac{1}{2}} \right) } \right] F, \end{aligned}$$

(9)

$$\begin{aligned} M_b \left( x \right)= & {} \frac{1}{2k_F \tan \mathrm{h} \left( {{k_F }/2} \right) }\ln \frac{\cos \mathrm{h} \left( {{k_F }/2} \right) }{\cos \mathrm{h} \left[ {k_F \left( {\xi -\frac{1}{2}} \right) } \right] }FL. \end{aligned}$$

(10)

Equation (7), after integration and substitution of the expression (8), takes the following form

$$\begin{aligned} {\tilde{J}}_z \frac{\mathrm{d}v}{\mathrm{d}x}=C_1 +2\left( {1+\nu } \right) \frac{C_{v\psi } }{C_\psi }\frac{T\left( x \right) }{Ebh}-\frac{1}{Ebh^{3}}\mathop {\int }\limits {M_b \left( x \right) } \mathrm{d}x. \end{aligned}$$

(11)

The condition $\left. {{\mathrm{d}v}/{\mathrm{d}x}} \right| _{L/2} =0$ provides the following expression for the integration constant $C_{1}$

$$\begin{aligned} C_1 =\frac{J_1 }{2k_F \tan \mathrm{h} \left( {{k_F }/2} \right) }\frac{F\lambda ^{2}}{Ebh}, \end{aligned}$$

(12)

where $J_1 =\mathop {\int }\limits _0^{1/2} {\ln \frac{\cos \mathrm{h} \left( {{k_F }/2} \right) }{\cos \mathrm{h} \left[ {k_F \left( {\xi -\frac{1}{2}} \right) } \right] }} \mathrm{d}\xi , \lambda =\frac{L}{h}$—relative length of the beam.

Fig. 4

Scheme of the non-uniformly distributed load, the expression (1)

Fig. 5

Cross sections of the beam family

Integration of Eq. (11) gives

$$\begin{aligned} {\tilde{J}}_z v\left( x \right) =C_2 +C_1 x+2\left( {1+\nu } \right) \frac{C_{v\psi } }{C_\psi }\frac{M_b \left( x \right) }{Ebh}-\frac{1}{Ebh^{3}}\int {\int {M_b \left( x \right) } } \mathrm{d}x^{2}. \end{aligned}$$

(13)

The condition $v\left( 0 \right) =0$ zeroes the integration constant $C_2$ ($C_2 =0)$. Therefore, the maximum relative deflection of the beam reads

$$\begin{aligned} {\tilde{v}}_{\max }^{\left( {\mathrm{Analyt}} \right) } =\frac{v\left( {L/2} \right) }{L}={\tilde{v}}_{\max }^{0\left( {\mathrm{Analyt}} \right) } \frac{F}{Ebh}, \end{aligned}$$

(14)

where ${\tilde{v}}_{\max }^{0\left( {\mathrm{Analyt}} \right) } =C_{v0} \left\{ {1+\frac{C_{vs} }{\lambda ^{2}}} \right\} \frac{\lambda ^{2}}{{\tilde{J}}_z }$—dimensionless coefficient of the maximum deflection, $C_{v0} =\frac{J_1 -2J_2 }{4k_F \tan \mathrm{h} \left( {{k_F }/2} \right) }$—deflection coefficient, $J_2 =\mathop {\int }\limits _0^{1/2} {\int {\ln \frac{\cos \mathrm{h} \left( {{k_F }/2} \right) }{\cos \mathrm{h} \left[ {k_F \left( {\xi -\frac{1}{2}} \right) } \right] }} } \mathrm{d}\xi ^{2}$, $C_{vs} =4\frac{1+\nu }{J_1 -2J_2 }\ln \left[ {\cos \mathrm{h} \left( {{k_F }/2} \right) } \right] \left\{ {\mathop {\max }\limits _{k_s } \left[ {\frac{C_{v\psi } }{C_\psi }} \right] } \right\}$—shear coefficient.

Exemplary calculations of the dimensionless coefficient of maximum deflection ${\tilde{v}}_{\max }^{0\left( {\mathrm{Analyt}} \right) }$, the deflection coefficient $C_{v0}$ and the shear coefficient $C_{vs}$ are carried out for a beam family with selected bisymmetrical cross sections. The following data are assumed: the main dimensions of the cross sections $h=100$ mm, $b=50$ mm, the material constants $E=200$ GPa, $\nu =0.3$ and the values of dimensionless parameter of the non-uniformly distributed load $k_{F}=1, 3, 5$. The patterns of the distributed load are shown in Fig. 4.

The minimum value of the relative length $\lambda =8$ is assumed. In case of smaller $\lambda$ values, the structure cannot be considered as a beam and becomes a 3D problem of the elasticity theory.

The shapes of the cross sections are shown in Fig. 5.

Example 1

The shape of the cross section CS-1 (Fig. 5) corresponds to the values of the parameter $\beta _0 =0.5$ and exponent $k_c =1$. The results of the calculations are specified in Tables 1, 2 and 3.

Table 1 Values of dimensionless coefficient of the maximum deflection for $k_{F}=1$ (1)

Table 2 Values of dimensionless coefficient of the maximum deflection for $k_{F}=3$ (1)

Table 3 Values of dimensionless coefficient of the maximum deflection for $k_{F}=5$ (1)

Table 4 Values of dimensionless coefficient of the maximum deflection for $k_{F}=1$ (1)

Table 5 Values of dimensionless coefficient of the maximum deflection for $k_{F}=3$ (1)

Table 6 Values of dimensionless coefficient of the maximum deflection for $k_{F}=5$ (1)

The exponent of the function (4) after maximization amounts to $k_{s}=2$.

The values of the deflection and shear coefficients: $C_{v0} =0.013472$, $C_{vs} =4.0679$.

The values of the deflection and shear coefficients: $C_{v0} =0.015873$, $C_{vs} =4.1849$.

The values of the deflection and shear coefficients: $C_{v0} =0.017940$, $C_{vs} =4.3210$.

Example 2

The shape of the cross section CS-2 (Fig. 5) corresponds to the values of the parameter $\beta _0 =0.2$ and exponent $k_c =5$. The results of the calculations are specified in Tables 4, 5 and 6.

Maximization of the function (4) gives the exponent $k_{s}=2$.

The values of the deflection and shear coefficients: $C_{v0} =0.013472$, $C_{vs} =6.5732$.

The values of the deflection and shear coefficients: $C_{v0} =0.015873$, $C_{vs} =6.7623$.

The values of the deflection and shear coefficients: $C_{v0} =0.017940$, $C_{vs} =6.9822$.

Example 3

The shape of the cross section CS-3 (Fig. 5) corresponds to the values of the parameter $\beta _0 =0.09$ and exponent $k_c =8$. The results of the calculations are specified in Tables 7, 8 and 9.

Table 7 Values of dimensionless coefficient of the maximum deflection for $k_{F}=1$ (1)

Table 8 Values of dimensionless coefficient of the maximum deflection for $k_{F}=3$ (1)

Table 9 Values of dimensionless coefficient of the maximum deflection for $k_{F}=5$ (1)

Fig. 6

Diagram of the deflection coefficient $C_{v0} \left( {k_F } \right)$

The exponent of the function (4) after maximization is equal to $k_{s}=2$.

The values of the deflection and shear coefficient: $C_{v0} =0.013472$, $C_{vs} =10.5561$.

The values of the deflection and shear coefficients: $C_{v0} =0.015873$, $C_{vs} =10.8597$.

The values of the deflection and shear coefficients: $C_{v0} =0.017940$, $C_{vs} =11.2129$.

The value of the dimensionless parameter $k_F$ is decisive for the shape of the load distribution (1). This function describes the loads from uniformly distributed ($k_F \rightarrow 0$, then $C_{v0} =5/{384})$ to concentrated force—three-point bending ($k_F \rightarrow \infty$, then $C_{v0} =1/{48})$. The diagram of the deflection coefficient $C_{v0} \left( {k_F } \right)$ being a function of the dimensionless parameter $k_F$ is shown in Fig. 6.

3 Numerical-FEM models and calculations

The above results have been verified by numerical calculation performed with the use of finite element method. For purposes of the calculation, the dimensions $h=100$ mm and $b=50$ mm of the beam cross section have been assumed. Due to the symmetry, the FEM model included a quarter of the whole beam, i.e. a half of its length and width. In consequence, appropriate boundary conditions have been imposed.

Fig. 7

Model of the exemplary beam and a part of its finite element mesh

The model and mesh of the exemplary beam is shown in Fig. 7. The origin of the coordinate system is located in the beam middle. The longitudinal middle plane of the beam coincides with xy-plane and, as a result, the z-displacements are blocked on it. Similarly, the x-displacements are blocked on the yz-plane, being a central vertical plane of the beam symmetry. The beam end plane, located at L/2 distance from the origin of the coordinate system, is supported and, therefore, the y-displacements are blocked on it. The load q is applied to the upper surface of the beam.

Example of a part of the FEM mesh used for the computation is shown in Fig. 7. It is composed of 3D tetrahedral finite elements with four Jacobian points. The element dimensions vary according to the particular features of the beam cross-sectional shape.

In case of the shortest beam ($\lambda =8$), the mesh is composed of nearly 424,000 nodes and 280,000 elements.

4 Comparative analysis of deflections of the beams

The tables below provide comparison of the analytical $\tilde{v}_{\max }^{0\left( {\mathrm{Analyt}} \right) }$ and FEM numerical $\tilde{v}_{\max }^{0\left( \mathrm{FEM} \right) }$ results for subsequent beam cases.

The results for the cross section CS-1 ($k_c =1$ and $\beta _0 =0.5)$ are shown in Tables 10, 11 and 12.

The differences between analytical and numerical results are below 1% in this case.

Tables 13, 14 and 15 include the results for the cross section CS-2 ($k_c =5$, $\beta _0 =0.2)$.

Here the differences between analytical and numerical results do not exceed 1.3%.

In case of $k_c =8$ and $\beta _0 =0.09$ corresponding to the CS-3 cross section, the results are presented in Tables 16, 17 and 18.

Table 10 Comparison of maximum dimensionless deflections for $k_{F}=1$

Table 11 Comparison of maximum dimensionless deflections for $k_{F}=3$

Table 12 Comparison of maximum dimensionless deflections for $k_{F}=5$

Table 13 Comparison of maximum dimensionless deflections for $k_{F}=1$

Table 14 Comparison of maximum dimensionless deflections for $k_{F}=3$

Table 15 Comparison of maximum dimensionless deflections for $k_{F}=5$

Table 16 Comparison of maximum dimensionless deflections for $k_{F}=1$

Table 17 Comparison of maximum dimensionless deflections for $k_{F}=3$

Table 18 Comparison of maximum dimensionless deflections for $k_{F}=5$

This case is distinguished by the largest discrepancy between both series of the results, nevertheless, not exceeding 1.8%.

Good agreement between the analytical and FEM results confirms accurateness of the presented approach. The assumed hypothesis of deformation of the beam cross section may be acknowledged to be successful.

The above tables allow to conclude that compliance of both series of the results is very good.

5 Final remarks

The proposed approach to solving the problem of bending of the beams involves formulation of two original functions. One of them (1) allows to adjust characteristics of the load applied to the beam. According to the integer $k_{F}$ value, the load varies from uniform load intensity ($k_{F}=0$) to the force concentrated in the beam middle (three-point bending for $k_{F} \rightarrow \infty )$. The area under the loading force chart remains unchanged, which guarantees that total force is equal for any $k_{F}$ value.

The other function (3) controls the shape of the beam cross section. The cross section may take various shapes according to $\beta _{0}$ and $k_{c}$ values. These shapes change from rectangular profile up to typical I-beam. The value of the shear coefficient $C_{vs}$ increases for more slender shapes of the cross section, taking the highest level for an I-beam.

Such a unified approach enables to consider the whole families of the beams subjected to various load cases using the same formulae. The influence of the shear effect on the deflection of the bent beam decreases with growing beam length (14).

The FEM (SolidWorks) models have been developed with a view to check advisability of the proposed approach. Its correctness was satisfactorily verified and confirmed by the FEM computation.