1 Introduction

With the increase in exploitation level of oil and gas resource, drilling engineering faces more complex geological environment and the exploration efficiency is also decreasing [1, 2]. Due to the hardness difference of the rock formation, the friction torque constantly changes at the bottom of the drill string, especially in the drilling process of deep well or ultra-deep well [3, 4]. The drill string is tightened like clockwork and then released suddenly, which results in the generation of the stick–slip phenomenon. The stick–slip phenomenon not only reduces the rate of penetration (ROP) of the drilling system, but also influences the service life of the drill bit and the drill string, which bring in economic losses for the drilling engineering [5,6,7].

In order to solve the stick–slip problem in the drilling system [8], many studies have been conducted by worldwide scholars to research the influence factors of the stick–slip phenomenon, which include rotation speed of rotary disk and weight on bit (WOB) and so on [9,10,11]. The gravitational stiffening effect and the associated tension and compression fields within the drill string are taken into account when the stick–slip model is analyzed in Ref. [9]. The modified Cosserat rod element method is used to study the complex dynamic and geometric behavior of the drill string, which allows analysis of the main vibration modes, torsional, axial and lateral, and also their couplings in Ref. [10]. A statistic model is constructed for the stick–slip dynamics, and the system response was analyzed from a probabilistic viewpoint which is composed of a sequence of stick and slip modes in Ref. [11]. And another model has been constructed to solve the stick–slip phenomenon. The drill string model considered axial stiffness and viscous friction is researched [12, 13]. Two modeling approaches for stick–slip in drilling system is considered and a physical interpretation linked the two models are proposed to study their differences [14].

The existing researchers provide broad ideas to solve the stick–slip of drill string. However, the force condition of the drill string has not been changed fundamentally. Therefore, the stick–slip problem of drill string cannot be solved essentially and efficiently. Based on this, a new torsional oscillator is proposed which can achieve energy conversion. The hydraulic energy is transformed into the mechanical energy by utilizing drilling fluid. A circumferential torque is applied cyclically to the drill string system and the force condition of the system is changed in the drilling process. Thus the drill string stick–slip and the sticking phenomenon can be reduced. It is of significance to research the working mechanism and dynamic characteristics of the new torsional oscillator.

2 Structure design and work principle

The components of the torsional oscillator include upper case, upper joint, center tube, fork switch, hydraulic hammer, valve body, hammer block, ball bearing, lower cage and bit sub as shown in Fig. 1.

Fig. 1
figure 1

The structure of the torsional oscillator

Full size image

Drilling fluid flows into torsional oscillator from upper case to drive torsional oscillator work. If the cavity of hydraulic hammer is connected to center tube, the cavity channel will close between valve body and fork switch. Drilling fluid flows into the cavity of hydraulic hammer through the orifice of center tube. Thus, hydraulic hammer and fork switch are driven to motion clockwise together (Fig. 2a). When hydraulic hammer collides with valve body, hydraulic hammer stops motion and fork switch continues to rotate clockwise (Fig. 2b) until fork switch collides with hydraulic hammer (Fig. 2c). Then the channel between valve cavity and fork switch cavity opens, hydraulic hammer and fork switch together begin to generate counterclockwise motion (Fig. 2d). Similarly, when hydraulic hammer collides against with valve body, hydraulic hammer remains stationary and fork switch keeps counterclockwise movement (Fig. 2e) until colliding with hydraulic hammer (Fig. 2f). At this moment, a collide period has been completed and since then the previous movement will be repeated. A periodic and circumferential torque is applied to valve body which can provide high-frequency pulse torque for drill bit.

Fig. 2
figure 2

The motion diagram of the fork switch and the hydraulic hammer. a The clockwise motion of hydraulic hammer and fork switch together, b The single clockwise motion of fork switch, c The fork switch collides with hydraulic hammer, d The anticlockwise motion of hydraulic hammer and fork switch together, e The single anticlockwise motion of fork switch and f The fork switch collides against with hydraulic hammer

Full size image

3 Theory analysis models

3.1 Kinetic characteristic analysis

Based on the performance characteristics of the torsional oscillator and the requirements of the analysis model, related assumptions are proposed. Drilling fluid is steady and incompressible fluid. The pressure variation of drilling fluid is ignored approximately flowing past a single orifice of center tube. At the initial moment, the hydraulic hammer head is contacted to the cavity wall and hydraulic hammer is about to generate an anticlockwise motion. The change of the experiment resulted from the temperature is ignored.

Since there are orifices, when flowing into center tube, the drilling fluid meets the flow conservation law as \(q_{1}= q_{2}+ q_{3}\), Where \(q_{1}\) is the inlet flow of the torsional oscillator, \(q_{2}\) is the rest flow of drilling fluid flowed through a small orifice, \(q_{3}\) is the flow from the single orifice of center tube. The relationship among the inlet flow and velocity as well as the rest pressure and velocity flowing through a small orifice can be obtained as [15]

$$\begin{aligned} P_{2}-P_{1} =\kappa \rho \left( {u_{1}^{2} -u_{2}^{2}}\right) \end{aligned}$$
(1)

In which, \(P_{1}\) is the inlet pressure of the torsional oscillator, \(P_{2}\) is the rest pressure of drilling fluid flowing through the orifice, k is the correction coefficient, \(\rho \) is the density of drilling fluid, \(u_{1}\) is the inlet velocity, \(u_{2}\) is the velocity flowing through the orifice which meets \(u_2 =u_1 /\sqrt{1+0.03L_1 /0.08D_1 }\), wherein \( L_{1}\) is the orifice pitch of center tube, \(D_{1}\) is the inner diameter of center tube.

When a part of drilling fluid flows into the hydraulic hammer cavity from the orifice of center tube, the velocity of drilling fluid through the orifice can be written as

$$\begin{aligned} u_3 =0.62\sqrt{\left( {P_1 +P_2 -2P_3}\right) /\rho } \end{aligned}$$
(2)

where \(P_{3}\) is the pressure flowing out a single orifice. The relationship between the flow and the velocity of drilling fluid, flowing out from the orifice of center tub, can be written as \(u_{3}=q_{3}/A_{1}\). In which, \(A_{1}\) is the orifice area of the single orifice of center tube. Supposing that the flow of each orifice is approximately equal, the total flow of all orifices is satisfied with \( q_{4}=a{\cdot }q_{3}\), where a is the orifice number of center tube. Since there is symmetry in the torsional oscillator, the flow of drilling fluid, flowing into the unilateral cavity of hydraulic hammer, can be defined as \( q_{5}= q_{4}\)/2.

According to the Bernoulli’s equation, there is the relationship as

$$\begin{aligned} \frac{P_3 }{\gamma }+\frac{u_3 ^{2}}{2g}=\frac{P_4 }{\gamma }+\frac{u_6 ^{2}}{2g} \end{aligned}$$
(3)

where \(P_{4}\) is the internal pressure of the hydraulic hammer cavity, \(u_{6}\) is the velocity of drilling fluid in the hydraulic hammer cavity.

The total flow is equal when drilling fluid flows out from the orifice of center tube to the cavity of hydraulic hammer. That is \(q_{5}=q_{6}\), thus the flow of the hydraulic hammer cavity is defined as \(u_{6}=q_{6}/A_{2}\), where \(A_{2}\) is the cross-sectional area of hydraulic hammer.

When drilling fluid flows into the hydraulic hammer cavity, fork switch and hydraulic hammer are pushed to reciprocate. And it can be derived based on Newton’s second law as follows.

$$\begin{aligned} P_4 L_3 \left( {r_3 ^{2}-r_2 ^{2}}\right) =\left( J_1 +J_2\right) \frac{\hbox {d}^{2}\theta _1 }{\mathrm{d}t^{2}} \end{aligned}$$
(4)

where \(r_{3}\) is the outer diameter of hydraulic hammer, \(r_{2}\) is the inner diameter of hydraulic hammer, \(J_{1}\) is the moment of inertia of fork switch, \(J_{2}\) is the moment of inertia of hydraulic hammer, \(L_{3}\) is the hammerhead length of hydraulic hammer, \(\theta \)\(_{1}\) is the rotation angle of hydraulic hammer. In the initial moment, the rotation angle meets \(\theta _1 \left. {\left( t \right) } \right| _{t=0} =0\) and \(\left. {\frac{\mathrm{d}\theta _1 }{\mathrm{d}t}} \right| _{t=0} =0\), the rotation angle of hydraulic hammer can be solved as

$$\begin{aligned} \theta _1 =\frac{P_4 L_3 \left( {r_3 ^{2}-r_2 ^{2}} \right) }{2\left( {J_{1} +J_{2}} \right) }t^{2} \end{aligned}$$
(5)

The angular speed of hydraulic hammer can be obtained by taking the derivative of Eq. (5), and the result of derivation can be expressed as

$$\begin{aligned} \omega _1 =\frac{\mathrm{d}\theta _1 }{\mathrm{d}t}=\frac{P_4 L_3 \left( {r_3^2 -r_2^2 } \right) }{J_1 +J_2 }t \end{aligned}$$
(6)

Assuming that the rotation angle of hydraulic hammer is \(\alpha \) before the collision, then the rotation time of hydraulic hammer can be obtained as follows.

$$\begin{aligned} t_1 =\sqrt{\frac{2\alpha \left( {J_{1} +J_{2} } \right) }{P_4 L_3 \left( {r_3 ^{2}-r_2 ^{2}} \right) }} \end{aligned}$$
(7)

Before the collision, the line velocity of the center portion, located in the collision of hydraulic hammer, is determined by \(v_1 =\omega _1 \cdot \left( {r_3 +r_2 } \right) /2\). Supposing that the contact force of hydraulic hammer and valve body is \(F_{1}\) during the collision process, the velocity of hydraulic hammer is \(v_2\) and the speed of valve body is \(v_3\). The relative velocity of the two is \(v_r =v_2 -v_3 =\mathrm{d}\delta /\mathrm{d}t\), in which \(\delta \) is the decrement. Since the collision time is short, the force of hydraulic hammer from drilling fluid can be ignored. The relationship is written as

$$\begin{aligned} \frac{m_1 \mathrm{d}v_2 }{\mathrm{d}t}=-\frac{m_2 \mathrm{d}v_3 }{\mathrm{d}t}=-F_1 \end{aligned}$$
(8)

Equation (9) can be obtained after further derivation.

$$\begin{aligned} \frac{\mathrm{d}v_r }{\mathrm{d}t}=\frac{\mathrm{d}v_2 }{\mathrm{d}t}-\frac{\mathrm{d}v_3 }{\mathrm{d}t}=-\frac{F_1 }{m_1 }-\frac{F_1 }{m_2 }=-\frac{F_1 }{M} \end{aligned}$$
(9)

In which, \(m_{1}\) is the quality summation of hydraulic hammer and fork switch, \(m_{2}\) is the quality of valve body. M is the reduced mass and \(M=\left( {m_1 +m_2 } \right) /\left( {m_1 \cdot m_2 } \right) \). The relationship between the contact force and the compressed amount can be expressed as

$$\begin{aligned} F_1 =\frac{2E\delta ^{3/2}}{3\left( {1-\mu ^{2}} \right) }\cdot \sqrt{\frac{R}{2}} \end{aligned}$$
(10)

where E is the elastic modulus of the torsional oscillator, \(\mu \) is the Poisson’s ratio, R is the reduced radius of hydraulic hammer.

Equation (10) is modified as

$$\begin{aligned} \frac{1}{2}\mathrm{d}\left( {\left( {\frac{\mathrm{d}\delta }{\mathrm{d}t}} \right) ^{2}} \right) =\left( {-\frac{\lambda \delta ^{3/2}}{M}} \right) \mathrm{d}\delta \end{aligned}$$
(11)

The valve is static before the collision of hydraulic hammer and valve body, and the relative speed is \(v_{r0} =v_1 \). Integrated to Eq. (11) and the result can be obtained as

$$\begin{aligned} \frac{1}{2}\left[ {\left( {\frac{\mathrm{d}\delta }{\mathrm{d}t}} \right) ^{2}-v_{r0}^2 } \right] =-\frac{2\lambda }{5M}\delta ^{\frac{5}{2}} \end{aligned}$$
(12)

Since the compressive deformation amount is zero (\(\left. {\delta \left( t \right) } \right| _{t=0} =0)\) before the collision, the relationship between contact force and time is obtained by \(F_1 =\lambda \delta \left( t \right) ^{3/2}\). The torque of valve body subjected to the collision process can be written as

$$\begin{aligned} T_f =F_1 \cdot \left( {\frac{r_3 +r_2 }{2}} \right) \end{aligned}$$
(13)

According to the law of conservation of angular momentum, it can be derived

$$\begin{aligned} \left( {J_1 +J_2 } \right) \omega _{11} =\left( {J_1 +J_2 +J_3 } \right) \omega _2 \end{aligned}$$
(14)

In which \(J_{3}\) is the moment of inertia of valve body, \(\omega \)\(_{11}\) is the instantaneous angular velocity before the collision among fork switch, hydraulic hammer and valve body, \(\omega \)\(_{2}\) is the three’s common angular velocity after the collision.

When the collision completes between hydraulic hammer and valve body, the channel closes located in the orifice of center tube and the hydraulic hammer cavity and another channel opens between the valve cavity and the fork switch cavity. Drilling fluid flows into the valve body cavity and the fork switch cavity through the orifice of upper joint to drive fork switch generate counterclockwise motion. Applying the same theory as above, fork switch begins to produce uniformly accelerated motion before the collision under the effect of drilling fluid. The rotation angular velocity of hydraulic hammer related to the front of the collision can be achieved by

$$\begin{aligned} \omega _3 =\frac{\mathrm{d}\theta _2 }{\mathrm{d}t}=\frac{P_5 L_4 \left( {r_2^2 -r_1^2 } \right) }{J_1 }t \end{aligned}$$
(15)

The rotation angle of hydraulic hammer is \(\beta \) in the process. Taking the \(\beta \) into Eq. (15), the rotation time before the collision can be obtained as

$$\begin{aligned} t_2 =\sqrt{\frac{2\beta J_1 }{P_5 L_4 \left( {r_2 ^{2}-r_1 ^{2}} \right) }} \end{aligned}$$
(16)

where \(\beta \) is the rotation angular of fork switch with respect to hydraulic hammer, \(P_{5}\) is the pressure of drilling fluid flowing into the cavities of valve body and fork switch, \(L_{4}\) is the hammerhead length of fork switch, \(r_{1}\) is the inner diameter of fork switch.

Because the collision time is shortened, the influence of drilling fluid on the collision process can be ignored. Hydraulic hammer and fork switch are mainly subjected to the torque generated by the collision process, which can be given by

$$\begin{aligned} \frac{\left( {J_1 +J_2 } \right) \mathrm{d}\omega _a }{\mathrm{d}t}=-\frac{J_3 \mathrm{d}\omega _b }{\mathrm{d}t}=-T_a \end{aligned}$$
(17)

In which \(\omega _a\) is the angular velocity of hydraulic hammer and fork switch, \(\omega _b\) is the angular velocity of valve body, and the related angular velocity is \(\omega _{r1} =\omega _a -\omega _b\). According to the above-mentioned relationship, Eq. (17) can be written as

$$\begin{aligned} \frac{\mathrm{d}\omega _{r1} }{\mathrm{d}t}=\frac{\mathrm{d}\omega _a }{\mathrm{d}t}-\frac{\mathrm{d}\omega _b }{\mathrm{d}t}=-\frac{T_a }{J_1 +J_2 }-\frac{T_a }{J_3 }=-\frac{T_a }{J_M } \end{aligned}$$
(18)

where \(J_M \) is the reduced moment of inertia, and \(J_M =\left( {J_1 +J_2 } \right) \cdot J_3 /\left( {J_1 +J_2 +J_3 } \right) \)

The material of hydraulic hammer and valve body is same, so the compressive deformation is also same. Assuming the compression amount of hydraulic hammer and valve body as \(\delta _1 \), the relationship between the compression amount and the torque is defined as \(T_a =N\delta _1 \), wherein N is the proportionality coefficient. And the relationship between the compression amount and the related angular velocity is expressed as

$$\begin{aligned} \frac{\mathrm{d}\omega _{r1} }{\mathrm{d}t}=\frac{\mathrm{d}^{2}\delta _1 }{\mathrm{d}t^{2}} \end{aligned}$$
(19)

Taking Eq. (19) into Eq. (18) and the result is transformed as

$$\begin{aligned} \frac{1}{2}\mathrm{d}\left( {\left( {\frac{\mathrm{d}\delta _1 }{\mathrm{d}t}} \right) ^{2}} \right) =\left( {-\frac{N\delta _1 }{J_M }} \right) \mathrm{d}\delta _1 \end{aligned}$$
(20)

Integrate Eq. (20) and the following equation can be obtained.

$$\begin{aligned} \frac{1}{2}\left[ {\left( {\frac{\mathrm{d}\delta }{\mathrm{d}t}} \right) ^{2}-\omega _{r0}^2 } \right] =-\frac{N}{2J_M }\delta ^{2} \end{aligned}$$
(21)

According to the symmetry of the compression deformation process and the restoration process, the total time (\(t_1 )\) is twice to the compression time. For the first compression time, there is the relationship as

$$\begin{aligned} \mathrm{d}t_{01} =\frac{\mathrm{d}\delta }{\sqrt{\omega _{r0}^2 -\frac{N}{J_M }\delta ^{2}}} \end{aligned}$$
(22)

The average torque is \(T_{A1}\) and \(T_{A1} =H_1 /2t_{01} \), which is generated by hydraulic hammer, wherein \(H_1 \) is the first change type of the angular momentum.

According to the working principle of the torsional vibration oscillator, when hydraulic hammer and valve body motion together, fork switch rotates alone. At this moment, supposing that the angular velocity of fork switch is \(\omega _c\) and the angular velocity of hydraulic hammer and valve body is \(\omega _d\), the related angular velocity is defined as \(\omega _{r2} =\omega _c -\omega _d\). If the torque is \(T_b\), for the three rotating components, the interrelation is given by

$$\begin{aligned} \frac{\left( {J_2 +J_3 } \right) \mathrm{d}\omega _d }{\mathrm{d}t}=-\frac{J_1 \mathrm{d}\omega _c }{\mathrm{d}t}=T_b \end{aligned}$$
(23)

Equation (24) can be obtained by derivation.

$$\begin{aligned} \frac{\mathrm{d}\omega _{r2} }{\mathrm{d}t}=\frac{\mathrm{d}\omega _c }{\mathrm{d}t}-\frac{\mathrm{d}\omega _d }{\mathrm{d}t}=-\frac{T_b }{J_1 }-\frac{T_b }{J_2 +J_3 }=-\frac{T_b }{J_N } \end{aligned}$$
(24)

In which, \(J_N =J_1 \cdot \left( {J_2 +J_3 } \right) /\left( {J_1 +J_2 +J_3 } \right) \)

According to the solution process of the first compression time, the second compression time can be expressed as

$$\begin{aligned} \mathrm{d}t_{02} =\frac{\mathrm{d}\delta _2 }{\sqrt{\omega _{r2}^2 -\frac{N}{J_N }\delta _2 ^{2}}} \end{aligned}$$
(25)

Similarity, the average torque generated in the second collision type is \(T_{A2}\) and \(T_{A2} =H_2 /2t_{02}\) , wherein is the second change type of the angular momentum.

3.2 Vibration analysis model with impulse response

Because the collision time of the moving parts is short in the working process of the torsional vibration oscillator, the incentive function of valve body can be seen as a transient collision. Therefore, the generated vibration is also a transient vibration. Assuming that the width is \(T_0\) and the height is \(1/T_0\) in a rectangular pulse, the area of the whole rectangular pulse is 1. In order to obtain the whole unit pulse, in which the pulse width approaches 0 and the area remains constant, the pulse function is defined as

$$\begin{aligned} \left\{ \begin{array}{l} \delta \left( t \right) =0,\left( {t\ne 0} \right) \\ \int _{-\infty }^\infty {\delta \left( t \right) \mathrm{d}t=1} \\ \end{array} \right. \end{aligned}$$
(26)

The pulse occurs at the point (\(t=0)\) at this moment. If the unit pulse arises at \(t=a\), the pulse function can be written as

$$\begin{aligned} \left\{ \begin{array}{l} \delta \left( {t-a} \right) =0,\left( {t\ne a} \right) \\ \int _{-\infty }^\infty {\delta \left( {t-a} \right) \mathrm{d}t=1} \\ \end{array} \right. \end{aligned}$$
(27)

If the instantaneous impulse \({\tilde{F}}\) is applied at \(t=0\) and \(t=a\), the pulse force can be expressed as

$$\begin{aligned} {\tilde{F}}\left( t \right) =\left\{ \begin{array}{l} {\tilde{F}}\delta \left( t \right) ,\left( {t\ne 0} \right) \\ {\tilde{F}}\delta \left( {t-a} \right) ,\left( {t\ne a} \right) \\ \end{array} \right. \end{aligned}$$
(28)

The location of the torsional oscillator is shown in Fig. 3. For a single freedom degree of damping system, if the pulse force is \({\tilde{F}}={\tilde{F}}\delta \left( t \right) \), the system vibration equation can be given by Tian et al. [16]

$$\begin{aligned} m\ddot{x}+c{\dot{x}}+k{\dot{x}}={\tilde{F}}\delta \left( t \right) \end{aligned}$$
(29)
Fig. 3
figure 3

A typical drill string structure with a torsional oscillator

Full size image

The system keeps rest before the pulse force function, and the relationship is \((x\left( {0^{-}} \right) ={\dot{x}}\left( {0^{-}} \right) =0)\). The pulse force impacts at the moment (\(t=0)\) and the system is not subject to the pulse force when \(t\ge 0^{+}\). However, because of the existence of inertia, the system keeps vibrational state. In order to ensure the initial moment, the Eq. (30) is integrated in \(0^{-}\le t\le 0^{+}\) and the result is obtained as

$$\begin{aligned} m\left[ {x\left( {0^{+}} \right) -x\left( {0^{-}} \right) } \right] +\int _{0^{-}}^{0^{+}} {cx\mathrm{d}_t } +\int _{0^{-}}^{0^{+}} {\int _{0^{-}}^{0^{+}} {kx\mathrm{d}_t \mathrm{d}_t } } =\int _{0^{-}}^{0^{+}} {\int _{0^{-}}^{0^{+}} {{\tilde{F}}\delta (t)\mathrm{d}_t \mathrm{d}_t } } \end{aligned}$$
(30)

And

$$\begin{aligned} \int _{-\infty }^\infty {{\tilde{F}}\delta (t)} \mathrm{d}_t =\int _{0^{-}}^{0^{+}} {\int _{-\infty }^\infty {{\tilde{F}}\delta (t)} \mathrm{d}_t =} {\tilde{F}}=C \end{aligned}$$
(31)

The second and third terms almost approach to zero in the left side of Eq. (31). And because of \(x\left( {0^{-}} \right) =0\), the equation (\(x\left( {0^{+}} \right) =0)\) is held. It can be considered that there is no displacement change in the function of the pulse force.

Therefore, Eq. (32) is integrated into \(0^{-}\le t\le 0^{+}\) and the result is given by

$$\begin{aligned} m\left[ {{\dot{x}}(0^{+})-{\dot{x}}(0^{-})} \right] +c\left[ {x(0^{+})-x(0^{-})} \right] +\int _{0^{-}}^{0^{+}} {kx\mathrm{d}_t } =\int _{0^{-}}^{0^{+}} {{\tilde{F}}\delta (t)} \mathrm{d}_t \end{aligned}$$
(32)

Similarly, the right side of Eq. (32) is \({\tilde{F}}\) and the second term of the left end is zero while the third term is not equal to zero. It can be considered that the pulse force is applied at the time (\(t=0)\), which is equivalent to the initial time displacement \(x\left( 0 \right) =0\) and the initial velocity \(v_0 ={\tilde{F}}/m\). And Eq. (29) can be expressed as:

$$\begin{aligned} \left\{ \begin{array}{l} m\ddot{x}+c{\dot{x}}+kx=0 \\ x\left( 0 \right) =0,{\dot{x}}\left( 0 \right) =\frac{{\tilde{F}}}{m} \\ \end{array} \right. \end{aligned}$$
(33)

The solution of Eq. (33) can be obtained by mathematical deduction.

$$\begin{aligned} x(t)=\frac{{\tilde{F}}}{m\omega _d }\mathrm{e}^{-\zeta \omega _n t}\sin \omega _d t,t>0 \end{aligned}$$
(34)

In which, \(\omega _d =\sqrt{1-\zeta _n ^{2}}\omega _n\), wherein \(\omega _n\) is the natural frequency of the system and \(\zeta _n\) is the damping ratio. If the subjected impulse is \({\tilde{F}}_1 \) at \(t=0\) and the impulse is \({\tilde{F}}_2 \) at \(t=a\), the total impulse can be expressed as

$$\begin{aligned} {\tilde{F}}\left( t \right) ={\tilde{F}}_1 \delta \left( t \right) +{\tilde{F}}_2 \delta \left( {t-a} \right) \end{aligned}$$
(35)

According to the translation of the function, Eq. (37) can be obtained as

$$\begin{aligned} x_2 (t)=\frac{{\tilde{F}}}{m\omega _d }\mathrm{e}^{-\zeta _n \omega _n \left( {t-a} \right) }\sin \omega _d \left( {t-a} \right) ,\;\;\;t>a \end{aligned}$$
(36)

Equations (35) and (36) are added together, and the total response function is expressed as

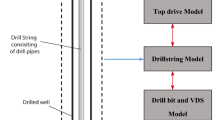
$$\begin{aligned} x(t)=\left\{ \begin{array}{ll} \frac{{\tilde{F}}_1 }{m\omega _d }\mathrm{e}^{-\zeta _n \omega _n t}\sin \omega _d t, &{} t>0 \\ \frac{{\tilde{F}}_2 }{m\omega _d }\mathrm{e}^{-\zeta _n \omega _n \left( {t-a} \right) }\sin \omega _d \left( {t-a} \right) , &{} t>a\\ \end{array} \right. \end{aligned}$$
(37)

To analyze the working characteristics of the torsional vibration oscillator, a simplified analysis model is established as shown in Fig. 4.

Fig. 4
figure 4

The simplified analysis model of the torsional vibration oscillator

Full size image

For the weak damping system, according to Newton’s second theorem, it can be defined as

$$\begin{aligned} J_d \ddot{\theta }_d +K_d \theta _d +C_d \dot{\theta }=0 \end{aligned}$$
(38)

In which, \(J_d \) is the rotational inertia, \(K_d \) is the stiffness of drill string, \(C_d \) is the damping stiffness, \(\theta _d \) is the angular displacement of vibration.

Wherein the rotational inertia and the stiffness of drill string are given by

$$\begin{aligned} \left\{ \begin{array}{l} J_d =\frac{1}{2}m_d \left( {\left( {\frac{D_{\mathrm{db}} }{2}} \right) ^{2}+\left( {\frac{d_{\mathrm{dl}} }{2}} \right) ^{2}} \right) \\ \\ K_d =\frac{\pi GD_{\mathrm{db}}^4 }{32l}\left( {1-\alpha ^{4}} \right) \end{array} \right. \end{aligned}$$
(39)

where G is the modulus of rigidity, \(D_{\mathrm{db}} \) is the external diameter of drill string, \(d_{\mathrm{dl}} \) is the inner diameter of drill string,\(\alpha \) is the ratio of inner diameter and outer diameter.

Assuming that the effect of damping on drill string is ignored, then Eq. (38) can be written as

$$\begin{aligned} J_d \ddot{\theta }_d +K_d \theta _d =0 \end{aligned}$$
(40)

According to the relationship between the angular momentum and the impact torque, the total impulse of the torsional vibration oscillator in a period can be obtained as

$$\begin{aligned} H_m \left( t \right) =H_1 \delta \left( {t-t_1 } \right) +H_2 \delta \left( {t-t_1 -t_2 } \right) +H_3 \delta \left( {t-2t_1 -t_2 } \right) +H_4 \delta \left( {t-2t_1 -2t_2 } \right) \end{aligned}$$
(41)

With the comparison of force and torque, the response function of vibration is derived as

$$\begin{aligned} \theta _d \left( t \right) =\left\{ \begin{array}{ll} 0, &{} 0<t<t_1\\ \frac{H_1 }{Jw_n }\sin w_n \left( {t-t_1 }\right) , &{} t_1<t<t_1 +t_2\\ \frac{H_1 }{Jw_n }\sin w_n \left( {t-t_1 } \right) +\frac{H_2 }{Jw_n }\sin w_n \left( {t-t_1 -t_2 } \right) , &{} t_1 +t_2<t<t_1+t_2 +t_3\\ \frac{H_1 }{Jw_n }\sin w_n \left( {t-t_1 } \right) +\frac{H_2 }{Jw_n }\sin w_n \left( {t-t_1 -t_2 } \right) +\\ \frac{H_3 }{Jw_n }\sin w_n \left( {t-t_1 -t_2 -t_3 } \right) , &{} 2t_1+t_2<t<2t_1 +2t_2\\ \frac{H_1 }{Jw_n }\sin w_n \left( {t-t_1 } \right) +\frac{H_2 }{Jw_n }\sin w_n \left( {t-t_1 -t_2 } \right) +\frac{H_3 }{Jw_n }\sin w_n \left( {t-2t_1 -t_2 } \right) +\\ \frac{H_4 }{Jw_n }\sin w_n \left( {t-2t_1 -2t_2 } \right) , &{} 2t_1+2t_2<t<2t_1 +2t_2\\ \end{array}\right. \end{aligned}$$
(42)

Equation (42) can be further derived and the angular velocity of vibration can be obtained as

$$\begin{aligned} \omega _d \left( t \right) =\left\{ \begin{array}{ll} 0, &{} 0<t<t_1\\ \frac{H_1 }{J}\cos w_n \left( {t-t_1 } \right) , &{} t_1<t<t_1 +t_2\\ \frac{H_1 }{J}\cos w_n \left( {t-t_1 } \right) +\frac{H_2 }{J}\cos w_n \left( {t-t_1 -t_2 } \right) , &{} 2t_1 +t_2<t<t_1 +t_2\\ \frac{H_1 }{J}\cos w_n \left( {t-t_1 } \right) +\frac{H_2 }{J}\cos w_n \left( {t-t_1 -t_2 } \right) +\\ \frac{H_3 }{J}\cos w_n \left( {t-t_1 -t_2 -t_3 } \right) , &{} 2t_1+t_2<t<2t_1 +2t_2\\ \frac{H_1 }{J}\cos w_n \left( {t-t_1 } \right) +\frac{H_2 }{J}\cos w_n \left( {t-t_1 -t_2 } \right) +\frac{H_3 }{J}\cos w_n \left( {t-2t_1 -t_2 } \right) +\\ \frac{H_4 }{J}\cos w_n \left( {t-2t_1 -2t_2 } \right) , &{} 2t_1+2t_2<t<2t_1 +2t_2\\ \end{array}\right. \end{aligned}$$
(43)
Fig. 5
figure 5

The experimental schematic diagram of the bench test

Full size image
Fig. 6
figure 6

The experimental test of the torsional oscillator

Full size image
Fig. 7
figure 7

Comparison between experiment result and calculation result

Full size image
Fig. 8
figure 8

The comparison results of the average torque

Full size image

4 Numerical analysis and experiment test

4.1 Experiment principle

According to the calculation method, kinematics analysis is carried out and example analysis is conducted by using the given parameters, including the relationship of collision period, inlet flow, angular velocity and angular displacement. Corresponding to the experimental test, the parameters used in numerical calculation are given as follows. \(L_{1}=0.018\,\hbox {m}\), \(a=48\), \(D_{1}=0.04\,\hbox {m}\), \(L_{2}=0.045\,\hbox {m}\), \(b=4\), \(D_{2}=0.057\,\hbox {m}\), \(J_{1}=0.687 \times 10^{-3}\,\hbox {kg}\,\hbox {m}^{2}\), \(r_{1}=0.0325\,\hbox {m}\), \(L_{4}=0.086\,\hbox {m}\), \(m_{1 }=4.018\,\hbox {kg}\), \(J_{2}=4.652 \times 10^{-3}\,\hbox {kg}\,\hbox {m}^{2}\), \(r_{2}=0.0465\,\hbox {m}\), \(r_{3}=0.0585\,\hbox {m}\), \(\alpha =0.7152\,\hbox {rad}\), \(J_{3}=38.772 \times 10^{-3}\,\hbox {kg}\,\hbox {m}^{2}\), \(L_{3}=0.096\,\hbox {m}\), \(\beta =0.3314\,\hbox {rad}\), \(\rho =1000\,\hbox {kg/m}^{3}\), \(m_{2}=15.764\,\hbox {kg}\), \(k=0.5\).

With the combination of the numerical example analysis, the experimental analysis is conducted. Referring to the experimental schematic diagram of the bench test (Fig. 5), the experimental test is designed. And experimental equipment includes the test bench of down-hole tool, two pumps, a water tank, a water inlet and a water outlet, two throttle valves, a bypass valve, data-acquisition instruments and the torsional oscillator. The torsional oscillator is held on the left of the bench and supported on the right. Water flows from the tank and the torsional oscillator is driven to motion by regulating the pump 1 and pump 2. Then the water flows to the tank from the return pipe. Figure 6 is the experimental test of the torsional oscillator.

Fig. 9
figure 9

The changing relationship between the inlet flow and the average torque

Full size image
Fig. 10
figure 10

The change of the angular velocity of valve body in counter clockwise motion

Full size image
Fig. 11
figure 11

The change of the angular displacement of the valve body

Full size image

4.2 Numerical results and comparison analysis

The changes of pressure, flow rate and collision frequency are recorded by data-acquisition instruments while the torsional oscillator is working. The experimental result is compared with the calculation result, which are depicted in Fig. 7. The changing relationship of the torque is described in Fig. 8, which shows the changing situation of the average torque when the inlet flow is 20 L/s. According to the comparison results, the sizes of the theoretical value and the experiment value are similar if the environmental conditions are consistent. The results indicate the accuracy of the theoretical model and it is reliable that the related research method is used to study the characteristics of the torsional vibration oscillator.

Fig. 12
figure 12

The results of the angular displacement in different inlet flow. a The angular displacement of vibration (\(q_{1}=20\,\hbox {L/s})\), b The angular displacement of vibration (\(q_{1}=25\,\hbox {L/s})\) and c The angular displacement of vibration (\(q_{1}=30\,\hbox {L/s})\)

Full size image

According to the previous theory research, combined with the example parameters, the changing relationship between inlet flow and average torque is shown in Fig. 4. The calculation results include different change rules in various inlet flow, which are 20, 25, 30 L/s respectively. The average torque is maximum when the inlet flow is 30 L/s and it is minimum on condition that the inlet flow is 20 L/s in a single period, which is shown in Fig. 9. In general, the average torque keeps increasing with the increase in the inlet flow rate, which is resulted from the torsional vibration oscillator.

Fig. 13
figure 13

The results of the angular velocity in different inlet flow. a The angular velocity of vibration (\(q_{1}=20\,\hbox {L/s})\), b the angular velocity of vibration (\(q_{1}=25\,\hbox {L/s})\) and c the angular velocity of vibration (\(q_{1}=30\,\hbox {L/s})\)

Full size image

Supposing that the counter clockwise motion is the positive direction, the clockwise rotation is negative direction. In the initial moment, the drilling fluid flows into the cavity of hydraulic hammer to generate counterclockwise motion. Valve body is not affected by forces and the angular velocity is 0 at this time. The angular velocity of valve body increases suddenly when hydraulic hammer collides with valve body. Since then the two components rotate counter clockwise together and the angular velocity of valve body remains the same. The angular velocity of valve body decreases rapidly until fork switch collides with hydraulic hammer. The change of the angular velocity of valve body in counter clockwise motion is shown in Fig. 10. When valve body stops the counter clockwise movement, it begins a clockwise motion. Meanwhile, with the increase in the inlet flow, the maximum value of the angular velocity is increasing.

Similar to the angular velocity of valve body, the angular displacement is 0 at the initial moment. When valve body begins to rotate counter clockwise, the angular displacement increases gradually until the anticlockwise motion completes. Then valve body generates clockwise rotation and the angular displacement continues to increase. When the clockwise motion stops, a movement period is completed. The change of the angular displacement of valve body is shown in Fig. 11. During the motion time, the angular displacement keeps increasing if the inlet flow increases gradually, which indicates the angular displacement of valve body is proportional to the inlet flow.

The cyclical and circumferential torque generated by the torsional vibration oscillator impacts on drill bit to improve the rock-breaking efficiency. During the generation process of the circumferential torque, the angular displacement of vibration of the drill string is shown in Fig. 12. In a single cycle, with the increase in the inlet flow, the angular displacement of vibration is increasing. When the inlet flow rate is 20 L/s, the angular displacement is related minimum. The angular displacement is relatively maximum, where the maximum value is about \(4\times 10^{4}\) in a single cycle.

Corresponding to the results of the angular displacement, the results of the angular velocity are obtained in different inlet flow, which are shown in Fig. 13. Similarly, the size of the angular displacement is greater if the inlet flow is increasing in a single cycle. With the increase in the inlet flow, the change cycle of the angular velocity is shortened gradually, which shows the collision cycle is shortened increasingly.

5 Conclusions

The relationship is analyzed by the established dynamic model including the inlet flow, the collision period, the angular velocity, the angular displacement and the average torque. The reliability and accuracy of the calculation method is verified by the comparison of the numerical example and experimental test results.

When the inlet pressure is constant, the average torque is more significant with the increase in the inlet flow rate. However, the collision period is shortened gradually with the increase in the inlet flow. And the angular displacement and velocity of the valve body are increasing. Similarly, the vibration angular velocity and displacement remain increase if the inlet flow increases gradually. The average torque, the angular velocity and displacement are proportional to the inlet flow, while the collision period is inversely proportional to the inlet flow.

The research conclusions, analyzing the relationship of collision period, angular velocity, angular displacement, average torque and inlet flow, can lay the foundation for the in-depth characteristics research of the torsional oscillator and provide technical reference for field application.