Investigation on the Effect of High-Frequency Torsional Impacts on the Torsional Vibration of an Oilwell Drill String in Slip Phase

Abstract

The drilling system usually encounters detrimental stick-slip vibration to the drilling process. One of the approaches for controlling the stick-slip vibration is using high-frequency torsional impact (HFTI). However, how the HTFI will affect the vibration of the drill string is still unknown. This study proposed a mechanical model of the drill string by using continuous system to investigate the effect of HFTI on the vibration of a drill string in slip phase, wherein the HFTI is considered in the model. The mechanical model is investigated through using mode superposition method and conducting case studies. Results show that the HFTI is more sensitive to the drill string close to the drill bit and that the HFTI has little effect on the vibration of drill string. During the drilling process, the HFTI aggravates the rock damage and rock failure, which actually improves the drilling efficiency and mitigates the stick-slip vibration.

1 Introduction

Oil and gas are two types of fossil energy generated by natural processes taking millions of years to form. Although oil and gas are continually being generated through natural processes, they are usually regarded as non-renewable resources [1, 2]. With the rapid development of economy, consumption of oil and gas in the world increases and the oil and gas are being consumed much faster than new ones are being made [3]. After the exploration and development of oil and gas in the past several decades, the drilling works are toward deep wells (≥3000 m) and ultra-deep wells (≥6000 m) [4]. The drilling cost occupies more than half of the fees used in the exploration and development of oil and gas. As a result, drilling companies all over the world try to reduce the drilling cost and improve the drilling efficiency.

In the drilling industry, one of the most popular drilling methods is the rotary steering drilling. Rotary steering equipment used to compose a drill string that is rotated to deepen the wellbore [5]. During the drilling process, the drill string encounters serious dynamic problems which may lead to drilling accident, such as buckling, vibration, and fracture. Due to the hostile environment of the drilling process, the dynamic behavior of the drill string is very complex [6]. Field observations show difference in vibration surveillance in downhole and on surface which indicates BHA undergoes severe vibrations. Drill string vibration is regarded as the primary reason for the premature failure of drilling tools, and the subject of vibration in the drilling system is an ongoing challenge for the engineers [7, 8].

Among the common vibration modes (including single modes and coupled modes), stick-slip vibration is considered as one of the primary reasons of drilling performance deterioration as it wastes drilling energy, leads to tool failure, reduces the penetration rate, and increases the drilling cost [9, 10]. Due to the large length-to-diameter (LTD) of a drill string, for example, the LTD of a 3,000 m drill string is bigger than 23,000, stick-slip vibration is very common [11]. It is reported that stick-slip vibration is more likely to appear in deep drilling systems [12,13,14]. Two reasons may be used to explain this (1) LTD of the drill string increases with an increase in the well depth and (2) rock hardness and rock strength increase with increasing the well depth. In field application, a large weight on bit is used to maintain the rate of penetration because of high rock strength, but this leads to a high possibility of generating or aggravating the stick-slip vibration.

Belokobyl’skii and Prokopov [15] studied the friction-induced vibration of drill string, which is thought to be the earliest publication related to stick-slip vibration of drill string. Their work was furthered by many other researchers. Richard et al. [16] investigated the root cause of stick-slip phenomenon of stick-slip in oilwell drill string using a simplified model that considered the interaction between the drill bit and rock formation. Patil and Teodoriu [17] studied the effects of system factors on the stick-slip vibration of drill string. Tang et al. [18,19,20] revealed the mechanism of stick-slip vibration and effects of drilling parameters on this type of phenomenon. Mihajlovic et al. [21] used an experimental drill string apparatus to study the causes of friction-induced stick-slip phenomenon. Lai et al. [22] reported the field measurement of stick-slip vibration using surface-based torque and presented the correlation between downhole and surface data. Puebla and Alvarez-Ramirez [23] developed a control method based on modeling error compensation to mitigate stick-slip motion in drill string. It is found that many literatures have focused on the stick-slip phenomenon, but there are still many challenges.

Many methods have been used to control the stick-slip vibration, including active ones and passive ones [10], and one of them is the high-frequency torsional impact (HFTI) drilling [24]. For this drilling technique, HFTI is supplemented to the drill bit through an impactor installed directly above the drill bit. Results of our previous studies showed that the HFTI can reduce the stick-slip vibration of the drill bit [18]. Since an additional impact is added onto the drill string, it is easy to believe that the HFTI may aggravate or be a source of drill string vibration.

For a drilling system with stick-slip vibration, the drill bit moves alternately between stick phase and slip phase. In the stick phase, the drill bit keeps still (referred to as being constrained). While in the slip phase, the drill bit is not constrained. In this paper, the investigation is conducted to know the effects of HFTI on the vibration of a drill string in slip phase.

2 Drill String Vibration Model

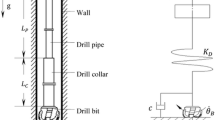
The drill string is regarded as vertical, elastic, homogeneous, and isotropic, and the flow of the drilling fluid and flow-induced vibration is neglected. The vibration model of the drill string is shown in Fig. 1, where x-axis is the longitudinal direction of the drill string, x = 0 means the rotary table, and x = l means the drill bit. θ(x, t) denotes the angular displacement of the cross section of the drill string at x and time t, and the gradient of the angular displacement can be expressed as

Fig. 1

Vibration model of the drill string: a general view of the drill string system; b vibration model of the continuous drill string

$$\frac{\partial \theta }{\partial x} = \frac{T}{{GI_{p} (x)}}$$

(1)

where T indicates the torque acted on the cross section of drill string, G means the shear modulus of the drill string, and I_p(x) represents the polar moment of inertia at x. For a drill string element dx shown in Fig. 1b, the motion differential equation of the torsional vibration can be expressed as

$$GI_{p} (x)\frac{{\partial^{2} \theta }}{{\partial x^{2} }}(x,t) - J(x)\frac{{\partial^{2} \theta }}{{\partial t^{2} }}(x,t) - \beta \frac{\partial \theta }{\partial t}(x,t) = M(x,t),x \in (0,l),t > 0$$

(2)

where J(x) denotes the rotational inertia, β represents the viscous damping coefficient of the drilling fluid, and M(x, t) refers to the external torque acted on the drill string.

For a dynamic mode that is feasible in physics, it can be realized by superposition of the basic modes of the system. The mode superposition method (MSM) transforms the geometric displacement coordinate into modal amplitudes and characterizes the system vibration as a linear combination of the mode shapes. Mode shape is an intrinsic parameter of the system like the density. To solve Eq. (2), its homogeneous form is firstly studied.

$$GI_{p} (x)\frac{{\partial^{2} \theta }}{{\partial x^{2} }}(x,t) - J(x)\frac{{\partial^{2} \theta }}{{\partial t^{2} }}(x,t) - \beta \frac{\partial \theta }{\partial t}(x,t) = 0,x \in (0,l),t > 0$$

(3)

One method of solving partial differential equations is the variable separation method. The solution is assumed in the form

$$\theta (x,t) = \phi (x)Q(t)$$

(4)

where ϕ(x) means a function representing the mode shape and is independent with t, and Q(t) indicates the generalized coordinate representing the amplitude and is dependent with t.

By substituting Eq. (4) into Eq. (3)

$$\frac{{\rho I_{p} \ddot{Q}(t) + \beta \dot{Q}(t)}}{Q(t)} = \frac{{GI_{p} \phi^{\prime \prime } (x)}}{\phi (x)}$$

(5)

where (.) denotes the derivation with respect to time t, $(^{{\prime }} )$ indicates the derivation with respect to x, and ρ represents the density of the drill string. By introducing a term C = −ω², two equations are satisfied.

$$\rho I_{p} \ddot{Q}(t) + \beta (x)\dot{Q}(t) + \omega^{2} Q(t) = 0$$

(6)

$$GI_{p} \phi^{\prime \prime } (x) + \omega^{2} \phi (x) = 0$$

(7)

The solution of Eq. (7) is then given as

$$\phi (x) = C_{1} \times \sin \left( {\omega \sqrt {\frac{\rho }{G}} x} \right) + C_{2} \times \cos \left( {\omega \sqrt {\frac{\rho }{G}} x} \right)$$

(8)

where C₁ and C₂ mean integration constant determined by the boundary condition and ω indicates the natural frequency of the drill string system.

3 Drill String Dynamics Under Torsional Impacts

3.1 Natural Frequency and Mode Shape

At the beginning of the slip phase, the driving torque acted on the drill string balances with the frictional torque acted on the drill bit. The drill string is twisty. After the slip phase is initiated, the bottom hole assembly vibrates violently and the rotary table moves steadily. For a drill string in slip phase, the relative movement between the drill bit and the rotary table can be regarded as the movement of a vertical beam with fixed boundary condition at the upper end and free boundary condition at the lower end. For the torsional vibration of a drill string, it can be obtained by superimposing the relative movement with effect of rotation of the rotary table on each mode shape. In the slip phase, kinetic frictional torque is acted on the drill bit. The kinetic frictional torque is regarded as external load. The boundary conditions can be given as

$$T(l,t) = GI_{p} \frac{\partial \theta }{\partial x} = 0$$

(9)

$$\theta (0,t) = 0$$

(10)

Upon substituting into Eq. (4), two equations can be obtained

$$\phi^{{\prime }} (l) = 0$$

(11)

$$\phi (0) = 0$$

(12)

Substituting Eqs. (11) and (12) into Eq. (8) gives

$$C_{2} = 0$$

(13)

$$\cos \frac{\omega l}{{\sqrt {{G \mathord{\left/ {\vphantom {G \rho }} \right. \kern-0pt} \rho }} }} = 0$$

(14)

The natural frequencies of the system can be found from Eq. (14) to be

$$\omega_{i} = \frac{{(2i - 1)\pi \sqrt {{G \mathord{\left/ {\vphantom {G \rho }} \right. \kern-0pt} \rho }} }}{2l},i = 1,2,3, \ldots$$

(15)

Hence, the expression for mode shape i can be of the form

$$\phi_{i} (x) = C_{1} \times \sin \frac{(2i - 1)\pi x}{2l},i = 1,2,3, \ldots$$

(16)

3.2 Generalized Moment of Inertia and Generalized Load

The generalized modes of the drill string, by determining C₁ = 1, is

$$\phi_{i} (x) = \sin \frac{(2i - 1)\pi x}{2l},i = 1,2,3, \ldots$$

(17)

And the generalized moment of inertia (generalized mass) is

$$\overline{J}_{i} = \mathop{\int}\limits_{0}^{l} {J\phi_{i}^{2} (x)\rm{d}x} = \mathop{\int}\limits_{0}^{l} {J\left( {\sin \frac{(2i - 1)\pi x}{2l}} \right)^{2} \rm{d}x = \frac{1}{2}Jl}$$

(18)

where J indicates the moment of inertia of each unit length of drill string. The generalized load is

$$\overline{M}_{i} (t) = \int\limits_{0}^{l} {\phi_{i} } (x)M(x,t)\rm{d}x$$

(19)

The HFTI generator is placed on a certain position of the drill string. The coordinate of this position is regarded as y in the x-axis. For the HFTI torque, it can be regarded as a distributed load which acts on a small segment (y − Δ, y + Δ), with its section length is 2Δ. The load intensity of the HFTI is ${{\left( {\frac{A}{2} + \frac{A}{\pi }\sin (\omega_{0} t) + \frac{A}{2\pi }\sin (2\omega_{0} t)} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{A}{2} + \frac{A}{\pi }\sin (\omega_{0} t) + \frac{A}{2\pi }\sin (2\omega_{0} t)} \right)} {2\Delta }}} \right. \kern-0pt} {2\Delta }}$ (the HFTI load is discussed in Appendix A). Based on Eq. (19), the generalized load of the HFTI can be given as

$$\begin{aligned} \overline{M}_{i1} (t) & = \int\limits_{0}^{l} {\phi_{i} } (x)M(x,t)\rm{d}x \\ & = \int\limits_{0}^{y - \Delta } {\phi_{i} (x)} M(x,t)\rm{d}x + \int\limits_{y - \Delta }^{y + \Delta } {\phi_{i} (x)} M(x,t)\rm{d}x + \int\limits_{y + \Delta }^{l} {\phi_{i} (x)} M(x,t)\rm{d}x \\ & = \int\limits_{y - \Delta }^{y + \Delta } {\sin \frac{{\left( {2i - 1} \right)\pi y}}{2l} \times } {{\left( {\frac{A}{2} + \frac{A}{\pi }\sin (\omega_{0} t) + \frac{A}{2\pi }\sin (2\omega_{0} t)} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{A}{2} + \frac{A}{\pi }\sin (\omega_{0} t) + \frac{A}{2\pi }\sin (2\omega_{0} t)} \right)} {2\Delta }}} \right. \kern-0pt} {2\Delta }}\rm{d}x \\ & = \sin \frac{(2i - 1)\pi y}{2l} \times \left( {\frac{A}{2} + \frac{A}{\pi }\sin (\omega_{0} t) + \frac{A}{2\pi }\sin (2\omega_{0} t)} \right) \\ \end{aligned}$$

(20)

Apart from the HFTI, kinetic frictional torque acts on the drill bit (y = l). The frictional torque is treated as external load, and its generalized form is expressed as

$$\overline{M}_{i2} (t) = \sin \frac{(2i - 1)\pi y}{2l} \times \mu_{K} W_{B} \overline{R}_{B} = \sin \frac{(2i - 1)\pi l}{2l} \times \mu_{K} W_{B} \overline{R}_{B} = \mu_{K} W_{B} \overline{R}_{B}$$

(21)

where $\mu_{K}$ indicates the kinetic frictional coefficient, W_B means the weight on bit, and $\overline{R}_{B}$ represents the equivalent diameter of the drill bit.

3.3 Generalized Coordinate

In complex systems, coordinates used to describe the system may not be independent; some of the coordinates may be related to each other by constraint equations. Generalized coordinate is a type of independent coordinate used to resolve the constraint equations. The MSM is to be used. Theoretically, there are infinitely many mode shapes should be superposed for a continuous system. Practically, however, only the mode shapes that provide the main contribution are included. For a drill string, using the MSM means the transformation of a continuous system into a discrete system. The solution of the equation of motion of the drill string is expressed as

$$\theta (x,t){ = }\sum\limits_{i = 1}^{\infty } {\phi_{i} (x)Q_{i} } (t)$$

(22)

where ϕ_i(x) represents the regularized modal function and Q_i(t) indicates the generalized coordinate that denotes the amplitude of the ith mode shape at time t.

By combining Eqs. (2) and (22), a differential equation of the generalized coordinate can be obtained (refers to Appendix C)

$$\ddot{Q}_{i} (t) + 2\xi_{i} \omega_{i} \dot{Q}_{i} (t) + \omega_{i}^{2} Q_{i} (t) = \frac{{\overline{M}_{i} }}{{\overline{J}_{i} }}$$

(23)

The problem of obtaining the system response is obtaining the generalized coordinates that are composed of a series of single degree of freedom (SDOF). The initial conditions of Eq. (23) are expressed by Eqs. (C.5) and (C.6). Once the generalized coordinates are obtained, the dynamics of the drill string can be obtained in terms of Eq. (22). The solution of Eq. (23) has two parts: a general solution related to the associated homogeneous equation and a particular solution. The associated homogeneous equation of Eq. (23) is

$$\ddot{Q}_{i} (t) + 2\xi_{i} \omega_{i} \dot{Q}_{i} (t) + \omega_{i}^{2} Q_{i} (t) = 0,i = 1,2,3 \ldots$$

(24)

Combining with Eqs. (C.5) and (C.6), the initial conditions of a drill string in the slip phase can be obtained

$$Q_{1} (0) = \frac{1}{{\overline{J}_{1} }}\int\limits_{0}^{l} {J\theta_{0} (x)\sin \left( {\frac{\pi x}{2l}} \right)\rm{d}x = } \frac{1}{{\overline{J}_{1} }}\int\limits_{0}^{l} {J\theta_{0} (l)\left[ {\sin \left( {\frac{\pi x}{2l}} \right)\rm{d}x} \right]^{2} } = \theta_{0} (l)$$

(25)

$$Q_{2} (0) = \frac{1}{{\overline{J}_{2} }}\int\limits_{0}^{l} {J\theta_{0} (x)\sin \left( {\frac{3\pi x}{2l}} \right)\rm{d}x = } \frac{1}{{\overline{J}_{2} }}\int\limits_{0}^{l} {J\theta_{0} (l)\left[ {\sin \left( {\frac{3\pi x}{2l}} \right)\rm{d}x} \right]^{2} } = \theta_{0} (l)$$

(26)

$$Q_{3} (0) = \frac{1}{{\overline{J}_{3} }}\int\limits_{0}^{l} {J\theta_{0} (x)\sin \left( {\frac{5\pi x}{2l}} \right)\rm{d}x = } \frac{1}{{\overline{J}_{3} }}\int\limits_{0}^{l} {J\theta_{0} (l)\left[ {\sin \left( {\frac{5\pi x}{2l}} \right)\rm{d}x} \right]^{2} } = \theta_{0} (l)$$

(27)

$$\dot{Q}_{1} (0) = \dot{Q}_{2} (0) = \dot{Q}_{3} (0) = 0$$

(28)

The generalized coordinate response determined by the initial conditions is then equals

$$Q_{i1} (t) = \eta_{i} e^{{ - \xi_{i} \omega_{i} t}} \sin (\omega_{id} t + v)$$

(29)

where

$$\eta_{i} = \sqrt {Q_{i}^{2} (0) + \left( {\frac{{\dot{Q}_{i} (0) + \xi_{i} \omega_{i} Q_{i} (0)}}{{\omega_{id} }}} \right)^{2} } = \sqrt {\left( {\theta_{0} (l)} \right)^{2} + \left( {\frac{{\xi_{i} \theta_{0} (l)}}{{\sqrt {1 - \xi_{i}^{2} } }}} \right)^{2} }$$

(30)

$$v_{i} = \arctan \frac{{\omega_{id} Q_{i} (0)}}{{\dot{Q}_{i} (0) + \xi_{i} \omega_{i} \dot{Q}_{i} (0)}} = \arctan \frac{{\sqrt {1 - \xi_{i}^{2} } }}{{\xi_{i} }}$$

(31)

For the drill string dynamics induced by initial conditions, the proportion of each generalized coordinate is inversely proportional to the square of frequency. Considering the first three orders of mode shape, their proportions are 225/259, 25/259, and 9/259, respectively.

For the drill string in slip phase, a kinetic frictional torque acts on the drill bit (y = l). The proportion of each generalized coordinate determined by the frictional torque is also inversely proportional to the square of the frequency, which can be described as

$$Q_{i2} (t) = \frac{{M_{F} }}{{\overline{J}_{i} \omega_{i}^{2} }}\sin \frac{(2i - 1)\pi y}{2l}$$

(32)

where M_F can be determined by Eq. (21).

The constant term of the generalized impact torque is $\frac{A}{2}\sin \frac{(2i - 1)\pi y}{2l}$, the corresponding generalized coordinate determined by it can be written as

$$Q_{i3} (t) = \frac{A}{{2\overline{J}_{i} \omega_{i}^{2} }}\sin \frac{{\left( {2i - 1} \right)\pi y}}{2l}$$

(33)

According to Eq. (19), the generalized impact torque of the second term (the term with ω₀) of Eq. (A.10) is $\frac{A}{\pi }\sin (\omega_{0} t)\sin \frac{(2i - 1)\pi y}{2l}$, and the corresponding generalized coordinate equals

$$Q_{i4} (t) = \frac{{\overline{M}_{i1} }}{{\overline{J}_{i} \omega_{i}^{2} }} \times \frac{1}{{\sqrt {(1 - \gamma_{i1}^{2} )^{2} + (2\xi_{i} \gamma_{i1} )^{2} } }} \times \sin (\omega_{0} t - \beta_{i1} )$$

(34)

where $\overline{M}_{i1} = \frac{A}{\pi }\sin \frac{(2j - 1)\pi y}{2l}$ indicates the coefficient of the jth generalized impact torque whose natural frequency is $\omega_{0}$, $\gamma_{i1}$ means the ratio of the excitation frequency $\omega_{0}$ and the ith natural frequency, $\beta_{i1}$ is the initial phase of the ith generalized coordinate when the harmonic term of natural frequency equals to $\omega_{0}$, and $\gamma_{i1}$ and $\beta_{i1}$ can be written as

$$\gamma_{i1} = {{\omega_{0} } \mathord{\left/ {\vphantom {{\omega_{0} } {\omega_{i} }}} \right. \kern-0pt} {\omega_{i} }}$$

(35)

$$\beta_{i1} = \arctan \frac{{2\xi_{i} \gamma_{i1} }}{{1 - \gamma_{i1}^{2} }}$$

(36)

According to Eq. (19), the generalized impact torque of the third term (the term with 2ω₀) of Eq. (A.10) is $\frac{A}{2\pi }\sin (2\omega_{0} t)\sin \frac{(2i - 1)\pi y}{2l}$, and the corresponding generalized coordinate equals

$$Q_{i5} (t) = \frac{{\overline{M}_{i2} }}{{\overline{J}_{i} \omega_{i}^{2} }} \times \frac{1}{{\sqrt {(1 - \gamma_{i2}^{2} )^{2} + (2\xi_{i} \gamma_{i2} )^{2} } }} \times \sin (2\omega_{0} t - \beta_{i2} )$$

(37)

where $\overline{M}_{i2} = \frac{A}{2\pi }\sin \frac{(2j - 1)\pi y}{2l}$ indicates the coefficient of the jth generalized impact torque whose natural frequency is $2\omega_{0}$, $\gamma_{i2}$ represents the ratio of the excitation frequency $2\omega_{0}$ and the ith natural frequency, $\beta_{i2}$ means the initial phase of the ith principal coordinate when the harmonic term of natural frequency equal $2\omega_{0}$, and $\gamma_{i2}$ and $\beta_{i2}$ can be written as

$$\gamma_{i2} = {{2\omega_{0} } \mathord{\left/ {\vphantom {{2\omega_{0} } {\omega_{i} }}} \right. \kern-0pt} {\omega_{i} }}$$

(38)

$$\beta_{i2} = \arctan \frac{{2\xi_{i} \gamma_{i2} }}{{1 - \gamma_{i2}^{2} }}$$

(39)

For a drill string with initial angular displacement and under the action of frictional torque and impact torque, the generalized coordinate [Eq. (23)] of using MSM can be expressed as

$$Q_{i} (t) = Q_{i1} (t) + Q_{i2} (t) + Q_{i3} (t) + Q_{i4} (t) + Q_{i5} (t)$$

(40)

4 Case Study

To obtain a quantitative understanding of the drill string dynamics, a case study is to be conducted with a specific drill string shown in Table 1 to be analyzed. The rotary table velocity is assumed to be 100 rpm (φ = 10.5 rad/s); the impact frequency is 600 times per minute (10 Hz); the first order of damping ratio is ξ₁ = 0.05; and the position of the impact torque is 1 m above the drill bit (y = 2999 m). For the impact generator, the impact torque is 366 N m when the impact frequency is 600 times per minute. The system parameters are $\overline{J}_{1} = \overline{J}_{2} = \overline{J}_{3} = 46.64$ Kg m², ω₁ = 1.672 rad/s, ω₂ = 5.015 rad/s, ω₃ = 8.358 rad/s, ξ₁ = 0.05, ξ₂ = 0.0167, ξ₃ = 0.01, l = 3000 m, A = 366 N m, y = 2999 m, ω₀ = 62.83 rad/s. Regarding the static frictional coefficient μ_S = 0.8, μ_K = 0.5, W_B= 160 kN, and $\overline{R}_{B} = 72$ mm, then $\overline{M}_{i2} (t) = 5760$ N m. Part of the parameters can be obtained from the works by Navarro-López and Cortés [25], Tang et al. [20], and Tang [26].

Table 1 Physical parameters of the drill string

For the drill string analyzed, the first three mode shapes are shown in Fig. 2

Fig. 2

First three mode shapes of the drill string

For the 3000-m-drill string, its torsional stiffness is 317 N m/rad. When the drill bit steps into the slip phase, the initial angular displacement of the drill bit is 29.07 rad (the drill bit lags behind the rotary table, and the value is determined by the static frictional torque). When there is no impact torque, the motion of the drill string is a type of damped vibration determined by the initial angular displacement and static frictional torque, the first three orders of generalized coordinate can be given as

$${Q_1}(t) = {{225 \times \left( \begin{array}{l} - 10.925 \times {e^{ - 0.05 \times 1.67t}} \times \sin (1.66t + 1.521)\\ - \left( {10.5t/{\phi _1}(x) + 18.17} \right) \end{array} \right)} \mathord{\left/ {\vphantom {{225 \times \left( \begin{array}{l} - 10.925 \times {e^{ - 0.05 \times 1.67t}} \times \sin (1.66t + 1.521)\\ - \left( {10.5t/{\phi _1}(x) + 18.17} \right) \end{array} \right)} {259}}} \right. \kern-\nulldelimiterspace} {259}} $$

(41)

$${Q_2}\left( t \right) = {{25 \times \left( \begin{array}{l} - 10.908 \times {e^{ - 0.0167 \times 5.015t}} \times \sin (5t + 1.554)\\ - (10.5t/{\phi _2}(x) + 18.17) \end{array} \right)} \mathord{\left/ {\vphantom {{25 \times \left( \begin{array}{l} - 10.908 \times {e^{ - 0.0167 \times 5.015t}} \times \sin (5t + 1.554)\\ - (10.5t/{\phi _2}(x) + 18.17) \end{array} \right)} {259}}} \right. \kern-\nulldelimiterspace} {259}} $$

(42)

$${Q_3}\left( t \right) = {{9 \times \left( \begin{array}{l} - 10.905{e^{ - 0.01 \times 8.358t}} \times \sin (8.32t + 1.561)\\ - (10.5t/{\phi _3}(x) + 18.17) \end{array} \right)} \mathord{\left/ {\vphantom {{9 \times \left( \begin{array}{l} - 10.905{e^{ - 0.01 \times 8.358t}} \times \sin (8.32t + 1.561)\\ - (10.5t/{\phi _3}(x) + 18.17) \end{array} \right)} {259}}} \right. \kern-\nulldelimiterspace} {259}} $$

(43)

For a drill string in slip phase and with the action of torsional impact, part of the frictional torque acted on the drill bit can be offset by the impact torque. The initial angular displacement of the drill bit is herein less than that of the conventional drilling (without impact torque). Under this condition, dynamics of the drill string are related to the initial condition, frictional torque, viscous damping, and impact torque (including constant term and the harmonic terms), the first three orders of generalized coordinate can be given as

$$\begin{aligned} Q_{1} (t) & = {{225 \times \left[ { - 10.925e^{ - 0.05 \times 1.67t} \times \sin \left( {1.66t + 1.521} \right) - \left( {10.5t/\phi_{1} (x) + 17.59} \right)} \right]} \mathord{\left/ {\vphantom {{225 \times \left[ { - 10.925e^{ - 0.05 \times 1.67t} \times \sin \left( {1.66t + 1.521} \right) - \left( {10.5t/\phi_{1} (x) + 17.59} \right)} \right]} {259}}} \right. \kern-0pt} {259}} \\ & \quad + \;6.33 \times 10^{ - 4} \times \sin \left( {62.83t + 0.0027} \right) + 7.91 \times 10^{ - 5} \times \sin (125.66t + 0.0013) \\ \end{aligned}$$

(44)

$$\begin{aligned} Q_{2} (t) & = {{25 \times \left[ { - 10.908e^{ - 0.0167 \times 5.015t} \times \sin (5t + 1.554) - (10.5t/\phi_{2} (x) + 17.59)} \right]} \mathord{\left/ {\vphantom {{25 \times \left[ { - 10.908e^{ - 0.0167 \times 5.015t} \times \sin (5t + 1.554) - (10.5t/\phi_{2} (x) + 17.59)} \right]} {259}}} \right. \kern-0pt} {259}} \\ & \quad + \;6.37 \times 10^{ - 4} \times \sin (62.83t + 0.0009) + 7.92 \times 10^{ - 5} \times \sin (125.66t + 0.0004) \\ \end{aligned}$$

(45)

$$\begin{aligned} Q_{3} (t) & = {{9 \times \left[ { - 10.905e^{ - 0.01 \times 8.358t} \times \sin (8.32t + 1.561) - (10.5t/\phi_{3} (x) + 17.59)} \right]} \mathord{\left/ {\vphantom {{9 \times \left[ { - 10.905e^{ - 0.01 \times 8.358t} \times \sin (8.32t + 1.561) - (10.5t/\phi_{3} (x) + 17.59)} \right]} {259}}} \right. \kern-0pt} {259}} \\ & \quad + \;6.44 \times 10^{ - 4} \times \sin (62.83t + 0.0005) + 7.94 \times 10^{ - 5} \times \sin (125.66t + 0.0003) \\ \end{aligned}$$

(46)

Substituting the above equations into Eq. (22), the following equation can be obtained by using MSM

$$\theta \left( {x,t} \right) = \phi_{1} (x)Q_{1} (t) + \phi_{2} (x)Q_{2} (t) + \phi_{3} (x)Q_{3} (t)$$

(47)

where ϕ₁(x), ϕ₂(x), and ϕ₃(x) are given by Eq. (16).

Figures 3 and 4 show the torsional dynamics of the drill string with and without the action of impact torque. From the figures, the torsional impact torque will aggravate slightly the drill string vibration. In general, the HFTI seems more significant to the vibration of the bottom hole assembly. The effect of HFTI on the rock breaking is not considered in this section.

Fig. 3

Angular displacement of the drill string during the slip phase in the case no HFTI acts on the drill string (assuming that the initial relative angular displacement between the drill bit and the rotary table is determined by the static frictional torque)

Fig. 4

Angular displacement of the drill string during the slip phase in the case HFTI acts on the drill string (assuming that the initial relative angular displacement between the drill bit and the rotary table is determined by the static frictional torque as well as the HTFI)

Figure 5 shows the time response of the relative angular displacement between the drill bit and the rotary table when the drill string is in slip phase. In this section, the drill bit is regarded to overcome a same frictional torque, though the HTFI can balance part of the frictional torque. From the figure, even in the drill bit, the effect of HFTI on vibration of the drill bit is very small.

Fig. 5

Relative angular displacement of the drill bit for the cases with and without HFTI

In the actual drilling process, the HFTI aggravates the rock damage and rock failure. As a result, the required torque developed to shear the rock reduces, which means the relative angular displacement between the drill bit and the rotary table is less than that of the drilling without HFTI. In our previous work [18], it is shown that the frictional torque becomes 8150 N m when the HFTI is 600 times per minute and the corresponding relative angular displacement is 25.71 rad/s (the drill bit lags behind the rotary table). When the effect of HFTI on rock breaking is considered, the first three orders of mode shape shall be given as

$$\begin{aligned} Q_{1} (t) & = {{225 \times \left[ { - 8.145e^{ - 0.05 \times 1.67t} \times \sin (1.66t + 1.521) - (10.5t/\phi_{1} (x) + 17.59)} \right]} \mathord{\left/ {\vphantom {{225 \times \left[ { - 8.145e^{ - 0.05 \times 1.67t} \times \sin (1.66t + 1.521) - (10.5t/\phi_{1} (x) + 17.59)} \right]} {259}}} \right. \kern-0pt} {259}} \\ & \quad + \;6.33 \times 10^{ - 4} \times \sin (62.83t + 0.0027) + 7.91 \times 10^{ - 5} \times \sin (125.66t + 0.0013) \\ \end{aligned}$$

(48)

$$\begin{aligned} Q_{2} (t) & = {{25 \times \left[ { - 8.128e^{ - 0.0167 \times 5.015t} \times \sin (5t + 1.554) - (10.5t/\phi_{2} (x) + 17.59)} \right]} \mathord{\left/ {\vphantom {{25 \times \left[ { - 8.128e^{ - 0.0167 \times 5.015t} \times \sin (5t + 1.554) - (10.5t/\phi_{2} (x) + 17.59)} \right]} {259}}} \right. \kern-0pt} {259}} \\ & \quad + \;6.37 \times 10^{ - 4} \times \sin (62.83t + 0.0009) + 7.92 \times 10^{ - 5} \times \sin (125.66t + 0.0004) \\ \end{aligned}$$

(49)

$$\begin{aligned} Q_{3} (t) & = {{9 \times \left[ { - 8.125e^{ - 0.01 \times 8.358t} \times \sin (8.32t + 1.561) - (10.5t/\phi_{3} (x) + 17.59)} \right]} \mathord{\left/ {\vphantom {{9 \times \left[ { - 8.125e^{ - 0.01 \times 8.358t} \times \sin (8.32t + 1.561) - (10.5t/\phi_{3} (x) + 17.59)} \right]} {259}}} \right. \kern-0pt} {259}} \\ & \quad + \;6.44 \times 10^{ - 4} \times \sin (62.83t + 0.0005) + 7.94 \times 10^{ - 5} \times \sin (125.66t + 0.0003) \\ \end{aligned}$$

(50)

Figure 6 presents the actual dynamics of the drill string by considering the effect of HFTI on rock breaking. Figure 7 shows the relative angular displacement between the drill bit and the rotary table with considering the effect of HFTI on rock breaking. From the figure, for the actual drilling, the HTFI will mitigate the torsional vibration of the drill string. In addition, the HFTI is more sensitive to the drill string close to the drill bit. The HFTI is beneficial to the drilling process as well as the mitigation of stick-slip vibration.

Fig. 6

Drill string dynamics with considering the effect of HFTI (600 times per minute) on the rock breaking

Fig. 7

Relative angular displacement of the drill bit for the cases with and without HFTI (for the case with HFTI, the effect of HFTI on rock breaking is considered)

5 Conclusions

This study addresses the problem of stick-slip vibration that usually occurs in the drilling of hard formation. In recent years, the HFTI is used to improve the drilling efficiency. Field applications show that the HFTI is beneficial to the rock breaking and mitigation of stick-slip vibration. Since the high-frequency torsional impact drilling is realized by adding HFTI onto the drill string, the HFTI may aggravate or be a source of drill string vibration. In this study, the effect of HFTI on the torsional vibration of a drill string in slip phase is investigated. Firstly, a mechanical model of the continuous drill string is developed, with the HFTI is treated as external load. Secondly, the motion equation of the drill string is resolved through using MSM, with the HFTI is regarded as Fourier series. Finally, case studies are conducted to reveal the effects of HFTI on drill string vibration, wherein a 3000-m-drill string is analyzed, and the impact parameters are obtained from the laboratory experiments. Results show that the HFTI has little influence on the vibration of a drill string in slip phase, which also means that the HFTI will not give rise to or aggravate the drill string vibration. In fact, the HFTI aggravates the rock damage and rock failure. In this way, the HFTI changes the response of angular displacement and finally leads to the mitigation of stick-slip vibration.

Appendices

Appendix A

In this appendix, the approach of processing the impact torque is presented. For the HFTI, it acts on a certain cross section of the drill string. The impact torque is assumed to be periodical pulses shown in Fig. A.1, wherein τ is the load period and A is the load amplitude.

Fig. A.1

Impact torque

According to the figure, the expression of the impact torque can be given as

$$p(t) = A \times \left(1 - \frac{t}{\tau }\right),\;0 \le t \le \tau$$

(A.1)

From the figure, the impact torque is piecewise, which leads to difficulties in solving the equations. The Fourier series is used to solve this matter. The p(t) can be given as

$$\begin{aligned} p(t) & = \frac{{a_{0} }}{2} + a_{1} \cos (\omega t) + a_{2} \cos (2\omega t) + \cdots + b_{1} \sin (\omega t) + b_{2} \sin (2\omega t) + \cdots \\ & = \frac{{a_{0} }}{2} + \sum\limits_{n = 1}^{\infty } {\left( {a_{n} \cos (n\omega t) + \cdots + b_{n} \sin (n\omega t)} \right)} \\ \end{aligned}$$

(A.2)

where ω = 2π/τ is the fundamental frequency, and a₁, a₂, …, b₁, b₂, … are given as

$$a_{0} = \frac{\omega }{\pi }\int\limits_{0}^{2\pi /\omega } {p(t)} dt = \frac{2}{\tau }\int\limits_{0}^{\tau } {p(t)} dt$$

(A.3)

$$a_{n} = \frac{\omega }{\pi }\int\limits_{0}^{2\pi /\omega } {p(t)} \cos (n\omega t)dt = \frac{2}{\tau }\int\limits_{0}^{\tau } {p(t)} \cos (n\omega t)dt$$

(A.4)

$$b_{n} = \frac{\omega }{\pi }\int\limits_{0}^{2\pi /\omega } {p(t)} \sin (n\omega t)dt = \frac{2}{\tau }\int\limits_{0}^{\tau } {p(t)} \sin (n\omega t)dt$$

(A.5)

By substituting Eq. (A.1) into Eqs. (A.1)–(A.5), the results become

$$a_{0} = \frac{\omega }{\pi }\int\limits_{0}^{2\pi /\omega } {p(t)} dt = A$$

(A.6)

$$a_{n} = \frac{\omega }{\pi }\int\limits_{0}^{2\pi /\omega } {p(t)} \cos (n\omega t)dt = 0,n = 1,2,3 \ldots$$

(A.7)

$$b_{n} = \frac{\omega }{\pi }\int\limits_{0}^{2\pi /\omega } {p(t)} \sin (n\omega t)dt = - \frac{A}{n\pi },n = 1,2,3 \ldots$$

(A.8)

The expression of impact torque can be given as

$$p(t) = \frac{A}{2} + \frac{A}{n\pi }\sum\limits_{n = 1}^{\infty } {\sin (n\omega_{0} t)}$$

(A.9)

where ω₀ is the impact frequency. By using the first three orders, Eq. (A.9) can be rewritten as

$$p(t) = \frac{A}{2} + \frac{A}{\pi }\sin (\omega_{0} t) + \frac{A}{2\pi }\sin (2\omega_{0} t)$$

(A.10)

Appendix B

The orthogonal character is presented. Equation (7) can be rewritten as

$$GI_{p} \phi_{i}^{\prime \prime } (x) = - \omega_{i}^{2} \phi_{i} (x)$$

(B.1)

Multiplying the first term of Eq. (B.1) by ϕ_j(x) and integrating it can obtain

$$\int\limits_{0}^{l} {GI_{p} \phi_{j} (x)} \phi_{i}^{\prime \prime } (x)\rm{d}x = {GI_{p} \phi_{j} (x)} \phi_{i}^{\prime } (x) |_{0}^{l} - \int\limits_{0}^{l} {GI_{p} \phi_{j}^{{\prime }} (x)} \phi_{i}^{{\prime }} (x)\rm{d}x$$

(B.2)

Eq. (B.2) can be rewritten as

$$\int\limits_{0}^{l} {GI_{p} \phi_{j} (x)} \phi_{i}^{\prime \prime } (x)\rm{d}x{ = }\int\limits_{0}^{l} {GI_{p} \phi_{j}^{\prime \prime } (x)} \phi_{i} (x)\rm{d}x$$

(B.3)

If fixed boundary condition or free boundary condition is applied on the drill string end, the second term of Eq. (B.2) equals 0. Equation (B.2) can then be written as

$$\int\limits_{0}^{l} {GI_{p} \phi_{j} (x)} \phi_{i}^{\prime \prime } (x)\rm{d}x{ = } - \int\limits_{0}^{l} {GI_{p} \phi_{j}^{{\prime }} (x)} \phi_{i}^{{\prime }} (x)\rm{d}x$$

(B.4)

Multiplying Eq. (B.1) by ϕ_j(x) and integrating it shall have

$$\int\limits_{0}^{l} {GI_{p} \phi_{j}^{{\prime }} (x)} \phi_{i}^{{\prime }} (x)\rm{d}x = \int\limits_{0}^{l} {\omega_{i}^{2} \phi_{i} (x)} \phi_{j} (x)\rm{d}x$$

(B.5)

Exchanging the corner marks i and j, Eq. (B.4) becomes

$$\int\limits_{0}^{l} {GI_{p} \phi_{i}^{{\prime }} (x)} \phi_{j}^{{\prime }} (x)\rm{d}x = \int\limits_{0}^{l} {\omega_{j}^{2} \phi_{j} (x)} \phi_{i} (x)\rm{d}x$$

(B.6)

Eqs. (B.5) and (B.6) lead to

$$\left( {\omega_{i}^{2} - \omega_{j}^{2} } \right)\int\limits_{0}^{l} {\phi_{i} (x)} \phi_{j} (x)\rm{d}x = 0$$

(B.7)

If i ≠ j, then ω_i ≠ ω_j; we therefore have

$$\int\limits_{0}^{l} {\phi_{i} (x)} \phi_{j} (x)\rm{d}x = 0$$

(B.8)

Equation (B.8) indicates that the mode shapes are orthogonal with respect to the mass and stiffness.

Appendix C

The derivation process of Eq. (23) is to be discussed. As the mode shapes are orthogonal with respect to the inertia (or mass) and stiffness, then we obtain

$$\int\limits_{0}^{l} {J\phi_{i} (x)\phi_{j} (x)} \rm{d}x = 0,i \ne j$$

(C.1)

$$\int\limits_{0}^{l} {J\phi_{i} (x)\phi_{j} } (x)\rm{d}x = 1,i = j$$

(C.2)

$$\int\limits_{0}^{l} {GI_{p} \frac{{d^{2} \phi_{i} (x)}}{{\rm{d}x^{2} }}\phi_{j} } (x)\rm{d}x = 1,i = j$$

(C.3)

Substituting Eq. (22) into Eq. (2), we have

$$\sum\limits_{i = 1}^{\infty } {GI_{p} \frac{{d^{2} \phi_{i} (x)}}{{\rm{d}x^{2} }}Q_{i} (t) - } \sum\limits_{i = 1}^{\infty } {J\phi_{i} (x)\ddot{Q}_{i} (t) - } \sum\limits_{i = 1}^{\infty } {\beta (x)\phi_{i} (x)\dot{Q}(t)} = M(x,t)$$

(C.4)

The corresponding initial conditions are

$$\theta (x,0) = \theta_{0} (x) = \sum\limits_{i = 1}^{\infty } {\phi_{i} (x)Q_{i} } (0)$$

(C.5)

$$\frac{\partial \theta (x,0)}{\partial t} = \dot{\theta }_{0} (x) = \sum\limits_{i = 1}^{\infty } {\phi_{i} (x)\dot{Q}_{i} (0)}$$

(C.6)

Multiplying Eq. (C.4) by ϕ_j(x) and integrating it, combining with Eqs. (C.1)–(C.3), and (B.3), we have

$$\begin{aligned} \int\limits_{0}^{l} {GI_{p} \frac{{d^{2} \phi_{j} (x)}}{{\rm{d}x^{2} }}} \phi_{j} (x)\rm{d}xQ_{j} (t) - \int\limits_{0}^{l} {J\phi_{j}^{2} (x)\rm{d}x\ddot{Q}_{j} (t)} \\ - \sum\limits_{i = 1}^{\infty } {\int\limits_{0}^{l} {\beta (x)\phi_{i} (x)\phi_{j} (x)\rm{d}x} } \dot{Q}_{i} (t) = \int\limits_{0}^{l} {\phi_{j} (x)} M(x,t)\rm{d}x \end{aligned}$$

(C.7)

By conducting similar operations to Eqs. (C.5) and (C.6), we have

$$Q_{j} (0) = \frac{1}{{\overline{J}_{j} }}\int\limits_{0}^{l} {J\theta_{0} (x)\phi_{j} (x)\rm{d}x}$$

(C.8)

$$\dot{Q}_{j} (0) = \frac{1}{{\overline{J}_{j} }}\int\limits_{0}^{l} {J\dot{\theta }_{0} (x)\phi_{j} (x)\rm{d}x}$$

(C.9)

Combining with Eqs. (18), (19), and (B.1), the first term of Eq. (C.7) can be written as

$$\int\limits_{0}^{l} {GI_{p} \frac{{d^{2} \phi_{j} (x)}}{{\rm{d}x^{2} }}\phi_{j} (x)\rm{d}xQ_{j} (t)} = - \omega_{j}^{2} \overline{J}_{j} Q_{j} (t)$$

(C.10)

and Eq. (C.7) becomes

$$\overline{J}_{j} \ddot{Q}_{j} (t) + \omega_{j}^{2} \overline{J}_{j} Q_{j} (t) + \sum\limits_{i = 1}^{\infty } {\int\limits_{0}^{l} {\beta (x)\phi_{i} (x)\phi_{j} (x)\rm{d}x} } \dot{Q}_{j} (t) = \overline{M}_{j}$$

(C.11)

For the third term of Eq. (C.11), the non-diagonal matrix will lead to difficulties in equation decoupling. In order to decouple the third term of Eq. (C.11), the viscous damping is assumed to be

$$\beta (x) = aJ$$

(C.12)

Defining the jth damping ratio ξ_j is

$$\xi_{j} = \frac{a}{{2\omega_{j} }}$$

(C.13)

where a is constant. By combining Eqs. (C.11)–(C.13), Eq. (23), which is a decoupled differential equation of the generalized coordinate, can be obtained.