Pochhammer–Chree waves: polarization of the axially symmetric modes

Abstract

The exact solutions of the linear Pochhammer–Chree equation for propagating harmonic waves in a cylindrical rod are analyzed. Spectral analysis of the matrix dispersion equation for longitudinal axially symmetric modes is performed. Analytical expressions for displacement fields are obtained. Variation of wave polarization on the free surface due to variation of Poisson’s ratio and circular frequency is analyzed. It is observed that at the phase speed coinciding with the bulk shear speed ($c_2$) all the components of the displacement field vanish, meaning that no longitudinal axisymmetric Pochhammer–Chree wave can propagate at $c_2$ phase speed.

1 Introduction

The equation for propagating harmonic waves in a cylindrical rod, now known as the Pochhammer–Chree equation, was for the first time derived in [1,2,3]. However, the corresponding solutions binding the phase or group speed with frequency remained unexplored until the middle of the last century, when the first branches of the dispersion curves were obtained numerically in [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22]. In [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20] longitudinal axially symmetric modes were explored, and in [21, 22] flexural and torsional modes were also considered. According to [16] the axially symmetric longitudinal modes are denoted by L(0, m), where m is the mode number.

In [4,5,6] by asymptotic methods were obtained analytical formulas for both short-wave ($c_{1,\mathrm{lim}})$ and long-wave ($c_{{2,\mathrm{lim}}} )$ limits for the phase speed for the lowest (fundamental) branch of the longitudinal axially symmetric modes. Following [6] (see also [15]), the short-wave limit speed ($c_{1,\mathrm{lim}})$ at $\omega \rightarrow \infty$

$$\begin{aligned} c_{1,\mathrm{lim}} =c_\mathrm{R} \end{aligned}$$

(1.1)

coincides with Rayleigh wave speed ($c_\mathrm{R})$, while the long-wave limit speed $c_{{2,}\mathrm{lim}}$ yields [15]

$$\begin{aligned} c_{{2,}\mathrm{lim}} =\sqrt{\frac{E}{\rho }}, \end{aligned}$$

(1.2)

where E is Young’s modulus and $\rho$ is the material density. In [6, 15] the long-wave limit $c_{{2,}\mathrm{lim}}$ was named as the “rod” wave speed.

One of the interesting peculiarities of propagating $L(0,m), m>1$, modes at $\gamma \rightarrow 0$, where $\gamma$ is the wave number ($\gamma =2\pi /\lambda$, where $\lambda$ is the wavelength), corresponds to the zero slope of the dimensionless frequency $\varOmega$ [15]:

$$\begin{aligned} \mathop {\lim }\limits _{\gamma \rightarrow 0} \frac{\partial \varOmega }{\partial \gamma }=0. \end{aligned}$$

(1.3)

In (1.3) $\varOmega =\omega R/c_2$; $\omega$ is a circular frequency, R is a radius of the rod; and $c_2$ is a speed of the bulk shear wave. Actually, condition (1.3) means the presence of the horizontal asymptote in the dispersion relation $\omega (c)$ at the phase speed $c\rightarrow \infty$ for higher longitudinal axially symmetric modes. Resemblance of the dispersion curves of Pochhammer–Chree waves with Lamb and Love ones is remarked in [23, 24].

Extensions of the Pochhammer–Chree waves to helical waves (longitudinal axially symmetric modes) that relate to non-integer coefficients at the angle coordinate in the corresponding potentials were analyzed in [25,26,27]. The analysis of rotational waves in cylinders of finite length was performed in [28].

2 Displacement representation

Equation of motion for an isotropic medium in the absence of body forces can be represented in a form

$$\begin{aligned} c_1^2 \nabla \hbox {div}\,\mathbf{u}-c_2^2 \hbox {rot}\, \hbox {rot} \,\mathbf{u} = \partial _{tt}^2 \mathbf{u}, \end{aligned}$$

(2.1)

where $\mathbf{u}$ is the displacement field, $c_1, c_2$ are speeds of bulk longitudinal and shear waves, respectively, and

$$\begin{aligned} c_1 =\sqrt{\frac{\lambda +2\mu }{\rho }},\quad c_2 =\sqrt{\frac{\mu }{\rho }}. \end{aligned}$$

(2.2)

In (2.2) $\lambda , \mu$ are Lame’s constants and $\rho$ is a material density.

The Helmholtz representation for the displacement field $\mathbf{u}$ yields

$$\begin{aligned} \mathbf{u}=\nabla \varPhi +\hbox {rot}{\varvec{\Psi }}, \end{aligned}$$

(2.3)

where $\varPhi$ and ${\varvec{\Psi }}$ are scalar and vector potentials, respectively. Substituting (2.3) into equation of motion (2.1) yields

$$\begin{aligned} c_1^2 \Delta {{\varPhi }} ={{\ddot{\varPhi }}}, c_2^2 \Delta {\varvec{\Psi }} ={\varvec{{\ddot{\Psi }}}}. \end{aligned}$$

(2.4)

For a harmonic wave propagating along axis z, potentials (2.4) can be represented in a form

$$\begin{aligned} \varPhi =\varPhi _0 ({{\varvec{x}}}')e^{i\gamma (z-ct)},\quad {\varvec{\Psi }} ={\varvec{\Psi }} _0 ({{\varvec{x}}}')e^{i\gamma (z-ct)}, \end{aligned}$$

(2.5)

where, as before, $\gamma$ is the wave number related to the phase speed c and circular frequency $\omega$ by equation

$$\begin{aligned} \gamma =\frac{\omega }{c}. \end{aligned}$$

(2.6)

In (2.5) ${{\varvec{x}}}'$ is the (vector) coordinate in the cross section of a rod ($\mathbf{{x}'}=\mathbf{x}-(\mathbf{n}\cdot \mathbf{x})\mathbf{n})$; $\mathbf{n}$ is the wave vector; and $z=\mathbf{n}\cdot \mathbf{x}$ (z is the coordinate along central axis of the rod).

Substituting representations (2.5) into Eq. (2.4) yields the Helmholtz equations for the potentials

$$\begin{aligned} \Delta \varPhi _0 +\left( {\frac{c^{2}}{c_1^2 }-1} \right) \gamma ^{2}\varPhi _0 =0,\quad \Delta {\varvec{\Psi }} _0 +\left( {\frac{c^{2}}{c_2^2 }-1} \right) \gamma ^{2}{\varvec{\Psi }} _0 =0. \end{aligned}$$

(2.7)

Now, taking into account (2.3)–(2.7), the desired vector field corresponding to the propagating longitudinal axially symmetric harmonic wave becomes [19]

$$\begin{aligned} u_r= & {} -\left[ {q_1 C_1 J_1 (q_1 r)+i\gamma C_2 J_1 (q_2 r)} \right] e^{i\gamma (z-ct)} \nonumber \\ u_\theta= & {} 0 \nonumber \\ u_z= & {} \left[ {i\gamma C_1 J_0 (q_1 r)+q_2 C_2 J_0 (q_2 r)} \right] e^{i\gamma (z-ct)}, \end{aligned}$$

(2.8)

where

$$\begin{aligned} q_{_1 }^2 =\left( {\frac{c^{2}}{c_1^2 }-1} \right) \gamma ^{2},\quad q_{_2 }^2 =\left( {\frac{c^{2}}{c_2^2 }-1} \right) \gamma ^{2}. \end{aligned}$$

(2.9)

3 Dispersion equation

Traction-free boundary conditions on a lateral cylindrical surface at $r=R$ have the form

$$\begin{aligned} \left. {\mathbf{t}_{\varvec{\upnu }} \equiv \left( {\lambda (\hbox {tr}{\varvec{\upvarepsilon }} ){\varvec{\upnu }} +2\mu {\varvec{\upvarepsilon }} \cdot {\varvec{\upnu }} } \right) } \right| _{r=R} =0, \end{aligned}$$

(3.1)

where ${\varvec{\upnu }}$ is the (outward) surface normal.

Substituting the displacement representation (2.8) into boundary conditions (3.1) yields the following equations written up to exponential multiplier $e^{i\gamma (z-ct)})$

$$\begin{aligned}&t_{rr} \equiv \lambda I_{\varvec{\varepsilon }} +2\mu {\varvec{\varepsilon }} _{rr} =-\left[ {\begin{array}{l} \lambda \left( {q_1^2 +\gamma ^{2}} \right) J_0 (q_1 r)C_1 \\ +\,\frac{2\mu }{r}\left[ {\begin{array}{l} q_1 C_1 \left( {q_1 rJ_0 (q_1 r)-J_1 (q_1 r)} \right) \\ +\,i\gamma C_2 \left( {q_2 rJ_0 (q_2 r)-J_1 (q_2 r)} \right) \\ \end{array}} \right] \\ \end{array}} \right] _{r=R} =0 \nonumber \\&t_{rz} \equiv 2\mu {\varvec{\varepsilon }} _{rz} =-\mu \left[ {\begin{array}{l} i\gamma \left[ {q_1 C_1 J_1 (q_1 r)+i\gamma C_2 J_1 (q_2 r)} \right] \\ +\left[ {i\gamma q_1 C_1 J_1 (q_1 r)+q_2^2 C_2 J_1 (q_2 r)} \right] \\ \end{array}} \right] _{r=R} =0. \end{aligned}$$

(3.2)

Equation (3.2) result in the desired dispersion equation

$$\begin{aligned} \det \mathbf{A}=0, \end{aligned}$$

(3.3)

where $\mathbf{A}$ is a square and generally non-symmetric $2\times 2$ matrix with complex coefficients:

$$\begin{aligned}&A_{11} =-\left( {\left( {q_1^2 +\gamma ^{2}} \right) \frac{c_1^2 }{c_2^2 }-2\gamma ^{2}} \right) J_0 (q_1 R)+\frac{2q_1 }{R}J_1 (q_1 R) \nonumber \\&A_{12} =-\frac{2i\gamma }{R}\left( {q_2 RJ_0 (q_2 R)-J_1 (q_2 R)} \right) \nonumber \\&A_{21} =-2i\gamma q_1 J_1 (q_1 R) \nonumber \\&A_{22} =-\left( {q_2^2 -\gamma ^{2}} \right) J_1 (q_2 R). \end{aligned}$$

(3.4)

Two-dimensional (right) eigenvectors related to vanishing eigenvalues (kernel eigenvectors) of matrix $\mathbf{A}$ define polarization of the corresponding Pochhammer–Chree waves.

4 Spectral analysis of matrix $\mathbf{A}$

Spectral analysis of matrix $\mathbf{A}$ splits into two cases.

4.1 Matrix $\mathbf{A}$ is (semi) simple

That is the case when matrix $\mathbf{A}$ contains no Jordan blocks and hence has two distinct eigenvectors. Spectral decomposition of $\mathbf{A}$ yields

$$\begin{aligned} \vec {\alpha }_{1} \leftrightarrow \lambda _{1},\quad \vec {\alpha }_{2} \leftrightarrow \lambda _{2}, \end{aligned}$$

(4.1)

where $\lambda _1, \lambda _2$ are right eigenvalues of matrix $\mathbf{A}$, and $\vec {\alpha }_1, \vec {\alpha }_2$ are two-dimensional eigenvectors. The characteristic equation for matrix $\mathbf{A}$ written in the form

$$\begin{aligned} \det \left( {\mathbf{A}-\lambda \mathbf{I}} \right) =0, \end{aligned}$$

(4.2)

where $\mathbf{I}$ is the unit diagonal matrix, yields the following representations for eigenvalues

$$\begin{aligned} \lambda _{1,2} =s \pm d, \end{aligned}$$

(4.3)

where

$$\begin{aligned} s=\frac{A_{11} +A_{22} }{2},\quad d=\sqrt{f^{2}+A_{12} A_{21} },\quad f=\frac{A_{11} -A_{22} }{2}, \end{aligned}$$

(4.4)

Note that coefficients $A_{ij}$ in (4.4) are defined by (3.4).

The corresponding (normed) eigenvectors have the form

$$\begin{aligned} \vec {\alpha }_{1,2} =\left( {{\begin{array}{l} {\frac{f\pm d}{\sqrt{\left| {A_{21} } \right| ^{2}+\left| {f\pm d} \right| ^{2}}}} \\ {\frac{A_{21} }{\sqrt{\left| {A_{21} } \right| ^{2}+\left| {f\pm d} \right| ^{2}}}} \\ \end{array} }} \right) . \end{aligned}$$

(4.5)

Analyses of expressions (4.3) and (4.5) allow formulating

Proposition 4.1

• (a) The necessary and sufficient condition for simplicity of matrix $\mathbf{A}$ is

  $$\begin{aligned} d\ne 0, \end{aligned}$$

  (4.6)

  where discriminant d is defined by (4.4).

• (b) Condition for degeneracy of matrix $\mathbf{A}$ takes the form

  $$\begin{aligned} A_{11} A_{22} =A_{12} A_{21}. \end{aligned}$$

  (4.7)

Proof

• (a) Expression (4.3) reveals that condition (4.6) gives a necessary and sufficient condition for simplicity of the considered matrix.

• (b) Due to (4.3), condition of degeneracy takes the form

  $$\begin{aligned} s^{2}=d^{2}. \end{aligned}$$

  (4.8)

Equation (4.8) with account of (4.4) yields the desired Eq. (4.7). $\square$

Remark 4.1

The straightforward analysis reveals that condition (4.7) is equivalent to the dispersion equation (3.3).

4.2 Matrix $\mathbf{A}$ is non-semisimple (contains Jordan block)

Condition for non-simplicity of matrix $\mathbf{A}$ following from expression (4.3) yields

$$\begin{aligned} d=0. \end{aligned}$$

(4.9)

At (4.9) the spectral decomposition of matrix $\mathbf{A}$ results in

$$\begin{aligned} \left( {{\begin{array}{l} {\frac{f}{\sqrt{\left| {A_{21} } \right| ^{2}+\left| f \right| ^{2}}}} \\ {\frac{A_{21} }{\sqrt{\left| {A_{21} } \right| ^{2}+\left| f \right| ^{2}}}} \\ \end{array} }} \right) \leftrightarrow \lambda _{1,2} =s. \end{aligned}$$

(4.10)

Thus, at (4.9) matrix $\mathbf{A}$ becomes not only non-simple matrix, but non-semisimple as well, since it has only one (right) eigenvector (4.10).

At (4.9) and in view of (4.3) the double degeneracy of $\mathbf{A}$ is equivalent to

$$\begin{aligned} s=0. \end{aligned}$$

(4.11)

Now, taking into account (4.4), the following proposition flows out

Proposition 4.2

• (a) The necessary and sufficient condition for non-semisimplicity of matrix $\mathbf{A}$ is

  $$\begin{aligned} f^{2}=-A_{12} A_{21}. \end{aligned}$$

  (4.12)

• (b) At condition (4.12) the double degeneracy of matrix $\mathbf{A}$ takes the form

  $$\begin{aligned} A_{11} =-A_{22}. \end{aligned}$$

  (4.13)

Proof

• (a) Proposition 4.1a ensures that at (4.9) matrix $\mathbf{A}$ becomes non-simple. But, at (4.9) both eigenvectors coincide due to (4.5), so actually $\mathbf{A}$ becomes non-semisimple. Then, substituting expressions (4.4) into (4.9) yields condition (4.12).

• (b) Due to (4.3), the degeneracy of matrix $\mathbf{A}$ at (4.9) is equivalent to

  $$\begin{aligned} s=0. \end{aligned}$$

  (4.14)

But, (4.14) is equivalent to (4.13). $\square$

Remark 4.2

For the considered case of degeneracy of the non-semisimple matrix, the corresponding dispersion equation takes the form

$$\begin{aligned} \left( {q_2^2 -\gamma ^{2}} \right) ^{2}\left( {J_1 (q_2 R)} \right) ^{2}-\gamma ^{2}q_1 q_2 J_0 (q_2 R)J_1 (q_1 R)+\frac{\gamma ^{2}q_1 }{R}J_1 (q_2 R)J_1 (q_1 R)=0. \end{aligned}$$

(4.15)

5 Displacement fields

Components of the kernel eigenvectors (4.5), (4.10), that correspond to vanishing eigenvalues, are coefficients $C_1, C_2$ in expressions (2.8). Depending on the spectral properties of matrix $\mathbf{A}$, two cases are considered.

5.1 Matrix $\mathbf{A}$ is (semi) simple

Substituting components of the kernel eigenvector (4.5) that corresponds to vanishing eigenvalue (4.3) into (2.8) at condition (4.7) yields

$$\begin{aligned} \begin{array}{l} u_r =\frac{-\,\left[ {q_1 \left( {f\pm d} \right) J_1 (q_1 r)+i\gamma A_{21} J_1 (q_2 r)} \right] }{\sqrt{\left| {A_{21} } \right| ^{2}+\left| {f\pm d} \right| ^{2}}}e^{i\gamma (z-ct)} \\ u_z =\frac{\left[ {i\gamma \left( {f\pm d} \right) J_0 (q_1 r)+q_2 A_{21} J_0 (q_2 r)} \right] }{\sqrt{\left| {A_{21} } \right| ^{2}+\left| {f\pm d} \right| ^{2}}}e^{i\gamma (z-ct)}, \\ \end{array} \end{aligned}$$

(5.1)

where f, d are defined by (4.4) and coefficients $A_{ij}$ of matrix $\mathbf{A}$ are defined by (3.4). In (5.1) and further vanishing component $u_\theta$ is not present.

Proposition 5.1

For (semi$-)$ simple matrix $\mathbf{A}$ the displacement component $u_z$ vanishes at $r=0$ and at $c=c_2$ regardless of frequency.

Proof

For the considered case condition (4.7) takes the form

$$\begin{aligned} i\gamma \left( {f\pm d} \right) =-q_2 A_{21}. \end{aligned}$$

(5.2)

Equation (5.2) with account of (4.4) can be transformed to the equivalent equation:

$$\begin{aligned} i\gamma q_2 \left( {A_{11} -A_{22} } \right) +q_2^2 A_{21} +\gamma ^{2}A_{12} =0. \end{aligned}$$

(5.3)

Substituting expressions (3.4) into (5.3) at $c=c_2$ ensures vanishing $u_z$ at $r=0$. $\square$

Corollary

For the considered simple matrix $\mathbf{A}$, expressions (5.1) are applicable for any axially symmetric mode L(0, m), $m>0$.

5.2 Matrix $\mathbf{A}$ is non-semisimple (contains Jordan block)

Substituting components of the kernel eigenvector (4.10) into (2.8) with account of conditions of degeneracy (4.12) and (4.13) yields

$$\begin{aligned} u_r= & {} \frac{-\left[ {q_1 f J_1 (q_1 r)+i\gamma A_{21} J_1 (q_2 r)} \right] }{\sqrt{\left| {A_{21} } \right| ^{2}+\left| f \right| ^{2}}}e^{i\gamma (z-ct)} \nonumber \\ u_z= & {} \frac{\left[ {i\gamma f J_0 (q_1 r)+q_2 A_{21} J_0 (q_2 r)} \right] }{\sqrt{\left| {A_{21} } \right| ^{2}+\left| f \right| ^{2}}}e^{i\gamma (z-ct)}. \end{aligned}$$

(5.4)

Proposition 5.2

For non-semisimple matrix $\mathbf{A}$ the displacement component $u_z$ does not vanish at $r=0$ and at $c=c_2$ regardless of frequency.

Proof

For the considered case condition (4.13) takes the form

$$\begin{aligned} i\gamma f=-q_2 A_{21}. \end{aligned}$$

(5.5)

Equation (5.5) with account of (4.4) can be transformed to the equivalent equation

$$\begin{aligned} i\gamma \left( {A_{11} -A_{22} } \right) +2q_2 A_{21} =0. \end{aligned}$$

(5.6)

Substituting (3.4) into (5.6) at $c=c_2$ reveals that condition (5.5) does not hold. $\square$

Corollary

For the considered non-semisimple matrix $\mathbf{A}$, expressions (5.1) are applicable for any axially symmetric mode L(0, m), $m>0$.

5.3 Displacement amplitudes on a lateral surface

Normalized amplitudes $U_r, U_z$ of the displacement fields on a cylinder lateral surface at $r=R$ can be defined by the following formulas

$$\begin{aligned}&U_r \equiv \left. {\frac{\left| {u_r } \right| }{\left| {u_r } \right| +\left| {u_z } \right| +1}} \right| _{r=R} \nonumber \\&U_z \equiv \left. {\frac{\left| {u_z } \right| }{\left| {u_r } \right| +\left| {u_z } \right| +1}} \right| _{r=R}. \end{aligned}$$

(5.7)

Remark 5.3

Generally, amplitude values of the components $\left| {u_r } \right|$ and $\left| {u_z } \right|$ can simultaneously vanish at some value of the radius, and particularly, they can vanish at $r=R$. For this reason unity is added to the denominators in (5.7).

6 Displacements for the fundamental mode

Displacement components are defined by expressions (5.1) for a simple matrix. (It can be shown that for the fundamental mode the non-semisimplicity cannot arise.) Amplitudes $U_r, U_z$ on a free surface of the cylinder are defined by Eq. (5.7). The amplitudes $U_r, U_z$ will be analyzed at different values of Poisson’s ratio from the interval ${l{\nu }} \in (0, 0.4]$.

6.1 Dispersion curves

For these values of Poisson’s ratio dispersion equation (3.3) allowed to obtain dispersion curves related to the fundamental axially symmetric mode L(0, 1). The corresponding curves are presented in Fig. 1 in terms of the dimensionless (1) phase speed $c/c_{2,\mathrm{lim} }$, where $c_{2,\mathrm{lim} }$ is defined by (1.2), and (2) dimensionless frequency $\omega R/c_2$, where $c_2$ is the bulk shear wave speed defined by (2.2).

The corresponding values of Poisson’s ratio are given in the legend. The dispersion curves in Fig. 1 clearly indicate the presence of two asymptotic phase velocities: $c_{1,\lim }$ at $\omega \rightarrow \infty$ and $c_{2,\lim }$ at $\omega \rightarrow 0$.

Fig. 1

Dispersion curves at different Poisson’s ratios

6.2 Amplitudes $U_r$

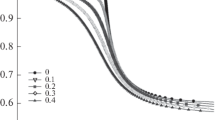
Variation of the displacement amplitude $U_r$ related to the fundamental mode with respect to variation of the phase speed is plotted in Fig. 2. The presented plots correspond to different values of Poisson’s ratio indicated in the legend.

Fig. 2

Variation of amplitude Ur vs relative phase speed

The most interesting in Fig. 2 is vanishing of the amplitude $U_r$ at the phase speed $c\rightarrow c_2 \pm 0$ and at $c\rightarrow c_{2,\mathrm{lim} } -0$.

6.3 Amplitude $U_z$

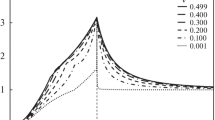
Variation of the displacement amplitude $U_z$ related to the fundamental mode with respect to variation of the phase speed is plotted in Fig. 3. The presented plots correspond to different values of Poisson’s ratio indicated in the legend.

Fig. 3

Variation of amplitude Uz vs relative phase speed

Herein, the displacement amplitude $U_z$ vanishes at two values of the phase speed related to $c_2$ and another speed $c_k$. The latter speed depends upon Poisson’s ratio and can be approximated by the following fraction-rational expression

$$\begin{aligned} c_k \approx \frac{c_{2,\mathrm{lim} } }{a+b{{\nu }}},\quad a= 1.0126,\quad b=0.8889. \end{aligned}$$

(6.1)

At higher speeds than $c_k$ the component $U_z$ gradually rises to about 0.5 almost independently of Poisson’s ratio. Parameters a, b in (6.1) are found by the regression analysis. The obtained values for a, b in (6.1) ensure relative error not exceeding 0.1% for the considered Poisson’s ratio values ${{\nu }} \in (0, 0.4]$.

Variation of the phase speed $c_k$ with respect to Poisson’s ratio is marked by dots in Fig. 4, where the dashed line corresponds to computations by approximate formula (6.1).

Fig. 4

Variation of phase speed ck vs Poisson’s ratio

Remark 6.1

• (A) Substituting phase speed $c=c_2$ into (3.4) reveals that at $c_2$ matrix $\mathbf{A}$ is simple with the following kernel (right) eigenvector

  $$\begin{aligned} \left( {{\begin{array}{l} 0 \\ 1 \\ \end{array} }} \right) \leftrightarrow \lambda =0. \end{aligned}$$

  (6.2)

  The kernel eigenvector (6.2) corresponds to the following coefficients in representation (2.8):

  $$\begin{aligned} C_1 =0,\quad C_2 =1. \end{aligned}$$

  (6.3)

  Analyzing expressions (5.1), (5.7) for the considered matrix $\mathbf{A}$ ensures that $U_r =U_z =0$ at $c\rightarrow c_2 \pm 0$.

• (B) Analogously, substituting coefficients (6.3) into expression (5.1) for the displacement components ensures that $u_r =u_z =0$ at $c\rightarrow c_2 \pm 0$ independent of circular frequency. This means that no longitudinal axisymmetric harmonic Pochhammer–Chree waves can propagate at $c_2$ phase speed.

7 Conclusions

The exact solutions of the linear Pochhammer–Chree equation for propagating harmonic axisymmetric longitudinal waves L(0, m) in a cylindrical rod were analyzed.

Spectral analysis of the matrix dispersion equation for longitudinal axially symmetric modes ($L(0, m), m>0)$ of Pochhammer–Chree waves was performed, revealing that no longitudinal modes can propagate at $c_2$ phase speed.

Variation of wave polarization on the free surface due to variation of Poisson’s ratio and circular frequency was analyzed. It was found that there was phase speed $c_k$ (value of this speed depends upon Poisson’s ratio) at which longitudinal component $U_z$ of the fundamental longitudinal mode vanishes.