1 Introduction

The purpose of the modal identification is based on the input and output data of a system to estimate modal parameters. In the process of modal estimation, the measurement data contaminated with noise and the extent of interference among the structural modes may often, however, affect the accuracy of identification results and even cause the problem of identifiability. Modal interference refers to the phenomenon that vibration energy of each mode of a system may overlap with other modes within certain frequency range. Major causes of modal interference include close frequencies, high damping ratios, and non-proportional damping. The serious problems of modal interference may result in the difficulty of modal identification, especially for a structure with axisymmetrical model, i.e., having close (even repeated) modes. Structures that are nearly axisymmetric play important roles in engineering applications, including disk and drum brakes, computer disk drives, gas turbine assemblies, and motor or railway vehicle system [1]. Consequently, it is desirable to develop techniques for modal identification without the influence on the serious problem of modal interference of structures and the effect of noise from measurement input and output data.

Numerous papers have been presented on system identification, acquiring the estimation of important parameters from measured data. During the 1970s, Ibrahim proposed a method developed in the time domain, which is usually referred to as the Ibrahim time domain method (ITD Method) [1]. The ITD method was employed to extract the modal characteristics of the structures such as the cantilever beams or the payload models [2]. The method is effective in identifying complex modes even for closely spaced modes with distinct damping ratios [3]. Although we can use the ITD method to perform modal identification via an eigenvalue analysis, the ITD method applies only to problems involving the free-decay response data of structures and sometimes its efficiency is low due to its large numerical computation. In addition, the modes identified by the ITD method generally include some fictitious modes due to numerical computation. In 1978, Ibrahim proposed the modal confidence factor (MCF) [4], which is to be computed for each and every identified mode, and the structural modes can then be separated from the computational modes accordingly, i.e., to decide whether a mode is a structural mode or not [5]. Gao and Randall further presented the so-called mode-shape coherence and confidence factor (MSCCF) [6] using the overall information of mode shapes to sort out physical modes from the identified modes. Because the calculation of MSCCF value is not just the information of a single mode as in the calculation of MCF, the MSCCF values are generally more reliable than the MCF values in distinguishing the structural modes from computational modes.

Based on the Prony’s theory, Brown et al. developed the least square complex exponential algorithm (LSCE) [7] using a squared output matrix constructed by multichannel impulse response functions, which is a well-known technique in conventional modal analysis yielding global estimates of residues and poles. The pseudo-inverse technique is employed to estimate the coefficients of the Prony’s polynomials and then extract the modal parameters of a system through the Prony’s technique. In 1982, Vold et al. further proposed poly reference complex exponential method (PRCE) [8] to perform modal identification for the case that one of the modes may not be present in the response data. Although repeated eigenvalues or closely spaced modes are said to be resolved by PRCE method, the judgment about the appropriate model order remains subjective and open to experimentation followed by construction of stabilization diagram to choose the proper model order and modal properties. In 1985, among follow-up developments on minimal realization algorithm and singular value decomposition (SVD) [9], Juang and Pappa [10] proposed the Eigensystem Realization Algorithm (ERA) using the impulse response or the free-vibration response of the system to construct the Hankel matrix, which is an augmented matrix containing Markov parameters, for reducing the effect of noise, and making the parameters estimation more accurate. The modal parameters of the system are identified through SVD of the Hankel matrix, and the accuracy of identification results will, however, be low when high noise levels are present in measurements. Subsequently, Fahey and Pratt [11] took up some applicable time domain algorithms by reviewing the complex exponential algorithm, Pisarenko harmonic decomposition, ITD method, and ERA. They also pointed out the quality of a fitting function of system damping is one significant difference between time and frequency domain techniques. In general, the time domain techniques outperform frequency domain techniques for a system with light damping [11]. A lightly damped response may distribute its effects over the entire duration of a time domain record, but produce only a few spectral lines when transformed to the frequency domain. Also, principal component analysis (PCA) may be used to resolve the issues of the number of degree of freedom of a system being less than the number of measured response channel. In 1986, Leuridan et al. [12] used a multivariate model in the form of a nonhomogeneous finite difference equation to identify modal parameters of a mechanical structure. By applying the multiple-input and multiple-output (MIMO) concept, the modal parameters of this equation are estimable from vibration data, and improved global estimates of modal parameters can then be obtained, including the highly coupled and pseudo-repeated modes of vibration.

In this paper, we propose a modification to the technique of channel-expansion in Ibrahim time domain method to improve the accuracy of system identification for structures with modal interference. In general, the accurate estimation the order of system matrix in Ibrahim time domain method is important for well-implemented modal identification. By introducing the singular value decomposition in conjunction with the method of least squares, the system matrix can be obtained and the order of system can be determined, the phenomenon of omitted modes can then be avoided. Additionally, the phase angle diagram of frequency response function can be used to more easily distinguish the structural modes influenced by modal interference and then improve the accuracy in parametric estimation of systems with modal interference.

2 Ibrahim time domain method

The Ibrahim time-domain method uses free-decay responses of several outputs of a structure under test to estimate its modal parameters in complex form [1] and has been extensively used in the engineering application [13,14,15]. From the measured free-decay responses at n stations on a structure under test, each with q sampling points, we define a system matrix \([\mathbf{A}]\), which is an \(n\times n\) matrix, such that

$$\begin{aligned} \mathbf{[A][X]}=\mathbf{[Y]} \end{aligned}$$
(1)

where \([\mathbf{X}]\) and \([\mathbf{Y}]\) are, respectively, \(n\times q\) data-expansion matrices of the free decay and its time-shifted response. The number q is generally chosen to be larger than the number of measurement channels n, and the system matrix \([\mathbf{A}]\) can be therefore estimated from \([\mathbf{X}]\) and \([\mathbf{Y}]\) through the least-squares method.

It can be shown that the natural frequencies and the damping ratios of the original vibrating system are directly related to the eigenvalues of the system matrix \([\mathbf{A}]\), and the mode shapes correspond to the eigenvectors of \([\mathbf{A}]\). Denote an eigenvalue of \([\mathbf{A}]\) and a characteristic root of the original vibrating system as \(\rho _\mathrm{r} =\beta _\mathrm{r} +i\gamma _\mathrm{r} \) and \(s_\mathrm{r} =\sigma _\mathrm{r} +iv_\mathrm{r} \), respectively. One can derive [1]

$$\begin{aligned} \left\{ {\begin{array}{l} \sigma _\mathrm{r} =\frac{1}{2\Delta \tau }\ln \left( {\beta _\mathrm{r} ^{2}+\gamma _\mathrm{r} ^{2}} \right) \\ v_\mathrm{r} =\frac{1}{\Delta \tau }\tan ^{-1}\left( {\frac{\gamma }{\beta }} \right) \\ \end{array}} \right. \end{aligned}$$
(2)

from which the natural frequencies \(\omega _\mathrm{nr} \) and damping ratios \(\zeta _\mathrm{r} \) of the structural system can be obtained to be

$$\begin{aligned} \left\{ {\begin{array}{l} \omega _\mathrm{nr} =\sqrt{\sigma _\mathrm{r} ^{2}+v_\mathrm{r} ^{2}} \\ \zeta _\mathrm{r} =\frac{\left| {\sigma _\mathrm{r}} \right| }{\sqrt{\sigma _\mathrm{r} ^{2}+v_\mathrm{r} ^{2}}} \\ \end{array}} \right. \end{aligned}$$
(3)

Hence, once the system matrix \([\mathbf{A}]\) is obtained via least-squares analysis from measured data, the modal parameters of the structural system can be determined by solving the eigenvalue problem associated with the system matrix \([\mathbf{A}]\).

2.1 Channel-expansion technique

In reality, we do not know in advance how many modes are required to describe the dynamic behavior of the observed structural system. The number of (real) modes m involved in the response determines the number of measurement channels, which is chosen to be at least twice of the number of modes of interest to appropriately identify the 2m complex modes. If the number of measurement channels does not actually reach 2m, we may employ the technique of channel expansion [3] with sampling time shifted to reach the total available number of measurement channels. It should be noted that, however, the identified mode shapes are composed of the components corresponding only to those physically measured response channels. In addition, due to the fact that the results of modal identification may be poor from the noise effect, through the channel-expansion technique in ITD method, which uses time-delayed sampling points from the original response to increase the total numbers of sampling points and measurement channels, we can therefore reduce the effect of noise to improve the accuracy of modal estimation based on the property of consistency in the theory of system identification. It should be mentioned that the channel-expansion technique requires significant computing capacity, so it is necessary to use appropriate and efficient sampling time shifted in ITD method, as described next.

2.2 Discussion of sampling time shifted

In this section, we will discuss the condition of sampling time shifted in ITD method to avoid the distortion of modal identification. Note that in driving Eq. (2), \(v_\mathrm{r} \) is a damped natural frequency \(\omega _\mathrm{dr} \) of a structural system. Therefore, the solution of \(\omega _\mathrm{dr} \) is not unique and can be expressed as

$$\begin{aligned} \omega _\mathrm{dr} =\frac{1}{\Delta \tau }\left[ \tan ^{-1}\left( {\frac{\gamma }{\beta }} \right) +k\pi \right] \end{aligned}$$
(4)

in which \(-\frac{\pi }{2}<\tan ^{-1}\left( {\frac{\gamma }{\beta }} \right) <\frac{\pi }{2}, k=0,1,2,3,\ldots \), and \(\Delta \tau \) is the sampling time shifted in ITD method. To avoid the ambiguous use of Eq. (4), it is necessary to specify that all the modes which contribute to the response corresponding to frequencies which can be calculated from the equation by using only a single value for k. Due to inequality of \(\tan ^{-1}\left( {\frac{\gamma }{\beta }} \right) \) in Eq. (4), and that all values of \(\omega _\mathrm{dr} \) in the frequency range of interest are required to be considered, Eq. (2) can be therefore written as the following inequality

$$\begin{aligned} \frac{k\pi }{\Delta \tau }<\omega _\mathrm{d} <\frac{(2k+1)\pi }{2\Delta \tau } \end{aligned}$$
(5)

Also, define the sampling frequency \(f_\mathrm{s} \) as \(f_\mathrm{s} =\frac{2\pi }{\Delta \tau }\), and consider the maximum and minimum of damped natural frequencies, say, \(f_\mathrm{min} \) and \(f_\mathrm{max} \), involved in free-decay response data of a system, and the following simplified inequality can be obtained from Eq. (4)

$$\begin{aligned} \frac{4f_\mathrm{max} }{2k+1}<f_\mathrm{s} <\frac{2f_\mathrm{min} }{k}, k=0,1,2,3,\ldots \end{aligned}$$
(6)

One can, therefore, derive

$$\begin{aligned} \frac{f_{\max } }{f_{\min } }<\frac{2k+1}{2k} \end{aligned}$$
(7)

Eq. (7) defines the maximum width of the frequency range used with the various k, and the appropriate k’s chosen for all the frequencies of interest can then employed in Eq. (6) to determine the allowable sampling frequencies. Consider two practically general cases of \(f_{\max } /f_{\min } \ge 3/2\) and \({4}/4<f_\mathrm{max} /f_\mathrm{min} <3/2\), respectively, for the conditions of \(k=0\) and \(k=1\), and the following inequality can then derived

$$\begin{aligned} \left\{ {\begin{array}{l} f_\mathrm{s}>4f_\mathrm{max} \\ 2f_\mathrm{min}>f_s >\frac{4}{3}f_\mathrm{max} \\ \end{array}} \right. \end{aligned}$$
(8)

or

$$\begin{aligned} \left\{ {\begin{array}{l} \Delta \tau<\frac{{1}}{{4}}T_\mathrm{min} \\ \frac{{1}}{2}T_\mathrm{max}<\Delta \tau <\frac{{3}}{{4}}T_\mathrm{min} \\ \end{array}} \right. \end{aligned}$$
(9)

where \(T_{\min } \) and \(T_{\max } \) correspond to the maximum and minimum of damped natural frequencies \(f_\mathrm{max} \) and \(f_\mathrm{min} \) of a system. It should be mentioned that, under the aforementioned conditions of properly chosen sampling time shifted \(\Delta \tau \)’s, modal identification can then be well performed in ITD method.

3 Determination of the system order using singular value decomposition

In general, the important modes of a system under consideration could be roughly found by examining the Fourier spectra associated with the measured response histories. The number of (real) modes involved in the response then determines the order n of the system matrix \([\mathbf{A}]\) in Eq. (1); however, it may lead to a distortion in the modal identification, especially for a system having a serious problem with modal interference among the modes. In this paper, we introduce the singular value decomposition (SVD) in the procedure of modal identification of ITD method to appropriately estimate the order of a system and then avoid the disadvantage of omitted mode. Through insertion of the SVD algorithm into eigenvalue analysis associated with the system matrix \([\mathbf{A}]\) in ITD method, Eq. (1) can be rewritten as follows:

$$\begin{aligned}{}[\mathbf{A}]=[\mathbf{Y}][\mathbf{X}]^{\mathrm{T}}([\mathbf{U}][{\varvec{\Sigma }} ][\mathbf{V}]^{{\mathrm{T}}})^{-1} \end{aligned}$$
(10)

where \([\mathbf{U}][{\varvec{\Sigma }}][\mathbf{V}]^{{\mathrm{T}}}=[\mathbf{X}][\mathbf{X}]^{T}\), \([\mathbf{U}]\) and \([\mathbf{V}]\) are both unitary matrices, and \([{\varvec{\Sigma }} ]\) is a rectangular matrix consisting of zero matrices with appropriate dimensions and a diagonal matrix with monotonically non-increasing singular values. Since \([\mathbf{U}]\) and \([\mathbf{V}]\) are the matrices with orthonormal property, (i.e., \([\mathbf{U}]^{{-1}}=[\mathbf{U}]^{\mathrm{T}}\), \([\mathbf{V}]^{{-1}}=[\mathbf{V}]^{\mathrm{T}})\), Eq. (10) can then be derived as

$$\begin{aligned}{}[\mathbf{A}]=[\mathbf{Y}][\mathbf{X}]^{\mathrm{T}}[\mathbf{V}][{\varvec{\Sigma }} ]^{-1}[\mathbf{U}]^{\mathrm{T}} \end{aligned}$$
(11)

It should be mentioned that, by examining the numbers of the nonzero singular values of \([{\varvec{\Sigma }} ]\) associated with the responses of the system, we could determine the order, as well as the number of modes to be identified, of a system, and also further confirm if the phenomenon of omitted modes exists. In addition, by performing the SVD analysis of \([\mathbf{X}][\mathbf{X}]^{\mathrm{T}}\), we could directly determine the order of a system without the procedures of examining the Fourier spectrum associated each of the response channels to roughly find the important modes of the system under consideration and also significantly reduce relatively much calculations required in the conventional channel-expansion technique.

4 Quantity estimation of identified modes from frequency response function

In the preceding, we introduce the singular value decomposition to improve the accuracy of the estimation the order of a system matrix when performing the ITD method. One can estimate the numbers of structural modes to be identified by examining the Fourier spectrum associated with each of the response channel; however, the modal interference among the modes with relatively high damping and closely spaced modes can generally lead to a distortion in the quantity estimation of identified modes. To verify the quantity estimation of the structural modes to be identified, the phase of frequency of response function will be employed in modal identification, as described in the following.

Consider a single-degree-degree-of-freedom system, whose frequency of response function \(H\left( \omega \right) \,\) can be expressed as follows

$$\begin{aligned} H\!\left( \omega \right) =\frac{1}{\left( {-\omega ^{2}M+i\omega C+K} \right) } \end{aligned}$$
(12)

In Eq. (12), \(H\left( \omega \right) \) is the complex function. Define the frequency ratio as \(\bar{\omega }=\frac{\omega }{\omega _0}\), where \(\omega \) and \(\omega _0 \) are the applied loading frequency and natural free-vibration frequencies, respectively, and introduce \(\bar{\omega }\) into the Eq. (12), \(H\left( \omega \right) \) can be rewritten as

$$\begin{aligned} H\!\left( \omega \right) ~ = \frac{1}{K}\left[ \frac{{1 - \bar{\omega }^{2} }}{{(1 - \bar{\omega }^{2} )^{2} + (2\xi \bar{\omega })^{2} }} + i\frac{{ - 2\xi \bar{\omega }}}{{(1 - \bar{\omega }^{2} )^{2} + (2\xi \bar{\omega })^{2} }}\right] \end{aligned}$$
(13)

Additionally, \(H\left( \omega \right) \,\) can also be expressed as

$$\begin{aligned} H\!\left( \omega \right) \,=H^\mathrm{R}\left( \omega \right) +H^\mathrm{I}\left( \omega \right) \end{aligned}$$
(14)

where \(H^\mathrm{R}\left( \omega \right) \) and \(H^\mathrm{I}\left( \omega \right) \) are, respectively, the real and imaginary parts of \(H\left( \omega \right) \,\). The phase \(\varphi _\mathrm{H} \) of \(H\left( \omega \right) \,\) can be defined as

$$\begin{aligned} \varphi _\mathrm{H} \left( \omega \right) =\hbox {tan}^{-1}\left( \frac{H^\mathrm{I}\left( \omega \right) }{H^\mathrm{R}\left( \omega \right) }\right) \end{aligned}$$
(15)

Through insertion of Eqs. (13) and (14) into Eq. (15), \(\varphi _\mathrm{H} \left( \omega \right) \) can also be rewritten as follows in the form of \(\xi \) and \(\bar{{\omega }}\),

$$\begin{aligned} \varphi _\mathrm{H} \left( \omega \right) =\hbox {tan}^{-1}\left( \frac{-2\xi \bar{\omega }}{1-\bar{\omega }^2}\right) \end{aligned}$$
(16)

It should be mentioned that, in Eq. (16), \(\varphi _\mathrm{H} \approx -90^{\circ }\), \(\varphi _\mathrm{H} \approx 0\), and \(\varphi _\mathrm{H} \approx 90^{\circ }\) are, respectively, in the case of \(\bar{{\omega }}=1^{-}\), \(\bar{{\omega }}\approx 0\), and \(\bar{{\omega }}>1^{-}\). The phase \(\varphi _\mathrm{H} \) of the frequency of response function \(H\left( \omega \right) \,\) will vary instantaneously from \(-90^{\circ }\) to \(90^{\circ }\) when natural free-vibration frequencies of a structure are equal to the applied loading frequency. We can therefore estimate the quantity of structural modes to be identified by examining the phase \(\varphi _\mathrm{H} \) of the frequency of response function \(H\left( \omega \right) \,\).

5 Numerical simulation

When a structure is subjected to dynamic tests under external force excitation, the modal parameters could be identified from the excitation and response data of a structural system. However, the implementation of the dynamic testing of large-scale structure is difficult and the exact modal information of a practical structure is not usually available, so it is necessary to verify in advance the effectiveness of the proposed theory and algorithm through the numerical simulations.

Fig. 1
figure 1

Schematic plot of the 7-dof system of a motor vehicle

Full size image

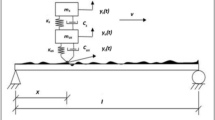
To demonstrate the effectiveness of the present method, we first consider a 7-dof system of the vehicle model with two pairs of closely spaced modes (frequency separation smaller than 0.03 Hz). A schematic representation of this model is shown in Fig. 1. The vehicle model is a 7-dof system with \(\mathbf{u}=\left[ {{u}_{1}, {u}_{2}, {u}_{3}, {u}_{4}, {u}_{5}, {u}_{6}, {u}_{7}} \right] \), where \(u_{2} =\varphi \) and \(u_{3} =\theta \) are the rotational displacement of pitch and roll behavior of the motor vehicle, respectively, and others are the vertical displacement of bounce behavior of the motor vehicle and four wheels as shown in Fig. 1. The mass matrix is a diagonal matrix, diag \(\mathbf{M}=\left[ {m_1, {m}_{2}, {m}_{3}, {m}_{4}, {m}_{5}, {m}_{6}, {m}_{7} } \right] \), where \({m}_{2} ={I}_{\mathrm{y}} \) and \({m}_{3} ={I}_{\mathrm{x}} \) are, respectively, the pitch and roll moment of inertia of the motor vehicle. The stiffness matrix can be obtained as

$$\begin{aligned} \mathbf{K}=\left[ {{\begin{array}{ccccccc} {k_1 +k_2 +k_3 +k_4 }&{} {-L_1 k_1 +L_2 k_2 -L_1 k_3 +L_2 k_4 }&{} {-L_3 k_1 -L_3 k_2 +L_4 k_3 +L_4 k_4 }&{} {-k_1 }&{} {-k_2 }&{} {-k_3 }&{} {-k_4 } \\ {-L_1 k_1 +L_2 k_2 -L_1 k_3 +L_2 k_4 }&{} {L_1^2 k_1 +L_2^2 k_2 +L_1^2 k_3 +L_2^2 k_4 }&{} {L_1 L_3 k_1 -L_2 L_3 k_2 -L_1 L_4 k_3 +L_2 L_4 k_4 }&{} {L_1 k_1 }&{} {-L_2 k_2 }&{} {L_1 k_3 }&{} {-L_2 k_4 } \\ {-L_3 k_1 -L_3 k_2 +L_4 k_3 +L_4 k_4 }&{} {L_1 L_3 k_1 -L_2 L_3 k_2 -L_1 L_4 k_3 +L_2 L_4 k_4 }&{} {L_3^2 k_1 +L_3^2 k_2 +L_4^2 k_3 +L_4^2 k_4 }&{} {L_3 k_1 }&{} {L_3 k_2 }&{} {-L_4 k_3 }&{} {-L_4 k_4 } \\ {-k_1 }&{} {L_1 k_1 }&{} {L_3 k_1 }&{} {k_1 +k_{11} }&{} 0&{} 0&{} 0 \\ {-k_2 }&{} {-L_2 k_2 }&{} {L_3 k_2 }&{} 0&{} {k_2 +k_{12} }&{} 0&{} 0 \\ {-k_3 }&{} {L_1 k_3 }&{} {-L_4 k_3 }&{} 0&{} 0&{} {k_3 +k_{13} }&{} 0 \\ {-k_4 }&{} {-L_2 k_4 }&{} {-L_4 k_4 }&{} 0&{} 0&{} 0&{} {k_4 +k_{14} } \\ \end{array} }} \right] \end{aligned}$$

where \(L_1 \) and \(L_2 \) are, respectively, the half of axle track of front and rear wheel, \(L_3 \) and \(L_4 \) are the distances to respectively, front and rear axle from the center of gravity of a motor, and the summation of \(L_3 \) and \(L_4 \) is the wheelbase of a motor. \(k_{1} \left( {=k_2 } \right) \) and \(k_{3} \left( {=k_{4} } \right) \) are front and rear suspension spring stiffness, respectively, \(k_\mathrm{{11}} =k_\mathrm{{12}} \) and \(k_\mathrm{{13}} =k_\mathrm{{14}} \) are front and rear tire stiffness, respectively. Throughout this numerical study, \(\left[ {m_{1}, {m}_{4}, {m}_{4}, {m}_{6}, {m}_{7} } \right] =\left[ {{1365,46.8,46.8,41.4,41.4}} \right] \,\mathrm{kg}\), \({m}_2 ={I}_\mathrm{y} =1.831\times 10^{3}\,\mathrm{{kg\, m^{2}}}\) and \({m}_{3} ={I}_\mathrm{x} =4.98\times 10^{2}\,\mathrm{{kg\, m^{2}}}\); \(k_{1} =k_2 =2.2428\times 10^{4}\,\mathrm{{N/m}}\), \(k_{3} =k_{4} =2.7022\times 10^{4}\,\mathrm{{N/m}}\), \(k_{{11}} =k_{{12}} =2.32342\times 10^{5}\,\mathrm{{N/m}}\), and \(k_{{13}} =k_{{14}} =2.92982\times 10^{5}\,\mathrm{{N/m}}\); \(L_1 =L_2 =0.7165\,\mathrm{m}\), \(L_3 =1.1135\,\mathrm{m}\), and \(L_4 =1.5415\,\mathrm{m}\); \({{{\varvec{C}}}}=0.1{{\varvec{M}}}+0.001{{\varvec{K}}}\,\mathrm{{N s/m}}\). Note that the system has proportional damping, because the damping matrix C can be expressed as a linear combination of M and K. The simulated impulse function serves as the excitation input acting on the seventh mass point of the system. The sampling interval is chosen as \(\Delta t=0.005\) s, and the sampling period is \(T=N_\mathrm{t} \cdot \Delta t=60.000\) s. Assume the system is initially at rest, and the displacement responses of the system can be obtained using Newmark’s method [16] as shown in Fig. 2.

Fig. 2
figure 2

Typical plots of the displacement responses and the corresponding amplitude frequency response functions and phases associated with impulse responses of the 1st and 4th DOF of the system of a motor vehicle

Full size image

The Newmark integration method is based on the assumption that the acceleration varies linearly between two instants of time. The parameters \(\alpha \) and \(\beta \) in the Newmark’s method indicate how much the acceleration at the end of the interval enters into the velocity and displacement equations at the end of the time interval \(\Delta t\) in the resulting expressions for the velocity and displacement vectors for a multi-degree-of-freedom system. \(\alpha \) and \(\beta \) can be chosen to obtain the desires accuracy and stability characteristics. In the numerical simulations of this paper, we choose the average acceleration method for the Newmark’s algorithm in the case of \(\alpha =1/4\) and \(\beta =1/2\), which correspond to the assumption of constant acceleration within \(\Delta t\). Noted that the average acceleration method is unconditionally stable no matter how \(\Delta t\) is large and it is accurate only if \(\Delta t\) is small enough.

In general, the important modes of a system under consideration could be roughly found by examining the Fourier spectra associated with the measured response histories. However, it may lead to a distortion in the modal identification, especially for a system with modal interference among the modes. The typical plots of amplitude frequency response functions of the system are also shown in Fig. 2, where we clearly see the serious problems of modal interference. According to the theory presented in the precious sections, the phase angle diagram of frequency response function, as also shown in Fig. 2, can be employed to distinguish the structural modes influenced by modal interference and then avoid the phenomenon of omitted modes from the distortion of system order determined by frequency response function. A typical plot of the phase frequency response function H47\((\omega )\) is shown at least the 5 excited modes of this 7-DOF system with modal interference.

Fig. 3
figure 3

Distribution of the singular values associated with (a) \([\mathbf{A}]\) and (b) \([\mathbf{X}][\mathbf{X}]^{\mathrm{T}}\), respectively, of the impulse responses of a 7-DOF motor vehicle subjected to an impulse excitation

Full size image
Fig. 4
figure 4

Comparison between the identified mode shapes and the exact mode shapes of the 7-DOF system of a motor vehicle subjected to an impulse input

Full size image

Furthermore, by referring to Sect. 3 in this paper, the singular value decomposition (SVD) in conjunction with least-squares analysis is introduced in the procedure of Ibrahim time domain method to obtain \([\mathbf{A}]\) and accurately determine the system order. The number of nonzero singular values is the rank of \([\mathbf{X}][\mathbf{X}]^{\mathrm{T}}\) and is also the system order. By performing the SVD algorithm of \([\mathbf{X}][\mathbf{X}]^{\mathrm{T}}\), we could directly determine the system order without the procedures of examining the Fourier spectrum associated each of the response channels to roughly find the important modes of the system under consideration. Comparing the singular values of \([\mathbf{A}]\) with those of \([\mathbf{X}][\mathbf{X}]^{\mathrm{T}}\) from the free-decay response data of a 7-DOF motor vehicle subjected to an impulse excitation, as shown in Fig. 3, the distribution of the singular values of \([\mathbf{X}][\mathbf{X}]^{\mathrm{T}}\) shows a relatively obvious drop around the singular value number 14, which determines system order and the number of modes to be identified and reduces more calculations. The results of modal parameter identification are summarized in Table 1, which shows that the errors in natural frequencies are less than 1% and the error in damping ratios is less than 10%. The identified mode shapes are also compared with the exact values in Fig. 4, in which we observe good agreement. The first three mode shapes are modal behavior with bounce, pitch, and roll modes of the global motor vehicle, while the last four mode shapes are modal behavior with bounce modes of the local left front, right front, left rear, and right rear wheels.

Table 1 Results of modal identification of the 7-dof system of a motor vehicle through the ITD method with channel-expansion technique
Full size table
Fig. 5
figure 5

Schematic plot of the 6-dof system of a linear two-dimensional model of one-half of a railway vehicle [16,17,18]

Full size image
Fig. 6
figure 6

Typical plots of free-decay responses and the corresponding amplitude frequency response functions and phases associated with impulse responses of the 1st and 3rd DOF of the system of a railway vehicle

Full size image
Fig. 7
figure 7

Distribution of the singular values associated with \([\mathbf{X}][\mathbf{X}]^{\mathrm{T}}\) of the impulse responses (contaminated with 5% noise) corresponding to an impulse input

Full size image

To further examine the effectiveness of the present method for the more complex structural, we consider a linear two-dimensional model of one-half of a railway vehicle excited by a simulated impulse loading. The dynamic system used in the numerical study (a sketch is shown in Fig. 5) is identical to that in Reference [17,18,19] and has the features of modal damping levels ranging from low (1.74%) to relatively high (18.78%) and a pair of closely spaced modes (frequency separation smaller than 0.25 Hz). The system is a 6-DOF system with \(\mathbf{u}=\left[ {{u}_{1}, {u}_2, {u}_{3}, {u}_{4}, {u}_{4}, {u}_{6} }\right] \), where \(u_{4} =\theta \) is the rotational displacement of pitch behavior of car body and others are the vertical displacement of bounce behavior of the car body, leading (trailing) bogies and leading (trailing) wheelsets. The mass matrix is a diagonal matrix, diag \(\mathbf{M}=\left[ {m_{1}, {m}_2, {m}_{3}, {m}_{4}, {m}_{4}, {m}_{6} } \right] \), where \({m}_{4} ={I}_\mathrm{B} \) is the mass moment of inertia of the rigid body B at the top of the structure. The stiffness and damping matrices can be obtained as

$$\begin{aligned} \mathbf K= & {} \left[ {{\begin{array}{cccccc} {k_1 +k_2 }&{} {-k_2 }&{} 0&{} 0&{} 0&{} 0 \\ {-k_2 }&{} {k_2 +k_3 }&{} {-k_3 }&{} {-k_3 L}&{} 0&{} 0 \\ 0&{} {-k_3 }&{} {k_3 +k_4 }&{} {k_3 L-k_4 L}&{} {-k_4 }&{} 0 \\ 0&{} {-k_3 L}&{} {k_3 L-k_4 L}&{} {k_3 L^{2}+k_4 L^{2}}&{} {k_4 L}&{} 0 \\ 0&{} 0&{} {-k_4 }&{} {k_4 L}&{} {k_4 +k_5 }&{} {-k_5 } \\ 0&{} 0&{} 0&{} 0&{} {-k_5 }&{} {k_5 +k_6 } \\ \end{array} }} \right] \\ \mathbf C= & {} \left[ {{\begin{array}{cccccc} {c_1 +c_2 }&{} {-c_2 }&{} 0&{} 0&{} 0&{} 0 \\ {-c_2 }&{} {c_2 +c_3 }&{} {-c_3 }&{} {-c_3 L}&{} 0&{} 0 \\ 0&{} {-c_3 }&{} {c_3 +c_4 }&{} {c_3 L-c_4 L}&{} {-c_4 }&{} 0 \\ 0&{} {-c_3 L}&{} {c_3 L-c_4 L}&{} {c_3 L^{2}+c_4 L^{2}}&{} {c_4 L}&{} 0 \\ 0&{} 0&{} {-c_4 }&{} {c_4 L}&{} {c_4 +c_5 }&{} {-c_5 } \\ 0&{} 0&{} 0&{} 0&{} {-c_5 }&{} {c_5 +c_6 } \\ \end{array} }} \right] \end{aligned}$$

where L is the horizontal distance between the center of the rigid body B and the springs/dashpots. Throughout this numerical study, \(\left[ {m_{1}, {m}_2, {m}_{3}, {m}_{4}, {m}_{6} } \right] =\left[ {{1200,850,4125,850,1220}} \right] \,\mathrm{{kg}}\), and \({m}_{4} =I_\mathrm{B} =1.25\times 10^{5}\,\mathrm{{kg\,m^{2}}}\); \(k_{1} =k_{6} =3.0\times 10^{7}\,\mathrm{{N/m}}\), \(k_2 =k_{4} =1.0\times 10^{6}\,\mathrm{{N/m}}\) and \(k_{3} =k_{4} =6.0\times 10^{6}\,\mathrm{{N/m}}\); \(c_{1} =c_{6} =0\), \(c_2 =c_{4} =6.0\times 10^{3}\,\mathrm{{N\,s/m}}\), and \(c_{3} =c_4 =1.8\times 10^{4}\,\mathrm{{N\,s/m}}\); \(L=8.53\) m. Note that this 6-DOF system of one-half of a railway vehicle has non-proportional damping, since the damping matrix \({{\varvec{C}}}\) cannot be expressed as a linear combination of \({{\varvec{M}}}\) and \({{\varvec{K}}}\). The simulated impulse function serves as the excitation input acting on the sixth mass point of the system. The sampling interval is chosen as \(\Delta t=0.001\) s, and the sampling period is \(T=N_\mathrm{t} \cdot \Delta t=1.000\) s. Assume the system is initially at rest, and the simulated impulse responses of the system can be obtained using Newmark’s method as shown in Fig. 6. The typical plots of amplitude frequency response functions of the system are also shown in Fig. 6, where we clearly see the serious problems of modal interference among the modes with relatively high damping and a pair of closely spaced modes. A typical plot of the phase frequency response function H16\((\omega )\) is shown at least the 5 excited modes of this 6-DOF system with modal interference. Through the SVD analysis, the distribution of the singular values of \([\mathbf{X}][\mathbf{X}]^{\mathrm{T}}\) shows a clear drop around the 12th singular value, as shown in Fig. 7, from which the order of the system model, i.e., the number of modes to be identified, is determined to be 12. The results of modal estimation obtained from the simulated impulse response data contaminated with 5% noise are summarized in Table 2, which shows that the both errors in natural frequencies and damping ratios are less than 3%. Note that for a system with non-proportional damping, the “exact” modal parameters listed in Table 2 are actually the equivalent values obtained by solving a simplified generalized eigenvalue problem of equation of motion in the state-space form for free-vibration analysis. Also, it is good agreement with the minimum value of MAC (Modal Assurance Criterion) [20] between the identified and exact mode shapes of about 0.90.

Table 2 Results of modal identification of the 6-dof system of a railway vehicle through the ITD method with channel-expansion technique (from simulated impulse response data contaminated with 5% noise)
Full size table

Note that in the formulations of motor and railway vehicles of the numerical simulations, the both mass matrices are diagonal; however, the both stiffness matrices are not diagonal, but are symmetric. It indicates that the resultant motion of the two types of vehicle is both translational and rotational when either a displacement or torque is applied through the center of gravity of the body as an initial condition [21]. Thus, using these coordinates, the models of motor and railway vehicles in the numerical simulations are both statically coupled, but not dynamically coupled.

6 Conclusions

Modal interference often degrades the accuracy of identification results and even causes problems of identifiability in the process of modal identification. An extended channel-expansion technique in Ibrahim time domain method (ITD) is presented in this paper for modal identification of structures with modal interference. In addition, the accurate estimation of the order of system matrix is important when performing the ITD method. By introducing the singular value decomposition in conjunction with least-squares analysis to solve the system matrix, without the procedures of examining the Fourier spectrum associated each of the response channels to roughly confirm the rich frequency content around the structure modes of interest, the order of the system can be determined to avoid the phenomenon of omitted modes and also significantly reduce relatively much calculations required in the conventional channel-expansion technique. Furthermore, the phase angle diagram of frequency response function can be employed to effectively distinguish the structural modes influenced by modal interference. Through numerical simulations, including two examples of a model of the motor vehicle, and a linear two-dimensional model of one-half of a railway vehicle, the proposed method has been confirmed the validity for modal identification of a system with modal interference.