1 Introduction

In recent years, vibration energy harvesting has become a superior technology for powering low-powered electronic devices and nano-sensors [1,2,3]. Vibration energy can be converted into electricity using electrostatic [4], electromagnetic [5], magnetostrictive [6], or piezoelectric effects. Piezoelectric transduction is the most suitable option for micro-electro-mechanical systems sensors, because it has large power densities, relatively high voltages and low currents [7]. Conventional linear piezoelectric energy harvester only exhibits a satisfactory performance with a large oscillation near its resonance frequency. The main problem of the linear resonant energy harvester is that the energy harvesting efficiency is significantly lowered when the excitation energy is distributed over a wider spectrum. To overcome this defect in efficiency, nonlinearities (such as mono-stability [8,9,10,11,12,13], bi-stability [14,15,16,17,18,19,20,21,22], tri-stability [21,22,23,24], even quad-stability [29,30,31]) are usually introduced using magnetic interaction to improve the output power over the wide range of frequency. In particular, bi-stable energy harvester (BEH) has been studied and utilized extensively due to sustaining interwell motions to extract high electrical power over a broad frequency band. Masana and Daqaq [14] investigated the relative performance of mono-stable energy harvesters and BEHs under sweep excitations, and the results illustrated that the BEH can outperform mono-stable one when BEH can be activated the interwell dynamics. Zhao and Erturk [15] numerically and experimentally investigated the mono- and bi-stable one subjected random excitation. They found that BEH can be preferred to mono-stable one if it is designed to operate in a known random excitation intensity. Mann and Owens [16] investigated the escape phenomena in a BEH and demonstrated that the escape from the potential wells can broaden the frequency spectrum of the energy harvester. Stanton et al. [17] performed dynamics feature of broadband vibration energy harvester in the investigations from a bi-stable piezoelectric inertial generator. The BEH is theoretically modeled, numerically simulated and experimentally verified. Vocca et al. [18] simulated the kinetic energy harvesting with BEH driven by random signals taken from: a microwave oven case, a train floor and a car hood. And it was shown that BEH outperformed the linear one in those three real-world cases. Recently, more complex energy harvesting systems were proposed to enhance the transferring energy efficiency. Gao et al. [19] and Leng et al. [20] analyzed the performance of the BEH with elastic support, which had a better power output than rigid-support BEH excited by weak random excitations. Wang and Tang [21] proposed a two-degree-of-freedom BEH, the numerical and experimental results showed that the responses with a wider bandwidth can appear at any of the two peaks or at both. Another two-degree-of-freedom piezoelectric energy harvester with stopper was theoretically modeled and analyzed to achieve wide operation frequency bandwidth [22]. Multi-stable energy harvesters [23], ranging from tri-stable to penta-stable, have been proposed, and several theoretical and experimental studies [23,24,25,26,27,28,29,30,31] show that as more potential wells are introduced, it is liable to take snap-through between potential wells and generate more output power than the BEH. In the classical bi-stable energy harvesters, the amplitude of snap-through motions has a great dependence on the separation distance between the tip magnet and the fixed one. However, as the magnetic field arrangements for TEH are much more complex than that for BEH, the capability of harvesting energy can be controlled to a certain degree by the gap distance between the two external magnets.

The aim of this paper is to theoretically and experimentally investigate the characteristics of a tri-stable nonlinear harvester and to make a comparison with the classical bi-stable energy harvester. The paper is organized as follows. In Sect. 2, the mathematical model of the energy harvester is established and formulated by the energy-based method and Euler–Lagrange principle. In Sect. 3, numerical simulations are performed based on derived model to investigate the efficient frequency bands of BEH and TEH under sweeping excitations. Section 4 presents the results of validation experiments at different excitation levels. The conclusions follow in Sect. 5.

Fig. 1
figure 1

Configurations of the piezoelectric energy harvesters: a BEH, b TEH

Full size image

2 Description and modeling of the tri-stable energy harvester

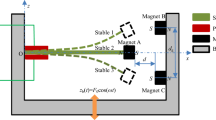
A typical BEH is shown in Fig. 1a, which is composed of a cantilever beam with a tip magnet and a fixed magnet. The cantilever beam is partially covered by piezoelectric layers connected to a collecting circuit. The separation distance between the tip and fixed magnets can be controlled to make the ferromagnetic beam own one unstable and two stable equilibrium positions, thereby becoming a bi-stable beam. It has been proved that interwell motions can improve the harvester’s performance and the large distance between potential wells can lead to a large amplitude in interwell motions. So it is desirable that the two magnets in BEH is close enough to produce a strong repulsive force. But unfortunately this strong repulsive force will create a high barrier between the potential wells simultaneously, which hinders the BEH in jumping between the potential wells. That is to say, the BEH requires a greater base excitation such as to maintain the continuous high-energy interwell motion. To overcome this defect, this paper focuses on a tri-sable energy harvester (TEH), which is maintained by attractive magnets. In contrast to the aforementioned repulsive magnet, the attractive magnetic force is preferable in getting the equilibrium positions accurately. The TEH’s configuration is shown in Fig. 1b. Two symmetrical external magnets are put on the bottom of a fixture with their opposite pole to that of the tip magnet. By adjusting the separation and the gap distances, the TEH can possess three stable equilibrium positions.

The kinetic energy of the TEH comes from the motion of the piezoelectric beam and the tip magnet. Thus, the kinetic energy can be given by

$$\begin{aligned} T_{pb} = \frac{1}{2}\int \nolimits _0^L m{\left[ {\dot{w}\left( {x,t} \right) + \dot{z}\left( t \right) } \right] ^2}\hbox {d}x + \frac{1}{2}{m_0}{\left[ {\dot{w}\left( {L,t} \right) + \dot{z}\left( t \right) } \right] ^2} \end{aligned}$$
(1)

where the overdot denotes the derivative with respect to time; L is the length of the piezoelectric beam; \(w\left( {x,t} \right) \) denotes the transverse displacement of the beam at a distance x from the clamped side; \(z\left( t \right) \) is the base displacement; \(m_0 \) is the mass of the tip magnet; m is the mass of the beam per unit length:

$$\begin{aligned} m=\left\{ {{\begin{array}{ll} {\rho _\mathrm{S} b_\mathrm{S} h_\mathrm{S} +2\rho _\mathrm{p} b_\mathrm{p} h_\mathrm{p} ,}&{}{\quad 0\le x< l_\mathrm{p} } \\ {\rho _\mathrm{S} b_\mathrm{S} h_\mathrm{S} ,}&{}{\quad l_\mathrm{p} \le x\le L} \\ \end{array} }} \right. \end{aligned}$$
(2)

where \(b_\mathrm{S} \) and \(h_\mathrm{S} \) are the width and thickness of substrate, respectively; \(\rho _\mathrm{S} \) and \(\rho _\mathrm{p} \) are the densities of the substrate and piezoelectric materials, respectively; \(b_\mathrm{p} \) and \(h_\mathrm{p}\) are the width and thickness of piezoelectric layer, respectively, and \(l_\mathrm{p} \) is its length.

The potential energy of the piezoelectric beam is

$$\begin{aligned} {U_{pb}} = \frac{1}{2}\int \nolimits _0^L \hbox {EI}w''{\left( {x,t} \right) ^2}\hbox {d}x - \frac{1}{2}\int \nolimits _0^L {\vartheta _\mathrm{p}}v\left( t \right) w''\left( {x,t} \right) \hbox {d}x + \frac{1}{2}{C_\mathrm{p}}v{\left( t \right) ^2} \end{aligned}$$
(3)

where the prime notation \(( )^{\prime }\) refers to \(\partial /\partial x\); \(v\left( t \right) \) is the voltage across the electrodes; the electromechanical coupling term \(\vartheta _\mathrm{p} \) is

$$\begin{aligned} \vartheta _\mathrm{p} =e_{31} E_\mathrm{p} b_\mathrm{p} l_\mathrm{p} \left( {h_\mathrm{s}^2 -h_\mathrm{p}^2 } \right) /h_\mathrm{p} \end{aligned}$$
(4)

The capacitance through the piezoelectric layers \(C_\mathrm{p} \) is

$$\begin{aligned} C_\mathrm{p} =\varepsilon _{33}^S b_\mathrm{p} l_\mathrm{p} /h_\mathrm{p} \end{aligned}$$
(5)

where \(\varepsilon _{33}^S \) is the piezoelectric material permittivity at constant strain, and EI is the bending stiffness of the cross section of the piezoelectric beam:

$$\begin{aligned} \hbox {EI}=\left\{ {{\begin{array}{ll} {\frac{1}{3}E_\mathrm{s} b_\mathrm{s} \left( {h_b^3 -h_a^3 } \right) +\frac{2}{3}E_\mathrm{p} b_\mathrm{p} \left( {h_c^3 -h_b^3 } \right) ,}&{}{\quad 0\le x< l_\mathrm{p} } \\ {\frac{1}{12}E_\mathrm{s} b_\mathrm{s} h_\mathrm{s} ,}&{}{\quad l_\mathrm{p} \le x\le L} \\ \end{array} }} \right. \end{aligned}$$
(6)

where \(h_a \), \(h_b \) and \(h_c \) represent the distances from the neutral axis to the bottom surface of the substrate, the bottom surface of the piezoelectric and the upper surface of the piezoelectric layer, respectively.

In calculating magnetic potential energy, the relative distances between the magnets are the determinant factors and must be given accurately. The geometric configuration of the tip magnet and two external fixed magnets is shown in Fig. 2.

Fig. 2
figure 2

Geometric configuration of the tip magnet and two external magnets

Full size image

The three magnets can be modeled as the point dipoles in calculating magnetic potential energy. The magnetic potential energy generated by magnet A and magnet B upon magnet C can be evaluated by [17]

$$\begin{aligned} U_\mathrm{m} =-\frac{\mu _0 }{4\pi }\left( {{\varvec{\nabla }} \frac{{\varvec{m}}_\mathrm{A} \cdot {\varvec{r}}_{\mathbf{A }\mathrm{C}} }{\Vert {\varvec{r}}_\mathrm{AC}\Vert ^{3}_{2} }} \right) \cdot {{\varvec{m}}}_c -\frac{\mu _0 }{4\pi }\left( {{\varvec{\nabla }} \frac{{\varvec{m}}_\mathrm{B} \cdot {\varvec{r}}_\mathrm{BC} }{\Vert {\varvec{r}}_\mathrm{BC}\Vert ^{3}_{2} }} \right) \cdot {{\varvec{m}}}_c \end{aligned}$$
(7)

where \({{\varvec{r}}}_\mathrm{AC} ({{\varvec{r}}}_\mathrm{BC})\) is the vector directed from the magnetic moment source of magnet A (B) to that of magnet \({C;\Vert \quad \Vert _{2}}\) and \({\varvec{\nabla }}\) denote L2-norm and vector gradient operator, respectively; \({{\varvec{m}}}_\mathrm{A}({{\varvec{m}}}_\mathrm{B}\hbox { or }{{\varvec{m}}}_{c})\)denote the magnetic moment vectors of magnet A (B or C), which can be estimated using magnetization intensity \({{\varvec{M}}}_\mathrm{A}({{\varvec{M}}}_\mathrm{B}\hbox { or }{{\varvec{M}}}_\mathrm{C})\) and material volume \(V_\mathrm{A}(V_\mathrm{B}\hbox { or }V_\mathrm{C})\) as \({{\varvec{M}}}_\mathrm{A}{{V}}_\mathrm{A}\) \(({\varvec{M}}_\mathrm{B} {{V}}_\mathrm{B}\hbox { or }{\varvec{M}}_\mathrm{C} V_\mathrm{C})\); \({{\varvec{\mu }}_0 }=4{\pi }\times {10^{-7}} {\hbox {Hm}^{-1}}\) is the magnetic permeability constant. As shown in Fig. 2, the horizontal displacement can be evaluated by \(\Delta x=\frac{a}{2}(1-\cos \alpha )\), where \(\alpha =\hbox {arctan}[w^{\prime }(L,t)]\) is the rotation angle of the tip magnet C and \(w^{\prime }(L,t)\) is the first-order derivative of the response of the beam tip. Since a is considerably small compared to L, \(\Delta x\approx 0\). Thus, the tip displacement can be approximated by w(L, t) [29]. Therefore, the potential energy expression can be written as

$$\begin{aligned} U_\mathrm{m}= & {} \frac{\mu _{0} {\varvec{M}}_\mathrm{A} {\varvec{M}}_\mathrm{C} {V_\mathrm{A} V_\mathrm{C}} \left( {-\left( {w\left( {L,t} \right) -C_\mathrm{A} } \right) ^{2}+2d^{2}-3d\left( {w\left( {L,t} \right) -C_\mathrm{A} } \right) w^{{\prime }\left( {L,t} \right) }} \right) }{4\pi \sqrt{w^{{\prime }({L,t})^{2}}+1} \left( \left( w\left( {L,t} \right) -C_\mathrm{A}\right) ^{2}+d^{2}\right) ^{5/2}}\nonumber \\&+\frac{\mu _0 {\varvec{M}}_\mathrm{B} {\varvec{M}}_\mathrm{C} V_\mathrm{BV_\mathrm{C}} \left( {-\left( {w\left( {L,t} \right) -C_\mathrm{B} } \right) ^{2}+2d^{2}-3d\left( {w\left( {L,t} \right) -C_\mathrm{B} } \right) w^{\prime }\left( {L,t} \right) } \right) }{4\pi \sqrt{w^{\prime }\left( {L,t} \right) ^{2}+1}\left( {\left( {w\left( {L,t} \right) -C_\mathrm{B} } \right) ^{2}+d^{2}} \right) ^{5/2}} \end{aligned}$$
(8)

where \(C_\mathrm{A}(C_\mathrm{B})\) represents the coordinate of magnet A (B) in z-direction \((C_\mathrm{A}=d_\mathrm{g},C_\mathrm{B}=-d_\mathrm{g})\); \({{\varvec{M}}}_\mathrm{A(B,C)}\) \({{\varvec{B}}}/r{\mu _0}\) where \({{\varvec{B}}}_\mathrm{r}\) is the residual flux density of magnet (if the magnet force is attractive; \({{\varvec{M}}}_\mathrm{A(B)}\) and \({{\varvec{M}}}_\mathrm{C}\) have the opposite signs; and if it is repulsive, they have the same signs).

Based on the given kinetic and potential energies above, the Lagrange function of the system can be expressed as

$$\begin{aligned} \mathcal{L}\left( {x,t} \right) =T_{pb} -U_{pb} -U_\mathrm{m} \end{aligned}$$
(9)

Assuming that the first mode plays a principal role in the dynamic responses, the deflection of the beam can be approximated by

$$\begin{aligned} w\left( {x,t} \right) =\phi \left( x \right) q\left( t \right) \end{aligned}$$
(10)

where \(\phi (x)\) is the first mode shape of the beam and can be expressed by \(\phi (x)=\varPsi \left[ 1-\cos \left( \frac{\pi x}{2L}\right) \right] , \varPsi \) is a constant; q(t) is the generalized temporal coordinate.

Substituting Eq. (10) into Eq. (9), the Lagrange function can be rewritten as

$$\begin{aligned} \mathcal{L}\left( t \right)= & {} \frac{1}{2}\dot{q}{\left( t \right) ^2} - \frac{1}{2}{\omega ^2}{q^2}\left( t \right) + \theta v\left( t \right) q\left( t \right) + \varGamma \dot{z}\left( t \right) \dot{q}\left( t \right) - \frac{1}{2}{C_\mathrm{p}}v{\left( t \right) ^2}\nonumber \\&+\frac{1}{2}\left( {{\rho _\mathrm{S}}{b_\mathrm{S}}{h_\mathrm{S}}L + 2{\rho _\mathrm{p}}{b_\mathrm{p}}{h_\mathrm{p}}{l_\mathrm{p}} + {m_0}} \right) \dot{z}{\left( t \right) ^2} - {U_\mathrm{m}}\left[ {q\left( t \right) } \right] \end{aligned}$$
(11)

where \({\omega }\) is the first natural frequency, and the electromechanical coupling term is

$$\begin{aligned} \theta = \frac{1}{2}{\vartheta _\mathrm{p}}\phi '\left( {{l_\mathrm{p}}} \right) \end{aligned}$$
(12)

The base excitation coefficient is

$$\begin{aligned} \varGamma = \left( {2{\rho _\mathrm{p}}{A_\mathrm{p}} + {\rho _\mathrm{S}}{A_\mathrm{S}}} \right) \int \nolimits _0^{{l_\mathrm{p}}} \phi \left( x \right) \hbox {d}x + {\rho _\mathrm{S}}{A_\mathrm{S}}\int \nolimits _{{l_\mathrm{p}}}^L \phi \left( x \right) \hbox {d}x + {m_0}\phi \left( L \right) \end{aligned}$$
(13)

The non-conservative virtual works done by the dissipative and the electric forces can be expressed as

$$\begin{aligned} \delta W = - \int \nolimits _0^L c\dot{w}\left( {x,t} \right) \delta w\left( {x,t} \right) \hbox {d}x + Q\left( t \right) \delta v \end{aligned}$$
(14)

where c is the mechanical damping coefficient and \(\dot{Q}(t)\) is the electric charge passing through the resistive load R, and \(Q(t)=v/R\).

The dynamical equations of the system can be derived by applying the Euler–Lagrange equations and we have

$$\begin{aligned} \ddot{q}{\left( t \right) ^2} + 2\zeta \omega \dot{q}\left( t \right) + {\omega ^2}q\left( t \right) - \theta v\left( t \right) + g\left[ {q\left( t \right) } \right]= & {} - \varGamma \ddot{z}\left( t \right) \end{aligned}$$
(15)
$$\begin{aligned} \nonumber \\ \theta \dot{q}\left( t \right) + {C_\mathrm{p}}\dot{v}\left( t \right) - v\left( t \right) /R= & {} 0 \end{aligned}$$
(16)

where \(\zeta =\hbox {c}\int \nolimits _0^L \phi \left( x \right) ^{2}\hbox {d}x\) and \(g\left[ {q\left( t \right) } \right] =\frac{\partial U_\mathrm{m} }{\partial q\left( t \right) }\).

3 Numerical simulation

The characteristics of BEH and TEH can be illustrated by potential energy diagram. The material properties and dimensions of the systems used in calculating the potential energies and numerical investigations are listed in Table 1.

Table 1 Material properties and dimensions of the system
Full size table
Fig. 3
figure 3

Potential energy shapes for TEH and BEH

Full size image
Fig. 4
figure 4

Potential energy shapes for TEH with different gap distances

Full size image
Fig. 5
figure 5

Tip displacement responses and the associated voltages for BEH under numerical frequency sweeps with excitation amplitude 0.5 g

Full size image
Fig. 6
figure 6

Tip displacement responses and the associated voltages for TEH under numerical frequency sweeps with excitation amplitude 0.5 g: a, b \(d_\mathrm{g} =32.2\) mm; c, d \(d_\mathrm{g} =31.2\) mm; e, f \(d_\mathrm{g} =30.2\) mm

Full size image
Fig. 7
figure 7

Tip displacement responses and the associated voltages for BEH under numerical frequency sweeps frequency sweeps with excitation amplitude 0.7 g

Full size image
Fig. 8
figure 8

Tip displacement responses and output voltages for TEH under numerical frequency sweeps with excitation amplitude \(a_b =0.7\) g: a, b \(d_\mathrm{g} =32.2\) mm, c, d \(d_\mathrm{g} =31.2\) mm, e, f \(d_\mathrm{g} =30.2\) mm

Full size image
Fig. 9
figure 9

Prototypes of the energy harvesters: a BEH, b TEH, c the two stable positions of BEH, d the three stable positions of TEH

Full size image
Fig. 10
figure 10

Experimental results of the strain and the voltage responses generated by the BEH under sweep excitation level of \(a_b =0.5\) g

Full size image
Fig. 11
figure 11

Experimental results of the strain and the voltage responses generated by the TEH under sweep excitation of \(a_b =0.5\) g: a, b \(d_\mathrm{g} =30.6\) mm, c, d \(d_\mathrm{g} =32.6\) mm, e, f \(d_\mathrm{g} =34.6\) mm

Full size image
Fig. 12
figure 12

Experimental results of the strain and the voltage responses generated by the BEH under sweep excitation level of \(a_b = 0.7\) g

Full size image
Fig. 13
figure 13

Experimental results of the strain and the voltage responses generated by the TEH under sweep excitation level of \(a_b =0.7\) g: a, b \(d_\mathrm{g} =30.6\) mm, c, d \(d_\mathrm{g} =32.6\) mm, e, f \(d_\mathrm{g} =34.6\) mm

Full size image
Fig. 14
figure 14

A brief time series sample of the strain measured in experiment at snap-through under excitation level of 0.7 g and frequency 10 Hz: a BEH, b TEH

Full size image

For both the TEH and BEH, the total potential energy consists of two components: the elastic potential energy and the magnetic one. We calculate them separately and add them to form the total potential energy. For example, at \(d=17\) mm and \(d_\mathrm{g} =32.2\) mm, the total potential energy diagrams of the BEH and TEH are plotted in Fig. 3. We know that now the BEH has two symmetric potential wells and one potential barrier, whose height \({\Delta }U_\mathrm{B1} \) is 48.2 mJ. In contrast, the TEH has three potential wells and two potential barriers, whose heights are \({\Delta }U_\mathrm{T1} = 8.9\) mJ and \({\Delta }U_\mathrm{T2} =4.2\) mJ, respectively. The fact that the TEH has the lower potential barrier implies that it needs the lower excitation energy for passing through the potential barriers to achieve interwell motion. Furthermore, from the perspective of the distance between potential wells, the two outer potential wells of the TEH is farther than that of the BEH, which means that the TEH can create a large amplitude of interwell motion and generate more electrical power. Thus, the advantage of the TEH in scavenging vibration energy lies in its ability to increase the amplitude of interwell motion.

Figure 4 shows the potential energies of the TEH for three different gap separation distances. Unlike the symmetrical potential wells of the BEH, the TEH own three potential wells with different depths. From the perspective of the well’s depth, the TEH can be classified into three categories: (a) the inner well is the deepest; (b) the three well’s depths are nearly the same; (c) the inner well is the shallowest. When the inner well is the deepest, the TEH is prone to oscillating in the inner potential well rather than jumping between the potential wells; when all the three well depths are nearly the same, the probability of oscillations in any one of the three potential wells is identical; thus, jumping between the wells is easy to occur; finally, in the case that the inner well is the shallowest, the TEH is likely to be trapped in one of the two outer potential wells, which is similar to the case of the BEH. In addition, it should be noted that in the case of identical well depths, the TEH possess the smallest well depth, which is in favor of interwell motions. Therefore, the TEH with identical well depths is expected to exhibit the best harvesting performance.

In order to show the frequency bandwidth over which the excitation energy can be effectively scavenged, frequency sweeping excitation is taken by linearly increasing frequency from 0 to 25 Hz at a constant rate of 0.1 Hz/s. The base acceleration amplitudes are designated as \(a_b =0.5\) g and 0.7 g (g is the gravitational constant) and the dynamic responses are acquired by numerical integration. Figure 5 illustrates the responses of the tip displacement and the output voltage for \(a_b =0.5\) g. At this relatively weak excitation, the BEH cannot pass through the potential barrier to achieve interwell oscillations, and thus, the corresponding output voltages are small.

In contrast, now the TEH’s interwell motion can be elicited by this weak excitation. Figure 6 shows its tip’s responses and the output voltages at \(a_b =0.5\) g for three gap distances. For the configuration of type (a), i.e., the inner well being deepest, most intrawell oscillations are confined in the inner potential well, and the interwell motion (chaotic motion) occurs over a fairly narrow frequency bandwidth of 8.4–10.7 Hz. As to the configuration of type (b), i.e., all potential well having the same depth, the TEH could easily go to interwell motion and the frequency bandwidth is from 6.8 to 16.1 Hz. In the case of type (c), i.e., the inner well being shallowest, it is easy for the TEH to escape from the inner well, but then the response will be restricted in the outer potential wells due to the quite deep outer wells. The interwell motion will occur over the frequency bandwidth of 5–8.7 Hz.

As for the TEH, from Fig. 8, we know that all three types of TEH have the wide frequency bandwidths of snap-through at this excitation (\(a_b =0.7\) g) (Fig. 8). Especially among them, type (b) has the widest frequency bandwidth of 6.4–17.5 Hz (Fig. 8b). So it can be deduced that there exists a best gap distance (\(d_\mathrm{g} )\), at which the TEH can attain the best performance of harvesting. This conclusion can be verified in the following experiments.

4 Experimental validation

Next as the excitation increases to \(a_b =0.7\) g, the BEH only maintains interwell motion over a narrow frequency bandwidth of 9.6–10.7 Hz, as shown in Fig. 7.

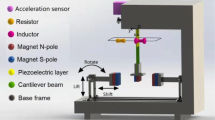
The corresponding experiments were carried out to validate the simulation results. The experimental setups are shown in Fig. 9a, b. Figure 9c, d shows the stable states of the BEH and TEH, respectively. The substrate layer is made of stainless steel with dimensions of 155 \(\,\times \,\) 7 \(\,\times \,\) 0.33 mm\(^{3}\). The piezoelectric patches have the dimensions of 8 \(\,\times \,\) 10 \(\,\times \,\) 0.25 mm\(^{3}\). The tip neodymium magnet has the dimensions of 10 \(\,\times \,\) 10 \(\,\times \,\) 0.5 mm\(^{3}\). All fixed neodymium magnets have the same dimensions of 20 \(\,\times \,\) 10 \(\,\times \,\) 0.5 mm\(^{3}\). The separate distance is adjusted in experiment such as to obtain the best performance of BEH and TEH, as a result, the best separate distances are 16 mm for BEH and 19 mm for TEH, respectively. The accelerometer was mounted on the top of shaker (DONGLING ES-3-150/LT0404) to monitor its acceleration. A data acquisition device (DH5922, DONGHUA) was used to record the open-circuit voltages and strains of the energy harvesters. The linearly increasing frequency sweeping tests were performed with the sweep rate of 0.1 Hz/s, and the frequency range was from 5 to 20 Hz. The accelerations of \(a_b =0.5\) g and \(a_b =0.7\) g were chosen as the excitation amplitudes.

Figure 10 shows the experimental results of the strain and voltage responses for the BEH under sweeping excitation of \(a_b =0.5\) g. It was apparent that no snap-through can be triggered now.

As for the TEH, at this excitation level, the interwell motions can take place for all three given gap distances (Fig. 11). Among them, we know that there is an optimal gap distance (\(d_\mathrm{g} =32.6\) mm), at which there exists the widest range of frequency of snap-through.

For a larger base excitation of \(a_b =0.7\) g, the experimental results of the strain and output voltage of the BEH and TEH are illustrated in Figs. 12 and 13, respectively. From the figures, the similar conclusion can be drawn. Comparing the experimental results with those of the simulations, we can find that they are in good agreement.

In order to see the snap-through characteristics of the BEH and TEH clearly, we choose a period of responses of the BEH and TEH in snap-through for comparison (Fig. 14). The curve in Fig. 14a reveals that the BEH must oscillate around an equilibrium position for a while and then starts jumping, and there exists a time interval between two jumps. As to that of the TEH (Fig. 14b), due to the lower potential well depths, jumping can occur between any two potential wells continuously, in which the jump between the farthest two wells is desirable since it can lead to a large amplitude and output voltage; furthermore, we can see that in the period the TEH owns a dense jump, which is benefit for obtaining a consecutive high output voltage.

5 Conclusions

This paper investigates the characteristics of a tri-stable energy harvester, which realizes the tri-stability by attractions between the beam tip’s magnet and the fixed magnets. The analytical model is established, and the dynamical equations are derived by the energy-based method and Euler–Lagrange principle. By analyzing the potential energy, we find that the case with three identical well depths is the best one for snap-through. Numerical simulations for sweeping frequency reveal that the TEH owns a broad bandwidth of frequency of snap-through and high output voltage. The validation experiments were performed at different excitation levels, and the results proved the TEH’s advantage. Moreover, the comparison between the TEH and the BEH is made experimentally, and the results indicate that the TEH is preferred to the BEH in harvesting energy.