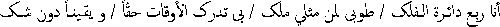Abstract
This paper is a technical study of the systematic observations and computations made by Muḥyī al-Dīn al-Maghribī (d. 1283) at the Maragha observatory (north-western Iran, c. 1259–1320) in order to newly determine the parameters of the Ptolemaic lunar model, as explained in his Talkhīṣ al-majisṭī, “Compendium of the Almagest.” He used three lunar eclipses on March 7, 1262, April 7, 1270, and January 24, 1274, in order to measure the lunar epicycle radius and mean motions; an observation on April 20, 1264, to determine the lunar eccentricity; an observation on August 29, 1264, to test the model; and another on March 15, 1262, for measuring the lunar parallax. In the second period of activity at the Maragha observatory, Shams al-Dīn Muḥammad al-Wābkanawī (c. 1254–1320) adopted all of al-Maghribī’s parameter values in his Zīj, but decreased his value for the mean longitude of the moon at epoch by 0;13,11\(^{\circ }\). By comparing the times of the new moons and lunar eclipses in the period of 1270–1320 as computed from the astronomical tables of the Maragha tradition with the true modern ones, it is argued that this correction was very probably the result of actual observations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The [Islamic] astronomers from the day of al-Ma’mūn to al-Battānī and afterwards did not mention their measurements in the same manner that Ptolemy mentioned his own computations, and did not manifest how they derived the planetary parameters from positions and motions of the planets through their continuous attempts to provide them. [...] He who elucidates his computational procedures is the most deserved to be followed.
\(\sim \)Abū al-Rayḥān al-Bīrūnī (973–1048)Footnote 1
The Marāgha observatory was built in 1259 by Hülegü (d. 1265), the founder of the Īlkhānīd dynasty of Iran. During its about fifty-eight years of operation, it represented the acme of Islamic astronomy.Footnote 2 It appears that some observations at Maragha had taken place before the construction of the observatory: In his treatise on the astrolabe, Fī kayfiyyat tasṭīḥ al-basiṭ al-kurī, Ibn al-Ṣalāh al-Hamadhānī (d. 1153) said that, at Maragha, he had found a magnitude of 23;\(35^{\circ }\) for the “total declination” (al-mayl al-kullī; i.e., obliquity of the ecliptic).Footnote 3 During the first two decades of the observatory, two zījes were written: al-Ṭūsī’s Īlkhānī zīj in Persian and Muḥyī al-Dīn al-Maghribī’s Adwār al-anwār in Arabic. Al-Ṭūsī (d. 1274) completed the Īlkhānī Zīj in about 1270. Although the majority of its underlying parameters are either Ptolemaic or borrowed from earlier zījes, nevertheless, some parameter values adopted in the Īlkhānī zīj were not known in any text prior to this work and appear to be the results of the observational program of the main staff of the observatory in the 1270s.Footnote 4 Muḥyī al-Dīn (d. June 1283) completed his zīj in the end of 1276 (see below). It was evidently based on the extensive observations done by him at the Maragha observatory. Muḥyī al-Dīn later wrote a treatise named Talkhīṣ al-majisṭī, “Compendium of the Almagest,” in which he describes his systematic observations and measurements of the solar, lunar, and planetary parameters. This treatise is our main concern in this paper. The two observational programs proceeded simultaneously and were conducted independently; none of Muḥyī al-Dīn’s new values for some parameters, except his value 23;\(30^{\circ }\) for the obliquity of the ecliptic resulting from observations performed on three successive days after the two dates of June 12 and December 7, 1264, were employed in the Īlkhānī zīj.
Little is known about Muḥyī al-Dīn except that his full name is Abū al-Shukr/Abu al-Karīm/Abu al-Fatḥ Yaḥyā b. Muḥammad b. Abī al-Shukr b. Ḥumīd of the Maghrib (of Tunis, of Andalus, or of Cordoba). He spent some years (after 1237 to October 2, 1260) in the service of King Nāṣir of Damascus (reign: 1237–1260) in Aleppo, before the king was killed by the Mongols and al-Maghribī was sent to the Maragha observatory. Other than a short-period migration to Baghdad in the second part of the 1270s (see below), he seems to have lived at Maragha and done his observations at the Maragha observatory until his death in June 1283. He taught some students in the observatoryFootnote 5 and wrote about 26 works on mathematics, astronomy, and astrologyFootnote 6 including two zījes: Tāj al-azyāj (Aleppo, about 1257)Footnote 7 and Adwār al-anwār (Maragha, 1276).
Muḥyī al-Dīn’s systematic observations at the Maragha observatory made him such an outstanding figure that his contemporaries and immediate successors called him by unique honorific titles denoting his skill in doing observations. For instance, Ibn al-Fuwaṭī, the librarian of the observatory, called him the “geometrician of the observations,” muhandis al-raṣadī.Footnote 8 His observational program is often named the “new Īlkhānīd observations,” raṣad al-jadīd al-Īlkhānī, in order to distinguish it from the purported observations conducted at Maragha for preparing the Īlkhānī zīj.Footnote 9 His fame was so widespread that his astrological doctrines were generally trusted (nine of his treatises are on astrology). An amazing example of this is the interpretation of the appearance of the comet C/1402 D1 based on his astrological doctrines which led to a very decisive war in the Middle East at the turn of the fifteenth century.Footnote 10
This paper deals with al-Maghribī’s lunar measurements as explained in the Talkhīs al-majisṭī. The work, its characteristics, and its place in the history of Islamic observational astronomy have already been introduced in three papers by George Saliba.Footnote 11 Despite its name, the treatise is neither a rewriting nor an abridgement of the contents of the Almagest, which, sometimes accompanied by criticisms about Ptolemy, was constituted as a genre with its own peculiar characteristics, playing a pivotal role in Islamic astronomy. Rather, in the same way of Ptolemy in the Almagest, Mūḥyī al-Dīn expounds how he proceeded to establish systematically his parameters starting from measuring the latitude of Maragha, the length of the tropical year, the solar mean angular velocity, ... up to the planetary parameters. In order to present his measurements, he first provides data obtained from his dated observations which are arranged chronologically, and then, he explains the mathematical procedure to determine the parameter in question. Finally, the procedures of applying the input observational data and doing computations are done, respectively, and described in detail. The obtained result is established as a new value or verified as an already existing one for that parameter. These materials as presented by Muḥyī al-Dīn allow one to pursue precisely his line of investigation, to uncover his mistakes and their effects on the final result, to recognize the probable circular arguments, etc, which is indeed very useful for making a comprehensive critical study. Regarding its contents, the Talkhīṣ has no counterpart in the medieval astronomical literature of the Middle East. Some sections of the treatise that are devoted to the measurement of planetary parameters may be considered as its most important parts, because it is hard to find any other work whose aim was to measure the planetary parameters in Islamic astronomy.
The Talkhīṣ is preserved in a unique copy (Leiden, Universiteitsbibliotheek, no. Orientalis 110) in al-Maghribī’s own handwriting. According to the table of contents given on fol. 2r, the treatise consists of ten books (maqāla). They discuss plane and spherical trigonometry (books I and II), time-reckoning (III), solar motion (IV), lunar motion (V), lunar parallax and the theory of eclipses (VI), longitudes and latitudes of the fixed stars (VII), planetary motions in longitude (VIII), retrograde motion and latitude of the planets (IX), and stereographic projection of the celestial sphere on the plane tangential to its north pole (X). The manuscript is, however, incomplete and corrupt where our author finishes his computations of Mars, while the reader expects he commences the computations related to the inferior planets. One may assume that it is the treatise itself that may have been left incomplete because of any possible reason. However, this does not appear to be the case here, because Wābkanawī reports three of Muḥyī al-Dīn’s values for the parameters of the inferior planets.Footnote 12 The last two books are also missing from this copy, but the contents of the last book may have been adopted from (possibly, a brief survey of) his treatise on the astrolabe, which deals with the same problem.Footnote 13
Muḥyī al-Dīn dedicated the Talkhīṣ to Ṣadr al-Dīn Abū al-Ḥasan ‘Alī b. Muḥammad b. Muḥammad b. al-Ḥasan al-Ṭūsī,Footnote 14 the son of Naṣīr al-Dīn al-Ṭūsī, who was appointed director of the observatory after the death of his father.Footnote 15 According to the Talkhīṣ, Muḥyī al-Dīn’s period of observations at the Maragha observatory was from March 7, 1262 (lunar eclipse; cf. Table 1) to August 12, 1274 (Jupiter). He applied the newly obtained parameters in his second zīj, the Adwār al-anwār, a copy of which has been preserved in the handwriting of the author (Mashhad, Holy Shrine Library, no. 332), which bears the date of Dhu al-qa‘da 674 H (April/May 1276) in the end of the canonsFootnote 16 and the date of Rajab 675 H (December 1276/January 1277) in the end of the tables.Footnote 17 These two dates may indicate when the canons and the tables were completed. It thus seems that he had finished his observations between August 12, 1274 and April/May 1276, and had engaged in constructing the tables in the period between April and December 1276. He also mentions in the prologue of this copy of the Adwār that he had commenced to write the zīj after completing a (now lost) treatise named Manāzil al-ajrām al-‘ulwiyya, “The mansions of the upper bodies.” We can therefore safely assume that the Talkhīṣ was written after Muḥyī al-Dīn completed the Adwār, i.e., after the end of the year 1276. According to Ibn al-Fuwaṭī,Footnote 18 Muḥyī al-Dīn left the observatory and spent a while in the service of Al-Ṣāḥib Sharaf al-Dīn b. al-Ṣāḥib Shams al-Dīn in Baghdad. The date of his departure was not given, but the migration had more likely been occurred after he finished the writing of the Adwār, i.e., after the end of 1276. From Ibn al-Fuwaṭī’s statements, it may be understood that this abandonment was due to some uncomfortable and inconvenient conditions at Maragha after the death of al-Ṭūsī, because he states immediately that after Muḥyī al-Dīn returned to Maragha, he was honored and supplied with the good amounts of regular stipend and honorarium. Thus, it is also possible that he has written the Talkhīṣ after his return from Baghdad to Maragha (i.e., a time after 1277 and, of course, before his death in 1283) when the observatory was directed by Ṣadr al-Dīn and, likely, its dedication to Ṣadr al-Dīn is as a response to his kind behavior toward the author.
In this paper, Sect. 2 concerns al-Maghribī’s observations of the three lunar eclipses at the Maragha observatory from which he determined the radius of the lunar epicycle and its mean motions. Section 3 introduces the other three lunar observations and explains al-Maghribī’s procedures, calculations, and numerical details in six separate parts that are arranged as follows: the first two parts explain how our author determined the size of the epicycle and the mean motions; in the third part, the eccentricity of the lunar orbit in the Ptolemaic model; in the fourth part, the distance between the point of prosneusis and the center of the earth; and in the fifth part, the inclination of the lunar orbit. Then, al-Maghribī’s tables of the lunar equations are briefly discussed. Finally, the last part deals with his determination of the lunar parallax. In all of these steps, the numerical values are al-Maghribī’s. The recomputed or true modern values will be indicated explicitly (the former within square brackets). In Sect. 4, some highlighted characteristics of Muḥyī al-Dīn’s observations, computations, methods, the instruments applied, and so on will be discussed and commented upon. His values for the lunar parameters will also be compared with the other medieval values obtained in the Middle East. Section 5 contains a comparative study between the times of the conjunctions and oppositions of the moon with the sun computed on the basis of modern theories and the times computed from the parameter values determined by al-Maghribī and those applied in the Īlkhānī zīj. This aims to evaluate the criticisms made by Wābkanawī (an astronomer who flourished about two decades later in the observatory) of the Īlkhānī zīj and his modification of al-Maghribī’s value for the lunar mean longitude, as will be explained there.
2 The observations of the lunar eclipses at the Maragha observatory
Table 1 presents the lunar eclipses observed by Muḥyī al-Dīn at the Maragha observatory, arranged chronologically, which have been used to determine the lunar parameters.
Col. 1 contains the numbers by which our author refers to each eclipse.
Col. 2 presents the dates of the observations given in the text according to the Yazdigird era and their corresponding dates in the Julian calendar and in Julian Days Number. In order to transform the dates from the Yazdigird era to the Julian one, it should be considered that in Islamic chronology, the day is traditionally reckoned from sunset, and hence, “night” precedes “day.” As a result, for example, the night of Wednesday, February 28, 631 Yazdigird, is the time interval between sunset on Tuesday, the 27th, and sunrise on the 28th. This confusion cannot occur when we use the equivalent Julian dates. Since our author has made the precise time of the maximum phase of each eclipse available (Col. 3), the dates can be converted conveniently.
Col. 3 presents the times of the eclipses, that is, the instants when the maximum phases occurred, counted from the beginning of the Yazdigird era. Our author counts the hours using a clepsydra (Pangān in Persian and Bankām in Arabic) from the instant of the meridian transit of the sun (true noon).Footnote 19 The instants of true noon for the days of the eclipses are, respectively, 12:10, 12:0, and 12:15 (–1 day), according to the mean local time of Maragha \(\approx \) UT \(+\) 3;5 h. The true times of the maximum phases of the three eclipses are 20:23, 22:8, and 2:12, respectively. Thus, the times of the eclipses after true noon, measured in hours, are as follows:
Nos. | Muḥyī al-Dīn | Modern | Error |
|---|---|---|---|
1 | 8;18 h | 8;13 h | \(+\)5 m |
2 | 10;13 h | 10;8 h | \(+\)5 m |
3 | 14;0 h | 13;57 h | \(+\)3 m |
Col. 4 indicates the type of the eclipse; TD denotes “Total eclipse with a perceptible duration (lit. “staying,” makth)”; P stands for “Partial.”
Col. 5 presents the magnitude of the eclipse. These might be a naked eye estimate; however, two optical devices for directly measuring eclipse magnitudes had been invented and constructed at the Maragha observatory.Footnote 20 Modern values are as follows:Footnote 21
Nos. | Muḥyī al-Dīn | Modern |
|---|---|---|
1 | Total | 1.77 |
2 | 0.833 | 0.823 |
3 | 0.8 | 0.77 |
Col. 6 gives the true longitude of the sun at the time of each eclipse, i.e., at the instant of the maximum phase. Our author has indeed calculated  based on his own parameters.Footnote 22 As we shall see below, in order to measure the radius of the lunar epicycle, it is necessary as the first step to obtain the moon’s longitudes at the instants of the maximum phases of a trio of the lunar eclipses, i.e., when the moon is in true opposition to the sun. Then, they can readily be calculated as
based on his own parameters.Footnote 22 As we shall see below, in order to measure the radius of the lunar epicycle, it is necessary as the first step to obtain the moon’s longitudes at the instants of the maximum phases of a trio of the lunar eclipses, i.e., when the moon is in true opposition to the sun. Then, they can readily be calculated as

. A comparison with modern values is as follows:
Nos. |
| |
|---|---|---|
Muḥyī al-Dīn | Modern | |
1 | 354;22,\(50^{\circ }\) | 354;\(20{,}4^{\circ }\) |
2 | 24;53,1 | 24;52,17 |
3 | 311;41,28 | 311;36,54 |
In the following, Muḥyī al-Dīn’s values for the lunar latitude and the longitude of its ascending node at the time of the eclipse no. 3 are compared with the corresponding modern data; cf. Sect. 3.2, (28) and (30).
Col. 7 shows the observed altitudes of some bright stars which were ordinarily used in order to determine the durations and times of the phases of the lunar eclipses. The position with respect to the horizon of a given celestial body may be given by means of its altitude plus its direction with respect to the meridian line; e.g., “\(51^{\circ }\) East” means an altitude of \(51^{\circ }\) at a given instant while it is located east of the meridian. An important note here is that in the case of the eclipse no. 1, the directions Mūḥyī al-Dīn cites for the measured altitudes do not express the direction of the star with respect to the meridian, but with reference to the lunar disk. Otherwise, the altitudes should have been expressed as \(51^{\circ }\) East for Regulus and \(17^{\circ }\) East for Spica at, respectively, the start and end of totality.
Based on what our author says (fol. 67v), these were the eclipses that he “dealt with observing them with the extreme accuracy,” and thus, he could rely on his observations and be confident about the correctness of the data obtained from them. In the period of his observations, nine other lunar eclipses were observable at their maximum phases from Maragha, and Muḥyī al-Dīn might have witnessed them as well.
3 Muḥyī al-Dīn’s lunar measurements
In Talkhīṣ V, chapter 1, Muḥyī al-Dīn reviews the situations of lunar motions in longitude, in anomaly, and in latitude, their periods, and explains the reason why ancient astronomers used lunar eclipses for measuring them (a recapitulation of Almagest IV, 1–3). In chapter 2, he suggests the equivalence of eccentric and epicyclic hypotheses (Almagest IV, 5) and gives the magnitudes of the radius of the lunar epicycle computed by Hipparchus, Ptolemy, and himself. In chapter 3, Ptolemy’s first (or Hipparchus’) model of the moon consisting of an epicycle rotating on a zero-eccentricity inclined deferent which intersects the ecliptic in the two orbital nodes is introduced. Our author, of course, mentions that the lunar motions cannot be explained by the aid of only an epicyclic hypothesis, but it needs to take the eccentric hypothesis into account as well (introductory remark in Almagest IV, 6). In chapter 4, our author computes the radius of the moon’s epicycle from the trio of lunar eclipses observed at the Maragha observatory (Table 1 and below, Sect. 3.1) (corresponding to Almagest IV, 6). In chapters 5 and 6, by comparing his third lunar eclipse and that of October 20, 134 observed by Ptolemy at Alexandria, he determines the rates of the lunar mean motions in longitude and in anomaly and that of the retrograde motion of the nodal line of the lunar orbit (below, Sect. 3.2) (Almagest IV, 7 and 9). In chapter 7, he computes the mean positions of the moon and the longitude of its ascending node at the epoch, i.e., for the end of the year 600 Yazdigird (= mean noon of January 17, 1232, JDN 2171062, at Maragha), from those in his eclipse no. 3 (Almagest IV, 8 and 9) and then constructs the tables of the lunar mean motions (Almagest IV, 4). In chapter 8, the second anomaly of the moon, which is related to its elongation from the sun, and then Ptolemy’s second lunar model based on an eccentric with the movable center to account for this anomaly are explained (Almagest V, 2 and 3). In chapter 9, our author computes the eccentricity of the now inclined eccentric deferent of the moon based on an observation done at Maragha in April 20, 1264 when the moon was near its last mean quadrature (below, Table 2 and Sect. 3.3) (Almagest V, 4). In chapter 10, he describes the idea of prosneusis (inḥirāf or muḥādhāt), that is, the point on the apsidal line of the lunar eccentric, in which the diameter passing through the lunar mean epicyclic apogee and perigee is directed is displaced from the earth’s center by the amount of eccentricity toward the lunar eccentric perigee. Our author measures the value of the displacement through an observation performed on August 29, 1264 when the moon was close to mean octant (below, Table 3 and Sect. 3.4) and verifies that it is equal to the eccentricity (Almagest V, 5). In chapter 11, our author instructs how to calculate trigonometrically the equations resulting from the lunar anomalies, constructs the tables for their components, and explains the procedure of computing the true ecliptical coordinates of the moon from the tables of the mean motions and equations (Almagest V, 6–9). The final parts of chapters 9 and 10 are specified to our author’s computations of the inclination of the moon’s eccentric from the last two observations (see below, Sect. 3.5). The book V ends with chapter 12 that explains the schemata of the four orbs of the moon (Ptolemy’s Planetary Hypotheses II).Footnote 23
A general overview of the contents of Talkhīṣ V shows that although Muḥyī al-Dīn describes and re-quantifies the Ptolemaic lunar model step-by-step through his own observations in the same way as Ptolemy did this, in fact, he has, a priori, the Ptolemaic ready-to-use model in his mindFootnote 24 and now wants, to a larger degree, to renew the computation of its underlying parameters and, to a lesser degree, to test it (especially, in the case of prosneusis). Figure 1 illustrates the Ptolemaic lunar model, its parameters and equations, and the conventional symbols used for referring to them. They will be explained further in the rest of the paper.
Ptolemy’s lunar model and the components of its equations: \(P=\hbox {Prosneusis};\,T = \hbox {Earth}\); Lunar eccentric of radius \(EC=R\) with center \(E;\,{\varvec{e}} = PT = TE= \hbox {Eccentricity}\); Lunar epicycle of radius \(MC=r\) with center \(C;\,\bar{{A}}= \hbox {Mean epicyclic apogee}\); \(A = \hbox {True epicyclic apogee}\);

 ;
; 
 \(=\) Mean motion in longitude with respect to
\(=\) Mean motion in longitude with respect to 

 ); \(i\)
\(=\) Inclination of the eccentric to the ecliptic; \(\beta \)
\(=\) Ecliptical latitude; \(q\)
\(=\) Equation of center; \(p_\mathrm{A}\)
\(\,=\,\) Epicyclic equation at the eccentric apogee; \(p_{\Pi }\)
\(\,=\,\) Epicyclic equation at the eccentric perigee. The tabular equation values and the calculation of the true longitude and latitude: \(c_{3} = q(2\bar{{\eta }}) \rightarrow \alpha = \bar{{\alpha }}\pm c_{3}\); \(c_{4} = p_\mathrm{A}(\alpha )\); \(c_{5} = p_{\Pi }(\alpha )-p_\mathrm{A}(\alpha )\); The coefficient of the interpolation: \(c_{6}(2\bar{{\eta }})\); \(p(\alpha ) = c_{4}+c_{5}\times c_{6}\);
); \(i\)
\(=\) Inclination of the eccentric to the ecliptic; \(\beta \)
\(=\) Ecliptical latitude; \(q\)
\(=\) Equation of center; \(p_\mathrm{A}\)
\(\,=\,\) Epicyclic equation at the eccentric apogee; \(p_{\Pi }\)
\(\,=\,\) Epicyclic equation at the eccentric perigee. The tabular equation values and the calculation of the true longitude and latitude: \(c_{3} = q(2\bar{{\eta }}) \rightarrow \alpha = \bar{{\alpha }}\pm c_{3}\); \(c_{4} = p_\mathrm{A}(\alpha )\); \(c_{5} = p_{\Pi }(\alpha )-p_\mathrm{A}(\alpha )\); The coefficient of the interpolation: \(c_{6}(2\bar{{\eta }})\); \(p(\alpha ) = c_{4}+c_{5}\times c_{6}\);  ; Argument of latitude:
; Argument of latitude:  . Equation of the inclined eccentric:
. Equation of the inclined eccentric:  ; True ecliptical longitude:
; True ecliptical longitude:  ; and
; and 
3.1 The measurement of the radius \(r\) of the lunar epicycle
In Almagest IV, 6, Ptolemy proposed a mathematical method to determine the radius \(r\) of the moon’s epicycle in terms of the radius of its deferent \(R = 60\) from the data obtained from the observations of three lunar eclipses.Footnote 25 Mūḥyī al-Dīn’s method in chapter 4 (fols. 69r–70v) is essentially that of Ptolemy; however, the application of the sine function makes the steps shorter and the whole procedure somewhat easier-to-reconstruct.
Assume that, in Fig. 2a, b, the points \(A,\,B\), and \(C\) show the position of the moon on its epicycle in the eclipses nos. 1, 2, and 3, respectively (Fig. 2a, b are copies of the diagrams drawn by our author in the manuscript, fol. 70v).Footnote 26
We know the times of the three eclipses since the epoch (cf. Col. 3 of Table 1). Thus, the time intervals between two successive eclipses are
\(\Delta t\) | |
|---|---|
From eclipse no. 1 \(\rightarrow \) no. 2 | 8 years 33 days 1;55 h |
From eclipse no. 2 \(\rightarrow \) no. 3 | 3 years 292 days 3;47 h |
Then, the differences in the lunar mean anomaly \(\Delta \bar{{\alpha }}\) and in its mean longitude \(\Delta \bar{{\hbox {\char 106}}}\) are
\(\Delta \bar{{\alpha }}\) | \(\Delta \bar{{\hbox {\char 106}}}\) | |
|---|---|---|
From eclipse no. 1 \(\rightarrow \) no. 2 | 61;57,\(26^{\circ }\) | 30;57,\(18^{\circ }\) |
From eclipse no. 2 \(\rightarrow \) no. 3 | 123;11,59 | 277;44,27 |
Thus, in Fig. 2a, b,
The difference in the lunar true longitude between two successive eclipses can be calculated from the true longitude of the sun at the instant of the maximum phase of each eclipse, already listed in Col. 6 of Table 1.
\(\Delta \hbox {\char 106}\) | |
|---|---|
From eclipse no. 1 \(\rightarrow \) no. 2 | 30;30,\(11^{\circ }\) |
From eclipse no. 2 \(\rightarrow \) no. 3 | 286;48,27 |
a The positions of the Moon in longitude and in anomaly in the three lunar eclipses observed by al-Maghribī in a lunar “epicycle zero-eccentricity deferent” model (i.e., Hipparchan model). b The transformation of the lunar anomalistic positions in the eclipses nos. 2 and 3 (the points \(B\) and \(C\)) to its orbital position in the eclipse no. 1
In Fig. 3a, the positions of the mean and true moon \((A,\,B,\,C)\) at the times of the three lunar eclipses are shown (drawn to scale). Figure 3b (which is the drawn-to-scale version of the same Fig. 2a, b) is produced through transforming DC and DB (the lines passing through the earth \(D\) and the moon in the eclipses nos. 2 and 3) in such a manner that each of them occupies their true position with respect to the mean moon. Then, it can easily be seen that \(\angle \) ADB and \(\angle \) ADC can be calculated from \(\left| {\Delta \hbox {\char 106}-\Delta \bar{{\hbox {\char 106}}}}\right| \):
Now, the problem is to find the radius \(TH (= r)\) of the circle \(ABC\) (= the lunar epicycle), so that the chords AB, BC, and AC appear from \(D\) (the earth) under the angles ADB, BDC, and ADC, respectively.
From (1),  , then \(\angle \textit{DBE} = \hbox {30;31,36}^{\circ }\). If we assign to ED an arbitrary length equal to 60, then with applying the sine rule to the plane triangle BED (Fig. 2a), we can calculate the length of BE in terms of ED. Our author computed it as
, then \(\angle \textit{DBE} = \hbox {30;31,36}^{\circ }\). If we assign to ED an arbitrary length equal to 60, then with applying the sine rule to the plane triangle BED (Fig. 2a), we can calculate the length of BE in terms of ED. Our author computed it as
(Hereafter, all numbers are Muḥyī al-Dīn’s; the recomputed numbers are given in brackets and the deviations are indicated in italics.) From (1), arc \(\textit{ABC} = \hbox {185;9,25}^{\circ }\). As a result, arc \(\textit{CA} = \hbox {174;50,35}^{\circ }\). Thus,  . From (2), \(\angle \textit{ADC} = \angle \textit{BDC} - \angle \textit{ADB} = \hbox {8;36,53}^{\circ }\). Thus, \(\angle \textit{ECD} = \hbox {78;48,24,30}^{\circ }\). Again, with applying the sine rule to the plane triangle CED, we have:
. From (2), \(\angle \textit{ADC} = \angle \textit{BDC} - \angle \textit{ADB} = \hbox {8;36,53}^{\circ }\). Thus, \(\angle \textit{ECD} = \hbox {78;48,24,30}^{\circ }\). Again, with applying the sine rule to the plane triangle CED, we have:
in terms of \(DE = 60\).
We also have \(\angle { BEC} = \angle { AEB} + \angle { AEC} = \hbox {118;24,0,30}^{\circ }\). We extend the chord EC from \(E\) to the right side and drop the perpendicular BZ that intersects it at \(Z\). Thus, \(\angle { BEZ} = \hbox {61;35,59,30}^{\circ }\), which is indeed, our author says, acute, and \(\angle \) BZE is right. Then, \(\angle { EBZ} = \hbox {28;24,0,30}^{\circ }\).
Now, we want to calculate the length of BC. First, in the triangle BEZ, we calculate the lengths of the lines BZ and EZ:Footnote 27
And we obtain, from the above-mentioned value for EZ and (4), \(CZ = EZ + EC = \hbox {9;36,46,49} \,[\hbox {9;36,}\textit{17,16}]\). Then
Until now, all of the lines have been calculated in terms of \({ DE} = 60\). We desire to express all of the lengths in terms of the radius of the lunar epicycle (circle ABC) taken as \(r = 60\). For this purpose, our author computes:
Here, the length of BC is in terms of \(r = 60\). Equations (5) and (6) establish the ratio for expressing the lengths of the lines, which were already computed in terms of \({ DE }=60\), in terms of \(r= 60\). We can then determine the length of DE in terms of \(r= 60\) as
Now, we want to compute the length of the chord AE. In the triangle BCZ:
And, indeed, arc \({ BE}=2\cdot (\angle { BCZ})=9{;}46{,}32^{\circ }\,[9{;}45{,}\textit{18}^{\circ }]\). From (1), arc \({ AE} = \hbox {arc}\, { BE} + \hbox {arc}\,{ AB} = 71{;}43{,}58^{\circ }\,[71{;}4\textit{2,44}^{\circ }]\). We can then calculate the length of the chord AE in terms of \(r = \) 60:
From (7) and (8), we can calculate the length of the line AD connecting the moon to the center of the earth at the instant of the maximum phase of the eclipse no. 1:
With regard to Fig. 2b, by Euclid III, 36,Footnote 28 from (7) and (9):
By Euclid II, 6,Footnote 29 from (10) and TH \(=\) \(r\) \(=\) 60, we have:
The line DT is the radius of the moon’s deferent and is now known in terms of \(r = 60\). If we assume \(R = DT = 60\), then we can conveniently calculate the length of \(r\) in terms of \(R = 60\) as
Muḥyī al-Dīn rounds the final result as 5;12. The errors befallen to our author are so small that their effect on the final result would not produce a rounded value other than 5;12. The maximum amount of the difference between the mean and true positions of the moon will then be Sin\(^{-1}\)(5;12) \(\approx \hbox {4;58}^{\circ }\), under the condition that the center of the lunar deferent coincides with that of the earth or, in other words, the moon revolves on a zero-eccentricity deferent (al-falak al-muwāfiq al-markaz). In his earlier zīj, Tāj al-azyāj, our author has 4;\(51^{\circ }\) (corresponding to \(r \approx 5{;}5\)),Footnote 30 which is the value ascribed to Ibn al-A‘lam (d. 985) (see below, Sect. 4.7).
3.2 The measurements of \(\omega _\mathrm{t},\omega _\mathrm{a}\), and 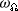
In chapters 5 and 6 (fols. 70v–72r) the procedure of determining the mean angular motions of the moon is described: the mean motion in anomaly, \(\omega _\mathrm{a}\), the mean motion in longitude, \(\omega _\mathrm{t}\), and the velocity of the retrograde motion of the lunar orbital nodes,

. In doing so, the author made use of the data obtained for the instant of the maximum phase of the eclipse no.3.
In Fig. 2b, we drop the perpendicular TKL from the center \(T\) of the epicycle to the line AE, so that it bisects the line AE at \(K\) and the arc AE at \(L\). Indeed, from (8), \({ KE} =\) 35;9,13,59,30 [35;8,42,21,53]. Then, with the length of DE from (7):
Applying the sine rule to the plane triangle KTD, with (11) and (13), we have:
Thus,
\(\angle \) KDT is the epicyclic equation of the moon at the instant of the maximum phase of the eclipse no. 1. From (2), \(\angle { ADC} = \angle { BDC}- \angle { ADB} =\hbox {8;36,53}^{\circ }\). Thus, from (15):
which is the epicyclic equation of the moon at the instant of the maximum phase of the eclipse no. 3. From (14): arc \(\textit{YL}=180^{\circ }-\angle \textit{DTK}= \hbox {94;1,20}^{\circ }\quad [\hbox {94;1,}\textit{8}^{\circ }]\); also, we previously computed arc \(AE = 71{;}43{,}58^{\circ }\). Thus,
The arc YA is the true lunar anomaly \(\alpha \) (khāṣṣa al-mu‘addala, lit. “adjusted anomaly,” named against mean anomaly \(\bar{{\alpha }}\), khāṣṣa al-wusṭā, which our author will introduce later) at the instant of the maximum phase of the eclipse no. 1. In this way, the true anomaly of the moon at the maximum phases of the other two eclipses, i.e., the arcs YB and YC, respectively, will be determined as follows. From (1), we have:
The true lunar anomaly in the eclipse no. 3, i.e., the arc YC, is indeed more than \(180^{\circ }\). Consequently, the lunar epicyclic equation calculated in (16) should be subtracted from its true longitude in order to obtain its mean longitude (i.e., the longitude of the center of the lunar epicycle). From Col. 3 of Table 1, \(\hbox {\char 106}_{\odot }= \hbox {311;41,28}^{\circ }\), and so

. Then from (16):

Now, we have the mean longitude of the moon in a well-measured time. In order to determine \(\omega _\mathrm{t}\), a mean longitude

for a given instant \(t_{0}\) should also be available. \(\omega _\mathrm{t}\) can then be computed from \(\Delta \bar{{\hbox {\char 106}}}/\Delta t\). In doing so, Muḥyī al-Dīn used the data presented by Ptolemy in Almagest IV, 6 for the second of the triple lunar eclipses observed by him at Alexandria (geographical longitude \(L=82^{\circ }\) from the Fortunate Isles, i.e., Canary Islands).Footnote 31 The data are as below:

Our author converts the time of the maximum phase of this eclipse (counted from the beginning of the Nabonassar era) from the local time of Alexandria to that of Maragha \((L = 62^{\circ })\) by adding 1;20 h:
The date of our author’s eclipse no. 3 corresponds to 18 Choiak 2022 Nabonassar. Thus, the time of the maximum phase of this eclipse counted from the beginning of the Nabonassar era is
Therefore, the time difference between the two eclipses is
Indeed, from (19) and (20), \(\Delta \bar{{\hbox {\char 106}}}=97{;}35{,}55^{\circ }\,[97{;}35{,}43^{\circ }\)]. Our author calculated that the moon completed 15230 revolutions \(+97{;}35{,}55^{\circ }\,[97{;}35{,}43^{\circ }]\) during the period (21); thus,
\(({ T}\bar{a}j\,al\hbox {-}azy\bar{a}j:\quad \quad \quad \ldots ,\hbox {36,32,17})\) Footnote 32
In order to determine \(\omega _\mathrm{a}\), we should also have two magnitudes \(\bar{{\alpha }}\) and \(\bar{{\alpha }}_0 \) for the mean anomaly of the moon measured, respectively, in the two times \(t\) and \(t_{0}\) sufficiently far from each other. From (20), it is clear that at the instant of the maximum phase of Ptolemy’s eclipse no. 2, the moon’s double mean elongation (Centrum) was \(2\bar{{\eta }}= 0{;}5{,}36^{\circ }\). By means of interpolation in the Almagest table for the lunar equation of center, our author obtains the equation of center \(q(0{;}5{,}36) = 0{;}50^{\circ }(0{;}49^{\circ })\).Footnote 33 The lunar mean anomaly in the Ptolemaic model is calculated by
Then, the mean anomaly of the moon at the time of Ptolemy’s eclipse no. 2 was
Muḥyī al-Dīn gives \(\bar{{\hbox {\char 106}}}_{\odot } = 310{;}20^{\circ }\) and

[above (19)] for the instant of the maximum phase of his eclipse no. 3. Thus, \(2\bar{{\eta }} \approx 353;32^{\circ }\). Now, by means of interpolation in the table of the lunar equation of center (so-called the “first equation”) calculated on the basis of his new value for the lunar eccentricity (cf. below, Sect. 3.3), the lunar equation of center is derived as \(q(353{;}32) = 0{;}51{,}44^{\circ }\).Footnote 34 Thus, from (18) and (23), the mean anomaly of the moon at the instant of our author’s eclipse no. 3 is
Thus, from (24) and (25), \(\Delta \bar{{\alpha }}= \hbox {180;22,30}^{\circ }\). The moon completed 15101 revolutions around the center of its epicycle \(+\,\hbox {180;22,30}^{\circ }\) in the period (21). Therefore,
In order to compute the rate of the retrograde motion of the lunar orbital node,  , our author first draws Fig. 4 (on folio 72r) which shows the position of the moon at the maximum phase of the eclipse no. 3 with respect to the ascending node \((A)\), to the ecliptic (AB), and to the circle of the earth’s shadow (the bigger circle with center \(B\)). Our author states that the angular apparent diameter of the moon at the time of this eclipse was
, our author first draws Fig. 4 (on folio 72r) which shows the position of the moon at the maximum phase of the eclipse no. 3 with respect to the ascending node \((A)\), to the ecliptic (AB), and to the circle of the earth’s shadow (the bigger circle with center \(B\)). Our author states that the angular apparent diameter of the moon at the time of this eclipse was

.Footnote 35 According to Almagest V, 14, the apparent radius of the earth’s shadow in the moon’s orbit is

The magnitude of the eclipse no. 3 was 4/5 (cf. Col. 5 of Table 1). Thus, we have:

BC is the latitude \(\beta \) of the moon. The modern value for the geocentric latitude of the moon at that moment is \(\beta = +0{;}34{,}52^{\circ }\).Footnote 36 In the triangle \(ABC,\,\angle B = 90^{\circ }\), and \(\angle A\) is the maximum latitude (= the inclination \(i\) of the orbit) of the moon, which is equal to \(5^{\circ }\) (cf. Sect. 3.5). Thus,
We know that the true longitude of the moon in the eclipse no. 3 was

; thus, the true longitude of the ascending node


in fair agreement with the modern value for  at the instant of the maximum phase of the eclipse no. 3:
at the instant of the maximum phase of the eclipse no. 3:  . In Ptolemy’s eclipse no. 2 [above (20)]:
. In Ptolemy’s eclipse no. 2 [above (20)]:  ; thus,
; thus,  . The ascending node therefore completed 61 revolutions \(+74{;}6{,}8^{\circ } [+74{;}6{,}30^{\circ }]\) in the direction of decreasing longitude in the time interval (21); then,
. The ascending node therefore completed 61 revolutions \(+74{;}6{,}8^{\circ } [+74{;}6{,}30^{\circ }]\) in the direction of decreasing longitude in the time interval (21); then,

In order to determine the lunar mean positions at the epoch, in chapter 7 (fol. 72v), our author computes back to the end of the year 600 Y (mean noon of January 17, 1232 at Maragha) from the eclipse no. 3 with the mean positions already calculated in (19), (25), and (30).

Now with (22), (26) and (31), Muḥyī al-Dīn constructs his own tables for the lunar mean motions in chapter 7.Footnote 38
3.3 The measurement of the Ptolemaic lunar eccentricity \(e\)
Through Ptolemy’s laborious lunar measurements, our author was well acquainted with the fact that the epicycle hypothesis is not enough in order to account for the moon’s motions at the times other than conjunctions and oppositions. He also knew that the lunar epicyclic equation at mean quadrature (when the moon’s mean elongation from the sun is \(180 \,\pm \, 90^{\circ }\)) is greater than any similar epicyclic position occupied at the other phases and that the moon has the least distance to the earth at quadratures. In order to determine how much greater the epicyclic equation may be at mean quadratures, which also makes possible to measure the lunar eccentricity, the moon should be observed when both (a) it is near mean quadrature and (b) it has an anomaly of about \(95^{\circ }\) to cause its epicyclic equation to be maximum. Our author starts his computations in chapter 8 (fols. 73r–76r) from the values observed for the altitudes of the sun and moon when the moon transited the meridian of Maragha on Sunday, April 20, 1264. At that moment, the moon was near its last mean qudrature (Table 2).
He gave the following quantities for the instant of this observation, by which he computed the moon’s ecliptical coordinates as follows (also see below, Sect. 4.6):

\(\hbox {Time elapsed since sunrise}: \quad \,\, \sim 10.5\,\hbox {min}=\hbox {2;37,20}^{\circ } \left[ \hbox {2;37,45}^{\circ }\right] \) Footnote 40
Our author draws Fig. 5 (fol. 76v) in which AB is an arc of the eastern horizon, CBL, the meridian and ADE, the eastern arc of the ecliptic, the southern pole of which is \(M.\) Thus, \(A\) is the ascendant ( ṭāli‘) and \(D\) is the mid-heaven or the transit degree (darajat al-tawassuṭ) whose longitude is denoted by  . CTY is the eastern arc of the celestial equator; thus, the arc TY is the oblique ascension of the arc TA (i.e., \(A_{\varphi }(TA) = TY\)). At the moment of the observation, the apparent moon is at \(Z\), but the true moon is at \(H\). ZH shows the lunar parallax in the vertical/altitude circle. Hence, ZB is the lunar apparent (topocentric) altitude and HB is its true (geocentric) altitude. We draw the orthogonal MHE to the ecliptic \((\angle { HED} = 90^{\circ })\); thus, \(E\) is the true position of moon on the ecliptic and HE is its latitude. With \(D\) as the pole, we draw a great circle passing through \(Y\) and \(M\), which intersects the ecliptic and the meridian, respectively, at \(K\) and \(L\,(\angle { TKY} = 90^{\circ };\,\hbox {arc}\,{ KYM} =90^{\circ })\).
. CTY is the eastern arc of the celestial equator; thus, the arc TY is the oblique ascension of the arc TA (i.e., \(A_{\varphi }(TA) = TY\)). At the moment of the observation, the apparent moon is at \(Z\), but the true moon is at \(H\). ZH shows the lunar parallax in the vertical/altitude circle. Hence, ZB is the lunar apparent (topocentric) altitude and HB is its true (geocentric) altitude. We draw the orthogonal MHE to the ecliptic \((\angle { HED} = 90^{\circ })\); thus, \(E\) is the true position of moon on the ecliptic and HE is its latitude. With \(D\) as the pole, we draw a great circle passing through \(Y\) and \(M\), which intersects the ecliptic and the meridian, respectively, at \(K\) and \(L\,(\angle { TKY} = 90^{\circ };\,\hbox {arc}\,{ KYM} =90^{\circ })\).
In the spherical triangle \({ KYT}\!,\,{ YT} = \hbox {24;31,12} + \hbox {2;37,20} = \hbox {27;8,32}^{\circ }\). \(\angle { KTY}\) is the obliquity of the ecliptic, \(\varepsilon = \hbox {23;30}^{\circ }\). Using the sine rule, we have \({ KY} = \hbox {10;29}^{\circ }\). \({ TC} = { YC} - { YT} = 90 - \hbox {27;8,32} = \hbox {62;51,28}^{\circ }\). Then the right ascension of the mid-heaven is  . Interpolating in our author’s table of the right ascension (fol. 34v), we then have:
. Interpolating in our author’s table of the right ascension (fol. 34v), we then have:

The arc DB is the altitude of the mid-heaven: \(h_\mathrm{mid}=\hbox {31;30}^{\circ }\). For the lunar apparent altitude \({ ZB}=h^{\prime }_\mathrm{max} = \hbox {28;34}^{\circ }\), our author calculates the lunar parallax (i.e., the arc HZ) as \(\varPi =\hbox {1;15}^{\circ }\) (cf. below, Sect. 4.3). Then the lunar true altitude is HB \(=\) \(h_\mathrm{max} = \hbox {29;49}^{\circ }\). As a result,
Since \(\angle \,{ TCD} = \angle { YKT} = 90^{\circ }\), we have:
Then, we can calculate the lunar latitude (the arc EH) using the sine rule to the triangle DEH:

In order to determine the lunar longitude, we should compute the arc DE. We know arc \(\textit{DE} = 90^{\circ } - \angle \textit{EML}\). Now, in the triangle \(\textit{MHL},\,\textit{MH} = 90^{\circ } - \textit{EH}= \hbox {88;21}^{\circ },\,\textit{LH} = 90^{\circ }- \textit{DH} = \hbox {88;19}^{\circ }\), and \(\angle \textit{HLM} =90^{\circ }\); thus, using the sine rule in the triangle \(\textit{HLM},\angle \,\textit{HML} = \hbox {89;39,11}^{\circ }\,[\hbox {89;40}^{\circ }]\). Therefore, \(DE=\hbox {0;20,49}^{\circ }\,[\hbox {0;20}^{\circ }]\). Now, from (34), the longitude of the moon is calculated as

The ecliptical coordinates computed by our author, compared with the modern ones, are summarized as follows:

Our author gives the mean longitudes of the sun and moon for mean noon of April 20, 1264 at Maragha as  and
and

; then \(\bar{{\eta }}= \hbox {269;38,15}^{\circ }\). Thus, a distance of \(y = 0{;}21{,}45^{\circ }\) should be travelled by both the mean sun and the mean moon until the last mean quadrature occurs when they are located in the angular distance of \(\bar{{\eta }}= 270^{\circ }\) from each other (Fig. 6). We wish to know how long it will take. This is easily calculated from

\(\omega _\mathrm{t}\) is given in (22) and \(\omega _{\odot } =\hbox {0;59,8,20,8,4,36,38}^{\circ }/\hbox {d}\). Thus,
During this time interval, the moon travels
and the sun,
along the ecliptic. Therefore, on the basis of our author’s results, the time of the last mean quadrature and the mean longitudes of the sun and moon when it took place were

The results are in fair agreement with the modern values:

As it is obvious, our author’s value for the time of the last mean quadrature has an error of about \(+\)18 min.
Our author gives half the hours of daylight as 6;43,\(31^\mathrm{h}\) [true \(\approx \) 6;40\(^\mathrm{h}\)]. Thus, the time of the last mean quadrature is \(6{;}43{,}31 + 0{;}42{,}48 = 7{;}26{,}19^\mathrm{h}\) after sunrise and \(7{;}\hbox {26,19} \,-\, (\hbox {2;37,20} \,\times \, 24/360) \approx 7{;}15{,}50^\mathrm{h}\) after the instant of the observation [above (33)]. The moon travels an arc of 3;59,\(17^{\circ }\) along the ecliptic during 7;15,\(50^\mathrm{h}\).Footnote 41 Thus, from (39), the true longitude of the moon at the instant of the last mean quadrature is

Therefore, the difference between the lunar true and mean longitudes, (41) and (42), is

We know that this is the amount of the angle subtended by the lunar epicycle radius at the earth’s center (or the same epicyclic equation of the moon) at the instant of the last mean quadrature. In the end of Sect. 3.1, we have calculated that if the moon revolves on a zero-eccentricity deferent, the radius of the lunar epicycle should always appear under the angle 4;\(58^{\circ }\) from the earth. Thus, the center of the moon’s deferent does not evidently coincide with that of the earth. Our author is well aware of this as well as the fact that the epicyclic equation will catch its maximum amount at mean quadratures.
In order to measure the lunar eccentricity \(e\), our author draws Fig. 7 (or extracts it from Almagest V, 4),Footnote 42 in which the earth is at \(D\). We previously assumed that the lunar deferent is a circle with center \(D\), whose radius AD is taken as \(R = 60\), but it is now known that the center \(C\) of the lunar deferent is displaced from \(D\). Thus, CD is the lunar eccentricity. We want to obtain the magnitude of CD in terms of \(\textit{AD} = R = 60\). Through the Almagest, we know that at mean quadrature, the center of the lunar epicycle is located at the perigee \(B\) of its eccentric. If the moon \((Z)\) has an anomaly (arc EZ) at that time such that the line DZ is tangential to the epicycle, then the epicyclic equation \((\angle \textit{BDZ})\) will be maximum. In the triangle \(\textit{DZB},\,\angle \textit{DBZ} = 180^{\circ }-\angle \textit{ZBE}\), where \(\angle \,\textit{ZBE}\) is the lunar anomaly, our author gives \(\alpha = \hbox {100;29,59}^{\circ }\) for the time of the last mean quadrature [above (41)]; then \(\angle \textit{DBZ} = \hbox {79;30,1}^{\circ }\). And from (43), \(\angle \,\textit{BDZ} =\hbox {7;7,32}^{\circ }\). Thus, \(\angle \,\textit{DZB} = \hbox {93;22,27}^{\circ }\). BZ is the radius of the epicycle, i.e., \(r= \hbox {5;12}\) in terms of \(R = 60\). Using the sine rule results \(\textit{BD} = \hbox {41;51}\). Our author rounds this to the nearest integer number, i.e., \(\textit{BD} = 42\). Thus, \(\textit{AB} = 60 + 42 = 102\). Therefore, the radius of the lunar eccentric deferent, AC, is calculated as 51, and the lunar eccentricity, CD, as
Then, the maximum amount of the lunar epicyclic equation (“second equation”) will be equal to sin\(^{-1}\)(5;12/42) \(\approx \hbox {7;8}^{\circ } [\hbox {7;7}^{\circ }]\). This is the case when at mean quadrature, the line passing through the centers of the earth and moon is tangential to its epicycle. And the difference between the maximum values of the second equation of the moon when the center of its epicycle is located at the eccentric apogee and at the eccentric perigee will be \(\hbox {7;8} - \hbox {4;58} = \hbox {2;10}^{\circ }\) [Ptolemy: \(\hbox {2;39}^{\circ }\)].
3.4 Prosneusis and the mean epicylic apogee in the Ptolemaic lunar model
In chapter 10 (fols. 77v–80r), our author introduces the last component of the Ptolemaic lunar model, i.e., prosneusis. This step is also like the testing of the model. In doing so, he makes use of his observation of the meridian transit of the moon on Friday, August 29, 1264, when the moon was near mean octant (Table 3).
The method of the determination of the ecliptical coordinates of the moon at the time of the observation is as described above, Sect. 3.3. In order to compute the longitude of the mid-heaven, our author first gives the solar mean longitude for the time of the observation as

So  , and hence, the right ascension of the solar longitude counted from the head of Capricorn is
, and hence, the right ascension of the solar longitude counted from the head of Capricorn is  . The revolution of the celestial sphere in this time interval is
. The revolution of the celestial sphere in this time interval is  . Then
. Then  (counted from the head of Capricorn). Thus,
(counted from the head of Capricorn). Thus,  . Accordingly, \(h_\mathrm{mid} = \hbox {34;52}^{\circ }\). Our author gives the lunar parallax in the vertical circle as \(\varPi = \hbox {1;3}^{\circ }\) (cf. below, Sect. 4.3). Hence,
. Accordingly, \(h_\mathrm{mid} = \hbox {34;52}^{\circ }\). Our author gives the lunar parallax in the vertical circle as \(\varPi = \hbox {1;3}^{\circ }\) (cf. below, Sect. 4.3). Hence,

and

. With regard to Fig. 8 which depicts the celestial sphere with respect to the local horizon at the instant of this observation, \(\delta ^{\prime } = \hbox {sin}^{-1}(\hbox {sin}(\hbox {317;35,46}-180)\times \hbox {sin}(\hbox {23;30})) = \hbox {15;35,53}^{\circ }\) [error \(\approx -2^{\prime \prime }\)]. We have \(\mu = 90^{\circ }- \delta ^{\prime }\) (cf. (36) and Fig. 5). Then \(\mu = \hbox {74;24,7}^{\circ }\). Like the procedure already described in Sect. 3.3, the latitude of the moon and the difference \(x\) between its longitude and the mid-heaven are determined by solving the highlighted triangles in Fig. 8; the results are

and \(x = \hbox {1;20,48}^{\circ } [\hbox {1;21,8}^{\circ }]\). Also, referring to the tables of the lunar mean motions, our author gives the mean and true positions of the moon at the instant of this observation as follows:

Now, our author draws Fig. 9 (fol. 79v) illustrating the orbital components of the Ptolemaic lunar model. \(\angle { AEB}\) is the mean double elongation of the moon; from (45) and (46), we have: \(2\bar{{\eta }}= \hbox {137;11,8}^{\circ }\). Then, \(\angle { BEG} = \hbox {42;48,52}^{\circ }\). Also, if \({ AE} = 60\), then \({ DE} = 9\) and \({ BD} = 51\). Thus, using the sine rule in the triangle BDE, we have \(\angle { DBE} = \hbox {6;53,18}^{\circ }\). Also, \(\angle { BDG}=\angle { BEG}-\angle { DBE}=\hbox {35;55,34}^{\circ }\). Applying the sine rule to the triangle BDE, we have:
From (46), the moon’s epicyclic equation at the time of this observation is

, and so, as our author mentions, the line passing through the centers of the earth and moon, i.e., EH, is located west of the line EZ. In the triangle BEH, BH is the radius of the lunar epicycle \(r = \hbox {5;12}\) and \(\angle { ZEH} =\hbox {2;24,22}^{\circ }\). Using the sine rule, we have: \(\angle { EHB}=\hbox {20;49,22}^{\circ }\) [error \(\approx +1^{\prime \prime }\)]. Thus,
This is the lunar anomaly. And it is evidently larger than the mean anomaly [cf. above, (46)]. From this, it results that the origin of the lunar mean motion in anomaly is not the point \(Z\), but the point \(T\) locating west of \(Z\) by the distance of \(\hbox {23;13,44}-\!\!\hbox {13;54,8} = \hbox {9;19,36}^{\circ } (= \angle { TBZ} = \angle { EBY})\) from it. Then, our author draws the line TB and extends it to meet AG at \(Y\). The problem is to verify \({ EY} = { ED}\). If so, the Ptolemaic lunar model is tested successfully. The proof is as follows: in the triangle \({ BEY}, \angle { BEG} =\hbox {42;58,52}^{\circ }\) and \(\angle { EYB} = 180^{\circ }- (\angle { BEG} +\angle { EBY}) = \hbox {127;51,32}^{\circ }\,[\hbox {127;41,32}^{\circ }]\). Then
which is approximately equal to ED, i.e., the Ptolemaic lunar eccentricity, computed earlier, cf. (44).
3.5 The measurement of the inclination of the lunar deferent (= maximum latitude)
In the end of both chapters 9 (folio. 77v) and 10 (fols. 79v–80r), our author devotes an unnumbered chapter to the calculation of the lunar parallax and orbital inclination from the data presented above. In order to compute the inclination \(i\) of the lunar deferent from the empirical data, we return to Fig. 4. AC is the angular distance of the moon from the node and BC is its latitude at the instant of the observation. \(\angle B = 90^{\circ }\). \(\angle BAC\) is the inclination of the lunar deferent. Our author gives  for the time of the observation no. 4 (cf. Table 2) from his table of the motion of the lunar ascending node. Also, from (39),
for the time of the observation no. 4 (cf. Table 2) from his table of the motion of the lunar ascending node. Also, from (39),

; thus,

. And

. Applying the sine rule to the triangle ABC, we have:
which in full agreement with the modern value calculated for April 20, 1264 AD.
For the time of the observation no. 5 (cf. Table 3), our author computes  from his table. With regard to Fig. 4, from (46):
from his table. With regard to Fig. 4, from (46):

and

. Applying the sine rule to the triangle ABC, we have:
The modern value for August 29, 1264 is \(i = \hbox {5;11}^{\circ }\).
After computing all of the lunar parameters, our author proceeded to prepare the tables for the equations, all of which are for each \(1^{\circ }\) of argument up to \(180^{\circ }\) (cf. Fig. 1): the table for the “first equation” or the “equation of center”: \(q(2\bar{{\eta }})=c_{3}\) and the “coefficient of the interpolation” due to the distance between the center of the lunar epicycle and that of the earth: \(c_{6}(2\bar{{\eta }})\) (fol. 82r); the table for the “second equation” or the “epicyclic equation at the eccentric apogee”: \(p_\mathrm{A}(\alpha )=c_{4}\) (fol. 82v); the table for the “third equation,”Footnote 43 i.e., the difference between the epicyclic equation at the eccentric perigee and at the eccentric apogee: \(p_{\Pi }(\alpha )-p_\mathrm{A}(\alpha )=c_{5}\) (fol. 83r); and the last lunar equation tabulated is the equation due to the shift of the moon from the inclined eccentric to the ecliptic: \(c_{7}\) (fol. 83v). The table for the lunar latitude is also on fol. 83r. The values of \(c_{7}\) and the moon’s latitude are for the argument of latitude

. Cf. Tables 4, 5, and 6. In the Adwār al-anwār, all of the equations are tabulated together (CB: fols. 81v–82r. The table of the latitude is on fol. 87v).Footnote 44
Neither in the Almagest, nor in the Handy Tables,Footnote 45 were the amounts of the equation \(c_{7}\) tabulated. To our best knowledge, a table for it first appeared in Yaḥyā b. Abī Manṣūr’s Zīj al-mumtaḥan.Footnote 46 He and later Ibn Yūnus gave \(\hbox {max}(c_{7}) = 0{;}6{,}0^{\circ }\) for  , and \(46^{\circ }\), presumably computed from the value \(i= 4{;}46^{\circ }\).Footnote 47 Al-Maghribī, in chapter 11, calls \(c_{7}\) as “the equation of the inclined sphere of the moon” (ta‘dīl al-falak al-mā’il) or “the equation of the shift” (ta‘dīl al-naql)Footnote 48 (fol. 83v) and explains how the equation to be calculated:
, and \(46^{\circ }\), presumably computed from the value \(i= 4{;}46^{\circ }\).Footnote 47 Al-Maghribī, in chapter 11, calls \(c_{7}\) as “the equation of the inclined sphere of the moon” (ta‘dīl al-falak al-mā’il) or “the equation of the shift” (ta‘dīl al-naql)Footnote 48 (fol. 83v) and explains how the equation to be calculated:

where \(i = 5^{\circ }\). Accordingly, \(\hbox {max}(c_{7}) = 0{;}6{,}33^{\circ }\) for  , while the Muḥyī al-Dīn’s table gives 0;6,\(40^{\circ }\) for
, while the Muḥyī al-Dīn’s table gives 0;6,\(40^{\circ }\) for  , and \(46^{\circ }\). The same table can be found in Khāzinī (Zīj, fol. 135r), the Īlkhānī zīj (C: p. 84), Kamālī (fols. 67r and 243v), Wābkanawī (T: fol. 156r), among others.Footnote 49 Bīrūnī (al-Qānūn, Vol. 2, p. 810), Kāshī (IO: fol. 133v; P: fol. 51v), and Ulugh Beg (P1: fol. 126v; P2: fol. 145r) accurately gave \(\hbox {max}(c_{7}) = 0{;}6{,}33^{\circ }\).
, and \(46^{\circ }\). The same table can be found in Khāzinī (Zīj, fol. 135r), the Īlkhānī zīj (C: p. 84), Kamālī (fols. 67r and 243v), Wābkanawī (T: fol. 156r), among others.Footnote 49 Bīrūnī (al-Qānūn, Vol. 2, p. 810), Kāshī (IO: fol. 133v; P: fol. 51v), and Ulugh Beg (P1: fol. 126v; P2: fol. 145r) accurately gave \(\hbox {max}(c_{7}) = 0{;}6{,}33^{\circ }\).
3.6 The measurement of the lunar parallax
In Talkhīṣ VI, our author deals with the lunar parallax, the solar and lunar distances from the earth, and the theory of eclipses (corresponding to Almagest V, 11–16, VI). In order to measure the lunar parallax in the circle of altitude, the observation should be made when (a) the moon is near the points of the solstices ( or \(270^{\circ }\)), (b) its ascending node is near the points of the equinoxes (
or \(270^{\circ }\)), (b) its ascending node is near the points of the equinoxes ( or \(180^{\circ }\)) to cause the moon to have the maximum northern or southern latitude, and (c) the moon transits the local meridian. Through our author’s period of the observations at Maragha, such a situation occurred in March 1262.Footnote 50 In VI, 2 (fols. 85v–86r), He used an observation made on March 15, 1262 (Table 7).
or \(180^{\circ }\)) to cause the moon to have the maximum northern or southern latitude, and (c) the moon transits the local meridian. Through our author’s period of the observations at Maragha, such a situation occurred in March 1262.Footnote 50 In VI, 2 (fols. 85v–86r), He used an observation made on March 15, 1262 (Table 7).
From the tables of the mean motions, he gives the following mean positions for the instant of this observation:

and then he proceeds to compute the lunar parallax as follows:
Muḥyī al-Dīn | Modern | ||
|---|---|---|---|
| 272;16,\(33^{\circ }\) | 272;9,\(9^{\circ }\) | |
\(\beta \) | \(-\)4;57,20 | \(-\)5;14,13 | |
Declination | \(\delta \) | \(-\)28;25,53 [\(-\)28;26,7]\(^{1}\) | \(-\)28;45,23 |
Co-latitude | \(90-\varphi \) | 52;39,30 | 52;36,14 |
Geocentric altitude | \(h_\mathrm{max}\) | 24;13,37 [24;13,23] | 23;50,51 |
Apparent altitude | \(h^{\prime }_\mathrm{max}\) | 22;48 | 22;58,41 |
Parallax | \(\varPi \) | 1;25,37 [1;25,23] | 0;52,\(10^{2}\) |
In Talkhīṣ VI, 3 (fols. 86r–87v), using \(h^{\prime }_\mathrm{max} = \hbox {22;48}^{\circ }\) and \(\varPi =\hbox {1;25,37}^{\circ }\), our author found that the moon–earth distance at the instant of this observation was 36;59,53 terrestrial radii (\({}^\mathrm{tr})\). Using \(R = 60, e \approx 9\), and \(r = \hbox {5;12}\), he also calculated that this distance is 37;37,42 in terms of \(R = 60\). All of the dimensions of the lunar model may then be expressed in the unit \({}^\mathrm{tr}\) through multiplying them by the factor of
as Ptolemy held in Almagest V, 13. In Talkhīṣ VI, 4 (fols. 87v–91v), our author constructed the table of the lunar parallax like Almagest V, 18 for the following four limits on the basis of the dimensions computed from his new values for \(e\) and \(r\):
\(\bar{{\eta }}(^{\circ })\) | \(\bar{{\alpha }}(^{\circ })\) | Distance \((^\mathrm{tr})\) |
|---|---|---|
0 | 0 | 64;6,48 |
0 | 180 | 53;53,12 |
90 | 0 | 46;24,48 |
90 | 180 | 36;11,12 |
Then, he instructed the operator how to calculate the lunar parallax from its geocentric altitude, elongation, and anomaly by the aid of the table. The table is given for the steps of \(3^{\circ }\), as in the Handy Table (an extract of this is shown in Table 8).
In the rest of the book VI, there is nothing else new except three interesting points as follows. Like Ptolemy, Muḥyī al-Dīn held the opinion that the angular diameters of the sun and moon are equal at their greatest distances from the earth. Nevertheless, he found that the minimum apparent diameters of the sun and moon are about 0;31,\(8^{\circ }\), instead of Ptolemy’s value 0;31,\(20^{\circ }\). This is not, of course, an observational achievement, but the result of a remedy of Ptolemy’s computations in Almagest V, 14. Ptolemy calculated the apparent diameter of the moon from the data obtained from the Babylonian observations of the two lunar eclipses on April 21/22, 621 BC and July 16/17, 523 BC, and arrived at 0;31,\(20^{\circ }\) as the minimum value.Footnote 51 Muḥyī al-Dīn realized that on the basis of the data given by Ptolemy, in both the eclipses, the moon was not at its maximum distance from the earth. As a result, 0;31,\(20^{\circ }\) cannot be the minimum amount of the lunar apparent diameter. Based on Ptolemy’s data, in these eclipses, the lunar anomaly was, respectively, \(20^{\circ }\) and \(28^{\circ }\). Simply adopting the mean value \(24^{\circ }\) results that the moon was in the distance of 64;50 \((R = 60)\) from the earth. Thus, the moon’s apparent diameter at its greatest distance from the earth should be equal to \(\hbox {64;50} \times \hbox {0;31,20}/\hbox {65;15}=\hbox {0;31,8}^{\circ }\) (Talkhīṣ, VI, 6: fols. 94r–v). I do not know another medieval astronomer objecting Ptolemy at this point. An indispensable consequence of the value 0;31,\(8^{\circ }\) is that the sun’s greatest distance from the earth is \(1420.5^\mathrm{tr}\) (Talkhīṣ, VI, 7: fols. 95r–v) while Ptolemy has \(1260^\mathrm{tr}\). The last issue that is worth mentioning is the existence of a comprehensive account of the annular solar eclipses (Talkhīṣ, VI, 17: fol. 106r). Some scatter (either incidental or passing) allusions to this phenomenon prior to al-Maghribī can be addressed; e.g., Simplicius (6th ct.), Bīrūnī (11th ct.), and al-Khāzinī (12th ct.), among others.Footnote 52
4 Some technical and historical comments
4.1 Process of measurements
The way in which our author presented his process of observations and computations for measuring the lunar parameters most likely does not cover all of what he in reality did to obtain them. It is quite possible that other observations that he performed (esp. the other nine lunar eclipses that he may have witnessed; see the quotation in the end of Sect. 2), some intervening turns of computation, and/or intermediate results have been discarded. He should have started his final computations after he observed the third lunar eclipse in 1274. The basic parameters \(r,\,\omega _\mathrm{t}\), and  could then be computed (Sects. 3.1, 3.2). After doing that, having referred to his recorded observations of 1264 (Tables 2 and 3), he first calculated \(e\) and \(\omega _\mathrm{a}\) and then examined the Ptolemaic model. He most likely dealt with the last computations documented in the Talkhīṣ in the period from August 1274 to December 1276, during which he was also busy with the preparation of the tables of second zīj, the Adwār. Meanwhile, he had thus to work with a preliminary set of parameters which resulted from his earlier unrecorded observations and undocumented computations at Maragha, were taken from his previous zīj, the Tāj al-azyāj, or were borrowed from his predecessors. It seems our author was utilizing his earlier parameters as well as Ptolemy’s.Footnote 53 He refers to his Islamic predecessors very rarely; besides the observations of the autumnal equinoxes by Yaḥyā b. Abī Manṣūr (Baghdad) and by al-Marwarūdhī and Sanad b. ‘Alī (Damascus), which he compared with his autumnal equinox observation of September 15, 1264 in order to determine the length of the tropical year (365;14,30 days),Footnote 54 no further allusion to his Islamic predecessors may be found in the Talkhīṣ.Footnote 55
could then be computed (Sects. 3.1, 3.2). After doing that, having referred to his recorded observations of 1264 (Tables 2 and 3), he first calculated \(e\) and \(\omega _\mathrm{a}\) and then examined the Ptolemaic model. He most likely dealt with the last computations documented in the Talkhīṣ in the period from August 1274 to December 1276, during which he was also busy with the preparation of the tables of second zīj, the Adwār. Meanwhile, he had thus to work with a preliminary set of parameters which resulted from his earlier unrecorded observations and undocumented computations at Maragha, were taken from his previous zīj, the Tāj al-azyāj, or were borrowed from his predecessors. It seems our author was utilizing his earlier parameters as well as Ptolemy’s.Footnote 53 He refers to his Islamic predecessors very rarely; besides the observations of the autumnal equinoxes by Yaḥyā b. Abī Manṣūr (Baghdad) and by al-Marwarūdhī and Sanad b. ‘Alī (Damascus), which he compared with his autumnal equinox observation of September 15, 1264 in order to determine the length of the tropical year (365;14,30 days),Footnote 54 no further allusion to his Islamic predecessors may be found in the Talkhīṣ.Footnote 55
4.2 Lunar maximum latitude
Our author’s step of measurement devoted to determine the value of the maximum latitude or the inclination of the orbit of the moon \(\beta _\mathrm{max}=i = 5^{\circ }\) (Sect. 3.5) does not seem so reasonable because, in order to measure  (Sect. 3.2), the value \(\beta _\mathrm{max} = 5^{\circ }\) has already been used to compute
(Sect. 3.2), the value \(\beta _\mathrm{max} = 5^{\circ }\) has already been used to compute  in the lunar eclipse no. 3. Now, using the table of
in the lunar eclipse no. 3. Now, using the table of  , the same value for
, the same value for  has in fact been redeployed in order to compute \(\beta _\mathrm{max}\). Thus, the procedure is indeed circular. It seems our author has only tried to justify why he has used the value \(\beta _\mathrm{max} = 5^{\circ }\) which had been accepted from the antiquity to the medieval period, and he himself did not attempt to measure this value.
has in fact been redeployed in order to compute \(\beta _\mathrm{max}\). Thus, the procedure is indeed circular. It seems our author has only tried to justify why he has used the value \(\beta _\mathrm{max} = 5^{\circ }\) which had been accepted from the antiquity to the medieval period, and he himself did not attempt to measure this value.
In order to determine the moon’s maximum latitude, one has to measure the apparent meridian altitude \(h^{\prime }_\mathrm{max}\) of the moon when its longitude is around \(90^{\circ }\) and its ascending node is near the vernal equinox, because, only under this condition, the lunar parallax will have its minimum amount. Then, the maximum latitude will be obtained as \(\beta _\mathrm{max}=h^{\prime } + \varPi - (90^{\circ } - \varphi + \varepsilon )\).Footnote 56 One attempt made during the medieval Islamic period for measuring \(\beta _\mathrm{max}\) is that of the Banū Mūsā at Baghdad, which has been documented in Bīrunī’s al-Qānūn al-mas‘ūdī:Footnote 57
Date | \(h^{\prime }\) | \(\varepsilon \) | \(\varphi \) | \(\varPi \) | \(\beta \) |
 | |
|---|---|---|---|---|---|---|---|
Monday, 28 Ābān 239 Y | Banū Mūsā: | 84;\(53^{\circ }\) | 23;\(33^{\circ }\) | 33;\(20^{\circ }\) | 0;\(5^{\circ }\) | 4;\(45^{\circ }\) | 90-0;\(3^{\circ }\) |
11 Dec. 870 AD, JDN 2039170 | Modern: | 84;56 | 23;35 | 33;20 | 0;5 | 4;56 | \(\sim \)81 |
The altitude value is expressed as  , which gives the impression that the instrument used had maybe been graduated for each \(3^{\prime }\). The input data are relatively correct and even the parallax had been calculated based on a horizontal parallax 0;\(56^{\circ }\) found in Indian sources, which is more accurate than Ptolemy’s 1;\(26^{\circ }\).Footnote 58 Nevertheless, the measured \(\beta \) is not \(\beta _\mathrm{max}\), simply because at the instant of the observation, the moon was not in
, which gives the impression that the instrument used had maybe been graduated for each \(3^{\prime }\). The input data are relatively correct and even the parallax had been calculated based on a horizontal parallax 0;\(56^{\circ }\) found in Indian sources, which is more accurate than Ptolemy’s 1;\(26^{\circ }\).Footnote 58 Nevertheless, the measured \(\beta \) is not \(\beta _\mathrm{max}\), simply because at the instant of the observation, the moon was not in  , but in
, but in  , and also
, and also  .
.
4.3 Lunar parallax in the observations nos. 4 and 5
Another example to show Muḥyī al-Dīn working with pre-existing parameters is the problem of the lunar parallax confronted in the observations nos. 4 and 5. In order to measure the eccentricity as well as to test the Ptolemaic lunar model, one of our author’s input observational data is the amount of the parallax while it can be calculated if and only if the lunar eccentricity, and thus the moon-earth distance are known. In the end of his computations as presented above in Sects. 3.3 and 3.4, our author computed the amounts of the lunar parallax for the instants of the observations nos. 4 and 5 from the distances resulting from the new value \(e= 9\) in order to verify that his input data in both observations are correct. The argument appears to be circular again.
In order to neutralize the effect of parallax on the lunar longitude, the observation should be made when the moon’s longitude equals the culminating point of the ecliptic. In such a situation, the ecliptic will be perpendicular to the lunar altitude circle and thus the longitudinal component of parallax becomes zero. As we have already seen in Sects. 3.3 and 3.4 and it will also be discussed below (cf. Sect. 4.6), our author did not directly measure longitudes, rather he measured the meridian altitude and time, and then converted them to the ecliptical coordinates. As a result, in order to neutralize the effect of parallax along with utilizing our author’s special method, the observation should be made when both the ecliptic is perpendicular to the meridian and the moon is appreciably near the points of the solstices, i.e., when the culminating point of the ecliptic, the mid-heaven, and the longitude of the moon are all equal. This situation occurs in observations like those employed to determine the maximum lunar latitude or parallax (e.g., the observation no. 6). Of course, it should also satisfy the other two conditions mentioned in the beginning of Sect. 3.3. Such a situation occurs very rarely and also gathering all conditions to allow doing such a measurement is very hard to achieve. For instance, in the observation no. 6 (Table 7), the moon was near, but not exactly in  and so the ecliptic was not firmly perpendicular to the local meridian. Moreover, at that instant, the moon’s anomaly was \(\alpha \approx 156^{\circ }\), far from the epicyclic quadrature. This observation could thus not serve for such a purpose.
and so the ecliptic was not firmly perpendicular to the local meridian. Moreover, at that instant, the moon’s anomaly was \(\alpha \approx 156^{\circ }\), far from the epicyclic quadrature. This observation could thus not serve for such a purpose.
Nevertheless, there may be an explanation for decoding the text at this point. It comes from our author’s style of rounding in the case of the value obtained for the minimum distance between the lunar epicycle center and the earth: he computed BD = 41;51 (Fig. 7) and rounded it to 42 and, as a result, \(e = 9\) is given instead of \(e = \hbox {9;4,30}\,(R = AD = 60)\). This gives impression that he started out the computation from some already-existed values for the lunar parallax to obtain an estimate for, or to find the amplitude of the variation in, \(e\). It may simply be shown that the Ptolemaic value for the lunar parallax in the altitude circle in a situation similar to the observations no. 4 is not more than \(\varPi =\hbox {1;19}^{\circ }\).Footnote 59 Working with the latter value (i.e., more than our author’s value by \(4^{\prime }\)) makes a difference of \(+\hbox {0;3,11}^{\circ }\) in

[cf. (38)] and so a difference of \(-\hbox {0;3,11}^{\circ }\) in

; i.e., 7;4,\(21^{\circ }\) instead of 7;7,\(32^{\circ }\) (cf. (43)). Therefore, \(BD = \hbox {42;9,29} \approx 42\) and hence \(e = \hbox {8;55,16} \approx 9\). (Note that working even with the drastically deviated values like \(\varPi = \hbox {1;0}^{\circ }\) and \(\hbox {1;30}^{\circ }\), making the differences of \(-\hbox {0;0,17}^{\circ }\) and \(+\hbox {0;5,11}^{\circ }\) in

, respectively, do not result in a rounded value other than \(e \approx 9\), i.e., 9;5 and 8;49, respectively.) This could make our author confident that \(e\) should be around 9, but he was probably and naturally not certain about its sexagesimal fractions. This appears to be the reason why our author gave the final result only in an integer number. It is deserved to notice that our author was likely aware of the fact that any change in the value of \(e\) by some minutes has a negligible effect on the lunar longitude.
4.4 Equation of time
The mean time intervals between the two eclipses [cf. Sect. 3.1 and 3.2(21)] contain the amounts due to the equation of timeFootnote 60, which must be taken into account in order to compute the true time intervals between them. The longitude values should also be modified by the correction amounts resulting from the equation of time. We have already shown that  recalculated for the instant of the maximum phase of the eclipse no. 1 based on our author’s tables coincides precisely with the value given by him (cf. note 22) as well as appreciably with the modern one. Following the same procedure to calculate
recalculated for the instant of the maximum phase of the eclipse no. 1 based on our author’s tables coincides precisely with the value given by him (cf. note 22) as well as appreciably with the modern one. Following the same procedure to calculate  for the other two eclipses results in the values given by our author (Col. 6 of Table 1). It thus seems that the correction due to equation of time has been neglected in each instance. This is apparently a consequence of the fact that our author did not believe that the equation of time exists. Wābkanawī reports that “if the day is counted from one midday to the next, the difference occurring in the [length] of days is only due to the equation of days [i.e., equation of time] according to the opinion of the majority of astronomers, except Mawlānā [i.e., our master] Muḥyī al-Dīn al-Maghribī. He believed that it does not exist. In his Majisṭī, he has presented a proof for his claim. And [in this case,] the opinion of the majority [of the astronomers] is correct.”Footnote 61 Accordingly, a table of the equation of time is found neither in the Talkhīṣ, nor in the Adwār. Although such a crude opinion indeed appears to be unjustifiable, it may be found at least in one other work from the thirteenth century: Kamāli reports concerning the Zīj al-Mughnī written by a certain Muntakhab al-Dīn Sakkāk (or Hakkāk) of Yazd (a city in central Iran) that its author did not put any difference between the mean and true solar days.Footnote 62
for the other two eclipses results in the values given by our author (Col. 6 of Table 1). It thus seems that the correction due to equation of time has been neglected in each instance. This is apparently a consequence of the fact that our author did not believe that the equation of time exists. Wābkanawī reports that “if the day is counted from one midday to the next, the difference occurring in the [length] of days is only due to the equation of days [i.e., equation of time] according to the opinion of the majority of astronomers, except Mawlānā [i.e., our master] Muḥyī al-Dīn al-Maghribī. He believed that it does not exist. In his Majisṭī, he has presented a proof for his claim. And [in this case,] the opinion of the majority [of the astronomers] is correct.”Footnote 61 Accordingly, a table of the equation of time is found neither in the Talkhīṣ, nor in the Adwār. Although such a crude opinion indeed appears to be unjustifiable, it may be found at least in one other work from the thirteenth century: Kamāli reports concerning the Zīj al-Mughnī written by a certain Muntakhab al-Dīn Sakkāk (or Hakkāk) of Yazd (a city in central Iran) that its author did not put any difference between the mean and true solar days.Footnote 62
4.5 Instruments
As we have already seen, our author’s observational data are altitudes and times of day. The majority of our author’s meridian altitude measurements, as explicitly mentioned by him in each case, were performed by the aid of the central quadrant of the observatoryFootnote 63 (engraved for each \(0.5^{\prime }\)), and most of the times by a clepsydra (see below).
Our author does not specify the instrument utilized for measuring the altitudes in the observations nos. 4–6. Although four of the large-sized instruments constructed in the observatory were altitude-azimuthal, only one of them, the so-called having the two quadrants, could be used for simultaneous observations of the horizontal coordinates of two celestial objects that appear in any angular distant from each other in the sky, as it is the case with the observations nos. 4 and 5.Footnote 64 We may thus suggest that the instrument “having the two quadrants” was utilized in the observations nos. 4–6, and more likely in other similar cases. Based on the times that our author gives for the observations nos. 4–6 (Tables 2, 3, and 7), it is evident that the moon had yet about one–two degrees of azimuth to travel until it reached the meridian of Maragha. This type of systematic error suggests the occurrence of a misalignment of about one degree toward the east in the meridian line marked on the azimuth circle of the instrument “having the two quadrants.” The error in the altitude of the sun and of the moon in observations nos. 4 and 5 was around \(\pm 10^{\prime }\) and \(\pm 20^{\prime }\), respectively, and that of the moon in observation no. 6 around \(-10^{\prime }\).
Muḥyī al-Dīn frequently referred to the application of a clepsydra or water-clock in his systematic observations. In Persian, the term pangān was used to refer to clepsydra,Footnote 65 which was Arabicized both as bankām and as fankān in the Islamic period; the first was utilized to name “water-clock,” in particular, and the latter was employed to call “clock,” in general. Al-Maghribī, however, mentions the name of the clepsydra as mankām which seems to be a corruption of bankām. Based on the information given by al-Maghribī, one may only speculate about its calibrations, but nothing more is known on its structure. The clepsydra used in al-Maghribī’s observations, of course, appears to have been of a good accuracy, so that it could fix the time intervals with a precision of only a few minutes (in the case of the lunar eclipses: error \(\approx \) +5 min; cf. Sect. 2). It may be mentioned that the use of the clepsydras having compound mechanical components was well established in Chinese astronomy since, at least, the eleventh century.Footnote 66 Due to the verified cultural relations between the two realms of Mongolian empire (i.e., Iran and China) and, especially, considering the fact that the Chinese astronomers (at least, a Fu Mengchi or Fu Muzhai) worked at the Maragha observatory,Footnote 67 perhaps, there was a connection between the clepsydra of the Maragha observatory and the Chinese elaborated technology of making time-measuring devices.
4.6 Al-Maghribī’s method of obtaining the ecliptical coordinates
The observational data achieved were converted to the ecliptical coordinates which served as the input data for the computation (cf. Sects. 3.3 and 3.4). We are not told the reason why our author preferred coping with this relatively lengthy process of doing computations over utilizing an armillary sphere through which he could read off the ecliptical coordinates directly. It is probable that he saw some difficulties in working with the instrument.Footnote 68 Throughout the treatise, the use of the armillary sphere is only mentioned in a passage in VII, 4, which is in fact a quotation from Almagest IX, 2Footnote 69 related to the observations of the planetary conjunctions with the stars. We know that a model of the armillary sphere had more likely been built in the observatory (radius of its ecliptic ring \(\approx \) 200 cm). Muḥyī al-Dīn’s specific treatment produced some restrictions on his measurements. For instance, when dealing with the stellar measurements in the Talkhīṣ, he complains that
“it is not possible for us to observe either Vega (\(\alpha \) Lyrae) or Capella (\(\alpha \) Aurigae), both of which transit the circle of meridian in its northern direction, because there is no northern quadrant [established] on the meridian line in this auspicious, blessed observation[-al program].”Footnote 70
4.7 Historical values
The more important values obtained for the lunar parameters by medieval Islamic astronomers in the Middle East are summarized in Table 9. As it may evidently be seen, some of these astronomers obtained values around Muḥyī al-Dīn’s \(r= 5{;}12\) (corresponding to \(\hbox {max}(c_{4}) = 4{;}58^{\circ }\)). Accordingly, it should not be considered as a sheer novel value (however, the independent result of a new set of observational data). Ibn al-A‘lam’s \(\hbox {max}(c_{4}) = 4{;}51^{\circ }\) is found in Muḥyī al-Dīn’s Tāj al-azyāj.Footnote 71 Although it is possible that he adopted it from Ibn al-A‘lam, it may also be the fruit of an independent observation done in Damascus, like his independently measured value \(\hbox {max}(c_{4}) = \hbox {4;58}^{\circ }\). The existence of other new parameters in the Tāj al-azyāj gives a preference to the latter possibility.
To my best knowledge, only two Islamic astronomers besides our author presented their observational data of a trio of lunar eclipses and explained how a value for \(r\) could be computed from them: al-Bīrūnī in al-Qānūn al-mas‘ūdī (the lunar eclipses of AD 1003–4)Footnote 72 and al-Kāshī in Khāqānī zīj (the lunar eclipses of AD 1406–7).Footnote 73 Considering the new values for \(e\) in the Islamic period, it may be mentioned that Bīrūnī’s \(e=\hbox {10;51}\) is not a value obtained from independent observations, but is the fruit of a remedy of Ptolemy’s computations in Almagest V, 3 (see below). The other value is \(e = \hbox {10;23}\) adopted in Ulugh Beg’s Sulṭānī zīj. Nevertheless, other than Muḥyī al-Dīn’s, no account of the measurement of \(e\) from independent observational data appears to exist.
[1] and [2] Kamālī, fols. 49r and 229v–230r. He also attributes \(\hbox {max}(c_{4}) = \hbox {4;56}^{\circ }\) to Indians and 5;\(0^{\circ }\) to Buzarjumihr denoting pre-Islamic Persian astronomy (the tradition of the Shāh zīj?).
[3] Ibn Yūnūs, pp. 121/176. From \(\hbox {max}(c_{4}) = \hbox {4;48}^{\circ },\,r= \hbox {5;1,14}\approx \hbox {5;1}\). Ibn Yūnus has \(\hbox {max}(c) = \hbox {7;38,34}^{\circ }\) (the sum of \(c_{4}(98) = \hbox {4;47,34}\) and \(\hbox {max}(c_{5})= c_{5}(98) = \hbox {2;51}\)). Note that these numbers are not in agreement with each other because one simply obtains from \(\hbox {max}(c_{4}) = \hbox {4;48}^{\circ }\) and \(\hbox {max}(c) = \hbox {7;38,34}^{\circ },\,e \approx \hbox {11;7}\) rather than \(e \approx \hbox {10;19}\). It seems that Ibn Yūnus accepted the value \(\hbox {max}(c_{5}) = \hbox {2;51}^{\circ }\) to keep the maximum amount of the lunar epicyclic equation near the Ptolemaic value 7;\(40^{\circ }\) without examining carefully whether or not they are in agreement with each other. See also below, Table 12, for Ibn Yūnus’ values for the lunar mean motions.
[4] Bīrūnī computed \(r = \hbox {5;11,43,36}\) from his observations of the three lunar eclipses occurred in the period of AD 1003–4 (al-Qānūn, Vol. 2, pp. 742–743, misprinted as \(4;\ldots \)) and obtained \(r \approx \hbox {5;13,45}\) from the data preserved by Ptolemy for the three Babylonian eclipses (Almagest IV, 11) (ibid., pp. 736/746, misprinted as 4;18,...and 5;38,..., respectively). He, however, gave \(r = \hbox {5;11,45,17}\) (ibid., p. 747, misprinted as 5;41,...) as his last result, from which he derived \(\hbox {max}(c_{4})=\hbox {4;58,4,38}^{\circ }\) and rounded it to 4;58,\(5^{\circ }\) (ibid., p. 792). His tables are asymmetrical, giving \(\hbox {Min} = \hbox {0;1,55}^{\circ }\) and \(\hbox {Max} = \hbox {9;58,5}^{\circ }\), from which \(\hbox {max}(c_{3}) = \hbox {4;58,5}^{\circ }\) is indeed resulted. Bīrūnī did not attempt to measure the lunar second anomaly and thus its eccentricity. He, who shows the considerable reliance upon the observations of the Banū Mūsā, mentions that it was not possible to the Banū Mūsā to measure carefully the lunar second anomaly, presumably because at the instant of the observation, “the moon was far distant from the qudrature.” Nevertheless, the value of the lunar second anomaly was roughly determined to be \(\hbox {2;40}\pm \hbox {0;48}^{\circ }\). Thus, “since we do not find,” Bīrūnī says, “the amount on which we can rely, we return back to Ptolemy’s computation and scrutinize it in the Almagest.” He examined Ptolemy’s calculations to determine the amount of the second lunar anomaly on the basis of the two observations made by Hipparchus and Ptolemy himself (Almagest V, 3) and obtained a value different from Ptolemy’s, i.e., \(\hbox {max}(c) = \hbox {7;48,8}^{\circ }\), and hence a “non-Ptolemaic” value \(e\approx \hbox {10;51}\) (ibid., pp. 793–794). He then computed \(q_\mathrm{max} = \hbox {13;50,2}^{\circ }\) (ibid., p. 803; the correct amount is 14;\(10^{\circ }\)).Footnote 74 From his asymmetrical table with \(\hbox {Min} = \hbox {1;2,48}^{\circ }\) and \(\hbox {Max} = \hbox {28;50,2}^{\circ },\,q_\mathrm{max} =\hbox {13;53,37}^{\circ }\) resulted, however.
[6] Kāshī, IO: fols. 132v–133r; P: pp. 132/135. His tables gives \(\hbox {max}(c) \approx \hbox {7;42,19}^{\circ }\) (= the sum of \(c_{4}(98) = \hbox {5;2,26}^{\circ }\) and \(c_{5}(98) =\hbox {2;39,53}^{\circ }\)), nearly in agreement with the desired value 7;42,\(27^{\circ }\).
[7] There is a table in Ulugh Beg’s Sulṭānī zīj giving the distance \(\varDelta \) of the moon from the earth when \(\bar{{\eta }}=0\!:\,\varDelta _\mathrm{max}= \hbox {65;12,24}\) and \(\varDelta _\mathrm{min} = \hbox {54;47,36}\), then \(r= \hbox {5;12,24}\) (P1: fol. 131v; P2: fol. 150v). The table for \(c_{3}\) (P1: fol. 128r; P2: fol. 143v) is asymmetrical, giving \(c^{\prime }_{3}(0) =\hbox {13;15,34}^{\circ },\,c^{\prime }_{3}(114) = \hbox {26;31,8}^{\circ }\) and \(c^{\prime }_{3}(246) = 0\). It is obvious that the constant \(k = \hbox {13;15,34}^{\circ }\) has been added to all of the entries of the corresponding symmetrical table, \(c_{3}\), to produce the asymmetrical table: \(c^{\prime }_{3}= c_{3}+k\). Thus, \(\hbox {max}(c_{3})=c_{3}(116) = \hbox {13;15,34}^{\circ }\), and hence \(e \approx \hbox {10;23}\). A re-computation of the table with \(e \approx \hbox {10;23}\) as the underlying parameter produces the results which are in excellent agreement with the entries of the original table (see Table 10; wherever there is a divergence between the tabulated and the corresponding true values, the difference (although all are about a few arc-seconds) is given within parentheses).
5 The historical and the modern testing of the times of the lunar synodic phenomena computed from the parameters of the zījes of the Maragha tradition
Table 11 presents the ecliptical coordinates of the moon calculated based on Muḥyī al-Dīn’s tables, i.e., taking the tabulated accumulation of the mean motions and interpolating in the tables of the equations, for a month since the epoch (i.e., from 17 January through February 16, 1232). Table 12 summarizes the epoch values for the mean longitude and mean anomaly of the moon and the longitude of its orbital ascending node as given by al-Maghribī (for mean noon of 5/13/600 Y, 17 January 1232, JDN 2171062, at Maragha; cf. above, (32)) as well as in the Īlkhānī zīj (for mean noon of 1/1/601 Y, 18 January 1232 at Maragha). The lunar mean positions of the Īlkhānī zīj for January 17, 1232 are simply produced by subtracting the daily mean motions given in the zīj from its mean positions at the epoch. The comparison with the modern values obviously shows that both the epoch values for the lunar mean longitude are nearly of the same accuracy (error \(\approx -11^{\prime }\) in the case of Muḥyī al-Dīn and \(-9^{\prime }\) in the case of the Īlkhānī zīj). But the Īlkhānī zīj has a better value for the lunar mean anomaly at the epoch (error \(\approx -23^{\prime })\) than al-Maghribī (error \(\approx +3^{\circ }\,44^{\prime })\). Considering the epoch values for the longitude of the lunar ascending node, al-Maghribī has a bit more accurate value (error \(\approx +7^{\prime })\) than the Īlkhānī zīj (error \(\approx +14^{\prime })\).
The underlying parameters of the Īlkhānī zīj, as its author clearly says in the prologue,Footnote 75 had been borrowed from the zījes of Ibn al-A‘lam and Ibn Yūnus. Of course, both \(r\) and \(e\) in the Īlkhānī zīj are Ptolemaic,Footnote 76 and thus none of the ‘new’ values observed by Ibn Yūnus and Ibn al-A‘lam (cf. Table 9, nos. 2 and 3) are employed in it. It thus seems that al-Ṭūsī refers to the mean motions adopted in the Īlkhānī zīj. Table 13 summarizes Ibn Yūnus’s solar and lunar mean motions in a Persian/Egyptian year given in the canons of his zīj, the daily mean motions resulting from them (I), and the rounded values tabulated in his zīj (II)Footnote 77 in comparison with the Īlkhānī zīj (III), Ptolemy (IV), and Muḥyī al-Dīn (V). Therefore, the mean motions of the sun and moon in the Īlkhānī zīj appear to have been borrowed from Ibn Yūnus. However, this conclusion needs a further mathematical analysis to be verified completely.Footnote 78
(1) Counted from the apogee. (2) The table has \(\hbox {226;46,22}^{\circ }\), but since the table for \(c_{4}\) is asymmetric giving \(c^{\prime }_{4}(0) = +\hbox {7;40}^{\circ }\), it is evident that all of the mean longitudes were decreased by \(\hbox {7;40}^{\circ }\) and then tabulated; thus, \(\hbox {226;46,22} + \hbox {7;40} = \hbox {234;26,22}^{\circ }\). This is in agreement with the tabulated value for the double mean elongation at the epoch, \(\hbox {220;50,31}^{\circ }\), because the Īlkhānī zīj has the solar mean anomaly at the epoch = 215;36,\(15^{\circ }\) and the longitude of the solar apogee at the epoch = 86;24,\(21^{\circ }\) and gives an asymmetric table for the solar equation of center, whose maximum value is \(+\)2;0,\(30^{\circ }\).Footnote 79 Then, the sun’s mean position at the epoch is 304;1,\(6^{\circ }\). Therefore, the moon’s double mean elongation at the epoch is \(2 \times (\hbox {234;26,22} - \hbox {304;1,6}) =\hbox {220;50,31}^{\circ }\). (3) Table has \(\hbox {245;1,27}^{\circ }\) and the table for \(c_{3}\) is asymmetric giving \(c^{\prime }_{3}(0) = +\hbox {13;8}^{\circ }\). It is then known that all of the entries of the table for the lunar mean anomaly were decreased by 13;\(8^{\circ }\) and then tabulated; therefore, \(\hbox {245;1,27} + \hbox {13;8} = \hbox {258;9,27}^{\circ }\).
A good time after the two zījes, i.e., al-Maghribī’s Adwār and the Īlkhānī zīj, appeared, al-Zīj al-muḥaqqaq al-sulṭānī (completed between 1316 and 1324) was written by Shams al-Dīn Muḥammad al-Khwāja Shams al-Munajjim al-Wābkanawī al-Bukhārī at the Maragha observatory.Footnote 80 The period of Wābkanawī’s observations, as he himself says, extended over 40 years. The first observation documented in his zīj is the measurement of the lunar altitude on 3 December 1272, which, as he explicitly mentioned, had been done at Maragha and shows that he was there at least since 1272.Footnote 81 The last observation documented is that of the triple conjunctions of the two superior planets, i.e., Jupiter and Saturn, in 1305–6 (we are not told the place of this observation).Footnote 82 Meanwhile, he mentioned the observation of the annular
eclipse of 30 January 1283 in MughānFootnote 83 and that of the great conjunction of 1286 (the place of the observation was not given).Footnote 84 Based on the explanations given in the prologue of the zīj, these observations were mainly focused on testing the data derived from the various zījes against observations. With regard to his explanations, it appears he paid considerable attention to test the Īlkhānī zīj, which was regarded as the main achievement of the observatory, and Muḥyī al-Dīn’s Adwār against the observations. He gives the numerical results concerning his comparative studies. He finally was convinced that the times of the occurrence of the astronomical phenomena such as conjunctions and oppositions as well as the planetary ecliptical coordinates calculated based on the Īlkhānī zīj did not coincide with the data derived from the observations, and added that, especially in the case of magnitudes and the instants of the eclipses’ phases, heavy disagreements and evident differences were observed.Footnote 85 Conversely, the Adwār al-anwār gave the results in good agreement with the observations, which persuaded him to adopt all of Muḥyī al-Dīn’s new values for the Ptolemaic parameters in his zīj: “we observed all of them [i.e., the previously mentioned phenomena] based on the principles established in this zīj and found the calculated [position and/or time] in agreement with the observed [position and/or time].”Footnote 86 He also strictly criticized the Īlkhānī zīj especially for the reason that its fundamental planetary parameters were adopted from earlier zījes. He referred to Muḥyī al-Dīn’s Adwār as based on “the New Ilkhanid Observations” (i.e., Muḥyī al-Dīn’s own observations) for the sake of making a distinction between it and the Īlkhānī zīj which was assumed to be obtained through the “Ilkhanid Observations” (i.e., the observational program supervised by al-Ṭūsī and performed by his colleagues).Footnote 87 Wābkanawī, as he himself says in his zīj’s introduction, attempted to correct the minor disagreements found in “the principles of the Ilkhānīd observations” (i.e., al-Maghribī’s parameters) with regards to the results which, our author claims, had been obtained from observations during his 40-year career. One of them is the increase in Muḥyī al-Dīn’s value for the mean longitude of the moon by 0;13,\(11^{\circ }\), which is equivalent to a difference of about 24 min in the arrival of the mean moon at a specific longitude between the times computed from al-Maghribī’s and Wābkanawī’s zījes.Footnote 88 As a result, for the synodic phenomena such as new moons or full moons, it is expected that the times computed from Wābkanawī’s zīj precede those obtained from al-Maghribī’s.
That the author has presented such quantitative conclusions is significant and here is an appropriate opportunity to check them by means of testing the values derived from Īlkhānī zīj and al-Maghribī’s Adwār/Talkhīṣ against the true modern values.Footnote 89 In doing so, the times of the new moons for 135 lunations during the 1270s (from December 24, 1269 through November 24, 1280) were computed from the three zījes, Muḥyī al-Dīn’s, Īlkhānī zīj, and Wābkanawī’s, and then the found errors were plotted in the graphs of Fig. 10a–c, respectively.Footnote 90 The mean values of the errors are, respectively, \(+\)18.3, \(+\)21.3, and \(-\)7.3 min. In 85 cases (i.e., 62.5 percent), Wābkanawī has considerably better values than al-Maghribī. Accordingly, Wābkanawī’s modification of al-Maghribī’s value for the mean longitude of the moon seems to have improved the times computed.
The errors in the times computed for 136 new moons in the 1270s (from December 24, 1269 to November 24, 1280) based on the parameters of a al-Maghribī, b Īlkhānī zīj, and c Wābkanawī. The horizontal lines show the mean values of errors which are about \(+\)18.3, \(+\)21.3, and \(-\)7.3 min, respectively
Wābkanawī could test the theoretical values against the observations of the lunar eclipses in a sufficiently long period. He did so, as he claims, during his 40-year career. From the early 1270s to the end of the 1310s, the 15 lunar total eclipses were observable at their maximum phases from Maragha (cf. Table 14). Let us assume that Wābkanawī had observed them. What could he find then? We know that he had access to a clepsydra called Pangān, maybe the same model of which al-Maghribī made use. We already estimated its accuracy to be about 5 min (cf. Sect. 4.5). In his zīj (IV, 15, 8–9),Footnote 91 Wābkanawī mentions the two methods in order to measure the times of the phases of an eclipse: (1) the standard method of computing the time from the altitude of the sun (in the case of a solar eclipse) or the moon and reference stars (in the case of a lunar eclipse) and (2) using the clepsydra. They together, as Wābkanawī emphasized, constituted a method that might reduce the probable errors in measuring time. In Table 14, the times of the maximum phases of these 15 lunar total eclipses calculated based on these three zījes were compared with the true modern values. Comparing al-Maghribī’s times with those given by the Īlkhānī zīj shows that each set have more accurate values for about half number of the eclipses; the mean values of errors are about \(+\)24 and \(+\)30 min, respectively. Wābkanawī has nine values more accurate than the Īlkhānī zīj, while for the two eclipses (i.e., 1302-01-15 and 1320-07-21), the errors of the two zījes (regardless of sign) are equal. Comparing with Muḥyī al-Dīn, Wābkanawī has 11 more accurate values. In the case of Wābkanawī, the mean value of the errors is only \(-\)2 min. Therefore, it can obviously be seen that Wābkanawī’s modification of al-Maghribī’s value for the mean longitude of the moon significantly resulted in reducing errors by a mean value of 22 min. I believe that this statistically suggests that his correction of al-Maghribī’s value for the lunar mean longitude at the epoch was the result of doing observations. The similar conclusion may be drawn from the computation of the annular solar eclipse of January 30, 1283. The error in the time of the maximum phase of this eclipse as computed by Wābkanawī in his zīj for the latitude of Mughān (northwestern Iran, \(\varphi \approx 39^{\circ }\)) in comparison with the modern data is \(-\)4 min while the time computed according to al-Maghribī’s parameter values (i.e., only neglecting Wābkanawī’s modification of al-Maghribī’s value for the lunar mean longitude at the epoch) is +28 min.Footnote 92
6 Concluding remarks
In this paper, we presented Muḥyī al-Dīn al-Maghribī’s determination of the parameters of the Ptolemaic lunar model at the Maragha observatory in the 1270s and 1280s based on the contents of books V and VI of his Talkhīṣ al-majisṭī. As we already mentioned, besides al-Bīrūnī (11th ct.) and al-Kāshī (15th ct.), who documented their determinations of the size of the lunar epicycle and the lunar mean motions, al-Maghribī is the only Islamic astronomer who gave the account of his determination of all of the lunar parameters on the basis of the data obtained from observations. His observations and computations were explained in Sect. 3, and some of their distinct features were commented upon in Sect. 4. The results were compared with the values preserved from other medieval Middle Eastern astronomers (4.7). Al-Maghribī obtained new values for the lunar mean motions (3.2), eccentricity (3.3), and parallax (3.6). The value 5;12 our author found for the size of the epicycle (3.1) dates, at least, back to the early tenth century, and in the case of the inclination of the lunar orbit, he preferred to stay with the ancient value \(5^{\circ }\) (3.5). Our author also tested the Ptolemaic lunar model and verified that the distance between the point of prosneusis and the earth’s center is equal to the eccentricity.
Muḥyī al-Dīn, as the contents of the Talkhīṣ illustrate, was a well-experienced astronomer who knew when and under what conditions he could find what he sought after. For example, the lunar observation no. 6 was done when only three years had been elapsed after laying of the cornerstone of the observatory while its buildings and instruments had not yet been constructed completely; as already discussed (cf. Sect. 3.6 and note 50), the specific situation concerning the positions of the moon in connection with the ecliptic and the position of the ecliptic with respect to the local horizon at the instant of this observation, which satisfied the essential conditions for measuring the lunar parallax, did not occur again at Maragha until nine years later.
We also dealt, as a case study, with Wābkanawī’s attempts for reconciling theory and observation as regard the times of the lunar synodic phenomena computed from the zījes of the Maragha tradition. It was concluded that al-Maghribī’s parameter values resulted in times that agree only a bit better with the true modern values than those computed from the Īlkhānī zīj. But Wābkanawī’s modification of al-Maghribī’s value for the lunar mean longitude appears to make a remarkable improvement on times computed from al-Maghribī’s values for the lunar parameters that were determined at the Maragha observatory.
Notes
A tentative translation of Bīrūnī, Vol. 3, p. 1193, lines 2–5.
Cf. (Lorch (2000), p. 401). MS. Iran, the library of parliament, no. 6412, fol. 62r: wa huwa ‘alā mā wajadnāhu bi-’l-raṣad bi-Marāgha 23 \(juz^{an}\) wa 35 daqīqa. Nevertheless, in some later copies of it (e.g., MS. Iran, Library of Parliament, no. 602, pp. 33–52, written originally by Qāḍī-zādih al-Rūmī in Rajab 892/July 1487, and MS. Iran, Library of Parliament, no. 6329, pp. 24–35), the second part (maqāla) of the treatise is the “Projection of the Astrolabe” (Tasṭīh al-asṭurlāb) of Muḥyī al-Dīn al-Maghribī, wherein that author stated his own found magnitude for the total declination, 23;\(30^{\circ }\) (bi-qadr al-mayl al-a‘zam, huwa 23;30 ‘alā mā wajadnāhu bi-’l-raṣad; the edited text in the present author’s thesis for receiving M. Sc. degree in the history of astronomy, cf.Mozaffari 2007).
Cf. below, Sect. 5. Some parameter values applied to the Īlkhānī Zīj that may not be found in earlier works are: (1) the values tabulated for the longitude of the solar apogee for the years 601 Yazdigird (AD 1232) onwards; no relation between them and earlier zījes may be found. Quṭb al-Dīn al-Shīrāzī, a member of the observatory, associated these values with the “new observations” done at the Maragha observatory (al-Shīrāzī, Tuḥfa, fol. 38v; al-Shīrāzī, Ikhtiyārāt, fol. 50v). (2) The radius of Mars’ epicycle: the table for the epicyclic equation of Mars for the adjusted anomaly is symmetrical with the maximum value 42;\(12^{\circ }\) at mean distance (i.e., when the distance between the center of the planet’s epicycle and that of the earth is equal to the radius of the deferent, which is taken as \(R = 60\)) (Īlkhānī Zīj, C: p. 116, P: fols. 38v–39r, M: fols. 70v–71v). This amount corresponds to the value 40;18 for the radius of the epicycle. (3) A star table in which the ecliptical coordinates of 16 stars observed at the Maragha observatory are tabulated, accompanied by their coordinates according to Ptolemy and Ibn Yūnus (d. 1007) as well as those attributed to Ibn al-A‘lam (d. 985). All longitudes were converted to the epoch of the zīj, i.e., January 18, 1232. The coordinates attributed to Ibn al-A‘lam appear to have been derived indirectly from the Mumtaḥan zīj (Baghdad, \(c.\) 830) (van Dalen 2004a, pp. 27–28).
Of them, Ibn al-Fuwaṭī (1995, Vol. 1, 146–147) mentions of a certain ‘Izz al-Dīn al-Ḥasan b. al-Shaykh Muḥammad b. al-Shaykh al-Ḥasan al-Wāsiṭī al-‘aṭṭār Shaykh Dār Mūsīyān (also cf. below, note 65).
Cf. (Suter (1902), p. 155), Brockelmann, Vol. 1, p. 626, \(\hbox {S}_{1}\), p. 868, (Sarton (1953), pp. 1015–1016), (Sezgin (1978), p. 292); (Rosenfeld and Ihsanoglu (2003), p. 226). Some of his mathematical works were studied, cf.Voux (1891), Hogendijk (1993). S. Tekeli’s short entry about al-Mghribī in DSB (Gillipsie et al. 1980, Vol. 9, p. 555) only covers his mathematical works. Also, cf. M. Comes’ entry in (Hockey et al. (2007), pp. 548–549).
Cf.Dorce (2003).
Ibn al-Fuwaṭī, 1995, Vol. 5, p. 117.
In the prologue of his Zīj al-muḥaqqaq al-sulṭānī, Shams al-Dīn Muḥammad Wābkanawī (c. 1254–1320) employs the term “new Īlkhānīd observations” specifically for Muḥyī al-Dīn’s observations; cf. below, Sect. 5. In Mozaffari and Zotti (2013), all of the indications of the term, found in the treatises written either during the lifetime of the observatory or after that are introduced.
Cf. (Mozaffari (2012), pp. 363–364).
The contents of the treatise were introduced in Saliba (1983). The computations related to the eccentricity of the sun and of Jupiter were subject to two critical studies by Saliba (1985; 1986; for al-Maghribī’s solar observations, cf.Mozaffari 2013a, pp. 318, 330). The present author analyzed al-Maghribī’s measurements of the Ptoemaic orbital elements of Saturn in his Ph. D. dissertation. A detailed study of al-Maghribī’s planetary and stellar observations is being prepared by him.
They are the eccentricities of Mercury and Venus: 3;10 and 1;2,49, respectively, and the radius of the epicycle of Mercury: 22;30,30 (Wābkanawī, IV, 15, 10: T: fols 93r–93v, Y: 160v–161r).
Cf.Mozaffari (2007). This treatise is interesting in various aspects; e.g., its clear mention of the infinite geometrical spaces.
Al-Maghribī, Talkhīṣ, fol. 2r.
(Sayılı (1960), p. 205).
Al-Maghribī, Adwār, M: fol. 55v.
Al-Maghribī, Adwār, M: fol. 124v.
Ibn al-Fuwaṭī, 1995, Vol. 5, p. 117.
Cf. below, Sect. 4.5.
Ptolemy (Almagest, V, 14) used a dioptra originally described by Hipparchus that was four cubits in length(\(\approx \) 185.28 cm) (Toomer 1998, p. 56). This dioptra has a fixed lower pinnula on which there is a hole for sighting, and a movable outer one, which is placed in front of the sun. The solar/lunar angular diameter is calculated based on the movable pinnula’s width and the distance between the two pinnulas. In his Fī kayfīyya al-arṣād (“How to make the observations”), Mu’ayyad al-Dīn al-‘Urḍī, the instrument maker of the Maragha observatory (d. 1266), presented an addition for the antique dioptra to determine the eclipsed area/diameter of the sun or the moon (Seemann 1929, pp. 61–71). Thus, Muḥyī al-Dīn had a specific instrument for measuring the magnitude of eclipses at his disposal, which he may have applied to these lunar eclipses. In the Risāla al-Ghāzāniyya fi ’l-ālāt al-raṣadiyya (“Ghāzān’s treatise on observational instruments”) (cf.Zotti and Mozaffari 2010, pp. 165–167; Mozaffari and Zotti 2012, pp. 419–421) and in Wābkanawī’s Zīj (IV, 15, 8: Y: fols. 159r–159v, T: fols. 92r–92v), an instrument as a pinhole image device is introduced that fulfills the measuring of the magnitude of solar eclipses. The treatise contains the physical descriptions and applications of 12 new observational instruments in the second period of the Maragha observatory, which were presumably the inventions of Ghāzān Khān, the seventh ruler of the Īlkhānīd dynasty of Iran (reg. 21 October 1295-17 May 1304). About it, also see Mozaffari and Zotti (2013).
Based on NASA’s Five Millennium Catalog of Lunar Eclipses (http://eclipse.gsfc.nasa.gov/lunar.html), which is now the standard: nos. 07878, 07897, and 07907.
For example, for the time of the maximum phase of the eclipse no. 1, the true longitude of the sun is calculated as follows:

Cf. (Neugebauer (1975), Vol. 2, pp. 922–926).
E.g., see note 33, below.
We use the standard proposed by (Kennedy (1991/1992), p. 21) to transliterate the letters in the diagrams.
Throughout the paper, Sin \(\alpha \) indicates the sine of the angle \(\alpha \) under the condition that the radius of the trigonometric circle is assumed to be \(R = 60\), i.e., Sin \(\alpha = 60\) sin \(\alpha \). Similarly for Crd \(\alpha \).
(Heath (1952), p. 33).
(Heath (1952), pp. 64–66). Like Ptolemy, our author does not refer to Euclid.
(Dorce (2003), p. 203).
(Dorce (2003), p. 197).
Note that our author computes here the mean anomaly of the moon according to the Ptolemaic lunar model introducing the second anomaly of the moon and the prosneusis while he has not yet expounded this model and that the correction due to the prosneusis, i.e., the lunar equation of center, should be taken into account in order to compute the lunar mean anomaly from its true anomaly. In the situations like this, he refers reader to the future chapters. Another note is that Ptolemy in Almagest IV, 7 (Toomer 1998, p. 204; Neugebauer 1975, Vol. 1, pp. 78–79) computes \(\omega _\mathrm{a}\) according to his first (i.e., Hipparchan) lunar model, but never comes back to revise it after completing his lunar model. On the four-eclipse method for determining the length of the lunar anomalistic month (i.e., \(360^{\circ }/\omega _\mathrm{a})\) described by Ptolemy and a more coherent formulation of it by Jābir b. Aflaḥ (fl. Spain, the 12th ct.), cf.Bellver (2006).
Talkhīṣ, fol. 82r; Adwār, CB: fol. 81v; Wābkanawī, fol. 154v (cf. below, Table 4): \(q(353) = 0{;}56^{\circ }\) and \(q(354) = 0{;}48^{\circ }\rightarrow q(353{;}32) = 0{;}51{,}44^{\circ }\). However, the trigonometric formula for \(q\) results 0;50,\(35^{\circ }\).
Our author discussion on the solar and lunar angular diameters as well as his non-Ptolemaic value for the minimum apparent diameter of the moon and sun, i.e., 0;31,\(8^{\circ }\), appear in VI, 6 (fol. 93v onwards).
Note that although the input data for the calculation of \(\beta \) is the magnitude of the eclipse, which was obtained from the observation, the value of \(\beta \) in (28) should be compared with the modern value of the geocentric \(\beta \) (not with the topocentric/apparent \(\beta \), which is about \(+\)0;11,\(30^{\circ }\)), simply because both
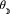
and \(r_{\bullet }\) have been calculated according to the geocentric hypotheses of the Ptolemaic model.
Note that the arc AB of the ecliptic, instead of the arc AC, should be subtracted from
 . However, the two arcs are approximately equal: \(AB \approx 6{;}\hbox {26,12}^{\circ }\).
. However, the two arcs are approximately equal: \(AB \approx 6{;}\hbox {26,12}^{\circ }\).Mean motion in longitude: Talkhīṣ, fol. 73r; Adwār, M: fol. 76v, CB: fol. 74v; in anomaly: Talkhīṣ, fol. 73v; Adwār, M: fol. 77r, CB: fol. 75r;
 : Talkhīṣ, fol. 74r; Adwār, M: fol. 78r, CB: fol. 76r; the Adwār has also the table for \(2\bar{{\eta }}\): M: fol. 77v, CB: fol. 75v. All of the tables have been prepared for each 30 years, one month, one day, and one hour (up to 30 h).
: Talkhīṣ, fol. 74r; Adwār, M: fol. 78r, CB: fol. 76r; the Adwār has also the table for \(2\bar{{\eta }}\): M: fol. 77v, CB: fol. 75v. All of the tables have been prepared for each 30 years, one month, one day, and one hour (up to 30 h).By means of interpolation in the table of the oblique ascension for the latitude of Maragha on folio 35v.
The time expressed in the sun’s apparent diurnal motion as projected onto the celestial equator, the so-called dā’ir. Our author calls it “Altitude dā’ir,” indicating that this time was computed from the solar altitude, not measured with the clepsydra. With our author’s parameters, i.e., the geographical latitude of Maragha \(\varphi = 37{;}20{,}30^{\circ }\), the obliquity of the ecliptic \(\varepsilon = 23.5^{\circ }\), and
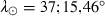 , half the sun’s apparent diurnal motion = 100;56,\(31^{\circ }\) (and so, half the duration of daylight = 6;43,46 h; our author later gives 6;43,31 h) and, therefore, the sun’s hour angle when it had the altitude \(h = 2^{\circ }\) was 98;18,\(46^{\circ }\).
, half the sun’s apparent diurnal motion = 100;56,\(31^{\circ }\) (and so, half the duration of daylight = 6;43,46 h; our author later gives 6;43,31 h) and, therefore, the sun’s hour angle when it had the altitude \(h = 2^{\circ }\) was 98;18,\(46^{\circ }\).Note that when the last mean quadrature occurred [above, (41)], the moon had an anomaly near \(100^{\circ }\) (see below), and so the line of sight to it was tangential to the epicycle. Thus, the lunar epicyclic equation was maximum, and therefore, its true motion was equal to its mean motion.
(Toomer (1998), p. 226); Arabic Almagest, fol. 63v.
In the other zījes, it is called the “extra difference.”
Our author’s tables for the lunar equations can be found in Kamālī, fols. 243v–251r, and his values for the lunar mean motions on fols. 232v–233r. The tables in Wābkanawī’s zīj are all based on Muḥyī al-Dīn’s parameter values.
Cf. (Neugebauer (1975), Vol. 2, pp. 988–989).
Cf. (Kennedy and Pingree (1981), pp. 168 and 310).
Zīj al-mumtaḥan has \(\beta _\mathrm{max} = 4{;}30^{\circ }\) and \(\beta _\mathrm{max} =5{;}0^{\circ }\) (fols. 54r and 57r). Ḥabash (fol. 36r) and Bīrūnī (al-Qānūn, Vol. 2, pp. 776 and 779) have associated \(i= 4{;}46^{\circ }\) with the Banū Mūsā (cf. below, Sect. 4.2). However, Bīrūnī mentions that some people erroneously cast doubt on the correctness of this attribution and consider this value as the average of the Indian and Ptolemaic values, respectively, 4;\(30^{\circ }\) and 5;\(0^{\circ }\). Another source (Kamālī, fol. 53v) has attributed \(\beta _\mathrm{max} = \hbox {4;46}^{\circ }\) to the Mumtaḥan tradition and \(\beta _\mathrm{max} =4{;}55^{\circ }\) to Thābit b. Qurra, ‘Alī b. ‘Īsā, Sanad b. ‘Alī, Khālid b. ‘Abd- al-Malak al-Marwarūdhī, and the Banū Mūsā.
In the other zījes, it is called “the third equation.” In the modern astronomy, it is called “the reduction to the ecliptic.”
\(\hbox {Max}(c_{7}) = 0;6,40^{\circ }\) is derived from \(i= 5;3^{\circ }\) which al-Fārisī (fol. 119v) (about him, cf.Pingree 1985, pp. 8–9) attributes to Ibn Yūnus.
The next appropriate opportunity was on March 19, 1271. Of course, the moon transited the meridian of Maragha about 17:47 MLT, before the sunset in \(\sim \) 18:15 MLT. Our author’s tables give
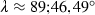 and \(\beta = -4{;}59{,}59^{\circ }\) for this time.
and \(\beta = -4{;}59{,}59^{\circ }\) for this time.For example, the amounts our author gave for the difference in mean anomaly between the two lunar eclipses (cf. Sect. 3.1) are better matched with taking Ptolemy’s value for \(\omega _\mathrm{a}\) to compute them while those given for the difference in mean longitude are in better agreement with taking the value adopted in Tāj al-azyāj for \(\omega _\mathrm{t}\) (the differences are in parentheses):

The medieval astronomers measured the length of the tropical year with taking the autumnal equinox as the zero-point over the long periods. Thus, the result achieved should be considered as a “mean” value. The mean value for the length of the tropical year between the two consecutive autumnal equinoxes in the period from AD 0 to 2000 is 365;12,32 days (cf.Meeus 2002, pp. 357–366). Muḥyī al-Dīn’s value is thus more exact than those given, say, by Hipparchus/Ptolemy \((365{;}14{,}48^\mathrm{d})\), Thābit b. Qurra \((365{;}14{,}24^\mathrm{d})\), and al-Battānī \((365{;}14{,}26^\mathrm{d})\); cf. Mozaffari (2013a).
As far as the present author knows, in his mathematical treatises as well as his treatise on the astrolabe, he refers to Avicenna (e.g., Hogendijke 1993, p. 134).
Bīrunī, al-Qānūn al-mas‘ūdī, Vol. 2, p. 779.
Cf. (Pedersen (1974), p. 206).
The center of the epicycle is at the perigee of the eccentric deferent (mean quadrature), and the moon is near its maximum elongation from it; so, the moon–earth distance \(\varDelta = \hbox {0;59} \times ((60 - 2 \times \hbox {10;19})^{2} -\hbox {5;15}^{2})^{1/2} = \hbox {38;21,53}\) terrestrial radii. Thus, with \(h' = \hbox {28;34}^{\circ },\, \varPi = \hbox {sin}^{-1}(\hbox {cos}\,h'/\varDelta ) \approx \hbox {1;19}^{\circ }\).
Equation of days (Ar. ta‘dīl al-ayyām, La. equatio dierum) in the medieval astronomical context. However, it may be noted that the modern term “equation of time” (Ar. ta‘dīl al-zamān) may be found in Ibn Yūnus, p. 92 (line 13) and Bīrūnī, Vol. 2, p. 720; cf.Neugebauer 1975, Vol. 1, p. 61 (n. 2).
Wābkanawī, II, 1, 1: T: fol. 16r; Y: fol. 26v. The Majisṭī to which Wābkanawī refers is probably Muḥyī al-Dīn’s Khulāṣa al-majisṭī which is now lost.
Kamālī, fol. 52v. In other sources, the work has been ascribed to ‘Abd al-Karīm al-Fahhād (cf.Kennedy 1956, no. 64). The two works may, however, be independent from each other.
Muḥyī al-Dīn appears to have been so interested in the central quadrant that composed a poem during the observations of 1265–6 AD to praise it, which a certain The Astrologer Majd al-Dīn Abū Muḥammad al-Ḥasan b. Ibrāhīm b. Yūsūf al-Ba‘albakī had engraved on the instrument (cf. Ibn al-Fuwaṭī 1995, Vol. 4, pp. 413–414):
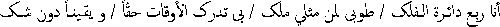
.
Cf.Seemann (1929). The other two instruments could be used in order to measure simultaneously the horizontal coordinates of the two celestial objects having the diametrical opposed azimuths. The last instrument was solely applicable to the measurement of the coordinates of one object in a given time.
E.g., cf. (Needham (1981), p. 136).
In the Ghāzān’s treatise on observational instruments (see note 20), the adequacy of the classic instruments described in the Almagest is rejected for the various reasons; in the case of the armillary sphere, cf. (Mozaffari and Zotti (2012), pp. 400–401).
(Toomer (1998), p. 423, lines 10–13).
Al-Maghribī, Talkhīṣ, fol. 114v. The declinations of Vega and Capella were about, respectively, \(+44^{\circ }\) \(51.5^{\prime }\) and \(+38^{\circ }\) \(17.5^{\prime }\) at the time, and thus both transited the Maragha’s meridian \((\varphi = \hbox {37;23,46}^{\circ })\) in its northern half. The non-Ptolemaic star table of Īlkhānī Zīj includes the coordinates of both Vega and Capella (al-Ṭūsī, C: p. 195, T: fol. 100r).
(Dorce (2003), p. 203).
Bīrūnī, al-Qānūn al-mas‘ūdī, Vol. 2, pp. 742–743. For the analysis these eclipses (nos. 07224, 07225, and 07227 in NASA’s Five Millennium Catalog of Lunar Eclipses), cf. (Said and Stephenson (1997), pp. 45–46), Stephenson (1997, pp. 491–492). The analysis of Bīrūnī’s lunar measurements will appear in a separate paper.
Kāshī, IO: fols. 4r–6r, P: pp. 24–28. The eclipses nos. 08220, 08221, and 08222 in NASA’s Five Millennium Catalog of Lunar Eclipses. The analysis of Kāshī’s lunar measurements will come in a separate paper.
Based on the wrong assumption (likely from the false analogy drawn between the Ptolemaic lunar and planetary models) that \(q\) reaches its maximum when the line dropped from the epicycle’s center to the prosneusis is perpendicular to the apsidal line.
Al-Ṭūsī, C: p. 7, T: fol. 3r.
All of the tables for the lunar equations are asymmetric giving (i) \(\hbox {max}(c^{\prime }_{3}) = \hbox {13;8}^{\circ }\), (ii) \(c^{\prime }_{4} = \hbox {7;40}^{\circ }\) for the arguments 0, \(180^{\circ }\), and \(360^{\circ }\) and \(\hbox {max}(c^{\prime }_{4})= c^{\prime }_{4}(265) = \hbox {12;41,0}^{\circ }\) (thus, \(\hbox {max}(c_{4}) = \hbox {5;1}^{\circ }\)), and (iii) \(\hbox {max}(c_{5}) = \hbox {2;39}^{\circ }\). Cf. al-Ṭūsī, C: pp. 67–85; P: fol. 23v–28v; M: fols. 40r–50v.
Ibn Yūnus, pp. 120, 158, 160, 162.
For the solar daily mean motion, Wābkanawī’s Zīj has evidentially the same value obtained by al-Maghribī, i.e., \(\omega _{\odot }= \hbox {0;59,8,20,8,4,36,38}^{\circ }/\hbox {d}\) (cf. Wābkanawī, T: fol. 149r). Also, al-Kāshī’s value for \(\omega _{\odot }\) is Ibn Yūnus’ (Khāqānī zīj, IO: fol. 128v, gives the solar mean motion in a Persian year as \(\hbox {359;45,40,4}^{\circ }\); cf. Table 14). Al-Kāshī’s adoption of this value appears to be a consequence of his project of the revision of the Īlkhānī zīj. Support comes from the fact that the solar maximum equation of center and eccentricity in al-Kāshī’s zīj (IO: fol. 131r, 157r) are Ibn Yūnus’, as is in the Īlkhānī zīj. Al-Kāshī did not, of course, mention his source.
It is borrowed from Ibn Yūnus’ zīj (p. 174), corresponding to the solar eccentricity = 2;6,10 \((R = 60)\).
For a biographical outline of him, cf.van Dalen (2007). About his zīj and some studies of it, cf. Kennedy 1956a, no. 35, (King et al. (2001), p. 46), (Kennedy (1958), p. 251), Haddad and Kennedy (1971, p. 91), (Kennedy (1964), p. 443), (King (1986), pp. 138–140), (Kunitzsch (1964), pp. 398–399). Kennedy (1960, p. 211) employed the explanations given by Wābkanawī as regards the Maragha observatory to verify some remarks by al-Kāshī in a letter to the latter’s father and, in another paper (1962, p. 24), quoted a section of the zīj related to chronology and astrology.
Wābkanawī, T: fol. 89v–90r, Y: fol. 155r.
Wābkanawī, T: fol. 125r; Y: fol. 235r.
Wābkanawī, T: fol. 3r, Y: fol. 4v.
Wābkanawī, T: fol. 2v, Y: fol. 3v. Concerning the conjunctions, the differences that Wābkanawī found are:
\(\begin{array}{lll} \hbox {Mars and Saturn:}&{} \hbox {in the period of direct motion of Mars:} &{}6 \hbox { days} \\ &{}\hbox {in the period of retrograde motion of Mars:}&{} 8 \hbox { days}\\ \hbox {Mars and Jupiter:}&{} \hbox {in the period of direct motion of Mars:}&{} 5 \hbox { days}\\ \end{array}\)
Wābkanawī, T: fol. 2v, Y: fol. 3v.
E.g., Wābkanawī, III, 3, 1: T: fol. 53r, Y: fol. 96r; III, 9, 5: T: fol. 60r, Y: fol. 108v; III, 13, 6: T: fol. 67r, Y: fol. 120v. Since Wābkanawī contends the Īlkhānī zīj to be majorly based on earlier astronomical tables, rather than obtained from making independent observations, he goes further to call only Muḥyī al-Dīn’s Adwār as the “Īlkhānīd Observations.” Cf. Wābkanawī, T: fol. 3r, Y: fol. 4v.
The other three modifications made by Wābkanawī are concerning (1) the mean longitude of Mars (increased by 1;\(5^{\circ }\)), (2) the mean anomaly of Venus (increased by 2;\(30^{\circ }\)), and (3) the latitudes of the two inferior planets; cf. Wābkanawī, T: fol. 3r; Y: fol. 4v; P: fols. 4r–v. Wābkanawī also differently arranged the entries of al-Maghribī’s equations tables.
The modern values in this paper are extracted from the software Alcyone, applying the estimates of Morrison and Stephenson 2004 for \(\Delta \hbox {T}\) (the difference between the Dynamical Time and Universal Time).
For the present study, a PC-program was used, which can compute the solar, lunar, and planetary ecliptical coordinates; the times of the synodic phenomena; etc, from the three zījes of the Maragha tradition. In this program, the equations, of course, are computed from the corresponding trigonometric formulas, instead of interpolating in the equations tables of these zījes. The differences, however, are small enough to be less effective when testing a historical claim. In addition, rendering ineffective the errors and/or differences in the equations tables, this procedure makes a unified scale in order to make the comparison merely between the two sets of the parameter values adopted in these three zījes.
Wābkanawī, T: fols. 92r–v, Y: fols. 159r–160r, P: fols. 139r–140r. The passage in question may also be found in the “Ghāzān’s treatise on the observational instruments” (cf. note 20). In it, the time-measuring device is, however, called the “time-glass” (shīsha-i sā‘at).
Cf. (Mozaffari (2013b), Section 4.III).
References
Anonymous, Sulṭānī zīj, MS. Iran, Parliament Library, no. 184.
Bellver, J. 2006. Jābir b. Aflaḥ on the four-eclipse method for finding the lunar period in anomaly. Suhayl 6: 159–248.
Bellver, J. 2008. Jābir b. Aflaḥ on lunar eclipses. Suhayl 8: 47–91.
Bīrūnī, Abū al-Rayḥān. 1954. al-Qānūn al-mas‘ūdī. Hyderabad: Osmania Oriental Publication Bureau.
Bowen, A.C. 2008. Simplicius’ commentary on Aristotle, De Caelo 2.10-12: An annotated translation (Part 2). SCIAMVS 9: 25–131.
Brockelmann, K. Geschichte der arabischen Literatur, Vols. 1–2, 2nd ed., Leiden, 1943–1949, Supplementbände 1–3, Leiden, 1937–1942.
van Dalen, B. 2002a. Islamic and Chinese astronomy under the Mongols: A little-known case of transmission. In From China to Paris: 2000 years transmission of mathematical ideas, ed. Dold-Samplonius Yvonne, 327–356. Stuttgart: Franz Steiner.
van Dalen, B. 2002b. Islamic astronomical tables in China: The sources for the Huihui Ii. In History of oriental astronomy (Proceedings of the joint discussion 17 at the 23rd general assembly of the international astronomical union, organised by the Commission 41 (History of Astronomy), Held in Kyoto, August 25–26, 1997), ed. Ansari Razaullah, 19–30. Dordrecht: Kluwer.
van Dalen, B. 2004a. A second manuscript of the Mumtaḥan Zīj. Suhayl 4: 9–44.
van Dalen, B. 2004b. Science, techniques et instruments dans le monde Iranien. In The activities of Iranian astronomers in Mongol China, ed. N. Pourjavady, and Ž. Vesel, 17–28. Téhéran: Institut Français de Recherche en Iran.
van Dalen, B. 2007. Wābkanawī. In The biographical encyclopedia of astronomers, ed. Thomas Hockey, 1187–1188. London: Springer.
Dorce, C. 2002–2003. The Tāj al-azyāj of Muḥyī al-Dīn al-Maghribī (d. 1283): methods of computation. Suhayl 3:193–212.
Duke, D. 2005. Hipparchus’ eclipse trios and early trigonometry. Centaurus 47: 163–177.
Espenak, Fred. NASA’s five millennium catalog of lunar eclipses. http://eclipse.gsfc.nasa.gov/LEcat5/LEcatalog.html.
Al-Fārisī. Zīj al-muẓaffarī, MS. Cambridge Gg.3.27, no. 508.
Gillipsie C.C. et al. (ed.). 1970–1980. [DSB] Dictionary of Scientific Biography, 16 Vols. New York: Charles Scribner’s Sons.
Haddad, F.I., and E.S. Kennedy. 1971. Geographical tables of medieval Islam. Al-Abhath 24:87–102. Reprinted in Kennedy, SIES, pp. 636–651.
Heath, T.L. 1952. [the 5th ed. 1994], The thirteen books of euclid’s elements. In Great books of the Western World, vol. 10. Chicago: Encyclopedia of Britannica.
Hockey, Thomas (ed.) et al. 2007. The biographical encyclopedia of astronomers. New York: Springer.
Hogendijk, J.P. 1993. An Arabic text on the comparison of the five regular polyhedra: ‘Book XV’ of the ‘Revision of the Elements’ by Muḥyī al-Dīn al-Maghribī. Zeitschrift fur Geschichte der Arabisch-Islamischen Wissenschaften 8: 133–233.
Ḥunayn, b. ’Isḥāq and Thābit b. Qurra (tr.), Arabic Almagest, MS. Iran, Tehran, Sipahsālār Library, no. 594 (copied at H 480/ AD 1087–1088).
Ibn al-Fuwatī, Kamāl al-Dīn ‘Abd al-Razzāq b. Muḥammad. 1995. Majma‘ al-ādāb fī mu‘jam al-alqāb, ed. Muḥamamd Kāẓim. Tehran: Ministry of Culture.
Ibn al-Ṣalāh al-Hamadhānī. Fī kayfiyyat tasṭīḥ al-basīṭ al-kurī. MSS. Iran, Parliament, Library, no. 6412; no. 602, pp. 33–52; no. 6329, pp. 24–35.
Ibn Yūnus, Abu al-Ḥasan \(^{\rm c}\)Alī b. \(^{\rm c}\)Abd al-Raḥmān b. Adhmad. Zīj al-kabīr al-ḥākimī. MS. Leiden, Or. 143.
Kamālī, Muḥamamd b. ’Abī \(^{\rm c}\)Abd-Allāh Sanjar. Ashrafī Zīj. MS. Paris, Biblithèque Nationale, suppl. Pers. No. 1488.
Kāshī, Ghiyāth al-Dīn Jamshīd. Khāqānī Zīj. MS. P: Iran, Parliament Library, No. 6198; IO: London, Inida Office, no. 430.
Kennedy, E.S. 1956. A survey of Islamic astronomical tables. Philadelphia: American Philosophical Society.
Kennedy, E.S. 1958. The Sasanian astronomical handbook Zīj-i Shāh and the astronomical doctrine of transit (Mamarr). Journal of American Oriental Society 78: 246–262. Reprinted in Kennedy, SIES, pp. 319–335.
Kennedy, E.S. 1960. A letter of Jamshīd al-Kāshī to his father: Scientific research at a fifteen century court. Orientalia 29: 191–213. Reprinted in Kennedy, SIES, pp. 722–744.
Kennedy, E.S. 1964. The Chinese-Uighur calendar as described in the Islamic sources. ISIS 55:435–443. Reprinted in Kennedy, SIES, pp. 652–660.
Kennedy, E.S. 1991/1992. Transcription of Arabic letters in geometric figures. Zeitschrift fur Geschichte der Arabisch-Islamischen Wissenschaften 7: 21–22.
Kennedy, E.S., and D. Pingree (eds.). 1981. The book of the reasons behind astronomical tables. New York: Scholars’ Facsimiles & Reprints.
Kennedy, E.S., colleagues, and former students. 1983. Studies in the Islamic exact sciences [SIES]. Beirut: American University of Beirut.
Al-Khāzinī, Abd al-Raḥmān. Zīj al-Mu‘tabar al-Sanjarī, MS. V: Vatican Library, No. 761.
Al-Khāzinī, A. Wajīz [Abridgment of] al-Zīj al-Mu‘tabar al-Sanjarī [Considered Zij of Sultan Sanjar], MS. Istanbul, Suleymaniye Library, Hamadiye Collection, No. 859.
King, D. 1986. The earliest Islamic mathematical methods and tables for finding the direction of Mecca. Zeitschrift fur Geschichte der Arabisch-Islamischen Wissenschaften 3: 82–149.
King, D., J. Samsó, and B.R. Goldstein. 2001. Astronomical handbooks and tables from the Islamic World. Suhayl 2: 9–105.
Kunitzsch, P. 1964. Das Fixsterverzeichnis in der ,,Persischen Syntaxis“ des Georgios Chrysokokkes. Byzantinische Zeitschrift 57: 382–411.
Lorch, R. 2000. Ibn al-Ṣalāḥ’s treatise on projection: A preliminary survey. In Sic Itur ad Astra: Studien zur Geschichte der Mathematik und Naturwissenschaften, ed. Folkerts Menso, and R. Lorch, 401–408. Wiesbaden: Harrassowitz Verlag.
Al-Maghribī, Mūḥyī al-Dīn. Adwār al-anwār, MS. M: Iran, Mashhad, Holy Shrine Library, no. 332, MS. CB: Ireland, Dublin, Chester Beaty Library, no. 3665.
Al-Maghribī, Mūḥyī al-Dīn. Talkhīṣ al-majisṭī, MS. Leiden, Universiteitsbibliotheek, Or. 110.
Meeus, J. 2002. More mathematical astronomy morsels. Richmond: William-Bell.
Mozaffari, S.M. 2007. The mathematical basis and functions of astrolabe with focus on the old texts: “Projection of Astrolabe” by Muhyiddin Al-Maghribi, Thesis for receiving M. Sc. degree in History of Science (Majoring in Astronomy), Tehran: University of Tehran, 2007, unpublished.
Mozaffari, S.M. 2009. Wābkanawī’s and the first scientific observation of an annular eclipse. The Observatory 129: 144–146. [It should be read accompanied with Mozaffari, S. Mohammad, 2010. Wābkanawī’s annular eclipse. The Observatory 130: 39–40].
Mozaffari, S.M. 2012. The effect of astrological opinions on society: A preliminary view. Trames 16: 359–368.
Mozaffari, S.M. 2013a. Limitations of methods: The accuracy of the values measured for the Earth’s/Sun’s orbital elements in the Middle East, A.D. 800–1500. Journal for the History of Astronomy 44: 313–336 and 389–411.
Mozaffari, S.M. 2013b. Wābkanawī’s observation and calculations of the annular solar eclipse of 30 January 1283. Historia Mathematica 40: 235–261.
Mozaffari, S.M., and G. Zotti. 2012. Ghāzān Khān’s astronomical innovations at Marāgha observatory. Journal of American Oriental Society 132: 395–425.
Mozaffari, S.M., and G. Zotti. 2013. The Observational Instruments at the Maragha Observatory after AD 1300. Suhayl (to appear).
Needham, J. 1981. Science in traditional China: A comparative perspective. Cambridge, MA: Harvard University Press.
Neugebauer, O. 1975. A history of ancient mathematical astronomy. Berlin: Springer.
Pedersen, O. 1974. A survey of the Almagest. Odense: Odense University Press. [With annotation and new commentary by A. Jones, New York: Springer, 2010].
Pingree, D. ed. 1985. Astronomical works of gregory chioniades, vol. 1: Zīj al-‘alā’ī. Amsterdam: Gieben.
Rosenfeld, B.A., and E. Ihsanoglu. 2003. Mathematicians, astronomers, and other scholars of Islamic civilization and their works, Istanbul.
Said, S.S., and F.R. Stephenson. 1997. Solar and Lunar Eclipse measurements by medieval Muslim astronomers, II: Observations. Journal for the History of Astronomy 28: 29–48.
Saliba, G. 1983. An observational notebook of a thirteenth-century astronomer. ISIS 74: 388–401. Repr. in Saliba 1994, pp. 163–176.
Saliba, G. 1985. Solar observations at Maragha observatory. Journal for the History of Astronomy 16:113–122. Repr. in Saliba 1994, pp. 177–186.
Saliba, G. 1986. The determination of new planetary parameters at the Maragha observatory. Centaurus 29: 249–271. Repr. in Saliba 1994, pp. 208–230.
Saliba, G. 1994. A history of Arabic astronomy: Planetary theories during the golden age of Islam. New York: New York University.
Sarton, G. 1953. Introduction to the history of science, Vol 2. Part 2, Baltimore.
Sayılı, A. 1960. The observatory in Islam. Ankara: Turk Tarih Kurumu Basimevi.
Seemann, H.J. 1929. Die Instrumente der Sternwarte zu Maragha nach den Mitteilungen von al-‘Urḍī. In Sitzungsberichte der Physikalisch-medizinischen Sozietät zu Erlangen, ed. Oskar Schulz, vol. 60 (1928), 15–126. Erlangen: Kommissionsverlag von Max Mencke.
Sezgin, F. 1978. Geschichte Des Arabischen Scrifttums, Vol. 6, Leiden.
Al-Shīrāzī, Quṭb al-Dīn. Ikhtīyārāt-i Muẓaffarī. MS. Iran, National Library, no. 3074f.
Al-Shīrāzī, Quṭb al-Dīn, Tuḥfa al-Shāhiyya. MS. Iran, Parliament Library, no. 6130.
Simplicius. 1894. Simplicii in Aristotelis De Caelo Commentaria, ed. by I. L. Heiberg, Berlin.
Steele, J. 2000. A re-analysis of the Eclipse observations in Ptolemy’s Almagest. Centaurus 42: 89–108.
Stephenson, F.R. 1997. Historical Eclipses and Earth’s Rotation. Cambridge University Press, Cambridge.
Al-Ṣūfī, Abd al-Raḥmān. 1995. Al-‘amal bi-l-Aṣṭurlāb. Morocco: ISESCO.
Suter, H. 1902. Die Mathematiker und Astronomen der Araber und Ihre Werke, Amsterdam.
Thurston, H. 1994. Early astronomy. London: Springer.
Toomer, G.J. (ed.). 1998. Ptolemy’s Almagest. Princeton: Princeton University Press.
Al-Ṭūsī, Naṣīr al-Dīn. Ilkhānī zīj. MS. C: California, no.; MS. T: Iran, University of Tehran, no. 165-Ḥikmat; MS. P: Iran, Parliament Library, no. 181; MS. M: Iran, Mashhad, Holy Shrine Library, no. 5332a.
Ulugh Beg. Sulṭānī Zīj (or Gūrkānī Zīj), MS. T: Tehran University Central Library, no. 13J; MS. P1: Iran, Parliament Library, no. 72; MS P2: Iran, Parliament, Library, no. 6027.
Voux, C. 1891. Remaniement des Spheriques de Theodes Par Iahia ibn Muhammed ibn Abi Shukr Almaghribi Alandalusi. Journal Asiatique 17: 287–295.
Wābkanawī, Shams al-Dīn Muḥammad. Zīj-i muhaqqaq-i sulṭānī. MS. T: Turkey, Aya Sophia Library, No. 2694; MS. Y: Iran, Yazd, ‘Ulūmī Library, no. 546, its microfilm is available in Tehran University Central Library, no. 2546; MS. P: Iran, Parliament Library, no. 6435.
Zotti, G., and S.M. Mozaffari. 2010. Ghāzān Khān’s astronomical instruments at Maragha Observatory. In Astronomy and its instruments before and after Galileo, ed. Luisa Pigatto, and Valeria Zanini, 157–168. Padova: Cooperativa Libraria Editrice Università di Padova (CLEUP).
Acknowledgments
The author notes with the best thanks and gratitude the suggestions and comments of Dr. Benno van Dalen (Germany). This work has been supported financially by Research institute for Astronomy and Astrophysics of Maragha (RIAAM) under research Project No. 1/2782-55.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by George Saliba.
Rights and permissions
About this article
Cite this article
Mozaffari, S.M. Muḥyī al-Dīn al-Maghribī’s lunar measurements at the Maragha observatory. Arch. Hist. Exact Sci. 68, 67–120 (2014). https://doi.org/10.1007/s00407-013-0130-4
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00407-013-0130-4









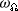











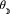
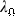 . However, the two arcs are approximately equal:
. However, the two arcs are approximately equal:  : Talkhīṣ, fol. 74r; Adwār, M: fol. 78r, CB: fol. 76r; the Adwār has also the table for
: Talkhīṣ, fol. 74r; Adwār, M: fol. 78r, CB: fol. 76r; the Adwār has also the table for 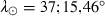 , half the sun’s apparent diurnal motion = 100;56,
, half the sun’s apparent diurnal motion = 100;56,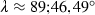 and
and