Capillary flow of a suspension in the presence of discontinuous shear thickening

Abstract

The rheology of suspensions showing discontinuous shear thickening (DST) is well documented in conventional rheometer with rotating tools, but their study in capillary flow is still lacking. We present results obtained in a homemade capillary rheometer working in an imposed pressure regime. We show that the shape of the experimental curve giving the volume flow rate versus the wall stress in a capillary can be qualitatively reproduced from the curve $\dot{\gamma }(\tau )$ obtained in rotational geometry at imposed stress but instead of a sharp decrease of the volume flow rate observed at a critical stress, this transposition predicts a progressive decrease in flow rate. The Wyart-Cates theory is used to reproduce the stress-shear rate curve obtained in rotational geometry and then applied to predict the volume flow rate at imposed pressure. The theoretical curve predicts a total stop of the flow at high stress, whereas experimentally it remains constant. We propose a modification of the theory which, by taking into account the relaxation of the frictional contacts in the absence of shear rate, well predicts the high stress behavior. We also hypothesized that the DST transition propagates immediately inside the capillary, once the wall shear stress has reached its critical value: τ_R = τ_c, even if the internal shear stress τ(r < R) is below the critical one. In this way the whole experimental curve can be well reproduced by the modified W–C model.

Graphical abstract

Introduction

The rheology of concentrated suspensions is quite complex since it can exhibit a broad diversity of behavior like a yield stress, shear thinning or shear thickening or both and even sudden jumps of viscosity. These different behaviors are related to structural changes when the applied stress is increased. Depending on the balance between hydrodynamic shear forces imposed by the applied stress and local interparticle forces (lubrication, Van der Waals, Debye–Huckel, hydration, entropic etc..) individual particles can gather into different types of aggregates whose shape and life time will depend both on the applied shear rate and on the local interactions between the particles. A common feature is the fact that the suspending fluid imprisoned inside these aggregates move as if it was a solid part of the aggregates, then increasing the effective solid volume fraction and so the viscosity of the suspension. Such an approach can describe several rheological behaviors of concentrated suspensions (Quemada and Berli 2002; Bossis and Brady 1989). In monodisperse suspensions of colloidal particles, a sudden jump of viscosity during a ramp of stress was attributed to the transition from a low viscosity configuration made of a stacking of sheets of particles sliding over each other to a disordered one (Hoffman 1972). This transition is specific to monodisperse particles which can arrange in layers of hexagonally packed particles, thus increasing the average distance between sheared layers and lowering the viscosity compared to a disordered state.

Nevertheless, the presence of a sudden jump of viscosity was also observed in suspensions of polydisperse suspensions of Latex particles (Laun et al. 1991) and it was proved, by neutron scattering (Laun et al. 1992; Bender and Wagner 1996) that there was no layered pattern before the transition. Also suspensions of particles of irregular shape like corn-starch (Fall et al. 2008) or acicular calcium carbonate (Egres and Wagner 2005) or gypsum (Neuville et al. 2012) show this jump of viscosity whereas their irregular shape prevents the formation of ordered sliding layers. This discontinuous shear thickening (DST) was studied mostly in conventional rotational rheometry coupled with different techniques like dichroism (d’Haene et al. 1993), magnetic resonance imaging MRI (Fall et al. 2010), shearing of photo-elastic beads (Bi et al. 2011) neutron scattering (Laun et al. 1992; Bender and Wagner 1996) to obtain some information on the evolution of the structural properties during this transition. Both numerical simulations (Seto et al. 2013; Mari et al. 2014; Johnson et al. 2017; Singh et al. 2018; Guy et al. 2020) and experiments have shown that the onset of the transition was ruled by the competition between the shear forces and the repulsive forces which prevent the surfaces to come in contact and to experiment friction forces. For instance, by varying the pH in suspensions of silica or alumina at a constant salt concentration, Franks et al. (Franks et al. 2000) have shown that an increase of the magnitude of the repulsive force was correlated with an increase of the shear stress needed to obtain the transition. More recently Clavaud et al (2017), using a suspension of silica spheres in a rotating drum to measure the friction coefficient,  have shown that the DST could only be observed if the suspension was initially in a frictionless state. There is now a large consensus that, in order to experimentally observe a DST transition, the particles should initially be separated by a repulsive force and that this transition will occur when the shear forces dominate the repulsive ones, allowing a frictional contact between the surfaces of the particles. It is the formation of a percolated network of particles in frictional contacts, as the ones observed in numerical simulations (Mari et al. 2014; Gameiro et al. 2020), able to support the stress through elastoplastic contacts, which explains the jump of viscosity (see for example reviews Brown and Jaeger 2014; Denn et al. 2018; Morris 2020)). The correlation between an increase of the normal force between particles and the one of the interparticle friction has been confirmed by AFM (Comtet et al. 2017; Hsu et al. 2018; Madraki et al. 2020).

A model which explains qualitatively this rheological behavior was proposed by Wyart and Cates (W–C) (Wyart and Cates 2014) and is based on the idea that the volume fraction at which the viscosity diverges, depends on the imposed stress. In the W–C model, this process was characterized by a jamming fraction Φ_J(τ) lower than the usual jamming fraction of a perfect hard sphere suspension at random close packing (RCP), Φ₀, but higher than a volume fraction Φ_j^μable to mechanically support a stress without flowing: Φ_j^μ < Φj(τ) <  Φ₀. This last limit reached for τ$\to \infty$ is not well defined since it depends on macroscopic properties like the stiffness of the boundaries or the anisotropy of the structure and of local properties like the particle friction coefficient, μ. At high friction (μ > 1), a possible value for monodisperse spheres could be the loose random packing fraction ${\Phi }_{{j}}^{\upmu }\sim {\Phi }_{RLP}$~0.55–0.56 (Jerkins et al. 2008; Singh et al. 2018). In this model, for volume fraction between Φ_j^μ and Φ₀, it exists a domain of stress above which the suspension cannot flow, called the shear jammed domain. On the other hand, for Φc < Φ<${\Phi }_{{j}}^{\upmu }$ where Φ_c is the volume fraction under which there is no DST transition, the DST transition takes place with a S-shape of the shear stress versus shear rate curve, followed at high enough stresses by a Newtonian regime when Φ_J(τ) becomes constant (Bi et al. 2011; Singh et al. 2018). These predictions are quite well verified by numerical simulations, but large disagreements persist when the parameters of the W–C model obtained by numerical simulations are transposed to represent the experimental data (Lee et al. 2020) or with polydisperse suspensions (Guy et al. 2020). An improved version of the model where the breakdown of the percolated force chains are allowed in the shear jammed zone was recently proposed (Baumgarten and Kamrin 2019). Also, attempts to introduce adhesive contacts, responsible for the presence of a yield stress, with a similar approach as in the W–C model, will help to generalize this model to a larger class of suspensions (Singh et al. 2019; Richards et al. 2020). The aim of this work is to bring some experimental data which can help to progress in the prediction of the rheological behavior of these concentrated suspensions, in particular with new experiments obtained with capillary flows. Usually, experimental data on DST phenomena are obtained in conventional rotational rheometry and very few papers present results obtained in capillary rheometry. A comparison between a cone-plate geometry and a capillary at imposed pressure on latex particles of diameter 0.3–0.4μm, has shown an apparent critical shear rate about two times larger in capillary geometry (Laun et al. 1991) which was attributed to wall slip. Pressure gradient in a square microchannel with confocal microscopy was used to study the velocity and concentration profiles of PMMA spheres of diameter 2.6μm at Φ = 0.63; they found unexpected flow profiles, compared to yield stress fluids which were explained by taking into account the stress fluctuations (Isa et al. 2007). In situations of high confinements (R/a < 30) a regime of oscillations of the flow rate was observed and explained by a local change of volume fraction associated with the permeation of the solvent through jammed domains (Isa et al. 2009). Recently, we have studied the flow of a concentrated magnetorheological suspension in a capillary at imposed flow rates (Bossis et al. 2020) showing that we recover the jamming transition but at a higher critical shear rate compared to conventional rheometry, both in the absence and presence of a magnetic field.

In the first section, we shall present new experimental results for the flow of a suspension of magnetic particles in the regime of imposed pressure. The stress-shear rate curve obtained in conventional rheometry will be used to predict the volume flow rate at imposed pressure. The similarity between the predicted curve and the experimental one, despite the difference in flow geometry will be outlined but the reduction of the volume flow rate when the stress is increased is much more gradual than in experiments. In the second part we apply the W–C model to fit the experimental curve obtained in rotational rheometry and then we use it to predict the volume flow rate in the capillary configuration. As in rotational rheometry, the model predicts a total stop of the volume flow rate as the stress is increased contrary to what is observed experimentally. In the last section, we propose a modification of the W–C model to explain the fact that the flow is not totally blocked above the transition, and we also show that it is necessary to consider a non-local rheology above the transition if we want to explain the abrupt transition observed in the capillary at imposed pressure.

Materials and methods

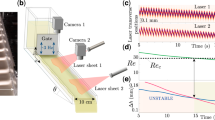
We are using suspensions of carbonyl iron particles, grade HQ, from BASF, supplied by Imhoff & Stahl Gmbh; their density is ρ_p = 7.8 g/cm³ and their average diameter d = 2a = 0.6μm. They are suspended in a mixture of 85% ethylene–glycol and 15% water which is used to minimize the evaporation at room temperature. The viscosity of the suspending fluid is η₀ = 0.011 Pa.s. The additive used to prevent the aggregation between the particles is a plasticizer used in cement industry called Optima100 and sold by the company Chryso. The Reynold number based on the size of the particles is ${Re}_{p}=\rho \dot{\gamma }{d}^{2}/\eta$. For a typical shear rate of 10 s⁻¹ and the minimum viscosity of the suspension we have used: η = 1 Pa.s, the particle Reynold number is of order 10^–8, so inertial effects at the level of the particle are totally negligible in these suspensions. The sedimentation velocity of a particle ${v=2({\rho }_{p}-\rho }_{f})g{a}^{2}$/9η is of order 0.01 μm/s so we can also neglect sedimentation effects in the capillary. Practically, all the commercial capillary rheometers impose the volumetric flow rate through the motion of a piston. In this case the DST transition results in a jump of pressure at a critical shear rate (Bossis et al. 2020) but more information on the physics of the transition can be obtained by driving the pressure since in this case, it is possible to observe the decrease of the shear rate and its subsequent behavior. For these experiments, we have used a homemade capillary rheometer described in Fig. 1.

Fig. 1

Sketch of the equipment for capillary flow at imposed pressure

It is composed of a tank with a pressure regulating valve (MDG-3 from Seflid) and a piezoelectric manometer (LEO 2 from Serv’instrumentation; resolution 10^–3 bar, maximum pressure 3 bars) connected to a 3-way ball valve (SS-43GXS4 from Swagelok). For the gas, we use dry compressed air. The vertical output of the 3-way valve is connected to the liquid tank in plexiglass, itself connected to the capillary through an interchangeable flange whose output is a part of the capillary. This part can be prolongated through a tube fitting union (for instance SS-400–6 for a tube of ¼ in external diameter) to easily change the length of the capillary. The third way of the valve is connected to a water vacuum pump through a 2-way valve and a vacuum manometer. The suspension is first pumped from a container placed on a balance (STX from Ohaus) into the liquid tank at a known negative pressure and the change of weight recorded each second. Then the path of the 3-way valve is turned towards the pressurized gas tank, which is regulated at a given pressure, for instance during 60 s, then the pressure is changed to another value and so on until emptying of the liquid tank; the change of weight is recorded during this time for typically ten different pressures. The procedure can be repeated several times until enough different pressure points have been recorded. The internal diameter of the tank is 2.5 cm and its height 10 cm. The radius of the capillary was R = 1.5 mm. The imposed pressure was corrected to consider the change of height of the column of fluid in the tank which was deduced from the change of mass. The mass flow rate Q(P) at a given pressure P, was obtained from the fit by a straight line of the mass versus time. The integration time of a mass measurement was 1 s, still we did not observe a decrease of flow rate at constant pressure which could have been attributed to clogging effects at the entrance of the capillary as predicted for small values of R/a (Koivisto and Durian 2017) since we have R/a ~ 5000. The wall shear stress is related to the pressure by: ${\tau }_{R}=P.\frac{R}{2L}$ where L is the length of the capillary. In these experiments we have used two different lengths L = 36 cm and L = 18 cm of a stainless-steel tube for the capillary and there was no difference between the data recorded for these two lengths.

On the other hand, the measurement of the viscosity was made with an imposed stress rheometer MCR 502 from Anton Paar. We used a cylindrical geometry with a small gap to minimize the change of shear rate inside the gap and to avoid particle migration.

Experimental results

The rheograms are represented in Fig. 2 for three volume fractions: Φ = 0.6; Φ = 0.64; Φ = 0.65. For the two highest volume fractions, we have a strong signature of the DST transition with an abrupt decrease of the shear rate followed by strong oscillations around an average value which remains approximatively constant during the increase of stress.

Fig. 2

Rheograms in cylindrical Couette cell for three volume fractions: Φ = 0.6; Φ= 0.64; Φ = 0.65. The dashed black lines are a polynomial fit of the experimental curve

The behavior is different at Φ = 0.6 where the transition is still accompanied by oscillations of the shear rate but without a sudden decrease of its value. In a forthcoming paper focused on the rheology of MR suspensions at high volume fractions, we shall see that the volume fraction of 0.60 is approaching the one corresponding to the random loose packing of this suspension which is estimated to be Φ_rlp = 0.58 whereas the close packing is Φ₀ = 0.681. The critical shear rate strongly decreases with the increase of volume fraction passing from 200 s⁻¹ at Φ = 0.6 to 10 s⁻¹ at Φ = 0.65 whereas the critical stress decreases slightly. Above Φ_rlp, the Wyart-Cates (W–C) model predicts that at high enough stress the suspension will be completely jammed and will stop. Actually, we rather observe, as many other authors (d’Haene et al. 1993; Laun 1994; Frith et al. 1996; Fagan and Zukoski 1997; Fall et al. 2015; Hermes et al. 2016), that above the transition, the shear rate remains approximately constant whatever the value of the stress. In practice at high stresses, it ends up by an expulsion of the suspension in plate-plate or cone-plate geometry or by foaming in cylindrical Couette geometry. We shall come back to the analysis of the W–C model in the context of the capillary flow in the next sections. The results obtained in capillaries for the wall shear stress as a function of the volume flow rates are presented in the three following figures (Figs. 3, 4, 5). On these figures we have also plotted the predicted curve obtained from the fitted curve of the experimental rheogram $\dot{\gamma }\left(\tau \right)$(cf Fig. (2)) through the equation:

Fig. 3

Volume fraction Φ = 0.6. Red dots are the flow rates measured at different imposed pressures. The solid line is obtained from Eq. (1) with $\dot{\gamma }\left(\tau \right)$ given by the dashed curve of Fig. (2) for Φ = 0.6

Fig. 4

Volume fraction Φ = 0.64. Red dots are the flow rates measured at different imposed pressures. The solid line is obtained from Eq. (1) with $\dot{\gamma }\left(\tau \right)$ given by the dashed curve of Fig. (2) for Φ = 0.64

Fig. 5

Volume fraction Φ = 0.65. Red dots are the flow rates measured at different imposed pressures. The solid line is obtained from Eq. (1) with $\dot{\gamma }\left(\tau \right)$ given by the dashed curve of Fig. (2) for Φ = 0.65

$$Q\left({\tau }_{R}\right)=\pi{\int }_{0}^{R}{r}^{2}\dot{\gamma }\left(r\right)dr=\frac{\pi {R}^{3}}{{\tau }_{R}^{3}}{\int }_{0}^{{\tau }_{R}}{\tau }^{2}\dot{\gamma }\left(\tau \right)d\tau$$

(1)

This equation is always valid whatever the rheological law since it just comes from the definition of the volume flow rate as the integral from r = 0 to r = R of the velocity field v_z(r) and of the change of variable r = R. τ (r)/ τ_R, where τ_R is the wall shear stress.

The previous figures show that, qualitatively, the predicted result from the use of rheometry through Eq. (1) is in agreement with the experimental points showing a decrease of the flow rate above a critical flow rate whose value is nevertheless smaller than the experimental one for Φ = 0.64 and Φ = 0.65. At Φ = 0.60, where the rheometry does not show a sudden decrease of the shear rate (Fig. 2), the predicted curve has the same aspect as the experimental one with a rounded part at the transition. This is quite different for Φ = 0.64 and Φ = 0.65 (Figs. 4 and 5) because the predicted curves do not reflect the sudden decrease of the flow rate.

We have seen that both in rotational rheometry and in capillary flow we have a sharp transition but that, if we introduce the experimental curve $\dot{\gamma }$ (τ) obtained from rheometry in Eq. (1), the predicted transition for the capillary flow is a soft one; (cf. Figures 4–5). Still Eq. (1) is general and applies whatever the rheological law. We will see what the reason is for this contradiction in the last section, but first let us see how the W–C model applies to a capillary flow.

Application of the Wyart-Cates model

In the W–C model, the volume fraction where the viscosity diverges, depends on the applied stress in the following way:

$${\Phi }_{J}\left(\tau \right)=\left({\Phi }_{{RLP}}-{\Phi }_{0}\right)f\left(\tau ,\uplambda ,q\right)+{\Phi }_{0}$$

(2)

As explained in the introduction Φ_RLP can be approximated by the random loose packing which is 0.58 for our suspension and the frictionless packing is Φ₀ = 0.681. The function f represents the proportion of frictional contacts in the suspension and increases from 0 to 1 while increasing the stress. Different expressions have been proposed for the function f; we shall take the following one (Guy et al. 2020):

$$f\left({\uptau }^{*},\lambda ,q\right)={e}^{-{\left(\frac{\lambda }{{\uptau }^{*}}\right)}^{q}}with\; {\uptau }^{*}\uptau /{\uptau }_{c}$$

(3)

The parameters λ and q are taken to fit the experimental curve obtained in conventional rheometry and τ_c is the critical stress at the transition.

The viscosity and the shear rate dependence are given by the usual relation for concentrated suspensions, with the only difference that Φ₀ has been replaced by Φ_J(τ). The yield stress in Eq. (4) is the dynamic yield stress of a Bingham law which fits quite well the beginning of the stress-shear rate curve:

$$\dot{\gamma }\left(\uptau \right)=\frac{\uptau -{\tau }_{y}}{{\eta }_{c}\left(\Phi ,\tau \right)}\; with\; {\eta }_{c}\left(\Phi ,\tau \right)={\alpha }{(1-\frac{\Phi }{{\Phi }_{j}\left(\tau \right)})}^{-2}$$

(4)

The values of α and τ_y are obtained from the fit by Eq. (4) of the first part of the curve for τ < τ_c and λ and q are obtained by the condition that the fitted curve should have a zero slope for $\frac{d\dot{\gamma }}{d\tau }$ at the experimental turning point ${\tau }_{c},{\dot{\gamma }}_{c}$. The result is represented in Fig. 6 by the solid black line with the following values:τy=19.4Pa,α=0.02,λ=1.29,q=6.08.

Fig. 6

Fit of the rheometric curve (blue solid line) by the Wyart-Cates model (solid black line). The shear rate for the results at imposed pressure (red squares) is deduced from the flow rate by:$\dot{\gamma }=4Q/(\pi {R}^{3}$)

$${\tau }_{\text{y}}=19.4{ Pa},{ \alpha }=0.02,\uplambda =1.29,{ q}=6.08$$

We see that the W–C model predicts a zero shear rate when the jamming fraction Φ_J(τ) becomes equal to the actual value, Φ, whereas, as already pointed out, the experimental shear rate does not cancel and remains approximatively constant (solid blue line). It is also interesting to note that, on this figure, the shear rate for the results at imposed pressure is the Newtonian shear rate ${\dot{\gamma }}_{N}=4Q/(\pi {R}^{3})$. This shear rate is not the real wall shear rate which is obtained by the derivative of Eq. (1):

$${\dot{\gamma }}_{R}=\frac{1}{\pi {R}^{3}}\left[{\tau }_{R}\frac{dQ({\tau }_{R})}{d{\tau }_{R}}+3Q({\tau }_{R})\right]$$

(5)

The derivative of the volume flow rate relatively to the stress is not well defined experimentally, especially during the transition; this is the reason why we have decided to compare in Figs. 3, 4, and 5, the wall stress versus volume flow rate rather than versus the shear rate. The quite large difference between the critical shear rate in conventional rheometry and in capillary flow in Fig. 6 is partly due to the use of the Newtonian shear rate instead of the real one, and we can see in Fig. 4 that the agreement is better if we consider the volume flow rate instead of the Newtonian shear rate.

Since, the Eq. (4) represents the W–C model for the function $\dot{\gamma }\left(\tau \right)$ in rotational rheometry, we can use this analytical equation in Eq. (1) to compare the prediction of this model with the experiment in the case of a capillary flow. This is the solid blue line in Fig. 7.

Fig. 7

Prediction of the stress versus flow rate in the frame of the W–C model. The experimental points for the capillary flow are the red dots at Φ = 0.64

As this model predicts a complete jamming above a given stress (τ_m = 233 Pa for Φ = 0.64), the predicted volume flow rate will also progressively stop when the stress rises. In this model, since the stress remains low at the center of the capillary, the central part will continue to flow even if a solid zone has begun to form on the wall where the stress is larger than the jamming stress τ_m. This zone will progressively extend towards the center until it fills all the section of the capillary when the flow stops. There are two striking differences between the prediction of the W–C model and the experiment. The first concerns the soft transition instead of the abrupt one and was expected since it was already observed with the fitted experimental rheometric curve that the W–C theory try to represent. The second is that the volume flow rate decreases towards zero while experimentally it remains constant above the transition.

A possible reason for the soft transition could be related to shear induced migration which would gradually modify the volume fraction profile and could then be responsible for this behavior. Actually, shear induced migration above DST was observed in a Couette cell of large gap by magnetic resonance imaging with cornstarch particles (Fall et al. 2010) so we have to analyze its possible role on the stress-volume flow rate curve. In the appendix we develop an analysis of shear induced migration in the presence of aggregates based on the work of Mills and Snabre (Mills and Snabre 1995). The predicted effect of migration on the wall stress versus flow rate curve is shown to increase the volume flow rate between 50 and 100% at the vicinity of the critical stress compared to the experimental values which on the other hand, are well predicted in the absence of migration (cf Appendix, Fig. 11). The lack of migration could be surprising at first glance given that it was observed with cornflake particles by magnetic resonance imaging in a large gap Couette cell where the shear rate is also inhomogeneous. In fact, our particles are more than an order of magnitude smaller and the diffusion coefficient being proportional to the square of the radius of the particles we expect a much smaller migration as long as the particles are not aggregated. On the other hand, above the transition, in the presence of a percolated network of frictional contacts, the transverse motion of particles during the deformation and rearrangement of this network is probably a rarer event than when particles do not stick to each other. This analysis shows that shear induced migration cannot explain why the use of the rheometric data obtained in rotational geometry, as well as the W–C model based on these data, fail to reproduce the sharp change of volume flow rate in capillary flow. In the last section, we will propose an explanation of this disagreement, but first we need to investigate why the volume flow rate does not stop above the transition as predicted by the W–C model.

Modification of the W–C model to get a constant flow rate above the transition

If the flow stops, we expect that the normal force will relax either through remaining Brownian motion or lubricated contacts still present in the percolated network or because the polymer molecules which were strained or removed from the surface by the local flow will come back to their initial position. In this case, the percolated structure will be momentaneously isotropized and destroyed, but the high applied stress will make the suspension to flow again and the cycle between arrested flow and flowing states will start again. This qualitative explanation is based on an equilibrium between forces which on one hand tend to destroy the percolated network of frictional contacts and on another hand to reinforce it. This approach is generally used to describe the evolution of a structural parameter like for instance, the sizes of the aggregates in the presence of shear and of attractive or Brownian forces and to predict the rheological law related to this structural parameter (Quemada and Berli 2002). In this kind of approach, the flowing state observed above the transition can be the result of an average of unstable flows which depends on the ratio between the measurement time and inertial time t_m/t_I. Another way to describe this phenomenon is to say that the structure at the jamming volume fraction Φ_J(f) (which is smaller than the RCP one, Φ₀), can still deform and yield so, depending on the difference between the applied stress and the yield stress generated by the percolation of frictional contacts, the suspension can still flow through rupture and reformation of frictional bonds. In a recent paper (Baumgarten and Kamrin 2019), a similar reasoning was applied to the fraction, f, of frictional contacts (here defined by Eq. (3)); a constant shear rate in the limit of high stress was obtained thanks to the introduction of a “hardening function” H(τ) scaling as τ^3/2. A simpler way to obtain a constant shear rate when the jamming fraction approaches the actual volume fraction is to introduce a divergence of the viscosity at a given non-zero shear rate. As already said, the fraction of frictional contact must tend to zero with time when the suspension no longer flows and that, whatever the value of the initial stress. Let us then write the fraction of frictional contact as:

$${f}^{^{\prime}} ({\tau }^{*},\dot{\gamma })=f\left({\tau }^{*}\right)*L({t}_{L}.\dot{\gamma })$$

(6)

Here f(τ*) is the function already defined by Eq. (3) and L(x) is a function which tends to zero when x tends to zero and which saturates to unity like for instance the Langevin function: L(x) = coth(x)-1/x. The parameter t_L is related to the relaxation time of the stress during the blockage phase: the larger, the closer we approach a complete stop of the flow. We call f_jam the value of f for which we have Φ_J(f_jam) = Φ (here using Eq. (2) and (3) give f_jam = 0.44 for Φ = 0.64). Since at high stresses $f\left({\tau }^{*}\right)\to 1$, the equation $L({t}_{L}.\dot{\gamma })={f}_{jam}$ will give the limiting shear rate, ${\dot{\gamma }}_{l}$, for which the viscosity $\eta \left({f}^{^{\prime}}\right)$ diverges; in our example for Φ = 0.64 and t_L = 0.18 s, ${\dot{\gamma }}_{l}=8.49 {s}^{-1}$. Due to this divergence, the shear rate $\dot{\gamma }=(\tau -{\tau }_{y})/\eta \left({\tau }^{*},\dot{\gamma }\right)$ approaches quickly its asymptote. We have added here the presence of a dynamic yield stress which is present in our case and the viscosity is the one given by Eq. (4) with f ’ instead of f in Eq. (2). The resulting curve is shown in Fig. 8 with the relaxation time t_L = 0.18 s together with the original prediction of the W–C model. We see that this simple modification allows to well represent the experimental data.

Fig. 8

Comparison of the prediction of the W–C model (green line) with the modified value of f: Eq. (6) and t_L = 0.18 s (red line). The solid blue line is the experimental result in Couette geometry at Φ = 0.64

As it is not the scope of this paper we did not try to reproduce the oscillations of the shear rate which can be obtained by including the inertia of the rotating part of the rheometer in the equation of motion of the tool (Bossis et al. 2017, 2019; Richards et al. 2019). We do not see any fluctuations of the flow rate at imposed pressure although they could appear due to the inertia of the fluid itself (Nakanishi et al. 2012) but the averaging time of 1 s for the mass measurement is too large to observe them if any, because the inertia time: ${\tau }_{I}$=ρ ${R}^{2}/2\eta$,which rules the relaxation of a shear rate fluctuation, is typically smaller than 1 ms in our experimental conditions. It should also be noted that, for the analytical curve $\dot{\gamma }$(τ) derived from the rotational rheometry data, we have used an average value of the fluctuating shear rate, implicitly assuming that this average was the equilibrium curve in the absence of inertia and that it is the right value to introduce in Eq. (1) since, in the capillary flow, the inertia is negligible and its effect is not observed. Now that we have an equilibrium curve from the modified W–C model we could also use the theoretical curve $\dot{\gamma }$(τ) of Fig. 8 instead of the fitted curve in Eq. (1) but the result would be very close from the one obtained with the fitted rheometric curve: there will be no sharp transition of the volume flow rate as observed experimentally. So, the modification of the W–C theory does not help to explain this discrepancy.

On the other hand, Eq. (1) is always valid, but we have done the hypothesis that the rheological law inside the capillary was the same as in the cylindrical shear cell, or in other words that the law $\dot{\gamma }$ (τ) fitted from the rheometry applies locally inside the capillary with $\tau =(r/R){\tau }_{R}$. This is not very realistic: as soon as the transition takes place close to the wall where the shear stress is maximum, the radial stress will provoke the propagation of the percolation towards the center of the cell. We can assume that above the transition, we suddenly move towards a regime where we have a uniform viscosity given by the modified W–C model. Said differently, the jamming volume fraction is the one at the wall Φ_J(τ_R) and does not depend on the radial coordinate. Assuming a constant viscosity independent of the radial coordinate means that we have now in Eq. (1):

$$\dot{\gamma }\left(\tau \right)=\frac{\tau }{\eta \left({\tau }_{R}\right) } \Rightarrow Q\left({\tau }_{R}\right)=\frac{\pi {R}^{3}}{4 }\dot{\gamma }({\tau }_{R})$$

(7)

Above the transition, even if the percolated structure extends to the center of the capillary, it is likely that the contact forces between the particles will be lower at the center and consequently that the viscosity will also be lower; nevertheless, as it can be seen in Fig. 9, this approximation represented by Eq. (7) well reflects the experimental behavior.

Fig. 9

Different models used to predict the volume flow rate at imposed pressure. Solid black line: Eq. (1) with fitted value of $\dot{\gamma }({\tau }_{R})$ (cf. Figure 2). Green solid line: Eq. (7) with $\dot{\gamma }({\tau }_{R})$ from the modified W–C model. Blue solid line: Eq. (7) with the fitted values of $\dot{\gamma }\left({\tau }_{R}\right).$ Red dots: experimental points at Φ = 0.64

The green curve is the result of Eq. (7) applied to the prediction of $\dot{\gamma }({\tau }_{R})$ by the W–C model modified with the help of Eq. (6) and the blue curve is the same Eq. (7) applied to $\dot{\gamma }({\tau }_{R})$ fitted from the rheometry cf. (Fig. 2). Even if this approach is an “oversimplification,” the important point to underline is that the comparison between the data obtained in the capillary at imposed pressure and those obtained in Couette cell geometry cannot be explained above the transition without abandoning the hypothesis of a local rheology represented by the solid black line in Fig. 9. This point would be quite trivial for small value of R/a but here we have R/a ~ 5000 proving the long-range effect of the transmission of normal forces above the DST transition.

Conclusion

We have presented new experiments based on capillary flow at imposed pressure of a suspension in the regime of discontinuous shear thickening. The rheological law $\dot{\gamma }\left(\tau \right)$ of the same suspension was measured in conventional rheometry using a cylindrical Couette cell. At high enough volume fraction, we well recover the DST transition in this capillary flow with a strong and abrupt decrease of the volume flow rate for a critical stress. The experimental curves Q(τ_R) of the volume flow rate as a function of the wall stress were compared with the ones predicted using the rheological law from Eq. (1). The agreement was qualitative but did not reflect the abrupt transition observed experimentally. A possible reason could have been the migration of particles towards the center, but an analysis of shear induced migration shows that it would give a volume flow rate much larger than the experimental one. The use of the Wyart-Cates model to predict the volume flow rate does not help and furthermore predicts a flow stop above the critical stress which is not observed experimentally. On the contrary, as in conventional rheometry for the shear rate, the volume flow rate remains approximatively constant when the stress is increased. It is possible to explain this behavior considering that, if the flow stops for a given stress, the absence of shear flow will allow to reactivate the interparticle repulsive forces and will lead to a deformation of the percolated structure and a new start of the flow. Allowing the fraction, f, of frictional contacts to cancel at low shear rate independently of the value of the applied stress (cf. Equation (6)) allows us to well reproduce the zone of constant flow rate at high stress. The other discrepancy stands in the fact that, the use of the curve $\dot{\gamma }\left(\tau \right)$ obtained in a Couette cell to predict the one observed in the capillary shows a gradual decrease of the volume flow rate above the DST transition rather than the abrupt one observed experimentally. If we consider that, in the presence of a percolated network of contacts, the viscosity does not depend on the radial position and is equal to the one on the wall: η (τ_R), (or in other words that the frictional network has extended over the entire section of the capillary), then it is possible to recover the volume flow rate obtained at imposed pressure from the rheometry in a Couette cell.

Appendix: Effect of Shear induced migration on the volume flow rate

Shear induced migration in a gradient of shear rate is related to the gradient of the number of collisions between particles since each collision induces a random transverse motion of order of magnitude a, relatively to the average velocity direction which induces a migration from the higher rate of collision domain (high$\dot{\gamma }$) to the lower one. This migration was first observed by NMR in concentric cylinders (Abbott et al. 1991; Graham et al. 1991; Chow et al. 1994) and in Poiseuille flow (Hampton et al. 1997). The shear induced diffusion coefficient is proportional to $\dot{\gamma }{a}^{2}$ with a coefficient which depends on the volume fraction and of the interparticle force but that remains usually smaller than unity for reasonable values of the range of roughness (Leighton and Acrivos 1987; Da Cunha and Hinch 1996; Zarraga and Leighton, 2001) or of the interparticle forces (Meunier and Bossis 2008). In our case with an average radius of 0.3μm, the typical time for a migration of 1 mm—the characteristic value of the radius of the capillary- would be ${T}_{m}\propto \frac{1}{\dot{\gamma }}{\left(\frac{R}{a}\right)}^{2} \approx {10}^{5}s$ for a typical wall shear rate of 10 s⁻¹. The time needed for the transfer of the suspension from the input to the output of the capillary is T_tr = πR ²L/Q then, with a radius of 1.5 mm and the maximum length used of 36 cm and a minimum flow rate of 0.01cm³/s, we get T_tr = 250 s which is more than two orders of magnitude smaller than the migration time. Nevertheless, if below the transition we can neglect the migration, this not so obvious anymore above the transition since it is related to the formation of aggregates of particles in frictional contact which are supposed to percolate between the walls of the capillary. Instead of the radius of the particles which determines the transverse change of trajectory, it is rather a typical size of the aggregates, which means that now the migration time becomes just proportional to ${\dot{\gamma }}^{-1}$ which in turns, is now much smaller than the transfer time of the suspension. Of course, this analysis is only indicative because the collision between big aggregates will mainly result in their deformation rather than in a global change of trajectory. As already underlined, the size of the aggregates formed during the transition can play a major role in shear induced migration. We shall use the work of P. Mills and P. Snabre (Mills and Snabre 1995) who have introduced in a simple way a correlation length, ξ, in order to estimate its influence on the migration. They obtain the following result for the volume fraction Φ (r) in a circular capillary:

$$\frac{\Phi \left(r\right)}{1-\Phi \left(r\right)/{\Phi }_{0}}={\left(\frac{r}{R}\right)}^{L}\frac{{\Phi }_{R}}{1-{\Phi }_{R}/{\Phi }_{0}}$$

(8)

where ${\Phi }_{0}$ is the closed-packed volume fraction,Φ_R = Φ(R) and L an exponent which is equal to 2 for 0 < r < ξ and 1 for ξ < r < R. The correlation length ξ is the one over which the stress is transmitted from one particle to the other inside a chain through frictional or lubricated contacts. The factor 2 comes from the integral of the stress along a chain of length ξ. Note that the value L = 1 gives a density profile with a cusp at the center (Phillips et al. 1992). In the frame of the W–C model Eq. (8) can be re-written as:

$$\frac{\Phi (r)}{{\Phi }_{R}}={\left(\frac{R}{r}\right)}^{L}\sqrt{\frac{\eta (R)}{\eta (r)}}$$

(9)

With

$$\eta \left(r\right)={\alpha } {(1-\frac{\Phi \left(r\right)}{{\Phi }_{J\left(r\right)}})}^{-2}$$

(10)

In Eq. (10) the jamming volume fraction now will depend on r since in the capillary the stress: τ (r) = τ_R (r/R) varies from zero at the center to τ_R on the wall so the jamming volume fraction will depend on r* = r/R:

$${\Phi }_{J}\left({r}^{*}\right)=\left({\Phi }_{{RLP}}-{\Phi }_{0}\right)f\left({r}^{*}{\tau }_{R},\uplambda ,q\right)+{\Phi }_{0}$$

(11)

Combining Eq. (9) and (10) gives the variation of the volume fraction:

$$\Phi \left({r}^{*},{\tau }_{R}\right)=\frac{{\Phi }_{R}}{{r}^{*l}\left(1- \frac{{\Phi }_{R}}{{\Phi }_{JR}}\right)+\frac{{\Phi }_{R}}{{\Phi }_{J}({r}^{*})}}$$

(12)

Due to the divergence of the viscosity for $\Phi \left(r\right)={\Phi }_{j}(r)$, the volume fraction in Eq. (12) remains bounded by ${\Phi }_{j}(r)$. The unknown in Eq. (12) is Φ_R the volume fraction at r = R. It is derived from the condition of recovering the average volume fraction:

$$\Phi =2{\int }_{0}^{1}\Phi \left({r}^{*},{\tau }_{R}\right){r}^{*}d{r}^{*}$$

(13)

In Fig. (10) we have represented the volume fraction profile deduced from Eq. (12), (13) for four different stresses. These are equilibrium profiles when the migration is ended. For τ_R = 100 we are well below the critical stress and the maximum volume fraction at the center (r* = 0) is equal to Φ₀ and decreases almost linearly from the center to the wall. For τ_R = 200, even if we are slightly above the transition, the profile is rather the same as for τ_R = 100 except close to the wall where the volume fraction is slightly lower. The change is important at τ_R = 275 Pa and still more important at τ_R = 340, both values being above the jamming stress in the W–C model in the absence of migration. It is only at this last stress that the profile becomes blunted with, at the center of the capillary the maximum volume fraction Φ = Φ₀. This kind of profile was experimentally observed on suspensions of non-Brownian spheres with R/a ~ 40 at Φ = 0.55 by magnetic resonance imaging (Oh et al. 2015).

Fig. 10

Predicted volume fraction profiles Φ(r*) for four different wall stresses: τ = 100, τ = 200, τ = 275, τ = 340 at an average volume fraction of Φ = 0.64

Fig. 11

Prediction of the stress versus flow rate in the frame of the W–C model. In blue without migration; in green with an exponent 1 < L < 2 (cf. Equation (8) with L = 1 + f_e(r^*. τ_R, λ, q))) depending on the value of the stress; in red with L = 2 whatever the value of the stress. The experimental points are the red dots at Φ = 0.64

The wall stress versus flow rate for different profiles of volume fraction, including the case of a constant volume fraction already presented in Fig. (7) in the absence of migration, is represented in Fig. (11)). In the presence of migration we use, instead of Eq. (4), the following one:

$$\dot{\gamma }\left({r},{\uptau }_{R}\right)=\frac{\uptau ({r})-{\tau }_{y}}{{\eta }_{r}\left(\Phi ,\tau \right)}\;with\;{\eta }_{r}\left(\Phi ,r\right)={\alpha }{(1-\frac{\Phi ({r})}{{\Phi }_{j}\left(r\right)})}^{-2}$$

where r = r* τ_R and Φ(r) the solution of Eqs.(12),(13).

When the stress has exceeded the transition value, τ_c, the jamming fraction Φ_J decreases with the stress until it reaches everywhere the local volume fraction Φ(r) making the flow to stop due to the divergence of the viscosity. We have taken in Eq. (8) a value of the exponent L = 1 + f_e(r^*. τ_R, λ,q)) which changes from 1 to 2 with the value of the stress to consider the progressive increase of the correlation length, ξ, with the stress. This correlation length is related to the presence of clusters of particles which transport the particles during their rotation on a length equivalent to the diameter of the cluster. Since, even in the absence of friction, the hydroclusters can also play this role, we can use L = 2 also below the transition. In this case, we obtain the red curve which is still more different from the experimental results. It appears that, whatever the migration model, the increase in volume fraction at the center of the capillary will result in an important increase of the volume flow rate which is not compatible with the experimental data especially concerning the maximum volume flow rate. From this comparison between the models without and with migration and the experimental values we can conclude that we do not have migration.