A study on the flow of moderate and high viscosity ratio emulsion through a cylindrical tube

Abstract

This work deals with asymptotic and numerical solutions for emulsion flowing driven by a pressure gradient. The average macroscopic description of a homogeneous continuous emulsion of high viscosity drops is modeled. A parameter involving the product of the squares of the capillary number and the aspect ratio is the key parameter for developing a new asymptotic solution. Explicit expressions of the velocity profile, the flow rate correction due to the drops stress contribution, drop deformation, and the relative viscosity of the emulsion are shown as function of the capillary number ranging from 0 to 10 and emulsion viscosity ratio ranging from 2 to 20. The theoretical predictions by asymptotic theories developed in this work are compared with those computed results by boundary integral method (BIM) for different viscosity ratios of a dilute emulsion undergoing both pressure-driven flow and linear shear flow. Some discrepancies observed for moderate viscosity ratio are identified and discussed. The present study for emulsion with moderate and high viscosity ratio and arbitrary capillary number are still few explored in the current literature.

Introduction

Pipeline transportation of emulsions is difficult to predict or control due to the complex interplay between the detailed drop-level microphysical evolution and the macroscopic flow. Consequently, the flow of emulsions in pipelines has attracted the interest of several researchers (Derkach 2009). Axisymmetric calculations have precisely mapped out the condition for studies of drop deformation, orientation, breakup, and the consequences of the individual and collective drop behavior to emulsion rheology (e.g., Rallison 1980; Stone 1994; Derkach 2009). There have been a few theoretical studies of the influence of the viscosity ratio on the emulsion the flows in capillaries. In fact, the studies reported in the current literature are mainly focused on flow of emulsions with unitary viscosity ratio. The pipeline flow of emulsions with moderate and high viscosity ratio has received less attention.

Some rigorous theoretical descriptions are available for the effect of drop deformation on the rheology of a dilute emulsion (e.g., Schowalter et al. 1968; Frankel and Acrivos 1970; Barthés-Biesel and Acrivos 1973b; Cho and Schowalter 1975; Nika and Vernescu 2016). In addition, asymptotic analyses in the limit of small drop deformation were developed by Barthés-Biesel and Acrivos (1973a) and Rallison (1980). The theoretical calculations developed by Barthés-Biesel and Acrivos (1973a) explored the limit of drop deformation limited by surface tension, i.e., Ca_o ≪ 1, where Ca_o is the standard capillary number $\left(\upmu \mathrm{a}\dot{\gamma }/{\sigma}_o\right)$ with a being the radius of the nondeformed drop, $\dot{\gamma}$ the shear rate, and σ_o the uniform interfacial tension. Their theory is very important to the prediction of drop breakup, essentially because it occurs far from a spherical shape as imposed by a high drop-to-medium viscosity ratio theory with $\mathcal{O}\left(1/\lambda \right)\ll 1$ (λ = μ_drop/μ_medium) such as the one used in the present paper. The theory of Barthés-Biesel and Acrivos (1973a) takes the near sphere analysis up to third order. They solved the truncated series exactly and examined the stability of the exact solution of the truncated equations. From this, they predicted the breakup of droplets with a reasonable agreement with available data. Davis et al. (1989) coupled lubrication theory with boundary integral theory to describe the relative motion of two unequal drops in near contact. They showed that the interfacial mobility and internal circulation within the drops allow the surrounding fluid to drain from between two approaching spherical drops so that coalescence can occur even in the absence of an attractive force. A key finding is that the coalescence rates decrease significantly with an increasing ratio of the drop viscosity to solvent viscosity because the internal flow is then reduced and it becomes more difficult for the solvent fluid to be squeezed out from between two approaching drops. Guido et al. (2004) reported experimental observations of a single high viscosity drop dynamics under large amplitude oscillatory shear. They provided experimental evidence of a quite complex frequency response in drop dynamics. A review paper discussing isolated drop deformation, breakup, including cross-stream migration, and the effect of surfactants under pressure-driven flow was written by Guido and Preziosi (2010). More recently, Oliveira and Cunha (2011) presented results of small deformation analysis for an emulsion undergoing unsteady shear flows. They explored the nonlinear frequency response for high strain amplitudes for a dilute emulsion, where hydrodynamic drop interaction is a negligible effect.

Computer simulations of emulsions have been developed to help the interpretation of experimental observations (Mason et al. 1997) and to predict the complex microstructure of drop size distributions such as those shown by experimental techniques of emulsion characterization (Xu et al. 2005). The viscous behavior of oil-in-water emulsions was investigated by Pal (2000) over a broad range of volume fraction of the drops. The influence of shear rate and concentration applied on droplet deformation was systematically investigated experimentally by Tufano et al. (2008). In that work, the non-Newtonian behavior of the emulsion was interpreted in terms of relative viscosity versus particle Reynolds number. Although most of the theoretical works have been concerned with axisymmetric or two-dimensional interface drop deformations, which require numerical treatment of line integrals, several studies have considered the more difficult case of three-dimensional drop distortion (e.g., Youngren and Acrivos 1975; Rallison 1981; Tanzosh et al. 1992; Mo and Sangani 1994; Kennedy et al. 1994; Loewenberg and Hinch 1996, 1997; Coulliette and Pozrikids 1998; Zinchenko and Davis 2002; Zinchenko and Robert 2003; Cristini et al. 2001; Bazhlekov et al. 2004; Oliveira and Cunha 2015). Large-scale multidrop numerical simulations for investigating emulsion flow through porous media and general rheology of concentrated emulsion of deformable drops in extensional and shear flow have been performed by Zinchenko & Davis in a series of recent works (Zinchenko and Davis 2013, 2015, 2017a, b).

The regime of emulsion flow under a pressure gradient with high and moderate viscosity ratios has not been much explored in the current theoretical and experimental literature . In this work, we examine a pressure-driven emulsion-flow using the regular asymptotic method in order to present new calculations for the regime of small deformation theory in the limit of high viscosity ratio dilute emulsion. The regime for a moderate viscosity ratio and drop deformation is investigated by a three-dimensional boundary integral method developed by Oliveira and Cunha (2015). The relevant parameters for the problem that we have investigated include the dispersed to continuous phase viscosity ratio λ, the capillary number Ca_λ, and the capillary number evaluated using the wall shear rate Ca_w. We develop a theory for drop deformation and relative viscosity (i.e., intrinsic viscosity) of a dilute emulsion as function of the capillary number and viscosity ratio under influence of a shear rate gradient. The theoretical prediction developed in the present article for high viscosity ratio dilute emulsions are compared with results of numerical simulations based on boundary integral method. A good quantitative agreement is observed in the limit of dilute emulsion with moderate and high viscosity ratio drop-ambient fluid. The discrepancies observed mainly for moderate viscosity ratio are identified and discussed.

Pressure-driven flow in cylindrical tubes

The fluid velocities within the dispersed and continuous phases obey Stokes equations. The fluid velocity is everywhere continuous but the normal component of stress has a discontinuity on drop surfaces due to interfacial tension; tangential traction may be discontinuous if Marangoni stresses are important. We assume unidirectional flow so that the effect of fluid inertia is absent, i.e., u ⋅∇u = 0. Body forces are also ignored in the present analysis. Under these conditions, one can write the governing equations as follows:

$$ \nabla \cdot \boldsymbol{u}=0,\kern1em \mathrm{and}\kern2.00em \nabla \cdot \boldsymbol{\sigma} =\mathbf{0}, $$

(1)

where u is the velocity vector, and σ = −pI + 2μD denotes the stress tensor of the fluid with p being the mechanical pressure and D = (1/2)(∇u + (∇u)^T) the rate of deformation tensor.

Now, considering also that the fluid flowing through a cylindrical tube is an dilute emulsion, an additional particle stress tensor σ^d must to be added to the standard Newtonian stress contribution in order to account the bulk nonlinear behavior from the complex dynamics of the drops in the microscale (Batchelor 1970). In this sense, σ^d is the stress contribution of the disperse phase to the bulk stress tensor of the emulsion assumed as being a continuous homogeneous material. Actually, σ^d denotes the bulk stresslet per unit of volume produced by the drops on the ambient fluid. In this work, the emulsion viscosity ratio, λ, is considered moderate or high (i.e., in general λ ∼ 1 or greater than it), and the particle volume fraction is always assumed very small (dilute regime). The microscale flow around the drop (inside and outside the particle) is assumed creeping flow and consequently both having a very small Reynolds number, i.e., $\operatorname{Re}=\rho \dot{\gamma}{a}^2/\mu \ll 1$, and Re_λ = Re(ρ_s/ρ)λ^− 1 ≪ 1 where ρ and ρ_s are the drop and ambient fluid density, respectively. In addition, the macroscopic flow in the tube scale is considered unidirectional (i.e., free of inertia as well) since Re_R = (ρUR/μ)(R/L) ≪ 1. Here, the aspect ratio R/L, in general, is a small parameter in capillaries. Thus, the emulsion flow is a laminar (or parallel) flow. Since, in this paper, the flow in the macro- and microscales are free of inertia, we shall use a viscous scale for pressure given by $\mu \dot{\gamma}=\upmu \mathrm{U}/a$ instead of the common one used ρU². So, the Reynolds number will not appear explicitly in our calculations.

A shear-induced particle diffusion has been shown to play an important role on the rheology as involving concentrated suspensions (e.g., Eckstein et al. 1977; Leighton and Acrivos 1987). However, the phenomenon as described in Cunha and Hinch (1996) at a infinitely dilute limit (i.e., non-interacting drops) can be taken as a second-order effect. The shear-induced particle diffusion in an emulsion would require at least two drops interactions in order to a small deformation during the drops collision breaks the time reversibility of the Stokes flow (i.e., a small amount of deformation could produce irreversible drops trajectories) (Loewenberg and Hinch 1997). In a quadratic shear like the flow explored here, there is still a shear rate gradient. Therefore, even in the absence of inertia, the drops could migrate radially toward the centreline (i.e., from the wall-high shear to the center-low shear). The flux particle-drift due to a shear rate gradient scales like ${a}^2{\phi}^2\nabla \dot{\gamma}$ (Phillips et al. 1992). Since this contribution is proportional to ϕ², it is just a second-order effect. In addition, the induced deformation drift velocity v_d by the asymmetrical stresslet on the deformable drop close to the wall scales like ${v}_d\sim {\lambda}^{-1} Ca\dot{\gamma}{a}^3/{y}_d^2$ (Chaffey et al. 1965). In this paper, the drops are always very small compared with the tube diameter, the viscosity ratio is moderate or high and the capillary number Ca ∼ 1. Consequently, this drift velocity being proportional to ${a}^3/{y}_d^2$, where y_d is the distance between the center of the drop and the wall, gives very small values of the migration velocity compared to a typical velocity of the flow $\dot{\gamma}$. Therefore, this migration effect will not produce a substantial effect on the rheology of a high viscosity emulsion composed of small drop.

The effect of drop-drop interactions on the rheology is unimportant in the limit of very dilute emulsion explored here. The coefficients O(ϕ) and O(ϕ²) of the shear-induced diffusivities are always very small for dilute suspensions or emulsions as compared with the diffusivities in concentrated suspensions (Leighton and Acrivos 1987). We can justify the assumption of neglecting drop shear-induce migration here by considering the relative importance between the timescale for a drop diffuses its own radius a, i.e., τ_d ∼ a²/D_h and a convective time scale ${\tau}_c\sim \lambda /\dot{\gamma}$. Here, D_h is the hydrodynamic diffusion for instance the one proposed by Cunha and Hinch (1996) for a dilute regime, ${D}_h\sim \dot{\gamma}{a}^2\phi$. A hydrodynamic Péclet number in the present context can be defined as being Pe_h = τ_d/τ_c = (ϕλ)^− 1. Now, since λ ∼ 1 and ϕ ≪ 1, then Pe_h ≫ 1, that means deformation of the drop by the flow dominates drop shear-induced dispersion.

Under these conditions, we can write the governing equation of the equivalent continuous emulsion in the absence of a coupling between particle volume fraction ϕ and the flow at high Pe_h, as follows:

$$ -\nabla p+\mu {\nabla}^2\boldsymbol{u}+\nabla \cdot {\boldsymbol{\sigma}}^d=\boldsymbol{0}. $$

(2)

Setting up an axisymmetric cylindrical coordinate system, the velocity field takes the form u = u(r)e_z, where e_z is the unit vector parallel to the axial direction and r is the radial coordinate. In this case, Eq. 2 written in terms of cylindrical coordinates takes the form:

$$ \kern0.5em -\kern0.5em \frac{\partial p}{\mathrm{\partial z}}+\mu \frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial u}{\partial r}\right)+\frac{1}{r}\frac{\partial }{\partial r}\left(r{\sigma}_{rz}^d\frac{}{}\right)=0\kern2em \mathrm{and} $$

(3)

$$ \kern0.5em -\kern0.5em \frac{\partial p}{\partial r}+\frac{1}{r}\frac{\partial }{\partial r}\left(r{\sigma}_{rr}^d\frac{}{}\right)-\frac{\sigma_{\uptheta \uptheta}^d}{r}=0. $$

(4)

In general, we may have a radial pressure gradient in order to balance eventual normal stresses yielded from the nonlinear part of the fluid stress tensor, like shows the Eq. 4 . Here, the extra stress tensor due the action of the disperse phase is a function of the radial coordinate only, namely, σ^d = σ^d(r). Therefore, analyzing Eq. 4, we argue that ∂p/∂r = f(r), in such way that p = F(r) + M(z), where f(r) and F(r) are functions of the radial coordinate, related by dF(r)/dr = f(r). M(z) is some function of the axial coordinate only. In this context, if we proceed the differentiation of the expression for the pressure, p, in relation to the variable, z, one obtains ∂p/∂z = m(z), where m(z) = dM(z)/dz. From this, we found that ∂p/∂z = h(r), where h(r) is a function of r only. In particular, h(r) = m(z) is valid only in the case as both functions are constants. This condition leads G = −∂p/∂z to be constant even for regime of non-Newtonian fluids.

The governing equations are made nondimensional by considering typical characteristic quantities of the flow. The reference length and velocity are L_c = R and U_c = Q/πR², where R is the tube radius and Q is the flow rate. We define a typical shear rate and a characteristics pressure gradient as being ${\dot{\gamma}}_c={U}_c/R$ and G_c = μU_c/R², respectively. Since our flow is free of inertia we have used a typical viscous scale for the pressure gradient instead of Bernoulli scale $\rho {U}_c^2/R$. Now, in terms of nondimensional quantities, (3) takes the form:

$$ \frac{1}{\tilde{r}}\frac{d}{d\tilde{r}}\left(\tilde{r}\frac{d\tilde{u}}{d\tilde{r}}\right)+\frac{1}{\tilde{r}}\frac{d}{d\tilde{r}}\left(\frac{}{}\tilde{r}{\tilde{\sigma}}_{rz}^d\right)=-\tilde{G}, $$

(5)

where,

$$ \tilde{r}=\frac{r}{R},\kern1em \tilde{u}=\frac{u}{U_c},\kern1em \tilde{G}=\frac{G}{G_c},\kern1em {\tilde{\sigma}}^d=\frac{\sigma^d}{\mu {\dot{\gamma}}_c}, $$

(6)

Integrating the momentum, (5) one finds out as follows:

$$ \frac{d\tilde{u}}{d\tilde{r}}+{\tilde{\sigma}}_{rz}^d\kern0.5em =\kern0.5em -\frac{\tilde{G}}{2}\tilde{r}.\kern2em \tilde{r}\in \left[0,1\right]. $$

(7)

The differential equation (7) is subjected to the nonslip condition at the tube walls, $\tilde{u}(1)=0$. The same equation results in the classical Hagen-Poiseuille solution in the absence of a drop volume fraction, i.e., ϕ = 0. In this case, $\tilde{G}=8$. Equation 7 and the boundary condition $\tilde{u}(1)=0$ alone do not define a well-posed problem since the nondimensional pressure gradient, $\tilde{G}$, is an unknown quantity as ϕ is not null. In other words, if we impose a pressure gradient through a tube, the fluid will flow at a certain flow rate which defines the mean velocity U_c for a given ϕ. Since the nondimensional flow rate is always the unit for a given ϕ, consequently the following condition must always verified:

$$ \tilde{Q}=2{\int}_0^1\tilde{u}\left(\tilde{r}\right)\tilde{r}d\tilde{r}=1. $$

(8)

Therefore, for ϕ ≠ 0, an iterative method is necessary to find $\tilde{G}$ such the integral equation (8) is satisfied.

Emulsion relative viscosity or intrinsic viscosity

The flow rate can also be used to define the relative or effective viscosity in the flow through a cylindrical tube. In principle, for any type of fluid, we can carry out an experiment for measuring the flow rate as function of the pressure gradient. From the linear part of the plot ∇p versus Q, we can define the emulsion relative viscosity ${\tilde{\mu}}_{\phi }={\mu}_{\phi }/\mu$ by using the equivalent Poiseuille law in terms of nondimensional quantities. This leads to as follows:

$$ {\tilde{\mu}}_{\phi }=\frac{\tilde{G}}{8}, $$

(9)

Again, note that for a Newtonian fluid μ_ϕ/μ = 1, Eq. 9 gives that $\tilde{G}=8$. However, for the case of a non-Newtonian fluid, i.e., ϕ ≠ 0, and it implies $\tilde{G}>8$. In addition, we define the nondimensional wall relative viscosity as follows:

$$ {\tilde{\mu}}_w=\frac{\mu_w}{\mu }=\frac{\tilde{G}}{2\tilde{\dot{\gamma_w}}}. $$

(10)

In Eq. 10, $\tilde{\dot{\gamma_w}}={\left(d\tilde{u}/d\tilde{r}\right)}_{r=1}$ is the nondimensional shear rate in the wall (r = 1). The wall viscosity can be also be also examined as function of the viscosity ratio, λ, and the macroscopic capillary number defined in the next section. Since ${\tilde{\mu}}_w$ depends on the shear rate of the flow, it should be also interpreted as being an apparent viscosity of the emulsion and should be equivalent to the apparent viscosity measured in simple shear flow rheometry, at the same shear rate.

Equations 7 and 8 together with the nonslip boundary condition at the tube wall define a closed nonlinear differential problem for solving the flow as the additional stress tensor due the disperse phase, σ^d, is specified.

Constitutive equation for dilute emulsions

From this point, we suppress the tilde used for nondimensional quantities in order to make the nomenclature as simpler as possible.

Now, in order to solve Eq. 7, we propose a constitutive equation for the stress ${\sigma}_{rz}^d$. This work deals with the flow of dilute emulsions of high viscosity drops. In this case, a constitutive model may be derived from the complete description of the hydrodynamics in the drop scale (e.g., Schowalter et al. 1968; Frankel and Acrivos 1970; Barthés-Biesel and Acrivos 1973b; Rallison 1980; Oliveira and Cunha 2011). A volume average over the drop stress can be used in order to compute the bulk effect of the drop stress contribution. In this way, it is possible to characterize a homogeneous emulsion on the level of the material macroscale (e.g., Landau and Lifshitz 1987; Batchelor 1967, 1970). For a dilute emulsion, we compute the rheology just adding the particle stress contribution (i.e., drop stresslet) on the fluid produced by each isolated drop separately. Therefore, the hydrodynamic interactions between drops are neglected in the present work.

For emulsions of high viscosity ratios undergoing shear flows, the time for drop rotates being much smaller than the time scale for distortion leads to a small deformation condition of the drop. Under this conditions, the theoretical pair of constitutive equations for drop shape and stress adopted for conditions of high viscosity ratio λ are given respectively by Barthés-Biesel and Acrivos (1973a), Rallison (1980), and Frankel and Acrivos (1970)

$$ {\displaystyle \begin{array}{rcl}\frac{d\boldsymbol{A}}{dt}& =& C{a}_p\varrho \boldsymbol{W}\cdot \boldsymbol{A}-C{a}_p\varrho \boldsymbol{A}\cdot \boldsymbol{W}+\frac{5}{\lambda }C{a}_p\varrho \boldsymbol{E}-c\boldsymbol{A},\\ {}& & \end{array}} $$

(11)

$$ \frac{{\boldsymbol{\sigma}}^d}{\phi}\kern0.5em =\kern0.5em \left(5-\frac{25}{2\lambda}\right)\boldsymbol{E}+4{\left(C{a}_p\varrho \right)}^{-1}\boldsymbol{A}+\frac{15}{7}\mathcal{F}\left[\boldsymbol{A},\boldsymbol{E}\right], $$

(12)

where Ca_p is the capillary number defined for the flow through a cylindrical tube, ϱ is the aspect ratio between the radius of the drop and the cross-section, λ is the ratio of the drop and continuous phase viscosities, c = 20/19 is a constant related to the drop relaxation time due the action of the surface tension, ϕ is the drop volume fraction , A is symmetric second-order tensor related to the distortion of the drop from the equilibrium spherical shape, E and W are, respectively, the symmetric and anti-symmetric parts of the nondimensional velocity gradient. Here, the operator $\mathbf{\mathcal{F}}\left[\boldsymbol{A},\boldsymbol{E}\right]=\boldsymbol{A}\cdot \boldsymbol{E}+\boldsymbol{E}\cdot \boldsymbol{A}-2/3\left(\boldsymbol{A}:\boldsymbol{E}\right)\boldsymbol{I}$, where I is the unit tensor.

In general, the capillary number is defined as being $Ca=\mu {\dot{\gamma}}_ca/\sigma$, where μ is the dynamic viscosity of the ambient liquid, ${\dot{\gamma}}_c$ is a characteristic shear rate, a is the drop radius, and σ is the interfacial surface tension coefficient. This nondimensional physical parameter represents the ratio between the surface tension relaxation time, τ_σ ∼ μa/σ, and a characteristic time of the nondisturbed flow, ${\tau}_f\sim 1/{\dot{\gamma}}_c$. In this study, the capillarity makes a similar role of the Deborah number for flows of elastic liquids. However, for an emulsion of high viscosity drops, the choice of the drops viscosity instead of the continuous phase viscosity seems to be more adequate, because, at moderate and high λ, drops rotates much faster than it deforms (Rallison 1980; Oliveira and Cunha 2011). Therefore, we have opted to define the capillary number as being $C{a}_{\lambda }=\lambda \mu {\dot{\gamma}}_ca/\sigma$. In pressure-driven flow through a tube the shear rate is not constant ${\dot{\gamma}}_c={U}_c/R$, but we can relate the local capillary number definition based on the drop radius with a global capillary based on the tube radius by the equation

$$ C{a}_{\lambda }=\frac{\lambda \mu {\dot{\gamma}}_ca}{\sigma }=\frac{\lambda \mu {U}_c}{\sigma}\frac{a}{R}=C{a}_p\varrho . $$

(13)

The aspect ratio ϱ is the geometric parameter linking the macroscopic flow capillary number, Ca_p, to the drops scale capillary, Ca_λ. Actually, ϱ makes the role of the Knudsen number, where a is a characteristic length of the emulsion internal scale and R is a global scale of the flow. In this sense, this analysis is restricted to cases where ϱ ≪ 1, in order to describe the emulsion as a continuous homogeneous non-Newtonian liquid.

In the flow of the emulsion through a tube, the velocity gradient is not constant, and consequently equations (11) and (12) are coupled, and it must to be solved simultaneously. The velocity field for an axisymmetric steady unidirectional laminar flow in cylindrical coordinates (r,z) is given by u = u(r)e_z and, consequently E = (1/2)(du/dr)(e_ze_r + e_re_z) and W = (1/2)(du/dr)(e_ze_r −e_re_z). The steady-state condition is assumed and dA/dt = 0. Under this condition, Eq. 11 reduces simply to a system of algebraic equation in the components of A whose solution is straightforward, resulting as follows:

$$ {A}_{zz}\kern0.5em =\kern0.5em \frac{5\varepsilon }{4\lambda }{\left(\frac{du}{dr}\right)}^2{\left[\varepsilon {\left(\frac{du}{dr}\right)}^2+1\right]}^{-1}\kern2em \mathrm{and} $$

(14)

$$ {A}_{rz}\kern0.5em =\kern0.5em \frac{5\sqrt{\varepsilon }}{4\lambda}\frac{du}{dr}{\left[\varepsilon {\left(\frac{du}{dr}\right)}^2+1\right]}^{-1}, $$

(15)

where ε is the parameter defined as ε = (Ca_pϱ/c)².

Drop deformation

Drop deformation can be quantified for small and moderate distortion using the nondimensional Taylor’s parameter (Taylor 1934)

$$ {D}_T=\frac{L-B}{L+B}, $$

(16)

where L and B are the maximal and the minimal deformation lengths measured in the shear plane, respectively. In the context of the small deformation theory (Rallison 1980; Oliveira and Cunha 2011), the nondimensional drop’s shape equation is given by r = 1 + n ⋅A ⋅n, where n is the nondimensional normal vector point out from the nondeformed drop and r is the nondimensional distance from the drop centroid to a point on its interface. Therefore, the principal radii of deformations are given by r_i = 1 + α_i, where α_i are the eigenvalues of A. In the present case, the distortion tensor A is a rank two, symmetric, and traceless matrix, with both eigenvalues of the same magnitude and opposite signals, i.e., α₁ = α and α₂ = −α, with the following:

$$ \alpha =\sqrt{A_{zz}^2+{A}_{rz}^2}. $$

(17)

Thereafter, it follows that L = 1 + α and B = 1 − α so that D_T = α. Substituting Eqs. 15 and 14 in Eq. 17, one has the following:

$$ {D}_T=\frac{5}{4\lambda }{\left[\frac{\varepsilon {\left( du/ dr\right)}^2}{\varepsilon {\left( du/ dr\right)}^2+1}\right]}^{1/2}. $$

(18)

Equation 18 gives the Taylor deformation along the radial coordinate depending on ε. At the wall (r = 1), one has that $\varepsilon {\left( du/ dr\right)}_{r=1}^2={\left(C{a}_{\lambda }{\dot{\gamma}}_w/c\right)}^2={\left(C{a}_w/c\right)}^2$, where $C{a}_w=C{a}_{\lambda }{\dot{\gamma}}_w$ is the capillary number evaluated using the wall shear rate. Defining the wall Taylor deformation, D_Tw, as being D_T evaluated at the wall and attempting to the definition of Ca_w, one can show as follows:

$$ {D}_{Tw}=\frac{5}{4\lambda }{\left(\frac{C{a}_w^2}{C{a}_w^2+{c}^2}\right)}^{1/2}. $$

(19)

Equation 19 is used to compute the maximal deformation reached by a drop in a dilute high viscosity emulsion, of monodisperse drops, flowing through a circular tube, for arbitrary Ca_w. It is worthy to mention that Eq. 19 predicts the same behavior for drop deformation that is predicted by Oliveira and Cunha (2011), for simple shear flow. The expression for D_Tw is quite consistent with Taylor theory (Taylor 1934) for small capillary numbers. In that case, as Ca_w ≪ 1, one can use series expansion to show that, as Ca_w → 0,

$$ {D}_{Tw}=\frac{19}{16\lambda }C{a}_w+\mathcal{O}\left(C{a}_w^2\right), $$

(20)

recovering the Taylor deformation law, toked for high viscosity ratios.¹ On the other hand, for ε →∞,

$$ {D}_{Tw}\to \frac{5}{4\lambda }, $$

(21)

characterizing the constant shape of high viscosity ratio drops observed for high capillary number (Oliveira and Cunha 2011). Series expansion can also be employed to produce asymptotic law for high capillary numbers, such that, in the limit of Ca_w ≫ 1 (but not infinity),

$$ {D}_{Tw}=\frac{5}{4\lambda}\left(1-\frac{c^2}{2C{a}_w^2}\right)+\mathcal{O}\left(C{a}_w^{-4}\right). $$

(22)

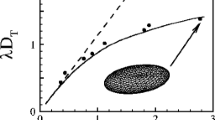
Figure 1 shows the Taylor deformation at the wall as function of the capillary number evaluated at the wall. The general theory given by Eq. 19 is represented by the solid line. For low capillary numbers, we include the Taylor limit for deformation (Eq. 20), represented by a double dot-dashed line, both in the semilog scale (in the main chart) as well in linear scale (in the insert). A close agreement between the arbitrary capillary number theory and Taylor limit is observed for Ca_w < 0.1. For high capillary numbers, the single dot-dashed line shows the asymptotic limit given by Eq. 22, which is almost coincident to Eq. 19 for Ca_w > 1. The dashed line marks the deformation upper limit, given by Eq. 21. Drop orientation could be determined computing the angle between the eigenvector associated with the larger eigenvalue of A and the unitary vector parallel to the axial direction. In this way, the drop orientation is also a function of the capillary number (Rallison 1984), such that, at low shear rates (i.e., in Taylor regime), the drop orientation is equal to π/4 and, for high shear rates, drops aligns to the axial direction.

Fig. 1

Drop Taylor’s deformation at wall. Solid line: Eq.(19); dashed line: Eq.(21) giving the $\lambda \to \infty$ limit; double dot-dashed line: small capillary limit, Eq.(20); single dot-dashed line: high capillary theory, Eq.(22). The insert shows Taylor’s theory for the small capillary number departing from Eq.(19) in linear scale chart

Stress contribution from disperse phase

By substituting the components of tensor A (15) and (14) in the stress tensor given by Eq. 12, one obtains the following:

$$ {\sigma}_{rz}^d=\phi \left(\frac{5}{2}-\frac{25}{4\lambda}\right)\frac{du}{dr}+\frac{5\phi }{c\lambda}{\left[\varepsilon {\left(\frac{du}{dr}\right)}^2+1\right]}^{-1}. $$

(23)

Now, substituting Eq. 23 into to Eq. 7, we have as follows:

$$ {\mu}_T\frac{du}{dr}+\varepsilon \left[{\mu}_B{\left(\frac{du}{dr}\right)}^3+\frac{G}{2}r{\left(\frac{du}{dr}\right)}^2\right]=-\frac{G}{2}r,\kern1.00em $$

(24)

where r ∈ [0, 1]. Additionally to Eq. 24, the boundary condition u(1) = 0 must be kept. The parameters μ_T and μ_B appearing in this solution are the emulsion viscosities at the limit of low and high shear rates, respectively. Actually, it corresponds to Taylor (Taylor 1932, 1934) and blob viscosities, respectively, such as we have already defined in our previous publication on dilute emulsion with high viscosity ratio undergoing steady and oscillatory shear flow (Oliveira and Cunha 2011). The expressions we have found are

$$ {\mu}_T=1+\phi \left(\frac{5}{2}-\frac{3}{2\lambda}\right)\kern1em \mathrm{and}\kern1em {\mu}_B=1+\phi \left(\frac{5}{2}-\frac{25}{4\lambda}\right). $$

(25)

Equation 24 is a first-order, ordinary nonlinear differential equation. For ϕ = 0, we have μ_T = μ_B = 1, and Eq. 24 can be factored and written in the form

$$ \left[\varepsilon {\left(\frac{du}{dr}\right)}^2+1\right]\left[\frac{du}{dr}+\frac{G}{2}r\right]=0. $$

(26)

Since ε ≥ 0, the first term on the left-hand side of Eq. 26 is always positive. This condition implies that du/dr + (G/2)r = 0, that leads to classical Hagen-Poiseuille flow for the Newtonian ambient fluid. On the other hand, for ϕ ≠ 0, the limit of low shear rate as ε → 0, Eq. 24 reduces to μ_Tdu/dr + (G/2)r = 0, and the emulsion behaves like an equivalent Newtonian fluid with an effective viscosity μ_T(ϕ). At the limit of very high shear rates as ε →∞, the term inside the brackets in Eq. 24 dominates and Eq. 24 takes the form μ_Bdu/dr + (G/2)r = 0. In this case, the emulsion behaves like a Boger liquid with effective viscosity μ_B(ϕ).

Asymptotic solutions

In summary, the equation governing the axisymmetric flow of a dilute emulsion of high viscosity drop is given by the following:

$$ \left\{\begin{array}{c}{\mu}_T\frac{du}{dr}+\varepsilon \left[\kern-0.2em {\mu}_B{\left(\frac{du}{dr}\right)}^3+\frac{G}{2}r{\left(\frac{du}{dr}\right)}^2\right]=-\frac{G}{2}r,\kern0.5em r\in \left[0,1\right],\\ {}\kern0.60em u(1)=0,\\ {}\kern0.60em Q(G)=1.\end{array}\right. $$

(27)

Asymptotic solution for ε ≪ 1: low shear rates

In Eq. 27, the physical parameter ε can assume small values as Ca_p ≪ 1. Under condition of ε ≪ 1 (Hinch 1991), we propose a regular asymptotic solution $\mathcal{O}\left({\varepsilon}^2\right)$ for the axial velocity component in the form as follows:

$$ u(r)={u}_0(r)+\varepsilon {u}_1(r)+{\varepsilon}^2{u}_2(r)+\mathcal{O}\left({\varepsilon}^3\right). $$

(28)

Now substituting u given by Eq. 27 into Eq. 28 and collecting terms of the same order in ε, we obtain the governing differential equations associated with $\mathcal{O}(1)$, $\mathcal{O}\left(\varepsilon \right)$, $\mathcal{O}\left({\varepsilon}^2\right)$ of the approximated solution, respectively,

$$ \kern1.00em {\mu}_T\frac{d{u}_0}{dr}+\frac{G}{2}r=0, $$

(29)

$$ \kern1.00em {\mu}_T\frac{d{u}_1}{dr}+{\mu}_B{\left(\frac{d{u}_0}{dr}\right)}^3+\frac{G}{2}r{\left(\frac{d{u}_0}{dr}\right)}^2=0, $$

(30)

$$ {\displaystyle \begin{array}{rcl}& & {\mu}_T\frac{d{u}_2}{dr}+3{\mu}_B{\left(\frac{d{u}_0}{dr}\right)}^2\frac{d{u}_1}{dr}+\frac{G}{2}r\left(\frac{d{u}_0}{dr}\frac{d{u}_1}{dr}\right)=0.\\ {}& & \end{array}} $$

(31)

The ordinary differential equations given by the Eqs. 29–31 are solved with the associated boundary conditions u₀(1) = u₁(1) = u₂(1) = 0. After some algebraic manipulations, we found the following approximated velocity profile at $\mathcal{O}\left({\varepsilon}^2\right)$ as follows:

$$ {\displaystyle \begin{array}{rcl}u(r)& =& {f}_1\left(\lambda \right)\frac{G}{2}\left(1-{r}^2\right)+\varepsilon {f}_2\left(\lambda \right)\frac{G^3}{32}\left(1-{r}^4\right)\\ {}& & +{\varepsilon}^2{f}_3\left(\lambda \right)\frac{G^5}{192}\left(1-{r}^6\right)+\mathcal{O}\left({\varepsilon}^3\right),\end{array}} $$

(32)

where,

$$ {\displaystyle \begin{array}{rcl}& & {f}_1\left(\lambda \right)=\frac{1}{\mu_T},\kern1em {f}_2\left(\lambda \right)=\frac{\mu_T-{\mu}_B}{\mu_T^4}\kern1em \mathrm{and}\\ {}& & {f}_3\left(\lambda \right)=\frac{\left({\mu}_T-{\mu}_B\right)\left(2{\mu}_T-3{\mu}_B\right)}{\mu_T^7}.\end{array}} $$

(33)

Since the nondimensional pressure gradient G is an unknown quantity and consequently part of the solution, Eq. 32 alone is not sufficient to fully describe the radial velocity profile. In addition, the integral relation (8) for the nondimensional flow rate must be satisfied for a given G, i.e. Q(G) = 1. Therefore, for the velocity given in Eq. 32 we have:

$$ {f}_1\left(\lambda \right)\frac{G}{8}+{f}_2\left(\lambda \right)\frac{G^3}{48}\varepsilon +{f}_3\left(\lambda \right)\frac{G^5}{256}{\varepsilon}^2+\mathcal{O}\left({\varepsilon}^3\right)=1. $$

(34)

We can rewrite (34) in terms of the nondimensional emulsion relative viscosity defined in Eq. 9 in the following form

$$ {f}_1\left(\lambda \right){\mu}_{\phi }+\frac{32}{3}{f}_2\left(\lambda \right)\varepsilon {\mu}_{\phi}^3+128{f}_3\left(\lambda \right){\varepsilon}^2{\mu}_{\phi}^5+\mathcal{O}\left({\varepsilon}^3\right)=1. $$

(35)

Equation 35 is a polynomial of fifth order with respect to μ_ϕ. The coefficients of the polynomial are rational functions of λ and ε. For exploring the ε ≪ 1 limit, we can use the method of successive substitution in order to obtain solution for the Eq. 35. Based on the expression of Eq. 35, we propose the following recursive formula

$$ {\mu}_{\phi, n}=\frac{1}{f_1\left(\lambda \right)}\kern0.3em \left(\kern0.3em 1-\frac{32}{3}\kern0.3em {f}_2\left(\lambda \right)\varepsilon {\mu}_{\phi, \left(n-1\right)}^3-128{f}_3\left(\lambda \right){\varepsilon}^2{\mu}_{\phi, \left(n-1\right)}^5\kern0.60em \right), $$

(36)

where n = 1,2,… and μ_ϕ,0 is the emulsion viscosity for ε = 0. Preserving the order of the approximation considered in the method of our regular asymptotic expansion (36) can be used for n = 1 and 2. Therefore, we obtain

$$ {\displaystyle \begin{array}{rcl}{\mu}_{\phi }& =& \frac{1}{f_1\left(\lambda \right)}+\frac{32{f}_2\left(\lambda \right)}{3{f}_1^4\left(\lambda \right)}\varepsilon +\kern0.3em \left(\kern0.3em \frac{1024{f}_2^2\left(\lambda \right)}{3{f}_1^7\left(\lambda \right)}-\frac{128{f}_3\left(\lambda \right)}{f_1^6\left(\lambda \right)}\kern0.3em \right){\varepsilon}^2\\ {}& & +\mathcal{O}\left({\varepsilon}^3\right).\end{array}} $$

(37)

Now substituting the expressions for f₁(λ), f₂(λ) and f₃(λ) give in Eq. 33, we obtain the following expression $\mathcal{O}\left(\phi, {\varepsilon}^2\right)$ for the emulsion relative viscosity as follows:

$$ {\mu}_{\phi }={\mu}_T-\frac{\phi }{\lambda}\left[\frac{152}{3}\varepsilon +608{\varepsilon}^2\right]+\mathcal{O}\left({\varepsilon}^3\right). $$

(38)

The expression of the Eq. 38 already indicates the existence of a pseudo-plastic behavior of the emulsion even at low shear rate, once for ε → 0, μ_ϕ → μ_T.

Asymptotic solution for ε ≫ 1: high shear rate

In order to calculate an expression of the relative viscosity μ_ϕ for high ε, i.e., Ca_p ≫ 1, we divide (24) by ε and make the following change of variable 1/ε = ε^′. This procedure allows us to rewrite the governing equation given by the Eq. 27 in the nondimensional form:

$$ {\mu}_B\frac{du}{dr}+\frac{G}{2}r=-{\varepsilon}^{\prime}\left[{\mu}_T\frac{du}{dr}+\frac{G}{2}r\right]{\left(\frac{du}{dr}\right)}^{-2}. $$

(39)

For high shear rates (ε^′→ 0), Eq. 39 recovers the Boger fluid regime of a constant viscosity, i.e., μ_ϕ → μ_B. In this limit, ε^′≪ 1, we also propose an recursive equation in order to obtain an approximate solution for Eq. 39 by using the successive substitution method. We have as follows:

$$ {\displaystyle \begin{array}{rcl}{\left(\frac{du}{dr}\right)}_n& =& -\frac{G}{2{\mu}_B}r\\ {}& & -\frac{\varepsilon^{\prime }}{\mu_B}\left[{\mu}_T{\left(\frac{du}{dr}\right)}_{n-1}+\frac{G}{2}r\right]{\left(\frac{du}{dr}\right)}_{n-1}^{-2},\end{array}} $$

(40)

as n = 1, the first-order approximation is given by the following:

$$ \frac{du}{dr}=-\frac{G}{2{\mu}_B}r+\frac{2\left({\mu}_T-{\mu}_B\right)}{Gr}{\varepsilon}^{\prime }+\mathcal{O}\left({\varepsilon}^{\prime 2}\right). $$

(41)

The velocity profile at this limit is calculated by integrating Eq. 41 considering the boundary condition u(1) = 0:

$$ u(r)=\frac{G}{4{\mu}_B}\left(1-{r}^2\right)+\frac{2\left({\mu}_T-{\mu}_B\right)}{G}\ln (r){\varepsilon}^{\prime }+\mathcal{O}\left({\varepsilon}^{\prime 2}\right). $$

(42)

Now, we use the same procedure that has been applied to the limit ε ≪ 1 with Q − 1 = 0 and G = 8μ_ϕ. This leads to the following:

$$ {f}_4\left(\lambda \right){\mu}_{\phi }+\frac{f_5\left(\lambda \right)}{8{\mu}_{\phi }}{\varepsilon}^{\prime }+\mathcal{O}\left({\varepsilon}^{\prime 2}\right)=1, $$

(43)

where f₄(λ) = 1/μ_B and f₅(λ) = (μ_B − μ_T). Equation 43 can be written as a second-order polynomial whose positive root is obtained in terms of $\sqrt{\varepsilon^{\prime }}$. As the solution of the interest is $\mathcal{O}\left({\varepsilon}^{\prime}\right)$, we expand the results in a MacLaurin series in ε^′ and one collect the first two terms. Through this procedure, we obtain ${\mu}_{\phi }={\mu}_B+\left[\left({\mu}_T-{\mu}_B\right)/8\right]{\varepsilon}^{\prime }+\mathcal{O}\left({\varepsilon}^{\prime 2}\right)$, that corresponds to the following:

$$ {\mu}_{\phi }={\mu}_B+\frac{19\phi }{32\lambda }{\varepsilon}^{-1}+\mathcal{O}\left({\varepsilon}^{-2}\right). $$

(44)

A numerical solution of the governing equation for arbitrary ε

For emulsion flow regimes out of the range where the asymptotic solutions presented in the previous section are not valid, i.e., as ε ∼ 1 (or even arbitrary), a numerical procedure is proposed in order to solve the governing equation and the boundary condition given in Eq. 27. Hence, the emulsion relative viscosity is obtained using the relation μ_ϕ = G/8. For the case, ϕ = 0, the solution is given by the classical Poiseuille flow with G = 8 and consequently, μ_ϕ = 1.

Instead of working with the governing equation in the form of the Eq. 27, Eq. 24 is replaced by the Eq. 7. In this way, the final numerical procedure might be easily changed to consider different constitutive equations or even material data provided numerically. The numerical integration starts considering an initial shear rate profile of du/dr for given G and ε. Typically, we take as initial guess the one given by the parabolic velocity profile of an equivalent Newtonian emulsion with Taylor’s viscosity μ_T (Taylor 1932). Actually, it is equivalent to make ε = 0 so that Eq. 24 reduces to du/dr = −Gr/(2μ_T). The radial coordinate of the unidirectional flow was divided into N control points, following a standard finite differences approach.

Now, considering the Eq. 7 and also that G and r are fixed, we define a function $\mathbf{\mathcal{M}}\left( du/ dr\right)$ as follows:

$$ \mathbf{\mathcal{M}}\left( du/ dr\right)=\frac{du}{dr}+{\sigma}_{rz}^d+\frac{G}{2}r. $$

(45)

We have used a Newton-Raphson procedure in order to find root of Eq. 45 for each control point over the radial direction. In this procedure, we treat $\mathcal{M} \left( du/ dr\right)=0$ as an algebraic equation in the variable du/dr, whose the solution allows us to rewrite the original governing equation in the form:

$$ \left\{\begin{array}{c}\frac{du}{dr}\left({r}_i\right)=F\left({r}_i\right),\kern2em i=1\dots N,\\ {}u\left({r}_N\right)=0,\end{array}\right. $$

(46)

where F(r_i) is the result of the Newton-Raphson computation at each control point r_i. Once having the problem in the form of Eq. 46, a second-order finite differences method is used to get the algebraic differences equation given by the following:

$$ {u}_{i-1}-{u}_{i+1}=-2\Delta rF\left({r}_i\right), $$

(47)

where Δr = r_i+ 1 − r_i is the constant radial incremental step. Equation 47 leads to a three-diagonal linear system readily solved by a TDMA algorithm. Then, the flow rate is computed using standard trapezoidal rule applied to the integral in Eq. 8.

From a global perspective, the numerical procedure is for a given parameter ε, taking G as an input, the Newton-Raphson method finds the shear rate as function of r using Eq. 45; the finite differences procedure determines the velocity profile by solving linear equations system (47); and the trapezoidal rule computes the flow rate. Symbolically, that procedure might be taken as a real function $\mathcal{I}:\mathbb{R}\to \mathbb{R}$, whose the input is the pressure gradient G and the output is the flow rate Q, i.e., $\mathbf{\mathcal{I}}(G)=Q$. Finally, we have used Newton-Raphson iterations to vary G enforcing the integral constraint Q = 1.

The whole process is computationally cheap such that small tolerances and refined grids can be handled by conventional desktop computers. In our simulations, we have used a 10⁶ points in the grid along radius and tolerances about 10^− 10 for both Newton-Raphson procedures.

Figure 2 shows a comparison of the numerical solution and the asymptotic solution for a dilute emulsion of high viscosity ratio. The asymptotic solution is shown for the limits at low and high ε. It is seen two plateaus of constant relative viscosity at low and high shear rates. Numerical and the asymptotic solutions coincide for both asymptotic limits. In particular, for moderate shear rates (i.e., ε ∼ 1), the numerical integration predicts typical shear-thinning behavior of the high viscosity ratio emulsion. Our asymptotic solutions indeed break down in this shear-thinning region of the relative viscosity since drops presents a significant deformation by the quadratic shear existing in a pressure-driven flow through a circular tube.

Fig. 2

Emulsion relative viscosity as function of ε. Solid line: numerical solution; dashed lines: asymptotic solutions developed here. The inserts show more details of the asymptotic solutions $\mathcal{O}\left(\varepsilon \right)$, $\mathcal{O}\left({\varepsilon}^2\right)$ (ε ≪ 1) and $\mathcal{O}\left(1/\varepsilon \right)$ (ε ≫ 1)

A theory for a dilute emulsion of high viscosity drops undergoing arbitrary shear rates in a cylindrical tube flow

In the limit case of a dilute emulsion of high viscosity ratio undergoing a pressure-driven flow, the velocity profile of the flow may be decomposed in the form u(r) = u^∞(r) + u^′(r), where u^∞(r) is the quadratic part of u(r) proportional to r² and, u^′(r) the nonlinear contribution of the drop phase. In this asymptotic limit, we assume that the nonlinear contribution is much smaller than the leader order quadratic flow, i.e., ∣u^′∣/∣u^∞∣≪ 1. In this way, we make a simple approximation of the local capillarity number using the well-known Poiseuille law for an equivalent fluid with viscosity μ_B² in order to compute the shear rate ∣du/dr∣. This assumption implies that the local capillarity can be taken approximately as being Ca_ℓ ≈ 4Ca_λr. In addition, considering the ε definition, Eq. 24 can be rewritten in the following form:

$$ {\mu}_T\frac{du}{dr}+\frac{1}{c^2}{\left(C{a}_p\varrho \frac{du}{dr}\right)}^2\left[{\mu}_B\frac{du}{dr}+\frac{G}{2}r\right]=-\frac{G}{2}r. $$

Now, applying the approximation Ca_ℓ ≈ 4Ca_λr, we obtain that ${\left(C{a}_p\varrho du/ dr\right)}^2=C{a}_{\ell}^2=16C{a}_{\lambda}^2{r}^2$, and therefore:

$$ \frac{du}{dr}=-\frac{G}{2}\left(r+\frac{16C{a}_{\lambda}^2{r}^3}{c^2}\right){\left({\mu}_T+\frac{16{\mu}_BC{a}_{\lambda}^2{r}^2}{c^2}\right)}^{-1}. $$

(48)

Equation 48 is a linear first-order differential with a straightforward solution. Applying the nonslip boundary condition u(1) = 0, the velocity profile is determined and using the nondimensional flow rate continuity constraint Q − 1 = 0, we finally derive a more general expression for the relative viscosity μ_ϕ of a dilute high viscosity ratio emulsion undergoing a pressure-driven for arbitrary capillary numbers Ca_λ. After few algebraic manipulations, we find an expression for the emulsion relative viscosity only in terms of ϕ, Ca_λ and λ resulting in the following:

$$ {\displaystyle \begin{array}{rcl}{\mu}_{\phi }& =& {\mu}_BC{a}_{\lambda}^4\left[C{a}_{\lambda}^4-\frac{c^2\left({\mu}_T-{\mu}_B\right)}{2^3{\mu}_B}C{a}_{\lambda}^2\right.\\ {}& & +\kern1em {\left.\frac{\mu_T\left({\mu}_T-{\mu}_B\right){c}^4}{2^7{\mu}_B}\ln \left(\frac{16{\mu}_B}{c^2{\mu}_T}C{a}_{\lambda}^2+1\right)\right]}^{-1}.\end{array}} $$

(49)

Of more interest, however, is the expression in the limit of high viscosity dilute emulsion. So, we must retain only the order $\mathcal{O}\left(\phi /\lambda \right)$ of the Eq. 49 as considering the theoretical limit of a high λ dilute emulsion. Therefore, performing a Taylor expansion of Eq. 49 in the variable ϕ/λ, and truncating at $\mathcal{O}\left(\phi /\lambda \right)$, we obtain the following:

$$ {\mu}_{\phi }={\mu}_B+\frac{25}{38}\left[C{a}_{\lambda}^2-\frac{c^2}{16}\ln \left(\frac{16}{c^2}C{a}_{\lambda}^2+1\right)\right]\frac{\phi }{\lambda C{a}_{\lambda}^4}, $$

(50)

that represents the approximation $\mathcal{O}\left(\phi /\lambda \right)$ at arbitrary capillary numbers for the Eq. 49.

Now, we verify the high and low shear rate limits of the equation (50). Firstly, taking the limit of Ca_λ → ∞, one may see as follows:

$$ \frac{25}{38}\left[C{a}_{\lambda}^2-\frac{c^2}{16}\ln \left(\frac{16}{c^2}C{a}_{\lambda}^2+1\right)\right]\frac{\phi }{\lambda C{a}_{\lambda}^4}\to 0, $$

and consequently μ_ϕ → μ_B as Ca_λ →∞, as expected. On the other hand, at very low shear rates as Ca_λ → 0, the second contribution on the right-hand side equation of the Eq. 50 reduces to the following:

$$ \frac{25}{38}\left[C{a}_{\lambda}^2-\frac{c^2}{16}\ln \left(\frac{16}{c^2}C{a}_{\lambda}^2+1\right)\right]\frac{\phi }{\lambda C{a}_{\lambda}^4}\to \frac{19\phi }{4\lambda }, $$

and we found that as Ca_λ → 0, μ_ϕ → μ_T = 1 + ϕ(5/2 − 3/(2λ)), that corresponds to the Taylor viscosity at the limit of very high viscosity ratio, as defined before (Taylor 1932, 1934). We emphasize that Eq. 50 is one important theoretical result of this paper which predicts for arbitrary capillary numbers (or shear rates) the relative viscosity of a dilute emulsion of high viscosity drops undergoing a pressure-driven laminar flow throughout a tube of circular cross-section.

Comparison between theoretical prediction and numerical integration

The main plot of Fig. 3 shows a shear-thinning behavior of the relative viscosity, of a dilute emulsion of high viscosity drops in pressure-driven flow, as considered in this work. The emulsion relative viscosity decreases with increasing Ca_λ, ranging from 0.01 to 100 . This occurs because the increase in drop deformation produces a decrease in the global energy dissipation of the flow as compared with the condition of lower Ca_λ, leading to a diminution of the emulsion relative viscosity. This shear-thinning behavior of emulsions was previously reported in the context of boundary integral numerical simulations for emulsions undergoing linear simple shear flow (e.g., Kennedy et al. 1994; Loewenberg and Hinch 1996; Cunha and Loewenberg 2003; Oliveira and Cunha 2015). We can see also from this plot the asymptotic limits of low and high nondimensional shear rates corresponding to the plateaus of constant relative viscosities. A very good agreement between the numerical solution for the flow governed by the Eq. 27 and the theoretical prediction given by Eq. 50 can be observed. Actually, the maximum relative deviation from the numerical and analytic results was less than 0.05%, for Ca_λ ≈ 0.2.

Fig. 3

Emulsion viscosity as function of the capillary number. Main plot: solid line is the relative viscosity calculated by Eq.(50); circles are computed numerically as described in this section; in the main plot Ca_λ = ε^1/2. Insert: solid line is the emulsion viscosity undergoing simple shear flow as predicted by the $\mathcal{O}\left(\phi /\lambda \right)$ asymptotic theory (Oliveira and Cunha 2015); diamonds is the wall relative viscosity as defined in Eq.(10), computed using numerical simulation; in the insert $C{a}_w=\lambda \mu \dot{\gamma_w}a/\sigma$, where $\dot{\gamma_w}={\left( du/ dr\right)}_{r=1}$

The symbols in the insert of Fig. 3 show the behavior of the wall relative viscosity as defined in Eq. 10, as function of the capillary number evaluated at the wall, given by $C{a}_w=\lambda \mu \dot{\gamma_w}a/\sigma$. The solid line represents the emulsion viscosity undergoing simple shear flow as predicted by a $\mathcal{O}\left(\phi /\lambda \right)$ asymptotic theory (Oliveira and Cunha 2015)³, at the same shear rate. In the present work, μ_w is calculated considering the definition given by Eq. 10 and numerically computing du/dr(1), as described in this section. The wall relative viscosity in pressure-driven flow is a rheological meaningful quantity comparable to the viscosity measured in uniform shear rate flows like simple shear. In fact, a very good agreement between numerical predictions and simple shear relative viscosity is achieved, such that the maximum relative deviation between this two measures is less than 0.1%, happening again for Ca_w ≈ 1, where the shear thinning is stronger. In the constant viscosity plateaus, at low and high capillary numbers, the difference between μ_ϕ and μ_w vanishes.

A distinctive difference between the plots in Fig. 3 is a shift in the shear thinning. While μ_ϕ shear-thinning practically stops for Ca_λ ≈ 1, it is very intense for μ_w for Ca_w ≈ 1. Now, we argue that this discrepancy can be attributed to the difference in the capillary number experiment by the drop. We can show that for a given Ca_λ in the main plot of Fig. 3 the local shear rate (and consequently the local capillary number) experienced by a drop is stronger for r > 1/4, resulting in a stronger viscosity decreasing. Actually, even if Ca_λ = Ca_p, the mean local capillary number experienced by the fluid in the cross-section of a tube is larger than Ca_λ. The spatial average of the local capillary in a tube cross-section can be computed as follows:

$$ {Ca}_{\ell }=\frac{\lambda \mu a}{\sigma}\frac{1}{\pi {R}^2}{\int}_0^R\frac{du}{dr}2\pi rdr, $$

(51)

where du/dr = 4U_cr/R². Using du/dr = 4U_cr/R² into the Eq. 51, we find the following:

$$ {Ca}_{\ell }=\frac{8}{3}\frac{\lambda \mu a}{\sigma}\frac{U}{R}=\frac{8}{3}C{a}_{\lambda }. $$

(52)

Consequently, Ca_ℓ ∼ 4rCa_λ and Ca_ℓ > Ca_λ for r > 1/4. Therefore, along 3/4 of the tube radius, the local capillary is larger than it would be in simple shear flow at Ca_λ.

Boundary integral method: drop surface velocity and drop stress contribution

One of the main goals of the present work is to study the pressure-driven flow of an emulsion of moderate viscosity ratio, λ, such that asymptotic theory as described in “Constitutive equation for dilute emulsions” is no longer valid. For this end, a boundary integral method (BIM) implementation has been used in order to generate constitutive data on dilute emulsions for several viscosity ratios in the range 2 ≤ λ ≤ 20. Actually, the numerical method is not the focus of the present paper and only a brief description will be presented here, for the sake of completeness. For a detailed description of the boundary integral method applied to emulsion flows, see Bazhlekov et al. 2004; Oliveira and Cunha 2015 and Siqueira et al. 2017, 2018.

We have used a boundary integral representation of the velocity field at drop interface for an isolated drop in the free space, valid for dilute emulsion flows. The nondimensional fluid velocity at the drop surface u^s(x_o) is given by the following:

$$ {\boldsymbol{u}}^s\left({\boldsymbol{x}}_o\right)-\frac{\lambda -1}{4\pi \left(\lambda +1\right)}\underset{S}{\int}\boldsymbol{u}\left(\boldsymbol{x}-{\boldsymbol{x}}_o\right)\cdot \mathbf{\mathcal{T}}\left(\boldsymbol{x}-{\boldsymbol{x}}_o\right)\cdot \boldsymbol{n}\left(\boldsymbol{x}\right) dS\left(\boldsymbol{x}\right)=\mathbf{\mathcal{L}}\left({\boldsymbol{x}}_o\right),\kern1.00em $$

(53)

where,

$$ {\displaystyle \begin{array}{rcl}\mathbf{\mathcal{L}}\left({\boldsymbol{x}}_o\right)& =& \frac{2C{a}_{\lambda }}{\lambda \left(\lambda +1\right)}{\boldsymbol{u}}^{\infty}\left({\boldsymbol{x}}_o\right)\\ {}& & -\frac{1}{4\pi \left(\lambda +1\right)}\underset{S}{\int}\Delta \boldsymbol{f}\left(\boldsymbol{x}\right)\cdot \mathbf{\mathcal{G}}\left(\boldsymbol{x}-{\boldsymbol{x}}_o\right) dS\left(\boldsymbol{x}\right).\end{array}} $$

(54)

In Eqs. 53 and 54, x_o is a point on the drop surface S, n is the exterior normal vector related to S, and u^∞ represents the nondisturbed velocity field, far from the drop. In this work, u^∞ is always a simple shear flow, with origin in the center of the nondeformed drop. The nondimensional traction jump across the surface Δf considers a clean drop (i.e., the absence of Marangonni effects) with a homogeneous interfacial tension coefficient. Under this condition, Δf = κn, where κ = ∇⋅n is the nondimensional local mean curvature. The tensorial kernel functions $\mathbf{\mathcal{G}}$ and $\mathbf{\mathcal{T}}$ are, respectively, the stokeslet and stresslet in the free space and this Green functions are given by the following:

$$ \mathbf{\mathcal{G}}\left(\boldsymbol{x}-{\boldsymbol{x}}_o\right)=\frac{\boldsymbol{I}}{r}+\frac{\left(\boldsymbol{x}-{\boldsymbol{x}}_o\right)\left(\boldsymbol{x}-{\boldsymbol{x}}_o\right)}{r^3} $$

(55)

and

$$ \mathbf{\mathcal{T}}\left(\boldsymbol{x}-{\boldsymbol{x}}_o\right)=-6\frac{\left(\boldsymbol{x}-{\boldsymbol{x}}_o\right)\left(\boldsymbol{x}-{\boldsymbol{x}}_o\right)\left(\boldsymbol{x}-{\boldsymbol{x}}_o\right)}{r^5}, $$

(56)

where I is the unit tensor and $r=\sqrt{\parallel \boldsymbol{x}-{\boldsymbol{x}}_o\parallel }$. The drop surface was discretized using a mesh of planar triangular faces. Nonplanar control surfaces were defined around the nodes by connecting neighbor triangles around. The Stokes’ theorem was used to compute n and κ for each grid node. The singular integrals in Eqs. 53 and 54 were transformed to regular contour integrals by assuming constant curvature in the surface containing a pole x_o (Bazhlekov et al. 2004; Siqueira et al. 2017) and no numerical singularity subtraction is needed. A second-order trapezoidal rule based on two-points Newton-Cotes formula was used to compute the resulting regular contour integrals. For λ ≠ 1, Eq. 53 is a second kind Fredholm equation, requiring iterative solution. The existence of eigensolutions of Eq. 53, related to rigid body motion and isotropic expansion, severely reduces the convergence rate of iterative methods. Wielandt deflation was employed to purge that eigensolutions, allowing fast convergence of Gauss-Seidel iterations. Once velocity has been computed, drop shape can be updated by moving grid nodes as material particles traveling with velocity u^s. In other words, the equation dx_o/dt = u^s(x_o) is evolved in time from a initial shape. A second-order Runge-Kutta method, equipped with adaptive time-step and nontopological mesh relaxation procedure, was used to this end (Siqueira et al. 2017).

The stress contribution from the disperse phase in a dilute emulsion is given by Batchelor (1970) as follows:

$$ {\boldsymbol{\sigma}}^d=\frac{3\phi }{4\pi}\underset{S}{\int}\left[\boldsymbol{x}\Delta \boldsymbol{f}+\left(\lambda -1\right)\left(\boldsymbol{un}+\boldsymbol{nu}\right)\right] dS. $$

(57)

Trapezoidal surface integration was employed to compute the integral in Eq. 57. For each simulation, three different meshes, progressively finer (1002, 1212, and 1442 nodes respectively), were used in order to allow extrapolation to mesh-independent results, as described in Siqueira et al. (2017).

Stress data tabulation

A new set of numerical simulation has also been performed using BIM as described in the section “Boundary integralmethod: drop surface velocity and drop stress contribution.” An important innovation has also been that our boundary numerical procedure may compute the solution of the nonlinear emulsion undergoing pressure-driven flow by using an additional stress tensor, σ^d, provided from a table of stress data. In this case, instead of applying the theoretical expression restrict to very high viscosity ratios λ given by Eq. 23, a table of ${\sigma}_{rz}^d$ as function of the shear rate has been used in order to provide disperse stress contribution in the range 2 ≤ λ ≤ 20. This is done assuming that in the neighborhood of a small droplet such that a/R ≪ 1, the local parabolic flow may be approximated by a local simple shear. In terms of nondimensional quantities, a local capillary number Ca_ℓ can be defined for each radial position of the flow around an isolated droplet as follows:

$$ C{a}_{\ell }=\frac{\lambda \mu a\dot{\gamma}(r)}{\sigma }. $$

(58)

where $\dot{\gamma}(r)$ is the shear rate evaluated at the drop’s centroid. The dimensional local shear rate is given by $\dot{\gamma}(r)=\left({U}_c/R\right)\mid du(r)/ dr\mid$, and Eq. 58 leads to the following:

$$ C{a}_{\ell }=C{a}_p\varrho \left|\frac{du(r)}{dr}\right|. $$

(59)

Thus, if Ca_p and ϱ are known parameters, a table of numerical data for ${\sigma}_{12}^d$ versus Ca_λ can be generated under simple shear flow condition and directly accessed by making Ca_λ = Ca_ℓ. In another words, Eq. 59 gives the ratio between the capillary number in a simple shear and the equivalent parameter in the pressure-driven flow at the same viscosity ratio.

In our simulations, we have generated σ^d data for capillary numbers in the interval Ca_λ ∈ [10^− 2, 10²] using 250 points logarithmically spaced. The tabulated stress is then used in the numerical procedure described in the section “A numerical solution of the governing equationfor arbitrary ε” by replacing the algebraic expression for ${\sigma}_{rz}^d$ in Eq. 45 by a linear interpolation procedure in the σ^d table. In order to check the validity of our method, we have tested the tabulation procedure by generating a σ^d table with 250 points in the same capillary number range but using the asymptotic theory in the form of Eq. 23. Then, we have compared results from stress tabulation method and the conventional numerical solution, observing that the maximal deviation from μ_ϕ results were less than 0.05%.

The real motivation behind this numerical approach is the possibility of using tabulated stress data, generated by numerical simulations (e.g., BIM) or even by experimental data to perform more robust simulations of pressure-driven flow of emulsions. The focus of the present work is on dilute emulsions of λ ∼ 1, but this numerical procedure might be used for simulations of higher drop volume fractions of homogeneous or disperse drop radius distributions, generated in the simple shear flow.

Emulsion relative viscosity for moderate viscosity ratios

In this work, we have used the BIM and tabulation procedure as described in the section “Boundary integralmethod: drop surface velocity and drop stress contribution” and “Stress data tabulation,” in order to compute the emulsion relative viscosity as function of the viscosity ratio ranging from λ = 2 to λ = 20. The tabulation procedure using boundary integral simulation data were used to simulate pressure-driven flow for Ca_λ = 0.1 and Ca_λ = 0.5 with a drop volume fraction of ϕ = 0.05. Figure 4 shows a comparison between numerical results of the emulsion viscosity as function of the viscosity ratio λ using tabulation of BIM stress data and the results theoretically predicted by Eq. 50. The theory gives a good quantitative picture of the phenomenon for λ around 5 and Ca_λ = 0.1. The emulsion viscosity increases for increasing λ because the drop at very high λ describes approximately a rigid body motion and the emulsion viscosity tends to an upper bound limit equivalent to the effective Einstein viscosity (Einstein 1956). For Ca_λ = 0.5, at the same low volume fraction, the theoretical predictions are systematically smaller than those observed by tabulation of BIM stress data, because the drop starts having a substantial degree of deformation for λ = 10, where we can see already a perceptible discrepancy even at this high-drop viscosity ratio. For smaller λ, the results indicate a fast decreasing of the relative emulsion viscosity as λ decreases. This variation can be observed for both Ca_λ = 0.1 and Ca_λ = 0.5. For λ < 10, the emulsion relative viscosity is strongly dependent on λ as Ca_λ is $\mathcal{O}(1)$. Consequently, the behavior of this intrinsic rheological quantity as predicted by the theory proposed in this work is at best only of qualitative value for smaller values of λ, because BIM simulations attained drop deformations that were larger than those found theoretically. Even this limited agreement is gratifying for engineering applications.

Fig. 4

Emulsion relative viscosity as function of the viscosity ratio drop fluid λ. In this plot, 2 ≤ λ ≤ 20. Solid line and circles: Ca_λ = 0.1 and ϕ = 0.05. Solid line: theoretical prediction by (50), circles: tabulation of BIM stress data. Dashed line and squares: Ca_λ = 0.5 and ϕ = 0.05. Dashed line: theoretical prediction by (50), squares: tabulation of BIM stress data. The upper bounder limit represented by the horizontal dotted line corresponds to the Einstein viscosity (Einstein 1956), which is independent of λ

Comparison with previous works available in the literature: linear and quadratic shear flows

The physical parameter we have defined in this work in general are slightly different of the ones defined in previous works available in the literature. For instance, in the paper by Coulliette and Pozrikids (1998) on drops in pressure-driven flow they used boundary integral numerical method for viscosity ratio always equal to unity. Their problem is slightly different of the one explored here. They have examined the pressure-driven transient motion of a periodic file of deformable liquid drops through a cylindrical tube with circular cross-section, at low Reynolds number condition. A flow similar to the one assumed by red blood cells in flow through capillaries (i.e., microvessels).

Despite the limitations mentioned above, there are some promising results. We made a comparison of the emulsion relative viscosity determined in the present work with the equivalent quantity for the motion of an isolated drop in simple shear performed numerically using a boundary integral method (BIM) by Kennedy et al. (1994), for a viscosity ratio λ = 6.4. It is worth to mention that the nondimensionlization employed in this reference work is different of ours, and it is necessary to compatibilize it prior to perform the comparisons. In addition, our results for λ = 4 were also compared with BIM results of Coulliette and Pozrikids (1998) for a periodic array of drops undergoing pressure-driven flow in a cylindrical tube for λ = 1 (the only λ available in that paper). These result are shown in Fig. 5.

Fig. 5

Comparison of the present results with those ones of previous works available in the literature. In the main chart, white squares indicate a result of disperse phase contribution to the effective viscosity in linear shear from Kennedy et al. (1994); Solid line: numerical solution for quadratic shear using small deformation theory; dashed line: numerical solution for quadratic shear using stress data tabulation. In the insert, we compare our results for λ = 4 to the results of Coulliette and Pozrikids (1998), for λ = 1

Figure 5 shows a comparison between the results of this work with those of we compare our results to those of Kennedy et al. (1994). Those authors report results for the disperse phase stress contribution ${\sigma}_{12}^d$, that is equivalent to the whole contribution of the stresslet integral (Eq. 57). In order to isolate only the disperse phase contribution of the nondimensional viscosity in our results, the quantity μ_w − 1 must be computed. The range of capillary is right in the shear-thinning region and a good qualitative agreement among the curves in the plot is observed. Actually, the maximal relative difference observed between the wall relative viscosity μ_w computed using the small deformation theory and Kennedy’s et. al. BIM work is around 10%. When using our tabulation procedure, the results are even closer, and the maximal relative difference is 8%. Considering the comparisons presented in the main chart of Fig. 5, we argue that the differences observed could be mainly associated to the type of the flow, since in our case the flow is quadratic in contrast with the linear shear used by Kennedy et al. (1994). A regression analysis was used to fit a power law to the curves in the shear-thinning region. For the pressure-driven flow, a scaling law like $C{a}_w^{-1/5}$ is found for both asymptotic results and for tabulated stress, as well. The results indicate a remarkable agreement of the shear-thinning behavior between our theoretical predictions and the BIM based on the tabulated stresses. In contrast, for the linear flow the decaying is proportional to $C{a}_{\lambda}^{-1/10}$. The stronger shear thinning observed in the pressure-driven flow could be related to the quadratic velocity profile, with high shear rates at the tube wall. It is not surprising because an emulsion is a non-Newtonian fluid and no universal law with respect the flow is expected. In addition In addition, the insert of Fig. 5 shows a comparison between our results and three values of relative viscosity available in Coulliette and Pozrikids (1998), for ϕ = 4.6%. In that case, the range of capillary number is in the low shear rate plateau and the shear-thinning behavior is not perceptible. The difference between results is always less than 3%. We can see that the apparent viscosities reported by Coulliette and Pozrikids (1998) for λ = 1 are slightly greater than our predictions for λ = 4. This difference can be attributed to the strong effect of the wall on the drop in a pressure-driven flow as the size of the drop is comparable to the diameter of the cylindrical capillary tube, in the reference situation. In this case, a drift velocity produced by wall-drop interaction and deformation-induced migration are significant in the pressure-driven flow of aligned drops in a capillary tube as explored by Coulliette and Pozrikids (1998). Certainly, the different viscosity ratios (i.e., λ = 1 in the reference and λ = 4 in the present work) also should contribute to the differences between results.

In general, from all comparisons done, we can see at least a good qualitatively agreement between the results. In particular, our findings are consistent with the conclusions drawn by Kennedy et al. (1994) and Coulliette and Pozrikids (1998) in linear shear as well as for the array of drops in pressure-driven flow. It was difficult to obtain a direct experimental result test of our theoretical prediction for the emulsion relative viscosity and wall viscosity of a dilute emulsion with moderate or high viscosity ratios under pressure-driven flow.

Concluding remarks

Our understanding on the behavior of emulsion flows with moderate and high viscosity contrast drop fluid through a tube has been significantly broadened by the present theoretical investigation, even in a dilute regime. Equation 50 was one of the most significant theoretical propose of this paper, which predicts the relative viscosity (or intrinsic viscosity) of a dilute emulsion of high viscosity drops flowing through a tube of circular cross-section. This high λ theory proposed for dilute emulsion in quadratic flow is valid for any arbitrary capillary or shear rates.

We have found that a dilute emulsion with moderate and high viscosity ratio under pressure-driven flow presents a shear-thinning behavior like the one observed in linear shear. Both the wall viscosity and the relative intrinsic viscosity decrease as the capillary number increases for all values of viscosity ratios examined. The theoretical calculations and the boundary integral simulations showed the same dependence of the relative viscosity on the emulsion viscosity ratio for both capillary number tested with a drop volume fraction of 5%.

We have shown that our analysis predicts the relative viscosity of a dilute emulsion of high viscosity drop as function of the capillary number Ca_λ and the viscosity ratio λ. For Ca_λ = 0.1 and ϕ = 5%, our theoretical predictions and numerical results performed by using a tabulation of stress data from BIM simulations were found to be in very good agreement even for a moderate viscosity ratio, i.e., λ = 5. For smaller values of λ and Ca_λ > 0.2, the agreement was found to be only qualitative. From all comparisons of our results with previous work, it was seen at least a qualitatively agreement between the results. In general, our findings were consistent with the conclusions draw by Pozrikids and co-authors for the array of drops in pressure-driven flow as well as for a drop in linear shear. On the other hand, it was difficult to obtain a direct experimental result test of our theoretical prediction for the emulsion relative viscosity and wall viscosity of a dilute emulsion with moderate or high viscosity ratios under pressure-driven flow.

The present study for emulsions with moderate and high viscosity ratios and arbitrary capillary numbers are still few explored in the current literature. The present work may elucidate some of the relevant physical consideration governing the high viscosity ratio oil-water emulsion flooding mechanisms in practical applications of oil recovery processes.

In this paper, the small contributions of shear-induced migration of microdrops were neglected, but this phenomenon could be considered even in the dilute limit involving two particle interactions as have been shown by Cunha and Hinch (1996) and Loewenberg and Hinch (1997). In the case of pressure-driven flow, we can have a diffusion process associated with a gradient in particle volume fraction added to a particle migration induced by a shear rate gradient. We plan in the future to incorporate this phenomenon for describing emulsion flow in pressure-driven flow by coupling the governing equations of the flow already explored here with a new nonlinear diffusion equation for the drop volume fraction ϕ.