Introduction

The development of an accurate theory for the flow dynamics of polymer melts is the key to predict their processing and shaping into plastic products. Traditionally, the flow of nearly monodisperse polymer melts (Vinogradov et al. 1975; Bach et al. 2003) has been seen as the ideal system to gain insight into melt flow. Extensional flows, commonly of the uniaxial type, are particularly important as they are very sensitive to changes in flow dynamics and material properties, whereas shear flow is not. Ideally consisting of two monodisperse polymers (Nielsen et al. 2006; Auhl et al. 2009) bi-disperse systems are considered the step towards a general understanding of the interaction between polymers of different length in flow (Wagner et al. 2008; Dhole et al. 2009; Khaliullin and Schieber 2010; van Ruymbeke et al. 2010; Read et al. 2012).

All of the experimental works by Vinogradov et al. (1975), Bach et al. (2003), Nielsen et al. (2006), Auhl et al. (2009) and Read et al. (2012) consider polymer melt systems meaning that solvents are not involved. Classic assumption about the flow dynamics of polymers is that polymer melts and solutions thereof have identical flow physics with the same entanglement number. With exceptions (van Ruymbeke et al. 2010; Desai and Larson 2014) this assumption has been the main guideline for the evolution (Dhole et al. 2009; Park et al. 2012) of the original tube model (Doi and Edwards 1986) to cope with the experimental findings. Experimentally, it is less complicated to measure on dissolved monodisperse polymers (Bhattacharjee et al. 2002) than undissolved ones, as these in most cases require temperatures differentiating from room temperature, typically elevated ones. Recent extensional experiments on oligomer-diluted narrow molecular weight distributed (narrow molar mass distribution, NMMD) polystyrene (PS) melts by Huang et al. (2013a, b), show that the assumptions of a unified flow physics for melts and solutions with the same entanglement numbers, are unlikely to be correct (Rasmussen and Huang 2014a). The flow physics of entangled polymer systems seems to be more complex than expected. Preceding the experimental studies by Huang et al. (2013a, b), Yaoita et al. (2012) explained this difference between solvent-diluted and pure monodisperse melt as a result of chain-chain interaction of nematic character, consequently changing the segmental friction. The effect of nematic solvent-chain interactions was originally studied theoretically by Doi et al. (1989) expecting the effect on flow to be unimportant in linear flow, whereas its role in on nonlinear flow is more unclear (Doi and Watanabe 1991). Whether or not nematic interactions have an effect on chain-chain interaction in the flow of melt systems, as discussed in Huang et al. (2013b), is to be seen.

Rasmussen and Huang (2014a) also concluded that there seems to be a fundamental difference between bi-disperse and monodisperse polymer melts. Likewise, this is as important as the difference between solutions and melts. Rasmussen and Huang (2014a) defined a bi-disperse blend as a system consisting of an entangled ideally monodisperse polymer diluted in a shorter polymer, containing at least two Kuhn steps. The short polymers need to be a chain in terms of Kuhn step. Naturally, this definition of a bi-disperse system also includes the blends in the work of Nielsen et al. (2006), Auhl et al. (2009), and Read et al. (2012). Here, the blends consist of NMMD polymers all being considerably larger than the entanglement length. The length of the short polymers used in Huang et al. (2013a, b) was less than the entanglement length and stayed in a random state at all experimental conditions. These dilutions from Huang et al. (2013a, b) are theoretically ideal materials that seem to provide the basis for gaining basic insight into melt flow. Rasmussen and Huang (2014a) derived a constitutive equation indicating an identical flow dynamics of these systems independent of the length of the short polymer. This independency is valid if the short polymer is a chain in term of Kuhn step, e.g. it should contain at least two Kuhn steps.

This paper will extend the ideas from Rasmussen and Huang (2014a) to general bi-disperse systems, as they still seem to be the direction toward an general understanding of polymer melt flow. Constitutive ideas still struggle with attempts to integrate monodisperse melts and solutions into a unified theoretical framework (Desai and Larson 2014). The increased complexity due to the difference between these fluids and diluted systems, where the diluent should contain at least two Kuhn step, has not yet been addressed theoretically except by Rasmussen and Huang (2014a, b).

Linear dynamics

The linear viscoelastic dynamics of bi-disperse polymer melts Struglinski and Graessley (1985) has been studied in a series of papers. Particularly, des Cloizeaux (1988) presented mixing rules for blends of monodisperse polymers, and the understanding has continued to evolve (Park and Larson 2004; Khaliullin and Schieber 2010; Read et al. 2012). Here, to obtain the most accurate description of measured mechanical spectroscopic data, the semi empirical method by Baumgaertel, Schausberg and Winter (BSW) (Baumgaertel et al. 1990) is applied. The BSW method was initially developed to handle monodisperse polymers (Baumgaertel et al. 1990). The corresponding method for bi-disperse blends of monodisperse polymers was developed by Jackson and Winter (1995). Although it is a very accurate method, it should not be interpreted as a blend rule, as all involved parameters cannot be predicted based on the composition of the blend.

The BSW memory function containing the linear dynamics is

$$\begin{array}{@{}rcl@{}} M(t\!-t^{\prime})\!&=&\!M_{1}(t-t^{\prime})+M_{2}(t-t^{\prime}), \end{array} $$
(1)
$$\begin{array}{@{}rcl@{}} M_{i}(t\!-t^{\prime})\!&=&\!{\int}_{0}^{\infty} \frac{H_{i}(\tau)}{\tau^{2}} e^{(-(t-t^{\prime})/\tau)}d \tau , \quad \end{array} $$
(2)
$$\begin{array}{@{}rcl@{}} H_{i}(\tau)\!&=&\!n_{e} G_{N,i}^{0} \left[ \!\left (\!\frac{\tau}{\tau_{\text{max},i}} \right)^{n_{e}}\!+\left (\frac{\tau}{\tau_{c}} \right)^{-n_{g}} \!\right] h(1\,-\,\tau/\tau_{\text{max},i}). \quad \end{array} $$
(3)

t is the time and h(x) is the Heaviside step function. n e , n g and τ c are parameters with a unique value for each type of polymer. τ c is the time scale for the transition to the glassy regime. The values obtained in Rasmussen and Huang (2014a, b) of n e =0.2, n g =0.7 and τ c =0.4s (at 130 ∘C) are used for the PS blends. These seem to be the optimal choice for the involved NMMD polystyrene melts and should be used for the corresponding bi-disperse systems as well (Jackson and Winter 1995). \({G_{N}^{0}}\) is the plateau modulus for the particular polymer given as \({G_{N}^{0}}\) = 250 kPa at 130 °C (Bach et al. 2003) for the polystyrene (PS) melts and \({G_{N}^{0}}= 476\) kPa at 25 ∘C (Auhl et al. 2009) for the polyisoprene (PI) melts are used.

Table 1 lists the relevant molecular weights for the involved NMMD PS and PI with reference to their origin. M w and M n are the weight and number average molecular weight, respectively. These NMMD polymer melts are blended into bi-disperse systems where the composition can be found in Table 2 which includes the necessary references. The long and short chains are the same type of polymer where 𝜃 is the weight fraction of the long chain in the blend. The references in Table 2 refer to the sample preparation as well as the corresponding measured mechanical spectroscopic data. The actual BSW fittings are shown in Figs. 1, 2 and 3, where the values n e =0.25, n g =0.65 and λ c =11 μs at 25 ∘C have been obtained as the optimal values for all the involved PI blends. All remaining BSW parameters are calculated by data fittings using the method from Rasmussen et al. (2000). The remaining unknown parameters to be least square fitted to the mechanical spectroscopic data are the two maximal time constants (τ max,1 and τ max,2) and one of the \(G_{N,i}^{0}\). The methodology outlined here is identical to the one used in Nielsen et al. (2006), actually on the same polystyrenes as used here. A more detailed discussion can be found in Nielsen et al. (2006).

Table 1 Molecular weights for the involved NMMD PS and PI
Full size table
Table 2 Composition and molecular weights for the involved bi-disperse PS and PI blends
Full size table
Fig. 1
figure 1

Loss, \(G^{\prime \prime }\) (open circles) and storage moduli, \(G^{\prime }\) (closed circles), both as a function of the angular frequency ω at 25 ∘C, for the PI483_34_XX data series (from Read et al. (2012) its Fig. 5) where XX = 40, 20, 10 and 04 for the left/top to the right/bottom series. The solid lines are the least-square fittings to the BSW model in Eq. 3

Full size image
Fig. 2
figure 2

Loss, \(G^{\prime \prime }\) (open circles) and storage moduli, \(G^{\prime }\) (closed circles), both as a function of the angular frequency ω at 25 ∘C, for the PI226_23_XX data series (from Read et al. (2012) its Fig. 4) where XX = 40 and 20 for the left/top and the right/bottom series, respectively. The solid lines are the least-square fittings to the BSW model in Eq. 3

Full size image
Fig. 3
figure 3

Loss, \(G^{\prime \prime }\) (open circles) and storage moduli, \(G^{\prime }\) (closed circles), both as a function of the angular frequency ω at 130 ∘C, for the PS Blend X data series (from Nielsen et al. 2006) where X = 1, 2 and 3 for the right/bottom and left/top series, respectively. The solid lines are the least-square fittings to the BSW model in Eq. 3

Full size image

Constant interchain pressure

To explain the extensional dynamics of oligomer-diluted NMMD polystyrene melts, (Rasmussen and Huang 2014b) suggested a tube-based reptation model based on the idea of a constant interchain pressure (CIP). The nonlinear dynamics was explained as a consequence of a constant thermal interchain pressure originating from the short polymer chains on the wall of the tube containing the long chains. The short polymer chain should have a length of at least two Kuhn steps as it needs to be a chain in term of Kuhn step. It is the random motion of the chain which imposes the constant thermal pressure (Doi and Edwards 1986). The tube changes the diameter both affinely and by convective constraint release (Marrucci 1996) in the model by Rasmussen and Huang (2014b). They incorporated the CIP into the molecular stress function (MSF), following the method of Wagner et al (2005). In the MSF approach, the components of the stress tensor, σ ij, are given as

$$\begin{array}{@{}rcl@{}} \boldmath \sigma &=& \int\limits_{-\infty}^{t} \left[ \sum\limits_{i=1}^{M} M_{i}(t-t^{\prime}) f_{i}(\boldmath {x},t,t^{\prime})^{2} \right]\\ &5& \left\langle \frac{ [ \mathbf{E}(\boldmath{x},t,t^{\prime})\cdot\mathbf{u}] [ \mathbf{E}(\boldmath{x},t,t^{\prime})\cdot\mathbf{u} ]} {|\mathbf{E}(\boldmath{x},t,t^{\prime}) \cdot\mathbf{u}|^{2}} \right\rangle dt^{\prime} , \end{array} $$
(4)

where \(f_{i}(\boldmath {x},t,t^{\prime })\) is a stretch evolution with an initial value \(f_{i}(\boldmath {x},t^{\prime },t^{\prime })=1\). All the angular brackets are a unit sphere integral defined as \(\langle {\dots } \rangle = 1/(4 \pi ) {\int }_{|\mathbf {u}|=1} {\dots } d\mathbf {u}\) where u is a unit vector. The components of the displacement gradient tensor \(\mathbf {E}(\boldmath {x},t,t^{\prime })\) are \(E_{\text {ij}}(\boldmath {x},t,t^{\prime }) = {\partial x_{\mathrm {i}} / \partial x_{\mathrm {j}{'}}}\), i=1,2,3 and j=1,2,3 in Cartesian coordinates. \((x^{\prime }_{1} ,x^{\prime }_{2} , x^{\prime }_{3})\) are the coordinates of a particle in the reference state at time \(t^{\prime }\) displaced to the coordinates (x 1,x 2,x 3) in the present time t.

In this constitutive (5), the original MSF equation is extended to include multiple stretch evolution functions (Huang et al. 2012), similarly to the approach introduced by Wagner et al. (2008) for bi-disperse systems. They introduced separate stretch evolution functions for the long and the short polymer. In the original CIP method presented in Rasmussen and Huang (2014b), the constitutive equation was independent of the theoretical choice for the linear dynamics, as long as it was an accurate prediction of the measures data. Here, it requires that it is possible to distinguish between the linear dynamics of the long and the short polymer.

The stretch evolution of the CIP type, omitting the dependence of x, t and \(t^{\prime }\) in the notation,was

$$ \frac{df_{i}}{dt} = f_{i} \frac{\partial}{\partial t} \left\langle \ln | \mathbf{E}\cdot \mathbf{u} | \right\rangle - c(f_{i},\lambda_{\text{max},i}) \cdot f_{i} \frac{(f_{i}-1)}{\tau_{R,i}} $$
(5)

where τ R,i is the Rouse time. This is an extension of the original CIP approach to a multimode form where M=1 is the original equation. The relative Padé inverse Langevin function (Ye and Sridhar 2005) was used to represent the maximum extensibility of the long polymer as

$$ c(f,\lambda_{\text{max}}) = \frac{ (3-f^{2}/\lambda_{\text{max}}^{2})(1-1/\lambda_{\text{max}}^{2})}{(3-1/\lambda_{\text{max}}^{2})(1-f^{2}/\lambda_{\text{max}}^{2})}. $$
(6)

The square of the maximal relative stretch, \(\lambda _{\text {max}}^{2}\), of a polymer chain is given as the number of Kuhn steps between entanglements. In Rasmussen and Huang (2014b), this was given as \(\lambda _{\text {max}}^{2}=22/\theta \) for the long polystyrene chains. The relation between the molecular weight and the Rouse time was found as

$$ \tau_{R}/\tau_{\text{max}} = 4050 \cdot (\text{kg/mol} / M_{w} )^{2} , $$
(7)

valid for both the NMMD polystyrene melts and the oligomer diluted ones.

The use of this MSF constitutive concept in Eq. 5 is not an exclusive approach. The CIP idea can be incorporated in other constitutive concepts (Dhole et al. 2009; van Ruymbeke et al. 2010).

Bi-disperse polystyrene blends

The oligomers diluent in Huang et al. (2013a, b) is in random configuration at all experimental conditions. The length of the short chains in Nielsen et al. (2006) is at least 12 times larger than the short ones in Huang et al. (2013a, b). Consequently, one difference between the bi-disperse blends from Huang et al. (2013a, b) and Nielsen et al. (2006) is the presence of a significant time constant of the short polymer in the blends in Nielsen et al. (2006). The maximal time constants connected to the dynamics of the short ones (τ max,2) is about two decades lower than the corresponding time constants of the long polymers (τ max,1) as it appears in Table 3. The value of τ max,2 related to the dynamics of the short polymer has been added on Figs. 4, 5 and 6. Of course, these two decades ensure that the short polymer will stay in a virtually random configuration for a time scale in-between one to two decades from the maximal time constant of the large polymer. Here, the nonlinear dynamics would be expected to be controlled

Table 3 Fitted BSW parameters in Eq. 3 based on the method by Rasmussen et al. (2000) containing the linear dynamics of the blend. The values of n e =0.2, n g =0.7 and τ c =0.4 s for the PS blends and n e =0.25, n g =0.65 and λ c =11 μs for the PI blends
Full size table
Fig. 4
figure 4

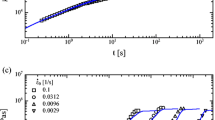
Corrected extensional viscosity, \(\bar {\eta }^{+}\) for the PS blend 1 at 130 ∘C as a function of the time t from Nielsen et al. (2006). The extension rates are 0.3, 0.1, 0.03, 0.01 and 0.003 s −1 from the left to the right data series. The dotted lines are the linear viscoelastic predictions based on the parameters listed in Table 3 using (3). The dashed lines are the corresponding predictions to the data from Eqs. 5 based on the Rouse time in Eq. 9. The solid lines are the corresponding predictions to the data from the Eqs. 5 based on the Rouse time in Eq. 7

Full size image
Fig. 5
figure 5

Corrected extensional viscosity, \(\bar {\eta }^{+}\) for the PS blend 2 at 130 ∘C as a function of the time t from Wagner et al. 2008. The extension rates are 0.1, 0.03, 0.01, 0.003 and 0.001 s −1 from the left to the right data series. The dotted lines are the linear viscoelastic predictions based on the parameters listed in Table 3 using Eq. 3. The dashed lines are the corresponding predictions to the data from the Eqs. 5 based on the Rouse time in Eq. 9. The solid lines are the corresponding predictions to the data from the Eq. 5 based on the Rouse time in Eq. 7

Full size image
Fig. 6
figure 6

Corrected extensional viscosity, \(\bar {\eta }^{+}\) for the PS blend 3 at 130 ∘C as a function of the time t from Nielsen et al. (2006). The extension rates are 0.3, 0.1, 0.03, 0.01, 0.003, 0.001, 0.0003 and 0.00015 s −1from the left to the right data series. The dotted lines are the linear viscoelastic predictions based on the parameters listed in Table 3 using Eq. 3. The dashed lines are the corresponding predictions to the data from the Eq. 5 based on the Rouse time in Eq. 9. The solid lines are the corresponding predictions to the data from Eq. 5 based on the Rouse time in Eq. 7. The dotted-dashed lines are the corresponding predictions to the data from the Eq. 5 with a maximum extensibility of \(\lambda _{\text {max} }^{2}=22\). This is the value expected for undiluted NMMD polystyrenes melts

Full size image

Figures 4, 5 and 6 show the startup of extensional viscosities, \(\bar {\eta }^{+}\), with a constant extension rate, \(\dot {\epsilon }\) from Nielsen et al. (2006). This extensional viscosity is defined as \(\bar {\eta }^{+}~=~(\sigma _{\text {33}}~-~\sigma _{\text {11}})/\dot {\epsilon }\) where x 3 represents the direction of the extension. The strain is here given as \(\epsilon (t)~=~\dot {\epsilon } \cdot t\), where the extension is initiated at time t=0. The extension measurements in Figs. 4, 5 and 6 were performed using the filament stretching rheometer (FSR). Using the FSR, a shear contribution, may add to the measured elongational viscosity during the initiation of the extension (Spiegelberg et al. 1996; Szabo 1997; Kolte et al. 1997; Rasmussen et al. 2010). Here, the correction formula from Rasmussen et al. (2010) has been applied. It ensures a maximal 3 % deviation from the correct evaluation of the initial extensional stress. The formula from Spiegelberg et al. (1996) was applied in the original paper from Nielsen et al. (2006). The deviation may be as large as 13 % using this approach.

For oligomer chain-diluted systems, the constant thermal interchain pressure on the wall of the tube containing the long chains originates from the short chains in a random configuration (Rasmussen and Huang 2014b). It is a consequence of the random motion of the chains imposing a thermal pressure on the tube wall of the larger molecule. According to Doi and Edwards (1986), the relation for the thermal pressure on the tube wall is

$$ p = \frac{\pi^{2}}{3}\frac{Nb^{2}}{{L_{V}^{2}}} \frac{kT}{V}. $$
(8)

where T is the temperature and k is the Boltzmann constant, where k T represents the thermal energy. N is the number of Kuhn segments in the short chain, where b is the length of one Kuhn segment. V is the volume, where L V is its length dimension, containing a chain. Notice that this thermal pressure is not dependent on entanglements. It is a consequence of the random motion from a polymer chain physically consisting of Kuhn segments, e.g. at least two of these, on the tube wall. Assuming the surrounding short chains are in a random configuration, a constant thermal pressure is imposed orthogonal to the tube interface. As derived in details in Rasmussen and Huang (2014b), this leads to the constitutive equation presented in the section “Constant interchain pressure”.

All blends should have identical flow physics if the length (in term of Kuhn step) of the short polymers does not have an effect on the flow dynamics, as long as they stay in a random configuration. In this case, a Rouse time would be expected to be of the type

$$ \tau_{R,i}/\tau_{\text{max},i} = 4050 \cdot (\text{kg/mol} / (\theta M_{\text{long}}) )^{2} , $$
(9)

where M long is the (weight based) molecular weight of the long NMMD polystyrene. The value of τ max,2 relates to the dynamics of the short polymer. This time constant should not contribute to the constitutive equation except as Newtonian dynamics. The time scale of any experiment should be several times larger than τ max,2 to ensure that the short polymer stays in a random configuration.

The calculated extensional viscosities, corresponding to the experiments based on the CIP (5) using the above Rouse time (9), have been inserted in Figs. 4, 5 and 6. These are the dashed lines. All the corresponding viscosities are inserted, although comparison should only be made at the lowest extensional rates. The deviation from the measured values are on a scale of several hundred percent. This is the case even before the transition to the steady extensional viscosities, where the viscosity is controlled by the maximal extensibility. As a result of a too large Rouse time, the calculated initial strain hardening is too severe. The presence of the short chains at least changes the Rouse time.

The semi-empirical relation of the Rouse time in Eq. 7 is based on a MSF framework. The relation in Eq. 7 is valid as long as the dilutions (or the lack of it) are ideal. It can be seen as monodisperse polymers diluted in the same polymer. The constitutive nonlinearity changes depending on the character of blend, e.g. whether it is a solution, a dilution or a pure melt, according to Rasmussen and Huang (2014a). The particular values of the Rouse time (e.g. τ R /τ max) depend somewhat on the used concept (Larson et al. 2003; Osaki et al. 2000, 2001; Likthman and McLeish 2002; Menezes and Graessley 1982). Theoretically, these concepts imply a unique dependence of the entanglement number on the Rouse time. In the concepts, the tube basically consists of the entanglements surrounding the polymer. Based on published extensional experiments, the dynamics of any ideal dilution of a polymer can be explained as a consequence of the change of entanglements. It is clear from the above discussion involving Figs. 4, 5 and 6 that the random configuration of the short polymer changes the value of the Rouse time if the short polymer is sufficiently large. This does not necessarily imply that the polymer is entangled, but the short polymer in the work of Nielsen et al. (2006) is so. Interpreted within the entanglement idea, it is clear from the above discussion that the random configuration of the short polymer does not remove the entanglements. An extension of the entanglement idea is cumbersome (Read et al. 2012), whereas the basic ideas of Doi and Edwards, represented by Eq. 8, constitute a more straightforward explanation. Here, the tube consists of the motion of the polymer chains, physically represented by Kuhn chains, in direct contact with the (long) polymer. Opposite of the entanglements, the Kuhn steps in a polymer chain do not change with any kind of dilution effect, considering an ideal diluent. Inspecting the Eq. 7 for the Rouse time, which is semi-empirically based but confirmed experimentally, the Rouse time depends on the total number of Kuhn steps of the polymers in direct contact with the (long) polymer. Extending this idea to general bi-disperse system, the relation in Eq. 7 should still be valid. The total number of Kuhn steps is proportional to M w , independently of the composition of the melt.

Based on the Rouse time in Eq. 7 inserted into the CIP (5), the calculated elongational viscosities corresponding to the experiments are showed in Figs. 4, 5 and 6, as the solid lines. The expected agreement with the experiments is obtained at the lowest rate, confirming the idea of a tube consisting of the Kuhn steps of the polymers in direct contact with the (long) polymer. More surprisingly, the agreement seems to extend past the time constant of the short polymer. This indicates a more general application of the idea of a tube consisting of the Kuhn chains which are independent of the rate, where the Rouse time should be evaluated relatively to the characteristic time constant of the particular polymer inside the tube. One particular exception is observed in Fig. 6. This happens in the extension at high extensional rates. Here, the maximal extensibility seems to be too high, particularly at the highest rate, as the steady extensional viscosities are over predicted by the solid lines. The used definition of the maximal extensibility is the same as in Figs. 4 and 5. It is the number of Kuhn steps between entanglements where the short polymer is assumed to be in a random state, effectively removing entanglements. This increases the entanglement length. This assumption is expected to lose its validity considerably beyond the inverse time constant of the short polymer. This will reduce the entanglement length and as a consequence the maximal extensibility as well. A model prediction based on a maximal extensibility for an undiluted polystyrene melt, \(\lambda _{\text {max} }^{2}=22\), has been inserted in Fig. 6 as the dotted-dashed lines. The entanglements from the short polymers seem to be reinstated at the fastest elongational rate and the maximal extensibility changes accordingly, predicting the correct steady extensional viscosity. Below this rate, the measure-steady extensional viscosity is in between the solid and dashed line. Actually, blend 3 represents the smallest difference between the short and the long polymer, for all the involved bi-disperse melts presented here, and it seems to have a consequence for the value of the maximal extensibility.

Bi-disperse polyisoprene blends

The lowest value of the maximal extensability should be the number of Kuhn steps between entanglements, N e , in an undiluted state. N e is defined as the number of Kuhn steps in an entanglement strand. Due to the different possible structural configurations in polyisoprene, the N e value highly depends on the particular composition of the sample. Its various structural composition changes the value of N e and according to Fetters et al. (2007), it may at least be between 14 and 54. This value would be expected to be about 50 (Krishnamoorti et al. 2002; Fetters et al. 2007) for the melts in the work by Auhl et al. (2008). The extensional experiments by Auhl et al. (2009) and Read et al. (2012) are all performed on the (SER) Sentmanat Extension Rheometer equipment equipment (Sentmanat 2004). The SER has a limit on the maximal strain of 3.8 on all experiments. Due to this limit and the value of N e it is not necessary to include the maximal extensibility in the theoretical analysis. It only has a minor effect of a few percent and only at the highest strain values. Most of the experiments are actually performed considerably below the maximal strain of 3.8.

Extensional measurements on bi-disperse polymer melt systems using the SER equipment have been presented subsequent to the work by Auhl et al. (2009). Wang et al. (2011) measured on styrene-butadiene random (SBR) copolymer bi-disperse systems. Here, only the polyisoprene measurements from Auhl et al. (2009) and Read et al. (2012) are considered, as all the applied extensional rates in Wang et al. (2011) were considerably higher than the inverse time constant of the short polymer. Actually, most of the presented extensions were at rates where the measurements were affected by the glassy regime.

The constitutive (5) for bi-disperse blends without maximal extensibility only depends on the values of the Rouse time. Although the idea of a unified flow physics of melts and dilutions with the same entanglement numbers has been shown to be incorrect, all available experimental evidence still confirms the unique relation between entanglement numbers and the Rouse time. Of course, this only considers NMMD melts and ideal dilutions thereof. Although the original work by Vinogradov et al. (1975) considered extension of NMMD polyisoprene, necessary data to establish an accurate relation between monodisperse polyisoprene and the Rouse time seem to be unavailable. Start-up of shear flow has been studied experimentally (Boukany et al. 2009) by Auhl et al. (2008); Schweizer et al. (2004) but shear flow is not sufficiently sensitive to the value of the Rouse time to enable the development of an accurate relation.

Equation 7 can be applied using the classical assumption where the Rouse time solely depends on the entanglement number. It needs the establishment of the entanglement number of both the polystyrene and isoprene. Values of the entanglement molecular weight have been reported within the range of 3.25 to 6.4 kg/mol for the polyisoprene and from 13.3 to 18.1 kg/mol for the polystyrene (Fetters et al. 2007). The ratio between these Rouse times is needed to extend (7) to polyisoprenes. Here, the entanglement molecular weights used in Read et al. (2012) of 4.816 kg/mol for polyisoprene and 18.1 kg/mol polystyrene, that actually represents an intermediate value of the ratio. Therefore, a relation for the Rouse time for polyisoprenes is expected to follow a relation of

$$ \tau_{R,i}/\tau_{\text{max} ,i} = 4050 \cdot ((4.816/18.1) \text{kg/mol} / M_{w} )^{2}. $$
(10)

It is very important that the used constitutive approach represents an appropriate description of the flow physics, not only in extension but also in shear. Read et al. (2012) also measured the startup of shear for two of the polyisoprene blends. Particularly, the PI226_23_40 blend is measured in both shear and extension. Both of these sets of startup data from Read et al. (2012) are shown in Fig. 7 where η + is the startup of the shear viscosity. The corresponding start-up of extension (left curves) and shear (right curves) flow to the experiments based on the CIP model in Eq. 5 and Eq. 10 are the solid lines in Fig. 7. The expected agreement with these experiments is found. As for the polystyrene blend, the agreement extends past the time constant of the short polymer. Further, the start-up of shear flow confirms that (5) is accurate in both shear and extension. In Fig. 8, the start-up of shear for the PI226_23_20 blend from Read et al. (2012) with the CIP model prediction is shown as well. Notice that the maximal extensibility is not needed in shear, as the (square of the) molecular stress function stays considerably below this value.

Fig. 7
figure 7

The startup of extensional viscosity, \(\bar {\eta }^{+}\) (top data series) and startup of shear viscosity η + (bottom data series) for the PI226_23 blend at 25 ∘C as a function of the time t from Read et al. (2012). The extension rates are 2190, 225.5, 67.64, 22.65, 6.796 and 0.2321 s −1 from the left to the right data series. The shear rates are 679.6, 226.5, 67.96, 22.65, 9.676, 2.903, 0.9676, 0.2903 and 0.02903 s −1 from the left to the right data series. The dotted lines are the linear viscoelastic predictions based on the parameters listed in Table 3 using Eq. 3. The are the corresponding predictions to the data from Eq. 5 based on the Rouse time in Eq. 10

Full size image
Fig. 8
figure 8

The startup of shear viscosity η +for the PI226_23_20 blend at 25 ∘C as a function of the time t from Read et al. (2012). The shear rates are 222, 132.5, 66.61, 44.16, 22.2, 13.25, 6.661, 4.416, 2.22, 1.164, 0.4416 and 0.03493 s −1 from the left to the rightdata series. The dotted lines are the linear viscoelastic predictions based on the parameters listed in Table 3 using Eq. 3. The solid lines are the corresponding predictions to the data from the Eq. 5 based on the Rouse time in Eq. 10

Full size image

The extensional data from Read et al. (2012) for the remaining four blends are shown in Figs. 9 and 10. In three of these, the expected agreement with the experiments in extension flow is observed. An exception is the most diluted polyisoprene blend (PI483_34_04) where the calculated extensional viscosities are severely below measurements at all extensional rates. This is inexplainable within this CIP concept.

Fig. 9
figure 9

The startup of extensional viscosity, \(\bar {\eta }^{+}\) at 25 ∘C as a function of the time t from Read et al. (2012). The top data series are the PI483_34_40 blend where the extension rates are 100.4, 10.4, 1.2 and 0.12 s −1 from the leftto the right data series. The bottom data series are the PI483_34_10 blend where the extension rates are 9.85, 2, 1 and 0.1 s −1 from the left to the right data series. The dotted lines are the linear viscoelastic predictions based on the parameters listed in Table 3 using Eq. 3. The solid lines are the corresponding predictions to the data from the Eq. 5 based on the Rouse time in Eq. 10

Full size image
Fig. 10
figure 10

The startup of extensional viscosity, \(\bar {\eta }^{+}\) at 25 ∘C as a function of the time t from Read et al. (2012). The top data series are the PI483_34_20 blend where the extension rates are 101.6, 9.91, 1.24, and 0.1 s −1 from the left to the right data series. The bottom data series are the PI483_34_04 blend where the extension rates are 224, 46.7, 9.81, 2, 0.5 and 0.1 s −1 from the left to the right data series. The dotted lines are the linear viscoelastic predictions based on the parameters listed in Table 3 using Eq. 3. The solid lines are the corresponding predictions to the data from the Eq. 5 based on the Rouse time in Eq. 10

Full size image

Summary and conclusion

A tube-based constitutive equation to predict the flow dynamics of bi-disperse polymer melts has been derived. It was based on the idea of a tube consisting of a constant interchain pressure (CIP). This was originally suggested to explain the nonlinearity of extensional flow of oligomer diluted NMMD polystyrene (Rasmussen and Huang 2014b), if the oligomers consist of at least two Kuhn steps. The oligomer needs to be a chain in term of Kuhn step. An assumption of a tube consisting of (the Kuhn chains of) the polymers in direct contact with the polymer have been suggested. It seems to be a valid extension of the CIP idea to general bi-disperse system. This assumption allows a calculation of the involved Rouse times depending on M w , and at the same time, sustains the original nonlinearity. It therefore contains the original CIP model. Here, the CIP model was incorporated into the molecular stress function method as in Rasmussen and Huang (2014b). The methodology was similar to the approach introduced by Wagner et al. (2008) for bi-disperse systems. Experimentally, the dynamics of the bi-disperse polystyrene systems of Nielsen et al. (2006) and polyisoprene systems by Read et al. (2012)—with one exception—were within quantitative agreement with the derived model. This included both startup of extension as well as shear flow.

The startup of extension continued to its steady extensional viscosity in the data from Nielsen et al. (2006). A model prediction based on a maximal extensibility, proportional to the Kuhn steps between entanglements was applied here. It accurately described the viscosity at the steady flow, where the short chains are in a random state and therefore effectively act as a diluent. Further maximal extensibility comprises that of an undiluted melt at the highest elongational rate, where all polymers are in a structured state.