Introduction

Investigation of internal flow constitutes a problem of fundamental interest in the fluid mechanic discipline. The problem is of particularly interest for the cases with non-Newtonian fluids which are showing a yield stress such as Bingham plastics and Herschel-Bulkley fluids. Internal flow of these materials divides into two regions: yielded and un-yielded. In yielded region, the value of shear stress is greater than yield stress and the material deforms like as viscous liquids, while in un-yielded central region, plug region, the shear stress is less than yield stress and it deforms plastically. It is interesting to mention that in complex geometry and regimes, prediction of this plug region boundary could be a problem. For instance, in this field, an interesting analytical approach by Bahadori et al. (2013) is presented to predict plug boundaries of laminar Bingham plastic fluid flows through annulus. The obtained correlations for this flow are achieved as a function of dimensionless yield stress and aspect ratio parameters for given values of rheological properties, pressure gradient, and dimensions of annulus. More recently, Swamee and Aggarmal (2011) provided explicit equations for Bingham plastic fluids to calculate the friction factor in closed pipes by laminar flow assumption. They also provided an explicit equation for critical Reynolds number to determine the flow regime. Nirmalkar et al. (2012) extended this scenario to analyze the creeping flow of Bingham plastic passing a square cross-sectional duct. The governing equations are numerically solved over a wide range of Bingham number as 1 ≤ Bn ≤ 105 to investigated the influence of the Bingham number on the size of yield and un-yield regions. Furthermore, Min et al. (1997) focused their numerical study to investigate the developing region of Bingham plastic flows in pipes. A four-step fractional method combined with an equal order bilinear finite element method is used. The results are obtained for various values of the yield stress and Bingham, Reynolds, and Prandtl numbers. It is shown that for larger values of yield stress, the entrance length is shorter to reach fully developed velocity field, and the un-yielded region near the centerline becomes thicker. In the micro scale situation, wall roughness could be an important parameter on laminar flow of Bingham plastic fluids. Engin et al. (2004) numerically studied the effect of this parameter in the micro channels. They assumed that friction factor is a function of only Reynolds number. It is presented that roughness-affected viscosity increase exponentially from the tube centerline based on modified viscosity model, Meokle-Kubota-Ko. The effect of wall roughness is also shown to play an important role on the friction factor even in laminar flow conditions. The combined effects of wall roughness and yield stress appear to have a considerable impact on the flow behavior through micro tubes. Vola et al. (2003) presented a numerical method to deal with Bingham fluid flows which able them to cope with convection-dominated problems using low-order finite elements. They applied Fortin-Glowinski decomposition coordinate method to offer wide flexibility in the choice of the rheological constitutive relations. The three-dimensional Bingham fluid flow is solved by Laaber (2008). They presented two methods for solving this problem. The idea of using a time-dependent problem in order to approximate the steady-state problem led to an Uzawa-type method coupled with fixed point iteration together with stabilization for the projection. The stabilization is necessary due to the non-uniqueness of the dual variable. Discretization with finite elements was done for both three-dimensional approaches. In other problem dealing with Bingham fluids, Soleimani and Sadeghy (2011) investigated the instability of Bingham fluids numerically in pressure-driven flow between two infinity long concentric cylinders, using pseudo-spectral collocation method for both Taylor-Dean and Dean flows. They showed that the yield stress has a stabilizing effect on Taylor-Dean flow, but it depends on the amount of Bingham number and gap size for the Dean flow. They employed second order of finite difference method to solve the constitutive equation and inspected the effect of normal stress differences on the flow stability. Furthermore, Wang and Ho (2008) analyzed planar geometry, a 2:1 sudden expansion, for Bingham flow in a planar channel using Lattice-Boltzmann method. They captured corner vortices and shape of yield and un-yield regions for a wide range of Bingham and Reynolds numbers (0 ≤ Bn ≤ 2, 000 and 0.2 ≤ Re ≤ 200).

Among the internal flow investigations, those which deal with analysis of the effects of centripetal forces on the flow characteristics of viscous fluids passing through curved pipes are of great value and essential because of frequent occurrence of them in industries, heat engines, heat exchangers, chemical reactors, and biophysical equipment. Presence of pressure gradient, arisen from centripetal acceleration, in radial direction makes the flow to leave its rectilinear distribution and a pair of secondary flow to appear. Pioneering investigations in this field were first carried out by Dean (1927, 1928) who omitted all the effects related to the curvature except centripetal acceleration to simplify the equations of motion. An analytical solution based on perturbation method was obtained in curved pipes and spots on most of significant feature of the flow such as Taylor-Gortler secondary flows which previously was unveiled on empirical investigation of Eustice (1911). Following to the revolutionary works of Dean (1927, 1928), Topakoghlu (1967) conducted the same approach for Newtonian fluid and derived a full solution for circular and annular. Clegg and Power (1963) extended this type of investigations to Bingham materials in small values of the Dean number. In following, Batra and Jena (1991) studied the flow of a Casson fluid in a curved tube for different values of Dean number. An indeed interesting investigation in this among is carried out by Das (1992) who studied the Bingham fluids in curved tubes. There, the influence of yield number on the velocity distribution and frictional resistance in the high Dean number were obtained and compared with Casson fluid showing the same yield values.

In the past few years, a notable attention is also allocated to study the viscoelastic category in curved pipes. An interesting investigation in the field of internal flows of viscoelastic fluids is the study of Oldroyd-B fluid flow in both circular and annular curved pipes which is carried out by Robertson and Muller (1996). They employed a perturbation method and considered the curvature ratio as perturbation parameter. In following of this work, instability of creeping viscoelastic flow in a curved rectangular duct has been studied numerically by Norouzi et al. (2012). They investigated the creeping and inertial flow of second-order fluid in square cross-sectional curved ducts employing finite difference method. They provided some detailed results on the effect of centrifugal force and normal stress differences on the secondary flows. Moreover, they presented an analytical correlation for the axial velocity and flow resistance ratio of creeping flow. Related to the curvature effect, Mashelkar and Devarajan (1976) described the origin of the secondary flows by the means of forces’ balance. They used order of magnitude technique and showed that the centrifugal force is balanced with the radial pressure gradient in the core region of flows. The core region is the area located in the middle of cross section which is far from the walls. Therefore, a high value of centrifugal force causes a large radial pressure gradient in the core region. This equilibrium is invalid near to the outer wall, where the amount of main flow velocity and centrifugal force is negligible. The amount of radial pressure gradient is still large near to the outer wall, so to counterbalance the forces, the momentum mechanism is activated and secondary flows are generated. Additionally, Helin et al. (2009) studied three-dimensional viscoelastic Dean flows of modified Phan-Thien-Tanner fluids in a curved channel with a square cross section using finite volume method. The authors showed that the Dean flows are steady for the range of 125 ≤ Dn ≤ 150. In following, they showed that the elasticity of the extensional parameter of viscoelastic fluid and Dean parameter enhances the size and number of secondary flows.

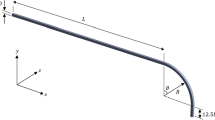
There is a dearth literature on exact solutions for Bingham flow in curved non-circular ducts. These solutions are useful in microfluidics, where lithographic methods typically produce channels of square or rectangular cross section. These channels are widely used in biochemistry, nanotechnology, and biotechnology, with practical applications to the design of systems in which small volumes of fluids will be handled. In this paper, an EXACT analytical solution for the creeping Dean flow of Bingham plastics through curved rectangular ducts is presented for the first time. The schematic geometry of problem is shown in Fig. 1. According to the figure, the cylindrical coordinate system is used to analyze the flow field. The rectangular shape is considered for cross section, and the radius of curvature is assumed to be constant. The solution of fluid flow for yielded and un-yielded regions is derived using bounded Fourier transformation. Based on the present analytical solution, the effect of Hedstrom number, curvature ratio, and aspect ratio on axial velocity distribution, flow resistance ratio, and wall shear stress is discussed in detail.

Fig. 1
figure 1

Geometry of curved duct in current study

Full size image

Governing equations

The governing equations of an incompressible steady flow including continuity and momentum equations are written as follows:

$$ \nabla \cdot \tilde{V}=0 $$
(1)
$$ \rho\;\tilde{V}\cdot \nabla \tilde{V}=-\nabla \tilde{P}+\nabla \cdot \tilde{\boldsymbol{\uptau}} $$
(2)

where \( \tilde{V} \) is velocity vector, ρ is density, \( \tilde{P} \)is static pressure, and \( \tilde{\boldsymbol{\uptau}} \) is the stress tensor. To solve this problem for flow in a curved duct, cylindrical coordinate system has been employed. The governing equations in this coordinates can be expressed as follows (Bird et al. 1987):

$$ \frac{1}{\tilde{r}}\frac{\partial }{\partial r}\left(r{\tilde{v}}_r\right)+\frac{1}{\tilde{r}}\frac{\partial {\tilde{v}}_{\theta }}{\partial \theta }+\frac{\partial {\tilde{v}}_z}{\partial \tilde{z}}=0 $$
(3)
$$ \rho \left({\tilde{v}}_r\frac{\partial {\tilde{v}}_r}{\partial \tilde{r}}+\frac{{\tilde{v}}_{\theta }}{\tilde{r}}\frac{\partial {\tilde{v}}_r}{\partial \theta }-\frac{{{\tilde{v}}_{\theta}}^2}{\tilde{r}}+{\tilde{v}}_z\frac{\partial {\tilde{v}}_r}{\partial \tilde{z}}\right)=-\frac{\partial \tilde{P}}{\partial \tilde{r}}+\left[\frac{1}{\tilde{r}}\frac{\partial }{\partial \tilde{r}}\left(\tilde{r}{\tilde{\tau}}_{rr}\right)+\frac{1}{\tilde{r}}\frac{\partial {\tilde{\tau}}_{r\theta }}{\partial \theta }+\frac{\partial {\tilde{\tau}}_{rz}}{\partial \tilde{z}}-\frac{{\tilde{\tau}}_{\theta \theta }}{\tilde{r}}\right] $$
(4)
$$ \rho \left({\tilde{v}}_r\frac{\partial {\tilde{v}}_{\theta }}{\partial \tilde{r}}+\frac{{\tilde{v}}_{\theta }}{\tilde{r}}\frac{\partial {\tilde{v}}_{\theta }}{\partial \theta }+\frac{{\tilde{v}}_r{\tilde{r}}_{\theta }}{\tilde{r}}+{\tilde{v}}_z\frac{\partial {\tilde{v}}_{\theta }}{\partial \tilde{z}}\right)=-\frac{1}{\tilde{r}}\frac{\partial \tilde{P}}{\partial \theta }+\left[\frac{1}{{\tilde{r}}^2}\frac{\partial }{\partial \tilde{r}}\left({\tilde{r}}^2{\tilde{\tau}}_{r\theta}\right)+\frac{1}{\tilde{r}}\frac{\partial {\tilde{\tau}}_{\theta \theta }}{\partial \theta }+\frac{\partial {\tilde{\tau}}_{\theta z}}{\partial \tilde{z}}+\frac{{\tilde{\tau}}_{\theta r}-{\tilde{\tau}}_{r\theta }}{\tilde{r}}\right] $$
(5)
$$ \rho \left({\tilde{v}}_r\frac{\partial {\tilde{v}}_z}{\partial \tilde{r}}+\frac{{\tilde{v}}_{\theta }}{\tilde{r}}\frac{\partial {\tilde{v}}_z}{\partial \theta }+{\tilde{v}}_z\frac{\partial {\tilde{v}}_z}{\partial \tilde{z}}\right)=-\frac{\partial \tilde{P}}{\partial \tilde{z}}+\left[\frac{1}{\tilde{r}}\frac{\partial }{\partial \tilde{r}}\left(\tilde{r}{\tilde{\tau}}_{rz}\right)+\frac{1}{\tilde{r}}\frac{\partial {\tilde{\tau}}_{\theta z}}{\partial \theta }+\frac{\partial {\tilde{\tau}}_{zz}}{\partial \tilde{z}}\right] $$
(6)

Non-dimensional parameters related to governing equations and coordinate system are defined as follows:

$$ \begin{array}{c}\hfill \begin{array}{llllll}r=\frac{\tilde{r}}{d_{\mathrm{h}}},\hfill & z=\frac{\tilde{z}}{d_{\mathrm{h}}},\hfill & R=\frac{\tilde{R}}{d_{\mathrm{h}}},\hfill & \delta =\frac{\tilde{a}}{2\tilde{R}},\hfill & a=\frac{\tilde{a}}{d_{\mathrm{h}}},\hfill & b=\frac{\tilde{b}}{d_{\mathrm{h}}}\hfill \end{array}\hfill \\ {}\hfill \begin{array}{lllll}{v}_i=\frac{{\tilde{v}}_i}{W_0},\hfill & {\tau}_{ij}=\frac{{\tilde{\tau}}_{ij}{d}_{\mathrm{h}}}{\eta {W}_0},\hfill & P=\frac{\tilde{P}{d}_{\mathrm{h}}}{\eta {W}_0},\hfill & \mathrm{B}\mathrm{n}=\frac{{\tilde{\tau}}_0{d}_{\mathrm{h}}}{\eta {W}_0},\hfill & \mathrm{He}=\frac{\rho {\tilde{\tau}}_0{d_{\mathrm{h}}}^2}{\eta^2}\hfill \end{array}\hfill \end{array} $$
(7)

where \( \tilde{r} \) and \( \tilde{z} \) are the coordinates, and \( \tilde{a}\kern0.5em \mathrm{and}\kern0.24em \tilde{b} \) are the length and width of the duct cross section shown in Fig. 1. Here, d h is the hydraulic diameter, \( \tilde{R} \)is the pitch radius of curvature, W 0 is the reference velocity, η is the viscosity of yielded region, δ is the curvature ratio, \( {\tilde{\tau}}_0 \) is the yield stress of the Bingham plastic, Bn is the Bingham number, and He is the Hedstrom number. Here, the reference velocity (W 0) is the maximum velocity of Newtonian flow in a straight circular pipe by the same hydraulic diameter and pressure gradient of Bingham flow in curved rectangular duct which is presented as follows (Robertson and Muller (1996)):

$$ {W}_0=\frac{G{a}^2}{16\eta } $$
(8)

Bingham number is proportional to the ratio of yield stress to viscous stress. In our problem, the Hedstrom number is used because of its suitability in creeping Bingham plastic flow, and it could be defined based on the production of Reynolds and Bingham numbers:

$$ \mathrm{He}=\mathrm{R}\mathrm{e}\mathrm{B}\mathrm{n} $$
(9)

The problem discussed in this study is a creeping Dean flow of Bingham plastic. Therefore, it is clear that the left hand side of the momentum equation can be ignored. Furthermore, assuming fully developed flow in curved ducts, derivatives of all variables with respect to θ are zero except the static pressure. The pressure gradient of this flow is expressed as follows:

$$ \frac{\partial P}{\partial \theta }=-16R=-C $$
(10)

It is well-known in Bingham materials that a fluid with a yield stress (\( {\tilde{\tau}}_{{}_0} \)) flows only under the condition that the applied stress exceeds the yield value. It is pertinent to be noted that this stress component is proportional to pressure gradient. Around the core region of the rectangular curved duct which stress tensor obtains a value less than the yield stress, there will appear a solid plug-like region. In steady and rectangular curve duct, the constitutive equations of Bingham fluid can be written as:

$$ \left\{\begin{array}{l}{\tilde{\tau}}_{r\theta }={\tilde{\tau}}_0+\eta \left(\tilde{r}\frac{\partial }{\partial \tilde{r}}\left(\frac{{\tilde{v}}_{\theta }}{\tilde{r}}\right)+\frac{1}{\tilde{r}}\frac{\partial {\tilde{v}}_r}{\partial \theta}\right)\kern0.6em \mathrm{f}\mathrm{o}\mathrm{r}\kern0.48em \left|{\tilde{\tau}}_{r\theta}\right|\ge {\tilde{\tau}}_0\\ {}\overset{\cdot }{\gamma }=0\kern12.1em \mathrm{f}\mathrm{o}\mathrm{r}\kern0.48em \left|{\tilde{\tau}}_{r\theta}\right|<{\tilde{\tau}}_0\end{array}\right. $$
(11)
$$ \left\{\begin{array}{l}{\tilde{\tau}}_{z\theta }={\tilde{\tau}}_0+\eta \left(\frac{1}{\tilde{r}}\frac{\partial {\tilde{v}}_z}{\partial \theta }+\frac{\partial {\tilde{v}}_{\theta }}{\partial \tilde{z}}\right)\kern2.04em \mathrm{f}\mathrm{o}\mathrm{r}\kern0.48em \left|{\tilde{\tau}}_{z\theta}\right|\ge {\tilde{\tau}}_0\\ {}\dot{\gamma}=0\kern11.4em \mathrm{f}\mathrm{o}\mathrm{r}\kern0.48em \left|{\tilde{\tau}}_{z\theta}\right|<{\tilde{\tau}}_0\end{array}\right. $$
(12)

It is important to remember that due to the absence of centripetal force in creeping fully developed Dean flow of viscous fluids, the velocity field keeps its rectilinear distribution. In other words, the lateral parts of velocity components can be omitted in comparison with the order of magnitude of main velocity. Therefore, only the θ-momentum equation should be solved. The dimensionless style of θ-momentum equation in the cylindrical coordinate system can be expressed as follows:

$$ \frac{C}{r}+\left[\frac{1}{r^2}\frac{\partial }{\partial r}\left({r}^2{\tau}_{r\theta}\right)+\frac{\partial {\tau}_{\theta z}}{\partial z}\right]=0 $$
(13)

Substituting Eq. (11) into the Eq. (13), the θ-momentum equation can be derived as follows:

$$ \frac{C}{r}+\left\{\frac{1}{r^2}\frac{\partial }{\partial r}\left({r}^2\mathrm{B}\mathrm{n}+{r}^3\frac{\partial }{\partial r}\left(\frac{v_{\theta }}{r}\right)\right)+\frac{\partial }{\partial z}\left(\mathrm{B}\mathrm{n}+\frac{\partial {v}_{\theta }}{\partial z}\right)\right\}=0 $$
(14)

Considering the Bingham plastic flow constitutive equation, two regions of yielded and un-yielded regions should be separately solved. In yielded region, this fluid behaves like a linear flow, while in un-yielded region, the stress is less than the yield stress and shear rate is zero. It is obvious that there is a boundary between the two regions, which is the locus of the points that the stress is equal to τ 0 for both of them (Chhabra and Richardson (2008)).

In outer region, yielded region, Eq. (14) should be solved with respect to the boundary condition expressing as:

$$ \begin{array}{l}\mathrm{A}\mathrm{t}\kern0.24em r={r}_i\kern0.36em \mathrm{and}\kern0.36em r={r}_o\to {v}_{\theta }=0\\ {}\mathrm{A}\mathrm{t}\kern0.24em z=0\kern0.36em \mathrm{and}\kern0.24em z=b\kern0.36em \to {v}_{\theta }=0\end{array} $$
(15)

Equation (14) can be solved using Fourier Transformation in the z-direction. The transformation and its reverse relation are expressed as follows (Bronshtein et al. 2007):

$$ {F}_s\left\{{v}_{\theta}\left(r,z\right)\right\}=U\left(r,n\right)=\frac{2}{b}{\displaystyle \underset{0}{\overset{b}{\int }}{v}_{\theta}\left(r,z\right) \sin \left(\frac{n\pi z}{b}\right)dz} $$
(16)
$$ {v}_{\theta}\left(r,z\right)={F_s}^{-1}\left\{U\left(r,n\right)\right\}={\displaystyle \sum_{n=1}^{\infty }U\left(r,n\right)} \sin \left(\frac{n\pi z}{b}\right) $$
(17)

Applying Fourier Transformation (Eq. (16)) into all terms of Eq. (14), the differential equation below is obtained:

$$ r\frac{d}{dr}\left(r\frac{dU}{dr}\right)-\left(\frac{n^2{\pi}^2{r}^2}{b^2}+1\right)U+\frac{32r}{n\pi}\left(R+\frac{1}{8}\mathrm{B}\mathrm{n}\right)\left[1-{\left(-1\right)}^n\right]=0 $$
(18)

The solution of this ordinary differential equation is as follows:

$$ U\left(r,n\right)={a}_n{I}_1\left(\frac{n\pi r}{b}\right)+{b}_n{K}_1\left(\frac{n\pi r}{b}\right)-\frac{32{b}^2}{n^3{\pi}^3r}\left(R+\frac{1}{8}\mathrm{B}\mathrm{n}\right)\left[-1+{\left(-1\right)}^n\right] $$
(19)

Applying inverse Fourier transformation (from Eq. (17)) on above solution, the velocity distribution is derived as follows:

$$ {v}_{\theta}\left(r,z\right)={\displaystyle \sum_{n=1}^{\infty}\left\{{a}_n{I}_1\left(\frac{n\pi r}{b}\right)+{b}_n{K}_1\left(\frac{n\pi r}{b}\right)+\frac{32{b}^2}{n^3{\pi}^3r}\left(R+\frac{1}{8}\mathrm{B}\mathrm{n}\right)\left[-1+{\left(-1\right)}^n\right]\right\}} \sin \left(\frac{n\pi z}{b}\right) $$
(20)

where a n and b n are calculated using boundary conditions (Eq. (15)) as follows:

$$ {a}_n=\frac{4{b}^2}{n^3{\pi}^3}\left[1-{\left(-1\right)}^n\right]\left\{\frac{\left(-\frac{8R}{r_o}-\frac{\mathrm{Bn}}{r_o}\right){K}_1\left(n\pi {r}_i/b\right)+\left(\frac{8R}{r_i}+\frac{\mathrm{Bn}}{r_i}\right){K}_1\left(n\pi {r}_o/b\right)}{I_1\left(n\pi {r}_o/b\right){K}_1\left(n\pi {r}_i/b\right)-{I}_1\left(n\pi {r}_i/b\right){K}_1\left(n\pi {r}_o/b\right)}\right\} $$
(21)
$$ {b}_n=-\frac{4R{b}^2}{n^3{\pi}^3}\left[1-{\left(-1\right)}^n\right]\left\{\frac{\left(\frac{8R}{r_i}+\frac{\mathrm{Bn}}{r_i}\right){I}_1\left(n\pi {r}_o/b\right)-\left(\frac{8R}{r_o}+\frac{\mathrm{Bn}}{r_o}\right){I}_1\left(n\pi {r}_i/b\right)}{I_1\left(n\pi {r}_o/b\right){K}_1\left(n\pi {r}_i/b\right)-{I}_1\left(n\pi {r}_i/b\right){K}_1\left(n\pi {r}_o/b\right)}\right\} $$
(22)

The flow resistance of a fluid flow in curved ducts is generally defined as follows (Fan et al. (2001)):

$$ \frac{f_{\mathrm{c}}}{f_{\mathrm{s}}}={\left(\frac{Q_{\mathrm{c}}}{Q_{\mathrm{s}}}\right)}^{-1} $$
(23)

Here, Q c represents the flow rate passing through the curved duct and Q s is the flow rate of a Newtonian fluid in the straight duct under same pressure gradient with similar shape of the cross section. The flow rate in a curved duct is calculated by integrating the axial velocity Eq. (20) over the duct cross section:

$$ {Q}_{\mathrm{c}}={Q}_{\mathrm{c}\hbox{-} \mathrm{yielded}}+{Q_{\mathrm{c}}}_{\hbox{-} \mathrm{u}\mathrm{n}\hbox{-} \mathrm{yielded}} $$
(24)

where,

$$ \begin{array}{l}\mathrm{f}\mathrm{o}\mathrm{r}\kern0.36em \left\{\begin{array}{l}{r}_i\le r\le {r}_{p1}\kern0.6em ,\kern0.72em {r}_{p2}\le r\le {r}_o\\ {}0\le z\le {z}_{p1}\kern0.72em ,\kern0.6em {z}_{p2}\le z\le b\end{array}\right.\kern0.24em :\\ {}{Q}_{\mathrm{c}\hbox{-} \mathrm{yielded}}={\displaystyle \sum_{n=1}^{\infty}\frac{2{z}_{p1}^2\left[1-{\left(-1\right)}^n\right]}{n^2{\pi}^2}\left\{\begin{array}{l}\kern0.36em {a}_n\left[{I}_0\left(\frac{n\pi {r}_{p1}}{b}\right)+{I}_0\left(\frac{n\pi {r}_o}{b}\right)-{I}_0\left(\frac{n\pi {r}_i}{b}\right)-{I}_0\left(\frac{n\pi {r}_{p2}}{b}\right)\right]-\\ {}{b}_n\left[{K}_0\left(\frac{n\pi {r}_{p1}}{b}\right)+{K}_0\left(\frac{n\pi {r}_o}{b}\right)-{K}_0\left(\frac{n\pi {r}_i}{b}\right)-{K}_0\left(\frac{n\pi {r}_{p2}}{b}\right)\right]-\\ {}\kern1.2em \frac{32b\left(R+\frac{1}{8}\mathrm{B}\mathrm{n}\right)\left[1-{\left(-1\right)}^n\right]}{n^2{\pi}^2}\left(Ln\left(\frac{r_{p1}}{r_i}\right)+Ln\left(\frac{r_o}{r_{p2}}\right)\right)\end{array}\right\}}\\ {}\end{array} $$
(25)
$$ \begin{array}{l}\;\mathrm{f}\mathrm{o}\mathrm{r}\kern0.24em \left\{\begin{array}{l}{r}_{p1}\le r\le {r}_{p2}\\ {}{z}_{p1}\le z\le {z}_{p2}\end{array}\right.\;:\\ {}{Q}_{\mathrm{c}\hbox{-} \mathrm{unyielded}}={\displaystyle \underset{r_{p1}}{\overset{r_{p2}}{\int }}{\displaystyle \underset{z_{p1}}{\overset{z_{p2}}{\int }}{v}_{\theta } drdz}}\kern0.84em ,\kern0.36em {v}_{\theta }=\mathrm{Linear}\kern0.5em \mathrm{distribution}\end{array} $$
(26)

In order to calculate the flow resistance ratio (Eq. (23)), we also need the flow rate of Newtonian flow in straight ducts with rectangular cross section. This solution was reported previously in literature (White (1991)):

$$ W\left(r,z\right)={\displaystyle \sum_{n=1}^{\infty}\left[{a}_{n,s}\ \cosh\ \left(\frac{n\pi x}{b}\right)+{b}_{n,s}\ \sinh\ \left(\frac{n\pi x}{b}\right)+\frac{32{b}^2}{n^3{\pi}^3}\left[1-{\left(-1\right)}^n\right]\right]}\ \sin\ \left(\frac{n\pi y}{b}\right) $$
(27)

where,

$$ {a}_{n,s}=\frac{32{b}^2}{n^3{\pi}^3}\left[{\left(-1\right)}^n-1\right] $$
(28)
$$ {b}_{n,s}=\frac{32{b}^2}{n^3{\pi}^3}\left[{\left(-1\right)}^n-1\right]\left(\frac{1- \cosh\ \left(\frac{n\pi a}{b}\right)}{\ \sinh\ \left(\frac{n\pi a}{b}\right)}\right) $$
(29)

The flow rate can be obtained by integrating the above solution on the area of cross section (White (1991)):

$$ {Q}_{\mathrm{s}}={\displaystyle \sum_{n=1}^{\infty}\frac{b^2\left[1-{\left(-1\right)}^n\right]}{n^2{\pi}^2}\left[\begin{array}{l}{a}_{n,s}\ \sinh\ \left(\frac{n\pi a}{b}\right)-{b}_{n,s}\left(1- \cosh\ \left(\frac{n\pi a}{b}\right)\right)+\\ {}\kern3em \frac{32 ab\left[1-{\left(-1\right)}^n\right]}{n^2{\pi}^2}\end{array}\right]} $$
(30)

Finally, the flow resistance ratio of Bingham plastic creeping flow in curved rectangular ducts can be calculated by substituting Eqs. (24) and (30) into Eq. (23).

Results and discussion

In this section, the obtained results for steady creeping Bingham flow in curved ducts with different aspect ratios, curvature ratios, and Hedstrom numbers are studied in detail. Accuracy of present solution is tested via exact solution of Newtonian creeping flow through a straight rectangular duct and also by comparing the results with computational fluid dynamic (CFD) simulation. The corresponding results are expected to be identical with Newtonian solution at zero yield stress. It is important to mention that a solution for flow in a curved duct should tend to solve for the corresponding flow in a straight duct at r → ∞. In this condition, we have r ≈ R ≈ r i  ≈ r o . If we substitute zero yield stress and consider r → ∞ in solution of Bingham flow in curved ducts Eq. (20), the result is identical with exact solution that presented in literature for Newtonian flow in straight rectangular ducts Eqs. (27). The deviation between these two exact solutions by considering 30 terms of Fourier series is in the order of 10− 5 − 10− 6 for different aspect ratios and curvature ratios. This deviation has arisen from truncation of Fourier series and also the error related to calculation of Bessel functions at large arguments.

In order to investigate the validation of present study with more generalized results, we compared our exact solution with results of numerical simulation. For this purpose, we used a CFD code which is prepared by the first author of the present paper, and it has been used previously for solving the Newtonian and viscoelastic flows in curved non-circular ducts (Norouzi et al. 2009; Norouzi et al. 2010; Norouzi et al. 2012). The governing equations have been discreted using first-order forward finite difference for time and second-order central finite difference for space in a staggered mesh. The pressure is estimated using artificial compressibility approach to obtain a physical solution for steady-state situation. We developed this code to solve the Bingham Dean flow in curved rectangular ducts. We used 80 × 80 and 60 × 100 grids for a square (d/h = 1) and a rectangular cross section (d/h = 2/5), respectively. Hedstrom number and curvature ratio for both cases are 0.05 and 0.1, respectively. Here, the maximum value of error for axial velocity distribution is 0.1075 % for square and 0.3579 % for rectangular cross section. Also, the error of flow resistance ratio between these two solutions is 0.0318 % for square and 0.0745 % for rectangular cross section. Therefore, it is obvious that the present exact solution has a suitable agreement with numerical solution.

Due to the large number of dimensionless groups important for this problem, finding all of trustable situations is difficult. By comparing with CFD simulations, it is evident that the present exact solution is reliable for 0.25 < AR < 4, 0.05 < δ < 0.95, He < 0.15 and Re < < 1. In these conditions, the average relative error of axial velocity distribution between the exact solution and second-order numerical simulation is less than 1 %.

Figure 2 shows the axial dimensionless velocity distribution along the symmetry boundary (at z = b/2) for a rectangular curved duct at AR = 2 and δ = 2/5. Unlike the inertia cases that centrifugal force makes the position of maximum velocity to shift toward outer wall, due to elimination of inertia forces corresponding to the creeping flow assumption, it is shown that this position can shift even toward the inner wall which is related to the larger value of axial pressure gradient in this region. For He > 0, the axial velocity consisted of two parts. In first part (0 < r < r p1 , r p2 < r < r o ), near wall region, the total shear stresses (τ rz  and τ rθ ) are larger than yield stress and behaves like a viscous fluid, while in second part, core region (r p1 < r < r p2), the total shear stresses are less than the yield stress, in this scenario Bingham plastic acts as a rigid body. An interesting result is related to straight pipe scenario that the flow distribution between r p1 and r p2 is linear and constant. As it is mentioned previously, these contours are obtained at z = b/2; further results present the flow pattern of whole region.

Fig. 2
figure 2

Distributions of axial velocity along the symmetry line (z = b/2) at AR = 2, R = 2.5 and δ = 2/5 for different Hedstrom numbers

Full size image

Variations of axial velocity for creeping Bingham plastic fluid in rectangular curved ducts for different Hedstrom numbers, curvature ratios, and aspect ratios are presented in Figs. 3 and 4. According to Fig. 3, the location of maximum axial velocity shifts toward to the inner wall by increasing the curvature ratio which is related to the larger value of axial pressure gradient near to the inner wall for sharp curvatures. Figure 4 shows off that increasing the Hedstrom number is followed by extension of un-yielded area which is obviously related to increasing the amount of yield stress. In other words, by increasing the Hedstrom number, the region in which the stress is greater than the yield stress (near wall region) is became smaller. Figure 5 presents aspect ratio effect on distribution of main flow velocity at He = 0.02. This figure shows that, in scenario with curved ducts, the position of maximum flow shifts toward the inner wall, and by enhancing aspect ratio (AR), this scenario intensifies. According to this figure, the maximum value of velocity increases by an increment in aspect ratio since the maximum values for AR = 0.5, 2, 3, and 5 against AR = 1 are −0.583, 0.833, 109.275, and 250 %, respectively.

Fig. 3
figure 3

Contours of axial velocity at AR = 1 and He = 0.03 for different curvature ratios

Full size image
Fig. 4
figure 4

Contours of axial velocity at AR = 1, R = 1.5, and δ = 1/3 for different Hedstrom numbers

Full size image
Fig. 5
figure 5

Contours of axial velocity (\( \raisebox{1ex}{${V}_{\theta }$}\!\left/ \!\raisebox{-1ex}{$U$}\right. \)) at He = 0.02 and δ = 1/3 for different aspect ratios

Full size image

Substituting Eqs. (25) and (31) into Eq. (23), the flow resistance ratio of creeping Bingham plastic flow in a curved duct can be determined analytically. In Fig. 6, flow resistant ratio versus curvature ratio in creeping flows for different aspect ratios and Hedstrom numbers are plotted. Here, AR represents the ratio of length of duct in r-direction on length of duct in z-direction. According to the figure, for Newtonian case (He = 0), which depends on the value of aspect ratio, flow resistance ratio is more or less than 1. This issue is related to the radial dependency of axial pressure gradient (see term of C/r in Eq. (13)) and form of velocity distribution in different aspect ratios. Figure shows that there is a critical aspect ratio equal to 0.89077 in which the flow resistance ratio of Newtonian flow is always equal to one. In this case, the flow resistance is independent from curvature ratio. Another interesting phenomenon is related to aspect ratios larger than 0.89077 in which the flow resistance ratio is less than 1. In other words, the flow rate in a curved duct could be larger than straight duct for a same pressure gradient and similar shape of cross section! This phenomenon is also previously observed for creeping flows of Newtonian (Topakoglu (1967)), UCM, and second-order fluids (Bowen et al. (1991) in curved circular pipes. It is shown that at He < 0.005, variation of flow resistant ratio with curvature ratio at large radius of curvature is insignificant and the trend of diagrams is approximately similar to Newtonian cases. As Hedstrom number is increased from 0.005, flow resistant ratio is generally dropped and the trend of diagrams is changed. This issue is better shown in Fig 7. This figure depicts the variation of flow resistant ratio in terms of Hedstrom numbers at δ = 0.6 and AR = 1. According to the figure, a drag reduction has occurred in creeping Dean flow of Bingham fluid by increasing the Hedstrom number. This issue could be attributed to growing the size of un-yielded region (as the high-speed region) by enhancing the Hedstrom number that causes an increment in flow rate.

Fig. 6
figure 6

Flow resistance ratio versus curvature ratio for different aspect ratios and Hedstrom numbers

Full size image
Fig. 7
figure 7

Flow resistance ratio versus Hedstrom number at δ = 0.6 , AR = 1, r i  = 0.5

Full size image

Figures 8, 9, and 10 plot variation of Poiseuille number in curved channels for creeping flow of viscoplastic materials in different Hedstrom numbers and aspect ratios. The Poiseuille number is generally defined as (White (1991)):

Fig. 8
figure 8

Distributions of Poiseuille number in lateral walls of curved rectangular ducts at r i  = 0.3

Full size image
Fig. 9
figure 9

Distributions of Poiseuille number in upper wall of curved rectangular ducts at r i  = 0.3

Full size image
Fig. 10
figure 10

Distributions of Poiseuille number in inner wall of curved rectangular ducts at r i  = 0.3

Full size image
$$ \mathrm{P}\mathrm{o}={C}_{\mathrm{f}}\times \mathrm{R}\mathrm{e} $$
(31)

where \( {C}_{\mathrm{f}}=\frac{{\tilde{\tau}}_w}{\frac{1}{2}\rho {W_0}^2} \) is friction coefficient.

Taking the advantages of dimensionless form of parameters, we have:

$$ \mathrm{P}\mathrm{o}=2{\tau}_{\mathrm{w}} $$
(32)

where τ w is dimensionless wall shear stress. For Newtonian flow, the Poiseuille number is independent of fluid material properties, velocity, temperature, or duct size. It is solely a function of the duct shape (Shah and London (1978)). It can be noted that τ rθ is wall shear stress at walls located at inner and outer radius of curvature, while τ zθ plays this role in lateral walls (the walls located at z = 0 and z = b). Arising from symmetry along z = b/2, τ zθ has the same distribution in lateral walls. According to Figs. 8, 9, and 10, it can be also noted that the value of Poiseuille number is zero at the edge of channels for Newtonian fluids. Here, in following of an increment in Hedstrom number, the value of Poiseuille number is enhanced and at the edges obtains a non-zero value. The enchantment of Poiseuille number by increasing the Hedstrom number is related to shrinking the size of yielded region which causes more velocity gradient at walls and subsequently increasing the wall shear stress. In accordance with Fig. 8, an decrement in aspect ratio increases the Poiseuille number at lateral walls in a way that the maximum value of Poiseuille number for different Hedstrom numbers at AR = 0.25 is around six times larger than corresponding cases at AR = 4. It is also observed that enchantment in Hedstrom number is followed by an increment in Poiseuille number in lateral walls. Rate of increment in Poiseuille number is increased by an increment in aspect ratio. As an example, maximum difference in Poiseuille number at He = 0.1 in comparison with Newtonian fluid (He = 0) for AR = 0.25 and 4 is 184 and 29 %, respectively. On the other hand, Fig. 8 shows that shear stress distribution in lateral walls tends to migrate toward inside of channel.

Figure 9 plotted the Poiseuille number at upper wall of curved rectangular ducts for different aspect ratios and Hedstrom numbers. It can be noted that for cases with He > 0, shear stress in some aspect ratios can change their directions. Data in Fig. 10 shows that an increment in He and AR can enhance the maximum value of Poiseuille number.

Figure 11 depicts values of Poiseuille number at walls of curved channels for AR = 1 and r i  = 0.2 scenarios in different Hedstrom numbers. An increment in Hedstrom number increases the Poiseuille number at edges. It is also shown that as Hedstrom number is increased, the value of Poiseuille number is enhanced at walls. According to the obtained results, curvature ratio causes the shear stress to show an asymmetry distribution and to shift its position toward curvature center line.

Fig. 11
figure 11

Poiseuille number in AR = 1 and r i  = 0.2 at walls of curved duct

Full size image

Conclusions

In the current investigation, an exact analytical solution for Bingham plastic fluid flows in curved rectangular ducts is presented for the first time. The results of the present study could be useful for microfluidics especially in biomechanics and biotechnology. The main results of present research are summarized as follows:

  • By increasing the curvature ratio (decreasing the radius of curvature), the location of maximum axial velocity shifts toward to the inner wall. It is important to remember that this effect is completely reveres in inertia flows. In creeping flow, due to the absence of centripetal force, the axial pressure gradient plays the main role in axial velocity distribution. In other words, due to the higher of axial pressure gradient near to the inner wall, the axial velocity is more in this region. The present analytical solution indicated that this effect has existed for both Newtonian and Bingham plastic fluids.

  • Flow resistance ratio is decreased by increasing the Hedstrom number. In other words, a drag reduction is observed in creeping Dean flows of Bingham plastic by increasing the yield stress. This issue could be attributed to growing the size of un-yielded region (as the high-speed region) by enhancing the Hedstrom number that causes an increment in flow rate.

  • In Newtonian creeping flow, there is a critical aspect ratio in which the flow resistance ratio is independent from curvature ratio. The present analytical solution indicated that this critical aspect ratio has not existed at large enough Hedstrom numbers.

  • It is shown that as Hedstrom number is increased, the value of Poiseuille number is enhanced. Unlike the Newtonian flows, the value of Poiseuille number is not zero at edges of cross section for Bingham plastic flows.

  • Unlike to the Newtonian creeping flows in which the dependency of flow resistance ratio to curvature ratio is canceled at small curvature ratios, this dependency is considerable for Bingham plastic creeping flows especially at large Hedstrom numbers (see Fig. 6).