1 Introduction

Fluid flow in the curved non-circular ducts is a common phenomenon in engineering applications [1]. For example, this fluid flow is recognizable in cooling parts of the turbines [2], fluid machineries [3], heat exchangers [4], lab-on-a chip devices [5, 6], etc. In addition, flow in the curved duct is an important prototype to study the hydrodynamic instability. In 1927, Dean [7] presented pioneering study related to hydrodynamic stability of flow in the curved direction. According to this study, Dean instability theory and Dean number (i.e., De as control parameter) are defined.

Based on the literature, investigating the influences of Dean number (De) on fluid flow instability is an attentive subject in the context of hydrodynamic instability in the curved non-circular ducts. Therefore, there are several experimental and numerical investigations on this subject [8,9,10,11,12,13,14,15,16,17,18,19,20,21]. For example, Mori et al. [8] presented both experimental test and analytical study on fully developed flow in the curved square duct. Cheng et al. [9] numerically studied the steady laminar flow in the non-circular curved ducts at various Dean numbers ranging from 5 to 715. Humphrey et al. [10] studied laminar flow through the square section curved duct with turning angle of 90° at De = 368, experimentally and numerically. Their results show that the local position of the maximum of flow velocity is around the 85% of duct’s width (near the outer wall). Ghia and Sokhey [11] conducted three-dimensional analysis on incompressible viscous flow in the curved ducts using alternating direction implicit (ADI) method. Their results show that the inception of hydrodynamic instability through the curved square ducts is corresponding to De = 143. In another study, Ghia et al. [12] investigated fully developed flow through the curved duct at De < 900 using a multi-grid technique. They reported the onset of hydrodynamic instability at Dean number 600. Hille et al. [13] conducted an experimental investigation on steady flow in the 180° curved square duct at Dean numbers ranging from 150 to 300. They found a pair of second vortex nearby the outer curved wall. Yang and Camarero [14] numerically analyzed the viscous flow through the 90° curved duct at Dean number 55 by vorticity–potential method. Mees et al. [15] studied steady incompressible flow through the square curved duct at Dean numbers ranging from 200 to 600, experimentally and numerically. In both numerical and experimental studies, Fellouah et al. [16, 17] studied the laminar fluid flow through the curved ducts with turning angle 180°. In Refs [16, 17], radial gradient of velocity in the stream-wise direction is suggested as Dean instability criteria. In 2013, Mondal et al. [18] numerically investigated the flow instability through the rotating rectangular curved duct. In their study, the effects of different types of rotations (i.e., positive and negative) on flow instability are evaluated. In 2014, impression of centrifugal and Coriolis instabilities in the rotating rectangular curved duct is studied by Mondal et al. [19]. In 2015, Mondal et al. [20] presented a numerical study on nonlinear unsteady solution arising from heat transfer and flow in the curved duct with aspect ratio 0.5 and curvature ratio 0.1.

Recently, Dutta et al. [21] have simulated the flow in the 90° curved duct using k-ε turbulence model. Their results show that the reason of flow separation is the secondary motion movement that is also observed by Helal et al. [22]. Krishna et al. [23] conducted experimental tests with computational fluid dynamics (CFD) analysis on unsteady pulsatility flow through the highly curved duct. Their results show that the secondary flow is the origin of flow separation through the highly curved square duct. Adegun et al. [24] simulated convective heat transfer through the curved ducts. Their results show that the influence of inclination on flow behavior is remarkable for Reynolds number upper than 200. Islam et al. [25] studied the stability of flow through the coiled duct with rectangular cross section by spectral method. Their results show an improved heat transfer through the curved duct by combination of centrifugal and Coriolis instabilities. In 2017, they also investigated the interaction of centrifugal, Coriolis and buoyancy forces through the rotating curved duct at Dean number 1000 [26]. In 2018, Islam et al. [27] numerically investigated the influence of Coriolis force on instability of unsteady Dean–Taylor flow through the curved duct. Elsamni et al. [28] conducted a CFD investigation on hydrodynamic stability of laminar flow through the semicircular curved duct at 100 < Re < 1500. Their results show an improved heat transfer for curved duct with semicircular cross section compared to fully circular cross section. In 2019 by semi-analytical study, Nowruzi et al. [29] performed an investigation on hydrodynamic instability of fluid flow through the curved duct with rectangular cross section by using linear hydrodynamic stability method. In their study, the effects of different aspect ratios and curvature ratios on Dean flow stability are evaluated.

Until now, various theories [30,31,32,33] are proposed to analysis of hydrodynamic stability. Recently, Dou [34, 35] have suggested “energy gradient theory” to study the hydrodynamic stability. Energy gradient theory has high potential to identify the local regions via highest probability to onset of instability in the entire flow field. This method is successfully tested for different problems [36,37,38,39].

According to the cited works, hydrodynamic stability and behavior of flow in the curved non-circular ducts are significantly corresponding to the flow parameter of Dean number. However, a comprehensive analysis on the mechanisms behind of Dean hydrodynamic instability at different Dean numbers is still missing. Moreover, the local regions of instability inception are not well recognized at various Dean numbers. In addition, the lack of study to evaluate the capability of energy gradient theory to analysis of Dean instability in the curved square duct is evident.

Therefore, following our investigation in Ref [39], the principle intention of the present paper is to examine the instability of flow through the curved square duct at various Dean numbers. To this accomplishment, various Dean numbers ranging from 19.69 to 1181.25 (i.e., corresponding to 50 ≤ Re ≤ 3000) are considered. Computational fluid dynamics (CFD) is employed to simulate of an incompressible fluid flow in the curved duct with square cross section. Then, stability of the flow is examined via energy gradient method.

2 Physic of the problem

Flow in the curved path known as Dean flow. In this fluid flow type, centrifugal forces will be induced a counter-rotating vortex motion on the stream-wise flow in the duct’s cross section, which is known as the main secondary flow. An imbalance of the pressure gradient in radial direction and centrifugal forces will be resulted to hydrodynamic instability (i.e., Dean hydrodynamic instability) in fluid flow domain. At this critical condition, Dean vortices as an additional counter-rotating vortex will be emerged on the cross-stream flow.

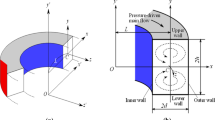
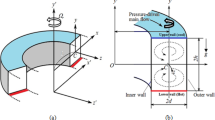
Figure 1 shows the schematic of intended curved square duct. As shown in Fig. 1b, inlet of curved duct is equipped with long straight duct to guarantee smoothing and fully developed inflow. Indeed, upstream straight duct as inlet section makes large enough (i.e., 50 \(D_{h}\)) to prevent from outlet effects on our solutions and to generate fully developed fluid flow in the inlet of the square curved duct [40]. Now, we can define Dean number (De) as control parameter in Dean flow as follows:

$$De = Re.\sqrt {\frac{1}{\delta }} = \text{Re} .\sqrt {\frac{{D_{h} }}{R}} = \frac{{D_{h} u_{\text{avg}} }}{\nu }.\sqrt {\frac{{D_{h} }}{R}}$$
(1)

where Re and \(u_{\text{avg}}\) are Reynolds number of the basic flow and average of velocity in stream-wise direction, respectively. Moreover, \(\nu\) is kinematic viscosity and \(\delta = {R \mathord{\left/ {\vphantom {R {D_{h} }}} \right. \kern-0pt} {D_{h} }}\) is the curvature ratio (curvature radius is shown by \(R\)) and \(D_{h}\) is representative of hydraulic diameter as follows:

$$D_{h} = \frac{{2\left( {a.b} \right)}}{a + b}$$
(2)
Fig. 1
figure 1

(taken from Ref [41])

a Schematic of considered curved square duct and b long straight duct as inlet of curved duct

Full size image

According to Eq. (1), the proportion among the inertial and viscous forces is shown by Dean number. In addition, one can be concluded that the aspect ratio \({\text{Ar}} = {b \mathord{\left/ {\vphantom {b a}} \right. \kern-0pt} a}\) (see Fig. 1) is equal to one for curved square duct.

Table 1 shows the intended test cases. As illustrated in Table 1, Dean number is varied in the range 19.69 to 1181.25 at fixed curvature ratio and aspect ratio equal to 6.45 and 1, respectively.

Table 1 Characteristics of intended test cases
Full size table

2.1 Governing equations

In the present paper, we considered laminar flow through the curved square duct. In addition, steady flow of an incompressible fluid is considered according to the physic of the problem. Standard Navier–Stokes equation and continuity equation are as follows:

$$\left\{ {\begin{array}{*{20}l} {\varvec{u}.\nabla \varvec{u} = - \frac{1}{\rho }\nabla p + \nu \nabla^{2} \varvec{u},} \\ {\nabla .\varvec{u} = 0.} \\ \end{array} } \right.$$
(3)

where \(\varvec{u}\) is the velocity vector and open form of Eq. (3) is as follows:

Momentum in x-direction:

$$w\frac{\partial u}{\partial z} + v\frac{\partial u}{\partial y} + \frac{u}{(R + z)}\frac{\partial u}{\partial x} + \frac{uw}{(R + z)} = - \frac{1}{(R + z)}\frac{\partial p}{\partial x} + \left[ {\frac{{\partial^{2} u}}{{\partial z^{2} }} + \frac{1}{(R + z)}\frac{\partial u}{\partial z} + \frac{{\partial^{2} u}}{{\partial y^{2} }} + \frac{1}{{(R + z)^{2} }}\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{1}{{(R + z)^{2} }}\left( {2\frac{\partial w}{\partial x} - u} \right)} \right].$$
(4)

Momentum in y-direction:

$$w\frac{\partial v}{\partial z} + v\frac{\partial v}{\partial y} + \frac{u}{(R + z)}\frac{\partial v}{\partial x} + = - Re^{2} \frac{\partial p}{\partial y} + \left[ {\frac{{\partial^{2} v}}{{\partial z^{2} }} + \frac{1}{(R + z)}\frac{\partial v}{\partial z} + \frac{{\partial^{2} v}}{{\partial y^{2} }} + \frac{1}{{(R + z)^{2} }}\frac{{\partial^{2} v}}{{\partial x^{2} }}} \right].$$
(5)

Momentum in z-direction:

$$w\frac{\partial w}{\partial z} + v\frac{\partial w}{\partial y} + \frac{u}{(R + z)}\frac{\partial w}{\partial x} - \frac{{u^{2} \text{Re}^{2} }}{(R + z)} = - Re^{2} \frac{\partial p}{\partial z} + \left[ {\frac{{\partial^{2} w}}{{\partial z^{2} }} + \frac{1}{(R + z)}\frac{\partial w}{\partial z} + \frac{{\partial^{2} w}}{{\partial y^{2} }} + \frac{1}{{(R + z)^{2} }}\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{1}{{(R + z)^{2} }}\left( { - w - 2\frac{\partial u}{\partial x}} \right)} \right].$$
(6)

Continuity equation:

$$\frac{1}{(R + z)}\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z} + \frac{w}{(R + z)} = 0.$$
(7)

where velocity components in x-, y- and z-directions are shown by u, v and w. Moreover, \(p\) is representative of the pressure. Commercial CFD package ANSYS-CFX [42] is used to solve of governing Eqs. (4) to (7) for flow through the considered duct.

Spatially stream-wise uniform velocity is considered for inlet boundary condition, and no-slip boundary condition is applied for rigid walls. Moreover, opening boundary condition is used for flow exits. This selection is due to that the details of velocity of fluid flow are not known and this boundary condition has no impression on the upstream fluid flow [43, 44]. In the present paper, we used element-based finite volume method by coupled solver of ANSYS-CFX. In addition, standard Rhie–Chow interpolation is used to interpolate the pressure [45]. In addition, second-order accurate scheme shape functions are computed for the diffusion term. Moreover, high-resolution scheme is implemented for the advection term. Then, we studied the grid independency analysis and model validation to select an appropriate mesh structure for considered computational domain.

2.2 Model validation

We conducted a comprehensive mesh sensitivity analysis to find proper mesh structure for our computational domain. This model validation is performed with details in our previous paper (see Ref [41]). However, for convenience of the readers, some details are presented in this subsection. Results of grid independency analysis on velocity profile in the curved square duct compared to experimental data in Ref. [13] at Re = 574 are shown in Fig. 2. According to Fig. 2, we tested four different mesh resolutions. Quantitative comparison between our numerical results of stream-wise velocity with experimental data in Ref. [13] for angular positions of 36° and 144° is also tabulated in Table 2. For more details, total number of cells and calculated root mean square error (RMSE) are presented in Table 3. The results of mesh sensitivity analysis in case of Re = 3000 (i.e., the highest considered Reynolds number) are also provided in Fig. 3. As illustrated in Fig. 3 and Table 3, the differences on the maximum, minimum and RMSE of the velocity profile between Mesh 3 and Mesh 4 are obtained less than 1.15E − 3. Now, according to Figs. 2 and 3, one can be concluded that Mesh 3 with ∆grid = 4.52 × 10−4 in the cross section of the duct, ∆grid = 2×10−3 for the straight duct (in stream-wise direction) and ∆grid = 9.61 × 10−4 for the curved duct (in stream-wise direction), is an appropriate selection for considered computational domain. Figure 4 presents the schematic of selected structured hexahedral mesh applied on our computational domain.

Fig. 2
figure 2

(taken from Ref [41])

Obtained numerical stream-wise velocity profile in comparison with experimental results in Ref. [13] at Re = 574 for angular positions of a 36°, b 90° and c 144°

Full size image
Table 2 Quantitative comparison between the obtained numerical results of stream-wise velocity with Ref. [13] at Re = 574 for angular positions of 36° and 144°
Full size table
Table 3 Number of total cells used in validation case (i.e., Reynolds number = 574) and RMSE of each case in comparison with the archival experimental data in Ref. [13] (taken from Ref [41])
Full size table
Fig. 3
figure 3

(taken from Ref [41])

Numerical profile of stream-wise velocity at Re = 3000 under different mesh resolutions for angular positions of a 36°, b 90° and c 144°

Full size image
Fig. 4
figure 4

(taken from Ref [41])

Considered mesh structure

Full size image

Then, the formulation of the 3D energy gradient function K for flow through the curved duct is obtained.

3 Energy gradient method

In energy gradient theory (see more details of this theory in Refs. [34, 35, 46]), fluid flow field is considered as the energy field. Based on this theory, one of the main reasons behind of fluid motion is the energy gradient. Indeed, in case of no external force acting on fluid, the power of motion and change of fluid flow state is energy gradient. Kinematic energy gradient in transverse direction of fluid flow will be generated a driving force that leads to the increase in flow disturbance. These disturbances will be absorbed by the flow viscous friction gradient. Amplifying disturbances is due to large gradient of energy in the transversal direction, while viscous friction generated with shear stress will be resulted to stability of flow via damping the fluctuations. By increasing the transversal energy gradient, laminar state will lose its capability to balance the fluctuations and this will result in the inception of hydrodynamic instability. In summary, energy gradient in cross-stream is the reason for growth of small perturbations on the basic fluid flow, while stream-wise viscous loss is the reason for decay of these disturbances. So, the proportion of energy gradient amplification in cross-stream direction to the friction damping in stream-wise direction can be defined as hydrodynamic stability criteria as follows [34, 35]:

$$F = \frac{\Delta E}{\Delta H} = \frac{{\left( {\frac{\partial E}{\partial n}\frac{{2\bar{A}}}{\pi }} \right)}}{{\left( {\frac{\partial H}{\partial s}\frac{\pi }{\omega }\varvec{u}} \right)}} = \frac{2}{{\pi^{2} }}K\frac{{\bar{A}\omega }}{\varvec{u}} = \frac{2}{{\pi^{2} }}K\frac{{u^{\prime}_{m} }}{\varvec{u}} < Const.$$
(8)

where \(\Delta E\) is representative of total energy in the cross-stream direction (in unit volumetric fluid) and the loss of stream-wise total energy (in unit volumetric fluid) is shown by \(\Delta H\). Moreover, \(E = p + 0.5\rho \varvec{u}^{2}\) is total mechanical energy and hydrodynamic pressure is \(p\). In addition, \(\bar{A}\) is the amplitude of the distance of disturbance, \(u^{\prime}_{m}\) is the amplitude of the velocity disturbance corresponding to \(u^{\prime} = u^{\prime}_{m} \cos \left( {\omega t + \varphi_{0} } \right)\) and \(\omega\) is the disturbance frequency. The indicators of \(n\) and \(s\) are representative of directions in cross-stream and in the stream-wise, respectively. Moreover, in Eq. (8), the parameter of K has the following form:

$$K = \frac{{{\raise0.7ex\hbox{${\partial E}$} \!\mathord{\left/ {\vphantom {{\partial E} {\partial n}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\partial n}$}}}}{{{\raise0.7ex\hbox{${\partial H}$} \!\mathord{\left/ {\vphantom {{\partial H} {\partial s}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\partial s}$}}}}$$
(9)

Based on Eq. (8), we have hydrodynamically unstable flow by an increase in magnitude of F. Therefore, we have stable state for fluid below the constant certain value of F. Moreover, according to Eqs. (8) and (9), one can be concluded that two main affective parameters on the instability are K function and value of relative disturbance velocity (\({{u^{\prime}_{m} } \mathord{\left/ {\vphantom {{u^{\prime}_{m} } \varvec{u}}} \right. \kern-0pt} \varvec{u}}\)). For \(K_{\rm{max} } < K_{c}\), the fluid flow is hydrodynamically stable, while the fluid flow is unstable at \(K_{\rm{max} } > K_{c}\) (where \(K_{\rm{max} }\) and \(K_{c}\) are maximum of \(K\) and critical value of \(K_{\hbox{max} }\), respectively). In case of the curved duct, cross-stream gradient of total mechanical energy for flow is (see Fig. 1):

$$\frac{\partial E}{\partial n} = \frac{{\partial \left( {p + \rho \varvec{u}^{2} /2} \right)}}{\partial n} = \frac{\partial p}{\partial n} + \rho \varvec{u}\frac{{\partial \varvec{u}}}{\partial n}$$
(10)

where, in case of the pressure driven flow through the curved square duct, energy loss is [35]:

$$\frac{\partial H}{\partial s} = \frac{2\tau }{r} + \frac{\partial \tau }{\partial r}$$
(11)

where \(\tau\) as shear stress has the following form:

$$\tau = \mu \left( {\frac{{\partial \varvec{u}}}{\partial r} - \frac{\varvec{u}}{r}} \right)$$
(12)

where \(\mu\) is the dynamic viscosity and we can redefine Eq. (11) as follows:

$$\frac{\partial H}{\partial s} = 2\frac{\mu }{r}\left( {\frac{{\partial \varvec{u}}}{\partial r} - \frac{\varvec{u}}{r}} \right) + \mu \left( {\frac{{\partial^{2} \varvec{u}}}{{\partial r^{2} }} + \frac{\varvec{u}}{{r^{2} }} - \frac{1}{r}\frac{{\partial \varvec{u}}}{\partial r}} \right) = \frac{\mu }{r}\frac{{\partial \varvec{u}}}{\partial r} - \frac{{\mu \varvec{u}}}{{r^{2} }} + \mu \frac{{\partial^{2} \varvec{u}}}{{\partial r^{2} }}$$
(13)

Assumption of \(\frac{1}{r} = \frac{1}{{\rho \varvec{u}^{2} }}\frac{\partial p}{\partial n}\) will be resulted to redefinition of Eq. (13) in form of:

$$\frac{\partial H}{\partial s} = \mu \left( {\frac{{\partial^{2} \varvec{u}}}{{\partial n^{2} }} + \frac{1}{{\rho \varvec{u}^{2} }}\frac{{\partial \varvec{u}}}{\partial n}\frac{\partial p}{\partial n} - \frac{1}{{\rho^{2} \varvec{u}^{3} }}\left( {\frac{\partial p}{\partial n}} \right)^{2} } \right)$$
(14)

Now, energy gradient function K as stability parameter will be achieved via substitution of Eqs. (10) and (14) into Eq. (9) as follows:

$$K = \frac{{\frac{\partial p}{\partial n} + \rho \varvec{u}\frac{{\partial \varvec{u}}}{\partial n}}}{{\mu \left( {\frac{{\partial^{2} \varvec{u}}}{{\partial n^{2} }} + \frac{1}{{\rho \varvec{u}^{2} }}\frac{{\partial \varvec{u}}}{\partial n}\frac{\partial p}{\partial n} - \frac{1}{{\rho^{2} \varvec{u}^{3} }}\left( {\frac{\partial p}{\partial n}} \right)^{2} } \right)}}$$
(15)

Geometrical relations among the gradient of a variable such as \(\varphi\) in s–n coordinate system and considered Cartesian system is shown in Fig. 5. Based on Fig. 5, we have the following geometrical relation:

$$\frac{\partial \varphi }{\partial n}_{3D} = \sqrt {\left( {\frac{\partial \varphi }{\partial n}_{2D} } \right)^{2} + \left( {\frac{\partial \varphi }{\partial y}} \right)^{2} }$$
(16)

where \(\frac{\partial \varphi }{\partial n}_{2D}\) is:

$$\frac{\partial \varphi }{\partial n}_{2D} = \sqrt {\left( {\frac{\partial \varphi }{\partial x}} \right)^{2} + \left( {\frac{\partial \varphi }{\partial z}} \right)^{2} } \sin \left( \delta \right)$$
(17)
Fig. 5
figure 5

(taken from Ref [41])

Parameter \(\varphi\) between two considered coordinates

Full size image

Now, we can extract 3D dimensionless function of K for flow through the curved duct via substitution of Eqs. (16) and (17) into Eq. (15):

$$K = \frac{{\sqrt {\left( {\sqrt {\left( {\frac{\partial p}{\partial x}} \right)^{2} + \left( {\frac{\partial p}{\partial z}} \right)^{2} } \sin \left( \delta \right)} \right)^{2} + \left( {\frac{\partial p}{\partial y}} \right)^{2} } + \rho \varvec{u}\sqrt {\left( {\sqrt {\left( {\frac{{\partial \varvec{u}}}{\partial x}} \right)^{2} + \left( {\frac{{\partial \varvec{u}}}{\partial z}} \right)^{2} } \sin \left( \delta \right)} \right)^{2} + \left( {\frac{{\partial \varvec{u}}}{\partial y}} \right)^{2} } }}{B}$$
(18)

where

$$B = \mu \left( \begin{aligned} &\sqrt {\left( {\sqrt {\left( {\frac{{\partial^{2} \varvec{u}}}{{\partial x^{2} }}} \right)^{2} + \left( {\frac{{\partial^{2} \varvec{u}}}{{\partial z^{2} }}} \right)^{2} } \sin \left( \delta \right)} \right)^{2} + \left( {\frac{{\partial^{2} \varvec{u}}}{{\partial y^{2} }}} \right)^{2} } \hfill \\ &+ \frac{1}{{\rho \varvec{u}^{2} }}\sqrt {\left( {\sqrt {\left( {\frac{{\partial \varvec{u}}}{\partial x}} \right)^{2} + \left( {\frac{{\partial \varvec{u}}}{\partial z}} \right)^{2} } \sin \left( \delta \right)} \right)^{2} + \left( {\frac{{\partial \varvec{u}}}{\partial y}} \right)^{2} } \sqrt {\left( {\sqrt {\left( {\frac{\partial p}{\partial x}} \right)^{2} + \left( {\frac{\partial p}{\partial z}} \right)^{2} } \sin \left( \delta \right)} \right)^{2} + \left( {\frac{\partial p}{\partial y}} \right)^{2} } \hfill \\ &- \frac{1}{{\rho^{2} \varvec{u}^{3} }}\left( {\left( {\sqrt {\left( {\frac{\partial p}{\partial x}} \right)^{2} + \left( {\frac{\partial p}{\partial z}} \right)^{2} } \sin \left( \delta \right)} \right)^{2} + \left( {\frac{\partial p}{\partial y}} \right)^{2} } \right) \hfill \\ \end{aligned} \right)$$
(19)

It is also notable that, based on the Prandtl [47] investigation, two kinds of steady secondary motions are detectable in flow. Mean flow corresponding to the curvature effect (i.e., pressure driven) is the reason for generation of the first kind. Second kind is also corresponding to the turbulence in transverse plane. One of the main scenarios behind of Prandtl’s second kind is an imbalance on the normal Reynolds stress in cross-stream [48, 49]. This scenario is corresponding to “Dean number” and “dimensionless energy gradient function”. Indeed, as may be seen in Eq. (1), De is corresponding Re (i.e., inertial forcers per viscous forces) at specified curvature ratio. So, rate of the inertial forcers per viscous forces and imbalance of Reynolds stress can be controlled by Dean number. In addition, as shown in Eqs. (9) to (19), dimensionless energy gradient function K (i.e., total cross-stream mechanical energy per total viscous friction in the stream-wise direction) is another control parameter on hydrodynamics instability and secondary flow formation.

Moreover, one can be concluded that the essence of Dean number is relevant by dimensionless energy gradient function K. Therefore, critical Dean number and physical phenomenon such as Dean vortices are directly effective on energy distribution in the curved duct. Indeed, Dean vortices are local regions where the total cross-stream mechanical energy is significantly greater than viscous friction in the stream-wise direction. Consequently, higher value of dimensionless energy gradient function K is detectable in these local regions.

4 Results and discussion

4.1 Effects of Dean numbers (Reynolds numbers)

At first, the influences of various Dean numbers in the range of 19.69 up to 1181.25 (equal to 50 ≤ Re ≤ 3000) on fluid flow behavior and instability through the considered duct are investigated. For this purpose, as shown in Fig. 6, nine sections with their mid-plane lines at y = 0 are selected.

Fig. 6
figure 6

(taken from Ref [41])

Considered sections along the azimuthally angular positions via their mid-plane line at y = 0

Full size image

In order to investigate the instability through the curved square duct, distributions of velocity and total pressure are analyzed. Then, we evaluated the parameter of K at different Dean numbers.

Velocity and total pressure distribution vs. dimensionless radius r − R from − 0.5 (i.e., inner curvature wall) to 0.5 (i.e., outer curvature wall) on the mid-plane lines (see Fig. 6) in the considered duct at different De are presented in Fig. 7. According to Fig. 7, for De > 78.75 similar trend on velocity profiles is detected at all considered angular positions. At entry flow region (i.e., θ ≤ 18°), maximum of velocity profiles is located at r − R = 0. Afterward, the peak of velocity profiles moved toward the curvature wall at r − R = 0.4 for 18° < θ < 36°. Peak of velocity profiles remains there with progress of fluid flow up to θ = 72°, especially for De > 590.62. However, for 78.75 < De < 590.62, peak of velocity profiles is moved to r − R about 0.27 – 0.3. It is notable that the maximum of velocity is diminished at θ > 36° for 78.75 < De < 590.62, while we found this reduction on peak of the velocity profiles at θ > 72° for De > 590.62. This may be related to the tendency of the flow regime to conserve the initial momentum at the entry flow region via strong flow nearby the outer curvature wall. According to transfer of momentum toward the interior curvature wall at 78.75 < De < 590.62, values of velocity profiles in the distance of r − R = (− 0.2, 0.3) are enhanced by flow progress from θ = 36° up to θ = 108°. This is also observed for flow progress from θ = 36° up to θ = 162° for 590.62 < De < 1181.25, and it is in accordance with Helal et al. [22] study. Due to intrinsic tendency of flow regime to being fully develop at θ = 108° to θ = 126°, we have insignificant changes on velocity profiles via progress of fluid flow for 78.75 < De < 590.62. However, for De > 590.62, more fluctuations on the velocity profiles are achieved, especially for θ > 108°. In addition, maximum of velocity profiles are moved toward the ducts’ center, which may be related to generate of additional vortex pair on the stream-wise flow.

Fig. 7
figure 7figure 7

Velocity and total pressure distribution at various Dean numbers in the range of 19.69 up to 1181.25

Full size image

At the entrance zone, due to smaller centrifugal force compared to inertial and viscous forces (i.e., θ < 18°), we found symmetry structure on the total pressure profiles at low Dean numbers. As flow progresses through the duct, the peak of the pressure is shifted into the outer wall. This is because of the increase in centrifugal force effects by increasing the Dean number. Therefore, for higher Dean numbers, during the momentum transfer into the exterior wall, maximum of total pressure is located nearby the outer curvature wall at θ < 72°. According to imbalance among the radial pressure gradient and centrifugal forces in the vicinity of outer curvature wall, partial back-transfer of flow momentum (i.e., maximum of total pressure) into the center of the duct is achieved for θ > 90° under 226.01 < De < 590.62. Generation of counter-rotating vortex motion (i.e., Dean roll cells as main secondary flow) is related to the partial back-transfer of flow momentum. For θ > 108° at De > 590.62, peaks on velocity and total pressure profiles are representative of Dean hydrodynamic instability with additional Dean vortices which are also observed in Krishna et al. [23] study.

Figure 8 shows distribution of velocity contours on different computational sections (see Fig. 6) for Dean numbers ranging from 19.69 to 1181.25. Based on Fig. 8, local regions with highest velocity are moved to the exterior curvature wall by increasing the De and via progress of flow in the duct. These local zones are back-transferred toward the duct’s center as counter-rotating motion. Then, we observed an insignificant change on these local regions nearby the outer curvature wall. It is notable that the fluid flow behavior in these contours is in agreement with distribution of velocity profiles in Fig. 7.

Fig. 8
figure 8figure 8figure 8

Velocity contour distribution on the considered computational sections at different Dean numbers in the range of 19.69–1181.25

Full size image

For more details on flow behavior, Fig. 9 shows stream-wise contour of the velocity via vorticity contours at θ = 36° to θ = 144°. Based on Fig. 9, concentration of fluid momentum is moved toward the outer curvature wall. Afterward it is expanded in the local zone between the outer wall and the center of the duct.

Fig. 9
figure 9

Stream-wise velocity contour distribution via of cross-stream vorticity contours at θ = 36° up to θ = 144° under two Dean numbers 226.01 and 1181.25

Full size image

Figure 10 presents the distribution of K at various Dean numbers. As shown in Fig. 10, values of K on the mid-plane lines are decreased nearby the inner and outer duct’s walls for 19.69 < De < 393.75. Moreover, maximum of K-value is achieved at the outlet region (i.e., θ > 162°) nearby the inner wall for Dean numbers of 393.75 and 590.62. In addition, average of the K-value is remarkably enhanced for De ≥ 787.5. We also found that the K-value is decreased in the local zone among the center of the duct and exterior curvature wall for De = 78.75. However, similar trends on K-value are obtained by progress of flow in the duct for Dean number up to 590.62. For De > 590.62, significant increase in the K-value is detected in the local zone among the center of the duct and exterior curvature wall via progress of fluid flow from θ = 108° to θ = 162°. It should be noted that the peaks on the diagrams of K are in accordance with inflection points on velocity profiles (see Fig. 7).

Fig. 10
figure 10

Distribution of K at various Dean numbers in the range of 19.69 to 1181.25

Full size image

For better assessment of K-values, contours of K-distribution on the sections of 54°, 90° and 126° at various Dean numbers are presented in Fig. 11. Based on Fig. 11, for Dean number up to 78.75, the highest K-value are detected at the local regions of the main secondary flow. Consequently, the flow is unstable in these local regions. Subsequently, maximum of K-values is found nearby the upper and lower duct’s wall, especially on margins of additional Dean vortices for De = 226.01 at θ = 54°. It is notable that these local zones are the most possible regions to onset of hydrodynamic instability. At De = 226.01, the local region with highest K-value is moved to the corner vortices nearby the upper and lower duct’s wall by flow progress up to θ = 126°. At De > 226.01, local regions with the highest K-value are formed among the center of the duct and exterior wall, especially for θ = 54° up to θ = 90°. In addition, the vortex-like lines with highest K-values (i.e., additional pair of Dean vortices) are enhanced by increasing the Dean number from 226.01 up to 1181.25. This is related to the growth of the centrifugal forces effects (i.e., transversal pressure gradient) by increasing the De. It should be pointed that local regions with the highest K-values are positions where the impressions of centrifugal forces have been strengthened there.

Fig. 11
figure 11figure 11

Distribution of K-value on the sections of 54°, 90° and 126° at various Dean numbers in the range of 19.69–1181.25

Full size image

Figure 12 shows the isosurface of dimensionless function K (under the constant value 20) with cross-sectional K-contours from θ = 36° to θ = 144° at two Dean numbers of 78.75 and 1181.25. As shown in Fig. 12, the isosurface of K is placed on the local regions with highest dimensionless function K. Moreover, the local areas of the K-isosurface are expanded on the main secondary flow on the lower and upper duct’s walls by an increase in the Dean number.

Fig. 12
figure 12

Isosurface of K-value (under constant value 20) with cross-sectional K-contours from θ = 36° to θ = 144° at two Dean numbers: 78.75 and 1181.25

Full size image

As stated before, position of \(K_{\rm{max} }\) is the local place where fluid flow is initially losing its hydrodynamic stability. For more quantitative details about the critical K-values, Table 4 presented for values of \(K_{\rm{max} }\) and its cylindrical coordinates (see Fig. 1) under different Dean numbers. According to Table 4, the value of \(K_{\rm{max} }\) has become greater by an enhancement in Dean number. As given in Table 4, angular position of \(K_{\rm{max} }\) with the highest possibility to onset of instability is generally located at θ < 72° (i.e., the entrance and overshoot regions). In addition, radial position of \(K_{\rm{max} }\) is generally located in the local zone among the center of the duct center and exterior curvature wall.

Table 4 Local positions and values of \(K_{\rm{max} }\) under different Dean numbers
Full size table

5 Conclusions

We used CFD simulation and energy gradient method to study the hydrodynamic stability of 3D flow through the curved duct with square cross section under different Dean numbers ranging from 19.68 to 1181.249 (i.e., corresponding to Reynolds numbers in the range of 50 to 3000). Three significant findings of the current paper are as follows:

  1. 1.

    Imbalance of pressure gradient among the center of the duct and outer wall is strengthened, and the \(K_{\rm{max} }\) is enhanced by increasing the Dean number. As a result, as Dean number increases, the fluid flow becomes more hydrodynamically unstable.

  2. 2.

    By increasing the Dean numbers, more additional Dean vortices are detected on the fluid flow domain which are corresponding to bifurcation on velocity and total pressure profiles.

  3. 3.

    Azimuthally angular position of \(K_{\rm{max} }\) is generally achieved at θ < 72° (i.e., entrance and overshoot regions), and the radial position of \(K_{\rm{max} }\) is occurred in the local zone among the center of the duct and outer curvature wall. According to energy gradient theory, these zones have the highest probability for onset of instability in the entire flow field of our problem.

Finally, we reported \(K_{\rm{max} }\) and its coordinates at various Dean numbers. More assessment on the other geometrical designs for inflow to achieve an improved energy distribution can be intended in future studies.