Introduction

The nonlinear mechanical response of many materials, when subjected to large deformation or stress, changes from being predominantly elastic (solid-like) to predominantly plastic (liquid-like) (Stokes et al. 2008). This transition is called yielding. One of the experimental techniques to investigate the nonlinear response of soft materials involves subjecting them to oscillatory shear flow in which the shear strain \(\gamma =\gamma _{0} \sin \left ( {\omega t} \right )\) is varied by ramping its amplitude \(\gamma _{0}\) at a constant frequency. For an arbitrary strain amplitude, the measured stress \(\sigma (t)\) can be deconvoluted into an in-phase response, characterized by the elastic modulus \(G^{\prime }\), and an out-of-phase response, characterized by the viscous modulus \(G^{\prime \prime }\). An accurate representation of the stress response would consist of Fourier harmonics of the elastic and viscous moduli (Ewoldt et al. 2008). However, harmonics higher than the first can be neglected for moderate strain amplitudes at which yielding is most often seen in soft materials. Thus in an amplitude sweep test, the mechanical response of soft materials changes from being elastic (\(G^{\prime }>G^{\prime \prime }\)) at small strain to viscous (\(G^{\prime }<G^{\prime \prime }\)) at large strain.

At intermediate strain, many metastable soft materials show a characteristic response in which the viscous modulus increases from its linear value up to a maximum value \(G_{\text {max}}^{\prime \prime }\) before falling off, while the elastic modulus decreases monotonically with strain and crosses below the viscous modulus at the yield point. This nonmonotonic \(G^{\prime \prime }\) response, also called the type III LAOS behavior (Hyun et al. 2002), has been reported earlier for carbon composites of butyl rubber (Payne 1963), soft colloidal glasses (Brader et al. 2010), emulsions (Mason et al. 1995; Bower et al. 1999), gels (Altmann et al. 2004), electrorheological fluids (Parthasarathy and Klingenberg 1999; Sim et al. 2003), associating polymer solutions (Tirtaatmadja et al. 1997a, b), and weakly structured materials such as xanthan gum solutions (Song et al. 2006). On the other hand, polymeric fluids such as solutions and melts, which are ergodic, are typically known to exhibit strain-softening response (Doi and Edwards 1986) in which chain orientation causes both moduli to decrease monotonically with increasing shear strain.

Recently, Miyazaki et al. (2006) proposed an elegant qualitative argument for explaining the origin of the nonmonotonic \(G^{\prime \prime }\) response based on the reasoning that yielding involves a strain-induced decrease in the characteristic relaxation time of the material. The authors proposed that the nonmonotonic \(G^{\prime \prime }\) behavior should be observable in all complex fluids. In this work, we validate this hypothesis by demonstrating experimentally the universality of the yielding response. We also extend the argument further to infer an interesting dynamical feature.

Model

Following Miyazaki et al. (2006), we may represent any viscoelastic fluid by a parallel combination of N Maxwell elements, each consists of linear springsFootnote 1 in series with nonlinear dashpots so that the relaxation times (\(\lambda _{i}\)) of the Maxwell elements are given by some decreasing function of the strain amplitude such as

$$ \frac{1}{\lambda_{i} \left({\gamma_{0}}\right)}=\frac{1}{\lambda_{i}^{\text{LVE}}}+k\left({\omega \gamma_{0}}\right)^{m}. $$
(1)

In Eq. 1, \(\lambda _{i}^{\text {LVE}}\) represents the characteristic relaxation time for the ith mode in the linear regime, i.e., under small imposed strain. The validity of Eq. 1 with \(m \approx 1\) for nonlinear deformations of metastable materials was demonstrated by Wyss et al. (2007), Yamamoto and Onuki (1998), Leonardo et al. (2005), and Kalelkar et al. (2010). Incidentally, Eq. 1 also describes the so-called convective constraint release mechanism of stress relaxation in entangled polymer melts subjected to high shear (Marrucci 1996). Thus, the use of Eq. 1 for describing the strain dependence of relaxation times of many soft materials in the nonlinear regime appears justified. Indeed, Eq. 1 is a simplified version of the model proposed by Derec et al. (2001) who, in addition to considering the strain dependence of relaxation times, have also taken into account the influence of possible aging effects.

The elastic and viscous moduli for the Maxwell model can be written as

$$\begin{array}{@{}rcl@{}} G^{\prime} \left({\omega ,\gamma_{0}}\right)&=&\sum\nolimits_{i}^{N} \frac{g_{i}\left[{\omega \lambda_{i} \left({\gamma_{0}}\right)} \right]^{2}}{1+\left[{\omega \lambda_{i} \left({\gamma_{0}}\right)}\right]^{2}};\\ G^{\prime\prime}\left({\omega ,\gamma_{0}}\right)&=&\sum\nolimits_{i}^{N} {\frac{g_{i}\left[{\omega \lambda_{i}\left({\gamma_{0}}\right)} \right]}{1+\left[{\omega \lambda_{i} \left({\gamma_{0}}\right)}\right]^{2}}}. \end{array} $$
(2)

Here, \(\lambda _{i}(\gamma _{0}\)) is given by Eq. 1. Miyazaki et al. (2006) explained the strain dependence of \(G^{\prime \prime }\) by considering a single mode (\(N = 1\)) in Eq. 2. The frequency regime of interest is one in which the material is predominantly elastic at small strains so that the Deborah number is given by \(\omega \lambda _{C}^{\text {LVE}} \gg 1\), where \(\lambda _{C}^{\text {LVE}}\) is a strain-independent characteristic time of the material that is experimentally measured as the inverse of the crossover frequency. At small strain amplitudes, \(G^{\prime }\sim g\) and \(G^{\prime \prime }\hspace *{-2pt}\sim \hspace *{-2pt}g\left /\right . {\omega \lambda _{C}^{\text {LVE}}}\) so that \(G^{\prime }>G^{\prime \prime }\) and both are independent of the applied strain. At moderate strain amplitudes, just after the linear regime, the Deborah number is still \(\omega \lambda _{c} \left ( {\gamma _{0}} \right )>1\) but the relaxation time decreases upon increasing strain so that \(G^{\prime \prime }\hspace *{-2.5pt}\sim \hspace *{-2.5pt}g\left /\right . {\omega \lambda _{c} \left ({\gamma _{0}} \right )}\) is an increasing function of strain. For large strain amplitudes, the effective strain rate reduces the relaxation time to the extent where \(\omega \lambda _{C} \left ({\gamma _{0}} \right )\ll 1\), so that the moduli in Eq. 2 can be approximated as \(G^{\prime \prime } \sim g_{i}\left [ {\omega \lambda \left ( {\gamma _{0}} \right )} \right ];G^{\prime } \sim g_{i} \left [ {\omega \lambda \left ( {\gamma _{0}} \right )} \right ]^{2}\) indicating both \(G^{\prime }\) and \(G^{\prime \prime }\) to be decreasing functions of strain, with \(G^{\prime \prime }>G^{\prime }\). Further, the model also predicts the crossover point, i.e., the macroscopic yield point at

$$ \omega \lambda_{C} \left( {\gamma_{0,\mathrm{y}}}\right)=1,\;\text{where}\;G^{\prime}=G_{\text{max}}^{\prime \prime} =g\left/\right.2. $$
(3)

In Eq. 3, \(\gamma _{0,y}\) is the yield strain, which is unity when normalized as \(\widetilde {\gamma }_{0,y} =k\gamma _{0,y} \cong 1\) [cf. Eq. 1].

Since Eq. 1 invokes neither the microstructural details of soft materials nor their dynamical details, the Miyazaki argument presented above should be equally valid for all viscoelastic fluids as long as they are probed in an appropriate frequency window. In what follows, we demonstrate this experimentally for different complex fluids, which are chosen such that under near-quiescent conditions, some of them are in equilibrium state (polystyrene melt, surfactant lamellar phase) and some in metastable state (microgel dense suspension, hair gel, xanthan gum, and gelatin). The chosen materials also have very different microstructures.

Experimental procedures

Sample preparation

Poly(N-isopropylacrylamide) microgels

Poly(N-isopropylacrylamide) (PNIPAm) microgels (Pelton and Chibante 1986) were synthesized by free radical precipitation polymerization as prescribed by Senff and Richtering (2000). Sodium dodecyl sulfate (0.15 g) was used as a stabilizer and potassium per sulfate (KPS 0.3 g) as an initiator, and cross-linking was done by poly(ethylene glycol) diacrylate (\(\text {Mw} = 700\) kg/mol, 0.157 g). Polymerization was carried out in a double-jacketed glass kettle reactor connected to a temperature-controlled water circulator and an overhead stirrer. All reactants except the initiator were mixed in 480 ml of deionized water at 25 °C and stirred at 300 rpm for 30 min under inert atmosphere. The reaction mixture was heated to \(70~\circ\)C followed by addition of the initiator (0.3 g of KPS in 20 ml deionized water). The reaction was allowed to proceed for 4 h under nitrogen. The temperature was then reduced to 25\(~\circ\)C, and the reaction mixture was stirred overnight at 100 rpm. Finally, the dispersion was dialyzed (using dialysis bags having a molecular weight cutoff of 10,000 g/mol) against deionized water for 2 weeks. The dialyzed sample was lyophilized for 8 h and stored in a desiccator. Concentrated suspension (6 wt %) was then prepared by dispersing a known amount of polymer in deionized water. As these microgels are soft and compressible, they seldom crystallize at very high concentrations. The hydrodynamic radius \(R_{h} = 137\) nm at 25\(~\circ\)C was measured from dynamic light scattering experiments (Brookhaven Instruments).

Xanthan gum

A 2-wt % aqueous suspension of xanthan gum gives a soft colloidal glass (Song et al. 2006). Ninety-eight milliliters of water was taken in a beaker and stirred at \(\sim 500\) rpm with the help of an overhead stirrer. Two grams of xanthan gum powder was added very slowly to the continuously stirred water. This ensured complete and homogenous mixing of the powder. Stirring was continued for another 30 min, and the suspension was stored at 5\(~\circ\)C in a screw-capped container.

Surfactant lamellar phase

A 90-wt % aqueous suspension of a nonionic surfactant C\(_{12}\textit {E}_{9}\) (Rylo) was prepared using deionized water. The suspension was heated above the isotropic temperature (\(\sim 40~\circ\)C) on a water bath. This warm solution was then mixed vigorously using a vibrato meter. Bubbles trapped were removed by sonication and multiple cycles of heating and cooling above the isotropic melting temperature. A thermodynamically stable homogenous lamellar phase was formed at room temperature (\(\sim 25~\circ\)C) as confirmed by small-angle X-ray scattering (Kulkarni et al. 2011).

Gelatin

A 14-wt % gelatin solution was prepared in deionized water. The gel was made in a petri dish. Heating the solution above 40\(~\circ\)C helps to homogenize the gelation powder. On cooling the solution to room temperature, the gel takes the shape of the container at room temperature (\(\sim 25~\circ\)C).

Hair gel

A commercial hair gel (Park Avenue) was used as received.

Polystyrene melt

Polystyrene (\(\text {Mw}\sim 550,000\) g/mol, \(\text {PDI}\sim 1.05\)) was purchased from Sigma-Aldrich (GPC grade), and disk samples (25 mm in diameter) were prepared by compression molding at 170\(~\circ\)C.

Rheological measurements

Rheological experiments for all samples except polystyrene were done on a MCR 301 (Anton Paar) rheometer. The geometry used was a cone–plate (cone angle 1°, diameter 25 mm). Polystyrene disks were tested on an ARES-G2 (TA Instruments) rheometer using 25-mm parallel plates. Oscillatory strain sweep tests were performed at constant frequency and temperature. Experiments were conducted at various frequencies and at temperatures so chosen that the samples exhibited dominantly elastic response at small strain. Linear viscoelastic frequency response was measured by performing frequency sweep tests at a constant strain chosen from the linear viscoelastic (LVE) regime.

Results and discussions

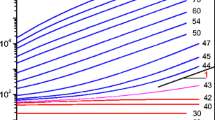
Figure  1(a–f) shows that all materials, including the entangled polystyrene melt and the lamellar surfactant phase, show a nonmonotonic \(G^{\prime \prime }\) response followed by a crossover of the moduli, which we define as the macroscopic yielding event. Figure 1(g–l) shows that the LVE frequency response of all these materials, irrespective of their microstructure and thermodynamic state, is qualitatively similar: \(G_{\text {LVE}}^{\prime } >G_{\text {LVE}}^{\prime \prime }\), suggesting that in the frequency–temperature–density window of observation, the fluid is predominantly elastic at small strain, \(G_{\text {LVE}}^{\prime \prime } \) increases monotonically but weakly with frequency, whereas the \(G_{\text {LVE}}^{\prime \prime }\) shows nonmonotonic frequency dependence with a minimum at intermediate frequency. Thus, the data corroborate the simple arguments presented in the Section “Model” and underline the similarity of patterns observed in the yielding process in complex fluids.

Fig. 1
figure 1

Amplitude sweep at frequency where maximum in normalized \(G^{\prime \prime }\) is observed (a–f). Frequency sweep (in LVE) and normalized \(G^{\prime \prime }\) at different frequencies for different materials (g–l). PNIPAm suspension at \(20~\circ\)C and frequency of 1 rad/s (a, g), lamellar phase of C\(_{n}\textit {H}_{2n+1}\) surfactant at 25\(~\circ\)C and frequency of 1 rad/s (b, h), hair gel at 25\(~\circ\)C and frequency of 0.5 rad/s (c, i), xanthan gum solution at 25\(~\circ\)C and frequency of 1 rad/s (d, j), gelatin at 25\(~\circ\)C and frequency of 1.6 rad/s (e, k), and polystyrene at 170\(~\circ\)C and frequency of 16 rad/s (f, l). \(G^{\prime }\) is represented by open circles, \(G^{\prime \prime }\) by filled circles, maximum normalized \(G^{\prime \prime } \left ({\widetilde {G}_{\text {max}}^{\prime \prime }} \right )\) by filled stars, \(G^{\prime \prime } \left ( {\widetilde {G}_{\text {max}}^{\prime \prime } } \right )\) and dotted lines are guides to the eye

Full size image

The predictions of the multimode Maxwell model (Eq. 2) are shown in Fig. 2 for the representative case of the PNIPAm microgel suspension. For this calculation, an eight-mode relaxation spectrum was obtained by fitting the model to the experimental linear viscoelastic frequency response shown in Fig. 2a. The prediction of the multimode Maxwell model for an amplitude sweep experiment carried out at a representative frequency of 1 rad/s is compared with experimental data in Fig. 2b. Different values of the parameter m in Eq. 1 were tried, and it was found that \(m= 1\) gave the best fit to the experimental data. Previous experimental investigations have also suggested the value of \(m=1\) (Wyss et al. 2007; Kalelkar et al. 2010). The model provides only a qualitative prediction of the nonmonotonic \(G^{\prime \prime }\) response. The poor agreement between model prediction and experimental data in the nonlinear region could be due to contributions from higher harmonics that have not been accounted for in the model. However, in our earlier work (Kalelkar et al. 2010), we have shown that for a 14-wt % suspension of PNIPAm microgels, the ratio of the third harmonic stress signal to the first harmonic stress signal is small (\(I_{3}\) / \(I_{1} = 0.06\)). This suggests that the contribution of the higher harmonics is likely to be small and may not be the main reason for the observed differences between the model and experiments. In the present work, our interest is in seeking broader understanding of the phenomenon rather than aiming for quantitative predictions, for which more sophisticated models will be required. Hence, we present below only qualitative trends predicted by the Maxwell model.

Fig. 2
figure 2

a Frequency sweep data at low strain amplitude (linear viscoelastic response) of PNIPAm microgel suspension along with fit of the multimode Maxwell model. b Amplitude sweep data at 1 rad/s for the same suspension together with predictions of the multimode Maxwell model, for \(m=1\)

Full size image

While the multimode Maxwell model predicts similar nonlinear response as the single-mode version of Miyazaki et al. (2006), it allows us to interrogate what happens to the dissipation component when the strain sweep experiments are done at different frequencies. To answer this, we define the normalized viscous modulus \(\widetilde {G}_{\text {max}}^{\prime \prime } ={G_{\text {max}}^{\prime \prime } } / {G_{\text {LVE}}^{\prime \prime } \left (\omega \right )}\) so that the dissipation can be compared for different frequencies relative to the linear limit. Figure 3a shows that \(G_{\text {max}}^{\prime \prime } \) has a weaker dependence on frequency relative to \(G_{\text {LVE}}^{\prime \prime } \left (\omega \right )\), which has a frequency dependence shown in Fig. 2a. Therefore, the normalized viscous modulus \(\widetilde {G}_{\text {max}}^{\prime \prime }\) has a maximum at the characteristic frequency at which the \(G_{\text {LVE}}^{\prime \prime } \left ( \omega \right )\) shows a minimum. To illustrate this, Fig. 3b shows the predictions of \(\widetilde {G}_{\text {max}}^{\prime \prime }\) at different frequencies as calculated from the multimode Maxwell model for the case of the PNIPAm microgel suspension. Also shown are experimentally determined values of \(\widetilde {G}_{\text {max}}^{\prime \prime }\) and the linear frequency response for this material. Indeed, the maximum in \(\widetilde {G}_{\text {max}}^{\prime \prime }\) is seen to occur at the frequency where \(G_{\text {LVE}}^{\prime \prime }\left (\omega \right )\) shows a minimum. That this is a common feature of yielding for all soft materials is seen in Fig. 1(g–l), which shows \(\widetilde {G}_{\text {max}}^{\prime \prime }\) at various frequencies for all materials investigated here. In each case, the maximum in \(\widetilde {G}_{\text {max}}^{\prime \prime }\) is seen at the frequency where \(G_{\text {LVE}}^{\prime \prime } \left ( \omega \right )\) shows a minimum. It may be noted that in a LAOS experiment, the energy dissipated per cycle is \(\mathrm {{\O }}=\int _{0}^{{2\pi } / \omega } {\tau \dot {\gamma } dt=\pi G_{1}^{\prime \prime } \gamma _{0}^{2}}\), where \(G_{1}^{\prime \prime }\) is the first harmonic of the loss modulus (Ganeriwala and Rotz 1987). Thus, the maximum relative dissipation defined as \(\mathrm {{\O }}_{\text {max}} =\pi \gamma _{0}^{2} \widetilde {G}_{\text {max}}^{\prime \prime } \) (assuming that \(G^{\prime \prime }\cong G_{1}^{\prime \prime } )\) will have the same frequency dependence as \(\widetilde {G}_{\text {max}}^{\prime \prime } \). In other words, the maximum relative dissipation will be the highest at the frequency where \(G_{\text {LVE}}^{\prime \prime } \left ( \omega \right )\) shows a minimum.

Fig. 3
figure 3

a Maxwell model predictions of the strain dependence of normalized \(G^{\prime \prime }\) for various frequencies. b Comparison of experimentally determined normalized \(\widetilde {G}_{\text {max}}^{\prime \prime } \)(filled circles) as a function of frequency with predictions of the Maxwell model (dotted line) for the normalized \(\widetilde {G}_{\text {max}}^{\prime \prime }\). The dashed–dotted line through the experimental data only serves as guide to the eye. The figure also shows the experimental linear viscoelastic frequency response (triangles) and model fit for the same (bold and dashed lines). c Prediction of the Maxwell model for the frequency dependence of \(G^{\prime }\) and \(G^{\prime \prime }\) at different strains \(\gamma _{0} = 1~\%\) (LVE), 5 %, 20 %, 40 %, 60 %, and 90 % (arrows indicate increasing strain amplitudes). The closed and open symbols represent the experimental \(G^{\prime }\) and \(G^{\prime \prime }\), respectively, for \(\gamma _{\text {LVE}} = 0.6~\%\)

Full size image

In order to better understand this phenomenon, we show in Fig. 3c the predictions of Maxwell model for frequency dependence of viscoelastic moduli at various strain amplitudes starting from small strain (linear response) to large strains (nonlinear response). The relaxation spectrum used here as an example is that for the PNIPAm suspension; however, similar features will be predicted for any other complex fluid. The calculations are extrapolated to low frequencies where the Maxwell model predicts a crossover of moduli corresponding with the structural relaxation time \(\lambda _{C}\). For increasing strain amplitude, several features are worth noticing in the figure: In the low-frequency region \(\omega <\omega _{C}^{\text {LVE}}\), the moduli decrease with increasing strain, suggesting a strain-softening behavior with \(G^{\prime \prime }>G^{\prime }\). At higher frequencies \(\omega >\omega _{C}^{\text {LVE}} \), while \(G\prime \) decreases with strain, \(G^{\prime \prime }\) increases with strain. This corresponds with the upturn in \(G^{\prime \prime }\) seen in the amplitude sweep predictions. It can be seen that the ratio \({\widetilde {G}^{\prime \prime } =G^{\prime \prime } \left ({\omega ,\gamma _{0}} \right )} / {G_{\text {LVE}}^{\prime \prime } \left ( \omega \right )}\), i.e., the normalized loss modulus, is always the highest for the frequency corresponding to the minimum in \(G_{\text {LVE}}^{\prime \prime } \left (\omega \right )\), indicating the maximum relative dissipation at this frequency. The crossover frequency \(\omega _{C} \left ( {\gamma _{0}} \right )\) increases with strain amplitude, indicating a decrease in the structural relaxation time in accordance with Eq. 1. Thus, the slow structural relaxation time scale approaches the fast time scale monotonically with increasing strain amplitude. At 90 % strain for this material, the \(\omega _{C}\) approaches the frequency at which \(G_{\text {LVE}}^{\prime \prime } \left (\omega \right )\) shows a minimum. Above this strain, \(G\prime \) decreases below \(G^{\prime \prime }\) (indicating yielding), and \(G^{\prime \prime }\) also decreases over the entire frequency range. Thus, the maximum relative dissipation is obtained at 90 % strain for this fluid and at frequency close to \(\omega _{\beta }\), which is the frequency corresponding to the minimum in \(G_{\text {LVE}}^{\prime \prime } \) and is referred to as the beta relaxation frequency of cage dynamics in the framework of the mode-coupling theory (Mason and Weitz 1995).

The above observations together with Eq. 3 imply that the maximum relative dissipation \(\left ({\widetilde {G}_{\text {max}}^{\prime \prime }}\right )\) just before macroscopic yielding will occur in an amplitude sweep experiment when the imposed frequency satisfies \(\omega =1 /\lambda _{c} =1/{\lambda _{\beta }}\); here, \(\lambda _{C}(\gamma _{0})\) is the structural relaxation time (i.e., the so-called alpha relaxation time) and \({\lambda _{\beta } =1}/{\omega _{\beta }} \) is the beta relaxation time. For soft glassy materials consisting of particles trapped in a local “cage,” \(\lambda _{C}\) represents the time scale over which a trapped particle would escape its cage, while \(\lambda _{\beta }\) corresponds to the cooperative motion of the particles within the cage (Roldan-Vargas et al. 2010). Thus, the maximum relative dissipation prior to macroscopic yielding is seen to occur when the dynamics of alpha relaxation are accelerated by the imposed shear to an extent where they become equal to the beta relaxation dynamics so that, effectively, a particle in the fluid does not feel the presence of topological constraints.

For entangled polymers, whose dynamics may be understood using the tube model, Marrucci (1996) argued that the tube renewal time scale \(\lambda _{C}\) will decrease upon imposition of large and rapid deformation by the so-called convective constraint release process in which neigboring entangled chains are convected away from the test chain, releasing entanglements locally along its contour. Under sufficiently strong flows, if the rate of CCR is of the same order as the relaxation of a disentangled polymer, then the polymer chain would not experience the presence of topological constraints tube in a dynamical sense. The latter is approximately given by the Rouse reorientation time \(\lambda _{R}\) of half the chain in its tube. Hence, when the imposed frequency of a large amplitude oscillatory flow approaches \(\lambda _{R}\), a complete destruction of the tube is possible. This is akin to the destruction of the cage structure in a soft glassy material. It is well known that the Rouse frequency \(\omega _{\mathrm {R}} =1/{\lambda _{\mathrm {R}}}\) is slightly lower than the frequency at which \(G_{\text {LVE}}^{\prime \prime } \) shows a minimum (Rubinstein and Colby 2003; Doi and Edwards 1986). If the imposed frequency equals the Rouse frequency, a polymer chain would not feel the presence of topological constraints of the entanglements. Therefore, the criterion \(\omega =1/{\lambda _{\mathrm {C}}} =1 / {\lambda _{\beta }}\) results in the maximum relative dissipation in the case of entangled polymers as well.

In summary, we have ascertained that soft materials exhibit universal features of yielding in an oscillatory shear test when conducted in an appropriate frequency–temperature–concentration window. Specifically, the linear frequency response and the nonlinear strain response are related such that the maximum relative dissipation prior to macroscopic yielding is obtained when the imposed frequency resonates with the microscopic time scale of the material. Under this condition of high shear, the microscopic structural entities that make up the material do not feel topologically constrained any more.