Flow of concentrated solutions of starlike micelles under large-amplitude oscillatory shear

Abstract

The non-linear viscoelasticity of concentrated solutions and glasses of soft starlike micelles has been studied by large-amplitude oscillatory shear (LAOS). The non-linear response has been analysed using current schemes of Fourier transform (FT) rheology, and its character has been determined by the phase of the third harmonic contribution to the stress. The limitations of FT rheology and related analysis methods are discussed, and an alternative method is presented that takes into account all the higher harmonics. This method reveals a strain-hardening character of intracycle non-linearities at large strain amplitudes for all volume fractions. We also show that, although the relation of LAOS with steady shear measurements works qualitatively, due to inherent limitations of LAOS, steady shear data cannot be reproduced quantitatively.

Introduction

The non-linear rheological response of concentrated disordered soft materials (such as colloidal suspensions, emulsions, foams) presents many interesting problems of both fundamental and diverse practical significance (Larson 1999; Mewis and Wagner 2009). Typically, such materials at high volume fractions and/or strong intermolecular attractions exhibit strong viscoelasticity and yield stress (Larson 1999; Moller et al. 2006). In general, such behaviour stems from frozen or very slowly relaxing structures that are due to strong entropic or enthalpic energy barriers imposed at a microscopic scale on the constituents of the system, creating glasses and gels, respectively. These states behave as weak solids at low stresses but can flow if the imposed stress or strain exceeds a certain value. By increasing the volume fraction, hard- or soft-sphere colloids exhibit a diverging zero-shear viscosity (Shikata and Pearson 1994; Mason and Weitz 1995) and suppression of long-time out-of-cage diffusion forming a glassy state where individual particles are kinetically trapped by their neighbours (Pusey and Van Megen 1987; van Megen et al. 1998; Brambilla et al. 2009). Under external shear, colloidal glasses and gels yield due to cage breaking and/or bond breaking, i.e. via a shear-induced weakening of the entropic barrier allowing particles to escape from their cage (Petekidis et al. 2002, 2004; Pham et al. 2008; Laurati et al. 2011; Koumakis and Petekidis 2011; Koumakis et al. 2012a). Such shear-induced solid-to-liquid transition (yielding) has been studied in a variety of systems, both under steady and oscillatory shear (Mason et al. 1996; Cloitre et al. 2003; Petekidis et al. 2003; Carrier and Petekidis 2009; Helgeson et al. 2007).

A main feature of colloidal glasses and gels (similarly with other concentrated disordered soft materials) is that they show pronounced non-linear stress response in steady or oscillatory shear. Common examples of such behaviour is the reduction of viscosity at high shear rates (i.e. shear thinning) (Larson 1999; Mewis and Wagner 2009) and the anharmonic stress response to large-amplitude oscillatory shear (Philippoff 1966; Hyun et al. 2011). Their non-linear response is quite important in most applications and processes of biological or industrial significance, where large deformations and non-unidirectional flows are present. A straightforward, and thus commonly used, method to study non-linear viscoelasticity is to extend the linear small-amplitude oscillatory measurements to large strain amplitudes. Thus, in a large-amplitude oscillatory shear (LAOS) experiment, the moduli G′ and G″ are measured even at strain amplitudes where the stress exhibits strong deviations from simple harmonic response. This approach is very useful in determining the onset of non-linear behaviour, but it is also fraught with difficulties. The most critical problem is that G′ and G″, due to the large anharmonic contributions in the stress, lack the commonly accepted physical interpretation that they have in the linear regime.

Here, we extend a previous LAOS study on yielding of soft colloidal glasses (Renou et al. 2010) presenting experimental data at different volume fractions, above and below the glass transition. An additional aim of this paper was to discuss the relative merits of some of the different methods currently used for the analysis of LAOS experiments and further suggest a simple approach to look into the non-linear intracycle response. In this way, we compare the LAOS response of a concentrated viscoelastic liquid, where shear thinning (i.e. drop of the complex viscosity) is detected, to that of a colloidal glass where yielding (i.e. shear-induced solid-to-liquid transition) takes place when the yield strain is exceeded leading to a similar drop of G′ below G″.

Large-amplitude oscillatory shear (LAOS)

In a LAOS experiment, a sinusoidal strain of large amplitude is applied to the sample and the non-sinusoidal stress response is measured (Philippoff 1966; Onogi et al. 1970; Gadala-Maria and Acrivos 1980). In the last 10 years, LAOS has become one of the most common techniques to study non-linear viscoelasticity since one can change independently the oscillation amplitude γ0 and frequency ω, probing the whole range of rheological behaviour, from steady viscosimetric flow (ω → 0) and linear viscoelasticity (γ0 → 0) to non-linear viscoelasticity (Dealy and Wissbrun 1999).

Several methods of analysis of LAOS data have been proposed and recently reviewed in the literature (Hyun et al. 2011). The most common method is Fourier transform (FT) analysis, where the non-sinusoidal but periodic stress response to LAOS is expressed as a Fourier series (Matsumoto et al. 1973; Wilhelm et al. 1998). The magnitude of non-linear response can thus be quantified by the relative amplitudes of higher harmonics with respect to the fundamental. This approach has been used extensively to analyse LAOS results on a variety of systems such as linear polymers (Wilhelm et al. 1999, 2000), branched polymers (Schlatter et al. 2005; Hyun et al. 2013), cubic phases of diblock copolymer micelles (Daniel et al. 2001; Nicolai and Benyahia 2005), lamellar phases of diblock copolymer melts (Langela et al. 2002) and concentrated colloidal suspensions (Heymann et al. 2002; Le Grand and Petekidis 2008; Carrier and Petekidis 2009). However, although it quantifies very accurately the magnitude of the non-linear response, it is not straightforwardly related with the physical processes that cause it, although the phase of the harmonics has been used to indicate shear-thinning or shear-thickening response within a cycle (Neidhofer et al. 2003).

Based on symmetry arguments, a conceptually different approach has been suggested where the total stress is decomposed into an elastic stress and a viscous stress (Cho et al. 2005). This decomposition is used to construct non-linear moduli that specifically refer to the elastic stress and viscous stress separately and hence give an indication of the character of the non-linear response, without the need for a Fourier transformation.

Both approaches were combined by Ewoldt et al. who used Chebyshev polynomials as an orthonormal basis for the decomposition of the periodic stress signal (Ewoldt et al. 2008). Crucially though, they have provided a physical interpretation of higher harmonics by assigning meaning to mainly the third-order Chebyshev polynomials. The non-linear behaviour of materials was classified into strain-hardening/softening and shear-thickening/thinning contributions according to whether the maximum non-linear stress occurs at maximum strain or shear rate and whether it augments or reduces the linear stress. Of course, the classification of non-linearity based on the third harmonic is expected to be valid only when it dominates the non-linear response, i.e. at small strain amplitudes. It has also been shown that Chebyshev decomposition is equivalent in all respects to FT analysis, with the role of the nth Chebyshev polynomial sign played by the phase of the nth harmonic, although one has to be careful with the definition of the oscillatory input (Ewoldt 2013).

On the other hand, some studies have sought to understand LAOS by comparing the response to simpler steady shear experiments. In the early 1980s, Gadala-Maria and Acrivos could predict the LAOS response of non-Brownian concentrated suspensions from their rheological response to step shear rates of opposite directions (Gadala-Maria and Acrivos 1980). More specifically for concentrated suspensions with a yield stress, Doraiswamy et al. (1991) have constructed a model, also applied to LAOS, that combines perfectly elastic deformation below a yield stress and viscous shear-thinning behaviour after yielding (Doraiswamy et al. 1991). More recently, it has been similarly suggested that the stress waveform can be viewed as a succession of elastic and viscous processes (Renou et al. 2010; Rogers et al. 2011). Rogers et al. used this approach to quantitatively extract an elastic modulus from the elastic part of the waveform and further determine the flow curve (stress versus strain rate in steady shear) from the viscous part of the oscillatory stress waveform (Rogers et al. 2011).

Fourier transform (FT) rheology

FT rheology decomposes the stress response into a Fourier series of higher harmonics:

$$ \sigma(t)=\gamma\,_{0}\left\{\sum\limits_{n\;\mathrm{odd}}G^{'}_{n}\mathrm{sin}\left(n\omega t\right)+\sum\limits_{n\;\mathrm{odd}}G^{''}_{n}\mathrm{cos}\left(n\omega t\right)\right\} $$

(1)

or, in the intensity-phase representation, as:

$$ \sigma(t)=\sum\limits_{n\;\mathrm{odd}}I_{n}\mathrm{sin}\left(n\omega t+\phi_{n}\right) $$

(2)

A physical interpretation of higher harmonics can be extracted from the phase difference of the nth harmonic with respect to the strain, $\delta _{n}(0-2\pi ).$ ¹ This can be understood in simple terms by considering the effect of the third harmonic on an arbitrary linear viscoelastic stress response. In Fig. 1(a), a typical linear response is displayed along with a third harmonic stress response that is in phase ($\delta _{3}=0$) with the strain. It can be clearly seen that the third harmonic is zero at the point of maximum shear rate and negative at the point of maximum strain. Thus, the non-linear response, of mainly elastic character, can be classified as pure strain softening within the cycle; as the maximum strain is approached, the total stress falls below the harmonic stress. Similarly, for $\delta _{3}=\pi$, the total stress at maximum strain is found to be larger than the harmonic stress (Fig. 1(b)), indicating intracycle strain hardening. In the same way, $\delta _{3}=\pi /2$ is associated with shear thickening (Fig. 1(c)), since the stress at maximum rate (mainly of viscous origin) is larger than the harmonic stress, while $\delta _{3}=3\pi /2$ indicates shear thinning (Fig. 1(d)) along the same lines.

Fig. 1

Simulated data of arbitrary harmonic viscoelastic response (red dashed line) to a sinusoidal strain input (black dashed line). A third stress harmonic of lower amplitude is added with a fixed phase difference with respect to the strain, and the resulting total stress is shown (grey line). This phase difference is in (a) δ ₃ = 0°, (b) δ ₃ = 180°, (c) δ ₃ = 90° and (d) δ ₃ = 270°. The contribution of the third harmonic to the total stress is examined at two points within the period of oscillation, at maximum shear rate and maximum strain, and the non-linear response is classified accordingly (the equations used to generate the figure are $\sigma _{1}=\sin \left (2\pi x\right )+\cos \left (2\pi x\right )$, $\gamma =\sin \left (2\pi x\right )$ and $\sigma _{3}=0.25\sin \left (6\pi x + \delta _{3}\right )$)

It is important to realise that in the most general case, δ ₃ will be between the phase differences that correspond to the above pure intracycle non-linear phenomenologies, suggesting that the material exhibits both strain-hardening (or softening) and shear-thickening (or thinning) response. We should also note that the nomenclature above, i.e. shear thinning/thicknening and strain hardening/softening, in the context of the phase of the third harmonic strictly describes a non-linear response within the LAOS cycle (Ewoldt et al. 2008; Hyun et al. 2011). This is not a priori related to the decrease or increase of G′₁ and G″₁ at high strain amplitudes due to shear melting or hydrodynamic effects which are also usually described as shear thinning and shear thickening, respectively.

Materials and methods

Starlike micelles from poly(ethylene-alt-propylene)–poly(ethylene oxide) (PEP-PEO) block copolymers

PEP-PEO block copolymers were prepared by a two-step anionic polymerization (Allgaier et al. 1997). In this study, we used PEP1-PEO20 block copolymers where the hydrophobic PEP part has 1/20 of the molecular volume of the hydrophilic PEO part. The number average molar mass (M _n) determined by size-exclusion chromatography in THF/DMA at 40 °C was 1,300 g/mol for the PEP block and 20,300 g/mol for the PEO block corresponding to an overall M _n = 21,600 g/mol for the block copolymer. Their polydispersity indices (M _w/M _n) were 1.04 and 1.08, respectively.

Previous work has demonstrated that PEP-PEO block copolymers in deuterium oxide (D₂O) form micelles with an aggregation number of 120 and a core where no kinetic exchange of arms between micelles is possible (Stellbrink et al. 2004; Lund et al. 2006). The absence of kinetic exchange ensures that the aggregation number remains constant with varying concentration and temperature. Furthermore, it has been seen that the pair interaction potential between micelles is similar to the interaction potential of regular star polymers (Laurati et al. 2005). The micelles can thus be treated as stable colloidal entities with starlike pair interactions.

Clear solutions were obtained by dissolving the PEP-PEO polymer in D₂>O (99.8 at.% D, purchased from Armar Chemicals). The solutions were left to equilibrate at room temperature for at least 1 week before measuring. The dependence of the micellar hydrodynamic radius R _h on temperature has been established by dynamic light scattering on dilute solutions. It decreases from R _h = 37.4 nm at 10 °C to R _h = 34.4 nm at 40 °C due to the decreasing solvation of the corona in marginal solvent D₂O. The micellar solutions are labelled by their polymer concentration normalised by the overlap concentration $c^{\ast }$ which was calculated using the R _h at each specific temperature. At 20 °C, the overlap concentration was found to be $c^{\ast }=3fM_{\mathrm {w}}/\left (4\pi R_{\mathrm {h}}^{3}N_{\mathrm {a}}\right ) = 21.7$ g/l.

Experimental methods

An Anton Paar Physica MCR 501 stress-controlled rheometer was used in strain control mode for the linear viscoelasticity and the LAOS experiments. We used a stainless steel cone-and-plate geometry, with a cone diameter of 50 mm, an angle of 0.04 rad and a truncation (gap) of 50 μm. The temperature was controlled by a Peltier system, and a home-made solvent trap was used to minimise evaporation during measurements typically lasting up to 4 h.

The linear viscoelastic data were acquired between 100 and 0.1 rad/s. In the case of glassy solutions, the sample was rejuvenated by an oscillatory preshear of strain amplitude 1,000 % at 1 rad/s for 200 s and measurements were performed after a waiting time of 200 s. A series of dynamic strain sweeps at different frequencies and temperatures were performed. The strain amplitude was varied between 1 and 1,000 %. When constant LAOS response (denoted as alternance by Giacomin et al. (2011)) was reached, the last full waveform of stress and strain was recorded and stored. Crucially, the Direct Strain Oscillation option of the Physica MCR 501 is used to ensure a perfect sinusoidal strain at all amplitudes. The ability to perform LAOS experiments with a stress-controlled rheometer has been recently demonstrated for a variety of different samples (Laeuger and Stettin 2010). For the present system, no indication of slip was detected in steady or oscillatory shear (Ballesta et al. 2008, 2012). The flow curves do not show the characteristic stress drop at low shear rates, while in oscillatory shear, the absence of even harmonics is another indication of the absence of transient slip (Renou et al. 2010).

The stress signal is Fourier-transformed using a discrete FFT macro included in the data analysis software IGOR Pro 6 extracting the phase difference, $\delta _{n}$, and the $G_{n}^{^{\prime }}$, $G_{n}^{^{\prime \prime }}$ coefficients. For all the samples studied here, the even harmonics are negligible compared to the odd harmonics. We should note that the values of G′ and G″ directly provided by the rheometer software in the non-linear oscillatory regime are actually the first harmonic coefficients G′₁ and G″₁.

Results

Linear viscoelasticity of starlike micelle system

The linear viscoelastic moduli of four samples measured at 10 °C can be seen in Fig. 2a. The high concentration sample (3$c^{\ast }$) shows all the characteristics of a soft glass. The elastic modulus G′ is constant over a wide range of frequencies and, with a value of around 1,000 Pa, much higher than G″. The increase of G″ at low frequencies can be attributed to out-of-cage hopping mechanisms that might take place at even lower frequencies. Furthermore, the sample exhibits ultra-slow structural relaxations measured by multispeckle DLS, with characteristic relaxation times of more than 100 s that are evolving with time (ageing) (Renou et al. 2010). The sample at the immediately lower concentration (2.6$c^{\ast }$) has G′ > G″ at all frequencies probed; therefore, it can be termed as glassy. However, G′ decreases and G″ increases at low frequencies, indicating a slow relaxation with crossover frequency outside our experimental window. Upon decreasing the concentration further (2.4$c^{\ast }$), the crossover frequency moves inside the experimental window at 3 rad/s. The sample is solid-like above and liquid-like below that frequency, and it can be termed a concentrated viscoelastic solution. The low-concentration sample (2.1$c^{\ast }$) has a crossover frequency of 40 rad/s. The terminal liquid-like regime at low frequencies $\left (G^{^{\prime }}\sim \omega ^{2}, G^{^{\prime \prime }}\sim \omega \right )$ is visible; the sample behaves like a Maxwell fluid at long timescales. The dynamic frequency sweeps of a sample at a fixed polymer concentration (2.3$c^{\ast }$ at 20 °C) and at three different temperatures, 10, 15, and 20 °C, are shown in Fig. 2b. The same transition from a solid-like, non-ergodic solution to a liquid-like solution can be seen just by increasing the temperature, with the crossover frequency scaling well with $c/c^{\ast}$ at different temperatures (Koumakis et al. 2012b). In multiarm star polymers, such transitions are well documented both in athermal solvents by increasing concentration (Ozon et al. 2006; Laurati et al. 2007) as well as in intermediate quality solvents by increasing temperature due to the swelling of the star (Kapnistos et al. 2000).

Fig. 2

Dynamic frequency sweeps in the linear regime ($\protect \gamma =0.5$ %) for six different effective volume fractions. $G^{^{\prime }}$ is indicated with filled symbols and $G^{^{\prime \prime }}$ with unfilled symbols. a Samples measured at 10 °C. The polymer concentration varies from 3$c^{\ast }$ (red), 2.6$c^{\ast }$ (black), 2.4$c^{\ast }$ (green), to 2.1$c^{\ast }$ (blue). b A single sample at a fixed polymer concentration measured at three different temperatures: 10 °C (black) (2.6$c^{*}$), 15 °C (2.5$c^{*}$) (dark grey) and 20 °C (2.3$c^{*}$) (light grey). The arrow indicates $1/t_{\protect \alpha }$

The samples presented above are at concentrations greater than two times the overlap concentration. It is perhaps surprising that strongly interpenetrated micelles can show terminal liquid-like behaviour. However, this is a direct manifestation of the softness of the interparticle potential, where limited interpenetration is not sufficient to induce a liquid-to-solid transition. In order for the micelles to be caged and form a glass, one has to reach much higher number densities compared to hard-sphere colloids or microgel particles (Koumakis et al. 2012b). In multiarm star polymers of similar functionalities, the glass transition was determined at 1.4$c^{\ast }$ (Kapnistos et al. 2000; Helgeson et al. 2007).

Non-linear rheology

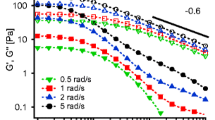
Four micellar solutions at increasing concentrations have been studied by LAOS experiments. The dynamic strain sweeps at a fixed frequency of 1 rad/s can be seen in Fig. 3. All dynamic strain sweeps show some common features. At small strain amplitudes, both $G^{^{\prime }}$ and $G^{^{\prime \prime }}$ are constant. This defines the linear regime for a specific temperature and polymer concentration. At large amplitudes, both $G^{^{\prime }}$ and $G^{^{\prime \prime }}$ decrease below their linear values with $G^{^{\prime \prime }}$ becoming larger than $G^{^{\prime }}$ for glassy samples, indicating a liquid-like response. The major qualitative difference between solid-like (glassy) and liquid-like samples is that for the former, $G^{^{\prime \prime }}$ exhibits a maximum and a yield point as the strain amplitude is increased beyond a critical strain amplitude. Such non-monotonic behaviour of $G^{^{\prime \prime }}$ with strain amplitude is a typical manifestation of yielding and has been observed in a variety of colloidal glasses and pastes (Mason et al. 1996; Pham et al. 2008; Helgeson et al. 2007; Renou et al. 2010). Moreover, different theoretical approaches such as mode-coupling theory (MCT) (Miyazaki et al. 2006; Brader et al. 2010), soft glassy rheology (Sollich 1998) or other phenomenological models (Craciun et al. 2003; Derec et al. 2003; Carrier and Petekidis 2009) predict such behaviour and relate it to a maximum energy dissipation per unit strain amplitude around the yield point of the material. In colloidal glasses, this has been related to cage breaking due to which individual particles are assisted by shear to diffuse out of the cages formed by their neighbours (Petekidis et al. 2002; Pham et al. 2008). The peak is more pronounced at higher volume fractions because the initial caging is stronger and the additional energy dissipated when the cages are broken higher. The yield strain$\gamma _{\mathrm {y}}$ of the solid-like samples, determined at the strain amplitude where $G^{^{\prime }}=G^{^{\prime \prime }}$, is increasing with $c/c^{\ast }$ acquiring values of $\gamma _{\mathrm {y}}=7.9$ % at 3$c^{\ast }$, $\gamma _{\mathrm {y}}=5$ % at 2.6$c^{\ast }$ and $\gamma =2.5$ % at 2.5$c^{\ast }$.

Fig. 3

Dynamic strain sweeps at a frequency of $\protect \omega = 1$ rad/s for four different concentrations. $G^{^{\prime }}$ is indicated with filled symbols and $G^{^{\prime \prime }}$ with unfilled symbols. a Samples measured at 10 °C. The polymer concentration varies from 3$c^{\ast }$ (red), 2.6$c^{\ast }$ (black), 2.4$c^{\ast }$ (green), to 2.1$c^{\ast }$ (blue)

We may also briefly discuss the decrease of $G^{^{\prime }}$ and $G^{^{\prime \prime }}$ at large oscillatory strain amplitudes. A common report in the literature is that both $G^{^{\prime }}$ and $G^{^{\prime \prime }}$ follow a power law decrease with strain amplitude, $G^{^{\prime }}\propto \gamma \,_{0}^{\nu ^{^{\prime }}}$, $G^{^{\prime \prime }}\propto \gamma \,_{0}^{\nu ^{^{\prime \prime }}}$, with power law exponents $\nu ^{^{\prime }}\simeq 2\nu ^{^{\prime \prime }}$. Within Maxwell-type models, $\nu ^{^{\prime }}$ and $\nu ^{^{\prime \prime }}$ acquire the values of $-$2 and $-$1, respectively (Miyazaki et al. 2006), whereas numerical MCT predictions yield less trivial, lower values in better agreement with experiments keeping however the ratio $\nu ^{^{\prime }}/\nu ^{^{\prime \prime }}=2$ (Brader et al. 2010; Miyazaki et al. 2006). Such behaviour has been asserted at least approximately in a variety of systems such as colloidal glasses of hard spheres (Mason and Weitz 1995; Derec et al. 2003; Miyazaki et al. 2006), concentrated emulsions (Mason et al. 1997), depletion gels (Pham et al. 2006), multiarm star polymers (Helgeson et al. 2007; Rogers et al. 2011; Christopoulou et al. 2009) and core–shell particles (Carrier and Petekidis 2009). However, looking carefully at several of these experiments, one may see deviations from the $\nu ^{^{\prime }}\simeq 2\nu ^{^{\prime \prime }}$ relation (Koumakis et al. 2012a). Here, the $G_{1}^{^{\prime }}$ and $G_{1}^{^{\prime \prime }}$ power law exponents for the highest concentration sample shown in Fig. 3 are $-1.37$ and $-0.93$, respectively, with the ratio $\nu ^{^{\prime }}/\nu ^{^{\prime \prime }}=1.47$ significantly lower than 2. Similar ratios of 1.5 are found for different frequencies between 0.1 and 2 rad/s, indicating that the value of 2 is not universal and therefore calling for better theoretical predictions beyond the Maxwell-type approximations.

Stress waveforms and Lissajous figures

In LAOS experiments, it is customary to plot the stress as a function of strain in an elastic Lissajous figure (or the stress as a function of shear rate in a viscous Lissajous figure). In the linear regime, since both stress and strain are sinusoids with the same frequency, the Lissajous figure is an ellipse. Any deviation from an elliptical shape signals the existence of higher harmonics in the stress response, and hence the onset of non-linear behaviour. The elastic and viscous Lissajous figures for four different concentrations measured at 1 rad/s are shown in Fig. 4. Three strain amplitudes are plotted (1, 10 and 100 %), which correspond roughly to the linear response, yielding and beyond yielding.

Fig. 4

(Top) Elastic Lissajous figures of the steady-state stress response at 1 rad/s for four different samples and three strain amplitudes at 10 °C. The concentrations are $c/c^{\ast } =$ 2.1 (blue), $c/c^{\ast } = 2.4$ (green), $c/c^{\ast } = 2.6$ (black) and $c/c^{\ast } = 3$ (red). The values of the stress at zero strain are also noted in the plot. The arrows in the Lissajous curve for $c/c^{\ast } = 3$ and $\protect \gamma _{0}=10$ % indicate the elastic (1) and post-yield (2) regimes. The vertical double arrow indicates the stresses at a point in the elastic (A) and post-yield (B) region with the same strain within the cycle. (Bottom) Viscous Lissajous figures of the same samples

Qualitatively, we can make the following observations: at $\gamma_{0}=1$ %, all samples respond linearly; the corresponding Lissajous figures are ellipses and clearly show the difference between a liquid-like response at low concentration and a solid-like response at high concentration. As the strain amplitude is increased to 10 %, the shapes become progressively less elliptic. The non-linear behaviour is much more evident at high concentrations, where the Lissajous figures develop sharp edges and abrupt changes of stress with strain. At the highest concentration, there are clearly two different regimes within the oscillation cycle. In the first regime, the stress increases almost linearly with strain, while in the second regime, the stress is almost independent of strain. The two regimes are indicated by two arrows on one of the Lissajous plots in Fig. 4. The first regime which follows immediately after strain reversal is separated from the second regime by a stress overshoot, i.e. a pronounced peak in stress. The LAOS response of a colloidal glass after strain reversal is thus very similar to the response to a start-up step rate experiment (Renou et al. 2010). The stress overshoot peak has been observed in step rate experiments on a number of different samples (Mewis and Meire 1984; Liddel and Boger 1996; Stokes and Telford 2004; Carrier and Petekidis 2009; Renou et al. 2010; Koumakis et al. 2012a, b), and it occurs due to the distortion of the quiescent structure faster than it can relax through Brownian motion (Sollich 1998; Zausch et al. 2008; Koumakis et al. 2012a). To avoid giving the impression that a simple one-to-one correspondence exists between the LAOS and steady shear stress overshoots, we should note that often there are no stress peaks in LAOS although they exist under the same conditions (rates and volume fractions) in steady shear (Koumakis 2011).

At even higher strain amplitudes, the non-linear behaviour becomes obvious even at the lowest concentration studied here. The general phenomenological behaviour of the samples at these large strain amplitudes is as follows: At maximum strain (zero rate), the direction of deformation is changed and the stress starts to increase linearly with strain, indicating an elastic response. When the elapsed strain from reversal exceeds a characteristic strain, which for samples with solid-like response represents the yield point within the cycle, a stress overshoot with concentration- and frequency-dependent magnitude is observed. Beyond this yield point, solid-like samples flow with a stress that remains almost constant and independent of strain (and shear rate) within the cycle (upper right plots of Fig. 4). For the frequencies probed here, this indicates mainly plastic flow. Note that this characteristic strain within the cycle is similar but not necessarily identical, at all frequencies, with the yield strain amplitude determined at the overlap of $G^{^{\prime }}=G^{^{\prime \prime }}$ in dynamic strain sweeps. This sequence of elastic and plastic (or viscous at higher frequencies) behaviour is quite commonly found in yield stress systems within a LAOS cycle (Renou et al. 2010; Rogers et al. 2011).

The viscous Lissajous figures (stress versus shear rate) of the same samples can be seen in Fig. 4. Again, the appearance of higher harmonics is manifested by the distortion of the initially elliptical shape of the figures. What is more interesting is the self-intersection of the stress signal at 2.4$c^{\ast }$, 2.6$c^{\ast }$ and 100 % strain amplitude. The appearance of this kind of secondary loops has recently been explained as coming from a strong elastic non-linearity leading to an apparent negative local elastic modulus around zero strain (Ewoldt and McKinley 2010). More generally, this reflects the difference in the behaviour upon increasing the rate as zero strain is approached compared to that of decreasing rate in the quadrant following zero strain.

Fourier transform analysis

We first use Fourier transform analysis to decompose the stress response into a linear response and higher harmonics. In Fig. 5a, b, the relative intensities of the third and fifth harmonics are displayed as a function of strain amplitude for the four samples at different concentrations shown in Fig. 3a.

Fig. 5

FT analysis results for the four samples at different concentrations measured at 10 °C and 1 rad/s. a Amplitude of the third harmonic divided by that of the first. b Amplitude of the fifth harmonic divided by that of the first

Both $I_{3}/I_{1}$ and $I_{5}/I_{1}$ increase monotonically and then reach a plateau at most concentrations. It is immediately evident that as the concentration is increased, the non-linear response becomes stronger at all strain amplitudes and the linear regime extends to lower strain amplitudes. The maximum relative amplitude of the third (fifth) harmonic is $\sim$0.28 ($\sim$0.15) for the most concentrated sample and then decreases to 0.26 (0.14) at 2.6$c^{\ast }$, 0.22 (0.11) at 2.4$c^{\ast }$ and 0.18 (0.08) at 2.1$c^{\ast }$. These values can be contrasted to the maximum intensity of higher harmonics, $I_{3}/I_{1}=1/3$ and $I_{5}/I_{1}=1/5$, expected for a material that exhibits perfect plastic response, i.e. a square-wave stress response (Wilhelm et al. 2000; Ewoldt et al. 2010). Thus, as the concentration is increased, the response approaches that of a perfect plastic material. The weak decrease observed at 2.6$c^{\ast }$ and 3$c^{\ast }$ is due to the approach towards a simpler liquid-like response at high strain amplitudes as explained previously in similar studies of soft core–shell microgels (Le Grand and Petekidis 2008; Carrier and Petekidis 2009) and also recently observed in multiarm star polymers (Rogers et al. 2011).

In Fig. 6, the phase difference, δ ₃, between the third harmonic and the strain is plotted as a function of $\gamma \,_{0}$. From these, we can deduce the intracycle character of the non-linearities as discussed above. It can be seen that the character of the third harmonic for the two highest concentrations follows the same trend, from mostly non-linear shear thickening at $4~\%\leq \gamma _{0}\leq 10$ %, to non-linear strain hardening at $10~\%\leq \gamma _{0}\leq 50$ % and finally to non-linear shear thinning at $\gamma _{0}\geq 50$ %. For the 2.4$c^{\ast }$ concentration sample, the third harmonic has mostly non-linear strain-hardening character at $5~\%\leq \gamma _{0}\leq 20$ % while at $\gamma _{0}\geq 50$ %, this turns into non-linear shear-thinning character. The lowest concentration sample behaves similarly, but with non-linearities becoming important at even larger strain amplitudes, $\gamma _{0}\geq 15$ %. As mentioned before, yielding is associated with a characteristic peak of $G_{1}^{^{\prime \prime }}$, which indicates increased energy dissipation as the microstructure is broken down (Fig. 3). At the same strain amplitudes, the non-linear response exhibits a shear-thickening intracycle character. It is therefore conceivable that the non-linear shear thickening present at high concentrations is due to the same mechanisms that contribute to the increase and peak of $G_{1}^{^{\prime \prime }}$. The absence of non-linear shear thickening for the two lower concentrations should thus reflect the absence of yielding (related microscopically to shear-induced cage breaking) as the terminal flow (thermally activated structural relaxation) regime is probed here at 1 rad/s.

Fig. 6

Phase difference between the third harmonic and the strain, plotted only for amplitudes where $I_{3}$ is more than 1 % of $I_{1}$. The horizontal lines mark the phase differences corresponding to pure strain softening (0°), pure strain hardening (180°), pure shear thickening (90°), pure shear thinning (270°) within the oscillation period

Discussion

Non-linear waveform analysis

All FT analysis methods essentially compare the deviations from harmonic response (i.e. the higher harmonics) to the first harmonic of the material under study. This idea underpins all FT rheology efforts to provide a physical interpretation of LAOS results. Since most rheometer’s software extracts directly the first harmonic, we here propose a more direct and simpler way to classify the non-linear response of materials based on the framework of Ewoldt et al. (2008). The alternative method is based on decomposing the full stress waveform into the harmonic response represented by $G_{1}^{^{\prime }}$ and $G_{1}^{^{\prime \prime }}$ values and an anharmonic response which contains all higher harmonics. The total stress is thus decomposed into a ‘linear’ harmonic stress (1st harmonic) and a ‘non-linear’ anharmonic stress. This can be implemented simply by noting that the harmonic stress, calculated directly from the $G_{1}^{^{\prime }}$ and $G_{1}^{^{\prime \prime }}$ output of the rheometer during a dynamic strain sweep, is:

$$ \sigma _{1}\left( t;\omega \right) =\gamma_{0}\left[G_{1}^{^{\prime }}\mathrm{ sin}\left( \omega t\right) +G_{1}^{^{\prime \prime }}\mathrm{cos}\left(\omega t\right) \right] $$

(3)

At the same time, the waveform of the total stress $\sigma _{\mathrm {tot} }\left ( t;\omega \right )$ at each $\gamma_{0}$ can be used to define the anharmonic stress, $\sigma _{\mathrm {anh}}$, by simply subtracting from the total stress waveform the harmonic waveform:

$$ \sigma _{\mathrm{anh}}\left( t;\omega \right) =\left\vert \sigma _{\mathrm{ tot}}\left( t;\omega \right) \right\vert -\left\vert \sigma _{\mathrm{1} }\left( t;\omega \right) \right\vert $$

(4)

Note that $\sigma _{\mathrm {anh}}$ is then the sum of all higher harmonics.

The procedure described above is illustrated in Fig. 7 for one measurement of the sample at 3$c^{\ast }, T = 10$ °C at $\gamma_{0}=100$ %.² The total stress waveform is plotted together with the harmonic stress response, calculated from the dynamic strain sweep values of $G_{1}^{^{\prime }}$ and $G_{1}^{^{\prime \prime }}$ (Fig. 3) using Eq. 3. The resulting plot (Fig. 7(a)) shows clearly the extent of the difference between the real waveform and the harmonic response. The anharmonic stress waveform calculated according to Eq. 4 is shown in Fig. 7(b). The values of $\sigma _{\mathrm {anh}}$ at maximum strain and maximum shear rate can be read directly off the graph and can be used to determine the strain-softening/hardening and the shear-thinning/thickening character of the intracycle non-linearity, with the former detected at maximum strain while the latter at maximum rate. In this case, at maximum strain, the total stress is 64.9 Pa whereas the harmonic stress is 21.3 Pa ($G_{1}^{^{\prime }}=21.3$ Pa at $\gamma_{0}=100$ %). This can be clearly classified as strong strain-hardening behaviour since $\sigma _{ \mathrm {anh}}(\gamma =\gamma_{0})=43.6$ Pa. At the same time, the total and harmonic stresses at maximum shear rate are 93.6 and 113 Pa, respectively, yielding $\sigma _{\mathrm {anh}}(\gamma =0)=-19.4$ Pa. This reveals a shear-thinning behaviour which is however weaker than the strain-hardening one, both in absolute (19.4 versus 43.6 Pa) and in relative terms (20 versus 70 % of total stress). We can thus conclude that the dominant non-linear response within the oscillatory cycle for this sample is strain hardening.

Fig. 7

Decomposition of total stress response $\protect \sigma _{\mathrm {tot}}$ into a harmonic response and an anharmonic response for the 3$c^{\ast }$, 10 °C sample at $\protect \gamma \,_{0} = 100$ %. (a) Total stress waveform (black solid line) and harmonic stress waveform (grey dashed line) plotted over one-half period. (b) Anharmonic stress waveform resulting from the substraction of the harmonic stress from the total stress shown on the left. The strain waveform in this case is a pure sine with $\protect \omega = 2\protect \pi /T$, so that maximum $\protect \gamma \,_{0}$ occurs at $T/4$ and maximum rate at 0 and $T/2$

The main advantage of this method becomes clear when one compares this result to the classification based on the phase of the third harmonic performed earlier. In Fig. 6, we have seen that the same sample at that particular strain has δ ₃ = 231° which is very close to a pure non-linear shear-thinning material (δ ₃ = 270°). Recalling the discussion on FT rheology in the introduction, we can calculate the contribution of the third harmonic at the two points of interest. At maximum rate, $\sigma _{3}\left ( \gamma =0\right ) =I_{3}\sin (\delta _{3})=-0.78I_{3}=-28$ Pa, and at maximum strain, $\sigma _{3}\left ( \gamma =\gamma_{0}\right ) =I_{3}\sin (3\pi /2+\delta _{3})=0.63I_{3}=23$ Pa. This is obviously classified as shear thinning. On the other hand, the subtraction of waveforms gives $-19.4$ and 43.6 Pa, respectively. The additional harmonics with $n>3$ have reduced the magnitude of the shear-thinning contribution and have substantially increased the magnitude of the strain-hardening contribution, so that now it is evident that the dominant intracycle non-linearity has a strain-hardening character. For this sample, this is actually true at all strain amplitudes greater than 20 %.

The example above shows clearly that a classification of non-linear response based on the third harmonic alone can be very misleading. The argument for neglecting higher harmonics is that, in most cases, their amplitude tends to be smaller than the third harmonic. However, this argument neglects the fact that higher harmonics have also a phase. Thus, it is possible that all harmonics higher than the third add in phase, enhancing or acting against the strain softening/hardening (or shear thickening/thinning) of the third harmonic alone.

Anharmonic moduli

Based on the anharmonic stress waveform, one can also define moduli that describe the LAOS behaviour of the sample at two points inside the period, maximum strain and maximum rate. For simplicity, we determine these in the first quarter of the period (as shown in Fig. 7) where the stress is positive, as follows:

$$G^{^{\prime }}_{\mathrm{anh}}=\frac{\sigma_{\mathrm{anh} }(\gamma=\gamma\,_{0})}{\gamma_{0}}$$

(5)

$$ G^{^{\prime \prime }}_{\mathrm{anh}}=\frac{\sigma_{\mathrm{anh}}(\gamma=0) }{\gamma_{0}} $$

(6)

The two anharmonic moduli, $G^{^{\prime }}_{\mathrm {anh}}$ and $G^{^{\prime \prime }}_{\mathrm {anh}}$, can be directly compared with the linear harmonic moduli $G^{^{\prime }}_{1}$ and $G^{^{\prime \prime }}_{1}$ to give a more complete representation of LAOS. The anharmonic moduli can be either positive or negative; a negative modulus means that the total stress is less than the harmonic stress.

In Fig. 8a, c, e, g, the harmonic modulus $G_{1}^{^{\prime }}$ and the absolute value of the anharmonic modulus, $\left |G_{\mathrm {anh}}^{^{\prime }}\right |$, are displayed, with the sign of the anharmonic modulus also indicated (open and solid symbols). This figure contains all the information for the LAOS behaviour of the sample at maximum strain. More specifically, it shows clearly that the anharmonic contribution to the stress starts to be important close to the yield strain, at $\gamma_{0}\sim 10$ %, while above $\gamma_{0}\sim 40$ %, the anharmonic contribution becomes equally important with the harmonic contribution $G_{1}^{^{\prime }}\sim G_{\mathrm {anh}}^{^{\prime }}$. At large amplitudes, the now-dominant anharmonic contribution exhibits a linear decrease with strain amplitude similarly with $G_{1}^{^{\prime \prime }}$. Moreover, the anharmonic contribution is always positive, indicating a strain-hardening intracycle response essentially at all amplitudes. The power law exponent of $-$1 is quite interesting, because it means that the stress at maximum strain $\left (\approx \gamma_{0}G_{\mathrm { anh}}^{^{\prime }} \text {when}~G_{1}^{^{\prime }}<<G_{\mathrm {anh}}^{^{\prime }}\right )$ remains constant with strain amplitude. As at maximum strain the shear rate is zero, the stress at this point is only of structural origin. A constant stress would then indicate that after yielding the structure of the micellar solution remains the same for any strain amplitude (and thus average shear rate) when the shear flow is stopped and reversed.

Fig. 8

a, c, e, g $G^{^{\prime }}_{1}$, $|G^{^{\prime }}_{\mathrm {anh }}|$. b, d, f, h $G^{^{\prime \prime }}_{1}$, $|G^{^{\prime \prime }}_{\mathrm {anh}}|$. The harmonic moduli are shown with lines, while the absolute values of the anharmonic moduli are shown with symbols. A filled triangle indicates a positive anharmonic modulus, while an open triangle indicates a negative anharmonic modulus

Similarly, in Fig. 8b, the harmonic modulus $G_{1}^{^{\prime \prime }}$ and the absolute value of the anharmonic modulus at maximum rate $\left |G_{\mathrm {anh}}^{^{\prime \prime }}\right |$ are shown for the highest concentration glassy sample (3$c^{\ast }$). In this case, the behaviour is more complicated. In comparison with $\left |G_{\mathrm {anh}}^{^{\prime }}\right |$, the anharmonic contribution to the viscous stress becomes important at lower strain amplitudes, $\gamma_{0}\sim 4$ %, coinciding with the peak in $G_{1}^{^{\prime \prime }}$. Between $\gamma_{0}\sim$4 and 10 %, $G_{\mathrm {anh}}^{^{\prime \prime }}$ is positive, indicating intracycle shear thickening. At strain amplitudes $\gamma_{0}>15,$ %, $G_{\mathrm {anh}}^{^{\prime \prime }}$ changes sign revealing shear thinning which is almost equal to 15 % of the harmonic viscous contribution.

The above methodology allows a complete description of the LAOS intracycle non-linearities in the framework of FT rheology. At low strain amplitudes $\gamma_{0}<$4 %, the response is dominated by harmonic elasticity. At intermediate amplitudes, $4~\%<\gamma_{0}<10$ %, the harmonic elastic and viscous contributions are important; however, now the anharmonic shear-thickening response is also strong as revealed by the high positive value of $G_{\mathrm {anh}}^{^{\prime \prime }}$. At larger strain amplitudes, the response is dominated by harmonic viscous response and anharmonic contributuon with dominant strain-hardening character and a weaker shear-thinning component.

We can further compare the LAOS response for different volume fractions (Fig. 8). Qualitatively, the behaviour at maximum strain is similar (Fig. 8a, c, e, g). Beyond the linear regime, the anharmonic elastic contribution is always positive. The anharmonic strain-hardening stress decreases with a power law exponent of −1 with strain amplitude, but it becomes progressively more important compared to the harmonic elastic stress. At the largest strain amplitude attained, the anharmonic stress is at least 1 order of magnitude above the harmonic one. On the other hand, the behaviour at maximum rate is quite different at high (Fig. 8b, d) and low concentrations (Fig. 8f, h). At high concentrations, the peak of $G_{1}^{^{\prime \prime }}$ is always accompanied by an anharmonic shear-thickening peak (Fig. 8b, d). This is not present at the low-concentration samples. At large amplitudes and for all samples, the anharmonic shear-thinning contribution decreases almost linearly and is about an order of magnitude smaller than the harmonic viscous stress.

Comparison with other methods of LAOS analysis

Local non-linear coefficients calculated at specific points within the period have been introduced before, most notably by Ewoldt et al. (2008). The modulus at minimum resolvable strain $G_{\mathrm {M}}^{^{\prime }}$ is the gradient of the stress with respect to strain calculated at zero strain, and the modulus at maximum strain $G_{\mathrm {L}}^{^{\prime }}$ is simply the stress at maximum strain divided by $\gamma _{0}$. The definition of viscosities $\eta ^{^{\prime }}$ and $\eta _{\mathrm {L}}^{^{\prime }}$ is similar but with the strain replaced by the shear rate. Based on these moduli and viscosities, a further two non-linear coefficients are defined: S, which gives the strain-hardening/softening character, and T, which gives the shear-thickening/thinning character. It is clear that $G_{\mathrm {L}}^{^{\prime }}$ and $\eta ^{^{\prime }}$ are trivially related to $G_{\mathrm {anh}}^{^{\prime }}$ and $G_{\mathrm {anh}}^{^{\prime \prime }}$ by the following relations:

$$ G_{\mathrm{anh}}^{^{\prime }} = G_{\mathrm{L}}^{^{\prime }}-G_{\mathrm{1}}^{^{\prime }}$$

(7)

$$ G_{\mathrm{anh}}^{^{\prime \prime }} =\omega \eta _{\mathrm{L}}^{^{\prime }}-G_{ \mathrm{1}}^{^{\prime \prime }} $$

(8)

On the other hand, $G_{\mathrm {M}}^{^{\prime }}$ and $\eta _{\mathrm {L}}^{^{\prime }}$ cannot be expressed simply in our scheme or any other scheme based on FT rheology, and the same is true for S and T.

The key difference between the method of analysis presented in this paper and the previous methods is that here we compare the non-linear stress directly to the harmonic stress and not to the stress gradient. Hence, the anharmonic moduli may also serve as indicators of the inaccuracy in the representation of non-linear data by $G_{\mathrm {1}}^{^{\prime }}$ and $G_{\mathrm {1}}^{^{\prime \prime }}$ as in conventional dynamic strain sweeps.

There is a further subtle but important conceptual difference; here, we do not decompose the total stress into an elastic stress and a viscous stress (Cho et al. 2005). We refrain from doing so because in our view, the elastic–viscous decomposition does not represent correctly the physics within the period, at least for the highly concentrated and glassy samples undergoing yielding. More specifically, the requirement for an identical elastic stress at the same values of strain within the LAOS period is not always true since in some cases, at the same values of strain, the material can be either flowing or deforming elastically. This is illustrated in Fig. 4 with an arrow that marks two points inside the period at the same strain. Although according to the elastic–viscous stress decomposition (Cho et al. 2005) they should have the same elastic (and viscous) stress, this is clearly not the case since these two points correspond to different rheological states of the material: In point A, we have mainly an elastic response after strain reversal, whereas in point B, a viscous (or plastic) post-yielding response is approaching strain reversal. Moreover, the decomposition includes in the viscous stress all the $G_{n}^{^{\prime \prime }}$ terms of Eq. 1. However, as it has been pointed out before, all of these terms with the exception of $G_{1}^{^{\prime \prime }}$ have an elastic character that renders their inclusion in the viscous stress problematic (Onogi and Matsumoto 1981; Dealy and Wissbrun 1999). In our scheme, the whole non-linear behaviour is discussed using the stress at two points inside the period: maximum rate, where the contribution from the hydrodynamic stress is at a maximum, and maximum strain, where the contribution from the hydrodynamic stress is zero. This is certainly a simplification but has the merit of being able to describe the waveform of the stress response much better than the first harmonic moduli alone. The failure of the decomposition in pure elastic and viscous contributions in the stress within the period of oscillation in a generic manner provides further justification for the choice of determining the character of the higher harmonics only at the points of zero and maximum rate as discussed above.

Any method of analysis, such as FT rheology or Chebyshev decomposition, that compares the total stress waveform to a harmonic waveform suffers from the vague physical meaning of the harmonic contribution. Nevertheless, we know that $G_{1}^{^{\prime \prime }}$ is proportional to the total energy dissipation and $G_{1}^{^{\prime }}$ to the average elasticity. A possible way to interpret the harmonic waveform would then be to associate it with the response of a linear viscoelastic system that dissipates the same energy and has the same average elasticity. Thus, the strain hardening/softening and shear thinning/thickening are defined with respect to this ideal viscoelastic system.

Relation of LAOS with steady shear

Another approach to LAOS analysis seeks to understand the non-linear response in relation to simpler steady shear experiments, as discussed above. For colloidal glasses, a qualitative relation between LAOS and steady shear (e.g. step rates) has been discussed here and elsewhere (Renou et al. 2010; Rogers et al. 2011). It is based on the fact that following flow reversal, the stress increases linearly with strain, indicating an elastic response, while near the maximum shear rate, the material flows with a shear rate-dependent viscosity. A quantitative relation between LAOS and steady shear has been proposed by Rogers et al. along two lines: firstly, that the the linear $G^{^{\prime }}$ (called the cage modulus or $G_{\mathrm {cage}}$) can be determined from the slope of the stress versus strain at zero stress and, secondly, that the LAOS stress in the post-yield regime plotted against shear rate may reproduce the steady shear flow curve (Rogers et al. 2011). The cases were applied to experimental data from a colloidal glass of multiarm star polymers probed at a single frequency of 1 rad/s. Below, we test these propositions in the current system.

In Fig. 9, we compare the dynamic strain sweep values of G′₁ with G _cage extracted from the elastic part of the LAOS stress for two solid-like samples. The agreement between the two is quite good, confirming the validity of this approach for our system at an angular frequency of 1 rad/s.

Fig. 9

Comparison of $G^{^{\prime }}$ with $G_{\mathrm {cage}}$, calculated from the gradient of stress with strain of the LAOS experiments at zero stress. The horizontal lines are an extension of the linear $G^{^{\prime }}$ values to all strain amplitudes. Two solid-like samples are shown with 3$c^{\ast }$ (grey) and 2.6$c^{\ast }$ (black) measured at 10 °C

As the strain amplitude increases, the slope of the stress versus strain is less well defined, leading to a larger error in the determination of G _cage. In our view, this approach is based on the assumption that the cage is undeformed at zero stress, which allows the calculation of a cage elastic modulus. However, one should bear in mind that although this seems to hold here, it is not necessarily true in general as in other systems, the microstructure might be very anisotropic at zero stress (Koumakis et al. 2012b).

In Figs. 10a and 11a, we show Lissajous plots from LAOS experiments in a liquid and glassy sample, respectively. Figures 10b and 11b depict the corresponding stresses extracted from the LAOS cycle in the regime between the maximum and zero rate, i.e. the flowing post-yield regime as a function of the shear rate. In line with Rogers et al. (2011), these are contrasted with the flow curve (stress versus shear rate) measured under steady shear. The latter was measured by progressively lowering the shear rate and with long enough averaging at each rate to ensure that a steady state is reached. It can be seen that Qualitatively, the LAOS data follow the flow curve at high shear rates. However, there are important quantitative differences mainly at low shear rates for both frequencies shown. The same disagreement is found for the more concentrated sample ($c=2.9c^{\ast }$) exhibiting yield stress behaviour (Fig. 11). Note that the discrepancy in the measured stresses upon approaching zero strain (maximum rate) and going beyond, manifested in the viscous Lissajous plots as secondary loops (Fig. 4b), justifies the use of only the viscoplastic flow regime of LAOS cycle between zero and maximum strain.

Fig. 10

a Stress versus normalised strain in an elastic Lissajous representation of LAOS results at same maximum shear rate . b The LAOS stress between zero and maximum strain plotted against shear rate for two different pairs of frequency and strain amplitude, but with the same maximum shear rate. The flow curve of the material is shown as a red line (sample at 2.4$c^{\ast }$ was measured at 15 °C). Note that for the data presented here, $\mathrm {Wi}_{\protect \alpha } = 1.67$ while $\mathrm {Pe}_{\protect \omega }=4.2\;10^{-5}$ (for 0.1 rad/s)

Fig. 11

a Elastic Lissajous figure (grey line) with the stress between zero and maximum strain indicated by crosses. b The LAOS stress between zero and maximum strain is plotted against shear rate for different frequencies and strain amplitudes. The flow curve of the material is shown as a red line (sample at 2.9$c^{\ast }$ was measured at 10 °C). Note that for the data presented here, $\mathrm {Wi}_{\protect \alpha } > 10$ (for 0.1 rad/s, $\protect \gamma _{0} = 1{,}000$ % and 1 rad/s, $\protect \gamma _{0} = 107$ %) and $\mathrm {Wi}_{\protect \alpha } > 40$ (for 1 rad/s, $\protect \gamma _{0} = 409$ %) while $\mathrm {Pe}_{\protect \omega }=4.2\;10^{-5}$ (for 0.1 rad/s)

A rationalisation for this difference can be provided by considering the relaxation times in the system. The dimensionless number quantifying the interplay of the terminal relaxation and shear is given by the Weissenberg number, $\mathrm {Wi}_{\alpha }=t_{\alpha }(\omega \gamma _{0})$, where $t_{\alpha }$ is terminal $\alpha$-relaxation related with the out-of-cage diffusion, determined here at the crossover point of $G^{^{\prime }}$ and $G^{^{\prime \prime }}$ at low frequencies (see Fig. 2). For the 2.6$c^{\ast }$ sample, $\mathrm {Wi}_{\alpha }=1.67$, while for comparison, the ‘bare’ Peclet number $\mathrm {Pe}_{\omega }=t_{\beta }(\omega \gamma _{0})$ with $t_{\beta }=R_{\mathrm {h}}^{2}/D_{0}$ ($D_{0}$ is the free Brownian diffusion coefficient) is only $4.2\;10^{-5}$, for $\omega =0.1$ rad/s. For the highest concentration, 3$c^{\ast }$, the linear viscoelastic measurement (Fig. 2a) does not indicate a terminal relaxation within the frequency range of the experiment. Therefore, we can conclude that $\mathrm {Wi}_{\alpha }>10$ for the 0.1 rad/s, $\gamma _{0}=1{,}000$ % and for the 1 rad/s, $\gamma _{0}=107$ % measurements shown. Such large $\mathrm {Wi}_{\alpha }$ values are expected for any glassy sample where the $\alpha$-relaxation is either infinite or very long compared to any measurement time. Here, it is obvious that the LAOS stress data, extracted from the part of the period where the sample qualitatively is showing a viscous/plastic response (past the yield point after strain reversal), do not superimpose with the properly measured flow curve. Moreover, there is a clear discrepancy among the LAOS data at different frequencies (0.1 and 1 rad/s) as well as different strain amplitudes (107 and 409 %) at the same frequency (1 rad/s) especially for low rates. This should not be unexpected as only in the limit of zero frequency, a LAOS experiment may be considered identical to steady shear; however, when the frequency is finite, the relaxation time of the material starts to affect the stress response within the oscillatory cycle. Furthermore, we should keep in mind that a proper flow curve measurement requires averaging of the stress over a time period typically of the order $1/\dot {\gamma }$ in order to allow steady state to be reached at each rate. In comparison, LAOS measurements even at low frequencies do not involve similar long averages per point measured that would allow steady state to be approached. For example, even at 0.1 rad/s, each of the 256 points measured within a LAOS cycle is taken in 0.25 s. However, this duration is not sufficient to reach steady state for rates roughly smaller than 1 s$^{-1}$, and therefore, it is not surprising that low rate values from LAOS deviate from those of steady shear flow curves.

Conclusions

We have studied the non-linear response of model soft starlike micelles at different volume fractions, both in the concentrated viscoelastic liquid and glassy state by large-amplitude oscillatory shear experiments. We discuss the evolution of the Lissajous figures and use Fourier transform analysis to quantify the progressively non-linear behaviour with increasing strain amplitude. With increasing volume fraction, the linear regime shrinks and the magnitude of the non-linearity, as measured by $I_{3/1}$, increases faster with strain amplitude, although the yield strain itself $\left (\textrm {determined at}~G^{^{\prime }}=G^{^{\prime \prime }}\right )$ also increases with concentration.

The character of the dominant intracycle non-linearity was first determined by the phase of the third harmonic. However, we further propose an alternative method through which all higher harmonics are taken into account by subtracting the harmonic stress from the total stress waveform. The new method shows that by taking into account all higher harmonics, the character of the intracycle non-linearities may by altered: For example, for the high concentration glassy systems, the intracycle non-linear behaviour at large amplitudes has a stronger strain-hardening than shear-thinning contribution contrary to what is suggested by the third harmonic alone. Therefore, glassy samples during yielding exhibit a progressive transition from non-linear shear thickening at intermediate strain amplitudes $\left (\textrm {near the}~G^{^{\prime \prime }}~\text {peak}\right )$ to strain hardening at larger strains (with similar order but weaker shear thinning). For liquid-like samples, the initial shear-thickening character, which may be related to yielding, is absent. The new method proposed is easier to implement than Fourier transform rheology or Chebyshev decomposition, fully accounting of all higher harmonics. However, similarly with the above, it brings out the need for a physical understanding of the harmonic response with which one naturally compares in this approach.

Furthermore, we point out here that although the glassy systems may be considered shear-melted at strains above the yield strain, there is a considerable elastic component at flow reversal even at very large strain amplitudes, in agreement with previous studies in hard and soft-sphere glasses showing strong strain recovery even after being shear-melted at high shear rates (Petekidis et al. 2004; Le Grand and Petekidis 2008; Christopoulou et al. 2009). This is also manifested by the almost constant cage modulus determined from the elastic regime of the LAOS cycle even at high strain amplitudes. Finally, in contrast to the cage modulus that is in a quantitative agreement with the linear $G^{^{\prime }}$, the quantitative determination of the steady shear flow curve from the viscous part of the Lissajous plot suggested previously (Rogers et al. 2011) does not work in the present system neither for liquid nor glassy samples. We consider the latter to be representative of a generic behaviour of glassy or highly concentrated systems with very long or infinite structural relaxation times rather than the exception, since practically a steady state equivalent to that in constant shear rate cannot be reached at each point within the LAOS period.