Non-Newtonian deterministic lateral displacement separator: theory and simulations

Abstract

Deterministic lateral displacement devices have been proved to be an efficient way to perform continuous particle separation in microfluidic applications (Huang et al. Science 304:987–990, 2004). On the basis of their size, particles traveling through an array of obstacles follow different paths and can be separated in outflow. One limitation of such a technique is that each device works for a specific critical size to achieve particle separation, and a new device with different geometrical properties needs to be fabricated, as the dimensions of the particles to be separated change. In this work, we demonstrate the possibility to tune the critical particle size in a deterministic lateral displacement device by using non-Newtonian fluids as suspending liquid. The analysis is carried out by extending the theory developed for a Newtonian constitutive law (Inglis et al. Lab Chip 6:655–658, 2006) to account for fluid shear-thinning. 3-D finite element simulations are performed to compute the dynamics of a spherical particle flowing through the deterministic ratchet. The results show that fluid shear-thinning, by altering the flow field between the obstacles, contributes to decrease the critical particle diameter as compared to the Newtonian case. Numerical simulations demonstrate that tunability of the critical separation size can be achieved by using the flow rate as control parameter. A design formula, relating the separation diameter to the fluid rheology and the relevant geometrical parameters of the device, is derived. Such a formula, originally developed for a power-law model, is proved to work for non-Newtonian liquids with a general viscosity trend.

Introduction

Separation of particles suspended in fluids in microfluidic devices is a crucial step in many chemical and biochemical processes (Pamme 2007). Several separation techniques have been proposed, based on magnetic fields (Pamme and Manz 2004; Xia et al. 2006), electric fields (Mazereeuw et al. 2000; Fonslow and Bowser 2008), acoustic waves (Laurell et al. 2007; Nam et al. 2011), gravity (Huh et al. 2007), and hydrodynamic forces (Yamada et al. 2004; Yamada and Seki 2005).

Within the context of separators based on hydrodynamic effects, Huang et al. (2004) developed an efficient, size-based, continuous separation technique known as “deterministic lateral displacement” (DLD). The separation device consists in a sequence of rows of obstacles that are shifted by a fixed displacement along the flow direction. The displacement is chosen such that, after a number of rows, the obstacles aligned again. The suspension containing particles with different sizes is pumped through the array of obstacles in laminar flow. Small particles follow the direction of the flow, and there is no net displacement when traveling through the device (“zigzag motion”). On the other hand, bigger particles hydrodynamically interact with the obstacles and are pushed from the original flow stream to the adjacent one, resulting in a net displacement between the inlet and outlet position (“displacement motion”). Such a technique is “deterministic” as, if diffusion is negligible, the path followed by the particles is completely determined by the geometry of the device. The deterministic ratchet has been successfully used in biological applications for separation of DNA, cells, and blood (Huang et al. 2004; Davis et al. 2006; Inglis et al. 2008a, b, 2010; Green et al. 2009), showing improved performances over alternative techniques in terms of speed and separation resolution.

The critical particle size, i.e., the particle diameter dividing the displacement from the zigzag behavior, depends on the geometrical parameters of the device, e.g., the gap between two posts and the displacement between two consecutive rows of obstacles (Inglis et al. 2006). Therefore, once a device has been fabricated, it can be only used to separate two classes of particles having sizes lower and higher than the critical diameter which the device has been designed for. For this reason, most practically used DLD devices are made with several sections in series, each with a different critical particle size. In this way, a discrete set of characteristic dimensions can be separated. However, because of the high variability of sizes in biological particles, an existing device may not have the adequate geometrical properties to achieve particle separation. Therefore, a limitation of the DLD technique is the need to fabricate a new device able to process suspensions with the desired critical separation size.

Recently, a couple of techniques to tune the critical particle size in a DLD device have been proposed. Beech and Tegenfeldt (2008) showed that a variation of the critical particle size can be attained by stretching the deterministic ratchet along the direction orthogonal to the flow. Indeed, as an effect of the applied strain, the inter-obstacle distance increases, leading to an increase in the critical separation size as well. Of course, the device needs to be fabricated by an elastomeric material as PDMS and, as remarked by the authors, a uniform stretching of the device is required, avoiding, at the same time, the deformation of the pillars. A second possibility to tune the critical size has been proposed by Beech et al. (2009) by combining the DLD principle with dielectrophoresis. By applying a nonuniform electric field, a dielectrophoretic force acts on the particles leading to a “jump” to the adjacent flow stream. By modulating the external voltage, such a force can be varied, thus tuning the critical separation size.

In this work, we present an alternative method to tune the critical size in a DLD device. We propose to use non-Newtonian fluids as suspending liquid in order to exploit their rheological properties to modify the critical particle size. Therefore, instead of applying an external force (e.g., by stretching the device or by using dielectrophoresis), we propose to attain tunability of the critical size by exploiting the “internal” properties of the liquid.

The use of non-Newtonian fluids as suspending liquids in microfluidic devices has been proved to be an efficient way to achieve operations that commonly require complex apparati. For instance, viscoelastic fluids promote particle focusing in straight channels (Leshansky et al. 2006; Yang et al. 2011; Villone et al. 2011; D’Avino et al. 2012), and size-based separation by exploiting the particle migration phenomenon induced by fluid elasticity (Nam et al. 2012). Very recently, non-Newtonian fluids have also been used as suspending liquids to manipulate DNA, cells, and nanoparticles (Yang et al. 2012; Kim et al. 2012).

The aim of this work is to investigate the effect of the rheology of non-Newtonian fluids on the dynamics of particles flowing in a deterministic ratchet. More specifically, the study is finalized to relate the critical size to the fluid shear-thinning and test the possibility to modulate the particle separation diameter by properly selecting the fluid rheology for a given geometry of the device.

The theory developed by Inglis et al. (2006) for predicting the critical particle size for Newtonian liquids is firstly extended to take into account fluid shear-thinning. This is done by considering the power-law model because of its simplicity and the availability of analytical expressions for the flow field in simple geometries.

The theoretical results are, then, confirmed by 3-D direct numerical simulations whereby the dynamics of a rigid, spherical particle in the DLD device is computed by solving the governing equations. The finite element method with a mesh-deforming procedure to follow the particle motion is adopted. A Newtonian suspending liquid is firstly considered to validate the numerical code by a comparison with the available experimental data. The simulations are, then, extended to the power-law and the Bird–Carreau constitutive models. From the numerical results, a design formula relating the critical particle diameter to the fluid rheology and the geometry of the DLD device is derived.

Problem formulation and numerical method

Problem description and governing equations

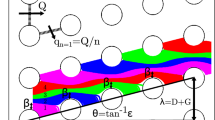
A top view of the deterministic ratchet (also referred as bumper array) is schematized in Fig. 1. Each gray circle is a cylindrical obstacle with radius $R_{\textrm {cyl}}=D_{\textrm {cyl}}/2$ and height $L_{\textrm {cyl}}$ which is generally chosen much larger than the radius. The gap between two obstacles along the y-direction is denoted by H, whereas the distance between two consecutive rows of obstacles (computed from the cylindrical surfaces) is denoted by $\Delta x$. Each row is shifted with respect to the previous one by a quantity $\Delta \lambda$. The ratio $N_{\textrm {post}}=\Delta \lambda /\lambda$, with $\lambda =H+D_{\textrm {cyl}}$, is called the periodicity number of the bumper array. Indeed, such a parameter represents the number of rows that identifies the characteristic cell of the device, i.e., the whole device can be obtained by replicating along the $x-$ and $y-$directions of such a cell. In Fig. 1, the device periodicity is $N_{\textrm {post}}=4$. The number of periodic posts is a fundamental design parameter as it is directly related to the critical particle size. Previous studies have reported that, by choosing an integer periodicity number, typically the particles follow two possible paths (see below), whereas a more complicated scenario occurs for noninteger values of $N_{\textrm {post}}$ (Long et al. 2008; Frechette and Drazer 2009). In this work, we always set an integer periodicity number.

Fig. 1

Schematic top view of the deterministic ratchet. The cylindrical obstacles are the gray circles and the relevant geometrical parameters are reported. The computational domain used in the simulations is also shown (dashed lines)

A dilute suspension of spherical rigid particles flows by imposing a flow rate along the x−direction. We denote the particle radius by $R_{\textrm p}=D_{\textrm p}/2$. Assuming negligible inertia and no external forces and torques, the governing equations for the fluid domain read as follows:

$$ \nabla\cdot\boldsymbol{u}=0 $$

(1)

$$ \nabla\cdot\boldsymbol{\sigma}=-\nabla p+2\nabla\cdot\left[\eta(\dot\gamma)\boldsymbol{D}\right]=\boldsymbol{0} $$

(2)

Equations 1 and 2 are the mass and momentum balance, respectively. In these equations, $\boldsymbol {\sigma }$, $\boldsymbol {u}$, $p$, $\eta (\dot \gamma )$, and $\boldsymbol {D}$, are the stress tensor, the velocity vector, the pressure, the viscosity, and the rate-of-deformation tensor $\boldsymbol {D}=(\nabla \boldsymbol {u}+\nabla \boldsymbol {u}^T)/2$, respectively. Notice that, in general, the viscosity is not constant, but it is assumed to be a function of the magnitude of the rate-of-deformation tensor $\dot \gamma =\sqrt {2\boldsymbol {D}:\boldsymbol {D}}$ (Bird et al. 1987). The expression for the viscosity is determined by choosing a constitutive equation for the fluid. In this work, we consider the Newtonian constitutive law characterized by a constant viscosity:

$$ \eta(\dot\gamma)=\mu $$

(3)

and two non-Newtonian fluids, i.e., the power-law model:

$$ \eta(\dot\gamma)=m \dot\gamma^{n-1} $$

(4)

and the Bird–Carreau model:

$$ \eta(\dot\gamma)=\eta_{\infty}+(\eta_0-\eta_{\infty})\frac{1} {\left[1+(K \dot\gamma)^2\right]^{\frac{1-n}{2}}} $$

(5)

In both non-Newtonian equations, the parameter n sets the fluid shear-thinning. For n = 1, the Newtonian case is recovered, with viscosity given by m and $\eta _0$, for the power-law, and Bird–Carreau models, respectively. For $n<1$, both models predict shear-thinning. In Eq. 5, $\eta _0$ and $\eta _{\infty }$ are the viscosities at low and high shear rates, and $1/K$ is the shear rate value corresponding to the start of viscosity thinning in simple shear flow. In Fig. 2, we show the viscosity trends for the Newtonian case ($\mu =1$), the power-law fluid with $m=1$ and two values of the parameter n ($n=0.7$ and $n=0.4$), and for the Bird–Carreau model with $\eta _0=1$, $\eta _{\infty }=0.1$, $K=1$, $n=0.1$. It is important to remark that both non-Newtonian constitutive equations do not predict normal stresses and fluid elasticity, and they can be regarded as a generalization of the Newtonian constitutive equation (Bird et al. 1987).

Fig. 2

Viscosity trends in simple shear flow for a Newtonian fluid ($\mu =1$, dashed–dotted line), power-law model ($n=0.7$, long dashed line; $n=0.4$, short dashed line, and $m=1$), Bird–Carreau model ($\eta _0=1$, $\eta _{\infty }=0.1$, $K=1$, $n=0.1$, solid line)

Because of the assumption of dilute system, we can consider the dynamics of a single flowing particle, neglecting particle–particle hydrodynamic interactions. Under the assumptions of absence of particle inertia, and no external forces and torques, the total force $\boldsymbol {F}$ and torque $\boldsymbol {T}$ acting on the particle surface are zero:

$$ \boldsymbol{F}=\int_{\partial S_{{\textrm p}}}\boldsymbol{\sigma}\cdot \boldsymbol{n}\, dS=\boldsymbol{0} $$

(6)

$$ \boldsymbol{T}=\int_{\partial S_{{\textrm p}}}(\boldsymbol{x}-\boldsymbol{x}_{{\textrm p}})\times(\boldsymbol{\sigma} \cdot \boldsymbol{n})\, dS=\boldsymbol{0} $$

(7)

where $\boldsymbol {n}$ is the outwardly directed unit normal vector on the particle surface $\partial S_{{\textrm p}}$, $\boldsymbol {x}$ is a generic point on the surface, and $\boldsymbol {x}_{{\textrm p}}$ is the particle center. Notice that, in writing Eqs. 6–7, we neglected particle diffusion (i.e., Brownian motion). Although diffusion has been proven to have an effect on the behavior of DLD devices (Heller and Bruus 2008; Long et al. 2008), we recall that non-Newtonian fluids usually have viscosities much larger than water, thus reducing the particle diffusion coefficient.

Finally, the particle position and rotation are updated by integrating the following kinematic equations:

$$ \frac{d\boldsymbol{x}_{{\textrm p}}}{dt}=\boldsymbol{U}_{{\textrm p}},~~~ \boldsymbol{x}_{{\textrm p}}|_{t=0}=\boldsymbol{x}_{{\textrm p,0}} $$

(8)

$$ \frac{d\boldsymbol{\Theta}}{dt}=\boldsymbol{\omega}_{{\textrm p}},~~~ \boldsymbol{\Theta}|_{{\textrm t=0}}=\boldsymbol{\Theta}_{{\textrm 0}} $$

(9)

with $\boldsymbol {U}_{{\textrm p}}$ and $\boldsymbol {\omega }_{{\textrm p}}$ the translational and angular particle velocity, and $\boldsymbol {\Theta }$ the angular rotation.

To prevent a severe mesh distortion between the particle and pillars, a short-range repulsive force needs to be included (Frechette and Drazer 2009; Kulrattanarak et al. 2011b). Following Glowinski et al. (1999), in this work, we model the repulsive force as

$$ \boldsymbol{F}_{\textrm{p,j}}=\boldsymbol{0},\quad d_{\textrm{p,j}}>R_{\textrm p}+R_{\textrm{cyl}}+\rho $$

(10)

$$ \begin{array}{rll} \boldsymbol{F}_{\textrm{p,j}}&=&F(\boldsymbol{x}_{\textrm p}-\boldsymbol{x}_{\textrm{cyl,j}})(R_{\textrm p}+R_{\textrm{cyl}}+\rho- d_{\textrm{p,j}})^2,\\ d_{\textrm{p,j}}&\leq& R_{\textrm p}+R_{\textrm{cyl}}+\rho \end{array} $$

(11)

where $d_{\textrm {p,j}}=|\boldsymbol {x}_{\textrm p}-\boldsymbol {x}_{\textrm {cyl,j}}|$, $\boldsymbol {x}_{\textrm {cyl,j}}$ is the center of the circular section of the cylinder j (all the cylinders have the same radius $R_{\textrm {cyl}}$), $F$ modulates the magnitude of the force and $\rho$ is the force range. Such a force is added to the Eq. 6. Preliminary tests have been performed to evaluate the force parameters. In this work, we set $F=5,000$ and $\rho =0.035$. With this choice, the mesh deformation between the particle and a pillar is not critical, still allowing the particle to closely approach the cylinders. Furthermore, as shown by the validation tests presented in Section “Simulation procedure and code validation”, with those values for F and ρ, the simulation results fairly describe the experimental data.

To solve the system of equations, boundary conditions for the velocity field need to be specified. This is postponed to the next section, after the computational domain is discussed.

The governing equations are made dimensionless by taking the gap H as characteristic length, the ratio Q/H as characteristic velocity, where Q is the flow rate per unit of height of the device crossing the gap H (see below), and $\eta Q/H^2$ as characteristic stress, with η a viscosity depending on the constitutive equation. For brevity, we report in dimensionless form only the mass and momentum balance equations, after substituting the three constitutive models. Denoting with starred symbols the dimensionless quantities, they read as

$$ \nabla^{*}\cdot\boldsymbol{u}^{*}=0 $$

(12)

$$ -\nabla^{*} p^{*}+2\nabla^{*}\cdot\boldsymbol{D}^{*}=\boldsymbol{0} $$

(13)

$$ -\nabla^{*} p^{*}+2\nabla^{*}\cdot\left[(\dot\gamma^{*})^{n-1}\boldsymbol{D}^{*}\right]=\boldsymbol{0} $$

(14)

$$ \begin{array}{rll} && -\nabla^{*} p^{*}+\\ && 2\nabla^{*}\cdot\left[\left(\eta_r+(1-\eta_{\textrm r})\frac{1}{[1+(\Theta \dot\gamma^{*})^2]^{\frac{1-n}{2}}}\right)\boldsymbol{D}^{*}\right]=\boldsymbol{0} \end{array} $$

(15)

where Eqs. 13–15 refer to the Newtonian, power-law, and Bird–Carreau model, respectively. In Eq. 15, $\eta _{\textrm r}=\eta _{\infty }/\eta _0$ is the viscosity ratio and $\Theta =K Q/H^2$.

From the dimensionless equations, it is evident that, for a Newtonian liquid, there is no constitutive dimensionless parameter, whereas the exponent n is the only parameter for the power-law model. Therefore, in both cases, the particle dynamics and, consequently, the critical separation size are expected to be independent of the flow rate (in terms of dimensionless quantities). On the contrary, the flow rate appears in the parameter Θ of the Bird–Carreau model, that, together with the viscosity ratio $\eta _{\textrm r}$ and the exponent n, completely describes the fluid rheology. The effects of the flow rate on the critical size for the Bird–Carreau model will be discussed in Section “Bird–Carreau model”.

Finally, the dimensionless geometrical parameters are the blockage ratio $D_{\textrm p}/H$, the distance between two consecutive rows $\Delta x/H$, the diameter of the cylinders $D_{\textrm {cyl}}/H$, and the number of periodic posts $N_{\textrm {post}}$. In this work, we fix the following geometrical parameters $D_{\textrm {cyl}}/H=1$ and $\Delta x/H=2$, whereas the influence of the fluid rheology and periodicity of the device $N_{\textrm {post}}$ is analyzed by varying the blockage ratio $D_{\textrm p}/H$ to identify the critical particle separation size.

Computational domain and boundary conditions

As discussed above, the structure of the deterministic ratchet can be obtained by periodically replicating a characteristic cell, as the one depicted in Fig. 1. Of course, it is assumed that the influence of the inlet and outlet as well as the lateral bounding walls is negligible. Therefore, the numerical investigation of the critical particle size can be limited to a periodic cell, as done in Kulrattanarak et al. (2011b). For analyzing the flow field without particles, a further reduction of the computational domain is possible. Indeed, the domain delimited by the dashed–dotted lines in Fig. 1 is representative of the whole system, i.e., the flow field within such a reduced domain is the same in any region of the deterministic ratchet. Now the two periodic directions are along the lines connecting the centers of the pillars.

When a particle is taken into account, the latter still holds, provided that the lengths of the reduced domain are sufficiently larger than the particle diameter such that the particle path is not influenced by the images of the particle itself across the periodic boundaries. The periodicity implies that, when the particle leaves the domain crossing a boundary surface, it appears on the opposite surface, at the same relative position with respect to the periodic directions. However, the dashed–dotted domain shown in Fig. 1 cannot be directly used as it would require the splitting of the particle when crossing the domain boundaries. To overcome this problem, the domain enclosed by the dashed line can be used as computational domain, but the relocation of the particle is still performed when its center crosses one of the boundaries of the dashed–dotted domain. In this way, the particle surface is always enclosed within the computational domain and the domain size is increased, thus leading to a larger distance between the particle and their images. It is important to remark that the jump of the particle from one surface to the opposite one is allowed as no velocity/stress time-derivative appears in the governing equations (no inertia/no elasticity). In other words, each step of the simulations is independent of the previous ones as the velocity/stress field previously computed are not required to calculate the solution at the current time level. Preliminary tests have been carried out to verify that the lengths of the computational domain allows to neglect the influence of the periodic images of the particle on its dynamics. Further details are given in the next section.

Concerning the size of the domain along the x−axis, we assume (in agreement with the ratchets used in the experiments) that the height of the pillars is much larger than the particle diameter. This allows us to study one-half of the full geometry obtained by cutting the sphere in two halves by a symmetry plane (the xy−plane). As a consequence, the translational particle velocity has two components (along x− and y−direction) and the angular velocity has one nonzero component (rotation around the z−axis).

In conclusion, the computational domain used in this work is shown in Fig. 3. Notice that the angle between the planes parallel to the z−axis depends on the periodic number of posts $N_{\textrm {post}}$, as it directly affects the position of the pillars.

Fig. 3

Computational domain used in the simulations. Notice that the flow direction does not coincide with the plane $\partial S_5$ and $\partial S_6$

Referring to the notation in Fig. 3, the boundary conditions read as follows:

$$ \boldsymbol{u}=\boldsymbol{0}\quad{\textrm{on}}~\partial S_{{\textrm{cyl,i}}}~~~i=1,...,4 $$

(16)

$$ \boldsymbol{u}|_{\partial S_1}=\boldsymbol{u}|_{\partial S_3} $$

(17)

$$ \boldsymbol{u}|_{\partial S_5}=\boldsymbol{u}|_{\partial S_6} $$

(18)

$$ -\int_{\partial S_1}\boldsymbol{u}\cdot\boldsymbol{n}\,dS=Q_{\textrm{in}} $$

(19)

$$ u_z=0,\,f_x=f_y=0\quad{\textrm{on}}~\partial S_2~{\textrm{and}}~\partial S_4 $$

(20)

$$ \boldsymbol{u}=\boldsymbol{U}_{{\textrm{p}}}+\boldsymbol{\omega}_{{\textrm p}}\times(\boldsymbol{x}- \boldsymbol{x}_{{\textrm p}})\quad{\textrm{on}}~\partial S_{{\textrm p}} $$

(21)

Equation 16 is the no-slip condition on the pillar surfaces, Eqs. 17–18 express the periodic conditions for the velocity, a flow rate $Q_{\textrm {in}}$ is imposed in inflow (Eq. 19 with $\boldsymbol {n}$ the outwardly directed unit normal vector on $\partial S_1$), and Eq. 20 is the symmetry condition applied on the upper and lower boundaries where $f_j$ is the force directed along the direction j. Finally, Eq. 21 is the rigid-body motion on the particle boundary. Notice that, because of the chosen computational domain, the flow rate $Q_{\textrm {in}}$ is twice the flow rate Q crossing the section between two posts. Because of the arbitrary size of the domain along the z−axis, both flow rates are expressed for unit length of z−dimension. Therefore, the characteristic velocity Q/H introduced in the previous section is the average velocity of the fluid crossing the gap between two obstacles.

Numerical method and preliminary tests

The governing equations are solved by the finite element method. A second-order Adams–Bashforth scheme is used for time integration of Eqs. 8–9. The particle translational and the angular velocity are treated as additional unknowns and are included in the weak form of momentum equation. The force- and the torque-free conditions are imposed through Lagrange multipliers in each node of the spherical surface (D’Avino et al. 2008, 2010; Snijkers et al. 2011). Therefore, at each time step, the velocity and pressure fields, together with the x− and y−components of the particle translational velocity and the angular velocity around the z−axis are simultaneously computed.

A boundary-fitted mesh with tetrahedral elements is used to discretize the domain. During a simulation, the particle changes its position following the flow direction. The mesh nodes describing the particle surface are moved in order to follow the particle motion. The internal mesh nodes (representing the fluid) need to be moved as well in order to reduce the mesh distortion. The mesh displacement, calculated in terms of velocity $\hat {\boldsymbol {u}}$, is computed by solving a Laplace equation, assuring smooth variation (Hu et al. 2001). Due to the mesh distortion as the particle moves, the mesh needs to be regenerated after some time steps. Following Hu et al. (2001), the mesh is considered too much distorted when one of the two following parameters $f_1$ and $f_2$ exceeds the threshold of 1.39:

$$ f_1=\max_{1\leq e \leq N_{\textrm{el}}}(f_1^{\textrm{e}}) $$

(22)

$$ f_2=\max_{1\leq e \leq N_{\textrm{el}}}(f_2^{\textrm e}) $$

(23)

with $N_{\textrm {el}}$ as the total number of elements and

$$ f_1^e=|\log(V^e/V_0^{\textrm e})| $$

(24)

$$ f_2^e=|\log(S^e/S_0^{\textrm e})| $$

(25)

where $V^{\textrm e}$, $S^{\textrm e}$, $V_0^{\textrm e}$, and $S_0^{\textrm e}$ are the volume and the aspect ratio of the element e and their values in the initial undeformed mesh, respectively. The aspect ratio is defined as $S^{\textrm e}=(l^{\textrm e})^3/V^{\textrm e}$ with $l^{\textrm e}$ as the maximum side length of the element e.

Because of the inertialess assumption, the computations are greatly simplified as (a) no convective term appears in the governing equations and, hence, we do not need to take into account for the relative motion of the mesh nodes with respect to the fluid velocity, and (b) the absence of time-dependent terms does not require to project the velocity field from the old mesh to the new one.

The mesh generation is automatically performed by using the software Gmsh (Geuzaine and Remacle 2009). As the particle–pillar distance can be very small, to accurately solve the flow field in between the gap, we guarantee that at least six to eight tetrahedral elements are generated between the particle and cylinder surfaces. An example of the mesh is shown in Fig. 4, when the particle is quite close to a pillar. For the sake of clarity, only the elements on the domain boundaries are shown, and the mesh reported in the figure is coarser than the ones typically used in the simulations. In the inset, the nonuniform distribution of the elements on the particle and the closest pillar is readily observed, assuring a sufficiently fine discretization within the gap.

Fig. 4

Typical mesh used in the simulations. For sake of clarity, only the mesh on the domain boundaries is reported and the discretization is coarser than the one used in the computations. In the inset, the element distribution between the particle and the closest cylinder is shown

A number of preliminary tests have been carried out. Mesh and time convergence has been checked by changing the number of elements and the time-step size. A representative convergence test is reported in Fig. 5 where particle trajectories in the bumper array with $N_{\textrm {post}}=4$ are shown. The solid line is the trajectory for $D_{\textrm p}/H=0.6$ with a mesh with about 20,000 elements and a (dimensionless) time-step size $\Delta t=0.05$. The symbols refer to the same case with $\Delta t=0.025$ (black circles) and about 35,000 elements (white circles). It is readily seen that the symbols and the solid line cannot be distinguished. By changing the geometrical parameters, similar results are obtained. In all the simulations, we adopt meshes with about 20,000 elements and a time-step size $\Delta t=0.05$. Finally, Fig. 5 also shows the two dynamics followed by the particle, i.e., the zigzag motion for $D_{\textrm p}/H=0.6$ (solid line and symbols) and the displacement motion obtained by increasing the particle size to $D_{\textrm p}/H=0.8$ (dashed line).

Fig. 5

Particle trajectories for two different particle sizes: $D_{\textrm p}/H=0.8$ (dashed line) and $D_{\textrm p}/H=0.6$ (solid line). Both simulations have been performed with $\Delta t=0.05$ and about 20,000 elements. The symbols are the trajectories for $D_{\textrm p}/H=0.6$ with $\Delta t=0.025$ (black circles) and about 35,000 elements (white circles)

To check the possibility of using the reduced domain as discussed in the previous section, we perform 2-D numerical simulations by comparing the particle trajectories obtained in the reduced domain and in the whole periodic cell. The choice of using 2-D simulations is twofold: (a) the computational effort to simulate the periodic cell is much less expensive than the full 3-D computations and (b) more importantly, if the 2-D results confirm that no appreciable change in the particle dynamics occurs by using the small computational domain, this is surely verified by the 3-D case as well because the perturbations due to the presence of the particle images die out faster in 3-D than in 2-D case. Simulations have been performed by taking the largest particle diameter considered in this work as it gives the most critical situation in terms of particle–particle interactions. The results evidence that only slight deviations between the particle trajectories occur, and the critical particle size is unaffected. We remark that the possibility to use the reduced domain reported in Fig. 1 is strictly related to the geometrical parameters considered in this work. We expect that by reducing the cylinder radius and/or the distance between two rows of posts $\Delta x$, a larger computational domain may be required.

Finally, the height of the domain $L_{\textrm c}$ has to be chosen in order to exclude any interaction between the sphere and its image across the symmetry boundaries. This is done by monitoring the particle dynamics by progressively enlarging the domain. We found that $L_{\textrm c}/H=2$ suffices to fulfill such a condition.

Simulation procedure and code validation

The aim of this work is to investigate how the (dimensionless) critical particle diameter $D_{\textrm c}/H$, i.e., the diameter of the particle dividing the displacement and the zigzag motion, is related to the fluid rheology. The computation of $D_{\textrm c}$ is done by initially locating the particle with center in the middle of two posts and monitoring its position after passing through $N_{\textrm {post}}$ pillars, i.e., after covering a distance equal to the length of the periodic cell. In agreement with Kulrattanarak et al. (2011b) and Frechette and Drazer (2009), we found that the initial particle position does not affect the computation of the critical particle size. At each time step the governing equations are solved and the particle position is updated. During the motion, when the particle center crosses the plane between the two rightmost pillars of the computational domain, it is relocated at the same position (according to the periodic direction) along the opposite plane. A similar procedure is done when the particle crosses the lower boundary (that occurs when traveling in zigzag motion).

To evaluate the critical particle diameter $D_{\textrm c}$, several simulations have been carried out by changing the particle diameter. We start from a diameter comparable to the gap size so that the particle travels following the displacement motion. The diameter is, then, progressively reduced by a constant step size in order to detect the limiting value $D_{\textrm {p,up}}$ such that the displacement motion occurs. By further reducing the diameter to the next value $D_{\textrm {p,down}}$, the particle experiences the zigzag behavior. The value $D_{\textrm c}$ belongs to the interval $[D_{\textrm {p,down}},D_{\textrm {p,up}}]$. Finally, we improve the accuracy of $D_{\textrm c}$ by running simulations with particle diameters in this interval. For all the simulation data, the uncertainty in the computation of $D_{\textrm c}$ is 0.005 (in dimensionless units), i.e., particles with $D_{\textrm p}>D_{\textrm c}+0.0025$ follow the displacement motion and particles with $D_{\textrm p}<D_{\textrm c}-0.0025$ follow the zigzag motion.

The code is validated by comparing the numerical predictions for a Newtonian suspending fluid with the experimental data reported in Inglis et al. (2006). Figure 6 reports the dimensionless particle diameter as a function of the inverse of the device periodicity number $1/N_{\textrm {post}}$. The circles are experimental observations for several combinations of $D_{\textrm p}/H$ and device periodicity. Particles observed in displacement motion are reported as white circles, whereas particles in zigzag motion are shown as black circles. Therefore, the critical particle size is identified as the region in between the black and white circles. The solid line is the theory developed in Inglis et al. (2006) for predicting the critical particle diameter as a function of $N_{\textrm {post}}$. The numerical predictions are reported in the same figure as gray diamonds for $N_{\textrm {post}}$ ranging from 3 to 8. A good quantitative agreement is found and both experimental and theoretical trends are correctly captured. Finally, it is worthy to mention that the experimental data reported in Fig. 6 refer to different post size to gap size ratios $D_{\textrm {cyl}}/H$ (Inglis et al. 2006). Therefore, it seems that such a parameter does not have a significant influence on the critical separation size.

Fig. 6

Dimensionless particle diameter $D_{\textrm p}/H$ as a function of the inverse of the number of periodic posts $\/N_{\textrm {post}}$. The circles are the experimental data from Inglis et al. (2006) for the zigzag motion (black circles) and the displacement motion (white circles). The solid line is the theoretical prediction from Inglis et al. (2006). The gray diamonds are the simulation results

Results and discussion

Theory

Inglis et al. (2006) proposed a model for determining the critical particle diameter as function of the number of array periodicity and the gap between the posts. The theory is based on the assumption that the critical radius is identified by the width of the first flow lane (see below) that is calculated by assuming a parabolic velocity profile through the gap between two posts. In this section, we generalize such a theory for non-Newtonian fluids by taking into account the effect of the shear-thinning on the velocity field. For the sake of simplicity, the fluid is modeled by the power-law constitutive equation, as the shear-thinning behavior is described by a single parameter. The velocity field through the bumper array for a Newtonian fluid is firstly presented and the methodology developed by Inglis et al. (2006) is briefly reviewed. The theory is, then, extended to shear-thinning fluids.

In Fig. 7a, the velocity field in the bumper array for a Newtonian fluid is reported. The number of periodic posts is chosen as $N_{\textrm {post}}=4$, thus the region represented in the figure is a periodic cell of the device. The colors are the (dimensionless) velocity magnitude. In the same figure, we also show the streamlines dividing the flow lanes between two posts. The latter have been computed by integrating the motion equation of a material point $d\boldsymbol {x}/dt=\boldsymbol {u}(\boldsymbol {x})$ with $\boldsymbol {u}$ the computed velocity field. A fourth-order Runge–Kutta algorithm is used for time integration. Notice that, assuming that the height of the pillars is much larger than the radius, the results in this figure can be obtained by 2-D simulations. Each streamline begins and ends on a post. The number of flow lanes coincides with the bumper periodicity (in this case, $N_{\textrm {post}}=$4). It is worth to mention that such a condition is not always verified but depends on the geometrical parameters of the device, as remarked in Kulrattanarak et al. (2011a). For the device geometry considered in this work, the number of flow lanes always matches the bumper periodicity, in line with numerical calculations reported in Kulrattanarak et al. (2011a).

Fig. 7

a Velocity field within the bumper array for a Newtonian fluid. The flow lane distribution is also shown. b Closer view of the velocity field between two posts. The analytical velocity profile for a wide-slit channel (solid line) is compared with the profile computed along the gap by solving the governing equations in the real geometry (dashed line)

Inglis et al. (2006) assumed that the critical particle radius $R_{\textrm c}=D_{\textrm c}/2$ is equal to the width $\beta$ of the first flow lane (see Fig. 7a). Indeed, particles with radius lower than $R_{\textrm c}$ are expected to flow within the same flow lane experiencing the zigzag motion. On the other hand, particles larger than $R_{\textrm c}$ are bumped to the adjacent flow lane at each subsequent row because of the hydrodynamic interactions with the obstacles, thus traveling in the displacement mode. Assuming also that the total fluid flux through the gap H is equally partitioned into $N_{\textrm {post}}$ flow streams, the following relationship holds (in dimensional form):

$$ \int_{-H/2}^{-H/2+\beta}u_x(y)dy=\frac{1}{N_{\textrm{post}}}\int_{-H/2}^{H/2}u_x(y)dy $$

(26)

where $u_x(y)$ is the $x-$component of the velocity field through the gap H. The left-hand side is the flow rate through the first flow lane that is equal to the total flux divided by the number of flow lanes. Notice that, in writing Eq. 26, the origin of a Cartesian reference frame has been chosen in the middle of the gap. To calculate $\beta /H$, Inglis et al. (2006) considered the velocity $u_x(y)$ given by the fully developed profile of a Newtonian fluid through a wide-slit channel:

$$ \frac{u_x(y)}{\bar{u}}=\frac{3}{2}\left[1-\left(\frac{2y}{H}\right)^2\right] $$

(27)

By solving the Eq. 26 with the velocity field in Eq. 27, the dimensionless critical diameter $D_{\textrm c}/H=2\beta /H$ can be related to the number of periodic posts $N_{\textrm {post}}$. The solution of Eq. 27, reported as solid line in Fig. 6 and as a solid line with white squares in Fig. 8, shows that the critical diameter is a decreasing function of $N_{\textrm {post}}$.

Fig. 8

Theoretical predictions of the dimensionless critical particle size $D_{\textrm c}/H$ as a function of the number of periodic posts $N_{\textrm {post}}$ for a power-law fluid with different values of the parameter n. The Newtonian and plug-flow cases, corresponding to $n=1$ and $n=0$, are also reported. The calculations have been carried out by assuming the velocity profile in a wide-slit channel

The assumption of a parabolic profile for $u_x(y)$ is, however, an approximation of the real velocity field developed between two posts. To verify how much such an approximation affects the critical particle size for the geometry considered in this work, we compare in Fig. 7b the parabolic velocity profile (solid line) with the profile computed by numerically solving the flow field within the device (dashed line). It is observed that the computed velocity field has a lower maximum and, consequently, higher values towards the obstacles. Those deviations are due to perturbations to the velocity field between two posts coming from the pillars of adjacent rows. Therefore, deviations can be even more pronounced for lower $\Delta x/H$ ratios (the rows of obstacles are closer) (Kulrattanarak et al. 2011a). For quite low $\Delta x/H$ values, an asymmetric velocity profile can also occur, and, as mentioned above, the number of flow lanes may be higher than $N_{\textrm {post}}$.

By substituting the computed velocity field $u_x(y)$ in Eq. 26, we obtain the dashed curve with white squares in Fig. 9. It is observed that the critical separation size slightly decreases as compared to the prediction for a parabolic profile (solid curve with white squares). Although the approximation with a wide-slit channel flow does not introduce a big error (at least for the chosen set of geometrical parameters), the computation of $D_{\textrm c}/H$ through the velocity field obtained via 2-D simulations is a more rigorous procedure as it takes into account the real geometry of the device (Loutherback et al. 2010).

Fig. 9

Dimensionless critical particle size $D_{\textrm c}/H$ as a function of the number of periodic posts $N_{\textrm {post}}$ predicted from the theoretical analysis by assuming the velocity profile in a wide-slit channel (solid lines) and by computing the velocity field in the real device geometry (dashed lines). The Newtonian (squares) and the power-law model with $n=0.4$ (circles) are considered

Let us consider now the velocity field obtained in the bumper array for a power-law fluid, reported in Fig. 10a. The same geometrical parameters as before are considered. The power-law index is chosen as $n=0.4$, denoting a strong shear-thinning behavior. It is well known that the viscosity thinning leads to a flat profile around the maximum (Bird et al. 1987), as confirmed by the red zones in the figure (compare with Fig. 7a). As a consequence of the modified velocity field, we expect that the flow lane distribution as well as the partition of the flux through each flow lane is affected as well, thus leading to a variation of the critical particle diameter $D_{\textrm c}$. To estimate the critical size for the shear-thinning fluid we can solve the Eq. 26 by using the velocity field modified according to the non-Newtonian fluid rheology. As above, we start by approximating the $x-$component of the velocity $u_x(y)$ with the fully developed flow field of a power-law fluid in a wide-slit channel given by Bird et al. (1987):

$$ \frac{u_x(y)}{\bar{u}}=\frac{1+2n}{1+n}\left[1-\left(\frac{2y}{H}\right)^{1+\frac{1}{n}}\right] $$

(28)

By solving the Eq. 26 with $u_x(y)$ given by the expression in Eq. 28, we obtain the normalized critical particle diameter $D_{\textrm c}/H$ as a function of the number of periodic posts $N_{\textrm {post}}$ for any value of the parameter n. The results are reported in Fig. 8. As for the Newtonian case, a reduction in the critical particle size is found as the periodicity of the device increases. However, for a fixed value of $N_{\textrm {post}}$, i.e., for a given geometry of the device, the normalized critical diameter decreases as the fluid shear-thinning is more pronounced (higher n). This opens up the possibility to tune the critical dimension to achieve particle separation by properly selecting the rheology of the suspending liquid. It is worth to notice that the amount of reduction of $D_{\textrm c}/H$ has its lower limit corresponding to a plug-flow profile ($n\rightarrow 0$). The reduction of the critical size as compared to a Newtonian suspending liquid has also some remarkable advantages as discussed in Loutherback et al. (2010), e.g., the possibility to separate smaller particles by using the same device, and, for the same critical particle size, to increase the gap size (thus reducing the pressure drop and the clogging) and to use a lower number of periodic posts (thus reducing the overall length of the array).

Fig. 10

a Velocity field within the bumper array for a power-law fluid with $n=0.4$. The flow lane distribution is also shown. b Closer view of the velocity field between two posts. The analytical velocity profile for a wide-slit channel (solid line) is compared with the profile computed along the gap by solving the governing equations in the real geometry (dashed line)

As for the Newtonian case, we repeat the calculations by using the velocity field between two posts computed by 2-D simulations in the full geometry. Figure 10b compares the velocity profile from Eq. 28 with $n=0.4$ (solid line) with the one from 2-D simulations in the real device geometry (dashed line). As before, the presence of adjacent pillars leads to slight discrepancies, making the profile even more flatter around the maximum (but still symmetric). Therefore, a similar behavior as for the Newtonian case is expected when the critical size is computed from Eq. 26 by using the actual velocity field. This is confirmed in Fig. 9 where a comparison between the dashed and solid line with white circles evidences a reduction of the critical size.

Numerical simulations

The theoretical analysis carried out in the previous section showed the possibility to modulate the critical particle size by changing the rheology of the suspending fluid. The procedure is based on the identification of the critical size with the width of the first flow lane (Inglis et al. 2006), that is calculated by computing (or assuming) the velocity field between two posts without particles. However, the presence of inclusions strongly alter the velocity field and, as the particle approaches the obstacles, the hydrodynamic interactions lead to deviations from the path followed by the object. To quantify the effective variation of the critical particle size and relate it to the shear-thinning property of the suspending liquid, we perform 3-D direct numerical simulations of the motion of a spherical particle through the array of obstacles, as described in Section “Simulation procedure and code validation”. In Section “Power-law model”, the power-law fluid is considered as suspending liquid. The analysis is, then, extended to the Bird–Carreau constitutive equation in Section “Bird–Carreau model”.

Power-law model

In Fig. 11, the computed normalized critical particle diameter $D_{\textrm c}/H$ is reported as a function of the number of periodic posts $N_{\textrm {post}}$ for different values of the power-law exponent n. The white squares are the Newtonian calculations (reported as gray diamonds in Fig. 6). The simulation results confirm that a reduction in the critical particle size can be attained by suspending the particles in a shear-thinning fluid. It is worth to note that a significant variation of $D_{\textrm c}/H$ is found for strong shear-thinning fluids as compared to the Newtonian case, especially for high values of $N_{\textrm {post}}$. For instance, for $N_{\textrm {post}}=8$ and $n=0.2$, the predicted $D_{\textrm c}/H$ is 37 % lower than the Newtonian value, leading to a wide operating window for a fixed device geometry. A comparison with the data reported in Figs. 8 and 9 shows that the critical size predicted by the theory based on the undisturbed velocity profile is overestimated. We remark that such discrepancies are likely due to the finite dimension of the flowing particle that alters the fluid velocity field, especially near the pillars where strong particle–wall hydrodynamic interactions arise.

Fig. 11

Dimensionless critical particle size $D_{\textrm c}/H$ as a function of the number of periodic posts $N_{\textrm {post}}$ computed from 3-D direct numerical simulations. The Newtonian (squares) and the power-law suspending fluid for different values of the parameter n (circles) are reported. The dashed lines are fitting curves through Eq. 29

The data reported in Fig. 11 show a similar trend as the power-law exponent n is varied. Such a trend can be fairly described by the following equation:

$$ \frac{D_{\textrm c}}{H}=\frac{A(n)}{A(n)+N_{\textrm{post}}-2} $$

(29)

where $A(n)$ is a function of the parameter n. By fitting the simulation data, we find that $A(n)=1.86+1.08n+1.38n^2$. The Eq. 29 with such an expression for $A(n)$ is reported as dashed lines in Fig. 11 for different values of the parameter n. A good quantitative agreement with the numerical predictions is found. We point out that the formula given in Eq. 29 as well as the expression for $A(n)$ do not come from any physical consideration, but they are just the simplest functions able to fairly describe the simulation results (at least in the investigated range of parameters). Equation 29 can be viewed as a design formula for the bumper array, relating the critical particle diameter for separation $D_{\textrm c}$ to the gap between the pillars H, the number of periodic posts $N_{\textrm {post}}$ and the degree of fluid shear-thinning n.

Some remarks about the applicability of Eq. 29 are in order. The design formula has been empirically derived by simulation data for a power-law suspending liquid. As such, it is strictly usable for fluids characterized by a similar rheology (see e.g., Zhang et al. 1996), or in those ranges of flow rates where the viscosity vs shear rate trend is well described by a power-law function. Although this seems a quite strong limitation, we will show in the next section that the application of Eq. 29 is much more general. Concerning the geometrical parameters, we have investigated the effect of the device periodicity $N_{\textrm {post}}$ on the critical size by keeping fixed both the cylinder diameter $D_{\textrm {cyl}}$ and the distance between two consecutive rows of pillars $\Delta x$. As mentioned above, the choice of $\Delta x$ is critical as, if it is chosen too low compared to the gap size, it directly alters the velocity field within two obstacles leading, in case, to asymmetric profiles. As reported in Kulrattanarak et al. (2011a), our choice of $\Delta x/H$ is around the limiting value. Therefore, we expect that the formula in Eq. 29 still works for those devices characterized by $\Delta x/H>2$ as the velocity profile within the gap only slightly changes by increasing the distance between two rows of pillars (the disturbance induced by the adjacent obstacles dies out). Of course, strong deviations are, instead, expected as $\Delta x$ is reduced. On the other hand, the dimension of the pillar diameter does not seem to play an important role as demonstrated by the experimental investigation of Inglis et al. (2006) (see also Fig. 6 and the relative discussion).

Bird–Carreau model

The simplicity of the power-law constitutive equation considered so far allowed to easily extend the theory developed by Inglis et al. (2006) to take into account the shear-thinning of the suspending fluid. The simulation results also provided a general formula relating the critical particle size to the number of periodic posts and the power-law index. However, such a model has some limitations as it does not predict the typical constant-viscosity regimes at low and high shear rates that are a characteristic feature of non-Newtonian fluids (Bird et al. 1987). As a consequence of the power-law relationship between viscosity and shear rate, the results previously reported are independent of the flow rate, as shown by the dimensionless equations in Section “Problem description and governing equations”.

In this section, we extend the numerical analysis to a suspending liquid modeled by the Bird–Carreau constitutive equation. We choose the following dimensional parameters: $\eta_{0} = 1$, $\eta_{\infty} =0.1$, $K=1$, $n=0.1$, corresponding to the viscosity curve reported in  Fig. 2. At variance with the power-law model, the velocity profile through the bumper array now qualitatively changes as the flow rate is varied. It is known that the critical particle size $D_{\textrm {c}}$ is related to the profile of the velocity field (Inglis et al. 2006; Loutherback et al. 2010), as also demonstrated in the previous section. Therefore, we expect that, for a given device geometry and fluid rheology, the critical separation size can be tuned by properly modulating the external flow rate.

To investigate how the critical size can be related to the flow rate through the velocity field, let us first analyze the simple case of a fluid (without particles) with the viscosity curve depicted in Fig. 2 flowing in a wide-slit channel. Fig. 12a reports the computed fully developed velocity profile across the channel section for different Θ-values. We recall that, for a fixed geometry and fluid rheology, changing Θ is equivalent to modify the flow rate. The velocity is normalized by the maximum velocity obtained for a Newtonian fluid at the same flow rate $u_{\textrm {N,max}}$. For low Θ-values, the Newtonian parabolic profile is obtained due to the viscosity plateau at low shear rate values. As Θ is increased, the shear-thinning leads to a flat profile around the maximum, similarly to the power-law model. For even higher Θ-values, the velocity field tends to the Newtonian one again because of the plateau at high shear rates. Needless to say, at high Θ-values the Newtonian profile cannot be reached as the local shear rate ranges from zero to a maximum value, thus covering the range characterized by the viscosity thinning.

Fig. 12

a Velocity profile in a wide-slit channel for a Bird–Carreau model for different values of the parameter $\Theta$. b Percentage difference in the maximum velocity in a wide-slit channel between a Newtonian fluid $u_{\textrm {N,max}}$ and a Bird–Carreau model $u_{\textrm {BC,max}}$ for different values of the parameter $\Theta$. c Velocity profile in a wide-slit channel for a Bird–Carreau model for two values of the parameter $\Theta$ (lines) and the velocity field for a power-law model obtained by fitting the parameter n (symbols)

To quantify the deviations of the non-Newtonian velocity profile from the parabolic one, we report in Fig. 12b the percentage difference between the maximum velocity attained for a Newtonian liquid and for the shear-thinning Bird–Carreau model, as a function of Θ. The nonmonotonic trend confirms the different behavior at low, intermediate, and high Θ-values. Therefore, on the basis of the data shown in Fig. 12a and the results reported in the previous section, we expect that for low values of the parameter Θ, the critical particle size essentially coincides with the Newtonian one. A reduction is, instead, expected for higher Θ-values up to a minimum value beyond which it raises again.

Direct numerical simulations are performed to confirm and quantify the reduction in the critical size as Θ is varied. Figure 13 shows the normalized critical particle diameter $D_{\textrm {c}}/H$ as a function of the number of periodic posts for different Θ-values. The Newtonian results are also plotted as white squares. It is readily observed that the data corresponding to the lowest Θ ($=0.05$) superimpose the Newtonian ones, whereas a minimum is achieved around $\Theta \cong 0.5$. The nonmonotonic trend can be better appreciated in Fig. 14 where $D_{\textrm {c}}/H$ is reported for several values of the parameter Θ for three values of $N_{\textrm {post}}$. Starting from the Newtonian value, the fluid shear-thinning contributes to reduce the critical size. After a minimum is achieved, $D_{\textrm {c}}/H$ goes up again. It is worth to mention that the curves reported in Fig. 14 show a similar trend. Therefore, the device geometry does not qualitatively alter the functional form relating the critical separation size to the flow rate, which is, instead, strictly related to the fluid rheology. Needless to say, the minimum value of the critical particle diameter depends on the viscosity thinning. Therefore, to achieve wider operating windows (in terms of tunability of the critical size) strong shear-thinning suspending liquids have to be chosen.

Fig. 13

Dimensionless critical particle size $D_{\textrm c}/H$ as a function of the number of periodic posts $N_{\textrm {post}}$ computed from 3-D direct numerical simulations. The Newtonian (squares) and the Bird–Carreau suspending fluid for different values of the parameter $\Theta$ (circles) are reported. The dashed lines are fitting curves through Eq. 29. For sake of clarity, only the Newtonian case and the Bird–Carreau model with $\Theta =0.5$ are reported. The dark gray and white triangles are the data for a power-law suspending fluid computed from Eq. 29 with the parameter n obtained by fitting the velocity field of the Bird–Carreau fluid for $\Theta =0.5$ and $\Theta =2.5$, respectively

Fig. 14

Dimensionless critical particle size $D_{\textrm c}/H$ as a function of the parameter $\Theta$ for a Bird–Carreau suspending fluid for different values of the number of periodic posts $N_{\textrm {post}}$ computed from 3-D direct numerical simulations

It is interesting to note that the Θ-values corresponding to the Newtonian-like behavior (both at low and high rates) as well as to the maximum reduction in $D_{\textrm c}/H$ can be fairly deduced from Fig. 12b. For instance, the minimum $D_{\textrm c}/H$-value is found for $\Theta \cong 1$ corresponding to the maximum deviation from the Newtonian and the non-Newtonian velocity profile. This is not surprising, as a close relationship between the critical particle size and the velocity field holds. However, no quantitative information about the effective reduction of $D_{\textrm c}/H$ can be deduced from the data in Fig. 12b. Quantitative predictions require, in fact, the simulation of finite-sized particles flowing in the actual geometry.

The similarity of the velocity fields for the power-law and the Bird–Carreau model suggests that the trends in Fig. 13 can be well described by Eq. 29. For sake of clarity, we report in Fig. 13 with dashed lines the curves for the Newtonian case (already shown in Fig. 11) and for the Bird–Carreau model with $\Theta =0.5$. The latter has been obtained by fitting the parameter $A$ in Eq. 29 that is now regarded as a constant. It is readily observed that the formula in Eq. 29, in fact, well describes the trend.

It would be useful, at this point, to extend the design formula in Eq. 29 to account for all the parameters of the Bird–Carreau constitutive equation. As this equation well describes the viscosity trend over a wide range of shear rates for several non-Newtonian fluids (Bird et al. 1987), a general criterion for designing the non-Newtonian deterministic lateral displacement separator can be devised. However, even if we assume that the functional form in Eq. 29 still holds for any fluid rheology, to find a general expression for $A=A(\eta _{\textrm r},\Theta ,n)$ is not straightforward because of the relatively large number of model parameters. The direct relationship between the critical particle size and the velocity field evidenced in the previous section comes in handy. Indeed, we expect that the formula in Eq. 29 (with the expression for $A(n)$ computed for a power-law fluid) can be applied to predict the critical size for a given fluid rheology and flow rate, provided that the velocity field can be approximated by the one obtained for a power-law fluid for some value of the parameter n. In other words, instead of directly relating the critical separation size to the fluid rheology, we link it to the velocity field stemming from such a rheology.

To test this idea, we apply Eq. 29 to try to predict the simulation results in Fig. 13 for $\Theta =0.5$ (dark gray circles). First, we need to estimate the power-law index n in order to match the velocity profile obtained for the Bird–Carreau model. Strictly speaking, this should be done by accounting for the velocity field through the real geometry of the bumper array. However, we have shown above that the approximation with the velocity profile developed in a wide-slit channel only leads to slight deviations. Therefore, we can take advantage of the analytical form in Eq. 28 for the velocity in a wide-slit channel and fit the parameter n. The fitting procedure gives n = 0.437 corresponding to the velocity profile reported with open circles in Fig. 12c (that well describes the Bird–Carreau profile shown as dashed–dotted curve). By using this value for n in Eq. 29, we get the dark gray triangles in Fig. 13. A comparison with the dark gray circles (and the dashed line) shows that the quantitative prediction of $D_{\textrm c}/H$ is excellent. The same procedure is repeated for the case $\Theta =2.5$ (white circles in Fig. 13). The fitted power-law index is n = 0.613 and the corresponding velocity profile is shown as black circles in Fig. 12c. The critical sizes predicted from Eq. 29 are shown as white triangles in Fig. 13. Again, a very good quantitative agreement with the simulation results is found. Needless to say, the successful application of the simple formula in Eq. 29 stems from the fact that the velocity field corresponding to a given rheology and flow rate can be appropriately described by the one resulting from the power-law model.

To conclude this section, some remarks are in order. In this work, we have assumed rigid particles. It has been recently reported that the deformability of the particles influences their effective size (Beech et al. 2012). More specifically, as the flow rate increases, the deformation leads to a reduction of the effective size (Beech et al. 2012). Therefore, when a non-Newtonian DLD device is used to process deformable particles, a suspending liquid with a sufficient degree of shear-thinning needs to be chosen in order to guarantee that the decrease in the critical separation size for increasing flow rates related to the shear-thinning is more effective than the reduction of the particle effective size due to the deformation, thus making the separation still possible. Finally, all the theoretical and numerical results presented above are based on the assumption of negligible inertia. Furthermore, fluid elasticity is not taken into account. The small length scales involved in microfluidics generally lead to Reynolds numbers lower than 1 (Squires and Quake 2005), thus making, in fact, inertial effects to be irrelevant. Moreover, non-Newtonian fluids typically are characterized by high viscosities that contribute to reduce the Reynolds number further on. On the other hand, the small length scales enhance elastic effects, giving rise to nonlinear phenomena that would require extreme conditions in macroscopic systems. It is not straightforward to deduce the effects of fluid elasticity on the critical particle size. Elasticity brings in nonlinear effects that alter the particle dynamics. For instance, viscoelasticity-induced particle migration can occur during the motion through the obstacles leading to “jumps” of the particle to an adjacent flow lane. As an immediate consequence, the critical particle size would not be independent of the particle initial position anymore. In this case, a flow-focusing device can be integrated to the bumper array to align in inflow the particles along a streamline. Therefore, shear-thinning fluids with low elasticity (e.g., Zhang et al. 1996) have to be preferred for an efficient use in deterministic ratchets. A rigorous analysis about the effect of fluid elasticity, i.e., whether and in which direction it may alter the particle dynamics, requires simulations with viscoelastic constitutive equations and will be part of future work.

Conclusions

In this work, we showed that the critical particle size in a deterministic lateral displacement device can be tuned by using non-Newtonian fluids as suspending liquid. The theory developed for Newtonian fluids (Inglis et al. 2006) is extended to a power-law constitutive model. 3-D direct numerical simulations are, then, performed to quantitatively relate the critical particle size to the device geometry and the fluid rheological properties. The governing equations are solved by the finite element method and the dynamics of a spherical particle flowing through the deterministic ratchet is computed.

The theoretical results show that fluid shear-thinning leads to a lower critical particle size as compared to the Newtonian case. Indeed, the viscosity thinning modifies the velocity profile through the ratchet, altering the flow lane distribution and, in turn, the critical separation size.

Numerical simulations are firstly performed by considering the power-law constitutive equation to confirm the theoretical results. The effect of fluid shear-thinning (through the power-law exponent) as well as the number of periodic posts is related to the critical particle diameter normalized by the gap size. The results show a general trend that allows us to derive a formula to design the non-Newtonian deterministic ratchet.

The simulations are, then, extended to the more realistic Bird–Carreau model. It comes out that the flow rate can be conveniently used to tune the critical particle size, once the device geometry and the suspending liquid have been chosen. Finally, we demonstrated that the simple design formula derived for a power-law model also works for the Bird–Carreau constitutive equation (and in general for any viscosity curve) provided that the velocity field coming from a given viscosity function can be approximated by the one obtained from the power-law model (with a proper choice of the parameter n). The proposed technique allows to achieve arbitrarily small steps in the critical size in real time, something that is not possible with a conventional DLD device.

The results presented in this work can be extended in several directions. Firstly, it would be interesting to investigate the effect of fluid elasticity on the path followed by the particles. As remarked in the previous section, if fluid elasticity is relevant, it may alter the particle dynamics giving rise to nonlinear phenomena (e.g. migration). The quantification of such effects requires numerical simulations by choosing viscoelastic constitutive equations able to describe both shear-thinning and normal stresses.

The influence of the geometrical parameters, i.e., the distance between the rows of obstacles and the cylinder diameter, on the critical particle size can be studied in order to define the region of validity for the design formula. The shape of the obstacles, which affects the velocity field through the ratchet and, as such, has been proved to have a strong impact on the device performances (Loutherback et al. 2010), can be also analyzed.

Finally, experimental data are required to validate the theoretical results presented in this paper and to test the applicability of the design formula derived for a simple constitutive equation to real cases.