Introduction

Magnetorheological (MR) fluids are magnetically responsive colloidal suspensions with tunable mechanical properties (de Vicente et al. 2011a; Park et al. 2010). In the case of conventional MR fluids, dispersed micron-sized particles become magnetized in the presence of external magnetic fields, eventually aggregating in the direction of the field and forming elongated chain-like structures. MR fluids are typically characterized by a field-dependent yield stress (i.e., the minimum stress value required for the suspension to flow).

Because of their unique mechanical properties, MR fluids are already used in a wide range of commercial applications including automobile suspension systems, shock absorbers, etc. (Carlson 2007; Olabi and Grunwald 2007). In general, available devices using these fluids can be classified according to their flow mode as direct-shear flow mode, pressure-driven flow mode and squeeze-film flow mode. Among the three modes, it is well-known that the squeeze flow mode provides the largest yield stress under the same field (Havelka and Pialet 1996). The rheological properties of MR fluids under shearing flows (i.e., direct-shear and pressure-driven flows) have been extensively investigated in the literature. However, the understanding of the behavior of MR fluids under non-shearing elongational flows, and particularly in squeeze flow mode is still far to be complete mainly because of the lack of both a thorough understanding of the basic MR mechanisms and reliable experimental data (de Vicente et al. 2011b).

First reports on squeeze flow magnetorheology were devoted to investigate the enhancement of MR performance by the so-called compression-assisted aggregation process (Tang et al. 2000; Zhang et al. 2004, 2009). This consists of enhancing the yield shear stress by the formation of thick strong columns under compression. Later, See (2003) reported a series of low-strain tests on MR fluids where the behaviors under constant velocity squeezing flow and shear flow were compared. A field dependence of H 0.91 was found for compression in contrast to the H 1.4 dependence observed under shearing. Constant area squeeze flow MR experiments were carried out by Mazlan et al. (2007; Mazlan et al. (2008). More recently, Gstöttenbauer et al. (2008) designed a test rig to explore the flow behavior of MR fluids under sinusoidal loading modes.

Traditionally, the squeeze flow behavior of field-responsive fluids has focused on the electric counterparts of MR fluids; i.e. electrorheological (ER) fluids (El Wahed et al. 1998; Meng and Filisko 2005; Stanway et al. 1987; Tian et al. 2002a, 2003b). Currently, the use of MR fluids under non-shearing flows has received attention mostly because of two reasons: (a) border effects, that are unavoidably present when working with ER fluids, are not an issue for MR fluids; (b) the magnetic field strength can be kept essentially constant (when neglecting/controlling the change in magnetic resistance when decreasing the gap) if compared to ER analogues working under constant voltage operation. However, a thorough investigation of the stress–strain characteristics of MR fluids in compression mode is still not complete. To the best of our knowledge, only the effect of magnetic field strength has been investigated under slow-compression, no-slip, constant-volume squeeze mode (de Vicente et al. 2011b; See 2003).

On the one hand, the effect of medium viscosity in the squeeze flow performance has been scarcely investigated. Chu et al. (2000) observed that the normal stresses in ER fluids containing lower medium viscosity not only possessed larger value but also increased more rapidly with the strain. These findings were explained in terms of a smaller drag force acting on field-induced structures. Interestingly, the medium viscosity does also influence the sedimentation rate of the dispersed particles. Experimental work and particle-level simulations demonstrate that body forces can significantly influence the structure and rheology of ER and MR suspensions even when the magnitude of the body force is small compared to the field-induced force (e.g., in the filtration-dominated squeeze regime; Klingenberg et al. 2007). On the other hand, the understanding of the effect of particle concentration has been traditionally impeded by the fact that most experiments reported in the literature concern ER fluids working under constant area operation. For these systems, once the field is applied, the volumetric concentration increases under compression due to the “sealing/condensation effect” originated by the field intensification near the electrodes edges (Chu et al. 2000; Lynch et al. 2006; McIntyre and Filisko 2007; Tian et al. 2002a).

In the current work, we follow a previous paper where we investigated the effect of magnetic field strength in the appearance of normal forces under no-slip compression in the filtration dominated regime (de Vicente et al. 2011b). In that paper, we demonstrated a good scaling when normalizing by the low-strain normal force and a reasonably good agreement with macroscopic plastic models at large enough magnetic fields and particle-level dynamic simulations—see Fig. 9 in de Vicente et al. (2011b). In the present manuscript, we report new experimental data to better understand the effect of dispersing liquid viscosity and particle content in the squeeze flow behavior. We also address a macroscopic model that may capture dependencies with magnetic field strength, dispersing medium viscosity and particle concentration. The development of a general constitutive framework for MR fluids would find use in the design of better MR engineering devices.

Theory

The squeeze flow behavior of inelastic yield stress fluids under no-slip conditions has been extensively investigated in the literature since the pioneering work by Scott (1929). Usually, a plasticity number S is defined that separates the preyield and postyield regimes (Covey and Stanmore 1981):

$$ \label{eq1} S=\frac{\eta_p \emph{v}R}{h^2\tau_y } $$
(1)

Here η p is the Bingham plastic viscosity, \(\emph{v}\) is the approaching speed, R is the radius of the sample, h is the gap thickness and τ y is the yield shear stress.

Starting from the Bingham constitutive equation, Covey and Stanmore (1981) obtained an analytical relation between the normal force F and the gap thickness h for small S numbers (S < 0.5):

$$ \label{eq2} F=\frac{2\pi \tau_y R^3}{3h}+\frac{4\pi }{7h^2}\sqrt {2\tau_y \eta_p \emph{v}R^7} $$
(2)

Later Williams et al. (1993) analytically solved the squeeze flow problem for a bi-viscous fluid instead of a Bingham plastic. The final result reads as follows:

$$ \label{eq3} F=\frac{2\pi \tau_y R^3}{h\chi^3}\left[ {\frac{\gamma ^3}{108}+\int_{\gamma \mathord{\left/ {\vphantom {\gamma 3}} \right. \kern-\nulldelimiterspace} 3}^\chi {S^2G\,dS} } \right] $$
(3)

where γ, χ, and G are parameters defined by:

$$ \label{eq4} \gamma =\frac{\eta }{\eta_r };\chi =S\left( {r=R} \right);G=-\frac{h}{{2}\tau_{y} }\frac{dp}{dr} $$
(4)

Here η r is the preyield viscosity and η the viscosity above the yield point in the bi-viscous model.

Interestingly, for S < < 1, in the so-called filtration dominated regime (McIntyre and Filisko 2010), both Eqs. 2 and 3 converge to the following analytical expression:

$$ \label{eq5} F=\frac{2\pi \tau_y R^3}{3h} $$
(5)

After some algebra, the normal force in the case of constant-volume tests can be written as follows:

$$ \label{eq6} F=\frac{2\tau_y V^{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}{3\sqrt \pi h_0^{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-\nulldelimiterspace} 2} \left( {1-\varepsilon } \right)^{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-\nulldelimiterspace} 2}} $$
(6)

where V represents the total volume of the sample \(\left( {V=\pi R^2h} \right)\) and the elongational strain ε is defined here as the ratio of the moving distance of the upper plate to the initial distance between the plates \(\varepsilon ={\left( {h_0 -h} \right)} \mathord{\left/ {\vphantom {{\left( {h_0 -h} \right)} h}} \right. \kern-\nulldelimiterspace} h_0 \).

It is worth to remark here that in the derivation of Eq. 6, we have assumed a small gap to radius ratio and a constant plastic yield stress that is independent of the deformation rate. Also, surface tension effects are neglected. Importantly, Eq. 6 reveals that the resistance to deformation for low plasticity numbers comes from the yield shear stress component while viscous stresses are negligible. Equation 6 has been validated in the literature for the compression of ER fluids under constant area operation (Tian et al. 2002b). However, deviations from this description have been also reported (Tian et al. 2003b).

Experimental

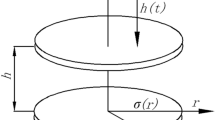
Conventional MR fluids were prepared by carefully mixing carbonyl iron microparticles (HQ grade, BASF) in silicone oil (Sigma-Aldrich). A parallel plate magnetorheometer MCR-501 (Anton Paar) was used to perform constant-volume squeeze flow experiments in the presence of magnetic fields. The schematic of the compression test system is shown in Fig. 1. Non-magnetic titanium plates (diameter 2 cm) were employed. The initial separation was \(h_{0\, }= 300~\upmu \)m. Plates were supposed to be perfectly parallel even though a small misalignment exist (Andablo-Reyes et al. 2010; Andablo-Reyes et al. 2011). The distortion of the force sensor under pressures generated in this work was neglected. Previous work suggested that no-slip assumptions do apply for all experiments reported in this manuscript (de Vicente et al. 2011b). Also, magnetic fields are expected to be reasonably uniform in the MRD-180 magnetocell employed as the typical magnetic field strength values remained smaller than 300 kA/m (Laun et al. 2008).

Fig. 1
figure 1

Schematic view of the constant-volume squeeze flow experiment and typical behavior of normal force growth for a 5 vol% MR fluid. Magnetic field strength 177 kA/m. Dispersing medium viscosity 200 mPa·s. Approaching speed \(v = 10~\upmu \)m/s

Full size image

Compression experiments were run at constant volume V, and constant velocity ν = 10 \(\upmu \)m/s (elongational rate range: \(\dot{{\varepsilon }}\sim 0.03-0.2\;{\rm s}^{-1})\). This corresponds to low plasticity numbers S < 0.5 and low Reynolds numbers Re~10 − 3 ≪ 1 so lubrication and creeping flow approximations can be used. Additionally, preliminary tests were performed under different approaching speeds and constant compressive rates to ensure that the tests were safely done in the so-called “filtration” regime (McIntyre and Filisko 2010). Prior to the test, the sample was equilibrated at rest in the presence of a suddenly applied external magnetic field during 60 s. Results presented below are always averages over at least three separate runs. All experiments were run at 25 °C.

Static and dynamic yield shear stress measurements were carried out in controlled shear stress mode. In the first step, a preshear \(\left( {\dot{{\gamma }}=200s^{-1}} \right)\) is applied in the absence of a magnetic field for 30 s. Then, the magnetic field is turned on without any shear applied yet. After 30 s of equilibration the shear stress was logarithmically increased from 0.1 Pa at a rate of 10 points per decade. On the one hand, the static yield stress is determined from the low-shear extrapolation in double logarithmic representations of shear stress versus shear rate. On the other hand, the dynamic yield stress is obtained from curve fitting using the Bingham model at large shear rates in a lin–lin representation.

Results and discussion

A series of unidirectional slow-compression tests has been carried out with different magnetic field strengths, dispersing medium viscosities and particle volume fractions. As a way of example, a typical result is shown in Fig. 1. In general, when a MR fluid is compressed under the presence of a magnetic field, its compressive resistance increases with the gap reduction. At large gaps (i.e., low strains), the normal force tends towards a limiting plateau value that is associated to the yield compressive stress of the field-induced structure.

In a previous work we reported on the collapse of slow-compression curves obtained for different magnetic field strengths when normalizing by the low-strain normal force plateau (de Vicente et al. 2011b). In Fig. 2, we reproduce these data along with new experiments for a wide range of dispersing liquid viscosities and particle volume fractions. As observed, a reasonably good collapse is also found. As a reference, included in Fig. 2 we also show the theoretical prediction according to Eq. 6 for yield stress fluids. At first glance, the theoretical prediction satisfactorily explains experimental data.

Fig. 2
figure 2

Dimensionless normal force F as a function of compressive strain ε for different magnetic field strength, dispersing medium viscosity and particle volume fraction. The force F is normalized by the low-strain normal force value A. Solid line corresponds to the prediction by the continuous media theory for plastic materials Eq. 6. Approaching speed v = 10 \(\upmu \)m/s

Full size image

Next, we will take a closer look to the experimental data in a more convenient way by plotting the normal force F versus 1 − ε in a log–log representation (see Fig. 3). Results show a reasonably good linear relationship as theoretically predicted (cf Eq. 6). Deviations from linearity appear at large 1 − ε values may be due to inertia and initial transient effects. A least squares fitting routine was used to fit normal force data according to \(F=A \mathord{\left/ {\vphantom {A {\left( {1-\varepsilon } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {1-\varepsilon } \right)}^B\) in a log–log representation. Intercept A and slope B fitting parameters are included in Table 1.

Fig. 3
figure 3

Log–log representation of normal force F vs. 1 − ε curves. Solid lines are best fits to \(F=A \mathord{\left/ {\vphantom {A {\left( {1-\varepsilon } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {1-\varepsilon } \right)}^B\) with fitting parameters included in Table 1. a η = 20 mPa·s, ϕ = 5 vol%; b H = 177 kA/m, ϕ = 5 vol%; and c H = 177 kA/m, η = 20 mPa·s. Approaching speed v = 10 \(\upmu \)m/s

Full size image
Table 1 Fitting parameters (A and B) and correlation coefficients (R 2) for normal force vs. 1 − ε curves reported in Fig. 3 according to \(F=A \mathord{\left/ {\vphantom {A {\left( {1-\varepsilon } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {1-\varepsilon } \right)}^B\)
Full size table

On the one hand, intercept values A do increase with increasing the magnetic field strength, medium viscosity and particle concentration. This finding suggests that the yield compressive stress is a function of these quantities. On the other hand, the slopes of the experimental curves B approach the theoretical value of 2.5 (in agreement with results presented in Fig. 2). However, non-negligible deviations in B parameters with respect to the theoretical value exist (ranging from 2.4 to 3.1). These deviations may suggest that the compression resistance increases generally faster than the prediction of the squeeze flow theory, for example with a τ y that increases when decreasing the gap. To check this hypothesis we took pictures of the MR fluids under compression using a rheomicroscopy device. In Fig. 4, we show a typical example where field-induced structures are seen to actually evolve under compression leading to thicker columnar aggregates. These thicker structures are presumably more resistant to deformation and eventually would give a larger τ y in view of the squeeze strengthen effect (Tang et al. 2000).

Fig. 4
figure 4

Structure evolution of a 5 vol% suspension in a 20 mPa·s silicone oil under compression, in the presence of an external magnetic field that is perpendicular to the paper. a Initial gap h 0 = 300 \(\upmu \)m in the absence of an external magnetic field; b initial gap h 0 = 300 \(\upmu \)m in presence of an external magnetic field; c intermediate gap h 0 = 190 \(\upmu \)m in presence of an external magnetic field

Full size image

A further insight into the compressive behavior of MR fluids can be obtained by directly measuring the static yield shear stress τ y of the samples using conventional steady simple shear rheometry (de Vicente et al. 2011a). With this, compressive stresses can be calculated from Eq. 6 as follows:

$$ \label{eq7} \tau_{C,C} =\frac{2\tau_y V^{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}{3\pi^{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}h_0^{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-\nulldelimiterspace} 2} r_0^2 }=\frac{2\tau_y r_0 }{3h_0 } $$
(7)

where r 0 is the initial sample radius (r 0 = 3.8 ± 0.3 mm). For a comparative analysis, in Fig. 5 we show experimentally measured compressive yield stresses \(\tau_{C,E} =A \mathord{\left/ {\vphantom {A {\pi r_0^2 }}} \right. \kern-\nulldelimiterspace} {\pi r_0^2 }\) (solid symbols) as well as calculations τ C,C using Eq. 7 (open symbols). As demonstrated, calculated compressive yield stresses compare reasonably well with experimental measurements especially taking into account that there are not free parameters in these calculations. The yield compressive stress does increase with increasing the magnetic field strength, medium viscosity and particle content. A power law dependence is found in the three cases. Even though similar values are obtained for the experimental and calculated yield compressive stresses, the slopes seem to differ from each other (see Table 2).

Fig. 5
figure 5

Low-strain compressive stresses as a function of magnetic field strength H (squares), dispersing medium viscosity η (circles) and particle volume fraction ϕ (triangles). a Comparison between experiments τ C,E and calculations τ C,C using Eq. 7 for the static yield shear stress; solid symbols, experimental; open symbols, calculations. b Calculations of the low-strain compressive stresses using dynamic yield shear stress measurements in Eq. 7

Full size image
Table 2 Power law exponent α for the yield compressive stress τ C according to τ C according to \(\tau_{C} \propto X^{\alpha }\) being X = H, η, or ϕ
Full size table

The experimentally measured yield compressive stress τ C, E varies with the magnetic field strength as H\(^{2.0\, \pm \, 0.1}\). This H dependency of normal stresses in the squeezing flow turns out to be larger than the well-known H1.5 dependence of shear stresses in simple shearing flow (de Vicente et al. 2011a; Ginder et al. 1996; See 2003). In agreement with the literature, our MR fluid exhibited a yield shear stress that scaled as H1.47 (see Table 2). Similarly to our results, Tian et al. (2003b) reported that the yield compressive stress in ER fluids was proportional to the square of the external electric field for large gap separations. They argued that the exponent should be 2 if there is no saturation effect in ER fluids according to the polarization model (Wen et al. 2008). On the contrary, Chu et al. (2000) measured an exponent larger than 4 in ER fluids for the E dependence, and See (2003) found that in the case of highly concentrated MR fluids the normal force varies with H0.91 under the higher fields investigated.

The dispersing medium viscosity dependence is significantly low as expected in a slow-compression filtration-dominated regime (≈η \(^{0.33\, \pm \, 0.08})\). The slight increase in the stress with increasing viscosity may be due to an enhancement in the kinetic stability and hence slightly stronger field-induced structures (Klingenberg et al. 2007). This hypothesis is confirmed from yield shear stress measurements; actually, the yield shear stress did also slightly increase with increasing the medium viscosity (≈η \(^{0.46\, \pm \, 0.02}\), see Table 2).

As expected, the effect of particle concentration is found to be significantly more important than the effect of oil viscosity. Again, a power law dependence is found between the yield compressive stress and the volume fraction (≈ϕ \(^{2.0\, \pm \, 0.2})\). This result is larger than the slope obtained from yield shear stress measurements, that predict a power law of approximately 1.5 (see Table 2), and in qualitative good agreement with Tian et al. (2003a). It is worth to remark here that contrary to ER fluids where ϕ increases with decreasing the electrode separation, in our experiments, ϕ remains constant as the magnetic field is presumably uniform (Laun et al. 2008).

For completeness, in Fig. 5b, we show calculated compressive stresses by substituting the dynamic yield shear stress—instead of the static yield shear stress—in Eq. 7. By comparing Fig. 5a and b, we observe that a much better accordance between experiments and calculations is obtained when using the static yield stress data. This was expected as the field-induced structures were not supposed to slip on the plates.

Conclusions

Most of the squeeze flow results reported in the literature on field-responsive fluids deal with ER fluids where both the electric field strength and particle concentration change during compression. Many efforts have been done in the past to better understand their squeeze flow behavior under the framework of continuum media theories. In some cases, experimental data are satisfactorily explained using a continuum squeeze flow theory whereas it has been recently reported that this theory fails for small initial gaps and high voltages (Meng and Filisko 2005; Tian et al. 2003b).

In this paper, we performed a systematic experimental study of conventional MR fluids under conditions of slow-compression, no-slip, and constant volume. We proposed a unified description of the behavior of MR fluids in terms of a continuous media theory for plastic materials. This allowed us to collapse compression curves obtained for a wide range of magnetic field strengths, medium viscosity and particle concentration. Deviations from the theory were explained in terms of the squeeze strengthening effect. On the one hand, a quadratic dependence with the magnetic field strength (2.0 ± 0.1) and particle concentration (2.0 ± 0.2) is found. On the other hand, a η \(^{0.33\, \pm \, 0.08}\) dependence of the compressive stress is found. Experiments reported here suggest another procedure to determine static yield shear stresses when slowly compressing the MR fluids.