Transport Phenomena in Viscoplastic Materials

Abstract

This chapter focuses on various transport phenomena in yield stress materials. After a brief introduction, an overview of the phenomenology of the solid–fluid transition is given in Sect. 2. Section 3 introduces a microscopic theory able to describe the solid–fluid transition in both thixotropic and non-thixotropic yield stress materials. A discussion of the hydrodynamic stability of yield stress materials is presented in Sect. 4. Some non-isothermal transport phenomena are discussed in Sect. 5.

1 Introduction

A broad class of materials exhibits a dual response when subjected to an external stress. For low applied stresses, they behave as solids (loosely speaking they may deform but they do not flow) but, if the stress exceeds a critical threshold generally referred to as the “yield stress”, they behave as fluids (typically non-Newtonian) and a macroscopic flow is observed. This distinct class of materials has been termed as “yield stress materials” and, during the past several decades, it attracted a constantly increasing level of interest from both theoreticians and experimentalists. The motivation behind this issue is twofold. From a practical standpoint, such materials have found a significant number of applications in several industries (which include food, cosmetical, pharmaceutical, oil field engineering, etc.) and they are encountered in daily life in various forms such as food pastes, hair gels and emulsions, cement, mud, etc. More recently, hydrogels which exhibit a yield stress have found a number of future promising applications including targeted drug delivery (Jeong et al. 1997; Qiu and Park 2001), contact lenses, noninvasive intervertebral disc repair (Hou et al. 2004) and tissue engineering (Beck et al. 2007).

From a fundamental standpoint, yield stress materials continue triggering intensive debates and posing difficult challenges to both theoreticians and experimentalists from various communities: soft matter physics, rheology, physical chemistry and applied mathematics. The progress in understanding the flow behaviour of yield stress materials made the object of several review papers (Nguyen and Boger 1992; Coussot 2014; Balmforth et al. 2014; Bonn et al. 2017). The best known debate concerning the yield stress materials is undoubtedly that related to the very existence of a “true” yield stress behaviour (Barnes 1999; Barnes and Walters 1985). During the past two decades, however, a number of technical improvements of the rheometric equipment made possible measurements of torques as small as 0.1 n Nm and of rates of deformation as small as $10^{-7}\,\mathrm{s}^{-1}$). Such accurate rheological measurements proved unequivocally the existence of a true yielding behaviour (Putz and Burghelea 2009; Bonn and Denn 2009; Denn and Bonn 2011). The physics of the yielding process itself on the other hand remains elusive. The macroscopic response of yield stress fluids subjected to an external stress, $\sigma$, has been classically described by the Herschel–Bulkley model (Herschel and Bulkley 1926a, b):

$$\begin{aligned} \sigma = \sigma _y + K \dot{\gamma }^{N}. \end{aligned}$$

(1)

Here, $\sigma _y$ is the yield stress, $\dot{\gamma }$ is the rate of shear, i.e. the rate at which the material is being deformed, $\sigma$ is the macroscopically applied stress (the external forcing parameter), K is a so-called consistency parameter that sets the viscosity scale in the flowing state and N is the power law index which characterises the degree of shear thinning of the viscosity beyond the yield point.

In spite of its wide use by rheologists, fluid dynamicists and engineers, the Herschel–Bulkley model (and its regularised variants, e.g. Papanastasiou 1987) is in fact applicable only for a limited number of yield stress materials, sufficiently far from the solid–fluid transition, i.e. when $\sigma > \sigma _y$, and in the conditions of a steady-state forcing, i.e. when a constant external stress $\sigma$ is applied over a long period of time. The behaviour of a large number of the yield stress materials encountered in daily life applications cannot be accurately described by the simple Herschel–Bulkley model. This fact has initiated the “quest” for a “model” yield stress fluid.

A “model” yield stress material should fulfil a number of quite restrictive conditions:

• 1. As the externally applied stresses are gradually increased, a solid–fluid transition occurs at a well-defined value of the applied stress, $\sigma =\sigma _y$.

• 2. Past the yield point the relationship between the applied stress $\sigma$ and the macroscopic rate of shear $\dot{\gamma }$ follows faithfully the Herschel–Bulkley model described by Eq. (1).

• 3. The solid–fluid transition is reversible upon increasing/decreasing forcing, that is, no thixotropic effects are present.

For nearly two decades, aqueous solution of Carbopol^® has been chosen as the best candidates as “model” yield stress materials (Curran et al. 2002; Ovarlez et al. 2013). Carbopol^® is the generic trade name of an entire family of cross-linked polyacrylic acids with the generic chemical structure $H-A$. Upon dissolution in water, the polyacrylic acid dissociates as $H-A\Longleftrightarrow H^{+} + A^{-}$, resulting in a mixture with $pH \approx 3$. Upon neutralisation with an appropriate basic solution (e.g. a sodium hydroxide solution, NaOH) the micro-gel particles swell up to 2000 times and a physical gel is obtained. The Carbopol gels are optically transparent, chemically stable over long periods of time which makes them ideal candidates for experimental studies.

To illustrate the limitations of the classical Herschel–Bulkley picture in accurately describing the solid–fluid transition even in the case of a Carbopol^® gel, we discuss below several experimental observations performed in kinematically “simple” flows of aqueous solutions of Carbopol^® that are at odds with the picture of a “model” yield stress fluid.

1.1 Sedimentation of a Spherical Object in an Elasto-Viscoplastic Material (Carbopol^® 940)

The first experimental observation relates to the flow patterns around a spherical object freely falling in an aqueous solution of Carbopol^® 940 discussed in detail by Putz et al. (2008).

The experiment consisted of measuring time series of the velocity fields around a sphere freely falling in a container filled with a Carbopol^® solution via digital particle image velocimetry (DPIV). To test the reliability of the method, flow fields were first measured in a Newtonian fluid (an aqueous solution of Glycerol), as shown in Fig. 1a. As the Reynolds numbers (calculated using the size and the terminal speed of the spherical object) did not exceed unity, a perfect fore-aft symmetry of the flow pattern is observed and a quantitative agreement with the analytical solution (Landau and Lifschitz 1987) is found, which fully confirms the reliability of both the experimental procedure and data analysis technique.

Fig. 1

Experimentally measured flow field around a sphere freely falling in a Newtonian fluid (glycerol) at $Re<1$ (1a). Experimentally measured flow fields around a sphere freely falling in Carbopol^® solutions at $Re<1$ (1b). The radii of the spheres and the yield stresses of the solutions in each panel are (1)—$R= 3.2$ mm, $\sigma _y = 0.5$ Pa, (2)—$R= 1.95$ mm, $\sigma _y = 0.5$ Pa, (3)—$R= 3.2$ mm, $\sigma _y = 1.4$ Pa, (4)—$R= 1.95$ mm, $\sigma _y = 1.4$ Pa. The colour maps in all panels refer to the modulus of velocity and the full lines are streamlines. The acceleration of gravity is oriented from right to left

For several cases involving different Carbopol^® solutions and different sizes of the spherical object, however, the flow patterns are strikingly different though the Reynolds number was kept in the same range, as shown in Fig. 1b. As compared to Newtonian flow patterns, two distinct features may be observed:

• 1. For each of the cases illustrated in Fig. 1b, the fore-aft symmetry of the flow patterns is broken in spite of the laminar character of the flow.

• 2. For each of the cases illustrated in Fig. 1b, a negative wake manifested through a reversal of the flow direction is clearly visible.

None of these distinctive features can be understood in the classical Bingham/Herschel–Bulkley frameworks. Numerical simulations using either the Bingham or the Herschel–Bulkley constitutive equations predict fore-aft symmetry of the flow pattern (Beris et al. 1985; Fraggedakis et al. 2016). The second feature is even more intriguing as the negative wake phenomenon has been observed in strongly elastic shear-thinning solutions with no yield stress (Arigo and McKinley 1998).

We have proposed the following phenomenological explanations (Putz et al. 2008). Bearing in mind that the material in the fore region of the object is subjected to a forcing that gradually increases past the solid–fluid transition and the aft region is subjected to a forcing that gradually decreases past the fluid–solid transition, we have conjectured that the solid–fluid transition is not reversible upon increasing/decreasing stresses. As the emergence of the negative wake is concerned, we have conjectured that, around the solid–fluid transition, the elastic effects are dominant which, in conjunction with the curvature of the streamlines, leads to the emergence of a first normal stress difference that ultimately causes a “flow reversal” or negative wake. Although quite debated for nearly a decade by part of the viscoplastic community, these phenomenological explanations have been confirmed by the recent numerical simulations (Fraggedakis et al. 2016).

1.2 The Landau–Levich Experiment with an Elasto-Viscoplastic Material (Carbopol^® 980)

A second and equally simple experiment one can perform is to withdraw a vertical plate at a constant speed U from a bath filled with a Carbopol^® gel. This is referred to in the literature as the “Landau–Levich” problem (Landau and Levich 1972). An instantaneous flow field measured using DPIV is exemplified in Fig. 2. Similar to the case of the sedimentation experiment previously illustrated, a negative wake is clearly visible behind the moving plate. As in the previous case, the material located in the wake region of the flow is subjected to a decreasing stress and gradually transits from a fluid state to a solid one. The emergence of a negative wake is once again associated to the presence of elasticity.

Fig. 2

The Landau–Levich flow problem: instantaneous flow field around a rigid plate being withdrawn at constant speed from a bath filled with a Carbopol^® gel

1.3 The Solid–Fluid Transition in a Carbopol^® Gel Revisited

The “simple flows” examples presented above bear two common features:

• 1. The material is subjected to an external forcing (stress) around the solid–fluid transition.

• 2. The material is forced in an unsteady manner. By this, we mean that the stress locally applied changes with a characteristic time $t_0$ set by the characteristic scale of the speed U and a characteristic space scale L by $t_0 = L/U$. In the case of the sedimentation problem, L is just the size of the spherical object $L=R$ and U is its terminal speed which, for the experiments illustrated in Fig. 1b, give $t_0< 1s$.

The points above prompted us to revisit the macroscopic solid–fluid transition. The solid–fluid transition may be investigated during macroscopic rheological experiments by subjecting the material to a controlled stress ramp and monitoring its response (the rate of shear $\dot{\gamma }$). Prior to yielding negligibly, small shear rates are measured whereas above the yield point non-zero values are recorded which allows one to “guess” the yield point. We have implemented a rheological protocol that “$\textit{mimics}$” an unsteady forcing rather than following the rheological “golden rule” of imposing a steady-state forcing ($t_0 \rightarrow \infty$).

Fig. 3

a Schematic illustration of the controlled stress flow ramp. b Rheological flow curve measured via the controlled stress ramp illustrated in (a) for a $0.1 \%$ (wt) solution of Carbopol^® 940. The full line is a nonlinear fitting functions according to the Herschel–Bulkley model. The full/empty symbols refer to the increasing/decreasing branches of the stress ramp schematically illustrated in (a). The inset presents the dependence of the hysteresis area on the characteristic forcing time $t_0$. The full line in the inset is a guide for the eye $P_h\propto t_0^{-1}$

In Fig. 3b, we illustrate such measurements performed on a controlled stress rheometer (Mars III from Thermo Fischer Scientific) equipped with a serrated plate–plate geometry with a $0.1\%$ (wt) solution of Carbopol^® 940 by using the forcing scheme illustrated in Fig. 3a with $t_0=0.5$ s. As opposed to previous measurements by others that seemed to indicate that the Carbopol^® gels are “model” or “ideal” yield stress fluids—i.e. free of thixotropic effects and with a rheological behaviour well described by the Herschel–Bulkley constitutive law—the data presented in Fig. 3b reveals the following features of the solid–fluid transition:

Fig. 4

Rheological flow curves measured via controlled stress ramps for various materials: a mayonnaise (Carrefour, France) b mustard (Carrefour, France) c $0.08 \%$ (wt) aqueous solution of Carbopol^® 980. For each stress value, the response of the material was averaged during $t_0 = 10$ s. The range of applied stresses corresponding to the yielding transition is highlighted in each subplot. The full lines are nonlinear fitting functions according to the Herschel–Bulkley model. The full/empty symbols in each panel refer to the increasing/decreasing branches of the stress ramp schematically illustrated in Fig. 3a

• 1. The solid–fluid transition is not direct (does not occur at a well-defined value of the applied stress $\sigma = \sigma _y$) but gradual and spanning a finite interval of the applied stresses.

• 2. The Herschel–Bulkley law describes well the rheometric response only in a range of large applied stresses, the full line in Fig. 3b.

• 3. The data corresponding to the increasing/decreasing branches of the controlled stress ramps overlap only far above the solid–fluid transition. Additionally, a cusp visible on the decreasing stress branch is visible. At this point, the rate of shear $\dot{\gamma }$ changes sign which indicates an elastic recoil effect typically observed with viscoelastic fluids. This feature has not been reported before and may phenomenologically explain the emergence of a negative wake in Figs. 2, 1b.

• 4. The degree of the irreversibility of the deformation states upon increasing/decreasing forcing quantitatively described by the area of the hysteresis visible in Fig. 3b scales as a power law with the degree of steadiness of the controlled stress ramp $t_0$—see the inset in Fig. 3b.

Fig. 5

Dependence of the hysteresis area on the characteristic forcing time $t_0$ (see text for description) measured with several yield stress materials via controlled stress flow ramps: circle ${(\circ )}$—mayonnaise (Carrefour, France), square ${(\square )}$—mustard (Carrefour, France), up triangle ${(\bigtriangleup )}$—$0.08 \%$ (wt) aqueous solution of Carbopol^® 980. The dashed lines are log-normal fitting functions (see text for the discussion); the full lines are power law fitting functions indicated in the inserts

A natural question arises at this point: How universal is the irreversible flow behaviour observed with a Carbopol^® gel? To answer this question, we present in Fig. 4 controlled rheological stress ramps performed with three microstructurally distinct yield stress materials: a commercially available mayonnaise, a commercially available mustard and a different type of Carbopol^® gel (Carbopol^® 980). Each of these rheological tests reveals a gradual solid–fluid transition characterised by a more or less pronounced hysteresis that departs from the Herschel–Bulkley constitutive relation. This indicates that, irrespective to the chemical identity of the material, the solid–fluid transition follows a rather universal scenario. It is equally interesting to monitor how the magnitude of the hysteresis depends on the degree of steadiness of the external forcing—the time $t_0$ the stress is maintained constant during the stress ramp (see Fig. 3a).

We present in Fig. 5 the dependence of the magnitude of the rheological hysteresis on the characteristic time $t_0$ for each of the materials characterised in Fig. 4.

For the case of mayonnaise and mustard (the circles and the squares in Fig. 5), a non-monotonic dependence of the magnitude of the hysteresis on the characteristic forcing time $t_0$ is observed. Corresponding to low values of $t_0$ (fast forcing), the hysteresis area first increases and then, for large values of $t_0$ (slow forcing), decreases following a power law. This non-monotone behaviour agrees well with the measurements of Divoux and his coworkers performed for several yield stress materials: mayonnaise, Laponite gel and carbon black gel (Divoux et al. 2013). As pointed out by Divoux et al. (2013), these non-monotone dependencies may be fitted by a log-normal function (the dashed lines in Fig. 5). The presence of a local maximum of these curves has been attributed to the existence of a critical timescale $t_0^{\star }$ specific to each material which describes the restructuration dynamics of the solid material units.

It has been shown recently that a clear departure from the Herschel–Bulkley behaviour can be observed even for “simple” yield stress fluids such as the Carbopol^® gels particularly during unsteady flows taking place around the yield point (Putz and Burghelea 2009; Weber et al. 2012; Divoux et al. 2013; Poumaere et al. 2014). The yielding behaviour of a Carbopol^® gel is illustrated here in Fig. 3b and in panel (c) of Fig. 4. As compared to the mayonnaise and the mustard, no local maximum was observed in the dependence of the hysteresis area on the characteristic forcing time but a negative power law scaling which indicates that in the limit of very slow forcing (large $t_0$) the Carbopol^® gels behave as non-thixotropic yield stress fluids.

2 Phenomenological Modelling of the Solid–Fluid Transition in an Elasto-Viscoplastic Material

As argued in the previous section, the simple Herschel–Bulkley picture cannot accurately describe the solid–fluid transition even in the case when the time-dependent effect (thixotropy) are not very pronounced, e.g. for the case of a Carbopol^® gel. This prompted the development of more sophisticated phenomenological models. It is widely believed that the macroscopic yield stress behaviour originates from the presence of a microstructure which can sustain a finite local stress prior to breaking apart and allowing for a macroscopic flow to set in. To illustrate this, we present in Fig. 6 micrographs (acquired in a quiescent state) of several materials that exhibit a yield stress behaviour. In spite of clear differences in the chemical nature (and, consequently, physico-chemical properties) of these materials, heterogeneous and soft-solid-like aggregates are visible in each of the micrographs presented in Fig. 6. A microscopic experimental study of the yielding would require monitoring in real time both the motion of such aggregates and the dynamics of their break-up (and, possibly, reforming) during flow. This experimental approach is difficult to implement, and we are aware of very few previous works that describe the evolution of the microstructure during yielding (Dimitriou and McKinley 2014). Although the structural heterogeneity and the characteristic space scales of a Carbopol^® gel are quite clearly probed by diffusion experiments (Oppong et al. 2006; Oppong and de Bruyn 2007), a detailed experimental description of the Carbopol^® microstructure is still missing. This is mainly due to practical difficulties in visualising the microstructure without altering it Piau (2007). We present in the following a minimalistic model that uses no explicit microstructural assumption but is yet able to describe both shear and oscillation rheological experiments. As previously suggested by several authors (Möller et al. 2006; Dullaert and Mewis 2006), the fluidisation process of a physical gel sample under shear can be interpreted in terms of a “dissociation” reaction, $\mathbf {S \rightleftharpoons S+F}$ which can be modelled by the following kinetic equation:

Fig. 6

Micrographs of several yield stress materials: a commercial shaving gel (Gillette Series) b mayonnaise (Carrefour, France) c $5 \%$ bentonite in water d suspension of Chlorella Vulgaris unicellular microalga (reproduced from Souliès et al. 2013)

$$\begin{aligned} \frac{d \bar{a}(t)}{dt}=R_d\left[ \bar{a}(t),t,\Gamma \right] +R_r\left[ \bar{a}(t),t,\Gamma \right] +\delta , \end{aligned}$$

(2)

where S, F denote the solid and fluid phases, respectively, $\bar{a}(t)=[S]$ is the concentration of the solid phase, $\Gamma =\frac{\sigma }{\sigma _y}$ is the non-dimensional forcing parameter, $R_d$ is the rate of destruction of solid units, $R_r$ is the rate of fluid recombination of fluid elements into a gelled structure and $\delta$ is a small thermal noise term.

The exact form of the terms $R_r$ and $R_d$ is usually chosen on an intuitive basis: the destruction of solid structural units increases monotonically with increasing applied forcing, whereas the recombination probability may be even constant or monotonically decreasing with increasing forcing.

One of the simplest choices of a microstructural equation was introduced by Coussot and coworkers (Coussot et al. 2002a).

It considers an evolution equation for a microstructural parameter $\lambda$ in the following form:

$$\begin{aligned} \frac{d \bar{a}}{dt} = \frac{1}{\tau } - \alpha \dot{\gamma }\bar{a}, \end{aligned}$$

(3)

where $\tau$ is a characteristic timescale of the aggregation of microstructural units and $\alpha$ is a positive constant related to role of the external shear in destroying the solid structural units. Furthermore, the model considers a viscosity function that depends on the microstructure in the following form:

$$\begin{aligned} \eta =\eta _0 \left( 1 + \bar{a} ^n\right) , \end{aligned}$$

(4)

where $\eta _0$ is a constant asymptotic viscosity when the microstructure is entirely destroyed, $\eta _0 = \lim _{\bar{a} \rightarrow 0} \eta \left( \bar{a}\right)$.

The parameter $\bar{a}$ can be loosely defined as the degree of flocculation for clays, a measure of the free energy landscape for glasses or as the fraction of particles in potential wells for colloidal suspensions (Coussot et al. 2002a). An obvious difficulty of this microstructural approach relates to the fact that the parameter $\bar{a}$ is not easily accessible experimentally and, consequently, a direct comparison with rheometric measurements remains elusive (Coussot 2007).

Due to its simplicity and formal elegance, this model is quite appealing to both physicists and rheologists.

In a recent publication, it has been claimed that this simple microstructural model is able to accurately fit rheological flow curves measured during a controlled stress ramp (Dinkgreve et al. 2018)—see Fig. 7 therein. This result is highly questionable. Even if one neglects the emergence of a hysteresis of the deformation states illustrated in Fig. 3, far above the yield point Carbopol^® gels are shear-thinning fluids. On the other hand, in a fluid state ($\bar{a} \rightarrow 0$) the above-mentioned model predicts a constant viscosity $\eta _0$ according to Eq. (4). This is at odds with any rheological tests performed with Carbopol^® gels we are aware of. As a cautionary note to the reader, we point out that in spite of their appeal, phenomenological models that are too simple may be deceptive when compared to experimental results.

We present in the following a minimalistic phenomenological model able to describe the main features of the solid–fluid transition of a Carbopol^® gel subjected to stress (Putz and Burghelea 2009; Moyers-Gonzalez et al. 2011b).

We make the following assumptions concerning the terms $R_r$ and $R_d$ involved in the microstructural equation Eq. (2):

• 1. $R_d(\bar{a}(t),t,\dot{\gamma })$ is proportional to the relative speed of neighbouring solid units and the existing amount of solid, i.e. $R_d(\bar{a}(t),t,\dot{\gamma })=-g(\Gamma ) \bar{a}(t)$ and $g(\Gamma )=K_1 |\Gamma |$ is a linear amplitude of shear-induced destruction.

• 2. Unlike in solutions of micelles or suspensions, where the external shear may induce aggregation (Goveas and Olmsted 2001; Heymann and Aksel 2007), in the case of a physical gel the rate of fluid recombination decreases with the relative speed of neighbouring fluid elements being practically zero in a fast enough flow. Therefore, we consider $R_r(\bar{a}(t),t,\Gamma ) = f(\Gamma ) \bar{a}(t) (1-\bar{a}(t))$, where $f(\Gamma )=K_r \left[ 1- \tanh \left( \frac{\Gamma -1}{w} \right) \right]$ is a smooth decaying function of the applied forcing. Here, we have considered that recombination of the gel network takes place via binding of single polymer molecules to already existing solid blobs. Although we are not aware of any theoretical prediction in this sense, different recombination schemes (S + S$\rightarrow$ S, L + L$\rightarrow$ S, S + S + L$\rightarrow$ S, etc.) are in principle possible and we note here that they actually lead to a qualitatively similar behaviour of the phase parameter $\bar{a}(t)$.

With the assumptions above, the kinetic Eq. 2 may be written as

$$\begin{aligned} \frac{d \bar{a}}{dt}=-K_d \Gamma \bar{a}+K_r \left[ 1- \tanh \left( \frac{\Gamma -1}{w} \right) \right] \bar{a}(1-\bar{a})+\delta . \end{aligned}$$

(5)

We would like to point out that a constant recombination term as previously employed by several authors (Möller et al. 2006; Roussel et al. 2004) seems to us somewhat unphysical in this context. Precisely, if one solves the phase equation (Eq. 5) with a constant recombination term and a forcing parameter linearly increasing with time, $\Gamma \propto t$, one obtains a non-monotone dependence $\bar{a}=\bar{a}(t)$ which we consider to be unrealistic for a Carbopol^® gel as it will further imply a non-monotone stress rate of strain dependence.

The phase equation admits two steady-state solutions:

$$\begin{aligned} \bar{a}_{SS1} = \left\{ \begin{array}{cc} 1-\frac{g}{f} &{} , g<f \\ 0 &{} \text {otherwise} \\ \end{array} \right. ,\,\, \text {stable} \end{aligned}$$

(6)

and

$$\begin{aligned} \bar{a}_{SS2} = \left\{ \begin{array}{cc} 1-\frac{g}{f} &{} , g \ge f \\ 0 &{} \text {otherwise} \\ \end{array} \right. ,\,\, \text {unstable.} \end{aligned}$$

(7)

It can be easily noted that the first steady state $\bar{a}_{SS1}$ is stable, whereas $\bar{a}_{SS2}$ is unstable and their separation is insured by the small parameter $\delta$.

As a constitutive equation, we use a thixoelastic Maxwell (TEM)-type model (Quemada 1998a, b, 1999):

$$\begin{aligned} \frac{\eta \left( \dot{\gamma }\right) }{G} \bar{a} \frac{d \sigma }{dt} + \sigma = \eta \left( \dot{\gamma }\right) \dot{\gamma }, \end{aligned}$$

(8)

where the viscosity is given by a regularised Herschel–Bulkley model, $\eta =K~\left( \epsilon +|\dot{\gamma }|\right) ^{N-1}+\frac{\sigma _y}{\epsilon + \left| \dot{\gamma }\right| }$. Here, G is the static elastic modulus, K is the consistency, N is the power law index and $\epsilon$ is the regularisation parameter (typically of order of $10^{-12}$). A detailed discussion of several regularisation techniques is presented by Frigaard and Nouar (2005).

Fig. 7

a Rheological flow curve measured via the controlled stress ramp illustrated in Fig. 3a for a $0.1 \%$ (wt) solution of Carbopol 940. The full/empty symbols refer to the increasing/decreasing branches of the stress ramp schematically illustrated in Fig. 3a. b. Normalised strain measured during a controlled stress oscillatory sweep. c Lissajoux figure corresponding to the controlled stress oscillatory sweep. The full line in each panel is the prediction of the model

The choice of this constitutive equation is motivated by the presence of elastic effects in the intermediate deformation regime (see the cusp in decreasing stress branch in Figs. 3b and 4c, and the corresponding discussion). It is easy to note that in the limit $\bar{a} \rightarrow 1$, Eq. (8) reduces to Hooke’s law, $G=\sigma \gamma$, and in the limit $\bar{a} \rightarrow 0$ it reduces to a regularised Herschel–Bulkley model.

A nonlinear fit of the controlled stress ramp presented in Fig. 3b is presented in Fig. 7a (the full line). Quite remarkably, without any other adjustment of the fit parameters, the model is able to fit controlled stress oscillatory tests performed with the same material (Fig. 7b) and the corresponding Lissajoux figure (Fig. 7c).

A central conclusion of this part is that the usage of an evolution equation that describes a smooth change of a microstructural parameter $\bar{a}$ coupled to a constitutive equation that contains information on both the viscous and the elastic behaviours suffices to describe rheological measurements.

Though able to model sufficiently complex rheological data (ranging from controlled stress/strain unsteady flow ramps, creep tests and oscillatory tests in a wide range of frequencies and amplitudes), the phenomenological model has a number of limitations:

• 1. As the functional dependence of the microstructural parameter Eq. (5) is generally chosen on an intuitive basis rather derived from first principles, the model by Putz and Burghelea (2009) can teach little about the microscopic-scale physics of the yielding process.

• 2. The model involves a rather large number of parameters some of which are not directly and easily measurable and can be obtained only by fitting the experimental data, e.g. $K_r$, $K_d$, w.

• 3. The model is not inherently validated from a thermodynamical standpoint as the choice of $R_d$, $R_r$ is not made based on first principles. The second law of thermodynamics is not necessarily satisfied and such a validation is not always straightforward as it requires the derivation of a thermodynamic potential (Picard et al. 2002; Bautista et al. 2009; Hong et al. 2008).

To circumvent these limitations, we present in the next section a different and more fundamental approach for the yielding of a soft material subjected to a varying external stress based on principles of Statistical Physics and Critical Phenomena.

3 Microscopic Modelling for the Yielding of a Physical Gel as a Critical Phenomenon

For a detailed account of these theoretical developments, the reader is referred to two recent publications (Sainudiin et al. 2015b; Burghelea et al. 2017).

We propose in the following a microscopic model for the yielding or gelation, corresponding to $\overline{a}$ approaching 0 or 1, respectively, of a physical gel using an essentially bi-parametric family of a correlated site percolation that is inspired by the two-dimensional Ising model for the $+1$ or $-1$ magnetization of a ferromagnet (Ising 1925; Stanley 1987). Our model builds on the analogy between the local agglomerative interactions in terms of assembly/disassembly of neighbouring gel particles in a microscopic gel network (see Slomkowski et al. 2011, (2.5, 2.6, 5.9, 5.9.1, 5.9.1.1, 8.1.4) and Jones (2009) for standardised nomenclature subjected to an external stress and the local ferromagnetic interactions in terms of spin up ($+1$)/spin down ($-1$) of neighbouring particles in a microscopic ferromagnetic network subjected to an external magnetic field).

By the analogy with the Ising model for the ferromagnetism, we are placing the problem of yielding of a soft solid under stress in the more general context of “Phase Transitions and Critical Phenomena” and fully benefit from a number of theoretical tools developed during the past five decades for gaining physical insights into the solid–fluid transition.

This thermodynamically consistent microscopic model with only two parameters that reflect the chemical nature of the gel and only two energy-determining configuration statistics the number of gelled particles and the number of gelled pairs of neighbouring particles is able to capture the macroscopic behaviours of yielding and gelation for any stress regime given as a function of time, including hysteretic effects, if any. This approach is fundamentally probabilistic and formalises Gibbs fields as time-homogeneous and time-inhomogeneous Markov chains over the state space of all microscopic configurations. It not only provides simulation algorithms to gain insights but also allows one to derive an approximating nonlinear ordinary differential equation for $\overline{a}(t)$, the expected volume fraction of the unyielded material at a rescaled time t, which we show to be a robust qualitative determinant of the probabilistic dynamics of the system.

3.1 A Microscopic Gibbs Field Model for the Macroscopic Yielding of a Yield Stress Material

Let us model an idealised yield stress material or viscoplastic fluid as a network of microscopic constituents in an appropriate solvent that are capable of assembling by “forming bonds” or disassembling by “breaking bonds” with their neighbours. Without making any assumption about either the nature of the bonds or the physical nature of the interactions among neighbouring microscopic constituents, we investigate the model when the network of particles is the regular graph given by the toroidal two-dimensional square lattice as illustrated in Fig. 8 and the bonds/interactions are accounted for in a generic manner as detailed in the following.

Fig. 8

a The regular graph represented for $n=5$. The vertices labelled with 1/0 represent micro-gel particles in a unyielded/yielded state, respectively. The labels 1/0 of the edges indicate whether two sites are connected/unconnected. b 2D toroidal lattice suggesting the periodic boundary conditions used through the simulations

Let the set of nodes or sites be

$$\mathbb {S}_n=\{1,2,\ldots ,n\}^2 = \{(1,1),(1,2),\ldots ,\ldots ,(n,n) \} .$$

Let $N_s = \{ r : \Vert \overline{(r-s)}_n \Vert =1\}$ denote the set of four nearest neighbouring sites of a given site $s \in \mathbb {S}_n$, where $\overline{(r-s)}_n$ denotes coordinate-wise subtraction modulo n and $\Vert \cdot \Vert$ denotes the Euclidean distance. Then the set of edges between pairs of sites is

$$\mathbb {E}_n = \bigcup _{s \in \mathbb {S}_n} \{\langle s,r\rangle : r \in N_s \}\subset \mathbb {S}_n^2 .$$

Let |A| denote the size of the set A. Note that $|\mathbb {S}_n|=n^2$ and $|\mathbb {E}_n|=2n^2$. Each site $s \in \mathbb {S}_n$ can be thought to represent a microscopic clump of particles in a particular region of the material and each edge $\langle s,r\rangle \in \mathbb {E}_n$ represents a potential connection between neighbouring clumps at sites s and r. At the finest resolution of the model, each site can be a monomer molecule in the material and each edge can represent a potential bond between neighbouring molecules. Let $x_s \in \Lambda =\{0,1\}$ denote the phase at site s. Phase 0 corresponds to being yielded or un-gelled and phase 1 corresponds to being unyielded or gelled. The phase at a site directly affects its connectability with its neighbouring sites. We assume that only two gelled sites can be connected with one another. Thus, the connectivity between sites s and r is given by

$$\begin{aligned} y_{\langle s,r \rangle }= {\left\{ \begin{array}{ll} 1 &{} \text { if } r \in N_s \text { and } x_r x_s=1 \\ 0 &{} \text { otherwise.} \end{array}\right. } \end{aligned}$$

(9)

In other words, we say that sites s and r are connected, i.e. $y_{\langle s,r \rangle }=1$, if and only if $x_s=x_r=1$ and s and r are neighbours. Otherwise, we say s and r are unconnected, i.e. $y_{\langle s,r \rangle }=0$. These definitions are schematically illustrated in Fig. 8a. Since the phase of sites determines their connectedness, we refer to sites in phase 1 as connectable and those in phase 0 as un-connectable. Thus, every site configuration $x \in \mathbb {X}_n := \Lambda ^{\mathbb {S}_n}$ has an associated edge configuration $y \in \mathbb {Y}_n := \Lambda ^{\mathbb {E}_n}$ which characterises the connectivity information between all pairs of neighbouring sites. We use X to denote a random site configuration and $Y=Y(X)$ to denote the associated random edge configuration. Two extreme site configurations are $\mathbf {1} := \{x_s=1: s \in \mathbb {S}_n\} \in \mathbb {X}_n$, with all sites gelled, and $\mathbf {0} := \{x_s=0: s \in \mathbb {S}_n\} \in \mathbb {X}_n$, with all sites un-gelled. Their corresponding extreme edge configurations are $\mathbf {1} := \{y_{\langle s, r \rangle }=1: \langle s, r \rangle \in \mathbb {E}_n\} \in \mathbb {Y}_n$, with all neighbouring pairs of sites connected, thus making the material to be in a fully solid state, and $\mathbf {0} := \{y_{\langle s, r \rangle }=0: \langle s, r \rangle \in \mathbb {E}_n\} \in \mathbb {Y}_n$, with all neighbouring pairs of sites unconnected, thus making the material to be in a fully fluid state, respectively. Note that $Y(x):\mathbb {X}_n \rightarrow \mathbb {Y}_n$ is neither injective nor surjective.

Let $\mathcal {E}(x)$ be the energy of a site configuration x, k be the Boltzmann constant and T be the temperature. Then the probability distribution of interest on the site configuration space $\mathbb {X}_n$ is

$$ \pi (x) = \frac{1}{Z_{kT}} \exp \left( -\frac{1}{kT} \mathcal {E}(x) \right) , $$

where $Z_{kT}$ is the normalising constant or partition function

$$ Z_{kT} = \sum _{x \in \mathbb {X}_n} \exp \left( -\frac{1}{kT} \mathcal {E}(x) \right) . $$

By $X \sim \pi$, we mean that the random site configuration X has probability distribution $\pi$, i.e.

$$\Pr (X=x)={\left\{ \begin{array}{ll}\pi (x) &{} \text { if } x \in \mathbb {X}_n\\ 0 &{} \text { otherwise} .\end{array}\right. }$$

Next we show that $\pi$ is a Gibbs distribution by expressing the energy in terms of a potential function describing local interactions. Due to $\{N_s: s \in \mathbb {S}_n\}$, the neighbourhood system, we have only singleton and doubleton cliques. Therefore, the Gibbs potentials over the two types of cliques are

$$ V_{\{s\}}(x) = (\sigma - \alpha ) x_s = {\left\{ \begin{array}{ll} 0 &{} \text { if } x_s=0 \\ \sigma - \alpha &{} \text { if } x_s=1 , \end{array}\right. } $$

and

$$ V_{\langle s,r\rangle }(x) = -\beta x_s x_r = {\left\{ \begin{array}{ll} 0 &{} \text { if } (x_s,x_r)=(0,0) \\ 0 &{} \text { if } (x_s,x_r)=(1,0) \\ 0 &{} \text { if } (x_s,x_r)=(0,1) \\ -\beta &{} \text { if } (x_s,x_r)=(1,1) , \end{array}\right. } $$

where $\{s\}$ is the singleton clique, $\langle s,r\rangle$ is the doubleton clique with $r\in N_s$, $\sigma \ge 0$ is the external stress applied, $\alpha \ge 0$ is the site-specific threshold, and $\beta \in (-\infty ,\infty )$ is the interaction constant between neighbouring sites. The parameters $\alpha$ and $\beta$ can be thought to reflect fundamental rheological properties of the material under study.

The energy function corresponding to this potential is therefore

$$\begin{aligned} \mathcal {E}(x)= & {} \sum _{C} V_C(x) \\= & {} \sum _{s \in \mathbb {S}_n} V_{\{s\}}(x) + \sum _{\langle s,r \rangle \in \mathbb {E}_n} V_{\langle s,r \rangle }(x) \\= & {} \left( - \beta \sum _{\langle s,r \rangle \in \mathbb {E}_n} x_s x_r + (\sigma -\alpha ) \sum _{s \in \mathbb {S}_n} x_s \right) . \end{aligned}$$

Since $\mathcal {E}(x)$, the energy of a configuration x, only depends on $\beta$ and the difference $(\sigma -\alpha )$, we can define this difference as the parameter $\tilde{\sigma } := \sigma -\alpha \ge -\alpha$ in order to reparametrize

$$ \mathcal {E}(x) = \left( - \beta \sum _{\langle s,r \rangle \in \mathbb {E}_n} x_s x_r + \tilde{\sigma } \sum _{s \in \mathbb {S}_n} x_s \right) , $$

through $(\tilde{\sigma },\beta ) \in [-\alpha ,\infty ) \times (-\infty ,\infty )$.

Let the expectation of a function $g : \mathbb {X}_n \rightarrow \mathbb {R}$, with respect to $\pi$, be

$$ \mathbf {E}_{\pi }(g) := \sum _{x \in \mathbb {X}_n} g(x)\pi (x)$$

then the internal energy of the system is

$$ \mathcal {U} = \mathbf {E}_{\pi }\left( \mathcal {E} \right) = \sum _{x \in \mathbb {X}_n} \mathcal {E}(x) \pi (x) , $$

and the free energy of the system is

$$ \mathcal {F} = -k T \ln (Z_{kT}) . $$

Our model satisfies the standard thermodynamic equality:

$$\begin{aligned}&-T^2 \frac{\partial }{\partial T} \left( \frac{\mathcal {F}}{T}\right) = -T^2 \frac{\partial }{\partial T} \left( \frac{-k T \ln (Z_{kT})}{T} \right) = kT^2 \frac{\partial }{\partial T} \left( {\ln (Z_{kT})} \right) \\&= kT^2 {\frac{1}{Z_{kT}}} \frac{\partial }{\partial T} \left( Z_{kT} \right) = kT^2 {\frac{1}{Z_{kT}}} \frac{\partial }{\partial T} \left( \sum _{x \in \mathbb {X}_n} \exp \left( -\frac{1}{kT} \mathcal {E}(x) \right) \right) \\&= kT^2 {\frac{1}{Z_{kT}}} \left( \sum _{x \in \mathbb {X}_n} \exp \left( -\frac{1}{kT} \mathcal {E}(x) \right) \frac{\mathcal {E}(x)}{kT^2} \right) = \sum _{x \in \mathbb {X}_n} \mathcal {E}(x) \pi (x)\\&= \mathcal {U} . \end{aligned}$$

We sometimes emphasise the dependence of the energy and the corresponding distribution upon $\alpha$, $\beta$ and $\sigma$ by subscripting as follows:

$$ \mathcal {E}(x) = \mathcal {E}_{\alpha ,\beta ,\sigma }(x) \quad \text { and } \quad \pi (x) = \pi _{\alpha ,\beta ,\sigma }(x) . $$

Let the number of neighbours of site s that are in phase 1 be $x_{N_s} := \sum _{r \in N_s}x_r$. Then, $\mathcal {E}_s(x)$, the local energy at site s of configuration x, is obtained by summing the Gibbs potential $V_C(x)$ over all $C \ni s$, i.e. over cliques C containing site s, as follows:

$$\begin{aligned} \mathcal {E}_s(x)= & {} \sum _{C \ni s} V_C(x) = V_{\{s\}}(x) + \sum _{r \in N_s} V_{\langle s,r \rangle }(x)\\= & {} (\sigma - \alpha )x_s - \beta \sum _{r \in N_s} x_sx_r \\= & {} x_s \left( (\sigma - \alpha ) - \beta \sum _{r \in N_s} x_r \right) \\= & {} x_s \left( (\sigma - \alpha ) - \beta x_{N_s} \right) . \end{aligned}$$

Let $(\lambda ,x(\mathbb {S}\setminus {s}))$ denote the configuration that is in phase $\lambda$ at s and identical to x everywhere else. Then the local specification is

$$\begin{aligned} \pi _s(x)= & {} \frac{\exp (-\frac{1}{kT} \mathcal {E}_s(x))}{\sum _{\lambda \in \Lambda }\exp (-\frac{1}{kT} \mathcal {E}_s(\lambda ,x(\mathbb {S}\setminus {s})))} \nonumber \\= & {} {\left\{ \begin{array}{ll} \frac{\theta }{1+\theta } &{} \text { if } x_s=0\\ \frac{1}{1+\theta } &{} \text { if } x_s=1 \end{array}\right. }, \end{aligned}$$

(10)

where

$$\begin{aligned} \theta = \theta (s,\alpha ,\beta ,\sigma ) = \exp \left( -\frac{1}{k T} \left( \beta x_{N_s}-(\sigma -\alpha ) \right) \right) . \end{aligned}$$

(11)

We focus on the effect of varying external stress $\sigma$ at a constant ambient temperature, and therefore without loss of generality, one may set $kT=1$ and work with $\pi (x) = Z_1^{-1}\exp (-\mathcal {E}(x))$.

We can think of this model as an $\mathbb {X}_n$-valued Markov chain $\{X(m)\}_{m = 0}^{\infty }$, where $X(m)=\left( X_s(m), s \in \mathbb {S}_n\right)$ and $X_s(m) \in \Lambda$, in discrete time $m \in \mathbb {Z}_+ := \{0,1,2,\ldots \}$. Let the initial condition, $X(0)=x(0)$, be given by the initial distribution $\delta _{x(0)}$ over $\mathbb {X}_n$ that is entirely concentrated at state x(0). Then the conditional probability of the Markov chain at time step m, given that it starts at time 0 in state x(0), is

$$\begin{aligned} \Pr \left\{ \, X(m) \, | \, X(0)=x(0) \, \right\} = \delta _{x(0)} \left( P_{\alpha ,\beta ,\sigma }\right) ^m , \end{aligned}$$

(12)

where the $|\mathbb {X}_n| \times |\mathbb {X}_n|$ transition probability matrix $P_{\alpha ,\beta ,\sigma }$ over any pair of configurations $(x,x') \in \mathbb {X}_n \times \mathbb {X}_n$ is

$$\begin{aligned} P_{\alpha ,\beta ,\sigma } (x,x') = {\left\{ \begin{array}{ll} \frac{1}{n^2} \frac{1}{1+\theta } &{} \text { if } || x-x' || = 1, 0 = x_s \ne x'_s = 1 \\ \frac{1}{n^2} \frac{\theta }{1+\theta } &{} \text { if } || x-x' || = 1, 1 = x_s \ne x'_s = 0 \\ \frac{1}{n^2} \frac{1}{1+\theta } &{} \text { if } || x-x' || = 0, 1 = x_s = x'_s = 1 \\ \frac{1}{n^2} \frac{\theta }{1+\theta } &{} \text { if } || x-x' || = 0, 0 = x_s = x'_s = 0 \\ 0 &{} \text{ otherwise }. \end{array}\right. } \end{aligned}$$

(13)

$\theta =\theta (s,\alpha ,\beta ,\sigma )$ is indeed a function of the site s and the three parameters: $\alpha$, $\beta$ and $\sigma$. By $|| x-x' || = 1$, we mean that the configurations x and $x'$ differ at exactly site s, i.e. $x_s \ne x'_s$. Similarly, by $|| x-x' || = 0$ we mean that the two configurations are identical, i.e. $x=x'$ or $x_s=x'_s$ at every site $s \in \mathbb {S}_n$. We can think of our Markov chain evolving according to the following probabilistic rules based on Eqs. (10) and (11):

• Given the current configuration x, we first choose one of the $n^2$ sites in $\mathbb {S}_n$ uniformly at random with probability $n^{-2}$;

• Denote this chosen site by s and let the number of bondable neighbours of s be $i=N_s(x) \in \{0,1,2,3,4\}$; and

• Finally, change the phase at s to 1, i.e. set $x_s=1$ with probability

  $$\begin{aligned} p_i := (1+\theta )^{-1} = (1+\theta (s,\alpha ,\beta ,\sigma ))^{-1} = 1/(1+e^{(\sigma -\alpha -i\beta )}) \end{aligned}$$

  (14)

  and set $x_s=0$ with probability $1-p_i$.

Fig. 9

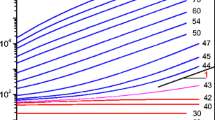
Plots of $p_i$, the probability that site s with $i=x_{N_s}$ neighbours in phase 1, is also in phase 1, as a function of external stress $\sigma$ for different values of $\alpha$, $\beta$. From the plots it is clear that $\alpha$ is a location parameter while $\beta$ controls the scale of the relative difference between $p_i$’s

We emphasise the dependence of $p_i$ on the parameters $\alpha$, $\beta$ and $\sigma$ by $p_i(\alpha ,\beta ,\sigma )$. This is illustrated in Fig. 9 for different parameter values. Just as in the Ising model, our model can be classified into three behavioural regimes depending on the sign of the interaction parameter $\beta$. When the interaction parameter $\beta >0$ the model is said to have “agglomerative interactions” analogous to the ferromagnetic interactions of the Ising model whereby the probability of a site being in phase 1 increases with the number of its neighbouring sites also being in phase 1, i.e. if $\beta >0$, then $0< p_0< p_1< p_2< p_3< p_4 < 1 .$ When $\beta =0$, the model is said to be “non-interactive” since the probability of a site being in phase 1 is independent of the phase of the neighbouring sites and identically p at each site, i.e. $0< p = p_0 = p_1 = p_2 = p_3 = p_4 = 1/\!\left( 1+e^{\sigma - \alpha }\right) < 1.$ When $\beta <0$, our model captures the “anti-agglomerative” interactions that are analogous to the “anti-ferromagnetic” interactions of the Ising model since the probability of a site being in phase 1 decreases with the number of its neighbouring sites also being in phase 1, i.e. if $\beta <0$ then $1> p_0> p_1> p_2> p_3> p_4 > 0.$

Note that our transition probabilities allow self-transitions, i.e. there is a positive probability that we will go from a configuration x to itself. Although we think of $\{X(m)\}_{m = 0}^{\infty }$ on the state space of all configurations $\mathbb {X}_n$ as a discrete-time Markov chain, with transition probability matrix $P_{\alpha ,\beta ,\sigma }$ in Eq. (13), we can easily add exponentially distributed holding times with rate 1 at each configuration and use Eq. (13) to choose a possibly new configuration and thereby obtain a continuous-time Markov chain $\{X(t)\}_{t \ge 0}$ in the usual way from $\{X(m)\}_{m = 0}^{\infty }$. This Markov chain over $\mathbb {X}_n$ is nothing but our Gibbs field (or Markov random field) model (Brémaud 1999 see, e.g. Chap. 7).

If the external stress varies as a function of discrete-time blocks of length $\underline{h} = \lfloor hn^2 \rfloor$ and given by the function $\sigma (m)$ for each time block $m=0,1,\ldots ,M$, then we have the time-inhomogeneous Markov chain $\{X(k)\}_{k=0}^{M\underline{h}}$ with the transition probability matrix at time k given by

$$\begin{aligned} P(k) = P_{\alpha ,\beta ,\sigma (\lfloor k/\underline{h}\rfloor )} , \end{aligned}$$

(15)

and the k-step configuration probability, with $k < M \underline{h}$ under initial distribution $\delta _{x(0)}$, given by

$$\begin{aligned} \Pr \Big \{ \, X(k) =\,&x(k) \, | \, X(0)=x(0) \, \Big \} \nonumber \\&= \delta _{x(0)} \left( \prod _{m=0}^{\lfloor k/\underline{h} \rfloor } \left( P_{\alpha ,\beta ,\sigma (m)}\right) ^{\underline{h}} \right) \left( P_{\alpha ,\beta ,\sigma ({\lfloor k/\underline{h} \rfloor + 1})}\right) ^{\overline{(k)}_{\underline{h}}} . \end{aligned}$$

(16)

As before, ${\overline{(k)}_{\underline{h}}}$ is k modulo $\underline{h}$.

We can use the local specification to obtain the Gibbs sampler, a Monte Carlo Markov chain (MCMC), to simulate from $\{X(m)\}$. Let h denote the average number of hits per site. Thus, $\lfloor h \,|\mathbb {S}_n|\rfloor =\lfloor hn^2 \rfloor$ gives the number of hits on all $n^2$ sites in $\mathbb {S}_n$ chosen uniformly at random. Given h and the parameters determining the local specification, i.e. $\alpha$, $\beta$ and $\sigma$, $\mathtt {GibbsSample}(x(0),\alpha ,\beta ,\sigma ,h)$ produces a sample path of configurations from the Markov chain $\{X(k)\}_{k = 0}^m$ given by Eqs. (12) and (13) and initialized at x(0) as it undergoes $m=\lfloor hn^2\rfloor$ transitions in $\mathbb {X}_n$.

If we are interested in simulating configurations with stationary distribution $\pi _{\alpha ,\beta ,\sigma }$, then for large $m=\lfloor hn^2 \rfloor$, the m-step probabilities, $\Pr \left\{ \, X(m) \, | \, X(0)=x(0) \, \right\}$, by construction will approximate samples from $\pi _{\alpha ,\beta ,\sigma }$ Brémaud (1999, see, e.g. Chap. 7, Sect. 6), i.e.

$$ \lim _{m \rightarrow \infty } d_{TV} \left( \Pr \left\{ \, X(m) \, | \, X(0)=x(0) \, \right\} , \pi _{\alpha ,\beta ,\sigma } \right) = 0 . $$

Here, $d_{TV} \left( \varpi , \pi \right) = 2^{-1} \sum _{x \in \mathbb {X}_n} |\varpi (x)-\pi (x)|$ is the total variation distance between two distributions $\varpi$ and $\pi$ over $\mathbb {X}_n$.

Two informative singleton clique statistics of a configuration x(m) at time m are the number and fraction of gelled sites given, respectively, by

$$ a(x) := \sum _{s \in \mathbb {S}_n} x_s \quad \text {and} \quad \overline{a}(x) := |\mathbb {S}_n|^{-1} a(x) = \frac{a(x)}{n^2}. $$

Similarly, two informative doubleton clique statistics of a configuration x are the number and fraction of connected pairs of neighbouring sites given, respectively, by

$$\begin{aligned} b(x)&:= \sum _{\langle s,t \rangle \in \mathbb {E}_n} y_{\langle s,r \rangle } = \sum _{\langle s,r \rangle \in \mathbb {E}_n} x_r x_s \quad \text {and} \\ \overline{b}(x)&:= |\mathbb {E}_n|^{-1} b(x) = \frac{b(x)}{2n^2} . \end{aligned}$$

When the configuration is a function of time m and given by x(m), then the corresponding configuration statistics are also functions of time and are given by $a(m)=a(x(m))$, $\overline{a}(m) = \overline{a}(x(m))$, $b(m)=b(x(m))$ and $\overline{b}(m) = \overline{b}(x(m))$. The energy of a configuration x can be succinctly expressed in terms of $\overline{a}(x)$ and $\overline{b}(x)$ as

$$ \mathcal {E}(x) = -\beta b(x) + (\sigma - \alpha ) a(x) = - \beta 2n^2 \overline{b}(x) + (\sigma - \alpha ) n^2 \overline{a}(x) , $$

and therefore

$$\begin{aligned} \mathcal {E}(x) \propto -2\beta \overline{b}(x) + (\sigma - \alpha ) \overline{a}(x) = -2\beta \overline{b}(x) + \tilde{\sigma } \overline{a}(x), \end{aligned}$$

(17)

where $\beta \in (-\infty ,\infty )$ and $\tilde{\sigma } = \sigma - \alpha \ge -\alpha$ for a given $\alpha \ge 0$. Since the energy of a configuration x, given n, only depends on its $\overline{a}(x)$ and $\overline{b}(x)$, we can easily visualise any sample path $\left( \, x(0),\ldots ,x(m) \, \right) \in \mathbb {X}_n^{m+1}$ in configuration space as the following sequence of $(m+1)$ ordered pairs in the unit square:

$$ \left( \, \left( \overline{a}(x(0)), \overline{b}(x(0))\right) , \ldots , \left( \overline{a}(x(m)), \overline{b}(x(m))\right) \, \right) \in \left( [0,1]^2\right) ^{m+1} . $$

Finally, we reserve upper case letters for random variables. Thus, A(X), $\overline{A}(X)$, B(X) and $\overline{B}(X)$ are the statistics of the random configuration X. And the notation naturally extends to A(m), $\overline{A}(m)$, B(m) and $\overline{B}(m)$ when X(m) is a random configuration at time m.

The macroscopic behaviour of a configuration x can be described by other statistics of x. We can obtain the connectivity information in the site configuration x through y, its edge configuration, according to (9). By representing the connectivity in y and/or x as the adjacency matrix of the graph whose vertices are $\mathbb {S}_n$, we can obtain various alternative graph statistics:

• 1. $C_x=\left\{ C_x^{(1)}, C_x^{(2)},\ldots ,C_x^{(n_y)}\right\}$, a partition of $\mathbb {S}_n$ that gives the set of connected components of x;

• 2. $C^{(*)}_x = argmax_{C_x^{(i)} \in C_x} |C_x^{(i)}|$, the first largest connected component;

• 3. $|C^{(*)}_x|/n^2$, the size of the first largest connected component per site; and

• 4. $F^{(*)}_x$, the fraction of the rows of $\mathbb {S}_n$ that are permeated (from top to bottom) by $C^{(*)}_x$.

3.1.1 Equilibrium Behaviour Under Constant Stress

We are interested in the effect of applying constant external stress $\sigma$ for a long period of time to an yield stress material with rheological properties specified by parameters $\alpha$ and $\beta$.

The subplot (a) of Fig. 10 approximates the time asymptotic behaviour of $\overline{a}$ when the Monte Carlo simulation of Gibbs field was initialized from $\mathbf {1}$ ( $h=100$ hits per site were performed) and subplot (b) presents the same information when the Gibbs field was initialized from $\mathbf {0}$. For both simulations, we have used $n=100$ and $(\tilde{\sigma },\beta )$ taken from a grid of linearly spaced points in $[-10,15]\times [0,4]$. In both panels (a–b) of Fig. 10, one can note that if the interaction parameter is smaller than a critical value of the interaction parameter $\beta < \beta _c$ ($\beta _c \approx 1.5$), both the solid–fluid and fluid–solid transitions are smooth. When the interaction parameter $\beta$ is gradually increased past this critical value both transitions become increasingly sharp.

Fig. 10

The value of $\overline{a}$ at rescaled time $t=100$ from Monte Carlo simulations of the Gibbs field for fixed parameters $(\tilde{\sigma },\beta )$ when initialized from $\mathbf {1}$ (panel (a)) and from $\mathbf {0}$ (panel (b)). The difference in $\overline{a}$ between the subplots (a) and (b) is shown in panel (c). The horizontal dashed lines indicate the critical value of the interacting parameter $\beta _c$ (see the discussion in the text)

To assess the reversibility of the deformation states in the time asymptotic limit, we focus at the difference between the subplots (a) and (b) which is presented in Fig. 10c. In the range $\beta < \beta _c$, the steady-state transition from solid to fluid evolves through the same intermediate states as the steady-state transition from fluid to solid and no hysteresis effect can be observed. When the interaction parameter $\beta$ exceeds the critical value $\beta _c$, a triangular hysteresis region may be observed in Fig. 10c.

This is an interesting result as it tells us that in the presence of strong interactions a “genuine” hysteresis of the deformation states would be observed even in conditions of a steady-state forcing. At a given applied stress $\tilde{\sigma }$, the size of the hysteresis region increases when the strength of the interactions is increased.

3.1.2 Configurations at the Solid–Fluid Interface

Let us now focus on the nature of the configuration x for a given $\beta$ at the solid–fluid interface, i.e. when $\overline{a}=1/2$, as $\tilde{\sigma }$ reaches a specific value. Site configurations at the solid–fluid interface provide the random environment for restricted diffusion of small tracer particles near gel transition. This phenomenon is of experimental and theoretical interest (Oppong et al. 2006; Oppong and de Bruyn 2007; Putz and Burghelea 2009) and has been recently studied for the case of $\beta =0$ (de Bruyn 2013). We are interested here in gaining insights on the nature of the site configurations at the solid–fluid interface for values of $\beta$ below, above and equal to zero.

Fig. 11

Effect of $\beta$ on preferred energy minimising configurations. Two sample configurations are shown for each $\beta \in \{-2,0,+2\}$ over a toroidal square lattice of $100\times 100$ sites. Sites in phase 0 and 1 are shown in black and white, respectively, at the solid–fluid interface when $\overline{a}\approxeq 1/2$

Figure 11 shows two random site configurations at the solid–fluid interface when $\overline{a}\approxeq 1/2$ for three different values of $\beta$. Without loss of generality, we fixed $\alpha =8$ and focus on the properties of the material that is capable of forming a gel in the absence of external stress. Clearly, the site configurations are dependent on the magnitude and sign of the interaction parameter $\beta$. Recall that $\overline{a}$, the fraction of gelled sites, and $\overline{b}$, the fraction of pairs of neighbouring gelled sites, are the sufficient statistic of the configuration, i.e. the energy of the configuration only depends on its $(\overline{a},\overline{b})$.

Three distinct cases can be distinguished. If $\beta =0$, the non-interactive case of the classical site percolation model studied in de Bruyn (2013), and $\tilde{\sigma }$ is chosen so that $\overline{a}=1/2$, then due to the site-filling probability being independently and identically distributed across all $n^2$ sites $\overline{b}=\overline{a}^2=1/4$. Two typical configurations when $\beta =0$, $n=100$ and $t=100$ at the solid–fluid interface are shown by the subplots in the second row of Fig. 11. More configurations were visually explored, and their distinguishing site configuration feature is characterised by the independence of the site-filling probability over sites and is apparent by the concentration of their sufficient statistics $(\overline{a},\overline{b})$ about $(\overline{a},\overline{a}^2)=(1/2,1/4)$ at the solid–fluid interface. This is the only case considered by de Bruyn (2013) when obtaining the random environment for restricted diffusion of small tracer particles near gel transition.

When $\beta$ is increased from 0 to 2, we have a very different distribution over site configurations at the solid–fluid interface as shown by two samples in the first (top) row of Fig. 11. It is easy to understand this “patchy” pattern in site configurations with large positive $\beta$ by realising that new gelled sites can occur with a higher probability at sites neighbouring existing gelled sites that have a larger $i=x_{N_s}$, number of neighbours in phase 1, than at sites surrounded by un-gelled sites with a smaller $i=x_{N_s}$. As $\beta$ gets larger, the probability of forming gelled sites around existing gelled sites is much larger than that of forming gelled sites around un-gelled sites, and this concentrates $(\overline{a},\overline{b})$ about $(\overline{a},\overline{a})=(1/2, 1/2)$ at the solid–fluid interface.

Finally, when $\beta$ is decreased from 0 to $-2$, we have a “checkered” pattern of site configurations at the solid–fluid interface as shown by two samples in the third (bottom) row of Fig. 11. As $\beta$ gets negative, the probability of forming gelled sites around existing gelled sites gets much smaller (see top row of Fig. 9). In the extreme asymptotic case, as $\beta \rightarrow -\infty$, we obtain configurations with increasingly checkered patters with $(\overline{a},\overline{b}) \rightarrow (1/2, 0)$, the sufficient statistics of the extreme “chessboard” configuration (such patterns occur already for $\beta =-8$ with $n=100$ but are not shown here).

Thus, from the $\beta$-dependent site configurations at the solid–fluid interface depicted in Fig. 11, it is clear that the trajectories of tracer particles (see Fig. 1 of Putz and Burghelea 2009 from Oppong et al. 2006) that can only diffuse through the un-gelled (black) contiguous regions are heavily dependent on whether there is interaction between adjacent gelled sites. This interaction is captured in our correlated site percolation model by the interaction parameter $\beta$.

3.1.3 Behaviour Under Varying Stress

The energy of X(t), the random site configuration at time t, depends on two of its highly correlated statistics: $\overline{A}(t)$, the random fraction of gelled sites at time t, and $\overline{B}(t)$, the random fraction of connected sites at time t. One of our primary interests is to study $\overline{A}(t)$ and $\overline{B}(t)$ as X(t) is under the influence of time-varying externally applied stress $\sigma (t)$. This test will be the closest equivalent of a controlled stress ramp typically used in experiments (see Fig. 3a in Sect. 1.3).

Fig. 12

Results of five distinct Gibbs field simulations corresponding to an increasing/decreasing stress ramp (illustrated in the bottom panel) with $\alpha =8$ and $\beta \in \{0,1,2,4\}$ indicated on the top of each panel). The stress was increased from 0 to 25 in units of 0.01 and decreased back to 0 with a holding time of $h=1000$ (nearly asymptotic state for each value of the applied stress) as the site configuration varied from $\mathbf {1}$ to $\mathbf {0}$ and then back to $\mathbf {1}$. The arrows indicate the increasing/decreasing branches of the stress ramp

Using Monte Carlo simulations of the time-inhomogeneous Markov chain $\{X(m)\}_{m=0}^{M\underline{h}}$ given by Eqs. (15) and (16), under an initially increasing and subsequently decreasing time-dependent stress $\sigma (m)$ given in the bottom panel of Fig. 12, we obtained multiple independent trajectories of $\overline{A}(\sigma )$, the fraction of gelled sites as a function of the external stress $\sigma$. Five such simulated trajectories are shown in the first four panels of Fig. 12. In order to mimic an asymptotic steady state of deformation (which is typically what a rheologist would be interested in characterising during a rheological measurement), the holding time per stress value has been chosen large, $h=1000$ hits per site. We note that regardless the value of the interaction parameter $\beta$ the results of the five individual simulations overlap nearly perfectly which indicates that the grid size of the simulation is sufficiently large and the simulated trajectories are robust.

For low values of the interaction parameter ($\beta \in \{0,1\}$, top row of Fig. 12), the dependence $\overline{a}(\sigma )$ corresponding to the decreasing branch of the stress ramp overlaps with that corresponding to the increasing branch and no hysteresis is observed. This indicates that in the presence of weak interactions and provided that an asymptotically steady state is reached the deformation states are fully reversible upon increasing/decreasing the external forces. In this case, a smooth solid–fluid transition is observed.

As the value of the interaction parameter is increased ($\beta \in \{2,4\}$, middle row of Fig. 12), a significantly different yielding behaviour is observed. First, the deformation states are no longer reproducible upon increasing/decreasing stresses and a clear hysteresis is observed. Second, the larger the value of the interaction parameter is, the steeper the solid–fluid transition becomes.

To conclude this part, the realisations of the time-inhomogeneous Markov chain under time-dependent stress $\sigma (m)$ corresponding to an asymptotically steady forcing reveal a smooth and reversible solid–fluid transition if the interactions are either absent or weak and a steep and irreversible transition in the presence of strong interactions. This result is consistent with the result presented in Fig. 10 where we have seen that for $\beta >\beta _c$ a genuine irreversibility of the deformation state is observed during the steady yielding process. An experimental validation of these conclusions has been recently presented in Souliès et al. (2013). The rheological flow curves measured for a suspension of spherical and electrically charged non-motile microalgae (Chlorella Vulgaris) reveal an abrupt solid–fluid transition and exhibit a strong hysteresis even in the limit of very slow forcing, see Fig. 11 in Souliès et al. (2013). In the case of a Carbopol gel where the microscopic interactions are presumably weaker than the interactions between electrically charged Chlorella cells, a much smoother solid–fluid transition is observed and, in the asymptotic limit of steady forcing, the hysteresis effects become negligibly small, Putz and Burghelea (2009). This is perhaps the main reason why Carbopol gels have been considered for decades “model”, “simple” or “ideal” yield stress fluids.

3.1.4 Effect of Holding Time (Steadiness of the External Forcing) on the Hysteresis

A large number of flows of yield stress fluids are unsteady in the sense that the applied stress is maintained for a finite time $t_0$. For the case of a rheometric configuration, we have illustrated the unsteady response of the material in Figs. 3b and 4. An important feature of the deformation curves presented in these figures is the irreversibility of the deformation states upon increasing/decreasing applied stresses. The magnitude of this effect is found to depend systematically on the degree of steadiness of the forcing, the time $t_0$ the applied stress is maintained constant (Fig. 5).

The question we address in the following is to what extent is the Gibbs field model able to describe the unsteady yielding behaviour observed in macroscopic experiments, see the discussion in Sects. 1 and 2. To answer this question, we calculate trajectories $\overline{a}$ similar to those presented in Fig. 12 which are realised during an increasing/decreasing stress ramp (bottom panel).

To place ourselves in the conditions of an unsteady forcing, we chose during the simulations finite values of the holding time (or average number of hits per site). We note that the average holding time per site in our simulations is the closest equivalent we could find for the characteristic forcing time $t_0$ imposed during macroscopic rheological measurements (Figs. 3b and 4 and the discussion in Sect. 1). To quantify the degree of reversibility of the deformation states, we calculate after each run the area of the hysteresis encompassed by the increasing/decreasing branches of the dependence $\overline{a} = \overline{a} (\sigma )$.

Fig. 13

Effect of increasing $\beta$ on the relative hysteresis area for $\overline{a}$ for different holding times $t_0$ per stress level in a stress ramp from 0 to 25 in increments of 1 (with $\alpha =8$). The dash line is a log-normal fit and the full lines are the fitted power laws indicated in the inserts. The symbols refer to the value of the interaction parameter $\beta$: circles ${(\circ )}$—$\beta = 0$, up triangles ${(\bigtriangleup )}$—$\beta = 1.5$, down triangles ${(\triangledown )}$—$\beta = 3$, hexagons —$\beta = 3.5$

The dependencies of the hysteresis area on the holding time obtained from such simulations performed for a fixed value of the site threshold $\alpha$ and several values of the interaction parameter $\beta$ are presented in Fig. 13.

Regardless of the strength $\beta$ of the interaction, a non-monotone dependence of the hysteresis area on the holding time is obtained. By carefully inspecting the individual dependencies $\overline{a} = \overline{a} (\sigma )$, we have noticed that prior to the local maximum the lattice yields only partially ($\overline{a}$ never reaches 0) corresponding to the largest value of the applied stress $\sigma$. Corresponding to the local maxima $t_0^{\star }$ of the dependencies presented in Fig. 13, the lattice yields completely (the terminal value of $\overline{a}$ is 0) and the area of the hysteresis starts decaying with the holding time $t_0$. This behaviour of the degree of irreversibility of deformation states as a function of the steadiness of the forcing is qualitatively similar to the experimental results illustrated in Fig. 5. In the absence of interactions ($\beta =0$), the hysteresis area follows a log-normal correlation with the holding time (see the circles and the dashed line in Fig. 13), which once more comes into a qualitative agreement with the experimental results. For non-zero values of $\beta$, we could not accurately fit the data by a log-normal function. Corresponding to the largest values of the average number of hits per site we have tested, we have found a power law decay of the hysteresis area, the full lines in Fig. 13), which is once again similar to the behaviour illustrated in Figs. 3b and 4 and consistent with experimental results obtained with Carbopol gels (Putz and Burghelea 2009; Poumaere et al. 2014).

It is equally interesting to note that the stronger the interaction is (larger the parameter $\beta$ is), the weaker the decay of the hysteresis area with the characteristic forcing time $t_0$ is. This indicates that in the presence of strong interactions a full reversibility of the deformation states cannot be achieved regardless of the degree of steadiness of the external forcing. This is indeed the case of several highly thixotropic materials such as bentonite gels, Laponite gels where steady-state rheological measurements cannot be truly achieved even during very slow controlled stress flow ramps. Among the data we illustrate in Figs. 4 and 5, the mayonnaise seems to behave as such as well.

3.2 A Nonlinear Dynamical System Approach for the Yielding Behaviour of a Viscoplastic Material

Though able to capture most of the relevant features of the solid–fluid transition in a thermodynamically consistent manner and making use of solely two internal parameters, the microscopic Gibbs field model presented in the previous section is rather difficult to implement and requires a number of skills in both statistics and programming. As practical applications regarding the dynamics of the solid–fluid transition in a pasty materials are concerned, one would often prefer dealing with a continuum microstructural equation with a general form given by Eq. (2) which, unlike the simple phenomenological model described in the second part of Sect. 2, is derived from first principles.

Here, based on the microscopic Gibbs field model, we derive a nonlinear first-order differential equation to asymptotically approximate $\mathbf {E}(\overline{A}(t))$, the expected fraction of sites in the solid phase, in continuous time t that is measured in units of $n^2$ discrete time steps as the number of sites $n^2 \rightarrow \infty$, under a fixed externally applied stress $\sigma$ and fixed rheological parameters $\alpha$ and $\beta$.

First, consider the discrete-time Markov chain $\{X(m)\}_{m=0}^{\infty }$ of Eqs. (12) and (13) and recall that X(m) is the random site configuration of the chain at discrete time m and $A(m)=\sum _{s}X_s(m)$ is the number of sites that are in phase 1. We will derive the approximation first for the case when $\beta =0$ in Eq. (13) and then for the general setting of $\beta \ne 0$.

3.2.1 Non-interactive Case with $\beta =0$

If $\beta =0$ then the probability of the phase in site s at the next time step is independent of the current configuration, i.e.

$$\begin{aligned} \text {Pr} \Big \{ X_s(m+1)&=x_s(m+1) \, \vert \, X(m)=x(m) \Big \} \\ =\Pr&\Big \{ X_s(m+1)=x_s(m+1) \Big \} \\&= {\left\{ \begin{array}{ll} p = \left( 1+e^{\sigma -\alpha }\right) ^{-1} &{} \text { if } x_s(m+1)=1\\ 1-p = 1-\left( 1+e^{\sigma -\alpha }\right) ^{-1} &{} \text { if } x_s(m+1)=0\\ 0 &{} \text { if } x_s(m+1) \notin \{0,1\} . \end{array}\right. } \end{aligned}$$

Therefore, the probability that the total number of sites in phase 1 increases by 1 in one time step is obtained by adding the probability of a transition from phase 0 to phase 1 over every uniformly chosen site s as follows:

$$\begin{aligned}&\Pr \left\{ A(m+1)=a(m)+1 \, \vert \, A(m)=a(m) \right\} \\&= \sum _{s \in \mathbb {S}_n} \Pr \left\{ X_s(m+1)=1 , X_s(m)=0, S=s \, \vert \, A(m)=a(m) \right\} \\&= \sum _{s \in \mathbb {S}_n} \underset{p}{\underbrace{\Pr \left\{ X_s(m+1)=1 \, \vert \, X_s(m)=0, S=s, A(m)=a(m) \right\} }} \\&\qquad \qquad \qquad \times \, \underset{(n^2-a(m))/n^2}{\underbrace{\Pr \left\{ X_s(m)=0 \, \vert \, S=s, A(m)=a(m) \right\} }} \\&\qquad \qquad \qquad \qquad \times \, \underset{1/n^{2}}{\underbrace{\Pr \left\{ S=s \, \vert \, A(m)=a(m) \right\} }} \\&\qquad \qquad \qquad \qquad \quad = \sum _{s \in \mathbb {S}_n} p \left( 1-\frac{a(m)}{n^2}\right) \frac{1}{n^2} = p \left( 1-\overline{a}(m)\right) . \end{aligned}$$

Dividing both sides of the equality that defines the above event by $n^2$, we get

$$\begin{aligned} \Pr&\left\{ A(m+1)/n^2=a(m)/n^2+1/n^2 \, \vert \, A(m)/n^2=a(m)/n^2 \right\} \\&= \Pr \left\{ \overline{A}(m+1)=\overline{a}(m)+1/n^2 \, \vert \, \overline{A}(m)=\overline{a}(m) \right\} = p \left( 1-\overline{a}(m)\right) . \end{aligned}$$

By an analogous argument, we can obtain the probabilities for the remaining two possibilities

$$\begin{aligned}&\Pr \left\{ \overline{A}(m+1)=\overline{a}(m)-1/n^2 \, \vert \, \overline{A}(m)=\overline{a}(m) \right\} = (1-p) \overline{a}(m),\\&\Pr \left\{ \overline{A}(m+1)=\overline{a}(m) \, \vert \, \overline{A}(m)=\overline{a}(m) \right\} = p\overline{a}(m) + (1-p) (1-\overline{a}(m)) . \end{aligned}$$

Now we can define a continuous-time Markov chain $\{\overline{A}(t)\}_{t \ge 0}$ on the unit interval [0, 1] by a rescaling of the discrete-time Markov chain $\{\overline{A}(m)\}_{m = 0}^{\infty }$ and letting the number of sites $n^2 \rightarrow \infty$. These two Markov chains are notationally distinguished only by their time indices. The rescaled time t is m in units of $n^2$, i.e. $m=\lfloor tn^2 \rfloor$ and $m+1=\lfloor (t+1/n^2)n^2\rfloor$. Then by taking $\Delta _t=O(1/n^2)$ and letting

$$\Delta _A = \overline{A}(t+\Delta _t)-\overline{a}(t) = \overline{A}(\lfloor (t+\Delta _t)n^2 \rfloor )-\overline{a}(\lfloor tn^2 \rfloor ) ,$$

we get

$$\begin{aligned} \Pr \Bigg \{ \frac{\Delta _A}{\Delta _t}=\frac{\Delta _a}{\Delta _t} \,&\Bigg \vert \, \overline{A}(t)=\overline{a}(t) \Bigg \} \nonumber \\ =&{\left\{ \begin{array}{ll} p \left( 1-\overline{a}(t)\right) + O(\Delta _t) &{} \text { if } \frac{\Delta _a}{\Delta _t}=1 \\ (1-p) \overline{a}(t) + O(\Delta _t) &{} \text { if } \frac{\Delta _a}{\Delta _t}=-1 \\ p \overline{a}(t)+ (1-p)(1-\overline{a}(t))+O(\Delta _t) &{} \text { if } \frac{\Delta _a}{\Delta _t}=0 \\ O(\Delta _t) &{} \text { otherwise}. \end{array}\right. } \end{aligned}$$

(18)

Finally, by considering the instantaneous rate of change of the expected fraction of sites in phase 1

$$ \frac{d}{dt}\overline{\mathbf {a}}(t) := \lim _{\Delta _t \rightarrow 0} \mathbf {E} \left( \frac{\overline{A}(t+\Delta _t) - \overline{A}(t)}{\Delta _t} \, \vert \, \overline{A}(t) \right) , $$

we get the limiting differential equation approximation as

$$n^2 \rightarrow \infty , \quad \Delta _t \rightarrow 0, \quad \Delta _a \rightarrow 0 ,$$

such that

$$\Pr \{ \, \Delta _a/\Delta _t \in \{0,-1,+1\} \, \} \rightarrow 1$$

based on Eq. (18) as follows:

$$ \dot{\overline{\mathbf {a}}} = \frac{d}{dt}{\overline{\mathbf {a}}(t)} = p(1-\overline{\mathbf {a}}(t)) - (1-p) \overline{\mathbf {a}}(t) = p-\overline{\mathbf {a}}(t) , $$

or simply by

$$\begin{aligned} \dot{\overline{\mathbf {a}}} = p-\overline{\mathbf {a}} = (1+e^{\sigma -\alpha })^{-1} - \overline{\mathbf {a}} . \end{aligned}$$

(19)

The simple relationship above is mathematically very similar to the so-called “lambda-model” introduced by Coussot et al. (2002a, b) with the remark that we consider the stress $\sigma$ as a forcing parameter rather than the rate of deformation. Given the initial condition $\overline{\mathbf {a}}(0)=\overline{\mathbf {a}}_0$, the analytic solution is

$$ \overline{\mathbf {a}}(t) = p + (\overline{\mathbf {a}}_0-p)e^{-t} = (1+e^{\sigma -\alpha })^{-1} + (\overline{\mathbf {a}}_0 - (1+e^{\sigma -\alpha })^{-1}) e^{-t} $$

with only one asymptotically stable fixed point

$$\begin{aligned} \overline{\mathbf {a}}^* = p = (1+e^{\sigma -\alpha })^{-1} . \end{aligned}$$

(20)

Thus, $\overline{\mathbf {a}}(t)$ in the above differential equation is the expected fraction of sites in phase 1 at time t in the limit of an infinite toroidal square lattice with $|\mathbb {S}_n|=n^2\rightarrow \infty$ and a realisation of the continuous-time Markov chain $\{\overline{A}(t)\}_{t\ge 0}$ is $\overline{a}(t)$. Since $\beta =0$, the probability of a site being in a given phase is independent of the phases of its neighbouring sites. Thus, we can obtain $\overline{\mathbf {b}}(t)$, the expected fraction of bonds, by simply multiplying $\overline{\mathbf {a}}(t)$, the probability of finding a randomly chosen site in phase 1, by itself, i.e.

$$\begin{aligned} \overline{\mathbf {b}}(t) = \overline{\mathbf {a}}(t)^2 \text { and } \overline{\mathbf {b}}^*=\left( \overline{\mathbf {a}}^*\right) ^2. \end{aligned}$$

(21)

3.2.2 Interactive Case with $\beta \ne 0$

If $\beta \ne 0$, then the probability of site s being in phase 1 at time $m+1$ depends on the configuration of the neighbouring sites of s at time m through $X_{N_s}(m)=\sum _{r \in N_s}X_r(m)$, the number of neighbouring sites of s in phase 1 at time m.

$$\begin{aligned} \Pr \Big \{ X_s(m+&1)=x_s(m+1) \, \vert \, X(m)=x(m) \Big \} \\&=\Pr \Big \{ X_s(m+1)=x_s(m+1) \, \vert \, X_{N_s}(m)=i \Big \} \\ =&{\left\{ \begin{array}{ll} p_i = \left( 1+e^{\sigma -\alpha -i\beta }\right) ^{-1} &{} \text { if } x_s(m+1)=1\\ 1-p_i = 1-\left( 1+e^{\sigma -\alpha -i\beta }\right) ^{-1} &{} \text { if } x_s(m+1)=0\\ 0 &{} \text { if } x_s(m+1) \notin \{0,1\} . \end{array}\right. } \end{aligned}$$

Thus the probability that the phase changes from 0 to 1 in one time step at site s given that a(m) is the total number of sites in phase 1 at time m is

$$\begin{aligned} \Pr \Big \{ X_s(m&+1)=1 , X_s(m)=0 \, \vert \, S=s, A(m)=a(m) \Big \} \\&= \sum _{i=0}^{4} \Pr \left\{ X_s(m+1)=1 , X_{N_s}(m)=i , X_s(m)=0 \right. \\&\qquad \qquad \qquad \qquad \qquad \left. \, \vert \, S=s, A(m)=a(m) \right\} \\ =\sum _{i=0}^{4}&\Pr \left\{ X_s(m+1)=1 \, \vert \, X_{N_s}(m)=i ,\right. \qquad \qquad \qquad \qquad \\&\underset{p_i}{\underbrace{\left. \qquad \qquad \qquad \qquad X_s(m)=0, S=s, A(m)=a(m) \right\} }} \\ \times&\Pr \left\{ X_{N_s}(m)=i \, \vert \, X_s(m)=0, S=s, A(m)=a(m) \right\} \\&\qquad \times \underset{(n^2-a(m))/n^2=1-\overline{a}(m)}{\underbrace{\Pr \left\{ X_s(m)=0 \, \vert \, S=s, A(m)=a(m)\right\} }}. \end{aligned}$$

Since there are $4!/((4-i)!i!)$ distinct neighbourhood configurations with i of the four nearest neighbours of site s in phase 1, one can make the following approximation for $\Pr \left\{ X_{N_s}(m)=i \, \vert \, X_s(m)=0, S=s, A(m)=a(m) \right\}$ in the above expression and obtain

$$\begin{aligned} \Pr \Big \{ X_s(m+1)=1 , X_s(m)=0 \,&\vert \, S=s, A(m)=a(m) \Big \} \\ =\sum _{i=0}^{4} p_i (1-\overline{a}(m))&\\ \qquad \qquad \times \Pr \Big \{ X_{N_s}(m)=i \,&\vert \, X_s(m)=0, S=s, A(m)=a(m)\Big \}\\ \approxeq \sum _{i=0}^{4} p_i \big (1-&\overline{a}(m)\big ) \, \begin{pmatrix}{4}\\ {i}\end{pmatrix} \, \left( \overline{a}(m)\right) ^i \, \left( 1-\overline{a}(m)\right) ^{4-i}. \end{aligned}$$

Therefore, the probability that the total number of sites in phase 1 increases by 1 in one time step is obtained by adding the probability of a transition from phase 0 to phase 1 over every uniformly chosen site s as follows:

$$\begin{aligned} \Pr \big \{ A(m+1)=a(m)+1 \, \vert&A(m)=a(m) \big \}\\ = \sum _{s \in \mathbb {S}_n} \Pr \big \{ X_s(m+1)&=1 , X_s(m)=0, S=s \, \vert \, A(m)=a(m) \big \}\\ = \sum _{s \in \mathbb {S}_n} \Pr \big \{ X_s(m+1)&=1, X_s(m)=0 \, \vert \, S=s, A(m)=a(m) \big \} \\ \times&\underset{1/n^{2}}{\underbrace{\Pr \left\{ S=s \, \vert \, A(m)=a(m) \right\} }} \\ \approxeq \sum _{s \in \mathbb {S}_n} \Bigg ( \sum _{i=0}^{4} p_i \big (1-\overline{a}&(m)\big ) \, \begin{pmatrix}{4}\\ {i}\end{pmatrix} \, \left( \overline{a}(m)\right) ^i \, \left( 1-\overline{a}(m)\right) ^{4-i} \Bigg ) \frac{1}{n^2}\\ = \big (1-\overline{a}&(m)\big ) \sum _{i=0}^{4} p_i \, \begin{pmatrix}{4}\\ {i}\end{pmatrix} \, \left( \overline{a}(m)\right) ^i \, \left( 1-\overline{a}(m)\right) ^{4-i} . \end{aligned}$$

Dividing both sides of the equality that defines the above event by $n^2$, we get

$$\begin{aligned} \Pr \Big \{ \overline{A}(m+1)=\overline{a}(m)&+1/n^2 \, \vert \, \overline{A}(m)=\overline{a}(m) \Big \} \\ \approxeq&\left( 1-\overline{a}(m)\right) \sum _{i=0}^{4} p_i \, \begin{pmatrix}{4}\\ {i}\end{pmatrix} \, \left( \overline{a}(m)\right) ^i \, \left( 1-\overline{a}(m)\right) ^{4-i}. \end{aligned}$$

By an analogous argument, we can obtain the probability that $\overline{A}(m+1)$ decreases by $1/n^2$ as

$$\begin{aligned} \Pr \Big \{ \overline{A}(m+1)=\overline{a}(m)&-1/n^2 \, \vert \, \overline{A}(m)=\overline{a}(m) \Big \} \\ \approxeq \,&\,\overline{a}(m) \sum _{i=0}^{4} \left( 1-p_i \right) \, \begin{pmatrix}{4}\\ {i}\end{pmatrix} \, \left( \overline{a}(m)\right) ^i \, \left( 1-\overline{a}(m)\right) ^{4-i} . \end{aligned}$$

Using the same limiting approximation in the previous section, we can obtain the following differential equation approximation for $\overline{\mathbf {a}}=\overline{\mathbf {a}}(t)$ one obtains:

$$\begin{aligned} \dot{\overline{\mathbf {a}}}\quad = \quad&\frac{d}{dt}\overline{\mathbf {a}}(t)\\ \quad = \quad&(1-\overline{\mathbf {a}}) \left( p_0 \, (1-\overline{\mathbf {a}})^4 + p_1 \, 4 \overline{\mathbf {a}} (1-\overline{\mathbf {a}})^3 \right. \\&\left. + p_2 \, 6 \overline{\mathbf {a}}^2 (1-\overline{\mathbf {a}})^2 + p_3 \, 4 \overline{\mathbf {a}}^3 (1-\overline{\mathbf {a}}) + p_4 \, \overline{\mathbf {a}}^4 \right) \\&-\,\overline{\mathbf {a}} \left( (1-p_0)\,(1-\overline{\mathbf {a}})^4 + (1-p_1)\, 4\overline{\mathbf {a}}(1-\overline{\mathbf {a}})^3 \right. \\&\left. +\,(1-p_2) \, 6 \overline{\mathbf {a}}^2 (1-\overline{\mathbf {a}})^2 + (1-p_3) \, 4 \overline{\mathbf {a}}^3 (1-\overline{\mathbf {a}}) \right. \\&\left. +\,(1-p_4) \, \overline{\mathbf {a}}^4) \right) . \end{aligned}$$

This simplifies after factoring and extracting coefficients of $\overline{\mathbf {a}}$ as follows:

$$\begin{aligned} \dot{\overline{\mathbf {a}}}(t)&= \quad p_{0} -{\left( 4 \, p_{0} - 4 \, p_{1} + 1\right) } \overline{\mathbf {a}} + 6 \, {\left( p_{0} - 2 \, p_{1} + p_{2}\right) } \overline{\mathbf {a}}^{2} \nonumber \\&\quad -4 \, {\left( p_{0} - 3 \, p_{1} + 3 \, p_{2} - p_{3}\right) } \overline{\mathbf {a}}^{3} \nonumber \\&\quad + {\left( p_{0} - 4 \, p_{1} + 6 \, p_{2} - 4 \, p_{3} + p_{4}\right) } \overline{\mathbf {a}}^{4} . \end{aligned}$$

(22)

We can understand Eq. (22) directly as a quartic polynomial in $\overline{\mathbf {a}}$ whose coefficients are given by an alternating binomial series corresponding to the increase and decrease in $\overline{\mathbf {a}}$ based on a combinatorial averaging over the transition diagram of site configurations at the four nearest neighbours of a given site.

We now focus on the stability of the fixed points of the evolution equation for the volume of fraction of solid $\bar{a}$ (Eq. 22). In the left panel of Fig. 14, we present three different stability scenarios for the fixed points of Eq. (22) in the $(\tilde{\sigma },\beta )$ plane: (i) In the blue-shaded region, the right-hand side of Eq. (22) has four real roots and only one of them is in [0, 1]; this fixed point is stable. (ii) In the yellow region, starting at point (2.589145, 1.2945725), we have four distinct real roots with three of them in [0, 1]. Only one of the three distinct real roots is an unstable fixed point, while the other two roots are stable fixed points. This naturally corresponds to a family of pitchfork bifurcations and the associated hysteresis depending on where the system is initialised from. (iii) The unshaded region in the left panel of Fig. 14 corresponds to the parameter space where the quartic discriminant $\Delta _4$ is negative and thus implying the existence of two real roots (with one of them in [0, 1], stable fixed point) and two complex conjugate roots.

The real roots and their derivatives over each $(\tilde{\sigma },\beta )$ in a grid of parameter values from $[-8, 12]\times [-4, 4]$ were obtained through interval analytic methods (Hofschuster and Krämer 2003).

Fig. 14

Four real roots of the quartic occur in the shaded regions (blue and yellow) over $\tilde{\sigma }=\sigma -\alpha$ and $\beta$ is shown in the left panel. The black line is $\beta =\tilde{\sigma }/2$ started at (2.589145, 1.2945725). The parameter space with only three distinct real roots in [0, 1] is shown in the right panel

Figure 15 shows the set of fixed points $\overline{\mathbf {a}}^*$ of the dynamical system as a function of $(\tilde{\sigma },\beta )$. The parameter space corresponding to the central shaded region of Fig. 14 containing the line $\beta =\tilde{\sigma }/2$ is evident in Fig. 15 with three fixed points in [0, 1]. The pitchfork bifurcations along the plane $\tilde{\sigma }=2\beta$ or $\beta =\tilde{\sigma }/2$ determined by the non-negative sign of the cubic discriminant along the black line in Fig. 14 is displayed to highlight the dynamics with one unstable fixed point at 1/2 and two other stable fixed points that are equidistant on either side of 1/2.

We are interested in varying the externally applied stress $\sigma$ for a given material characterised by fixed rheological parameters $\alpha$ and $\beta$. This amounts to varying $\tilde{\sigma }$ for a fixed $\beta$ since the fixed $\alpha$ is absorbed into $\tilde{\sigma }=\sigma -\alpha$. The asymptotic dynamics when we apply a constant external stress for a long period of time are given by the fixed points $\overline{\mathbf {a}}^*$ in Fig. 15. Note that the ODE model for $\beta \ne 0$ is only in qualitative agreement with $\overline{\mathbf {a}}(t)$, the expected volume fraction of the unyielded material at time t. This is because we are ignoring the dependent statistic $\overline{\mathbf {b}}(t)$, the expected fraction of bonds or pairs of neighbouring unyielded material at time t. Despite this simplification, as we will see through this section, there is qualitative agreement between the ODE and the Gibbs simulations presented in Sect. 3.1. Furthermore, an admittedly ad hoc correction of the ODE through a translation of the vector field by $(\alpha _0,\beta _0)$ even improves the quantitative approximation. We postpone a formal quantitative approximation of the ODE using perturbation theoretic methods to the future and focus here on obtaining insights from the Gibbs sampler that is in qualitative agreement with the ODE approximation.

Fig. 15

The fixed points $\overline{\mathbf {a}}^*$ as a set-valued function of the parameters $\tilde{\sigma }=\sigma -\alpha$ and $\beta$. The blue, black and azure points are the stable fixed points, while the red and green points are the unstable fixed points of the system. There is a pitchfork bifurcation along $\tilde{\sigma }=2\beta$ that starts at (2.589145, 1.2945725) where the fixed point at 0.5 becomes unstable with two stable fixed points on either side

3.2.3 Comparison Between Microscopic Gibbs Field Model Described in Sect. 3.1 and ODE Approximation Under Varying Stress

The energy of X(t), the random site configuration at time t, depends on two of its highly correlated statistics: $\overline{A}(t)$, the random fraction of gelled sites at time t, and $\overline{B}(t)$, the random fraction of connected sites at time t. One of our primary interests is to study $\overline{A}(t)$ and $\overline{B}(t)$ as X(t) is under the influence of time-varying externally applied stress $\sigma (t)$. Using Monte Carlo simulations from Algorithm 2 in Sainudiin et al. (2015a) of the time-inhomogeneous Markov chain $\{X(m)\}_{m=0}^{M\underline{h}}$, under a time-dependent stress $\sigma$ ramp, we can obtain multiple independent trajectories of $\overline{A}(\sigma )$, the fraction of gelled sites as a function of the external stress $\sigma$. This is to emulate conditions of an unsteady forcing during macroscopic rheological measurements. In the following, h is the average hits per site in the Gibbs sampler algorithm and we define it also as the characteristic forcing time $t_0$ for the stress ramp in our ODE simulations. We set $h=1000$ in order to reach steady state for each value of $\sigma$. In Fig. 16, the trajectories are shown as thin lines and the curves for the ODE approximation have the $\square$ symbol on them. Note the reversibility of the response of the material when $\beta \in \{0,1\}$ (top row of Fig. 16) upon increasing/decreasing applied stresses. The microscopic model and the ODE approximation quantitatively agree quite well when $\beta <\beta _c$ ($\beta _c \approx 1.3$), the threshold for three fixed points in [0, 1] for the ODE model. As we increase $\beta$ beyond the aforementioned threshold $\beta _c$, we see that irreversible behaviour in the material appears and the comparison between the two models (discrete and continuous) is only qualitative in nature. This is due to the fact that our ODE approximation only models $\overline{\mathbf {a}}$, instead of modelling the dependent pair $(\overline{\mathbf {a}},\overline{\mathbf {b}})$ that is sufficient for the energy, see Sect. 3.1. This effect can also be seen if we compare the right panel of Fig. 14 with Fig. 10c. Clearly, the light region of Fig. 10c corresponds to the yellow region where the hysteresis is always present. The main discrepancy is the value of $\beta _c$. In the ODE approximation, the calculated value is $\beta _c\approx 1.3$, whereas from the Gibbs sampler simulations one obtains $\beta _{c}^{GS}\approx 1.5$. As mentioned above this difference is due to the fact that in the ODE approximation all bond interactions between neighbours have been disregarded. Further details on improving the agreement between the predictions of the approximating nonlinear dynamical system model with those of the Gibbs field model are given in Sect. 4.4 and in Fig. 9 of Sainudiin et al. (2014).

As a qualitative remark, one can note that even in the presence of strong interactions $\beta >\beta _c$, both models predict an increase of the steepness of the solid–fluid transition (defined as the slope of the dependence $\bar{a}(t)$ on $\sigma$ around the point where $\bar{a} \approx 1/2$).

Fig. 16

Gibbs field and ODE approximation simulations with $\alpha =8$ and $\beta \in \{0,1,3\}$. The stress was increased from 0 to 25 in units of 0.01 and decreased back to 0 with a holding time of $t_0=1000$ (nearly asymptotic state for each distinct stress) as the site configuration varied from $\mathbf {1}$ to $\mathbf {0}$ and then back to $\mathbf {1}$. The curves with the symbol ($\square$) are the ODE simulations

3.2.4 Comparison Between Model by Putz and Burghelea Putz and Burghelea (2009) and ODE Approximation

In this section, we will consider the model developed by Putz and coworkers (Putz and Burghelea 2009; Moyers-Gonzalez et al. 2011b). As already highlighted in Sect. 2, this model is phenomenological in the sense that, unlike the Gibbs field model presented in Sect. 3.1 it is not derived from first principles. In this type of modelling, one mimics the behaviour of the microstructure through the definition of a macroscopic structural variable with range in [0, 1], where 0 means completely unstructured or fluid and 1 means completely structured or solid. As explained in Sect. 2, the structural variable $a_p$ satisfies a kinematic equation and usually depends explicitly on the stress and/or rate of strain. In the case of the model by Putz and Burghelea (2009), we have

$$\begin{aligned} \frac{d}{dt}a_p(t)= & {} k_r\left[ 1-\tanh \left( \frac{\sigma -\sigma _y}{w}\right) \right] (1-a_p(t))\nonumber \\- & {} k_d\left[ 1+\tanh \left( \frac{\sigma -\sigma _y}{w}\right) \right] a_p(t), \end{aligned}$$

(23)

where $k_r$ is the rate of recombination of microstructural units, $k_d$ is the rate of destruction of the solid phase, $\sigma _y$ is the yield stress and w is a constant that controls how steep the change in the microstructure from solid to fluid and fluid to solid is.

In Fig. 17, we present the simulations of Eqs. (22) and (23) for three characteristic forcing times $t_0$. As expected we have very good agreement between the models. This could be considered as a qualitative “proof” that the phenomenological models can actually approximate the behaviour of the microscopic models derived from first principles.

Fig. 17

Comparison between ODE approximation and the model by Putz and Burghelea (2009) detailed in Sect. 2 for different holding times $t_0$. ODE model with $\alpha =8$ and $\beta =1$, the model by Putz and Burghelea (2009) with $k_d=k_r=0.3$, $w=0.5$ and $\sigma _y=10$. Full lines are the ODE approximation and broken lines the model by Putz and Burghelea (2009)

3.2.5 Determination of the Yield Point in the Limit of a Steady-State Forcing

A reliable estimation of the yield point is important to many practical applications involving yield stress materials. This is typically done by fitting steady-state rheological measurements with models with various degrees of complexity ranging from the mathematically simple and classical Herschel–Bulkley correlation up to structural models. Thus, it appears natural to attempt in the following to obtain an estimate of the yield point for the case of a steady-state forcing from the nonlinear dynamical system model presented herein.

To get an approximation for the yield point $\sigma _y$ during a steady-state forcing process, we will make the assumption (well supported by the results presented in Figs. 12 and 17) that, corresponding to the yield point, the absolute value of the slope of the dependence $\bar{a}^*(\sigma )$ passes through a maximum:

$$\begin{aligned} \left| \frac{d \bar{a}^*}{d \sigma } \right| \overset{\sigma \approx \sigma _y}{\longmapsto } Max. \end{aligned}$$

(24)

For simplicity, let us focus first on the non-interacting case, $\beta = 0$. From Eq. (20), one can readily show that the condition given in Eq. (24) reduces to $\sigma _y = \alpha$. Thus, in the non-interactive case, the yield point obtained during a steady-state stressing practically coincides with the site-specific threshold $\alpha$ of the Gibbs field model.

Fig. 18

Dependence of the approximate yield stress shifted by the site-specific threshold $\tilde{\sigma }_y = \sigma _y -\alpha$ on the interaction parameter $\beta$. The dashed line is $\tilde{\sigma }_y = \beta$, and the dash-dotted line is $\tilde{\sigma }_y = 2 \beta$. The circles mark the critical point corresponding to $\beta _c \approx 1.3$

We now consider the interactive case $\beta \ne 0$. To a leading order in $\bar{a}^*$ and assuming that around the yield point $\bar{a}^* \approx 1/2$, it can be shown using Eq. (22):

$$\begin{aligned} \left. \frac{d \bar{a}^*}{d \tilde{\sigma }} \right| _{\sigma \approx \sigma _y} \approx e^{\tilde{\sigma }} \left[ \frac{1}{\left( 1+ e^{\tilde{\sigma }} \right) ^2}-2 \frac{e^{-\beta }}{\left( 1+ e^{\tilde{\sigma }} e^{-\beta } \right) ^2} \right] . \end{aligned}$$

(25)

The implicit dependence of the approximate yield stress $\tilde{\sigma }_y$ on the interaction parameter $\beta$ may be obtained by solving numerically $\left| \frac{d \bar{a}^*}{d \tilde{\sigma }}\right| = 0$. The result is presented in Fig. 18. For interactions weaker than the critical threshold $\beta _c$, the apparent yield stress scales as $\tilde{\sigma }_y = \sigma -\alpha = \beta$ (the dash-dotted line in Fig. 18). Beyond this threshold, the scaling becomes steeper, $\tilde{\sigma }_y = \sigma -\alpha = 2 \beta$ (the dashed line in Fig. 18). To conclude this part, the yield stress assessed via steady-state controlled stress ramps is (according to our model) expected to depend linearly on both the site-specific threshold $\alpha$ which may be intuitively understood as a measure of the strength of the microscopic constituents of the fluid and the strength $\beta$ of their interaction and the slope of this behaviour switches when the strength of the interaction passes through the threshold $\beta = \beta _c$.

In Fig. 19, we investigate the dependence of right-hand side of Eq. (25) with respect to $\tilde{\sigma }$ (left panel) and with respect to $\beta$ (the right panel).

Fig. 19

a Dependance of the slope of $\bar{a} ^*$ on the applied stress on the yield stress for various values of $\beta$ ranging from 0 to 2 ($\beta$ increases from bottom to top). b Dependance of the maximum value of the slope $\left. \frac{d \bar{a}^*}{d \tilde{\sigma }} \right| _{\sigma \approx \sigma _y}$ given by Eq. 24 calculated around the yield point on the interaction parameter $\beta$

Regardless of the value of the interaction parameter, the stress dependence of the slope passes through a local maximum marked by a full symbol in Fig. 19a. As previously explained, this may be considered as an indicator of the yield point. While $\beta$ increases, the location of this maximum shifts towards larger stress values as already illustrated in Fig. 18. The value of this maximum slope increases monotonically with $\beta$, as shown by the dashed line in Fig. 19a. As we approach $\beta _c$, the slope diverges Fig. 19b. This is consistent with the fact that our steady solution becomes discontinuous as a function of $\tilde{\sigma }$. Recall that we have a pitchfork bifurcation with stable fixed points $\{0,1\}$; hence, the value of $\sigma _y$ is not unique and depends on the initial condition.

3.2.6 Description of Linear Controlled Stress Flow Ramps

To demonstrate the practical usefulness of our approach, we focus in the following on the description of an experimentally measured data set acquired during a linear controlled stress flow ramp with a $0.2 \%$ (wt) aqueous solution of Carbopol 980, the symbols in Fig. 20. The characteristic forcing time for the rheological test was $t_0=2$ s, and the empty/full symbols refer to the increasing/decreasing branch of the stress ramp. As already pointed out, the control parameter of our model is an energy supplied to the lattice rather than a true stress. Yet, in order to describe a one-dimensional data set, one can interpret the stress as the energy supplied per unit volume of material and attempt to couple the evolution equation for the number of sites in a gelled state to a constitutive relation.

To describe the experimentally measured flow ramp, Eq. (22) describing the evolution of the microstructural parameter $\bar{a}(t)$ is complemented by a Maxwell-type thixoelastic constitutive equation (as in the case of the model by Putz and Burghelea (2009) discussed in Sect. 2):

$$\begin{aligned} \frac{\eta (\dot{\gamma })}{G}\bar{a} \frac{d \sigma }{ dt} +\sigma = \eta (\dot{\gamma }) \dot{\gamma }, \end{aligned}$$

(26)

where G is the elastic modulus, $\dot{\gamma }$ is the rate of shear and $\eta (\dot{\gamma }) = K \dot{\gamma }^{N-1} + \sigma _y\frac{1-e^{-m \left| \dot{\gamma }\right| }}{\left| \dot{\gamma }\right| }$ is a Papanastasiou regularised Herschel–Bulkley viscosity function.

Fig. 20

Flow curve measured for increasing (empty symbols) and decreasing (full symbols) values of the applied stress. The full line is a fit by the model by Putz and Burghelea (2009), and the dashed line is the prediction of the nonlinear dynamical system model

The best fits using both the model by Putz and Burghelea (2009) and the current approach are presented in Fig. 20 as full and dashed lines, respectively.

The fit parameters for the model (the full line in Fig. 20) are $\sigma _y^u=66.2$ Pa, $\sigma _y^d=63.45$ Pa, $k_d^u = k_d^d=0.1 \mathrm{s}^{-1}$, $k_r^u=0.263~\mathrm{s}^{-1}$, $k_r^d=0.95~\mathrm{s}^{-1}$, $w_u=0.93$ Pa, $w_d=0.143$ Pa, $N_u=N_d=0.31$, $K_u=24.33~\mathrm{Pa s}^N$, $K_d = 27.12~\mathrm{Pa s}^N$, $G_u = 2036$ Pa and $G_d = 457$ Pa.

The fit parameters for the nonlinear dynamical system approach (the dashed line in Fig. 20) are $\sigma _y^u=64.38~\mathrm{Pa}$, $\sigma _y^d=63.48~\mathrm{Pa}$, $\alpha _u = 64.72$, $\alpha _d = 62$, $\beta _u = 0.73$, $\beta _d = 0.98$, $N_u = 0.31$, $N_d = 0.3$, $K_u=26.21~\mathrm{Pa s}^N$, $K_d = 27~\mathrm{Pa s}^N$, $G_u = 3929$ Pa and $G_d = 451$ Pa.

The goodness of the fit by the current model is comparable to that by the model (the PMM, see Sect. 2) which demonstrates the practical usefulness of this approach. It is equally worth noting that, for the Carbopol gel used in the rheological test illustrated in Fig. 20, the interactive parameter $\beta$ obtained for each branch of the stress ramp is smaller than the critical value $\beta _c \approx 1.3$ that defines the cross-over from a reversible to irreversible yielding scenario. This indicates that the Carbopol gels fall into the class of weakly interactive viscoplastic materials that show no thixotropic effects in the limit of a steady-state forcing.

To conclude this section, a fundamental understanding of the yielding of a viscoplastic material may be obtained via a probabilistic approach developed using the main tools of the Statistical Physics similar to the Ising model of magnetisation. Unlike the phenomenological approaches that typically involve a rather large number of parameters some of which have an unclear physical meaning (and, consequently, are difficult to assess experimentally), this approach involves only two internal parameters: a site-specific threshold and the strength of interaction of neighbouring building blocks of the viscoplastic material. These two parameters are responsible for a number of experimentally observed features of the solid–fluid transition: its onset (the yield stress), its reversibility upon increasing/decreasing stresses and its steepness.

4 Viscoplasticity and Hydrodynamic Stability

The flows discussed so far through this chapter were hydrodynamically stable and the only source of nonlinearity in the momentum equation was related to the constitutive relation describing the viscoplastic material. The aim of this section is to introduce the reader into the hydrodynamic stability of yield stress materials. We discuss two distinct types of instabilities involving viscoplastic materials. In Sects. 4.1, 4.2, we discuss the inertial instability of flows of a viscoplastic material in a pipe flow and in a plane channel flow, respectively. In Sect. 4.3, we discuss a low Reynolds number hydrodynamic instability triggered by a fast chemical reaction occurring at the interface between two fluids which locally creates a yield stress material or, in other words, a strong stratification of stresses.

4.1 Transition to Hydrodynamic Turbulence in a Shear-Thinning Physical Gel

In this section, we summarise some key results of an experimental study of the laminar, transitional and turbulent flows of a viscoplastic fluid in a cylindrical pipe (Hagen–Poiseuille flow). For a more comprehensive account of the main results, the reader is referred to Güzel et al. (2009). As compared to the laminar flows previously studied through this chapter, such flows are expected to be significantly more complex as two sources of nonlinearity are present in the Navier–Stokes equation: inertial (related to large Reynolds numbers) and rheological (related to the dependence of the stresses on the rate of strain).

The motivation of studying the hydrodynamic stability of yield stress fluids is threefold:

• 1. Fluids of shear-thinning type with a yield stress abound in industrial settings, as well as some natural ones. The particular motivation here comes from both the petroleum industry and the pulp and paper industry, where design/control of the inherent processes often requires knowledge of the flow state at different velocities. Similar fluid types and ranges of flows occur in food processing, polymer flows, and in the transport of homogeneous mined slurries. Although many of these industrial fluids exhibit more complex behaviour (e.g. thixotropy, viscoelasticity, etc.), as noted by Bird et al. (1977), the shear-dependent rheology is often the dominant feature.

• 2. In line with the above, there is a demand from industrial application to predict the Reynolds number ($Re=UD/\nu$, where U is the average velocity, D is the diameter of the pipe and $\nu$ is the kinematic viscosity), or other bulk flow parameter, at which transition occurs, for a range of fluid types, so that different frictional pressure closures may be applied to hydraulics calculations above/below this limit. One of the such earliest attempts, and probably still the most popular, was that of Metzner and Reed (1955). Perhaps, the most obvious weakness with such phenomenological formulae is that turbulent transition occurs over a wide range of Reynolds numbers and not at a single number. For example, in careful experiments, Hof et al. (2003) report retaining laminar flows in Newtonian fluids up to $Re = 24 000$, whereas the common observation of transition initiating in pipe flows is at $Re \approx 2000$. Thus, there is a difficulty with interpreting the predictions of phenomenological formulae, many of which we note were either formulated before a detailed understanding of transitional phenomena has developed.

• 3. A third and most important motivation of such study is of a scientific nature. Since Reynolds’ famous experiment (Reynolds 1883), transition in pipe flows has been an enduring unsolved problem in Newtonian fluid mechanics. It is thus natural that there have been far fewer studies of non-Newtonian fluids in this regime, either experimental or numerical/theoretical. The intellectual challenge is related to dealing with two sources of strong nonlinearity in the momentum equation discussed in the Introduction: inertial and rheological—coming from nonlinearity of the stress rate of strain relationship. The existing studies that have been conducted for shear-thinning viscoplastic fluids leave a large number of intriguing questions unanswered. In the first place, experimental studies by Escudier and Presti (1996) using Laponite suspensions and by Peixinho et al. (2005b) using Carbopol^® solutions have revealed interesting flow asymmetries in the mean axial velocity profile during transition, which have been largely unexplained. These have been summarised by Escudier et al. (2005).

4.1.1 Experimental Setup and Procedures

All the results we report herein are from tests performed in a $L=10$-m-long flow loop with an inner diameter of $2R=50.8$ mm. The setup is illustrated schematically in Fig. 21. The flow is generated by a variable-frequency-driven screw pump fed to a carbon steel inlet reservoir $\mathbf {R_{1}}$ of approximately 120 L capacity to an outlet reservoir $\mathbf {R_{2}}$ of the same capacity. The pump can provide a maximum flow rate of ${\approx }22~\mathrm{l/s}$, which is equivalent to a maximal mean flow velocity of ${\approx }10~\mathrm{m/s}$. Two honeycomb sections are placed inside the reservoir $\mathbf {R_{1}}$ before the tube inlet in order to suppress any swirl or other fluid entry effects. We used a Borda style entry condition in which the pipe extended backwards approximately 50 cm into the tank. Two honeycomb elements were inserted into this section. The fluid reservoir $\mathbf {R_{2}}$ is pressurised to damp mechanical vibrations induced by the pump motor and a flexible hose is used between the pump and reservoir in order to diminish flow pulsations.

Fig. 21

Schematic view of the experimental setup: $\mathbf {R_{1,2}}$—fluid reservoirs, P—pump, FM—flowmeter, $\mathbf {PT_{1,2}}$—pressure transducers, FT—fish tank, CCD—digital camera, PB—laser Doppler velocimetry probe, PMT—photomultiplier, BSA—burst spectrum analyzer

The flow structure has been investigated using the laser Doppler velocimetry (LDV) technique. A detailed description of the LDV optical arrangement is given in Güzel et al. (2009). Two pressure transducers ($\mathbf {PT_{1,2}}$) are located near the inlet and outlet of the flow channel (Model 210, Series C from www.gp50.com). These are bonded strain gauge transducers with internal signal conditioning to provide a Vdc output signal in direct proportion to the input pressure. The accuracy of each transducer is $0.02\%$ of the full scale, and they were calibrated with an externally mounted pressure gauge. Pressure drop readings $\Delta p$ were averaged over 150 s and used to estimate the radius of the plug according to

$$\begin{aligned} r_p=2L\frac{ \sigma _y}{R \Delta p}. \end{aligned}$$

(27)

Flow rates were estimated using two methods: (i) using an electromagnetic flowmeter (FM) installed near the outlet reservoir, as shown in Fig. 21; (ii) by numerically integrating the measured axial velocity profiles. The latter estimate is used to calculate the relevant flow parameters reported through this section. The transversal profiles of the axial velocity have been measured at a position $L_m = 108 D$ downstream where the flow is fully developed (corresponding to a Reynolds number $Re \approx 3000$ the entry length was estimated $L_e \approx 100D$).

The Reynolds number can be defined in a number of ways for a non-Newtonian fluid. Here, we define a generalised number that accounts for the shear thinning of the solution across the pipe by

$$\begin{aligned} Re_G=\frac{4 \rho }{R} \int _0^R \frac{\bar{u}(r)}{\eta \left[ \dot{\gamma }(r)\right] }rdr, \end{aligned}$$

(28)

where $\rho$ and $\eta$ are the density and the effective viscosity of the fluid. The latter depends on the strain rate of the base flow $\dot{\gamma }(r)$ which is calculated locally from the transversal profile of the time-averaged axial velocity $\bar{u}(r)$. As a yield stress material, we have used several aqueous solutions of Carbopol^® 940. As a first approximation, we consider here for simplicity a Herschel–Bulkley constitutive relationship, $\eta = \sigma _y \dot{\gamma }^{-1} + K \dot{\gamma }^{N-1}$. As already discussed in Sects. 1 and 2, the Herschel–Bulkley constitutive relationship does not accurately describe the yielding of a Carbopol^® gel. In our context, the main problem arises from the term $\eta (\dot{\gamma })$ which around the solid–fluid transition diverges. The experimental measurements presented in Sect. 1 indicate that prior to yielding the viscosity is very large but finite. The Herschel–Bulkley correlation, however, remains useful to get an estimate for the yield stress.

4.1.2 Transition to Turbulence in the Pipe Flow of a Shear-Thinning Yield Stress Fluid: Phenomenological Observations

Before proceeding to the main findings, it is instructive to first examine representative transversal profiles of the time-averaged velocity. To this end, we plot transversal profiles of the time-averaged velocity $\bar{u}$ as a function of $Re_{G}$, see Fig. 22 measured with a $0.1\%$ Carbopol^® solution at various $Re_G$. At each radial position, over one-hundred thousand instantaneous velocity measurements were used in the ensemble average and the confidence interval for each point is very small. It should be noted that the results have been made dimensionless by scaling the ensemble average with the centreline velocity $u_c$. Under laminar conditions, that is, with $Re_G < 1700$, the fully developed laminar profiles are included in these graphs as the solid lines. This was performed in order to ascertain the validity of our results. For the higher flow rates, we present cases for both transitional and turbulent flows. Dashed lines are drawn to highlight an apparent asymmetry in the measurements. The dashed lines were constructed by averaging the data at equivalent radial positions on either side of the central axis. The asymmetry is apparent and disappears once a fully turbulent flow regime is achieved. It is worth noting that the asymmetry is systematic, i.e. these data were taken from time-averaged data and the asymmetry is consistently in the same part of the pipe for the same fluid. This persistent flow asymmetry runs contrary to the intuitive notion that transitional flow structures, when ensemble averaged over a suitably long time, should occur with no azimuthal bias. A similar asymmetry has been reported by other groups in their experiments (Escudier and Presti 1996; Peixinho et al. 2005b; Escudier and Presti 1996). The initial reaction to this rather unexpected flow asymmetry was to look for and eliminate any directional bias in the apparatus or in the flow visualisation technique. However, even after extensive precautions the asymmetry still persists and is fully reproducible in subsequent tests and for several concentrations of Carbopol^®(a more comprehensive discussion and additional data are presented in Güzel et al. 2009).

Fig. 22

The transversal profiles of the time-averaged velocity $\bar{u}$ for $0.1\%$ (wt) Carbopol: a $Re_{G}$=378 ($\bigcirc$), 937 ($\square$), 1160 ($\bigtriangleup$), 1735 ($\bigtriangledown$) and 2920 ($\vartriangleleft$) b $Re_{G}$=397 ($\bigcirc$), 914 ($\square$), 2001 ($\bigtriangleup$), 2238 ($\bigtriangledown$) and 2612 ($\vartriangleleft$). These data are from replicate tests obtained from similar experimental conditions

To characterise the transition to turbulence in a Carbopol^® gel, the turbulence intensity is monitored at various radial positions r/R. The turbulence intensity is defined as $I = \frac{u_{rms}}{\bar{u}}$ where $u_{rms}$ stands for the root mean square of the fluctuations of the point-wise velocity.

Fig. 23

Turbulence intensity measured at $r/R=0$ (circles), $r/R=-0.75$ (up triangles) and $r/R=0.75$ (down triangles) for a $0.1\%$ (wt) solution of Carbopol^® 940

After a rapid increase through transition, the turbulent intensity relaxes as we enter the fully developed turbulent regime, as shown in Fig. 23. An important experimental observation is that transition does not involve a simultaneous and sharp increase in turbulent intensity across the pipe radius. Instead, one may notice in Fig. 23 that the turbulent intensity begins to increase at $r/R=\pm 0.75$ at markedly lower generalised Reynolds numbers than at the centreline. This observation was systematically reproduced for several other Carbopol^® solutions indicating that this transition scenario is rather universal.

To get additional insights into the evolution of the flow structure around the onset of the laminar–turbulent transition, we resort to a qualitative imaging of the flows. For this purpose, the flow was seeded with a minute amount of Kalliroscope reflective flakes. Thus, turbulent “puffs” passing the point of observation cause mixing of the tracer particles which result in “grainy” flow image due to local changes in mean orientation (i.e. reflectance) of the seeding particles. Instant puff images obtained for a 0.075% (wt) solution of Carbopol^® at a $Re_G$ close to the onset of the instability are illustrated in Fig. 24. With these images, we attempted to characterise the size and velocity of the leading and trailing edges of the puff by an object tracking method. We have also produced spatiotemporal plots of the images. Here, the images are filtered and the variation of greyscale intensity at one axial position is reported as a function of time, see Fig. 25. What is clear in this sequence of images is that an asymmetry is once more evident. As compared to the Newtonian case (data not shown here but shown in Fig. 10 of Güzel et al. 2009), the leading edge of the puff is elongated and is located in the vicinity of the wall. Moreover, the puffs observed with the Carbopol^® solution will spread axially at a significantly slower rate than those typically observed with Newtonian fluids. Another observation for the case of a Carbopol^® solution is that the elongation of the leading edge gets smaller with decreasing concentrations of Carbopol^®, i.e. the tip observed in Fig. 25 is both reduced in size and located closer to the centre line of the pipe.

Fig. 24

Instant puff images taken for $0.075 \%$ solution of Carbopol^® 940 at $Re_G = 1850$ at different time instants: a $t =130$ ms, b $t =225.5$ ms, c $t =255.5$ ms, d $t =320$ ms, e $t =422.5$ ms, f $t =447.5$ ms, g $t =497.5$ ms, h $t =600$ ms, i $t =755$ ms, j $t =1117.5$ ms, k $t =1155$ ms and l $t =1187.5$ ms

Fig. 25

Space-time plot measured with a 0.075%(wt) Carbopol^® at $Re_G=1850$ a obtained from raw images b obtained from filtered, background subtracted and binarised images. The puff length is ${\approx }1.69\,\mathrm{m}$. The images sequence consisted of 320 frames

To summarise our observations, we measured the axial velocity as a function of radial position using the LDV for several aqueous solutions of Carbopol^® solutions undergoing Hagen–Poiseuille flow within a wide range of Reynolds numbers. We find that for all the fluids tested there exists a persistent asymmetry in the velocity profiles present during transition. Symmetrical flows were found for both laminar and fully turbulent cases. These observations were confirmed using high-speed imaging. No physical explanation is given at this point. We do, however, attempt to quantify the transition more precisely by presenting a more in-depth statistical analysis of these results. To this is dedicated the next section.

4.1.3 Statistics of Weak Turbulence

Landau and Lifschitz indicate that inertially turbulent flows are traditionally characterised by random fluid motion in a broad range of spatial and temporal scales (Landau and Lifschitz 1987). We have attempted to characterise these relevant scales using several statistical measures as indicated by Frisch (1995).

A first statistical measure is the Eulerian autocorrelation of the velocity defined by

$$\begin{aligned} C(t) = \frac{\langle u(t) u(t+\tau ) \rangle _{\tau }}{u_{rms}^2} \end{aligned}$$

(29)

and determined using the LDV data. This quantity is a measure of the time over which the instantaneous velocity u(t) is correlated with itself. In other words, C(t) is bounded by unity as t approaches zero and by zero as $t \rightarrow \infty$, because a process becomes un-correlated with itself after a long time.

We report measurements of the temporal autocorrelation function as a function of both $Re_G$ and the radial position in the pipe, Fig. 26. Before we proceed to interpret these figures, we must spend some time explaining how the data is represented. Each figure is given as three panels, i.e. at three different radial positions. Within each panel, four data sets are presented representing four different Reynolds numbers. The data series labelled $\mathbf {(1)}$ and $\mathbf {(2)}$ represent laminar flow while $\mathbf {(3)}$ is in the transitional regime and $\mathbf {(4)}$ in a turbulent regime. With regards to $\mathbf {(1)}$, which corresponds to the lowest $Re_G$, in each of the panels the velocity signal is probably dominated by high-frequency noise which results in a fast decay of C(t) with a characteristic decay time which we find to be of the order of the inverse data rate of the LDV signal. Proceeding through $\mathbf {(4)}$, we find the fully turbulent state characterised by rapid decay of the autocorrelation to the noise level.

Fig. 26

Correlation functions measured for a $0.1\%$ solution Carbopol^® at three different radial positions: a $r/R=-0.75$ b $r/R=0$ c $r/R=0.75$. The data sets in each panel are $\mathbf {(1)}$ $Re_G=397$, $\mathbf {(2)}$ $Re_G=914$, $\mathbf {(3)}$ $Re_G=2238$, $\mathbf {(4)}$ $Re_G=3309$

A striking difference is found in curve $\mathbf {(2)}$ in comparison to the other curves. We observe that there are plateaus in these curves, for some radial positions for each of the fluids, e.g. at $C(\tau )\sim 0.4$ for both $r/R = {\pm }0.75$. Although this data was obtained in a region which we define as laminar, it is clear that there are some weakly correlated structures at this radial position in the pipe. For the Newtonian fluid, the plateau in the autocorrelation is at a lower value than for the non-Newtonian fluids and is visible also at the centreline (data are not shown here but detailed in Güzel et al. 2009). For the case of the Carbopol^® solution illustrated in Fig. 26, the plateau is strongly attenuated at the centreline but evident at the radial positions $r/R = {\pm }0.75$. Using Taylor’s frozen flow hypothesis (Taylor 1938), we may estimate the axial length scale of these structures to be ${\sim }10^{-1}$ m, being longer for the Newtonian fluids than for the non-Newtonian fluids (again, for a full account of this issue the reader is referred to Güzel et al. 2009). This is significantly lower than the size of the puffs and slugs estimated via the high-speed imaging technique. We comment also that consistently with the flow asymmetry of the velocity profiles illustrated in Fig. 22 an asymmetry is observed in many of the autocorrelations curves as well.

4.1.4 Evolution of the Plug Region During Transition

For yield stress fluids, the role of the plug region in retarding transition is largely unknown. If one interprets the yield stress fluid to be fully rigid below the yield stress, then the laminar flow is analogous to that with the plug replaced by a solid cylinder moving at the appropriate speed. Presumably, since the effective viscosity becomes infinite at the yield surface, the flow should be locally stabilised. Two different scenarios may be postulated at transition:

• 1. Transition may occur in the yielded annulus around the plug, leaving intact the plug region;

• 2. Transition is retarded until the plug region thins to such an extent that the Reynolds stresses (in the annular region) can exceed the yield stress.

In the first scenario (Peixinho 2004; Peixinho et al. 2005a), during the first stage of transition the turbulence intensity level on the centreline is reported as being similar to laminar levels. This is also the scenario assumed explicitly in some phenomenological theories of transition (Slatter 1999) treats the plug as a rigid body in developing his formula for transition. In Fig. 27, we present the ratio of averaged Reynolds stress at the centreline (where the level of velocity fluctuations is minimum) to the yield stress, as a function of the generalised Reynolds number Re$_G$ for the four different Carbopol concentrations that we have used. The filled symbols in Fig. 18 mark the lowest value of Re$_G$ for which puffs or slugs were detected in the experiments, for each of the different concentrations of Carbopol.

Fig. 27

Axial Reynolds stresses normalised by yield stress for four different concentration levels of Carbopol^®. The filled symbols indicate points where the flow becomes transitional, with puffs/slugs first observed

One can observe that the mean Reynolds stress exceeds the yield stress in each case. This remains true even if we subtract the laminar flow fluctuations from the Reynolds stresses, interpreting them as instrumental noise. This suggests that the second explanation given above is the more plausible, i.e. the viscoplastic plug has broken when transition starts. This is further reinforced by the results of the previous section on the structure functions, i.e. at these transitional/weak turbulent Reynolds numbers we have observed very similar intermittency characteristics with Carbopol, right across the pipe radius, as with Xanthan, where there is no yield stress. We should also comment that for the concentrations of Carbopol that we have used, if we calculate the (laminar) unyielded plug diameters using Eq. (27), for the largest flow rates for which puffs or slugs are not detected (see Fig. 28) these plug diameters are at most of the order 2 mm. Thus, we do not anyway have a strong plug close to transition.

Fig. 28

Plug radius normalised by pipe radius for four different concentration levels of Carbopol^® indicated in the insert

There is no contradiction with the data from other works (Peixinho 2004; Peixinho et al. 2005a), simply with its interpretation. Even with this thinning and break-up of the plug, in the Reynolds number range preceding transition flow instabilities are not sustained. Peixinho et al. (2005a) report measuring low-frequency oscillations away from the central region. Such low-frequency forcing, presumably with slow axial variation, could easily be responsible for slow extensional straining that yields the true plug of the base flow into a pseudo-plug. This type of psuedo-plug also occurs, for example, in thin-film flows (Balmforth and Craster 1999), and in channels of slowly varying width (Frigaard and Ryan 2004). In such flows the velocity remains asymptotically close to the base flow solutions, while shear and extensional stresses combine to maintain the pseudo-plug at just above the yield stress. Such flows are laminar but yielded and the psuedo-plug is characterised by large effective viscosity, which would presumably give similar characteristics to the base laminar flow in controlling fluctuation level, Peixinho (2004), Peixinho et al. (2005a). From our measurements of the velocity profiles, the mean velocity remains very plug-like in the centre of the pipe in this upper range of laminar Reynolds numbers and it is simply not possible to discern whether what is observed is a true plug or not. Evidently, the ideal situation would be to visualise transition within a plug region of significant size in comparison to the pipe. Interestingly, this was the intention of our experiments. Our study was started after discussions with C. Nouar about ongoing experiments (Peixinho 2004; Peixinho et al. 2005a). These were conducted in a 30 mm pipe at lower speeds, and for the flow rates at which transition occurred the plug region had radius of the order of 1 mm: too small to detect if broken or not. This prompted our interest in the role of the plug during transition, and we therefore designed our experiments at a larger scale so that we could potentially achieve transition with higher yield stress fluids, in larger diameter pipes and at higher speeds, hopefully also with a larger plug radius at transition. This objective could not be attained, as the small values of $r_p/R$ in Fig. 28 indicate. Together with these experiments (Peixinho 2004; Peixinho et al. 2005a), the results described above contribute to the evidence that the plug region must thin to such an extent that the Reynolds stresses can break it, before transition commences.

4.2 Hydrodynamic Stability of a Plane Poiseuille Flow of a Carbopol^® Solution Within the PMM Framework

We have argued in Sect. 1 of this chapter that the yielding scenario of a Carbopol^® gel is somewhat more complex that one would have expected and it cannot be accurately described by the classical Herschel–Bulkley framework. To circumvent these difficulties, we have proposed in Sect. 2 a phenomenological model able to both account for a gradual solid–fluid transition and describe the elastic effects observed in both rheological (controlled stress ramps) and tabletop (e.g. the sedimentation problem discussed in Sect. 1 and illustrated in Fig. 1b).

The fundamental question we address in this section is: To what extent the novel yielding scenario proposed in Sect. 2 could influence our understanding of hydrodynamic stability?.

At a first glance, this question might appear groundless: the yielding transition occurs at very low Re (typically $Re\ll 1$), whereas the loss of hydrodynamic stability due to the inertial term in the momentum equation occurs at significantly larger Re (typically $Re>1000$); therefore, what is the physical connection between the two phenomena? Given a second thought, the relevance of the yielding scenario to the hydrodynamic problem may be defended as follows. The base flows usually considered in the linear analysis of the hydrodynamic stability of channel flows of yield stress fluids are characterised by a significant stratification of the velocity gradients: large values near the channel boundaries which are consistent with a yielded flow region and vanishing values near the centre line, which are consistent with a plug region. The experimental investigation of the laminar–turbulent transition in the pipe flow of a yield stress fluids we have briefly presented in Sect. 4.1 (Güzel et al. 2009) demonstrates that the transition to turbulence occurs when the Reynolds stresses balance the yield stress of the fluid, that is, when the plug is broken. These findings corroborate well with the idea that, contrary to our initial intuition, the nature of the solid–fluid transition and the yielding scenario may actually play a role in the hydrodynamic stability problem.

To test this, we briefly discuss in the following the linear stability of a plane channel flow of an elasto-viscoplastic material described by the phenomenological presented in Sect. 2 and compare our results with the results obtained from a Casson regularised constitutive relationship. For the details of this analysis, the reader is referred to Moyers-Gonzalez et al. (2011a).

The plane channel flow of the elasto-viscoplastic fluid is described by the following set of equations depending on the variables $(p, \mathbf {u}, \varvec{\sigma }, \bar{a})$:

$$\begin{aligned} \rho \left( \frac{\partial \mathbf {u}}{\partial t} + \left( \mathbf {u} \cdot \nabla \right) \mathbf {u}\right) =-\nabla p + \eta _s \nabla \cdot \dot{\gamma } + \nabla \cdot \varvec{\sigma } \end{aligned}$$

(30)

$$\begin{aligned} \nabla \cdot \mathbf {u}=0, \end{aligned}$$

(31)

where $\eta _s$ is the solvent viscosity and $\dot{\varvec{\gamma }}$ is the rate of strain tensor. The constitutive relation is the one we have proposed in Sect. 2 in the framework of the phenomenological yielding model but adapted to a tensorial form in order to be coupled to the Navier–Stokes (Eq. 30):

$$\begin{aligned} \varvec{\sigma }+\lambda \left( \dot{\varvec{\gamma }}, \bar{a} \right) \underset{-}{\nabla }\varvec{\sigma } = \eta \left[ \dot{\gamma }(\mathbf {u})\right] \dot{\varvec{\gamma }}, \end{aligned}$$

(32)

where $\underset{-}{\nabla } \cdot = \frac{D \cdot }{Dt} - \nabla {\mathbf {u}}\cdot - \cdot \nabla \mathbf {u}^T$ is the upper convected derivative ($\frac{D \cdot }{Dt}$ is the classical material derivative), $\lambda \left( \dot{\gamma }, \bar{a} \right) = \frac{\eta \left[ \dot{\gamma }(\mathbf {u}) \right] }{G} \bar{a}$ is the relaxation time and G is the elastic modulus. The concentration of the unyielded material $\bar{a}$ satisfies the kinematic equation below:

$$\begin{aligned} \frac{\partial \bar{a} }{\partial t} + \left( \mathbf {u} \cdot \nabla \right) \bar{a} = R_d\left[ \bar{a}, \sigma (\mathbf {u}) \right] + R_r\left[ \bar{a}, \sigma (\mathbf {u}) \right] . \end{aligned}$$

(33)

As detailed in Sect. 2, $R_d, R_r$ are the rates of destruction and re-formation of solid structural units, respectively. The hydrodynamic stability problem is governed by the Reynolds (Re), the Weissenberg (Wi) and the Bingham (Bi) number defined as

$$\begin{aligned} Re=\frac{\rho L U_{max}}{\eta } \end{aligned}$$

(34)

$$\begin{aligned} Wi=\frac{\lambda _H U_{max}}{L}\end{aligned}$$

(35)

$$\begin{aligned} Bi=\frac{\sigma _y L}{\eta U_{max}} \end{aligned}$$

(36)

The relaxation time $\lambda _H$ is defined here as $\lambda _H=\frac{\eta _{\infty }}{G}$ with $\eta _{\infty }$ being the infinite shear viscosity and G the elastic modulus. The plasticity number, $Pl=Re Bi=\frac{\sigma _y \rho L}{\eta ^2}$, is defined as the product between the Reynolds number and the Bingham number. Note that Pl depends solely on the rheological properties of the fluid and the geometry of the problem, thus as we increase Re in our analysis Pl will remain fixed. For this reason, we chose Pl as control parameter through our analysis.

As is common in linear stability analysis, we consider an infinitesimal perturbation ($\epsilon u'$, $\epsilon p'$) superimposed upon the base flow and linearise the momentum Eq. (30) around the base flow solution. We do not show here the full development of the linear stability analysis (for these mathematical details, the reader is referred to Moyers-Gonzalez et al. 2011a) but solely focus on the main results. Unlike pipe flows of Newtonian fluids which are linearly stable at all Re, the plane Poiseuille flow becomes linearly unstable at $Re_{Newt} = 5772$.

We have studied the onset of instability for two cases: the case of an yield stress fluid described by the classical Herschel–Bulkley constitutive relation and the case of a fluid described by the model by Putz and Burghelea (2009). The dependence of the normalised onset of the instability on the plasticity number for each case is illustrated in Fig. 29.

Fig. 29

Normalised critical Re for increasing Pl

As with the regularised Herschel–Bulkley model, the existence of a pseudo-plug region (spatially stratified viscosity) is sufficient to greatly enhance the stability of the flow. The critical Reynolds number appears to be a monotone increasing function of plasticity number Pl, just as with the regularised viscoplastic model. We should also note that the inclusion of a highly viscous viscoelastic fluid as a plug destabilises the flow when comparing it with the regularised model (shown as the lower curve in Fig. 29). In relative terms, when $Pl = 1000$ the critical Reynolds number for the elasto-viscoplastic model is $2.66\%$ smaller than the critical Reynolds number for regularised model. For $Pl = 10^5$, this percentage increases to around $6\%$; this is due to the fact that the pseudo-plug and solid–fluid regions increase and are closer to the wall. Thus, the central conclusion of this study is that the presence of a solid–fluid coexistence transitional regime marked by the presence of elastic effects which is properly accounted for by the model by Putz and Burghelea (2009) proposed in Sect. 2 has a destabilising role.

4.3 Unstable Flows Triggered by a Fast Chemical Reaction

Generating high Reynolds number flows as illustrated in Sect. 4.1 may sometimes prove to be un-practical, e.g. in the case of highly viscous fluids flowing in spatially confined environments. An alternative way of breaking the hydrodynamic stability in the absence of any significant inertial contribution ($Re \ll 1$) is to “switch on” another source of nonlinearity in the Navier–Stokes equation. This can be done by inducing a strong spatial heterogeneity of the viscosity (and/or yield stress) in the flow. Although the hydrodynamic stability of miscible shear flows with a strong monotonic variation in viscosity has been analysed theoretically (Ern et al. 2003), we have found no clear experimental demonstration of these instabilities. With flows of simple Newtonian fluids, it is difficult to vary the viscosity locally to induce an instability. With complex or “structured” fluids, however, the situation is significantly different: the rheology is strongly coupled to the molecular-scale organisation of the fluid. This opens a new possibility of locally controlling the viscosity by inducing local changes in the molecular structure via a chemical reaction taking place at the interface between two complex fluids as schematically illustrated in Fig. 30. The advantage of such a method is that a chemical reaction may be controlled by either mass transfer or by local heating or cooling.

Fig. 30

Schematic overview of the reactive flow configurations: a displacement configuration b Hele–Shaw parallel flow configuration. The colours in each panel refer to the pH of the fluid—see text for description

Here, we demonstrate experimentally that a fast (acid–base) chemical reaction taking place at the interface between two miscible fluids and resulting in the local formation of a gel may indeed destabilise the flow in the absence of any relevant inertial contribution. The chemical reaction takes place at the interface between a Newtonian fluid (an aqueous of sucrose) at $pH \approx 13$ and an un-neutralised aqueous solution of Carbopol^® 980 at $pH \approx 3.5$. The neutralised Carbopol^® located around the interface of the reacting fluids exhibits an yield stress behaviour and thus a large viscosity contrast is generated in the flow. The pH-dependent rheology is illustrated in Fig. 31.

Fig. 31

a Strain rate dependence of the effective viscosity of the two reacting fluids: circle—displaced Carbopol solution at $pH=3$, squares—displacing sucrose solution at $pH= 13$, triangles—neutralised Carbopol^® solution($pH=7$). b pH dependence of the viscosity of the Carbopol^® solution measured at $\dot{\gamma }= 1s^{-1}$. c pH dependence of the yield stress of the Carbopol^® solution

In a neutral state, the viscosity of the Carbopol^® solution is two orders of magnitude larger than in the initial acid state ($pH \approx 3$), panel (b) in Fig. 31 and the Carbopol^® solution exhibits yield stress, panel (c) in Fig. 31.

We show through this section that this spatially inhomogeneous fluid rheology triggered by the acid–base reaction that locally neutralises the Carbopol^® structural units leads to an inertia free hydrodynamic instability. We have focused on two distinct flow configurations:

• 1. a displacement flow configuration where the less viscous Newtonian fluid displaces the more viscous Carbopol^® solution, as shown in Fig. 30a.

• 2. a parallel flow configuration where the two reacting fluids are injected side by side, displayed in Fig. 30b.

Besides the fundamental interest in understanding how a stratification of the viscosity influences the hydrodynamic stability of the flow, each of the aforementioned flow configurations had a clearly defined practical motivation. The motivation for the displacement flow configuration illustrated in Fig. 30a came from the construction of oil and gas wells. Since the early 1990s, there have been an increasing number of wells that are constructed with long horizontal sections. The worlds longest extended reach wells have horizontal sections in the 10–15 km range, but these are exceptional. More routinely, wells are built with horizontal extensions of up to 7 km. One of the key barriers in constructing longer wells comes from simple hydraulic friction. In a vertical well, both the pore pressure of reservoir fluids and the fracture pressure of the reservoir rock increase with depth, approximately linearly. Judicious choice of fluid density and circulating flow rates keeps the well-bore pressure inside the so-called “pore-frac envelope”, i.e. the region where the porous rock does not fracture. In a horizontal well section, the pore-frac envelope is unchanged with length along the well, but the frictional pressure increases with length, leading to eventual breaching of the envelope.

To avoid large pressure drops but yet achieve an efficient displacement, our original idea was to locally increase the viscosity of the fluid only in the vicinity of the interface (see the sketch in Fig. 30a rather than using a high viscosity displacing fluid over the entire length of the pipe. A brief discussion of the main experimental findings for this flow configuration is given in Sect. 4.3.1. For a detailed account, these findings the reader is referred to Burghelea et al. (2007).

The second flow configuration illustrated in Fig. 30b might find some useful applications in efficiently mixing viscous fluids in the absence of significant inertial contributions, e.g. in micro-channels. A brief discussion of the main experimental findings for this flow configuration is given in Sect. 4.3.2. For a detailed account of these findings, the reader is referred to Burghelea and Frigaard (2011).

4.3.1 Unstable Displacement Flows in the Present of a Fast Chemical Reaction

A typical stable displacement experiment performed with two Newtonian fluids at low Re is illustrated in Fig. 32. A small amount of fluorescein has been added to the displacing fluid in order to visualise the interface between the two fluids. The fluid displacement process laminar, steady and dominated by a long finger of the displacing fluid penetrating into the displaced fluid.

Fig. 32

Example fluorescent images of the interface in an experiment from control sequence: displacing fluid 65% saccharose solution, displaced fluid $-66\%$ saccharose solution. The flow rate $\hat{Q} =0.145$ ml/s. The two images are separated in time by 5 s

Fig. 33

a–f Fluorescent images of the interface in a reactive displacement: displacing fluid—-$65\%$ saccharose solution, displaced fluid—$0.1\%$ Carbopol^® in $66\%$ saccharose solution. e–f Fluorescent flow images long after the entrance of the unstable interface in the field of view; the images are separated in time by approximately 5 s. The dotted lines highlight gelled structures tumbling downstream. The direction of the flow in each panel is from right to left

The flow behaviour was significantly different from the control experiments in the reactive case, when the Carbopol^® solution at $pH=3$ was displaced by a saccharose solution at $pH=11$, at different flow rates. The initial interface penetrates in a sharp spike as before, but this is destabilised and the finger rapidly widens to nearly fill the pipe. A complex secondary flow develops at the interface between fluids. The flow seems to be dominated by large vortices advected by the flow, with a typical size of the order of the pipe radius. Typical images are shown in Fig. 33. As the front of the finger passes, the secondary flow instabilities persist along the sides of the finger. The secondary flow provides a feedback mechanism for the instability by bringing into contact new unreacted fluid elements and taking away reacted highly viscous fluid. The initial pass of the finger front does not remove all the fluid 2 from the walls. However, the secondary flows result in a fairly rapid erosion of the residual layers. After the initial instability, small parcels of fluid 2 pulled into the fluid 1 stream react to form gelled solid regions that are advected along with the fluid. Close observation of video images reveals that some of these parcels appear to be in rigid motion as shown in Fig. 33e and f.

To quantitatively assess the impact of the instability on the efficiency of the fluid displacement, we monitor the dependence of the normalised width of the finger $\frac{W}{2 \hat{R}}$ (here $\hat{R}$ stands for the radius of the pipe) versus the strain $\gamma = \frac{\hat{U}_0 \hat{t}}{\hat{R}}$. Here $U_0$ stands for the mean flow velocity and $\hat{t}$ for the time.

When a Newtonian fluid pair is used, the displacement efficiency depends strongly on the flow rate and, at the higher rate, does not exceed 0.9, as shown in Fig. 34. This is what one would expect for a laminar flow and a displacing fluid less viscous than the displaced one. The picture is quite different when a reactive fluid pair is used. Due to the flow instability, efficient mixing occurs near the interface (Fig. 33). As compared to the Newtonian case, two major differences are observed. First, the temporal evolution of the displacement efficiency is little sensitive to the flow rates: the points measured for various flow rates collapse onto a single master curve. Second, the displacing efficiency reaches now 0.98 indicating that the instability leads to a nearly complete displacement which the desirable case for the oil well engineering context we described in the beginning of this section.

Fig. 34

a Normalised width of the tip versus the normalised displacement distance, $\hat{U}_0\hat{t}/\hat{R}$, for several values of the flow rate: $\hat{Q} =0.063$ ml/s, $\hat{Q} =0.145$ ml/s, $\hat{Q} =0.19$ ml/s, $\hat{Q} = 0.3$ ml/s. The experiments with the Newtonian fluids pair that undergoes a stable displacement flow. b Normalised width of the tip versus the normalised displacement distance, $\hat{U}_0\hat{t}/\hat{R}$, for several values of the flow rate: $\hat{Q} = 0.13$ ml/s, $\hat{Q} = 0.18$ ml/s, $\hat{Q} = 0.2$ ml/s, $\hat{Q} =0.31$ ml/s, $\hat{Q} =0.47$ ml/s. The experiments belong to the reactive sequence

4.3.2 Unstable Parallel Flows in the Present of a Fast Chemical Reaction

We now focus on reactive flows in a parallel flow configuration (Fig. 30b) where the reacting fluids are injected side by side. As in the case of the displacement flow configuration discussed in Sect. 4.3.1, in the absence of a chemical reaction, the flow is linear, laminar and steady. Thus, the mixing of the fluids is poor as it is carried on by molecular diffusion alone.

Fig. 35

Space-time diagrams measured at a fixed driving pressure drop $\Delta p = 500$ Pa at several locations downstream: a $y = 3.2$ cm, b $y = 14$ cm, c $y = 17$ cm, and d $y = 35$ cm. The flow patterns have been visualised using the laser-induced fluorescence (LIF) technique. LIF flow images acquired in the horizontal plane corresponding to each space-time diagram are presented on the top row. The dotted lines in the bottom row indicate the time instant when the LIF flow images have been acquired. The concentration of Carbopol^® in the acid fluid was $0.1\%$

The spatial development of the flow downstream in the channel for the reactive fluid pair is presented in Fig. 35, at an intermediate pressure drop $\Delta p = 500$ Pa. Four positions downstream are selected. The top row presents a snapshot of the spatial structure at each position, while the bottom row presents space-time diagrams for a time period of 500 s including the snapshot. The space-time diagrams are obtained by monitoring a single brightness profile acquired at a fixed location across successive laser-induced fluorescence (LIF) images evenly spaced in time. The interface between the two fluids is unstable from the very entry of the channel $y = 3.2$ cm (Fig. 35a). As one advances downstream, the interface between the two fluids becomes increasingly unstable and the degree of mixing increases, panels (b)–(d) in Fig. 35. The diffuse layer visible near the interface in Fig. 35a is suggestive of a spreading reaction–diffusion front. We can observe unevenness of the diffuse layer thickness at small spatial scales (which could correspond to a reactive–diffusive instability), but we also see larger wavy variations in the interface itself which are likely to have a hydrodynamic origin. This larger scale waviness is evident in the spatiotemporal plot and appears to evolve spatially along the channel, while the diffuse interfacial layer is lost. On the scale of the channel, the characteristic diffusion timescale is much larger than the advection timescale. This implies that the apparently random mixing patterns illustrated in panels (b)–(d) are not related to molecular diffusion but rather to a (chaotic) advection phenomenon. The degree of mixing increases, extending across the entire channel (Fig. 35c and d), but it is remains intermittent with significant regimes of black and white showing in the LIF images. This suggests that the mixing mechanism is interfacially controlled, rather than by bulk fluid motion. Presumably, those interfacial regions that react quickly on mixing will form highly viscous (or unyielded) layers. These layers may either separate regions of pure fluid or may even encapsulate such regions through advective instability. Fluid which is bounded by highly viscous (or unyielded) layers will respond much less to local stress gradients. At the same time, unstable motions will continue to bring new unreacted fluids into contact. This probably explains the preservation of some larger scale structures together with seemingly diffuse well-mixed regions, as the flow progresses. In Fig. 35d, we see a more longitudinal spatial structure developing. A plausible mechanism for this is that the regions of unreacted fluid will move relatively fast along the channel and help to orient near rigid regions with the flow. These regions may agglomerate, but in doing so will move slower and hence have an increased possibility of further growth via agglomeration.

5 Non-isothermal Problems Involving Yield Stress Materials

5.1 Thermo-Rheological Behaviour of a Shear-Thinning Yield Stress Material

Whereas a clear progress towards understanding the isothermal deformation of viscoplastic materials has been made, there exist a limited number of studies dealing with temperature-dependent viscometric and non-viscometric flows of Carbopol^® solutions. An experimental study of the heat transfer in the transitional pipe flow of a Carbopol^® solution is presented in Peixinho et al. (2008). The authors of this study consider a Herschel–Bulkley-type yielding scenario and analyse their rheological measurements accordingly. The hydrodynamic stability of the flow and the heat transfer problem are discussed in terms of the rheological properties of the material and their temperature dependence.

The previous studies regarding the thermo-rheology of Carbopol^® gels may be divided into two classes. A first class of previous rheological studies found a “normal” temperature correlation of the rheological properties that can be modelled by the Arrhenius law (Islam et al. 2004; Peixinho et al. 2008; Alain and Bardet 1982; Fresno Contreras et al. 2001). Islam et al. (2004) found an Arrhenius scaling of the viscosity of the Carbopol^® gel with temperature which gave rather low values of the activation energy, $\Delta E_a$ consistent with a low-temperature sensitivity. The gels studied in this work were prepared in a glycerol solvent which behaves as a rheologically simple fluid and has a rather large flow activation energy (Magazu et al. 2007) which could potentially “mask” a significantly weaker anomalous behaviour related to the swollen gel network. Peixinho et al. (2008) found no temperature dependence of the power law index and yield stress and an Arrhenius-type decay of the consistency. They used a neutralised $0.2\%$ (wt) aqueous solution of Carbopol^® 940 and a controlled stress rheometer (AR2000 from TA Instruments) equipped with a steel 0.5 deg cone/40 mm plate and truncation of 15 $\upmu$m. It is worth noting that the maximum temperature investigated in this work is as large as 85 $^\circ$C (and therefore the fluid evaporation could have played a significant role during the measurements) and that the scatter of their yield stress measurements accounts for nearly $30\%$ of the measured values which makes the observation of a particular trend difficult. There exists a second class of previous rheological studies which observe an anomalous temperature–viscosity correlation, i.e. an increase of the viscosity with the temperature (Owen et al. 2003; Park and Jr. 1997; Park and Irvine 1997; Todica et al. 2010).

Barry and Meyer (1979a, b) were among the first to provide a very complete description of the rheological properties of Carbopol^® at various temperatures by combined shear measurements, creep measurements and small amplitude oscillatory measurements. Although the general conclusion is that the rheological properties of Carbopol^® gels are practically insensitive to temperature variations (their flow activation energy is small), the authors did observe an anomalous temperature dependence of the viscosity (see the discussion in page 8 of Barry and Meyer 1979a) but they discard the observation by noting “As an increase in apparent viscosity is inconsistent with an activation energy for viscous flow these data were not used to derive such values”. By using a Brookfield Model DV-III Digital Rheometer (Brookfield Engineering Laboratories Inc., Stoughton, MA, USA) and a cone and plate configuration, Owen et al. (2003) observed an anomalous temperature viscosity correlation for two neutralised polyacrylic acid derivatives used in contraception under the trade names “Advantage-S” and “KY-Plus”. In the same study, however, for two other contraceptive gel formulations, “Ginol II” and “Conceptrol” and by using the same rheological procedure, a “normal” (Arrhenius-like) temperature correlation of the viscosity is observed. This indicates that the correlation between the temperature and the rheological behaviour is intrinsically related to the physico-chemical properties of the gel mixture.

By using a falling needle viscometer, Park and Jr. (1997); Park and Irvine (1997), an anomalous temperature dependence of the viscosity of Carbopol^® 934 is at three distinct concentrations (which they express in parts per million): $c = 5000$ ppm, $c = 7500$ ppm and $c = 10 000$ pm. They did not elaborate any further on this rather unexpected result but they did note, however, that “Perhaps this phenomenon originates from a structural change of the polymer molecules with concentration and temperature”. The most recent observation of an anomalous behaviour we are aware of is due to Todica et al. (2010). They performed their measurements on a Brookfield DV II Pro viscometer, using cylindrical spindle. A detailed explanation for this anomalous behaviour is not given in this paper either.

Both classes of previous works briefly discussed above have, most probably, a limited number of things in common which makes a pertinent comparison quite difficult. Although they use a variety of rheometric equipment (note that these studies span the last four decades during which the rheometric devices have significantly evolved), it is, in our opinion, unlikely that the differences in the observed temperature correlations are due to this. This idea corroborates with the fact that sometimes, within the same study (thus using the same device and rheological method) both “normal” and “anomalous” behaviours are found, depending on grade of Carbopol^® used (Owen et al. 2003).

At a second analysis of the bibliography given above, one can find, however, other significant differences between these studies: the physico-chemical properties of the gels. Thus, various studies used various grades of Carbopol (934, 940, Ultrez 10, etc.) or even custom gel formulations (Owen et al. 2003). Additionally, many of these studies do not discuss in detail the chemical nature of the cross-linking agent, the ionic content and the interaction of the polyacrylic acid molecules with various types of solvent used (water, water/ethanol mixtures, water ethylene/glycol mixtures and glycerol).

To conclude this part, a pertinent comparison and analysis of the existing body of literature on the thermo-rheological properties of Carbopol^® is difficult to make based on the published results. This is due in our opinion to an incomplete understanding and control of the physico-chemical interactions that govern the cross-linking, ionisation, swelling and jamming dynamics of the individual molecules. Each of these molecular-scale physico-chemical processes is temperature-dependent (and they are characterised by their own chemical activation energies which are largely unknown) and the overall temperature dependence observed in a macroscopic rheological experiment is the result of a highly non-trivial “average” of these microscopic dependencies. We discuss in the following the thermo-rheological properties of a Carbopol^® gel under shear. For a more comprehensive account of the main results, the reader is referred to Weber et al. (2012).

5.1.1 Experimental Setup and Methods

To prevent the wall slip, a parallel plate geometry with cleated surfaces has been used, Fig. 36a. The radius of the parallel plates is $R = 40$ mm, and the gap measured by the rheometer is $d = 1$ mm. The cleats have an equal height $H = 600\,\upmu \mathrm{m}$ and are disposed in a rectangular grid over each plate. Several advantages of cleated geometries over other methods of preventing the wall slip effect (such as using a sandblasted geometry or a vane tool) have been recently demonstrated experimentally (Nickerson and Kornfield 2005). Among these advantages, the cleated geometry allows suppression of the wall slip effect even in the absence of significant normal forces and creates a well-defined shear.

Fig. 36

a Schematic illustration of the cleated parallel plate geometry. b Temperature calibration measurements. The symbols are circles—the top plate, squares—the bottom plate. A thermo-rheologically simple silicon oil with a known activation energy has been used

The flow between neighbouring cleats is restricted and stops over a finite distance $\Delta$ (the flow penetration length) along the vertical axis (see Fig. 36a) and thus, two parallel no-slip surfaces are formed at an effective distance $d_e=d+2\Delta$. Consequently, the stress measurements should be corrected according to $\sigma = \sigma _a \frac{d_e}{d}$ where $\sigma _a$ is the apparent stress value recorded by the rheometer. A second concern was related to the possible artefacts introduced by fluid evaporation during long experimental runs. In order to prevent this, a solvent trap has been placed around the free fluid meniscus. The sealing of the solvent trap on the base plate of the rheometer has been insured by a thin layer of vacuum grease. After each experimental run, it has been carefully checked (by visual inspection) that no significant changes in the shape of the meniscus occurred. Additionally, we have checked at the end of each run that one can reproduce the viscosity measured during the pre-shear step which indicated us that the evaporation effects were either minimal or absent. A third concern is related to the temperature gradient which develops within the space between the parallel plates of the measuring geometry. To monitor and account for this effect, two temperature probes have been embedded in each of the parallel plates of the geometry. The temperature of each plate $(T_t, T_b)$ has been measured as a function of the temperature set to the Peltier plate of the rheometer $T_{pp}$ in the range 5–55 $^\circ$C. Beyond this range of temperatures, we have found that the measurements are not reproducible (a scatter of nearly $75\%$ over several subsequent runs with fresh samples was observed) and, consequently, unreliable. During these measurements, a Carbopol^® sample was loaded but the top plate of the rheometer was held static. The transient temperature signals have been monitored using a digital oscilloscope and each temperature reading has been made only after the temperature of each plate has reached a steady state. Calibration measurements of the temperature at the top and bottom plate of the rheometer as a function of the temperature set to the Peltier plate are presented in Fig. 36b.

Fig. 37

Validation of the cleated geometry and stress correction. The symbols are circles—cone and plate geometry; squares—the cleated geometry illustrated in Fig. 36b. A thermo-rheologically simple silicon oil with a known activation energy has been used

As the temperature set to the Peltier plate, $T_{pp}$, departs the room temperature, a linear increase of temperature difference between the top and the bottom plates is observed. By measuring the temperature difference between the plates at a fixed temperature of the Peltier plate for various values of the distance d between the plates, it was checked that the temperature varies linearly within the gap. This allowed us to define an effective temperature of the sample as an arithmetic mean of the temperatures of the top and the bottom plates of the rheometer, $T= (T_t + T_b)/2$. The reliability of the stress and temperature corrections described above was assessed by comparative thermo-rheological measurements performed on a calibrated silicon using both the cleated geometry described above (together with the stress and the temperature corrections) and a standard cone and plate geometry. The result of this comparison is presented in Fig. 37.

The viscosity measurements performed on the two geometries come into a perfect agreement which indicates that both the stress correction related to the cleated geometry and the temperature correction related to the temperature gradient between the parallel plates are reliable and can be safely employed in the thermo-rheological measurements concerning the Carbopol^® gel.

5.1.2 Thermo-Rheological Properties of a Carbopol^® Gel

Each of the thermo-rheological measurements performed with Carbopol^® gels followed the procedure in Sect. 1. More specifically, corresponding to each average temperature T the material has been subjected to a controlled stress stepped ramp similar to the one schematically illustrated in Fig. 3a, and flow curves qualitatively similar to those illustrated in Figs. 3b, 4c and 7a were recorded. The characteristic forcing time (see Sect. 1 for a detailed discussion) has been kept constant, $t_0=0.66$ s. For each ascending/descending controlled stress ramp, 1000 linearly spaced stress values have been explored ranging between 0.1 and 20 Pa.

The advantage of this rheological protocol is twofold. First, it allows the simultaneous assessment of both elastic and viscous rheological parameters. Second, it allows a more accurate measurement of the yield stress within the phenomenological framework briefly introduced in Sect. 2 (and detailed in Putz and Burghelea 2009), thus avoiding the inherent inaccuracies related to the classical Herschel–Bulkley nonlinear fitting procedure.

Fig. 38

a Temperature dependence of the elastic moduli, measured from the increasing (the empty symbols) and decreasing (the full symbols) branches of the controlled stress ramp. b Temperature dependence of the consistency. c Temperature dependence of the power law index. The symbols in each panel refer to different Carbopol^® weight concentrations: squares—$c = 0.1 \%$; triangles—$c = 0.15 \%$; circles—$c = 0.2 \%$

At low values of the applied stress corresponding to the solid deformation regime ($\bar{a} \rightarrow 1$) the elasto-viscoplastic constitutive relation defined by Eq. 8 reduces to the Hooke’s law, $\sigma =G \gamma$. Bearing in mind that the controlled stress ramp is linearly spaced in time, this provides us with a quick way of estimating the elastic modulus by monitoring the plateau observed in the solid range on each branch of the stress ramp (increasing/decreasing stresses). The measured dependence of the elastic moduli $G_u,G_d$ measured on the increasing/decreasing branches of the flow ramp (full/empty symbols) performed with Carbopol^® is presented in Fig. 38a. The error bars have been calculated to be repeating each test four times with a fresh sample. Within the accuracy of the measurements, no sensitive temperature dependence of the elastic moduli is observed (but only an obvious dependence on the concentration of Carbopol^®). Thus, the solid-like deformation observed in a range of low applied stresses is inconsistent with a rubber-like behaviour, which typically manifests through a proportional increase of the elastic modulus with the temperature (Larson 1999).

By fitting controlled stress ramps measured at various temperatures with the phenomenological model presented in Sect. 2, one obtains the temperatures dependencies of the consistency K, power law index n and the yield stress, $\sigma _y$. Similarly, neither the consistency presented in Fig. 38b nor the power law index presented in Fig. 38c depends on the temperature but solely on the polymer concentration. The invariance of the consistency with the temperature is at odds with the observations by Peixinho et al. (2008), which indicate an Arrhenius-type exponential decay of the consistency with the temperature.

Fig. 39

Temperature dependence of the yield stress measured for three distinct values of the Carbopol^® concentration: squares—$c = 0.1 \%$; triangles—$c = 0.15 \%$; circles—$c = 0.2 \%$. The dashed line marks the transition from an Arrhenius temperature dependence to a non-Arrhenius one

A strikingly different behaviour is observed for the temperature dependence of the yield stress, $\sigma _y$ (Fig. 39). Corresponding to a critical temperature $T_c$, a local minimum of the dependence is observed. This unexpected behaviour has been observed for each value of the Carbopol^® concentration, and the non-monotone trend of the curves clearly highlighted by the dashed line in Fig. 39 falls beyond the error bars of the measurements. The critical temperature $T_c$ marks the transition from a Arrhenius-like behaviour described by $\sigma _y = \sigma _y^0 e^{\frac{\Delta E_a}{RT}}$ (the full lines in Fig. 39) to a anomalous non-Arrhenius one and decreases with increasing Carbopol^® concentration. Here, $\Delta E_a$ and R stand for the activation energy and the universal gas constant, respectively.

As the observation of an anomalous temperature dependence of the yield stress (and implicitly of the viscosity measured at a given applied stress, because the consistency and the power law index are temperature invariant, as shown in Fig. 38b and c) was quite unexpected and intriguing (particularly the increase of $\sigma _y$ for $T > T_c$ ), the calibration measurements presented in Fig. 39 have been repeated several times and subsequently reproduce this result. As the same stress calibration and temperature correction have been employed for all the measurements performed on the various Carbopol^® gels as in the case of the calibration measurements illustrated in Fig. 37, we may safely rule out the possibility that the anomalous temperature dependence observed in Fig. 39 is the result of an experimental artefact.

Attempting to qualitatively understand the temperature dependence of the yield stress above the critical temperature within the classical framework of the Arrhenius law would quickly lead to an unphysical conclusion: the activation energy is negative which apparently violates the second law of thermodynamics. This prompts one to seek an explanation for the experimentally observed anomalous behaviour beyond the “classical” Arrhenius framework. To this discussion, we dedicate the next subsection.

5.1.3 A Possible Qualitative Explanation for the Anomalous Temperature Dependence of the Yield Stress

The Arrhenius viscosity–temperature correlation emerges as a particular case from the more general theory developed by Henry Eyring which described the fluid flow as an activation process (Eyring 1936; Ree and Eyring 1955). At its turn, the Eyring theory of flow as an activated process emerged as a particular case of the Theory of Rate Processes which has significantly reshaped the modern chemical physics (Glasstone et al. 1941). We briefly present in the following the main results of the Eyring theory.

For a detailed discussion, we refer the reader to the classical textbook by Bird et al. (2002). Similarly to the excitation of atoms from their ground state to various energetic levels, Eyring has interpreted the motion of a “flow unit” (we use the term originally employed in Eyring 1936) along a given direction x as a tunnelling process of an energy barrier. Although the Eyring flow activation theory has been employed by several authors to explain the yielding in extension of amorphous polymers (Richeton et al. 2005; Bauwens-Crowet et al. 1972), we are not aware of any similar work for viscoplastic materials under shear.

In the absence of a shear force, the energy barrier associated to the displacement of the neighbouring material layers along the x-direction is symmetric and, consequently, the probabilities of hopping (or hopping rates) along and opposite to the x-direction are equal, $\nu _{+} = \nu _{-}= \nu _0e{\frac{\Delta E_a}{RT}}$. Here, $\nu _0$ is the equilibrium hopping frequency, $\Delta E_a$ is the activation energy per mol of material and R is the universal gas constant.

When an external shear force $f_{+}$ is applied onto the material layers along the direction x, the symmetry of the activation energy barrier is broken, $\Delta E_{-,+} = \Delta E_a \pm f_{+} D N_A)$ where $N_A$ stands for the Avogadro’s number and D is a characteristic space scale (measured along the shearing direction, “$+$”) associated to the gel network. Consequently, the hopping rates along and opposite to the direction of the shearing force $\nu _{+}, \nu _{-}$ are no longer equal and an effective hopping rate along the direction of the imposed shear can be calculated by the difference:

$$\begin{aligned} \nu = \nu _{+}-\nu _{-}= 2\nu _0 e^{-\frac{\Delta E_a}{R T}} sinh \left[ \frac{f_+ D}{2k_BT}\right] . \end{aligned}$$

(37)

Denoting by A the characteristic shearing area between two neighbouring gel elements and interpreting the effective hopping rate as a microscopic rate of shear $\nu = \dot{\gamma }$, one can invert Eq. (37) and obtain the viscosity¹:

$$\begin{aligned} \eta \left( \dot{\gamma }, T\right) = \frac{2k_B T}{V^* \dot{\gamma }}sinh^{-1}\left[ \frac{\dot{\gamma }}{ 2 \nu _0}e^{\frac{\Delta E_a}{R T}}\right] , \end{aligned}$$

(38)

where $V^*=AD$ stands for a characteristic volume of the gel network. In the case of a Carbopol^® gel, we expect $V^*$ to be a non-trivial function of the molar mass of the polyacrylic acid, the polymer concentration and the pH which controls the degree of swelling of individual molecules (Gutowski et al. 2012).

For simple fluids, it is often assumed that

$$\begin{aligned} \frac{f_+ D}{2 k_B T} \ll 1, \end{aligned}$$

(39)

and Eq. (38) reduces to the well-known Arrhenius law²:

$$\begin{aligned} \eta \left( \dot{\gamma }, T\right) = \frac{k_B T}{V^* \dot{\gamma }}e^{\frac{\Delta E_a}{R T}}. \end{aligned}$$

(40)

To test the applicability of the simplifying condition given by the inequality Eq. (39) for the case of a Carbopol^® gel, one can consider as a typical space scale related to the gel network $D \approx 1\, \upmu \mathrm{m}$, $A \approx 1\, \upmu \mathrm{m}^2$, which are of the same order of magnitude with the values assessed via diffusion measurements (Oppong et al. 2006; Oppong and de Bruyn 2007), and $\sigma = 1$ Pa which leads to $\frac{f_+D}{2k_B T} \approx 240$.

These simple numerical estimates indicate that, in the case of a percolated Carbopol^® gel structure, one should not expect the simplified Arrhenius law to apply in the whole range of temperatures and one should consider instead the full Eyring dependence given by Eq. (38).

If one assumes that $V^*$ is temperature invariant,³ it can readily be shown that there exists a critical temperature $T_c$ corresponding to which the viscosity given by Eq. (38) passes through a local minimum. By solving numerically the equation $\frac{\partial \eta \left( \dot{\gamma }, T \right) }{\partial T} = 0$, it can be readily shown that the critical temperature $T_c$ which marks the transition from a thermo-rheologically simple (Arrhenius-like) behaviour to a anomalous one is a decreasing function of $\frac{\dot{\gamma }}{ \nu _0}$ at a fixed value of the activation energy $\Delta E_a$.

We emphasise once more that the Eyring model does not directly refer to the temperature dependence of the yield stress but to that of the viscosity. However, within a Herschel–Bulkley framework and due to the temperature invariance of both the consistency and the power law index (see the data presented in Fig. 38b and c), the yield stress $\sigma _y$ at a given temperature T is a linear function of the viscosity measured at the same temperature and a fixed rate of shear, $\sigma _y= \eta \left( \dot{\gamma }, T \right) \dot{\gamma }- K \dot{\gamma }^n$. Thus, one can conclude that the Eyring theory may qualitatively describe the anomalous temperature dependence of the yield stress illustrated in Fig. 39.

We propose in the following a simplistic phenomenological interpretation for the existence of a critical temperature $T_c$ beyond which an anomalous temperature correlation is observed. The microstructure of a polyacrylic micro-gel system statistically described by the characteristic volume $V^*$ is the result of two competing effects: swelling of individual micro-gel particles and osmotic de-swelling.

Following Cloitre et al. (2003) and Borrega et al. (1999), the swelling behaviour of a polyelectrolyte gel is governed by three contributions: the mixing entropy of the polymer molecules, the balance of osmotic pressure exerted by the counter-ions trapped within the micro-gel particles and the pressure of the ions present in the solution and the elasticity of the gel network. At a neutral pH, the degree of ionisation of individual polyacrylic acid molecules is high and, consequently, the mixing entropy can be neglected in the swelling equation:

$$\begin{aligned} \Pi _{in}+\Pi _e=\Pi _{out}. \end{aligned}$$

(41)

Here, $\Pi _e$ stands for the elastic pressure exerted upon the micro-gel particles and $\Pi _{in}$, $\Pi _{out}$ stand for the osmotic pressures due to the mobile ions inside and outside the micro-gel particles. The osmotic pressures are related to the concentrations of ions $C_{in}$, $C_{out}$ via $\Pi _{in,out}=RT C_{in,out}$. Assuming that all ions are contained within the micro-gel particles (which is reasonable provided that no salt is added to the system), Eq. (41) reduces to $\Pi _{in}=\Pi _e$. The concentration of ions trapped into the micro-gel particles may be written as $C_{in}= \alpha C_0 z Q^{-1}$ where $C_0$ is the average concentration of polyacrylic acid inside the micro-gel particles, $\alpha$ is the degree of ionisation, z is the molar fraction of acidic groups and $Q=V^*/V_0$ is the swelling ratio ($V_0$ is the characteristic volume of the un-swollen micro-gel particles).

Because the macroscopic elastic modulus reflects the microscopic-scale elasticity of the micro-gel structure, the temperature invariance illustrated in Fig. 38a indicates that the elastic pressure of the gel network $\Pi _e$ is temperature invariant. With these considerations, a simple algebraic manipulation of Eq. (41) would lead to the conclusion that the swelling ratio is proportional to the temperature or, equivalently $V^* \propto T$. Thus, within this regime, the pre-factor in Eq. (38) is practically temperature independent which explains why the temperature dependence of yield stress (viscosity) can be fairly well described by an Arrhenius-type correlation, see the full lines in Fig. 39. The osmotic de-swelling occurs when counter-ions may escape from the core of micro-gel particles into the solution by penetrating the outer shell of the particles where the local electro-neutrality condition is not fulfilled. The fraction $\Gamma$ of these counter-ions is proportional to the Debye length, $\Gamma \propto \lambda _D$, (Cloitre et al. 2003; Israelachvili 2010). Bearing in mind that the Debye length scales as $T^{1/2}$ one can conclude that an increase of the temperature translates into an increase of the number of counter-ions that leave the micro-gel particles which promotes the de-swelling process. According to Cloitre et al. (2003), if one accounts for the competing effects of the swelling and osmotic de-swelling and if one denotes the volume fraction of micro-gel particles by $\Phi$, the concentrations $C_{in,out}$ may be rewritten as

$$\begin{aligned} C_{in}=\frac{\alpha \left( 1-\Gamma \right) z C_0}{Q} \end{aligned}$$

(42)

$$\begin{aligned} C_{out}=\frac{\alpha \Gamma z C_0}{Q} \frac{\Phi }{1-\Phi }. \end{aligned}$$

(43)

A dynamical equilibrium between the swelling and the osmotic de-swelling may be achieved when the concentration of ions trapped within the micro-gel particles becomes comparable to that of the counter-ions that leave the micro-gel particles, $C_{in} \approx C_{out}$. This, together with Eq. (42) and with the square root temperature scaling of $\Gamma$, indicates the existence of a critical temperature $T_c$ and a critical characteristic volume defied implicitly via $\Gamma _c=1-\Phi _c$. Beyond this critical temperature $T_c$, the osmotic de-swelling wins over the swelling and a further increase of the characteristic volume $V^*$ with the temperature is no longer possible. Consequently, the pre-factor in Eq. (38) is proportional to the temperature which translates into the anomalous behaviour observed in Fig. 39. For high polymer concentration, the range of temperatures within which individual molecules can freely swell upon an increase of the temperature becomes narrower and the critical condition will be fulfilled at a lower temperature $T_c$. As a consequence, within this phenomenological picture, one should expect a decrease of the critical temperature $T_c$ with increasing Carbopol^® concentration. This trend is apparent in Fig. 39. A quantitative description of the data presented in Fig. 39 by the Eyring model could not be obtained. The reason behind this might be that Eq. (38) considered a single (plastic) “flow unit” characterised by a single specific volume $V^*$ related to the average size of the percolated gel network. A more realistic model should account for the presence of the Newtonian solvent (in our case the water trapped into the swollen polymer network) and a realistic statistical distribution of $V^*$. Such a statistical distribution is difficult to predict theoretically from first principles and, most probably should be tackled experimentally by direct visualisation of the polymer network, as very recently performed (Gutowski et al. 2012).

5.2 Rayleigh–Bénard Convection in a Shear-Thinning Yield Stress Material

The Rayleigh–Bénard convection in a fluid heated from below is a paradigm of pattern-forming systems (Cross and Hohenberg 1993).

Imposing a vertical temperature gradient within a Newtonian fluid by heating it from below translates into a vertical gradient of the fluid density or buoyancy which, beyond a critical value of the temperature gradient $\Delta T_c$, may overcome the viscous dissipation and trigger an upward motion of the fluid elements. Within a finite-size system and in the virtue of the mass conservation, this instability results in a regular and steady fluid motion in the form of rolls or hexagons which is classically referred to as the Rayleigh–Bénard thermal convection.

The transition to laminar Rayleigh–Bénard convection in Newtonian fluids has been intensively studied during the past five decades both theoretically and experimentally. Among a large amount of published work on the topic, we can refer the reader to textbook of Koschmieder (1993) and the review article by Bodenschatz et al. (2000).

A Newtonian fluid heated from below loses its hydrodynamic stability when the stresses associated to the buoyancy forces exceed those associated to the viscous dissipative forces.

The balance between the buoyancy and the viscous forces is quantified by the Rayleigh number:

$$\begin{aligned} Ra = \frac{\beta \Delta T g H^{3}}{k \cdot \nu }, \end{aligned}$$

(44)

where $\beta$ is the coefficient of thermal expansion, g is the gravitational constant, k is the thermal diffusivity, $\nu$ is the kinematic viscosity, $\Delta T$ is the temperature difference measured between the plates and H is the distance between plates. It has been shown both theoretically and experimentally that the onset of the convection corresponds to $Ra_c \approx 1708$.

Within the Boussinesq approximation, it has been demonstrated theoretically that the Rayleigh–Bénard convection emerges via a backward bifurcation (which may become an imperfect bifurcation in a finite system) and its onset can be described via a linear theory (Joseph 1970; Sani 1964). Moreover, it is demonstrated that a finite-amplitude bifurcation is not possible in this case.

If Q is the amount of heat transported between plates via the thermal convection, the balance between the convective and conductive heat transfer is quantified by the Nusselt number:

$$\begin{aligned} Nu = \frac{QH}{\alpha \Delta T}, \end{aligned}$$

(45)

where $\alpha$ is the thermal conductivity of the fluid.

Whereas there exist an overwhelming number of fundamentally important studies of the Rayleigh–Bénard convection in Newtonian fluids, much less progress has been achieved in understanding the thermal convection in non-Newtonian fluids. The reason for this most probably originates in the highly non-trivial coupling between the hydrodynamic problem, the rheological properties of the fluids and their thermal dependence.

A systematic theoretical analysis of the Rayleigh–Bénard convection in shear-thinning fluids is presented by Albaalbaki and Khayat (2011). Using the Carreau–Bird rheological model, they show that although the onset of the thermal convection is the same as in the Newtonian case, the non-Newtonian fluids can convect in the form of rolls, squares or hexagons, depending on the degree of shear thinning. They also predict that in the case of a strong enough degree of shear thinning the bifurcation may turn sub-critical.

The experimental investigation presented by Lamsaadi and his coworkers for a power law fluid revealed an increase of the Nusselt number with the shear-thinning index (Lamsaadi et al. 2005). There exist several systematic studies of the Rayleigh–Bénard convection in viscoelastic fluids focusing on the role of elasticity (quantified by the Weissenberg number) on the onset of convection and on the main features of the transition (Park and Ryu 2001; Park and Park 2004). The experimental investigation presented by Martinez-Mardones and his coworkers for a viscoelastic fluid has captured the influence of the rheological parameters on the critical conditions (Martinez-Mardones et al. 2000). The experiments performed on viscoelastic shear-thinning fluids by Liang and Acrivos (1970) indicate that the transition to convective states emerges as a supercritical bifurcation. They also conclude that the experimentally observed convective patterns are similar to the Newtonian ones. The main effect of the non-Newtonian rheological behaviour on the Rayleigh–Bénard convection is an increase of the Nusselt number as compared to a Newtonian fluid with the same viscosity.

The practical interest in understanding thermo-convective instabilities in viscoplastic originates from the fact that such materials are relevant to various geophysical flows such as magma flows within the Earth’s mantle (Griggs 1939; Meinesz 1947; Orowan 1965; Le Bars and Davaille 2004).

Systematic studies of the hydrodynamic stability of yield stress fluids have been performed only recently (Frigaard et al. 1994; Landry et al. 2006; Metivier et al. 2005). In this context, there exist several fundamental mathematical and physical problems yet to be understood. One of these problems concerns with the occurrence of the Rayleigh–Bénard instability in yield stress materials.

The very first theoretical study of the Rayleigh–Bénard convection in a yield stress fluid was performed by Zhang et al. (2006). Using a linear stability approach formulated within the framework of the Bingham rheological model, they show that base state is stable to infinitesimally small perturbations regardless the finite value of the yield stress. This is due to the fact that, corresponding to the stable base flow state, the Bingham model predicts an infinite viscosity which cannot be destabilised by infinitesimally small perturbations.

The weakly nonlinear stability analysis performed by Balmforth and Rust (2009) carried out within the framework of the Bingham rheological model indicates that a sufficiently large finite-amplitude perturbation of the base state of a viscoplastic fluid may trigger Rayleigh–Bénard convection.

The experiments that complement their theoretical investigation confirm that the presence of the yield stress generally suppresses the convection in the sense that the fluids will not spontaneously convect unless a perturbation of a finite amplitude is applied. The magnitude of the perturbation needed to initiate the convection increases with the yield number Y which characterises the competition between the buoyancy-induced stresses and the yield stress of the fluid.

A numerical simulation study of the Rayleigh–Bénard convection of a Bingham fluid in a square enclosure is presented by Turan et al. (2012). By a systematic scaling analysis Turan and his coworkers assess the scaling of the relevant non-dimensional numbers corresponding to the onset of the instability and relate the results to the strength of the gel.

An experimental study of the development of thermal plumes within a Carbopol^® gel due to local heating was recently presented by Davaille et al. (2013). Depending on the yield number Y, they have observed three distinct dynamic regimes: stable, small-scale convective (the convection is localised around the heater) and thermal plumes. A systematic description of the morphology of the thermal plumes is provided as a function of the yield number. The study by Davaille et al. (2013) reinforces the main conclusion of the study by Balmorth and Rust that finite-amplitude perturbations may indeed destabilise the base flow of fluids with a finite yield stress.

Darbouli et al. (2013) have studied experimentally the Rayleigh–Bénard convection within various Carbopol^® gels confined in a cylindrical cavity and heated from below. Although they did not intentionally applied a finite-amplitude perturbation, they did observe convective states various values of the yield stress that cover a limited range (0.0047–0.104 Pa) (according to their Table 1). Bearing in mind that the accuracy of the determination of the yield stress via classical rheometry is somewhat limited and the uncertainties becomes increasingly larger when the yield stress is diminished, it is not fully clear whether their materials truly possessed a yield stress or they were merely shear-thinning fluids (which is the case when the concentration of Carbopol^® is smaller than the overlap concentration even at neutral pH).

In the case of a viscoplastic fluid, the onset of the Rayleigh–Bénard convection coincides with the onset of the solid–fluid transition (yielding) and thus, the viscous stresses are infinite at the onset. This suggests that, in the case of a viscoplastic fluid, the onset condition should be reconsidered. For this purpose, the force balance criterion can be modified by considering that the thermal convection is triggered when the stresses associated to the buoyancy overcome the yield stress $\tau _y$ of the gel and by replacing the viscous timescale with a characteristic timescale associated to the microstructure of the gel:

$$\begin{aligned} Ra = \frac{\rho \beta \Delta T g H}{\tau _y} \frac{t_d}{t_g} \ge Ra_c \end{aligned}$$

(46)

Here, $t_d= \frac{H^2}{\kappa }$ is the characteristic timescale associated to the thermal diffusion and $t_g$ is a characteristic timescale associated to the gel microstructure near the onset of the convection (i.e. near the yield point) which will be discussed in detail through our paper in connection to the rheological properties of the Carbopol^® gels. As the yield stress has been considered as a scale for the stresses, the definition above is valid only around the onset of the instability which coincides with the onset of the solid–fluid transition (yielding). Far beyond the onset, the Rayleigh number should be rewritten in terms of a shear-thinning viscosity.

From a phenomenological point of view and following the basic ideas of the (energy) balance theorem initially introduced by Chandrasekhar (1961), one can alternatively consider that the thermal convection in a yield stress fluid is initiated when the energy dissipated per unit volume of material by the buoyancy forces becomes comparable in magnitude to the maximal elastic energy that the gel network can locally store per unit volume prior to yielding: $W_b \ge W_e$. Here, $W_e = \rho g \beta \Delta T$ is the energy dissipated per unit volume by the buoyancy forces and $W_e = \tau _y$ is the elastic energy per unit volume. With these considerations, the energy criterion for the convective instability in a yield stress fluid can be formulated in terms of the yield number Y:

$$\begin{aligned} Y = \frac{\tau _y}{\rho \beta g H \Delta T } \le Y_c \end{aligned}$$

(47)

To the best of our knowledge, there exists no experimental assessment of the validity of the force and energy balance criteria for the transition to thermal convective states in a Carbopol^® gel given by Eqs. (46) and (47).

The present study concerns with an experimental investigation of the Rayleigh–Bénard convection in Carbopol^® gels with various concentrations (yield stresses). Among the primary goals of the study, we mention the accurate detection of the onset of the instability in relation with the rheological properties of the gel (yield stress), the characterisation of the convective flow patterns as a function of the control parameter. Of particular interest is the assessment of the nature of the bifurcation towards convective states which is little documented by the existing body of experimental work. In addition to these goals, we are interested in the scaling of the physical parameters characterising the onset of the convective instability with the rheological properties of the solutions which will allow one to probe the applicability of the force and energy balance stability criteria discussed above.

5.2.1 Experimental Setup and Methods

The Rayleigh–Bénard convection cell is schematically illustrated in Fig. 40. It consists of a rectangular cavity with acrylic-made flat transparent walls. The length of the fluid cavity is $L=386$ mm, the width is $W=186$ mm and its height is $H= 20$ mm. The length-to-height aspect ratio of the cavity is $L/W = 19.3$. The bottom and the top enclosures of the cavity are 3-cm-thick polycarbonate plates. The smooth surfaces of the plates have not been treated neither chemically nor mechanically, and thus the wall slip phenomenon was present during the experiments with Carbopol^® gels. The significant width of these two plates and their small thermal conductivity coefficient have been purposely chosen in order to obtain a uniform temperature distribution along the entire fluid cavity. The bottom plate was heated electrically by a resistive circuit fed by a constant current I supplied by the stabilised current supply CS. The heating power was calculated as $P=R I^2$ where $R= 25.5~\Omega$ is the resistance of the electrical heater. To avoid the thermal damage of the bottom polycarbonate plate, a copper plate CP is interposed in between the polycarbonate plate and the resistive heater.

The top plate was uniformly cooled by means of a circulating fluid bath CFB. The circulating fluid is a mixture of glycerin and anti-freeze, and its temperature is maintained constant through our experiments, $T_{wb}=-10\,^\circ$C.

The transition to the Rayleigh–Bénard convection was simultaneously investigated by both integral measurements of the temperature difference $\Delta T$ between plates and local measurements of the amplitude of the convective states.

Fig. 40

Schematic view of the experimental setup L—solid-state laser, CO—cylindrical optics block, CP—copper plate, TP—top plate, BP—bottom plate, CFB—cooling fluid bath, $\mathbf {A_2D}$—analogical to digital signal conditioning block, RB—reference box

Prior to characterising the transition to the Rayleigh–Bénard convection within a Carbopol^® gel, we have focused on a systematic validation of the experimental system and the measuring techniques with a Newtonian fluid, pure Glycerin. The experimentally measured values of the physical parameters for the Glycerin are $\beta = 5\cdot 10^{- 4}\mathrm{K}^{-1}$, $g=9.8\,\mathrm{m}^2/\mathrm{s}$, $\kappa =1.37 \cdot 10^{-7}\,\mathrm{m}^2/\mathrm{s}$ and $\nu = 872 \cdot 10^{-6}\,\mathrm{m}^{2}\,\mathrm{s}^{-1}$.

Fig. 41

a Temperature measurements within the bottom plate BP (the empty circles) and within the top plate TP (the empty squares). The full lines are linear fitting functions and the full symbols are the linear extrapolations of the temperature measurement at the contact points with the fluid. b Time series of the temperature difference $\Delta T$. $t_d$ stands for the characteristic thermal diffusion time, and $t_c$ stands for the characteristic slowing downtime. The dependence of the thermal diffusion time td on the heating power, P, measured for three Carbopol^® solutions with the concentrations $c = 0.06, 0.075, 0.08\%$ for both increasing (full symbols) and decreasing (empty symbols) heating powers is presented in the inset. The full line is the theoretical estimate, $t_d \approx 2730$ s (see text)

Measurements of the temperature difference $\Delta T$ between the plates performed with a Glycerin solution for both increasing and decreasing values of the heating power P are presented in Fig. 41a. A linear increase of the integral temperature difference between the plates $\Delta T$ with P which corresponds to a purely conductive heat transfer regime (the slope of this dependence is proportional to the thermal conductivity $\alpha$ of fluid) is observed below a critical value of the heating power $P_c \approx 16.32$ W. Beyond this onset, the dependence becomes nonlinear consistently with a mixed conductive–convective heat transfer regime. Based on the material parameters enumerated above, the critical Rayleigh number corresponding to the onset of the thermal convection can be estimated $Ra_c \approx 1774$ which is in a very good agreement (within $4\%$) with the theoretical value $Ra_c^t = 1708$ given in Chandrasekhar (1961).

The dependence of the reduced temperature difference $\Delta T_{r}=\frac{\Delta T}{\Delta T_{lin}}-1$ on to the reduced power $P_{r}=P/P_c-1$ is presented in the top panel of Fig. 41b. Here $\Delta T_{lin}$ represents the linear temperature difference measured within the conductive regime (see the full line in Fig. 41a). It can be observed that the reduced temperature difference $\Delta T_{r}$ increases linearly with the reduced heating power $P_r$ consistent with a supercritical bifurcation towards convective states.

Measurements of the convection amplitude obtained via the DPIV technique as a function of the heating power are presented in Fig. 41b.

Around the onset of convection, the velocity amplitude follows the Landau theory of imperfect bifurcations, Landau and Lisfshits (1980):

$$\begin{aligned} P_r V -a V^3+h=0 \end{aligned}$$

(48)

Here, a is the amplitude coefficient and h is the imperfection coefficient which quantifies the degree of smearing of the bifurcation. This result agrees with both theoretical predictions (Newell and Whitehead 1969; Segel 1969) and previous experimental findings, Dubois and Bergé (1978).

To conclude this part, the measurements illustrated and discussed above clearly identify the transition to convective states within a Newtonian fluid as an imperfect bifurcation.

After having probed by these measurements the reliability of our experimental setup and measuring methods, we focus in the following section on the transition to the Rayleigh–Bénard convection in various Carbopol^® gels.

Fig. 42

a Dependence of the temperature gradient $\Delta T$ within Glycerin on the heat flux P. The full/empty symbols refer to increasing/decreasing heat flux. The vertical dashed line marks the transition between the conductive and convective regimes. A typical DPIV measured convection pattern is illustrated in the inset. b (Top) Dependence of the reduced temperature $\Delta T_{r}$ on the reduced power. The line is a linear fit. (Bottom) Dependence of the pattern amplitude V on the reduced power $P_{r}$. The line is a nonlinear fit according to Landau’s theory of imperfect bifurcations, Eq. (48)

5.2.2 Experimental Observation of the Thermal Convection in a Carbopol^® Gel

To study the thermo-convective stability of a physical gel, we have used various Carbopol^® solutions with weight concentrations ranging in between 0.05 and $0.11\%$ as working fluids and the same experimental procedures as for the Newtonian test case discussed in the previous section. The chosen polymer concentrations all lie above the overlap concentration $c^{*}$ which ensures that our working fluids are indeed yield stress fluids not just weakly shear thinning. A more systematic account of the experimental observations is given in Kebiche et al. (2014).

As for the case of a Newtonian fluid, the transition to convective states within various Carbopol^® gels is simultaneously assessed by both local flow speed measurements by the DPIV technique and integral measurements of the temperature difference between the top and the bottom plates, $\Delta T$ (Fig. 42).

For each value of the concentration of the Carbopol^® solution, no measurable flow is observed if the integral temperature difference between plates does not exceed a critical value, $\Delta T < \Delta T_c$. As the temperature difference is increased past this onset, the energy dissipated per unit volume of material by the buoyancy forces overcomes the elastic energy associated with the gel microstructure. Consequently, the gel locally yields and roll flow patterns are observed. The unstable flow patterns are observed in the absence of an external perturbation of a finite amplitude.

The evolution of the flow patterns as the control parameter is varied right above the onset of the convection monitored within a $0.08\%$ Carbopol^® solution is illustrated in Fig. 43.

Fig. 43

Evolution of the flow patterns corresponding to several values of the integral temperature difference $\Delta T$ indicated in the inserts. The up/down arrows indicate the increasing/decreasing branch of the heating ramp. The false colour map refers to the absolute value of the flow velocity. A 0.08% Carbopol^® solution was used and the onset of the Rayleigh–Bénard convection corresponds to $\Delta T_c =2.58\,{^{\circ }\mathrm{C}}$

Right above the onset of the convection ($\Delta T=3.18\,^{\circ }\mathrm{C}$), the flow pattern has a slightly asymmetric appearance. This may be due to the large characteristic times $t_c$ needed for the pattern to reach a steady state or the so-called critical slowing down phenomenon which will be discussed in detail through the paper. Upon an increase of the temperature difference between plates, the flow patterns become more regular and the horizontal extent $\lambda$ of the convection rolls decreases (equivalently with an increase of the horizontal wave number $q_x= \frac{2 \pi }{\lambda }$). It is important to note that the flow states are reversible upon a decrease of the heating power (or temperature difference) which is a first indicator that, similarly to the Newtonian case, the transition to the Rayleigh–Bénard convection in the Carbopol^® gel is a continuous one and exhibits no hysteresis. This qualitative similarity with the transition to convective states within a Newtonian fluid that deserves being studied in depth.

Integral measurements of the dependence of the temperature difference between plates $\Delta T$ performed for six values of the Carbopol^® concentration and for both increasing (the full symbols) and decreasing (the empty symbols) values of the heating power P are presented in Fig. 44.

Fig. 44

Dependence of temperature gradient on the heat flux for six values of the Carbopol^® concentration: ($\bigtriangleup$, $\blacktriangle$)—$c = 0.11 \%wt$, ($\circ$, $\bullet$)—$c = 0.1 \%wt$, (, )—$c = 0.08 \%wt$, ($\blacklozenge$, $\diamond$)—$c = 0.075 \%wt$, ($\star$, )—$c = 0.06 \%wt$, ($\square$, $\blacksquare$)—$c = 0.05 \%wt$. The full/empty symbols refer to increasing/decreasing heat flux. The full line is a linear fit

For each value of the Carbopol^® concentration, a linear conductive part of the dependence is observed below a critical heating power $P_c$. The slopes of these linear dependencies are independent on the polymer concentration (see the full line in Fig. 44) indicating that the polymer addition does not significantly alter the thermal conductivity of the aqueous solutions. This result is fully consistent with direct measurements of the thermal conductivity coefficient $\kappa$ performed for each solution separately (Kebiche et al. 2014). Beyond the onset $P_c$, the dependence of the temperature difference between plates on the heating power becomes sub-linear and a convective regime is observed.

Regardless of the yield stress of the Carbopol^® solution, the transition from a conductive to a convective regime is reversible upon increasing/decreasing values of the heating power and a strong qualitative similarity of these integral measurements to the similar ones performed with a Newtonian fluid previously discussed is observed.

To gain a deeper insight into the nature of the bifurcation towards convective states within the Carbopol^® solutions, we present the same data in terms of the reduced variables $\Delta T_r$, $P_r$. The dependence of the reduced temperature $\Delta T_r$ on the control parameter $P_r$ for each Carbopol^® solution is presented in Fig. 45a.

Fig. 45

a Dependence of the reduced temperature $\Delta T_{r}$ on the reduced power $P_{r}$ for various Carbopol concentrations, see Fig. 44. The full lines are linear fitting functions. b Dependence the DPIV measured amplitude of the convection pattern V on the reduced power $P_{r}$. The line is nonlinear fit function according to the Landau theory of imperfect bifurcation, Eq. 48

Above the onset of the bifurcation, the reduced temperature $\Delta T_r$ scales linearly with the control parameter and this result is, as in the Newtonian case illustrated in Fig. 42a, typical for a supercritical bifurcation. This fundamentally important conclusion on the nature of the bifurcation towards convective states is reinforced by the local measurements of the convective amplitude V presented in Fig. 45b. Indeed, above the onset of the bifurcation, the amplitude data can be well fitted by the Landau prediction for a supercritical bifurcation. The smearing of the transition data observed near the onset indicates that the bifurcation is an imperfect one. The degree of smearing of the bifurcation is rather small ($h \approx 0.05$), and the bifurcation is rather close to a perfect one.

The dependence of the onset parameters on the yield stress of the Carbopol^® solution is illustrated in Fig. 46.

Fig. 46

a Dependence of the critical heating power $P_c$ corresponding to the onset of the Rayleigh–Bénard convection on the yield stress $\sigma _y$ of the Carbopol^® solution. The line is an exponential fit. b Dependence of the critical yield number $Y_c$ (squares, bottom-left axis) and of the critical Rayleigh number $Ra_c$ (circles, bottom-right axes) on the yield stress $\sigma _y$

The critical heating power needed to trigger convective states increases exponentially with the yield stress of the Carbopol^® solution, Fig. 46a. This indicates that in solutions with a sufficiently large yield stress the thermal convection cannot be experimentally observed as it would require heating powers practically unsustainable.

Another important issue relates to the right control parameter to describe the transition towards convective states. In the case of Newtonian fluids, this is the Rayleigh number (Chandrasekhar 1961). To test if this the case for a Carbopol^® gel, we have calculated the critical Rayleigh number corresponding to the onset of convection according to Eq. (46). The result is displayed in Fig. 46b (the circles). Quite remarkably, as the yield stress of the solution varies, the critical Rayleigh number $Ra_c$ spans nearly three orders of magnitude. This clearly indicates that, unlike for the case of Newtonian fluids, Ra is not the right control parameter. On the other hand, the yield number Y calculated at the onset of the instability according to Eq. (47) remains of order of unity over the entire range of yield stresses explored. This indicates that the right control parameter for the thermo-convective instability in a Carbopol^® gel is the yield number.

To conclude this section, we have demonstrated that, contrary to the existing theoretical predictions, thermal convection can be triggered in a Carbopol^® gel in the absence of any finite-amplitude perturbation and the bifurcation towards convective states is an imperfect one (described by the Landau–Ginzburg formalism). A first physical ingredient that probably needs to be accounted for in the theoretical studies is related to the rather new scenario of the yielding illustrated in Sect. 2 that accounts for a gradual yielding process characterised by both a solid–fluid phase coexistence and elastic effects that are not captured by the classical rheological pictures. Indeed, measurements of the second invariant of the rate of strain (not shown here as shown in Figure 19 of Kebiche et al. 2014) indicate that the onset of convection is practically located within the non-trivial solid–fluid coexistence zone (hysteresis) visible in Figs. 3b and 4. Thus, any theoretical attempt to describe this instability using the Herschel–Bulkley law that is applicable at much larger rates of strain is not expected to accurately predict the transition. A second theoretical ingredient worth to be accounted for in future theoretical developments is related to the non-trivial (and rather unexpected) thermo-rheological behaviour of the Carbopol^® gel presented in Sect. 5.1.

6 Concluding Remarks

During the past decade, the fluid dynamics of viscoplastic materials has emerged as a distinct field of the hydrodynamics of complex fluids rivalling, perhaps, with the well-established field of hydrodynamics of viscoelastic fluids. This intellectually very rich discipline brings together several scientific communities: fluid dynamics, rheology, applied mathematics, thermal science, engineering. The dynamics of yield stress materials poses highly non-trivial problems even in isothermal flow conditions.

The first class of isothermal flows we have studied was that of low Reynolds number flows and the main scope was understanding the physics of the solid–fluid transition in a physical gel subjected to a gradually increasing external stress. The physical complexity of this problem comes from a strong nonlinearity of the stress term in the momentum conservation and a highly non-trivial coupling between the flow field and the microstructure of the material. In this context, the Carbopol^® gels have been considered as “model” yield stress materials for over two decades and their flows have been traditionally studied within the classical Herschel–Bulkley model. Yet, it has been shown only recently that this classical picture is unable to describe several “simple” fluid dynamics problems: the low Re sedimentation of a spherical object (Sect. 1), the slow withdraw of a rigid plate at a constant speed (Sect. 1). These rather unexpected experimental facts have prompted us to reconsider the solid–fluid transition by careful and more systematic rheological tests, Sect. 1. Contrary to the common belief that Carbopol^® gels behave as “model” yield stress fluids accurately described by the Herschel–Bulkley constitutive equation, we have found a gradual and irreversible yielding scenario together with significant elastic effects. Thus, the Herschel–Bulkley constitutive relationship is applicable only far above the transitional region, i.e. at large enough rates of deformation. In an attempt to “rationalise” these findings, we have proposed a phenomenological model that we have coined “The Poor Man Model”, Sect. 2. These results initially published in Putz and Burghelea (2009) have been received with a fair amount of scepticism by the viscoplastic community which prompted us for an additional validation in simple low Reynolds number pipe flow upon an increase/decrease of the driving pressures (Poumaere et al. 2014). This particular experiment has finally dissipated any doubts on the nature of the solid–fluid transition: a hysteresis of the deformation states is equally observed in a pipe flow. Reassured by this result, we have started to develop a scientifically more solid theoretical approach to explain the solid–fluid transition, Sect. 3. This time we have resorted to the tools of Statistical Physics and Critical Phenomena and derived from first principles a model somewhat similar to the Ising model of the ferromagnetism. The model depends on solely two internal parameters and, as it is formulated from first principles, it is inherently validated from a thermodynamic standpoint. The central conclusion of the approach is that, when the magnitude of the interactions between the microscopic building blocks of a yield stress material exceeds a threshold, an irreversible solid–fluid transition will be observed regardless the manner the material is forced: steadily or unsteadily. This threshold is the exact physical equivalent of the Curie temperature in a magnetic system. For weakly interacting systems such as Carbopol^® gels, a reversible yielding scenario may be retrieved in the asymptotic limit of a steady-state external forcing.

An extra level of complexity is added to the flow problem of a yield stress material if the Reynolds numbers are sufficiently high. Thus, a fundamental question how does the viscoplasticity couples to the inertial hydrodynamic instability observed at $Re>1000$, Sect. 4. The complexity of this question comes from two sources of nonlinearity in the momentum equation: inertial and due to the highly nonlinear dependence of the stresses on the rate of strain. An experimental study of the laminar–turbulent transition in a Carbopol^® gel is presented in Sect. 4.1. The central conclusion of this study is that the inertial instability sets in when the Reynolds stresses become comparable in magnitude with the yield stress. This suggests that, somewhat peculiarly, the loss of the hydrodynamic stability cannot be fully decoupled from the solid–fluid transition although the onset Reynolds number is large. We have pursued this idea in Sect. 4.2 where we have addressed the question of how the inertial instability of a plane Poiseuille flow is affected by the yielding scenario. The central conclusion of this part was that switching from the classical Herschel–Bulkley yielding scenario to the model by Putz and Burghelea (2009) framework developed in Sect. 2 changes significantly the stability picture: the elasticity present in the model by Putz and Burghelea (2009) has a destabilising role. In Sect. 4.3, we show that if one generates strong spatial gradients of stresses via a chemical reaction that locally produces a Carbopol^® gel one obtains a sharp hydrodynamic instability in the absence of any inertial contribution. We have shown that this novel instability may turn useful in both efficiently displacing very viscous fluids from a flow channel and obtaining efficient mixing in situations where increasing Re is un-practical, e.g. micro-fluidics systems.

Yet, a third layer of complexity is added to the flow problem of a viscoplastic material if one considers the non-isothermal case (Sect. 5). What looked at a first glance the most basic and straightforward problem was related to the temperature dependence of the rheological properties of a Carbopol^®, Sect. 5.1. Quite surprisingly, the thermo-rheology of a Carpobol^® gel departs from the classical Arrhenius picture. We provide a phenomenological explanation in terms of the physico-chemical properties of a swollen system of polyacrylic acid spongy particles in conditions of neutral pH.

In Sect. 5.2, we have shown that, contrary to the existing theoretical predictions, the Rayleigh–Bénard convection can be triggered in a Carbopol^® gel in a wide range of measurable yield stresses. Although we do not yet have a detailed theoretical explanation for this fact, we believe this discrepancy originates from the non-trivial yielding scenario observed experimentally in Sect. 1 and theoretically described in Sects. 2 and 3.