Introduction

The rheological behavior of hydrophobic alkali-soluble emulsion (HASE) polymers has been the subject of intense research over the past 10–15 years because of their ample applications in the paint and coating industry, in water treatment, and in enhanced oil recovery, where thickening efficiency is an important factor (Seng et al. 1999; Ng et al. 2001; Kästner 2001). Essentially, these polymers consist of a long-chain hydrophilic backbone to which small amounts of hydrophobic constituents are incorporated (Tan et al. 2000; Tam et al. 2000; Dai et al. 2002). When these polymers are dissolved in water, hydrophobic groups aggregate to minimize their water exposure. In semidilute aqueous solutions at basic pH, hydrophobic groups form intramolecular and intermolecular associations that give rise to a three-dimensional network, which can be disrupted by flow. The formation and breakdown of the network have often been followed by rheological measurements (English et al. 1997, 1999).

The dynamic response of HASE polymer solutions is characteristic of a viscoelastic liquid, in such a way that linear viscoelastic spectra reflect two types of interactions: those produced via topological entanglements and those produced via hydrophobic associations. Consequently, linear viscoelastic response differs significantly from that observed in other types of associative polymers, namely, hydrophobic ethoxylated urethane (HEUR) polymers, since the network dynamics of HASE-type polymers cannot be represented by the Maxwell model. In fact, the elastic modulus (G′) and the loss modulus (G″) of HASE systems in the terminal region display a weaker dependence on frequency than that exhibited by HEUR polymers, which can be attributed to the broadening of the terminal relaxation spectrum due to the combined effects of topological entanglements and hydrophobic associations.

The dynamics of the associative network structure formed by hydrophobic interactions in HASE systems has been investigated by a number of techniques, including superposition of oscillations on steady shear flows (English et al. 1997, 1999; Tirtaatmadja et al. 1997; Mewis et al. 2001). These techniques have provided information on the balance between entanglement depletion and intermolecular association under steady shear. As superposed steady shear is increased, the entire terminal region of the moduli shifts to higher frequencies, implying that longer time modes of relaxation are lost. This behavior is ascribed to a reduction in the steady state entanglement density of the polymer network, in which longer modes due to entanglements vanish and shorter modes due to hydrophobic associations remain. Similar information is obtained from unsteady shear flows and from comparisons of dynamic viscosity and steady-shear viscosity.

Modeling of the rheological behavior of associative polymers has concentrated mainly on low molecular weight HEUR solutions due to their similarities with simple Maxwellian behavior (Annable et al. 1993; Tanaka and Edwards 1992). Developments in HASE systems are more complicated due to the presence of molecular entanglements. The dynamics of entangled networks formed by linear chains with temporary junctions has been investigated. The model of Leibler et al. (1991) predicts, similarly to the theory of Doi and Edwards (1986), two basic relaxation processes. The slower process is related to the reptation of polymer chains and is found to be a function of association degree; the faster process is due to the relaxation of segments between entanglement points and is related to the average lifetime of associations. Some other studies have fitted the fast relaxation process to a Rouse or Zimm spectrum (Tirtaatmadja et al. 1997), inasmuch as the short time process is related to fast movements of segments of the hydrophilic backbone and to hydrophobic chains.

Other associative polymers, such as hydrophobically modified hydroxyethyl cellulose (HMHEC), show two relaxation processes (Maestro et al. 2002). The longer relaxation process corresponds to chain relaxation after a hydrophobic junction is broken (inverse of the exit rate of a hydrophobe from a micelle) and the shorter relaxation time observed at high frequencies is attributed to rapid movements of free chains and may follow the Rouse or Zimm model (Tirtaatmadja et al. 1997). For telechelic HEUR polymers, on the other hand, disengagement of a hydrophobe necessarily implies the relaxation of the whole chain and the breakage of elastic chains (Annable et al. 1993). In polymers with comb structures, such as HASE and HMHEC, a spectrum of relaxation times is necessary to explain their viscoelastic behaviors (Maestro et al. 2002).

The modeling of associative polymers has been analyzed by transient network models (Vaccaro and Marrucci 2000) that introduce a nonlinear entropic law for network segment deformations to predict the shear-thickening regime observed in the experimental data of viscosity vs shear rate. In addition, others (Maestro et al. 2002) have introduced a spectrum of relaxation times to capture the relaxation process of long chains and the relaxation involved in the disengagement of hydrophobic groups of the molecule in HASE- and HMHEC-type polymers. In this regard, attention is given in this work to the modeling of the rheological behavior of HASE-type polymers. For this purpose, we use a multimode version of a model that combines a rheological equation of state with a kinetic equation, which represents the breakage and reformation process of the structure as it is modified by the flow (Bautista et al. 1999). This model has been proposed elsewhere (Manero et al. 2002) to predict the behavior of complex fluids where a kinetic process of flow-induced structure modification is involved. The present analysis generalizes this model by considering a spectrum of relaxation times, which is consistent with transient network formulations (Manero et al. 2002). This kinetic approach is justified in systems where the molecular weight between hydrophobic associations is small compared to the physical entanglement molecular weight. In this situation, the number density of hydrophobic associations exceeds the number density of entanglements, and the dynamics is governed by the formation and destruction of hydrophobic associations. In the deformation range that corresponds to a linear viscoelastic regime, this model reduces to a multimode linear Maxwell model.

The objective of the present analysis is the prediction of behavior in the shear flow of a commercial HASE polymer currently employed in the painting industry that contains small surfactants and additive contents. We are aware that, in industrial samples, surfactants and additives are added to stabilize latex and that their presence can modify the rheology of the system substantially. In this regard, this work is not intended to draw conclusions on the relationship between chemical structure and the rheology of pure HASE polymers, but rather to deal with a complex system actually used in industrial processes. This analysis is therefore focused on the rheological modeling of complex commercial systems constituted by transient networks where, besides the kinetic process of breakage reformation, a spectrum of relaxation times is implied.

Experimental

Aqueous solutions of 0.5 M 2-amino-2-methylpropanol (AMP) or KOH and 2 wt% HASE polymer (Primal TT-935; Rohm and Haas) were prepared and left to rest for 48 h prior to measurements. In addition, aqueous solutions of TT-935 at various pH values were prepared by subsequently adding AMP or KOH solutions to a freshly made 2 wt% TT-935 solution under stirring. The pH after each addition was recorded in a Solution Analyzer 5800-05 pH meter with an Ag/AgCl electrode (Thermodyne S-7805). The pH meter and the electrode were calibrated with two buffer solutions (pH 4.0±05 and 10.0±0.05).

Steady simple-shear and linear oscillatory measurements were made in a TA Instruments AR-1000 N stress-controlled rheometer with a stainless-steel cone and a plate fixture (diameter, 6 cm; angle, 2°). Time-dependent simple-shear measurements were performed in a Rheometrics 3LS-1A Ares strain-controlled rheometer (stainless-steel cone and plate; diameter, 5 cm; angle, 2.28°). Sinusoidal response wave was tested at each measurement to ensure that inertial effects were not important at the frequencies used. Shear viscosities of TT-935 solutions at different pH values made with any of the alkali solutions were measured with the stress-controlled rheometer, covering a shear rate range from 0.01 to 300 s−1. From these data, the dependence of zero shear rate viscosity on pH was obtained. Experiments in small-amplitude oscillatory flows of a solution of 2 wt% HASE + 0.5 M AMP (to keep the pH at 9.0) were performed from 5 to 25°C, covering 4.5 decades in frequency (0.01–500 s−1). Sufficient time was allowed for thermal equilibration before changing the sample temperature.

The equilibrium surface tension of aqueous solutions maintained at pH 9.0 (using 0.5 M AMP) as a function of HASE concentration was measured in a Whilhemy plate tensiometer. The Gibbs adsorption isotherm and the Volmer equation (Gracia-Fadrique et al. 2002) were used to calculate the amount of components absorbed at the interface from surface-tension-vs-concentration plots, the surface area at the interface per adsorbed molecule, and the critical aggregation concentration (CAC).

The model

The equations of the single-mode model (Bautista et al. 1999; Manero et al. 2002) are written here in terms of the ith contribution to stress according to:

$${\mathop \tau \limits_ = } = {\sum\limits_{i = 1}^n {{\mathop {\tau _{i} }\limits_ = }} }$$
((1))
$${\mathop {\tau _{i} }\limits_ = } + \lambda '{\left( {{\mathop {\tau _{{\text{i}}} }\limits_ = },{\mathop D\limits_ = }} \right)}{\mathop {\tau _{i} }\limits_ = ^\nabla } = 2G_{{0i}} {\text{ $ \lambda $ }}^{\prime }_{i} {\left( {{\mathop {\tau _{{\text{i}}} }\limits_ = },{\mathop D\limits_ = }} \right)}{\mathop D\limits_ = }$$
((2))
$${\text{ $ \lambda $ }}^{\prime }_{i} {\left( {{\mathop {\tau _{i} }\limits_ = },{\mathop D\limits_ = }} \right)} = {\eta _{i} {\left( {{\mathop {\tau _{i} }\limits_ = },{\mathop D\limits_ = }} \right)}} \mathord{\left/ {\vphantom {{\eta _{i} {\left( {{\mathop {\tau _{i} }\limits_ = },{\mathop D\limits_ = }} \right)}} {G_{{0i}} }}} \right. \kern-\nulldelimiterspace} {G_{{0i}} } = A^{{ - 1}}_{i} \lambda _{{0i}} $$
((3))
$$\frac{{dA_{i} }}{{dt}} = \frac{1}{{\lambda _{i} }}{\left( {1 - A_{i} } \right)} + \frac{1}{{G_{{0i}} }}{\left( {{\lambda _{{0{\text{i}}}} } \mathord{\left/ {\vphantom {{\lambda _{{0{\text{i}}}} } {\lambda _{{\infty i}} }}} \right. \kern-\nulldelimiterspace} {\lambda _{{\infty i}} } - A_{i} } \right)}{\mathop {\tau _{i} }\limits_ = }:{\mathop D\limits_ = }$$
((4))

where \(\underline{\underline \tau } \) and \(\underline{\underline D} \) are the stress and rate of deformation tensors, respectively; \({\mathop \tau \limits_ = ^\nabla }\) denotes the upper-convected derivative of the stress tensor; and λ’, η, and G 0 stand for variable relaxation time, viscosity, and elastic shear modulus, respectively. A i are scalars that reflect changes in viscosity due to changes in the structure induced by flow. The three characteristic times λ 0, λ ∞, and λ are Maxwell relaxation time, relaxation time at high frequencies, and structure relaxation time, respectively.

For a single-mode model (i=1), Eq. (2) is the upper-convected Maxwell equation with variable relaxation time, which itself is a function of the scalar A that follows the evolution equation (Eq. 4). The limit of A is one in creeping flows and λ0/λ∞ in strong flows. Equation (4) represents changes in the structure due to flow through a kinetic equation that follows the process of breakage and reformation of the structure. The first term on the right-hand side of Eq. (4) is identified with reformation process, which is governed by the characteristic time λ. The second term is a function of the dissipation (\(\underline{\underline \tau } \):\(\underline{\underline D} \)) and represents the breakage of the structure. When the ratio of the two time scales λ/λ0 is much larger than one, the structure does not reform during the time scale of the external flow process, and the system exhibits thixotropy. In steady state, the single-mode versions of Eqs. (1, 2, 3, 4), according to Bautista et al. (1999) and Manero et al. (2002), are reduced to:

$$\frac{{1 + {\left( {\lambda \mathord{\left/ {\vphantom {\lambda {G_{0} }}} \right. \kern-\nulldelimiterspace} {G_{0} }} \right)}{\left( {{\lambda _{{\text{0}}} } \mathord{\left/ {\vphantom {{\lambda _{{\text{0}}} } {\lambda _{\infty } }}} \right. \kern-\nulldelimiterspace} {\lambda _{\infty } }} \right)}{\left( {{\mathop \tau \limits_ = }:{\mathop D\limits_ = }} \right)}}}{{1 + {\left( {\lambda \mathord{\left/ {\vphantom {\lambda {G_{0} }}} \right. \kern-\nulldelimiterspace} {G_{0} }} \right)}{\left( {{\mathop \tau \limits_ = }:{\mathop D\limits_ = }} \right)}}}{\mathop \tau \limits_ = } + \lambda _{0} {\mathop \tau \limits_ = ^\nabla } = 2G_{0} \lambda _{0} {\mathop D\limits_ = }$$
((5))

where the time derivative contained in the upper-convected derivative is equal to zero. In small deformation flows, Eq. (5) reduces to the linear Maxwell model. In small-amplitude oscillatory flow, the multimode version of Eq. (5) renders well-known expressions of storage and loss moduli:

$$G' = {\sum\limits_{i = 1}^n {G_{{0i}} } }\frac{{\omega ^{2} \lambda _{{0i}} ^{2} }}{{1 + \omega ^{2} \lambda _{{0i}} ^{2} }}$$
((6a))
$$G = {\sum\limits_{i = 1}^n {G_{{0i}} } }\frac{{\omega \lambda _{{0i}} }}{{1 + \omega ^{2} \lambda _{{0i}} ^{2} }}$$
((6b))

provided that the zero strain rate viscosity is:

$$\eta _{0} = {\sum\limits_{i = 1}^n {G_{{0i}} \lambda _{{0i}} } }$$
((7))

Steady simple-shear flow

In steady simple-shear flow, prediction for shear viscosity from the multi-mode version of Eq. (5) is as follows:

$$\eta {\left( {{\mathop \gamma \limits^\cdot }} \right)} = {\sum\limits_{i = 1}^n {\eta _{{0i}} \frac{{{\left( {\lambda _{{0i}} \lambda _{i} {\mathop {\gamma ^{2} }\limits^\cdot } - 1} \right)} + {\left[ {{\left( {\lambda _{{0i}} \lambda _{i} {\mathop {\gamma ^{2} }\limits^\cdot } - 1} \right)}^{2} + 4{\left( {{\lambda _{i} } \mathord{\left/ {\vphantom {{\lambda _{i} } {\lambda _{{\infty i}} }}} \right. \kern-\nulldelimiterspace} {\lambda _{{\infty i}} }} \right)}\lambda _{{0i}} ^{2} {\mathop {\gamma ^{2} }\limits^\cdot }} \right]}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} }}{{2{\left( {{\lambda _{i} } \mathord{\left/ {\vphantom {{\lambda _{i} } {\lambda _{{\infty i}} }}} \right. \kern-\nulldelimiterspace} {\lambda _{{\infty i}} }} \right)}\lambda _{{0i}} ^{2} {\mathop {\gamma ^{2} }\limits^\cdot }}}} }$$
((8))

where the contributions to zero shear rate viscosity are given by η0i =G0i λ0i . The limits of Eq. (8) at low and high shear rates are given by:

$$\eta {\left( {{\mathop \gamma \limits^ \cdot }} \right)} = {\sum\limits_{i = 1}^n {\eta _{{0i}} } } = \eta _{0} \quad {\text{as}}\quad {\mathop \gamma \limits^ \cdot } \to 0$$
((9a))
$$\eta {\left( {{\mathop \gamma \limits^ \cdot }} \right)} = {\sum\limits_{i = 1}^n {G_{{0i}} \lambda _{{\infty i}} = \eta _{\infty } } }\quad \operatorname{as} \quad {\mathop \gamma \limits^ \cdot } \to \infty $$
((9b))

Equation (8) has two asymptotic limits: at moderate shear rates\({\left( {\lambda _{{0i}} \lambda _{i} {\mathop {\gamma ^{2} }\limits^ \cdot } \ll 1} \right)}\) and at very high shear rates\({\left( {\lambda _{{0i}} \lambda _{i} {\mathop {\gamma ^{2} }\limits^ \cdot } \gg 1} \right)}\). For moderate shear rates, Eq. (8) becomes:

$$\eta {\left( {{\mathop \gamma \limits^ \cdot }} \right)} = {\sum\limits_{i = 1}^n {\eta _{{0i}} \frac{{{\left[ {1 + 4{\left( {{\lambda _{i} } \mathord{\left/ {\vphantom {{\lambda _{i} } {\lambda _{{\infty i}} }}} \right. \kern-\nulldelimiterspace} {\lambda _{{\infty i}} }} \right)}\lambda _{{0i}} ^{2} {\mathop {\gamma ^{2} }\limits^ \cdot }} \right]}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} - 1}}{{2{\left( {{\lambda _{i} } \mathord{\left/ {\vphantom {{\lambda _{i} } {\lambda _{{\infty i}} }}} \right. \kern-\nulldelimiterspace} {\lambda _{{\infty i}} }} \right)}\lambda _{{0i}} ^{2} {\mathop {\gamma ^{2} }\limits^ \cdot }}}} }$$
((10))

As shear rate increases within this regime, viscosity approaches the following behavior, provided that \(\lambda _{\infty } {\mathop \gamma \limits^ \cdot } \ll 1:\)

$$\eta {\left( {{\mathop \gamma \limits^ \cdot }} \right)} = {\sum\limits_{i = 1}^n {\frac{{\eta _{{0i}} }}{{\lambda _{{0i}} {\mathop \gamma \limits^ \cdot }}}{\left( {\frac{{\lambda _{{\infty i}} }}{{\lambda _{i} }}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} \quad as\quad {\mathop \gamma \limits^ \cdot } \to \infty } }$$
((11))

Stress relaxation after cessation of steady simple shear

In stress relaxation, Eqs. (1), (2), (3), (4) give the following expression:

$$\tau = {\sum\limits_{i = 1}^n {\tau _{i} } } = {\sum\limits_{i = 1}^n {\eta _{{ssi}} {\mathop \gamma \limits^ \cdot }_{{ss}} \exp {\left[ {{ - t} \mathord{\left/ {\vphantom {{ - t} {\lambda _{{0i}} + \lambda _{i} {\left( {\frac{1}{{\lambda _{{0i}} }} - \frac{{G_{{0i}} }}{{\eta _{{ssi}} }}} \right)}{\left( {1 - e^{{{ - t} \mathord{\left/ {\vphantom {{ - t} {\lambda _{i} }}} \right. \kern-\nulldelimiterspace} {\lambda _{i} }}} } \right)}}}} \right. \kern-\nulldelimiterspace} {\lambda _{{0i}} + \lambda _{i} {\left( {\frac{1}{{\lambda _{{0i}} }} - \frac{{G_{{0i}} }}{{\eta _{{ssi}} }}} \right)}{\left( {1 - e^{{{ - t} \mathord{\left/ {\vphantom {{ - t} {\lambda _{i} }}} \right. \kern-\nulldelimiterspace} {\lambda _{i} }}} } \right)}}} \right]}} },$$
((12))

In this equation, \({\mathop \gamma \limits^ \cdot }_{{ss}} \) is the steady-state shear rate and η ssi is the spectral contribution to steady shear viscosity prior to cessation of flow. In the limit of vanishing shear rate, η ssi →η 0i and, hence, λ0i →η ssi /G 0i ; thus, Eq. (12) reduces to the expression corresponding to the monoexponential relaxation of stress, consistent with linear Maxwell model expressions in oscillatory flow (Eqs. 6a and 6b):

$$\tau = \eta _{{ss}} {\mathop \gamma \limits^ \cdot }_{{ss}} \exp {\left( {{ - t} \mathord{\left/ {\vphantom {{ - t} {\lambda _{0} }}} \right. \kern-\nulldelimiterspace} {\lambda _{0} }} \right)}$$
((13))

Here, the characteristic time λ0 is the longest relaxation time of the system. For arbitrary shear rates, Eq. (12) has two limits for short and long times, namely:

$$\tau = \eta _{{ss}} {\mathop {\gamma _{{ss}} }\limits^ \cdot }\exp {\left( {{ - tG_{0} } \mathord{\left/ {\vphantom {{ - tG_{0} } {\eta _{{ss}} }}} \right. \kern-\nulldelimiterspace} {\eta _{{ss}} }} \right)}\quad {\text{as}}\quad t \to 0$$
((14))
$$\tau = {\sum\limits_{i = 1}^n {\eta _{{ssi}} {\mathop {\gamma _{{ss}} }\limits^ \cdot }\exp {\left[ {{ - t} \mathord{\left/ {\vphantom {{ - t} {\lambda _{{0i}} }}} \right. \kern-\nulldelimiterspace} {\lambda _{{0i}} } + \lambda _{i} {\left( {\frac{1}{{\lambda _{{0i}} }} - \frac{{G_{{0i}} }}{{\eta _{{ssi}} }}} \right)}} \right]}} }\quad {\text{as}}\quad t \to \infty $$
((15))

where G 0 is the instantaneous modulus (elastic modulus). According to Eq. (13), the domain of η ss is bounded (η 0≥η ss≥η ∞, η 0≡G 0λ0, and η ∞≡G 0λ∞). For small shear rates, η ss→η 0, and Eq. (14) becomes Eq. (13). On the contrary, for large shear rates, η ss→η ∞; hence, Eq. (14) predicts a straight line with a steep slope governed by the characteristic time λ∞ on a semilogarithmic plot. According to Eqs. (14) and (15), for single-mode relaxation, the stress relaxes monoexponentially at short times with a time constant that depends on the previous shear rate, followed by another monoexponential relaxation with characteristic time equal to the Maxwell relaxation time, and with an intercept that depends on two time constants (λ 0,λ) and on the characteristic time of the flow η ss/G 0 . From these expressions, it is clear that, for a multimode expansion, λ 0i and λ i can be evaluated straightforwardly from tangents to the stress relaxation curve. The tangent taken at the longest time has a slope with the longest time constant λ 0 and an intercept that depends on the ratio λ/λ ∞.

Stress relaxation after a step strain

In stress relaxation after a step strain, the time-dependent shear relaxation modulus consistent with Eqs. (1, 2, 3, 4) is given by:

$$G{\left( t \right)} = G_{0} \exp {\sum\limits_{i = 1}^n {{\left[ {\frac{{ - t}}{{\lambda _{{0i}} }} + \lambda _{i} {\left( {\frac{1}{{\lambda _{{0i}} }} - \frac{{G_{{0i}} }}{{\eta {\left( {\gamma \mathord{\left/ {\vphantom {\gamma {\Delta t}}} \right. \kern-\nulldelimiterspace} {\Delta t}} \right)}}}} \right)}{\left( {1 - e^{{{ - t} \mathord{\left/ {\vphantom {{ - t} {\lambda _{i} }}} \right. \kern-\nulldelimiterspace} {\lambda _{i} }}} } \right)}} \right]}} }$$
((16))

where G 0 is the instantaneous modulus, γ is the applied strain, and Δt is the experimental time of the deformation process, which, in most instruments, lies around 0.05 s. Hence, η(γ/Δt) is taken as the viscosity calculated at the shear rate of (γ/0.05). The limits at short and long times can be expressed as:

$$G{\left( t \right)} = G_{0} \exp {\left[ {\frac{{ - tG_{0} }}{{\eta {\left( {\gamma \mathord{\left/ {\vphantom {\gamma {\Delta t}}} \right. \kern-\nulldelimiterspace} {\Delta t}} \right)}}}} \right]}\quad {\text{as}}\quad t \to 0$$
((17))
$$G{\left( t \right)} = G_{0} \exp {\sum\limits_{i = 1}^n {{\left[ {\frac{{ - t}}{{\lambda _{{0i}} }} + \lambda _{i} {\left( {\frac{1}{{\lambda _{{0i}} }} - \frac{{G_{{0i}} }}{{\eta {\left( {\gamma \mathord{\left/ {\vphantom {\gamma {\Delta t}}} \right. \kern-\nulldelimiterspace} {\Delta t}} \right)}}}} \right)}} \right]}\quad {\text{as}}\quad t \to \infty } }.$$
((18))

Let us consider a single-mode relaxation process. At long times, the plot of log[G(t)/G 0] vs time follows a straight line with slope (−1/λ 0) and intercept \(\lambda {\left( {\frac{1}{{\lambda _{0} }} - \frac{{G_{0} }}{{\eta {\left( {{\text{ $ \lambda $ }} \mathord{\left/ {\vphantom {{\text{ $ \lambda $ }} {\Delta t}}} \right. \kern-\nulldelimiterspace} {\Delta t}} \right)}}}} \right)}\). In fact, the single-mode version of Eq. (18) can be written as:

$$G{\left( t \right)} = G_{l} h{\left( \gamma \right)}$$
((19))

where G l is the linear relaxation modulus:

$$G_{l} = G_{0} \exp {\left( {{ - t} \mathord{\left/ {\vphantom {{ - t} {\lambda _{0} }}} \right. \kern-\nulldelimiterspace} {\lambda _{0} }} \right)}$$
((19a))

and

$$h{\left( \gamma \right)} = \exp {\left[ {\lambda {\left( {\frac{1}{{\lambda _{0} }} - \frac{{G_{0} }}{\eta }} \right)}} \right]}$$
((19b))

is the damping function. The limits of η(γ/Δt) are η 0 and η ∞. In the first case, h(γ)→1 and the stress relaxation function becomes monoexponential with time constant λ 0 [G(t)=G l]. For increasing strains, the damping function diminishes down to a limiting value at very large strains given by:

$$h{\left( {\gamma \to \infty } \right)} = \exp {\left( {{ - \lambda } \mathord{\left/ {\vphantom {{ - \lambda } {\lambda _{\infty } }}} \right. \kern-\nulldelimiterspace} {\lambda _{\infty } }} \right)},\quad \lambda _{\infty } \equiv {\eta _{\infty } } \mathord{\left/ {\vphantom {{\eta _{\infty } } {G_{0} }}} \right. \kern-\nulldelimiterspace} {G_{0} }.$$
((20))

As it will be shown later in the case of associative polymers, in the high-strain region, the form of the damping function becomes:

$$h{\left( \gamma \right)} = \exp {\left( { - K^{'} \gamma } \right)}$$

where K′ is the damping coefficient. This form of the damping function has been reported in polymer melts (Bird et al. 1987). However, in the limit of very large strains, the damping function reaches a limiting value given by Eq. (20). From the limiting value of the damping function and the value of the damping coefficient, it is possible to estimate the values of the time constants separately.

Stress growth upon inception of steady shear flow

For the inception of steady shear flow, the following expression of stress growth coefficient derived from the model is obtained at vanishing imposed shear rates:

$$\eta ^{ + } {\left( t \right)} = G_{0} \lambda _{0} {\left( {1 - e^{{{ - t} \mathord{\left/ {\vphantom {{ - t} {\lambda _{0} }}} \right. \kern-\nulldelimiterspace} {\lambda _{0} }}} } \right)}$$
((21))

where λ 0 is the longest relaxation time. For arbitrary shear rates, there are two possible analytical expressions derived from Eqs. (1, 2, 3, 4), which are valid for short and long times, namely:

$$\eta ^{ + } {\left( t \right)} = {\sum\limits_{i = 1}^n {G_{{0i}} {\left[ {\frac{1}{{\lambda _{{\infty i}} }}e^{{{ - t} \mathord{\left/ {\vphantom {{ - t} {\lambda _{i} }}} \right. \kern-\nulldelimiterspace} {\lambda _{i} }}} + \frac{1}{{\lambda _{{0i}} }}{\left( {1 - e^{{{ - t} \mathord{\left/ {\vphantom {{ - t} {\lambda _{i} }}} \right. \kern-\nulldelimiterspace} {\lambda _{i} }}} } \right)}} \right]}^{{ - 1}} \quad {\text{as}}\quad t \to 0} }$$
((22))
$$\eta ^{ + } {\left( t \right)} = {\sum\limits_{i = 1}^n {G_{{0i}} {\left[ {\frac{1}{{\lambda _{{\infty i}} ^{2} }}e^{{{ - 2t} \mathord{\left/ {\vphantom {{ - 2t} {\lambda _{i} }}} \right. \kern-\nulldelimiterspace} {\lambda _{i} }}} + {\mathop {\gamma ^{2} }\limits^ \cdot }{\left( {{\lambda _{i} } \mathord{\left/ {\vphantom {{\lambda _{i} } {\lambda _{{\infty i}} }}} \right. \kern-\nulldelimiterspace} {\lambda _{{\infty i}} }} \right)}{\left( {1 - e^{{{ - 2t} \mathord{\left/ {\vphantom {{ - 2t} {\lambda _{i} }}} \right. \kern-\nulldelimiterspace} {\lambda _{i} }}} } \right)}} \right]}^{{ - 1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} \quad {\text{as}}\quad t \to \infty } }.$$
((23))

Equation (22) has two limits itself, but it only describes the behavior of the real system at short times. Similarly, Eq. (23) also has two limits, but it only describes the behavior of the real system at long times. At very short times, Eq. (22) yields:

$$\eta ^{ + } {\left( t \right)} = G_{0} \lambda _{\infty } {\left( {{1 + t} \mathord{\left/ {\vphantom {{1 + t} \lambda }} \right. \kern-\nulldelimiterspace} \lambda } \right)}$$
((24))

where the modulus and characteristic times are defined at very high frequencies. At time equal to zero, the viscosity attains its lowest possible value (η ∞≡G 0 λ ∞) and initially follows a linear variation with time, as in Eq. (24). At long times, Eq. (22) has the following limit:

$$\eta ^{ + } {\left( {t \to \infty } \right)} = {\sum\limits_{i = 1}^n {G_{{0i}} \lambda _{{0i}} = \eta _{0} } }.$$
((25))

As it will be shown later, Eq. (22) is a monotonically increasing function and describes the short time nonlinear behavior of the system up to the maximum of the stress growth coefficient curve, but it does not describe correctly the decrease of η + at longer times. On the other hand, Eq. (23) has the following limit at long times:

$$\eta ^{ + } {\left( {t \to \infty } \right)} \equiv \eta _{{ss}} = {\sum\limits_{i = 1}^n {\frac{{G_{{0i}} }}{{{\mathop \gamma \limits^ \cdot }}}{\left( {\frac{{\lambda _{{\infty i}} }}{{\lambda _{i} }}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} } }$$
((26))

This limit coincides with the steady-state solution given in Eq. (11). Equation (23) is a monotonically increasing function, describing a behavior similar to that of Eq. (24) at short times, but it does not follow the behavior of real systems, except near the range of validity of Eq. (26). This is demonstrated later in “Results” (Fig. 10).

Results

Measurements of equilibrium surface tension vs concentration allow the estimation of the critical association concentration and the surface area of the adsorbed species at the interface (Adamson 1976). According to the Gibbs adsorption isotherm and the Volmer equation (Gracia-Fadrique et al. 2002), the CAC can be determined from the discontinuity of a plot of ln(π/c) vs π, where π is the surface tension of the solution and c is the solute (HASE + surfactant and additives), as well as the maximum area per adsorbed molecule A (i.e., at saturation conditions) from the slope of the same plot. In the case analyzed here, polymer accumulation on the surface produces a decrease in surface tension (Table 1). The surface activity of HASE depends mainly on hydrophobic tails and, to a lesser degree, on carboxyl group content. From the data in Table 1, we found that discontinuity in surface tension occurs at a HASE concentration around 0.55–0.6 wt%. At this concentration, we found that the area per molecule at the interface is ca. 30–40 Å2. These results imply that polymer molecules are surface-active, inasmuch as these values are too large for common surfactant molecules. Therefore, the polymer behaves like a surfactant with high molecular weight.

Table 1 Surface tension data for several HASE polymer concentrations at various pH values
Full size table

Prior to rheological studies, the zero shear rate viscosity behavior of the associative polymer was examined as a function of pH by varying the concentration of KOH or AMP. Figure 1 shows the zero shear rate viscosity vs pH obtained for 2-wt% aqueous solutions of the HASE polymer. The plot of zero shear rate viscosity vs pH depicts four regions. The first region is located at pH values from 6 to ca. 6.8, where the viscosity is low and almost does not change with increasing pH. For values larger than ca. 6.8, the viscosity starts to rise, signaling the occurrence of the critical association concentration. In this region, the viscosity values of both solutions are similar. In region II, the viscosity rises rapidly with pH (in the range 7–8), where polymer–solvent interactions and hydrophobic interactions increase drastically. Region III covers the asymptotic part of the curves located at pH values larger than 7.5 for KOH or 8 for AMP. For pH larger than 9.8, the viscosity decreases with pH (region IV). These results are consistent with the reported behavior of model HASE solutions: at low pH (<7.0), HASE is insoluble in water and has a compact structure (hence, low solution viscosity); at pH ca. 6.8–7.0, the acid groups from the initiator used in HASE synthesis are neutralized (Wang et al. 2000); with addition of further amounts of the base, the superficial and internal (at higher pH values) methyl methacrylate (MMA) segments of the HASE are neutralized, which leads to the swelling (transient network formation) and dissolution of the HASE polymer. In fact, the dissolution, according to our data, occurs at pH values larger than ca. 10, which is consistent with potentiometric results in model HASE systems (Wang et al. 2000). With AMP, the polymer solution attains viscosities (around 5 Pa s) larger than those observed in the solution with KOH (4 Pa s). The larger viscosity level of the solutions made with AMP may be ascribed to the larger polymer–polymer repulsive interactions among the ionic groups of macromolecules that lead to larger hydrodynamic volumes of polymer molecules. The solution made with AMP was more stable than that made with KOH. In fact, the first Newtonian viscosity of the solution with AMP in steady and oscillatory flows maintained the same value (5.1 Pa s at pH 9.5) for times longer than those of the solution with KOH, which exhibited variations in the range of 3.5–4.2 Pa s at the same pH. The differences observed in the neutralization behavior of AMP and KOH can be ascribed to different degrees of dissociation and neutralization in the presence of additives other than the polymer itself. In fact, Wang et al. (2000) showed that the mechanism of neutralization (and hence of swelling of the dissolution of HASE polymers) differs when a strong (base i.e., KOH) and a weak base (i.e., AMP) are used, which can explain the two-plateau regions of the viscosity-vs-pH curve.

Fig. 1
figure 1

Zero shear rate viscosity vs pH of the HASE polymer with two alkali solutions: (■) AMP, (○) KOH

Full size image

Small-amplitude oscillatory flow and relaxation spectrum

Master curves of the storage modulus (G′) and of the loss modulus (G″) vs frequency, referred to 20°C of a 2-wt% HASE solution at pH 9, are shown in Fig. 2. These master curves were obtained by a horizontal shifting of data and were fitted with Eqs. (6) and (7) of the multimode Maxwell model with ten modes, the values of which are given in Table 2. The global error in the fitting was less than 5%. The loss modulus has two regions of behavior, implying two relaxation processes. In HEUR-type polymers, the longer relaxation (<100 s−1) is ascribed to the exit of hydrophobes from the micelles (Annable et al. 1993), and the shorter relaxation observed at high frequency (≈1000 s−1) is attributed to Rouse-type relaxations of free chains. In comb associative polymers, complete relaxation of the molecule requires the disentanglement of at least one hydrophobic group. The random distribution of hydrophobic groups along the macromolecular backbone gives rise to this distribution of relaxation times.

Fig. 2
figure 2

Master curves of the moduli vs frequency. The multimode Maxwell model predictions are shown as continuous lines. Data correspond to a temperature range of 5–25°C and frequencies of 0.01–500 s−1

Full size image
Table 2 Discrete viscoelastic spectrum obtained from oscillatory flow measurements
Full size table

The Arrhenius plot of the factor a T, which is the ratio of relaxation time at T to that at 20°C (not shown), indicates a thermally activated process of the form λ(t)=λ(T 0)exp(E α /RT), where R is the gas constant and E α is the activation energy. The value of the activation energy calculated here is 57.5 kJ/mol, which is similar to that found in other associative polymers, such as in HMHEC (Maestro et al. 2002) or in HEUR-type telechelic polymers (Annable et al. 1993). The interpretation given by several authors to thermally activated relaxation times (Tanaka and Edwards 1992) is that linear viscoelasticity is dominated by junction dissociation.

From values reported in Table 2, a logarithmic distribution of relaxation times was calculated (Fig. 3, curve a). This distribution represents a global relaxation spectrum of the system and, of course, it can be extended to the five decades covered by the master curve. The generalized Maxwell model used here requires three parameters for the distribution of chain disentanglement times around a main relaxation time. In this regard, the relaxation spectrum can be fitted with an analytical distribution of the form suggested by Maestro et al. (2002):

Fig. 3
figure 3

a Logarithmic distribution of relaxation times obtained from the fitting of Fig. 2. b Distribution of relaxation times obtained from the fitting of the shear viscosity curve (Fig. 4)

Full size image
$$H{\left( {\ln \lambda } \right)} = \frac{{G_{0} }}{{\ln \sigma {\sqrt {2\pi } }}}\exp {\left[ { - \frac{{{\left( {\ln \lambda - \ln \lambda _{M} } \right)}^{2} }}{{2{\left( {\ln \sigma } \right)}^{2} }}} \right]}$$
((27))

where G 0,λ M, and σ are the storage modulus, mean relaxation time, and variance, respectively. Figure 3 (curve a) shows the fitting of Eq. (27) to the experimental oscillatory data taken from the discrete values of Table 2. Clearly, the experimental data follow the distribution proposed by Maestro et al. (2002).

Steady shear viscosity

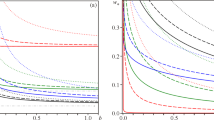
The shear viscosity of the 2 wt% HASE + 0.5 M AMP solution was predicted with Eq. (8), with ten discrete modes reported in Table 3. It is interesting that “good” predictions can also be obtained using only four discrete modes for complex viscosity and two modes for shear viscosity in the model. The first Newtonian viscosity is located at small shear rates and coincides with the Newtonian plateau of the complex viscosity (Fig. 4). Shear thinning begins at a shear rate of 0.6 s−1 , and both viscosities attain a slope close to −1 for strain rates larger than 500 s−1. The complex viscosity is always smaller than the shear viscosity for frequencies larger than 0.5 s−1; hence, the Cox–Merz rule is not satisfied.

Fig. 4
figure 4

Complex viscosity (○) and shear viscosity (●) vs strain rate. Model predictions are shown as continuous lines

Full size image
Table 3 Discrete viscoelastic spectrum obtained from the steady shear viscosity (Eq. 8)
Full size table

It is known that, at intermediate shear rates and low HASE-type polymer concentration, relatively weak shear thickening is observed (English et al. 1997). Shear thickening is less pronounced than in the case of HEUR polymers observed by Annable et al. (1993). Shear-induced structuring through hydrophobic associations is a possible cause of shear thickening, which becomes more pronounced with decreasing polymer concentration. In the concentration range analyzed in this work, the thickening region is absent. Nonetheless, our model can predict this behavior if a balance that favors reformation upon destruction of structure is considered in the kinetic equation.

The effect of the steady-shear flow on the associative polymer network is reflected in the disappearance of long relaxation times and the increase in the number of short relaxation times. Thus, the global effect of shear on such systems is the destruction of long-range (e.g., intermolecular) links. This enables the formation of additional short-range (e.g., intramolecular) links, thus increasing the contribution from relaxation modes at intermediate frequencies (Mewis et al. 2001). From these data, a distribution of relaxation times analogous to that of the oscillatory regime can be obtained from the model (Fig. 3, curve b). In this case, both (linear and nonlinear) distributions coincide with the longer time part of the spectrum, but they diverge in the region of shorter relaxation times, where smaller relaxation times are present in the case of shear flow. In fact, the mean relaxation time shifts to lower values and the distribution broadens; thus, standard deviation (σ) increases. Deviations from the Cox–Merz rule are ascribed to a flow-induced structure modification process, in which the network is disrupted, favoring intramolecular links with shorter relaxation times. Flow affects the relaxation spectrum by shifting the curve to shorter times under steady shear.

The comparison of values reported in Tables 2 and 3 reveals that the discrete modes of the modulus in the shear viscosity are larger than those of the complex viscosity. An average length scale 〈R 2〉1/2 for links or segments between entanglement points that are elastically active can be defined as follows:

$${\left\langle {R^{2} } \right\rangle }^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} \alpha {\left( {\frac{{K_{B} T}}{{G_{0} }}} \right)}^{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}} $$
((28))

A shift of the spectrum to larger values of the discrete modulus can then be attributed to a reduction in length between entanglement points, or to an increase in network connectivity.

Stress relaxation after cessation of flow

As is usual in rheological analyses, a linear viscoelastic spectrum is used to predict nonlinear viscoelastic properties. Unsteady-state predictions require determination of the time material constants λ and λ ∞ for each mode, in addition to values of λ0 and G 0 reported in Table 1. This can be carried out with Eqs. (15, 20 and 24), which contain asymptotic expressions for stress relaxation function at long times, the damping function at large step strains, and the initiation of flow at short times, respectively. Equation (15) reveals that the tangents drawn to the stress relaxation curve have a slope, which is a function of λ 0, and an intercept from which λ can be obtained for each tangent. This provides a unique relationship between λ 0 and λ for each tangent that represents a single mode.

Stress relaxation after cessation of flow data for various shear rates is depicted in Fig. 5. For shear rates lower than ca. 0.5 s−1, the relaxation is monoexponential. For larger shear rates, nonlinear behavior is observed, where a sudden decrease of the stress with time, followed by a more gradual decrease for longer times, is apparent. The stress relaxation curve for a shear rate of 9 s−1 was predicted in the region of short to moderate times with Eqs. (14) and (15) using only two modes (Fig. 5, solid line). The values of the time material constants corresponding to these modes are disclosed in Table 4, and they are located in the long-time part of the spectrum. As mentioned previously, the stress relaxation curves display a two-step relaxation process. One relaxation is fast, and its duration depends on the previous shear rate, whereas the second occurs in time scales comparable to the main relaxation time λ 0. The behavior of the relaxation at short and long times follows a simple exponential pattern, as predicted by Eqs. (14) and (15), although the wide distribution of relaxation times (Fig. 3) masks the transition between the two regions, producing a gradual (instead of sharp) change between two single-exponential regions. In fact, some authors have predicted the relaxation behavior as the sum of two functions: one monoexponential decay for rapid initial decrease and one stretched exponential form (i.e., a distribution of relaxation times) in the intermediate and long times (Séréro et al. 2000; Pellens et al. 2004), as in Eq. (15).

Fig. 5
figure 5

Stress relaxation after cessation of shear flow vs time for various shear rates (s−1): 0.01 (□); 0.5 (▪); 1 (•); 3 (▴); 5 (◆); 7 (★); 9 (∇). Predictions for an applied shear rate of 9 s−1 are shown as a continuous line

Full size image
Table 4 Model material parameters
Full size table

Stress relaxation after a step strain

The stress relaxation modulus as a function of time for various applied strains (from 1 to 250%) is shown in Fig. 6a as a semilogarithmic plot and in Fig. 6b as a log–log plot. In both plots, model predictions (Fig. 6a and b, solid lines) are included using the material constants disclosed in Table 4. Notice that these material constants are equal to those of stress relaxation, except the second mode of λ. It is interesting that linear single-exponential behavior is not attained even at the lowest applied strains (1%). Instead, a limiting curve is observed for applied strains larger than 50% [i.e., the same dependence of G(t) with time is obtained for strains larger than this value]. On the other hand, at short times, some authors (Séréro et al. 2000; Pellens et al. 2004) have found a region of strain-hardening behavior when the applied strain was small, followed by a strain-thinning region for larger strains. In the inset of Fig. 6b, the same effect is reproduced for strains in the range of 1–10%. At long times, the relaxation curves superimpose and can be factored into a time-dependent and a strain-dependent term because all curves have the same slope, which depends on the time scale λ 0 as Eq. (18) predicts. This is not the case at short times, where the data depend on the time scale of the applied strain, as predicted by Eq. (17). This double relaxation process predicted by the model is observed in the experimental data. Most stresses relax by a fast process attributed to a rapid breaking of the chains that are highly stretched (Séréro et al. 2000; Pellens et al. 2004). A slower relaxation has been ascribed to the continuous breaking and reformation of hydrophobic groups. Between the two single-exponential regions, a continuous and gradual decrease in the relaxation modulus is due to the broad distribution of relaxation times. As in Séréro et al. 2000, data at moderate to long times can be described by a stretched exponential or with a distribution of relaxation times, as proposed in Eq. (18). The model parameters needed to predict the experimental data at high strains are the same two modes used in the stress relaxation after cessation of flow, corresponding to the long-time part of the spectrum.

Fig. 6
figure 6

a Semilog plot of the stress relaxation curves for various imposed strains (%): 1 (▪); 5 (□); 10 (▴); 100 (▾); 150 (•); 200 (★); 250 (◆). Model predictions are shown as a continuous line. b Log–log plot of the stress relaxation modulus vs time for the same strains as in a. Inset: stress relaxation modulus vs strain

Full size image

From the intercepts of the linear region at long times in Fig. 6a (dashed line), the damping function can be evaluated for various strains. At the highest strain (250%), the intercept corresponds to the ratio λ/λ ∞, according to Eq. (20), manifesting a leveling off of the damping function and attaining a lower plateau for large applied strains.

Stress growth upon inception of shear flow

The normalized stress growth coefficient is plotted in Fig. 7 as a function of time for various imposed shear rates. At low applied shear rates, the stress growth is monotonic, whereas for values larger than 1 s−1, a maximum appears, which shifts to shorter times as the applied shear rate increases. The magnitude of the maximum increases with imposed shear rate, as observed in polymer solutions and melts. However, when the normalized stress growth coefficient is plotted against the strain (Fig. 8), the maximum shifts from approximately 2.5 strain units at the lowest applied shear rate (0.5 s−1) to 7.24 strain units under imposed shear rates larger than 3 s−1. These data show a distinct behavior compared to that observed in polymer melts, where the maximum always occurs at the same value of the strain for a given polymer, which is on the order of two to three units (Bird et al. 1987).

Fig. 7
figure 7

Stress growth coefficient vs time for several imposed shear rates (s−1): 0.01 (•); 0.5 (▪); 1 (◆); 3 (□); 7 (▾); 20 (•); 150 (★)

Full size image
Fig. 8
figure 8

Stress growth coefficient vs strain for several applied shear rates (s−1): 0.5 (▪); 1 (★); 3 (•); 5 (○); 7 (▾); 15 (□); 50 (△); 100 (◊); 200 (+)

Full size image

A very interesting observation reveals that, at shear rates between 15 and 100 s−1, the magnitude of the maximum increases up to the largest value (at 100 s−1; see Fig. 8) and then it decreases for larger shear rates. This behavior is predicted qualitatively by the model. The predicted overshoot increases with increasing applied shear rates up to a maximum and then it decreases, recovering the single-exponential behavior with time constant λ ∞ at very high shear rates (Fig. 9).

Fig. 9
figure 9

Model predictions of the stress growth coefficient for applied shear rates between 0.01 s−1 (uppermost curve) and 500 s−1 (lowermost curve)

Full size image

Figure 10 depicts the normalized stress growth coefficient against the nondimensional time (t/λ 0) for applied shear rates of 0.1 s−1 (inset) and 5 s−1, respectively. For low shear rates (Fig. 10, inset), Maxwellian behavior is predicted in accordance to Eq. (21), and the predictions closely follow the experimental data. For larger applied shear rates, the predictions from Eqs. (22) and (23) agree with the data obtained at short and long times, respectively. This comparison clearly shows the range of applicability of Eqs. (22) and (23) and the validity of asymptotic analysis. Quantitative predictions of the full curve can be made only for relatively low shear rates, such as those considered in Fig. 7, with the values disclosed in Table 4. Notice that they are the same as those used in stress relaxation predictions.

Fig. 10
figure 10

Stress growth coefficient vs normalized time for applied shear rates of 0.1 s−1 (inset) and 15 s−1. Model predictions are shown as continuous lines. Predictions (lines) in the inset are from the Maxwell model, whereas those for data at 9 s−1 are from Eq. (22) (for short times) and Eq. (23) (for long times)

Full size image

Discussion

The rheology of associative polymers differs markedly from polymer solutions without cross-links. It has been observed that there is a significant amount of shear thickening (at low polymer concentrations), a deviation from the Cox–Merz rule, and the presence of relaxation modes that give rise to high values of the dynamic moduli in the low-frequency range of the spectrum. Due to the presence of temporary cross-links between macromolecules, analysis of the behavior of associative polymers in the context of transient network theories is motivating. In these theories, junctions or cross-links are of temporary nature; thus, they can be created and destroyed. The creation of junctions is driven by diffusion, whereas the probability of destruction of a junction may depend on the average extension of the segments (Van den Brule and Hoogerbrugge 1995). The description of these theories and associated constitutive equations has been reviewed by Bird et al. (1987) and Larson (1988). The viscosity curves shown in Fig. 4 do not display a shear thickening region at intermediate shear rates, which is usually observed in associative polymers (English et al. 1997; Annable et al. 1993). At low HASE concentrations, the complex viscosity appears larger than the shear viscosity in this region. For concentrations larger than around 1 wt%, Mewis et al. (2001) observed the same trend as here. Shear thickening at intermediate shear rates has been attributed to either flow-induced change from intramolecular to intermolecular associations (English et al. 1999) or to flow-induced non-Gaussian stretching of the chains (Marrucci et al. 1993; Séréro et al. 2000). These structural changes would explain the deviations from the Cox–Merz rule. In fact, although shear thickening has not been detected in the present data, the appearance of larger values of the modulus in the discrete spectrum of the shear viscosity compared to those of the complex viscosity (see Tables 2 and 3) can be ascribed, however, to structural changes induced by flow, thus validating the increase in network connectivity and the decrease in segment length suggested by Eq. (28). In summary, the deviation from the Cox–Merz relationship suggests that there is a significant associative effect in this system under steady shear, even in the absence of a shear-thickening regime.

The model proposed in this work is consistent with the classical transient network theory formulation. In fact, as shown elsewhere (Bautista et al. 1999), the constitutive equations generated by transient network formulations give predictions similar to those of the model treated here. If the breakage probability function adopts the Warner approximation of the inverse Langevin function, the expressions obtained for simple shear are equal to those given in Eq. (8). The Warner form of the breakage probability accounts for the fact that the rate of detachment is dominated by thermal motions in weak flows, whereas in strong flows, the chains becomes extended and the breakage probability is forced to diverge (Vaccaro and Marrucci 2000).

Predictions of shear viscosity and complex viscosity at high strain rates show agreement with the observed inverse dependence on the strain rate (Fig. 4). The slope of −1 in the viscosity-vs-shear rate curve has also been predicted by Marrucci et al. (1993) following shear thickening in physically cross-linked networks. In fact, saturation of the shear stress at high strain rates is predicted to occur when all chains are fully extended and cannot extend any further. On the other hand, in HASE systems, the characteristic shear thickening observed in telechelic polymers of the HEUR type does not often occur in steady shear flow, particularly in the concentration range studied in this work. However, the deviation from the Cox–Merz rule at higher shear rates signals the presence of the flow-induced growth of fast relaxation modes during steady shear. In addition, strain hardening in stress relaxation confirms the fast relaxation phenomena occurring at short times.

Conclusions

The scope of the paper provides predictions of the rheological behavior of associative polymers of the HASE type, with a model that includes a spectrum of relaxation times. Important findings that have not been reported in the current literature include the limiting behavior of stress relaxation past a sudden applied strain that reveals a saturation of the damping function at high applied strains. Rheological modeling with a spectrum of relaxation times has not been analyzed in a form and in an amplitude exposed here. Moreover, the Maxwell behavior at high applied shear rates at the inception of shear flow has neither been reported nor predicted for associative polymers.

In stress relaxation, data show the presence of a limiting curve at high applied strains (Fig. 6), indicating saturation of the damping function in this region. In fact, for strains larger than two, the relaxation modulus does not decrease any further. To our knowledge, this behavior has not been reported for associative polymers, and the model exposed here predicts such behavior. A limiting behavior is also found at the inception of steady shear flow. At low applied shear rates, the stress growth coefficient is governed by a single-exponential time constant (λ 0) and the coefficient follows a monotonic increase (Figs. 7 and 8). Overshoots appear for larger applied shear rates (Figs. 7 and 8). Past a critical shear rate at which the maximum magnitude of the overshoot is observed, the overshoot becomes smaller as the applied shear rate is increased. The model proposed here predicts this behavior and a single-exponential one again at very high shear rates (Fig. 9). At these high shear rates, the stress growth coefficient is again governed by a single-exponential time constant (λ ∞). Once again, this behavior, to our knowledge, has not been reported for associative polymers and is also predicted by the model introduced here. In summary, the model proposed here predicts a limiting second Newtonian viscosity at very high shear rates (Eq. 9b) and, by extension, also a limiting behavior in the high-strain-rate region in unsteady flows.