Lattice gas simulations of two-dimensional liquid foams

Abstract

Liquid foam is a dense random packing of gas bubbles in a small amount of immiscible liquid containing surfactants. The liquid within the Plateau borders, although small in volume, causes considerable difficulties to investigations of the physical properties of foams, and the situation becomes even more complicated if the flow of the liquid through the foam is considered too. Here we propose a fresh approach to tackling these issues by introducing a discrete two-dimensional hybrid lattice gas model of liquid foams. While lattice gas models have been used to model two-phase liquids in the past, their application to the study of liquid foams is novel and proves promising. We represent bubble surfaces by a finite number of nodes, and model the surrounding liquid as a lattice gas (with a finite number of liquid particles). The gas in the bubbles is treated as an ideal gas at constant temperature. The model is tested by choosing an arbitrarily shaped bubble that evolves into a circular shape in agreement with Laplace’s law. The model is then employed to simulate periodic ordered and disordered dry and wet foams. Since our model is specifically designed to handle wet foams up to a critical liquid fraction of 0.16 (void fraction of random packing of disks), we are able to compute the variation in coordination number (average number of neighbours of a bubble) over the whole range of liquid fractions, and we find it to be a linear function of the shear modulus.

1 Introduction

An aqueous foam is a random packing of gas bubbles in a relatively small amount of liquid containing surface-active macromolecules, such as surfactants. These bubbles are separated by thin liquid films which are stabilized against rupture by physical–chemical effects arising from the presence of the liquid. Generally, if the volume fraction of liquid is greater than about 5%, the bubbles are nearly spherical; for drier foams, by contrast, the bubbles are more polyhedral, as dictated by the competition between surface tension and interfacial forces.

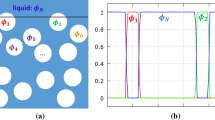
A good fundamental understanding of the properties of dry and static foams, such as coarsening and drainage, is well established ([1, 2, 3, 4] provide good general references on these topics). By contrast, wet foams provide a number of challenges to physicists and rheologists [5]. The rigidity loss for large values of the liquid fraction of the foam, the existence of a yield stress, and the possibility of convective bubble motion are just a few examples. Although the computation of the three-dimensional structure of foam is well advanced [6], a retreat to two dimensions still appears advantageous when foams with a high liquid content are studied. An example of such a 2-D foam, computed using our new simulation method, is shown in Fig. 1.

Fig. 1

Lattice gas simulation of a two-dimensional liquid foam containing 30 bubbles, with liquid fraction ϕ=0.078. Four periodic units are shown.

Previous work includes a geometrical model based on Laplace’s law [7] and a dynamical model where bubbles are represented as interacting soft disks [8]. These two models, with their specific application ranges will be analysed, in the following.

In wet foams, the bubbles experience more freedom to move than in dry foams where they are jammed together. This allows for the possibility of modelling a foam as individual bubbles interacting with nearest neighbours. The first such model was presented by Durian [8]. In this model, the bubbles constituting a foam are treated as interacting disks (similar to the treatment in granular dynamics [9] and their positions and velocities are determined by the contact forces using Newton’s equations of motion. Fluid flow in the channels between bubbles (Plateau borders) results in an additional viscous force acting on the bubbles. An obvious issue is the choice of an appropriate spring force between touching bubbles. Also, the model is only approximate when bubbles begin to jam into a foam structure as the liquid fraction is decreased. However, although not suitable for the simulation of dry foams, the model has proved valuable to the computation of rheological properties, such as yield strain and shear modulus, close to the rigidity loss transition.

Two-dimensional dry foams may be accurately simulated due to the simplicity of the underlying geometry (cell walls are arcs of circles due to Laplace’s law). Bolton and Weaire [7] used this as their basis, together with the decoration theorem [10], to simulate wet foams. The decoration theorem states that any two-dimensional dry foam structure can be decorated by small three-sided Plateau borders at each vertex, to give an equilibrated wet foam structure, provided such Plateau borders do not overlap. Wet foams can be successfully simulated for liquid fractions of up to ϕ=0.12–0.13, but numerical difficulties are encountered at higher values where the bubbles come apart to form a bubbly liquid. Nevertheless, this model was used extremely successfully to compute the mechanical properties of foams as a function of liquid fraction [11], and, more recently, to examine the effect of dilatancy in foams [12].

The shortcomings of the above models make it highly desirable to design a model that is equally suited to modelling both wet and dry foams. We used the concept of a lattice gas to achieve this. In addition, since the liquid in the foam is represented as fluid particles, this should also enable us to study aspects of foam drainage, although we have not yet undertaken such studies.

Lattice gas models are frequently used for flow situations involving moving interfaces, possibly due to the interaction with the fluid. This presents a problem that is difficult to handle with conventional fluid dynamics. Instead of considering the large number of individual molecules in a fluid (the molecular dynamics approach), a much smaller number of fluid particles are considered in the lattice gas method. A fluid particle represents a large group of molecules, which is still considerably smaller than the smallest length scale of the flow situation that is to be modelled. This is justified on the grounds that the macroscopic properties do not directly depend on the microscopic behaviour of the fluid. The fluid particles are restricted to move on the links of a regular lattice and their positions are updated in discrete time-steps. Mass and momentum conservation are incorporated into the update rules that are applied at each discrete time step. The FHP-III lattice gas has seven possible states for a fluid particle (movement in one of six possible directions, or rest) and 128 collision rules [13, 14]. At the start of each time step, the particles at each site collide according to the FHP-III collision rules, which are computed using either Boolean algebra [15] or using a table [16]. After these collisions, each particle travels at a new velocity along one of the lattice links (unless it is a particle at rest). Again the collision rules are applied, which determines the new particle velocities. After a sufficient number of time steps (which is dependent on the number density of fluid particles) the fluid evolves to an equilibrium state. Lattice gas models may be mapped exactly onto the incompressible Navier–Stokes equations [17], and so they are a valid representation of fluid flow.

Although there are various lattice gas models of binary liquids, none of these specifically address the problems of foams. Generally these models may be classified into “immiscible lattice gases” (ILG) and “liquid-gas models” [17]. In the former, two different types of fluid particles (distinguished by their “colour”) move along the lattice. While interactions of particles still conserve mass and momentum, the interaction rules are altered so as to favour the separation of the two particle types. This leads to phase separation. In liquid–gas models [18], there is only one species of particle, but two collision steps. While the first step is the same as in the standard lattice gas model, the second step considers interactions of particles over a specified distance. Choosing this interaction distance appropriately leads to the formation of coexisting areas of high or low number density of particles. These areas are identified as liquid or gas phases respectively.

Our work does not concern the modelling of foam formation (modelling the formation of high and low density regions) but the properties of a foam once it has been formed. We therefore start with the separation into a dispersed gaseous and continuous phase and design a model to specifically deal with this. We model the liquid between bubbles using the FHP-III lattice gas, while treating the gas inside the bubbles as ideal gas. The interface separating these two phases is modelled by a set of attracting surface nodes, mimicking the effect of surface tension. The resulting foam model may therefore be called a hybrid lattice gas model.

In the following, we shall provide details of our method and the test case of a bubble of arbitrary shape developing into a circle, demonstrating Laplace’s law. Finally we will present simulations of wet and dry foams.

2 A discrete model of liquid foams

2.1 Modelling Plateau borders: the lattice gas method

As mentioned in the introduction, the liquid in a foam is mainly contained in its Plateau borders. These are three-sided for values of liquid fraction ϕ≤0.03, but will eventually percolate throughout the entire foam as the foam reaches its critical liquid fraction ϕ_c≈0.16, corresponding to the void fraction of a random packing of hard disks [5]. To allow for such a complicated geometry, we have chosen to model this liquid using a FHP-III lattice gas.

Lattice gas models are an example of a cellular automata where lattice sites can take on a finite number of states and are updated in discrete time steps, based on the state of neighbouring sites at the previous time step. The FHP-III model of Frisch et al [14] consists of a hexagonal lattice and considers only the six nearest neighbours of a site in order to update its sites. Fluid particles (with unit mass) move along the hexagonal lattice with constant speed with the restriction that at most one particle moves along a particular direction at each site. The state of a site is given by the velocity directions of its occupying particles. An update consists of moving all of the particles to the next lattice site in the direction of their respective velocities, followed by a change in these velocities according to a set of defined collision rules [14]. These rules are designed to conserve both mass and momentum at each site. Some examples are shown in Fig. 2. Note that these also include rest particles—particles with velocity zero before a collision. Such rest particles lead to higher collision rates and so a faster relaxation to equilibrium [17].

Fig. 2

Shown are three of the total of 128 collision rules used in the FHP-III. Small solid circles denote lattice sites and open circles are rest particles (particles with zero velocity). All collision rules conserve momentum. A random choice is taken if there are two possible outcomes of a collision.

2.2 The gas inside the bubbles

At the beginning of our simulations, the bubbles are usually set as circles. N surface nodes are placed equidistantly along the bubble surface, and the bubble radius is given by

$$ r = \frac{{d_{0} }} {{2\pi }}N $$

(1)

where d₀ is the distance between neighbouring surface nodes. In our simulations, d₀ is 0.4, about three lattice length units.

The internal gas is treated as an ideal gas at constant temperature,

$$ PA = P_{0} A_{0} $$

(2)

where P and A are the bubble pressure and area, and P₀ and A₀ are the initial values of these quantities.

2.3 The gas–liquid interface

The most challenging aspect of our foam model is the treatment of the gas–liquid interface. We decided on a dynamic model, involving a finite set of surface nodes that are subject to a number of different forces, due to (1) surface tension, (2) internal gas pressure, (3) colliding liquid particles, and (4) the disjoining pressure in the vicinity of other interfaces. Positions and momenta of the surface nodes are then updated according to Newton’s equations of motion, followed by relaxation of the liquid particles within their new boundaries. Our iterative algorithm then computes the forces at the new positions and moves the surface nodes accordingly. This process will eventually converge to an equilibrated, converged foam structure.

Figure 3 shows a gas–liquid interface (small dots) represented by a set of surface nodes, marked as big solid circles. In our treatment of the interface as a flexible skin, the effect of surface tension is then a constant force that acts between neighbouring surface nodes. A similar approach can be found in the work of [19] for the model of a soap film. However, we model the film between two bubbles using two interfaces, since this enables us to simulate wet foams by inserting liquid particles between these interfaces.

Fig. 3

a The liquid–gas interface is represented by discrete surface nodes (solid circles). Solid squares are an approximation of this surface using only lattice sites. Open squares show the possible positions of fluid particles. Arrows indicate particles that interact with the interface (at the positions marked with the solid squares). b Shows the interactions when a second interface is present. When the distance between the two interfaces is of the order of one lattice unit, fluid particles are expelled, leading to direct interations between the interfaces at the locations aa′, bb′ and cc′.

In our simulation, we treat the gas contained in the bubbles as ideal gas. From the pressure acting on a surface element, we can compute the magnitude of the gas pressure force f_p on a surface node as $f_{{\text{p}}} = \frac{{2A_{0} P_{0} }} {N}{\sqrt {\frac{\pi } {A}} }.$ This force acts at all surface nodes in directions perpendicular to their links with neighbouring surface nodes.

The pressure force due to the liquid contained in the Plateau borders is given by the change in momenta of the fluid particles that collide with the interface. Since in our model the distance between neighbouring surface nodes is generally much larger than one lattice spacing, this requires the introduction of supplementary intermediate boundary sites, drawn as solid squares in Fig. 3. These are positioned on the lattice and are each associated with a specific nearby surface node. The velocities of the lattice gas particles colliding with these intermediate boundary sites are updated according to the link-bounce-back boundary condition (particles that are encountering a solid surface are reflected back in the direction from which they came from [20, 21, 22]). The force acting on the boundary is then given by the change in momentum.

Finally we have to consider the disjoining force due to other nearby interfaces. Neglecting the details of its physical origin (steric, electrostatic, and so on), we shall simply introduce the disjoining force as a mutual repulsive force between two neighbouring surfaces (as represented by the intermediate boundary sites) required to prevent them from overlapping. It is of a short-range nature and only active when bubbles are in contact. We model the force by a step function; it is only active when the distance between two supplementary boundary points (belonging to two different surfaces) is less or equal to one lattice unit. We find a magnitude of the order of the gas pressure forces to be a good heuristic choice.

Liquid pressure forces and disjoining forces are computed for the intermediate boundary sites. These forces are then added up and applied to the corresponding surface nodes, together with the forces due to surface tension and gas pressure.

Positions and velocities of the surface nodes are then updated using an Euler method. This propagation of the gas–liquid interface is followed by 500 steps of lattice gas calculations in order to allow for equilibration of the liquid particles and for the computation of the liquid pressure acting on the interfaces. This concludes one iteration. We find that several thousand such iterations are required for the computation of an equilibrium foam. Here we use the total interface length, which settles down to a constant (dependent on the number of bubbles and the liquid fractions) as a criterion of convergence.

2.4 Effect of discretisation on Laplace’s law

Since in our model we replace continuous boundaries by a finite number of surface nodes, it is essential to establish the minimum number of nodes required for a realistic simulation. This can be estimated by the following argument.

Let us consider the surface node A of a circular bubble (with neighbouring nodes A′ and A′′) as shown in Fig. 4 (here we have set the external pressure to zero). The net surface tension force and the gas pressure force on AA′ and AA′′ point in opposite directions and their magnitudes f _s and f _p are given by:

$$ f_{{\text{s}}} = 2\gamma \,\cos \,\alpha $$

(3)

$$ f_{{\text{p}}} {\text{ }} = 2{\text{ }}\Delta pr\,\cos \,\alpha \,\sin \,\alpha $$

(4)

where Δp is the pressure difference across the boundary and r is the bubble radius.

Fig. 4

Balance of surface tension force $\bar{f}_{{\text{s}}}$ and gas pressure forces $\bar{f}_{{\text{p}}}$ acting on surface node A (note that we have set the external pressure to zero here).

At equilibrium, the forces on node A balance,

$$ \Delta p = \frac{\gamma } {r}\frac{1} {{\sin \,\alpha }} $$

(5)

Inserting $\alpha = \frac{\pi } {2} - \frac{\pi } {N}$ therefore yields

$$ \Delta p = \frac{\gamma } {r}{\left[ {{\text{sin}}{\left( {\frac{\pi } {{\text{2}}} - \frac{\pi } {N}} \right)}} \right]}^{{ - 1}} $$

(6)

This is shown in Fig. 5, where we can see that even 20 nodes are sufficient to satisfy Laplace’s law (as given by the limit N→ ∞) to an accuracy of 2%.

Fig. 5

Laplace’s law for a discretized interface. As the number of surface nodes is increased, the exact form Δpr/γ is recovered.

2.5 Evolution of a single bubble

A simple test of our model consists of studying the evolution of a bubble of arbitrary initial shape surrounded by a lattice gas, as shown in Fig. 6. If the external pressure due to the lattice gas exceeds the initial internal gas pressure, the bubble will shrink. The final state in both cases is a circle, as governed by the equilibrium between pressure difference and surface tension. A comparison of radius and pressure difference, as is shown in Table 1, confirms Laplace’s law and therefore validates our model.

Fig. 6

A bubble of arbitrary shape (specified by 100 surface nodes) shrinks to a circle when its initial pressure is smaller than the constant external pressure due to interactions with the surrounding lattice gas. The dotted region is the initial shape; the thin solid outline is the developing bubble after 50 time steps; and the thick line is the circular bubble at the final steady state.

Table 1 Computational data for the evolution of a single bubble immersed in liquid (see Fig. 6)

3 Simulations of liquid foams

3.1 Dry foams

In our simulations, dry foams do not require the presence of any liquid particles. Therefore, the only forces acting on the surface nodes are due to surface tension, pressure differences and disjoining forces for bubbles in contact. In the simulations shown in Fig. 7a and b, thirty circular bubbles are located in a space of 250 by 259.8 lattice units (the dotted region in Fig. 7), which is a multiple of the basic unit required for an unstrained periodic foam system. Figure 7 shows three duplicates of this unit to illustrate the periodic boundary conditions used in this simulation. The 30 bubbles are assigned initial values for size and internal pressure. In Fig. 7a, each bubble is represented by 120 surface nodes (resulting in a radius as given by Eq. 1), while in Fig. 7b a random number between 50 and 200 was picked for every bubble. Values for initial pressure and surface tension were set to 0.05 and 0.04 in both simulations. Note that the initial size (determined by d₀ in Eq. 1) is chosen to be small enough to avoid bubble overlap at the beginning of computation. Since there are no liquid particles in these dry foams, the bubbles expand freely until the distance between the surface nodes of neighbouring bubbles is one lattice unit. Then, in addition the force due to surface tension forces and pressure forces, these nodes will also experience a disjoining force. This leads to relative adjustments of the nodes belonging to different bubbles until a steady state is reached. The resulting foam is determined by the initial conditions. In case Fig. 7a, where all bubbles have the same initial size and initial pressure, a perfectly ordered honeycomb structure with straight cell walls is formed. The initial conditions for case Fig. 7b result in a disordered foam. Note that, in agreement with Laplace’s law, cell walls in this case are generally curved, since there is a pressure difference between neighbouring bubbles of different sizes.

Fig. 7

Both ordered and disordered dry foams (ϕ=0) may be computed by setting the number density of fluid particles to zero (four period units are shown)

3.2 Wet foams

In our simulation of wet foams we use the same set-up as for the dry foam simulations of the previous section, but now liquid particles are added into the lattice spaces between the bubbles. For a sufficiently small number density of liquid particles, the bubbles will initially expand (as in the simulations of dry foams), pushing the liquid into locations where three bubbles meet and therefore forming three-sided Plateau borders. Increasing the number density of liquid particles leads to an increase in the wetness of the foam, accompanied by the formation of four (or more) sided Plateau borders. For values of the liquid fraction ϕ<0.05, the bubbles have polyhedral shapes; for higher values of ϕ they take on almost circular shapes; see Figs. 1 and 8.

Fig. 8

Example of two-dimensional wet foams: a ϕ=0.038, b ϕ=0.15, computed with our novel lattice gas method. The liquid fraction is determined by the number density of the fluid particles used in the simulation.

An important structural parameter for the characterisation of liquid foams is the coordination number Z(ϕ), the average number of neighbours of a bubble as a function of liquid fraction. In the dry limit (ϕ=0), the coordination number is given by Euler’s theorem as Z(0)=6. Increasing the liquid fraction leads to a decrease in Z until, at ϕ_c≈0.16, the foam is essentially a random packing of disks with a corresponding coordination number Z(ϕ_c)=4 [7].

The exact variation of Z(ϕ) has mainly been discussed for ϕ close to ϕ_c (close to the so-called rigidity loss transition where both shear modulus and yield stress vanish). Based on their simulations, which only cover a range of liquid fractions up to ϕ=0.12, Bolton and Weaire [7] concluded that Z(ϕ) decreases linearly. Using his bubble-scale model [8], which is valid only in the wet regime, Durian [23] found that it decreased in a non-linear fashion, with a power between 0.5 and 0.7.

The advantage of our lattice gas-based simulation is that we are able to compute Z(ϕ) for the entire range of liquid fractions, as shown in Fig. 9. We find the following empirical formula, which is correct in both dry and wet limits, to be a good description of our data:

$$ Z{\left( \phi \right)} = 2{\left( {1 - \frac{{\phi ^{2} }} {{\phi ^{2}_{{\text{c}}} }}} \right)} + {\text{4}} $$

(7)

Here the critical liquid fraction is determined from a least square fit as ϕ_c=0.162±0.001. (Fitting to ${\left( {\phi \mathord{\left/ {\vphantom {\phi {\phi _{{\text{c}}} }}} \right. \kern-\nulldelimiterspace} {\phi _{{\text{c}}} }} \right)}^{\alpha }$ in Eq. 7 gives α≈2.04±0.07 and ϕ_c=0.161±0.001.) From a Taylor expansion about ϕ_c we find that Z varies in a roughly linear way close to ϕ_c, which helps to reconcile the different previous findings. Also note that Z(ϕ) has a vanishing first derivative at ϕ=0, reflecting the Decoration Theorem [10].

Fig. 9

Variation of the coordination number Z with the liquid fraction ϕ. Note that our data reproduces and extends previous data by Bolton and Weaire [7] which did not cover the full range of liquid fractions. The thick solid line is a least square fit to Eq. 7.

Equation 7 is remarkable, since the same type of formula is found for the variation of the shear modulus G(ϕ) of liquid foams with liquid fraction [12], $G{\left( \phi \right)} = c_{0} \frac{\gamma } {{A^{{{\text{1/2}}}} }}{\left( {1 - \frac{{\phi ^{2} }} {{\phi ^{2}_{{\text{c}}} }}} \right)}.$ Here c₀ =(3^1/2/2)^1/2 is a geometrical constant, γ is the surface tension, and A is the area per cell in a foam. This allows us to link both quantities, shear modulus and coordination number, by writing

$$ G{\left( \phi \right)} = c_{0} \frac{\gamma } {{A^{{{\text{1/2}}}} }}\frac{{Z{\left( \phi \right)} - 4}} {{\text{2}}} $$

(8)

Although a linear relationship between G(ϕ ) and Z(ϕ ) has been suggested before [7, 23], Eq. 8 was not explicitly stated. No theoretical explanation of this relationship can be given at this stage, but it should be useful when relating the mechanical properties of disordered foam to its geometry.

4 Outlook

In this paper we have introduced a new hybrid lattice gas method for the computation of both dry and wet foam structures. While we focused on the structural properties of foams (the computation of Z(ϕ)), we are now in a position to study foam rheology, especially the role of topological changes (T1, or neighbour swapping changes) in wet foams under shear. These were reported to occur in the form of avalanches close to the rigidity loss transition [11]. However, this result was not reproduced in the simulations of Durian [23].

Note that in the code of Bolton and Weaire [7], used by Hutzler et al [11], the topological changes involved in yielding (plastic flow) require explicit programming. Whenever an edge is shorter than a defined critical length, a subroutine is called which performs the topological change. However, such a specific procedure is not required in our lattice gas model. Figure 10 shows an example of a T1 change. As the marked cell–cell edge decreases due to externally-applied shear, it reaches a point where the bubbles rearrange. Future work will therefore focus on obtaining reliable statistics for the occurrence of T1 changes in the wet regime.

Fig. 10

Dry foam under shear (simulations use boundary conditions). This results in several topological changes, as shown for example in the change of neighbours for bubbles 1, 2, 3 and 4.

Finally our model also lends itself to the study of liquid flow through a foam (foam drainage) and should give an insight into the resulting deformation of its structure, together with the effect of dilatancy (increase of local liquid fraction) due to shear [12].