Viscoelastic properties of magnetorheological fluids

Abstract

We have studied the rheological properties of some magnetorheological fluids (MRF). MRF are known to exhibit original rheological properties when an external magnetic field is applied, useful in many applications such as clutches, damping devices, pumps, antiseismic protections, etc. While exploiting parameters such as magnetic field intensity, particle concentration and the viscosity of the suspending fluid, we highlighted the importance of each one of these parameters on rheology in the presence of a magnetic field. We made this study by conducting rheological experiments in dynamic mode at very low strain which facilitates the comprehension of the influence of the structure on MRF rheology. Our results confirmed the link between the magnetic forces which ensure the cohesion of the particles in aggregates, and the elastic modulus. Moreover, we found that the loss modulus varies with the frequency in a similar manner than the elastic modulus. The system, even with the smallest deformations, was thus not purely elastic but dissipates also much energy. Moreover, we demonstrated that this dissipation of energy was not due to the matrix viscosity. Actually, we attributed viscous losses to particle movements within aggregates.

Introduction

Magnetorheological fluids (MRF) are magnetic suspensions made of particles with high permeability dispersed in a viscous or viscoelastic nonmagnetizable medium. Their flow in an external magnetic field undergoes a competition between magnetic and hydrodynamic forces. This competition gives rise to original rheological properties with creation of an apparent yield stress, therefore of a rapid and reversible liquid-solid transition, useful in many applications such as clutches which has been first described by Rabinow (1948), damping devices, pumps, antiseismic protection, etc. Despite these potential applications, there are only few commercially available devices due to the lack of suitable fluids. Good MR fluids should be stable against settling and should have a high magnetic saturation. However their major drawback is the particle erosion dues to frictions between particles in movement. Actually carbonyl iron particles have onion like structure and thus they can easily be peeled by shocks or frictions. This erosion makes the suspension to thicken irreversibly and thus decreases its performance. Surface treatments are currently investigated by makers in order to improve the life time of theirs MR fluids.

The flow modification is usually called the MR effect. It is attributed to the field-induced magnetization of the disperse phase relative to the continuous phase. At a first approximation, one particle can be made of one single magnetic domain and therefore is assimilated as one magnetic dipole. Klingenberg (1989) made some refinements to the calculus of the electrostatic force. Translated into magnetostatic, his expression for the magnetic force F may be written as shown in Eq. (1):

$$\matrix{ {{\bf{F}} = 3\mu _f a^2 \beta ^2 H^2 {\bf{f}}} \hfill \cr {{\rm{with}}} \hfill \cr {{\bf{f}} = {{a^4 } \over {r^4 }}\left[ {\left( {{\rm{2f}}_{{\rm{//}}} \cos ^2 \theta - f_ \bot \sin ^2 \theta } \right){\bf{e}}_{\bf{r}} + f_\Gamma \sin 2\theta {\bf{e}}_\theta } \right]} \hfill \cr } $$

(1)

with μ _p the particle permeability, μ _f the fluid permeability, $\beta = {{\mu _p - \mu _f } \over {\mu _p + 2\mu _f }} = {{\alpha - 1} \over {\alpha + 2}}$, r distance between sphere center to center and a particle diameter. f _‖ , f _⊥, and f _Γ are numeric terms which are function of ratios α and r/a.

In both limit cases when α→1 and a/r→0, parameters f _‖ , f _⊥, f _Γ→1 which correspond to the dipolar approximation. These parameters have been calculated for various α values (Klingenberg 1989; Clercx and Bossis 1993). Electrostatic forces increase tremendously while particles are coming closer up because of the divergence of the electrostatic field in the gap between sphere surfaces. In a same way, magnetic force between two magnetic spheres can also become very high up to the magnetization saturation.

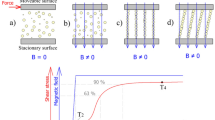
Because this force has two components along the radial and the orthoradial axis, a force momentum aligns particles into and head to tail configuration in the direction of the applied magnetic field (Fig. 1). This creates the experimentally observed fibrous structure.

Fig. 1

Relative positions of two spheres in regard to H

It has been reported by numerous publications that this structure must be broken in order to make the suspension flow. The force required to break these columns defines the yield stress τ_y. In steady state rheology, this type of flow is commonly modeled as a Bingham fluid (Eq. 2) (Bingham 1922) with a magnetic-field dependent yield stress τ _y (H):

$$ \begin{array}{*{20}l} {{\tau {\left( {\dot{\gamma },H} \right)} = \tau _{y} {\left( H \right)} + \eta \dot{\gamma }\;{\text{for }}\tau \geqslant \tau _{y} } \hfill} \\ {{\dot{\gamma } = 0\;{\text{for }}\tau < \tau _{y} } \hfill} \\ \end{array} $$

(2)

where τ is the shear stress and η is the viscosity at high shear rate. More models using a non-Newtonian shear can also be proposed as Eq. (3) (Casson 1959) or Eq. (4) (Hershel-Buckley 1926) which take into account the curve shape of the shear stress versus shear rate function:

$$\tau ^{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}} \left( {\dot \gamma ,H} \right) = \tau _y ^{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}} \left( H \right) + \left( {\eta \dot \gamma } \right)^{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}} $$

(3)

$$\tau \left( {\dot \gamma ,H} \right) = \tau _y \left( H \right) + \left( {K\dot \gamma } \right)^p $$

(4)

where parameter p is strictly positive and K called consistency is a viscosity-like parameter. However physical information drawn from such models is rather poor compared to what can be get from spectromechanical analysis. Indeed spectromechanical analysis has proven to be a very rich experimental method in polymer science because it makes it possible to separate the elastic and the viscous contribution of the material. Thus it can reveal all the different relaxation phenomena related to the microstructure.

That is why the main feature of this review will be about spectromechanical analysis and the influence of physical parameters like the magnetic field intensity H, the matrix viscosity η ₀ , the particle volume fraction Φ, and the shear strain γ.

Literature review

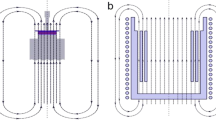
MR fluids are strongly structured fluids. In order to study its structure, spectromechanical analysis is the perfect tool. However until recently, it was rarely used in the case of MR suspensions. This is due to the failure of theoretical works to predict experimental behaviors. Two main contributors to the ER theoretical formalism held our attention: Klingenberg (1992) and McLeish et al. (1991). They have the merit to investigate the relaxation mechanism in ER fluids. However equations can be transposed to MR fluids by changing E into H and ε into μ. McLeish et al. (1991) modeled the suspension structure as single particle width chains (Fig. 2). They distinguished two kinds of chains: chains attached to both electrodes and “free” strings, chains attached to at most one electrode free. Under small amplitude oscillatory shear, attached chains deform affinely at all oscillation frequencies, producing no relaxation. As the storage modulus, G′, is a function of the magnetic tension within a string, it scales up with the squared field strength but is independent of the oscillation frequency (Eq. 5). For very small deformation and for the linear regime McLeish proposed the following expressions:

Fig. 2

Chain model for low concentrated MRF. n-th particle moves by translation of X_n

$$\left\{ {\matrix{ {G' \cong {{T\rho } \over {N2a}}\left( {1 - f} \right)} \hfill \cr {G \cong {{2T\rho } \over {N2a}}f\sum\limits_{q{\rm{ odd}}} {{{2\left( {1 - \cos q'} \right)i\omega ^* } \over {4\left( {1 - \cos q'} \right)^2 + \omega ^{*2} }}.{{\sin \left( {{{q'} \mathord{\left/ {\vphantom {{q'} 2}} \right. \kern-\nulldelimiterspace} 2}} \right)} \over {2\left( {1 - \cos q'} \right)}}} } \hfill \cr } } \right.$$

(5)

where T(H²) is the tension in a chain, N particle number per chain and ρ volume fraction of particles in suspension, f free chain fraction, non-dimensional pulsation ω*=ωτ with τ=t(T/(6πη ₀a²)), a= particle diameter, q’=πq/N where q is the number of modes.

The loss modulus, G″, arises essentially from the motion of the “free” chains, which may deform nonaffinely depending of the frequency.

This model is interesting as it predicts at intermediate frequencies a plateau for G″ in increasing the number of modes. Moreover both moduli scale up with the squared magnetic intensity. However, it predicts a Newtonian behavior at low oscillatory frequency and leads to a variation of G″ inversely proportional with the pulsation at high frequency which seems to be in contradiction with our observations. Their theory seems to match their experimental data but to our knowledge, it has not been successfully applied by others since then.

Klingenberg (1992) employed a similar model. However, the suspension structure was determined by computational simulation. At moderate to large particles concentration, the structure mainly consists of thick clusters as opposed to single particle chains. The relaxation process is associated to a frequency dependent dynamic structure within the cluster. As for McLeish, G′ scales up with the squared field intensity, but it varies between a low plateau for small value of the dimensionless frequency and a higher plateau at larger ones. G″ passes through a maximum near the transition between the small and large frequency regimes. This transition is defined by a characteristic time τ which allowed Klingenberg to define a property called time-field strength superposition, similar to the time-temperature superposition in polymer rheology. Thus, when scaled with the magnetic field strength squared, the complex shear modulus (G*) is only function of the frequency scaled by the magnetic field strength squared for a particular suspension at a given concentration:

$${G \over {{3 \over {16}}\pi \mu _0 \mu _c \beta ^2 H_0^2 }} = f\left( {{{16\eta _C \omega } \over {{3 \over {16}}\pi \mu _0 \mu _c \beta ^2 H_0^2 }}} \right) = f\left( {\omega \tau } \right).$$

(6)

Both models are based on linear viscoelastic rules. However, experimentally, linear viscoelastic behavior is often limited to very small strain amplitudes (Otsubo 1991; Ginder and Davis 1993; Parthasarathy et al. 1994; Yen and Achorn 1991). Several authors report for electrorheological fluids a very narrow linear domain and above that a strong decrease in the modulus values (Jordan et al. 1992; Otsubo et al. 1992) due to the break of the chain structure. Jordan et al. (1992) examined the viscoelastic behavior of a commercial ER fluid. They observed linear behavior for strain amplitudes below about 3%. Then, G′ and G″ decreased with further increases in strain amplitude. Otsubo et al. (1992) investigated the dynamic ER properties of silica particles in silicone oil. Linear viscoelastic behavior was observed for strain amplitudes below 1% for all field strengths investigated. G′ was found to decrease with further increases in strain amplitude, while G″ plotted against frequency passed through a maximum which shifted to smaller frequencies with increasing strain amplitude. Gamota and Filisko (1991) and Gamota et al. (1993) studied the dynamic properties of aluminosilicate particles in paraffin oil, focusing attention on the Fourier transform of the oscillatory shear flow response. Linear viscoelastic behavior was observed for sufficiently small strain amplitudes and field strengths, where at constant frequency, G′ and G″ increased with field strength. Experiments were performed by varying the electric field strength at constant strain amplitude (0.1 and 0.5) and frequency (1 Hz). The response was linear at small field strengths as determined by observing only a fundamental harmonic in the Fourier transform of the stress response. However, at large field strengths, higher order harmonies appeared, demonstrating that nonlinearity may be induced by other parameters other than the strain amplitude. Recently, Chin et al. (2001) have studied magnetic particles and carbonyl iron suspended in silicon oil. They could not reach small enough amplitude to reach the linear zone which was under a strain of 0.03% as both G′ and G″ were found to decrease with further increases in strain amplitude. Rankin et al. (1999) investigated the rheological properties of suspensions of iron particles in viscoplastic media. They concluded that carbonyl iron suspensions have a nonlinear MR response and that the field-dependence of the storage modulus reflects changes in the suspension structure. The mechanisms responsible for the onset of nonlinearity at very small strain amplitudes are not very well understood. Yen and Achorn (1991) associate the onset of nonlinearity with yielding at strains of 1%. Jordan et al. (1992) expect the transition to correspond to the breaking of chain linkages beyond their elastic limit which they view as the yield point of the material. However, Parthasarathy and Klingenberg (1995a, 1995b), while investigating by simulations the transition from linear to non linear at a particle-level, found that the slight rearrangements within structures as opposed to the column ruptures control the transition from linear to nonlinear rheological behavior at small deformation rates. For larger strains, the nonlinear behavior is attributed to breakdowns of percolating structures. Their conclusions are that any slight instability of the local magnetic field or any infinitesimal change of particle localization can induce a nonlinear rheological response.

Thus, it is not sure that true linearity can be reached in real experiment whatever the rheometer sensibility is, as local magnetic field is metastable.

This may explain why there are only few papers about ER fluids (McLeish et al. 1991; Jordan et al. 1992; Otsubo et al. 1992; Yen and Achorn 1991; Kim et al. 2001) and about MR fluids (Chin et al. 2001; Gans et al. 2000; Larrondo and van de Ven 1992) which show the frequency dependence of both storage and loss modulus. Results of spectromechanical analysis may look sometimes quite confusing. However, it is a consequence of the complex structure in such fluids. Even so, a tendency seems to appear in recent papers as people possess more precise tools. Actually, Kim et al. (2001) analyzing the electrorheological characteristics of a phosphate cellulose-based suspension at different electric field strengths and at a strain of 0.002 found that G′ and G″ are either constant or increase slightly above 10 Hz. G′ was found to be more affected by the electric field strength than G″ whereas G″ was more sensitive to the frequency. They concluded to a rubber-like behavior in the linear region. Studying an inverse ferrofluid, Gans et al. (2000) observed also such behavior for the G′ but their G″ showed an increase at low frequencies. They found that G′ scales up with the particle concentration and the square of the magnetic saturation (M_s). Thus, they proposed a normalization of G′ by (ϕ.M_s) in order to build a master curve. Recently, Chin et al. (2001) measured a G′ which also increases slightly with the frequency and a G″ which presents a plateau. Both moduli were found to be proportional to the applied magnetic field intensity (H₀) and the G″ was much more superior to the viscous contribution of the matrix. From all of these, it seems that each ER or MR material has its own viscoelastic behavior. Thus we find some interest to deeply study the viscoelastic properties of the most used and simple MR fluid, a carbonyl iron suspension.

Experimental

Preparation of MR fluids

Usually magnetorheological fluids are suspensions of thin colloidal ferromagnetic or ferromagnetic particles dispersed in a very fluid medium: magnetic latex made of polystyrene particles with inclusions of magnetite (Lemaire et al. 1992); suspensions of polymer-coated nano-sized ferrite particles in polar solvent (Kormann et al. 1996) and meso-scale carbonyl iron and nickel-zinc ferrites (Phulle and Ginder 1999), carbonyl iron stabilized by small aerosol particles (Volkova et al. 2000; Tang and Conrad 1996), by small magnetic particles (Chin et al. 2001), or by viscoplastic media (Rankin et al. 1999). From all of these systems, only carbonyl iron based suspensions have already enough performance to be used in magnetic devices such as dampers. As this kind of suspension is widely used, it seemed interesting to study them. We needed good magnetic properties which can only be provided by large particles. Carbonyl iron was chosen because of its high magnetic permeability and its low coercivity. It is suitable for reversible systems. These are characteristics of magnetic soft materials. Thus, we used 99% pure carbonyl iron particles from GoodFellow with a size of 7±1 μm and a density of 7.8 g/cm³. The shape of the particle is nearly spherical as seen by optical microscopy. Silicon oils from Rhodia (47V10000 and 47V500000 grades) with a density of 0.93 g/cm³ were used as received for the continuous phase of suspensions. Their Newtonian viscosities have been measured respectively equal to 13 Pa (47V10000) and 606 Pa (47V500000). They were high enough to slow down any settling during measurement time. Thus, we did not try to stabilize more by any means the dispersion.

Suspensions were prepared by first weighting a quantity of powder in a beaker. Then, the right mass of silicon oil was added on top of it. The suspensions were homogenized by the agitation of a mechanical stirrer at 200 rpm for several hours depending of the concentration until MR fluids got a homogeneous aspect. The obtained MR fluids were immediately frozen into liquid nitrogen to insure conservation without settling until use. In the case of the most viscous oil, we had to dissolve it with cyclohexane for a proper mixing. The solvent was then removed by cryo-distillation under vacuum. We used the following normalization for suspension names shown in Table 1.

Table 1 Table of samples

Magnetic properties

Magnetic properties were measured by a hysterisimeter. The magnetic field was produced by a large custom-built single coil powered by a stabilized d.c. supply. This coil allows a maximum magnetic intensity of 3.10⁴ A/m far from the saturation magnetization. Indeed, it is important to note that the magnetic field remains in the linear magnetic domain of carbonyl iron particles where Rayleigh’s law can be applied. From this one can deduce the relative permeability of the suspensions (Fig. 3) by formulae:

Fig. 3

Relative suspension permeability vs exterior magnetic intensity (filled diamonds 5%, open squares 10%, filled triangles 15%)

$$J = \mu _0 \left( {{\mu \over {\mu _0 }} - 1} \right)H$$

(7)

Thus, in our experiments relative permeabilities could be considered as constants. But these are average suspension permeabilities μ _s . In order to use theoretical models, we need to know the real particle permeabilities μ _p which is different from the average suspension permeability. One method to link the average permeability to the particle permeability is the Maxwell-Garnett (1906) theory based on the conservation of the magnetization in an effective medium. Thus, the total magnetization is the summation of each species weighted by their volume fraction. As a consequence, each particle is isolated in a magnetic field H from any interaction of other particles and the mutual magnetization between particles is negligible. This model is then limited to low volume fractions. The Maxwell-Garnett model gives the following equation:

$${{\mu _s - \mu _f } \over {\mu _s + 2\mu _f }} = \phi {{\mu _p - \mu _f } \over {\mu _p + 2\mu _f }}$$

(8)

Then μ _p can be calculated knowing μ _s and μ _f . If μ _f ≅μ ₀, Maxwell-Garnett formulae gives a straight line for the function, ${{\mu _s - \mu _0 } \over {\mu _s + 2\mu _0 }} = f\left( \phi \right)$. Its slope gives the value of μ _p . With our experimental values, we obtain a slope of 2.3, greater than 1 which gives an impossible negative value for the particle permeability. Volkova (1998) tried to solve this problem by making the assumption that the particles are not independent but aggregated in ellipsoidal clusters. She used the following modified Maxwell-Garnett equation:

$${{\mu _s } \over {\mu _0 }} = {{1 + \phi \beta _{//} } \over {1 - \phi n_{//} \beta _{//} }}{\rm{ with }}\beta _{//} = {{{{\mu _p } \mathord{\left/ {\vphantom {{\mu _p } {\mu _0 }}} \right. \kern-\nulldelimiterspace} {\mu _0 }} - 1} \over {1 + n_{//} \left( {{{\mu _p } \mathord{\left/ {\vphantom {{\mu _p } {\mu _0 }}} \right. \kern-\nulldelimiterspace} {\mu _0 }} - 1} \right)}}$$

(9)

Using Eq. (9), we found that the best fit is obtained with μ _p /μ ₀ =200 and n_//=0.1 for all magnetic intensity values.

In the literature, for 98% pure carbonyl iron we find μ _i /μ ₀ =132 and Ms=1,990,000A/m (Jiles 1995) and for 100% pure iron, μ _i /μ ₀ =320 and Ms=270,000kA/m (Durand 1968). Our particles are made of 99% pure iron. Thus our measures are accurately between the values of 100% pure and 98% pure iron. The β value would be considered near the unity.

Experimental rheological set-up

A wide variety of methods can be found in the literature for studying MR systems: concentric cylinder rotational viscometer (Laun et al. 1992), parallel plate geometry inserted into a coil (Volkova 1998), conventional stress and strain controlled rheometers with cone-plate (Larrondo and van de Ven 1992), parallel plate (Chin et al. 2001). All rheological experiments were done at room temperature. Dynamic rheological measurements were obtained on a strain controlled rheometer (ARES from Rheometrics) using a cone plate geometry. Steady rheological data were collected on a stress controlled rheometer (DSR from Rheometrics) using the same geometry. This geometry is particularly adapted to the study of our substances whose flow at a certain moment t depends on former mechanical history, i.e., the whole stress applied before this moment. Indeed because of constant stress, the mechanical history is constant all over the sample. We thus preferred this geometry for the study of our model MR fluids.

Figure 4 shows the schematic diagram of the apparatus for magnetorheological measurements. The sample was centered at best in the middle of the coil to insure the most homogeneous magnetic field inside and the measurement devices were made of non-magnetic aluminum. Thus, the magnetic induction, measured by a teslameter, presents a maximum deviation from the center of ±0.5% along the coil axis and ±6% in the radial direction. In a first approximation, the magnetic field would be considered as homogeneous. Its direction is then perpendicular to shear. Although gravitational settling of MRF samples was not observed during tests when the magnetic field is applied, all samples were well mixed before rheological experiments and changed with new ones at each measurement.

Fig. 4

Scheme of the magnetorheological setup attached on ARES rheometer

We also built a shearing cell on an optical microscope in order to see the evolution of the structure with the shear rate (Fig. 5). The cell is designed to reproduce the parallel plate geometry of rheometers. The bottom of the cell rotates thanks to the mobile axis of a viscosimeter while the independent top of the cell is maintained immobile. This creates a shear rate within the sample. The top of the cell is made of glass to let the light pass through. The microscope objective looks from above in reflective light mode. The whole cell can be moved in two horizontal directions with a precision of 0.01 mm. Unfortunately due to technical issues, we were not able to measure reliable viscosity data with this set-up. However, we could get pictures at given shear rate that we will later compare with the DSR data.

Fig. 5

Schematic diagram of the shearing cell

Steady state measurements were done using the stress controlled rheometer, DSR from Rheometrics. All experiments were carried out following a precise protocol. First the sample is sheared at low shear rate of 0.1 s^-1 over 1 min. This puts the sample in a so called zero state and removes any previous structural memory effect. The sample stays at rest for another minute. Then the magnetic field is applied for 1 h before starting the measure. Rheograms were obtained by programming a sequence of tests with a first test which increases the stress in a linear sweep from 1 to 1700 Pa immediately followed by a second test starting at 1700 Pa and decreasing down to 1 Pa. The entire sequence was done with a fixed sweep rate ranging from 2 Pa/min to 200 Pa/min. We choose 1 Pa as the starting point as previous experiments had shown that below this value the displacement cannot be measured by the optical sensor of this rheometer.

Dynamic tests were prepared by the following protocol. First, the suspension is sheared by a time sweep experiment at a strain of 0.05% and a frequency of 10 rad/s. Then at an instant t₀, the current of the induction coil is switched on at the desired intensity. We observe an exponential increase of both modulus G′ and G″ which reach a plateau value after a characteristic time τ as defined in Eq. (10). We choose to work on the storage modulus as it should be more sensitive to the structuring process:

$$\Delta G'\left( t \right) = \Delta G'_{\max } \left( {1 - e^{ - {\raise0.7ex\hbox{$t$} \!\mathord{\left/ {\vphantom {t \tau }}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$\tau $}}} } \right)$$

(10)

with ΔG’(t)=G’(t)−G’(t ₀) and ΔG’_max=G’(t _∞ )−G’(t ₀).

Figure 6 illustrates such an increase. The time origin represents the starting point when the current is abruptly applied. From these fits, we are able to build a master curve in logarithmic scale with the characteristic time vs the product of the magnetic intensity with the volume concentration (Fig. 7).

Fig. 6

Fit on elastic modulus for 15V5e5 (21350A/m, 10 rad/s)

Fig. 7

Time vs magnetic intensity and concentration for samples: filled diamonds 5V5e5, open squares 10V5e5, filled triangles 15V5e5 at 10 rad/s and 0.05% of strain

As moduli increase with the magnetic intensity over the time, we attributed this characteristic time to a structuring time. Then it is not surprising to find that this time is as low as the magnetic intensity and the concentration are high. Particles move faster with stronger magnetic attractive forces and the structure is also formed earlier with more particles by volume unit. Although we did not pursue further this kind of experiment, it could be interesting to deeper study this structuring regime.

Results and discussion

Static structure

Checked by optical microscopy, the application of a magnetic field causes the aggregation of the particles into chains in the magnetic field direction (Fig. 8). Thus, the formed structure should considerably modify the flow until transforming the fluid into gel. However we see here that even at relatively low concentration 5%, the structure is made with interlaced columns. This is far from the widely used chain model.

Fig. 8

Particles aggregation into a fibrous structure. Columns are about 17 μm in width

Steady state measurements

The steady-shear MR responses exhibits strong thixotropy effect in cone-plate geometry (Fig. 9) as already describe by Lemaire (1992). She attributed this fact to some structural changes inside the sample. We were able to follow the destruction effect in a rotational shear thanks to our custom-built shearing cell on an optical microscope (Fig. 10).

Fig. 9

Rheograms of 05V5e5 with 28460A/m (filled diamonds load curve, open diamonds unload curve) compared to the response with H=0 (continuous line) and microscopy under shear and magnetic field for the different zones

Fig. 10

Shear stress vs shear rate (15V5e5, H=28kA/m), Bingham (dashed line) and Cross (line)

Depending on how the material is solicited, we see a hysteresis formed by the loading and unloading curves. The loading curve has an original shape with two inflexions separating three zones. Zone A, is the first one defined by a sharp increase of the stress. According to our microscopic observation, the structure mainly remains intact. The material exhibits its strongest elasticity. Then if we further increase the stress (or the shear rate), we reach zone B which presents a shear thinning behavior due to the progressive disassemble of the columns. At high shear rate (zone C), the suspension is homogenized and has a Newtonian flow.

For an unknown reason, this thixotropy is less if not at all observed in a plate-plate geometry. Maybe it is caused by the non homogeneous chain deformation. Moreover, unlike the load curve the unload one does not depend on time. That is why we use unload curves for our analysis, as the unload data were very well reproducible.

Yield fluid models: Bingham (Eq. 2), Casson (Eq. 3), Hershell-Buckley (Eq. 4), will not be valid at low shear rates for this kind of rheograms as we did not observe any real yield stress due to the limitation of the angular resolution of the stress-controlled rheometer.

Looking for a more suitable model, we used a Cross model defined by the following equation:

$$\tau = \left[ {\eta _\infty + {{\eta _0 - \eta _\infty } \over {1 + \lambda \dot \gamma }}} \right]\dot \gamma $$

(11)

Then when γ̇→0, τ=η ₀ γ̇, the system has a Newtonian flow. Whereas when $\dot \gamma \to \infty {\rm{,}}\tau = {{\eta _0 - \eta _\infty } \over \lambda } + \eta _\infty \dot \gamma$, the system behaves like a Bingham fluid with a deduced apparent yield stress $\tau _s = {{\eta _0 - \eta _\infty } \over \lambda }$ and a plastic viscosity η _∞.

Cross model gives a good fit (Fig. 10) above all at low shear rates where our MR fluids behave as pseudoplastic materials. From Cross model, one can extract many interesting physical parameters (Table 2). First, the viscosity at high shear rates, η _∞, is slightly larger than the matrix viscosity. That means that the viscosity is the same as in the case of homogeneous suspension hindered by some hydrodynamic perturbation caused by remaining aggregates. As expected, we observed that this viscosity does not depend on the magnetic intensity and only a little with the concentration. Second, the initial viscosity at very low shear rates, η ₀, represents the viscosity of the structured fluid and has a value tremendously superior to the matrix viscosity. In spite of the high shear rate viscosity, the initial viscosity is very sensitive to the magnetic intensity as it varies in H ^2.9 but also to the concentration in Φ ^0.45. Third, the parameter λ has the dimension of a time. It is related to the transition from the “solid state” where aggregates are mainly intact to the “liquid state” where they are broken. As the initial viscosity, it scales up a lot in H ^2.8 and in Φ ^0.4. Therefore both former parameters should be physically linked.

Fig. 11

Yield stress vs magnetic field intensity and concentration 5%, 10%, 15%, 30% in 47V500000

Table 2 Parameters from Cross model (matrix viscosity=606 Pa.s)

Thanks to the apparent yield stress, $\tau _s = {{\eta _0 - \eta _\infty } \over \lambda }$, we were able to build a master curve from our data representing the yield stress vs the applied magnetic intensity and the concentration in a double logarithmic scale (Fig. 11). Thus, we deduced the following power law:

Fig. 12

Amplitude sweep for 15V1e4 at 10 rad/s (H=21350A/m: open triangles G′, filled triangles G″) and (H=0: filled diamonds G′, open diamonds G″)

$$\tau _s \propto \phi ^{0.5} H_0^{1.5} $$

(12)

Oddly, we did not find the squared variation in magnetic field, neither the linear dependency with the concentration as some other author did (Otsubo et al. 1992). We can easily imagine that this is due to the use of the external magnetic intensity instead of the local one applying in the particle neighborhood. Indeed a magnetic saturation may occur at the contact point between particles. However our exponent values (1.6±0.1) are in accordance with other authors like Chin et al. (2001).

Dynamic measurements

Unlike steady state experiments, oscillatory tests at sufficiently low deformations do not destroy the structure. We thus completed our study by rheological experiments in dynamic mode at very low strain which facilitate the understanding of the structure on MRF rheology. In spite of these advantages, this kind of mechanical spectrometry is rarely used in the literature concerning MR fluids. This is why we made a complete study of the complex shear modulus versus deformation and frequency. First of all, the deformation limit, which is also the limit of the linear viscoelastic range over which irreversible destruction of the structure begins, must be determined in an amplitude sweep test. Figure 12 shows strain sweeps of MRF sample (15V1e4) with H=21350A/m and without magnetic field.

As we can see in Fig. 12, the magnetic intensity increases both moduli. At small shear strain, the storage modulus increases one hundred times in this example whereas the loss modulus also increases by a factor of ten. At high shear strain, both curves show an analog behavior and the viscous component prevails over the elastic one.

We defined the critical strain as the strain value where loss modulus and elastic modulus are equal. This critical strain, γ_c, represents the transition between the viscoelastic solid at low strain and the viscoelastic liquid at high strain. Thus, this physical parameter is directly linked to the state of the structure. It is the witness of the competition between magnetic forces and hydrodynamic forces. That is why we investigate the values of the critical strain at various frequencies and magnetic field intensities. In general, we found a critical strain, γ_c, to be relatively small, between 0.05% and 1.8%, depending on the rotational frequency and the magnetic field intensity (Fig. 13). Data plotted in Fig. 13 show a linear variation of γ_c with Hω^-1/2.

Fig. 13

Variation of γ_C vs the frequency and magnetic intensity

We find that γ_c could be related to the non dimensional Mason number (Mn) which is here defined as the ratio between hydrodynamic and magnetic stresses:

$$Mn = {{6\eta _o \dot \gamma } \over {\mu _o \mu _f (\beta H)^2 }}$$

(13)

For oscillatory motions, the shear rate γ̇ is proportional to the frequency ω therefore Mn∝ωH ⁻². Then, we found that the critical strain changes with Mn following the power law:γ _c ∝Mn ^−1/2.

Depending on the strain domain, the frequency sweep experiments show a gel-like response below the critical strain (Fig. 14) and a liquid-like behavior above γ_c (Fig. 15).

Fig. 14

Complex shear moduli (filled squares G′, open squares G″) vs frequency (γ=10⁻⁴, η=13 Pa.s, ϕ=15%, H=21350A/m). Matrix moduli (G″ dashed line, G′ plain line)

Fig. 15

Complex shear moduli (G′ open squares, G″ filled diamonds) vs frequency (γ=1, η=13 Pa.s, ϕ=15%, H=21350A/m). Matrix moduli (G″ dashed line, G′ plain line)

As we can see in Fig. 14, at low strains the magnetic effect is much more pronounced as the frequency is lower. We defined G′₀ and G″₀ as the plateau values respectively of the elastic modulus and the loss modulus at low frequency (Fig. 14). Even at high frequency, the complex shear modulus of the structured suspension is much higher than the one of the matrix. Whereas, at high strains the flow is far from being Newtonian except at high frequency (Fig. 15). The Newtonian viscosity at high frequency is 26 Pa.s which is consistent with the viscosity of a suspension of free particles which should be calculated by a simple Einstein law which gives a value of 20 Pa. Indeed even at very low frequency and high deformation, the flow is not purely Newtonian. As we reduce the frequency, the apparent viscosity increases and the storage modulus levels off. This reveals relaxation mechanisms due to movements of different sized structures like aggregates. We calculated the relaxation time of Klingenberg s equation (Eq. 6) in the example of Fig. 15 which seems to match rather well. At low frequency, the partially broken aggregates have time to reorganize themselves in the direction of the magnetic field.

Moreover, we looked at the influence of the particle concentration, the intensity of the magnetic field, and the viscosity of the matrix on the MRF rheology for γ<<γ_c.

The magnetic field intensity scaling

Our results confirmed the link between the magnetic forces which ensure the cohesion of the particles in aggregates, and the elastic module as Klingenberg (1992) and McLeish et al. (1991) had proposed. Thus, under the application of a magnetic field, the elastic modulus can increase several orders of magnitude higher and become frequency independent for medium frequencies and lower (Fig. 16). To our knowledge only elastic modulus has been extensively studied as both Klingenberg’s and McLeish’s theory attached high frequency elastic modulus to a magnetic attraction within clusters. Whereas they do not propose a complete interpretation for the loss modulus as McLeish predicts a final Newtonian behavior that is still unseen by us (Fig. 17). That is why our interest has been essentially focused on the modulus plateau value on both G′ and G″, named respectively G′₀ and G″₀. We thus proposed some scaling laws on these values with characteristic parameters. Figure 18 shows that we could find a power law in $G_0^* \approx \left( {H.\phi } \right)^{1.65 \pm 0.5}$ for three concentrations.

Fig. 16

Storage modulus vs frequency for different magnetic intensities (15V1e4, γ=10⁻⁴)

Fig. 17

Loss modulus vs frequency for different magnetic intensities (15V1e4, γ=10⁻⁴)

Fig. 18

Plateau values (G′₀ open diamonds, G′₀ open squares) vs H.ϕ for 10V1e4, 15V1e4, 30V1e4 at γ=10⁻⁴

Such an exponent on the concentration is unexpected by the model of the single particle width chain disposed in a cubic organization. Indeed in this ideal case, it should be equal to 1. However, as we have seen above, structure is formed by several chains tightly interlaced. Thus, one can expect that such complex assembly could oddly influence the stress tensor within the material.

We looked at the effect of a change of the matrix viscosity. Stoke’s law teaches us that the hydrodynamic drag of dispersed objects is proportionally reduced by the matrix viscosity. We were not surprised to see that particles move faster for a lower matrix viscosity decreasing the structuring time. In Fig. 19 we applied a larger strain of 0.1%; that way we could see an inflexion of the rheological curves separating a high frequency regime from a low frequency one. Spectromechanical analyses show that the matrix viscosity does not change the plateau values of both moduli (Fig. 19). Thus it becomes easier to distinguish a difference in the characteristic times. Actually, the plateau values are strictly equivalent for the storage modulus at both viscosities: the elastic effect is internal to the columns and independent of the suspending fluid. However, the plateau of the storage modulus is also longer for lower viscosity which indicates that the matrix viscosity plays a role in a characteristic time. We observe that the crossover point is moved by a factor equal to the viscosity ratio. Indeed if we define a shift factor, a _η by

Fig. 19

Complex shear modulus vs frequency: H=14230A/m, 10%vol, η₂=13 Pa.s (G′ filled triangle▲, G″ open triangles), η₁=606 Pa.s (G′ filled squares, G″ open squares) at γ=10⁻³

$$a_\eta = {{\eta _1 } \mathord{\left/ {\vphantom {{\eta _1 } {\eta _2 }}} \right. \kern-\nulldelimiterspace} {\eta _2 }},$$

(14)

we obtain a time-viscosity superposition equivalent to the time-temperature superposition in polymer rheology:

$$G*\left( {\omega a_\eta ,\eta _1 } \right) = G*\left( {\omega ,\eta _2 } \right).$$

(15)

This gives the possibility to build a master curve from several spectromechanical analysis made at different viscosities (Fig. 19). This works perfectly for the elastic modulus. The loss modulus is slightly different at low frequency. However, its changes have little to do with the viscosity ratio. The loss modulus is thus not directly linked to the matrix viscosity. At last, the superposition overlaps well at high frequency.

Moreover we have observed that for high concentration and high magnetic intensity the shift factor needs to be increased in order to get the superposition. We think that under certain conditions which increase the number or the size of the suspended items, one aggregate’s movement is hindered by other aggregates. Thus we should use an effective viscosity higher than the matrix viscosity in the shift factor calculation.

If we summarize all these results, we can build some rheological master curve with the following equation (Fig. 20):

Fig. 20

Complex shear modulus vs frequency (γ=10⁻³, 5 vol.%, η=606 Pa.s) for three different magnetic intensities (G′ (filled symbols), G′ (open symbols))

$${{G^* } \over {\left( {\phi H} \right)^{1.7 \pm 0.1} }} = f\left( {{{\eta _0 \omega } \over {\left( {\phi H} \right)^{1.7 \pm 0.1} }}} \right) = f\left( {\omega \tau } \right)$$

(16)

This works pretty well with the storage and the loss modulus. For this latter, we see a little discrepancy at the lowest frequencies. This property had already been described in Klingenberg’s equation (Eq. 6).

Conclusion

We have presented an exhaustive experimental study of the viscoelastic behavior of MR fluids, structured under small deformations. Spectromechanical analyses are perfect for the simultaneous measurements of the elastic and viscous behavior over a large range of frequencies. Our results qualitatively agree with theoretical models for the storage modulus: the elastic effect comes from attractive magnetic interactions within aggregates. However, these models fail to interpret the loss modulus. Indeed fluctuations of the loss modulus are strictly linked to those of the storage modulus (master curve for the complex shear modulus), even if the behavior is not rheologically simple. Thus the origin of the loss of energy is not entirely due to the viscosity and to the hydrodynamic effects of the suspending fluid: the loss modulus under a magnetic field is several orders of magnitude higher than the matrix viscosity. In our opinion, viscous losses at low frequency should be attributed to internal movements within the aggregates, exactly to the relative movements of particles which also may be directly in contact between each other, creating some friction and lubrication effects.

To explore this idea more deeply, one should think of some local measurements of the friction and the lubrication in the interspace of two particles: direct contact between solid surface, thin layer of fluid trapped between the particles. All of this should highly depend on the surface state of the particles through some local roughness, chemical interaction, etc. We are thinking about doing some study of the viscoelastic properties of a confined polymer layer near a metal surface by nano-rheological measurements.